DOI:10.32604/csse.2022.017003

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.017003 |  |
| Article |
Relative Time Quantum-based Enhancements in Round Robin Scheduling
Department of Computer Information Systems, College of Computer Science and Information Technology, Imam Abdulrahman Bin Faisal University, P.O. Box No. 1982, Dammam, Saudi Arabia
*Corresponding Author: Hina Gull. Email: hgull@iau.edu.sa
Received: 18 January 2021; Accepted: 11 March 2021
Abstract: Modern human life is heavily dependent on computing systems and one of the core components affecting the performance of these systems is underlying operating system. Operating systems need to be upgraded to match the needs of modern-day systems relying on Internet of Things, Fog computing and Mobile based applications. The scheduling algorithm of the operating system dictates that how the resources will be allocated to the processes and the Round Robin algorithm (RR) has been widely used for it. The intent of this study is to ameliorate RR scheduling algorithm to optimize task scheduling. We have carried out an experimental study where we have developed four variations of RR, each algorithm considers three-time quanta and the performance of these variations was compared with the RR algorithm, and results highlighted that these variations performed better than conventional RR algorithm. In the future, we intend to develop an automated scheduler that can determine optimal algorithm based on the current set of processes and will allocate time quantum to the processes intelligently at the run time. This way the task performance of modern-day systems can be improved to make them more efficient.
Keywords: CPU scheduling; Round Robin; enhanced Round Robin; relative time quantum; operating systems
Operating systems are basic building blocks for the functioning of a computer-based system. Due to the transformation from a mainframe computer to smart devices, a similar shift has been observed in OS from batch processes to multi-tasking. Correspondingly, contemporary multi-user systems allow multiple threads to be shifted to the memory and run simultaneously [1]. This progression required categorization of the various processes and optimized utilization of resources such as memory and processor time. These processes keep moving among the various queues in the memory throughout their life cycles. Conventionally, the job of the operating system is to select processes from the queues and assign them to the central processing unit (CPU) by using CPU schedulers [2]. CPU schedulers works on different scheduling techniques and algorithms. These algorithms are based on diverse techniques, which laid the foundation for a particular algorithm to be selected and favored for one batch of processes over the other. Certain criteria are used to compare different algorithms based on their properties such as CPU consumption, turnaround time, time it waits in memory, throughput and response time [3]. Moreover, recent advancements, like Smart Systems, the Internet of Things (IoT) and Big data have additional implications on the scheduling decisions of underlying operating systems. Job quantity, Job variety and job priority are dynamic and therefore the scheduling algorithms need intelligence to optimize the distribution of resources in a real time environment. With the evolution of internet of things, modern day work and home environments have become intelligent. This has resulted in advances in e-healthcare (personal health trackers, hospital infrastructures), smart homes (lighting, home appliances, electricity, water and waste management, surveillance), Smart workplace (infrastructure management, attendance management, communication infrastructure, robots) and transportation (self-driven cars). In such systems sensors, cameras, and other computing devices coordinate to collect, monitor and review data in real time and to process this real time data, huge computing infrastructures are in place. The processing power and priority of computing jobs generated in these smart environments vary enormously. Therefore, it is highly important to take advantage of optimized utilization of CPU by increasing throughput, consequently minimizing the turnaround, response and waiting time of processes. One of the extensively used algorithms for time sharing and multiuser operating systems is Round Robin scheduling algorithm (RR). The functioning of the RR algorithm is reliant to the magnitude of time interval (fixed time assigned to each process). Based on the RR technique if the selected time quantum is very large, it will lead to the starvation problem (CPU held by a process for a long time) for the processes having large total execution time. On contrary, if the time interval is small, it will lead to several context switches (migration from one process to another) [1].
In this paper, we have developed four variations of the RR algorithm, which are selecting time quantum intelligently on the run time depending on the actual time of the candidate process. These variations will calculate a set of time quanta by taking aggregate values of the actual time of processes residing in the ready queue and assigning it to a process based on its technique.
Rest of the paper is structured as follows: Section 2 outlines related work and is followed by problem statement in Section 3. Section 4 presents developed algorithms and their results are discussed in Section 5 and followed by conclusion in Section 6.
There have been many studies in the computing literature focusing on scheduling algorithms. Balharith and Alhaidari, have carried out a review of Round Robin and its different variations. They have categorized different contributions based on static and dynamic time quantum. According to them, dynamic time quantum-based algorithms work on either selecting dynamic time quantum in each round or selecting dynamic time quantum for each job [4]. Similarly, Harki et al. [5] have carried out a rigorous review of different scheduling algorithms used by different operating systems. They described turnaround time, waiting time, response time and context switching as the key factors of a scheduling algorithm. Tyagi and Gupta have analyzed distributed computing environments and highlighted that task scheduling is very critical in improving the performance of distributed systems, therefore an effective scheduler in the distributed environment must be efficient, dynamic, transparent, and fair. They provide a comparison of different scheduling algorithms and develop a hierarchical classification of scheduling algorithms [6]. Reddy et al. have developed a variation of Round Robin scheduling algorithm to achieve optimal waiting and turnaround time and keeping the context switching to minimum. Their proposed algorithm calculates the mean of given processes before which improves its performance, however, if large time quantum is allocated then its performance becomes alike first come first serve algorithm [7]. Shafi et al. developed an improvement of Round Robin algorithm where burst time is adjusted cyclically based on processor performance. The simulation results highlighted that their algorithm outperformed Round Robin, improved Round Robin, priority-based Round Robin and optimum multilevel dynamic Round Robin schemes [8]. Dash et al. [9] have improved the Round Robin algorithm approach by proposing Dynamic Average Burst Round Robin. This improved algorithm works by allocating dynamic time quantum rather than static time quantum and algorithm showed improvements in average waiting time, turnaround time and context switching. Chandiramani, et al. have improved the priority scheduling algorithm which takes the time quantum equal to the shortest execution time of all the available processes. They found that the mean turnaround and waiting time were reduced as compared to priority preemptive scheduling [10]. Zouaoui et al. [11] have developed a scheduling approach by combining RR and priority-based scheduling algorithms to gain the advantages of both approaches. Nayak et al. [12] have proposed a variation of the RR algorithm, known as improved RR. In this approach, they arranged processes based on the shortest execution time and allocated appropriate time quantum to improve performance. Dinkar et al. [13] have developed a scheduling algorithm based on ant lion optimizer and the comparative results with first come first serve, shortest computation time first and RR showed less average waiting time. ElDahshan et al. have reviewed different variations of Round Robin algorithms and chalked out recommendations for an enhancement of RR algorithm that improves waiting and turnaround time of processes [14]. Rami has developed a self-adjusting RR scheduling algorithm based on the total execution time of the process. He has scheduled that optimal time quantum is based on taking median value, but if median is greater than 25, the value of time quantum can be adjusted to make it greater than 25. Based on his analysis, performance of RR scheduling can be improved by those methodologies as there will be less context switching between the processes [15]. Baccelli et al. [16] have discussed that scheduling strategy selection in IOT based operating systems should focus on task priorities, user interaction and real time response. Dhakad et al. [17] have proposed an Adaptive Round Robin Scheduling using Shortest Burst Approach which is based on smart time slice.
Despite these contributions there is a need for continuous improvement in the scheduling algorithms by optimizing processing time to respond the challenges of advanced computing paradigms and infrastructures.
As Internet of Things (IoT) and smart devices are on the rise and most of these applications are time bound and are running with strict time constraints, therefore, an optimal scheduling strategy is needed to improve the system performance. To meet the processing deadlines, scheduling strategy should be based on real time to complete the job in less time as well as to improve the waiting time of processes with less context switching [1]. Several scheduling algorithms and strategies have been developed in the past to deal with real time bound challenge of these applications and their scheduling problems [2]. Additionally, as modern gadgets and IoT has elevated the complexity of scheduling, so there is still room to develop an improved scheduling strategy that works intelligently to support such environment.
In this paper, we have developed four variations of Round Robin scheduling algorithm, which are selecting dynamic time quantum intelligently based on the total execution time of the candidate process. The main feature of these variations is to divide the list of processes and then apply their different technique to achieve maximum fair distribution of time quantum. Algorithms will assign time quantum to each process in real time, as each process will have its own time quantum. Complete descriptions of these algorithms are given below:
This algorithm (Plus Minus Mid PMM) works by dividing the ready queue of P processes into two lists. List 1 contains n processes while list 2 contains m processes, where n + m = P. Algorithm also takes the middle value v of the whole list of process lying in ready queue by using the following equation:
Algorithm works on generating three-time quantum and dynamically selecting and assigning the time quantum to the candidate process which is close to the total execution time (also called burst time) of that process. The algorithm follows the process by averaging the total execution times of the processes in each list, adding the averages to generate a first quantum s and subtracting the averages to generate a second quantum t. Average of list 1 is computed by the given equation:
where A1= Average of list 1, n= number of processes, x1 = the value of each item in the list of numbers being averaged. Similarly, average 2 can be computed by the same equation:
where A2= Average of list 2, m= number of processes, x1 = the value of each item in the list of numbers being averaged. Here rest of the two-time quantum s and t are calculated as follows:
The candidate process which needs to be assigned to CPU is compared with v, s and t. The value of the quantum that is near the total execution time of the candidate process is assigned to that process for running. Time quantum calculation, a block diagram of the process, flowchart and pseudocode of algorithm is shown in Figs. 1–4 respectively.
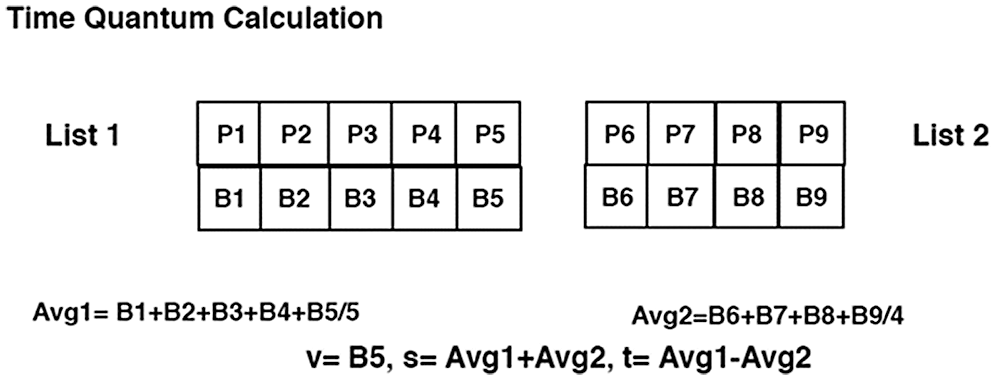
Figure 1: Time quantum calculation
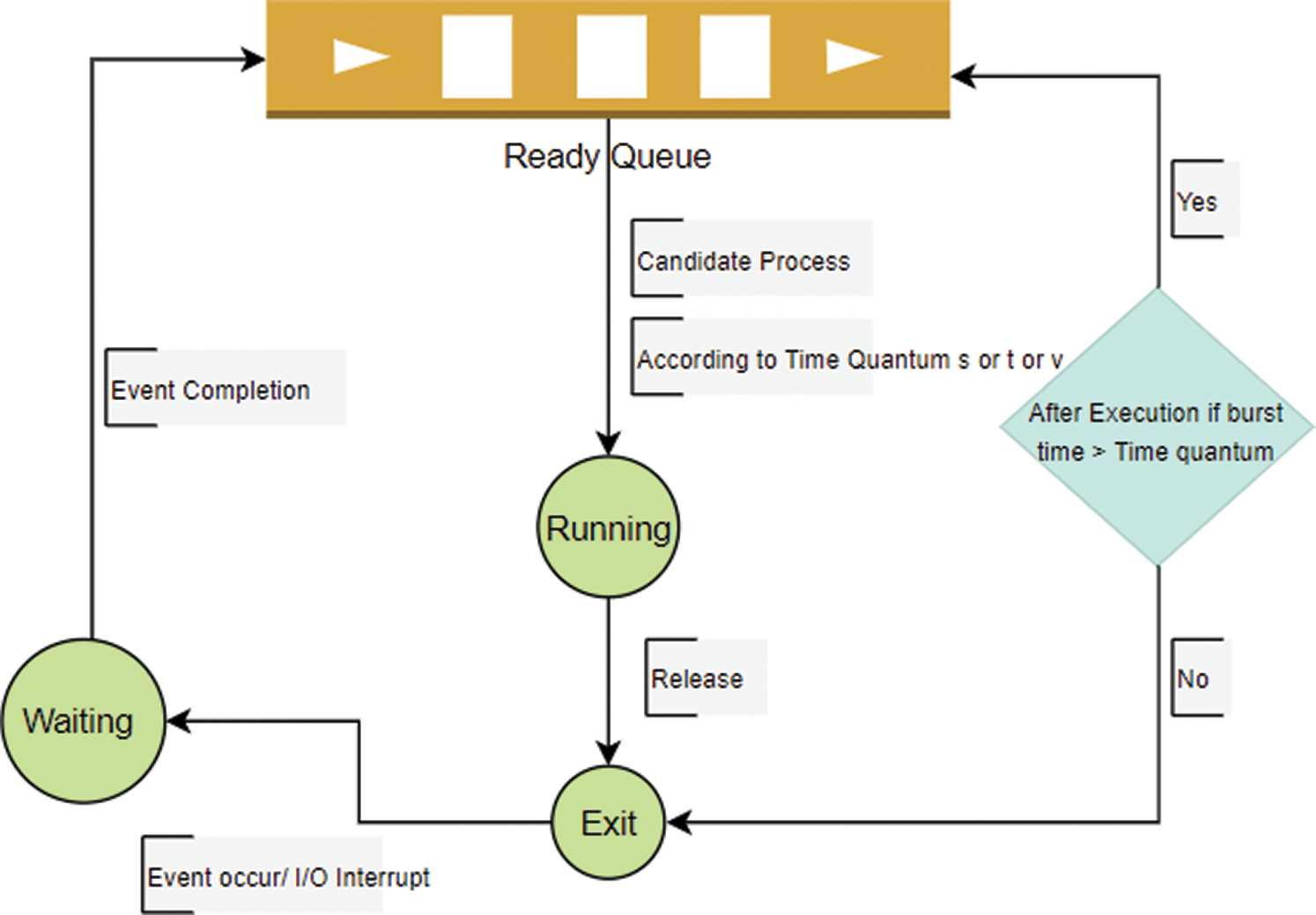
Figure 2: Block diagram

Figure 3: Pseudocode of Algorithm 1
This algorithm (called close to average CA) works by dividing the ready queue of P processes into two lists. List 1 contains n processes while list 2 contains m processes, where n+m=P. Algorithm generated a two-time quantum and dynamically selecting and assigning the time quantum to the candidate process which is close to the total execution time of that process. The algorithm follows the process by averaging the total execution times of the processes in each list, average of first list will be the first quantum s and the average of the second list will be the second quantum t. The candidate process which needs to be assigned to CPU is compared with s and t. The value of the quantum that is near the total execution time to the candidate process is assigned to that process for running. Averages and time quantum s and t are calculated by the formula given in Eqs. (1)–(3). Pseudocode and flowchart of the algorithm are given in Figs. 5 and 7.

Figure 4: Flowchart of Algorithm-1

Figure 5: Pseudocode of Algorithm 2
This algorithm (called close to Mid Value MC) works by dividing the ready queue of P processes into two lists. List 1 contains n processes while list 2 contains m processes, where n+m=P. Algorithm also takes the middle value v of the whole list of processes lying in ready queue. Algorithm works on generating three-time quantum and dynamically selecting and assigning the time quantum to the candidate process which is close to the total execution time of that process. Algorithm follows the process by averaging the total execution times of the processes in each list, average of first list will be the first quantum s and the average of second list will be the second quantum t. The candidate process which needs to be assigned to CPU is compared with v, s and t. The value of the quantum that is near the total execution time of the candidate process is assigned to that process for running. Averages and the time quantum s and t are calculated by the formula given in Eqs. (1)–(3). Pseudocode and flowchart are given in Figs. 6 and 8.
This algorithm works (CPU Max Min MM) by dividing the ready queue of P processes into two lists. List 1 contains n processes while list 2 contains m processes, where n+m=P. Algorithm works on generating two-time quantum and dynamically selecting and assigning the time quantum to the candidate process which is close to the total execution time of that process. Algorithm follows the process by averaging the total execution times of the processes in each list, larger average will be the first quantum s and smaller one will be second quantum t. The candidate process which needs to be assigned to CPU is compared with s and t. If the candidate process has total execution time more than t, it will be assigned time quantum s, otherwise it will be assigned as t. The time quantum calculation of the process is shown in Fig. 10. The pseudocode of the algorithm-4 is given in Fig. 9. Where processList is the list of processes lying in ready queue, list 1 is first half of process list, list 2 is the second half of process list, r1 is relative value of list 1, r2 is relative value of list 2, quantum is time quantum assigned to process, len is length of process list, waitTime is waiting time for each process, turnTIme is turnaround time for processes, avgWTime is average waiting time for all processes and avgTTime is average turnaround time for all processes. The flowchart is shown in Fig. 11. Averages are calculated by the formula given in Eqs. (1) and (2), while s and t are calculated as follows:

Figure 6: Pseudocode of Algorithm 3

Figure 7: Flowchart of Algorithm 2

Figure 8: Flowchart of Algorithm 3

Figure 9: Pseudocode of Algorithm 4

Figure 10: Time quantum calculation

Figure 11: Flowchart of Algorithm-4
Proposed algorithms are compared with each other as well as with Relative Concatenate algorithm (RC) and Relative Concatenate Minus (RCM) [3]. All these algorithms are also compared with RR (Round Robin) algorithm [1] for clearly evaluating the performance of these algorithms. Proposed algorithms, Round Robin and other algorithms [2,3] presented in literature are implemented in C# and are given same random data set to compare their performance. Algorithms are compared based on the average waiting and average turnaround time of these algorithms. As average waiting and average turnaround time depends on the number of processes residing in ready queue, an increase in the time leads to increase in cost. Fig. 12 shows the comparison of algorithms in terms of average waiting time. The stacked line chart is plotted for 10 to 200000 processes lying in the ready queue. The average waiting time taken by the processes is given in milliseconds and is plotted against y-axis, while x-axis plot the number of processes residing in ready queue. The performance of PMM is relatively better than other algorithms, followed by MC and CC. They show significant improvements in their performance if compared with RR which has almost double average waiting time. Results also indicate that as the number of processes is increasing in the ready queue PMM, MC and CC show significant change and improvement in their behavior. Relative Concatenate and Relative Concatenate Minus [3] shows almost similar behavior to Round Robin, whereas proposed algorithms show performance improvement in a large number of processes. Proposed algorithms can also be compared with efficient SJRR algorithm [2] which takes the average execution time of processes residing in a ready queue and assigns an average time slice to each process. Proposed algorithms behave similar, as far as a smaller number of processes is concerned, but as the number of processes increases, the performance of SJRR shows upward trends in waiting time of each process. Overall, as presented in line chart, the average waiting time for RR is constantly showing an upward trend as compared to proposed algorithms. It supports the fact that proposed algorithm can be used in optimized scheduling of processes in CPU.

Figure 12: Comparison-average waiting time
A similar pattern can be observed in the behavior of algorithms in terms of average turnaround time given in Fig. 13. PMM shows better performance as compared to the other algorithms. PMM does not show much of the difference as far as smaller number of processes is concerned. But as the number of processes is increasing, difference in average turnaround time is gradually increasing. This highlights the observation that the proposed algorithm can help resource optimization in CPU, if the CPU has many processes waiting in the ready queue. PMM is followed by MC, as performance is improved as compared to RR.

Figure 13: Comparison-average Turnaround time
This performance improvement can also be supported by the logic behind the algorithm which dynamically selects the time slice as compared to the RR which has a static time slice for all the processes residing in ready queue. All four proposed variations of RR algorithm have been compared with the earlier proposed work (RC and RCM algorithms) by authors where proposed algorithms showed significant improvements in average turnaround time of the processes as the number of processes is increasing in the ready queue. Overall, average turnaround time taken by proposed algorithms is less than that of Round Robin which highlights the fact that the performance of the proposed algorithm has significantly improved and aids the resource optimization in computers.
Literature shows several attempts to improve turnaround and waiting time as well as to minimize the context switching. Some of them are based on fixed time quantum while others are based on dynamic time quantum. Proposed algorithms are based on relative time quantum technique, as algorithms select the time quantum relative to the burst time of the process, which is ready to be assigned to the CPU. Unlike conventional RR based algorithms, where time quanta are selected randomly, the proposed variations calculate the time quantum based on the burst times of processes already in the ready queue. Each algorithm calculates three-time quantum (based on its methodology) and each time new process is ready to be assigned to CPU, proposed variations will intelligently select time quantum that is best suited in the real time. In short, each process will have its time quantum based on its burst time. It has been observed that if time quantum is selected intelligently and according to the burst time, it will lead to less context switching of the CPU. Experiments given above have shown that selecting time quantum intelligently decreases the waiting time and in turn reduces the turnaround time for each process. So, it is recommended to use these variations in different IoT devices based on the complexity and nature of these devices to improve their performance in the real time. In future, we intend to develop an automated scheduler that will decide the optimal algorithm for given set of processes and allocated time quanta accordingly.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. A. Silberschatz, P. B. Galvin and G. Gagne, “CPU Scheduling,” in Operating System Concepts, 7th edition, Newyork, USA: WILEY, pp.200–254, 2005. [Google Scholar]
2. S. Bibi, F. Azam, S. Amjad, W. H. Butt, H. Gull et al., “An efficient SJRR CPU scheduling algorithm,” International Journal of Computer Science and Information Security, vol. 8, no. 2, pp. 222–230, 2010. [Google Scholar]
3. H. Gull, S. Z. Iqbal, S. Saeed, M. Alqahtani and Y. A. Bamarouf, “Design and evaluation of CPU scheduling algorithms based on relative time quantum: Variations of Round Robin algorithm,” Journal of Computational and Theoretical Nanoscience, vol. 15, no. 8, pp. 2483–2488, 2018. [Google Scholar]
4. T. Balharith and F. Alhaidari, “Round Robin scheduling algorithm in CPU and cloud computing: A review,” in 2nd Int. Conf. on Computer Applications and Information Security, ICCAIS 2019, Riyadh, Saudi Arabia, pp. 1–7, 2019. [Google Scholar]
5. L. Harki, N. Ahmed and A. J. Haji, “CPU scheduling techniques: A review on novel approaches strategy and performance assessment,” Journal of Applied Science and Technology Trends, vol. 1, no. 2, pp. 48–55, 2020. [Google Scholar]
6. R. Tyagi and S. K. Gupta, “A survey on scheduling algorithms for parallel and distributed systems, ” in Advances in Intelligent Systems and Computing, pp. 51–64, 2018. [Google Scholar]
7. N. Reddy, H. Santhi, P. Gayathri and N. Jaisankar, “A new CPU scheduling algorithm using round-robin and mean of the processes,” Advances in Intelligent Systems and Computing, vol. 732, pp. 231–240, 2018. [Google Scholar]
8. U. Shafi, A. Munam, M. Shah, A. Wahid, K. Abbasi et al., “A novel amended dynamic round robin scheduling algorithm for timeshared systems,” Int. Arab Journal of Information Technology, vol. 6, no. 2, pp. 90–97, 2017. [Google Scholar]
9. A. R. Dash, S. K. Sahu and S. K. Samantra, “An optimized Round Robin CPU Scheduling algorithm with dynamic time quantum,” Int. Journal of Computer Science, Engineering and Information Technology (IJCSEIT), vol. 5, no. 1, pp. 7–26, 2015. [Google Scholar]
10. K. Chandiramani, R. Verma and M. Sivagami, “A modified priority preemptive algorithm for CPU scheduling,” Procedia Computer Science, vol. 165, no. 12, pp. 363–369, 2019. [Google Scholar]
11. S. Zouaoui, L. Boussaid and A. Mtibaa, “Priority-based round-robin (PBRR) CPU scheduling algorithm,” International Journal of Electrical and Computer Engineering, vol. 9, no. 1, pp. 190–202, 2019. [Google Scholar]
12. D. Nayak, S. Kumar Malla and D. Debadarshini, “Improved Round Robin scheduling using dynamic time quantum,” International Journal of Computer Applications, vol. 38, no. 5, pp. 34–38, 2012. [Google Scholar]
13. S. K. Dinkar and K. Deep, “A novel CPU scheduling algorithm based on ant lion optimizer,” Advances in Intelligent Systems and Computing, vol. 816, pp. 339–353, 2019. [Google Scholar]
14. K. Eldahshan, A. Elkader and N. Ghazi, “Round Robin based scheduling algorithms, A comparative study,” Automatic Control and System Engineering Journal, vol. 17, no. 2, pp. 29–42, 2017. [Google Scholar]
15. R. J. Matarneh, “Self-adjustment time quantum in round robin algorithm depending on burst time of the now running processes,” American Journal of Applied Sciences, vol. 6, no. 10, pp. 1831–1837, 2009. [Google Scholar]
16. E. Baccelli, O. Hahm, M. Gunes, M. Wahlisch and T. Schmidt, “RIOT OS: Towards an OS for the Internet of Things,” in IEEE Conf. on Computer Communications Workshops, (INFOCOM WKSHPSTurin, pp. 79–80, 2014. [Google Scholar]
17. V. K. Dhakad and L. Sharma, “Performance analysis of Round Robin scheduling using an adaptive approach based on smart time slice and comparison with SRR,” International Journal of Advances in Engineering & Technology, vol. 3, no. 2, pp. 2231–1963, 2012. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |