Computer Systems Science & Engineering DOI:10.32604/csse.2022.019549
Article

Decision Making on Fuzzy Soft Simply* Continuous of Fuzzy Soft Multi-Function

M. A. El Safty1,*, Samirah Al Zahrani1, Ansari Saleh Ahmar2 and M. El Sayed3

1Department of Mathematics and Statistics, College of Science, Taif University, Taif 21944, Saudi Arabia
2Department of Statistics, Faculty of Mathematics and Natural Sciences, Universitas Negeri Makassar, Makassar 90223, Indonesia
3Department of Mathematics, College of Science and Arts, Najran University, Najran, Saudi Arabia
*Corresponding Author: M. A. El Safty. Email: m.elsafty@tu.edu.sa
Received: 16 April 2021; Accepted: 24 May 2021

Abstract: Real world applications are dealing now with a huge amount of data, especially in the area of high dimensional features. In this article, we depict the simply*upper, the simply*lower continuous, we get several characteristics and other properties with respect to upper and lower simply*-continuous soft multi-functions. We also investigate the relationship between soft-continuous, simply*continuous multifunction. We also implement fuzzy soft multifunction between fuzzy soft topological spaces which is Akdag’s generation of the notion. We are introducing a new class of soft open sets, namely soft simply*open set deduce from soft topology, and we are using it to implement the new approximation space called soft multi-function approach space. Simply*space for approximation based on a simply*open set. The world must adopt modern studies in order to confront epidemics. Accordingly, we presented a new decision proposal in this article, compared our proposed approach to the soft relationship introduced by approximation of Xueyou, and concluded that our approach is better. We also used our proposal in the medical application that was studied in this paper.

Keywords: Soft multifunction; soft simply*lower; soft simply*upper approximation; upper inverse of a fuzzy soft multifunction; intelligence discovery; decision making

1  Introduction

Information about the world around is inaccurate and incomplete or uncertain. Granulation of information is very necessary to solve human problems, and thus have a very significant impact on the design and implementation of intelligent systems [1,2]. Decision making plays an important role in our daily life, there are many applications of decision making, such as [3,4]. Theory of topological spaces is a well-known theory that was combined with rough set theory to get new topological approximations for uncertain concepts in information systems, Trait reduction is one of the major steps in decision making problems. It refers to the determination of a minimum subset of attributes that preserves the final decision based on the entire set of attributes [5]. In addition to international schools in Germany and America, the Nobel Prize in Physics for topological uses of material transformation theory using topological applications in science and engineering was awarded in 2016 [6]. There exist many different types, functions that play an important role, topological space Mashhour et al. [7]. In addition, Mashhour et al. [8] introduced the concept of α-continuous function and studied some of their properties, at the final three contests, the notion of multi-function has developed at a different of methods and applications of this notion can be seen, in economic theory, non-cooperative games, artificial cleverness, medicine, knowledge sciences and resolution theory. Njastad [9] presented new class of the open sets it’s called α-open set. A big deal of studies on such functions has been developed for the show of multi-function. Decision making plays a critical role in our everyday lives, and among multiple alternatives, this mechanism offers the best alternative. There exist several decision making applications, such as [10–16].

Molodtsov et al. [17] present the idea of soft set theory as a mathematical method for answering doubts, also, Maji et al. [18]. He also introduced the fundamental results of the new soft set notion as well as presented some soft theory applications in several areas, e.g., soft functions, game theory, operations research, etc. Shabir et al. [19] began the study of soft topological space, and defined the soft topology over a soft set; they also introduced the fundamental notions of it. Aygunoğlu et al. [20] are researching on soft topological space. Recently, Kharal et al. [21] have recently learned about the concepts of a soft class function and studied some of its characteristics; they also applied these results to expert systems for medical diagnosis. Akdağ et al. [22] introduced the concept of upper and lower α-continuity of soft multi-function. These authors also investigated the relationship between a soft multifunction knowledge database.

The upper and lower reverse of a fuzzy soft multifunction from ordinary topological space to fuzzy soft topological space has been described by Metin et al. [23]. Our study of simply* upper and simply* lower continuous fuzzy soft applications has made great progress, especially in decision making, such as soft level sets applied by Feng et al. [24] to solve fuzzy soft set-based decision making.

We study some of their fundamental characteristics of this multi-function. Additionally, we study the relationship among soft continuous multifunction, soft alpha-continuous multi-function and soft pre-continuous multi-function. We also introduce the new approximation spaces called soft multifunction approximation space. Soft simply* approximation space based on soft simply* open set, and compare between these spaces and rough approximation induced by soft relation introduced by Xueyou [25]. We reach to the conclusion that our approximations are better than a rough approximation based on Yao. Also, we generalize the new concepts of fuzzy soft simply* lower and fuzzy soft simply* upper and their medical application. Our survey outlines a new model that gets major accuracies, competing with the Xueyou. To get the results a MATLAB program is applied.

The paper is structured as follows: The basic concepts of the soft set, fuzzy set and soft topological were explored in section two. Section three, we presented our proposed concept which is based on multi-function. In section four, some proposed concepts were introduced on fuzzy, soft and multi-function, and we also introduced a new concept to calculate the degree of accuracy, which has been applied in our paper, and section five concludes and highlights future scope.

2  Preliminaries

In this section, the present study is inspired by pointing out soft set and soft topological blind spots. We implement the notion of softness to overcome these challenge.

Definition 2.1 [11] A soft sub-set (F,I) of a soft space (U,τ~,I) it’s called soft simply* open set, if δints(cls(F,I))⊆~cls(δints(F,I)) . Also, soft simply* closed set, if intS(δclS(F,I))⊇~δclS(intS(F,I)) , and it’s called soft simply open set, if ints(cls(F,I))⊆~cls(ints(F,I)).

Definition 2.2 [20] A soft sub-set (F,I) of a soft topological space (U,τ~,I) it’s called:

i. Soft pre-open, if (F,I)⊆~intS(clS(F,I)) .

ii. Soft α - open, if (F,I)⊆~intS(clS(intS(F,I))) .

Definition 2.3 [12] A subset W of topological space (U,τ) it’s named simply*-open ( SM∗ -open) set if W∈{U,φ,G∪N:G is a proper-open set and N is a nowhere thick set}.

Proposition 2.1 [22] If (W,I) is set softly to Y . So, the next are true for a soft multi-function Π:(U,τ)→(Y,σ,I) :

i. Π+((W,I)C)=U−Π−(W,I) .

ii. Π−((W,I)C)=U−Π+(W,I) .

iii. (χ∘Π)(x)=G(Π(x)),∀n∈U.

Definition 2.4 [12] A topological space (U,γ) it’s called simply* consolidated if for all simply* - open cover of U has a finite sub-cover.

Definition 2.5 [26] Suppose R is a binary relation over U , for x∈X , r(x)={y:xRy} , then a pair of lower and upper approximations is defined: for M⊆U app_(M)={x:r(x)⊆M},app¯(M)={x:r(x)∩M≠ϕ}.

Definition 2.6 [27] Let U be a set and I be attributes set, then the mapping φ:I→2UXU is called a soft relation on U under I .

Definition 2.7 [8] Suppose ϕ is a soft relation, thus for every e∈I,φ(e) is a binary relation on U according to Yao’s definition, for x∈U we obtain re(x)={y:y∈U,(x,y)∈φ(e)} . Thus, for a soft set (C,B),C(e)⊆U , we define C(e)={x:re(x)⊆C(e)}, and C(e)={x:re(x)∩C(e)≠ϕ} . So, we obtain two soft sets (C¯,B) and (C_,B) .

Definition 2.8 [21] Let F:X→Y be fuzzy soft multifunction from the ordinary into fuzzy soft space (Y,σ,E) for each x∈X a soft set F(x) over (Y,σ,E) , F is said to be onto if for each fuzzy soft set GB over Y there exist x∈X such that F(x)=GB .

3  Simply*Continuity of Soft Multifunction

Definition 3.1 For soft multifunction Γ:(U,τ)→(Z,σ,I) the lower inverse F−(W,I) and the upper inverse Γ+(W,I) of a soft-set (W,I) upon Z know as follows: Γ−(W,I)={n∈U:Γ(n)⊆~(W,I)} , Γ+(W,I)={n∈U:Γ(n)∩~(W,I)≠φ} .

Definition 3.2 Let (V,δ) be a space moreover, (Z,γ~,I) be soft space. So, the soft multi-function Γ:(V,δ)→(Z,γ~,I) it is stated to be:

i. Soft- lower simply*-continuous at element n belongs to U if for each soft open set (W,I) such that Γ(n)⊆~(W,I) there is simply* -open neighborhood P(n) of n where Γ(m)⊆~(W,I) , ∀m∈P(n) .

ii. Soft -upper simply*-continuous at element n belongs to U if for each soft open set (W,I) such that Γ(x)∩~(W,I)≠ϕ there is simply* open neighborhood P(n) of n where Γ(n)∩~(W,I)≠ϕ , for all m∈P(n).

iii. Soft- lower (upper) simply*-continuous if Γ has this characteristic by via every of points U .

Theorem 3.1 A soft multi-function F:(U,δ)→(W,γ~,I) is a soft- lower simply*- continuous if for all soft open set (V,I) on top of W , F−(V,I) is simply*- open set in W.

Proof. Assume first F is soft -upper simply*-continuous. Suppose that {c,b} be soft open set upon V while v∈F−(V,I) . So, from definition 2.5 there is soft simply open vicinity P(v) of v where for each {b,a} , F(m)⊆~(V,I) which means that F−(V,I) is a soft simply* open. Conversely, is obvious from the definition of soft lower continuity of F.

Theorem 3.2 Let Π:(U,τ)→(Z,γ,I) be a soft multi-function and M is a simply*- open set of U . Then the restriction Π|M is soft-lower simply*- continuous if Π is soft-lower simply*-continuous.

Proof. Assuming that (K,I) be soft open set upon Z so that Π|M(v)⊆~(K,I) . If Π is soft lower simply* -continuous while Π(v)=Π|M(v)⊆~(K,I) , so, there are simply*- open set V⊆U include v so that Π(n)⊆~(K,I) for all n∈V . Put U1=V∩M then we have U1 is simply*-open set in M include v and Π(U1)=Π|M(U1)⊆~(K,I) . Consequently Π|M is soft lower simply* -continuous.

Theorem 3.3 Let Π:(U,δ)→(Z,γ) is multi-function, L:(U,δ)→(W,γ,I) is soft multi-function if Π is soft - upper (lower) simply* -continuous and L is soft - upper (lower) continuous consequently L∘F is soft -upper (lower) simply*-continuous.

Proof. Suppose that (V,I) is a soft open set upon W . As L is soft- upper continuous then L−(V,I) is open in Z . As Π is soft lower simply*continuous then Π−(L−(V,I)=(LoΠ)−(V,I) is simply*-open in U . Therefore LoΠ is soft - lower simply*- continuous. Similarly, we can show that LoΠ is soft- upper simply*-continuous.

Theorem 3.4 Suppose Π:(U,δ)→(V,γ~,I) be a soft-lower simply* -continuous surjective multi-function and U is simply*-compact thus (V,γ~,I) is soft- compact.

Proof. Assume Π:(U,δ)→(V,γ~,I) be an onto soft multi-function, suppose ζ={(Wk,E):k∈I} be a cover of V via soft open sets. As Π is soft- lower simply*- continuous, the class of all open sets of the form Π+(Wk,I) , for (Wk,I)∈ζ is a soft simply*- cover of V there is has a finite sub-cover. As Π is surjective, consequently, we get Π(Π−(Wk,I))=(Wk,I) for every soft set (Wi,I) over V . Then there exist the class images of elements of sub-cover is a finite sub-family of ζ which covers V . So (V,γ~,I) is soft- compact.

Remark 3.1 If F is a soft- lower simply*-continuous consequently F is soft – lower continuous but the reverse is not valid generally as illustrated the next example.

Example 3.1 Let τ={U,ϕ,{a},{c,a}} is a topology over U={a,b,c} and σ~={φ,W~,(V,I),(Z,I)} be a soft topology over W={y1,y2,y3} where I={e1,e2,e3} , V(e1)={y1} , V(e2)={y3} and V(e3)=ϕ , Z(e1)={y1,y2},Z(e2)={y3} and Z(e3)=W . Then the multi-function Π:(U,τ)→(W,σ~,I) is defined by Π(a)=(V,I),Π(b)=(Z,I) and Π(c)=W is soft upper simply*continuous multi-function but is not soft upper continuous multi-function. For Π−(V,I)={a} and Π−(V,I)={b,a} are upper (lower) simply*open sets but {b,a} is not open sets in U.

Remark 3.2 Let F be soft upper simply*continuous therefore F is continuous soft-semi upper and upper α -continuous however the reverse is not valid in generally as illustrated the next example.

Example 3.2 Assuming that τ={U,ϕ,{a},{b},{a,b}} be a topology on U={a,b,c} while σ~={φ,Z~,(V,I),(L,E)} be a soft topology over Z={y1,y2,y3} where I={e1,e2,e3} , V(e1)={y1} , V(e2)={y3} and V(e3)=ϕ , L(e1)={y1,y2},L(e2)={y3} while L(e3)=Z~ . Then the multi-function F:(U,δ)→(Z,γ~,I) defined out as follows F(a)=(V,I),F(b)=Z~ while F(c)=(L,I) is soft- lower simply*-continuous multi-function but is not soft upper α - continuous multi-function.

4  Approximation Based on Soft Multifunction and Its Application

Definition 4.1 Assume F:(U,δ)→(Z,γ,I) be soft multi-function, and F(v) is soft set over Z . Then (Z,F(v)) is called soft multi-function approximation space. We define a pair operator F− and F+ where F−,F+:SP(Z,I)→P(U) , we define the lower reverse F−(W,I) and the upper reverse F+(W,I) of a soft set (W,I) upon Z , are illustrated as follow: F−(W,I)={v∈U:F(v)⊆~(W,I)} and F+(W,I)={v∈U:F(x)∩~(W,I)≠φ} .

Definition 4.2 Assuming that Π:(U,δ)→(W,σ,I) be soft multifunction we define:

i. Π−(N,I) is devoted to the positive region of the soft set (N,I).

ii. Π+(N,I) is negative region and is equal to [Π+(N,I)]C.

iii. The boundary soft multi-function of soft set (N,I) denoted by BSM(N,I)= Π+(Π,I)−Π−(N,I) .

iv. (N,I) is called definable soft set and BSM(N,I)=ϕ otherwise is called soft multi rough set BSM(N,I)≠ϕ .

Definition 4.3 Let (U,SSM∗⁡O(U,I)) be soft simply*approximation space based on soft simply*open set and (W,I) is soft subset of soft topological space (U,δ~,I) , then we define a pair operator LSM∗(W,I) and USM∗(W,I), LSM∗(W,I),USM∗(W,I):SP(U,I)→SP(U,I) , we define the soft simply* lower F−(W,I) while upper inverse F+(W,I) of a soft set (W,I) upon U are defined as follows:

Definition 4.4 Let (X,SSM∗O(X,I)) be soft simply* approximation space we define:

i. LSM∗(W,I) is devoted to the positive region of the soft set (W,I).

ii. NEG(W,I)=X∖USM∗(W,I) is negative region.

iii. BSM∗(W,I)=USM∗(W,I)−LSM∗(W,I) is the boundary soft multi- function of soft set (W,I) .

iv. If USM∗(W,I)=LSM∗(W,I) , then (W,I) is called simply* definable soft set and BSM∗(W,I)=ϕ otherwise is called soft simply* rough set BSM∗(W,I)≠ϕ .

Definition 4.5 An accuracy measure of soft simply* approximation space of (A,I) in (X,F(x)) is defined as μSM∗(A,I)=|F−(A,I)|+|[F+(A,I)]C||X| where |.| is devoted to the cardinality of the set. Such that 0≤μMF(A,I)≤1 , if μMF(A,I)=1 , then (A,I) is definable soft set, if 0≺μMF(A,I)≺1 and μMF(A,I)≠1 then (A,I) is soft simply*undefinable soft set.

Next, we shall discuss the comparison between the Yao method and our method for approximations. We deduce that in our method the soft lower approximation of any soft subset in soft simply an approximation space is definable soft set or soft exact set with respect to the lower and upper approximations of the methods Xueyou Chen. Thus, the boundary region of our method is empty set, and the following application shows this comparison.

For U={b,a,c},I={e1,e2},σ~={U,φ,{(e1,{a,b}),(e2,{a,b})},{(e1,{b}),(e2,{a,c})},{(e1,{b,c}), (e2,{a})},{(e1,{b}),(e2,{a})},{(e1,{a,b}),(e2,U)},{(e1,U),(e2,{a,b})},{(e1,{b,c}),(e2,{a,c})}}, is soft topological space on set U , and τ={M,φ,{a1},{a1,c1}} , let R1={(a,a),(a,b),(b,a),(b,c),(c,b)}, R2={(a,a),(a,b),(b,a),(b,c),(c,a)} , be a binary relation on set U. we define soft relation ϕ:E→2UxU where ϕ(e1)=R1,ϕ(e2)=R2 . Then we define a binary relation such that re1(a)={a,b},re1(b)={c,a},re1(c)={b} , and re2(a)={b,a},re2(b)={c,a},re2(c)={a}, F:(V,τ)→(U,σ,E) be soft multi- function where V={a1,b1,c1,d1,e1,g1,h1}, F(a1)={(e1,{a,b}),(e2,{a,b})}, F(c1)={(e1,{b,c}),(e2,{a})},F(d1)={(e1,{b}),(e2,{a})},F(e1)={(e1,{a,b}),(e2,U)}, F(h1)={(e1,U),(e2,{a,b})}, F(g1)={(e1,{b,c}),(e2,{a,c})} , F(b1)={(e1,{b}),(e2,{a,c})}.

We have Xueyou approximation on soft simply* approximation space and we comparison between the soft simply* approximation space, inverse lower, inverse upper with respect to Yao approximation. As the following Tab. 1 shows the class of soft simply* open set, the lower and the upper soft simply* open set and the accuracy soft simply* open set.

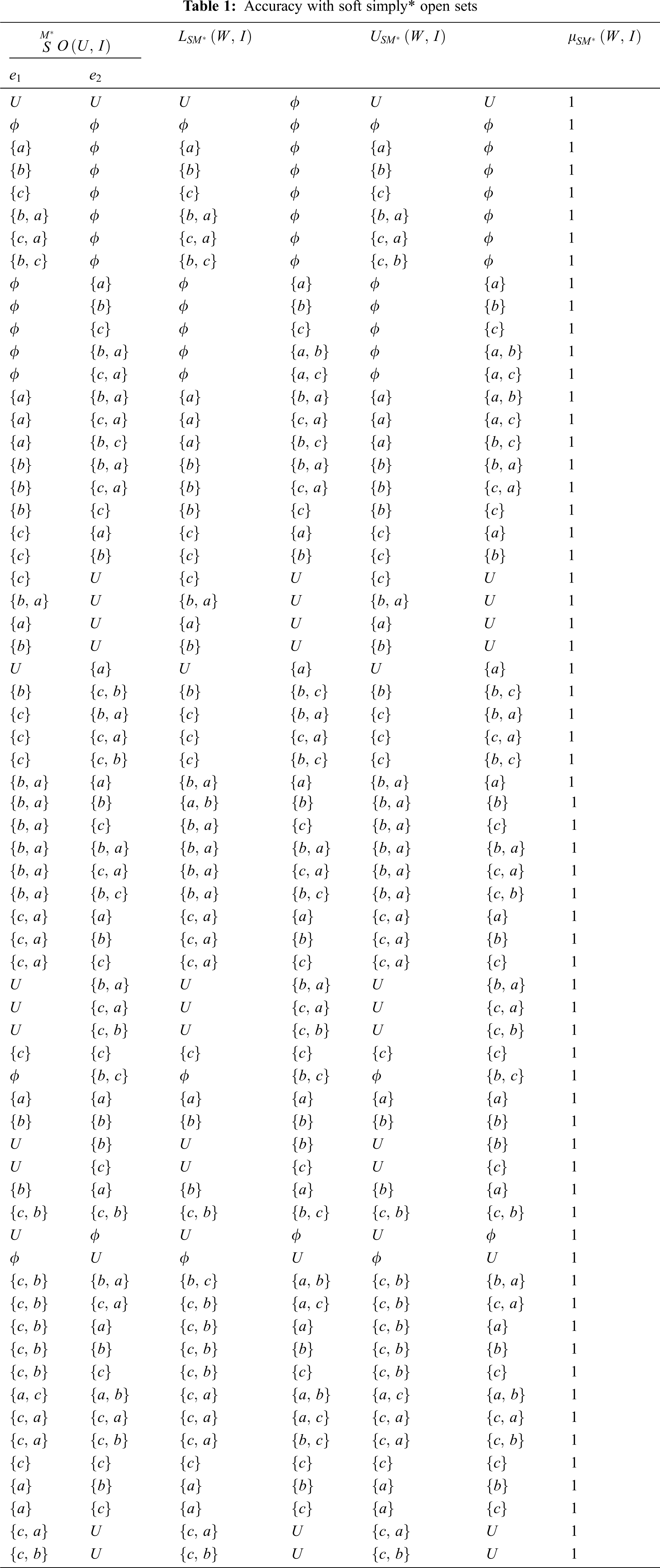
The next Tab. 2, gives the accuracy of soft multi-function approximation space w. r. to Xueyou method.

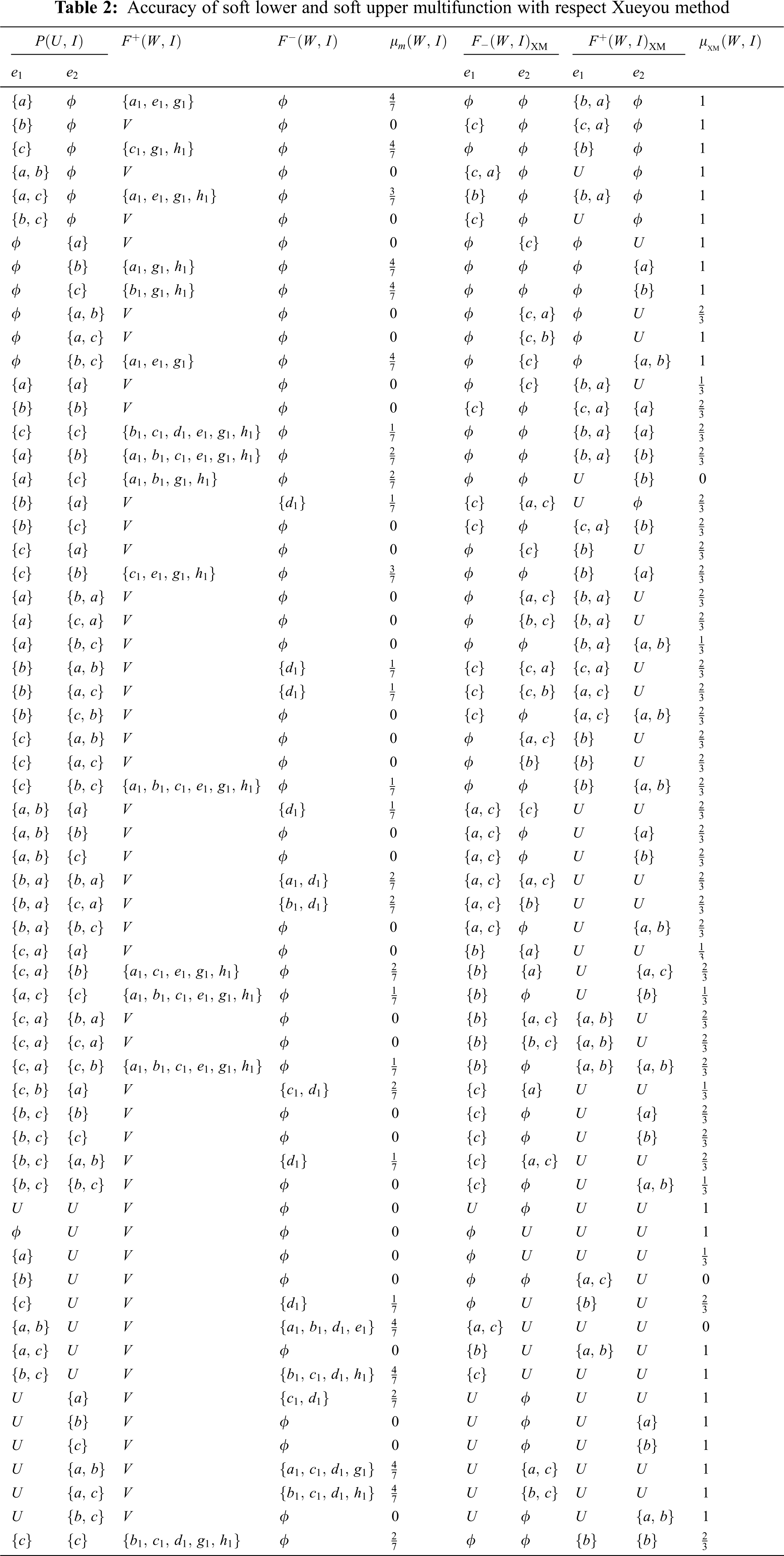
Tab. 3 show the comparison between the approximations.

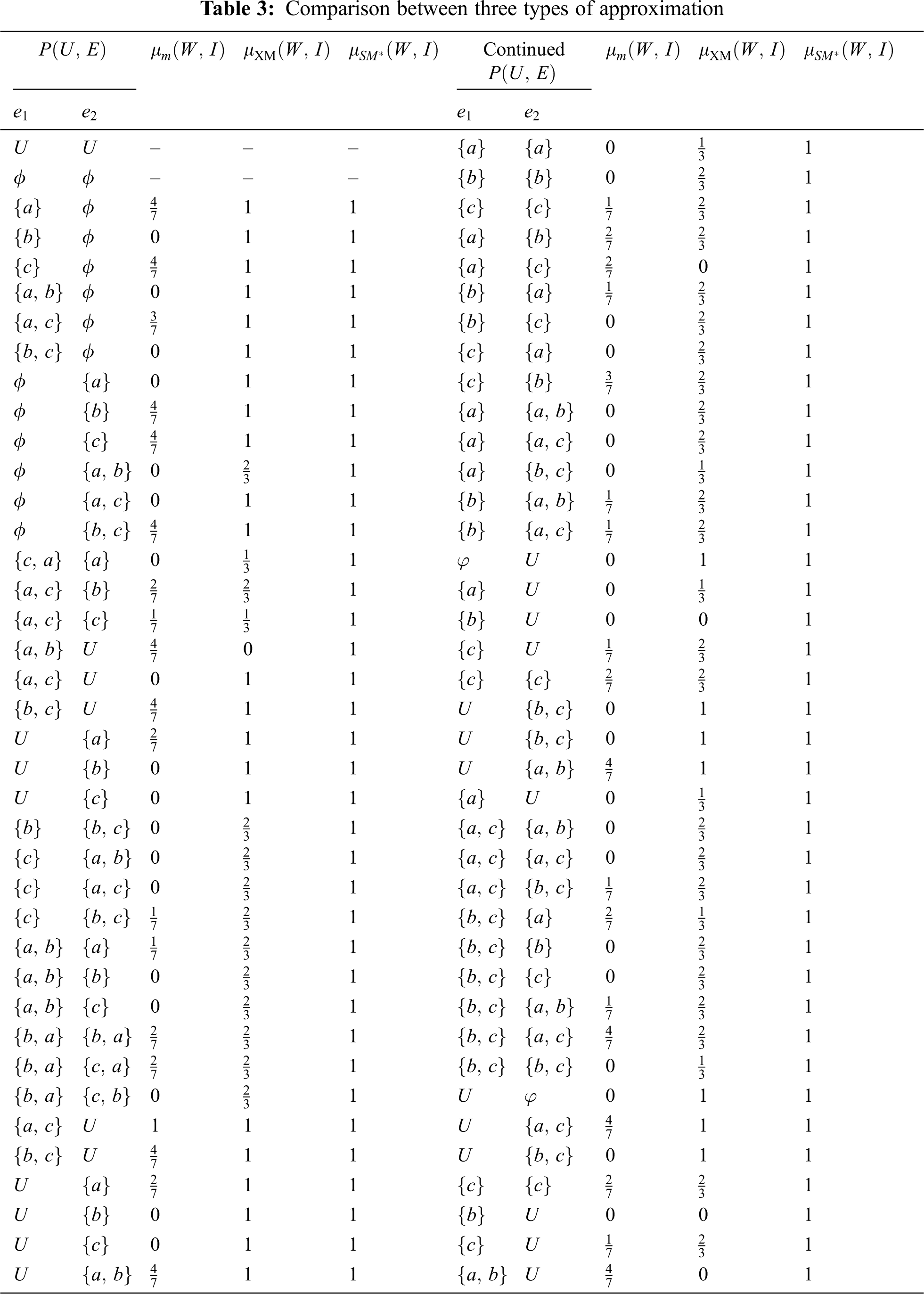
Previous Tabs. 3 and 4, we find out that the accuracy of soft simply* approximation space is the best of the accuracies of soft multifunction approximation space and Xueyou method based on Yao. From the above tables, we see that if the soft set {(e1,ϕ),(e2,{a,b})} is soft simply* open exact set. The accuracy of our approximation is better than the accuracy of the method Xueyou. Also, we get the best proposed accuracy on soft simply* approximation space.

Next, we shall introduce a new function called fuzzy soft simply* multifunction between two fuzzy soft topologies. Also, we introduce the concepts of fuzzy soft simply* lower and fuzzy soft simply* upper. We will use the new approximation in medical. Also, in this section, we shall present three algorithms.

Definition 4.6 For fuzzy soft multifunction Γ:(U,τ)→(Z,σ,I) the lower inverse F−(W,I) and the upper inverse Γ+(W,I) of a soft-set (W,I) upon Z as follows: Γ−(W,I)={n∈U:Γ(n)≤~(W,I)} , Γ+(W,I)={n∈U:Γ(n)∧~(W,I)≠φ} .

Definition 4.7 Let (V,δ) be a space moreover, (Z,γ~,I) be soft space. So, the fuzzy soft multi-function Γ:(V,δ)→(Z,γ~,I) it is stated to be:

i. fuzzy Soft- lower simply*-continuous at element n belongs to U if for each soft open set (W,I) such that Γ(n)≤~(W,I) there is simply* -open neighborhood P(n) of n where Γ(m)≤~(W,I) , ∀m∈P(n) .

ii. fuzzy Soft -upper simply*continuous at element n belongs to U if for each soft open set (W,I) such that Γ(x)∧~(W,I)≠ϕ there is simply*open neighborhood P(n) of n where Γ(n)∧~(W,I)≠ϕ , for all m∈P(n).

iii. fuzzy Soft- lower (upper) simply*-continuous if Γ has this characteristic by via every of points U .

Medical application explains the basic tasks performed by the medical expert in a group of patients and by transmitting their complaint into the possible causes of set that are of the cause of their disease. So, we get two soft classes (Y,E) , where (Y,E) is the soft class of symptoms and their importance for the patient, X symbolize the causes and medical advantage for treatment. Take Y={y1,y2,y3,y4,y5,y6,y7,y8},E={e1,e2,e3,e4} , where y1 is eczema, y2 migraine, y3 burning stomach, y4 joint Paine, y5 sleep massless, y6 headache, y7 herpes, y8 anxiety , and e1 high important, e2 medium important, e3 low important, e4 very low important, and X={x1,x2,x3,x4,x5,x6,x7,x8} where x1 allergy, x2 blood pressure, x3 acidity, x4 mod- disorder, x5 fatigue, x6 lock of appetite, x7 obesity, x8 depression. The fuzzy soft set of patients may be given as (G,E)={(e1,{y20.5,y40.4,y80.8}),(e2,{y20.3,y40.2,y50.6,y60.7}), (e3,{y40.2,y60.6}),(e4,{y20.2,y30.3,y81})}. The medical expert must first rely on the patient’s historical knowledge of the condition of the disease, which is stored in the doctor’s files. Map F:(X,τ)→(Y,τ~,E) is soft multi- function defined as follow:

f(x1)={(e1,{y3,y6}),(e2,{y7}),(e3,{y6}),(e4,{y6})}, f(x2)={(e1,{y4}),(e2,φ)},(e3,φ),(e4,φ)}, f(x3)={(e1,{y1,y2}),(e2,{y3,y4})},(e3,φ),(e4,{y8})},f(x4)={(e1,φ),(e2,{y1}),(e3,{y1,y2},),(e4,φ)}, f(x5)={(e1,{y1,y3,y4}),(e2,{y2,y6}),(e3,{y8}),(e4,{y6,y8})},

f(x6)={(e1,{y2,y8}),(e2,{y2,y6,y7}),(e3,{y3}),(e4,{y1,y7})}, f(x7)={(e1,{y6}),(e2,φ),(e3,{y3}),(e4,{y1,y7})},f(x8)={(e1,{y2}),(e2,{y5}),(e3,φ),(e4,{y8})}. So, from by computations give us the advantage causes and medical advantage for treatment as follows F−(G,E)={x2,x3,x5,x6,x8}. i.e., F−(G,E)={ Blood pressure, acidity, fatigue, locks of appetite, depression}.

Algorithm 4.1

Step 1: the finite universe U and the set of attributes I .

Step 2: compute the soft power set for (U,I)

Step 3: Compute the class of soft simply* open set for all soft power set.

Step 4: Compute the soft simply* lower LSM∗(W,I) and the soft simply* upper USM∗(W,I) .

Step 5: Compute the soft simply* accuracy μSM∗(W,I) .

Algorithm 4.2

Step 1: define soft multi-function Γ:(U,τ)→(Z,σ,I) .

Step 2: Compute the class of soft power set (U,I) .

Step 3: compute soft lower F−(W,I) and soft upper F+(W,I) multifunction

Step 4: Compute the accuracy of soft multi-function μm(W,I) .

Algorithm 4.3

Step 1: define soft multi-function Γ:(U,τ)→(Z,σ,I) .

Step 2: Compute the class of soft power set (U,I) .

Step 3: Compute soft lower F−(W,I)XM and soft upper F+(W,I)XM multifunction

Step 4: Compute the accuracy of soft multi-function μXM(W,I) .

Step 5: By comparison between our method based on soft simply* multi-function μSM∗(W,I) , other methods soft multi-function and μm(W,I) Xueyou method μXM(W,I) concerning the accuracy.

Step 6: From the Step 5 we deduce that our method is better than Xueyou method and soft multi-function.

5  Conclusion

The aim of this paper is to introduce a new definition of upper and lower soft-simply* multifunction as well as present basic properties. Furthermore, we also obtained the relationship between these concepts and other fuzzy soft multifunction. We generated that the new approximation spaces called soft and fuzzy multifunction approximation space. We got that the accuracy of our approximations is better than the accuracy of others. We achieve proposed accuracy that depends up on the fuzzy and soft simply* approximation space, which is better than of Xueyou and Yao method. Our method grants a very chance of maker to pick out a suitable for him. We also presented a medical application to demonstrate that our proposed concept is actually applicable. Thus, our method provides more flexibility to the decision-maker to choose which is suitable for him. In the future, based on some recent soft-topological studies, we will expand the research content of this paper further. Also, it is possible to use our approach to contribute to reducing Coronavirus (Covid-19).

Funding Statement: This research received funding from Taif University, Researchers Supporting and Project number (TURSP-2020/207), Taif University, Taif, Saudi Arabia.

Conflict of Interest: The authors declare that they have no interest in reporting regarding the present study.

References

 1.  M. A. El Safty, “Modeling uncertainty knowledge of the topological methods,” Poincare Journal of Analysis & Applications, vol. 8, no. 1, pp. 89–102, 2021. [Google Scholar]

 2.  M. A. El Safty and A. M. Alkhathami, “A topological method for reduction of digital information uncertainty,” Soft Computing, vol. 24, no. 1, pp. 385–396, 2020. [Google Scholar]

 3.  M. A. El Safty, A. A. Mousa, S. A. Alblowi and M. El Sayed, “Topological approach on fuzzy soft β-closure and β-interior and its application in decision making,” Nanoscience and Nanotechnology Letters, vol. 12, no. 11, pp. 1323–1328, 2020. [Google Scholar]

 4.  M. A. El Safty and S. Al Zahrani, “Topological modeling for symptom reduction of Coronavirus,” Punjab University Journal Mathematics, vol. 53, no. 3, pp. 47–59, 2021. [Google Scholar]

 5.  M. El Sayed, M. A. El Safty and M. K. El-Bably, “Topological approach for decision-making of COVID-19 infection via a nano topology model,” AIMS Mathematics, vol. 6, no. 7, pp. 7872–7894, 2021. [Google Scholar]

 6.  J. M. Kosterlitz, D. Haldane and D. J. Thouless, “Topological phase transitions and topological phases of matter, ” in Scientific Background on the Nobel Prize in Physics, 2016. [Google Scholar]

 7.  A. S. Mashhour, M. E. Abd El-Monsef and S. N. El-Deeb, “On pre continuous and weak pre continuous mappings,” Proceeding Mathematics and Physics Society Egypt, vol. 53, pp. 47–53, 1982. [Google Scholar]

 8.  A. S. Mashhour, I. A. Hasanein and S. N. El-Deeb, “α-continuous and α-open mappings,” Acta Mathematica Hungarica, vol. 41, pp. 41, 213–218, 1983. [Google Scholar]

 9.  O. Njastad, “On some classes of nearly open sets,” Pacific Journal of Mathematics, vol. 15, no. 3, pp. 961–970, 1965. [Google Scholar]

10. A. El Safty, “Topological method for a study of discriminating three categories of banks and its use in attributes reduction,” International Journal of Scientific Research in Science, Engineering and Technology (IJSRSET), vol. 7, no. 5, pp. 221–233, 2020. [Google Scholar]

11. M. El Sayed and M. K. El-Bably, “Soft simply open sets in soft topological space,” Journal of Computational and Theoretical Nano Science, vol. 14, pp. 4100–4113, 2017. [Google Scholar]

12. M. El Sayed, “Soft simply* generalized continuous mappings in soft topological spaces,” International Journal of Engineering and Applied Science, vol. 14, pp. 3104–3112, 2019. [Google Scholar]

13. M. El Sayed, Kh Abd-Rabou and M. A. El Safty, “New classes of soft open sets in soft generalized topological spaces,” Journal of Fuzzy Mathematics, vol. 28, pp. 721–732, 2020. [Google Scholar]

14. M. El Sayed, A. G. Al Qubati and M. K. El-Bably, “Soft pre-rough sets and its applications in decision making,” Mathematical Biosciences and Engineering MBE, vol. 17, no. 5, pp. 6045–6063, 2020. [Google Scholar]

15. A. A. Ojugo and R. E. Yoro, “Migration pattern as threshold parameter in the propagation of the COVID-19 epidemic using an Actor-based model for SI-social graph,” Journal of Information and Visualization, vol. 2, no. 2, pp. 93–105, 2021. [Google Scholar]

16. R. Patil, U. Patel and T. Sarkar, “COVID-19 cases prediction using regression and novel SSM model for non-converged countries,” Journal of Applied Science, Engineering, Technology, and Education, vol. 3, no. 1, pp. 74–81, 2021. [Google Scholar]

17. D. A. Molodtsov, “Soft set theory-first results,” Computers & Mathematics with Applications, vol. 37, no. 4–5, pp. 19–31, 1999. [Google Scholar]

18. P. K. Maji, R. Biswas and A. R. Roy, “Soft set theory,” Computers and Mathematics with Applications, vol. 45, pp. 555–562, 2003. [Google Scholar]

19. M. Shabir and M. Naz, “On soft topological spaces,” Computers & Mathematics with Applications, vol. 61, no. 7, pp. 1786–1799, 2011. [Google Scholar]

20. A. Aygunoğlu and H. Aygün, “Some notes on soft topological spaces,” Neural Computing and Applications, vol. 21, pp. 113–119, 2012. [Google Scholar]

21. A. Kharal and B. Ahmad, “Mappings on soft classes,” New Mathematics and Natural Computation, vol. 7, no. 3, pp. 471–481, 2011. [Google Scholar]

22. M. Akdağ and F. Erol, “Upper and lower α-continuity of soft multifunction,” American Scientific Research Journal for Engineering, Technology, and Sciences, vol. 8, pp. 96–107, 2014. [Google Scholar]

23. A. Metin, K. Serkan and E. Fethullah, “Fuzzy upper and lower continuity of fuzzy soft,” Journal of New Theory, vol. 1, pp. 59–68, 2015. [Google Scholar]

24. F. Feng, Y. Li and V. L. Fotea, “Application of level soft sets in decision making based on interval-valued fuzzy soft sets,” Computers & Mathematics with Applications, vol. 60, no. 6, pp. 1756–1767, 2010. [Google Scholar]

25. C. Xueyou, “Rough approximations induced by a soft relation,” Annals of Fuzzy Mathematics and Informatics, vol. 11, pp. 135–144, 2016. [Google Scholar]

26. Y. Y. Yao, “Constructive and algebraic methods of the theory of rough sets,” Information Sciences, vol. 109, no. 1–4, pp. 21–47, 1998. [Google Scholar]

27. Z. Li, X. Ningxin and G. Ninghua, “Rough approximations based on soft binary relations and knowledge bases,” Soft Computing, vol. 21, pp. 839–852, 2017. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.