Computer Systems Science & Engineering DOI:10.32604/csse.2022.018534
Article

On Vertex-Edge-Degree Topological Descriptors for Certain Crystal Networks

Sadia Husain1, Fouad A. Abolaban2, Ali Ahmad1,*, Muhammad Ahsan Asim1 and Yasir Ahmad1

1College of Computer Sciences and Information Technology, Jazan University, Saudi Arabia
2King Abdulaziz University, College of Engineering, Nuclear Engineering Department, Jeddah, 21589, Saudi Arabia
*Corresponding Author: Ali Ahmad. Email: ahmadsms@gmail.com
Received: 11 March 2021; Accepted: 30 April 2021

Abstract: Due to the combinatorial nature of graphs they are used easily in pure sciences and social sciences. The dynamical arrangement of vertices and their associated edges make them flexible (like liquid) to attain the shape of any physical structure or phenomenon easily. In the field of ICT they are used to reflect distributed component and communication among them. Mathematical chemistry is another interesting domain of applied mathematics that endeavors to display the structure of compounds that are formed in result of chemical reactions. This area attracts the researchers due to its applications in theoretical and organic chemistry. It also inspires the mathematicians due to involvement of mathematical structures. Regular or irregular bonding ability of molecules and their formation of chemical compounds can be analyzed using atomic valences (vertex degrees). Pictorial representation of these compounds helps in identifying their properties by computing different graph invariants that is really considered as an application of graph theory. This paper reflects the work on topological indices such as ev -degree Zagreb index, the first ve -degree Zagreb α index, the first ve -degree Zagreb β index, the second ve -degree Zagreb index, ve -degree Randic index, the ev -degree Randic index, the ve -degree atom-bond connectivity index, the ve -degree geometric-arithmetic index, the ve -degree harmonic index and the ve -degree sum-connectivity index for crystal structural networks namely, bismuth tri-iodide and lead chloride. In this article we have determine the exact values of ve -degree and ev -degree based topological descriptors for crystal networks.

Keywords: ev-degree; ve-degree; topological indices; crystal networks

1  Introduction

Computation of topological indices for large chemical structures becomes very challenging but still useful in depicting the structure and physico-chemical properties that are extremely important in reticular chemistry. Recently reticular Metal-organic frameworks MOFs are evolved as porous conductive solids with great applicability in fuel cells, batteries, capacitors, sensors and electronics. In MOFs covalent fibers of carbon atoms form mesh like crystals [1,2]. In reticular chemistry, the numerically representation of structural characteristics of molecules, are the topological indices, which are obtained by using the graphical methods. These indices play an important role in the area of mathematical chemistry and control theory, mainly in QSAR/QSPR investigations [3,4].

The networks that are topologically equivalent, although they exibit different labelings of distinct atoms but due to topological indices they are invariant. These indices describe the connections among the atoms and in this way they are basic invariants that show a relationship with biological activity and chemical reactivity. Topological study of a MOF means transforming the connectivity of any structure into a unique number representing an index of the metal-organic framework under consideration.

Wiener in his article [5], introduced the concept of topological index while he was studying the structural relationships to identify boiling points of paraffins. Many topological indices are used to reflect the structural arrangement of graphs. In general, they are classified into distance or degree-based topological indices along with these counting related indices of graphs have play a vital role in chemical characterization. Article [6–22] can give more deep insight as literature survey.

2  Preliminaries

Let G be a simple connected graph with vertex sets V(G) and edge sets E(G) . The degree of a vertex ε , denoted by d(ε) , is the number of edges that are incident to the ε . The open neighborhood of ε is defined as N(ε)={ε∈V(G):λε∈E(G)} and closed neighborhood N[ε]=N(ε)∪{ε} [23]. The ve -degree, denoted by dve(ε) , of any vertex ε∈V is the number of different edges that are incident to any vertex from the N[ε] . In [24] defined the ev -degree of the edge e=λε∈E, denoted by dev(e), the number of vertices of the union of the closed neighborhoods of λ and ε. For details see [25–30].

The ve -degree and ev -degree topological indices are defines as: ∑e∈E(G)(dev(e))2 , ∑ε∈Vdve(ε)2 , ∑λε∈E(dve(ε)+dve(λ)) , ∑λε∈E(dve(λ)×dve(ε)) , ∑λε∈E(dve(λ)×dve(ε))−12 , ∑e1∈Edve(e1)−12 , ∑λε∈E(dve(λ)+dve(ε)−2dve(λ)×dve(ε))12 , ∑λε∈E2(dve(λ)×dve(ε))12dve(λ)+dve(ε) , ∑λε∈E2dve(λ)+dve(ε) and ∑λε∈E(dve(λ)+dve(ε))−12 are ev -degree Zagreb ( Mev ) index, the first ve -degree Zagreb α ( Mαve1 ) index, the first ve -degree Zagreb β ( Mβve1 ) index, the second ve -degree Zagreb ( Mve2 ) index, ve -degree Randic ( Rve ) index, the ev -degree Randic ( Rev ) index, the ve -degree atom-bond connectivity ( ABCve ) index, the ve -degree geometric-arithmetic ( GAve ) index, the ve -degree harmonic ( Hve ) index and the ve -degree sum-connectivity ( χve ) index, respectively.

3  Crystal Structures

The physical structure of solid materials is significant for engineering applications. It depends on the arrangements of the atoms, ions, or molecules that becomes the reason for strength of solid materials. The connectivity pattern of ions or atoms in a solid and repetitive patterns in three dimensions is known as crystal structure and material is called crystalline solid or crystalline material. Due to different crystalline structure of a materials their performance and characteristics varies. The unit cell is the basic structure that explains the crystal structure and repetition of this unit cell forms the whole crystal. Some of the examples of crystalline materials are alloys, metals, and some ceramic materials. In this paper topological indices for the bismuth tri-iodide and lead chloride are determined by mapping their crystalline structures in the form of graphs.

4  Graph of Bismuth Tri-Iodide

Bismuth tri-iodide ( BiI3 ) is an inorganic compound. It is the result of the response of bismuth and iodine, which is important in qualitative inorganic analysis. Layered BiI3 crystal is considered to be a three-layered stacking structure, where bismuth atom planes are lying between iodide atom planes, which form the sequence I-Bi-I planes. The rhombohedral BiI3 crystal with R-3 symmetry is formed by the periodic stacking of three layers [31,32]. In 1995, Nason et al. [33] synthesized a unit crystal of BiI3 . The Fig. 1 shows one unit of bismuth tri-iodide.

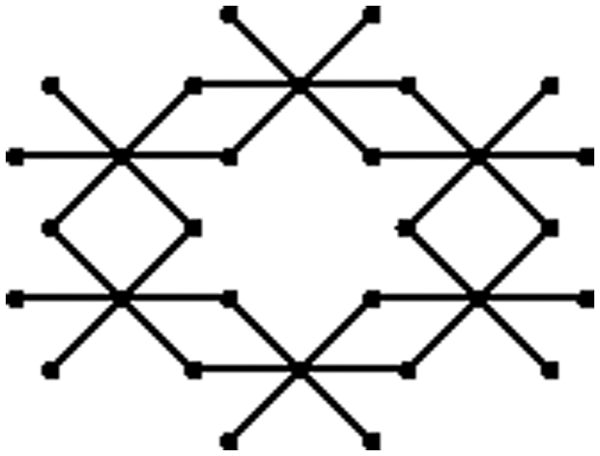
Figure 1: One unit of bismuth tri-iodide

The graph of a single unit of bismuth tri-iodide contains six 4-cycles of which two are at the bottom, two on the top and two in the middle. The unit cells of bismuth tri-iodide can be arranged either linearly or in a sheet form. A linear arrangement with q unit cells is called q -bismuth chain, p×q bismuth sheet is obtained by arrangements of pq unit cells into p rows and q columns. A p×q bismuth sheet throughout onward represented by BiI3 . A sheet of BiI3 contains 11pq+10p+7q+2 vertices and 18pq+12p+6q edges, which are shown in Tab. 1. The number of vertices corresponding to their degrees of BiI3 are shown in Tab. 2 and the edge partition based on degree of end vertices of each edge is shown in Tab. 3.

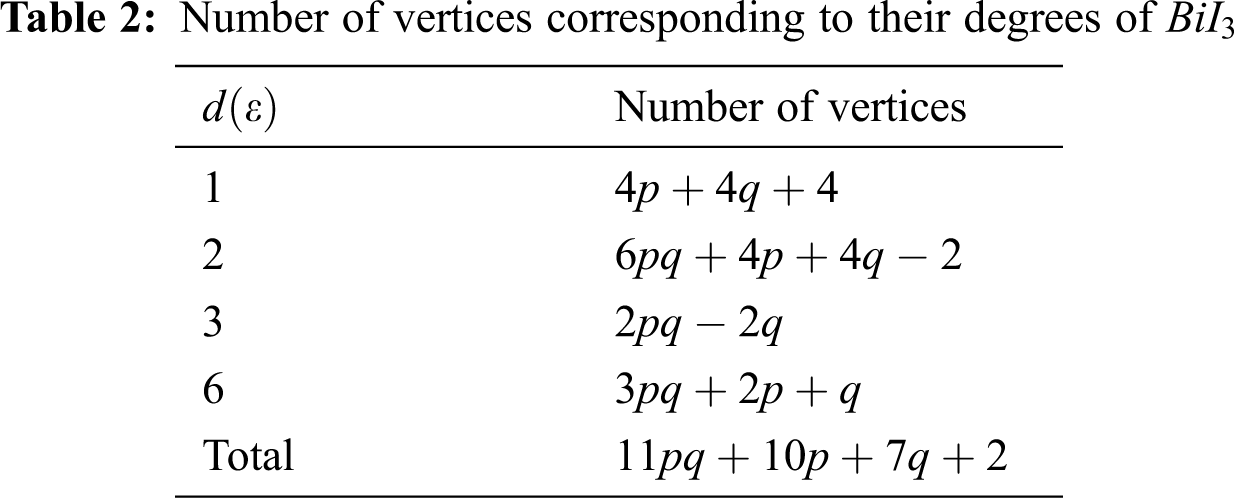
We partitioned the edges of BiI3 , based on ev -degree in Tab. 4.

In Tab. 5, we partitioned the vertices of BiI3 , based on ev -degree.

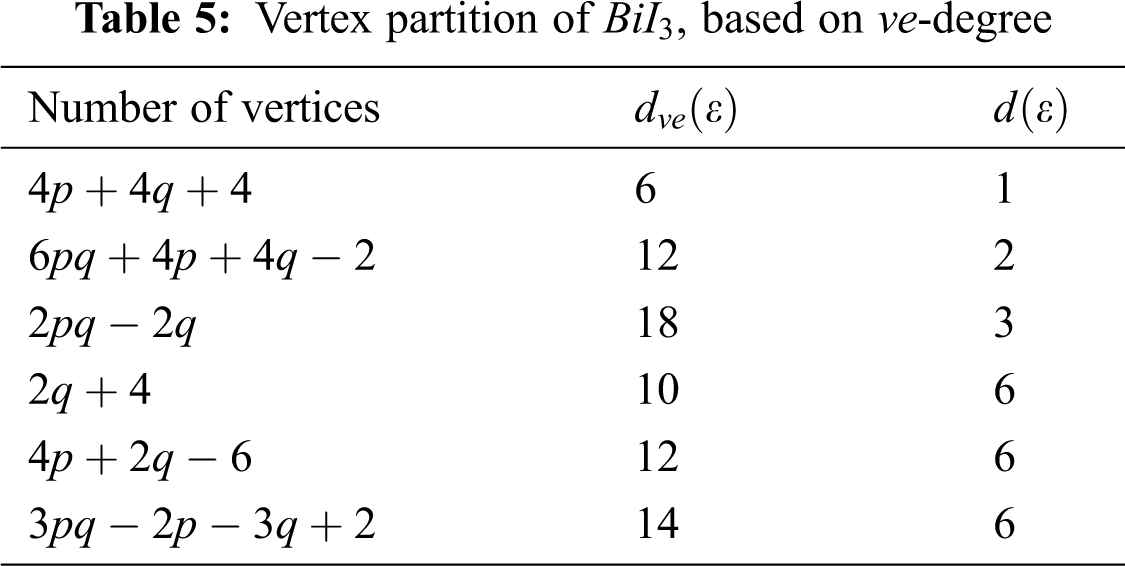
We partitioned the edge of BiI3 with respect to ve -degrees.

Now we calculated ev -degree and ve -degree based indices such as Mev index, Mαve1 index, Mβve1 index, Mve2 index, Rve index, Rev index, ABCve index, GAve index, Hve index and χve index for BiI3 .

4.1 ev-Degree Zagreb Index

By using ev -degree of BiI3 from Tab. 4, we compute the ev -degree based Zagreb index:

4.2 The First ve -degree Zagreb α Index

Using Tab. 5 we compute the first ve -degree Zagreb α index:

4.3 The First ve-degree Zagreb β Index

Using Tab. 6 we compute the first ve -degree Zagreb β index:

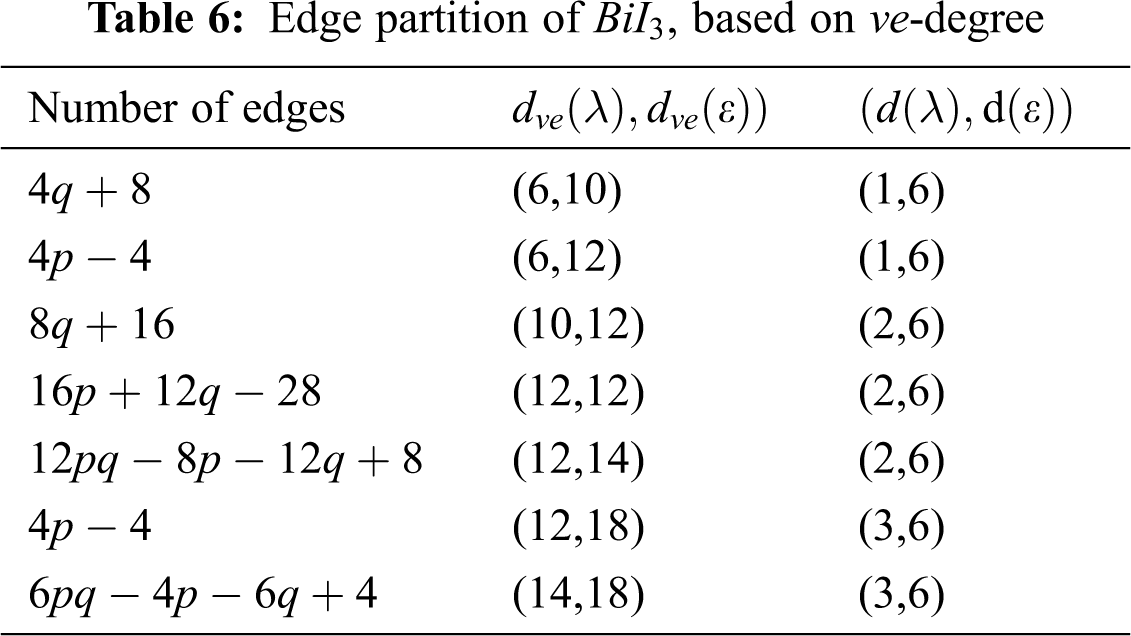
4.4 The second ve-degree Zagreb index

Using Tab. 6 we compute the second ve -degree Zagreb index:

4.5 ve-degree Randic Index

Using Tab. 6 we compute the ve -degree Randic index:

4.6 The ev-degree Randic Index

Using Tab. 4 we compute the ev -degree Randic index:

4.7 The ve-degree Atom-bond Connectivity Index

Using Tab. 6 we compute the ve -degree atom-bond connectivity index:

4.8 The ve-degree Geometric-arithmetic Index

Using Tab. 6 we compute the ve -degree geometric-arithmetic index:

4.9 The ve-degree Harmonic Index

Using Tab. 6 we compute the ve -degree harmonic index:

4.10 The ve-degree Sum-connectivity Index

Using Tab. 6 we compute the ve -degree sum-connectivity index:

5  The Graph of Lead Chloride

Lead chloride is a precious halide stone that usually occurs in mineral cotunnite. The structure of lead chloride is orthorhombic dipyramidal. The diagram of a solitary unit of lead chloride is obtained from bismuth tri-iodide by joining an extra vertex to only one 2-degree vertex of every one of the 4-cycles. Fig. 2 shows one unit of lead chloride.

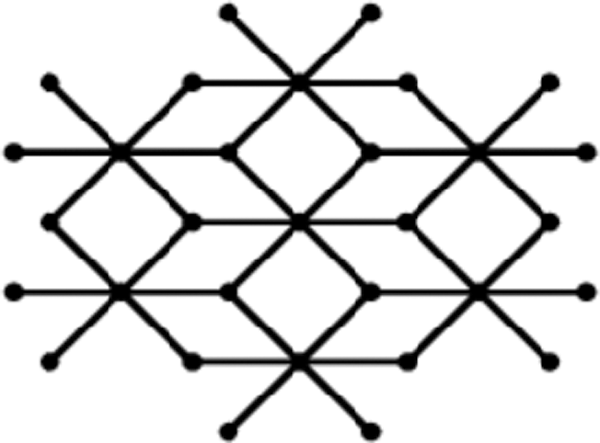
Figure 2: One unit of lead chloride

The unit cells of lead chloride can be arranged either linearly or in a sheet form. A linear arrangement with q unit cells is called q -lead chloride chain, p×q lead chloride sheet is obtained by arrangements of pq unit cells into p rows and q columns. A p×q lead chloride sheet throughout onward represented by LC . A sheet of LC contains 12pq+10p+7q+2 vertices and 24pq+12p+6q edges, which are shown in Tab. 7. The number of vertices corresponding to their degrees of LC are shown in Tab. 8 and the edge partition based on degree of end vertices of each edge is shown in the Tab. 9.

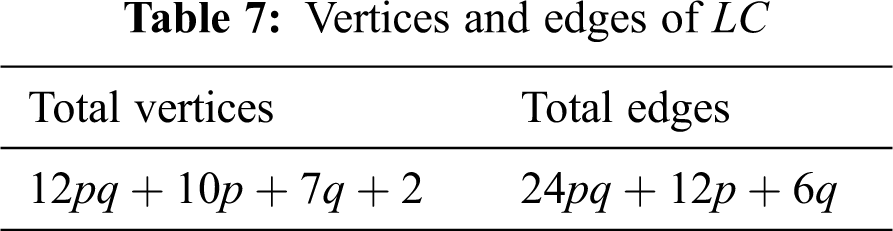
We partitioned the edges of LC , based on ev -degree in Tab. 10.

In Tab. 11, we partitioned the vertices of LC , based on ev -degree.

We partitioned the edge of LC with respect to ve -degrees.

Now we calculated ev -degree and ve -degree based indices such as Mev index, Mαve1 index, Mβve1 index, Mve2 index, Rve index, Rev index, ABCve index, GAve index, Hve index and χve index for LC .

5.1 ev-Degree Zagreb Index

By using ev -degree of LC from Tab. 10, we compute the ev -degree based Zagreb index:

5.2 The First ve-degree Zagreb α Index

Using Tab. 11 we compute the first ve -degree Zagreb α index:

5.3 The First ve-degree Zagreb β Index

Using Tab. 12 we compute the first ve -degree Zagreb β index:

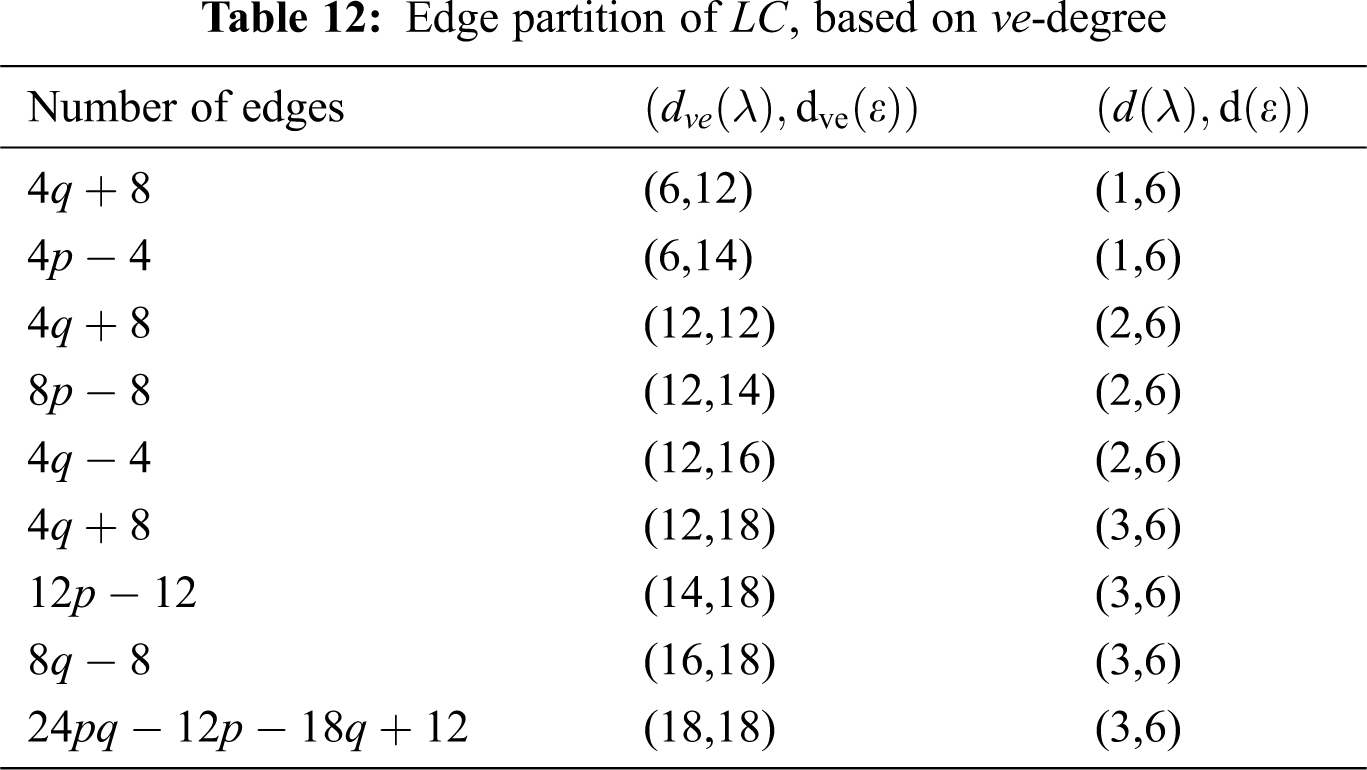
5.4 The second ve-degree Zagreb index

Using Tab. 12 we compute the second ve -degree Zagreb index:

5.5 ve-degree Randic Index

Using Tab. 12 we compute the ve -degree Randic index:

5.6 The ev-degree Randic Index

Using Tab. 10 we compute the ev -degree Randic index:

5.7 The ve-degree Atom-bond Connectivity Index

Using Tab. 12 we compute the ve -degree atom-bond connectivity index:

5.8 The ve-degree Geometric-arithmetic Index

Using Tab. 12 we compute the ve -degree geometric-arithmetic index:

5.9 The ve-degree Harmonic Index

Using Tab. 6 we compute the ve -degree harmonic index:

5.10 The ve-degree Sum-Connectivity Index

Using Tab. 12 we compute the ve -degree sum-connectivity index:

6  Graphical Representation and Discussion

Data or information visualization is becoming more popular due to ease of understanding and analysis in the modern scientific field. This section shows the graphical behavior of the above calculated topological descriptors for crystal networks (bismuth tri-iodide and lead chloride) is shown. It can be observed that by increasing the values of parameters values of topological descriptors are also increased. These graphical representations of ve -degree based topological descriptors are shown in Figs. 3–6.

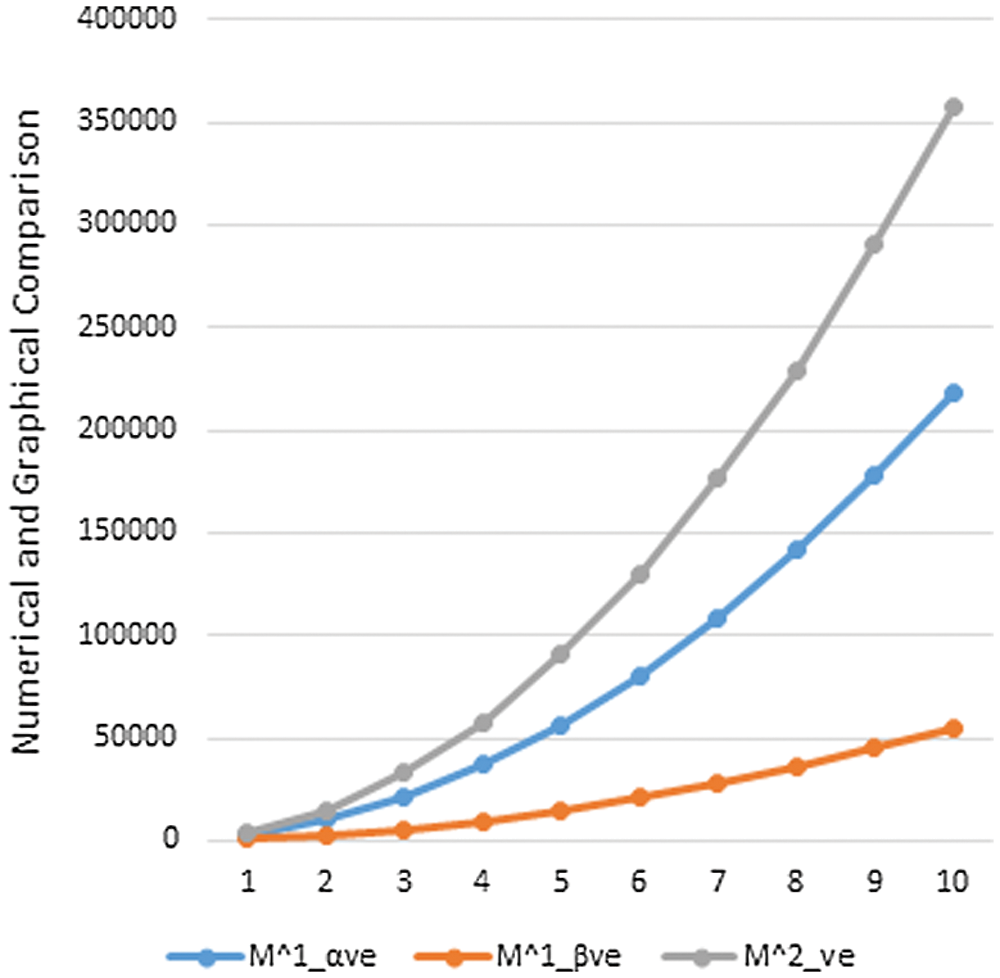
Figure 3: Graphical comparison of Mαve1,Mβve1,Mve2 for BiI3

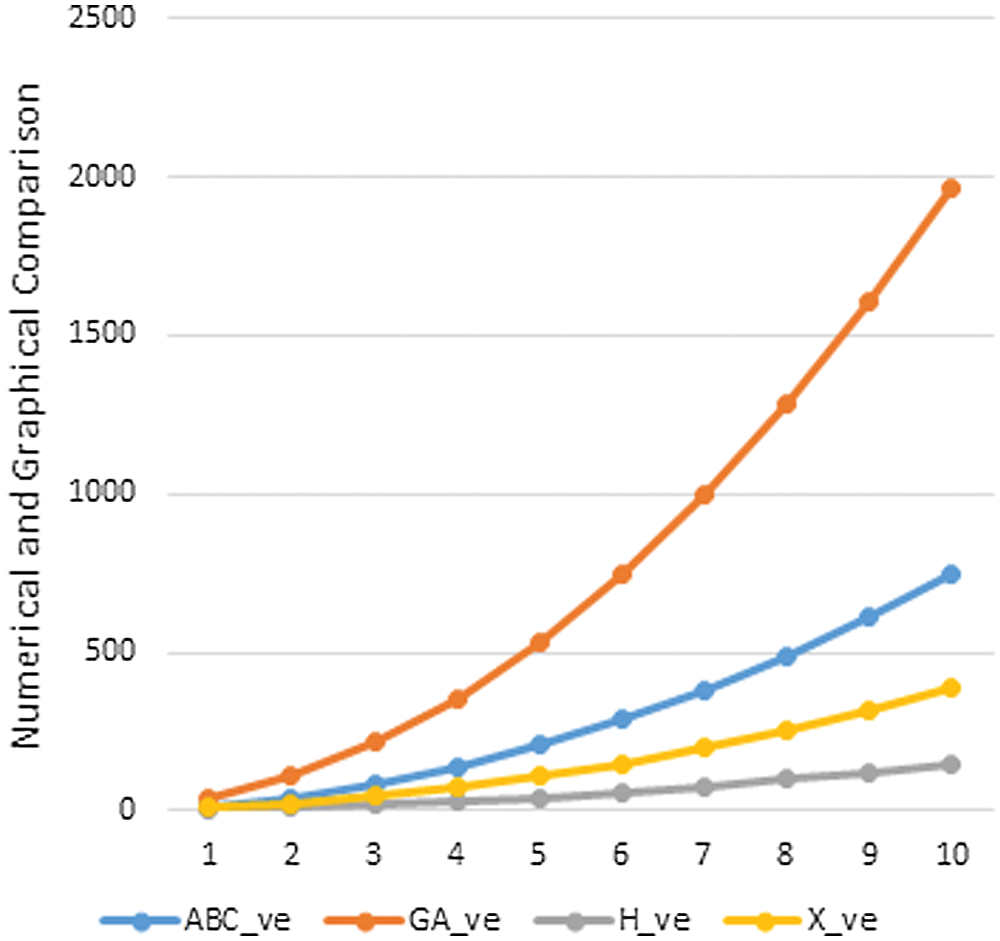
Figure 4: Graphical comparison of ABCve,GAve,Hve,χve for BiI3

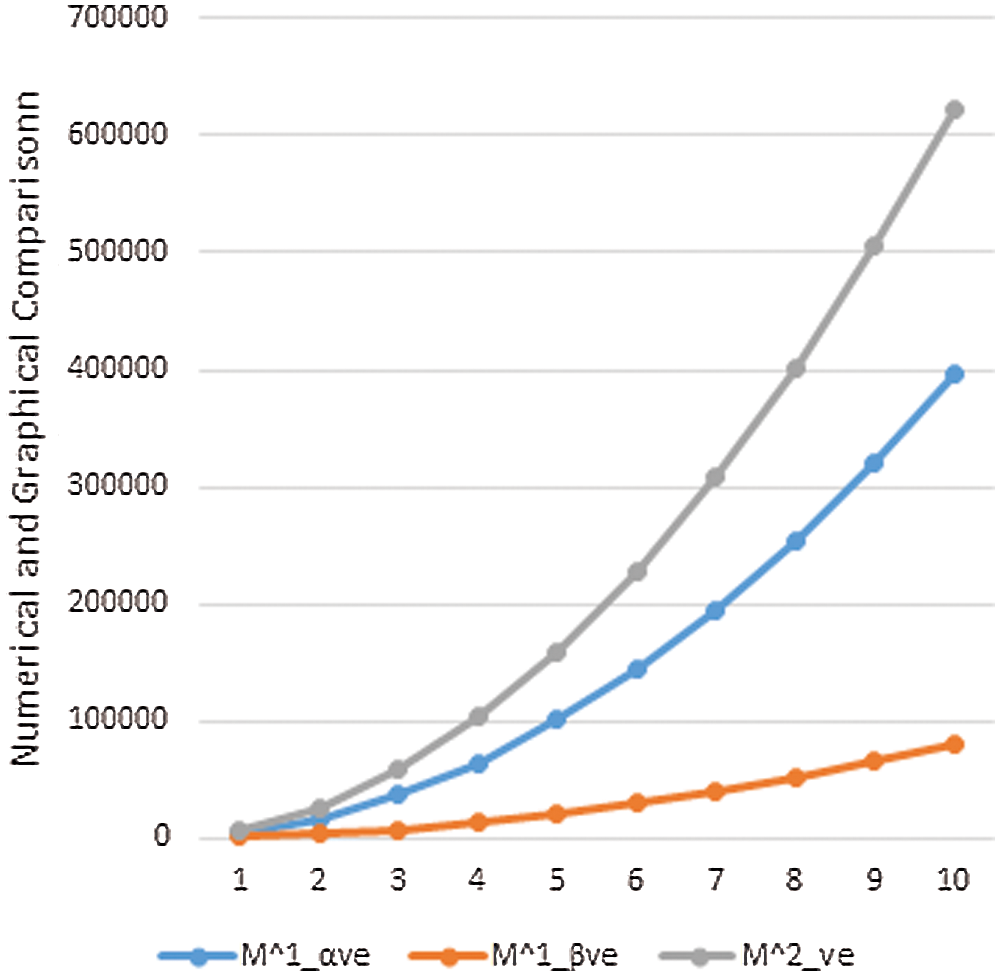
Figure 5: Graphical comparison of Mαve1,Mβve1,Mve2 for LC

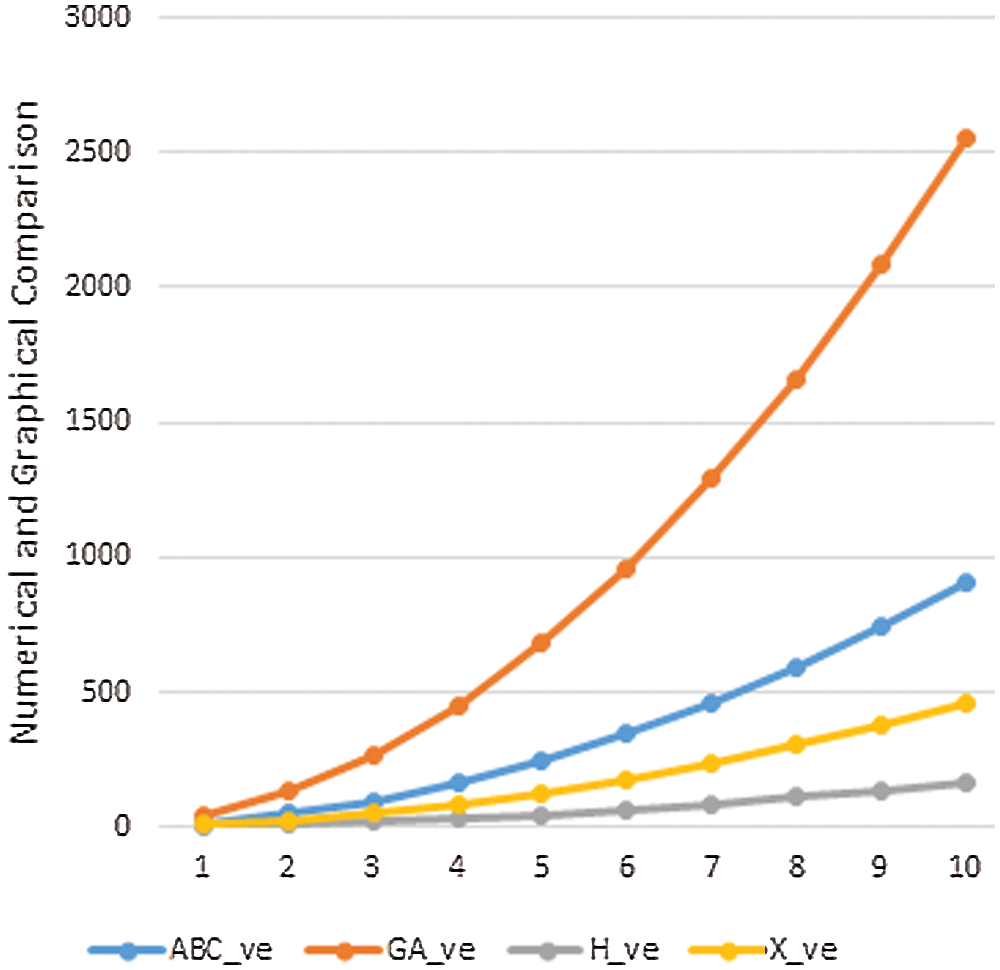
Figure 6: Graphical comparison of ABCve,GAve,Hve,χve for LC

In this section, we will discuss the graphical behavior of above calculated topological descriptors for crystal networks namely, bismuth tri-iodide and lead chloride. We observe that with the increase the values of parameters, the values of the defined topological descriptors are increased. The graphical representation of all above ve -degree based topological descriptors are shown in Figs. 3–6.

7  Conclusion

For numerical representaion of topologies for graphs or netwroks, topological descriptors are most useful invariants. That is why such investigations are widely used in computer applications and mathematical chemistry. Calculated results in this paper for ev -degree and ve -degree based topological indices for the crystal networks are shown pictorial in form of line chart from Figs. 3–6. In all the line charts it can be seen clearly that by increasing the values of p or q vlaues of topolgical decsriptors also incraese in a regular manner.

Funding Statement: This project was funded by the Deanship of Scientific Research (DSR) at King Abdulaziz University, Jeddah, under Grant No. RG-29-135-38.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  J. Jiang, Y. Zhao and O. M. Yaghi, “Covalent chemistry beyond molecules,” Journal of the American Chemical Society, vol. 138, no. 10, pp. 3255–3265, 2016. [Google Scholar]

 2.  Y. Liu, Y. Ma, Y. Zhao, X. Sun, F. Gándara et al., “Weaving of organic threads into crystalline covalent organic frameworks,” Science, vol. 351, no. 6271, pp. 365–369, 2016. [Google Scholar]

 3.  M. Karelson, Molecular Descriptors in QSAR/QSPR. New York: Wiley, 2000. [Google Scholar]

 4.  R. Todeschini and V. Consonni, Handbook of Molecular Descriptors. Weinheim: Wiley-VCH, 2000. [Google Scholar]

 5.  H. Wiener, “Structural determination of paraffin boiling points,” Journal of the American Chemical Society, vol. 69, pp. 17–20, 1947. [Google Scholar]

 6.  A. Ahmad, “On the degree based topological indices of benzene ring embedded in P-type-surface in 2D network,” Hacettepe Journal of Mathematics and Statistics, vol. 47, no. 1, pp. 9–18, 2018. [Google Scholar]

 7.  M. Bača, J. Horváthová, M. Mokrišová, A. Semaničová-Feňovčíková and A. Suhányiová, “On topological indices of carbon nanotube network,” Canadian Journal of Chemistry, vol. 93, no. 10, pp. 1157–1160, 2015. [Google Scholar]

 8.  M. Bača, J. Horváthová, M. Mokrišová and A. Suhányiová, “On topological indices of fullerenes,” Applied Mathematics and Computation, vol. 251, pp. 154–161, 2015. [Google Scholar]

 9.  A. Ahmad, “Computation of certain topological properties of honeycomb networks and graphene,” Discrete Mathematics, Algorithms and Applications (DMAA), vol. 9, no. 5, Article ID: 1750064, 2017. [Google Scholar]

10. M. Ajmal, W. Nazeer, M. Munir, S. M. Kang and Y. C. Kwun, “Some algebraic polynomials and topological indices of generalized prism and toroidal polyhex networks,” Symmetry, vol. 9, no. 1, pp. 5, 2017. [Google Scholar]

11. M. R. Farahani, W. Gao, M. R. R. Kanna, R. P. Kumar and J. B. Liu, “General Randić, sum-connectivity, hyper-Zagreb and harmonic indices, and harmonic polynomial of molecular graphs,” Advances in Physical Chemistry, Article no. 2315949, 2016. [Google Scholar]

12. M. Javaid, J. B. Liu, M. A. Rehman and S. Wang, “On the certain topological indices of Titania nanotube TiO2[m,n],” Zeitschrift Für Naturforschung A, vol. 72, no. 7, pp. 647–654, 2017. [Google Scholar]

13. M. Javaid, M. U. Rehman and J. Cao, “Topological indices of rhombus type silicate and oxide networks,” Canadian Journal of Chemistry, vol. 95, no. 2, pp. 134–143, 2017. [Google Scholar]

14. M. K. Siddiqui, M. Imran and A. Ahmad, “On Zagreb indices, Zagreb polynomials of some nanostar dendrimers,” Applied Mathematics and Computation, vol. 280, pp. 132–139, 2016. [Google Scholar]

15. T. Vetrík, “Degree-based topological indices of hexagonal nanotubes,” Journal of Applied Mathematics and Computing, vol. 58, no. 1, pp. 111–124, 2018. [Google Scholar]

16. G. Hong, Z. Gu, M. Javaid, M. H. Awais and M. K. Siddiqui, “Degree-based topological invariants of metal-organic networks,” IEEE Access, vol. 8, pp. 68288–68300, 2020. [Google Scholar]

17. A. Ahmad, “Topological properties of sodium chloride,” Scientific Bulletin-University Politehnica of Bucharest, Series B, vol. 82, no. 1, pp. 35–46, 2020. [Google Scholar]

18. A. Aslam, M. F. Nadeem, Z. Zahid, S. Zafar and W. Gao, “Computing certain topological indices of the line graphs of subdivision graphs of some rooted product graphs,” Mathematics, vol. 7, no. 5, 2019. [Google Scholar]

19. S. Imran, M. K. Siddiqui, M. Imran and M. F. Nadeem, “Computing topological indices and polynomials for line graphs,” Mathematics, vol. 6, no. 8, pp. article ID: 137, 2018. [Google Scholar]

20. Z. Ahmad, M. Naseem, M. K. Jamil, S. Wang and M. F. Nadeem, “Eccentric connectivity indices of titania nanotubes TiO2 [m;n],” Eurasian Chemical Communications, vol. 2, no. 6, pp. 712–721, 2020. [Google Scholar]

21. S. Hayat and M. Imran, “Computation of topological indices of certain networks,” Applied Mathematics and Computation, vol. 240, pp. 213–228, 2014. [Google Scholar]

22. N. A. Koam and A. Ahmad, “Polynomials of degree-based indices for three-dimensional mesh network,” Computers Materials and Continua, vol. 65, no. 2, pp. 1271–1282, 2020. [Google Scholar]

23. M. Chellali, T. W. Haynes, S. T. Hedetniemi and T. M. Lewis, “On ve-degrees and ev-degrees in graphs,” Discrete Mathematics, vol. 340, no. 2, pp. 31–38, 2017. [Google Scholar]

24. M. Cancan, “On ev-degree and ve-degree topological properties of Tickysim Spiking neural network,” Computational Intelligence and Neuroscience, vol. 8, pp. 11–31, 2019. [Google Scholar]

25. S. Ediz, “A new tool for QSPR researches: ev-degree Randic index,” Celal Bayar University Journal Science, vol. 13, no. 3, pp. 615–618, 2017. [Google Scholar]

26. B. Horoldagva, K. C. Das and T. A. Selenge, “On ve-degree and ev-degree of graphs,” Discrete Optimation, vol. 31, pp. 1–7, 2019. [Google Scholar]

27. S. Ediz, “On ve-degree molecular topological properties of silicate and oxygen networks,” International Journal Computational Science Mathematics, vol. 9, no. 1, pp. 1–12, 2018. [Google Scholar]

28. B. Sahin and S. Ediz, “On ev-degree and ve-degree topological indices,” Iranian Journal of Mathematical Chemistry, vol. 9, no. 4, pp. 263–277, 2018. [Google Scholar]

29. J. Zhang, M. K. Siddiqui, A. Rauf and M. Ishtiaq, “On ve-degree and ev-degree based topological properties of single walled titanium dioxide nanotube,” Journal of Cluster Science, 2020. [Google Scholar]

30. N. Zahra, M. Ibrahim and M. K. Siddiqui, “On topological indices for swapped networks modeled by optical transpose interconnection system,” IEEE Access, vol. 8, pp. 200091–200099, 2020. [Google Scholar]

31. K. Watanabe, T. Karasawa, T. Komatsu and Y. Kaifu, “Optical properties of extrinsic two-dimensional excitons in BiI3 single crystals,” Journal of the Physical Society of Japan, vol. 55, Article ID: 897, 1986. [Google Scholar]

32. R. W. G. Wyckoff, Crystal Structures, 2nd ed., vol. 2. New York, London, Sydney: John Wiley & Sons, Inc., 1964. [Google Scholar]

33. D. Nason and L. Keller, “The growth and crystallography of bismuth tri-iodide crystals grown by vapor transport,” Journal of Crystal Growth, vol. 156, no. 3, pp. 221–226, 1995. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.