Computer Systems Science & Engineering DOI:10.32604/csse.2022.017742
Article

An Adaptive Fuzzy Control Model for Multi-Joint Manipulators

Yanzan Han1,*, Huawen Zhang1, Zengfang Shi1 and Shuang Liang2

1Department of Mechanical and Electrical, Henan Polytechnic Institute, Nanyang, 473000, China
2University of Florence, Firenze, 50041, Italy
*Corresponding Author: Yanzan Han. Email: hanyanzan@163.com
Received: 09 February 2021; Accepted: 13 April 2021

Abstract: Multi-joint manipulator systems are subject to nonlinear influences such as frictional characteristics, random disturbances and load variations. To account for uncertain disturbances in the operation of manipulators, we propose an adaptive manipulator control method based on a multi-joint fuzzy system, in which the upper bound information of the fuzzy system is constant and the state variables of the manipulator control system are measurable. The control algorithm of the system is a MIMO (multi-input-multi-output) fuzzy system that can approximate system error by using a robust adaptive control law to eliminate the shadow caused by approximation error. It can ensure the stability of complex manipulator control systems and reduce the number of fuzzy rules required. Comparison of experimental and simulation data shows that the controller designed using this algorithm has highly-precise trajectory-tracking control and can control robotic systems with complex characteristics of non-linearity, coupling and uncertainty. Therefore, the proposed algorithm has good practical application prospects and promotes the development of complex control systems.

Keywords: Multi-joint manipulator; robust control law; adaptive fuzzy control; nonlinear MIMO system

1  Introduction

The intelligent manufacturing industry is developing rapidly in China. Manipulator technology has gradually become the most popular subject in the field of industrial control and has also become a focus of other fields. The core of a manipulator system is its control system. In recent years, great importance has been attached to the study of intelligent control. One goal is to control robotic arms with enough speed and precision that they can perform complex, demanding, monotonous and repetitive tasks normally performed by human beings. The requirements for robots are to achieve point-to-point tracking, general line tracking and complex curve tracking, as well as high-precision tracking of given paths. However, manipulator systems are subject to many influences, such as load variations, random disturbances and other external factors, as well as the uncertainty of their control model. These factors make it difficult to obtain accurate mathematical models of manipulator systems and greatly increase the difficulty of high-precision tracking control.

Xie et al. [1] designed an adaptive fuzzy control system for manipulator operation that eliminates the effects of approximation errors. Hui et al. [2] proposed an adaptive fuzzy control system based on state-observer, which can be used to deal with non-linear problems such as unmeasurable states, input saturation and actuator failure in complex systems. Fuzzy compensation and interference terms are included to enhance the robustness of the system and its resistance to interference. Wai et al. [3] proposed a fuzzy adaptive control algorithm based on an intelligent neural network, which can solve the problems of friction, external disturbance factors and parameter changes in an actual multi-link manipulator system. An on-line learning facility for manipulator control systems based on T-S fuzzy dynamic models of the dynamics of robotic systems has also been proposed. The fuzzy neural network is able to adjust the manipulator’s non-linear vector with a dynamic function to create a local fuzzy model of the control system; thereby deriving the control parameters of the manipulator’s fuzzy adaptive system. The results of this research show that the intelligent control algorithm can increase the robustness and stability of the system and facilitate its overall optimization. Li et al. [4] proposed a decentralized adaptive fuzzy control method based on an analysis of a multi-manipulator cooperative control system. A decentralized fuzzy control method with a combination of parameter adaptation and disturbance observer was established to compensate for the influences of dynamic uncertainty and external disturbances on system performance. Li et al. [5] proposed an adaptive fuzzy control system based on linear matrix inequality to suppress the effects of dynamic uncertainties, external disturbances and multiple random delays in the communication channel of a cooperative multi-robot system. Qiu et al. [6,7] designed a direct adaptive fuzzy control method based on a compound proportional differential control algorithm. This can optimise control hysteresis and compensate for the influences of cylinder length travel, gas compression and high-frequency modal vibration caused by non-linear factors in a pneumatic system. It improves the performance index of the multi-manipulator control system and ensures its stability and accuracy. Zhai et al. [8] proposed an adaptive fuzzy control method based on switching-error filtering to control errors in positional tracking and parameter estimation in a manipulator control system. Kumar et al. [9] designed a non-linear, adaptive, fractional-order-based, fuzzy PID controller that can effectively track the trajectory of a manipulator. Fateh et al. [10] proposed a discrete adaptive fuzzy control system to analyse influences on the progressive tracking control of a manipulator and thereby improve it. Sreekumar et al. [11] proposed an adaptive fuzzy control method to address the complexity and fuzziness of robotic systems. Su et al. [12] designed a discrete, indirect, adaptive fuzzy controller to eliminate uncertainties in a manipulator system. By using robust control terms, the approximation and discrete errors of the system were greatly reduced and asymptotic tracking of target trajectories was realized.

Because manipulators are prone to many uncertain disturbance factors and friction between their joints, it is difficult for conventional control methods to accurately track their trajectories. Fuzzy control is based on the operating experience of controlled equipment [13–15]. It does not require knowledge of the internal mechanism or mathematical model of the controlled object. The design of an adaptive fuzzy controller is independent of the mathematical model of the controlled device and is highly fault-tolerant in solving complex non-linear problems during the control process. An adaptive fuzzy control algorithm can uniformly approximate any non-linear function in the input space.

In this study, an adaptive fuzzy control algorithm is introduced into a multi-input and multi-output (MIMO) nonlinear system, which is used to compensate for uncertain disturbances in the manipulator control system to achieve accurate positional and speed tracking. To reduce approximation error and ensure the stability of the system, a robust term is added to the control algorithm based on Lyapunov stability theory. The proposed control algorithm is used to compensate for various uncertainty errors of the manipulator. Simulation results show that the robust adaptive control algorithm can eliminate the influences of approximation errors and improve the accuracy of trajectory tracking.

2  Basic Problem Description of Manipulators

It is assumed that a MIMO manipulator control system can be described in the following form.

{O1(a1)=α1(x)+∑j=1nβ1j(x)uj⋮O1(am)=αm(x)+∑j=1nβmj(x)uj (1)

The state variables x=[o1,o˙1,...,o1(a1−1),...,om,...,om(am−1)]T of the manipulator control system can be measured; u=[u1,...,um]T is the multi-joint input variable, o=[o1,...,om]T is the multi-joint output variable, and αi(x) and βij(x) are smooth unknown non-linear functions, where i=1,2,...,m;j=1,2,...,n .

Suppose that:

o(a)=[o1(a1),...,om(am)]T (2)

A(x)=[α1(x),...,αm(x)]T (3)

B(x)=[β11(x)⋯β1m(x)⋮⋱⋮βm1(x)⋮βmm(x)] (4)

Eq. (1) describing the MIMO manipulator nonlinear system can be changed into the following form:

o(a)=A(x)+B(x)u (5)

The control law u(t) of the manipulator control system can be designed such that the system variables of the closed-loop manipulator control system will be constrained so that the manipulator output will track a desired trajectory odt(t)=[odt1(t),odt2(t)...,odtp(t)]T .

Assumption 1: If the nonlinear function B(x) is a positive definite matrix and the real numbers are always greater than 0 ( σ0>0 ), then the manipulator control system will satisfy B(x)≥σ0Ip (where Ip is the unit matrix).

Assumption 2: The expected trajectory of the manipulator control system odti(t) ( i=1,...,p ) is bounded, its corresponding function has an n-order derivative, and all the derivatives of each order are bounded.

If Assumption 1 can guarantee the existence of the B(x) inverse matrix, then Eq. (5) can be expressed in the form of a linearised expression for static-state feedback. Although the assumption is strictly limited to the MIMO manipulator control system, the robot system needs to satisfy the assumptions.

The trajectory tracking error of the manipulator control system can be expressed by the following formula:

{te1(t)=odt1(t)−o1(t)⋮tem(t)=odtm(t)−om(t) (6)

The filter tracking error function of the manipulator control system can be defined using the following expression.

{κ1(t)=(ddt+γ1)(a1−1)te1(t),γ1>0⋮κm(t)=(ddt+γm)(am−1)tem(t),γm>0 (7)

Through analysis and deduction from Eq. (7), we can deduce that if the filter tracking error function of the manipulator control system approaches 0 ( κi→0 ), the trajectory tracking error will approach 0 ( tei→0 ), i=1,2,...,m , then the control objective of the manipulator control system will be changed to κi→0(i=1,2,...,m) .

According to the dynamic characteristics of the manipulator and Newton’s binomial theorem, a filter tracking error function formula can be obtained:

κi(t)=(ddt+γi)(ai−1)ei(t)=∑j=0ai−1(ai−1)!(ai−1−j)!j!(ddt)jtei(t)γiai−1−j=∑j=1ai(ai−1)!(ai−j)!(j−1)!(ddt)j−1tei(t)γiai−j (8)

Then, the differential equation of the filtering tracking error function can be obtained:

κ˙i(t)=odi(ri)−αi(x)−∑j=1iβij(x)uj+∑j=1ai−1(ai−1)!(ai−j)!(j−1)!tei(j)(t)γiai−j (9)

Hence, we can obtain the following formula:

{κ˙1=χ1−α1(x)−∑j=1mβ1j(x)uj⋮κ˙m=χm−αm(x)−∑j=1mβpj(x)uj (10)

In which,

{χ1=od1(a1)+φ1,a1−1te1(a1−1)+⋯+φ1,1te˙1⋮χm=odm(am)+φ1,am−1te1(am−1)+⋯+φm,mte˙m (11)

φi,j=(ai−1)!(ai−j)!(j−1)!γiai−j,i=1,2,...,m,j=1,2,...,n (12)

If the vector of the functions of the filter tracking error in the manipulator control system can be described as a formulation for κ(t)=[κ1(t),κ2(t),⋯,κm(t)]T , and the vector of the manipulator control system χ can be expressed as χ=[χ1(t)⋯χm(t)]T , then Eq. (1) can be changed to the following form:

κ˙=χ(t)−α(x)−β(x)u(t) (13)

If components α(x) and β(x) of the non-linear functions are given, the linear manipulator control can be described by:

u=β−1(x)(χ−α(x)+K0κ) (14)

In which K0=diag[k01,...,k0m] , k0i>0 , i=1,...,m .

By substituting Eq. (17) into Eq. (10), we can obtain:

κ˙(t)=−K0κ(t) (15)

κ˙i(t)=−K0iκi(t) (16)

Namely, by solving the differential equation, the following results can be obtained:

κi(t)=−κi(0)e−K0it (17)

When the time t tends to infinity ( t→∝ ), κi(t)→0 , the trajectory tracking error tei(t) and its ai−1 order derivatives will converge to 0.

Therefore, when αi(x) and βij(x) are known, it is easy to obtain the control law (17). However, in the actual system, the non-linear functions αi(x) and βij(x) are unknown, so it cannot design the control Eq. (17). Instead, the non-linear functions αi(x) and βij(x) of the manipulator control system can be used in the fuzzy systems to obtain an approximation.

3  Fuzzy System Design of a Multi-Joint Manipulator

Suppose that a fuzzy control system involves a mapping from set H⊆RN to set R . The l article fuzzy rule may be described in the following form [16–18]:

x=[x1,x2,...,xn]T∈H is the control input variable of the fuzzy manipulator system, and y∈H⊂R is the control output variable.

A singleton fuzzifier, a product inference engine, and a central mean defuzzifier are often used to design fuzzy systems. The output variable of the fuzzy control system can be represented as follows:

o(x)=∑l=1Mo¯l(Πi=1n⁡μαil(xi))∑l=1M(Πi=1n⁡μαil(xi)) (18)

In which o¯l is the value of the corresponding point whose maximum membership degree is μcl .

Then, Eq. (18) can be expressed as:

o(x)=ξT(x)ϑ (19)

In which ϑ=[o1,...,oM]T is the control parameter vector of the fuzzy manipulator system and ξ(x)=[ξ1(x),...,ξM(x)]T is the system regression vector, in which:

ξ(x)=(Πi=1n⁡μαil(xi))∑l=1M(Πi=1n⁡μαil(xi)) (20)

Then, the fuzzy system is used to approach the nonlinear functions of the unknown αi(x) and βij(x) components, and an adaptive control law is designed.

4  Design of an Adaptive Fuzzy Control System Based on a Known Upper Bound

4.1 Fuzzy Controller Design

The fuzzy system used to approach the unknown functions of the nonlinear αi(x) and βij(x) components are:

αi(x,ϑfi)=ξfiT(x)ϑfi,i=1,...,m (21)

β^ij(x,ϑgij)=ξgijT(x)ϑgiji=1,...,m (22)

In the above formulas, ξfi(x) and ξgij(x) are the manipulator vectors of fuzzy basis functions, and ϑαi and ϑβij are the vectors of adaptive adjustment parameters.

ϑαi∗ and ϑβij∗ are the optimal approximation vector forms of the system parameters ϑαi and ϑβij , while the minimum approximation error vectors of the fuzzy system are ξαi(x) and ξβij(x) . These parameters can be defined in the following forms:

ϑαi∗=arg⁡minϑαi⁡[supx∈Dx⁡|βi(x)−α^i(x,ϑαi)|] (23)

ϑβij∗=arg⁡minϑβij⁡[supx∈Dx⁡|βij(x)−β^ij(x,ϑβij)|] (24)

ϑ~αi=ϑαi∗−ϑαi,ϑ~βij=ϑβij∗−ϑβij (25)

ξαi(x)=αi(x)−α^i(x,ϑαi∗) (26)

ξβij(x)=βij(x)−β^ij(x,ϑβij∗) (27)

Suppose that the compact set Dx is large enough to ensure that for all x∈Dx , the minimum approximation error is bounded; that is, the absolute value of the vector of the fuzzy basis function is less than or equal to the average value of the vector of the fuzzy basis function. ξ¯αi(x) and ξ¯βij(x) are the known constants.

By using A^(x,ϑα) and B^(x,ϑβ) instead of A(x) and B(x) in control Eq. (10), the control law can be obtained:

uc=B^−1(x,ϑβ)(χ−A^(x,ϑα)+K0κ) (28)

The nonsingularity of B^(x,ϑβ) cannot be guaranteed by the online estimation of ϑβ . For this reason, the generalized inverse variable B^T(x,ϑβ)[ε0Ip+B^(x,ϑβ)B^T(x,ϑβ)]−1 takes the place of B^−1(x,ϑβ) , so we can obtain the control law:

uc=B^T(x,ϑβ)[(ξ0Ip+B^(x,ϑβ))B^T(x,ϑα)]−1(χ−A^(x,ϑα)+K0κ) (29)

where ξ0 represents a positive real number that can be arbitrarily small and Im represents an identity matrix.

4.2 Robust Adaptive Control Law Design

To minimize the error of the fuzzy manipulator control system, a robust term uc is included and its control law is:

u=uc+ur (30)

ur=κ|κT|(ξ¯α+ξ¯β|uc|+|u0|)σ0‖s‖2+δ (31)

u0=ξ0[ξ0Im+B^(x,ϑβ)B^T(x,θβ)]−1(χ−A^(x,ϑα)+K0κ) (32)

where δ is a time-varying parameter.

The adaptive control law of the multi-joint manipulator control system is:

ϑ˙αi=−ηαiξαiκi (33)

ϑ˙βij=−ηβijεβijκiucj (34)

δ˙=−η0|κT|(ξ¯α+ξ¯β|uc|+|u0|)σ0‖κ‖2+δ (35)

Theorem 1. When system (1) satisfies the assumptions, the control Eqs. (30)–(32) and adaptive Eqs. (33)–(35) are used to ensure that the system has the following characteristics:

(1) All multi-joint manipulator signals of the closed-loop control system are bounded;

(2) The trajectory tracking error and its derivatives of all orders converge uniformly to 0; that is, the tracking error of each trajectory converges to 0 as the system time tends to infinity.

By combining with Eq. (35), Eq. (14) can be transformed to:

κ˙=χ−A(x)−(B(x)−B^(x,θβ))uc−B^(x,θβ)uc+ξβ(x)u (36)

Combining this with Eq. (29), we can obtain the expression:

χ−B^(x,ϑβ)uc=χ−B^(x,ϑβ)B^T(x,ϑβ)[ξ0Im+B^(x,ϑβ)B^T(x,ϑβ)]−1(χ−A^(x,ϑα)+K0κ)=A^(x,ϑα)−K0κ+uc (37)

If Eq. (34) is substituted into Eq. (33), we can obtain the formula:

κTκ˙=−κTK0κ−∑i=1mεαiT(x)ϑ~αiγi−∑i=1m∑j=1nεβijT(x)ϑ~βijκiucj−κTB(x)ur+κTu0−κTξα(x)−κTξβ(x)uc (38)

In this study, the Lyapunov function of the control system can be defined in the following form:

X=12κTκ+12∑i=1m1ηαiϑ~αiTϑ~αi+12∑i=1m∑j=1n1ηβijϑ~βijTϑ~βij+12η0δ2 (39)

So,

X˙=κTκ+∑i=1m1ηαiϑ~αiTϑ˙αi+∑i=1m∑j=1n1ηβijϑ~βijTϑ˙βij+1η0δδ˙ (40)

Substituting Eq. (40) into the above formula, we obtain:

X˙=−κTK0κ+X˙1+X˙2 (41)

In which,

X˙1=−∑i=1pϑ˙αiT(εαi(x)κi+1ηfiϑ˙αi)−∑i=m∑j=1nϑβijT(εβij(x)κiucj+1ηβijϑ˙βij) (42)

X˙2=−κTG(x)ur+κTu0−κTξf(x)−κTξg(x)uc+1η0δδ˙ (43)

By substituting Eqs. (35) and (36) into Eq. (40), we can obtain X˙1=0 .

From Hypothesis 1 and Eq. (31), it can be deduced that κTBs≥σ0‖κ‖2 :

κTBur=κTBκ|κT|(ξ¯β+ξ¯β|uc|+|u0|)σ0‖κ‖2+δ≥σ0‖κ‖2|κT|(ξ¯α+ξ¯β|uc|+|u0|)1σ0‖κ‖2+δ=(σ0‖κ‖2+δ−δ)|κT|(ξ¯α+ξ¯β|uc|+|u0|)1σ0‖κ‖2+δ=|κT|(ξ¯α+ξ¯β|uc|+|u0|)−δ|κT|(ξ¯β+ξ¯β|uc|+|u0|)σ0‖κ‖2+δ (44)

By derivation from Eq. (44), we can obtain:

X˙2≤−κTX(x)ur+|κT|(ξ¯α+ξ¯β|uc|+|u0|)+1η0δδ˙ (45)

Substituting Eq. (45) into the above formula, we can get:

X˙2≤δ|κT|(ξ¯α+ξ¯β|uc|+|u0|)σ0‖κ‖2+δ+1η0δδ˙ (46)

Substituting Eq. (32) into the above formula, we can get X˙2≤0 .

Thus,

X˙≤−κTK0κ=−∑i=1mk0iκi2 (47)

It is concluded that if the differential of the Lyapunov function of the control system X˙ is negative semidefinite ( X∈L∞ ) and the Lyapunov function X(t) is not a monotonically-increasing function and is bounded, then the three signals of κi(t) , ϑ~αi(t) and ϑ~βij(t) will be bounded. So, the variables or parameters of ϑ~αi(t) , ϑ~βij(t) , x , u and κ˙i(t) are bounded.

4.3 Simulation of a Multi-Joint Manipulator Based on Fuzzy Adaptive Control Algorithms

For a rigid manipulator with two joints in plane motion, the dynamic equation is as follows:

[M11M12M21M22][q¨1q¨2]+[−vq˙2−v(q˙1+q˙2)vq˙10][q˙1q˙2]=[u1u2] (48)

The above formula can be transformed into:

[q¨1q¨2]=[a1+2a3cos⁡q2+2a4cos⁡q2a2+2a3cos⁡q2+2a4cos⁡q2a2+2a3cos⁡q2+2a4cos⁡q2a2]−1{[u1u2]−[−vq˙2−v(q˙1+q˙2)vq˙10][q˙1q˙2]} (49)

In which,

v=a3sin⁡q2−a4cos⁡q2 (50)

{a1=I1+m1lc12+Ie+melce2+mel12a2=Ie+melce2a3=mel1lcecos⁡δea4=mel1lcesin⁡δe (51)

The system parameters are m1=2 , me=3 , l1=1.2 , lc1=0.8 , lce=0.75 , I1=0.11 , Ie=0.23 , δe=π6 .

F(x)=[f1(x)f2(x)]=−M−1[−vq˙2−v(q˙1+q˙2)vq˙10][q˙1q˙2] (52)

G(x)=[g11g12g21g22]=M−1=[M11M12M21M22]−1 (53)

Then, the controlled object is:

o¨=F(x)+G(x)u (54)

The control objective of the designed method is that the system outputs q1 and q2 can track the desired trajectories od1=sin⁡t and od2=sin⁡t .

We define the membership function as:

{μFi1(xi)=exp⁡(−12(xi+1.250.5)2)μFi2(xi)=exp⁡(−12(xi0.5)2)μFi3=exp⁡(−12(xi−1.250.5)2)i=1,2,3,4, (55)

The design parameters are λ1=30 , λ2=30 , K0=5I2 , ε0=0.1 , ηfi=0.5 , ηgij=0.5 , η0=0.001 , δ(0)=0 , ξ¯g=[0.20.20.20.2] , ξ¯f=[0.20.2]T .

Simulation of the control object using the proposed robust adaptive fuzzy control algorithm leads to the following position- and element-tracking curves.

Figs. 1 and 2 show the position- and velocity-tracking curves of joints 1 and 2, respectively, without disturbance and robust terms. It is clear that the robust adaptive fuzzy control system based on known information tracks very well. The trajectory-tracking curves almost coincide with the desired trajectory curves, and the system error is close to zero.

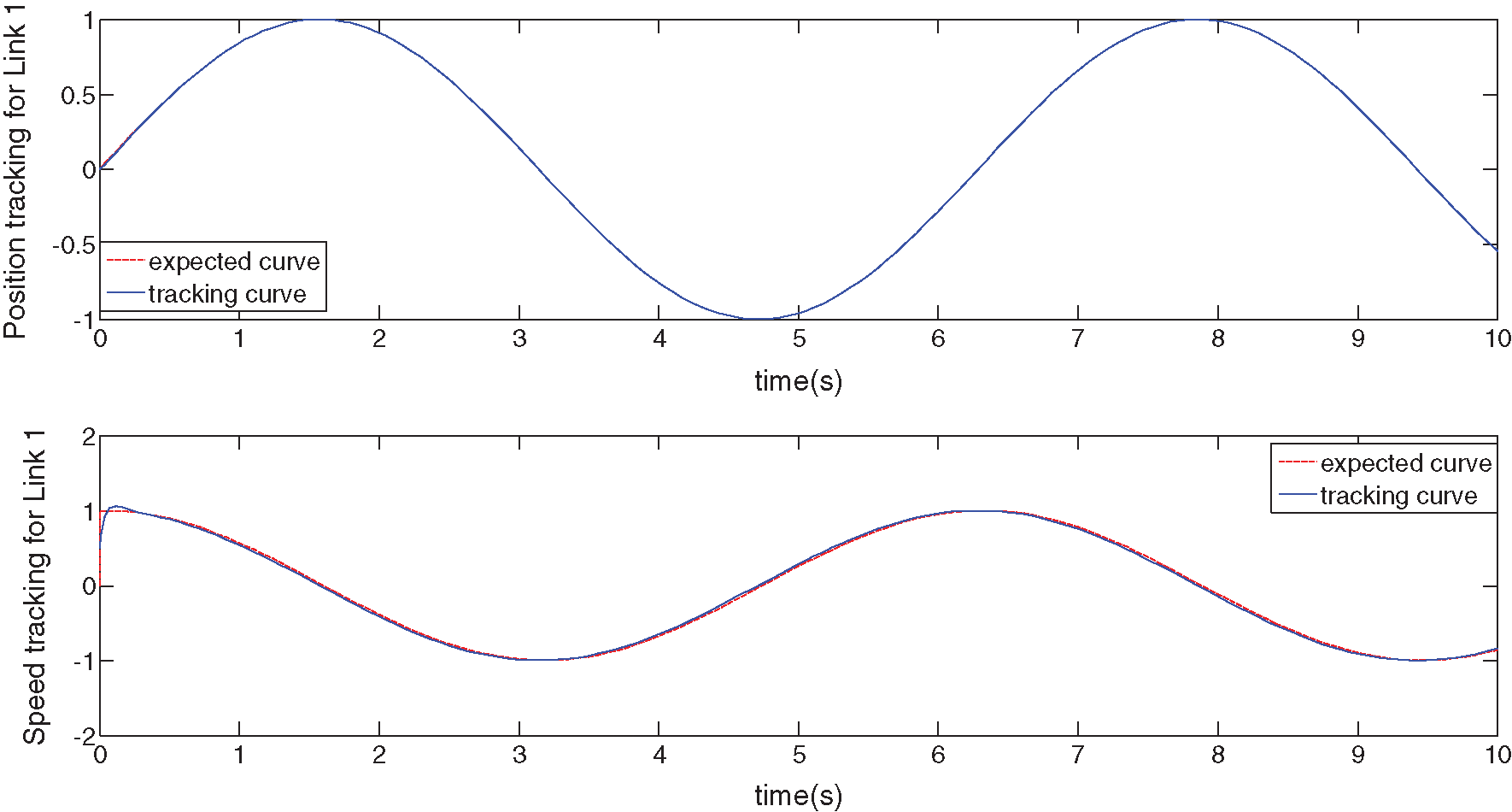
Figure 1: Position- and velocity-tracking curves of joint 1 (no disturbance and no robust term)

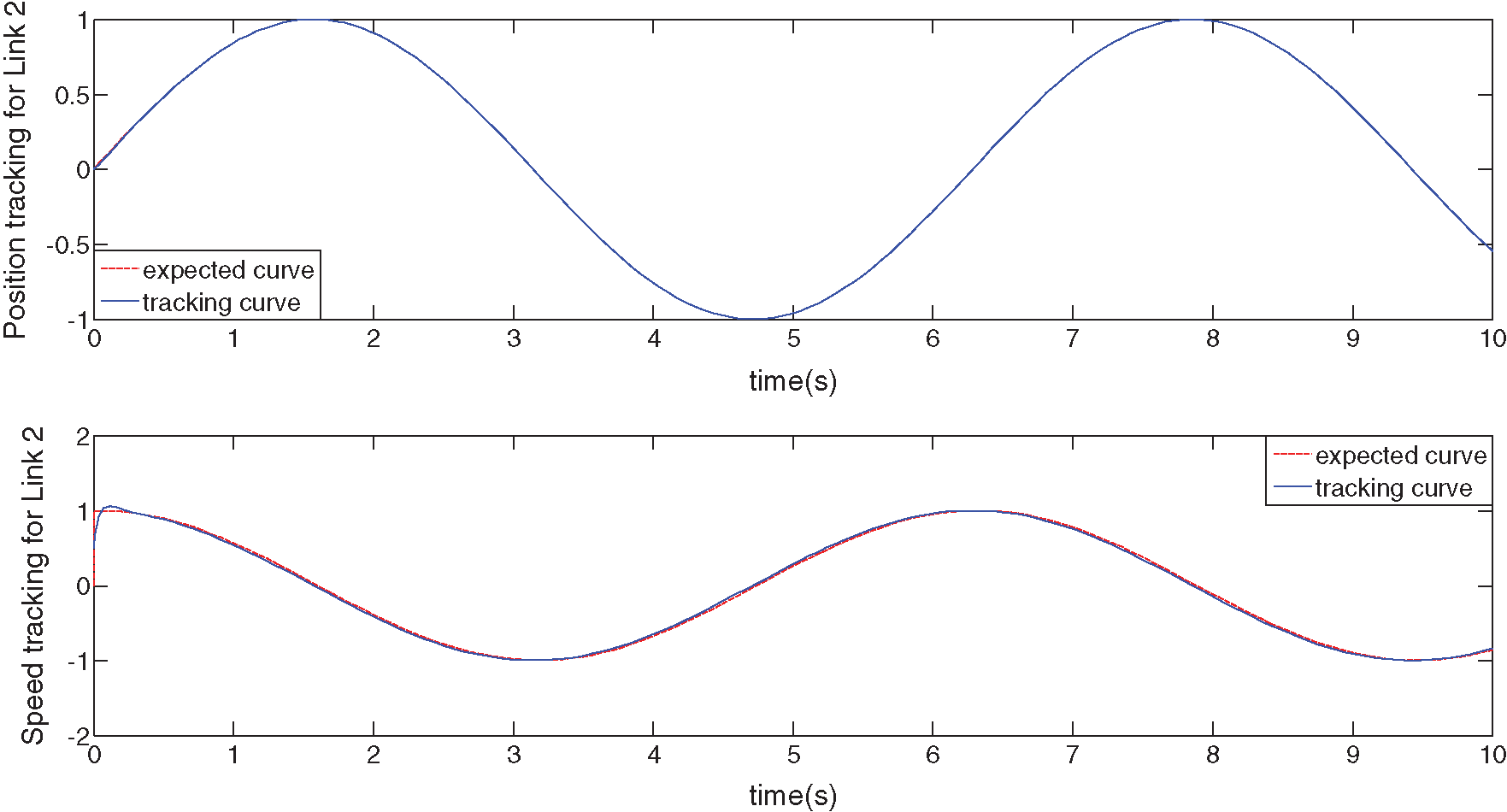
Figure 2: Position- and velocity-tracking curves of Joint 2 (no disturbance and no robust term)

Figs. 4 and 5 show the position- and velocity-tracking curves for joints 1 and 2 with perturbation and robustness terms. It can be seen that both show slight errors at the beginning, after which the tracking performance is good. The robust adaptive fuzzy control method can be used to quickly eliminate disturbances and achieve system stability and robustness [18–24]. By comparing Figs. 3 and 6, it can be seen that the control input in Fig. 3 tracks well in the absence of disturbances and robust terms, but there are some errors throughout the motion that are detrimental to its accuracy. The system in Fig. 6 has disturbances, but considering the inclusion of the robust term, the system error is slight in the initial stage and 0 after stabilisation. Hence, the proposed control algorithm can quickly eliminate disturbances and achieve stable control of the system.

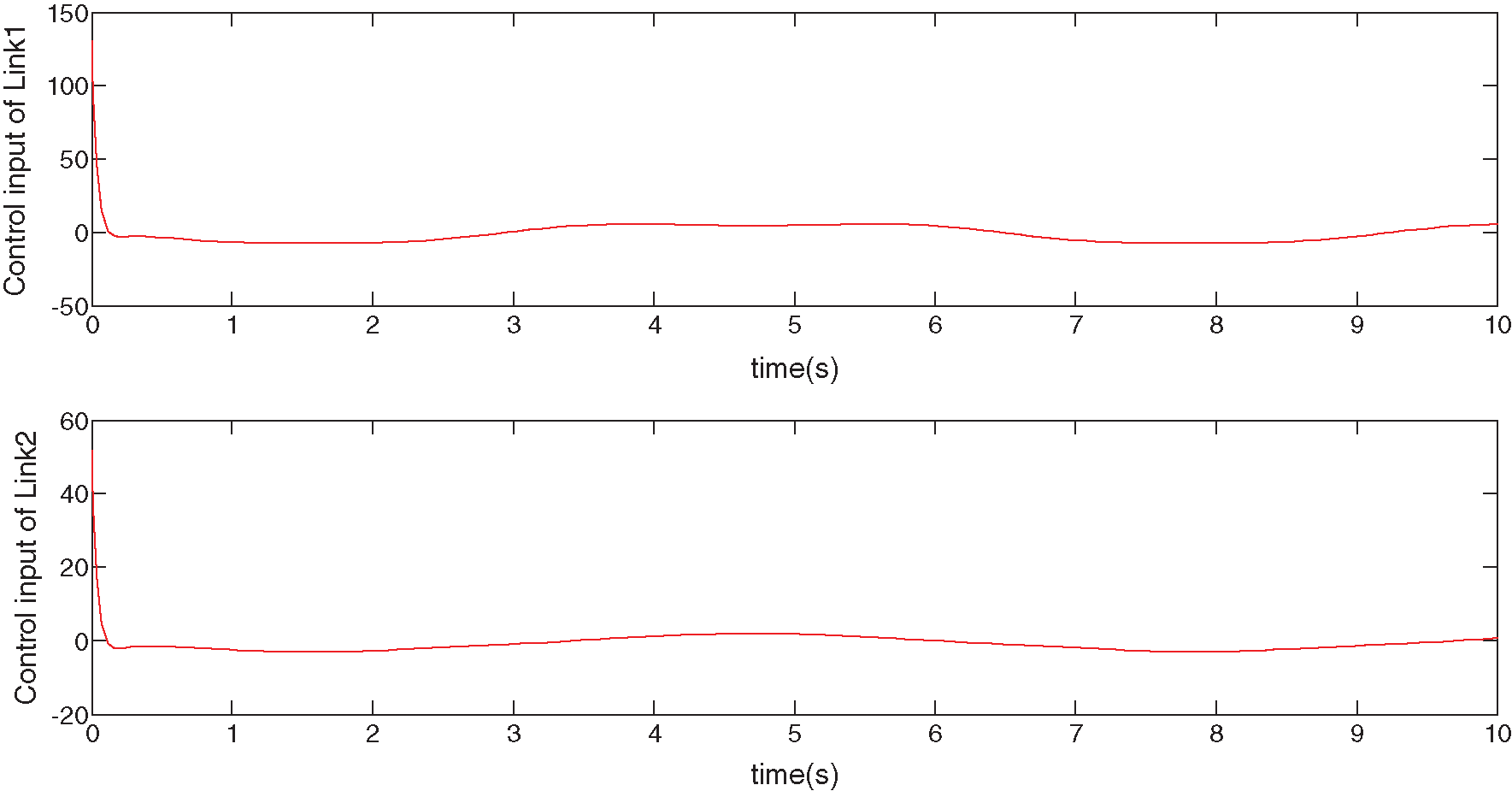
Figure 3: Control input curves of joints 1 and 2 (no disturbance and no robust term)

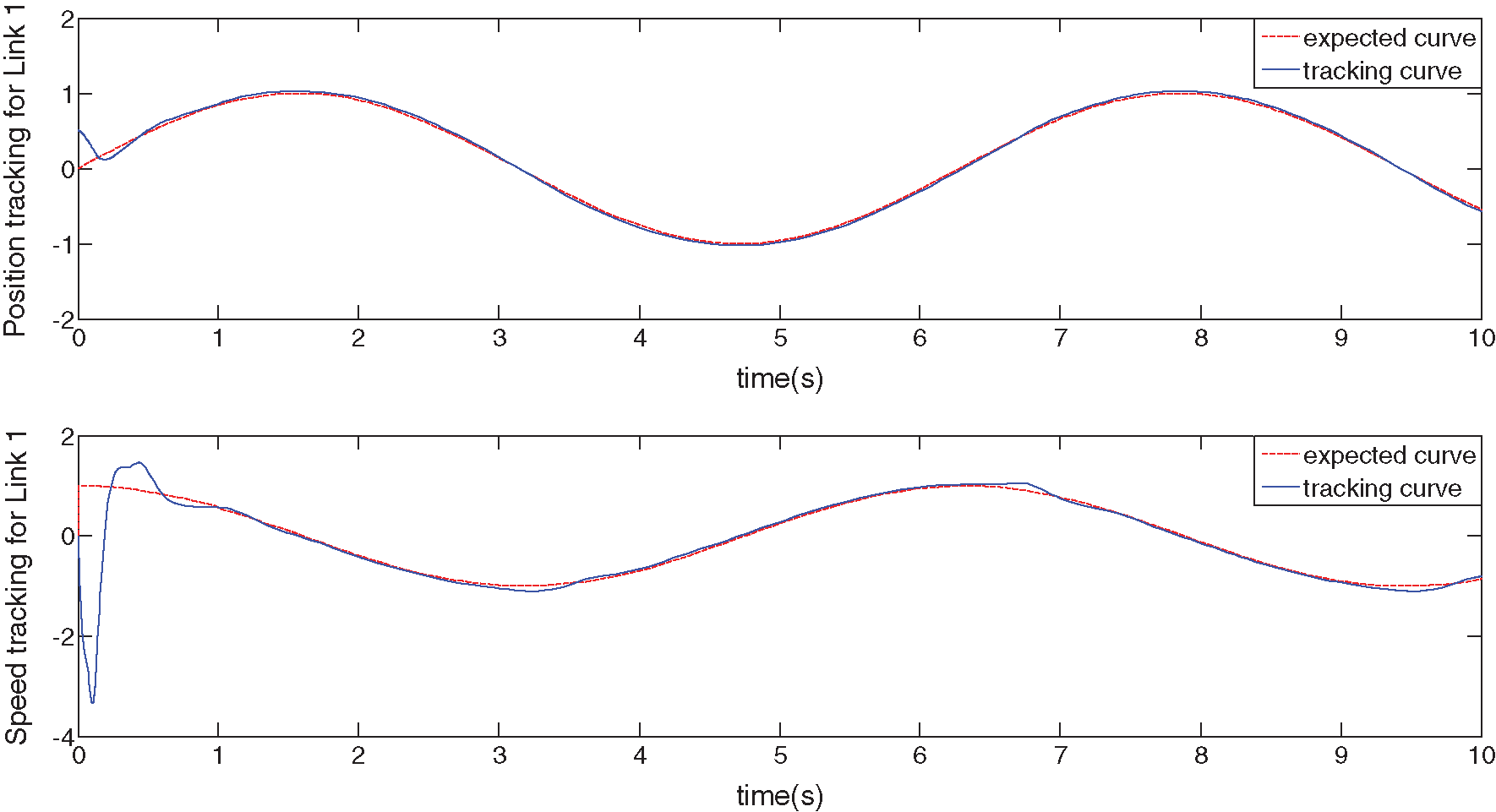
Figure 4: Position- and velocity-tracking curves of joint 1 (including disturbance and robust terms)

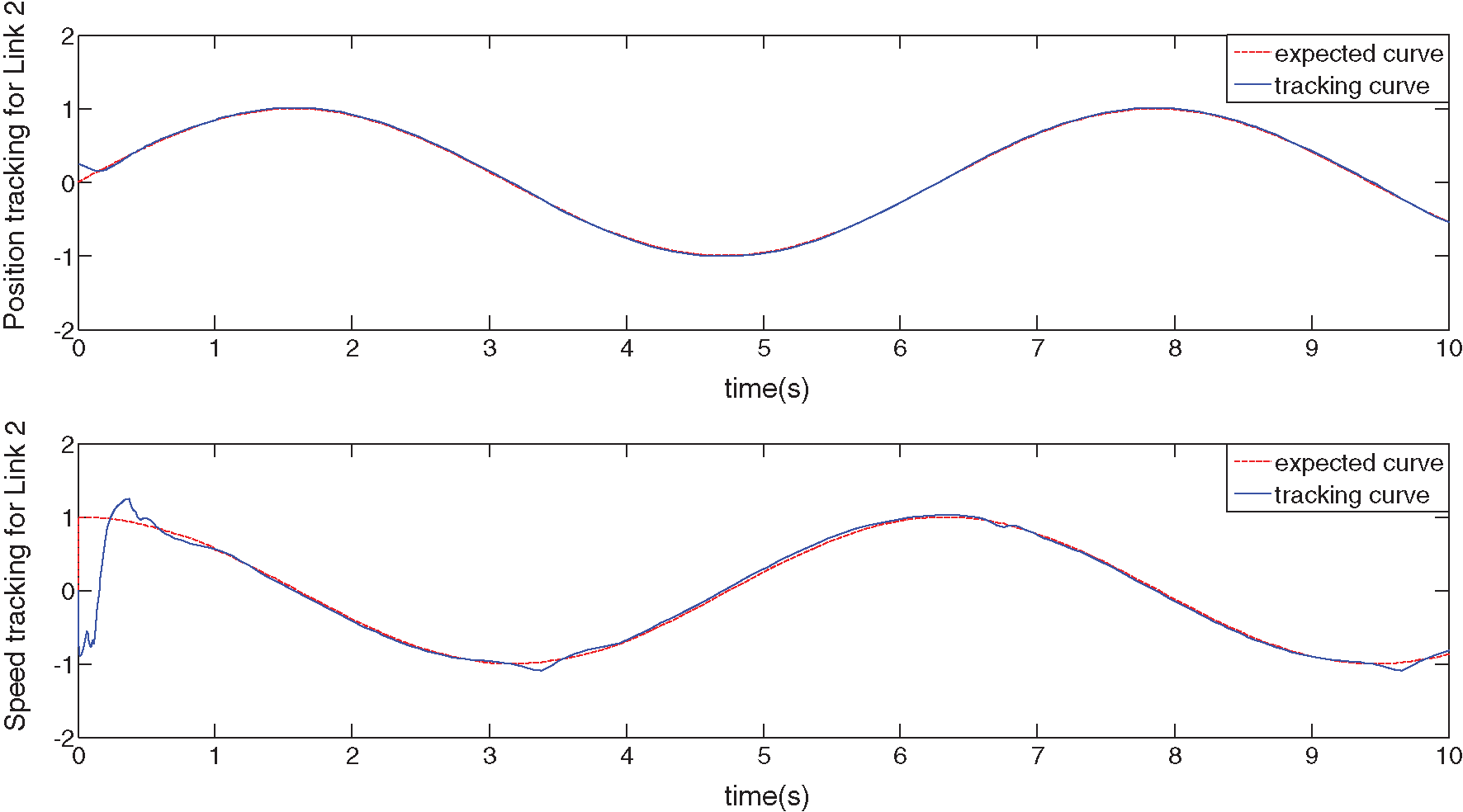
Figure 5: Position- and velocity-tracking curves of joint 2 (including disturbance and robust terms)

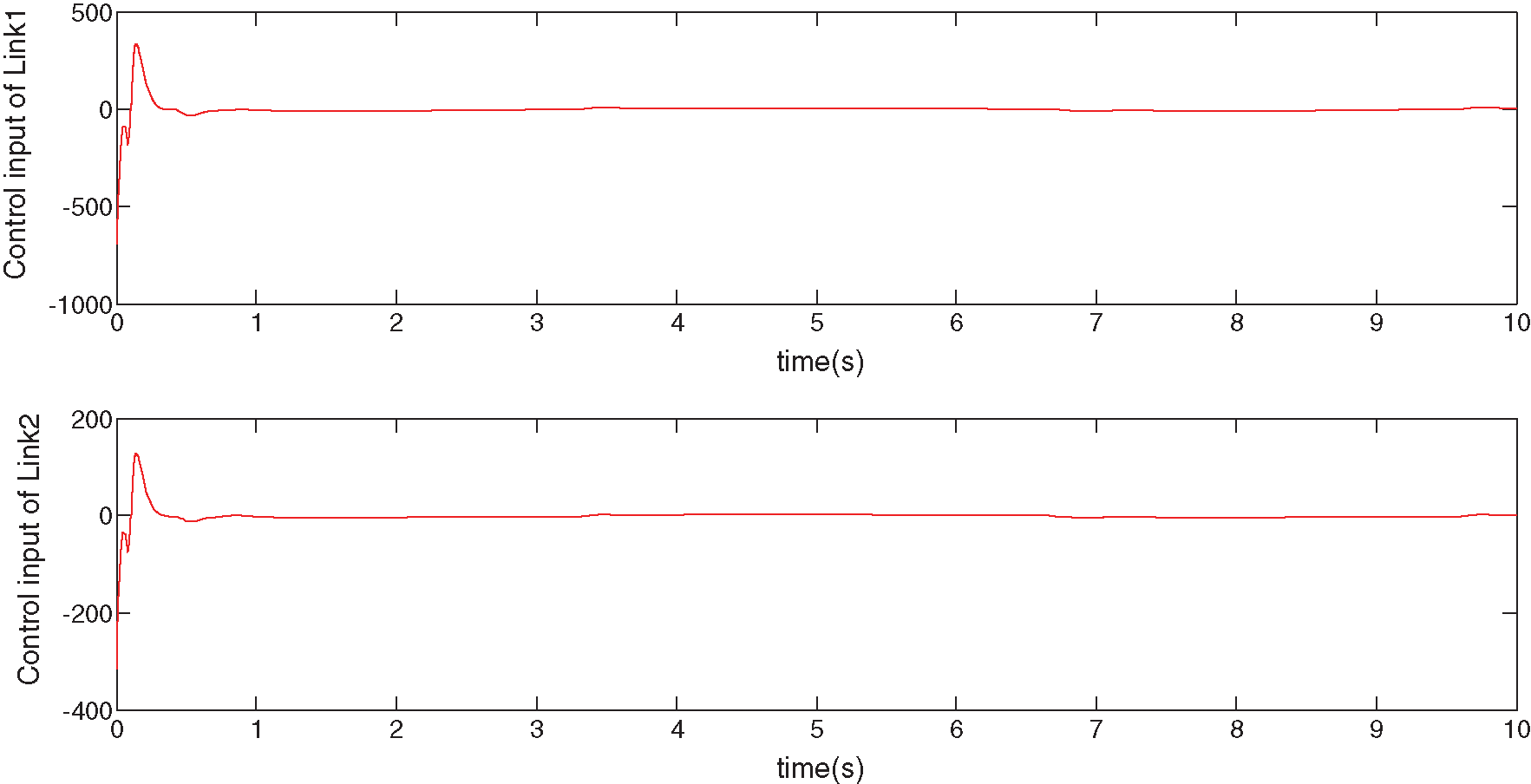
Figure 6: Control inputs curve of joints 1 and 2 (including disturbance and robust terms)

To better simulate and analyse the uncertain disturbances in the system, a controller design block diagram was designed in Simulink (Fig. 7).

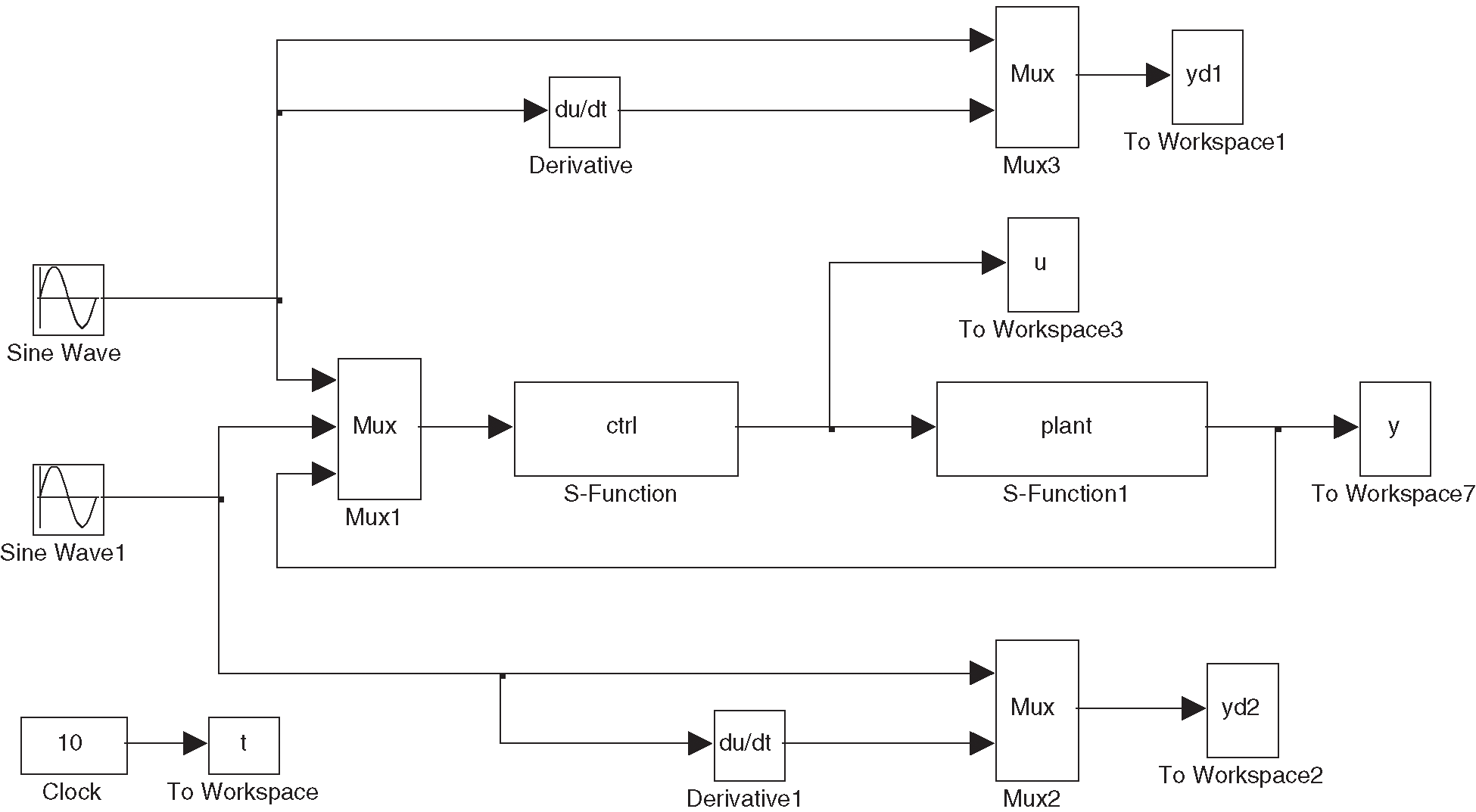
Figure 7: Simulink structural diagram of the manipulator adaptive model control system

A MIMO adaptive model control system for a joint manipulator was designed and two adaptive laws based on adaptive fuzzy compensation were simulated using MATLAB/Simulink software. The results show that the adaptive fuzzy control algorithm can effectively to compensate for various uncertainties in a multi-joint manipulator and can eliminate the influence of approximation errors. It can also improve the accuracy of trajectory tracking.

5  Conclusion

This study provides an in-depth study and analysis of the trajectory tracking problem in a manipulator control system based on a designed control algorithm. For complex multi-input and -output nonlinear systems, the robust adaptive fuzzy tracking control algorithm is completed by adding a robust controller to the adaptive control algorithm. They cooperate with each other to improve the control performance of the manipulator system as the adaptive fuzzy logic system is used to approximate the uncertain nonlinear function of the system, while the robust control is used to eliminate the error caused by approximation of the fuzzy system and the influences of external disturbance. After designing the controller, the tracking control algorithm was validated by software simulation experiments. The influence of uncertainties such as external disturbances was eliminated, resulting in very good trajectory tracking control performance. The control algorithm proposed in this study effectively solves the problem of dependence on a precisely-controlled object model, overcomes the influence of uncertainties such as system modelling errors and unknown disturbances, and improves the accuracy of trajectory tracking control in the manipulator system.

Acknowledgement: Thank the team members for their hard work, the scientific research platform provided by the University, and the strong support from the government funds.

Funding Statement: This work was supported by the project of science and technology of Henan province under Grant No. 14210221036.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  B. Xie, Z. J. Ding and W. Jiang, “Design of adaptive fuzzy control system for multi-joint manipulator based on MIMO system,” Journal of Qiqihar University (Natural Science Edition), vol. 32, no. 4, pp. 20–24, 2016. [Google Scholar]

 2.  M. Hui, Z. Qi and B. Lu, “Observer-based adaptive fuzzy fault-tolerant control for stochastic nonstrict-feedback nonlinear systems with input quantization,” IEEE Transactions on Systems Man & Cybernetics Systems, vol. 10, no. 99, pp. 1–12, 2018. [Google Scholar]

 3.  R. J. Wai and Z. W. Yang, “Adaptive fuzzy neural network control design via a T-S fuzzy model for a robot manipulator including actuator dynamics,” IEEE Transactions on Systems Man & Cybernetics Part B, vol. 38, no. 5, pp. 1326–1346, 2008. [Google Scholar]

 4.  Z. Li, C. Yang and T. Yong, “Decentralised adaptive fuzzy control of coordinated multiple mobile manipulators interacting with non-rigid environments,” IET Control Theory & Applications, vol. 7, no. 3, pp. 397–410, 2013. [Google Scholar]

 5.  Z. Li, Y. Xia and F. Sun, “Adaptive fuzzy control for multilateral cooperative teleoperation of multiple robotic manipulators under random network-induced delays,” IEEE Transactions on Fuzzy Systems, vol. 22, no. 2, pp. 437–450, 2014. [Google Scholar]

 6.  Z. C. Qiu, B. Wang and X. M. Zhang, “Direct adaptive fuzzy control of a translating piezoelectric flexible manipulator driven by a pneumatic rodless cylinder,” Mechanical Systems & Signal Processing, vol. 36, no. 2, pp. 290–316, 2013. [Google Scholar]

 7.  Z. Li, C. Yang and C. Y. Su, “Decentralized fuzzy control of multiple cooperating robotic manipulators with impedance interaction,” IEEE Transactions on Fuzzy Systems, vol. 23, no. 4, pp. 1044–1056, 2015. [Google Scholar]

 8.  D. H. Zhai and Y. Xia, “Adaptive fuzzy control of multilateral asymmetric teleoperation for coordinated multiple mobile manipulators,” IEEE Transactions on Fuzzy Systems, vol. 24, no. 1, pp. 57–70, 2016. [Google Scholar]

 9.  V. Kumar and K. P. Rana, “Nonlinear adaptive fractional order fuzzy PID control of a 2-link planar rigid manipulator with payload,” Journal of the Franklin Institute, vol. 354, no. 2, pp. 216–227, 2016. [Google Scholar]

10. M. M. Fateh and S. Azargoshasb, “Discrete adaptive fuzzy control for asymptotic tracking of robotic manipulators,” Nonlinear Dynamics, vol. 78, no. 3, pp. 2195–2204, 2014. [Google Scholar]

11. M. Sreekumar, “A robot manipulator with adaptive fuzzy controller in obstacle avoidance,” Journal of the Institution of Engineers, vol. 97, no. 3, pp. 469–478, 2016. [Google Scholar]

12. J. Su, R. Xu and J. Wang, “Idle slots skipped mechanism based tag identification algorithm with enhanced collision detection,” KSII Transactions on Internet and Information Systems, vol. 14, no. 5, pp. 2294–2309, 2020. [Google Scholar]

13. M. M. Fateh and S. Azargoshasb, “Discrete-time indirect adaptive fuzzy control for robot manipulators,” International Journal of Intelligent Computing & Cybernetics, vol. 7, no. 4, pp. 352–396, 2014. [Google Scholar]

14. S. Tabatabaei, “A novel fault tolerance energy-aware clustering method via social spider optimization (SSO) and fuzzy logic and mobile sink in wireless sensor networks (WSNS),” Computer Systems Science and Engineering, vol. 35, no. 6, pp. 477–494, 2020. [Google Scholar]

15. N. Chatti and A. Chatti, “Robust adaptive fuzzy control and strategy of avoidance of obstacles for a manipulator arm to serve the people disabilities,” IFAC Proceedings, vol. 43, no. 8, pp. 402–409, 2010. [Google Scholar]

16. C. R. Kumar and V. Jayanthi, “A novel fuzzy rough sets theory based CF recommendation system,” Computer Systems Science and Engineering, vol. 34, no. 3, pp. 123–129, 2019. [Google Scholar]

17. J. Xi, K. Zheng, J. Ma, J. Yang and Z. Liang, “Intuitionistic fuzzy petri nets model based on back propagation algorithm for information services,” Computers Materials & Continua, vol. 63, no. 2, pp. 605–619, 2020. [Google Scholar]

18. Y. Wu, Y. L. Du and W. Zhang, “Decentralized adaptive fuzzy control for manipulator based on extended state observer,” Journal of Southeast University, vol. 42, no. 1, pp. 192–195, 2012. [Google Scholar]

19. H. Q. Wang and Q. L. Wang, “Robust and adaptive fuzzy control for mobile manipulators,” Control & Decision, vol. 25, no. 3, pp. 461–465, 2010. [Google Scholar]

20. X. Wang, Q. Wang and S. Liang, “Predictive control algorithm for urban rail train brake control system based on T-S fuzzy model,” Computers Materials & Continua, vol. 64, no. 3, pp. 1859–1867, 2020. [Google Scholar]

21. J. Su, R. Xu and J. Wang, “Redundant rule detection for software-defined networking,” KSII Transactions on Internet and Information Systems, vol. 14, no. 6, pp. 2735–2751, 2020. [Google Scholar]

22. A. F. Amer, E. A. Sallam and W. M. Elawady, “Adaptive fuzzy sliding mode control using supervisory fuzzy control for 3 DOF planar robot manipulators,” Applied Soft Computing, vol. 11, no. 8, pp. 4943–4953, 2011. [Google Scholar]

23. S. Alavandar and M. J. Nigam, “New hybrid adaptive neuro-fuzzy algorithms for manipulator control with uncertainties–Comparative study,” ISA Transactions, vol. 48, no. 4, pp. 497–502, 2009. [Google Scholar]

24. Y. T. Kim, “Independent joint adaptive fuzzy control of robot manipulator,” Intelligent Automation & Soft Computing, vol. 11, no. 1, pp. 21–32, 2005. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.