Computer Systems Science & Engineering DOI:10.32604/csse.2022.017741
Article

Adaptive Sliding Mode Control Method for Onboard Supercapacitors System

Yanzan Han1,*, Hang Zhou1, Zengfang Shi1 and Shuang Liang2

1Department of Mechanical and Electrical, Henan Polytechnic Institute, Nanyang, 473000, China
2University of Florence, Firenze, 50041, Italy
*Corresponding Author: Yanzan Han. Email: hanyanzan@163.com
Received: 09 February 2021; Accepted: 14 April 2021

Abstract: Urban rail trains have undergone rapid development in recent years due to their punctuality, high capacity and energy efficiency. Urban trains require frequent start/stop operations and are, therefore, prone to high energy losses. As trains have high inertia, the energy that can be recovered from braking comes in short bursts of high power. To effectively recover such braking energy, an onboard supercapacitor system based on a radial basis function neural network-based sliding mode control system is proposed, which provides robust adaptive performance. The supercapacitor energy storage system is connected to a bidirectional DC/DC converter to provide traction energy or absorb regenerative braking energy. In the Boost and Buck modes, the state-space averaging method is used to establish a model and perform exact linearization. An adaptive sliding mode controller is designed, and simulation results show that it can effectively solve the problems of low energy utilization and large voltage fluctuations in urban rail electricity grids, and maximise the recovery and utilization of regenerative braking energy.

Keywords: Energy control; on-board supercapacitor; neural sliding mode control; urban rail train

1  Introduction

Urban rail transit systems can effectively alleviate urban traffic congestion due to their ability to carry large loads at high speeds for long distances. More than 300 cities around the world have developed urban rail transit systems, and their passenger volumes have reached 50%–80% in many developed cities. As of 31 December 2018, there was a total of 5,139 km of urban rail transit in 34 cities of mainland China. It is clear that city rail transit has entered a period of vigorous development.

Due to the short distances between stations on urban lines and the high density of vehicles, considerable braking energy is generated during frequent starting/braking processes. Vehicle speeds have increased in recent years, such that greater braking energy is involved [1–4]. Generally, about 30% of the electricity consumed by urban rail transit is used for auxiliary equipment such as lighting and air conditioning, 10% is used by other components, and the remaining 60% is used for traction power. Among them, the energy generated by regenerative braking accounts for at least 40% of the traction energy. To make better use of regenerative braking energy and suppress fluctuations in DC traction grid voltages, onboard supercapacitor control systems have been introduced [5].

Automotive supercapacitor control systems are nonlinear and uncertain control systems that are susceptible to end-to-end disturbance [6]. By switching the control quantity in sliding mode control, the system can slide along the sliding surface and gain good robustness and interference resistance. resistance. The algorithm used is independent of the system parameters and disturbances, so sliding mode control can be considered for the control of vehicle supercapacitor control systems. A hybrid vehicle supercapacitor system based on DC-DC electricity and batteries was proposed in Gao et al. [7] for energy recovery and utilization. A regenerative braking energy storage system for subway networks based on supercapacitors (SC) was proposed in Shetty et al. [8]. A method of optimal braking-force distribution based on an artificial neural network and sliding mode control was proposed in Ma et al. [9]. A controller composed of a radial basis function (RBF) neural network and sliding mode controller (SMC) was designed in Mao et al. [10] to recover energy from the braking process of mobile vehicles to extend driving distance and save energy. According to the requirements for fast and robust braking in automobile anti-lock braking systems, a sliding mode controller based on an RBF neural network was designed by Hung et al. [11]. An adaptive neural network sliding mode controller design method based on a decoupling method was proposed, and a trolley rod system and ball beam system were simulated.

However, in the design of practical control systems, chattering is prone to occur on both sides of the sliding mode surface when under sliding mode control. To alleviate the chattering problem effectively in traditional sliding mode control, the robustness of the neural network adaptive control system was improved to a certain extent. This study uses the advantages of RBF neural networks (excellent nonlinear function approximation, adaptiveness and self-learning abilities) to propose an onboard supercapacitor system with adaptive and robust sliding mode control. This can be used to recover regenerative braking energy and reduce the line losses of traction grids.

2  Description of a Vehicular Ultracapacitor System For Urban Rail Transit

A structural diagram of an onboard ultracapacitor control system is shown in Fig. 1.

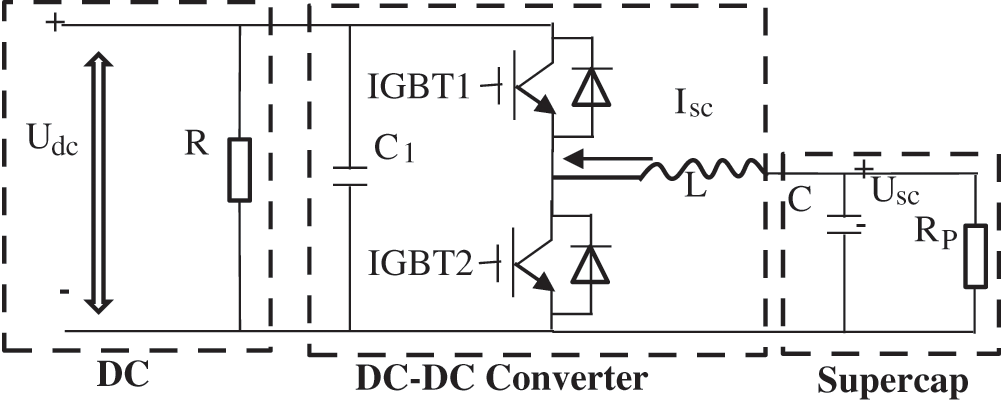
Figure 1: Structural diagram of an onboard ultracapacitor control system

2.1 Affine Nonlinear Model (Discharge Condition)

With an on-board ultracapacitor control system, if the train starts or accelerates, the system will supply power to the train and the supercapacitor will be in a discharged state to avoid supplying power to the train and causing a drop in grid voltage. In this state, circuit modelling using the state-space averaging method can be used to model the discharge state [12–16] as follows:

{LdiLdt=Usc−(1−μ1)UdcCdUscdt=(1−μ1)iL−UdcR (1)

where iL and Usc are the average values of the inductor current and ultracapacitor voltage within 1 switching period T, respectively; Udc is the voltage of the traction grid; L is the effective inductance; C is the vehicular ultracapacitor value; R is the load resistance and μ1 is the IGBT1 duty ratio.

If x1=iL , x2=Udc , a standard type of single-input, affine, nonlinear, vehicular supercapacitor system can be obtained as follows:

{x˙=f(x)+g(x)μ1y=h(x) (2)

Among them, f(x)=[−1Lx2+1LUsc1Cx1−1RCx2] , g(x)=[1Lx2−1Cx1] .

Then, the onboard ultracapacitor control system can be considered as a class of second-order nonlinear uncertain system:

{x˙1=x2x˙2=f(x)+g(x)u+d(t)y=h(x) (3)

Here, f(⋅) is the unknown nonlinear function; u and y are the control input and object output; and d(t) is the interference, where |d(t)|≤D .

If x1=θ , the ideal angle is θd . Then, the error is e=θd−θ and the sliding mode function is

s=e˙+ce. (4)

Among them, c>0 , then:

s˙=e¨+ce˙=θ¨d−θ¨+ce˙=θ¨d−f−gu−d(t)+ce˙ (5)

If f and g are known, the design control law is:

u=1g(−f+θ¨d+ce˙+ηsgn(s)) (6)

By substituting the control law into the above equation, it can be found that:

s˙=e¨+ce˙=θ¨d−θ¨+ce˙=θ¨d−f−gu−d(t)+ce˙=ηsgn(s)−d(t) (7)

If η≥D is certain, then:

ss˙=−η|s|−sd(t)≤0 (8)

So, the control system designed in this paper can meet the stability requirements of Lyapunov theory. The RBF neural network is used for approximating f(⋅) in the onboard ultracapacitor control system.

2.2 Precise Feedback Linearization of the Onboard Ultracapacitor Control System

Through the above analysis, it can be seen that the on-board ultracapacitor control system satisfies the precise linearization condition of the nonlinear system, so it can be linearized [17–20]. If z1 and z2 are the state variables used in linearized feedback linearization, the output function m(x) of the system model can be created.

If z1(x)=m(x) is set, then it can be obtained that:

dz1dt=dz1dxdxdt=Lf1m(x)+Lgm(x)μ1 (8)

In the above formula, Lf1m(x) and Lgm(x) are the lie derivatives along the direction of the sum.

If Lgm(x)=0 , Lf1m(x)=z2 are set, then it can be obtained that: dz1dt=z2 .

Similarly, it can be obtained that:

dz2dt=dz2dxdxdt=Lf2m(x)+LgLf1m(x)μ1 (9)

So,

z1(x)=m(x)=Lx12+Cx22 (10)

Then, the feedback linearized state variable system equation is:

{z˙1=z2=Lx12+Cx22z˙2=Lfm(x)=2Uscx1−2Rx22 (11)

3  Design of an Adaptive, Robust, RBF Neural Network Sliding Mode Controller

Due to the state discontinuity caused by frequent on-off events, the converter has nonlinear characteristics and is easily affected by disturbances, so the control effect is not ideal. A sliding mode variable structure control algorithm with independent parameter inputs and disturbances is used to design the controller [21–24], which is then switched by the control quantities in order to make the system slide along the sliding mode surface. To overcome the chattering phenomenon on both sides of the sliding mode surface, a neural network is added to approximate the nonlinear relationship between the sliding mode surface and the control quantity, so the system has good robustness and anti-interference characteristics.

According to the characteristics of the on-board supercapacitor system, a single, hidden-layer, three-layer, feed-forward, RBF neural network is adopted in this paper, which can approximate arbitrary nonlinear and linear functions. Its structure is shown in Fig. 2.

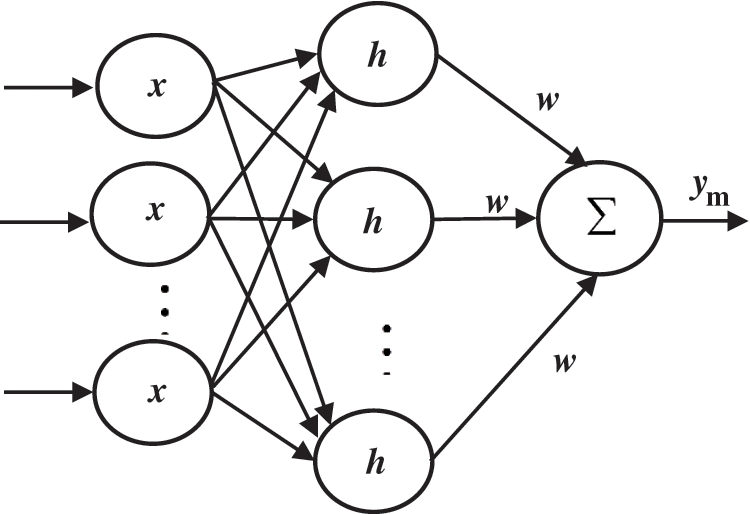
Figure 2: RBF neural network structural diagram

In this paper, an RBF neural network is used to approximate the nonlinear mapping relationship between the sliding mode surface and the control quantity, with the switching function s and the derivative s˙ used as inputs to the RBF neural network [25–29], while the sliding mode controller is the output. The structure of its adaptive sliding mode control system based on RBF is shown in Fig. 3.

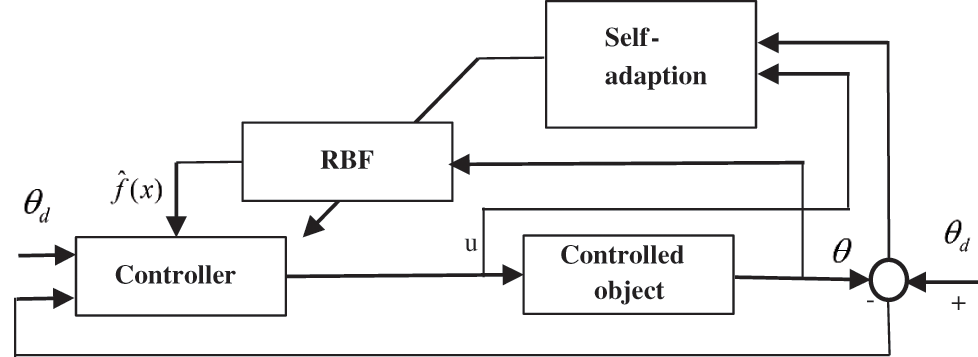
Figure 3: Structure of the adaptive sliding mode control system based on RBF

The input and output algorithms of the RBF network are supposed as:

hj=exp⁡(‖x−cj‖22bj2) (12)

f=W∗Th(x)+ε (13)

Among them, x is the input of the neural network, i is the network input of the first input layer, j is the network input of the hidden layer, h=[hj]T is the output of the Gaussian basis functions, W∗ is the ideal network weight, ε is the network approximation error ( ε≤εN ) and f is the output of the neural network.

The input of the neural network is x=[ee˙]T , then its output is:

f^(x)=W^Th(x) (14)

The control law is:

u=1g(−f^+θ¨d+ce˙+ηsgn(s)) (15)

Substituting control law Eq. (15) into Eq. (5), we can obtain:

s˙=θ¨d−f−gu−d(t)+ce˙=θ¨d−f−[−f^+θ¨d+ce˙+ηsgn(s)]−d(t)+ce˙=−f+f^−ηsgn(s)−d(t)=−f~−ηsgn(s)−d(t) (16)

Among them, f~=f−f^=W∗Th(x)+ε−W^Th(x)=W~Th(x)+ε , W~=W∗−W^ .

The Lyapunov function is designed as:

L=12s2+12γW~TW~ (17)

Among them, γ>0 .

From Eqs. (17) and (16), it can be obtained that:

L˙=ss˙+γW˜TW˜˙=s(−f˜−d(t)−ηsgn(s))−γW˜TW^˙=s(−W˜Th(x)−ε−d(t)−ηsgn(s))−γW˜TW^˙=−W˜T(sh(x)+γW^˙)−s(ε+d(t)+ηsgn(s)) (18)

The adaptation law can be derived as follows:

W^˙=−1γsh(x) (19)

Then,

L˙=−s(ε+d(t)+ηsgn(s))=−s(ε+d(t))−η|s| (20)

Because the RBF network’s approximation error ε is very small, we set η≥εN+D , then L˙≤0 . When L˙=0 , s≡0 , so according to the Lasalle principle of the invariant, the closed-loop system is asymptotically stable. When t→∞ , s→0 . It can be seen that the role of the robust term ηsgn(s) in the control law is to overcome interference and neural network approximation errors to ensure the stability of the system.

4  Simulation Verification

A simulation test was carried out on a certain track line with an operating interval of 1.98 km. The parameters of the supercapacitor are: capacitance = 30 F, rated voltage = 500 V and working current = −400–400 A. The parameters of the bidirectional DC/DC converter are: energy storage inductance = 7.5 mH and filter capacitance = 30,000 uF. The IGBT switching frequency = 10 kHz and the standard supply voltage of the DC traction network = 1500 V [30,31].

Simulink was used to establish a simulation model of a single train with an on-board ultracapacitor (Fig. 4), which can be used to robustly verify the absorption and utilization of regenerative braking energy by the designed control system.

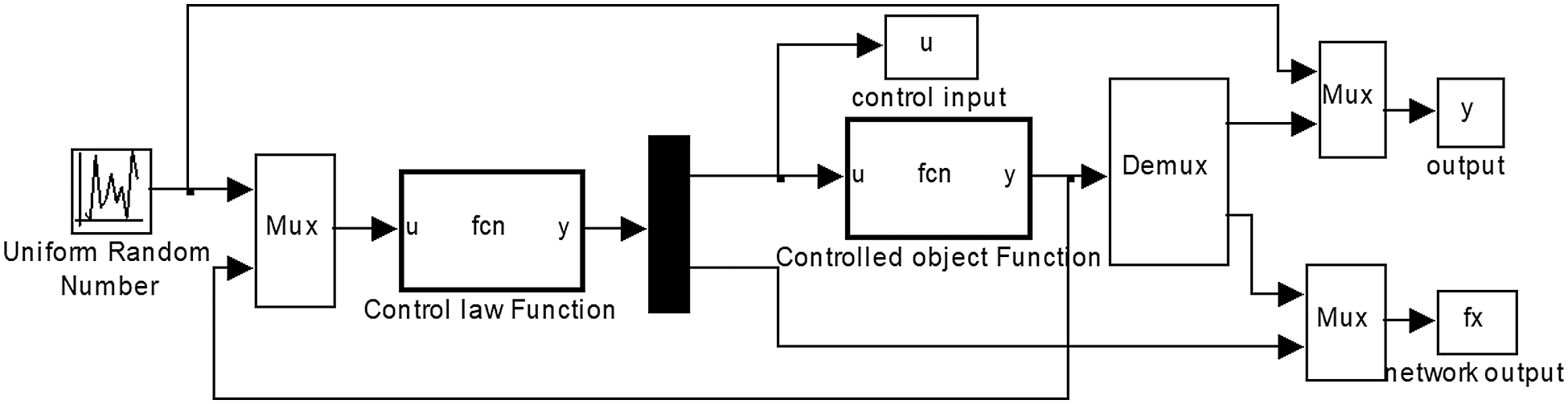
Figure 4: Simulink structural diagram of the onboard ultracapacitor sliding mode control system based on an RBF network

It can be seen from the simulation results (Fig. 5) that when the system is not connected to the on-board supercapacitor energy storage system and the train accelerates and tows, the network voltage fluctuation is about 400 V. The voltage difference between the train deceleration stage and the traction network is about 200 V. It can be seen that the voltage fluctuation of the traction network is high and braking energy cannot be recovered during this process. When the system is connected to the onboard supercapacitor energy storage system, the voltage difference between the train acceleration stage and the traction network is about 150 V, while that between the train deceleration and braking stages is about 90 V. Hence, the designed neural network adaptive sliding mode control system obviously reduces the dynamic amplitude of the traction grid voltage and, at the same time, effectively absorbs and utilizes regenerative braking energy.

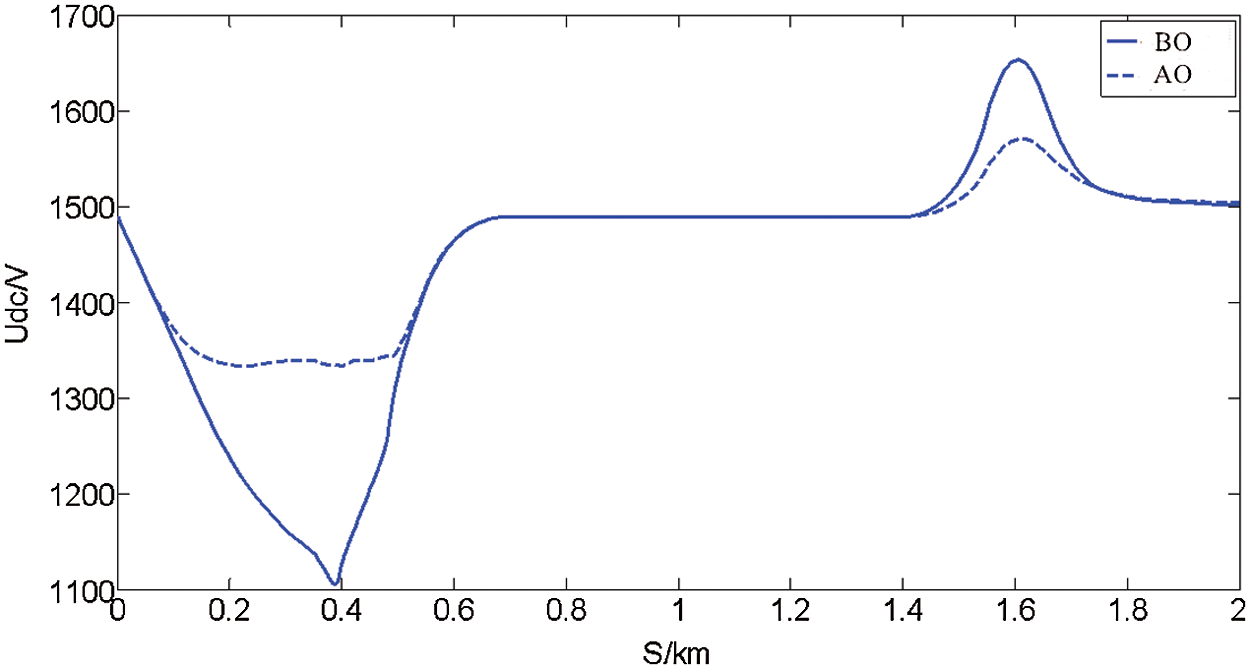
Figure 5: Voltage variation in the traction grid before (BO) and after optimization (AO)

It can be seen from Fig. 6 that, the designed control system can follow the ideal train operating speed curve well. This significantly improves the response speed and steady-state error of the control system, enhances the external anti-interference ability and improves its robustness, making driving more comfortable, safe and stable.

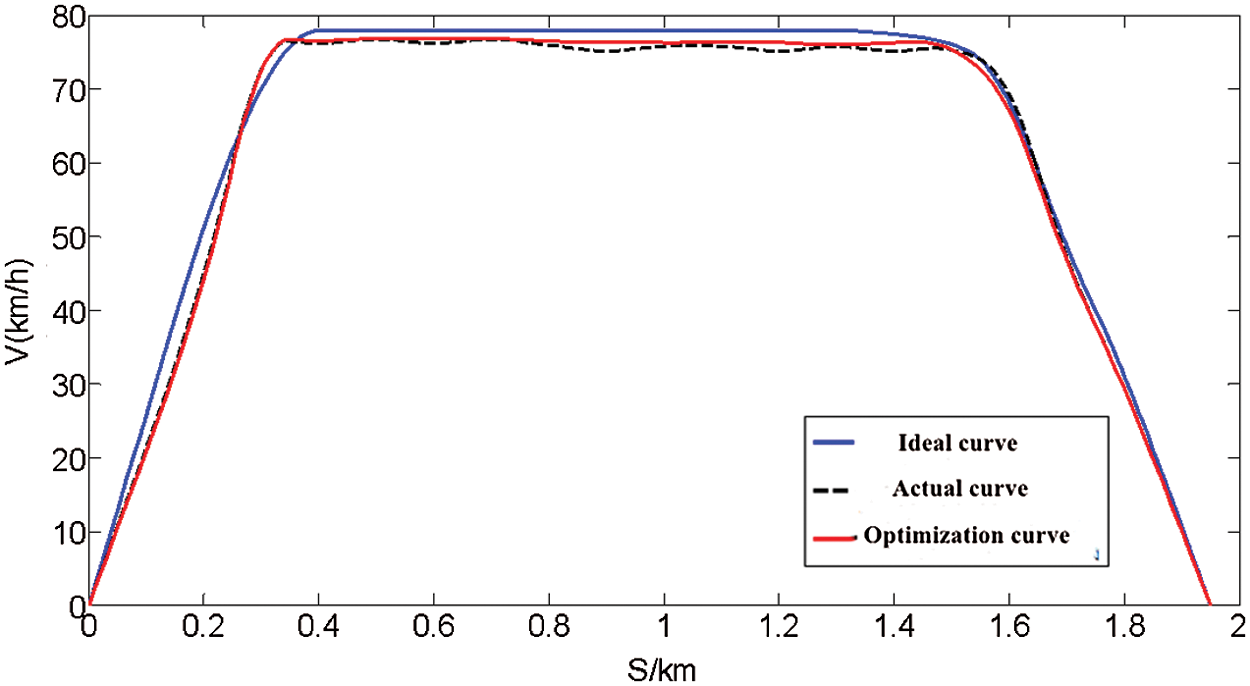
Figure 6: Train operation curve (velocity vs. distance) before and after optimization

Figs. 5–7 show that the designed on-board ultracapacitor control system can alleviate drops in traction grid voltage during train starts and absorb energy during braking, and can also prevent increases in grid pressure. When the braking resistor is used before optimization, the line losses of the traction grid are about 1.395 kWh. When the onboard ultracapacitor control system is used and the neural network adaptive sliding mode control method is adopted, the line loss of the traction grid is about 0.38 kWh. Hence, losses are reduced by 37.4%, which avoids energy wastage.

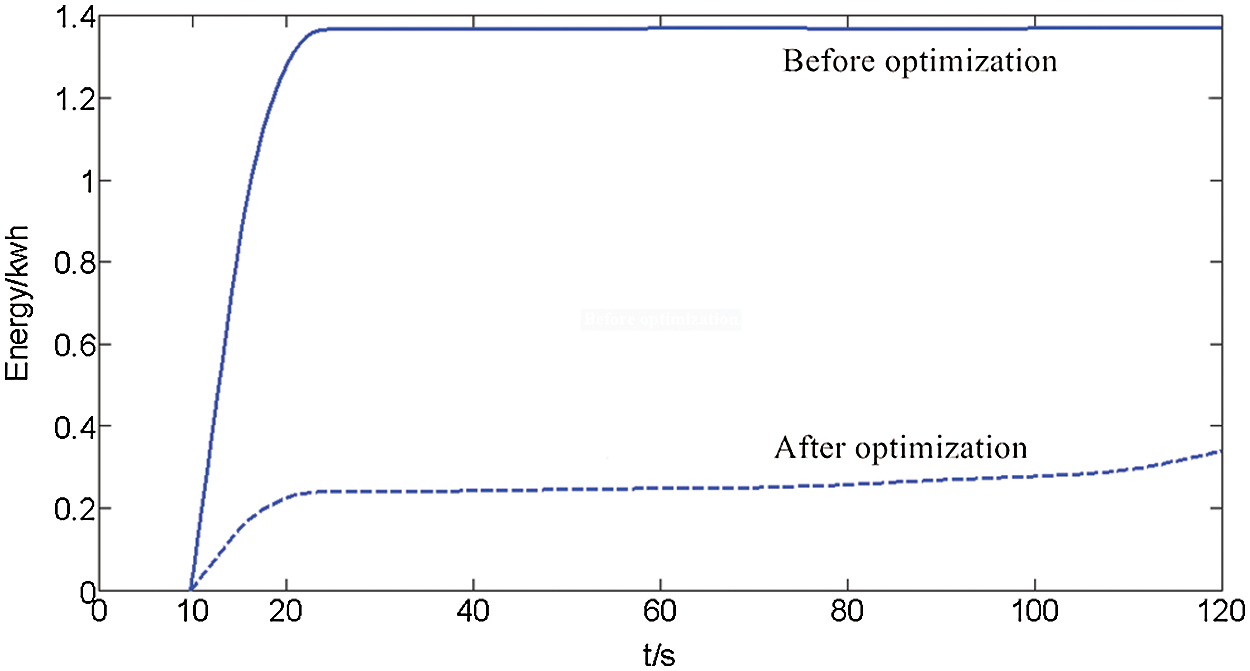
Figure 7: Variations in traction grid line losses before and after optimization

From the above analysis, it can be seen that the vehicle-mounted ultracapacitor energy storage system can effectively utilize regenerative braking energy, suppress fluctuations in grid voltage and reduce losses in the traction grid.

5  Conclusions

(1) With their high power density and long service life, ultracapacitors have unique advantages and development prospects in utilising regenerative energy in urban rail trains. They can improve the braking power of high-speed trains and allow operation without feeders, making trains more comfortable, safe and stable.

(2) An adaptive, neural network-based, sliding mode control system for supercapacitors was proposed in this paper. Through simulation, it was verified that the system can suppress fluctuations in network pressure, reduce losses in traction grids, and improve the utilization rate of regenerative braking energy.

Acknowledgement: We thank the team members for their hard work, the scientific research platform provided by the University, and the strong support from government funding.

Funding Statement: This work was supported by the Science and Technology Project of Henan Province under Grant No. 14210221036.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  X. A. Wang and S. Q. Xu, “An Analysis of energy saving strategies for vehicle-mounted ultracapacitor subway trains,” Shandong Industrial Technology, vol. 14, no. 1, pp. 39–42, 2019. [Google Scholar]

 2.  J. Chen and M. S. Deng, “Application of vehicle-mounted supercapacitor in energy recovery from subway braking,” Journal of Hunan University of Technology, vol. 32, no. 4, pp. 28–32, 2008. [Google Scholar]

 3.  J. P. Wang, “Optimal configuration method of vehicle-mounted ultracapacitor in urban rail transit,” Research on Urban Rail Transit, vol. 20, no. 3, pp. 36–39, 2017. [Google Scholar]

 4.  Y. Zhang, J. G. Cheng and J. Chen, “Analysis of regenerative braking energy utilization of subway trains based on ultracapacitor,” Urban Rail Transit Research, vol. 19, no. 9, pp. 56–65, 2016. [Google Scholar]

 5.  J. G. Cheng, S. R. Wu and J. Chen, “Research on vehicular ultracapacitor energy storage system of urban rail vehicles,” Modern Urban Rail Transit, vol. 12, no. 2, pp. 7–11, 2016. [Google Scholar]

 6.  L. J. Ma, W. J. Liao and Z. Y. Gao, “Research on control strategy of vehicular ultracapacitor energy storage in urban rail transit,” Journal of Electrical Technology, vol. 30, no. 11, pp. 63–68, 2015. [Google Scholar]

 7.  Z. Y. Gao, J. J. Fang and Y. N. Zhang, “Control of urban rail transit equipped with ground-based supercapacitor for energy saving and reduction of power peak demand,” International Journal of Electrical Power & Energy Systems, vol. 67, no. 16, pp. 439–447, 2015. [Google Scholar]

 8.  S. S. Shetty and O. Karabasoglu, “Regenerative braking control strategy for hybrid and electric vehicles using artificial neural networks,” Communications in Computer & Information Science, vol. 459, no. 64, pp. 103–112, 2014. [Google Scholar]

 9.  L. Ma, W. Liao and Z. Gao, “Research on ac side series supercapacitor regenerative braking energy storage system control strategy of railway vehicle,” Transactions of China Electrotechnical Society, vol. 12, no. 23, pp. 25–29, 2015. [Google Scholar]

10. Y. E. Mao, G. Stojanovski and Y. Jing, “Sliding mode controller employing RBF-ANN for vehicle anti-lock braking system,” Power Electronics & Motion Control Conference, vol. 14, no. 23, pp. 123–131, 2010. [Google Scholar]

11. L. C. Hung and H. Y. Chung, “Decoupled control using neural network-based sliding-mode controller for nonlinear systems,” Expert Systems with Applications, vol. 32, no. 4, pp. 1168–1182, 2007. [Google Scholar]

12. P. S. De, C. Chatzikomis and A. Sorniotti, “Comparison of traction controllers for electric vehicles with On-Board drivetrains,” IEEE Transactions on Vehicular Technology, vol. 14, no. 23, pp. 123–129, 2017. [Google Scholar]

13. J. Su, Z. Sheng, A. X. Liu and Y. Chen, “A partitioning approach to RFID identification,” IEEE/ACM Transactions on Networking, vol. 28, no. 5, pp. 2160–2173, 2020. [Google Scholar]

14. J. Su, Z. Sheng and Y. Chen, “Capture-aware identification of mobile RFID tags with unreliable channels,” IEEE Transactions on Mobile Computing, vol. 56, no. 12, pp. 1–14, 2020. [Google Scholar]

15. X. Li, Y. L. Li and X. Y. Chang, “A nonlinear control algorithm for supercapacitor energy storage system based on precise linearization theory,” Journal of Electrochemical and Technology, vol. 31, no. 21, pp. 12–16, 2016. [Google Scholar]

16. X. T. Feng, L. Zhang and C. X. Gao, “Bidirectional DC/DC converter experimental platform with supercapacitor energy storage,” Journal of Power Systems and Automation, vol. 30, no. 8, pp. 145–150, 2012. [Google Scholar]

17. Q. Ma, X. Guo, P. Luo and Z. W. Zhang, “Design of coordinated control strategy of new railway power regulator based on supercapacitor energy storage,” Journal of Electrical Technology, vol. 34, no. 4, pp. 765–776, 2019. [Google Scholar]

18. X. T. Feng, M. M. Wan, L. B. Han and L. X. Wu, “Power system control strategy of bidirectional DC/DC converter based on energy storage,” Power Electronics Technology, vol. 51, no. 7, pp. 8–19, 2015. [Google Scholar]

19. H. Xia, Z. P. Yang and X. Y. Li, “Control strategy of urban rail super-capacitor energy storage device based on train running state,” Journal of Electrical Technology, vol. 32, no. 21, pp. 16–23, 2017. [Google Scholar]

20. R. J. Wai, “Total sliding-mode controller for PM synchronous servo motor drive using recurrent fuzzy neural network,” IEEE Transactions on Industrial Electronics, vol. 48, no. 5, pp. 926–944, 2001. [Google Scholar]

21. F. J. Lin and P. H. Shen, “Robust fuzzy neural network sliding-mode control for two-axis motion control system,” IEEE Transactions on Industrial Electronics, vol. 53, no. 4, pp. 1209–1225, 2006. [Google Scholar]

22. S. Hao and H. Aschemann, “Sliding-mode control of a hydrostatic drive train with uncertain actuator dynamics,” Control Conference, vol. 64, no. 16, pp. 956–964, 2013. [Google Scholar]

23. B. Gu, W. Xiong and Z. Bai, “Human action recognition based on supervised class-specific dictionary learning with deep convolutional neural network features,” Computers Materials & Continua, vol. 63, no. 1, pp. 243–262, 2020. [Google Scholar]

24. M. D. Bougrine, A. Benalia and M. Benbouzid, “Nonlinear adaptive sliding mode control of a powertrain supplying fuel cell hybrid vehicle,” International Conference on Systems & Control, vol. 106, no. 64, pp. 1203–1301, 2013. [Google Scholar]

25. W. Yang, J. Li, W. Peng and A. Deng, “A rub-impact recognition method based on improved convolutional neural network,” Computers Materials & Continua, vol. 63, no. 1, pp. 283–299, 2020. [Google Scholar]

26. J. Su, R. Xu, S. Yu, B. Wang and J. Wang, “Idle slots skipped mechanism based tag identification algorithm with enhanced collision detection,” KSII Transactions on Internet and Information Systems, vol. 14, no. 5, pp. 2294–2309, 2020. [Google Scholar]

27. M. Ganesan, D. Ezhilarasi and J. Benni, “Hybrid model reference adaptive second order sliding mode controller for automatic train operation,” IET Control Theory & Applications, vol. 11, no. 8, pp. 1222–1233, 2017. [Google Scholar]

28. X. Yao, J. H. Park and H. Dong, “Robust adaptive nonsingular terminal sliding mode control for automatic train operation,” IEEE Transactions on Systems Man & Cybernetics Systems, vol. 64, no. 99, pp. 1–10, 2018. [Google Scholar]

29. G. Yang, J. Zeng and X. Wang, “Ott messages modeling and classification based on recurrent neural networks,” Computers Materials & Continua, vol. 63, no. 2, pp. 769–785, 2020. [Google Scholar]

30. S. Liu and W. Zhang, “Application of the fuzzy neural network algorithm in the exploration of the agricultural products e-commerce path,” Intelligent Automation & Soft Computing, vol. 26, no. 3, pp. 569–575, 2020. [Google Scholar]

31. Q. Y. Wang, W. U. Peng and X. Y. Feng, “An accurate stopping algorithm for urban rail transit based on adaptive terminal sliding mode control,” Acta Railway Sinica, vol. 38, no. 2, pp. 56–63, 2016. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.