DOI:10.32604/csse.2022.019655

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.019655 |  |
| Article |
Deterministic and Stochastic Fractional Order Model for Lesser Date Moth
1Department of Mathematics, Unaizah College of Sciences and Arts, Qassim University, P.O. Box 3771, Unaizah, 51911, Saudi Arabia
2Department of Mathematics, Buraydah College of Sciences and Arts, Qassim University, P.O. Box 1162, Buraydah, 51431, Saudi Arabia
*Corresponding Author: Moustafa El-shahed. Email: elshahedm@yahoo.com
Received: 21 April 2021; Accepted: 23 May 2021
Abstract: In this paper, a deterministic and stochastic fractional order model for lesser date moth (LDM) using mating disruption and natural enemies is proposed and analysed. The interaction between LDM larvae, fertilized LDM female, unfertilized LDM female, LDM male and the natural enemy is investigated. In order to clarify the characteristics of the proposed deterministic fractional order model, the analysis of existence, uniqueness, non-negativity and boundedness of the solutions of the proposed fractional-order model are examined. In addition, some sufficient conditions are obtained to ensure the local and global stability of equilibrium points. The occurrence of local bifurcation near the equilibrium points is investigated with the help of Sotomayor’s theorem. Numerical simulations are conducted to illustrate the properties of the proposed fractional order model with respect to the intrinsic growth rate of the LDM larvae, natural enemy’s mortality rate, predation rate, sex pheromone trap parameter, fractional order and environmental noise. The impact of mating disruption on lesser date moth is demonstrated. Also, a numerical approximation method is developed for the proposed stochastic fractional-order model.
Keywords: Lesser date moth; stochastic; stability; natural enemies; Sotomayor’s theorem; mating disruption
The palm tree is considered one of the oldest major and basic crops in Southwest Asia, North Africa and many other places of the world. Palm trees are affected by many agricultural pests that cause significant losses to the palm trees and their fruits, as well as affecting the age and growth of the palm tree if it is left without control [1]. The LDM is one of the most dangerous pests of young palm trees and immature palm fruits. The damage is mainly due to the way in which the LDM larvae feed, as soon as they leave the egg until the date of their entry the virgin dwelling develops feeding and causing tunnels in the affected part of the palm in all directions and depths without any early signs showing the infection [2–5]. One of the most promising strategies for controlling LDM is the use of a mating disruption using the sex pheromone traps [5]. Natural enemies’ use to stop pest infestation has long been recommended as a clean and environmentally friendly way to protect crops. The main natural enemies that are used in agricultural pest control are larval predators. Goniozus swirskiana can be considered as one of the most important natural enemies that can attack the LDM [6,7]. In the real world, plant diseases models are always affected by the environmental noise. Thus, the stochastic models may be a more appropriate way of modelling agricultural pests in many circumstances [8]. Recently, fractional calculus has been applied to describe different mathematical models, and it has been shown to be more accurate in some cases compared to the classical models [9]. The main objective of this paper is to propose and analyse a deterministic and stochastic fractional order LDM model with mating disruption and sex pheromone traps taking into consideration the effect of the natural enemy on LDM.
The paper is arranged as follows: In Section 2, the deterministic mathematical model is described as well as the existence, uniqueness, non-negativity, and boundedness of the solutions of LDM system are verified. The local and global stability of equilibrium points of the LDM system is analyzed in Section 3. Using Sotomayor’s theorem, the local bifurcation conditions are derived in Section 4. In Section 5, we extend the deterministic fractional-order LDM model to the stochastic case and a numerical approximation method developed for the proposed stochastic fractional-order case. Some numerical examples are given in Section 6 to illustrate the theoretical findings. Finally, the discussion and conclusion are given in Section 7.
2 Dynamic of the Deterministic Fractional Order Model
Following [10–14], the model of lesser date moth with mating disruption and sex pheromone
trap is describing by the following system
where

In this section, we investigate the existence and uniqueness of the solutions of the fractional order system (1) in the region
Theorem 1. For each
Proof. Define a mapping
For any
where
Hence,
2.2 Non-Negativity and Boundedness
The following results show the non-negativity of the solutions of the fractional order system (1). According to Cresson et al. [15], a model of the form
Theorem 2. All the solutions of the fractional-order LDM Model (1) starting in
Proof. The approach of [16,17] is utilized. Let
where,
where
Hence all the solutions of fractional-order LDM model (1) that start in
The LDM model (1) has the following three equilibrium points:
1)
2) The free natural enemy equilibrium point
The free natural enemy equilibrium point exists positively if
3) The coexistence equilibrium point
4) The coexistence equilibrium point
The locally and globally asymptotically stable of equilibrium points of LDM system (1) are now investigated. The stability analysis of the equilibrium point
The stability of free natural enemy equilibrium point
Theorem 3. If
Proof. The first three eigenvalues of
The roots of Eq. (3) have negative real parts. It can be observed that
Theorem 4. If
Proof. The following positive definite Lyapunov function is considered.
By calculating the time derivative of
Then
The stability of the coexistence equilibrium point
The first eigenvalue of
where
where
when
Theorem 5. If
The global stability of the coexistence equilibrium point is investigated in the following theorem.
Theorem 6. If
Proof. The following positive definite Lyapunov function is considered.
By calculating the time derivative of
Choosing
In this section the local bifurcations near the equilibrium points of LDM model (1) are inves-tigated with the help of Sotomayor’s theorem [22]. The Hopf bifurcation theorem given in Liu [23] is also presented to discuss the bifurcation analysis of the underlying system. One can compute
where
Theorem 7. The LDM system (1) undergoes a transcritical bifurcation with respect to the bifurcation parameter
Proof. Let
where
then
Thus, according to Sotomayor’s theorem, the LDM system (1) has a transcritical bifurcation at
Theorem 8. The LDM system (1) undergoes a transcritical bifurcation with respect to the bifurcation parameter
Proof. The Jacobian matrix of the LDM system (1) at the free enemy equilibrium point
where
where
then,
Thus, according to Sotomayor’s theorem, the LDM system (1) has a transcritical bifurcation at
In this part, we shall show that as the coexistence equilibrium loses stability, periodic solutions can bifurcate from the positive equilibrium. We first give the following lemma.
Lemma 9 . The characteristic Eq.(4) has a pair of purely imaginary roots and the remaining roots have negative real parts if and only if
Suppose (4) has two eigenvalues which have negative real parts and two complex conjugates eigenvalues (call them
Substituting (6) into (7), differentiating with respect to
Theorem 10. For the coexistence equilibrium point E2 of the integer order LDM system (1), the system around
1.
2.
3.
According to Theorem 10, there exists a Hopf bifurcation in the LDM model (1) with
5 Stochastic Fractional Order Model
This section extends the deterministic fractional-order LDM model (1) to the following stochastic fractional-order model.
where
where
According to Wang et al. [24,25], under some conditions on the coefficient functions, the global existence and uniqueness of solutions for the stochastic fractional-order system (8) can be investigated. Because Grunwald-Letnikov’s definition is the most straightforward from the point of view of numerical implementation, so we will use it to solve the LDM system of fractional order stochastic differential equations. Grunwald-Letnikov (
where
where
If
Now, the fractional order stochastic LDM model (8) can be written as
where,
In this section, we simulate the fractional-order LDM system (1) and stochastic fractional-order LDM (8) by the following parameters:
To show the effect of the intrinsic growth rate of the LDM larvae, we draw the bifurcation diagram concerning r as a bifurcation parameter. It can be seen that a transcritical bifurcation occurs at r = 0.51 as shown in Fig. 1 and stated in Theorem 7. It can also be observed that when r > 0.51, the coexistence equilibrium point E2 = (1.6667, 25.2475, 24.7525, 25.36, 157.407r − 85) is locally asymptotically stable. According to Theorem 10, it can be seen that the supercritical Hopf bifurcation value localized at r = 1.31143. For r > 1.31143 the LDM system (1) undergoes limit cycle behaviour.
To show the effect of the natural enemy’s mortality rate around the coexistence equilibrium points, we draw the bifurcation diagram for µ5 as a bifurcation parameter. It can be seen that the Hopf bifurcation value localized at µ5 = 0.0284692 as shown in Fig. 2. It can also be observed that when µ5 > 0.0284692, the coexistence equilibrium point E2 is locally asymptotically stable. For µ5 < 0.3235, the system undergoes limit cycle behaviour. According to Theorem 7, for µ5 > 0.0642346 the natural enemy goes extinct from the system and a transcritical bifurcation occurs at µ5 = 0.0642346 and the equilibrium point E1 = (26.94, 408.101, 400.009, 528.446, 0) is locally asymptotically stable.
In order to show the effect of the predation rate, we draw the bifurcation diagram with respect to β as a bifurcation parameter. It can be seen that a transcritical bifurcation occurs at β = 0.0501342 as shown in Fig. 3. It can also be observed that when β < 0.0501342, the free enemy equilibrium point E1 = (22.35, 338.569, 331.93, 436.688, 0) is locally asymptotically stable as indicated in Theorem 8. For 0.0501342 < β < 0.152449, the coexistence equilibrium point E2 is locally asymptotically stable. It can be seen that the supercritical Hopf bifurcation value localized at β = 0.152449. For β > 0.152449 the LDM system (1) undergoes limit cycle behaviour.
From Fig. 4a, it can be seen that the sex pheromone trap parameter p is important in that it affects the population density of the LDM male. One can observe from Fig. 4b. that the population density of LDM male decrease with increasing p. We conclude that the dynamics of LDM can be controlled by sex pheromone trap parameters p.
Fig. 5 shows that the deterministic fractional-order remains stable for different values of fractional-order α though solutions reach to equilibrium point E2(7.5, 113.614, 111.386, 140.149, 189) more slowly for a smaller value of fractional-order α. It is important to notice that when α = 1 the fractional order model for lesser date moth (1) reduces to the classical integer-order model [10–14].
When the strength of environmental noise is very close to zero, the fractional-order stochastic LDM system (8) behaves like the deterministic model. Fig. 6a indicates the dynamical behavior of stochastic LDM (8) without noise (i.e.,
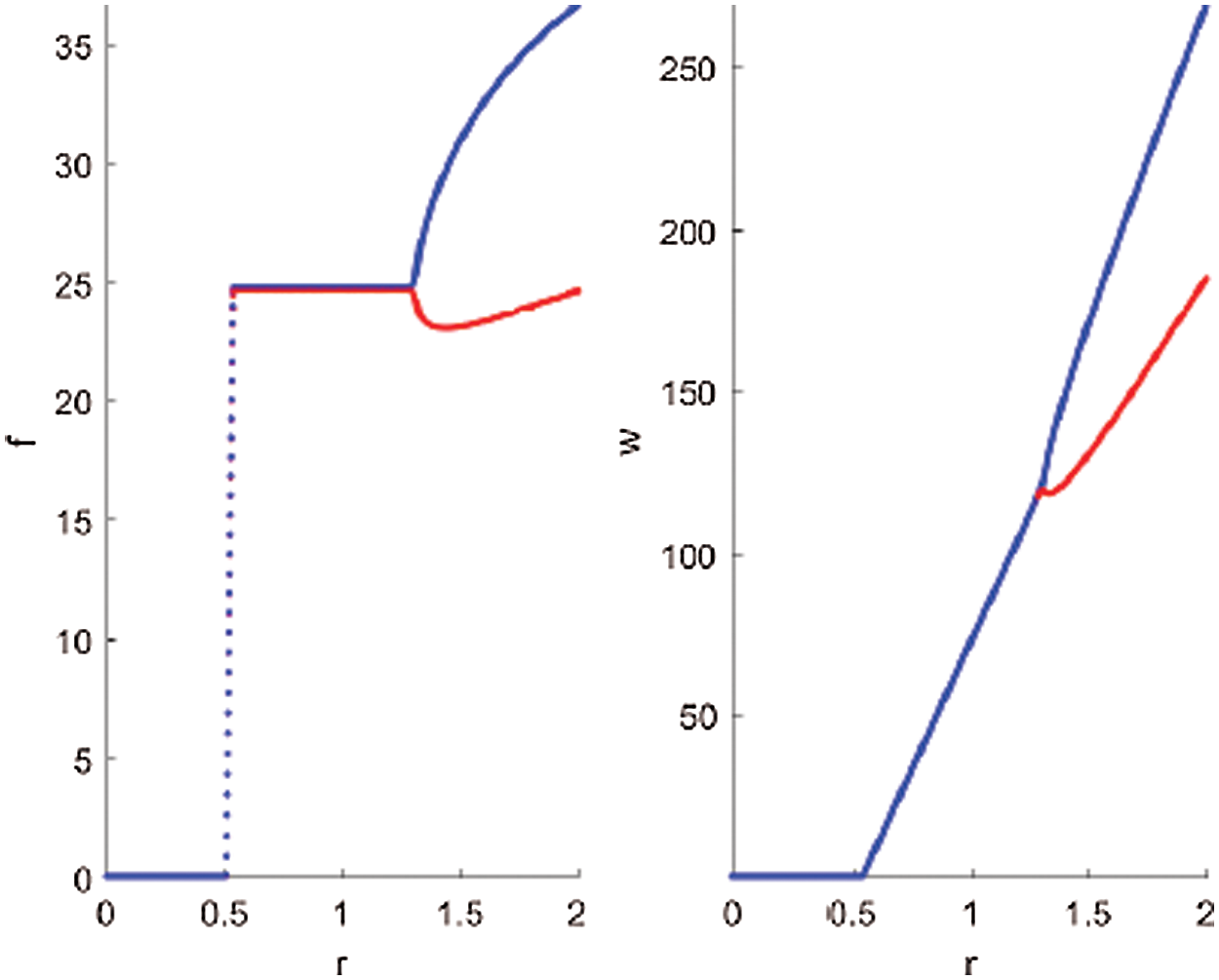
Figure 1: Bifurcation diagram of LDM model (1) with respect to r
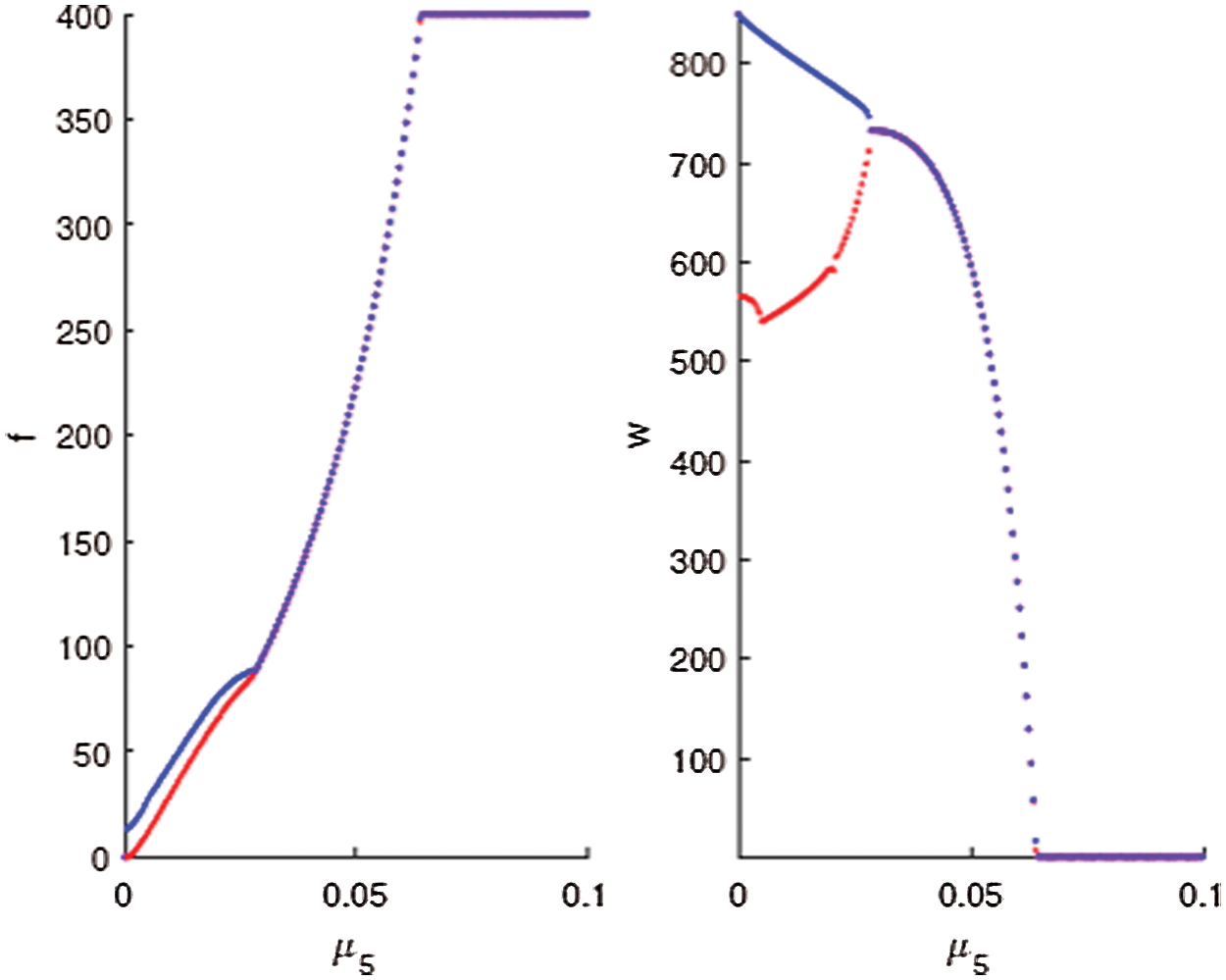
Figure 2: Bifurcation diagram of LDM model (1) with respect to µ5
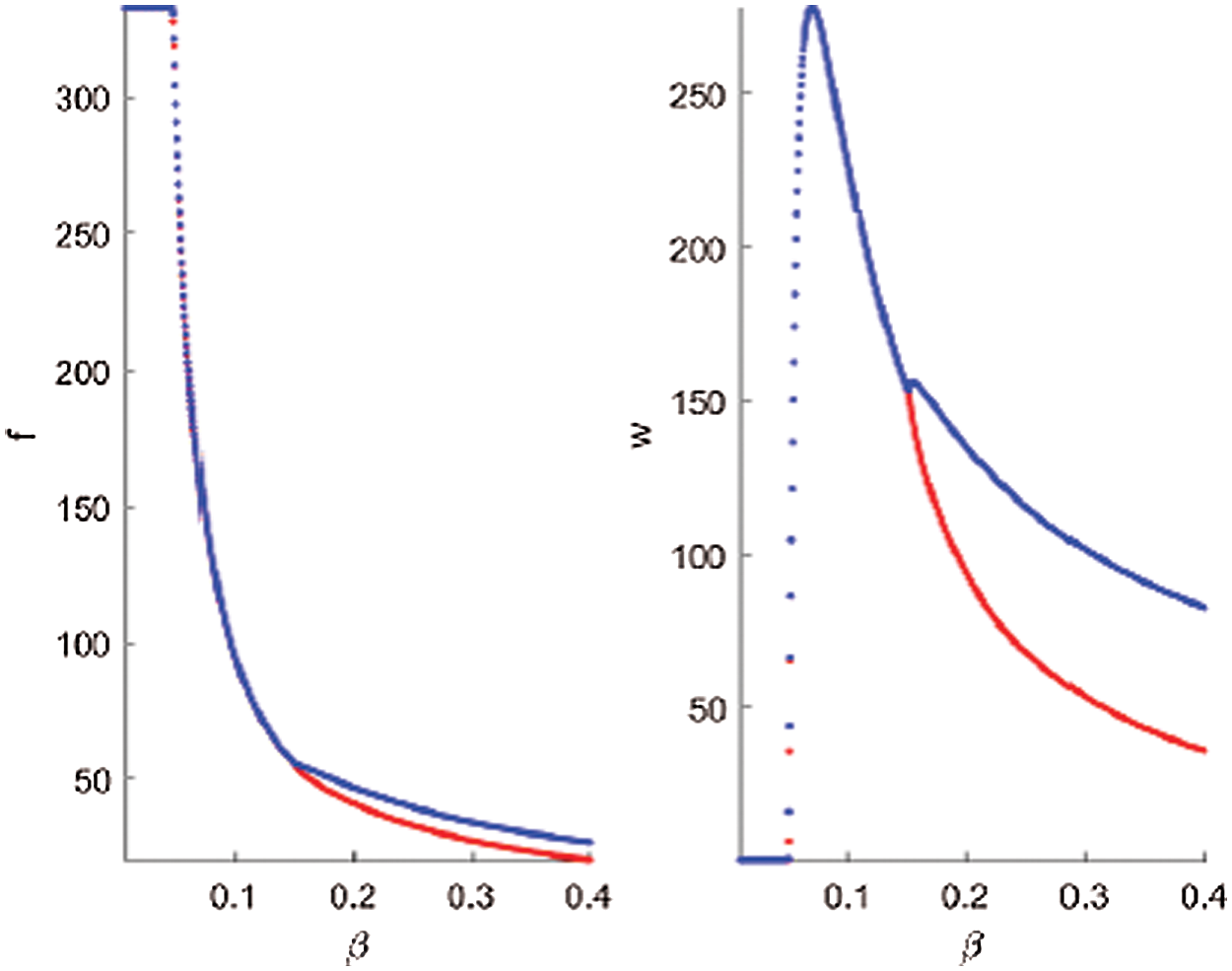
Figure 3: Bifurcation diagram of LDM model (1) with respect to β
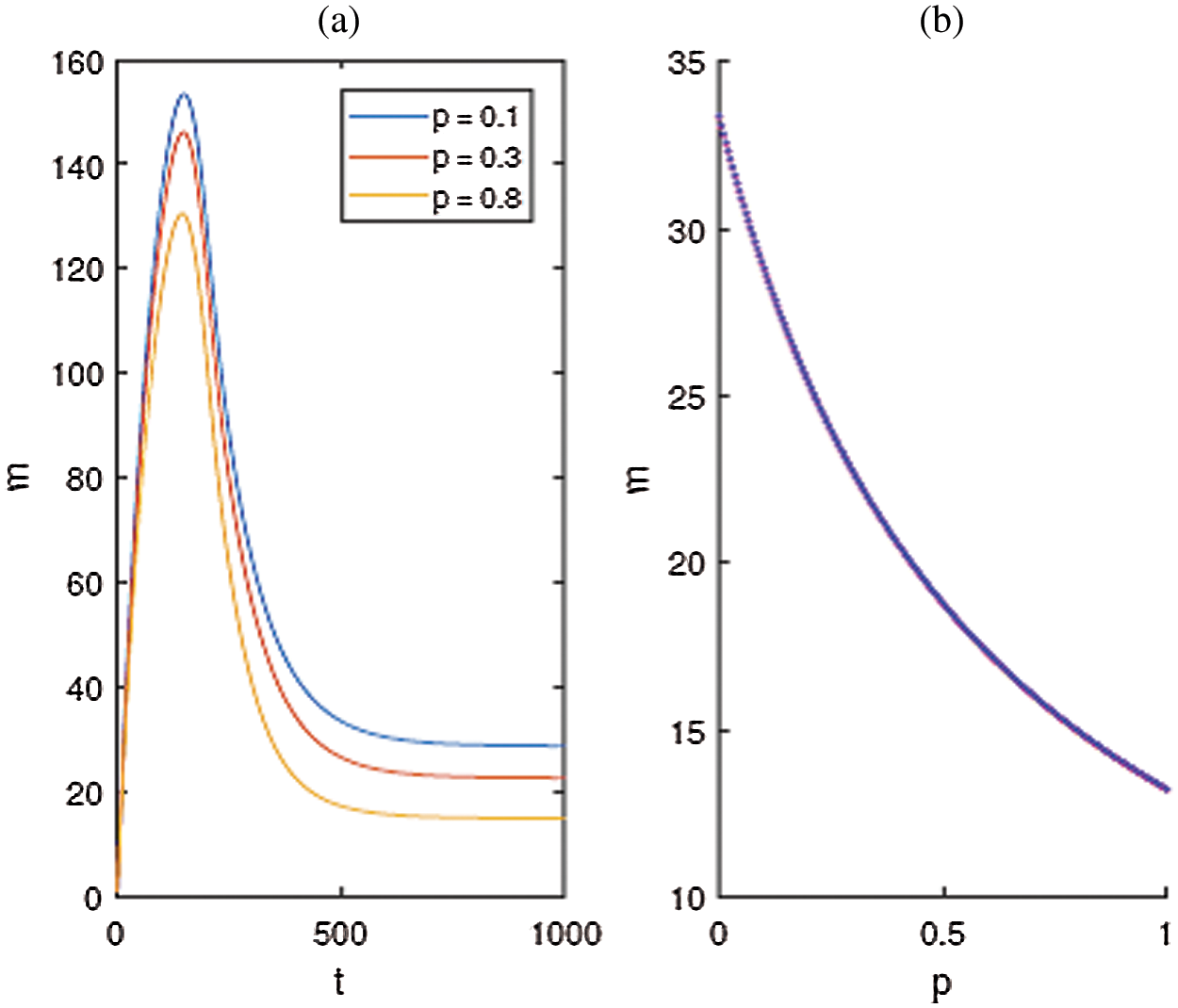
Figure 4: (a) Plot of the LDM male versus time with p = 0.1, 0.3, 0.8, (b) Plot of the LDM male versus time with 0 ≤ p ≤ 1
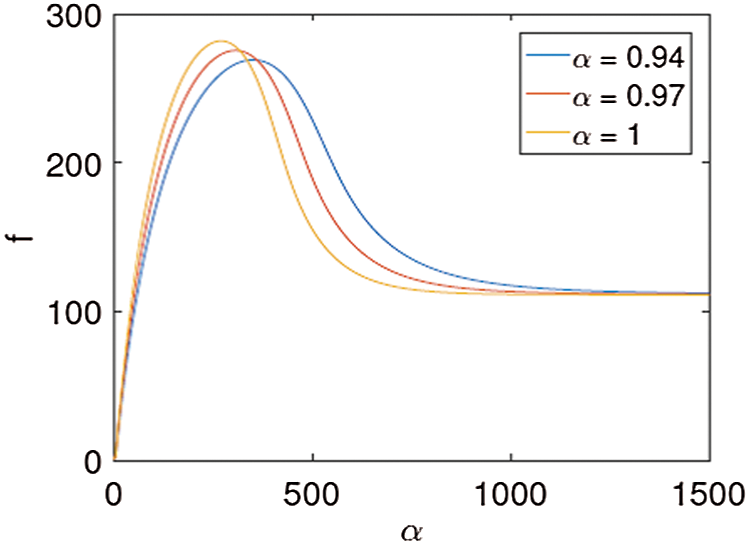
Figure 5: Time series of the LDM female with α = 0.94, 0.97, 1

Figure 6: Time series of the fractional order stochastic model (10) with σ = 0, 0.02, 0.05 (a) σi = 0 (b) σi = 0.02 (c) σi = 0.05
In this paper, we consider a deterministic and stochastic fractional order model for LDM using mating disruption and natural enemies. We obtain some sufficient conditions that ensure the local and global stability of equilibrium points. We conclude that sex pheromone trap parameters can control dynamics of LDM. The occurrence of local bifurcation near the equilibrium point is performed using Sotomayor’s theorem. Numerical simulations are performed to support and illustrate the theoretical findings. From the numerical results, one can realize that if the noise is not strong, the stochastic perturbation does not cause sharp changes in the dynamics of the LDM model. However, when the environmental noise is sufficiently large, the noise can force the population to become extinct.
Funding Statement: The authors gratefully acknowledge Qassim University, represented by the Deanship of Scientific Research, on the financial support under the number (cosao-bs-2019-2-2-I-5469) during the academic year 1440 AH/2019 AD.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. L. I. El-Juhany, “Degradation of date palm trees and date production in Arab Countries: Causes and potential rehabilitation,” Australian Journal of Basic and Applied Sciences, vol. 4, no. 8, pp. 3998–4010, 2010. [Google Scholar]
2. J. Al-Khayri, “Date palm phoenix dactylifera micropropagation,” in Protocols for Micropropagation of Woody Trees and Fruits, Springer, pp. 509–526, 2007. [Google Scholar]
3. A. Levi-Zada, D. Fefer, L. Anshelevitch, A. Litovsky, M. Bengtsson et al., “Identification of the sex pheromone of the lesser date moth, Batrachedra amydraula, using sequential SPME auto-sampling,” Tetrahedron Letters, vol. 52, no. 35, pp. 4550–4553, 2011. [Google Scholar]
4. M. A. Al-Deeb and H. A. Al-Dhaheri, “Use of a pheromone-baited trap to monitor the population of the lesser date moth Batrachedra amydraula (Lepidoptera: Batrachedridae) in the UAE,” Journal of Entomology and Zoology Studies, vol. 5, no. 6, pp. 2572–2575, 2017. [Google Scholar]
5. M. Hoddle, A. H. Al-Abbad, H. El-Shafie, J. Faleiro, A. Sallam et al., “Assessing the impact of areawide pheromone trapping, pesticide applications, and eradication of infested date palms for Rhynchophorus ferrugineus (Coleoptera: Curculionidae) management in Al Ghowaybah, Saudi Arabia,” Crop Protection, vol. 53, pp. 152–160, 2013. [Google Scholar]
6. E. Sadeghi, V. Baniameri and A. Marouf, “Oviposition behaviour of Goniozus swirskiana (Hymenoptera: Bethylidae: Bethylinae) a parasitoid of Batrachedra amydraula Meyrick from the warmest desert of Iran,” World Applied Sciences Journal, vol. 20, no. 11, pp. 1493–1498, 2012. [Google Scholar]
7. M. Abbas, S. Al-Khatry, R. Shidi and N. A. Al-Ajmi, “Natural enemies of the lesser date moth, Batrachedra amydraula Meyrick (Lepidoptera: Batrachedridae) with special reference to its parasitoid Goniozus sp,” Egyptian Journal of Biological Pest Control, vol. 24, no. 2, pp. 293–296, 2014. [Google Scholar]
8. L. Addison, “Analysis of a predator-prey model: A deterministic and stochastic approach,” Journal of Biometrics and Biostatistics, vol. 8, no. 4, pp. 359–368, 2017. [Google Scholar]
9. B. Ahmad, S. K. Ntouyas, A. Alsaedi and A. F. Albideewi, “A study of a coupled system of Hadamard fractional differential equations with nonlocal coupled initial-multipoint conditions,” Advances in Difference Equations, vol. 2021, no. 1, pp. 1–16, 2021. [Google Scholar]
10. R. Anguelov, C. Dufourd and Y. Dumont, “Mathematical model for pest-insect control using mating disruption and trapping,” Applied Mathematical Modelling, vol. 52, pp. 437–457, 2017. [Google Scholar]
11. J. P. Ntahomvukiye, A. Temgoua and S. Bowong, “Study of the population dynamics of Busseola fusca, maize pest,” Acta Biotheoretica, vol. 66, no. 4, pp. 379–397, 2018. [Google Scholar]
12. S. Xiang, Y. Pei and X. Liang, “Analysis and optimization based on a sex pheromone and pesticide pest model with gestation delay,” International Journal of Biomathematics, vol. 12, no. 5, pp. 1950054, 2019. [Google Scholar]
13. M. D. Tapi, L. Bagny-Beilhe and Y. Dumont, “Miridae control using sex-pheromone traps. Modeling, analysis and simulations,” Nonlinear Analysis: Real World Applications, vol. 54, pp. 103082, 2020. [Google Scholar]
14. M. El-Shahed and A. Al-Dubiban, “Mathematical modelling of lesser date moth using sex pheromone traps and natural enemies,” Mathematical Problems in Engineering, vol. 2021, pp. 1–14, 2021. [Google Scholar]
15. J. Cresson and A. Szafran´ska, “Discrete and continuous fractional persistence problems the positivity property and applications,” Communications in Nonlinear Science and Numerical Simulation, vol. 44, pp. 424–448, 2017. [Google Scholar]
16. H. Li, L. Zhang, C. Hu, Y. Jiang and Z. Teng, “Dynamical analysis of a fractional-order predator- prey model incorporating a prey refuge,” Journal of Applied Mathematics and Computing, vol. 54, pp. 435–449, 2016. [Google Scholar]
17. M. Sambath, P. Ramesh and K. Balachandran, “Asymptotic behavior of the fractional order three species prey-predator model,” International Journal of Nonlinear Sciences and Numerical Simulation, vol. 19, pp. 721–733, 2018. [Google Scholar]
18. S. K. Choi, B. Kang and N. Koo, “Stability for Caputo fractional differential systems,” Abstract and Applied Analysis, vol. 2014, pp. 1–6, 2014. [Google Scholar]
19. P. V. Driessche and J. Watmough, “Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission,” Mathematical Biosciences, vol. 180, pp. 29–48, 2002. [Google Scholar]
20. J. Huo, H. Zhao and L. Zhu, “The effect of vaccines on backward bifurcation in a fractional order HIV model,” Nonlinear Analysis: Real World Applications, vol. 26, pp. 289–305, 2015. [Google Scholar]
21. A. Matouk, “Stability conditions, hyperchaos and control in a novel fractional order hyperchaotic system,” Physics Letters A, vol. 373, no. 25, pp. 2166–2173, 2009. [Google Scholar]
22. L. Perko, Differential equations and dynamical systems. Vol. 7, Springer Science & Business Media, 2013. [Google Scholar]
23. W. M. Liu, “Criterion of Hopf bifurcations without using eigenvalues,” Journal of Mathematical Analysis and Applications, vol. 182, no. 1, pp. 250–256, 1994. [Google Scholar]
24. W. Wang, S. Cheng, Z. Guo and X. Yan, “A note on the continuity for Caputo fractional stochastic differential equations,” Chaos: An Interdisciplinary Journal of Nonlinear Science, vol. 30, no. 7, pp. 073106, 2020. [Google Scholar]
25. T. Doan, P. Huong, P. Kloeden and A. Vu, “Euler-Maruyama scheme for Caputo stochastic fractional differential equations,” Journal of Computational and Applied Mathematics, vol. 380, pp. 112989, 2020. [Google Scholar]
26. H. Aminikhah, A. H. R. Sheikhani, T. Houlari and H. Rezazadeh, “Numerical solution of the distributed-order fractional Bagley-Torvik equation,” IEEE/CAA Journal of Automatica Sinica, vol. 6, no. 3, pp. 760–765, 2017. [Google Scholar]
27. M. Hou, J. Yang, S. Shi and H. Liu, “Logical stochastic resonance in a nonlinear fractional-order system,” European Physical Journal Plus, vol. 135, no. 9, pp. 747, 2020. [Google Scholar]
28. I. Podlubny, Fractional Differential Equations. New York, NY, USA: Academic Press, 1999. [Google Scholar]
29. C. Huang and M. Stynes, “Error analysis of a finite element method with GMMP temporal discretisation for a time-fractional diffusion equation,” Computers & Mathematics with Applications, vol. 79, no. 9, pp. 2784–2794, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |