DOI:10.32604/csse.2022.019240

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.019240 |  |
| Article |
Design of Neural Network Based Wind Speed Prediction Model Using GWO
1Department of Computer Science and Engineering, Sri Ramakrishna Engineering College, Coimbatore, 641022, India
2Department of Computer Science and Engineering, PSG Institute of Technology and Applied Research, Coimbatore, 641062, India
*Corresponding Author: R. Kingsy Grace. Email: kingsygrace.r@srec.ac.in
Received: 07 April 2021; Accepted: 14 May 2021
Abstract: The prediction of wind speed is imperative nowadays due to the increased and effective generation of wind power. Wind power is the clean, free and conservative renewable energy. It is necessary to predict the wind speed, to implement wind power generation. This paper proposes a new model, named WT-GWO-BPNN, by integrating Wavelet Transform (WT), Back Propagation Neural Network (BPNN) and Grey Wolf Optimization (GWO). The wavelet transform is adopted to decompose the original time series data (wind speed) into approximation and detailed band. GWO – BPNN is applied to predict the wind speed. GWO is used to optimize the parameters of back propagation neural network and to improve the convergence state. This work uses wind power data of six months with 25, 086 data points to test and verify the performance of the proposed model. The proposed work, WT-GWO-BPNN, predicts the wind speed using a three-step procedure and provides better results. Mean Absolute Error (MAE), Mean Squared Error (MSE), Mean absolute percentage error (MAPE) and Root mean squared error (RMSE) are calculated to validate the performance of the proposed model. Experimental results demonstrate that the proposed model has better performance when compared to other methods in the literature.
Keywords: Wind speed; wavelet transform; back propagation neural network; grey wolf optimization; time series
The rapid growth of the world economy, the renewable energy sources such as solar, tidal, wind and geothermal energy has significantly shown its importance around the globe. Wind power is one of the most powerful ways to generate electricity from renewable sources. The amount of wind around the wind farm must be estimated to forecast the wind power. Wind speed is an important factor that affects the wind power. The other factors include location of wind farm and weather. There are two types of wind speed predictions, namely, short term and long term based on the time scale of the prediction. The farmer is more reliable than the later [1]. Numerical-Weather-Predictions [2] are based on physical methods and the statistical methods. They are also based on the historical data and not on the meteorological data such as temperature, pressure, surface conditions and obstacles. Time series data are used for the estimation of wind speed in statistical methods along with artificial intelligence.
Statistical and physical methods are also named as direct and indirect methods respectively. In direct method, there is a linear relationship among input time series data and the predicted results. Some of the direct method for prediction of wind speed are presented in [3–9]. Examples of indirect method for wind speed forecasting are reported in [10–12]. Both physical and statistical methods are also combined to provide better prediction of wind speed [13]. The reliability of the wind speed prediction is improved in hybrid approaches in Osório et al. [14–17]. Most of the proposed techniques use single learners and those are not steady in most of the changing weather conditions. If more predictors are included simultaneously, it increases the prediction error.
In Zhou et al. [17], after splitting into low frequency and high frequency data, two networks are used to train the input time series data. This will increase the prediction model's memory usage and computation cost. The proposed model WT-GWO-BPNN has single network with two hidden layers. To avoid the local minima and the over fitting problem, a Meta-heuristic algorithm, GWO is used. The steps involved in the proposed work are as follows: (i) A reliable wind speed prediction strategy is proposed and the wind speed is predicted with the help of wavelet transform, GWO and back propagation neural network. (ii) WT-GWO-BPNN is suitable for any type of wind farms and can be adopted for both wind power prediction and wind speed prediction. This paper is organized as follows. The related work in the literature is discussed in Section 2. Section 3 explains the preliminaries such as WT, BPNN and GWO. The proposed model WT-GWO-BPNN is presented in section 4 and the results are summarized in section 5. Section 6 concludes the paper with future directions.
WT is one of the prevailing tools to analyze variety of resolution images and time series data. During wavelet analysis the input signal is decomposed into shifted wavelets and scaled wavelets. Spare representation and non-redundant computation are the advantages of DWT than the Fourier Transform (FT), and Gabor transform while extracting features. DWT has been successfully used for feature extraction and achieve better results when compared to other methods [18]. DWT is a suitable method for extracting features of time series data. Furthermore, it allows the analysis of time series data on well localized in both time and frequency domain. Input data decomposition is done using Low Pass Filter (LPF) and High Pass Filter (HPF). At first level decomposition input image is divided into two components: approximation and detailed sub-band. The output of LPF is approximation band and the output of HPF is detailed sub-band. The vertical band, horizontal band and diagonal band are the three sub-bands in the detailed input signal. In approximation band further decomposition is done to divide into approximation and detailed data, and so on. The levels of decomposition can be determined based on the application [18].
BPNN is a variety of ANN, supervised learning, multilayer feed-forward network. The layers in BPNN are input layer, multiple hidden layers and output layer [19]. Fig. 1 shows the general structure of BPNN. The input data is processed by the input layer. All the neurons in the input layer are communicated with the hidden layer through a communication link named weight. The weight is multiplied with the input and the result is added with bias. Output neuron is computed based on the activation function.

Figure 1: General structure of BPNN
Eq. (2) defines the output of the neuron K. Xi indicates the input, Wi indicates the weights, input adder is represented by I, B is bias, output is Y and the activation function is ∅. In this method, BPNN is designed with an input layer, two hidden layers and an output layer. The number of neurons in the input layer depends on the number of feature vectors. The number of hidden layers and their neurons. Each hidden layer consists of 25 neurons. The number of output neurons in the output layer is equal to the number of registered individuals. Hidden layers activation function is Tan sigmoidal function. Purelin is employed as a transfer function in the output layer.
The GWO is one of the meta-heuristic algorithms based on the grey wolf’s hunting style [3]. The four varieties of grey wolves are: (i) alpha (ii) beta (iii) delta and (iv) omega. These variations are based on their leadership ladder. The hunting tread of grey wolves are: (i) searching for victim (ii) encircling victim and (iii) attacking the victim. Among the three classifications of the meta-heuristics, GWO comes under Swarm Intelligence (SI) algorithms and the others are evolutionary algorithms and physics-based algorithms. Some of the SI algorithms [20] are: MBO [21], AFSA [22], Termite Algorithm [23], Wasp Swarm Algorithm [24], Monkey Search [25], BCPA [26], Cuckoo Search [27], DPO [28], Firefly Algorithm [29], BMO [30], Krill Herd [31], FOA [32]. The Canidae family of grey wolf is in the crest of the food chain. Wolf are lived in a group average of 5 to 12. Fig. 2 shows the social ladder of grey wolf. The alphas are leaders and either male or female are in charge for all activities. The decision made by the alphas is followed by the betas. Scapegoat role is played by the omega which is in the lowest ladder. Delta is lower to alpha and beta and upper to omega. Deltas are usually the boundary keepers.
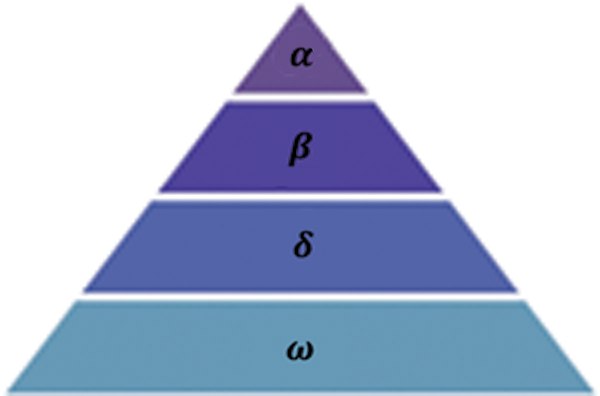
Figure 2: Grey wolf ladder [20]
In GWO α is the fittest solution and β, δ and Ω are the subsequent solutions. The mathematical equations in the GWO are given Eqs. (3) to (9) [20].
Where A and C are the coefficient vectors. The position of victim is Xp and the position of grey wolf is X. Both Xp and X are vectors. Vector a is decline from 2 to 0. The random vectors r1 and r2 takes the values in the range of [0,1]. The GWO algorithm is used to select the best solution from all the iterations. Coefficients A and C are random values and have different hyper-sphere for each random value. The GWO algorithm provides the possible solution to find the position of the victim and is shown in Fig. 3.

Figure 3: GWO algorithm
This section presents details of some of the prediction models of wind speed available in the literature. Jianguo Zhou et al. have proposed a wind power forecasting named ESMD-PSO-ELM [17]. It is a combination of three algorithms. The ESMD algorithm is used to split the wind energy into two components such as one residual and many intrinsic mode functions [17]. Both the components act as inputs to the hybrid PSO-ELM. The model developed in Zhou et al. [17] used the one-month data of April 2016 which has 2880 observations. The dataset was from china. The proposed model ESMD-PSO-ELM was compared with eight existing models in terms of MAPE (4.76), MAE (2.23) and RMSE (2.70). Aqsa and Asifullah have presented a wind power prediction model using ATL-DNN [33]. This method is a hybrid of transfer learning and deep learning. Intra TL and inter TL are the two classification of base learners training. The proposed algorithm is implemented using Matlab 2015(b) with DBN-Toolbox. The proposed method provides better results, when compared to ARIMA and SVR [33].
Han et al. [34] have introduced a wind power prediction based on Principle Component Analysis and Phase Space Reconstruction (PSR). The former used phase dimension and the latter used phase space reconstruction. The variance of forecasting is very small when compared to other approaches. The machine learning methods such as BPN, RBF and NARX are used for wind speed forecasting in [35] by Senthil Kumar. Significant features are selected from data set to minimize the complications in the prediction model. The proposed models demonstrated good results in terms of RMSE and MAE. Mutual information (MI) based feature selection is carried out. Six models are tested and the NARX with MIFS performs better than other algorithms. Wenlong Fu et al. [36] have introduced using GWO-SCA algorithm. The developed algorithm predicts the wind speed for short-term and multi-step. The designed method is named as IHGWOSCA and estimated optimal values are in PSR and ELM. The OVMD model performs better in terms of RMSE, MAE and MAPE than the standard models and PSR and ELM is better for multi-step prediction. IHGWOSCA converges faster than the other models [36].
Fredy H. Martínez S et al. [37] have discussed the prediction of wind speed with the help of LSTM. The wind energy is based on the speed of the wind in the corresponding area which is having wind farm. The proposed model is implemented using TensorFlow and backend with Keras. 10 years data is collected from Guajira and is the lowest electrical supply area. By predicting the wind speed, the power station in Jepírachi wind farm [38] can estimate the power generation through the farm. The LSTM method is not compared with any other methods but the RMSE value of LSTM is calculated as 4.223 km/h. Hao-FanYang et al. [39] have used E-S-ELM model to predict the wind speed. The proposed model is the combination of auto-encoders and ELM. This deep learning-based method uses 50 hidden layers and suggested to use shared hidden layers to improve the performance.
Jinli Dou et al. [40] have introduced CNN based wind speed prediction model for short-term. CNN plays a major role for improving time correlation between data among different stations. The prediction error rate is less in CNN. Hourly prediction on wind speed is proposed in [41] by Ghorban et al. using machine learning algorithm. Multi-Layer Perceptron (MLP) with feed forward technique, Genetic Programming (GP), multiple linear regression and Persistence method are used in the proposed system. seven years data is used for training and one year data is used for testing. 14 models are tested for both ANN and GP. Hui Liu et al. [42] have developed a wind prediction algorithm based on SSA, CNN, GRU and SVR was named SSA-CNNGRU-SVR. The input wind speed data is split into trend component using CNNGRU and detailed component using SVR. Even though SSA is extracting features efficiently, the proposed model predicts wind speed with satisfactory level.
Younes et al. [43] have explored both temporal and spatial forecasting of wind speed using ANN. The BPNN, RBFNN and ANFIS prediction models are evaluated. The BPNN learning algorithm [43] uses termination criteria to reduce the error rate during training. RBFNN is similar to BPNN and the algorithm of RBFNN is in Haque [44]. The properties of ANN and fuzzy is combined in ANFIS. The short-term wind prediction model is performed in two groups with the knowledge from the preceding step. The BPNN model prediction is efficient than other models RBFNN and ANFIS. Deep learning-based prediction of wind is explored in [45]. Tao et al. have tested the proposed neural network model deep belief network (DBN) to reduce the ambiguity and volatility nature of the wind power production. The prediction errors are very less in the proposed DBN method.
In order to predict wind power, a hybrid deep learning neural network system has proposed in Liu et al. [46]. The hybrid model consists of WT, Elman network and LSTM. After WT, the low frequency is given as input to LSTM and high frequency is given as input to elman network. Results are tabulated for 3-step predictions. Low and high frequencies are given to two separate networks and requires more memory during training. In Basaran Filik et al. [47], a multi-variable model using ANN is suggested. Three types of ANN network are tested for three substations in Eskisehir. The proposed network in Fonte Deea et al. [48] uses three-layer feed forward pattern and the MSE is less in training, testing and validation set. The DNN-MRT algorithm is proposed by Qureshi et al. in [49] for wind energy prediction wherein base-regressors and meta-regressors are used. The former is deep auto-encoders for training and the latter is DBN for learning. The transfer learning concept is used for reducing the shortcomings and the better learning is ensured by the proposed method ensemble based DNN-MRT. Tab. 1 presents the comparison on various wind speed prediction methods in the literature.
The proposed model WT-GWO-BPNN is used to predict the wind speed. The WT algorithm is used for decomposing the input signal ie., time series data. GWO-BPNN is used for predicting the wind speed based on the characteristics of the time series data. In this model GWO is used for tuning the weights during the BPNN training. The wind speed data is taken from the publicly available data sources for six months. Tab. 2 describes the statistical values of the input wind speed data. The flow of WT-GWO-BPNN is shown in Fig. 4.

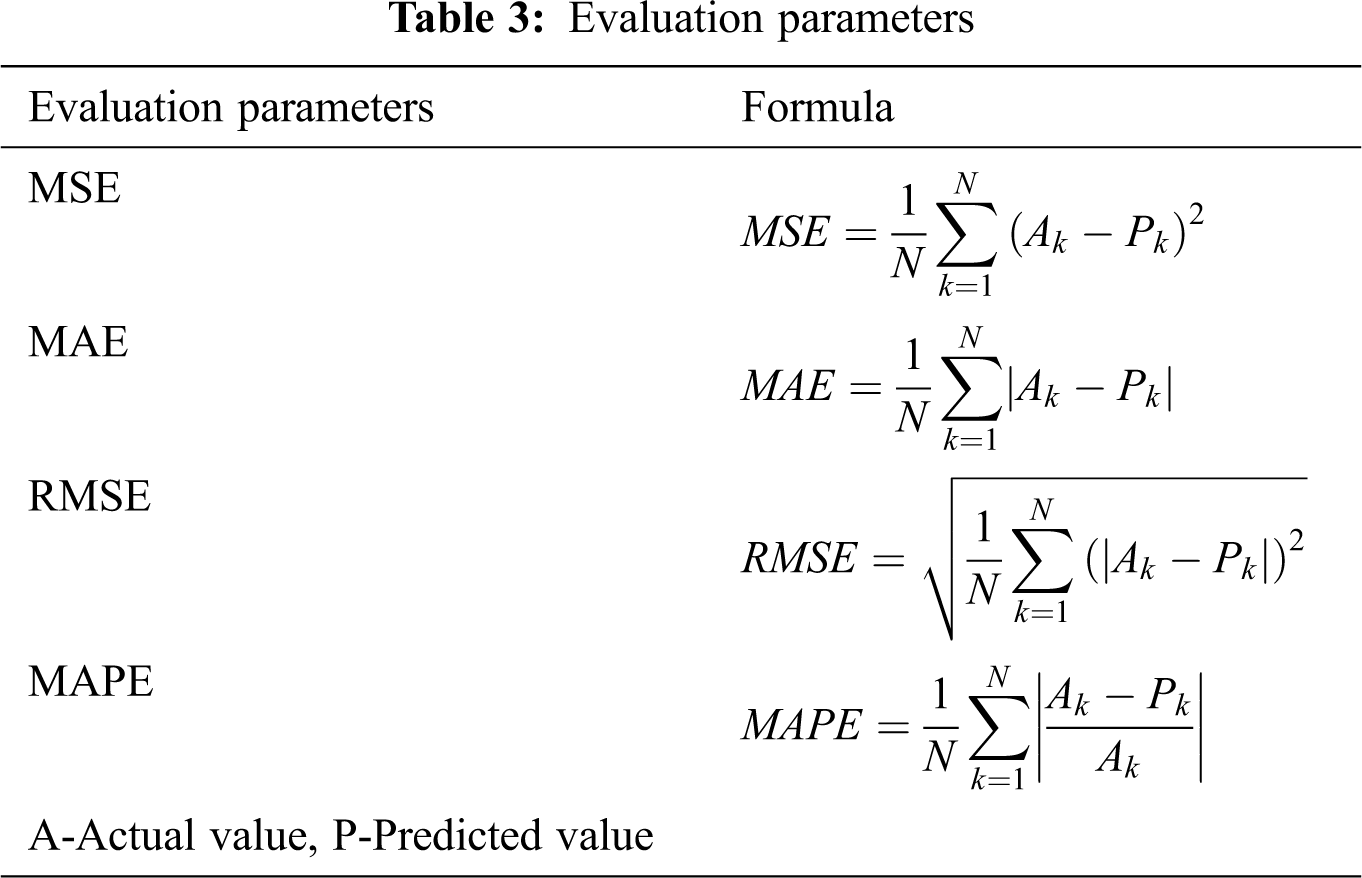
Usually, MAPE – Mean Absolute Percentage Error, MAE – Mean Absolute Error, RMSE – Root Mean Square Error and MSE – Mean Square Error are the performance measures for any predictive model [17]. At each input data point, the relative mean value is called as MAPE. The average distance between the actual value and the predicted value is called as MAE. The average magnitude of error is MSE and quadratic scoring of MSE is RMSE. The lower the error values show that there is less variation between the predicted and actual values [50]. Tab. 3 describes the evaluation parameters such as MSE, MAE, RMSE and MAPE used in the proposed model.
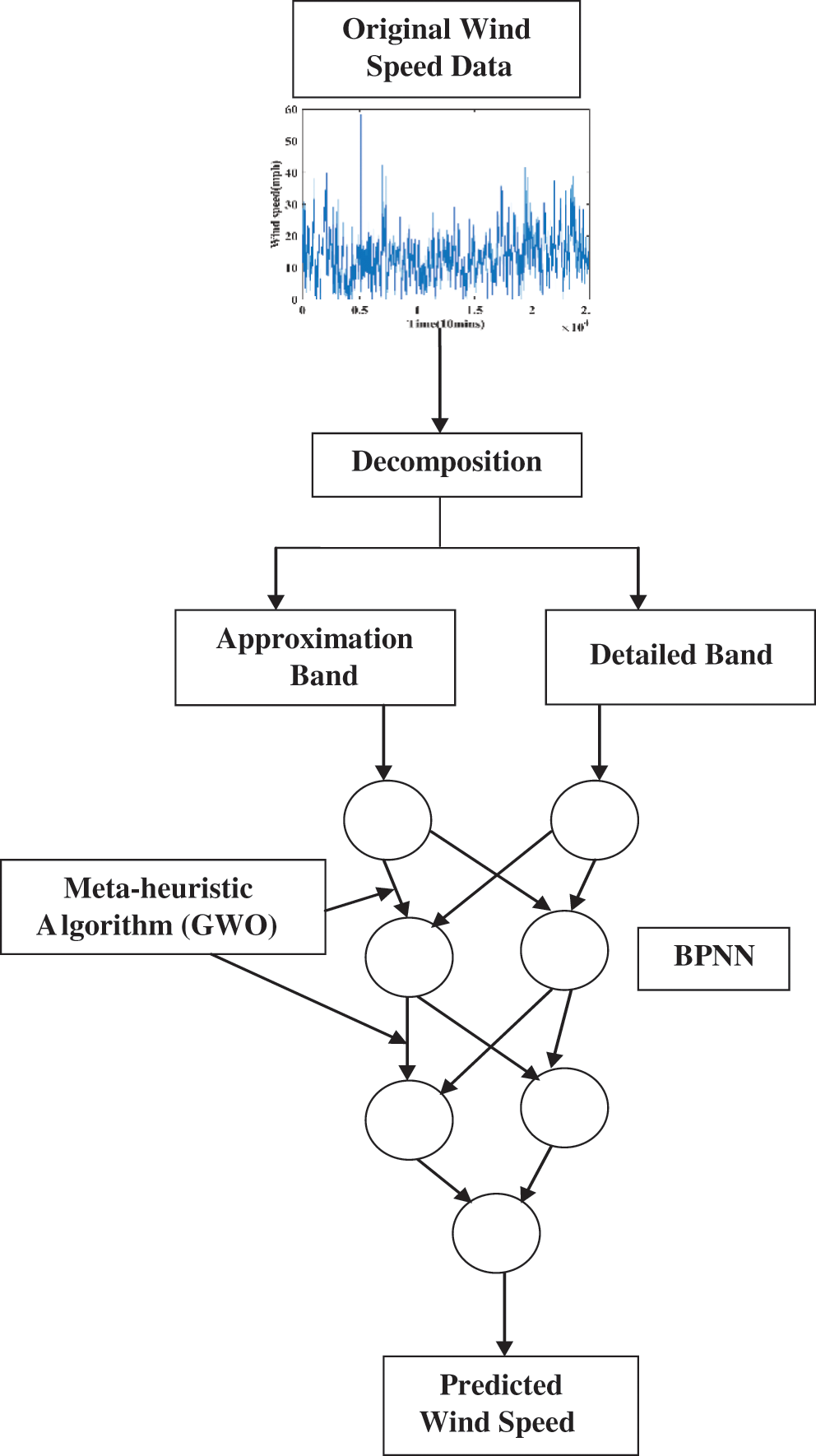
Figure 4: The flow chart of the proposed WT-GWO-BPNN model
This section deals with the experimental results obtained using the proposed system WT-GWO-BPNN. 25,086 data points are chosen as input for prediction. Seventy percentage of input data points are considered for training and remaining thirty percentage for testing. Fig. 5 indicates the original time series data of wind speed collected from internet sources. Initially, WT is applied on the dataset to split the input data into approximation band and detailed band. Fig. 6 shows the approximation band up to three levels. Fig. 7 indicates the detailed band for three levels. The prediction of training data and the testing data is illustrated in Figs. 8 and 9. From Figs. 8 and 9, it is obtained that the proposed method WT-GWO-BPNN performs better during prediction of wind speed.
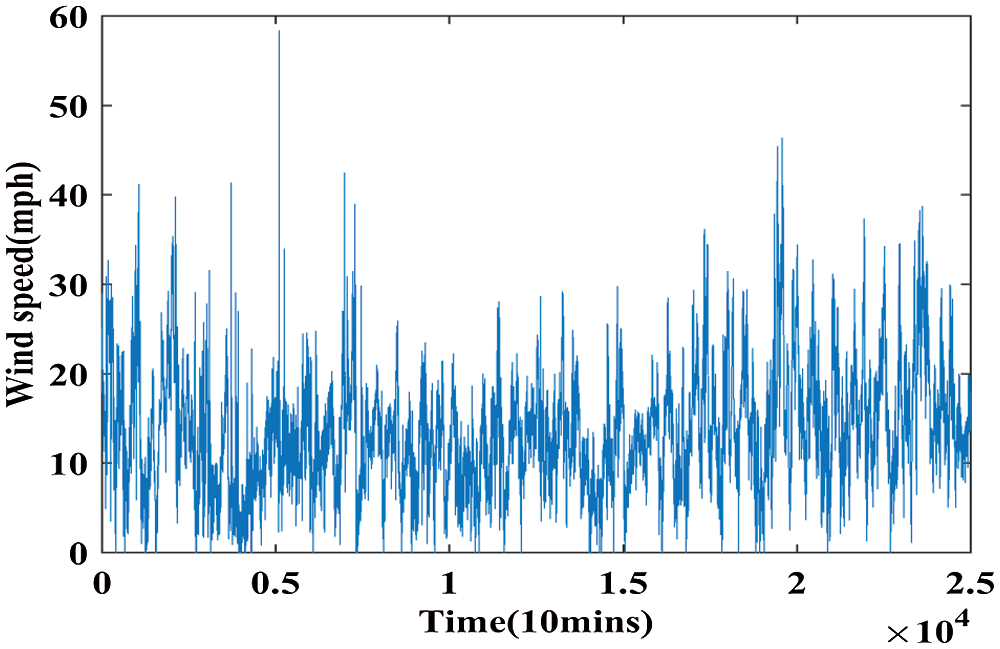
Figure 5: Time series of wind speed
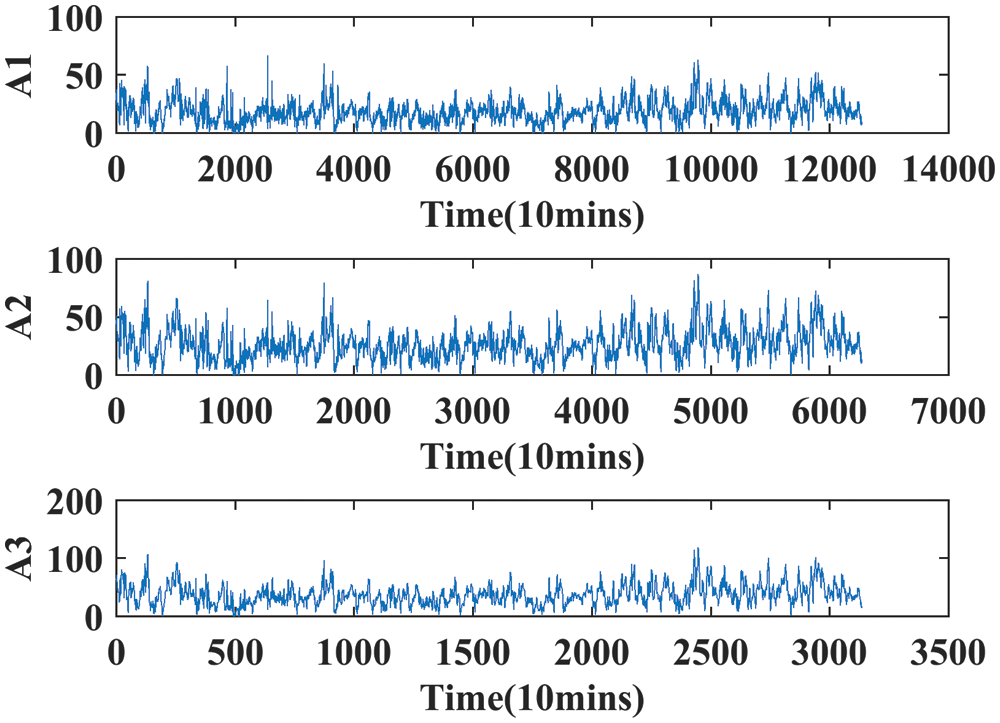
Figure 6: The approximation band of winder speed using WT
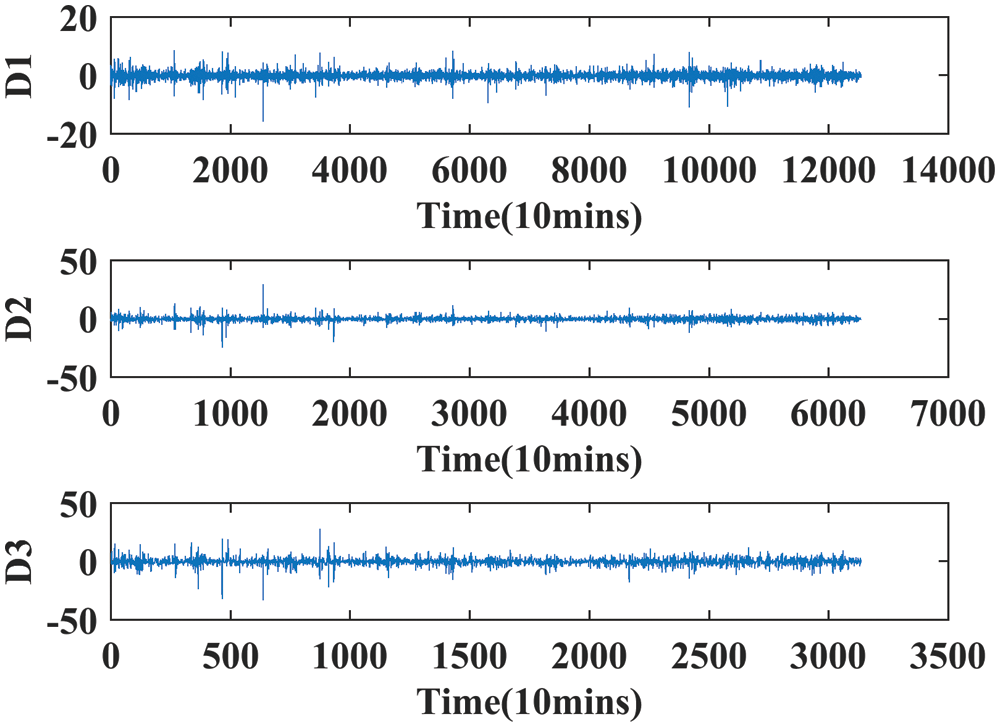
Figure 7: The detailed band of winder speed using WT
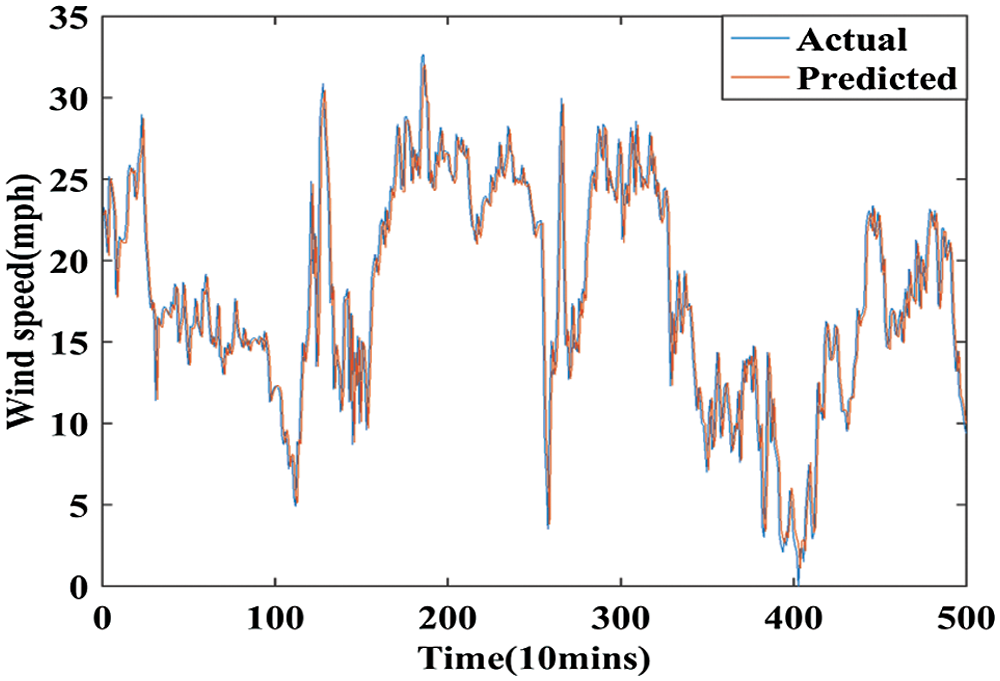
Figure 8: The prediction results of training data
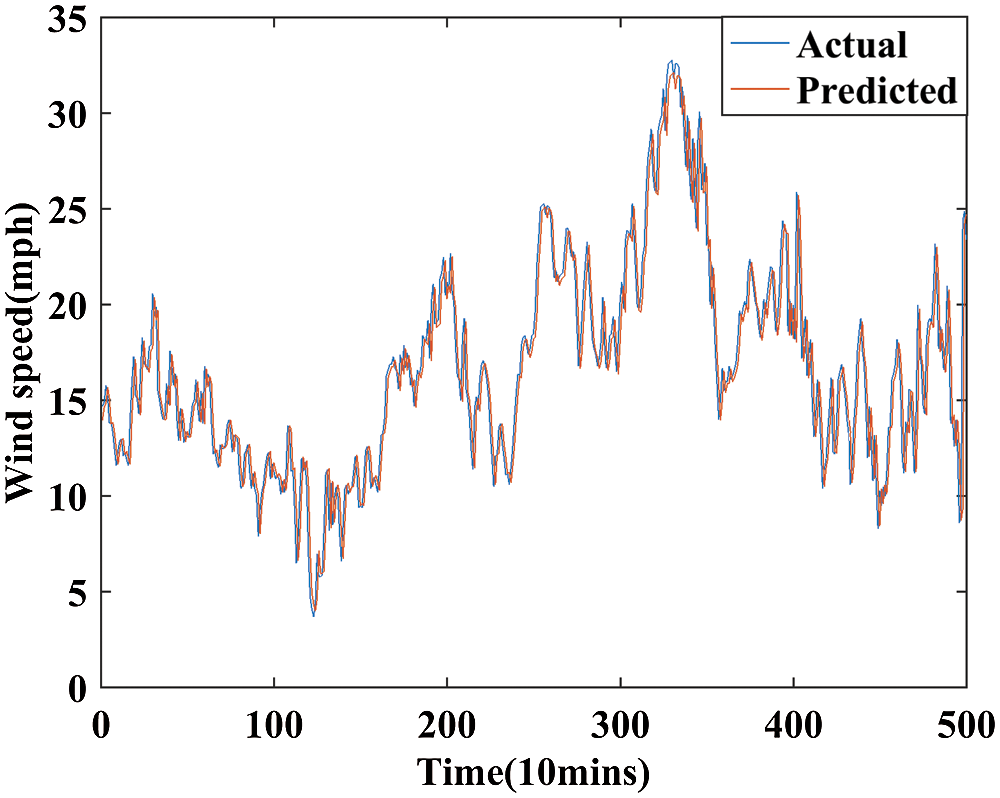
Figure 9: The prediction results of testing data
The error for training and testing data is shown in Figs. 10 and Fig. 11 respectively. As in Figs. 10 and 11, it is observed that the testing error is very less when compared to the training error. Tab. 4 summarizes 1-step, 2-step and 3-step performance comparison on different performance parameters for the proposed system WT-GWO-BPNN. The proposed system is compared with Elman [46], ARIMA [46], WPD-ELM [17], GRNN [46], EWT-Elman [46] and BPNN [17] in the literature and provides better results in terms of the performance parameters such as MSE, MAE, RMSE and MAPE. From Fig. 12, it is quite clear that the proposed model provides better results than other models taken for comparison.
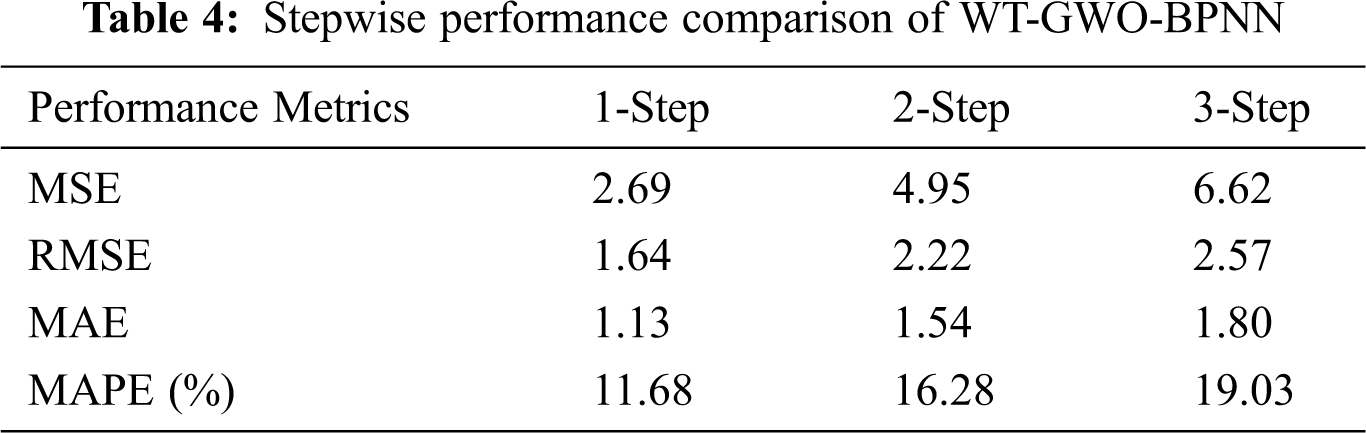
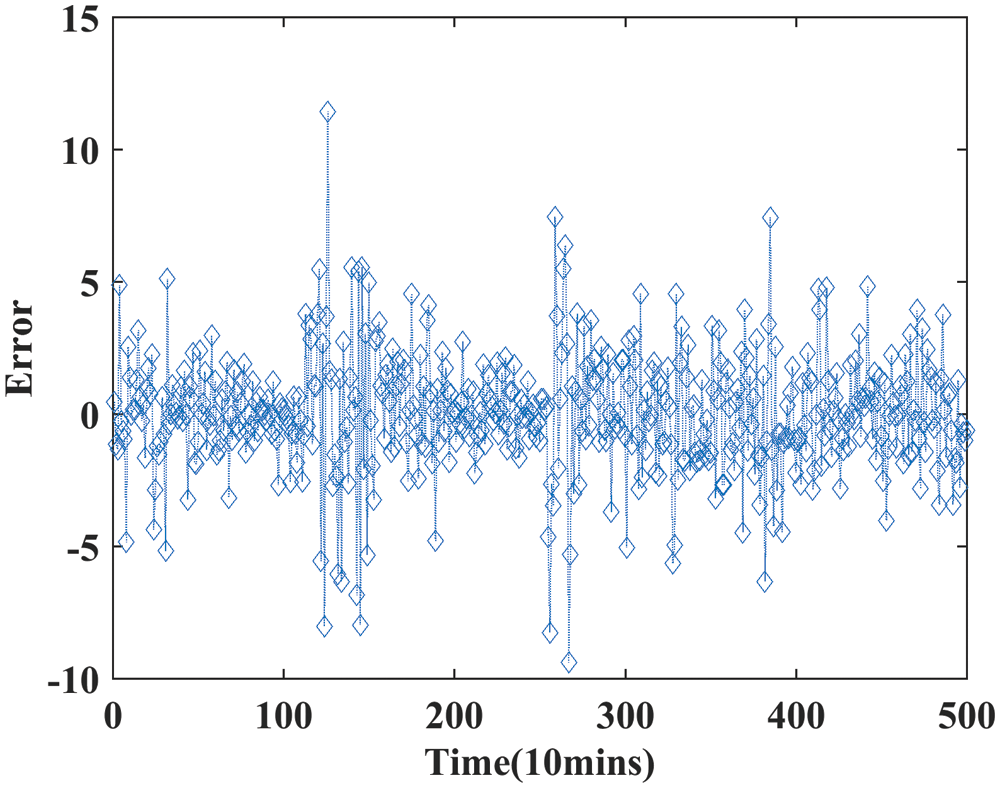
Figure 10: Error for training data
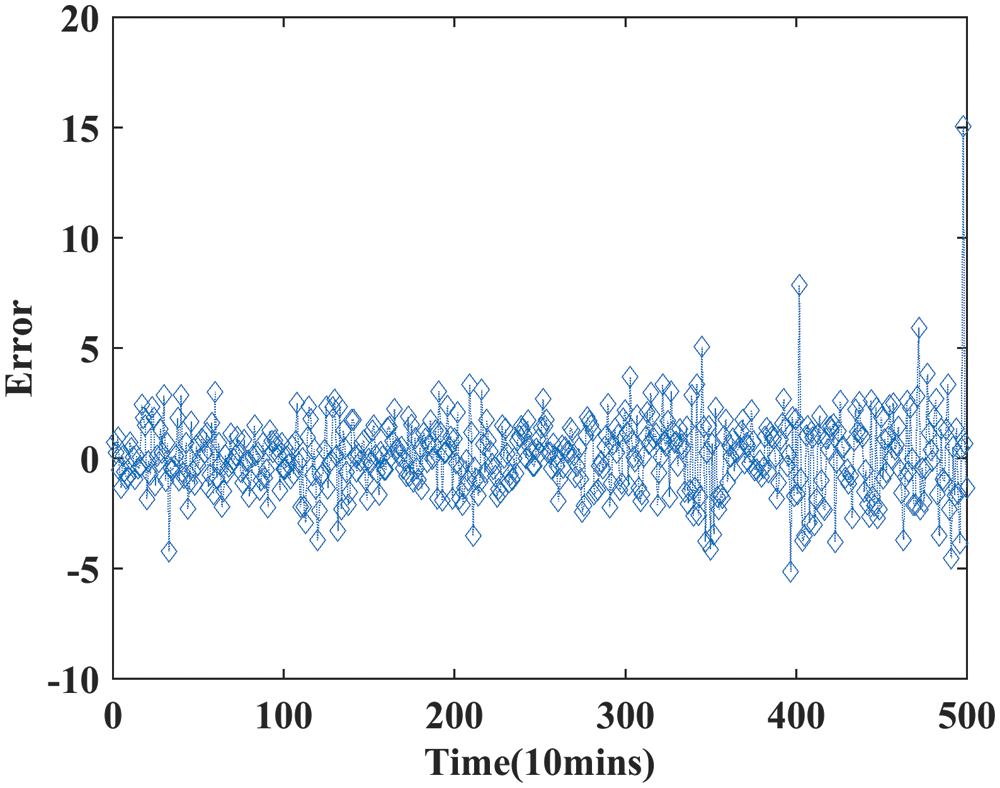
Figure 11: Error for testing data
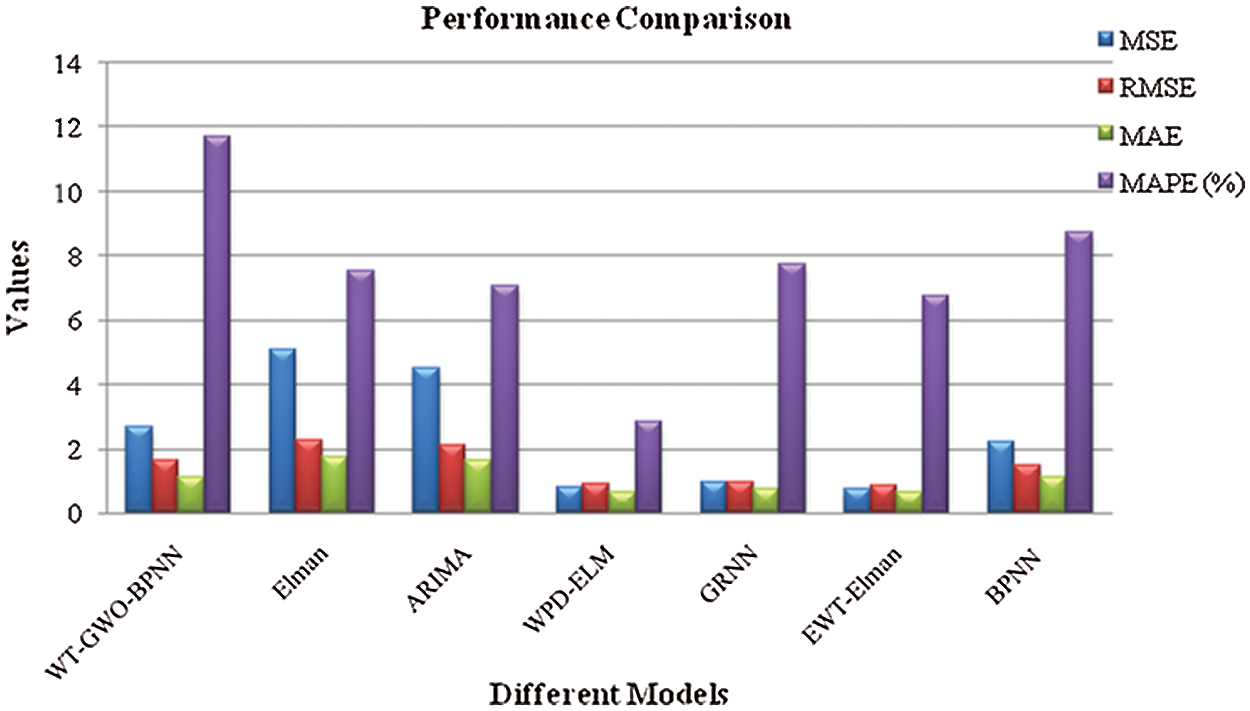
Figure 12: Performance metrics comparison of WT-GWO-BPNN with other models
Wind speed is one of the sources of renewable energy. Wind speed prediction is required to predict wind power. Due to the vague environment, the wind speed prediction is more difficult process. This paper has presented a wind speed prediction model employing a hybrid method named as WT-GWO-BPNN. The proposed method uses six months wind speed data of about 25,086 samples for prediction. The performance of the proposed model is evaluated and compared with the existing models in terms of MSE, MAE, RMSE and MAPE. It is observed that the proposed model poses low MAE when compared to all other models such as Elman, ARIMA, WPD-ELM, GRNN, EWT-Elman and BPNN. Additionally, the value of MSE and RMSE is better than Elman, ARIMA and BPNN. Stepwise performance comparison of WT-GWO-BPNN proved that the proposed method is used for prediction of wind speed during climatic changes. In future research, deep neural network methodologies can be applied with more sample data to improve the prediction of wind speed.
Acknowledgement: The authors acknowledge the support and encouragement of the management and Principal of Sri Ramakrishna Engineering College. We would also like to thank the referees and the editors for their helpful comments and suggestions.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. H. Liu, Z. Duan, F. Z. Han and Y. F. Li, “Big Multi-step wind speed forecasting model based on secondary decomposition, ensemble method and error correction algorithm,” Energy Conversion and Management, vol. 156, pp. 525–541, 2018. [Google Scholar]
2. M. Lange and U. Focken, “New developments in wind energy forecasting,” IEEE Power and Energy Society, General Meeting - Conversion and Delivery of Electrical Energy, Energy 21st Century, pp. 1–8, 2008. [Google Scholar]
3. M. A. Taher and N. M. Khooban, “Probabilistic wind power forecasting using a novel hybrid intelligent method,” Neural Computing and Applications, vol. 30, pp. 473–485, 2018. [Google Scholar]
4. P. L. Johnson, M. Negnevitsky and K. M. Muttaqi, “Short term wind power forecasting using adaptive neuro-fuzzy inference systems,” Australasian Universities Power Engineering Conf., Australas. University, pp. 1–6, 2007. [Google Scholar]
5. J. J. Wang, W. Zhang, Y. Li, J. J. Wang and Z. Dang, “Forecasting wind speed using empirical mode decomposition and elman neural network,” Applied Soft Computing, vol. 23, pp. 452–459, 2014. [Google Scholar]
6. J. Zhou, J. Shi and G. Li, “Fine tuning support vector machines for short-term wind speed forecasting,” Energy Conversion and Management, vol. 52, pp. 1990–1998, 2011. [Google Scholar]
7. K. Bhaskar and S. N. Singh, “AWNN-Assisted wind power forecasting using feed-forward neural network,” IEEE Transactions on Sustainable Energy, vol. 3, pp. 306–315, 2012. [Google Scholar]
8. K. Mohammadi, S. Shamshirband, P. L. Yee, D. Petković, M. Zamani et al., “Predicting the wind power density based upon extreme learning machine,” Energy, vol. 86, pp. 232–239, 2015. [Google Scholar]
9. J. F. Torres, A. M. Fernández, A. Troncoso and F. Martínez-Álvarez, “Deep learning-based approach for time series forecasting with application to electricity load,” Int. Work-Conf. on the Interplay Between Natural and Artificial Computation, pp. 203–212, 2017. [Google Scholar]
10. H. Chitsaz, N. Amjady and H. Zareipour, “Wind power forecast using wavelet neural network trained by improved clonal selection algorithm,” Energy Conversion and Management, vol. 89, pp. 588–598, 2015. [Google Scholar]
11. A. U. Haque, M. H. Nehrir and P. Mandal, “A hybrid intelligent model for deterministic and quantile regression approach for probabilistic wind power forecasting,” IEEE Transactions on Power Systems, vol. 29, pp. 1663–1672, 2014. [Google Scholar]
12. E. Mangalova and E. Agafonov, “Wind power forecasting using the k-nearest neighbors’ algorithm,” International Journal of Forecasting, vol. 30, pp. 402–406, 2014. [Google Scholar]
13. X. Wang, P. Guo and X. Huang, “A review of wind power forecasting models,” Energy Procedia, vol. 12, pp. 770–778, 2011. [Google Scholar]
14. G. J. Osório, J. C. O. Matias and J. P. S. Catalão, “Short-term wind power forecasting using adaptive neuro-fuzzy inference system combined with evolutionary particle swarm optimization, wavelet transform and mutual information,” Renewable Energy, vol. 75, pp. 301–307, 2015. [Google Scholar]
15. A. Troncoso, “Pattern sequence similarity-based techniques for wind speed forecasting pattern sequence similarity-based techniques for wind speed forecasting,” Int. Work-Conf. on Time Series (ITISE), vol. 2, pp. 789–794, 2017. [Google Scholar]
16. H. Peng, F. Liu and X. Yang, “A hybrid strategy of short-term wind power prediction,” Renewable Energy, vol. 50, pp. 590–595, 2013. [Google Scholar]
17. J. Zhou, X. Yu and B. Jin, “Short-term wind power forecasting: A new hybrid model combined extreme-point symmetric mode decomposition, extreme learning machine and particle swarm optimization,” Sustainability, vol. 10, pp. 3202, 2018. [Google Scholar]
18. C. Lin, Liu, “A tutorial of the wavelet transform,”Feb 23,2010. [Google Scholar]
19. K. L. Du and M. N. S. Swamy, “Multilayer perceptron: Architecture and error backpropagation,” Neural networks and statistical learning, pp. 83–126, 2014. [Google Scholar]
20. S. Mirjalili, S, Mohammad Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, pp. 46–61, 2014. [Google Scholar]
21. H. A. Abbass, “MBO: Marriage in honey bees’ optimization – A haplometrosis polygynous swarming approach,” in Proc. of the Evolutionary computation congress, pp. 207–214, 2001. [Google Scholar]
22. X. Li, “A new intelligent optimization-artificial fish swarm algorithm,” Doctor thesis. Zhejiang University of Zhejiang, China, 2003. [Google Scholar]
23. M. Roth, “Termite: A swarm intelligent routing algorithm for mobile wireless Ad-Hoc networks, ” in Stigmergic Optimization, J. Kacprzyk (ed.vol.31, pp. 155–184,2006. [Google Scholar]
24. P. C. Pinto, T. A. Runkler and J. M. Sousa, “Wasp swarm algorithm for dynamic MAX-SAT problems,” in 8th Int. Conf. on Adaptive and Natural Computing Algorithms, Part I, pp. 350–357, 2007. [Google Scholar]
25. A. Mucherino and O. Seref, “Monkey search: A novel metaheuristic search for global optimization,” in AIP Conf. Proc., pp. 162, 2007. [Google Scholar]
26. X. Lu and Y. Zhou, “A novel global convergence algorithm: Bee collecting pollen algorithm,” Advanced Intelligent Computing Theories and Applications with Aspects of Artificial Intelligence, ICIC 2008, Springer, pp. 518–525, 2008. [Google Scholar]
27. X. S. Yang and S. Deb, “Cuckoo search via lévy flights,” Nature & Biologically Inspired Computing, vol. 1, pp. 210–214, 2009. [Google Scholar]
28. Y. Shiqin, J. Jianjun and Y. Guangxing, “A dolphin partner optimization,” in WRI Global Congress on Intelligent systems, pp. 124–1282009. [Google Scholar]
29. X. S. Yang, “Firefly algorithm, stochastic test functions and design optimization,” International Journal Bio-Inspired Computing, vol. 2, pp. 78–84, 2010. [Google Scholar]
30. A. Askarzadeh and A. Rezazadeh, “A new heuristic optimization algorithm for modeling of proton exchange membrane fuel cell: Bird mating optimizer,” International Journal of Energy Research, vol. 37, no. 10, pp. 1196–1204, 2013. [Google Scholar]
31. A. H. Gandomi and A. H. Alavi, “Krill Herd: A new bio-inspired optimization algorithm,” Communications in Nonlinear Science and Numerical Simulation, vol. 17, no. 12, pp. 4831–4845, 2012. [Google Scholar]
32. W. T. Pan, “A new fruit fly optimization algorithm: Taking the financial distress model as an example,” Knowledge-Based Systems, vol. 26, pp. 69–74, 2012. [Google Scholar]
33. A. S. Qureshi and A. Khan, “Adaptive transfer learning in deep neural networks: Wind power prediction using knowledge transfer from region to region and between different task domains,” Computational Intelligence, vol. 5, no. 4, pp. 1088–1112, 2019. [Google Scholar]
34. L. Han, C. E. Romero and Z. Yao, “Wind power forecasting based on principle component phase space Reconstruction,” Renewable Energy, vol. 81, pp. 737–744, 2015. [Google Scholar]
35. P. Senthil Kumar, “Improved prediction of wind speed using machine learning,” EAI Endorsed Transactions on Energy Web, vol. 6, no. 23, pp. 1–7, 2018. [Google Scholar]
36. W. Fu, K. Wang, C. Li and J. Tan, “Multi-step short-term wind speed forecasting approach based on multi-scale dominant ingredient chaotic analysis, improved hybrid GWO-SCA optimization and ELM,” Energy Conversion and Management, vol. 187, pp. 356–377, 2019. [Google Scholar]
37. F. H. Martínez, C. A. Hernández and F. Martínez, “Multivariate wind speed forecasting with LSTMs for wind farm performance estimation,” International Journal of Engineering and Technology (IJET), vol. 10, no. 6, pp. 1626–1632, 2019. [Google Scholar]
38. Y. Ulianov and S. Laín, “Small signal stability analysis of jepirachi wind park,” IEEE Int. Sym. on Alternative Energies and Energy Quality (SIFAE 2012), pp. 1–6, 2012. [Google Scholar]
39. H. F. Yang and Y. P. Phoebe Chen, “Representation learning with extreme learning machines and empirical mode decomposition for wind speed forecasting methods,” Artificial Intelligence, vol. 277, pp. 103– 176, 2019. [Google Scholar]
40. J. Dou, C. Liu and B. Wang, “Short-term wind power forecasting based on convolutional neural networks,” 2nd Int. Sym. on Resource Exploration and Environmental Science, vol. 170, pp. 1–6, 2018. [Google Scholar]
41. M. A. Ghorbani, R. Khatibi, M. H. FazeliFard, L. Naghipour and O. Makarynskyy, “Short-term wind speed predictions with machine learning techniques,” Meteorology and Atmospheric Physics, vol. 128, no. 1, pp. 57–22, 2015. [Google Scholar]
42. H. Liu, X. Mi, Y. Li, Z. Duan and Y. Xu, “Smart wind speed deep learning based multi-step forecasting model using singular spectrum analysis, Convolutional gated recurrent unit network and support vector regression,” Renewable Energy, vol. 143, pp. 842–854, 2019. [Google Scholar]
43. Y. Noorollahi, M. Ali Jokar and A. Kalhor, “Using artificial neural networks for temporal and spatial wind speed forecasting in Iran,” Energy Conversion and Management, vol. 115, pp. 17–25, 2016. [Google Scholar]
44. A. U. Haque, “A new strategy for predicting short-term wind speed using soft computing models,” Renewable Sustainable Energy Reviews, vol. 16, no. 7, pp. 4563–4573, 2012. [Google Scholar]
45. Y. Tao, H. Chen and C. Qiu, “Wind power prediction and pattern feature based on deep learning method,” in IEEE PES Asia-Pacific Power and Energy Engineering Conf. (APPEEC2014. [Google Scholar]
46. H. Liu, X. Mi and Y. Li, “Wind speed forecasting method based on deep learning strategy using empirical wavelet transform, long short-term memory neural network and elman neural network,” Energy Conversion and Management, vol. 156, pp. 498–514, 2018. [Google Scholar]
47. U. Basaran Filik and T. Filik, “Wind Speed prediction using artificial neural networks based on multiple local measurements in eskisehir,” 3rd Int. Conf. on Energy and Environment Research, Spain, Energy Procedia, vol. 107, pp. 264–269, 2016. [Google Scholar]
48. P. M. Fonte Deea, G. X. Silva and J. C. Quadrado Deea, “Wind speed prediction using artificial neural networks,” in Proc. of the 6th WSEAS Int. Conf. on Neural Networks, Portugal, pp. 134–139, 2005. [Google Scholar]
49. A. S. Qureshi, A. Khan, A. Zameer and A. Usman, “Wind power prediction using deep neural network based meta regression and transfer learning,” Applied Soft Computing, vol. 58, pp. 742–755, 2017. [Google Scholar]
50. Y. Zhang, K. Liu and Q. Liang, “Short-term wind power multi-leveled combined forecasting model based on variational mode decomposition-sample entropy and machine learning algorithms,” Power System Technology, vol. 40, pp. 1334–1340, 2016. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |