DOI:10.32604/csse.2022.018369

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.018369 |  |
| Article |
Integrated Random Early Detection for Congestion Control at the Router Buffer
The World Islamic Sciences and Education University (WISE), Amman, Jordan
*Corresponding Author: Ahmad Adel Abu-Shareha. Email: ahmad.abushareha@wise.edu.jo
Received: 06 March 2021; Accepted: 01 May 2021
Abstract: This paper proposed an Integrated Random Early Detection (IRED) method that aims to resolve the problems of the queue-based AQM and load-based AQM and gain the benefits of both using indicators from both types. The arrival factor (e.g., arrival rate, queue and capacity) and the departure factors are used to estimate the congestion through two integrated indicators. The utilized indicators are mathematically calculated and integrated to gain unified and coherent congestion indicators. Besides, IRED is built based on a new dropping calculation approach that fits the utilized congestion indicators while maintaining the intended buffer management criteria, avoiding global synchronization and enhancing the performance. The results showed that IRED, compared to RED, BLUE, ERED, FLRED, EnRED and DcRED, decreased packet delay and loss under various network status. Specifically, the results showed that in heavy and moderate traffic, the proposed IRED method outperformed the state-of-the-art methods in loss and delay by 18% and 10.6%, respectively.
Keywords: Congestion; random early detection; active queue management
The widespread of computer networks increased data communication massively in the last decades. Data is communicated as packets transmitted over various network resources (e.g., links, switches and routers) before reaching its destination [1]. Because these resources have limited capacity, packets are queued at various network resources before being retransmitted to and via other resources. Due to the queuing mechanism, a problem at the router buffer occurs if the queue reaches the buffer’s limited capacity leading to packet loss and degrading network performance in what so-called congestion, as illustrated in Fig. 1 [2–4]. The early approach is the drop-tail method, which is implemented by dropping all the incoming packets when the queue reaches a specific limit to avoid buffer saturation. This mechanism is good enough if it operates under consistent traffic, which is not a real network case. Traffics transmitted over computer networks follow irregular patterns (bursty traffic) that suddenly change from the ideal state into heavy load and vice versa, which make the drop-tail method inapplicable of handling the task of router buffer management [5–7].
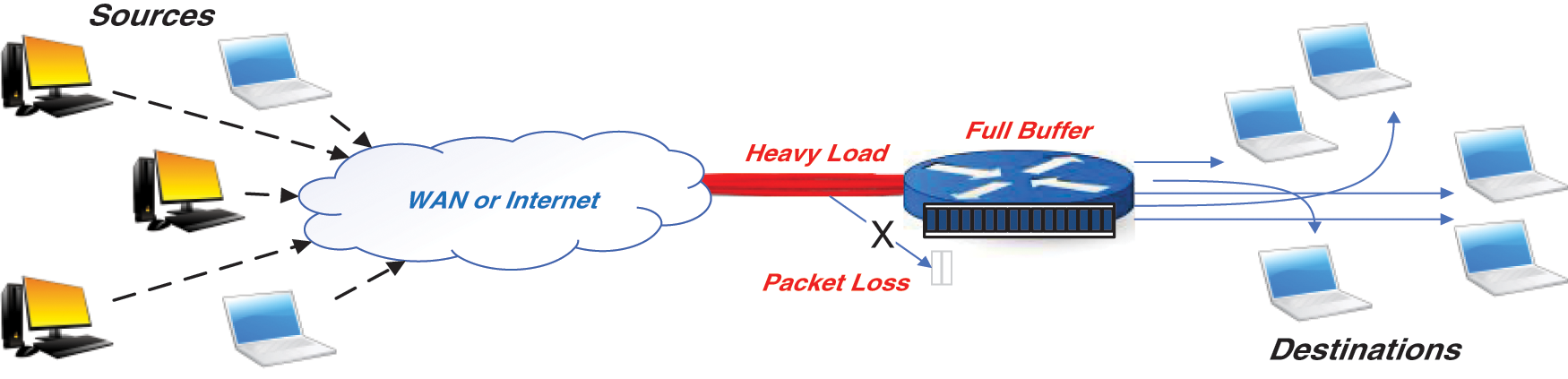
Figure 1: Congestion phenomenon at the router buffer
Active Queue Management (AQM) methods manage the router buffer and maintain the queue at a managed length to avoid packet loss, decrease delay and avoid congestion [8–11]. AQM uses packet dropping as a prevention mechanism against the congestion phenomenon that leads to bad network performance in term of delay, resource utilization, packet loss, etc. However, unnecessary dropping is considered a very serious drawback as it decreases the network performance by increasing the network’s load unnecessarily. Subsequently, dropping should be implemented rationally based on the network’s status in general and the router buffer in particular [4,12–14]. Accordingly, different AQM methods use different approaches to predict congestion at an early stage. Generally, AQM methods respond to the queue’s expansion at the buffer by dropping the incoming packets randomly to avoid global synchronization. Dropping is implemented based on the calculated dropping probability Dp, which is increased as the situation is getting more critical. As a response to that, senders decrease their sending rate before the buffer is saturated. Accordingly, AQM methods reduce the delay and packet loss resulting from the saturated buffer and alleviate TCP global synchronization and TCP starvation by dropping packets randomly [13,15–17]. Fig. 2 illustrates the difference between drop-tail and AQM techniques.
Random Early Detection (RED) [5], the first AQM method, depends on the average queue size (avg), which reflects the current and previous queue status as an indication of congestion at the router buffer. While RED has solved much of the drop-tail problems, unfortunately, RED suffers from various limitations that refers back to the low pass filtering mechanism, which causes slow varying in value with rapid changes in the queue and network status; subsequently, this causes packet loss when congestion occurs suddenly [2,9,10,18,19]. Various other AQM methods were proposed, such as Gentle Random Early Detection (GRED) [20], Dynamic Gentle Random Early Detection (DGRED) [3], Effective Random Early Detection (ERED) [21], Fuzzy Logic Random Early Detection [4], etc. These methods are similar in the technique but differ mainly in the calculation of Dp and the addressed RED’s limitations. These methods addressed RED’s drawbacks by depending on the load status or queue status as an indication of congestion. However, both indictor types fail to predict congestion accurately with network traffic’s bursty nature [19,22,23].
In this paper, a new Active Queue Management (AQM) method that integrates queue-status and load-status to manage queue in the router buffer is proposed. The contributions of this paper are as follows: 1) Resolve the queue-based AQM and load-based AQM, 2) Integrate the current and previous statues of the queue and the network through developed congestion indicators, 3) Develop a new AQM method for congestion indicator based on innovative Dp calculation, and 4) Evaluate the proposed method in comparison with the well-known AQM methods and Recently developed AQM methods. It gains the benefits of both of them in an integrated mechanism. The remaining sections of this paper are organized as follows. Section 2 reviews and analyzes the current methods used for buffer management and congestion control at the router buffer, the advantages and the key limitations of these methods. Section 3 discusses the proposed method in details and clarifies the mechanism that is used for congestion control. Section 4 discusses the simulation environment and parameters. Section 5 discusses the experiments and presents the results. Finally, Section 6 concludes the paper.
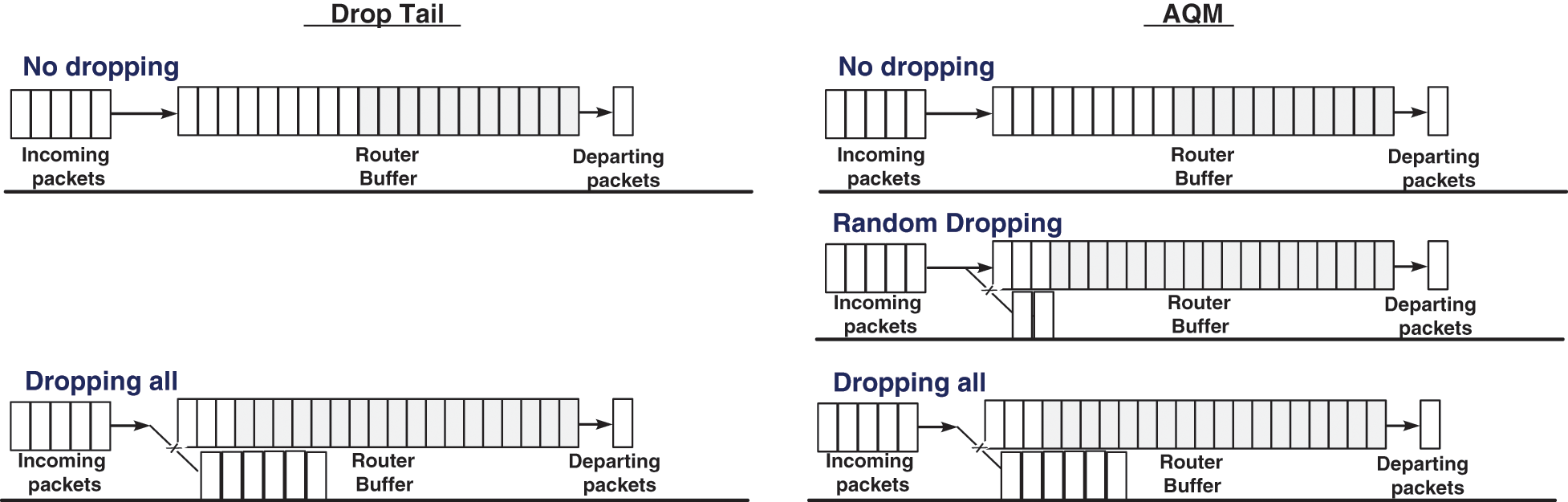
Figure 2: Drop Tail vs AQM techniques
Although the AQM method works at each router individually and independently, it depends on, besides the status of the queue, the estimated status of the network as a whole. The calculated or estimated statuses are used to calculate the Dp value for each arrival packet. Dp is finally used in a random procedure to decide whether to drop or accommodate the packet located in the router buffer [24–26]. Floyd and Jacobson [5] developed the RED method using an avg, reflecting the current and previous queue status as an indication of congestion at the router buffer. The avg is calculated and compared to two thresholds, representing safe and unsafe queue lengths, as illustrated in Fig. 3. Accordingly, if the avg is below the minimum threshold, RED drops no packets. In contrast, if the avg is above the maximum threshold, RED drops all arrival packets, and RED drop packet randomly when avg is between the minimum and maximum threshold. The purpose of using the avg instead of the instate queue length (q) is to reflect the previous status and draw a rough expectation of the future status, thus avoid unnecessary packet dropping. However, the avg varying slowly with rapid changes in the queue and network statuses; subsequently, it causes packet loss when congestion occurs suddenly.
As more AQM methods were developed to solve RED limitations, various congestion indicators have been used. Based on these indicators, the existing AQM methods can be classified into queue-based, load-based and hybrid-based, ass illustrated in Fig. 4 [12].
In the queue-based category, Suthaharan [27] proposed a method to “overcome the slowly varying nature of the avg computed using an exponentially weighted moving average (EWMA) used in the RED scheme, which causes the chaotic behaviour” [27]. Although the proposed solution overcome the slowly varying problem by allowing rapid variation on the value of the indicator when the queue length changes, rapid varying nature leads to the same results as using the q avoided initially. Accordingly, it gives false alarms on congestion on heavy, yet, short-duration traffic occurs, which causes unnecessary packet dropping. Patel and Bhatnagar [18] proposed reducing packet loss in RED by indicating the changing in the queue size.
Long, Zhao [28] proposed a method to overcome the slowly varying problem in the avg by using the estimated load as a congestion indicator in the load-based category. Using load as an indicator is more efficient than queue status with the network traffic’s busty nature. Thus, the proposed method efficiently managed the buffer in most of the cases. However, because load ignores the current and the buffer’s previous statuses, using load solely cause delay, packet loss, and unnecessarily dropping when the load changes while queue preserved and vice versa [29,30]. Other load-based methods, such as Adaptive Virtual Queue (AVQ) [31], used arrival rate estimation as a congestion indicator.
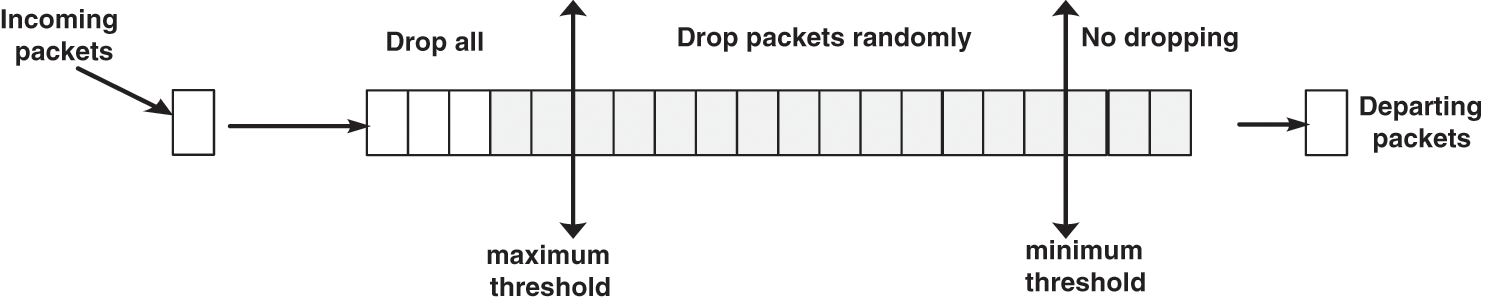
Figure 3: RED parameters
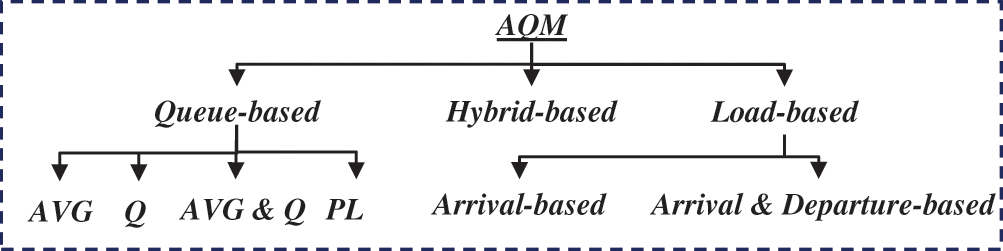
Figure 4: AQM methods classification
LUBA [16] used an estimation of the load factor, which is calculated as U=λ/μ (where λ is the aggregated arrival rate at the router and μ is the outgoing link capacity of the router). Accordingly, when the load is below the target link utilization, the router is non-congested, and packets are not marked nor dropped. When the load increased, all arriving packets are monitored while assigning each ingress flow at the router. While these methods achieved a good performance in buffer management, using load ignores the current and the buffer’s previous statuses, which causes packet loss and unnecessarily dropping when the load changes and the queue is preserved and vice versa.
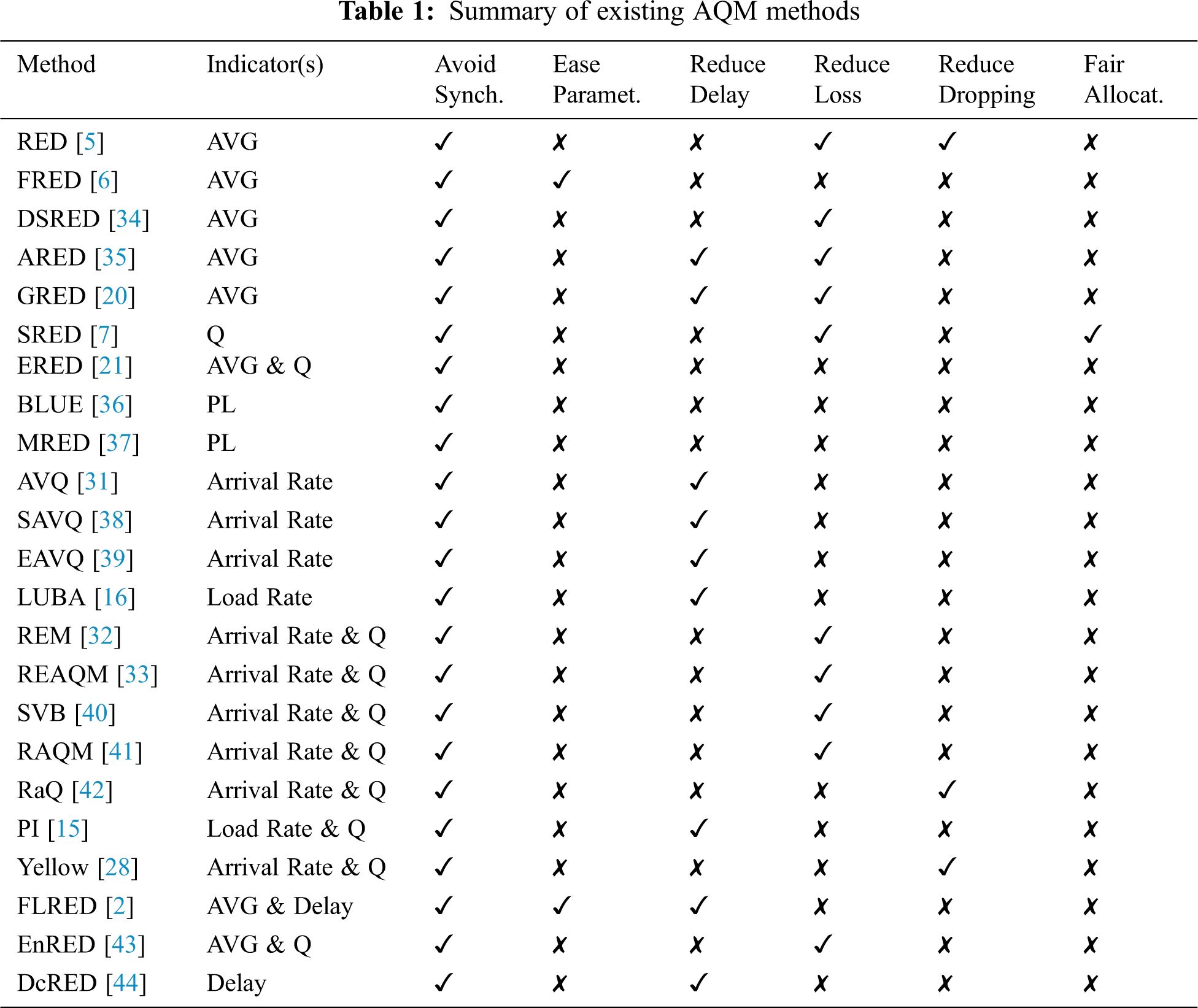
Hybrid-based methods were proposed in the literature to solve the problems of the queue-based and load-based methods. Hybrid-based methods, such as REM [32] and REAQM [33], used independent congestion indicators that speculate the queue status and the traffic load. Different strategies were used for combining these congestion indications. Accordingly, these methods provided better performance compared to the queue-based and load-based methods. A new challenge has been raised, which is related to how these indications should be combined. Thus, a new problem faced a hybrid method of unnecessary packet dropping as one indicator alert for congestion, while the other is not. Various other AQM methods have been proposed in the literature for different objectives and using different congestion indicators; these are summarized in Tab. 1.
In summary, RED depends on the avg, which combines the current and previous queue length, to predict congestion at the router buffer. Unfortunately, RED suffers from various limitations that resulted from the low-pass filtering mechanism of the indicator, which causes slow varying in value with rapid changes in the queue and network status; subsequently, this causes packet loss when congestion occurs suddenly. The other AQM methods are similar to RED in the technique but differ mainly in the utilized indicators. These methods address the drawbacks of RED by depending on the network status or buffer status; however, they fail to predict congestion accurately with the bursty nature of network traffic.
Generally, existing AQM methods differ in the goal to be achieved and the utilized congestion indicators. In terms of similarities, AQM methods have successfully adapted the RED-like mechanism for using the indicators to calculate the dropping probability. However, a new challenge raised in the attempt to use multiple indicators under the RED-like mechanism. ERED [21], one of these hybrid approaches, has achieved the best results in the literature. However, it has a shortage in terms of delay, which might be referred back to the adaptation of the RED-like mechanism in using multiple indicators. Accordingly, a new mechanism is required to use multiple congestion indicators efficiently. The problem lies in using integrated indicators that combine load and queue statuses.
The proposed AQM method, Integrated Random Early Detection (IRED), uses both queue-status and load-status to estimate congestion and manage the queue at the router buffer. Accordingly, two indicators are mathematically calculated and integrated to gain a singly and coherent congestion indicator at the router buffer. Besides, IRED proposed a new Dp calculation approach that fits the utilized congestion indicators while maintaining the intended buffer management criteria, which avoids global synchronization and enhances network performance. As illustrated in Fig. 5, the development of IRED is embodied in calculating the congestion indicators, followed by using the developed indicators to calculate the Dp and constructing the overall IRED mechanism. These processes are discussed in the following sub-sections.
The queue-status and load-status, used for congestion estimation in the router buffer, are estimated using two calculated factors: the integrated arrival factor and the integrated departure factor. These two factors differ from the commonly used arrival and departure rates in that both consider the status of the queue beside the rates.
The integrated arrival factor is calculated based on two parameters, the arrival rate and the queue length. The arrival rate is calculated as a weighted average of the current arrival value and the previous arrival value. The weight variable, w, specifies the share of each of these values, current and previous, towards the output value. Accordingly, with a value of weight above 0.5, the current rate takes more preferences over the old rates and vice versa. The queue length is calculated as the current queue combined with a pre-determined threshold value divided by the buffer’s total capacity. Accordingly, both parameters: arrival rate and queue length, are proportional to the integrated arrival value. Accordingly, the first factor, the integrated arrival factor, IA, is calculated as given in Eq. 1.
where Ai is the arrival rate at the time i, IAi-1 is the average integrated arrival rate before the time i, w is the weight that assigned to the current arrival rates to enforce preferences to the current or previous rates, q is the instant queue length, t is a threshold value and size is the capacity of the buffer.
The second factor, the integrated departure factor, ID, is calculated based on two parameters, the departure rate and the queue length, as given in Eq. 2.

Figure 5: IRED development process
where, Di-1 is the current departure rate, which is calculated at the time i-1, IDi-2 is the previous average integrated departure rate, w is the weight that is assigned to the current departure rates to enforce preferences to the current or previous rates, q is the instant queue length, t is a threshold value and size is the total capacity of the router buffer. Accordingly, ID calculation is identical to the IA calculation, except that it considers the previous slot’s departure rate, which follows the assumption of the discrete-time queue [45]. According to the discrete-time queue principles, as given in Fig. 6, the departure dn occurs before the arrival, and the departure of slot n occurs at the previous slot n-1.
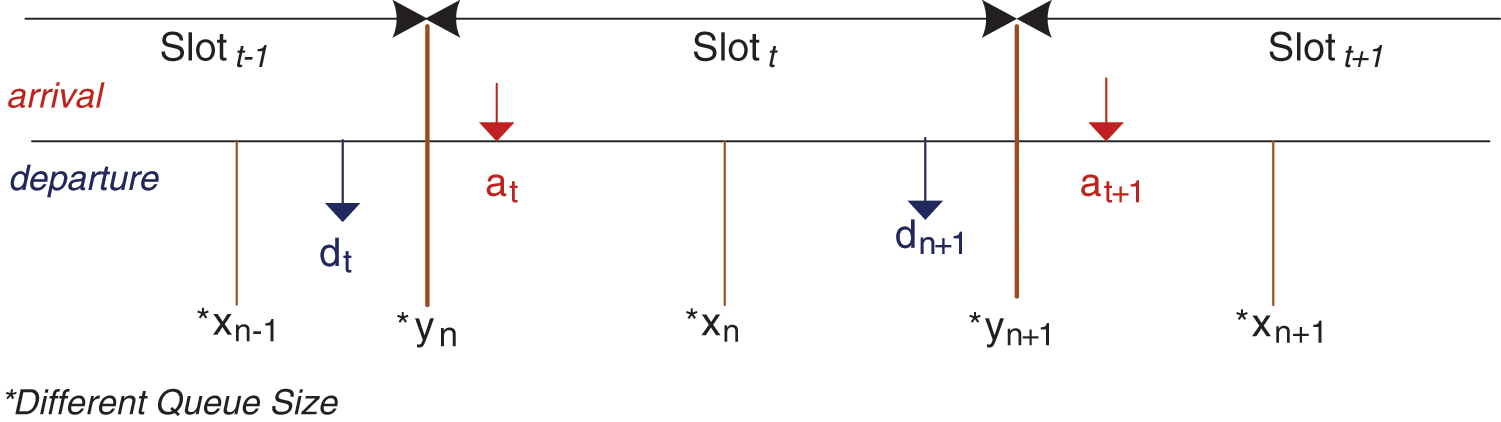
Figure 6: Discrete-Time queue model
Dp Calculation is implemented using multiple equations, each executed based on the arrival and departure indicators’ status. Accordingly, two thresholds are used to differentiate between three scenarios for the arrival/departure status: low, medium and high. The number of thresholds required is reduced in half by using the same calculations and principles for the departure and arrival status. Moreover, this identical principle reduces the number of Dp calculation scenarios, thus reducing the proposed mechanism’s complexity. Based on the arrival and departure status, the congestion status is determined, and the Dp is calculated accordingly. The first step towards calculating Dp is to investigate the effect of the integrated arrival factor and integrated departure factor on the buffer’s congestion. Then, investigate the combination of both factors. Finally, putting rules for calculating Dp based on the integrated arrival and integrated departure factors.
For the integrated arrival factor, the combination of both arrival rate and queue length affects the buffer as follows: If the arrival rate is high, while the queue length is small, the router is considered non-congested, and there is a high chance that the increase in the arrival rate is due to short false congestion. On the other hand, when the rate is high while the queue length is medium or high, either heavy congestion is approaching or considerable delay is facing. Different congestion status occurs with different arrival rates; each required a different decision about dropping vs accommodating the arrival packets, as given in Fig. 7(a).
Similarly, different congestion status occurs with different departure rates; each required a different decision about dropping vs accommodating the arrival packets, as given in Fig. 7(b). The decisions to be made about packet dropping according to integrated departure factors are opposite to the decisions made based on the integrated arrival, which is logically true and occurs in real situations. By combining these two tables, the final decision can be made based on integrated congestion indicators, as given in Fig. 7(c). Accordingly, based on the drawn conclusion about the expected congestion, dropping with different probabilities is utilized to eliminate congestion, as illustrated in Fig. 7(c). As noted, the dropping range is very aggressive to slight based on the expected congestion that is determined through the integrated arrival and departure indicators.
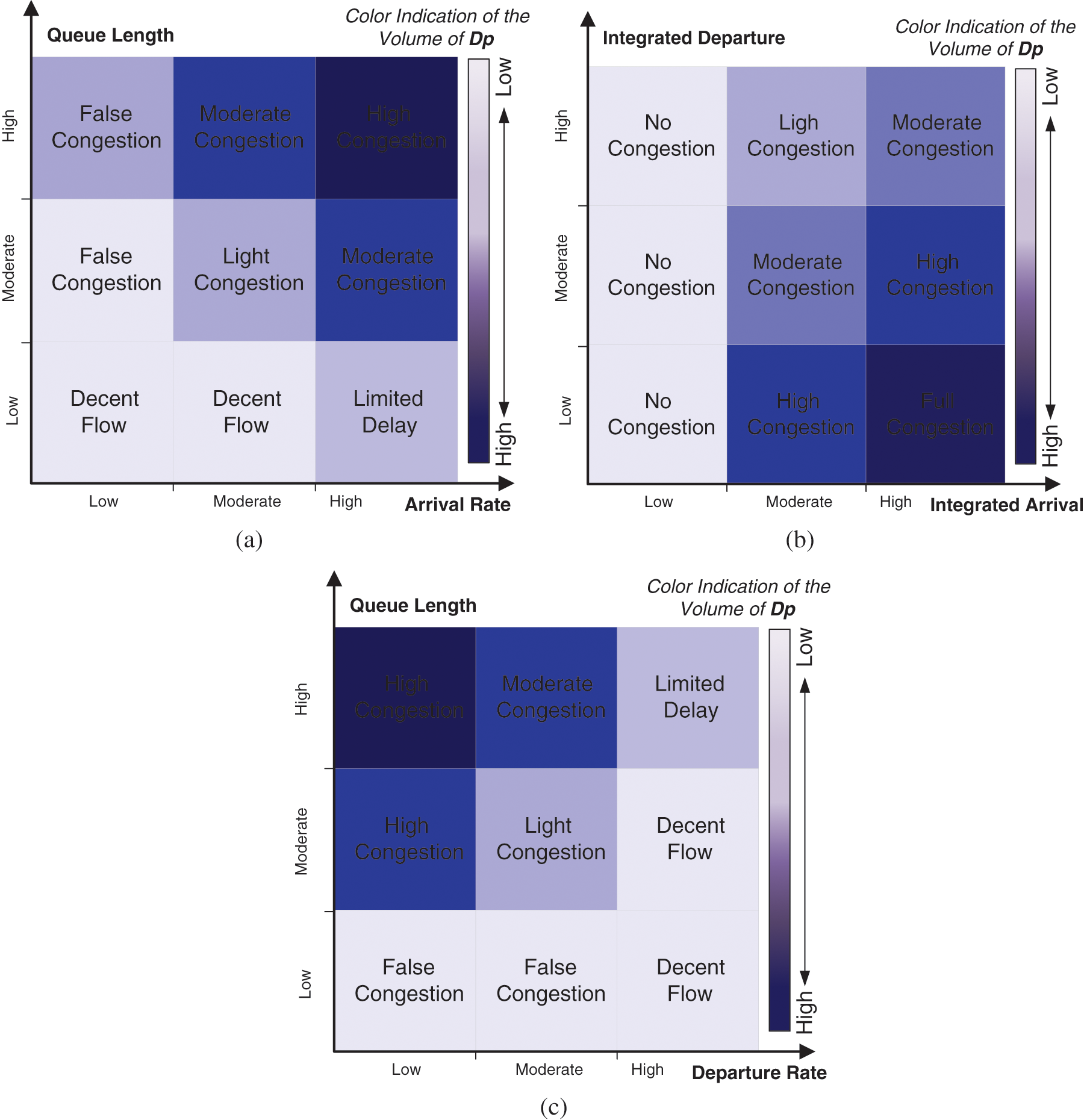
Figure 7: Congestion estimation based on the utilized sub-indicators: a) Congestion estimation as a function of integrated arrival, b) Congestion estimation as a function of integrated departure, c) Congestion estimation as a function of integrated arrival and integrated departure
According to the congestion estimation in Fig. 7, the proposed AQM method depends on three main sub-indicators: queue size, arrival and departure rate, each of which depends on other core indications. The proposed method allows for combining these core indications and sub-indicators by creating a logical relation between these indications to reach a final model for congestion estimation at the router buffer. Then, the Dp calculation is implemented based on the estimation mentioned above of the congestion.
Three equations for Dp calculation are utilized: one to address low dropping target, one for moderate dropping and one for high dropping. These calculations are given in Eqs. 3–5, respectively.
According to Eq. 3, Dp is calculated based on the parameter q. Dp is increased as q is increased, the parameter, count, is used to avoid global synchronization. In Eqs. 4 and 5, Dp is calculated based on q and the thresholds. The differences between these equations are the normalization parameters that are used with q. Using q in calculating Dp is more appropriate compared to avg. The best practice for avg is to use it for comparison, which is replaced here with integrated factors.
The parameter, count, is a float value ranging from 0 to 1 and increase as a factor of 1/size each time the packet is dropped and is set to 0 after a packet is accommodated. Accordingly, it reduces the chance of dropping subsequent packets to avoid the global synchronization problem. The tmax and tmin vales are determined empirically, and the relation “0 < tmin < tmax < 1” should always be true.
As an AQM, the proposed IRED is implemented by deciding about packet accommodation and dropping as each packet arrives at the buffer. This process required calculations of the congestion indicator and investigation of the buffer status, as discussed earlier. The complete process for IRED is implemented as given in Algorithm 1.

As given in Algorithm 1, there are four scenarios for Dp calculation given in line 4, line 6, line 9 and line 12. No dropping is implemented in the first case, and Dp is set to zero without any calculation. This case occurs when the IA is less than the minimum threshold. In such a case, there is no congestion expected as the arrival rate is low. In the second case, Dp is calculated using Eq. 4. This case occurs when the IA between the two thresholds while ID is greater than the maximum threshold. In such a case, light congestion is expected as the arrival rate is moderate and the departure rate is appropriate. In the third case, the dropping rate is increased, and Dp is calculated according to Eq. 3, in which the calculated dropping is more aggressive compared to the previous case. This case occurs when the IA and ID are between the two thresholds or when both IA and ID is higher than the maximum threshold. Accordingly, with almost equal arrival and departure, light congestion is expected, considering the routing time. Thus, for the second case, Dp is calculated as given in Eq. 1. In the fourth case, the dropping rate increases more, and Dp is calculated according to Eq. 5. This case occurs when the IA between the two thresholds while the ID is less than the minimum threshold or when the IA is greater than the maximum threshold while the ID is between the two thresholds. In such a case, congestion is expected as the arrival rate is high, and the departure rate is very low. In all these cases, packets are dropped probabilistically, and the value of the counter is adjusted to avoid global synchronization. Finally, in line 15, all the packets are dropped as the Dp is set to 1 with heavy congestion conditions. This case occurs when the IA is greater than the maximum threshold while ID is less than the minimum threshold. Accordingly, these cases matched the conceptual model in Fig. 7.
The proposed IRED is simulated according to the discrete-time queue model, which is commonly used to simulate AQM for its capabilities in capturing its performance accurately, compared to the continuous model. The discrete-time queue model uses multiple slots, representing equal periods, to capture the network performance [46,47]. In each slot, a packet may arrive, departed, or both depends on the arrival and departure rate of the simulated network. Accordingly, it allows for calculating accurate performance metrics at the router buffer and has been used for AQM simulations [4,19,23].
The following settings were implemented for the simulation environment; a single router buffer of twenty packets capacity is used with the first-in-first-out (FIFO) queuing model. The number of slots used is 2,000,000 slots for warm-up (800,000) and result collection (1,200,000). The warm-up period is enforced at the beginning of the experiments to ensure that the system reached a steady-state. Accordingly, no performance metrics are calculated during the warm-up period. The arrival rates that were implemented are 0.30–0.95 with intervals of 0.05, which generated different congestion status, given that the departure rate is set to a single value of 0.5. In the low arrival rate, non-congestion status is created, the average arrival rate creates light congestion, and the high rate creates a heavy congestion state. The minimum threshold and maximum threshold are set to 3 and 9, respectively, as determined by RED and ERED methods. The parameters of the IRED is set as follows: the threshold and the weight that are used to calculate the indicators are set to 3 and 0.5, respectively, and the minimum and maximum thresholds are set to 0.3 and 0.6, respectively.
The experiment is conducted by initializing and setting the values of the parameters. Then, in each slot, the following processes are implemented, the packet is generated stochastically based on the arrival rate value. If any, the generated packet is loosed, dropped or accommodated depends on the buffer and the running AQM method. Finally, after the pre-determined slots are completed, the results are collected, and the performance is evaluated. The implementation processes are illustrated in Fig. 8.
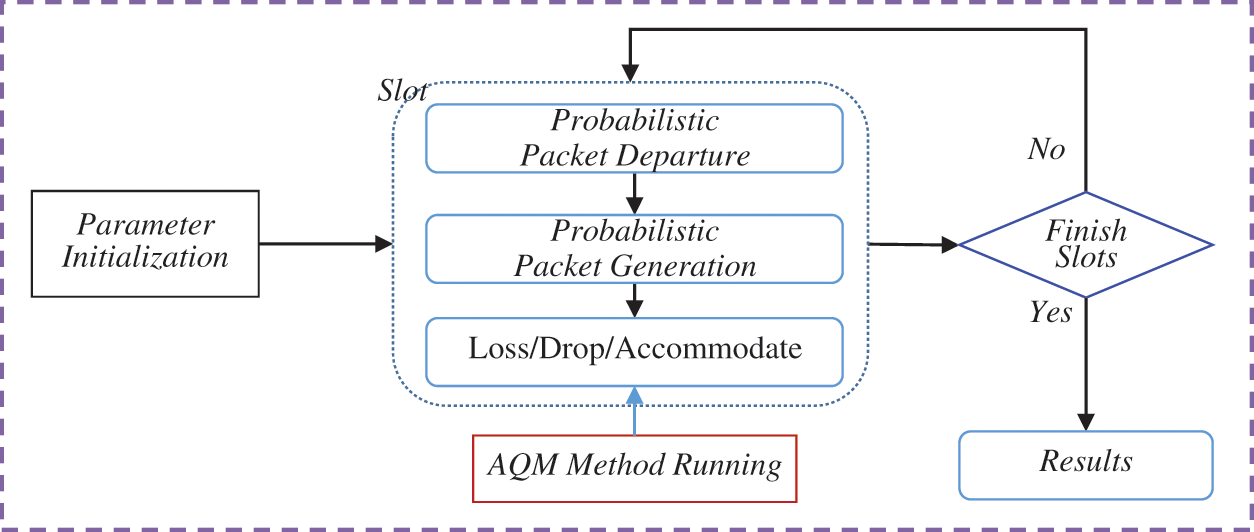
Figure 8: Experiments’ Flowchart
To evaluate the proposed method’s performance, in comparison with the existing AQM methods RED, BLUE and ERED and the recently developed methods FLRED and EnRED, the evaluation measures, packet loss, packet dropping, delay, were used. Packet loss is the consequences of buffer overflow and late congestion status. Dropping can be a prevention strategy implemented by AQM, or it can be a consequence of the wrong diagnosis of congestion when it is not occurring. Delay is the common consequences of congestion phenomena.
In the first case, with an arrival rate equal to 0.9 and a departure rate equal to 0.5, heavy congestion is expected to occur at the router buffer. Accordingly, loss, dropping and delay are expected to be faced in the router buffer. In results comparison, as illustrated in Fig. 9, the proposed IRED method and BLUE lost fewer packets compared to RED and ERED, while RED lost fewer packets compare to ERED as given in Fig. 9(a). For packet dropping, the proposed IRED method and RED dropped fewer packets than BLUE, while ERED dropped fewer packets than others, as given in Fig. 9(b). In heavy congestion, the AQM methods should drop packets to avoid loss; accordingly, dropping the necessary packets to avoid congestion is not a disadvantage. To clarify this point, the sum of packet dropping and packet loss is illustrated in Fig. 9(c), which shows that, in total, the proposed IRED method dropped fewer packets compared to RED and BLUE. The ERED methods and IRED dropped fewer packets, yet the IRED method is better than ERED as no loss occurs, as illustrated in Fig. 9(a).
These results showed that the proposed IRED method outperformed the compared methods RED, ERED and BLUE. Finally, the proposed IRED method outperformed the compared methods ERED in terms of the delay, as given in Fig. 9(d). Accordingly, IRED can predict congestion early and react to avoid buffer overflow, and packet loss lessens the delay, improves bandwidth utilization, and alleviates both global synchronizations.
In the second case, with an arrival rate equal to 0.5 and a departure rate equal to 0.5, light congestion is expected to occur at the router buffer. In results comparison, as illustrated in Fig. 10, the proposed IRED method, BLUE and ERED, lost fewer packets compared to RED as given in Fig. 10(a). The proposed IRED method dropped fewer packets than RED, BLUE, and ERED, while ERED dropped fewer packets than RED and BLUE, as shown in Fig. 10(b). Fig. 10(c) shows that, in total, the proposed IRED method dropped fewer packets than RED, BLUE, and ERED, while ERED dropped fewer packets than RED and BLUE. Finally, the proposed IRED method performed better than RED and ERED methods in terms of the delay, as given in Fig. 10(d). Accordingly, as given in Fig. 10, the proposed method outperformed RED and ERED and BLUE, enhancing network performance.
In the third case, with an arrival rate equal to 0.3 and a departure rate equal to 0.5, no congestion is expected to occur at the router buffer. Thus no delay, loss or dropping are expected in the ideal scenario. In results comparison, as illustrated in Fig. 11, the proposed IRED method and the compared methods, RED, BLUE and ERED, lost no packets as given in Fig. 11(a). Similarly, no packet dropping was reported for the proposed IRED method and the compared methods, RED, BLUE and ERED, as shown in Fig. 11(b). Fig. 11(c) shows the total loss and dropping for the proposed method IRED and the compared methods, RED, BLUE and ERED. Finally, the delay comparison is given in Fig. 11(d). The total loss, dropping, re-transmission and delay are given in Fig. 12.
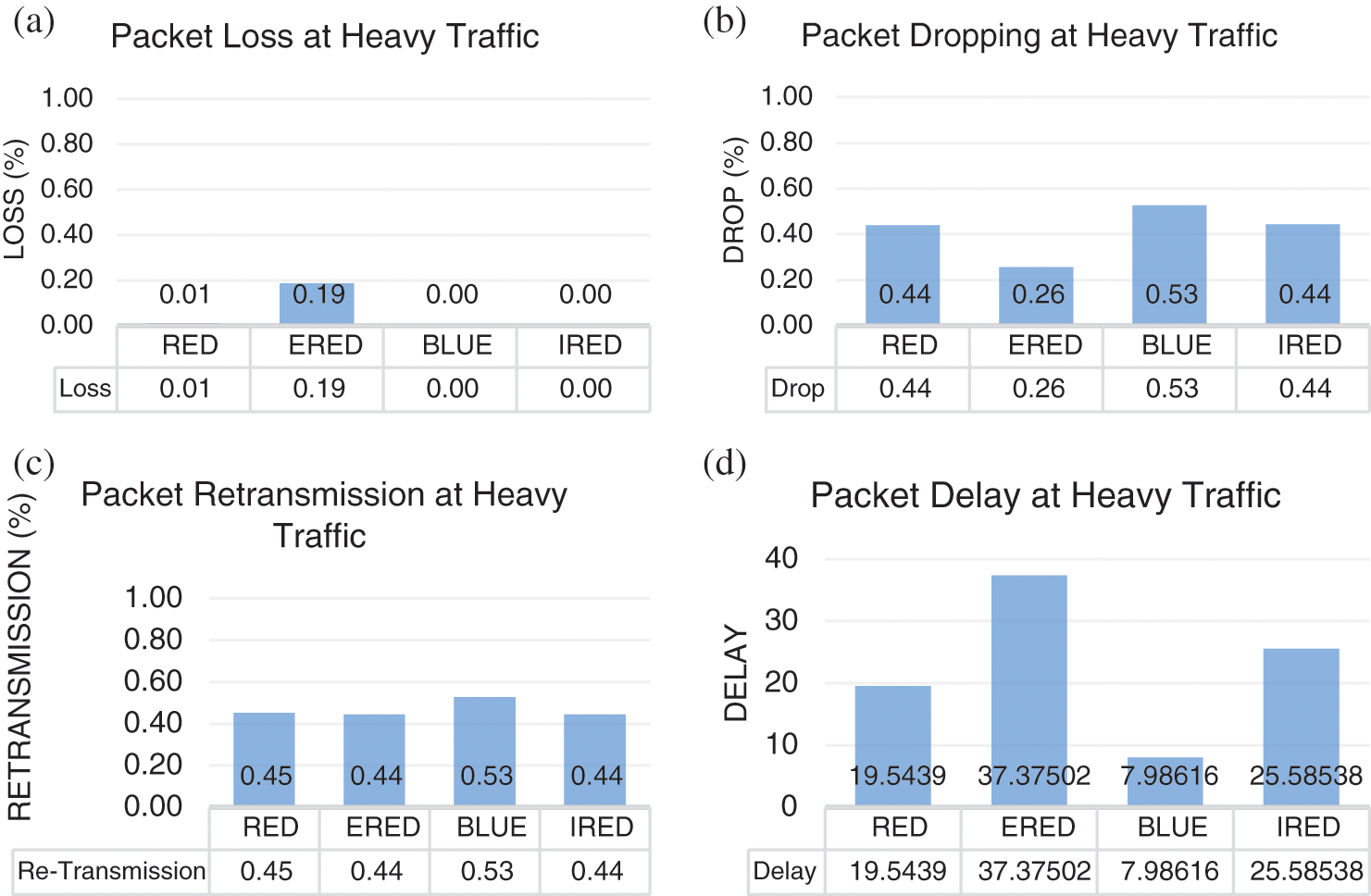
Figure 9: Results of the proposed and compared methods under heavy traffic. (a) Packet loss under heavy traffic. (b) Packet dropping under heavy traffic. (c) Packet re-transmission under heavy traffic. (d) Packet delay under heavy traffic
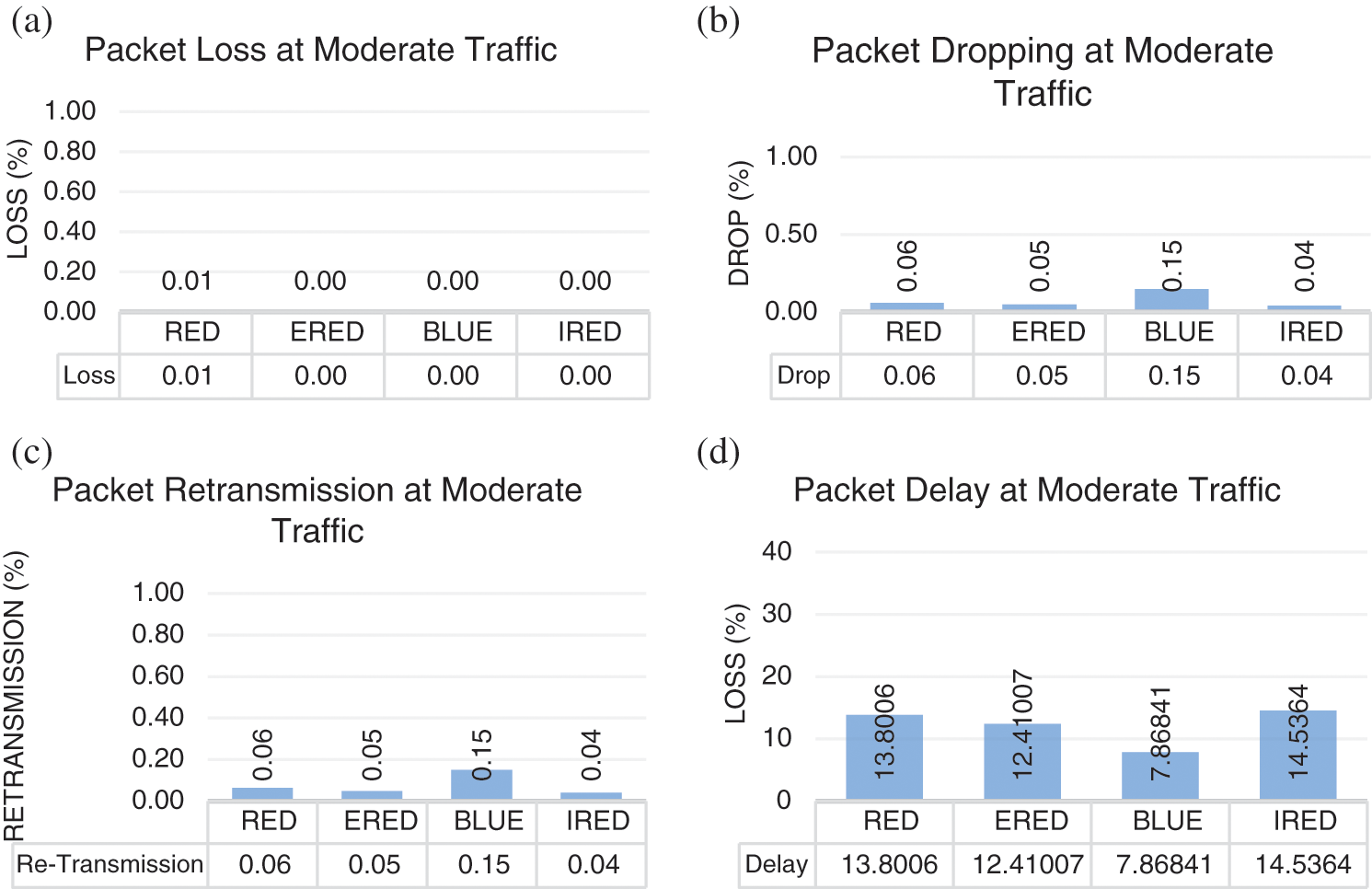
Figure 10: Results of the proposed and compared methods under moderate traffic. (a) Packet loss under moderate traffic. (b) Packet dropping under moderate traffic. (c) Packet re-transmission under moderate traffic. (d) Packet delay under moderate traffic
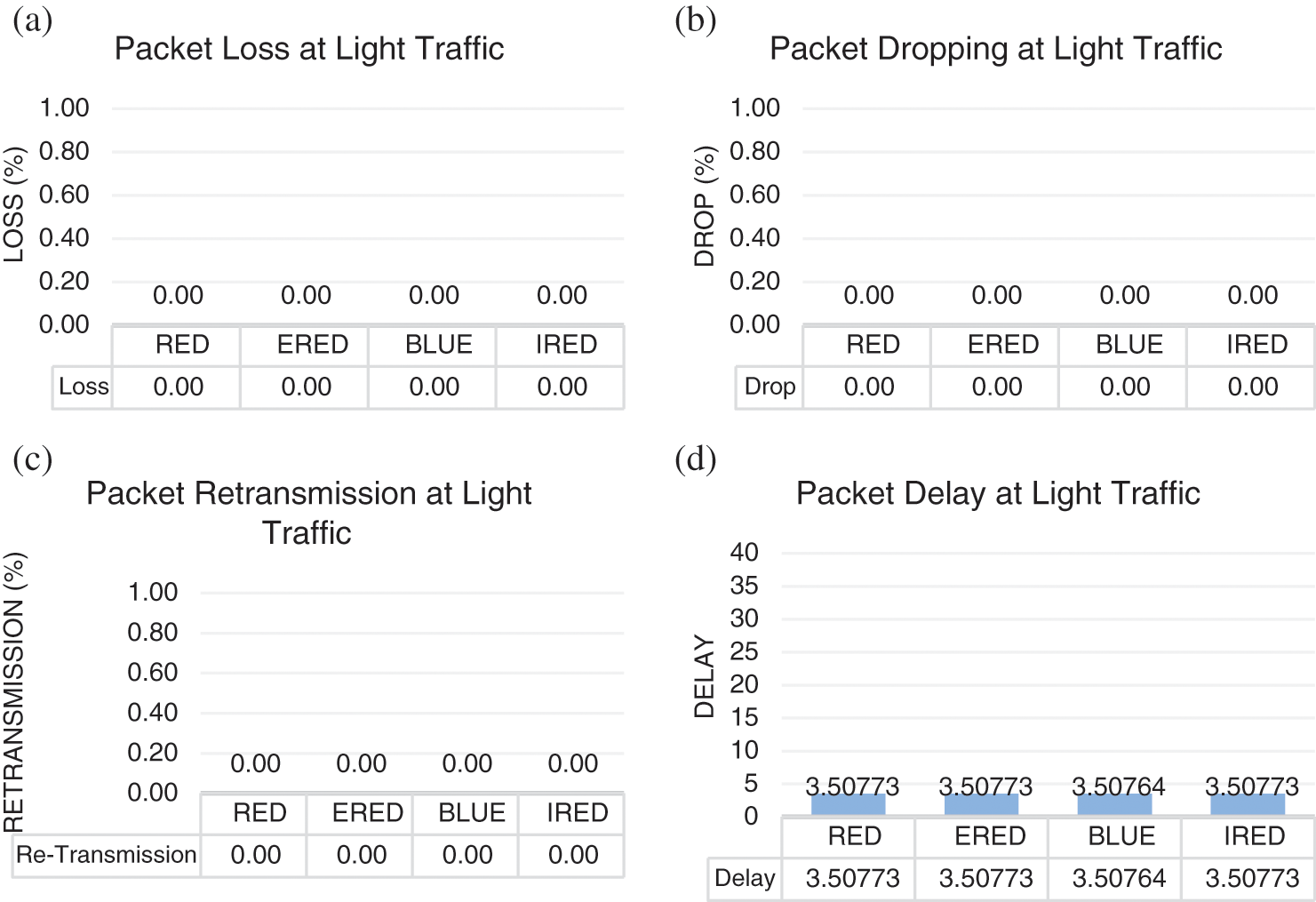
Figure 11: Results of the proposed and compared methods under light traffic. (a) Packet loss under light traffic. (b) Packet dropping under light traffic. (c) Packet re-transmission under light traffic. (d) Packet delay under light traffic
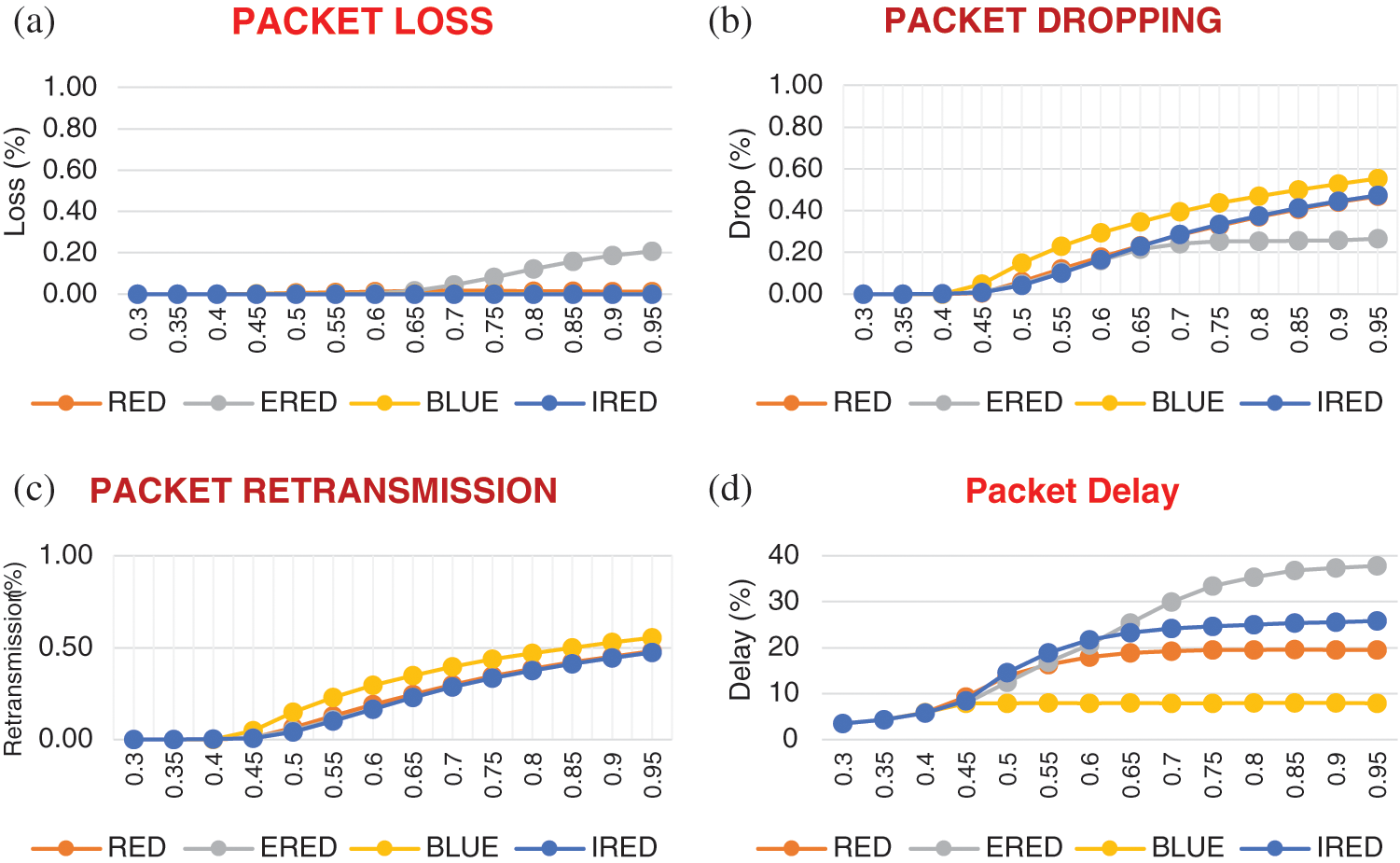
Figure 12: Results of the proposed and compared methods under various traffic load. (a) Packet loss under various traffic load. (b) Packet dropping under various traffic load. (c) Packet re-transmission under various traffic load. (d) Packet delay under various traffic load
Accordingly, the proposed IRED method achieved the intended goal to enhance the network performance in heavy and light congestion while preserving smooth network flow in the non-congestion state. As noted in the results, the proposed method outperformed the compared methods, the original RED, which is the commonly used method for buffer management and the state-of-the-art ERED method. Thus, IRED is a promising AQM method used in various network architectures for best performance results.
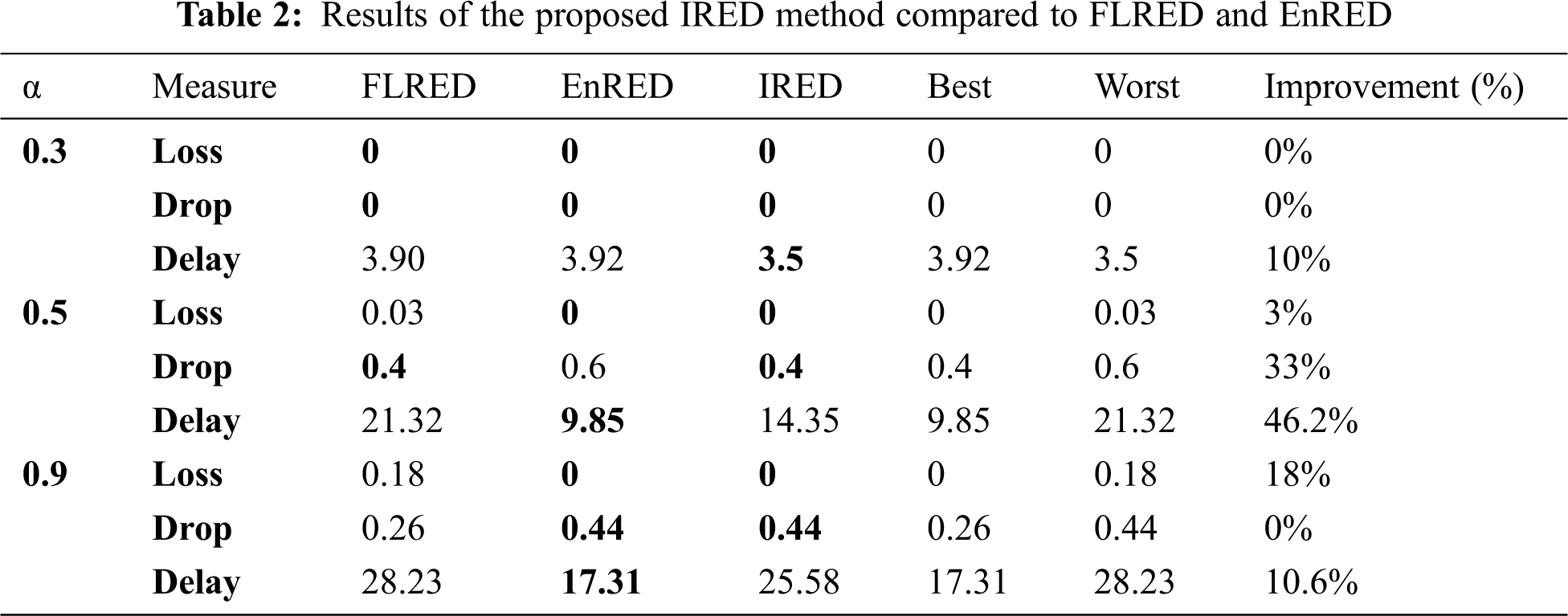
Compared to the recently developed AQM method, the proposed IRED method is evaluated with FLRED and EnRED with an α value of 0.3, 0.5 and 0.9, as shown in Tab. 2.
As noted, the proposed IRED outperformed the compared FLRED and EnRED in loss and dropping. At the same time, it is expected to have a higher delay, especially while the IRED try to avoid unnecessary loss in congested status.
This paper aimed to develop a congestion-aware AQM method based on integrated congestion indicators that speculate the queue and network statuses. Accordingly, integrated indicators, which speculate queue and load collectively, were proposed to manage the router buffer and achieve the computer network’s demanded optimized performance. The proposed IRED method extends the well-known RED method. It uses integrated indicators as a combination of the indicators used individually in various AQM methods: BLUE, SRED, AVQ, SAVQ and others. Accordingly, IRED combined the advantages of these methods and eliminated many of the AQM methods’ disadvantages, especially RED. IRED was simulated, and the performance results of IRED compared to the results obtained for RED and ERED. The simulation results showed that IRED outperformed both RED and ERED by decreasing packet loss and delay when heavy congestion occurs, while equally performed with RED and ERED in non-congestion status. Thus, it can be concluded that combining multiple indicators for congestion estimation and dropping calculation can be implemented by creating integrations of these indicators and logically combine them into a single framework. A mathematical investigation of the Dp calculation is also required to fit the developed indicators. Thus, relying on the existing well-known algorithms should be confined by implementing the necessary modification to such algorithms to fit the developed indicators. Future work will focus on eliminating the parameter-setting problem by extending IRED into Fuzzy-logic based technique (FIRED). Moreover, both IRED and FIRED will be implemented in the real environment. These methods’ performance will be compared by their influence on the TCP protocol in various network types, such as wireless networks and multi-hop network.
Funding Statement: The author received no specific funding for this study.
Conflicts of Interest: The author declares that they have no conflicts of interest to report regarding the present study.
1. S. Paul, J. Pan and R. Jain, “Architectures for the future networks and the next generation Internet: A survey,” Computer Communications, vol. 34, no. 1, pp. 2–42, 2011. [Google Scholar]
2. M. M. Abualhaj, A. A. Abu-Shareha and M. M. Al-Tahrawi, “FLRED: an efficient fuzzy logic based network congestion control method,” Neural Computing and Applications, vol. 30, no. 3, pp. 925–995, 2018. [Google Scholar]
3. M. Baklizi, H. Abdel-Jaber, M. M. Abu-Alhaj, N. Abdullah, S. Ramadass et al., “Dynamic stochastic early discovery: a new congestion control technique to improve networks performance,” International Journal of Innovative Computing, Information and Control, vol. 9, no. 3, pp. 1118–1126, 2013. [Google Scholar]
4. M. Baklizi, H. Abdel-Jaber, A. A. Abu-Shareha, M. M. Abualhaj and S. Ramadass, “Fuzzy logic controller of gentle random early detection based on average queue length and delay rate,” International Journal of Fuzzy Systems, vol. 16, no. 1, pp. 9–19, 2014. [Google Scholar]
5. S. Floyd and V. Jacobson, “Random early detection gateways for congestion avoidance,” IEEE/ACM Transaction on Networking, vol. 1, no. 4, pp. 397–413, 1993. [Google Scholar]
6. D. Lin and R. Morris, “Dynamics of random early detection,” in Proc. ACM SIGCOMM Computer Communication Review, Cannes, France, pp. 127–137, 1997. [Google Scholar]
7. T. J. Ott, T. V. Lakshman and L. Wong, “SRED: stabilized RED,” in Proc. INFOCOM ’99 Eighteenth Annual Joint Conference of the IEEE Computer and Communications Societies, New York, NY, USA, pp. 1346–1355, 1999. [Google Scholar]
8. A. Chydzinski and L. Chrost, “Analysis of AQM queues with queue size based packet dropping,” International Journal of Applied Mathematics and Computer Science, vol. 21, no. 3, pp. 567–577, 2011. [Google Scholar]
9. A. Kamra, S. Kapila, V. Khurana, V. Yadav, R. Shorey et al., “SFED: a rate control based active queue management discipline,” Research Report, IBM India Research Laboratory, India, 2000. [Google Scholar]
10. L. Rossides, A. Sekercioglu, A. Pitsillides, A. Vasilakos, S. Kohler et al., “Fuzzy RED: congestion control for TCP/IP Diff-Serv,” in Proc. Electrotechnical Conference, Lemesos, Cyprus, pp. 343–352, 2000. [Google Scholar]
11. M. H. Yaghmaee and H. AminToosi, “A fuzzy based active queue management algorithm,” Simulation Series, vol. 35, no. 4, pp. 458–462, 2003. [Google Scholar]
12. M. Kwon and S. Fahmy, “Comparison of load-based and queue-based active queue management algorithms,” Quality of Service over Next-Generation Internet, vol. 4866, pp. 35–46, 2002. [Google Scholar]
13. J. Koo, S. Ahn and J. Chung, “A comparative study of queue, delay, and loss characteristics of AQM schemes in QoS-enabled networks,” Computing and Informatics, vol. 23, no. 4, pp. 317–335, 2004. [Google Scholar]
14. M. Joshi, A. Mansata, S. Talauliker and C. Beard, “Design and analysis of multi-level active queue management mechanisms for emergency traffic,” Computer Communications, vol. 28, no. 2, pp. 162–173, 2005. [Google Scholar]
15. C. V. Hollot, V. Misra, D. Towsley and B. W., “On designing improved controllers for AQM routers supporting TCP flows,” in Proc. Twentieth Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOMAnchorage, AK, USA, 2001. [Google Scholar]
16. M. Agarwal, R. Gupta and V. Kargaonkar, “Link utilization based AQM and its performance,” in Proc. Global Telecommunications Conference, Dallas, TX, USA, 2004. [Google Scholar]
17. Z. Chuan and L. Xuejiao, “A robust AQM algorithm based on fuzzy-inference,” in Proc. International Conference on Measuring Technology and Mechatronics Automation, Zhangjiajie, China, pp. 534–537, 2009. [Google Scholar]
18. S. Patel and S. Bhatnagar, “Adaptive mean queue size and its rate of change: queue management with random dropping,” Telecommunication Systems, vol. 65, no. 2, pp. 281–295, 2017. [Google Scholar]
19. L. Tsavlidis, P. Efraimidis and R. A. Koutsiamanis, “Prince: an effective router mechanism for networks with selfish flows,” Journal of Internet Engineering, vol. 6, no. 1, pp. 355–362, 2016. [Google Scholar]
20. S. Floyd, “Recommendations on using the gentle variant of RED,” 2000. [Online]. Available at: http://www.aciri.org/floyd/red/gentle.html. [Google Scholar]
21. B. Abbasov and S. Korukoglu, “Effective RED: An algorithm to improve RED’s performance by reducing packet loss rate,” Journal of Network and Computer Applications, vol. 32, no. 3, pp. 703–709, 2009. [Google Scholar]
22. A. Fakharian and A. Abbasi, “Design of congestion controller for TCP networks based on LMI formulation,” Journal of Optimization in Industrial Engineering, vol. 8, no. 7, pp. 51–56, 2013. [Google Scholar]
23. Z. Yu-hong, Z. Xue-feng and T. Xu-yan, “Research on the improved way of RED algorithm S-RED, International Journal of u-and e-Service,” Science and Technology, vol. 9, no. 2, pp. 357–384, 2016. [Google Scholar]
24. A. G. Ali, M. Woodward and M. Etbega, “Two different approaches of active queue management,” in Proc. IEEE International Conference on Networking, Sensing and Control, London, UK, 2007. [Google Scholar]
25. S. Liu, T. Başar and R. Srikant, “TCP-Illinois: A loss-and delay-based congestion control algorithm for high-speed networks,” Performance Evaluation, vol. 65, no. 6, pp. 417–440, 2008. [Google Scholar]
26. S. Mohammadi, H. M. Pour, M. Jafari and A. Javadi, “Fuzzy-based PID active queue manager for TCP/IP networks,” in Proc. 10th International Conference on Information Science, Signal Processing and their Applications (ISSPA 2010Malaysia: Kuala Lumpur, pp. 434–439, May, 2010. [Google Scholar]
27. S. Suthaharan, “Reduction of queue oscillation in the next generation Internet routers,” Computer Communications, vol. 30, no. 18, pp. 3881–3891, 2007. [Google Scholar]
28. C. Long, B. Zhao, X. Guan and J. Yang, “The Yellow active queue management algorithm,” Computer Networks, vol. 47, no. 4, pp. 525–550, 2005. [Google Scholar]
29. J. Hong, C. Joo and S. Bahk, “Active queue management algorithm considering queue and load states,” Computer Communications, vol. 30, no. 4, pp. 886–892, 2007. [Google Scholar]
30. H. Abdel-jaber, M. Mahafzah, F. Thabtah and M. Woodward, “Fuzzy logic controller of random early detection based on average queue length and packet loss rate,” in Proc. Performance Evaluation of Computer and Telecommunication Systems (SPECTS 2008Edinburgh, UK, 2008. [Google Scholar]
31. S. Kunniyur and R. Srikant, “End-to-end congestion control schemes: Utility functions, random losses and ECN marks,” IEEE/ACM Transactions on Networking, vol. 11, no. 5, pp. 689–702, 2003. [Google Scholar]
32. D. Lapsley and S. Low, “Random early marking: an optimization approach to Internet congestion control,” in Proc. IEEE International Conference on Networks (ICON ‘99NW Washington, DC, United States, 1999. [Google Scholar]
33. J. Wang, M. Song and H. Yang, “Rate-based active queue management for congestion control over wired and wireless links,” in Proc. First International Conference on Communications and Networking in China, Hangzhou, China, 2006. [Google Scholar]
34. B. Zheng and M. Atiquzzaman, “DSRED: an active queue management scheme for next generation networks,” in Proc. 25th Annual IEEE Conference on Local Computer Networks, NW Washington, DC; United States, 2000. [Google Scholar]
35. S. Floyd, R. Gummadi and S. Shenker, “Adaptive RED: An algorithm for increasing the robustness of RED’s active queue management,” Research Report, AT&T Center for Internet Research at ICSI, University of California at Berkeley, United States, 2001. [Google Scholar]
36. W. C. Feng, D. Kandlur, D. Saha and K. Shin, “BLUE: A new class of active queue management algorithms,” Technical Report, University of Michigan, MI, United States, 1999. [Google Scholar]
37. J. Koo, B. Song, K. Chung, H. Lee and H. Kahng, “MRED: a new approach to random early detection,” in Proc. 15th International Conference on Information Networking, NW Washington, DC, United States, 2001. [Google Scholar]
38. C. N. Long, B. Zhao and X. P. Guan, “SAVQ: Stabilized adaptive virtual queue management algorithm,” IEEE Communications Letters, vol. 9, no. 1, pp. 78–80, 2005. [Google Scholar]
39. Q. Yanping, L. Xiangze, L. Qi and J. Wei, “A stable enhanced adaptive virtual queue management algorithm for TCP networks,” in Proc. IEEE International Conference on Control and Automation, Guangzhou, China, 2007. [Google Scholar]
40. X. Deng, S. Yi, G. Kesidis and C. R. Das, “Stabilized virtual buffer (SVB)-an active queue management scheme for internet Quality-of-Service,” in Proc. Global Telecommunications Conference, Taipei, Taiwan, 2002. [Google Scholar]
41. C. Wang, B. Li, Y. T. Hou, K. Sohraby and K. Long, “A stable rate-based algorithm for active queue management,” Computer Communications, vol. 28, no. 15, pp. 1731–1740, 2005. [Google Scholar]
42. J. Sun and M. Zukerman, “RaQ: A robust active queue management scheme based on rate and queue length,” Computer Communications, vol. 30, no. 8, pp. 1731–1741, 2007. [Google Scholar]
43. A. A. Abu-Shareha, “Enhanced random early detection using responsive congestion indicators,” International Journal of Advanced Computer Science and Applications(IJACSA), vol. 10, no. 3, pp. 358–367, 2019. [Google Scholar]
44. A. A. Abu-Shareha, “Controlling delay at the router buffer using modified random early detection,” International Journal of Computer Networks & Communications (IJCNC), vol. 11, no. 6, pp. 63–75, 2019. [Google Scholar]
45. L. Kleinrock, Queueing systems, 1st ed., New York: Wiley, 1976. [Google Scholar]
46. M. Khatari and G. Samara, “Congestion control approach based on effective random early detection and fuzzy logic,” MAGNT Research Report, vol. 3, no. 8, pp. 180–193, 2015. [Google Scholar]
47. M. Guizani, A. Rayes, B. Khan and A. Al-Fuqaha, Network modeling and simulation: a practical perspective, 1st ed., John Wiley & Sons, Chichester, UK, 2010. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |