DOI:10.32604/csse.2022.017733

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.017733 |  |
| Article |
Applying Non-Local Means Filter on Seismic Exploration
1College of Computer Science and Information Technology, Imam Abdulrahman Bin Faisal University, Dammam, P. O. 1982, Saudi Arabia
2Geophysical Application Division, Exploration Application Services Department, Saudi Aramco, Dhahran, Saudi Arabia
*Corresponding Author: Saleh Al-Dossary. Email: saleh.dossary.6@aramco.com
Received: 09 February 2021; Accepted: 09 April 2021
Abstract: The seismic reflection method is one of the most important methods in geophysical exploration. There are three stages in a seismic exploration survey: acquisition, processing, and interpretation. This paper focuses on a pre-processing tool, the Non-Local Means (NLM) filter algorithm, which is a powerful technique that can significantly suppress noise in seismic data. However, the domain of the NLM algorithm is the whole dataset and 3D seismic data being very large, often exceeding one terabyte (TB), it is impossible to store all the data in Random Access Memory (RAM). Furthermore, the NLM filter would require a considerably long runtime. These factors make a straightforward implementation of the NLM algorithm on real geophysical exploration data infeasible. This paper redesigned and implemented the NLM filter algorithm to fit the challenges of seismic exploration. The optimized implementation of the NLM filter is capable of processing production-size seismic data on modern clusters and is 87 times faster than the straightforward implementation of NLM.
Keywords: Seismic exploration; parallel programming; seismic processing; optimizing methods
Seismic exploration involves data acquisition, processing, and interpretation. This paper focuses on the seismic data processing stage, which is an analysis of recorded seismic signals to reduce noise and create an image of the subsurface to enable geological interpretation, and eventually to obtain an estimate of the distribution of material properties in the subsurface. This paper is extending the research work of Buades, Coll, and Morel [1]. There are three major challenges in applying NLM filter to seismic exploration data:
1. Long elapsed time.
2. Huge memory usage.
3. Poor scalability.
This paper discusses the redesign and implementation of the Non-Local Means filter algorithm using parallel programming to increase its feasibility for processing production-size seismic data, the optimized implementation has good performance and is capable of processing production-size 3D seismic data on modern clusters.
This section introduces some major key concepts of both NLM filter and seismic exploration.
The oil industry uses seismic exploration to find underground hydrocarbon reservoirs. There are three stages in seismic exploration data [2]. The first stage is the seismic acquisition, where the land and marine seismic signals are produced and recorded by field crews. The second stage is seismic processing, where seismic sections are created by removing noise from raw data recorded by the field crew. The third stage is seismic interpretation, where horizons and structures are identified, and potential reserves of hydrocarbons are mapped. This paper focuses on the second stage, seismic data processing.
2.2 Noise Filtering with Seismic Data
Seismic exploration data is unavoidably contaminated by coherent and random noise, which is known as seismic noise [3]. Therefore, noise reduction is necessary to enhance the seismic image to extract a real signal from raw seismic data. Among the most widely used filters for this purpose are the Mean, Median, and Non-Local Means filters [4]. This paper discusses the NLM filter for its effectiveness on noise reduction without damaging the data’s essential information.
One of the essential tasks of seismic image processing is edge detection. As the name implies, edge detection is a technique to define the boundaries of objects in images, especially after applying denoise techniques. The concept relies on using mathematical techniques to enhance the discontinuities in the data, as noise-filtering can often reduce the sharpness of these critical edges. One of the most promising edge detectors is the Sobel method [5]. It relies on a pixel-by-pixel gradient calculation [6]. As edge detection is a typical task performed after noise reduction, in this paper, we will use edge detection as a criterion to evaluate the results from different noise reduction algorithms.
Many algorithms can be broken down into subtasks that can be processed in parallel to improve the runtime performance [7]. OpenMP provides a multi-threaded programming facility based on a set of compilers and library calls directives. It supports parallel constructs in automatic parallel execution of for-loops without iteration dependencies [7]. This parallelism facility is not restricted to any specific processors or architecture and is applicable as long as shared memory is used for all the execution threads.
Buades et al. [1] developed the Non-Local Means (NLM) filter for image processing. This algorithm is capable of separating coherent and incoherent signals while preserving features, edges, and structures of the image. The NLM algorithm is based on a weighted mean. The weights depend on the measure of similarity between patches surrounding each sample of the image. This methodology allows for preserving the information integrity by saving the features and structures of the image and filtering out the noise. Bonar et al. [8] proved the effectiveness of NLM in seismic data processing compared to other techniques for noise attenuation like f-x deconvolution.
The NLM algorithm is based on non-local averaging of all pixels in a noisy image (a seismic section) I:
The weight between p and q depends on the measure of the relative distance d(p,q) and a harshness parameter h. It is computed using the formula:
The distance is computed to evaluate the similarity between two neighborhoods, p and q, and balanced by a convolutional kernel K. The formula of the distance is:
3.2 Noise Filtering Algorithm Comparison
In this section, we evaluate the effectiveness of Median, Mean and NLM filtering algorithms in removing noise. The edge detection algorithm applied to the result of each will show the most effective of the three in removing noise and enhancing edges in the image.
Figs. 1–4 show the original and the three filtered (denoised) seismic data together with the corresponding edge detection results, respectively. Comparing Figs. 1 and 2, it is observed that the Median filter did a minimal job of removing noise, but it preserved the structure of the image. Comparatively, the Mean filter (Fig. 3) removed more noise energy but some essential structures got blurred out in the process. The Non-Local Means filter (Fig. 4) reduced the noise the most and maintained the essential structures of the image intact. This proves the superiority of NLM over the other two filters and the quality of output is appropriate for the interpretation of seismic data.

Figure 1: Original image without applying any denoise filter and its edge detection result

Figure 2: Image after applying Median filter and its edge detection result

Figure 3: Image after applying Mean filter and its edge detection result

Figure 4: Image after applying Non-Local Means filter and its edge detection result
4 Apply the Non-Local Means Filter on Real Seismic Field Data
Straight forward implementation based on mathematical algorithm doesn’t always guarantee the best practical implementation. A practical implementation would be able to endure the speed required to process as much data as possible while consuming the smallest amount of time possible. Practicality also includes efficient memory usage where no memory exhaustion occurs due to the increasing demand or data size. In this section, each of the aforementioned challenges will be examined.
One of the most important advantages of parallel computing is to speed certain task by dividing it into several subtasks and perform these subtasks simultaneously [9]. Since the seismic data sizes are huge, parallel computing will reduce the execution time, and increase productivity such that more data is processed in less time.
Seismic data volumes are large, exceeding one terabyte, especially the 3D seismic data, which occupy massive (out-of-core) storage space that may be attached to a large scale SMP (Symmetric Multiprocessor) supercomputers or use a smaller scale cluster equipped with multicore CPU and OpenMP that provides the needed computational power at a fraction of the cost [10].
Parallel computers’ classification can be approximately comparable to the degree to which the hardware supports parallelism, given the fact that such machines include multiple cores and multiple processors shown within multiple processing units in a single machine [11]. Clusters, Massively Parallel Processors (MPPs), and grids use multiple machines to approximate the working strength and capacity of parallel computers [12]. As mentioned in 4.2, the alternative approach can further be cost-efficient and reliable by incorporating storage and computing scalability. As data size increases, more storage can be added. Also, better computing speed is needed to maintain a good ratio between data processing time and bulk data size. This can be achieved by adding more nodes to the clusters and computer grids [13].
4.4 Optimizing and Performance Comparison
We optimized the implementation of the NLM filter using OpenMP by creating a parallel region in the most intense task part of the NLM implementation, to guarantee the data dependency, and applying dynamic scheduling. Every thread takes one iteration in the dynamic scheduling, which is demand-based. A thread when finished takes the next iteration not being processed by anyone [14]. Therefore, it will never have one thread idle while others busy. Then, the optimization was tested to observe the impact of parallelization on the performance using OpenMP. The analysis included six different tests on the 3D implementation using various techniques to identify the best methods to use. This experiment compared the tests by the CPU utilization, consistency, execution time of each test, and whether it impacts the image quality by examining the original noisy image with the output image after NLM and used the edge detection algorithm on both noisy image and the output image to evaluate the quality. The same 3D noisy dataset was used in all the tests. Also, the tests were on the same device to ensure the comparison is accurate. The result showed that all output images using different optimization techniques were similar, and using the highest optimization level (O2), showed the best performance in terms of execution time.
The expectation for the implementation of the Non-Local Means filter in C++ without using parallelization was to be at least two times faster than the prototype, which is written in MATLAB. The results of the optimization were amazing and exceeded expectations since the serial C++ implementation became seven times faster than the prototype, as shown in Tab. 1 and Fig. 5.

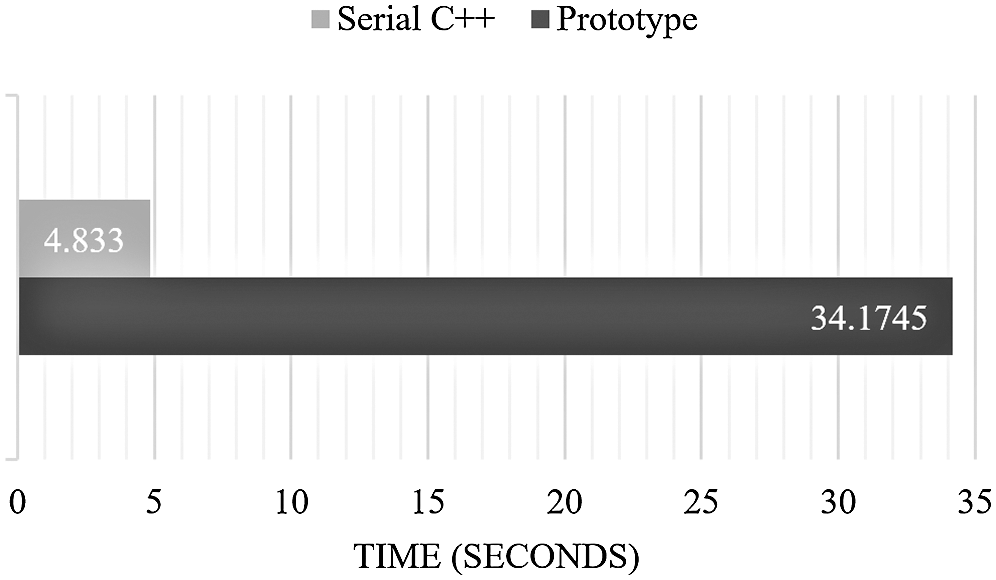
Figure 5: Execution time comparison for the NLM serial 2D code and the prototype
The parallelization was implemented on the 2D and 3D serial C++ implementation using OpenMP and enabled maximum speed optimization (/O2). The optimized 2D implementation is 12 times faster than the serial 2D C++ implementation and 87 times faster than the prototype (Tab. 2, Fig. 6). Also, the optimized 3D implementation is almost nine times faster than the serial 3D C++ implementation (Tab. 2, Fig. 7).
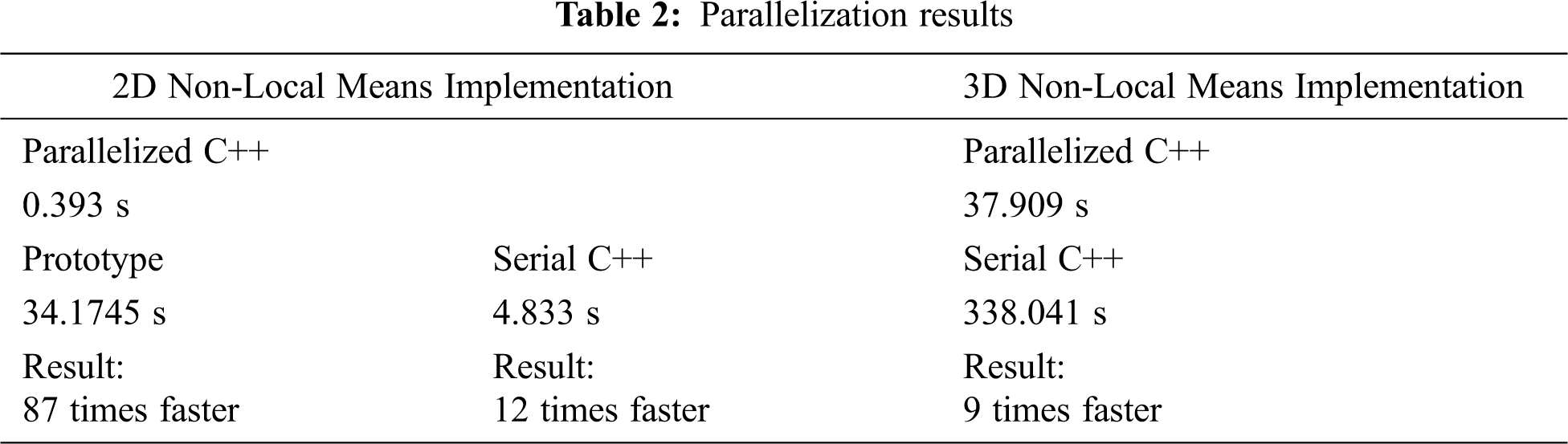
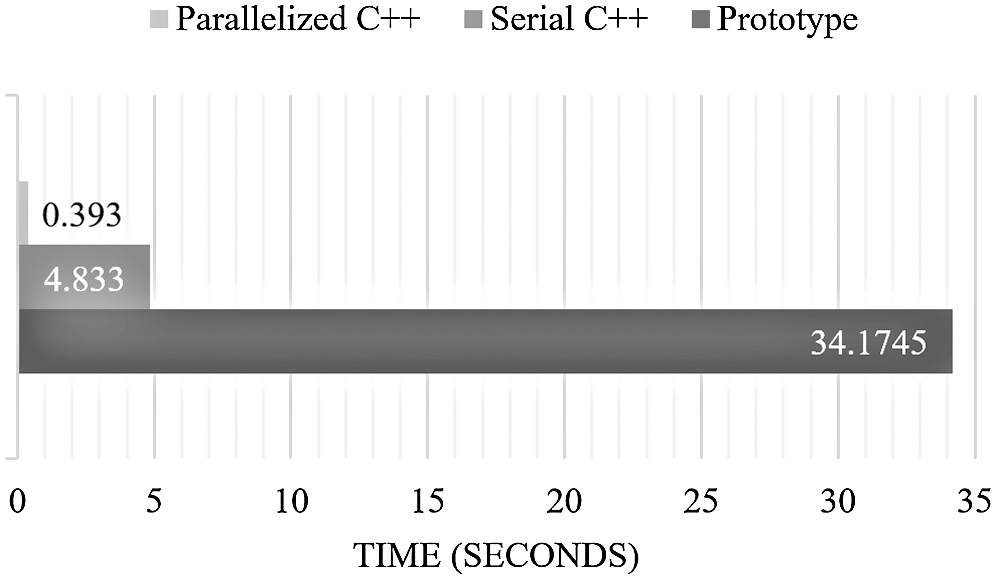
Figure 6: Execution time comparison for the prototype and NLM serial and parallelized 2D implementation
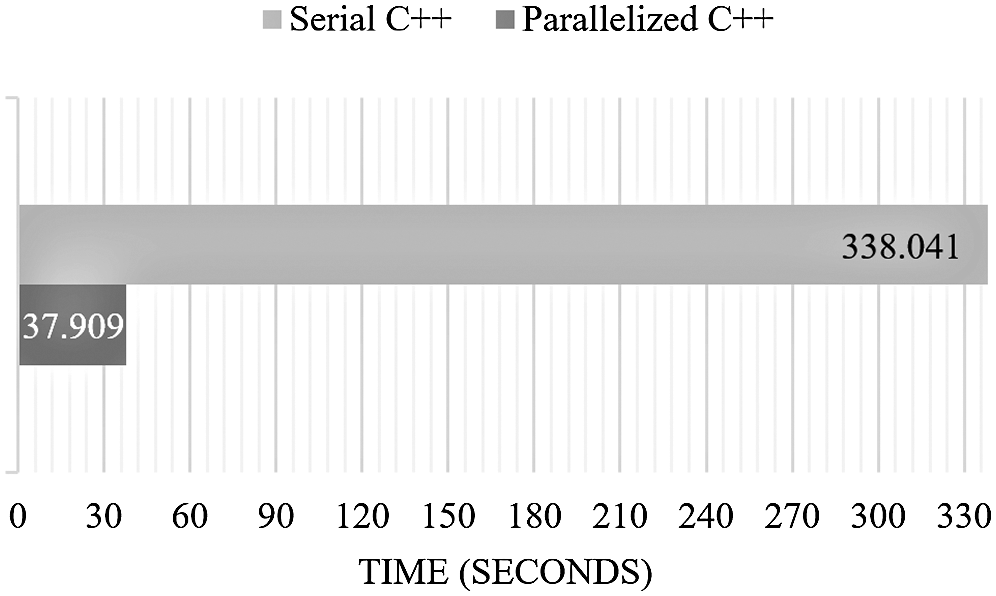
Figure 7: Execution time comparison for the NLM serial and parallelized 3D implementation
This paper proposed applying the Non-Local Means Filter on seismic exploration data. We demonstrated the superiority of the Non-Local Means filter over Median and Mean filters for denoise of seismic data. We also addressed the performance challenges of applying NLM on large 3D seismic exploration data. The redesigned Non-Local Means filter algorithm implemented using C++ language and OpenMP significantly improved the performance without compromising the quality of the image. After optimization and parallelization, the 2D version was 87 times faster than the straightforward implementation and the 3D version was nine times faster when 16 threads were used.
Acknowledgement: We are deeply grateful for our parents’ love, prayers, care, and sacrifices to educate and prepare us for our future.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. A. Buades, B. Coll and J. M. Morel, “A non-local algorithm for image denoising,” IEEE Computer Society Conf. on Computer Vision and Pattern Recognition, vol. 2, no. 7, pp. 60–65, 2005. [Google Scholar]
2. A. A. Al-Shuhail, S. A. Al-Dossary and W. A. Mousa, “Seismic Attributes,” in Seismic data interpretation using digital image processing, 1st ed. Henderson, NV, USA: John Wiley & Sons Inc, pp. 87–121, 2017. [Google Scholar]
3. K. Amitab, A. K. Maji and D. Kandar, “Speckle noise filtering in SAR images using fuzzy logic and particle swarm optimization,” Journal of Computational Methods in Sciences and Engineering, vol. 18, no. 4, pp. 859–873, 2018. [Google Scholar]
4. R. L. Weaver, “Information from seismic noise,” Science, vol. 307, no. 5715, pp. 1568–1569, 2005. [Google Scholar]
5. F. A. Alhaidari, S. A. Dossary, W. M. Al-Mattar, M. M. Kamaleldin, A. H. Abed et al., “Comparison of different edge detectors on general public images and two-dimensional seismic data,” Journal of Computational and Theoretical Nanoscience, vol. 16, no. 5, pp. 1794–1805, 2019. [Google Scholar]
6. S. Jingcheng, W. Zhengyan and L. Zenggang, “Implementation of Sobel Edge Detection algorithm and VGA display based on FPGA,” 2019 IEEE 4th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), vol. 1, pp. 2305–2310, 2019. [Google Scholar]
7. C. Terboven, D. an Mey and S. Sarholz, “OpenMP on multicore architectures,”3rd International Workshop on OpenMP,4935, pp. 2305–2310, 2007. [Google Scholar]
8. D. Bonar and M. Sacchi, “Denoising seismic data using the nonlocal means algorithm,” Geophysics, vol. 77, no. 1, pp. A5–A8, 2012. [Google Scholar]
9. J. Nakano, “Parallel Computing Techniques, ” in J. Gentle, W. Härdle, Y. Mori, Handbook of Computational Statistics, 1st ed. Berlin, Germany: Springer, pp. 243–271, 2011. [Google Scholar]
10. I. Said, P. Fortin, J. L. Lamotte and H. Calandra, “Leveraging the accelerated processing units for seismic imaging: A performance and power efficiency comparison against CPUs and GPUs,” International Journal of High Performance Computing Applications, vol. 32, no. 6, pp. 819–837, 2018. [Google Scholar]
11. A. C. Sodan, J. Machina, A. Deshmeh, K. Macnaughton and B. Esbaugh, “Parallelism via multithreaded and multicore CPUs,” Computer, vol. 43, no. 3, pp. 24–32, 2010. [Google Scholar]
12. R. Brightwell, L. A. Fisk, D. S. Greenberg, T. Hudson, M. Levenhagen et al., “Massively parallel computing using commodity components,” Parallel Computing, vol. 26, no. 2–3, pp. 243–266, 2000. [Google Scholar]
13. W. F. Mccoll, “Scalability, portability and predictability: The BSP approach to parallel programming,” Future Generation Computer Systems, vol. 12, no. 4, pp. 265–272, 1996. [Google Scholar]
14. R. Chandra, L. Dagum, D. Kohr, D. Maydan, J. McDonald et al., “Eploiting Loop-Level Parallelism,” in Parallel programming in OpenMP. San Francisco, CA, USA: Morgan Kaufmann Publishers, pp. 41–90,2001. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |