DOI:10.32604/csse.2021.016693

| Computer Systems Science & Engineering DOI:10.32604/csse.2021.016693 |  |
| Article |
Brain Storm Optimization Based Clustering for Learning Behavior Analysis
1School of Computer and Software, Nanjing University of Information Science and Technology, Nanjing, 210044, China
2Jiangsu Key Laboratory of Data Science and Smart Software, Jinling Institute of Technology, Nanjing, 211169, China
3Department of Electronics and Computer Science, Koszalin University of Technology, 75-453, Koszalin, Poland
*Corresponding Author: Yu Xue. Email: xueyu@nuist.edu.cn
Received: 08 January 2021; Accepted: 28 April 2021
Abstract: Recently, online learning platforms have proven to help people gain knowledge more conveniently. Since the outbreak of COVID-19 in 2020, online learning has become a mainstream mode, as many schools have adopted its format. The platforms are able to capture substantial data relating to the students’ learning activities, which could be analyzed to determine relationships between learning behaviors and study habits. As such, an intelligent analysis method is needed to process efficiently this high volume of information. Clustering is an effect data mining method which discover data distribution and hidden characteristic from uncharacterized online learning data. This study proposes a clustering algorithm based on brain storm optimization (CBSO) to categorize students according to their learning behaviors and determine their characteristics. This enables teaching to be tailored to taken into account those results, thereby, improving the education quality over time. Specifically, we use the individual of CBSO to represent the distribution of students and find the optimal one by the operations of convergence and divergence. The experiments are performed on the 104 students’ online learning data, and the results show that CBSO is feasible and efficient.
Keywords: Online learning; learning behavior analysis; big data; brain storm optimization; cluster
Online learning is becoming more popular as courses can easily and repeatedly be taken from anywhere and at any time. As such, the number of students is virtually unlimited, as even individuals who are not enrolled in a learning institution are able to sign up. With the outbreak of COVID-19 in 2020, many educational institutions were compelled to embrace online learning. As these learning platforms are able to capture substantial data related to the ongoing learning activities of each student, a considerable amount of information regarding learning behavior could be gathered. For example, analysis of the data can reveal relationships between learning behaviors and performance scores, enabling tailoring of lectures accordingly for better results, improving on the educational quality and experience [1,2].
Students have different learning manners, habits, basic knowledge, and interests. Manual analysis method are difficult to process this complex information. As such, intelligence methods are needed to solve these problems. This paper designs a clustering algorithm based on brain storm optimization (CBSO) to analyze online learning behaviors [3,4].
Brain storm optimization (BSO) simulates the brainstorming process, and is an optimization algorithm based on swarm intelligence [5]. As BSO has a good ability to solve optimization problems [6], it has been applied to fields such as classification [7–10], clustering [11], multi-objective optimization [12–14], and feature selection [15–17].
BSO combines swarm intelligence techniques with data mining and data analysis. The distribution of generated solutions can be changed according to the properties of a problem. However, BSO has the defects of converge slowly and falling into local optimum easily. As such, many BSO variants have been proposed. For example, Zhu proposed a BSO algorithm that replaced k-means with k-medians [18] and used the median to calculate the center point, which is the point that is closest to the other points in the cluster. Yang proposed a BSO algorithm which replaced Gaussian variation with differential variation [19], thereby improving greatly the running speed and search efficiency. Shi introduced the idea of a target space [20], which reduced the complexity of clustering by dividing solutions into elite and ordinary solutions. Zhang replaced k-means with SGM clustering [21], and Gaussian variation with differential variation to improve the operational efficiency and optimization accuracy. Wu used differential mutation and clustering to improve the search speed and accuracy [22]. Yang introduced a new method, which used the discussion mechanism to generate new individuals to avoid falling into a local optimum [23]. Wu proposed an adaptive inertial selection strategy to solve the problem of low accuracy and slow convergence [24]. Xue used BSO to solve multi-objective problems, and employed a non-dominant sort to update the archive set composed of non-inferior solutions [25]. Wu proposed a multi-dimensional BSO algorithm with high objectives to improve convergence and diversity, enhancing the efficiency in solving multi-objective problems [26].
The BSO algorithm has good robustness in solve clustering problems, and current clustering methods have some defects. For example, k-means depends on the selection of initial centers and is sensitive to noise and outliers. Density-based spatial clustering of applications with noise (DBSCAN) does not perform well on the problems that are high-dimensional or have large changes in density.
Clustering is an important technique which uses data mining to discover data distribution and hidden patterns. Through clustering, the relationship between learning behavior and performance can be found from uncharacterized online learning behavior data. As such, the characteristics of students are able to be obtained.
In this paper, CBSO is applied to cluster and analyze students’ online learning data. Our objectives are as follows:
1) to construct a clustering optimization model based on BSO;
2) to improve the accuracy of the cluster;
3) to apply the proposed model to data of students’ online learning behaviors;
4) to provide suggestions for students for better education quality.
The remainder of this paper is organized as follows. Section 2 provides background information. Section 3 describes the CBSO algorithm. Section 4 describes an experiment design. Section 5 presents results and discussion, and Section 6 relates our conclusions.
Human brainstorming is a method proposed by Osborne in 1953 to enable a group of people to come up with as many ideas as possible. Everyone can present ideas freely, find inspiration by listening to others. After all ideas are evaluated, the best is selected.
BSO simulates this process and has three corresponding steps of initializing individuals, generating new ones, and selecting the best one [27]. The steps are as follows:
Step 1: N individuals are initialized and grouped into k clusters, and the best individual in each cluster is selected as the cluster center.
Step 2: Updating strategies are selected according to probability functions. These strategies and random disturbances are used to generate new individuals.
Step 3: The fitness function is used to evaluate individuals and retain the better ones.
To strength the search ability of BSO, Gaussian variation is used to update individuals in Step 2. The updating method is shown in Eqs. (1) and (2).
where ζ is the step length,
3 Proposed Clustering Method Based on BSO Algorithm
Clustering method is dividing the samples with high similarity into a cluster. Hence samples in same cluster have high similarity, and in different clusters have high heterogeneity. In addition, the Euclidean distance is used as the fitness value to judge the similarity of samples. As the division of samples can be represented well by a solution of the intelligent swarm algorithm, and BSO is a good global optimization method, CBSO is used to find the optimal solution of clustering samples [28].
3.2 Initialization and Representation of Solutions
Algorithm 1 describes the initialization and representation of solutions for clustering problems. The value of each dimension of an individual is generated randomly in (0,1). This range is divided averagely into small intervals according to the number of clusters. A discrete value is obtained for each dimension by calculating which interval the corresponding continuous values fall in. The xi in individual x = {x1,x2,x3,…,xn} is the cluster label. The steps are shown in Algorithm 1.

The Euclidean distance is used as object function to gather similar samples into the same cluster. The closer the distance, the more similar the samples are. The object function is given as Eq. (3).
where k is the number of clusters, cj is the center of the jth cluster, xi is value of each sample in the jth cluster, mj is the number of members in the jth cluster, and F is the fitness value.
3.4 Clustering Method for Individuals in the Population of BSO
To reduce the search space and accelerate convergence, individuals in BSO are clustered by k-means [29–31]. Then, through the judgment of fitness value, the central individual can be obtained. In addition, A random probability p is used to judge whether to replace the current central individual with the new one to avoid premature convergence and falling into a local optimum. The steps are shown in Algorithm 2.

3.5 The Operations for Generating New Solutions
New individuals are generated according to Eqs. (1), (2), and (4). The probability parameters such as p1, p2, and p3 are used to avoid falling into a local optimum, as the specific operations are described in this section. The global optimal solution can be found by enhancing the search capability with these parameters in iterative processes [32]. Probability parameter p1 determines whether one or two clusters are selected. If the probability value generated is less than p1, we select one cluster; otherwise, we select two clusters. Probability parameter p2 is used to select the central or ordinary individual in a cluster to generate new individuals, and probability parameter p3 is used to select the central or ordinary individual from each of the two clusters and combine them to generate new individuals. The steps are shown in Algorithm 3.
where

We collected the online learning data of students in the spring of 2020, including student number, student name, course number, days and times logged in to the web, days and times logged in to a course, number of posts, number of replies, post points, and total points. To avoid the impact of abnormal and useless information, some abnormal samples were removed, 104 sample data without student number and name were reserved for subsequent analysis.
Since data in the collected dataset differed greatly, we standardized the data with a Z-score to reduce their impacts on CBSO.
where yi is the normalized value, xi is the original value, and
Since the original data had nine types of features, when drawing the graph of clustering results, we used principal component analysis (PCA) to reduce the dimensions to two.
In the CBSO algorithm, the maximum number of iterations was 12000, and runtimes was 30, ensuring the stability and accuracy of the experiment. The probability parameters of four updating strategies and initial number are shown in Tab. 1.
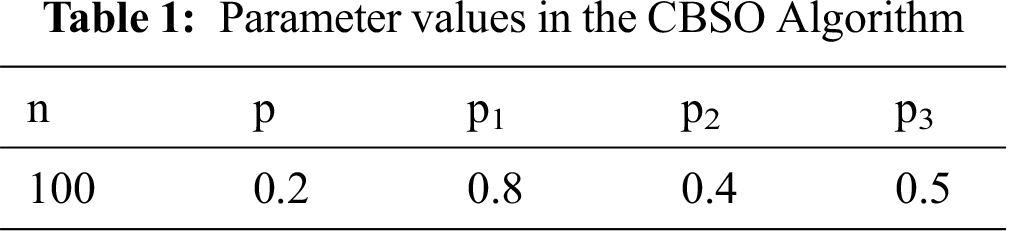
Students were clustered into four categories, and the average value of all student data for each category was calculated. Then, the characteristics of each category are able to be found by analyzing these values, enabling tailoring of lectures accordingly for better educational quality and high enthusiasm in learning.
5.1 Computational Results and Analysis
The cluster results are shown in Tab. 2, in which the value in each row is an average. The first through fourth classes had 23, 25, 37, and 19 students, respectively. In Tab. 2, the values of days logged in to web and courses, times logged in to web and courses, times released and replied posts can reflect the enthusiasm of students in learning. The posting integral and total integral can reflect students’ performance. Thus, four characteristics of students were defined according to enthusiasm and performance. For example, the values of the first-category were –0.3178, 0.4574, 0.9209, 0.7142, 0.6771, –0.0177, 1.1724, 1.1665, and 1.4339, respectively. Compared to the other three types of data, this kind of student’s learning enthusiasm and performance are the best. Therefore, such students are defined as those with good performance and high enthusiasm.
The same method is used to define the remaining three characteristics of students as follows: poor performance and high enthusiasm, good performance and low enthusiasm, and poor performance and low enthusiasm. Tab. 3 describes the four characteristics of students.
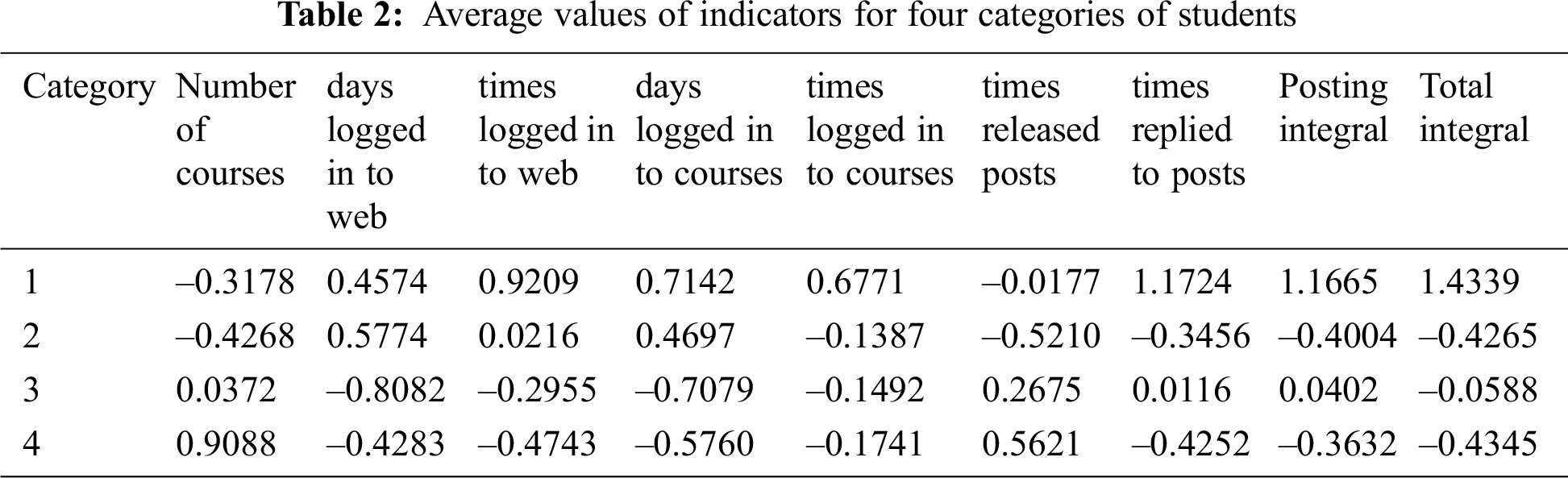

Fig. 1 shows the clustering situation of 104 students after dimensional reduction, which can reflect that the CBSO algorithm cluster samples with similar characteristics together.
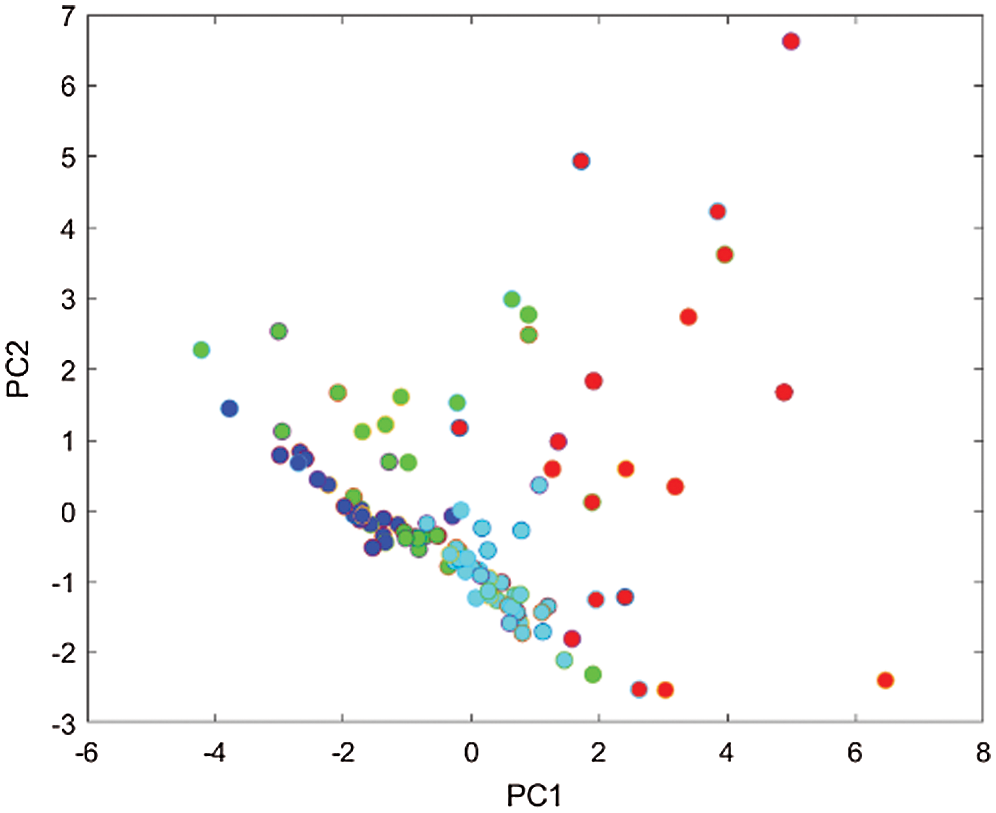
Figure 1: Cluster diagram after dimensionality reduction
Tailoring of lectures can be provided to help students achieve better learning results. For example, first-category students are highly motivated to learn and have strong learning capabilities. So, they should be provided with more learning resources for further improvement. Although the students in the second-category are motivated to learn, they do not achieve good results. They need to be given learning guidance to avoid study blindly. Conversely, students in the third-category have low learning enthusiasm, but their grades are acceptable. We should enhance teaching supervision and cultivate their interest in learning to raise their potential. Finally, students in the fourth-category have neither learning enthusiasm nor good grades. Thus, we should strengthen teaching supervision, cultivate their interest in learning, and change the manner of teaching to improve their performance.
The BSO algorithm takes advantage of swarm intelligence and data analysis, and can be used to solve efficiently clustering problems. Thus, the paper proposed a cluster algorithm based on BSO. Individuals were discretized to present the distribution of samples. Besides, Euclidean distance was used to calculate the similarity of individuals. Experiments showed that CBSO is feasible and efficient to solve clustering problems. As such, CBSO is applied to analyze the relationship between learning data and performance, so as to provide tailored guidance to each characteristic of student. However, BSO still falls easily into local optima. We look forward to optimizing the model to obtain more accurate clustering results.
Funding Statement: This work was partially supported by the National Natural Science Foundation of China (61876089, 61876185, 61902281, 61375121), the Opening Project of Jiangsu Key Laboratory of Data Science and Smart Software (No. 2019DS301), the Engineering Research Center of Digital Forensics, Ministry of Education, the Key Research and Development Program of Jiangsu Province (BE2020633), and the Priority Academic Program Development of Jiangsu Higher Education Institutions.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. O. Almatrafi and A. Johri, “Systematic review of discussion forums in massive open online courses (moocs),” IEEE Transactions on Learning Technologies, vol. 12, no. 3, pp. 413–428, 2019. [Google Scholar]
2. W. Chen, C. G. Brinton, D. Cao, A. Mason-Singh, C. Lu et al., “Early detection prediction of learning outcomes in online short-courses via learning behaviors,” IEEE Transactions on Learning Technologies, vol. 12, no. 1, pp. 44–58, 2019. [Google Scholar]
3. Z. Chen, M. Xu, G. Garrido and M. W. Guthrie, “Relationship between students’ online learning behavior and course performance: What contextual information matters,” Physical Review Physics Education Research, vol. 16, no. 1, pp. 1–15, 2020. [Google Scholar]
4. L. Wang, Z. Zhen, T. Wo, B. Jiang, H. Sun et al., “A scalable operating system experiment platform supporting learning behavior analysis,” IEEE Transactions on Education, vol. 63, no. 3, pp. 232–239, 2020. [Google Scholar]
5. Y. H. Shi, “Brain storm optimization algorithm,” in Proc. of Second Int. Conf. on Swarm Intelligence (ICSI 2011Chongqing, China, pp. 303–309, 2011. [Google Scholar]
6. Y. Xue, J. M. Jiang, B. P. Zhao and T. H. Ma, “A self-adaptive artificial bee colony algorithm based on global best for global optimization,” Soft Computing, vol. 22, no. 9, pp. 2935–2952, 2018. [Google Scholar]
7. Y. Zhang, D. W. Gong and J. Cheng, “Multi-objective particle swarm optimization approach for cost-based feature selection in classification,” IEEE/ACM Transactions on Computational Biology and Bioinformatics, vol. 14, no. 1, pp. 64–75, 2017. [Google Scholar]
8. X. Yu, Y. Chu, F. Jiang, Y. Guo and D. W. Gong, “SVMs classification based two-side cross domain collaborative filtering by inferring intrinsic user and item features,” Knowledge-Based Systems, vol. 141, no. 1, pp. 80–91, 2018. [Google Scholar]
9. Y. Xue, B. Xue and M. Zhang, “Self-adaptive particle swarm optimization for large-scale feature selection in classification,” ACM Transactions on Knowledge Discovery from Data, vol. 13, no. 5, pp. 1–27, 2019. [Google Scholar]
10. Y. Xue, T. Tang, W. Pang and A. X. Liu, “Self-adaptive parameter and strategy based particle swarm optimization for large-scale feature selection problems with multiple classifiers,” Applied Soft Computing, vol. 88, no. 4, pp. 106031, 2020. [Google Scholar]
11. S. Cheng and Y. H. Shi, “Brain storm optimization algorithms: Concepts, principles and applications,” Adaptation, Learning, and Optimization, vol. 23, pp. 1–299, 2019. [Google Scholar]
12. B. Cao, W. Dong, Z. Lv, Y. Gu, S. Singh et al., “Hybrid microgrid many-objective sizing optimization with fuzzy decision,” IEEE Transactions on Fuzzy Systems, vol. 28, no. 11, pp. 2702–2710, 2020. [Google Scholar]
13. B. Cao, X. S. Wang, W. Z. Zhang, H. B. Song and Z. H. Lv, “A many-objective optimization model of industrial Internet of things based on private blockchain,” IEEE Network, vol. 34, no. 5, pp. 78–83,2020. [Google Scholar]
14. A. Y. Hamed, M. H. Alkinani and M. R. Hassan, “Ant colony optimization for multi-objective multicast routing,” Computers, Materials & Continua, vol. 63, no. 3, pp. 1159–1173, 2020. [Google Scholar]
15. Y. Zhang, X. F. Song and D. W. Gong, “A return-cost-based binary firefly algorithm for feature selection,” Information Sciences, vol. 418–419, no. 3, pp. 561–574, 2017. [Google Scholar]
16. Y. Zhang, D. W. Gong, Y. Hu and W. Q. Zhang, “Feature selection algorithm based on bare bones particle swarm optimization,” Neurocomputing, vol. 148, no. 5, pp. 150–157, 2015. [Google Scholar]
17. Y. Xue, Y. H. Tang, X. Xu, J. Y. Liang and F. Neri, “Multi-objective Feature Selection with Missing Data in Classification,” in IEEE Transactions on Emerging Topics in Computational Intelligence, 2021. [Google Scholar]
18. H. Y. Zhu and Y. H. Shi, “Brain storm optimization algorithm swith k-medians clustering algorithms,” in The 7th Int. Conf. on Advanced Computational Intelligence, Zhengzhou, China, pp. 107–110, 2015. [Google Scholar]
19. Y. T. Yang, D. N. Duan and H. Zhang, “Kinematic recognition of hidden markov model based oncimproved brain storm optimization algorithm,” Space Medicine & Medical Engineering, vol. 28, no. 6, pp. 403–407, 2015. [Google Scholar]
20. Y. H. Shi, “Brain storm optimization algorithm in objective space,” in IEEE Congress on Evolutionary Computation, Sendai, Japan, 1227–1234, 2015. [Google Scholar]
21. Z. H. Zhan, J. Zhang, Y. H. Shi and H. L. Liu, “A modified brain storm optimization,” in Proc. of the 2012 IEEE Congress on Evolutionary Computation, Brisbane, Australia, pp. 1969–1976, 2012. [Google Scholar]
22. Y. L. Wu, Y. L. Fu, X. R. Wang and Q. Liu, “Difference brain storm optimization algorithm based on clustering in objective space,” Control Theory and Applications, vol. 34, no. 12, pp. 1583–1593, 2017. [Google Scholar]
23. Y. T. Yang, Y. H. Shi and S. R. Xia, “Discussion mechanism based on brain storm optimization algorithm,” Journal of Zhejiang University, vol. 47, no. 10, pp. 1705–1711, 2013. [Google Scholar]
24. Y. L. Wu, X. P. Wang, G. T. Li and A. T. Lu, “Brain Storm Optimization Algorithm based on adaptive inertial Selection strategy for the RCPSP,” 2019 Chinese Automation Congress (CAC), Hangzhou, China, pp. 2610–2615,2019. [Google Scholar]
25. J. Q. Xue, Y. L. Wu, Y. H. Shi and S. Cheng, “Brain storm optimization algorithm for multi-objective optimization problems,” Lecture Notes in Computer Science, vol. 7331, no. 4, pp. 513–519, 2012. [Google Scholar]
26. Y. L. Wu, Y. L. Fu, G. T. Li and Y. C. Zhang, “Many-objective brain storm optimization algorithm,” Control Theory and Applications, vol. 37, no. 1, pp. 193–204, 2020. [Google Scholar]
27. L. B. Ma, S. Cheng and Y. H. Shi, “Enhancing learning efficiency of brain storm optimization via orthogonal learning design,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, pp. 1–20, 2020. [Google Scholar]
28. T. Pan, Y. Song and S. Chen, “Wiener model identification using a modified brain storm optimization algorithm,” Intelligent Automation & Soft Computing, vol. 26, no. 5, pp. 934–946, 2020. [Google Scholar]
29. A. Maamar and K. Benahmed, “A hybrid model for anomalies detection in AMI system combining k-means clustering and deep neural network,” Computers, Materials & Continua, vol. 60, no. 1, pp. 15–39, 2019. [Google Scholar]
30. A. A. Ahmed and B. Akay, “A survey and systematic categorization of parallel k-means and fuzzy-c-means algorithms,” Computer Systems Science and Engineering, vol. 34, no. 5, pp. 259–281, 2019. [Google Scholar]
31. Y. Wang, X. Luo, J. Zhang, Z. Zhao and J. Zhang, “An improved algorithm of k-means based on evolutionary computation,” Intelligent Automation & Soft Computing, vol. 26, no. 5, pp. 961–971, 2020. [Google Scholar]
32. S. Cheng, L. B. Ma, H. Lu, X. J. Lei and Y. H. Shi, “Evolutionary computation for solving search-based data analytics problems,” Artificial Intelligence Review, in press, vol. 54, no. 2, pp. 1321–1348, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |