DOI:10.32604/csse.2021.05365

| Computer Systems Science & Engineering DOI:10.32604/csse.2021.05365 |  |
| Article |
A survey on the Metaheuristics for Cryptanalysis of Substitution and Transposition Ciphers
1Computer Engineering Department, Erciyes University, Kayseri, 38039, Melikgazi, Turkey
*Corresponding Author: Arkan Kh Shakr Sabonchi. Email: arkankhaleel@gmail.com
Received: 29 December 2019; Accepted: 31 August 2020
Abstract: This paper presents state-of-art cryptanalysis studies on attacks of the substitution and transposition ciphers using various metaheuristic algorithms. Traditional cryptanalysis methods employ an exhaustive search, which is computationally expensive. Therefore, metaheuristics have attracted the interest of researchers in the cryptanalysis field. Metaheuristic algorithms are known for improving the search for the optimum solution and include Genetic Algorithm, Simulated Annealing, Tabu Search, Particle Swarm Optimization, Differential Evolution, Ant Colony, the Artificial Bee Colony, Cuckoo Search, and Firefly algorithms. The most important part of these various applications is deciding the fitness function to guide the search. This review presents how these algorithms have been implemented for cryptanalysis purposes. The paper highlights the results and findings of the studies and determines the gaps in the literature.
Keywords: Cryptanalysis; metaheuristic algorithms; substitution cipher; transposition cipher
Cryptology is a research field focused on methods for secret communication; the field comprises two areas of study: cryptography and cryptanalysis. Cryptography is the study of secret communication methods while cryptanalysis is the study of methods for attacking ciphers. The purpose of cryptanalysis is to obtain the original text (plaintext) from the cipher text without having any information about the key that was used in the encryption process. There are three fundamental strategies for attacks: ciphertext-only, known-plaintext, and chosen-plaintext [1]. In a ciphertext-only attack, a cryptanalyst must decide the key exclusively from the ciphertexts, although the technique for encryption or certain plausible words might be obvious. In a known-plaintext attack, both the original text (plaintext) and the cipher text are known. A chosen-plaintext attack requires using randomly chosen plaintexts to obtain a cipher text [1]. Classical ciphers include two basic types: transposition ciphers and substitution ciphers. In security, classical ciphers do not match today’s ciphers. However, they still maintain some centrality, because the majority of generally used modern ciphers apply the operations of classical ciphers in their structure. Indeed, compounded algorithms are often framed by a blend of substitution and transposition ciphers. Current modern block ciphers, data encryption standard (DES) and advanced encryption standard (AES) ciphers. for example, are produced by repeating numerous levels of substitution and transposition [1].
The substitution cipher is the more established type of cryptography algorithm. This cipher replaces each letter and substitutes it with another letter in ciphertext. This substitution system is transformable in that it authorizes the expected text receivers to inverse-exchange cipher text letters to get the plaintext. The simple substitution cipher is the primary type of substitution cipher. Every letter in the original text maps to a letter in the cipher text [1]. There are four kinds of substitution ciphers:
• A simple substitution cipher, or monoalphabetic cipher, is one in which every letter in the original text is exchanged with an identical letter of ciphertext.
• A homophonic substitution cipher is as simple as the substitution cryptosystem, except that a letter of the original text can map to one of a few letters of the ciphertext.
• A polygram substitution cipher is outlines of the letters are encrypted in a set. The Playfair cipher and the Hill cipher are examples of this kind of cipher.
• A polyalphabetic substitution cipher combines several simple substitution ciphers. In this method, a certain cipher is used to change the position of all letters of the original text, such as in the Vigenere cipher.
• One-time pad is a large nonrepeating group of irregular key letters, which are written on a piece of a paper then glued to each other in a pad.
Another type of cryptography algorithm is transposition ciphers in which the main idea is breaking the original text into blocks of a specific size, depending on a specific permutation. In the substitution and transposition ciphers, the group of potential keys is the group of all potential permutations of the letter (for English alphabet letter); there are over 403 septillion possible permutations [2], so cryptanalysis by brute force is not effective. Instead, by utilizing a method which depends on unigrams’, bigrams’ and trigrams’ frequencies, we can create some assumptions about character substitutions and check them [3]. This operation takes a long time and includes a large amount of guesswork, as summarized in. Therefore, the target of any automated cryptanalysis operation must use this method to automate the operation. Due to the inefficiency of these methods, metaheuristic algorithms are employed to attack the ciphers. In this review, it is aimed to show how metaheuristic algorithms are used to obtain the key and investigate their fitness functions. Their efficiency in implementing automated cryptanalysis to attack the substitution and transposition ciphers are discussed.
2 Metaheuristic Algorithms to Attack Classical Cipher
Metaheuristic algorithms use randomization to discover near-optimal solutions to computationally unmanageable issues. In classical ciphers, because the group of potential keys is the group of all potential permutations of the letters (alphabet letter), there are many possibilities permutations. Therefore, due to the computational cost, cryptanalysis by brute force is not effective. For this reason, stochastic operations, guided by optimization algorithms, are used to get the optimal key.
Using the metaheuristics to attack the substitution and transposition ciphers requires a method to determine the viability of a key, called fitness function. The fitness functions are utilized to consider the validity of a certain key depending on the type of the frequency analysis. The aim of frequency analysis is to compare the frequencies in the decrypted text with the frequencies found in English literature. In other words, the frequency analysis authorizes us to evaluate precisely exact matches between a certain text and the language in which the original text was written. The frequency analysis is performed by extracting all unigrams i, bigrams ij, and trigrams ijk from the text, and then increasing a counter of Ctui, Ctbij, and Cttijk, respectively. When these tallies are classified, one can score the aggregate number of all unigrams, bigrams, and trigrams, as show in Eq. (1):
Finally, fractional indication frequencies are obtained for all unigrams, bigrams, and trigrams using Eq. (2):
In the frequency analysis, the message subjected to cryptanalysis must have sufficient length because implementing frequency analysis on short messages leads to low fitness values; therefore, only longer messages can be minutely analyzed by this method [2,4,5]. In the subsections how the algorithms are implemented for cryptanalysis purpose are given briefly and also some comparisons based on Genetic (GA), Simulated Annealing (SA), Tabu Search (TS), Particle Swarm Optimization (PSO), Artificial Bee Colony Algorithm (ABC) and Differential Evolution Algorithm (DE) are provided.
2.1 Genetic Algorithm (GA) Implementations
Holland, introduced the Genetic algorithms that modulate the idea of the Evolutionary Algorithm through the addition of a stage known as crossover. Usually, the crossover method takes apart from all chromosomes and exchanges them.
Matthews [4] used a genetic algorithm system, GENALYST, to break the transposition cipher. This system combined all the standard genetic algorithm features (crossover, point mutation, shuffle mutation). In the experiments, seven different key lengths were utilized which included the length of the target key. The population size was 20, and the number of generations was 25. The proportion of crossover was between 0.8 and 0.5. For point mutation and shuffle mutation, the proportion was 0.1, which then increased to 0.5 for point mutation and 0.8 for shuffle mutation. In total, GENALYST managed the case when the key length is 7 and 9.
Spillman et al. [5] applied a GA to break a monoalphabetic substitution cipher. The application generally recovered a key in less than a minute when the fitness value was 0.9 and the number of generations was 100, with a population size of 10. The fitness function used in the study is given by Eq. (3):
where SF[i] indicates the corresponding frequency of letter i in English, and DF[i] indicates the corresponding frequency of the decoded letter i in a text decrypted by key k. SDF[i][j] indicates the corresponding frequency of the bigram ij in English and DDF[i][j] indicates the corresponding frequency of that bigram in the decrypted text.
Clark [6] presented three algorithms, GA, TS, and SA, and applied them to cryptanalysis. Eq. (4) shows the fitness function that was used for the substitution cipher. Variables α and β are weighting parameters.
Lin and Kao [7] proposed a method based on GA to attack the Vernam cipher. They used a ciphertext-only attack and single point crossover operator in the GA. In their work, they tried to discover the optimal key from a cipher text and then utilized the key to attack the ciphertext. They created an array of match counters of a key, where Match[i] was the number of times in the key used to decrypt a ciphertext. Eq. (5) shows their fitness function.
Clark et al. [8] were the first to suggest using GA to attack a polyalphabetic substitution cipher. The parallel method they used in this work depended on several serial GA being applied to separate sections of the issue. The fitness function used weighted unigrams, bigrams, and trigrams, as shown in Eq. (6).
K1, K2, and K3 are known unigram, bigram, and trigram statistics, respectively. D1, D2, and D3 are statistics for the decrypted text, and W1, W2, and W3 are weights chosen to equal one. This study initially used unigrams and bigrams only, then later used trigrams. This method obtained 90% of the original by using 600 known cipher text letters for each key. In this test, the weights were W1 = 0.4, W2 = 0.6, and W3 = 0.0. After 100 iterations, the weights were gradually changed such that W1, W2, W3 {0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0}; the preferable outcome occurred when W3 = 0.8.
Clark and Dawson [9] extended the work proposed by Clark et al. [8]. They utilized a new strategy based on a parallel genetic algorithm to attack the Vigenere cipher. Their fitness function used weighted unigrams, bigrams, and trigrams, as seen in Eq. (7).
Suppose, L(1), L(2),and L(3) are the known unigram, bigram, and trigram statistics, respectively. D(1), D(2), and D(3) are statistics for the decrypted text, and w1 , w2, and w3 are weights chosen to equal one. When the algorithm was implemented 5 times on 10 different texts of text length 600 characters, 70% of the original key characters were restored correctly. An improved result was obtained when the values of w1, w2, and w3 were 0.1, 0.7 and 0.8 respectively.
Clark and Dawson [10] compared SA, GA, and TS on the cryptanalysis of simple substitution ciphers. They particularly investigated speed and efficiency. The overall attack used the fitness function given in Eq. (8).
where A is the language alphabet, K indicates the language statistics, D indicates the decrypted text statistics, and u, b, and t indicates the unigram, bigram, and trigram statistics, respectively. Through experimental results, the researchers obtained 100 various texts for each algorithm; they implemented the attack three times on each algorithm. The results showed that the most efficient algorithm was TS, followed by SA, then GA.
Dimovski and Gligoroski [11] presented three optimization heuristics that were used to break the transposition cipher: SA, GA, and TS. The experimental results showed that all three algorithms were effective methods for cryptanalysis. The technique they used for comparing statistics of the cipher text can be found in Eq. (9). The values of β and γ can be assigned to various weights of the bigrams and trigrams, respectively.
The results showed that each algorithm could successfully recover the key for periods less than 15 (13.25) with 1000 available cipher text characters. On average, the simulated annealing attacks could set 25 of the key elements for a transposition cipher of period 30.
Li et al. [12] hybridized TS and GA to break classical and modern ciphers. The results showed that the hybrid algorithms had the most effect on the transposition cipher, less effect on the hill cipher, and the AES cipher was the least affected among the three algorithms.
Toemeh and Arumugam [13] proposed an algorithm in which the recovered key was 15 for 1000 cipher text characters. In other words, there was an improvement of 13 percent. The goal key’s fitness function was calculated by Eq. (9).
Toemeh and Arumugam [14] implemented GA to attack the polyalphabetic (Vigenere) substitution cipher. They carried out the cryptanalysis by generating 10 Keys to get the original key. This method was used to compare target key word statistics with the decrypted text statistics in the language used. Eq. (9) was used to find the fitness of the key. The results showed that using GA in the cryptanalysis of the polyalphabetic (Vigenere) Substitution cipher decreased the time elapsed.
Song et al. [15] developed an automatic technique to cryptanalyze the transposition cipher. They used SAGA method on improved fitness value and compared the results with other experimental results of GA, TS, and SA. The results showed that an attack on the transposition cipher using improved SAGA is more powerful.
Garg [16] presented a method based on GA, TS, and SA algorithms to cryptanalyze the transposition cipher. They compared the efficiency of these three algorithms in automated attacks on a transposition cipher. The technique for comparing the target key was to compare n-gram statistics of the decrypted text with those of the used language, as shown in Eq. (8). He made two comparisons: the average number of key elements and the time taken by the algorithms. Results showed that TS was the most robust method for breaking the monoalphabetic cipher.
Erickson and Hausman [17] presented a method to attack the substitution cipher using dominate GA with unigram, bigram, trigram, and 4-gram statistics to create the key. These statistics identify which gene is the dominant, in addition to the goodness of a solution. In conclusion, they produced a well-balanced GA that can produce reasonable and acceptable solutions.
Omran et al. [18] developed a GA-based attack to cryptanalyze monoalphabetic ciphers. They used Eq. (8) to find the fitness function. This study was based on the work of Clark and Dawson [9], who discovered that the text is decrypted very fast when α = 0.1 and γ = 0.8 with a random crossover. This crossover is less informed than Spillman et al.’s [4] crossover method, because they do not use the letter frequency of the ciphertext. Results showed that the optimal keys for a population with 20 keys can be found after 400 generations. Because the crossover process was less optimized, the number of generations was larger.
Omran et al. [19] implemented a GA to attack the Vigenere cipher by using Eq. (8) with knowledge of the key length. This attack was completely successful, and usually discovered the true key in less than 100 generations.
Heydari et al. [20] proposed an approach to the cryptanalysis of transposition ciphers by using an improved GA with a modern fitness function. This was evaluated using very common bigrams and trigrams; the crossover and mutation factors were taken randomly. Eq. (10) was applied as the fitness function (Ff) for GA attack.
where Ci and Dj indicate the frequency of the bigram and trigram characters respectively, with 1 < i < 6 and 1 < j < 4. Likewise, Bi and Tj indicate the frequency of the very common characters, respectively. α and β are authorized to assign various weights to each of the bigrams and trigrams, respectively. Results indicated that the proposed algorithm is valuable for the cryptanalysis of transposition ciphers with long key lengths up to 25. Also, this proposed approach was found to be better and much faster than other GAs.
Dureha and Kaur [21] applied a generic genetic algorithm to cryptanalyze monoalphabetic, poly-alphabetic, and columnar transpositions. The algorithm could decode the ciphers by recovering 80.71%, 87.31%, and 77.66% of the correct characters, respectively. They used Eq. (11) to calculate the fitness function:
The results showed that the number of bits recovered was proportional (key-length and cipher-text length). Also, it was proportional to population size, which helps in preserving population divergence. In addition, the time was reduced by decreasing the number of generations to less than 50 generations, which gave the algorithm higher robustness.
Khalid et al. [22] concentrated on using GAs to cryptanalyze a transposition cipher. The used a particular technique focused on bigram and trigram frequencies of characters to discover the potential key length. The length of the message was 3000 characters, population sizes investigated were 10, 20, 30, 40, and 50, and the key size was 10 characters. They used Eqs. (12) and (13) to find the optimal solution. Eq. (12) was first applied to find the fitness of a proposed key (k). The proportion of correct characters was 7 of 10 after 300 generations for population sizes of 30 and 40.
Eq. (13) was also used to represent 6 bigrams and 4 trigrams characters.
where Pi refers to the frequency of the bigrams or trigrams in the text, Si refers to the fitness value to the ith bigram or trigram tested, and the result of the summation is over the Q bigram and trigram. This equation provided the right characters 10 out of 10. Both equations neglect the single character frequency because the number of all characters in the cipher text was same as in the original text. Also, the elapsed time for the second equation was less than that of the first equation.
Bhateja and Kumar [23] developed a technique to cryptanalyze a Vigenere cipher by GAs utilizing elitism with a novel fitness function. They used a roulette wheel technique, two point crossover, and cross mutation to generate a new population. They used different sizes of cipher text, such as 200, 400 and 600 letters with different key sizes, such as 3, 5… 25. They used GAs with and without elitism. Eq. (14) was used to find the fitness function of the key.
where SDM(i) indicates the standard frequency of the ith unigram in the original text, OFM(i) indicates the measured frequency of the decoded text ith unigram in the cipher text, SDB(i) indicates the standard frequency of the ith bigram in the original text, and OFB(i) indicates the measured frequency of the ith bigram in the cipher text. Experimental results showed that elitism improves the effectiveness and performance of the algorithm because it prevents the loss of the best key, which is possibly the right key.
Boryczka and Dworak [24] displayed how evolutionary algorithms such as GAs can be utilized to accelerate the procedure of cryptanalysis of the transposition cipher. The main target of this research was to explain that EAs (evolutionary algorithms) such as GAs can viably be utilized for cryptanalysis to optimize speed and memory.
Boryczka and Dworak [25] presented how evolutionary algorithms like GAs can optimize the complicated cryptanalysis operation and introduced an algorithm to implement an efficient cryptanalysis attack on a cipher text encoded with a transposition cipher.
Alkathiry and Al-Mogren [26] used a GA to attack the transposition cipher and applied 10 experiments to every key length. The rate accuracy of the results ranged from 65%–100%. That means that at least 10 of the results were readable. They performed the experiments on various texts with lengths of 200–500–1000 letters. The keys applied to encrypt the plain text were random keys with length from 5 to 20. They also used a modern crossover method that helped to produce better keys and arrive at the optimal key. They also used a dictionary for very common letters in the English language. In contrast to the bigram and trigram technique used in the other study, in this algorithm, the keys remained in the pool of keys and survived generations until reaching the optimal key. Finally, some factors that impact the GAs were dependent on the key size, which resulted in the same quality of results for all key lengths.
Saveetha et al. [27] studied reducing the computational complication of the cryptanalysis via GAs. They compared GAs with the TS. In addition, they presented the applicability of GAs for searching the key space in the Vigenere cipher. The frequency analysis was applied as a main factor in the objective function. The results showed that GAs displayed better results for transposition ciphers but produced bad results for substitution ciphers and modern ciphers. Overall, GAs displayed good results compared to TS. Based on the study, GAs and TS were more effective than other optimization methods.
Sadeghzadeha and Taherbaghalb [28] applied GAs for data encryption and compared the performance of GAs with other methods like SA and TS. They used Eq. (8) to find the fitness function. The results indicated that the implementation of a fixed permutation with a modification of GA techniques appears to perform better than other techniques. Also, TS performed well under particular circumstances. The performance of the proposed techniques built on the input parameters and might give good results when closely tuned.
Jadaun et al. [29] used evolutionary computing for the cryptanalysis of transposition ciphers. In this study, they used Eq. (15) for the fitness function of the key.
where F(key) denotes the fitness value, Kb(i,j) and Db(i,j),indicate the used language bigrams and decrypted text bigrams, respectively. The values of β assign various weights to the bigram model. The researchers used various population sizes, including 10, 20, 30, 40, 50, 60, 70, 80, and 90. The best fitness value was 50.074 when the population size was 60. It was observed that increasing key length leads to a decrease in the success average.
Bhateja et al. [30] described a technique for cryptanalysis of the Vigenere cipher. Simple substitution cryptosystems and linear feedback shift register cryptosystems based on a heuristic method fitness function were determined on the frequencies of unigrams and bigrams, depending on Eq. (16).
where SM(i) indicates the standard frequency of the ith unigram in standard English, OM(i) indicates the frequency of the ith unigram in the decrypted text, SB(i) indicates the standard frequency of the ith b-gram in standard English and OB(i) indicates the frequency of the ith bigram in the decrypted text. The Vigenere cipher was attacked by PSO and GA. The α and β were selected as 0.23 and 0.77, respectively. Each of the three cryptosystems were analyzed for 600 repetitions. A plain text of 600 letters was taken from 5000 letters randomly and the cipher text was made with all cryptosystems. Through analysis of the Vigenere cipher, the researchers concluded that GAs are a better method than PSO.
Khalid and Al-Khafagi [31] focused on the cryptanalysis of a Hill cipher by use of Gas, with various models for crossover, population size, and mutation, to get the optimal solution. To assess the quality of each population, they used a fitness function based on the character frequencies of the cipher and the English language as indicated in Eq. (17).
The sensitiveness to large values of the difference was reduced by scaling the summation terms. From the results, increasing population size leads to a decrease of the number of generations required to get to the optimal solution, but it leads to an increase in time required to perform a single generation. A lower mutation average decreases the prospect of genetic jump, as well. Also, the researchers applied two kinds of crossover, the single point crossover and the multipoint crossover, and stated that the multipoint crossover had better results compared to the single point crossover.
Bergmann et al. [32] introduced cryptanalysis based on GAs to attack different types of cryptosystems such as: polyalphabetic ciphers, transposition ciphers, DES and AES ciphers. Various text and ciphertexts were applied and cryptanalyzed 10 times for every cryptosystem using key lengths of 2 to 25. The results showed that generally GAs could characterize the true key in 200 generations with population size 20. The chance of success was very high up to a key length of 7. After this length of the key, the success average decreased.
Habeeb [33] presented a method based on GA to cryptanalyze the Vigenere cipher. The method used Arabic letters with different sizes and key lengths. The overall attack used the fitness function given in Eq. (16). In the experiments different sizes of cipher text, such as 400, 600 and 1000 letters with different key sizes, such as 5, 10 and 20. The experimental results showed that text with a short key length and a medium size of ciphertext were restored 100% of original key characters correctly, 90% of original key characters were restored correctly with medium key length and long size of ciphertext and 82% of original key characters were restored correctly with a long key and ciphertext.
Mudgal et al. [34] developed a technique to cryptanalyze a mono-alphabetic substitution cipher by three different types of GA. The first type of GA used random selection, one-point crossover and mutation techniques with elitism. As a second type of GA with roulette wheel selection, tow point crossover and mutation techniques were used. A third type of GA based on tournament selection, uniform crossover and mutation techniques were used. The fitness function used in the study is given in Eq. (16). Results showed that the first type of GA was the most robust method for breaking the monoalphabetic cipher.
Jain et al. [35] implemented a GA and SA to attack the affine cipher (which is a kind of mono-alphabetic substitution cipher) by using three types of attacks. They used only GA as a first attack, only SA as a second attack and the combination of GA and SA as the third attack. Eq. (18) was applied as the fitness function (Ff) for all three types of attacks.
Suppose, K(u), K (b) and K (t) are the known unigram, bigram, and trigram statistics, respectively. D(1), D(2), and D(3) are statistics for the decrypted text, and the value 0.1, 0.3 and 0.6 are weights chosen to equal one. Results showed that the combination of GA and SA was the most robust method for breaking the monoalphabetic cipher.
Forhad et al. [36] proposed an approach to the cryptanalysis of columnar transposition cipher by using GA with a combined fitness function. They used synchronic linguistics in order to check the sentences. Eq. (19) was applied as the fitness function.
Results indicated that the proposed algorithm is valuable for the cryptanalysis of columnar transposition ciphers with long key with lengths 1000. Also, this proposed approach was found to be better and much faster than Tomeh [13].
2.2 Simulated Annealing (SA) Implementation
Kirkpatrick et al., recommended SA which models the physical process of heating and cooling a material to minimize the energy related to the material. Some applications of SA on the cryptanalysis of classical ciphers are given below.
Forsyth and Safavi-Naini [37] were the first to used automated cryptanalysis based on SA to attack monoalphabetic substitution ciphers by comparing the frequencies of bigrams in the cipher text with those of the plaintext, as shown in Eq. (20). They then found the cost using Eq. (21).
where Fi is the value of the cost function,
Giddy and Safavi-Naini [38] applied cryptanalysis of the transposition cipher using SA to obtain the global minimum of a cost function based on a distance between decipherment of the given cipher text and a sample of original text language. The cost function C(s) is given by Eq. (22).
The cost function offered in this study was an improvement of the version used by Forsyth and Safavi-Naini [37]. Here, Pαβ indicate the probability of the bigram αβ in the plaintext, and N indicates the length of the ciphertext. To calculate C(s), the permutation s is applied to decrypt the cipher text and the proportional frequency of the bigram αβ in the resulting output is denoted by Cαβ. The success of the algorithm depends on the length of the ciphertext.
Nevertheless, in this study, comparing the result of the algorithm provided important information for guiding the cryptanalysis. The technique solved some transposition ciphers with periods of 25 and cipher lengths of 500 letters. In some cases, solutions reached 80% accuracy. The capability of the cost function to successfully identify the valid text from a series of letters depended on the algorithm’s decryption capability. Results showed that SA makes cryptanalysis of transposition ciphers easier and supplies a robust technique for analyzing most of the developed ciphers.
2.3 Tabu Search (TS) Implementation
Glover, used TS which finds the best neighbour solution for each iteration and acceptable changes are restricted using a tabu list which can prevent the cycling problem. Below are some applications of TS to the cryptanalysis of classical ciphers and some comparisons with GA.
Verma et al. [39] studied the cryptanalysis monoalphabetic substitution ciphers using both TS and GA. Both TS and GA employed the same fitness function. They compared the efficiency of TS and GA in terms of the cryptanalysis based on Eq. (8), which mainly depended on the frequencies (unigram, bigram, trigram) of the plaintext after decryption compared with the language frequencies. The results showed that TS found less correct than GA on a text with a length of less than 800 letters; however, TS found better results on a longer text. Generally, TS performed well, retrieving a correct solution in less time comparable with GAs.
2.4 Particle Swarm Optimization (PSO) Implementation
Kennedy and Eberhart, developed PSO based on the birds’ adaptation by information sharing to find rich food supplies and to avoid being hunted. In the algorithm, each particle uses its previous experience while setting its own position for the best position in the track. Below are some applications of PSO to the cryptanalysis of classical ciphers and some comparisons with SA, TS, and GA.
Uddin and Youssef [40] performed a PSO to break monoalphabetic ciphers in 2006. They used Eq. (17), and two different values for weights (1, 0) and (0, 1) were tested. The number of iterations did not exceed 200 repetitions. The results obtained with unigrams were better than the results obtained with bigrams. For a text of 500 letters, the PSO was capable of retrieving the correct key in less than 200 repetitions. However, when the number of letters was 300 or less, PSO could retrieve only 21 of the 26 true keys.
Hameed and Hmood [41] presented a new cryptanalysis transposition cipher based on PSO that automatically retrieves the correct key. The method compares n-gram statistics of the decrypted text with the statistics of the target language. Eq. (9) defines the fitness of a proposed key. The results showed that PSO is effective in defining the optimal selection of keys for the detection of the plaintext.
Rajkumar [42] introduced cryptanalysis based on PSO to attack different types of cryptosystems such as: simple substitution ciphers and AES ciphers. Various key length and ciphertexts were applied. Results showed that the PSO makes cryptanalysis of simple substitution ciphers easier and supplies a robust technique for analyzing AES ciphers.
2.5 Differential Evolution (DE) Implementation
Price and Storn, developed the DE algorithm for optimization problems through continuous scope based on crossover, mutation and greedy selection. Below is an application of Differential Evolution to the cryptanalysis of classical ciphers.
Wulandari et al. [43] applied DE to attack transposition ciphers with a shortened length of permutation, up to a size of 9. They found that the algorithm did not produce satisfactory results for longer keys, particularly well for shortened texts. In the cryptanalysis, Eq. (9) was applied to examine candidate keys. The values of β and λ were 0.4 and 0.6, respectively. All runs were repeated 10 times for permutation sizes of 5, 9, and 13. It was indicated that for permutation sizes of 5 and 9, the text length or topic did not affect the algorithm performance. Algorithm performance differs when the permutation size is 13. As the text size gets longer, the algorithm generates better results.
Sabonchi and Akay [44] used DE, GA and PSO algorithms for the cryptanalysis of polyalphabetic Vigenere ciphers and the results are compared based on the number of key characters recovered correctly. This shows the efficiency of the DE among the PSO and GA algorithms. In this study, they used Eq. (15) for the fitness function of the key. The researchers used various keywords sizes, including 5, 10, 15, 20 and 25, with four different plain texts sizes including 250, 500, 750 and 1000 in English as in Turkish. The result of this is that they find the DE algorithm can retrieve all 25 key elements when the size of ciphertext is over than 250 characters. Contrasting PSO and GA algorithms we find they can retrieve all 25 key elements correctly only if the length of keys is under 25. Through analysis of the Vigenere cipher, the researchers concluded that DE algorithm is a better method than both PSO and GA algorithms. In addition, they demonstrated that iteration cycles are related with the key and ciphertext length, although of the ciphertext is small than 250 character, they got good result in Turkish ciphertext than that in English ciphertext. Also, they proposed to study efficient fitness functions in further research.
2.6 Ant Colony Optimization (ACO) Implementation
The ACO algorithm developed by Dorigo, simulates the intelligent behaviours of ants related to selecting the path with a high concentration of pheromones. Below are some applications of the ACO to the cryptanalysis of classical ciphers and some comparisons with GA.
Russell et al. [45] proposed an implementation of ACO in the cryptanalysis of transposition ciphers. In the study, two heuristics are applied. The first is for recognizing plaintext. It utilizes a dictionary (Dict) as defined by Eq. (23). The second, for indicating adjacent Adj (i,j), employs bigrams, as shown in Eq. (24).
Nd is the number of d-letters in the dictionary and L indicates the length of the text. A list of 40000 letters was used as the basis dictionary. The researchers found that Dict(M) is maximum when M is the true text.
where Ix, and Jx, indicate the rth character in columns i and j, respectively. Pstd (xy) is the base prospect of the bigram “xy” and h is the number of rows in a column.
Uddint and Youssef [46] used ACO to attack simple substitution ciphers. They used the fitness function shown in Eq. (17). This fitness function did not use trigram statistics. The researchers only applied weights to the unigram and bigram frequencies. (λ1, λ2) were set to (1, 0) and (0, 1). The results showed that an attack based on the bigram is more effective than an attack based on the unigram.
Mekhaznia and Menai [47] applied two types of ACO algorithms for the cryptanalysis of classical ciphers, namely virtual ant system (VAS) and virtual MAX – MIN ant system (VMMAS). They investigated the efficiency of the algorithms on large number of ciphertexts based on six various encryption techniques, such as Feistel, Vigenere, simple substitution, affine, Polybe, and transposition algorithms. Then they compared their efficiencies with those of the ant colony system (ACS) and elitist ant system (EAS). The results showed the overall superiority of VMMAS over the other ant algorithms.
Grari et al. [48] used ACO to attack simple substitution ciphers. They presented a new fitness function as shown in Eq. (25). Because they thought that the good results are dependent on a good designed a fitness or a cost function.
Suppose, K is the known unigram and bigram. D is statistics for the decrypted text, M is a value used to reduce the effect of letters that have a large percentage, and w1, w2 are weights chosen to equal one. The results showed that the new fitness function displayed better results for simple substitution ciphers, and it will be useful with other encryption algorithms like AES.
2.7 Cuckoo Search (CS) Implementation
CS was presented based on the obligate brood parasitism of some cuckoo species that lay their eggs in the nests of other host birds. Below are some applications of CS to the cryptanalysis of classical ciphers and some comparisons based on TS, PSO, and GA.
Sadiq and Kareem [49] proposed the automated cryptanalysis of simple transposition ciphers established from an improved CS by combining a new sub operation to the CS procedure by harnessing resemblance among populations (nests). Tests showed the ability to attack 95% of encrypted texts with diverse key lengths. This gave better results in comparison with the classical CS algorithm on the amount of key recapture and time complication. Eq. (26) was used to locate the suitability of a proposed key.
where K indicates language statistics, b and t indicate bigram and trigram statistics, respectively. Results showed that the improved CS is efficacious in defining the correct key. Also, the improved CS can be used in the future to attack other cipher methods and can be applied to solve more problem variants.
Jain and Chaudhari [50] used CS to attack substitution ciphers. They compared different attack algorithms based on CS, GA, enhanced genetic algorithm, and TS and CS showed the best performance. The CS algorithm supplies a good and effective choice for solving similar permutation problems. Through the optimization method, all candidate keys were applied to decrypt the known ciphertext; at the same time, the n-gram statistics of the decrypted text were compared to the language statistics. Eq. (8) was applied for comparison of these statistics. Various weights in the domain (0.0–1.0) were assigned to α, β, and γ. They found that the CS attack showed the best efficiency between all attacks. Tests showed that the developed attack algorithm can supply results that are obviously better than previous attack algorithms for the substitution cipher and CS is said to be an efficacious alternative for solving this type of permutation problem.
Bhateja et al. [51] studied the suitability of the CS algorithm in the cryptanalysis of the Vigenere cipher. The fitness function of a particular cipher message was calculated by using Eq. (17). The supposed key K was used to decrypt the cipher message. The researchers applied GAs, PSO, and CS methods to attack the Vigenere cipher. The results showed that the GA and PSO methods can recapture the full key of the Vigenere cipher correctly for keys of small lengths. CS could recreate more than 90% of the key letters for keys of size up to 25 letters. Also, results showed that CS has faster convergence and better reliability in the cryptanalysis of the Vigenere cipher compared to PSO and GA, because GA and PSO get trapped in local minima.
Jain and Chaudhari [52] applied cryptanalysis of the transposition cipher using CS. and compared the performance of CS with GA. They used Eq. (8) to find the cost function C(s). The results showed that the CS is almost 1.5 times faster than GA. Moreover, CS methods can recapture key elements around 12% more than GA.
Jain and Chaudhari [53] presented a method based on improved GA, CS, and SA algorithms to cryptanalyze the substitution cipher by using Eq. (8). They compared the efficiency of these two algorithms with TS and default GA in automated attacks on a substitution cipher. They made three comparisons: the average number of key elements recovered correctly, average number of keys tested before finding the correct key and the time taken by the algorithms. Results showed that improved GA is better than the default GA in the average number of key elements recovered correctly and the time taken by the algorithms. CS is better than GA, improved GA, and TS in average number of key elements recovered correctly, average number of keys tested before finding the correct key and the time taken by the algorithms. Based on the study, CS was the most robust method for breaking the substitution cipher.
2.8 Firefly Algorithms (FA) Implementation
FA developed by Yang, is a modern evolutionary algorithm inspired by the flashing behavior of fireflies. Below is an application of the FA to the cryptanalysis of classical ciphers.
Luthra and Pal [54] investigated the integration of the factor of mutation and crossover with the FA for cryptanalysis of the monoalphabetic cipher. A hybrid FA uses genetic factors to solve the monoalphabetic cipher. English language statistics were used to determine the fitness rate of the possible solutions. The optimum swarm population size was found to be 35. The researchers found that the algorithm works better for large input cipher text lengths. Smaller cipher lengths require a larger number of generations.
2.9 Artificial Bee Colony Algorithm (ABC) Implementation
The ABC algorithm defined by Karaboğa, simulates the food source searching behaviors of honey bees. Because of the function division of the bees and their self-organization, the bees do many functions as a group in a good way. While food source position refers to the solution, amount of the nectar refers to the function of the solution in ABC algorithm. It has three phases; employed, onlooker and scout bees. Below are some applications of ABC algorithm to the cryptanalysis of classical ciphers and some comparisons with FA, CS, DE, PSO, and GA.
Sabonchi and Akay [55] were the first to used automated cryptanalysis based on ABC algorithm to attack monoalphabetic substitution ciphers by comparing the frequencies of cipher text with those of the plaintext, as shown in Eq. (8). They used different sizes of cipher text, such as 1000, 2000 and 3000 letters with different population sizes, such as 20, 50 and 100. Tests showed that the developed attack algorithm can present good result for attack algorithms for the substitution cipher and ABC algorithm can be an efficacious alternative for solving this type of permutation problem. Also, they supposed that ABC algorithm can use with modern encryption algorithms and comparing those result with results given from classical encryption algorithms.
Sabonchi and Akay [56] They were the first who apply ABC Algorithm to attack simple substitution ciphers using statistics-based fitness function as show in Eq. (8). They tested different sizes of cipher text with different same key sizes and different population sizes. The results indicated that the implementation of an ABC algorithm appear to perform well. ABC algorithm obtained 17 correct characters key from 26 characters when the populations is 50, and the limit is 100. While it obtains 18 in case of the populations is 100, and the limit number is 200.
Brezočnik et al. [57] presented five optimization heuristics that were used to break the Vigenere cipher: ABC, FA, PSO, DE and CS. They used the same cipher text with four different key sizes, to find the best, cryptanalyze technique among the presented algorithms. The experimental results showed that all five algorithms were effective methods for cryptanalysis. Furthermore, they made two comparisons based on the result of the algorithms: the average number of key elements and the time taken by the algorithms. Results showed that DE was the most robust method for breaking the Vigenere cipher. The technique they used for comparing statistics of the cipher text can be found in Eq. (15).
Sabonchi and Akay [58] used ABC algorithm for the cryptanalysis of polyalphabetic Vigenere ciphers and the results are compared based on the number of key characters recovered correctly. They modified ABC algorithm by employing a binomial crossover phase between employed bee and onlooker bee phases and referred as Binomial Crossover based Artificial Bee Colony algorithm (BCABC) In this study, they used Eq. (15) for the fitness function of the key. The researchers used various keywords sizes, including 5, 10, 15, 20 and 25, with four different plain texts sizes including 250, 500, 750 and 1000 in English as in Turkish. The result of this is that they find the BCABC algorithm can retrieve all 25 key elements when the size of ciphertext is over than 250 characters. Through analysis of the Vigenere cipher, the researchers concluded that BCABC algorithm is a better method than ABC algorithm. In addition, they demonstrated that iteration cycles are related with the key and ciphertext length, although of the ciphertext is small than 250 character, they got good result in Turkish ciphertext than that in English ciphertext. Also, they proposed to study efficient fitness functions in further research.
In this paper, 9 algorithms are reviewed about the applications of metaheuristic algorithms on the cryptanalysis of various classical ciphers, such as monoalphabetic, polyalphabetic, substitution, Hill, and Vernem ciphers. Among 55 papers, 33 papers employed GA, 2 papers employed SA algorithm, 4 papers employed ACO algorithm, 5 papers employed CS algorithm, 3 papers employed PSO algorithm, 4 papers employed ABC algorithm, 2 paper employed DE algorithm, 1 paper employed TS algorithm, and 1 paper employed FA algorithm. Tab. 1 summarizes a categorical view of the algorithms and their applications. From Tab. 1, it can readily be understood that cryptanalysis based on metaheuristic algorithms has been used for the attack of several types of classical ciphers.
Table 1: Categorical view of the algorithms and their applications

Fig. 1 shows the cryptanalysis of classical ciphers based on stochastic optimization algorithms with respect to years. Also, we can see that, although the number of papers on the cryptanalysis of classical ciphers based on stochastic optimization algorithms decreases in the years between 1998 and 2013, however; there are still published in this area in recent years, especially regarding to the new metaheuristic algorithms like ABC, FA and CS algorithms, as presented in Fig. 2.

Figure 1: The number of publications with respect to years
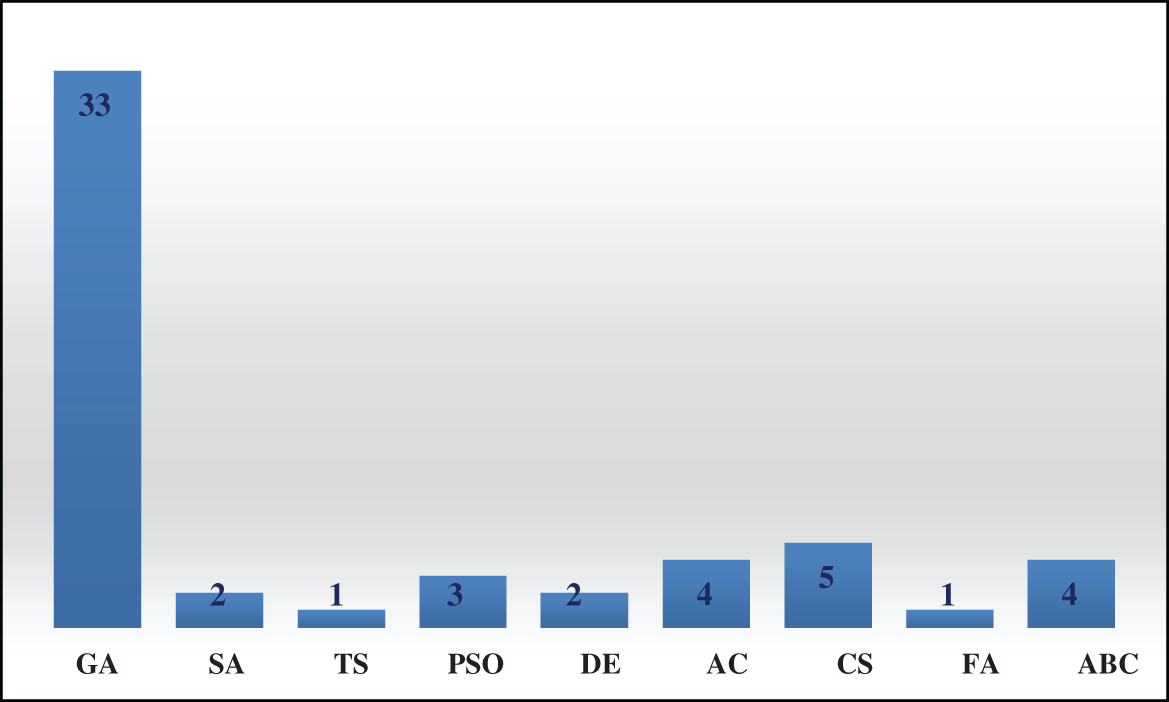
Figure 2: The published number of each algorithm from 2003 to 2020
We can see that there are still gaps in the literature, especially regarding the improvement of the algorithms’ efficiency for modern cryptographic techniques. We hope that this survey will be helpful for readers interested in cryptanalysis based on metaheuristic algorithms.
Acknowledgement: This study is supported by Erciyes University Research Projects Unit with grant number FDK-2016-7085.
Funding Statement: This study is supported by Erciyes University Research Projects Unit with grant number FDK-2016-7085, the initials of authors who received the grant are A and B and the URL to sponsors’ websites is http://bap.erciyes.edu.tr/
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. D. E. Robling Denning, “Cryptography and data security,” in The Addison-Wesley Longman Publishing Company, Massachusetts, Menlo Park, California London, Amsterdam, Don Mills, Ontario, Sydney, pp. 1–420, 1982. [Google Scholar]
2. R. Hilton, “Automated cryptanalysis of monoalphabetic substitution ciphers using stochastic optimization algorithms,” Ph.D. dissertation, University of Colorado, USA, 2012. [Google Scholar]
3. R. L. Solso, P. F. Barbuto and C. L. Juel, “Bigram and trigram frequencies and versatilities in the English language,” Behavior Research Methods & Instrumentation, vol. 11, no. 5, pp. 475–484, 1979. [Google Scholar]
4. R. A. Matthews, “The use of genetic algorithms in cryptanalysis,” Cryptologia, vol. 17, no. 2, pp. 187–201, 1993. [Google Scholar]
5. R. Spillman, M. Janssen, B. Nelson and M. Kepner, “Use of a genetic algorithm in the cryptanalysis of simple substitution ciphers,” Cryptologia, vol. 17, no. 1, pp. 31–44, 1993. [Google Scholar]
6. A. Clark, “Modern optimization algorithms for cryptanalysis,” in Proc. IEEE, Intelligent Information Systems, Australian, New Zealand, pp. 258–262, 1994. [Google Scholar]
7. F. T. Lin and C. Y. Kao, “A genetic algorithm for ciphertext-only attack in cryptanalysis,” in Proc. IEEE, Systems, Man and Cybernetics, Intelligent Systems for the 21st Century, Vancouver, BC, Canada, pp. 650–654, 1995. [Google Scholar]
8. A. Clark, E. Dawson and H. Nieuwland, “Cryptanalysis of polyalphabetic substitution ciphers using a parallel genetic algorithm,” in Proc. IEEE, Int. Sym. on Information and its Applications, Vancouver, BC, Canada, pp. 17–20, 1996. [Google Scholar]
9. A. Clark and E. Dawson, “A parallel genetic algorithm for cryptanalysis of the polyalphabetic substitution cipher,” Cryptologia, vol. 21, no. 2, pp. 129–138, 1997. [Google Scholar]
10. A. Clark and E. Dawson, “Optimisation heuristics for the automated cryptanalysis of classical ciphers,” Journal of Combinatorial Mathematics and Combinatorial Computing, vol. 28, pp. 63–86, 1998. [Google Scholar]
11. A. Dimovski and D. Gligoroski, “Attacks on the transposition ciphers using optimization heuristics,” in Proc. ICEST, Sofia, Bulgaria, pp. 1–4, 2003. [Google Scholar]
12. H. Y. Li, A. Samsudin and B. Belaton, “Heuristic cryptanalysis of classical and modern ciphers,” in Proc. IEEE, 7th Malaysia Int. Conf. on Communication, Kuala Lumpur, Malaysia, vol. 2, pp. 6, 2005. [Google Scholar]
13. R. Toemeh and S. Arumugam, “Breaking transposition cipher with genetic algorithm,”,” Elektronika ir Elektrotechnika, vol. 79, no. 7, pp. 75–78, 2007. [Google Scholar]
14. R. Toemeh and S. Arumugam, “Applying genetic algorithms for searching key-space of polyalphabetic substitution ciphers,” International Arab Journal of Information Technology (IAJIT), vol. 5, no. 1, pp. 87–91, 2008. [Google Scholar]
15. J. Song, F. Yang, M. Wang and H. Zhang, “Cryptanalysis of transposition cipher using simulated annealing genetic algorithm,” in Proc. Int. Sym. on Intelligence Computation and Applications, Berlin, Heidelberg, pp. 795–802, 2008. [Google Scholar]
16. P. Garg, “Genetic algorithms, Tabu search and simulated annealing: A comparison between three approaches for the cryptanalysis of transposition cipher,” Journal of Theoretical & Applied Information Technology, vol. 5, no. 4, pp. 387–392, 2009. [Google Scholar]
17. D. Erickson and M. Hausman, “A dominant gene genetic algorithm for a substitution cipher in cryptography,” CS 591 Project, vol. 1, no. 1, pp. 1–7, 2010. [Google Scholar]
18. S. S. Omran, A. S. Al-Khalid and D. M. Al-Saady, “Using Genetic Algorithm to break a mono-alphabetic substitution cipher,” in Open Systems IEEE, ICOS, Kuala Lumpur, Malaysia, pp. 63–67, 2010. [Google Scholar]
19. S. S. Omran, A. S. Al-Khalid and D. M. Al-Saady, “A cryptanalytic attack on Vigenere cipher using genetic algorithm,” in Proc. IEEE, (ICOSLangkawi, Malaysia, pp. 59–64, 2011. [Google Scholar]
20. M. Heydari, G. L. Shabgahi and M. M. Heydari, “Cryptanalysis of transposition ciphers with long key lengths using an improved genetic algorithm,” World Applied Sciences Journal, vol. 21, no. 8, pp. 1194–1199, 2013. [Google Scholar]
21. A. Dureha and A. Kaur, “A generic genetic algorithm to automate an attack on classical ciphers,” International Journal of Computer Applications, vol. 64, no. 12, pp. 20–25, 2013. [Google Scholar]
22. A. S. Al-Khalid, S. S. Omran and D. A. Hammood, “Using genetic algorithms to break a simple transposition cipher,” in Proc. 6th Int. Conf. on Information Technology ICIT, Amman, Jordan, pp. 1–9, 2013. [Google Scholar]
23. A. Bhateja and S. Kumar, “Genetic algorithm with elitism for cryptanalysis of vigenere cipher,” in Proc. IEEE, Issues and Challenges in Intelligent Computing Techniques (ICICTGhaziabad, India, pp. 373–377, 2014. [Google Scholar]
24. U. Boryczka and K. Dworak, “Genetic transformation techniques in cryptanalysis,” in Proc. Asian Conf. on Intelligent Information and Database Systems, Bangkok, Thailand, pp. 147–156, 2014. [Google Scholar]
25. U. Boryczka and K. Dworak, “Cryptanalysis of transposition cipher using evolutionary algorithms,” in Proc. Int. Conf. on Computational Collective Intelligence, Seoul, Korea, pp. 623–632, 2014. [Google Scholar]
26. O. Alkathiry and A. Al-Mogren, “A powerful genetic algorithm to crack a transposition cipher,” International Journal of Future Computer and Communication, vol. 3, no. 6, pp. 395–399, 2014. [Google Scholar]
27. P. Saveetha, S. Arumugam and K. Kiruthikadevi, “Cryptography and the optimization heuristics techniques,” International Journal, vol. 4, no. 10, pp. 408–413, 2014. [Google Scholar]
28. M. Sadeghzadeh and M. Taherbaghal, “A new method for decoding an encrypted text by genetic algorithms and its comparison with tabu search and simulated annealing,” Management Science Letters, vol. 4, no. 2, pp. 213–220, 2014. [Google Scholar]
29. A. S. Jadaun, V. Chaudhary, L. Sharma and G. P. Singh, “Deciphering of Transposition Ciphers u Deciphering of Transposition Ciphers using Genetic sing Genetic Algorithm.” International Journal of Computer Science and Network, vol. 3, no. 3, pp. 41–45, 2014. [Google Scholar]
30. A. Bhateja, S. Kumar and H. Chaudhary, “Analysis of different cryptosystems using meta-heuristic techniques,” in Proc. IEEE, Int. Conf. on Advanced Communication Control and Computing Technologies (ICACCCTRamanathapuram, India, pp. 1931–1934, 2014. [Google Scholar]
31. A. S. Al-Khalid and A. O. Al-Khfagi, “Cryptanalysis of a Hill cipher using genetic algorithm,” in Proc. IEEE, Computer Networks and Information Security (WSCNISWorld Sym., Hammamet, Tunisia, pp. 1–4, 2015. [Google Scholar]
32. K. P. Bergmann, R. Scheidler and C. Jacob, “Cryptanalysis using genetic algorithms,” in Proc. 10th Annual Conf. on Genetic and Evolutionary Computation, New York, NY, USA, pp. 1099–1100, 2008. [Google Scholar]
33. R. S. Habeeb, “Arabic text cryptanalysis using genetic algorithm,” Iraqi Journal for Electrical and Electronic Engineering, vol. 12, no. 2, pp. 161–166, 2016. [Google Scholar]
34. P. K. Mudgal, R. Purohit, R. Sharma and M. K. Jangir, “Application of genetic algorithm in cryptanalysis of mono-alphabetic substitution cipher,” in Proc. IEEE, Int. Conf. on Computing, Communication and Automation (ICCCAGreater Noida, pp. 400–405, 2017. [Google Scholar]
35. S. Jain, N. Chhibber and S. Kandi, “Cryptanalysis of mono-alphabetic substitution ciphers using genetic algorithms and simulated annealing,” IARS International Research Journal, vol. 8, no. 1, pp. 1–5, 2018. [Google Scholar]
36. M. S. A. Forhad, M. S. Hossain, M. O. Rahman, M. M. Rahaman, et al., “An improved fitness function for automated cryptanalysis using genetic algorithm,” Indonesian Journal of Electrical Engineering and Computer Science, vol. 13, no. 2, pp. 643–648, 2019. [Google Scholar]
37. W. S. Forsyth and R. Safavi-Naini, “Automated cryptanalysis of substitution ciphers,” Cryptologia, vol. 17, no. 4, pp. 407–418, 1993. [Google Scholar]
38. J. P. Giddy and R. Safavi-Naini, “Automated cryptanalysis of transposition ciphers,” Computer Journal, vol. 37, no. 5, pp. 429–436, 1994. [Google Scholar]
39. A. K. Verma, M. Dave and R. C. Joshi, “Genetic algorithm and Tabu search attack on the mono-alphabetic substitution cipher in Adhoc networks,” Journal of Computer Science, vol. 3, no. 3, pp. 134–137, 2007. [Google Scholar]
40. M. F. Uddin and A. M. Youssef, “Cryptanalysis of simple substitution ciphers using particle swarm optimization,” in Proc. IEEE, Evolutionary Computation, Vancouver, BC, Canada, pp. 677–680, 2006. [Google Scholar]
41. S. M. Hameed and D. N. Hmood, “Particles swarm optimization for the cryptanalysis of transposition cipher,” Journal of Al-Nahrain University Science, vol. 13, no. 4, pp. 211–215, 2010. [Google Scholar]
42. G. Rajkumar, “Linear cryptanalysis of substitution ciphers using particle swarm optimization,” Oriental Journal of Computer Science and Technology, vol. 10, no. 3, pp. 580–584, 2017. [Google Scholar]
43. G. S. Wulandari, W. Rismawan and S. Saadah, “Differential evolution for the cryptanalysis of transposition cipher,” in Proc. IEEE, Information and Communication Technology (ICoICTNusa Dua, Bali, Indonesia, pp. 45–48, 2015. [Google Scholar]
44. A. K. S. Sabonchi and B. Akay, “Cryptanalysis of polyalphabetic cipher using differential evolution algorithm,” Tehnički vjesnik, vol. 27, no. 4, pp. 1101–1107, 2020. [Google Scholar]
45. M. D. Russell, J. A. Clark and S. Stepney, “Making the most of two heuristics: Breaking transposition ciphers with ants,” in Proc. The Congress on Evolutionary Computation (CEC’03Canberra, ACT, Australia, vol. 4, pp. 2653–2658, 2003. [Google Scholar]
46. M. F. Uddin and A. M. Youssef, “An artificial life technique for the cryptanalysis of simple substitution ciphers,” in Proc. IEEE, Electrical and Computer Engineering Conf., Ottawa, ON, Canada, pp. 1582–1585, 2006. [Google Scholar]
47. T. Mekhaznia and M. E. B. Menai, “Cryptanalysis of classical ciphers with ant algorithms,” International Journal of Metaheuristics, vol. 3, no. 3, pp. pp 175–198, 2014. [Google Scholar]
48. H. Grari, A. Azouaoui and K. Zine-Dine, “A novel ant colony optimization based cryptanalysis of substitution cipher,” in Proc. Int. Afro-European Conf. for Industrial Advancement, Marrakesh, Morocco, pp. 180–187, 2016. [Google Scholar]
49. A. T. Sadiq, L. Ali and H. Kareem, “Attacking transposition cipher using improved cuckoo search,” Journal of Advanced Computer Science and Technology Research, vol. 4, no. 1, pp. 22–32, 2014. [Google Scholar]
50. A. Jain and N. S. Chaudhari, “A new heuristic based on the cuckoo search for cryptanalysis of substitution ciphers,” in Proc. Int. Conf. on Neural Information Processing, Istanbul, Turkey, pp. 206–215, 2015. [Google Scholar]
51. A. K. Bhateja, A. Bhateja, S. Chaudhury and P. K. Saxena, “Cryptanalysis of vigenere cipher using cuckoo search,” Applied Soft Computing, vol. 26, no. 4, pp. 315–324, 2015. [Google Scholar]
52. A. Jain and N. S. Chaudhari, “A novel cuckoo search technique for solving discrete optimization problems,” International Journal of System Assurance Engineering and Management, vol. 9, no. 4, pp. 972–986, 2018. [Google Scholar]
53. A. Jain and and N. S. Chaudhari, “An improved genetic algorithm and a new discrete cuckoo algorithm for solving the classical substitution cipher,” International Journal of Applied Metaheuristic Computing (IJAMC), vol. 10, no. 2, pp. 109–130, 2019. [Google Scholar]
54. J. Luthra and S. K. Pal, “A hybrid firefly algorithm using genetic operators for the cryptanalysis of a monoalphabetic substitution cipher,” in Proc. IEEE. In Information and communication technologies (WICTMumbai, India, pp. 202–206, 2011. [Google Scholar]
55. A. K. S. Sabonchi and B. Akay, “Cryptanalysis using artificial bee colony algorithm guided by frequency based fitness value,” in Proc. 1st Int. Sym. on Multidisciplinary Studies and Innovative Technologies, ISMSIT, Tokat, Turkey, pp. 334–338, 2017. [Google Scholar]
56. A. K. S. Sabonchi and B. Akay, “Cryptanalytic of substitution ciphers by artificial bee colony algorithm guided by statistics based fitness function,” in Proc. 8th Int. Advanced Technologies Sym. IATS17, Elazığ, Turkey, pp. 3999–4004, 2017. [Google Scholar]
57. L. Brezočnik, I. Fister and V. Podgorelec, “Nature-inspired cryptoanalysis methods for breaking Vigenère Cipher,” in Proc. Int. Conf. New Technologies, Development and Applications, Sarajevo, Bosnia and Herzegovina, pp. 446–453, 2020. [Google Scholar]
58. A. K. S. Sabonchi and B. Akay, “A binomial crossover based artificial bee colony algorithm for cryptanalysis of polyalphabetic cipher,” Tehnički vjesnik, vol. 27, no. 6, pp. 1825–1835, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |