DOI:10.32604/csse.2021.016633

| Computer Systems Science & Engineering DOI:10.32604/csse.2021.016633 |  |
| Article |
Mixed Attention Densely Residual Network for Single Image Super-Resolution
1School of Information and Communication Engineering, Hainan University, Haikou, 570228, China
2State Key Laboratory of Marine Resource Utilization in the South China Sea, Hainan University, Haikou, 570228, China
3Research Center for Healthcare Data Science, Zhejiang Lab, Hangzhou, 311121, China
4School of Computer Science and Cyberspace Security, Hainan University, Haikou, 570228, China
5Graduate School of Information Science and Engineering, Ritsumeikan University, 5258577, Japan
6College of Computer Science and Technology, Zhejiang University, Hangzhou, 311100, China
*Corresponding Author: Jingbing Li. Email: jingbingli2008@hotmail.com
Received: 01 January 2021; Accepted: 04 March 2021
Abstract: Recent applications of convolutional neural networks (CNNs) in single image super-resolution (SISR) have achieved unprecedented performance. However, existing CNN-based SISR network structure design consider mostly only channel or spatial information, and cannot make full use of both channel and spatial information to improve SISR performance further. The present work addresses this problem by proposing a mixed attention densely residual network architecture that can make full and simultaneous use of both channel and spatial information. Specifically, we propose a residual in dense network structure composed of dense connections between multiple dense residual groups to form a very deep network. This structure allows each dense residual group to apply a local residual skip connection and enables the cascading of multiple residual blocks to reuse previous features. A mixed attention module is inserted into each dense residual group, to enable the algorithm to fuse channel attention with laplacian spatial attention effectively, and thereby more adaptively focus on valuable feature learning. The qualitative and quantitative results of extensive experiments have demonstrate that the proposed method has a comparable performance with other state-of-the-art methods.
Keywords: Channel attention; Laplacian spatial attention; residual in dense; mixed attention
Single image super-resolution (SISR) is a low-level computer vision task that involves reconstructing accurate high-resolution (HR) images from their low-resolution (LR) counterpart [1]. This task has been widely used in numerous computer vision applications, such as video surveillance [2,3], medical imaging [4], and satellite remote-sensing [5]. However, despite the extensive activity in this field, the task remains highly challenging because LR images have a one-to-many relationship with their resulting HR images.
Early SISR research focused on prediction-based [6], patch-based [7], and learning-based [8,9] SISR methods. However, these methods suffer from two major problems: (1) they are optimized slowly with poor optimization performance; (2) most of them rely on the feature prior to the image, and the quality of the restored SR image is generally poor once the prior features are biased.
These issues have been addressed by the recent development of deep learning technology, which has achieved unprecedented success with SISR and other visualization tasks. Convolutional neural networks (CNNs) have a strong learning ability and the advantage of end-to-end training optimization. This strong learning capability is particularly valuable for SISR applications because LR images are almost completely composed of low-frequency information, and the SISR task can be regarded in general as a process of learning the high-frequency information lost in the original LR image. Dong et al. [8] proposed the super-resolution (SR) CNN (SRCNN) model, which was the first development of CNN-based SISR technology. The model employed a simple CNN with three convolutional layers and achieved a level of SISR performance surpassing all conventional SISR methods at that time. Then, Kim et al. [10] proposed very deep SR (VDSR) with a 20-layer residual structure and a recursive structure composed of a 20-layer deeply-recursive convolutional network (DRCN) [11], which greatly decreased the difficulty of training a deep model, and achieved better SISR performance than previous methods. Later, Tai et al. [12] proposed a very deep 52-layer deep recursive residual network (DRRN) structure, which repeated recursive blocks consisting of multiple residual units to increase the depth and reduce the number of training parameters. In addition, multi-path structures were used in the recursive blocks to reduce problems associated with gradient explosion and gradient disappearance, which increased training efficiency and achieved leading SISR performance. Later studies [13–16] achieved remarkable SISR performance by applying a generative adversarial network (GAN) proposed by Goodfellow et al. [17]. Comparable performance was achieved by Tai et al. [18], using the proposed MemNet, which is a network composed of multiple recursive persistent memory blocks. Although these models have achieved significantly improved SISR performance, they interpolate the LR input to the required size, which introduces artifacts into the output SR image, and suffer from high computational cost that greatly increases the time required for model training and testing.
Numerous efforts have focused on developing network models that can be more rapidly trained and tested. For example, Dong et al. [9], proposed a fast version of the original SRCNN model denoted as FSRCNN, which addressed slow model training and testing by applying post-up sampling, and further zooming and expanding the channel to make the model flops closer to real time. Lim et al. [19] achieved significant performance improvements by proposing enhanced deep SR (EDSR) and multi-scale deep SR (MDSR) technology, which removes unnecessary batch normalization (BN) layers in the residual structure because they are not required for SISR tasks. Zhang et al. [20] proposed a residual dense network (RDN) structure based on DenseNet [21], which learned the features of all previous layers via densely grouped connections (DGCs), and further introduced the residual long-skip connection (LSC) and the short-skip connection (SSC) to reduce training difficulties.
Recent work has demonstrated that applying an attention mechanism provides enhanced SISR performance. Here, the attention mechanism for humans can be regarded as the ability to focus on the most important and valuable information from a much larger set of information. The attention mechanism was first applied to natural language processing [22,23], and some recent studies have introduced it into the field of computer vision, such as image classification [24], and object detection [25]. Use of the attention mechanism can be very helpful in SISR tasks because it enables information to be treated selectively, resulting in greatly reduced computational cost and effective SISR performance improvement. For example, Zhang et al. [26] achieved surpassing SISR performance by proposing a 400-layer residual channel attention network (RCAN) model based on channel-wise attention [24], which improved SISR performance by modeling the relationship between channels. Channel-wise attention was later improved by Anwar et al. [27] in SENet [24]. This work further proposed Laplacian spatial attention (LSA), densely connected residuals blocks (RBs), and cascading residuals, which achieved improved SISR performance. However, the use of densely connected RBs dramatically increased the computational cost. Liu et al. [28] proposed a non-local recurrent network (NLRN) structure, which introduced non-local modules into a recurrent network to improve the SISR performance through spatial attention (SA). Efforts to improve the human visual system (HVS) performance of SISR have introduced models based on the GAN, including the SRGAN [14] model and the enhanced SRGAN (ESRGAN) [13] model. Although both of these models improve the perceptual quality of the image, the generated SR image is too bright.
Although many existing CNN-based SISR methods have achieved state-of-the-art performance, they also suffer from some problems. First, most models improve SISR performance by stacking multiple convolutional layers. In particular, ResNet [29] and DenseNet [21] are widely used in SISR methods [10,13,14,18–20,26–28,30–33] and image retrieval [34] to build very deep networks. However, simply stacking convolution layers to form deep network models cannot guarantee high SISR performance [26]. Other studies have demonstrated that a relatively deep network can be constructed by stacking several RBs connected by LSCs [19,20]. However, while this has been shown to achieve better performance in image recognition tasks, its application in the SISR task often causes the gradient to disappear or explode during the training process and fails to obtain better performance. Moreover, whether increasing the network depth can further improve SISR performance remains to be verified, and the optimum means of designing deeper models are still unclear. By contrast, while some models consider the relative dependencies between features or channels [26,33], most existing models do not [8–14,18–20,30–32,35–37]. Therefore, the means of extracting the most useful features and enhancing the discriminative learning ability of SISR models as much as possible under their limited capacities remains underdeveloped. In addition, most methods that apply the attention mechanism treat channels equally, while some models use either CA or SA and rarely combine both attention models, which reduces the discriminative learning ability of the model. Although Hu et al. [38] proposed SISR models based on both SA and CA, the attention models were inefficient.
The above discussed issues are addressed in the present work by proposing a mixed attention dense residual network (MADRN) to obtain a deep and powerful network for better feature correlation learning, which is a key component of the learning process. Specifically, we propose a mixed attention (MA) mechanism that effectively integrates LSA and CA to learn the most useful features adaptively, and thereby further improve the discriminative learning ability of the model. Additionally, the difficulty of training deep networks is decreased by applying a residual in dense (RID) structure, which is a basic unit for building a deep model with dense residual groups (DRGs). The use of DRGs addresses the gradient disappearance and explosion problems associated with stacking several RBs connected by LSCs to form a deep network. The RID structure not only can effectively promote feature reuse but can also avoid redundant feature learning and the transmission of low-frequency information through the network backbone to enable effective learning of the lost high-frequency information in LR images. The qualitative and quantitative results of extensive experiments demonstrate that the proposed method has a comparable performance with other state-of-the-art methods and can achieve superior visual quality, as demonstrated by Fig. 1.

Figure 1: Visual comparison. “img_046” from Urban100 and “Yumeiro Cooking” from Manga109 respectively perform visual results of 4× SR. Comparing other state-of-the-art methods, our method achieves better visual quality and restores more realistic image details
2 Mixed Attention Densely Residual Network (MADRN)
As shown in Fig. 2, the proposed MADRN architecture can be divided into four components: shallow feature extraction, RID structure for deep feature extraction, upscaling module and reconstruction module. It is assumed that the LR input and the SR output of the MADRN are represented by ILR and ISR, respectively, and Conv represents a convolutional layer. A shallow feature F0 is extracted from the LR input using only a single Conv layer as follows [20,37]:
where HConv (·) denotes the function that extracts the shallow feature from ILR. Then F0 is fed into the RID structure and forwarded to the front of the upscaling module by an LSC for the upscaling operation. In addition, a deep feature is extracted from F0 as follows:
where HRID(·) denotes the function that extracts the deep feature based on a very deep RID structure. To the best of our knowledge, HRID (·) is a novel function for use in SISR and has a very wide receptive domain Then, the low-frequency information in F0 is added to FN through an LSC, and thereby bypasses transmission through the network. Next, the upscaled feature FUP is obtained by fusing and scaling the shallow and deep features in the upscaling module as follows:
where HUP (·) represents the function of the upscaling module.
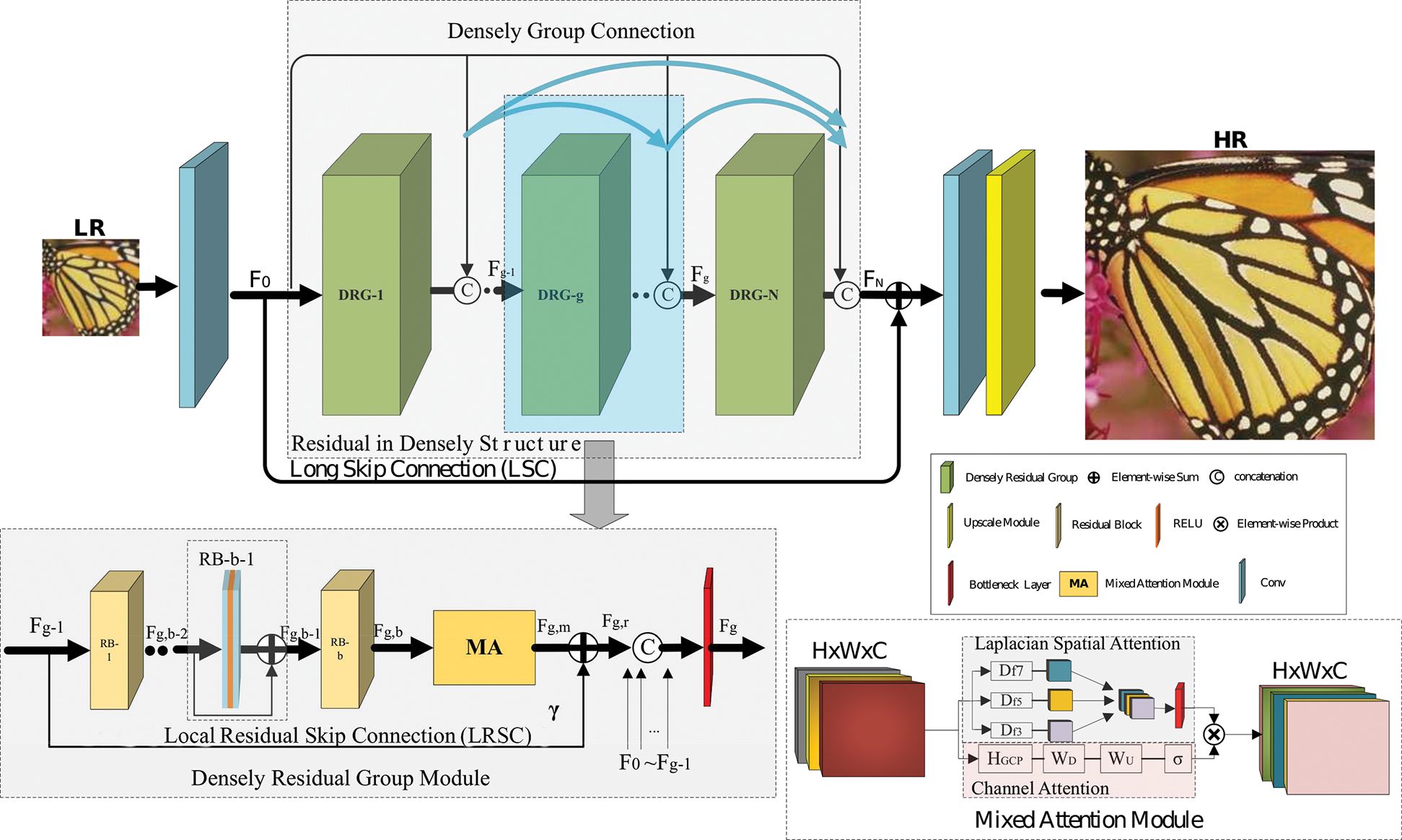
Figure 2: The frame of mixed attention densely residual network (MADRN)
Several options exist for implementing the upscaling module, such as the transposed convolution layer (also known as a deconvolution layer) [39], nearest-neighbor interpolation with convolution [40] and a sub-pixel convolution layer [41]. These types of post-upsampling methods consume less memory and provide a faster running speed, and better upsampling performance than pre-upsampling methods [8,11,12,42], while pre-upsampling methods often introduce more effect, such as noise and blurring [43]. Thus, we apply a sub-pixel convolution layer for the upscaling module, and then obtain the final reconstructed output ISR through a convolution layer as follows:
where HRECON (·) and HMADRN (·) represent functions of the reconstruction module and the entire MADRN structure, respectively.
A number of loss functions have been applied for optimizing SISR models, including the commonly employed L1 loss function [13,18,20,26,31,44,45], L2 loss function [8–11,35,46], and perceptual [36] and adversarial [13,14] losses. The validity of the proposed MADRN model can be best demonstrated by employing a common loss function. Therefore, we apply the L1 loss function in the present study. Given a training set comprising N LR images and their corresponding HR images, denoted
where
2.2 Residual in Dense (RID) Structure
The very deep RID structure is composed of N DRGs and an MA module with connections made by DGCs. Each DRG includes a stack of b RBs with a local residual skip connection (LRSC) between each block, and an MA module used to mine the dependency among features. This structure enabled the proposed network to exceed four hundred layers and achieve better performance SISR performance.
The output Fg of the g-th DRG can be expressed as:
where Hg (·) represents the function of the g-th DRG, and Fg−1 denotes its input. The use of DGCs in the residual groups to achieve a stable training effect and better SISR performance can be expressed as:
where Fg,r denotes the output of the local deep features of the g-th DRG, Hc,g(·) denotes the function of the DGC in the g-th DRG, which cascades the output of all previous DRGs and follows a Conv 1 × 1 bottleneck layer to reduce the dimension to that of Fg-1.
The output Fg,b of the b-th RB in the g-th DRG can be represented as:
where Hg, b(·) denotes the function of the b-th RB in the g-th DRG, which consists of two Conv layers sandwiching a rectified linear unit (ReLU) layer [47], and Fg,b−1 is its input. The use of LRSCs in each DRG to make the proposed model more focused on learning useful information can be expressed in terms of the output feature map Fg,m as follows.
Here, Hg, r (·) represents the function of the g-th DRG for learning high-frequency information, and
An MA module is embedded in the output of the last RB of each DRG to make the proposed model more discriminative for each feature by adaptively adjusting the weight of each feature. The proposed MA module is illustrated in Fig. 3. First, we propose a new mixed CA and LSA mechanism, and then implemented a channel and spatial information fusion mechanism via an element-wise product. Assuming that Fg,b, and Fg,m are the respective input and output feature maps of the MA module pertaining to the g-th DRG, the output feature map Fg,m is obtained as
where Hg,ma (·) represents the function corresponding to the CA, LSA and Fused Mechanism functions. Details regarding the specific implementation of these three functions are presented as follows.
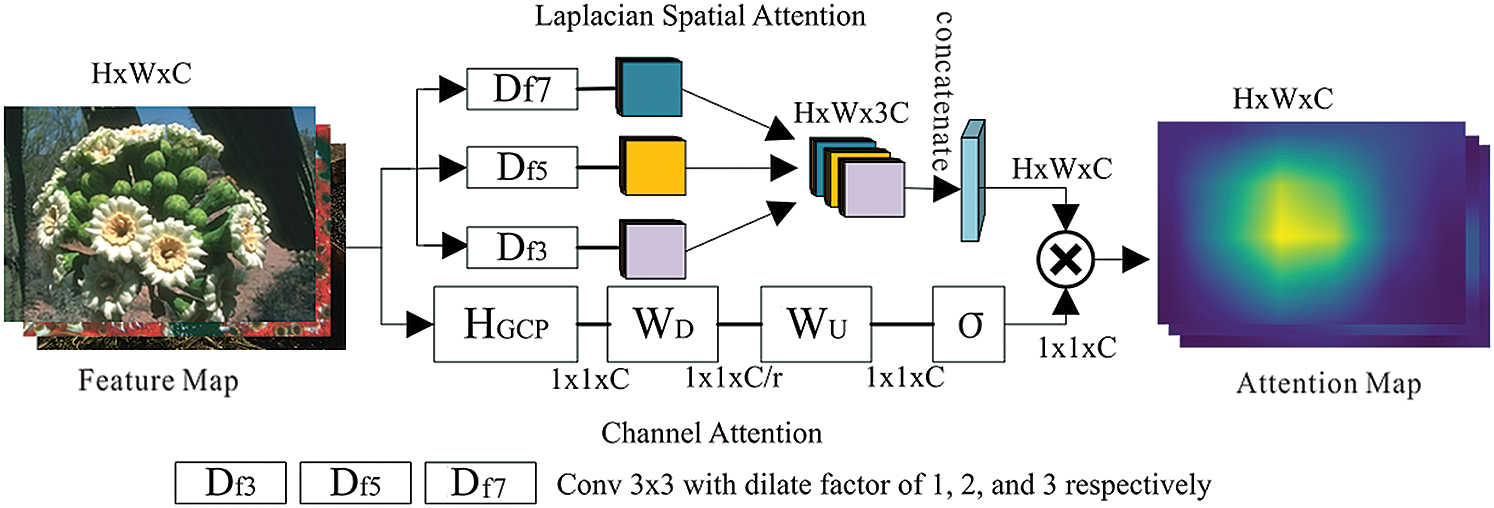
Figure 3: Mixed attention
Channel Attention (CA). In the present work, the output Fg,mca of the CA module in the g-th DRG can be expressed as follows [24]:
where Fg,b is its corresponding input, HGCP(·) is the corresponding global pooling function, which is used to collect channel statistics of the entire image. σ(·) and δ(·), respectively, represent the sigmoid gating function and the RELU function [47], and WD and WU are weights that respectively, represent channel-downscaling and channel-upscaling convolutional layers.
Laplacian Spatial Attention (LSA). The features in each feature map are relatively important, but most existing SISR methods treat the features in each feature map equally. The present study proposes an LSA mechanism to mechanism to exploit the potential relationships between features in SR images, and thereby create a more accurate representation of the visual experience. The proposed LSA differs substantially from the LSA proposed in previous studies [27,30]. Here, we use the convolutional layers of three different kernel dilations to estimate the relative importance of each feature. The output feature map Fg,msa of the LSA module in the g-th DRG can be expressed as follows.
Here, Fg,b is the corresponding input, and HD3(·), HD5(·), and HD7(·) denote Conv 3 × 3 operations with dilation factors 1, 2 and 3, respectively. The resulting three different levels of features Fg,msa3, Fg,msa5, and Fg,msa7, are concatenated as follows.
Then, we apply a Conv layer and δ(·) to further adjust the relative importance of the features and obtain an output feature map Fg,msa with the same size as Fg,b:
where Fg,msc is the corresponding input, and Hg,msd (·) is the function of the Conv Layer.
Fused Mechanism. The proposed CA and LSA modules, respectively, explore the relationship between different channels and features within each channel. Consequently, we take advantage of both attention mechanisms by applying the element-wise product, denoted as
Now we will introduce the implementation details of MADRN. We set the number N of DRGs in the RID structure of the MADRN model equal to 21, where each DRG has b = 10 RB blocks. In addition, we apply a Conv 3 × 3 layer with dilation factors of 1, 2, and 3 in the LSA module and a Conv 1 × 1 layer for channel downscaling and channel upscaling in the CA module, while the kernel size of all other Conv layers without special description is only 3 × 3. Except for Conv 1 × 1 layers, other convolution layers apply zero padding to ensure the same input and output size. In addition, with the exception of the channel-downscaling and bottleneck layers, all convolution kernel number are set as C = 64. In the bottleneck layer, the Conv filters number increases as the number of DRGs in the MADRN increases. Additionally, the reduction ratio of the channel-downscaling layer in the MA is set to r = 16. We followed a previously proposed scheme [20,44] for the upscaling module HUP(·) by applying the sub-pixel layer in the efficient sub-pixel CNN (ESPCNN) structure [41] for upsampling to obtain the coarse to fine feature, and finally applied a Conv layer with a filter number of 3 to output the color image. We stress that the proposed model is also applicable to gray-scale images.
Following a previously proposed experimental scheme [19,20,31,37], we employed 800 HR images from the DIV2K dataset [48] as the training dataset and adopted five benchmark datasets: Set5 [46], Set14 [49], BSD100 [50], Urban100 [51], and Manga109 [52], each with different characteristics as the testing datasets. The bicubic interpolation (BI) function in MATLAB was employed to obtain corresponding LR images based on ×2, ×3, and ×4 degradations applied to each image in the testing datasets. All experimental results were evaluated according to the peak signal to noise ratio (PSNR) and the structural similarity method (SSIM) of the transformed YCbCr space on the luminance channel. Moreover, we extended the limited training dataset, to avoid overfitting by randomly rotating the images in the training dataset by 90°, 180°, and 270°, and by horizontal flipping. We randomly selected 16 LR color image patches with a size of 48 pixels ×48 pixels as the input of each batch, and optimized our model using the ADAM optimizer with hyperparameters set to β1 = 0.9, β2 = 0.99, and
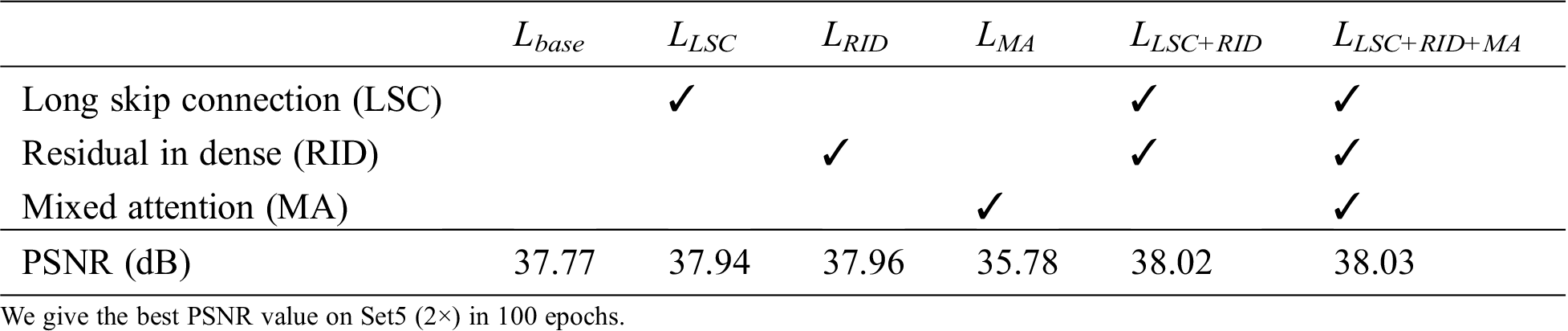
We investigated the effects of the proposed RID structure and MA mechanism on the SISR performance of the MADRN model. This was conducted by constructing a baseline (Lbase) model, composed of only 21 cascaded DRGs, and each DRG is composed of 10 cascaded RBs to form a very deep model with more than 400 layers. In particular, the Lbase model includes only LRSCs between the RBs and applies none between the other RBs and the DRGs. In addition, we constructed similar models with the LSC module (the LLSC model), the RID structure (the LRID model), and both the LSC module and RID structure (the LLSC+RID model). We also included the MA module within the Lbase model and the LLSC+RID model to obtain the Lbase+MA and LLSC+RID+MA models, respectively. It is noted from Tab. 1 that the Lbase model obtains a relatively low PSNR value of 37.77 dB for the Set5 dataset with ×2. degradation. However, the PSNR values obtained by the LLSC and LRID models increased to 37.94 dB and 37.96 dB, respectively. These increases can be attributed to the capability of the LLSC model to bypass the transmission of low-frequency information, while the LRID model is able to learn all previous hierarchical features. We also note that the LLSC+RID model obtains a higher PSNR value of 38.02 dB, indicating that the combined use of the LSC and RID structure can effectively build a very deep model, while simply stacking RBs, as is done in the Lbase model, cannot achieve good SISR performance. We also observe from Tab. 1 that the LLSC+RID+MA model obtains a PSNR value of 38.03 dB, which is slightly greater than that of the LLSC+RID model. This indicates that the MA module can improve the performance of the model by adaptively learning the dependencies between features and combining this information well. However, the Lbase+MA model provides significantly reduced SISR performance. This is mainly because the Lbase+MA model is composed of simply stacked very deep convolutional layers on the basic model and cannot employ the LSC module and RID structure to help propagate information in the previous layer and bypass low-frequency information. Therefore, we applied the LLSC+RID+MA model in the remainder of the experiments.
Table 1: Effects of various modules
3.3 Comparison with State-of-the-art SISR Methods
To validate our model, we compared the SISR performance of the MADRN model with that of13 state-of-the-art methods, including SRCNN [8], FSRCNN [9], VDSR [10], LapSRN [30], SRDenseNet [32], MemNet [18], EDSR [19], SRMDNF [37], NLRN [28], DBPN [31], RDN [20], RCAN [26] and CARN [35]. As has been done in previous studies [35,19], we also applied the self-ensemble method to further improve the performance of our MADRN model and denote this model herein as MADRN+.
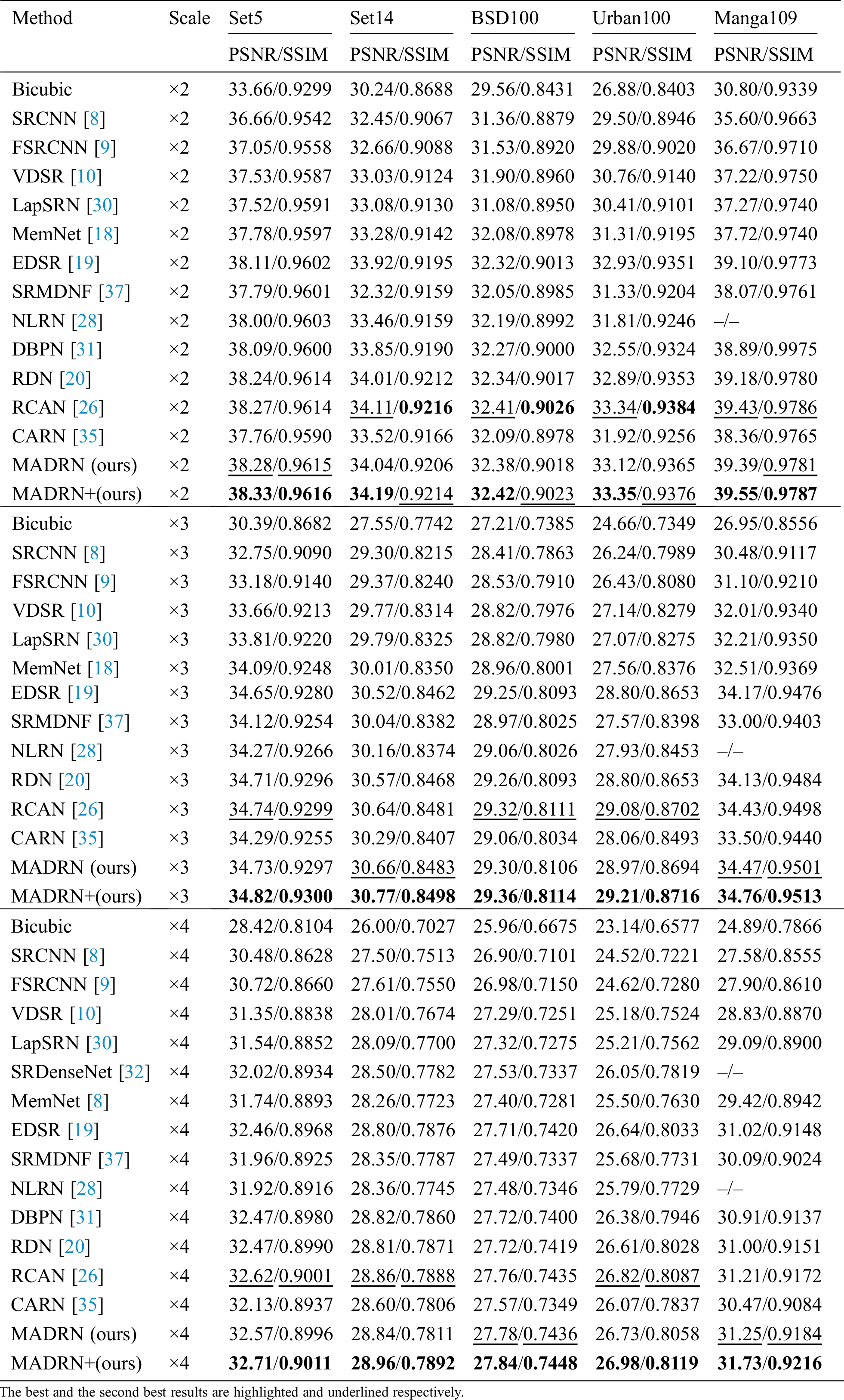
PSNR and SSIM Metric Results. The PSNR and SSIM results obtained by the various models considered are listed in Tab. 2 for the ×2, ×3, and ×4 LR images in the testing datasets. The results demonstrate that the MADRN+ model provided superior SISR performance compared with all other methods considered for the ×2, ×3, and ×4 LR images. Other than the MADRN+ model, the SISR performance of the proposed MADRN model and RCAN [35] is comparable and superior to all other methods. The main reason is that RCAN [35] uses channel-wise attention in each of the RBs to learn the interrelationships between channel-wise features, which makes the model more focused on useful features. However, the proposed MADRN model applied only one MA module in each DRG, whereas a total of 20 channel-wise attention modules were applied in each DRG in RCAN [35]. Accordingly, the proposed model is more efficient.
Table 2: Average PSNR/SSIM on five benchmark datasets
Qualitative Results. We further illustrated the advantages of the proposed MADRN model by comparing the visual results obtained by the various methods for the Manga100 dataset with ×4 LR images. The results shown in Fig. 4 indicate that most of the obtained SR images have not been accurately reconstructed and suffer severe blurring artifacts and somewhat ambiguous lines, whereas only the DBPN [31], RCAN [26], and the MADRN model recover sharp results that are close to the ground-truth SR images. This is particularly evident for “img_092” in the Urban datasets, which includes rich textural details. Here, most of the methods considered produce serious blur artifacts, and, even worse, the SR image results obtained by some of the older methods (i.e., SRCNN [8], FSRCNN [9], and LapSRN [30]) exhibit serious loss of image information. These issues are further illustrated by the results obtained for the “EverydayOsakanaChan” image in the Manga109 dataset. Here, the image includes a variety of structural information, and the SR images produced by most of the older methods suffer from very serious loss of structural information. Accordingly, these methods can only recover some of the main contour structures, and the finer textural information is affected by blur artifacts.

Figure 4: Visual comparison of our MADRN with other SR methods on the Urban100 dataset and the Manga100 datasets for 4×SR
The present work proposed the MADRN architecture to obtain a deep and powerful network for better feature correlation learning in SISR applications. Specifically, we effectively integrated LSA and CA modules into an MA mechanism to learn the most useful features adaptively, and thereby further improve the discriminative learning ability of the model. Additionally, we applied an RID structure with DRGs to reduce the difficulty of training deep networks. The RID structure not only promotes feature reuse but can also avoid redundant feature learning and the transmission of low-frequency information through the network backbone to enable effective learning of the lost high-frequency information in LR images. The qualitative and quantitative results of extensive experiments demonstrated that the proposed method has a comparable performance with other state-of-the-art methods and can achieve superior visual quality.
Funding Statement: This work was supported in part by the Natural Science Foundation of China under Grant 62063004 and 61762033, in part by the Hainan Provincial Natural Science Foundation of China under Grant 2019RC018 and 619QN246, and by the Postdoctoral Science Foundation under Grant 2020TQ0293.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. W. T. Freeman, E. C. Pasztor and O. T. Carmichael, “Learning low-level vision,” International Journal of Computer Vision, vol. 40, no. 1, pp. 25–47, 2000. [Google Scholar]
2. J. Zou, Z. Li, Z. Guo and D. Hong, “Super-resolution reconstruction of images based on microarray camera,” Computers, Materials & Continua, vol. 60, no. 1, pp. 163–177, 2019. [Google Scholar]
3. S. P. Mudunuri and S. Biswas, “Low resolution face recognition across variations in pose and illumination,” IEEE Transactions on Pattern Analysis & Machine Intelligence, vol. 38, no. 5, pp. 1034–1040, 2015. [Google Scholar]
4. H. Greenspan, “Super-resolution in medical imaging,” Computer Journal, vol. 52, no. 1, pp. 43–63, 2008. [Google Scholar]
5. M. W. Thornton, P. M. Atkinson and D. A. Holland, “Sub-pixel mapping of rural land cover objects from fine spatial resolution satellite sensor imagery using super-resolution pixel-swapping,” International Journal of Remote Sensing, vol. 27, no. 3, pp. 473–491, 2006. [Google Scholar]
6. R. Keys, “Cubic convolution interpolation for digital image processing,” IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 29, no. 6, pp. 1153–1160, 1981. [Google Scholar]
7. G. Freedman and R. Fattal, “Image and video upscaling from local self-examples,” ACM Transactions on Graphics, vol. 30, no. 2, pp. 1–11, 2011. [Google Scholar]
8. C. Dong, C. C. Loy, K. He and X. Tang, “Image super-resolution using deep convolutional networks,” IEEE Transactions on Pattern Analysis & Machine Intelligence, vol. 38, no. 2, pp. 295–307, 2015. [Google Scholar]
9. C. Dong, C. C. Loy and X. Tang, “Accelerating the super-resolution convolutional neural network,” in Springer ECCV. Amsterdam, The Netherlands, pp. 391–407, 2016. [Google Scholar]
10. J. Kim, J. K. Lee and K. M. Lee, “Accurate image super-resolution using very deep convolutional networks,” in IEEE CVPR. Las Vegas, NV, USA, pp. 1646–1654, 2016. [Google Scholar]
11. J. Kim, J. K. Lee and K. M. Lee, “Deeply-recursive convolutional network for image super-resolution,” in IEEE CVPR. Las Vegas, NV, USA, pp. 1637–1645, 2016. [Google Scholar]
12. Y. Tai, J. Yang and X. Liu, “Image super-resolution via deep recursive residual network,” in IEEE CVPR. Honolulu, HI, USA, pp. 3147–3155, 2017. [Google Scholar]
13. X. Wang, K. Yu, S. Wu, J. Gu, Y. Liu et al., “Esrgan: Enhanced super-resolution generative adversarial networks,” in Springer ECCV. Munich, Germany, pp. 63–79, 2018. [Google Scholar]
14. C. Ledig, L. Theis, F. Huszár, J. Caballero, A. Cunningham et al., “Photo-realistic single image super-resolution using a generative adversarial network,” in IEEE CVPR. Honolulu, HI, USA, pp. 4681–4690, 2017. [Google Scholar]
15. M. Zhao, X. Liu, X. Yao and K. He, “Better visual image super-resolution with Laplacian pyramid of generative adversarial networks,” Computers, Materials & Continua, vol. 64, no. 3, pp. 1601–1614, 2020. [Google Scholar]
16. W. Chen, T. Sun, F. Bi, T. Sun, C. Tang et al., “Overview of digital image restoration,” Journal of New Media, vol. 1, no. 1, pp. 35–44, 2019. [Google Scholar]
17. I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley et al., “Generative adversarial nets,” in Proc. NeurIPS, Montreal, Canada, pp. 2672–2680, 2014. [Google Scholar]
18. Y. Tai, J. Yang, X. Liu and C. Xu, “Memnet: A persistent memory network for image restoration,” in IEEE ICCV. Venice, Italy, pp. 4539–4547, 2017. [Google Scholar]
19. B. Lim, S. Son, H. Kim, S. Nahand and K. M. Lee, “Enhanced deep residual networks for single image super-resolution,” in IEEE CVPR. Honolulu, HI, USA, pp. 136–144, 2017. [Google Scholar]
20. Y. Zhang, Y. Tian, Y. Kong, B. Zhong and Y. Fu, “Residual dense network for image super-resolution,” in IEEE CVPR. Salt Lake City, Utah, USA, pp. 2472–2481, 2018. [Google Scholar]
21. G. Huang, Z. Liu, L. Van Der Maaten and K. Q. Weinberger, “Densely connected convolutional networks,” in IEEE CVPR. Honolulu, HI, USA, pp. 4700–4708, 2017. [Google Scholar]
22. J. Song, P. Zeng, L. Gao and H. T. Shen, “From pixels to objects: Cubic visual attention for visual question answering,” in Proc. IJCAI, Stockholm, Sweden, pp. 906–912, 2018. [Google Scholar]
23. L. Gao, X. Li, J. Song and H. T. Shen, “Hierarchical LSTMS with adaptive attention for visual captioning,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 42, no. 5, pp. 1112–1131, 2019. [Google Scholar]
24. J. Hu, L. Shen and G. Sun, “Squeeze-and-excitation networks,” in IEEE CVPR. Salt Lake City, Utah, USA, pp. 7132–7141, 2018. [Google Scholar]
25. J. Mai, X. Xu, G. Xiao, Z. Deng and J. Chen, “PGCA-Net: Progressively aggregating hierarchical features with the pyramid guided channel attention for saliency detection,” Intelligent Automation & Soft Computing, vol. 26, no. 4, pp. 847–855, 2020. [Google Scholar]
26. Y. Zhang, K. Li, K. Li, L. Wang, B. Zhong et al., “Image super-resolution using very deep residual channel attention networks,” in Springer ECCV. Munich, Germany, pp. 286–301, 2018. [Google Scholar]
27. S. Anwar and N. Barnes, “Densely residual Laplacian super-resolution,” IEEE Transactions on Pattern Analysis & Machine Intelligence, vol. 1, no. 01, pp. 1–12, 2020. [Google Scholar]
28. D. Liu, B. Wen, Y. Fan, C. C. Loyand and T. S. Huang, “Non-local recurrent network for image restoration,” in Proc. NeurIPS, Montreal, Canada, pp. 1673–1682, 2018. [Google Scholar]
29. K. He, X. Zhang, S. Ren and J. Sun, “Deep residual learning for image recognition,” in IEEE CVPR. Las Vegas, NV, USA, pp. 770–778, 2016. [Google Scholar]
30. W. S. Lai, J. B. Huang, N. Ahuja and M. H. Yang, “Deep Laplacian pyramid networks for fast and accurate super-resolution,” in IEEE CVPR. Honolulu, HI, USA, pp. 624–632, 2017. [Google Scholar]
31. M. Haris, G. Shakhnarovich and N. Ukita, “Deep back-projection networks for super-resolution,” in IEEE CVPR. Salt Lake City, Utah, USA, pp. 1664–1673, 2018. [Google Scholar]
32. T. Tong, G. Li, X. Liu and Q. Gao, “Image super-resolution using dense skip connections,” in IEEE ICCV. Venice, Italy, pp. 4809–4817, 2017. [Google Scholar]
33. J. H. Kim, J. H. Choi, M. Cheon and J. S. Lee, “Ram: Residual attention module for single image super-resolution. ArXiv Preprint ArXiv:1811.12043, 2018. [Google Scholar]
34. J. Song, T. He, L. Gao, X. Xu, A. Hanjalic et al., “Unified binary generative adversarial network for image retrieval and compression,” International Journal of Computer Vision, vol. 128, no. 1, pp. 2243–2264, 2020. [Google Scholar]
35. N. Ahn, B. Kang and K. A. Sohn, “Fast, accurate, and lightweight super-resolution with cascading residual network,” in Springer ECCV. Munich, Germany, pp. 252–268, 2018. [Google Scholar]
36. J. Johnson, A. Alahi and L. Fei-Fei, “Perceptual losses for real-time style transfer and super-resolution,” in Springer ECCV. Amsterdam, The Netherlands, pp. 694–711, 2016. [Google Scholar]
37. K. Zhang, W. Zuo and L. Zhang, “Learning a single convolutional super-resolution network for multiple degradations,” in IEEE CVPR. Salt Lake City, Utah, USA, pp. 3262–3271, 2018. [Google Scholar]
38. Y. Hu, J. Li, Y. Huang and X. Gao, “Channel-wise and spatial feature modulation network for single image super-resolution,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 30, no. 11, pp. 3911–3927, 2020. [Google Scholar]
39. M. D. Zeiler, D. Krishnan, G. W. Taylor and R. Fergus, “Deconvolutional networks,” in IEEE CVPR. San Francisco, CA, USA, pp. 2528–2535, 2010. [Google Scholar]
40. V. Dumoulin, J. Shlens and M. Kudlur, “A learned representation for artistic style,” in Proc. ICLR, Toulon, France, pp. 1–26, 2017. [Google Scholar]
41. W. Shi, J. Caballero, F. Huszár, J. Totz, A. P. Aitken et al., “Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network,” in IEEE CVPR. Las Vegas, NV, USA, pp. 1874–1883, 2016. [Google Scholar]
42. A. Shocher, N. Cohen and M. Irani, “Zero-shot super-resolution using deep internal learning,” in IEEE CVPR. Salt Lake City, Utah, USA, pp. 3118–3126, 2018. [Google Scholar]
43. Z. Wang, J. Chen and S. C. H. Hoi, “Deep learning for image super-resolution: A survey,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 1, no. 1, pp. 1, 2020. [Google Scholar]
44. Y. Zhang, K. Li, K. Li, B. Zhong and Y. Fu, “Residual non-local attention networks for image restoration,” in Proc. ICLR, New Orleans, LA, USA, pp. 1–18, 2019. [Google Scholar]
45. T. Dai, J. Cai, Y. Zhang, S. T. Xia and L. Zhang, “Second-order attention network for single image super-resolution,” in IEEE CVPR. Long Beach, California, USA, pp. 11065–11074, 2019. [Google Scholar]
46. M. Bevilacqua, A. Roumy, C. Guillemot and M. L. Alberi-Morel, “Low-complexity single-image super-resolution based on nonnegative neighbor embedding,” in Springer BMCV. Guildford, British, UK, pp. 135.1–135.10, 2012. [Google Scholar]
47. V. Nair and G. E. Hinton, “Rectified linear units improve restricted Boltzmann machines,” in Springer ICML. Haifa, Israel, pp. 807–814, 2010. [Google Scholar]
48. R. Timofte, E. Agustsson, L. Van Gool, M. H. Yang and L. Zhang, “Ntire 2017 challenge on single image super-resolution: Methods and results,” in IEEE CVPR. Honolulu, HI, USA, pp. 114–125, 2017. [Google Scholar]
49. R. Zeyde, M. Elad and M. Protter, “On single image scale-up using sparse-representations,” in Springer Curves and Surfaces. Avignon, France, pp. 711–730, 2010. [Google Scholar]
50. D. Martin, C. Fowlkes, D. Tal and J. Malik, “A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics,” in IEEE ICCV. Vancouver, BC, Canada, pp. 416–423, 2001. [Google Scholar]
51. J. B. Huang, A. Singh and N. Ahuja, “Single image super-resolution from transformed self-exemplars,” in IEEE CVPR. Boston, MA, USA, pp. 5197–5206, 2015. [Google Scholar]
52. Y. Matsui, K. Ito, Y. Aramaki, A. Fujimoto, T. Ogawa et al., “Sketch-based manga retrieval using manga109 dataset,” Multimedia Tools and Applications, vol. 76, no. 20, pp. 21811–21838, 2017. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |