Computer Systems Science & Engineering DOI:10.32604/csse.2021.015628
Article

Generalized Normalized Euclidean Distance Based Fuzzy Soft Set Similarity for Data Classification

Rahmat Hidayat1,2,*, Iwan Tri Riyadi Yanto1,3, Azizul Azhar Ramli1, Mohd Farhan Md. Fudzee1 and Ansari Saleh Ahmar4

1Faculty of Computer and Information Technology, Universiti Tun Hussein Onn Malaysia, Batu Pahat, Malaysia
2Department of Information Technology, Politeknik Negeri Padang, Padang, Indonesia
3Department of Information System, Universitas Ahmad Dahlan, Yogyakarta, Indonesia
4Department of Statistics, Universitas Negeri Makassar, Makassar, Indonesia
*Corresponding Author: Rahmat Hidayat. Email: rahmat@pnp.ac.id
Received: 30 November 2020; Accepted: 17 February 2021

Abstract: Classification is one of the data mining processes used to predict predetermined target classes with data learning accurately. This study discusses data classification using a fuzzy soft set method to predict target classes accurately. This study aims to form a data classification algorithm using the fuzzy soft set method. In this study, the fuzzy soft set was calculated based on the normalized Hamming distance. Each parameter in this method is mapped to a power set from a subset of the fuzzy set using a fuzzy approximation function. In the classification step, a generalized normalized Euclidean distance is used to determine the similarity between two sets of fuzzy soft sets. The experiments used the University of California (UCI) Machine Learning dataset to assess the accuracy of the proposed data classification method. The dataset samples were divided into training (75% of samples) and test (25% of samples) sets. Experiments were performed in MATLAB R2010a software. The experiments showed that: (1) The fastest sequence is matching function, distance measure, similarity, normalized Euclidean distance, (2) the proposed approach can improve accuracy and recall by up to 10.3436% and 6.9723%, respectively, compared with baseline techniques. Hence, the fuzzy soft set method is appropriate for classifying data.

Keywords: Soft set; fuzzy soft set; classification; normalized euclidean distance; similarity

1  Introduction

Nowadays, Big Data is used in Tuberculosis (TBC) patient data in healthcare, stock data in economics and business fields, and BMKG data (containing weather, temperature, and rainfall data), etc. Data mining is the process of extracting knowledge from large amounts of data [1], and is done by extracting information and analyzing data patterns or relationships [2,3].

Classification is one of the data mining processes used to predict predetermined target classes with data learning accurately. The classification has been used in health [4–6], economics, and agriculture fields [7,8]. Classifying data is challenging and requires further research [9].

In 1965, Zadeh [10] introduced a fuzzy set in which each element object had a grade of memberships ranging between zero and one. In comparison, Molodtsov [11] introduced soft set theory to collect parameters from the universal set subsets (set U). Soft set theory is widely used to overcome the presence of elements of uncertainty or doubt, such as those found in decision-making. Roy developed fuzzy soft set theory by combining soft set theory and fuzzy set theory. This theory was then used in decision-making problems [12,13]. Majumdar and Samanta [14] presented a fuzzy soft set for similarity measurement between two generalized fuzzy soft sets for decision-making.

The fuzzy soft set, an extension of the classical soft set, was introduced by Maji [15]. There have been many works about fuzzy soft set theory in decision-making. Ahmad et al. [16] defined arbitrary fuzzy soft union and fuzzy soft intersection and proved Demorgan laws using fuzzy soft set theory. Meanwhile, Aktas and Cagman [17] studied fuzzy parameterized soft set theory, related properties, and decision-making applications. Rehman et al. [18] studied some fuzzy soft sets’ operations and gave fuzzy soft sets the fundamental properties. Finally, Celik et al. [19] researched applications of fuzzy soft sets in ring theory.

The critical issue in fuzzy soft sets is the similarity measure. In recent years, similarity measurement between two fuzzy soft sets has been studied from different aspects and applied to various fields, such as decision-making, pattern recognition, region extraction, coding theory, and image processing. For example, similarity measurement [20] has been researched in fuzzy soft sets based on distance, set-theoretic approaches, and matching functions. Sut [21] and Rajarajeswari [22] used the notion of the similarity measure in Majumdar and Samanta [20] to make decisions. Several similarity measurement [23] based on four types of quasi-metrics were introduced to fuzzy soft sets. Sulaiman [24] researched a set-theoretic similarity measure for fuzzy soft sets, and applied it to group decision-making. However, some studies haphazardly investigated the similarity measurement of fuzzy soft sets based on distance, resulting in high computational costs [20,23]. Feng and Zheng [25] showed that the similarity measure based on the Hamming distance and normalized Euclidean distance in the fuzzy soft set is reasonable. Thus, the similarity of generalized normalized Euclidean distance is applied in the present paper to a fuzzy soft set for classification. The similarity is used to classify the label of data. The experimental results show that the proposed approach can improve classification accuracy.

2  The Proposed Method/Algorithm

This section presents the basic definitions of fuzzy set theory, soft set theory, and some useful definitions from Roy and Maji [12].

2.1 Fuzzy Set

Definition 2.1 [10] Let U be a universe. A fuzzy set A over U is a set defined by a function

μA:U→[0,1] (1)

where μ A is the membership function of A, and the value μ A (x) is the membership value of x ∈ U. The value represents the degree of x belonging to the fuzzy set U. Thus, a fuzzy set A over U can be represented as in (2).

A={μA(x)∣x∈U,μA(x)∈[0,1]} (2)

The notion that the set of all the fuzzy sets over U was denoted by F(U).

Definition 2.2 [10] Let A be a fuzzy set, where A ∈ F(U). Then, the complement of A is as in (3)

Ac={μAc(x)∣x∈U,μAc(x)=1−μA(x)} (3)

Definition 2.3 [10] Let A, B be the fuzzy set, where A, B ∈ F(U). The membership degree of union of A and B is denoted by μA∪B (x):

μA∪B(x)=max{μA(x),μB(x)}; (4)

for all x ∈ U and μA∪B (x) ∈ [0,1].

Definition 2.4 [10] Let A,B be the fuzzy set, where A,B ∈ F(U). The membership degree of intersection of A and B is denoted by μA∩B(x) :

μA∩B(x)=min{μA(x),μB(x)}; (5)

for all x ∈ U and μA∪B (x) ∈ [0,1].

2.2 Fuzzification

Fuzzification is a process that changes the crisp value to a fuzzy set, or a fuzzy quantity into a crisp quantity [26]. This process uses the membership function and fuzzy rules. The fuzzy rules can be formed as fuzzy implications, such as (x1 is A1) ° (x2 is A2) ° … ° (xn is An); then Y is B, with ° being the operator “AND” or “OR”. B can be determined by combining all antecedent values [14].

2.3 Fuzzy Soft Set (FSS)

Definition 2.5 [12] Let U be an initial universe set and E be a set of parameters. Let P(U) denote the power set of all fuzzy subsets of U, and A ⊆ E. ΓA is called a fuzzy soft set over U, where the function of γA is a mapping given by γA:A→P(U) such that γA(e)=∅ if e∉A.

Here, the function γA is an approximate function of the fuzzy soft set ΓA , and the value γA(e) is called an e-element of a fuzzy soft set for all e∉A . Fuzzy soft set ΓA over U can be represented by the set of ordered pairs:

ΓA={(e,γA(e))|e∈A,γA(e)∈P(U)}. (6)

Note that the set of all the fuzzy soft sets over U was denoted by FS(U).

Example 1 [14] Let a fuzzy soft set ΓA describe the attractiveness of the shirt concerning the given parameters, which the authors are going to wear. U={u1,u2,u3,u4,u5} is the set of all shirts under consideration. P(U) be the collection of all fuzzy subsets of U . Let E = {e1 = “colorful”, e2 = “bright”, e3 = “cheap”, e4 = “warm”}. If A={e1,e2,e3} can be the approximate value of the function fuzzy,

γA (e1) = {0.5|u1, 0.9|u2},

γA (e2) = {1|u1, 0.8|u2, 0.7|u3},

γA (e3) = {1|u2, 1|u5}.

The family {γA (ei); i = 1,2,3} of P(U) is then a fuzzy soft set ΓA . The tabular representation for fuzzy soft set ΓA is shown in Tab. 1.

Table 1: The representation of the fuzzy soft set ΓA

Definition 2.6 [14] Let ΓA, ΓB ∈ FS(U). ΓA is a fuzzy soft subset of ΓB, denoted by ΓA ⊆ ΓB, if γA(e) ⊆ γB(e) for all e ∈ A, A ⊆ B.

Definition 2.7 [14] Let ΓA, ∈ FS(U). The complement of fuzzy soft set ΓA is denoted by ΓAc such that γAc(e)=γAc(e) for all e ∈ A.

Definition 2.8 [14] Let ΓA, ΓB ∈ FS(U). The union of ΓA and ΓB is denoted by ΓA∪B(e) = γA(e) ∪ γB(e) for all e ∈ A ∪ B e∈A∪B.

Definition 2.9 [14] Let ΓA, ΓB ∈ FS(U). The intersection of ΓA and ΓB is denoted by ΓA∩B(e) = γA(e) ∪ γB(e) for all e ∈ A ∪ B e∈A∩B.

Definition 2.10 [14] Let ΓA, ∈ FS(U). The cardinal set of ΓA, denoted by cΓA, can be defined by cΓA = {µ cΓA (e)|e:e ∈ A}, where membership function µ cΓA of cΓA is defined by

cΓA:E→[0,1] (7)

μcΓA(e)=|μA(e)||U|. (8)

|U| is the cardinality of universe U , and

|μA(e)|=∑u∈U⁡μγA(e)(u). (9)

The set of all cardinal sets of fuzzy soft set over U can be denoted by cFS(U).

2.4 Classification

Classification involves learning a target function that maps each collection of data attributes to several groups of predefined classes. The purpose of the classification is to see the class’s target predictions as accurate as possible for each case in the data. The classification algorithm consists of two stages. In the training stage, the classifier is trained on predefined classes or data categories. An X tuple, represented by the n -dimensional vector attribute, X={x1,x2,…,xN} , describes by the measurements made on the tuples with n attributes A1,A2,…,AM . Each tuple belongs to a class, as identified by its attributes. Class attribute labels have discreet, non-consecutive values, and each value acts as a category or class. Next, the second step is Classification. In this step, the built-in classifier was used to classify the data by looking at the classification algorithm’s accuracy in the estimated data testing. The step is to see the accuracy in the first classification; the predicted classifier’s accuracy is estimated. If using a training set to measure the classifier’s accuracy, then the estimate would be optimal because the data used to form the classifier comprise the training set. Therefore, a test set (a set of tuples and their class labels selected randomly from the dataset) were used. Test sets are independent of the training sets because test sets were not used to build a classifier.

2.5 Similarity Measurement

A measurement of similarity or dissimilarity defines the relationships between samples or objects. Similarity measurements were used to determine which patterns, signals, images, or sets are alike. For the similarity measure, the resemblance is more critical when its value increases, but, conversely, for a dissimilarity measurement, the resemblance is more robust when its value decreases [27]. An example of the dissimilarity measure is a distance measure. Measuring similarity or distance between two entities is crucial in various data mining and information discovery tasks, such as classification and clustering. Similarity indicators calculate the degree that various patterns, signals, images, or sets are alike. A few researchers have measured the similarity between fuzzy sets, fuzzy numbers, and vague sets. Recently [14,20,28] studied the similarity measure of the soft set and fuzzy soft set. They explained the similarity between the two generalized fuzzy soft sets as follows.

Let U={x1,x2,…,xn} be the universal set of elements and E={e1,e2,…,em} be the universal set of parameters. Let Fρ and Gδ be two generalized fuzzy soft sets over the parameterized universe (U,E). Hence, Fρ={F(ei),ρ(ei),i=1,2,…,m} and Gδ={G(ei),δ(ei),i=1,2,…,m} . Thus, F={F(ei),i=1,2,…,m} and G={G(ei),i=1,2,…,m} are two families of fuzzy soft sets.

The similarity between F and G is found and denoted by M(F,G). Next, the similarity between the two fuzzy sets ρ and δ is found and denoted by m ( ρ , δ ). Then, the similarity between the two generalized fuzzy soft sets Fρ and Gδ is denoted as S( Fρ , Gδ ) = M(F,G) × m( ρ , δ ).

Therefore, M (F, G) = max Mi (F,G), where:

Mi(F-,G-)=1−∑j=1n⁡|F-ij−G-ij|∑j=1n⁡(F-ij+G-ij). (10)

Furthermore,

m(ρ,δ)=1−∑j=1n⁡|ρi−δi|∑j=1n⁡(ρi+δi). (11)

If we use the universal fuzzy soft set, then ρ=δ=1 and m( ρ , δ ) = 1. Now, the formula for similarity is

S(Fρ,Gδ)=Mi(F-,G-)=1−∑j=1n⁡|F-ij−G-ij|∑j=1n⁡(F-ij+G-ij). (12)

Example 2. In this example, U={x1,x2,x3,x4} and E={e1,e2,e3} . Let there be two generalized fuzzy soft sets over the parameterized universe (U,E) .

Here,

m(ρ,δ)=1−∑i=13⁡|ρi−δi|∑i=13⁡(ρi+δi)=1−0.1+0.1+.051.1+1.5+1.3=0.82

and M1(F,G) ≅ 0.73; M2(F,G) ≅ 0.43; M3(F,G) ≅ 0.50. Thus, max [ Mi(F,G) ] ≅ 0.73.

Hence, the similarity between the two GFSS Fρ and Gδ were S( Fρ , Gδ ) = M(F,G) × m( ρ , δ ) = 0.73 × 0.82 = 0.60 for a universal fuzzy soft set, where ρ=δ=1 and m( ρ , δ ) = 1. Then, the similarity S( Fρ , Gδ ) = 0.73.

2.6 Distance Measurement

In this study, the fuzzy soft set was calculated based on the normalized Hamming distance [25]. We assume fuzzy soft sets (F,A) and (G,B) have the same set of parameters, namely, A = B. The normalized Hamming distance and normalized distance in Fuzzy Soft Set (FSS) are obtained using Eqs. (13) and (14).

d1((F,A),(G,B))=1mn∑i=1m⁡∑j=1n⁡|F(ei)(xj)−G(ei)(xj)| (13)

d2((F,A),(G,B))=1mn(∑i=1m⁡∑j=1n⁡|F(ei)(xj)−G(ei)(xj)|2)12 (14)

Example 3. As in Roy and Maji [12], let U = {u1, u2, u3} be a set with parameters ={a1,a2,a3} . Two FSS (G,A) and (H,A) are represented by Tabs. 2 and 3, respectively.

Using Eqs. (13) and (14), respectively, the normalized Hamming distance and normalized distance in FSS between (G,A) and (H,A) can be calculated as follows:

d1((G,A),(H,A))=13×3∑i=13⁡∑j=13⁡(0.2+0.1+0.1+0.2+0.1+0+0.3+0.1+0.2)≈0.144

and

d2((F,E),(G,E))=13×3∑i=13⁡∑j=13⁡(0.22+0.12+0.12+0.22+0.12+02+0.32+0.12+0.22)12≈0.056

.

Table 2: Fuzzy set (G,A)

Table 3: Fuzzy set (H,A)

Feng and Zheng [13] extended Eq. (14) into a generalized normalized distance in FSS:

d4((F,A),(G,B))=1m∑i=1m⁡[1n∑j=1n⁡|F(ei)(xj)−G(ei)(xj)|p)1p],p∈N+. (15)

If p=1 , then Eq. (13) is reduced to Eq. (14).

From Eq. (14), it can be known that

d′=1n∑j=1n⁡|F(ei)(xj)−G(ei)(xj)| (16)

d′ indicates the distance between the ith parameter of (F,A) and (G,B) , and d1((F,A),(G,B)) indicates the distance among all parameters of (F,A) and (G,B) .

3  Discussion

In this section, the proposed approach and experimental results of the Fuzzy Soft Set Classifier (FSSC) using the normalized Euclidean distance are discussed.

3.1 Proposed Approach

This study proposed a new classification algorithm based on the fuzzy soft set; we call it the Fuzzy Soft Set Classifier (FSSC). This algorithm used the normalized Euclidean distance of similarity between two fuzzy soft sets to classify unlabeled data. Before training and classification steps, we first conducted fuzzification and created a fuzzy soft set.

3.1.1 Training Step

The goal of training the algorithm is to determine the center of each existing class.

Let U={u1,u2,…,uN} , E be the set of parameters, A⊆E,andA={ei,i=1,2,…M} . There are k classes with nr samples in each class, where r=1,2,…,k and ∑r=1k⁡nr=N . Let us say that Cr⊆U is r -class data, and ΓCr, is the set of fuzzy soft sets of the r -class data. Thus, the center set of class Cr is denoted as ΓPCr and be defined as in Eq. (17).

ΓPCr=cΓCr=μcΓCr(ei)=γCr(ei)|Cr|=∑j=1nr⁡μγCr(ei)(uj)nr

Thus,

ΓPCr=1nr∑j=1nr⁡μγCr(ei)(uj),∀ei,i=1,2,…,m,∀Cr,r=1,2,…,k (17)

3.1.2 Classification Step

The new data of the training step results were used to determine the classes in the new data; that is, by measuring the similarity of two sets of fuzzy soft sets acquired in the class center vector and new data.

Given ΓCr,r=1,2,…,k fuzzy soft set of new data ΓG . The formula for measuring similarity:

similaritymeasure=1−disctancemeasure .

We use the generalized normalized Euclidean distance for normalized Euclidean distance of the fuzzy set. With relation to Eq. (15), rather than the normalized Euclidean distance fuzzy set,

q(A,B)=1m∑i=1m⁡[1n∑j=1n⁡|F(ei)(xj)−G(ei)(xj)|p)1p],p∈N+. (18)

The generalized normalized Euclidean distance fuzzy soft set is as follows:

Q∗(ΓPCr,ΓG)=(1m.n(∑i=1m⁡∑j=1nr⁡(γPCr(ei)(xj)−γG(ei)(xj))p))1p, (19)

⇔Q∗(ΓPCr,ΓG)=(1m.1(∑i=1m⁡(γPCr(ei)(x1)−γG(ei)(x1))p))1p, (20)

⇔Q∗(ΓPCr,ΓG)=(1m(∑i=1m⁡(γPCr(ei)(x)−γG(ei)(x))p))1p. (21)

Thus, the formula for the similarity measure becomes:

S∗(ΓPCr,ΓG)=1−Q∗(ΓPCr,ΓG), (22)

⇔S∗(ΓPCr,ΓG)=1−(1m(∑i=1m⁡(γPCr(ei)(x)−γG(ei)(x))p))1p. (23)

After the value the similarity for each class was obtained, the algorithm looked for which class label is appropriate for new data ΓG by determining the maximum similarity.

prediction=arg[maxr=1kS∗(ΓPCr,ΓG)]. (24)

3.2 Experimental Results

We conducted experiments using the University of California (UCI) dataset to assess the accuracy of the proposed data classification method. The dataset samples were divided into training (75% of samples) and test (25% of samples) sets. Experiments were performed in MATLAB R2010a software. Figs. 1–4 show the classification results obtained by our fuzzy soft set method and other baseline techniques.

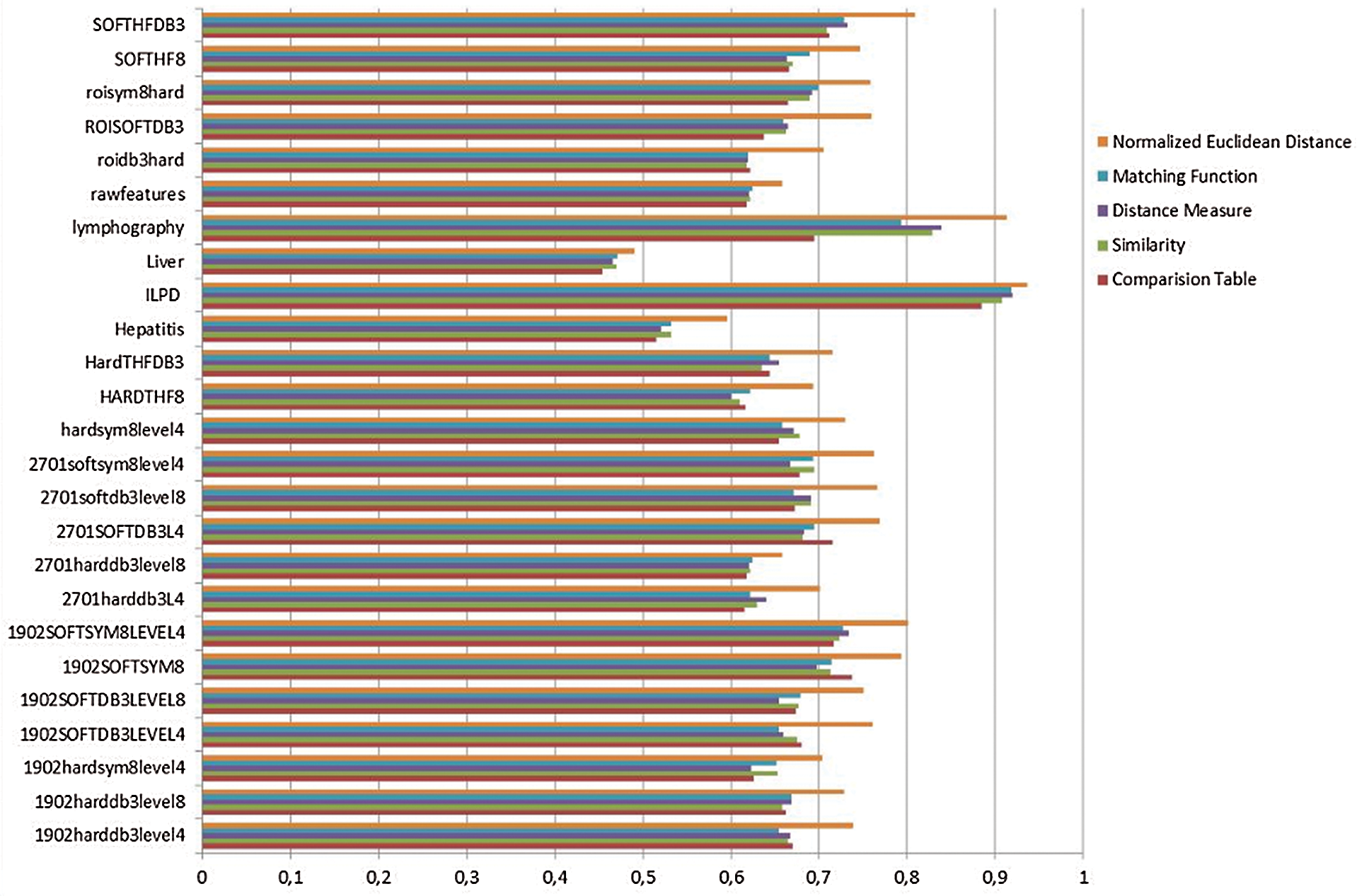
Figure 1: Comparison of accuracy

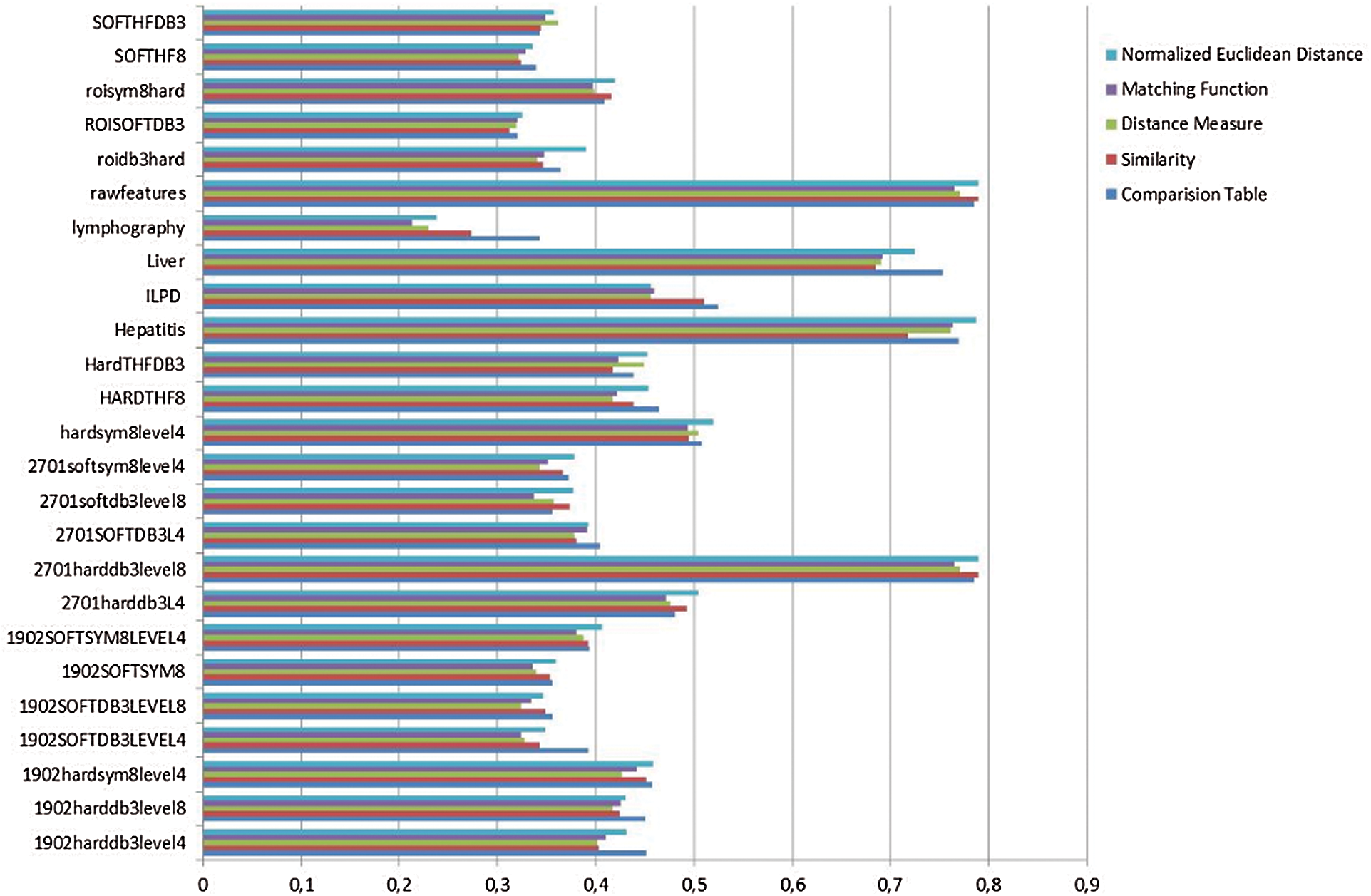
Figure 2: Comparison of precision

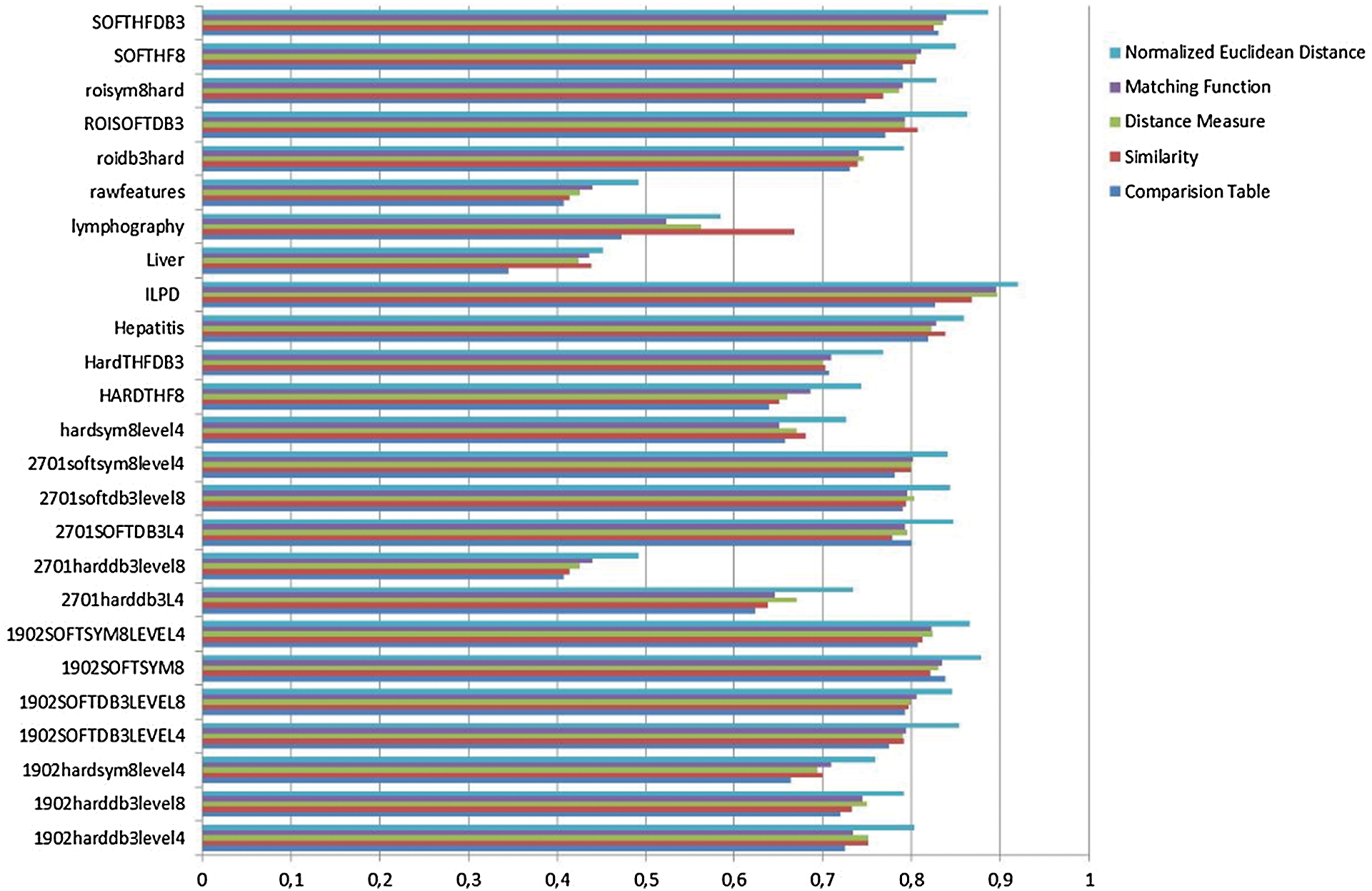
Figure 3: Comparison of recall

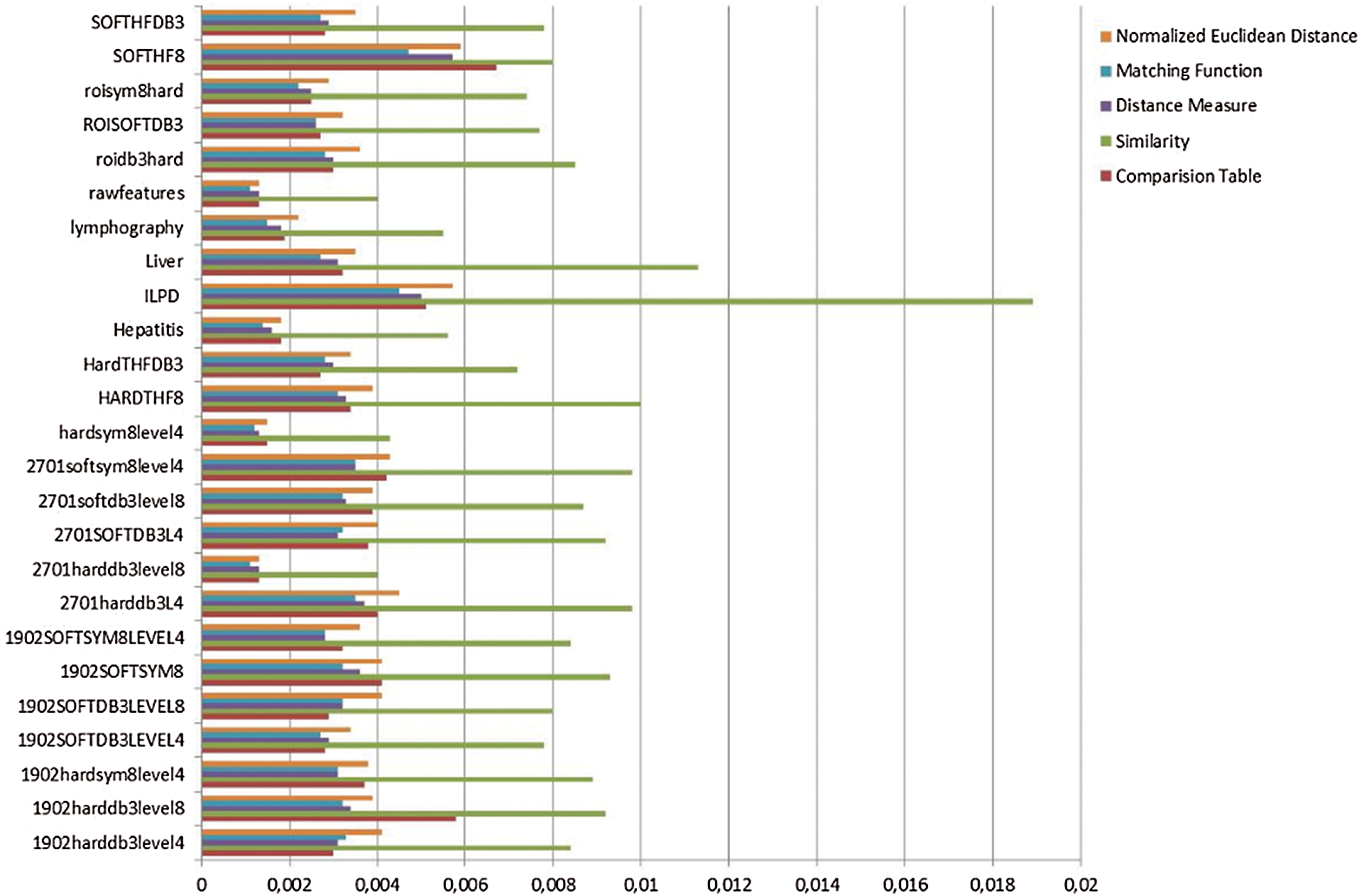
Figure 4: Comparison of computational time

As seen in Fig. 1, calculations using the normalized Euclidean distance method yield the highest accuracy results. Fig. 2 shows that the normalized Euclidean distance method obtains the second-highest precision; the highest precision is obtained by the comparison table method in MatLab.

Fig. 3 shows that the normalized Euclidean distance method produces the highest recall results, whereas Fig. 4 illustrates that the method has the highest computation time.

The fastest sequence is matching function, distance measure, similarity, normalized Euclidean distance. Comparisons are shown in Tab. 4.

Table 4: Improvement of accuracy and recall

4  Conclusions

In this study, a new classification algorithm based on fuzzy soft set theory was proposed. Experimental results show that the normalized Euclidean distance method improves accuracy by 10.3436% and increases by 6.9723%, compared to baseline techniques. We also find that all similarity measurements proposed in this paper are reasonable.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no interest in reporting regarding the present study.

References

 1.  J. Han, M. Kamber and J. Pei. (2012). “13 - Data mining trends and research rontiers BT - data mining,” In: J. Han (ed.The Morgan Kaufmann Series in Data Management Systems, 3rd edition, Boston: Morgan Kaufmann, pp. 585–631. [Google Scholar]

 2.  Y. Cheng, K. Chen, H. Sun, Y. Zhang and F. Tao. (2018). “Data and knowledge mining with big data towards smart production,” Journal of Industrial Information Integration, vol. 9, no. 9, pp. 1–13. [Google Scholar]

 3.  M. Azarafza, M. Azarafza and H. Akgün. (2021). “Clustering method for spread pattern analysis of corona-virus (COVID-19) infection in Iran,” Journal of Applied Science, Engineering, Technology, and Education, vol. 3, no. 1, pp. 1–6. [Google Scholar]

 4.  D. E. Lumsden, H. Gimeno and J.-P. Lin. (2016). “Classification of dystonia in childhood,” Parkinsonism & Related Disorders, vol. 33, pp. 138–141. [Google Scholar]

 5.  M. Zheng. (2016). “Classification and pathology of lung cancer,” Surgical Oncology Clinics, vol. 25, no. 3, pp. 447–468. [Google Scholar]

 6.  A. Ojugo and O. D. Otakore. (2021). “Forging an optimized bayesian network wodel with selected parameters for detection of the coronavirus in Delta State of Nigeria,” Journal of Applied Science, Engineering, Technology, and Education, vol. 3, no. 1, pp. 37–45. [Google Scholar]

 7.  X. Li and Y. Tang. (2014). “Two-dimensional nearest neighbor classification for agricultural remote sensing,” Neurocomputing, vol. 142, no. 10–12, pp. 182–189. [Google Scholar]

 8.  Y. Tang and X. Li. (2016). “Set-based similarity learning in subspace for agricultural remote sensing classification,” Neurocomputing, vol. 173, no. 10–12, pp. 332–338. [Google Scholar]

 9.  B. Handaga, T. Herawan and M. M. Deris. (2012). “FSSC: An algorithm for classifying numerical data using fuzzy soft set theory,” International Journal of Fuzzy System Applications (IJFSA), vol. 2, no. 4, pp. 29–46. [Google Scholar]

10. L. A. Zadeh. (1965). “Fuzzy sets,” Information and Control, vol. 8, no. 3, pp. 338–353. [Google Scholar]

11. D. Molodtsov. (1999). “Soft set theory—first results,” Computers & Mathematics with Applications, vol. 37, no. 4–5, pp. 19–31. [Google Scholar]

12. A. R. Roy and P. K. Maji. (2007). “A fuzzy soft set theoretic approach to decision making problems,” Journal of Computational and Applied Mathematics, vol. 203, no. 2, pp. 412–418. [Google Scholar]

13. P. K. Maji, A. R. Roy and R. Biswas. (2002). “An application of soft sets in a decision making problem,” Computers & Mathematics with Applications, vol. 44, no. 8–9, pp. 1077–1083. [Google Scholar]

14. P. Majumdar and S. K. Samanta. (2010). “Generalised fuzzy soft sets,” Computers & Mathematics with Applications, vol. 59, no. 4, pp. 1425–1432. [Google Scholar]

15. P. K. Maji, R. Biswas and A. R. Roy. (2001). “Fuzzy soft sets,” Journal of Fuzzy Mathematics, vol. 9, no. 3, pp. 589–602. [Google Scholar]

16. B. Ahmad and A. Kharal. (2009). “On fuzzy soft sets,” Advances in Fuzzy Systems, vol. 2009, pp. 586507. [Google Scholar]

17. H. Aktaş and N. Çağman. (2007). “Soft sets and soft groups,” Information Sciences, vol. 177, no. 13, pp. 2726–2735. [Google Scholar]

18. A. Rehman, S. Abdullah, M. Aslam and M. S. Kamran. (2013). “A study on fuzzy soft set and its operations,” Annals of Fuzzy Mathematics and Informatics, vol. 6, no. 2, pp. 339–362. [Google Scholar]

19. Y. Celik, C. Ekiz and S. Yamak. (2013). “Applications of fuzzy soft sets in ring theory,” Annals of Fuzzy Mathematics and Informatics, vol. 5, no. 3, pp. 451–462. [Google Scholar]

20. P. Majumdar and S. K. Samanta, “On similarity measures of fuzzy soft sets,” International Journal of AdvanceSoft Computing and Applications, vol. 3, no. 2, pp. 1–8, 2011. [Google Scholar]

21. D. K. Sut. (2012). “An Application of similarity of fuzzy soft sets in decision making,” Computer Technology and Application, vol. 3, no. 2, pp. 742–745. [Google Scholar]

22. D. P. Rajarajeswari and P. Dhanalakshmi. (2012). “An application of similarity measure of fuzzy soft set based on distance,” IOSR Journal of Mathematics, vol. 4, no. 4, pp. 27–30. [Google Scholar]

23. H. Li and Y. Shen. (2012). “Similarity measures of fuzzy soft sets based on different distances,” in 2012 Fifth International Symposium on Computational Intelligence and Design. Proceedings: IEEE Computer Society (IEEE, 6401247). Vol. 1. Hangzhou, China, pp. 527–529. [Google Scholar]

24. N. H. Sulaiman and D. Mohamad. (2012). “A set theoretic similarity measure for fuzzy soft sets and its application in group decision making,” in 20th National Symposium on Mathematical Sciences: Research in Mathematical Sciences: A Catalyst for Creativity and Innovation. Proceedings: AIP Conference, Putrajaya, Malaysia, vol. 1522, pp. 237–244. [Google Scholar]

25. Q. Feng and W. Zheng. (2014). “New similarity measures of fuzzy soft sets based on distance measures,” Annals of Fuzzy Mathematics and Informatics, vol. 7, no. 4, pp. 669–686. [Google Scholar]

26. L. Baccour, A. M. Alimi and R. I. John. (2014). “Some notes on fuzzy similarity measures and application to classification of shapes, recognition of arabic sentences and mosaic,” IAENG International Journal of Computer Science, vol. 41, no. 2, pp. 81–90. [Google Scholar]

27. S. Chowdhury and R. Kar. (2020). “Evaluation of approximate fuzzy membership function using linguistic input-an approached based on cubic spline,” JINAV: Journal of Information and Visualization, vol. 1, no. 2, pp. 53–59. [Google Scholar]

28. P. Majumdar and S. K. Samanta. (2008). “Similarity measure of soft sets,” New Mathematics and Natural Computation, vol. 04, no. 01, pp. 1–12. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.