DOI:10.32604/csse.2021.015619
| Computer Systems Science & Engineering DOI:10.32604/csse.2021.015619 | |
| Article |
New Fuzzy Fractional Epidemic Model Involving Death Population
1Department of Mathematics, Sri Ramakrishna Mission Vidyalaya College of Arts and Science, Coimbatore, 641020, India
2Department of Mathematics, Cankaya University, Ankara, 06530, Turkey
3Institute of Space Sciences, Magurele-Bucharest, Romania
4Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, Taiwan
*Corresponding Author: Dumitru Baleanu. Email: dumitru@cankaya.edu.tr
Received: 10 November 2020; Accepted: 18 December 2020
Abstract: In this research, we propose a new change in classical epidemic models by including the change in the rate of death in the overall population. The existing models like Susceptible-Infected-Recovered (SIR) and Susceptible-Infected-Recovered-Susceptible (SIRS) include the death rate as one of the parameters to estimate the change in susceptible, infected and recovered populations. Actually, because of the deficiencies in immunity, even the ordinary flu could cause death. If people’s disease resistance is strong, then serious diseases may not result in mortalities. The classical model always assumes a closed system where there is no new birth or death, no immigration or emigration, while in reality, such assumptions are not realistic. Moreover, the classical epidemic model does not report the change in population due to death caused by a disease. With this study, we try to incorporate the rate of change in the population of death caused by a disease, where the model is framed to reduce the curve of death along with the susceptible and infected populations. Since the rate of change turned out to be very small, we have tried to estimate it fractionally. Thus, the model is defined using fuzzy logic and is solved by two different methods: a Laplace Adomian decomposition method (LADM) and a differential transform method (DTM) for an arbitrary order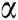 
. To test its accuracy, we compared the results of both DTM and LADM with the fourth-order Runge-Kutta method (RKM-4) at 
.
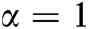Keywords: Susceptible-infected-recovered-dead; epidemic model; fractional-order; differential transformation method; Laplace Adomian decomposition method; Fourth-order; Runge-Kutta method
The present study on modeling epidemics like infectious diseases is an interesting topic in the fields of mathematical biology. The medical world is still struggling a lot to provide medicines that can cure deadly diseases and prevent recurring infections. For example, the Human Immunodeficiency Virus (HIV) disease already found is still being treated instead of being cured. The epidemic models are the pioneers of all mathematical models in studying the growth of diseases. Epidemics are the root of various diseases. The existing models in epidemiology are close-ended where no new birth or death occurs. Basically, a patient can die with or without the symptoms of a disease. So death is not only a parameter to make changes in susceptible, and infected. It is also subject to change depending on immunity, the dosage of medicine, age, etc. So, we are interested to propose a new model in epidemiology called Susceptible-Infected-Recovered-Dead (SIRD). In this paper, such a model is suggested and we convert it into a fuzzy fractional model. These models are studied with three methods of the same order to find the best out of them and the used methods are all fourth-order in Laplace Adomian decomposition method (LADM), differential transform method (DTM), and fourth-order Runge-Kutta method (RKM-4). In 1965 Zadeh introduced the fuzzy sets [1]. Bukley et al. [2] proposed the fuzzy differential equations in the year 2000. Abbasbandy [3] has extended Newton’s method for a system of nonlinear equations by modified the ADM in 2005. Allen [4] in 2007 studied an introduction to mathematical biology. In the same year, Makinde [5] suggested a SIR epidemic model with constant vaccination within ADM. Ongun [6] has applied the Laplace Adomian decomposition method for solving a model for HIV infection of CD4+T cells in 2011. Arafa et al. [7] studied the solutions of the fractional order model of Childhood disease with constant vaccination strategy in 2012. Farman et al. [8] analyzed and numerically found the solution of SEIR epidemic model of measles with non-integer time- fractional derivatives by using LADM in 2018. Moustafa et al. [9] and Palese et al. [10] mathematically solved the influenza type problems. Recently, many authors showed interest to study fractional-order mathematical models in HIV, Tuberculosis (TB), and cancer [11–13]. After the classical epidemic model [14], many research papers arrived at the advanced epidemic models. Authors of manuscripts [15–19] have regularly treated fuzzy differential equations numerically. Numerical solutions of epidemic models are studied by many authors [20–25]. Recently, many researchers discussed the coronavirus, a pandemic disease [26–30].
This manuscript consists of 8 sections. In Section 2, we are forming a new epidemic model. In Section 3, we are discussing the basic definitions and describing the parameters involved in solving this new model. In Section 4, we are analyzing the equilibrium and stability of the presented model. In Section 5, we are analytically finding the solution of the model by fourth-order DTM and fourth-order LADM. In Section 6, we are using the RKM-4 to find the numerical solution of the model. Section 7 presents numerical simulations of our study. In Section 8, the study of the whole paper was concluded.
2 SIRD-Epidemic Model-Formulation
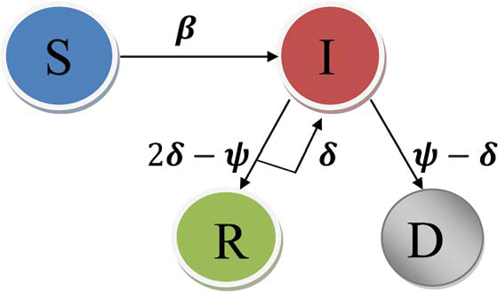
Figure 1: Model formulation
Let us consider a fuzzy fractional epidemic model-SIRD (See, Fig. 1) under Caputo derivative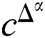 
, where ‘S’ denotes Susceptible, ‘I’ denotes the Infected, ‘R’ denotes the recovered hosts, and ‘D’ denotes death hosts. The model is considered to be close-ended i.e., no new birth or death can occur. So, we shall assume the following information as the background of the model. Let us consider an unknown disease spread in a place where it holds few susceptible, infected, recovered, and dead cases in the overall population. Also, at the stage of observation, it is noted that few people died out because of the severity of the disease, due to lack of immunity, or due to lack of medication. We also assert that no new people further died or were further assumed to be susceptible. The model is also framed to improve on the classical epidemic model SIR framed by Kermack-Mckendrick [14]. The classical epidemic model does not change for susceptible, infected, and dead cases (SID). For any common flu or severe disease, it is quite natural that few people can recover, few people can die and few recovered people may become infected. Recovered is also a part of susceptibility. Both recovered and dead people are free from infection, but the recovered people may become infected again, or even die naturally, whereas the dead people would not become infected, susceptible or recovered. With these ideas in mind the following model is assumed:
Throughout the paper, D represents the death population and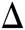 
represents d/dt.
3 Basic Definitions and Parameters
This section consists of some basic results in fractional differential equation in terms of fuzzy.
Definition 3.1: The fuzzy Caputo fractional order derivative of a function f on the interval [0,t] is defined as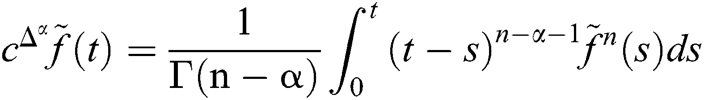 
, where 
and 
represents the integer part of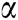 
.
Definition 3.2: The Laplace transform of fuzzy Caputo fractional derivative is given to b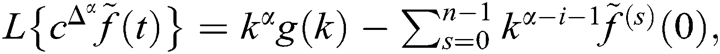e 
where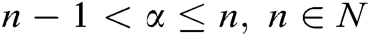
. For arbitrary 
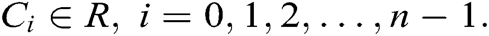where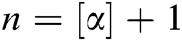 
and 
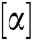represents the integer part of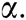 
The system of differential equations (1) is rewritten as the fractional system of differential equations (FDE) which is given as
It becomes a fuzzy fractional-order system of differential equation using the ideas given in preliminaries
where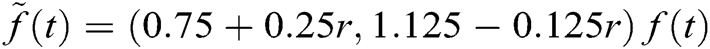 
is the fuzzy number with 
.
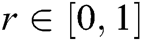The initial conditions are satisfied implying that the total population is constant with the size N.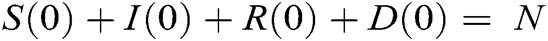 
. Here we shall take the initial populations as
The parameters are defined as follows:
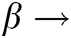The rate at which the susceptible become infected = 0.0006
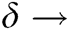The rate at which the infectious become recovered = 0.03
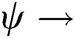The rate at which the infectious become dead because of disease = 0.02
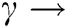The rate at which natural death occurs in each population = 0.01
4 Equilibrium Points and Stability Analysis
Calculation of Basic Reproduction Number (R0):
Basic reproduction number or ratio is defined as the number of secondary infections produced by an infected single individual during the total epidemic period. This number is calculated from the rate of change in the population of infected people when the time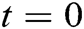 
. We found that, 
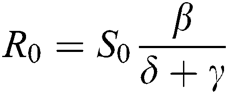. Suppose the critical value 
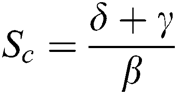then if 
the disease will not survive and if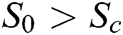 
then there is an epidemic. Also, if 
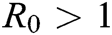, the disease will spread and for 
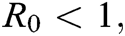the disease will die out.
Equilibrium Points:
In Eq. (3), we take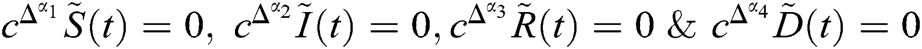 
. i.e.,
From Eqs. (4)–(7) we get the disease-free equilibrium point as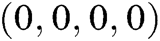 
and disease dependant equilibrium point as 
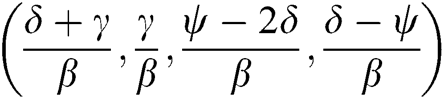. i.e., 
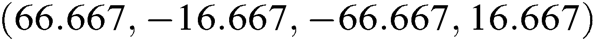is the disease dependant equilibrium point.
Theorem 1:
When all the real values of complex or non-complex eigenvalues of the linearized form of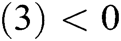 
then the model is asymptotically stable.
Proof:
Let us first linearize the model (3) in the form of Jacobian matrix and name it as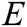
.
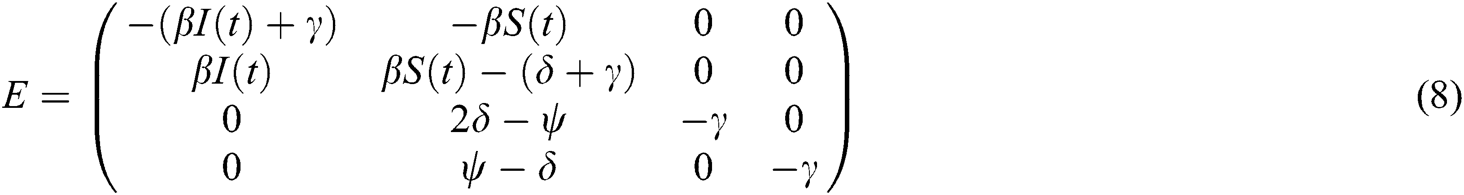
After substituting all values of all parameters we get, the characteristic polynomial of a matrix is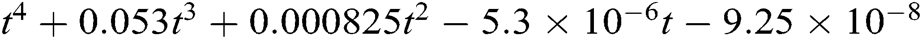 
. Equating the above polynomial to zero we have found the eigenvalues as 
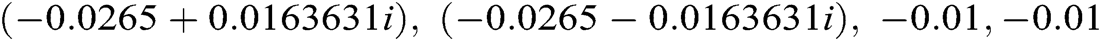. Since eigenvalues have the negative real parts we can conclude the system (3) is asymptotically stable.
5 Analytical Solution of the SIRD Model
5.1 Differential Transform Method (DTM)
For finding the analytical solution, we use DTM similar to [8]. The idea of differential transformation was derived from the Taylor series expansion. In this method, given the system of differential equations and the respected initial conditions are transformed into the system of recurring equations and at last, these equations become the Taylor series expansion about the point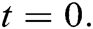 
The differential transform of the function 
when 
can be defined as 
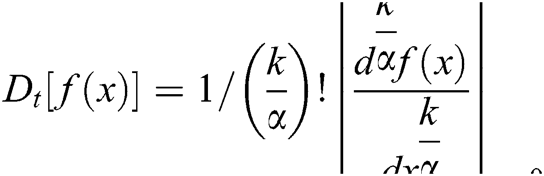. Also if 
, 
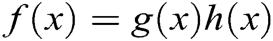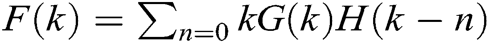. Now for 
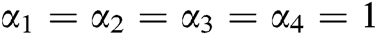. The system (3) becomes
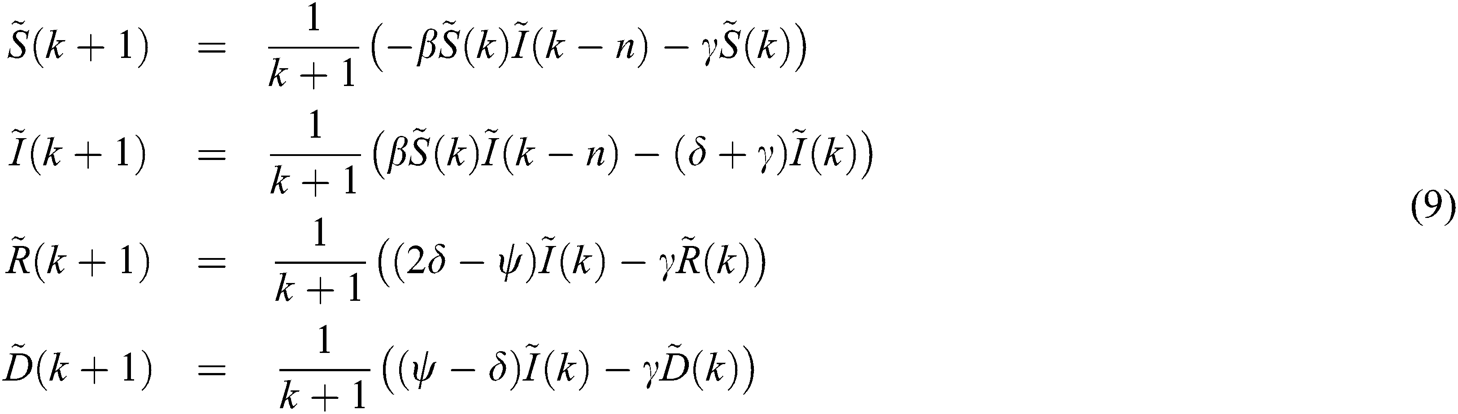
At 
, the inverse differential transform of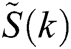 
, 
, 
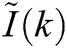and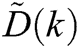 
are given by
, 
, 
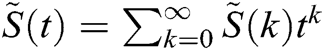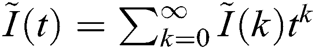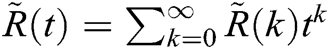and 
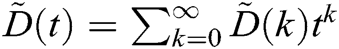. For the model (3), the solution obtained by DTM up to order 4 is
5.2 Laplace Adomian Decomposition Method (LADM)
In order to find the analytical solution of the new fractional epidemic model, we are using the second method called the LADM similar to [11], and the values of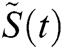 
, 
, 
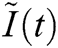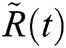, and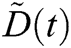 
are solved by the following procedures.
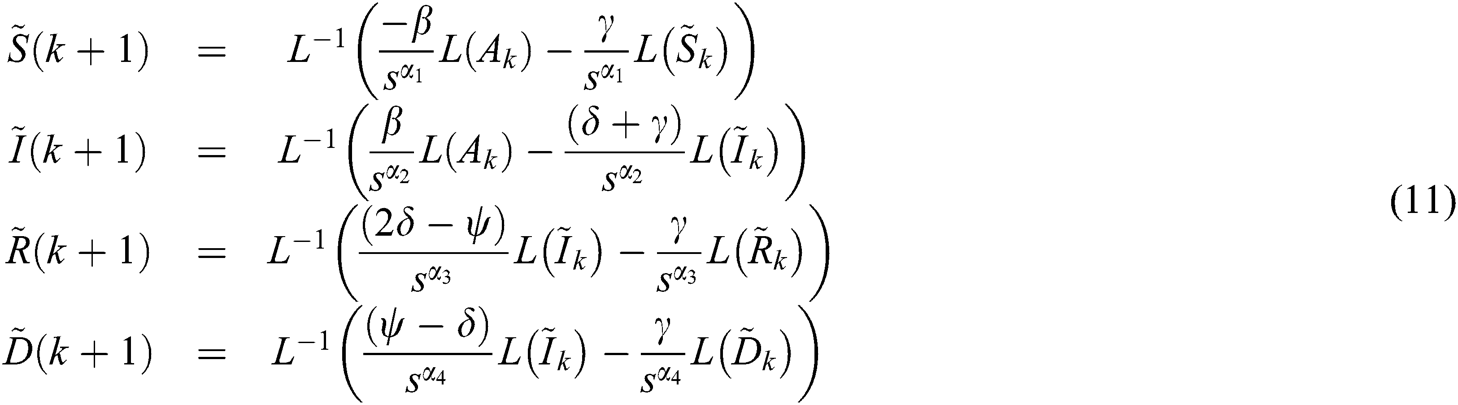
where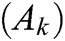
is an Adomian polynomial defined by 
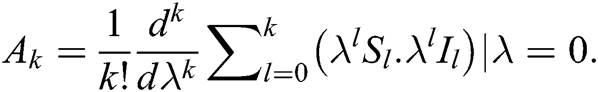i.e.,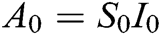 
, 
, 
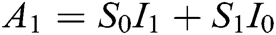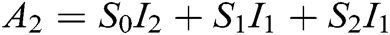, and so on. Also, 
, 
, 
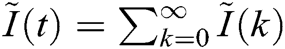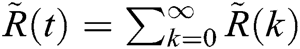and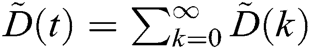 
. For model Eq. (3), after assigning the values to all the parameters, the solution obtained by LADM up to order 4 defining for 
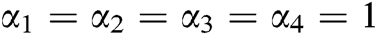is found as same as the solution obtained by DTM
6 Numerical Solution of the Suspected Infected Recovered and Dead (SIRD) Model by Runge-Kutta Method of Order 4 (RKM-4)
In this section, we are using RKM-4 with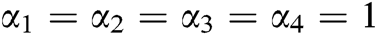 
. We are finding the values of 
, 
, 
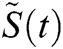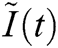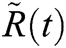and 
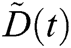at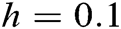 
for the best approximation. For 
,
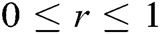We evaluate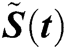 
, 
, 
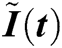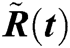and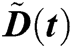 
:
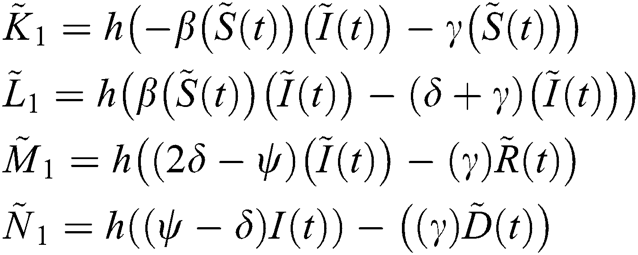
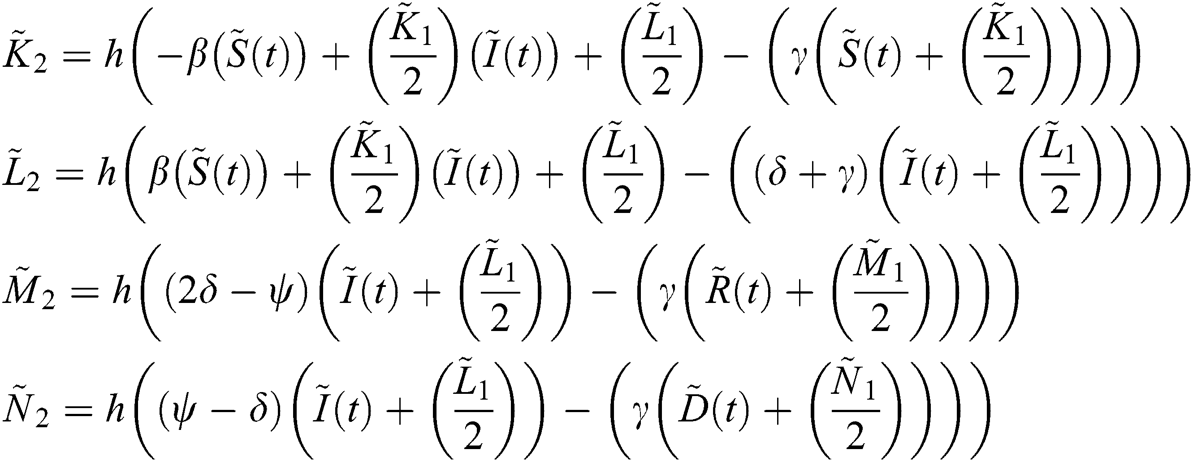
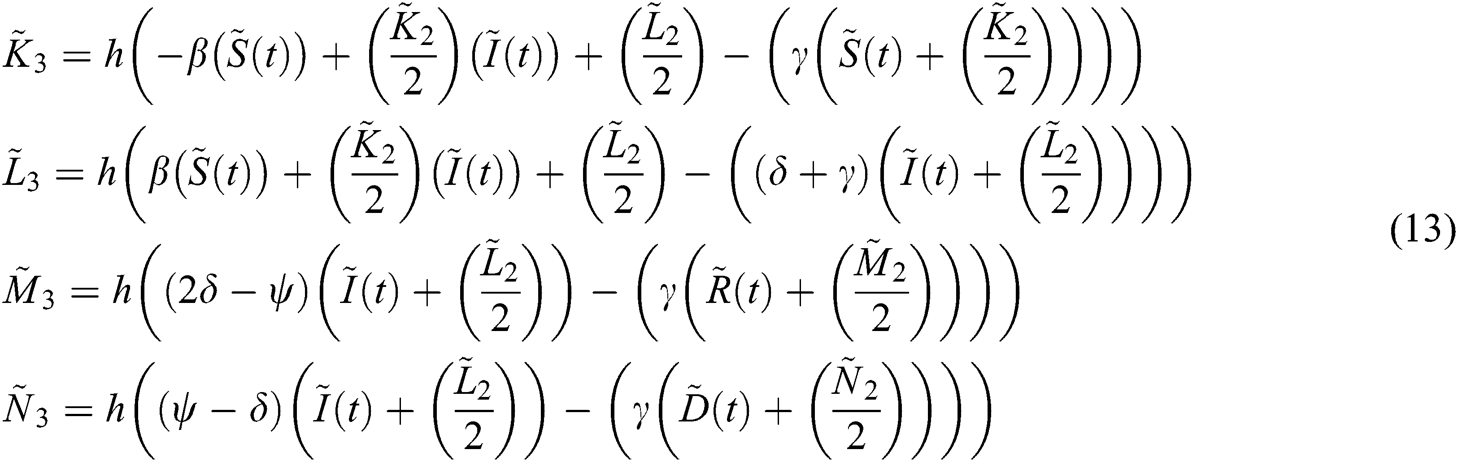
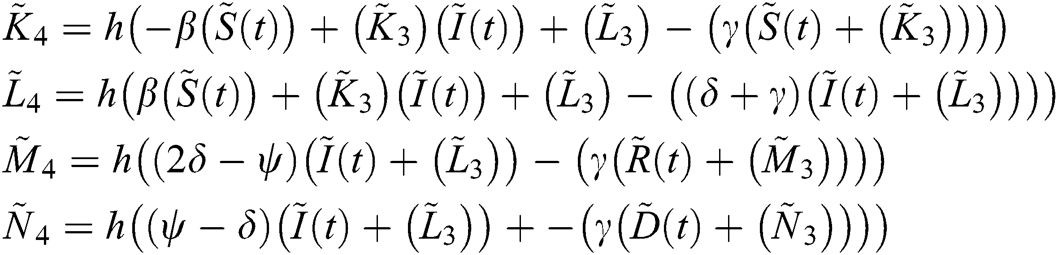
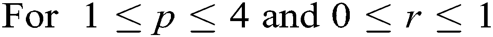
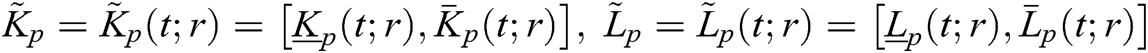
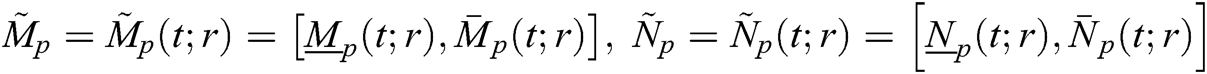
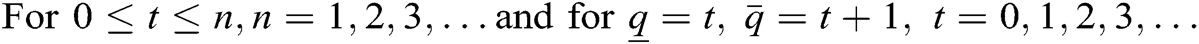
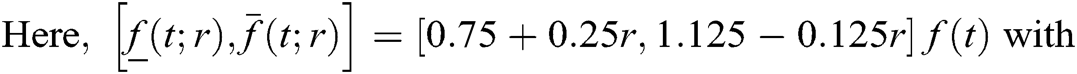
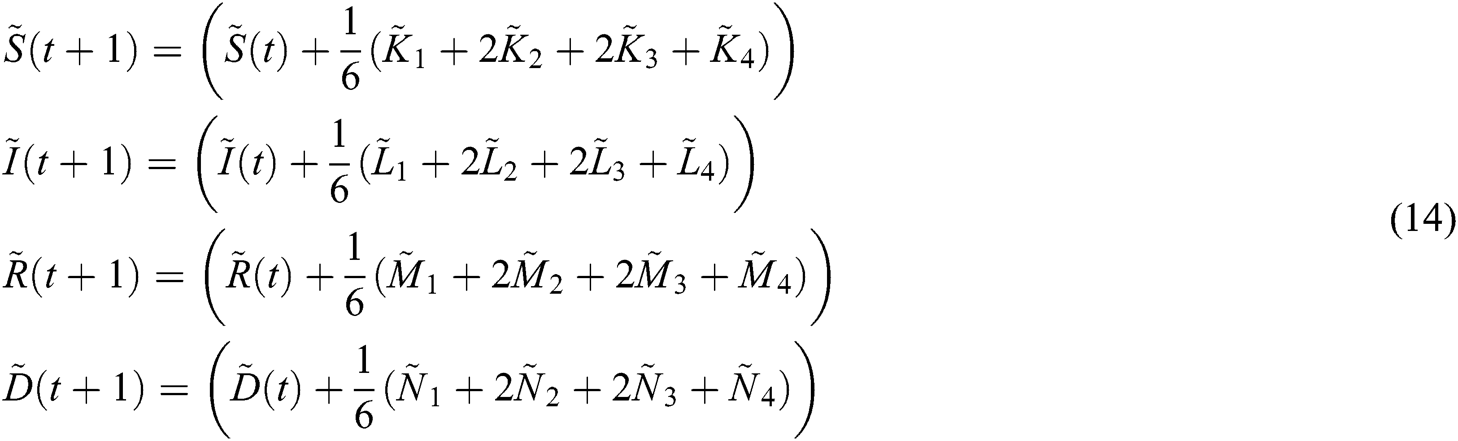
The relationship between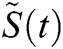
, 
, 
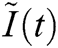and 
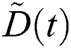at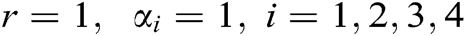 
for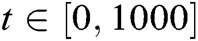 
for the fuzzy model Eq. (3) is given in Fig. 2.
Table 1: Susceptible population (S)
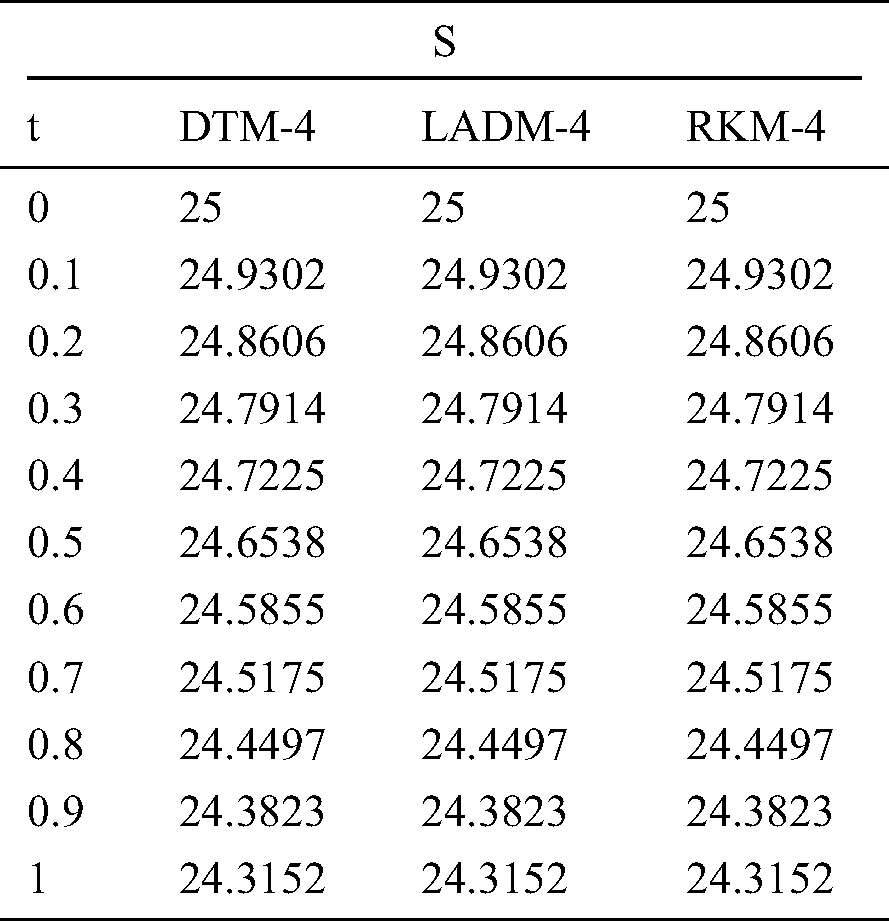
Table 2: Infected population (I)
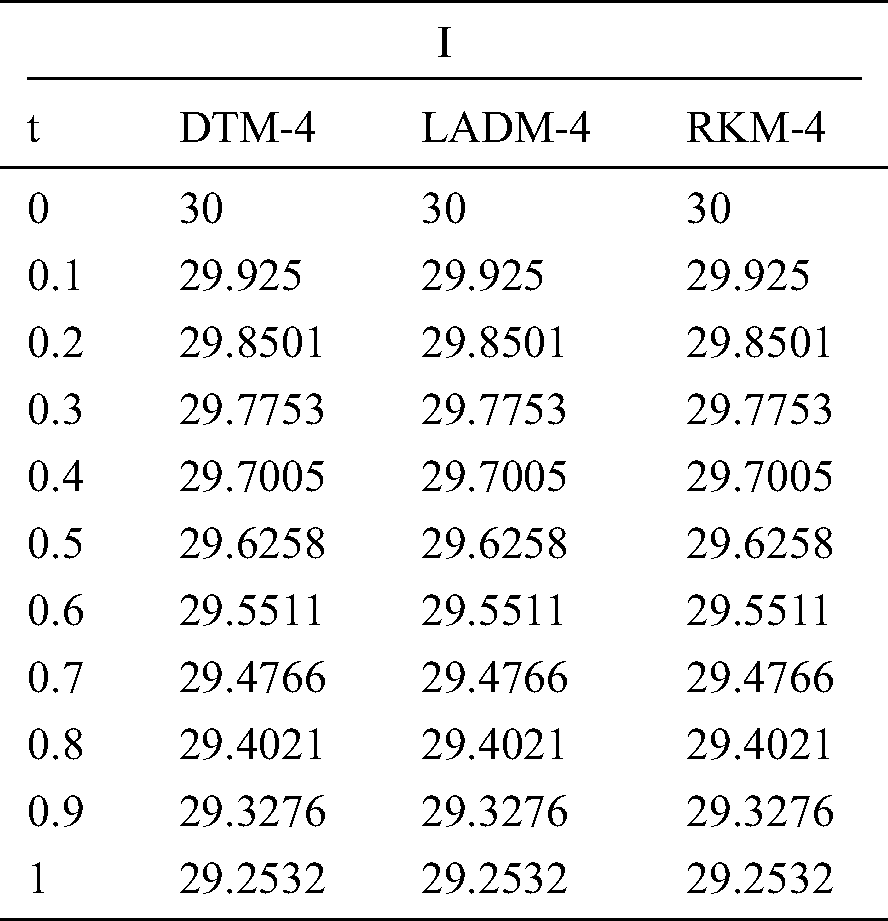
Table 3: Recovered population (R)
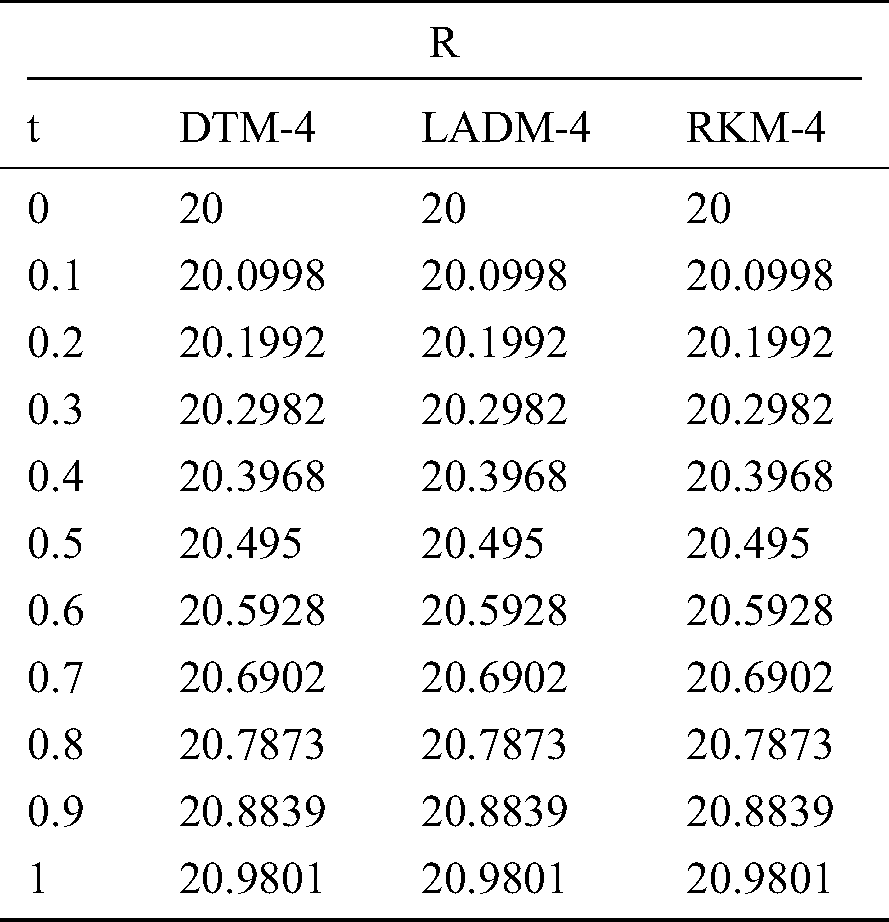
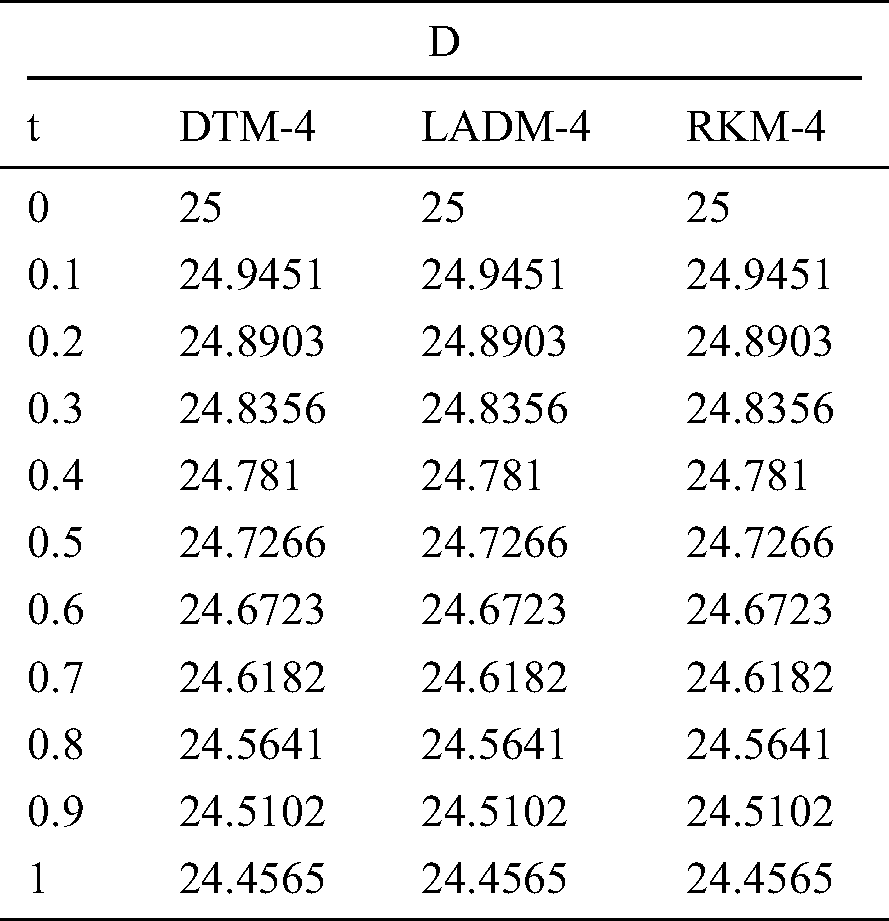
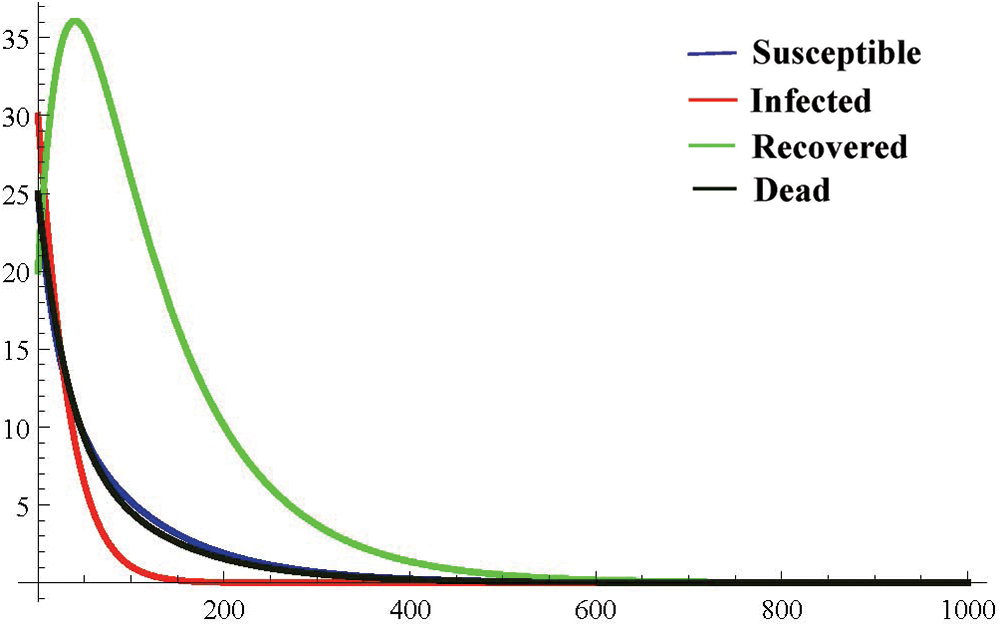
Figure 2: Fuzzy fractional SIRD model
Table 5: Fractional susceptible population (S)
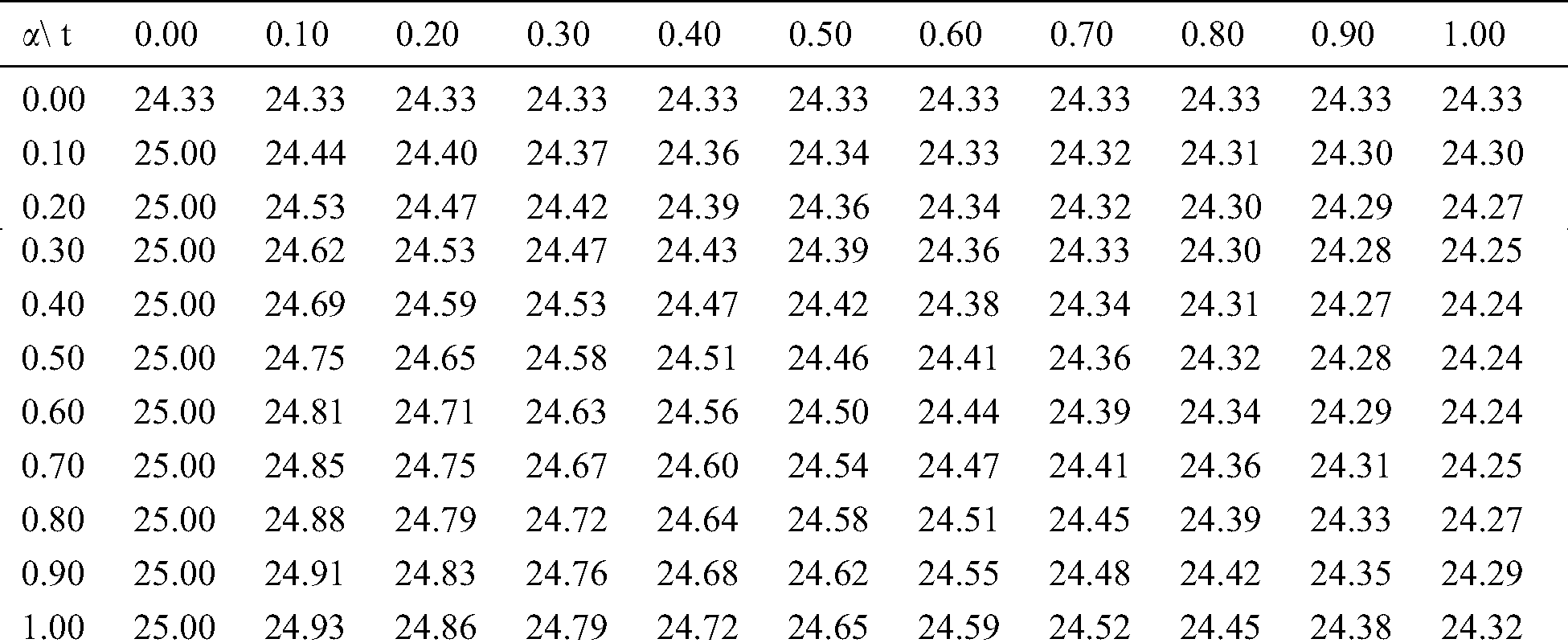
Table 6: Fractional infected population (I)
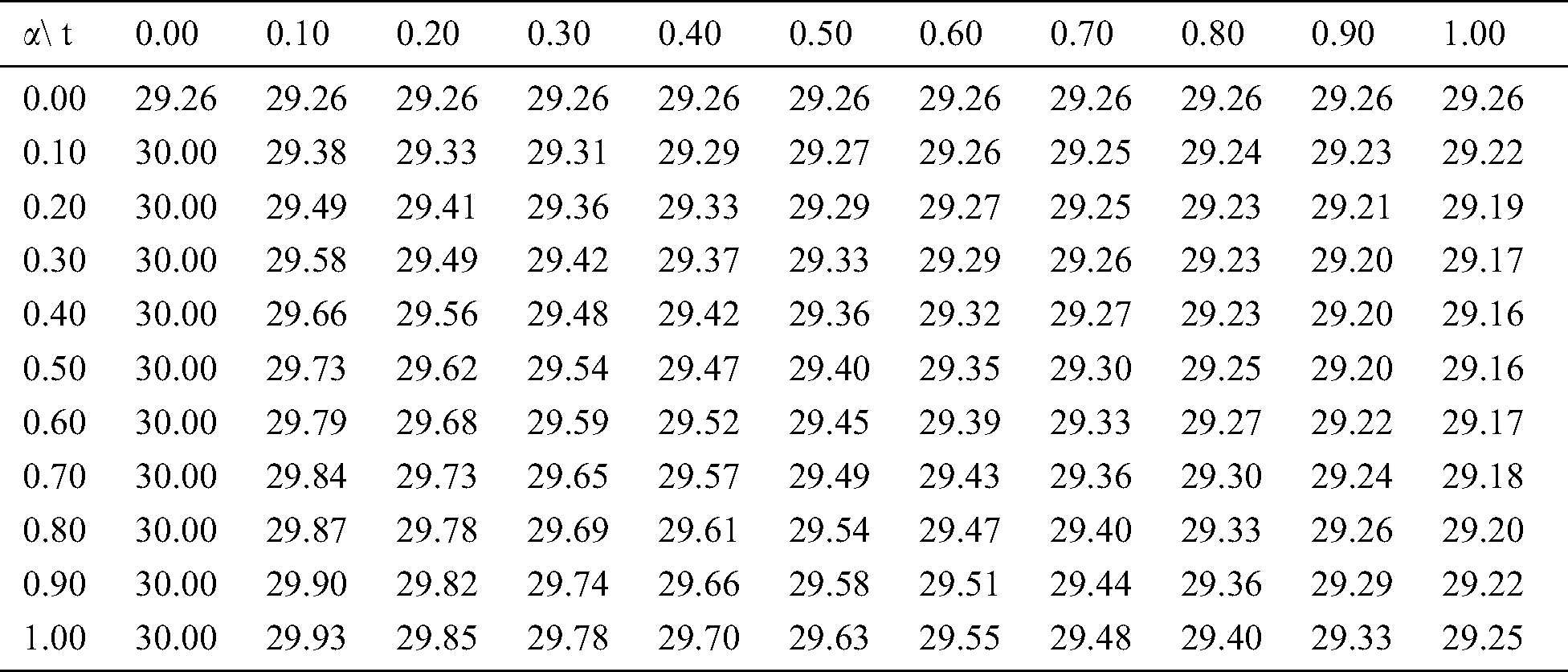
Table 7: Fractional recovered population (R)
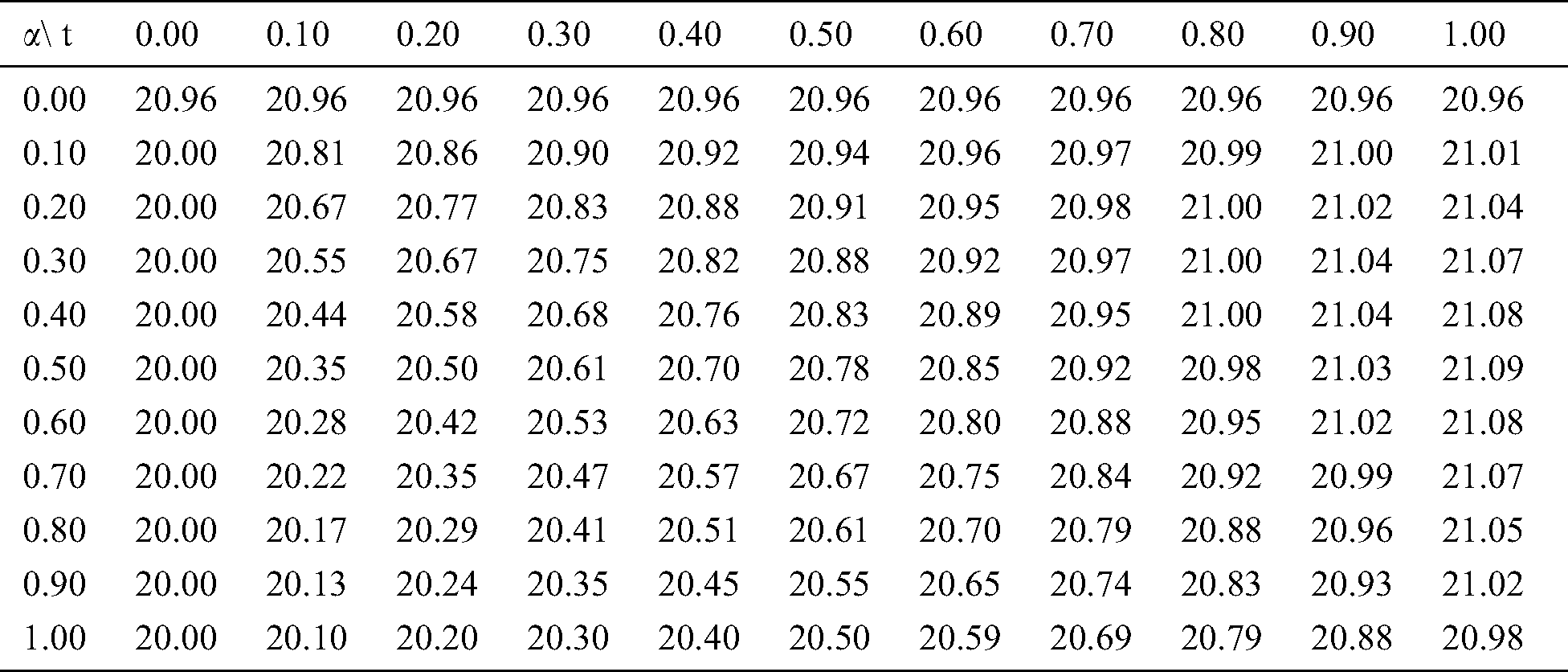
Table 8: Fractional dead population (D)
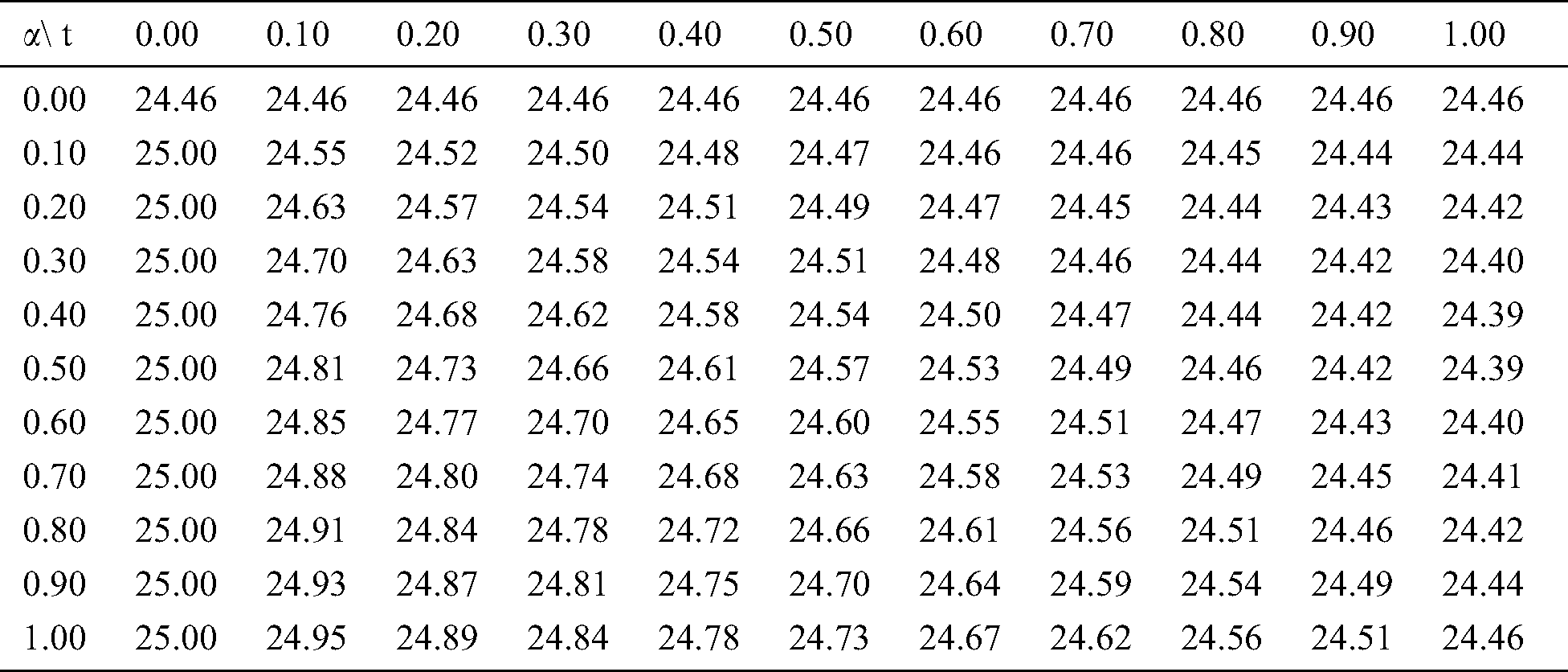
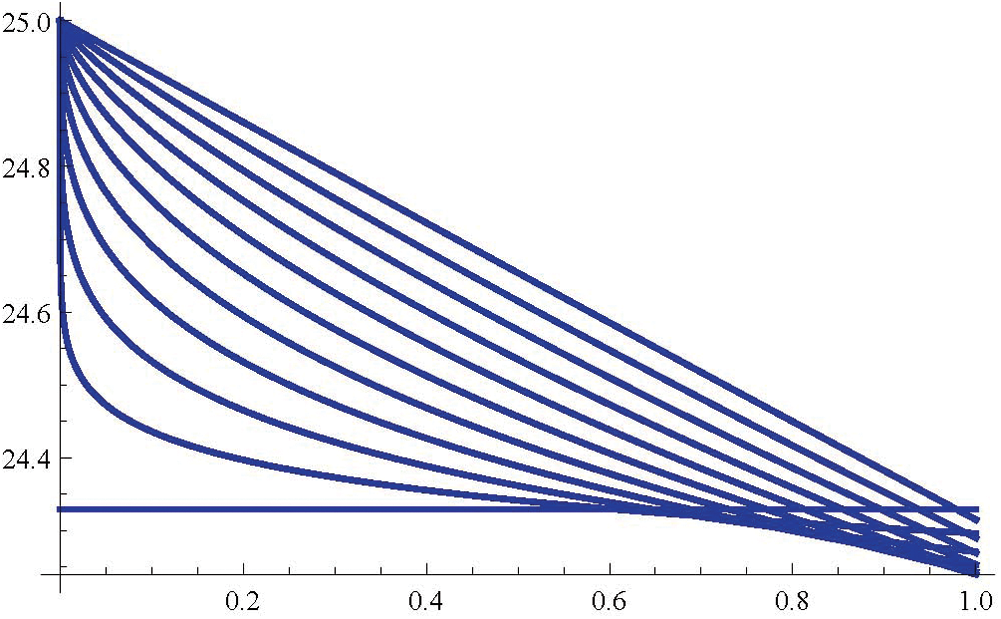
Figure 3: Fractional susceptible (S)
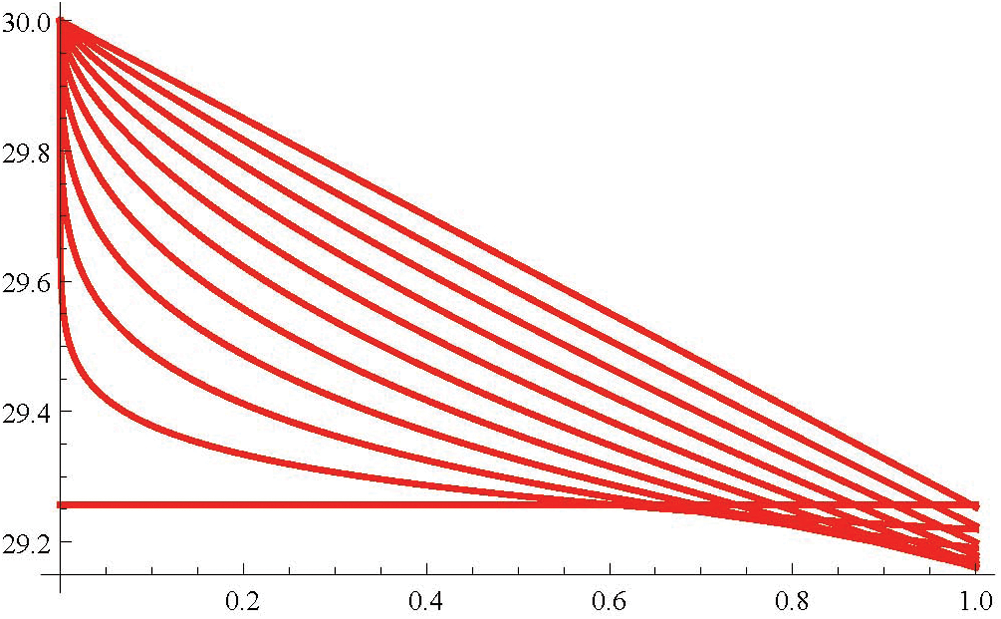
Figure 4: Fractional infected (I)
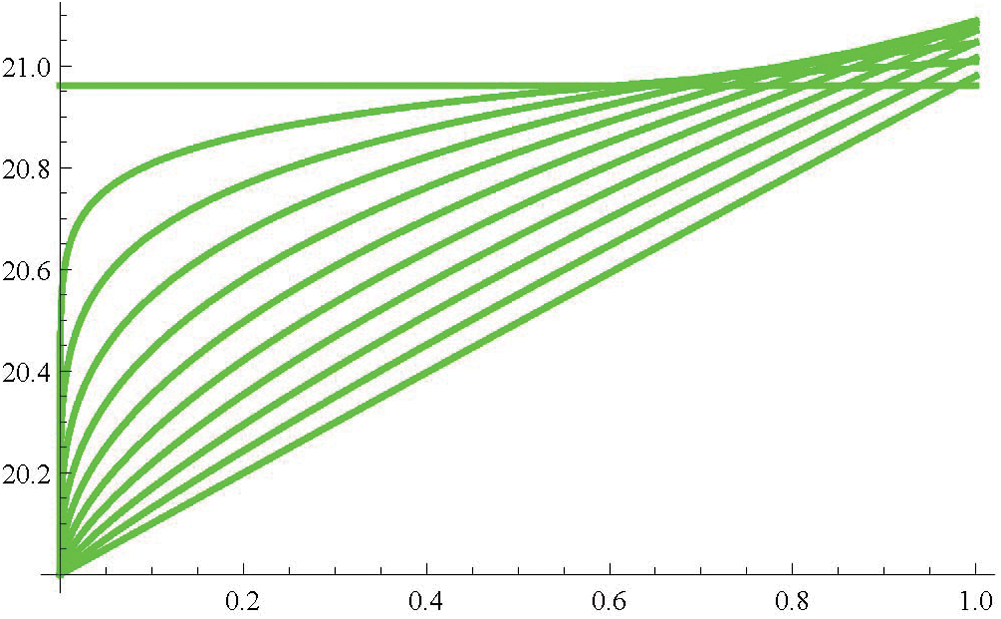
Figure 5: Fractional recovered (R)
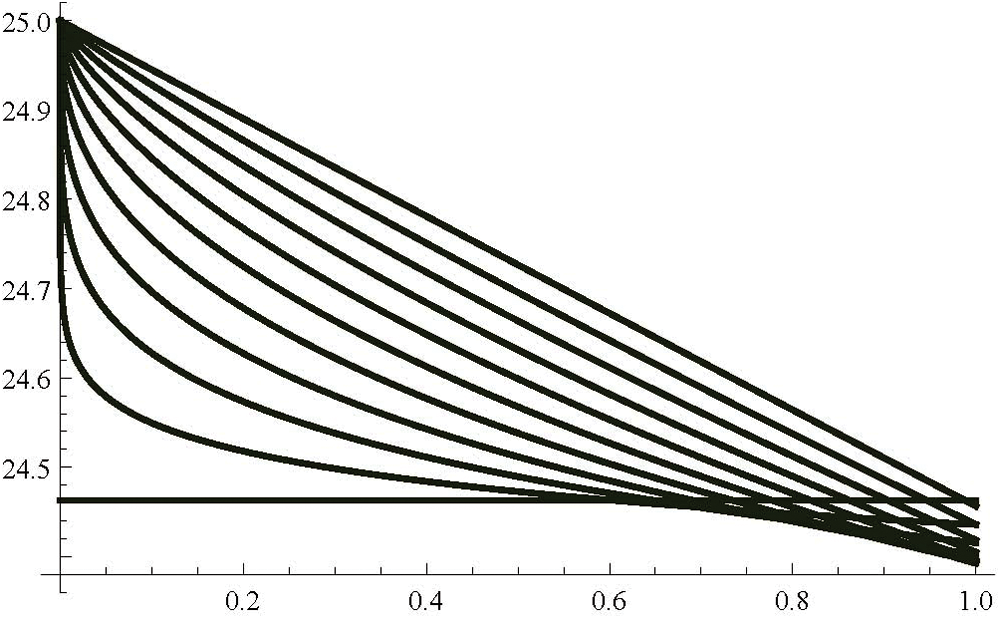
Figure 6: Fractional dead (D)
Table 9: Fuzzy fractional epidemic model
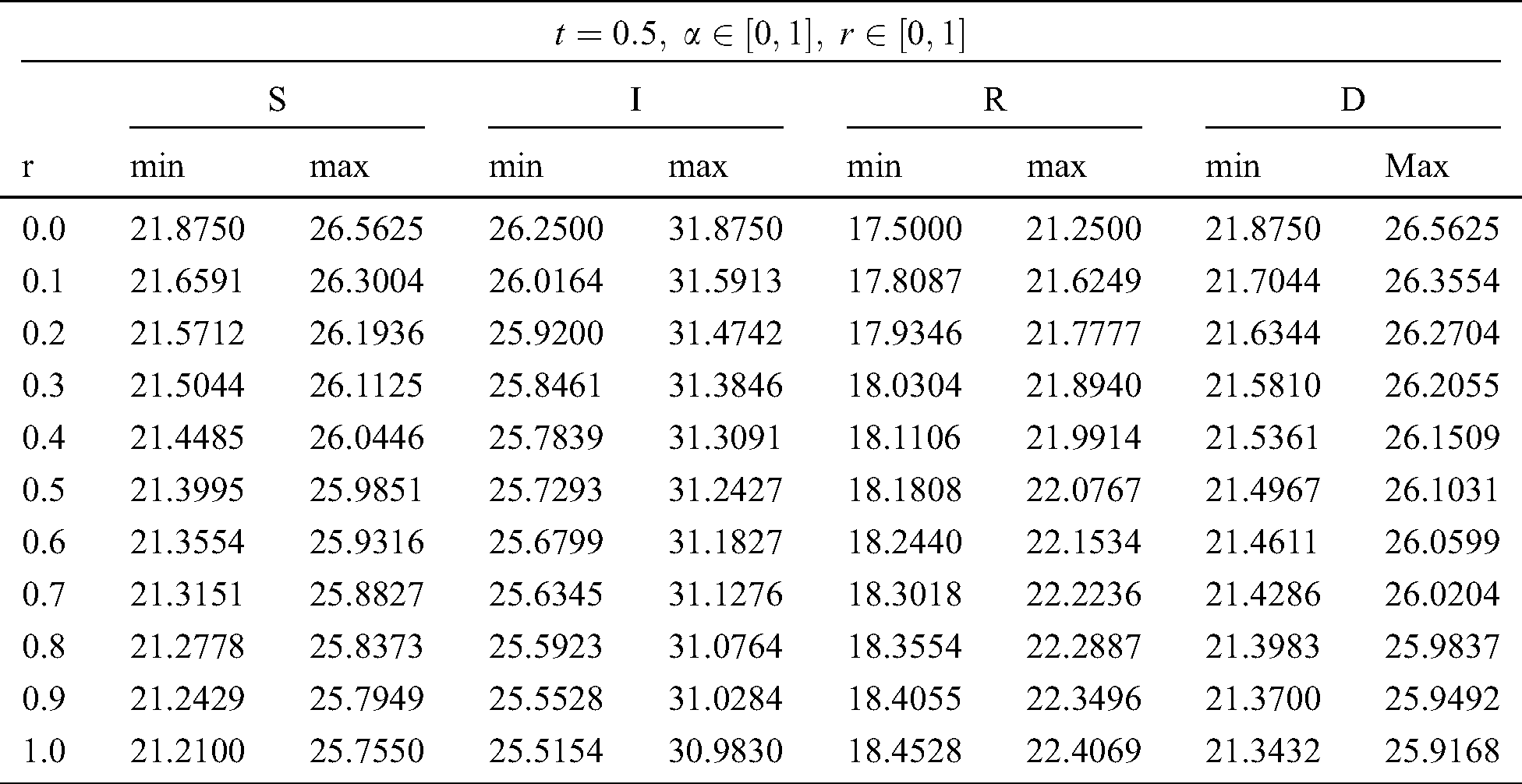
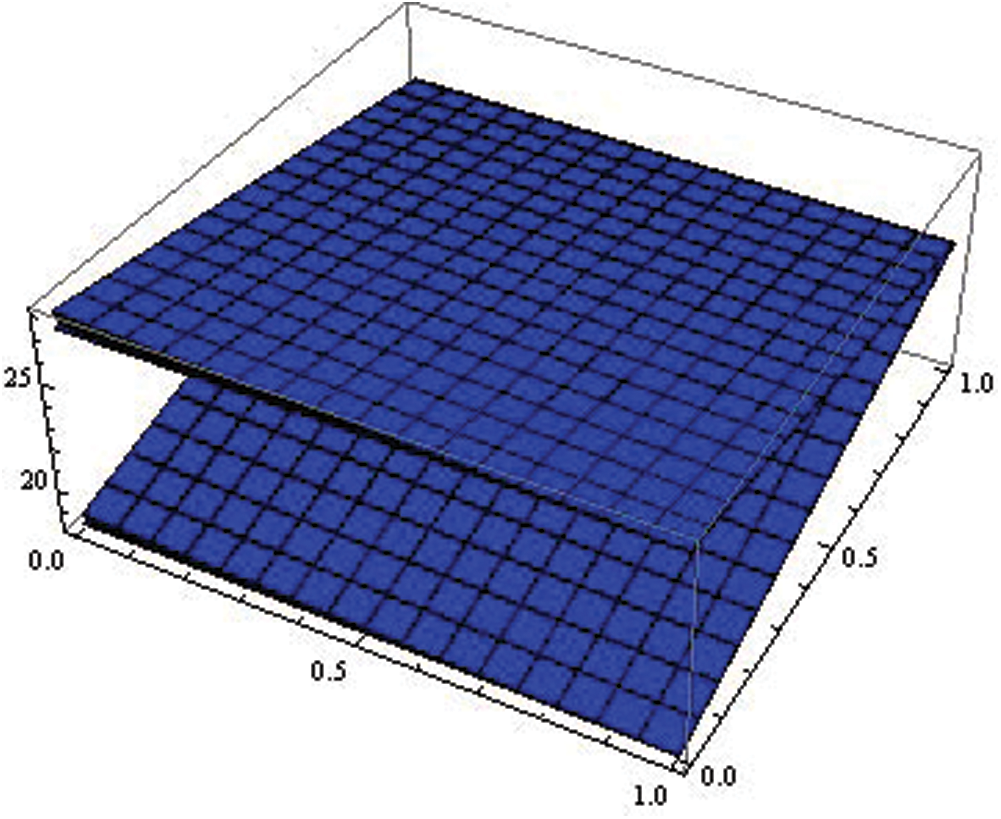
Figure 7: Fuzzy fractional susceptible (S)
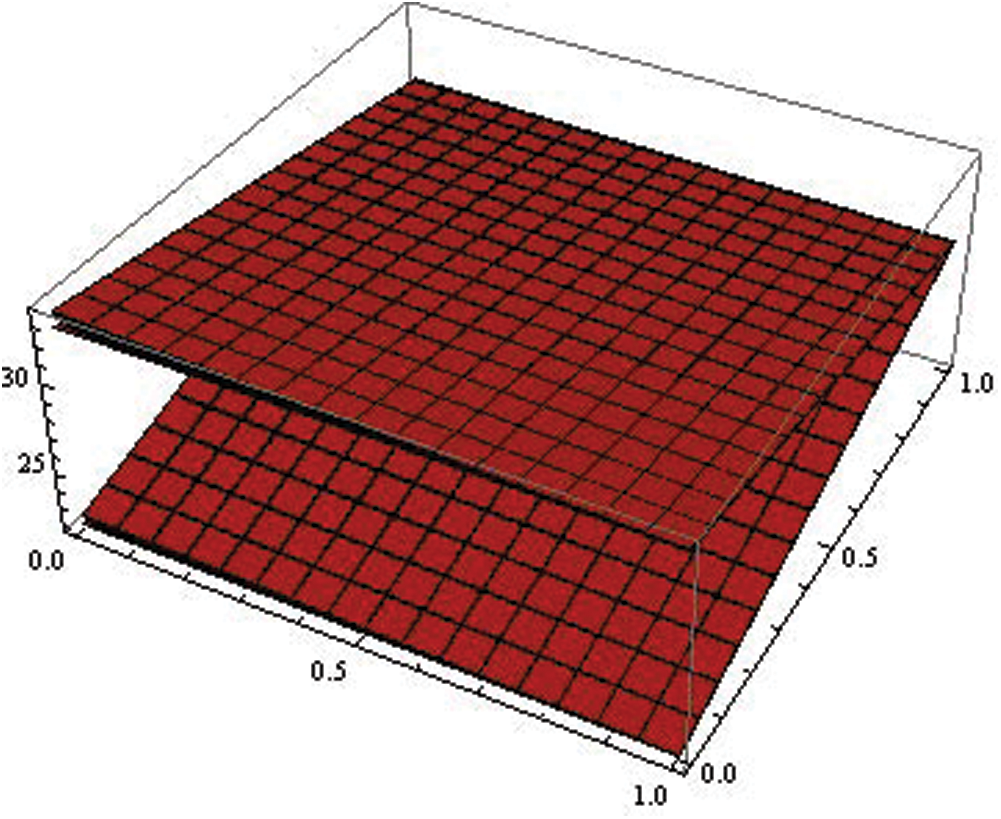
Figure 8: Fuzzy fractional infected (I)
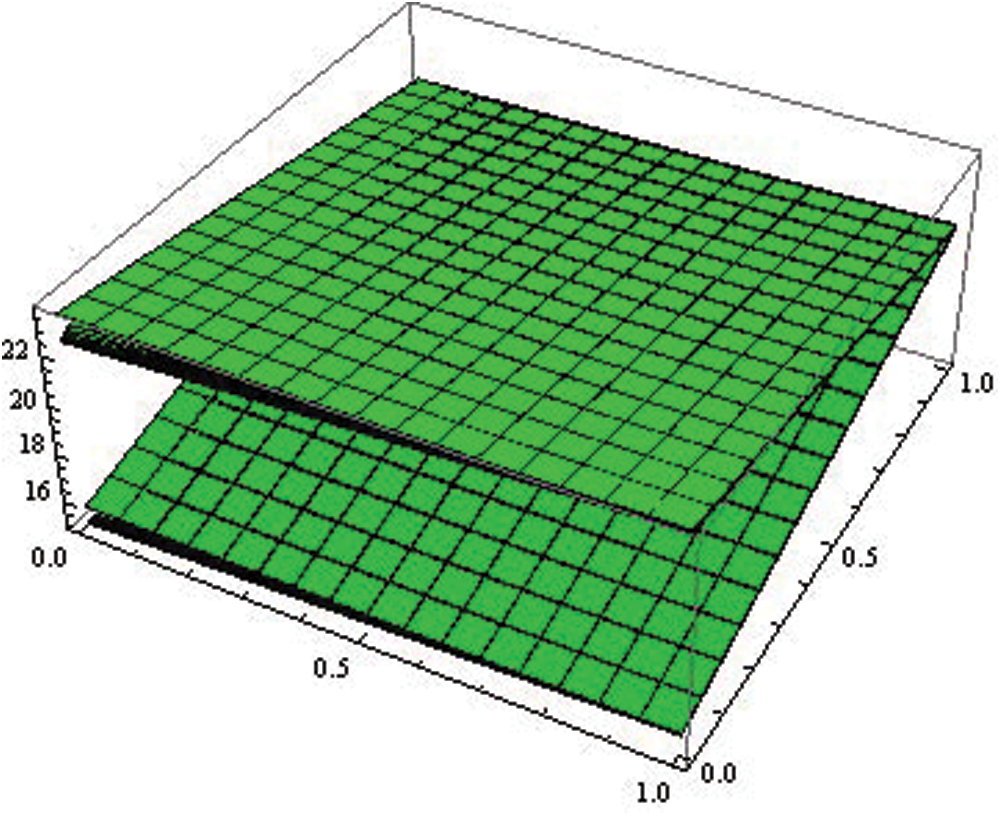
Figure 9: Fuzzy fractional recovered (R)
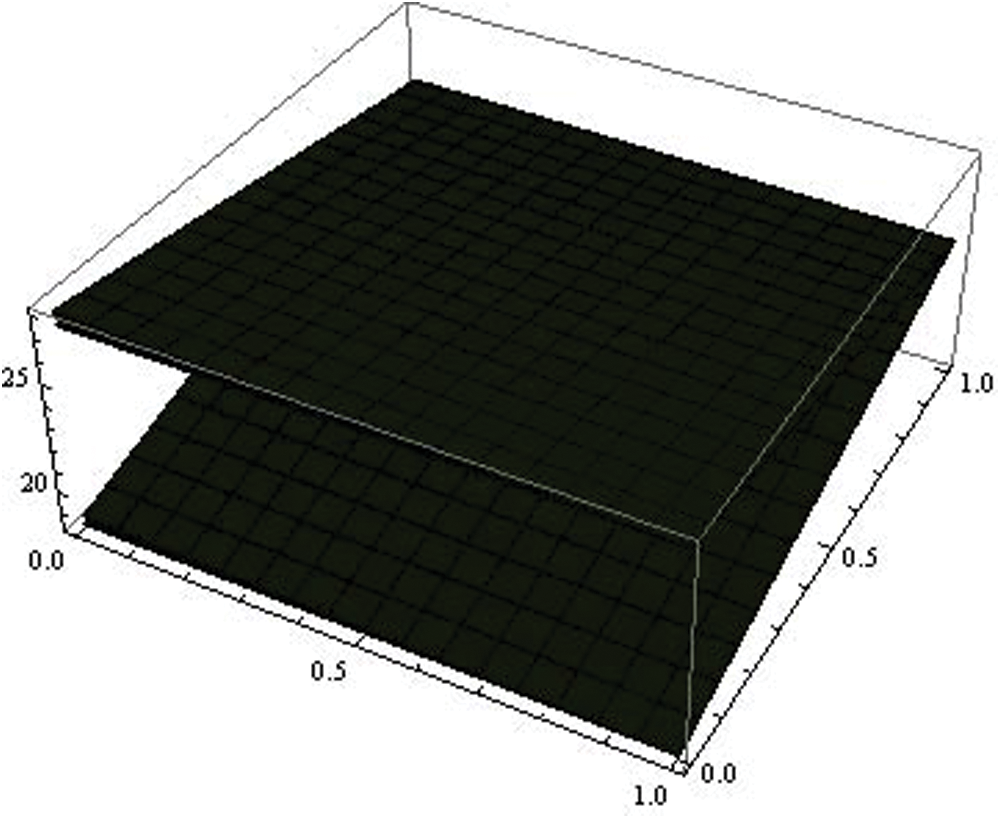
Figure 10: Fuzzy fractional dead (D)
In Tabs. 1–4, non-fuzzy, non-fractional valued susceptible infected, recovered and dead populations have been provided. In Tabs. 5–8, fractional valued susceptible infected, recovered, and dead populations have been provided and their respective plots have been given in Figs. 3–6. In Tab. 9 as a sample, fuzzy fractional SIRD populations are provided for 
But in Figs. 7–10, the plots of fuzzy fractional SIRD populations for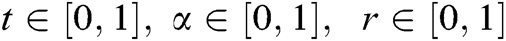 
are provided.
The stability of the epidemic model SIRD was confirmed by studying the nature of eigenvalues. Since the system is nonlinear, we applied and compared three different methods LADM-4, DTM-4, and RKM-4. Fuzzy valued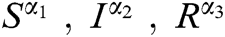 
and 
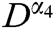at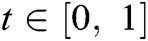 
and at 
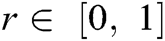are shown in the tables and figures. The solutions obtained by LADM-4, DTM-4, and RKM-4 were compared and it was noticed that all the above three methods are equally good in accuracy. Also, we have to keep in mind that all these three methods are very direct since there is no linearization made. The table values were presented only by fixing
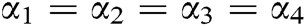. The graphical representations were plotted by considering all the values of 
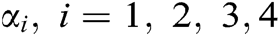irrespective of whether they are equal or not. As future works, we would like to frame the model of COVID-19 by using the fuzzy fractional differential equations and their solutions will be found by using any of the above three equally good accuracy methods.
Acknowledgement: The authors would like to thank the anonymous reviewers for their beneficial comments and suggestions towards improving the quality of the paper.
Funding Statement: The authors received no specific funding for this study.
Conflict of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. L. A. Zadeh. (1965). “Fuzzy sets,” Information and Control, vol. 8, no. 3, pp. 338–353. [Google Scholar]
2. J. J. Bukley and T. Feuring. (2000). “Fuzzy differential equations,” Fuzzy Sets and Systems, vol. 110, pp. 43–54. [Google Scholar]
3. S. Abbasbandy. (2005). “Extended Newton’s method for a system of nonlinear equations by modified Adomian decomposition method,” Applied Mathematics and Computation, vol. 170, no. 1, pp. 648–656. [Google Scholar]
4. L. J. S. Allen. (2007). An introduction to mathematical biology. Upper Saddle River, NJ: Prentice Hall. [Google Scholar]
5. O. D. Makinde. (2007). “Adomian decomposition approach to a SIR epidemic model with constant vaccination strategy,” Applied Mathematics and Computation, vol. 184, no. 2, pp. 842–848. [Google Scholar]
6. M. Y. Ongun. (2011). “The Laplace Adomian decomposition method for solving a model for HIV infection of CD4+T cells,” Mathematical and Computer Modelling, vol. 53, no. 5–6, pp. 597–603. [Google Scholar]
7. A. A. M. Arafa, S. Z. Rida and M. Khalil. (2012). “Solutions of the fractional order model of childhood disease with constant vaccination strategy,” Mathematical Science Letter, vol. 1, no. 1, pp. 17–23. [Google Scholar]
8. M. Farman, M. U. Saleem, A. Ahmad and M. O. Ahmad. (2018). “Analysis and numerical solution of SEIR epidemic model of measles with non-integer time fractional derivatives by using Laplace Adomian decomposition method,” Ain Shams Engineering Journal, vol. 9, no. 4, pp. 3391–3397. [Google Scholar]
9. E. Moustafa and A. Ahmed. (2011). “The fractional SIRC model and influenza A,” Mathematical Problems in Engineering, vol. 2011, no. 480378, pp. 1–9. [Google Scholar]
10. P. Palese and J. F. Young. (1982). “Variation of influenza A, B, and C,” Science, vol. 215, no. 4539, pp. 1468–1474. [Google Scholar]
11. Z. U. Malik, A. K. Abdullah and B. Dumitru. (2019). “An efficient numerical technique for a new fractional tuberculosis model with nonsingular derivative operator,” Journal of Taibah University for Science, vol. 13, no. 1, pp. 1147–1157. [Google Scholar]
12. U. Rahmat, R. Ellahi, M. S. Sadiq and S. T. Mohyud-Din. (2020). “On the fractional-order model of HIV-1 infection of CD4+ T-cells under the influence of antiviral drug treatment,” Journal of Taibah University for Science, vol. 14, no. 1, pp. 50–59. [Google Scholar]
13. D. Baleanu, A. Jajarmi, S. S. Sajjadi and D. Mozyrska. (2019). “A new fractional model and optimal control of a tumor-immune surveillance with non-singular derivative operator,” Chaos, vol. 29, no. 083127, pp. 1–15. [Google Scholar]
14. W. O. Kermack and A. G. Mckendrick. (1927). “Contribution to the mathematical theory of epidemics,” Proceedings of the Royal Society of London. Series A, vol. 115, no. 772, pp. 700–721. [Google Scholar]
15. P. B. Dhandapani, D. Baleanu, J. Thippan and V. Sivakumar. (2019). “Fuzzy type RK4 solutions to fuzzy hybrid retarded delay differential equations,” Frontiers in Physics, vol. 7, pp. 168. [Google Scholar]
16. D. P. Bharathi, T. Jayakumar and S. Vinoth. (2019). “Numerical solution of fuzzy multiple hybrid single retarded delay differential equations,” International Journal of Recent Technology and Engineering, vol. 8, no. 3, pp. 1946–1949. [Google Scholar]
17. D. P. Bharathi, T. Jayakumar and S. Vinoth. (2019). “Numerical Solution of fuzzy multiple hybrid single neutral delay differential equations,” International Journal of Scientific & Technology Research, vol. 8, no. 9, pp. 520–523. [Google Scholar]
18. T. Jayakumar, A. Parivallal and D. P. Bharathi. (2016). “Numerical solution of fuzzy delay differential equations by fourth order Runge-Kutta method,” Advances in Fuzzy Sets and Systems, vol. 21, no. 2, pp. 135–161. [Google Scholar]
19. D. P. Bharathi, T. Jayakumar and S. Vinoth. (2019). “Numerical solution of fuzzy mixed delay differential equations via Runge-Kutta method of order four,” International Journal of Applied Engineering Research, vol. 14, no. 3, pp. 70–74. [Google Scholar]
20. K. Abodayeh, M. S. Arif, A. Raza, M. Rafiq, M. Bibi et al. (2020). , “Numerical techniques for stochastic foot and mouth diseases with impact of vaccination,” Advances in Difference Equations, vol. 2508, no. 1, pp. 1–14. [Google Scholar]
21. M. A. Khan, M. Ismail, S. Ullah and M. Farhen. (2020). “Fractional order SIR model with generalized incidence rate,” AIMS Mathematics, vol. 5, no. 3, pp. 1856–1880. [Google Scholar]
22. A. Harir, S. Melliani, H. E. Harfi and L. S. Chadli. (2020). “Variational iteration method and differential transformation method for solving the SEIR Epidemic Model,” International Journal of Differential Equations, vol. 2020, pp. 1–7, Article ID. 3521936. [Google Scholar]
23. A. Ullah, T. Abdeljawad, S. Ahmad and K. Shah. (2020). “Study of a fractional-order epidemic model of childhood diseases,” Journal of Function Spaces, vol. 2020, pp. 1–8, Article ID. 5895310. [Google Scholar]
24. S. Kumar, A. Ahmadian, R. Kumar, D. Kumar, J. Singh et al. (2020). , “An efficient numerical method for fractional SIR epidemic model of infectious disease by using Bernstein wavelets,” Mathematics, vol. 8, no. 558, pp. 1–22. [Google Scholar]
25. S. Vinoth, T. Jayakumar and D. P. Bharathi. (2019). “Stability analysis of a mathematical model for the dynamics of HIV infection with cure rate,” International Journal of Applied Engineering Research, vol. 14, no. 3, pp. 87–90. [Google Scholar]
26. P. B. Dhandapani, D. Baleanu, J. Thippan and V. Sivakumar. (2020). “On stiff, fuzzy IRD-14 day average transmission model of COVID-19 pandemic disease,” AIMS Bioengineering, vol. 7, no. 4, pp. 208–223. [Google Scholar]
27. M. Naveed, D. Baleanu, M. Rafiq, A. Raza, A. H. Soori et al. (2020). , “Dynamical behaviour and sensitivity analysis of a delayed coronavirus epidemic model,” CMC, vol. 65, no. 1, pp. 225–241. [Google Scholar]
28. A. J. Kucharski, T. W. Russell, C. Diamond, Y. Liu, J. Edmunds et al. (2020). , “Early dynamics of transmission and control of COVID-19: A mathematical modeling study,” Lancet Infectious Diseases, vol. 11, no. 2, pp. 1–17. [Google Scholar]
29. C. Yang and J. Wang. (2020). “A mathematical model for the novel coronavirus epidemic in Wuhan,” China Mathematical Biosciences and Engineering, vol. 17, no. 3, pp. 2708–2724. [Google Scholar]
30. Y. Belgaid, M. Helal and E. Venturino. (2020). “Analysis of a model for coronavirus spread,” Mathematics, vol. 8, no. 820, pp. 1–30. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |