DOI:10.32604/csse.2021.015575
| Computer Systems Science & Engineering DOI:10.32604/csse.2021.015575 | |
| Article |
Average Convergence for Directed & Undirected Graphs in Distributed Systems
1Bahria University, Islamabad, 44000, Pakistan
2Comsats University Islamabad, Attock campus, 43600, Pakistan
3University of Engineering & Technology, Peshawar, 25000, Pakistan
*Corresponding Author: Salman Ahmed. Email: sahmed@uetpeshawar.edu.pk
Received: 28 November 2020; Accepted: 06 January 2021
Abstract: Consensus control of multi-agent systems is an innovative paradigm for the development of intelligent distributed systems. This has fascinated numerous scientific groups for their promising applications as they have the freedom to achieve their local and global goals and make their own decisions. Network communication topologies based on graph and matrix theory are widely used in a various real-time applications ranging from software agents to robotics. Therefore, while sustaining the significance of both directed and undirected graphs, this research emphases on the demonstration of a distributed average consensus algorithm. It uses the harmonic mean in the domain of multi-agent systems with directed and undirected graphs under static topologies based on a control input scheme. The proposed agreement protocol focuses on achieving a constant consensus on directional and undirected graphs using the exchange of information between neighbors to update their status values and to be able to calculate the total number of agents that contribute to the communication network at the same time. The proposed method is implemented for the identical networks that are considered under the directional and non-directional communication links. Two different scenarios are simulated and it is concluded that the undirected approach has an advantage over directed graph communication in terms of processing time and the total number of iterations required to achieve convergence. The same network parameters are introduced for both orientations of the communication graphs. In addition, the results of the simulation and the calculation of various matrices are provided at the end to validate the effectiveness of the proposed algorithm to achieve consensus.
Keywords: Multi-agent systems; average consensus; distributed estimation; directed graphs; undirected graphs; agent counting
Recent technological advancements in communication systems, control systems, and computer systems engineering attract many researchers to study the latest challenges and developments in the distributed control of multi-agent systems. It is a system with multiple agents, which are a self-managed and intelligent. The main objectives of such systems are to achieve their main objective in a cooperative manner that is essentially beyond the individual capabilities of a single agent. This is usually accomplished by properly designing a distributed protocol [1]. Multi-agent systems have numerous civil, military, and security applications and hold great promise in terms of scalability, robustness, and flexibility [2,3]. The design and implementation of such systems should have several advantages and some limitations. The advantages of such systems can be listed as follows: (1) such systems can solve large complex problems that cannot be solved with centralized systems due to their limited computing power and resources. (2) They can provide solutions in which information is spatially distributed among sources. (3) Multi-agent systems improve performance along with various domains such as computational efficiency, reliability, scalability, robustness, maintainability, responsiveness, and flexibility. Various researchers have conducted numerous studies in the field of multi-agent systems using the consensus algorithms. One of the main topics is the estimation of the distribution and the predictive control under different communication conditions [4]. Due to limited coverage, limited communication skills, and limited resources, each agent can only exchange information with its neighboring agent to calculate local metrics and obtain a distribution estimate. The entire network information account cannot be guaranteed in this way. Therefore, we have proposed to develop a distributed algorithm that cooperatively complements the estimated estimate using the average consensus that computes the average initial set of node values using the original information from the agents to communicate with their neighbors. This exchange of information leads to distributed systems with several agents. Consensus agents offer advantages over centralized systems that require statistics to be reported to a group of agents for decision making. Collaborative intrigues and the convergence of investigations from distributed estimation algorithms have gained immense importance. The results of such algorithms provide robustness for some failure factors, low communication and computational costs [5]. Multi-agent systems are of great importance in the context of network systems due to their distributed nature and are widely used in a variety of applications such as: Flocking [6–9], Wireless Sensor Networks (WSN) [10–13], robot coordination control [14–16], underwater vehicles, resource allocation and dynamic economic transport [17–20], control of an unmanned aerial vehicle (UAV) [21–23], training of vehicles [24,25], intelligent transport systems [26], robotic position control [27,28], formation control [29–31], satellite coordination and alignment [32], computer load balancing parallels [33], coordinated decision making [34], a smart decentralized mechanism for smart grids [35,36] and other multi-agent applications are discussed in detail in Cao et al. [37]. In multi-agent systems in particular, one of the techniques used for this purpose is consensus. In this study, we present a known distributed algorithm called the linear consensus algorithm. These algorithms have the quality of achieving mutual values to achieve their global objectives by calculating their local values. This type of algorithm is of great importance in multi-agent systems and network-controlled systems. In cooperative control of a networked multi-agent system, dynamic agent groups in multi-agent systems must interact with each other and ultimately agree on certain amounts of interest to achieve their common goals. These problems are commonly referred to as consensus problems, which are one of the fundamental research topics of decentralized control [38]. In other words, we can simply say that convergence on a common value is called consensus or agreement. The goal of consensus control is to develop algorithms for multi-agent systems so that the group of dynamic agents can reach an agreement on a certain amount of interest by communicating information with neighboring agents and with themselves [39]. Furthermore, in the areas of control systems theory, the consensus problem was initially discussed by Borkar et al. [40]. The problem of informatics, which focuses on the aggregation of animals using consensus control, is examined by the author in Reynolds [41]. In the later Consensus research horizons, Olfati-Saber and Murray promote control. They use the concepts of graph and matrix theories with directed and undirected graphs [42]. Subsequently, the authors implemented a consensus control for dynamically changing topologies in Ren et al. [43]. Furthermore, consensus in mediating network topologies is addressed in [44,45], Filter Design for Consensus [46], a convex solution optimized for large-scale industry using a distributed consensus algorithm from the authors in [47–49], Kalman filter design for the distributed consensus approach is discussed first in Li et al. [50]. Impulse control is an important mechanism that is highlighted in Guan et al. [51]. The event-driven convergence protocol for multi-agent linear distributed networks is examined by Cheng et al. [52]. The authors discuss time-synchronized algorithms for different applications in [53–55]. The concept of asynchronous consensus in different network environments is also presented by the authors in [56,57]. Similarly, the authors propose a consensus-based scheme in Zhao et al. [58] in which they calculate the binary values of neighboring states in the case of stochastic noise. Interestingly, in Zheng et al. [59] the researcher investigates a hybrid convergence scheme for continuous and discrete multi-agent systems. Furthermore, consensus algorithms for second and higher order orders in different scenarios and network conditions have been the focus of research in recent years based on a discrepancy in the event of breakdowns, restrictions on control inputs and agent speed [60]. Furthermore, specially directed diagrams are used on the World Wide Web, where the corner points are the web pages and the links between the different pages are the edges [61]. This is also implemented in the algorithm used by Google page ranking [62]. They are also implemented in operating systems, mainly for resource allocation, where processes and resources act as corner points and borders are drawn between the requesting process and the requested resource [63]. One of the examples of such a network are the Bayesian networks used by NASA’s space shuttle to select an operating system for multiple processes. Directed graphs are also used to represent Markov chains and their related applications, such as: For example: automatic speech recognition [64], neurobiology, chemical reaction networks, etc. Similarly, undirected charts are used in various applications for a navigation system to provide the best solution for the optimal search for the shortest route [65]. In addition, non-directional graphs from Facebook and other social networks are used, the cornerstone being users and the connection between friends as an advantage [66]. It is also worth noting that the algorithm for friend suggestions on multiple social media sources uses key concepts from graph theory.
In this study, we propose a distributed algorithm based on average consensus and using the concept of harmonic mean to quickly converge to its optimal value. The proposed algorithm is applied to both directed and undirected graphs for fixed networks in order to visualize their meaning for real word problems. The rest of the article is organized as follows. Section II provides a preliminary study on the design of a consensus algorithm. Section III deals with the formulation of the proposed consensus algorithm problem. The results of the simulation are presented in Section IV, and finally Section V concludes the article.
2 Preliminary Study for Designing of Consensus Algorithm
We use state space functions to model the proposed network control system. In cooperative control of multi-agent systems, graph theory and matrix theory are used as the main tools to study and design such systems together with the state space model.
In mathematics and in particular in graph theory, a graph is a representation of a set of objects in which certain pairs of objects are connected by links. Connected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges. The edges can be directed or undirected. The vertices that are directly connected to the other vertices of a network are considered its neighbors and are represented mathematically as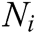 
for agent i. A graph is connected when there is a path between each pair of nodes. There are no inaccessible vertices in a joined diagram. In the network of interconnected agents, a graph is a tool for modeling a network topology and is denoted algebraically by G = (V, E). The agents identified in a graph are called the set of vertices and are indicated by V. In addition, the connections between vertices are known as the set of edges E = (i, j) [67]. Another important concept in graph theory is the spanning tree. If there is at least one corner point that has a route directed to all other agents in a network, we speak of a directed spanning tree [68,69]. A diagram can be classified based on the orientation of the information flow from one vertex to another using the edge. A graph can be directed or undirected.
If the graph does not have a specific direction for the edges, it is called an undirected graph. In undirected graph, the communication links for the information flow are bidirectional. For undirected graphs, A = AT, so the matrix is symmetric with respect to the diagonal. An ordered pair is used to denote the edge on a graph and can be written as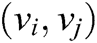 
. This simply means that agent i transmits its information to agent j directly connected. An undirected graph 
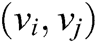means that both agents are connected and can transfer information bidirectional to each other. It is important to mention that in an undirected communication graph, the information is always available in due time, but at the same time it overloads the communication channel due to redundant information from the same node from multiple sources.
If the edges are directional, it is a directed graph. The edges are connected from node to node, and some of the same paths cannot be used to return to the original node. In directional diagrams, arrows on the edges indicate the direction of information flow. The source node can only use the specified address to reach the destination node, but must find an alternate route to return the start node. In some cases, a directed graph has problems related to the point of no return. This can lead to a blockage of communication networks. Furthermore, it can be said that a directed graph is a sequence of directed edges in the form of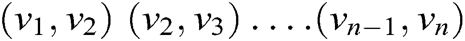 
where all 
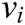belongs to V.
In addition to graph theory, convergence modeling for networked multi-agent systems depends mainly on matrix theory. When all the entries in a matrix are positive, the matrix is said to be a non-negative matrix. Similarly, with respect to the shape of the vector, the vector is not negative if all elements are positive. In matrix theory, different matrices are of great importance for convergence analysis. One of them is a stochastic matrix (row) P, which states that the total sum of rows in the matrix must be +1. Furthermore, this stochastic matrix P is called indecomposable and aperiodic (SIA) if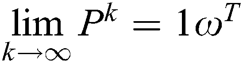 
is a column vector with all entries equal to 1, 
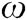is a vector column and T represents the transpose operation [67–69]. Likewise, a matrix of Rank 1 is a matrix in which all the rows are identical. An adjacency matrix is a matrix that provides information about connectivity within the elements of the matrix. The mathematical adjacency matrix of a graph G is denoted by 
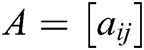and can be expressed as in Eq. (1):
One of the most important matrix for designing a consensus algorithms is the degree matrix. The Degree matrix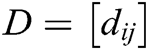 
of a graph G is a basically a diagonal matrix that possess a degree of vertex i.e., the number of agents adjacent to i. In addition, there is a concept of Laplace matrix that uses the definition of the degree matrix. Laplacian matrix of a graph is denoted by L where L = D – A. The Laplacian matrix is the utmost essential matrices in graph theory in terms of analysis and protocol design for distributed systems. Let 
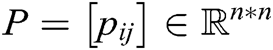be a stochastic matrix then G (P) is a graph associated with the matrix P, where G (P) has total N nodes and edges 
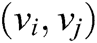if and only if 
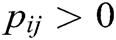. Also, a matrix with the majority of its elements equals to zero is called the sparsity matrix.
Consider a multi-agent system consisting of N agents. The communication topology for the whole system is designed by a graph G. Let A be the adjacency matrix with the associated graph. Similarly, D is the corresponding degree matrix and L is the Laplace matrix for the graph G. Each agent interacts with its neighbors, which is related to Ni for I agent. We consider mutual communication links between agents. In cooperative control of multi-agent networks, each agent has its local state variable yi. The agent should consider local state information as well as information from other connected agents. We investigate the following spatial state model in this investigation in Eq. (2):
In Eq. (2), zi is related to the control input generated by the agent. We have to design it so that all agents have to converge towards a common value based on their average. Furthermore, agent i must have the state value yi, which changes dynamically with time iteration. Furthermore, yi (0) is designated as the initial state value for agent i and the discrete moments in time are represented by k. Here we focus on two main objectives: one is to obtain the average consensus through the appropriate design of the fiscal contribution, and the second is to accurately estimate the total number of agents N. Our objective is that all local states yi (k) converge in a value that is the reciprocity of the total number of agents N in the network. This true approximation of the means N is given by Eq. (3).
The design of a control input zi (k) is considered a main objective and it must be ensured that Eq. (3) is satisfied. It is important to note that all agents in the communication network surely do the same as described in Eq. (3), regardless of whether the connection link between them has been established or even if there is no connection. Here we propose the draft of the control entry in Eq. (4):
In Eq. (4) α is a weight associated with the convergence factor to achieve immaculate coordination, and must be designed. To achieve the desired results more accurately and efficiently, we propose some conditions to design α for the objectives of the project algorithm. First, all agents i in a network must specify an initial condition for zero, where i = 2… N. Furthermore, an initial condition must be assigned specifically for the first agent in communication network equals to 1. The second condition is that the communication topology for the network under consideration is strongly connected and the third condition that must necessarily be fulfilled is the correct calculation of the weighting factor α, so that the substitution of this value in Eq. (4) ensures that the Eq. (3) is achieved. The weighting factor α and is proposed in Eq. (5).
Here, di and dj are the degrees of agent i and agent j. It is important to take into account that if all the steps are properly calculated and ensured for the proposed algorithm then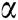 
surely gratifies the objective set in Eq. (3).
This section deals with the numerical and simulation results generated with the MATLAB simulation tool for the proposed algorithm. In this section we demonstrate the convergence analysis of our algorithm and also calculate the total number of agents in a network. A root mean square error is also recorded to ensure minimum error and achieve precision of results. Two cases are presented to reinforce our claim that the proposed algorithm achieves consensus with good results.
The following parameters need to be defined at the beginning of each simulation scenario.
a) Total number of agents (Network Size)
b) Initial conditions for all agents in a network
c) Computed value of weighting factor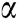 
d) Network topology (Adjacency): Fixed, directed, undirected
In the current scenario, we simulate it for directional and undirected orientations of the diagram. It also calculated the various matrices and provided a comparison for the performance of both graphs in the given network environment.
We consider a small undirected graphics network topology with 3 agents as shown in Fig. 1. The initial values for all agents except the first agent are set to zero. Where α is computed using Eq. (5). The convergence of the three network agents is 1/3 using Eq. (3). Also, the convergence of three means to a common value of 0.3333 is shown in Fig. 2.
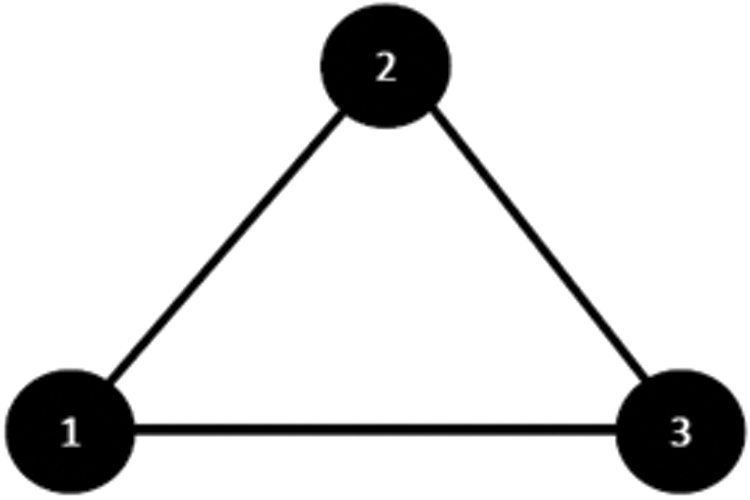
Figure 1: Undirected communication network of three networks agents with fixed network topology
We can formulate and compute the Adjacency matrix A, Degree matrix D, and the Laplacian matrix L for the undirected communication graph considered above as follows:
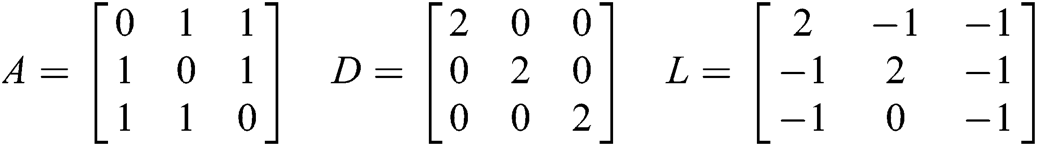
SIA Matrix =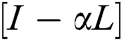 
and Rank1 Matrix = 
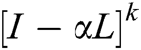associated with the undirected graph is computed as under:
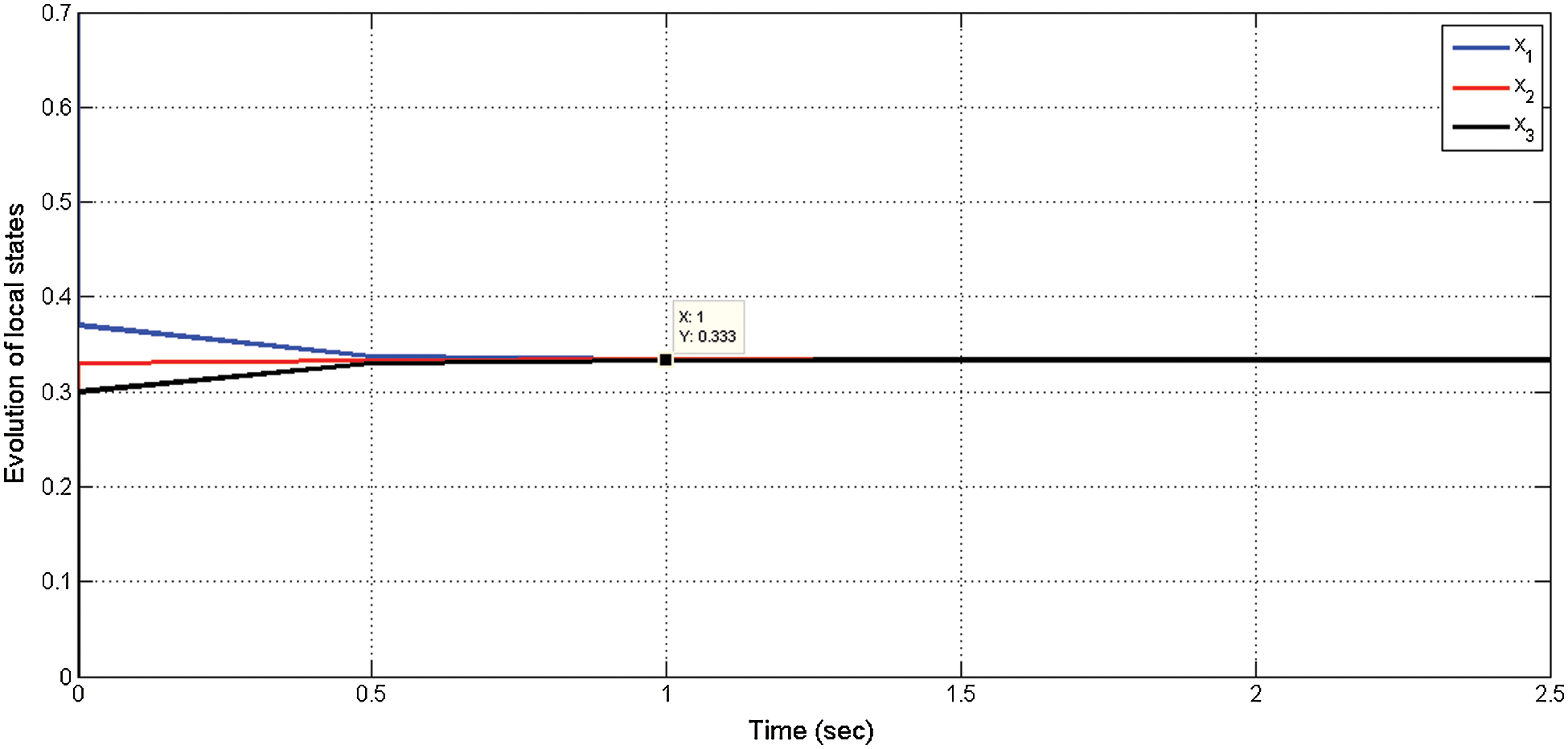
Figure 2: Consensus achieved by three agents in an undirected communication network
We consider a small undirected graphics network topology with 3 agents as shown in Fig. 3. The initial values for all agents except the first agent are set to zero. Where α is computed using Eq. (5). The convergence of the three network agents is 1/3 using Eq. (3). Also, the convergence of three means to a common value of 0.3333 is shown in Fig. 4.
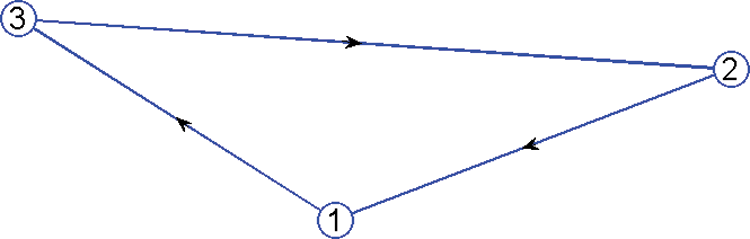
Figure 3: Directed communication network of three networks agents with fixed network topology
We can formulate and compute the Adjacency matrix A, Degree matrix D, and the Laplacian matrix L for the undirected communication graph considered above as follows:
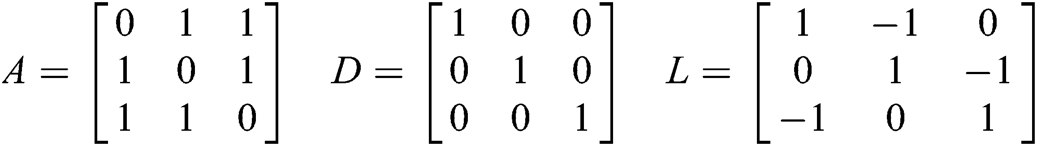
SIA Matrix =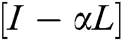 
and Rank1 Matrix = 
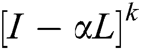associated with the undirected graph is computed as under:
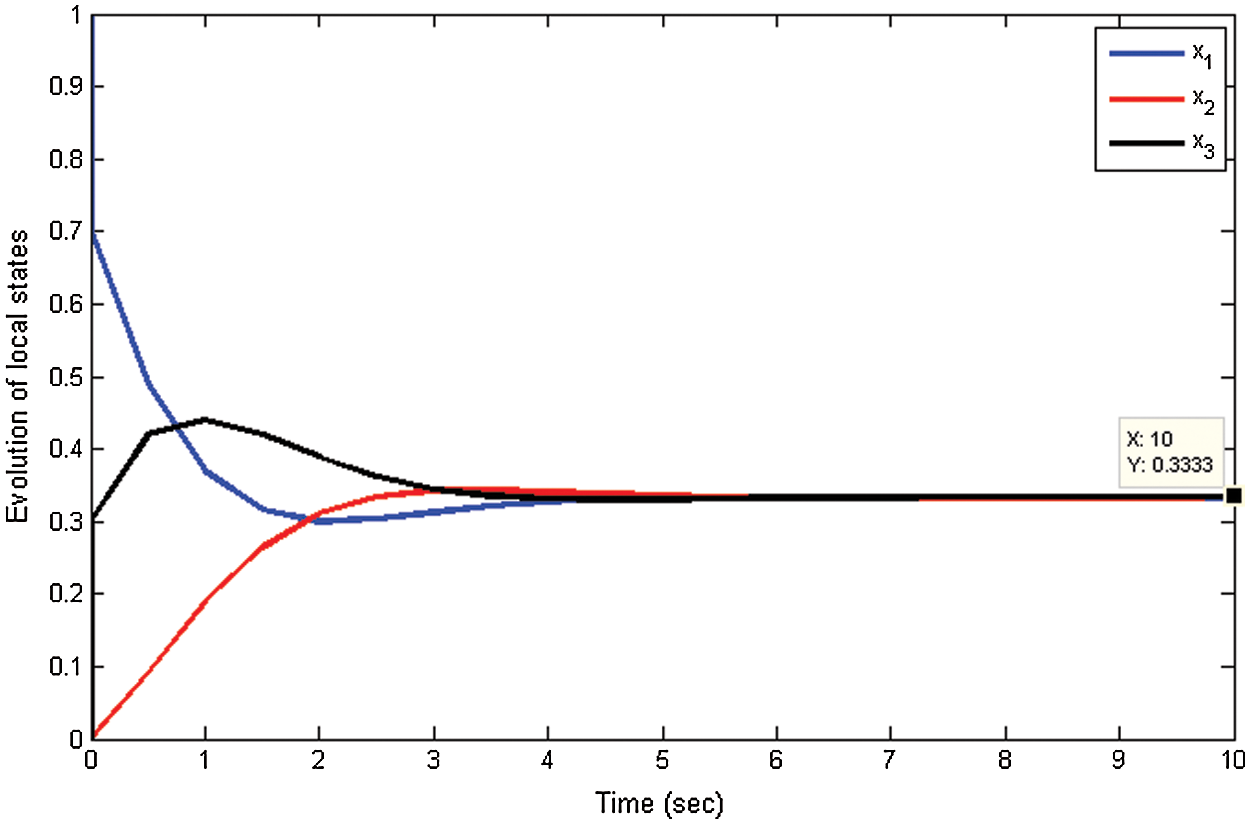
Figure 4: Consensus achieved by three agents in directed communication network
The convergence achieved in relation to several iterations and the time required for directional and undirected diagrams are shown in Tab. 1. It clearly showed that undirected graphs reach the consensus value in fewer iterations and are less time consuming in comparison with directed graphic.
Table 1: Comparison performance of undirected and directed for small communication network
In the current scenario, we simulate it for directional and undirected orientations of the diagram. It also calculated the various matrices and provided a comparison for the performance of both graphs in the given network environment with eight agents.
First, we consider a multi-agent network with 8 network agents with an undirected network topology. The initial state conditions are defined according to the specification established for the proposed algorithm, which are defined as x1 = 1 and xi = 0 and for all i = 2, 3, 4….8. The network topology of the communication graph is recorded and shown in Fig. 5. The weight is calculated based on the maximum degree of network connectivity implementing the proposed method. The total simulation time for this case remains constant for 25 seconds. The consensus agreement between the 8 agents is achieved with a mean value of 0.125, and the representation of the consensus within the communication network is shown in Fig. 6.
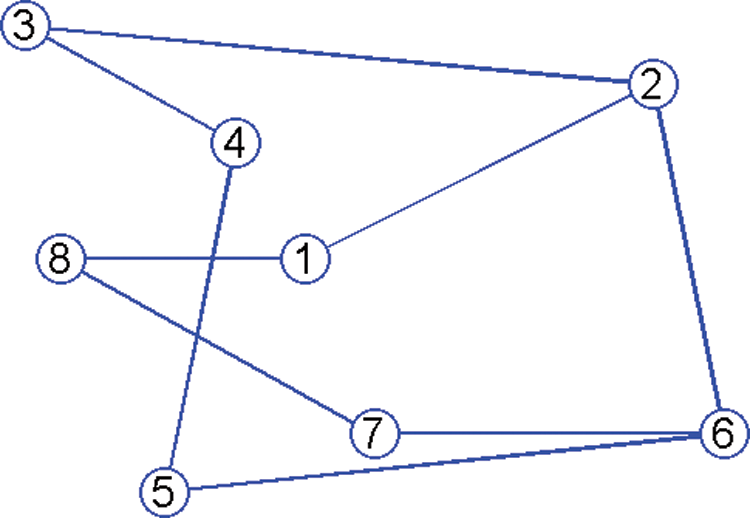
Figure 5: Undirected communication network of eight networks agents with fixed network topology
We can formulate the Adjacency, Degree, and the Laplacian matrix for the undirected graph considered above as follows:
SIA Matrix =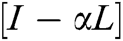 
and Rank1 Matrix = 
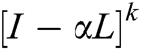associated with the undirected graph is computed as under:
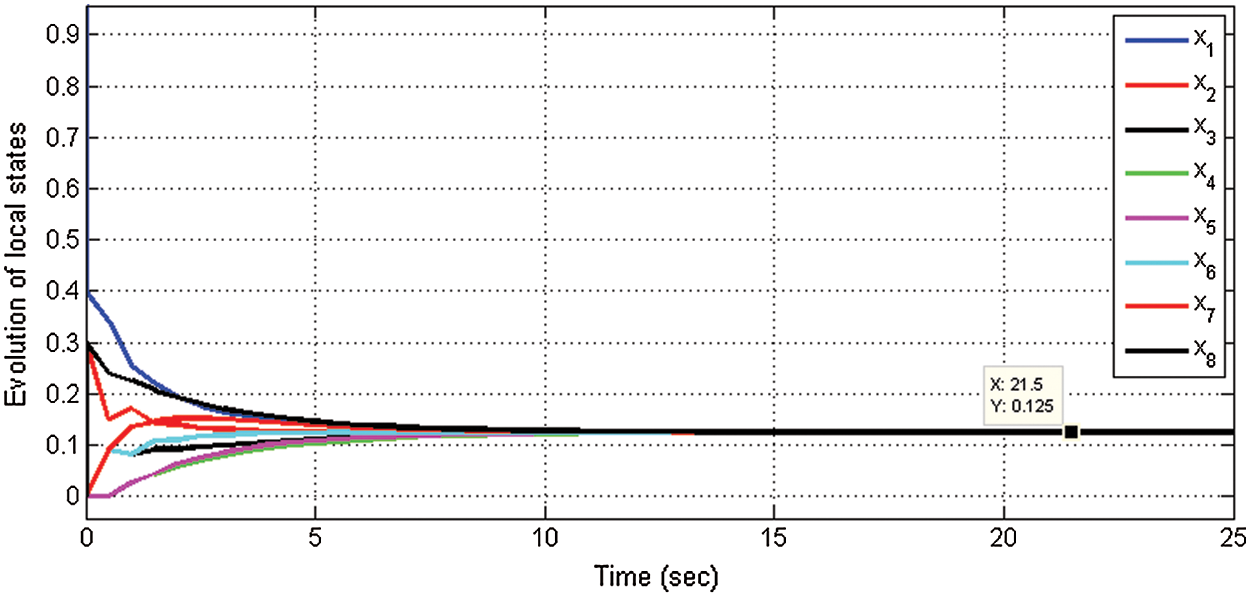
Figure 6: Consensus of the 8 network agents on the average value of 0.125 for undirected graph
We consider a multi-agent network with 8 network agents with a directed network topology. The initial state conditions are defined according to the specification established for the proposed algorithm, which are defined as x1 = 1 and xi = 0 and for all i = 2, 3, 4….8. The network topology of the communication graph is recorded and shown in Fig. 7. The weight is calculated based on the maximum degree of network connectivity implementing the proposed method. The total simulation time for this case remains constant for 70 seconds. The consensus agreement between the 8 agents is achieved with a mean value of 0.125 as shown in Fig. 8, and the representation of the consensus within the communication network is shown in Fig. 6.
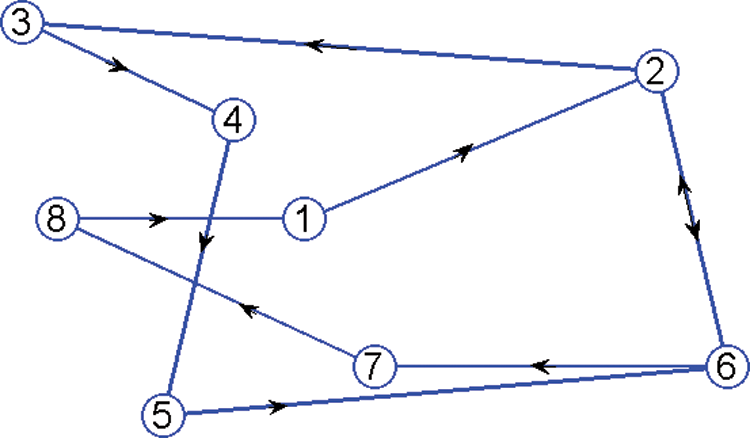
Figure 7: Directed communication network of eight networks agents with fixed network topology
We can formulate the Adjacency, Degree, and the Laplacian matrix for the undirected graph considered above as follows:
SIA Matrix =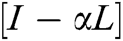 
and Rank1 Matrix = 
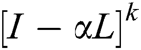associated with the undirected graph is computed as under:
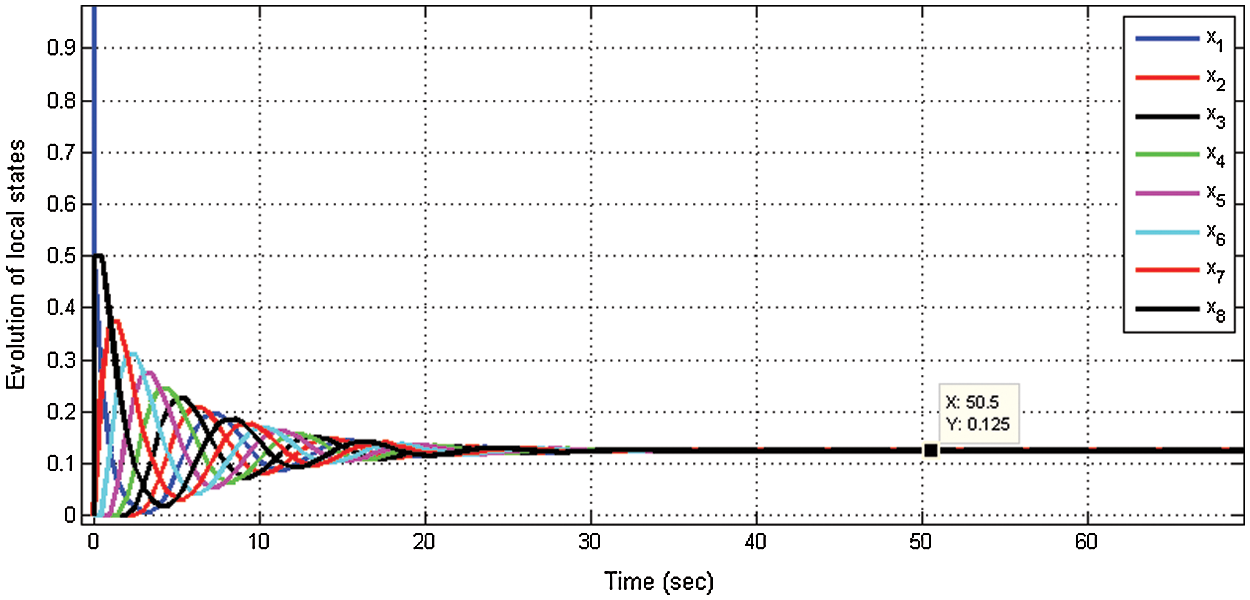
Figure 8: Consensus of the 8 network agents on the average value of 0.125 for directed graph
The convergence achieved in relation to several iterations and the time required for directional and undirected cases in scenarios are shown in Tab. 2. It is clear that the undirected graphs reaching the consensus value in fewer iterations and are less time consuming in comparison with directed graphic.
Table 2: Comparison performance of undirected and directed for communication network with 8 agents
This article presents an implementation of the proposed algorithm in directed and undirected graphs for the cooperative control of multi-agent systems. To determine the total number of agents in a network, the proposed algorithm converges with the reciprocal of the total number of agents. This implementation is done with stochastic matrix tools and algebraic graph theories. We simulate two cases of directional and non-directional alignment of the diagram to check the effectiveness of the proposed model for the multiple landscapes. Both objectives set for the research are achieved by attaining the convergence and the finding the agent count. The simulation results show that the proposed algorithm is very efficient in case of directed graphs with respect to a series of iterations and calculation time as compared for undirected graphs. One of the reasons is the bidirectional information flow, which can be easily evaluated on the undirected diagram. This work can be extended in the future by simulating the same network configuration in different network environments, e.g., adding noise and uneven delays. In addition, the update time of the agent states can be updated in an asynchronous clock mode and time-limited convergence. It can be further extended by adding more key performance indicators such as convergence time and the convergence factor to evaluate the convergence analysis of the proposed model.
Funding Statement: The author(s) received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. R. O. Saber, J. A. Fax and R. M. Murray. (2007). “Consensus and cooperation in networked multi-agent systems,” Proceedings of the IEEE, vol. 95, no. 1, pp. 215–233. [Google Scholar]
2. M. Vinyals, J. A. R. Aguilar and J. Cerquides. (2011). “A survey on sensor networks from a multiagent perspective,” Computer Journal, vol. 54, no. 3, pp. 439–454. [Google Scholar]
3. G. Antonelli. (2013). “Interconnected dynamic systems: An overview on distributed control,” IEEE Control Systems Magazine, vol. 33, no. 1, pp. 76–78. [Google Scholar]
4. X. Liang, Y. Hou, L. He, J. Zhang, J.Zhu . (2020). Consensus of multi-agent systems with input constraints based on distributed predictive control schemeComputers, Materials & Continua, vol. 62, no. 3, pp. 1335–1349. [Google Scholar]
5. Q. Zhang and J. F. Zhang. (2012). “Distributed parameter estimation over unreliable networks with markovian switching topologies,” IEEE Transactions on Automatic Control, vol. 57, no. 10, pp. 2545–2560. [Google Scholar]
6. Q. Zhang, P. Li, Z. Yang and Z. Chen. (2014). “Distance constrained based adaptive flocking control for multiagent networks with time delay,” Mathematical Problems in Engineering, vol. 2015, pp. 901282–901290. [Google Scholar]
7. R. Saber. (2006). “Flocking for multi-agent dynamic systems: Algorithms and theory,” IEEE Transactions on Automatic Control, vol. 51, no. 3, pp. 401–420. [Google Scholar]
8. J. Zhu, J. Lu and X. Yu. (2013). “Flocking of multi-agent non-holonomic systems with proximity graphs,” IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 60, no. 1, pp. 199–210. [Google Scholar]
9. M. M. Zavlanos, A. Jadbabaie and G. J. Pappas. (2007). “Flocking while preserving network connectivity,” IEEE Conference on Decision Control, pp. 2919–2924. [Google Scholar]
10. M. Khan, G. Pandurangan and V. Kumar. (2009). “Distributed algorithms for constructing approximate minimum spanning trees in wireless sensor networks,” IEEE Transactions on Parallel and Distributed System, vol. 20, no. 1, pp. 124–139. [Google Scholar]
11. B. K. N. Trigoni. (2012). “Sensor network algorithms and applications introduction,” Philosphical Transactions of the Royal Society, vol. 370, pp. 5–10. [Google Scholar]
12. H. I. Kobo, A. M. Abu-Mahfouz and G. P. Hancke. (2019). “Fragmentation-based distributed control system for software-defined wireless sensor networks,” IEEE Transactions on Industrial Informatics, vol. 15, no. 2, pp. 910. [Google Scholar]
13. Z. M., C. L. Liu and F. Liu. (2019). “Average-consensus tracking of sensor network via distributed coordination control of heterogeneous multi-agent systems,” IEEE Control Systems Letters, vol. 3, no. 1, pp. 132–137. [Google Scholar]
14. J. Dai, A. Benini, H. Lin, P. J. Antsaklis, J. Matthew et al. (2016). , “Learning-based formal synthesis of cooperative multi-agent systems with an application to robotic coordination,” Mediterranean Conf. on Control and Automation, pp. 1008–1013. [Google Scholar]
15. M. F. Ge, Z. H. Guan, B. Hu, D. X. He and R. Q. Liao. (2016). “Distributed controller–estimator for target tracking of networked robotic systems under sampled interaction,” Automatica, vol. 69, no. 5, pp. 410–417. [Google Scholar]
16. L. Jin and S. Li. (2018). “Distributed task allocation of multiple robots: A control perspective,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 48, no. 5, pp. 693–701. [Google Scholar]
17. C. Li, X. Yu, T. Huang and X. He. (2018). “Distributed optimal consensus over resource allocation network and its application to dynamical economic dispatch,” IEEE Transactions on Neural Networks and Learning Systems, vol. 29, no. 6, pp. 2407–2418. [Google Scholar]
18. G. Chen and Z. Zhao. (2018). “Delay effects on consensus-based distributed economic dispatch algorithm in microgrid,” IEEE Transactions on Power Systems, vol. 33, no. 1, pp. 602–612. [Google Scholar]
19. Z. Yang, J. Xiang and Y. Li. (2017). “Distributed consensus based supply–demand balance algorithm for economic dispatch problem in a smart grid with switching graph,” IEEE Transactions on Industrial Electronics, vol. 64, no. 2, pp. 1600–1610. [Google Scholar]
20. J. Qin, Q. Ma, Y. Shi and L. Wang. (2017). “Shi and L.Wang, Recent advances in consensus of multi-agent systems: A brief survey,” IEEE Transactions on Industrial Electronics, vol. 64, no. 6, pp. 4972–4983. [Google Scholar]
21. J. Gomes, I. Mas, C. Martinez, R. Pena and N. Quijano. (2016). “Distributed formation control of multiple unmanned aerial vehicles over time-varying graphs using population games,” in IEEE Int. Conf. on Decision and Control, pp. 5245–5250. [Google Scholar]
22. R. Beard, J. Lawton and F. Hadaegh. (2001). “A coordination architecture for spacecraft formation control,” IEEE Transactions on Control Systems Technology, vol. 9, no. 6, pp. 777–790. [Google Scholar]
23. W. Ren, R. Beard and E. Atkins. (2007). “Information consensus in multivehicle cooperative control,” IEEE Control Systems Magazine, vol. 27, no. 2, pp. 71–82. [Google Scholar]
24. O. Petter, E. Foirell and N. E. Leonard. (2004). “Cooperative control of mobile sensor networks: Adaptive gradient climbing in a distributed environment,” IEEE Transactions on Automatic Control, vol. 49, no. 8, pp. 1292–1302. [Google Scholar]
25. Y. Cao, W. Yu, W. Ren and G. Chen. (2013). “An overview of recent progress in the study of distributed multi-agent coordination,” IEEE Transactions on Industrial Informatics, vol. 9, no. 1, pp. 427–438. [Google Scholar]
26. R. Toyot and T. Namerikawa. (2017). “Formation control of multi-agent system considering obstacle avoidance,” in Proceedings of the SICE Annual Conference, pp. 446–451. [Google Scholar]
27. D. E. Soltero, M. Schwager and D. Rus. (2013). “Decentralized path planning for coverage tasks using gradient descent adaptive control,” International Journal of Robot Research, vol. 33, no. 3, pp. 401–425. [Google Scholar]
28. W. Ren, R. W. Beard and E. M. Atkins. (2005). “A survey of consensus problems in multi-agent coordination,” American Control Conf., pp. 1859–1864. [Google Scholar]
29. T. Han, Z. Guan, M. Chi, B. Hu, T. Li et al. (2017). , “Multi-formation control of nonlinear leader-following multi-agent systems,” ISA Transactions, vol. 69, no. 6, pp. 140–147. [Google Scholar]
30. J. Fax and R. Murray. (2004). “Information flow and cooperative control of vehicle formations,” IEEE Transactions on Automatic Control, vol. 49, no. 9, pp. 1465–1476. [Google Scholar]
31. H. Du, W. Zhu, G. Wen, Z. Duan and J. Lu. (2019). “Distributed formation control of multiple quadrotor aircraft based on non-smooth consensus algorithms,” IEEE Transactions on Cybernetics, vol. 49, no. 1, pp. 342–353. [Google Scholar]
32. A. Kashyap, T. Basar and R. Srikant. (2007). “Quantized consensus,” Automatica, vol. 43, no. 7, pp. 1192–1203. [Google Scholar]
33. D. Bauso, L. Giarre and R. Pesenti. (2003). “Distributed consensus protocols for coordinating buyers,” IEEE Conference on Decision and Control, vol. 1, pp. 588–592. [Google Scholar]
34. F. Karray, O. Basir, I. Song and H. Li, “A framework for coordinated control of multiagent systems,” Proc. of the 2004 IEEE Int. Symp. on Intelligent Control, pp. 156–161, 2004. [Google Scholar]
35. X. Hu, H. Zhou, Z. Liu, X. Yu and C. Li. (2017). “Hierarchical distributed scheme for demand estimation and power reallocation in a future power grid,” IEEE Transactions on Industrial Informatics, vol. 13, no. 5, pp. 2279–2290. [Google Scholar]
36. C. Li, X. Yu, W. Yu, T. Huang and Z. W. Liu. (2016). “Distributed event triggered scheme for economic dispatch in smart grids,” IEEE Transactions on Industrial Informatics, vol. 12, no. 5, pp. 1775–1785. [Google Scholar]
37. Y. Cao, W. Yu, W. Ren and G. Chen. (2013). “An overview of recent progress in the study of distributed multi-agent coordination,” IEEE Transactions on Industrial Information, vol. 9, no. 1, pp. 427–438. [Google Scholar]
38. H. Liu, L. Cheng, M. Tan, Z. Hou and Y. Wang. (2015). “Distributed exponential finite-time coordination of multi-agent systems: Containment control and consensus,” Int. Journal of Control, vol. 88, no. 2, pp. 237–247. [Google Scholar]
39. A. Pandey. (2012). “Consensusabilty of discrete-time multi-agent system,” Ph.D. dissertation. Visvesvaraya Technological University. [Google Scholar]
40. V. Borkar and P. Varaiya. (1982). “Asymptotic agreement in distributed estimation,” IEEE Transactions on Automatic Control, vol. 27, no. 3, pp. 650–655. [Google Scholar]
41. C. W. Reynolds. (1987). “Flocks, herds, and schools: A distributed behavioral model,” Computer Graphics, vol. 21, no. 4, pp. 25–34. [Google Scholar]
42. R. O. Saber and R. M. Murray. (2004). “Consensus problems in networks of agents with switching topology and time-delays,” IEEE Transactions on Automatic Control, vol. 49, no. 9, pp. 1520–1533. [Google Scholar]
43. W. Ren and R. W. Beard. (2005). “Consensus seeking in multiagent systems under dynamically changing interaction topologies,” IEEE Transactions of Automatic Control, vol. 50, no. 5, pp. 655–661. [Google Scholar]
44. L. Moreau. (2005). “Stability of multiagent systems with time-dependent communication links,” IEEE Transactions on Automatic Control, vol. 50, no. 2, pp. 169–182. [Google Scholar]
45. L. Moreau. (2004). “Stability of continuous-time distributed consensus algorithms,” IEEE Conf. on Decision and Control, vol. 4, pp. 3998–4003. [Google Scholar]
46. E. Kokiopoulou and P. Frossard. (2009). “Polynomial filtering for fast convergence in distributed consensus,” IEEE Transactions on Signal Processing, vol. 57, no. 1, pp. 342–354. [Google Scholar]
47. D. Yuan, D. W. Ho and S. Xu. (2016). “Regularized primal–dual subgradient method for distributed constrained optimization,” IEEE Transactions on Cybernetics, vol. 46, no. 9, pp. 2109–2118. [Google Scholar]
48. Q. Liu, S. Yang and Y. Hong. (2017). “Constrained consensus algorithms with fixed step size for distributed convex optimization over multiagent networks,” IEEE Transactions on Automatic Control, vol. 62, no. 8, pp. 4259–4265. [Google Scholar]
49. Z. Li, Z. Ding, J. Sun and Z. Li. (2018). “Distributed adaptive convex optimization on directed graphs via continuous-time algorithms,” IEEE Transactions on Automatic Control, vol. 63, no. 5, pp. 1434–1441. [Google Scholar]
50. W. Li, G. Wei, F. Han and Y. Liu. (2016). “Weighted average consensus-based unscented kalman filtering,” IEEE Transactions on Cybernetics, vol. 46, no. 2, pp. 558–567. [Google Scholar]
51. Z. Guan, D. J. Hill and X. Shen. (2005). “On hybrid impulsive and switching systems and application to nonlinear control,” IEEE Transactions on Automatic Control, vol. 50, no. 7, pp. 1058–1062. [Google Scholar]
52. B. Cheng and Z. Li. (2019). “Fully distributed event-triggered protocols for linear multi-agent networks,” IEEE Transactions of Automatic Control, vol. 64, no. 4, pp. 1655–1662. [Google Scholar]
53. Y. Wu, H. Su, P. Shi, Z. Shu and Z. Wu. (2016). “Consensus of multiagent systems using aperiodic sampled-data control,” IEEE Transactions on Cybernetics, vol. 46, no. 9, pp. 2132–2214. [Google Scholar]
54. G. S. Han, Z. H. Guan, J. Li, R. Q. Liao and X. M. Cheng. (2015). “Multi-consensus of multi-agent networks via a rectangular impulsive approach,” Systems & Control Letters, vol. 76, no. 4, pp. 28–34. [Google Scholar]
55. W. Yu, L. Zhou, X. Yu, J. Lu and R. Lu. (2013). “Consensus in multi-agent systems with second-order dynamics and sampled data,” IEEE Transactions on Industrial Informatics, vol. 9, no. 4, pp. 2137–2146. [Google Scholar]
56. M. T. Hale, A. Nedic and M. Egerstedt. (2017). “Asynchronous multiagent primal-dual optimization,” IEEE Transactions on Automatic Control, vol. 62, no. 9, pp. 4421–4435. [Google Scholar]
57. Z. Liu. (2017). “Asynchronous impulsive consensus of multi-agent systems,” in Eighth International Conference on Intelligent Control and Information Processing, pp. 278–281. [Google Scholar]
58. Y. Zhao, T. Wang and W. Bi. (2019). “Consensus protocol for multiagent systems with undirected topologies and binary-valued communications,” IEEE Transactions on Automatic Control, vol. 64, no. 1, pp. 206–221. [Google Scholar]
59. Y. Zheng, J. Ma and L. Wang. (2018). “Consensus of hybrid multi-agent systems,” IEEE Transactions on Neural Networks and Learning Systems, vol. 29, no. 4, pp. 1359–1365. [Google Scholar]
60. P. Lin, W. Ren, C. Yang and W. Gui. (2018). “Composite backstepping consensus algorithms of leader follower higher-order nonlinear multiagent systems subject to mismatched disturbances,” IEEE Transaction on Cybernetics, vol. 48, no. 6, pp. 1171–1176. [Google Scholar]
61. T. Munzner and P. Burchard. (1995). “Visualizing the structure of the world wide web in 3D hyperbolic space,” in Proc. of the First Sym. on Virtual Reality Modeling Language, pp. 33–38. [Google Scholar]
62. K. Wang, Y. Shi, L. Xiao, J. Wang, Y. N. Joglekar et al. (2020). , “Experimental realization of continuous-time quantum walks on directed graphs and their application in PageRank,” Optica, vol. 7, no. 11, pp. 1524–1530. [Google Scholar]
63. D. M. Chickering, D. Heckerman and C. Meek, “A Bayesian approach to learning Bayesian networks with local structure,” Proc. of 13th Conf. on Uncertainity in Aritifical Intelligence, pp. 80–89, 1997. [Google Scholar]
64. S. Sen, A. Dutta and N. Dey. (2019). “Speech processing and recognition system,” Audio Processing and Speech Recognition, pp. 13–43. [Google Scholar]
65. C. Guo, F. Li, Z. Tian, W. Guo and S. Tan. (2020). “Intelligent active fault-tolerant system for multi-source integrated navigation system based on deep neural network,” Neural Computing and Applications, vol. 32, no. 22, pp. 16857–16874. [Google Scholar]
66. B. Nick, C. Lee, P. Cunningham and U. Brandes. (2013). “Simmelian backbones: Amplifying hidden homophily in facebook networks,” in Proceedings of the IEEE/ACM Int. Conf. on Advances in Social Networks Analysis and Mining, pp. 525–532. [Google Scholar]
67. X. Meng and T. Chen. (2013). “Event based agreement protocols for multi-agent networks,” Automatica, vol. 49, no. 1, pp. 2125–2132. [Google Scholar]
68. X. Liu, H. Lin and B. M. Chen. (2013). “Graph-theoretic characterisations of structural controllability for multi-agent system with switching topology,” Int. Journal of Control, vol. 86, no. 2, pp. 222–231. [Google Scholar]
69. Y. Feng, S. Xu and B. Zhang. (2014). “Group consensus control for double-integrator dynamic multiagent systems with fixed communication topology,” Int. Journal of Robust and Nonlinear Control, vol. 24, no. 3, pp. 532–547. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |