DOI:10.32604/csse.2021.015543
| Computer Systems Science & Engineering DOI:10.32604/csse.2021.015543 | |
| Article |
Load Frequency Control of Multi-interconnected Renewable Energy Plants Using Multi-Verse Optimizer
1College of Engineering at Wadi Addawaser, Prince Sattam Bin Abdulaziz University, Wadi Addawaser, 11991, Saudi Arabia
2Electrical Engineering Department, Faculty of Engineering, Minia University, Minia, 61111, Egypt
*Corresponding Author: Hegazy Rezk. Email: hr.hussien@psau.edu.sa
Received: 27 November 2020; Accepted: 27 December 2020
Abstract: A reliable approach based on a multi-verse optimization algorithm (MVO) for designing load frequency control incorporated in multi-interconnected power system comprising wind power and photovoltaic (PV) plants is presented in this paper. It has been applied for optimizing the control parameters of the load frequency controller (LFC) of the multi-source power system (MSPS). The MSPS includes thermal, gas, and hydro power plants for energy generation. Moreover, the MSPS is integrated with renewable energy sources (RES). The MVO algorithm is applied to acquire the ideal parameters of the controller for controlling a single area and a multi-area MSPS integrated with RES. HVDC link is utilized in shunt with AC multi-areas interconnection tie line. The proposed scheme has achieved robust performance against the disturbance in loading conditions, variation of system parameters, and size of step load perturbation (SLP). Meanwhile, the simulation outcomes showed a good dynamic performance of the proposed controller.
Keywords: Load frequency control; multi-verse optimization; multi-area power system; renewable energy sources
The utilization of renewable energy expanded significantly everywhere throughout the world, soon after the primary huge oil crisis in the late seventies. Besides, with the worldwide ecological contamination and energy crisis, sustainable power sources, for example, photovoltaic (PV) and wind [1–7] have assumed an influential role in electricity generation. In any case, the yield of PV and wind power generation is normally oscillating because of the discontinuity and haphazardness of sun-powered and wind vitality, and results in a vigorous effect on the grid in case of grid-connected mode. As of late, the integration of energy storage (ES) into renewable energy sources (RES) has turned out to be a standout amongst the most pragmatic solutions for taking care of this issue [8–17]. The principal roles of ES are to level the variance and increment the infiltration of RES, update the transmission line capability, increment the power quality, keep up the system dependability and soundness [18]. With the integration of RES, the complexity of the power system operation is increasing. Moreover, the system operating point varies instantaneously, and subsequently the system encounter deviation in frequency [19]. This deviation leads to bothersome impacts. Load frequency control (LFC) is one of the essential auxiliary administrations which assume a critical role in keeping up the frequency of the system at its ostensible value [20]. Due to the viral role of LFC, optimal control-based controllers have been studied in many research. Parmar et al. [21] have studied the two-area LFC system with diverse power generation sources. The optimal feedback controller gains have been calculated to minimize the quadratic performance index. They have realized better dynamic performance for the system considering shunt DC/AC tie-line in the presence of parameter changes. The controller to the hybrid RES with Fuel Cell (FC) system has been introduced by Rawat et al. [22]. The system consists of a Micro-hydropower system (MHP), PV, Diesel Generator (DG) and (FC). They have proved the efficiency of the tuned proportional integral derivative (PID) rather than the proportional-integral (PI) controller over system stability and performance. Kabiri et al. [23] have proposed a controller to regulate thermal units and determine the amount of their generated power to compensate PV system and regulate frequency oscillations to improve the frequency in the smart grid. The authors in Liu et al. [24] have introduced PID and fuzzy logic controllers to the modeled hybrid hydro systems with the synthesis of wind, thermal, solar, and diesel plants. Satisfied performance and robustness were achieved for both controllers. Lotfy et al. [25] proposed a Polar Fuzzy (PF) control strategy for a multi-unit energy system. In this study, the authors have utilized the electric vehicle (EV) battery as an enormous energy storage unit to promote the system frequency stability. They have considered the error control signal of the power supply and frequency deviation. In Zeng et al. [26] have presented an adaptive model predictive load frequency control (MPC) method for the multi-area power system (MAPS) in discrete time form with PV generation. They have considered a dead band for governor and generation rate constraint for the steam turbine. They have ensured the priority of the proposed MPC method on the conventional PI control methods over dynamic and steady-state performance for the nominal condition, parameters uncertainties cases, load disturbance. In Mohamed et al. [27] have proposed several frequency control techniques for variable speed wind turbines and solar PV generators. These techniques have allowed renewable energy sources to keep a certain amount of reserve powers and then release the reserved power according to frequency events. Mu et al. [28] have investigated the LFC problem of a standalone microgrid with PV power and (EVs) which are used as large-scale energy storage units. An observer-based integral sliding mode (OISM) controller has succeeded to regulate the deviated frequency of the power system. Pandey et al. [29–31] have studied the LFC of MAPS with multi-power generation sources utilizing HVDC link parallel to AC two areas interconnection tie-line. They have applied differential evolution for tuning the controller parameters to their best values to realize a satisfying system performance. Other control schemes for LFC in power systems with or without integration of RES based on artificial intelligence and optimization algorithms have been introduced in Golpira et al. [32,33].
In this paper, a novel optimized controller based-Multi-Verse Optimization algorithm (MVO) has been presented to regulate the LFC. The proposed controller is applied for a single area and interconnected multi-area MSPS. MATLAB/SIMULINK has been utilized to simulate the control system with diverse operating conditions.
The proposed system includes hydro, thermal with reheat turbine, gas, PV, and wind power plants. Each unit has been modeled linearly for simulation as shown in Fig. 1. The symbols of the system have been presented in Appendix I. The following are the controller design for multi-source single area power system (SAPS) and MAPS:
Figure 1: Transfer function block diagram of the SAPS with integral controllers
2.1 Controller Design for Multi-Source SAPS
The main idea in this research is to decide the optimal LFC controller gains to quickly minimize the system frequency deviation. For this dilemma, the MVO algorithm has been applied for minimizing the defined objective function with desired specifications and constraints. The Integral of time multiplied squared error (ITSE) in automatic generation control (AGC) has been considered as an objective function and the controller parameters bounds as the constraint is expressed as the following:
where,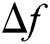 
is the deviation of the system frequency and Tmax is the simulation time. 
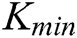and 
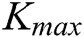are the boundaries of the controller parameters. The control system of SAPS is shown in Fig. 2.
Figure 2: Transfer function block diagram of SAPS with optimized controllers
2.2 Controller Design of Multi-Source MAPS
The proposed procedure has been utilized to design the controller for the system described in Fig. 3. Every system incorporates reheating thermal, gas, and hydro generating plants beside the PV and wind power plant. The block diagram of this system integrated with RES has appeared in Fig. 4.
Figure 3: The two-area power system interconnected through AC-DC parallel tie lines
Figure 4: Transfer function block diagram of the MAPS with HVDC link
The LFC scheme has been tested with the proposed optimized controller with two cases: one with AC tie-line only and the other with AC/DC tie-lines. Furthermore, the control scheme has been tested under change of load power and parameters variations. The transport delays have been neglecting for simplicity. The following is the objective function for MAPS:
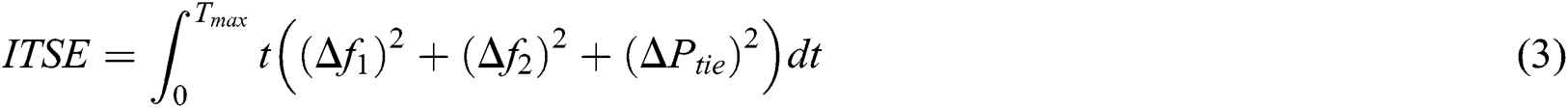
where,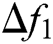 
and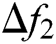 
are the deviations of system frequency, and 
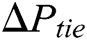is the power incremental change in tie line.
MVO algorithm has been inspired by the theory of multi-verse as presented in Mirjalili et al. [34,35]. The mathematical model of the MVO algorithm can be described as: firstly, the universes have to be sorted based on their rise rates and the roulette wheel select one universe to be the white holes in every sample, based on the following expressions:
where, d and z are the number of variables and universes, respectively.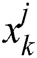 
specifies the j-th parameter of i-th universe, 
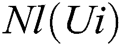is the normalized inflation rate of the i-th universe, r1 is a random number in [0,1], 
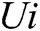displays the i-th universe, and 
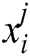designates the j-th parameter of k-th universe nominated by a roulette wheel.
The procedure described in Fig. 6 can be described as pursues:
where,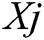 
demonstrates the j-th parameter of best universe so-far, 
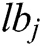displays the lower bound of j-th variable, 
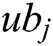is the upper bound of j-th variable, 
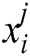demonstrates the j-th parameter of i-th universe, and r2, r3, r4 are random numbers in [0,1]. TDR, and WEP are the rate of traveling distance and the existence probability of wormholes, respectively and can be calculated as the following:
where, L expresses the maximum iterations, and l specifies the recent iteration. p is the exploitation accuracy over the iterations. Fig. 7 presents the flowchart of MVO.
The MVO algorithm has been utilized for the simulation and validation of the proposed control scheme. The simulation has been carried out using Core™ i5-4210U CPU, 1.7 GHz, and 8 GB RAM computer. The MVO has been simulated with 10 independent runs to validate the proposed procedure for each case. The obtained results by MVO are compared with PSO. The standard deviation values are 0.0565 and 0.1119 respectively for MVO and PSO methods. Also, the minimum cost values are 3.1626e-04 and 3.3e-03 respectively for MVO and PSO methods. A comparison between the convergence curves of MVO and PSO for several runs is presented in Fig. 5. The results confirmed the robustness of the MVO algorithm. The values of the best solution of the optimized PI controllers based on MVO and PSO have been recorded in Tab. 1.
Figure 5: MVO flowchart
Figure 6: Comparison between the convergence curves of MVO and PSO
Table 1: Optimal gains of PI controllers using MVO and PSO
To test the performance of the proposed controller with parameters variation, the wind power, and PV power variations have been assumed as shown in Fig. 7. To achieve this target, 5 cases of study have been introduced against load disturbance, frequency variation as the following:
Figure 7: Wind power and PV power variations
To ponder the dynamic behavior of the Multi-Source SAPS with MVO optimized controllers, 3 cases of study have been reproduced as the following:
The 1st case has studied the performance of the control system against the integration of PV and wind power plants into the system while maintaining the load disturbance unchanged at initial simulation at 0.01 pu. The integration of the PV and wind power plants into the system was at 10 s. The frequency deviation response has appeared in Fig. 8. As presented in Fig. 8, the proposed MVO optimized PI controller has quickly regulated the frequency against the penetration of the PV and wind power plants.
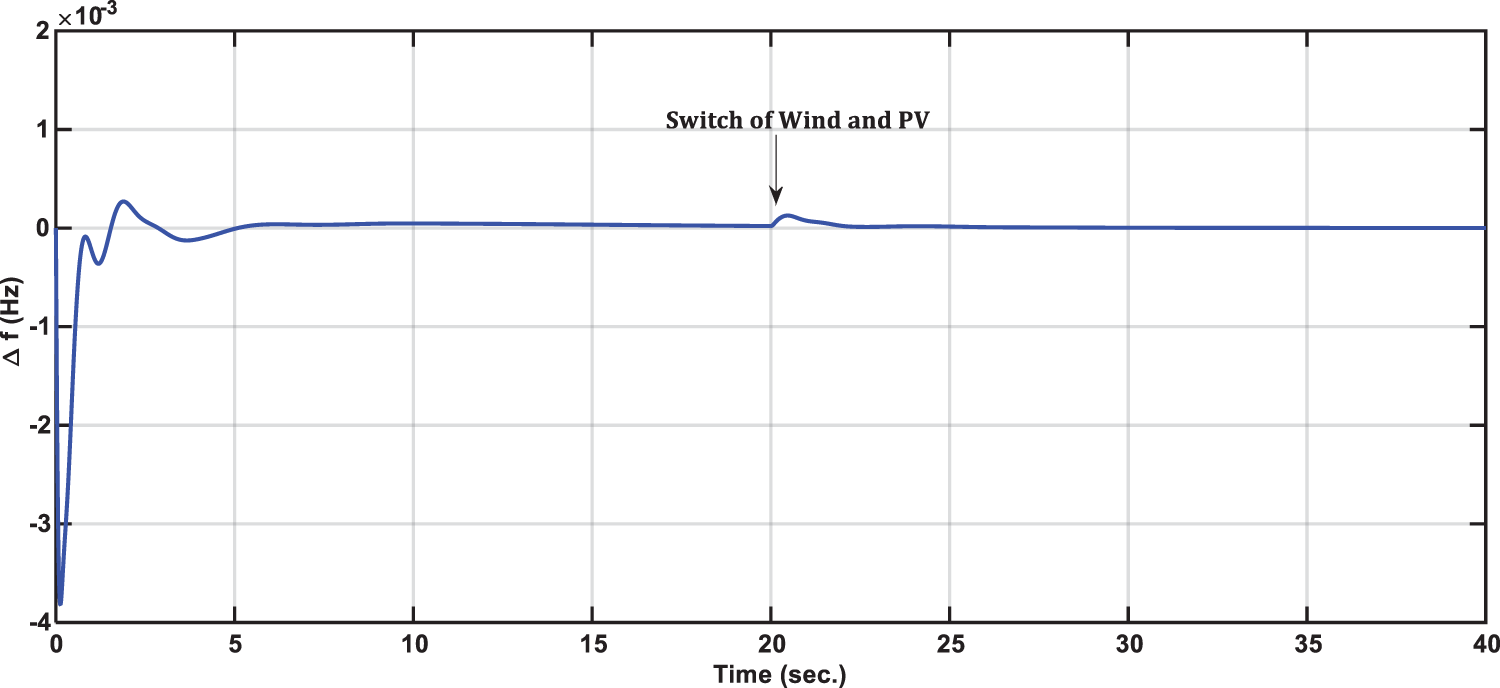
Figure 8: Time-domain system frequency response: Area frequency deviations (Case#1)
In this case of study, a 10% SLP is applied and removed while maintaining the other system parameters at nominal values as appeared in Fig. 9. It has proved that the proposed MVO optimized PI controller gives a good dynamic response, however having a small peak overshoot against load disturbance in presence of variation of PV and wind power.
Figure 9: Time-domain system response: Load disturbance variations and Area frequency deviations (Case#2)
In this case, a 10% SLP is applied as shown in Fig. 10. Moreover, the time constants of all power units in the system have been varied by +25% of their nominal values. The system performance with parameters uncertainty is shown in Fig. 10. This figure assures the ability of the optimized PI-MVO controller to interact with parameters variation, moreover, regulate the frequency deviation to zero.
Figure 10: Time-domain system response with parameters uncertainty: Load disturbance variations and Area frequency deviations (Case#3)
In this case, a 1% SLP has been applied at t = 0 sec for area 1, and at 20 sec for the area 2 while maintaining the other system parameters. The tie-line power and frequency deviation response have been presented in Fig. 11. Fig. 11 has proved a good dynamic response of the proposed optimized controller, however having a small peak overshoot against load disturbance, PV and wind plants variations.
Figure 11: Time-domain system responses of: Area frequency deviations for the two areas and Tie-line power (Case#4)
In case#5 the SLP has been applied as appeared in Fig. 12. In addition, the time constants of each power unit have been changed by +25% of their nominal value. The simulation results, Fig. 13 validate the quality of the proposed controller.
Figure 12: Time-domain system responses of load disturbance
Figure 13: Time-domain system responses of: Area frequency deviations for the two areas and Tie-line power (Case#5)
An MVO algorithm has been utilized in this paper to optimize the control parameters of the LFC of a predefined power system. This system comprises thermal, gas and hydro power plants as the conventional sources of power generation and PV, and wind power plants as RES. The algorithm has been applied to a single area and a two-area power system. The system performance has been observed on the basis of dynamic parameters and frequency overshoot. The Examination of dynamic responses revealed that the application of MVO improves the transient responses extraordinarily and enhances the frequency overshoot.
Funding Statement: This project was supported by the Deanship of Scientific Research at Prince Sattam Bin Abdulaziz University under the research project No 2020/01/11742.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. A. G. Olabi, T. Wilberforce, E. T. Sayed, K. Elsaid, H. Rezk et al. (2020). , “Recent progress of graphene based nanomaterials in bioelectrochemical systems,” Science of The Total Environment, vol. 749, p. 141225. [Google Scholar]
2. M. A. Abdelkareem, E. T. Sayed, H. O. Mohamed, M. Obaid, H. Rezk et al. (2020). , “Nonprecious anodic catalysts for low-molecular-hydrocarbon fuel cells: Theoretical consideration and current progress,” Progress in Energy and Combustion Science, vol. 77, p. 100805. [Google Scholar]
3. A. M. Eltamaly and M. A. Mohamed. (2018). “Optimal sizing and designing of hybrid renewable energy systems in smart grid applications,” Advances in Renewable Energies and Power Technologies, vol. 2, pp. 231–313. [Google Scholar]
4. M. A. Tolba, H. Rezk, V. Tulsky, A. A. Z. Diab, A. Y. Abdelaziz et al. (2018). , “Impact of optimum allocation of renewable distributed generations on distribution networks based on different optimization algorithms,” Energies, vol. 11, no. 1, p. 245. [Google Scholar]
5. A. M. Mohamed, A. M. Eltamaly, A. I. Alolah and A. Y. Hatata. (2018). “A novel framework-based cuckoo search algorithm for sizing and optimization of grid-independent hybrid renewable energy systems,” International Journal of Green Energy, vol. 16, no. 1, pp. 86–100. [Google Scholar]
6. M. A. Mohamed, A. A. Z. Diab and H. Rezk. (2019). “Partial shading mitigation of PV systems via different meta-heuristic techniques,” Renewable Energy, vol. 130, pp. 1159–1175. [Google Scholar]
7. A. A. Z. Diab and H. Rezk. (2017). “Global MPPT based on flower pollination and differential evolution algorithms to mitigate partial shading in building integrated PV system,” Solar Energy, vol. 157, pp. 171–186. [Google Scholar]
8. A. M. Eltamaly and M. A. Mohamed. (2016). “A novel software for design and optimization of hybrid power systems,” Journal of the Brazilian Society of Mechanical Sciences and Engineering, vol. 38, no. 4, pp. 1299–1315. [Google Scholar]
9. V. Khare, S. Nema and P. Baredar. (2015). “Optimisation of the hybrid renewable energy system by HOMER, PSO and CPSO for the study area,” International Journal of Sustainable Energy, vol. 36, no. 4, pp. 326–343. [Google Scholar]
10. A. Saha and L. C. Saikia. (2019). “Renewable energy source-based multiarea AGC system with integration of EV utilizing cascade controller considering time delay,” International Transactions on Electrical Energy Systems, vol. 29, no. 1, p. 2646. [Google Scholar]
11. S. S. Singh and E. Fernandez. (2018). “Modeling, size optimization and sensitivity analysis of a remote hybrid renewable energy system,” Energy, vol. 143, pp. 719–731. [Google Scholar]
12. A. M. Eltamaly and M. A. Mohamed. (2014). “A novel design and optimization software for autonomous PV/wind/battery hybrid power systems,” Mathematical Problems in Engineering, vol. 2014, pp. 1–16. [Google Scholar]
13. L. G. Acuña, M. Lake, R. V. Padilla, Y. Y. Lim, E. G. Ponzón et al. (2018). , “Modelling autonomous hybrid photovoltaic-wind energy systems under a new reliability approach,” Energy conversion and management, vol. 172, pp. 357–369. [Google Scholar]
14. M. S. Golsorkhi, Q. Shafiee, D. D. Lu and J. M. Guerrero. (2017). “A distributed control framework for integrated photovoltaic-battery-based islanded microgrids,” IEEE Transactions on Smart Grid, vol. 8, no. 6, pp. 2837–2848. [Google Scholar]
15. A. Giallanza, M. Porretto, G. L. Puma and G. Marannano. (2018). “A sizing approach for stand-alone hybrid photovoltaic-wind-battery systems: A Sicilian case study,” Journal of Cleaner Production, vol. 199, pp. 817–830. [Google Scholar]
16. A. Saha and L. C. Saikia. (2019). “Load frequency control of a wind-thermal-split shaft gas turbine-based restructured power system integrating FACTS and energy storage devices,” International Transactions on Electrical Energy Systems, vol. 29, no. 3, p. 2756. [Google Scholar]
17. H. Rezk and A. Fathy. (2017). “A novel optimal parameters identification of triple-junction solar cell based on a recently meta-heuristic water cycle algorithm,” Solar Energy, vol. 157, pp. 778–791. [Google Scholar]
18. A. Khosravi, R. N. N. Koury, L. Machado and J. J. G. Pabon. (2018). “Energy, exergy and economic analysis of a hybrid renewable energy with hydrogen storage system,” Energy, vol. 148, pp. 1087–1102. [Google Scholar]
19. D. Sharma and S. Mishra. (2018). “Power system frequency stabiliser for modern power systems,” IET Generation, Transmission & Distribution, vol. 12, no. 9, pp. 1961–1969. [Google Scholar]
20. H. Bevrani. (2014). “Frequency Control and Real Power Compensation,” in Robust Power System Frequency Control. Cham: Springer, p. 19–48. [Google Scholar]
21. K. P. S. Parmar, S. Majhi and D. P. Kothari. (2011). “Optimal load frequency control of an interconnected power system,” MIT International Journal of Electrical and Instrumentation Engineering, vol. 1, no. 1, pp. 1–5. [Google Scholar]
22. S. Rawat, S. Singh and K. Gaur. (2014). “Load frequency control of a hybrid renewable power system with fuel cell system,” in 2014 6th IEEE Power India Int. Conf. (PIICONDelhi, India: IEEE, pp. 1–6. [Google Scholar]
23. D. Kabiri, P. P. Shiani and B. Naeem. (2015). “Improving system frequency in smart grids in presence of wind and PV generation units using flywheel energy storage system,” Bulletin of Environment, Pharmacology and Life Sciences, vol. 4, no. 1, pp. 116–123. [Google Scholar]
24. Y. Liu, J. H. Park, B. Guo and Y. Shu. (2018). “Further results on stabilization of chaotic systems based on fuzzy memory sampled-data control,” IEEE Transactions on Fuzzy Systems, vol. 26, no. 2, pp. 1040–1045. [Google Scholar]
25. M. E. Lotfy, T. Senjyu, M. A. Farahat, A. Farouq and H. Matayoshi. (2017). “A polar fuzzy control scheme for hybrid power system using vehicle-to-grid technique,” Energies, vol. 10, no. 8, p. 1083. [Google Scholar]
26. G. Zeng, X. Xie and M. Chen. (2017). “An adaptive model predictive load frequency control method for multi-area interconnected power systems with photovoltaic generations,” Energies, vol. 10, no. 11, p. 1840. [Google Scholar]
27. T. H. Mohamed, H. Bevrani, A. A. Hassan and T. Hiyama. (2011). “Decentralized model predictive based load frequency control in an interconnected power system,” Energy Conversion and Management, vol. 52, no. 2, pp. 1208–1214. [Google Scholar]
28. C. Mu, Y. Tang and H. He. (2016). “Observer-based sliding mode frequency control for micro-grid with photovoltaic energy integration,” in 2016 IEEE Power and Energy Society General Meeting (PESGMBoston, MA, USA: IEEE, pp. 1–5. [Google Scholar]
29. S. K. Pandey, S. R. Mohanty and N. Kishor. (2013). “A literature survey on load-frequency control for conventional and distribution generation power systems,” Renewable and Sustainable Energy Reviews, vol. 25, pp. 318–334. [Google Scholar]
30. S. Panda, B. Mohanty and P. K. Hota. (2013). “Hybrid BFOA-PSO algorithm for automatic generation control of linear and nonlinear interconnected power systems,” Applied Soft Computing, vol. 13, no. 12, pp. 4718–4730. [Google Scholar]
31. B. Mohanty, S. Panda and P. K. Hota. (2014). “Controller parameters tuning of differential evolution algorithm and its application to load frequency control of multi-source power system,” International Journal of Electrical Power & Energy Systems, vol. 54, pp. 77–85. [Google Scholar]
32. H. Golpira and H. Bevrani. (2011). “Application of GA optimization for automatic generation control design in an interconnected power system,” Energy Conversion and Management, vol. 52, no. 5, pp. 2247–2255. [Google Scholar]
33. F. Daneshfar and H. Bevrani. (2012). “Multiobjective design of load frequency control using genetic algorithms,” International Journal of Electrical Power & Energy Systems, vol. 42, no. 1, pp. 257–263. [Google Scholar]
34. S. Mirjalili, S. M. Mirjalili and A. Hatamlou. (2016). “Multi-verse optimizer: a nature-inspired algorithm for global optimization,” Neural Computing and Applications, vol. 27, no. 2, pp. 495–513. [Google Scholar]
35. A. Fathy and H. Rezk. (2018). “Multi-verse optimizer for identifying the optimal parameters of PEMFC model,” Energy, vol. 143, pp. 634–644. [Google Scholar]
Appendix
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |
