DOI:10.32604/csse.2021.014557

| Computer Systems Science & Engineering DOI:10.32604/csse.2021.014557 |  |
| Article |
A Secure Signcryption Scheme for Electronic Health Records Sharing in Blockchain
1School of Cybersecurity, Chengdu University of Information Technology, Chengdu, 610225, China
2International Business Machines Corporation (IBM), New York, 10041, NY, 212, USA
*Corresponding Author: Jinquan Zhang. Email: zhjqcom@163.com
Received: 28 September 2020; Accepted: 28 November 2020
Abstract: In the existing Electronic Health Records (EHRs), the medical information of patients is completely controlled by various medical institutions. As such, patients have no dominant power over their own EHRs. These personal data are not only inconvenient to access and share, but are also prone to cause privacy disclosure. The blockchain technology provides a new development direction in the medical field. Blockchain-based EHRs are characterized by decentralization, openness and non-tampering of records, which enable patients to better manage their own EHRs. In order to better protect the privacy of patients, only designated receivers can access EHRs, and receivers can authenticate the sharer to ensure that the EHRs are real and effective. In this study, we propose an identity-based signcryption scheme with multiple authorities for multiple receivers, which can resist N-1 collusion attacks among N authorities. In addition, the identity information of receivers is anonymous, so the relationship between them and the sharer is not disclosed. Under the random oracle model, it was proved that our scheme was secure and met the unforgeability and confidentiality requirements of signcryption. Moreover, we evaluated the performance of the scheme and found that it had the moderate signcryption efficiency and excellent signcryption attributes.
Keywords: Electronic health records; blockchain; identity-based signcryption; multiple authorities; multiple receivers
Electronic Health Records (EHRs) are to digitize the paper-based health records, so that they can be stored, retrieved and accessed more conveniently and quickly in a network. However, some problems in the existing EHRs remain to be solved. Firstly, EHRs of patients are mainly stored on medical institutions sites, such as hospitals and clinics. Patients have the limited access to their personal medical data, while it is difficult to obtain such data from hospitals in real time, or to even share the data with family members and friends. In addition, medical workers in these institutions may access and disclose patients’ private medical data at will. Secondly, once a patient and a medical institution have any conflict or dispute, the latter can arbitrarily tamper with the EHRs of the patient, implicitly threatening the patient’s case. Thirdly, personal medical records are inherently confidential data and subject to personal privacy and security risks. As such, those records belong only to the corresponding individuals and only authorized users should be able to access relevant information. In order to solve the above problems, some researchers have made significant improvements in enabling patients to generate, manage and share their own EHRs, and ensure the privacy of their medical data.
In recent years, due to the extensive application of cloud computing technology in data processing [1], cloud-based EHRs have developed rapidly and more patients have been able to control their own medical data. In the cloud-based EHRs system, Premarathne et al. [2] and Ramu [3] set the access control to allow patients to share their medical data with doctors in a controlled way. However, a cloud server is not a fully trusted third party. In the cloud storage environment, it is difficult to guarantee the security of EHRs [4].
In 2008, blockchain was first proposed by Nakamoto [5] as a part of cryptocurrency bitcoin. At present, the application of the blockchain technology in the medical field is widely concerned among blockchain researchers [6]. With the decentralized, tamper-proof, traceable and publicly available blockchain technology [7], many problems in the medical field can be solved. Roehrs et al. [8] and Gordon et al. [9] proposed the basic framework of blockchain-based EHRs. Omer et al. [10] and Badr et al. [11] protected sensitive data of patients with the encryption technology in blockchain-based EHRs. Chen et al. [12] proposed a blockchain-based searchable encryption scheme for EHRs, which allowed patients to control the access to their EHRs.
In addition to the encryption protection, the authenticity of EHRs should be considered in the sharing process of EHRs. Authentication is crucial in blockchain [13] and cannot be ignored in blockchain-based EHRs [14]. Considering the characteristics of blockchain, many researchers proposed distributed signature schemes for blockchain-based EHRs. Tang et al. [14] constructed an identity-based signature scheme with multiple authorities to verify the identity of the signer and ensure the authenticity of the EHRs. Guo et al. [15] and Sun et al. [16] designed an attribute-based signature scheme with multiple authorities, which allowed the signer to hide their identity information when signing. However, these signature schemes lacked confidentiality of EHRs.
In order to satisfy both confidentiality and authenticity, in 1997, Zheng [17] first proposed the idea of signcryption, which could simultaneously realize the functions of signing and encrypting plaintext messages. Then, Malone-Lee [18] put forward the first practical identity-based signcryption scheme. Although many researchers have proposed more secure and efficient identity-based signcryption schemes [19,20], these schemes have only considered the case that a message was sent to one receiver. In 2006, Duan et al. [21] first proposed a multi-receiver identity-based signcryption scheme to send the same message to multiple receivers. In their scheme, the sender was only required to perform one pairing computation and n scalar multiplication in the signcryption phase, and each receiver could verify the validity of the message. Since then, the identity-based signcryption scheme for multiple receivers have been significantly improved based on the consideration of the efficiency and security properties [22–24].
In all the above identity-based signcryption schemes, only one key generation center (KGC) generates secret keys for all users, and the users must trust KGC unconditionally. However, KGC can use the public identity of users in the system to calculate the user’s secret key. Therefore, it can forge the sender’s signcryption or decrypt the signcryption obtained by the receiver. In addition, KGC may face a single point of failure.
A centralized KGC will have security risks, and the signcryption scheme of patient’s medical data in the blockchain was seldom explored. To enable patients to share the EHRs safely in the blockchain, in this paper, we made the following contributions.
Firstly, the distributed key generation method [13] is introduced into a centralized identity-based signcryption (IBSC) scheme. For multiple receivers, an identity-based signcryption with multiple authorities (MA-IBSC) scheme is developed. N authorities randomly construct their own polynomials and all authorities cooperatively generate the master secret key of the system by secret sharing, and embed their own secret key into the user’s secret key. Therefore, the scheme can resist the collusion attack of N-1 corrupt authorities. In addition, after signing EHRs, the patient encrypts the EHRs with the identities of other users whom the patient wants to share the data with. Thus, only authorized receivers can decrypt and access the EHRs. In this way, the authenticity of EHRs is ensured by verifying the signer’s signature. Furthermore, in the signcryption process, identity information of receivers can be hidden and the relationships between the patient and receivers are not exposed in the blockchain.
Secondly, signcrypted EHRs are directly uploaded to the blockchain, other nodes cannot verify them. Based on some adjustments of the on-chain and off-chain storage model [13], the signcrypted EHRs are recommended to be stored in the patient’s own off-blockchain database, so that the patient can control the EHRs. Then the patient extracts the storage address, signs it with the private key, and uploads it to the blockchain. Other users (nodes) in the system can verify the validity of the given address based on the patient’s public key.
Thirdly, based on the assumptions of computational Diffie-Hellman (CDH) problem and Bilinear Computational Diffie-Hellman (BCDH) problem, it is proved that our proposed sigcryption scheme is secure in the random oracle model. In other words, the unforgeability and confidentiality of signcryption are realized. Furthermore, the performance of the scheme is evaluated based on the two indices of signcryption efficiency and signcryption attributes.
The remainder of this paper is organized as follows. Section 2 presents the preliminaries, including Lagrange interpolation, bilinear map, computational assumption, syntax and secure model of the signcryption scheme. In Section 3, the EHRs system model in blockchain is described in detail. Section 4 demonstrates the specific MA-IBSC scheme for multiple receivers. The security analysis and performance evaluation are provided in Section 5. Finally, the conclusion is drawn in Section 6.
For a polynomial 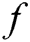 of degree
of degree  , given
, given 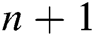
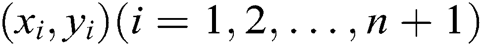 on
on 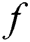 , we can uniquely determine a polynomial
, we can uniquely determine a polynomial 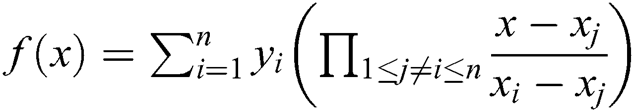 .
.
Let 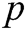 be a large prime number,
be a large prime number, 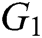 and
and 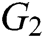 be two multiplicative cyclic groups of order
be two multiplicative cyclic groups of order 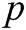 , and
, and 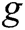 be the generator of
be the generator of 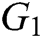 . We say that
. We say that  is not a bilinear map unless
is not a bilinear map unless 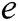 satisfies the following properties:
satisfies the following properties:
1. Bilinearity: for all  and
and 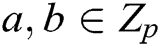 ,
, 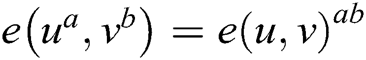 ;
;
2. 2) Non-degeneracy: there exists  , such that
, such that 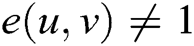 . That is to say, mapping
. That is to say, mapping  will not map all element pairs in
will not map all element pairs in  to the identity element of
to the identity element of  ;
;
3. Computability: for all , a valid algorithm can be used to calculate
, a valid algorithm can be used to calculate 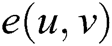 .
.
The security of the MA-IBSC scheme for multiple receivers is mainly based on the assumptions of Computational Diffie-Hellman (CDH) problem and Bilinear Computational Diffie-Hellman (BCDH) problem.
1) Computational Diffie-Hellman (CDH) problem. After  are randomly selected, for the given
are randomly selected, for the given 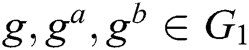 ,
, 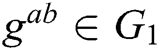 is calculated. If there is no probabilistic polynomial time (PPT) adversary A to calculate
is calculated. If there is no probabilistic polynomial time (PPT) adversary A to calculate 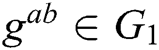 with the probability advantage that cannot be ignored, we call CDH in group
with the probability advantage that cannot be ignored, we call CDH in group 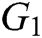 the assumption of the difficult problem.
the assumption of the difficult problem.
2) Bilinear Computational Diffie-Hellman (BCDH) problem. After 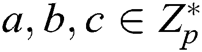 are randomly selected, for the given
are randomly selected, for the given 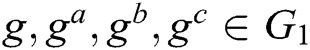 ,
, 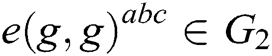 is calculated. If there is no probabilistic polynomial time (PPT) adversary A to calculate
is calculated. If there is no probabilistic polynomial time (PPT) adversary A to calculate 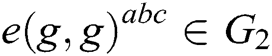 with the probability advantage that cannot be ignored, we call BCDH in group
with the probability advantage that cannot be ignored, we call BCDH in group  the assumption of the difficult problem.
the assumption of the difficult problem.
2.4 Syntax of the Signcryption Scheme
The identity-based signcryption with multiple authorities (MA-IBSC) scheme for multiple receivers involves the following seven algorithms:
Global Setup: The EHRs server takes a security parameter 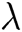 as the input and then outputs system public parameters
as the input and then outputs system public parameters 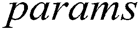 .
.
Authority Setup: All authorities perform this algorithm interactively. They input public parameters 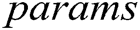 and their identity
and their identity 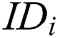 , then generate their respective secret key
, then generate their respective secret key 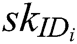 , system master secret key
, system master secret key 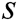 and master public key
and master public key 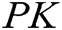 .
.
KeyGen: This algorithm is also cooperatively controlled by all authorities. They input the public parameters 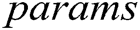 , their respective secret key
, their respective secret key 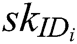 , and identity
, and identity 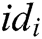 of a user, and then return secret key
of a user, and then return secret key 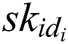 to the user.
to the user.
User-Sign: User 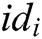 takes public parameters
takes public parameters  , his/her secret key
, his/her secret key 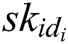 and message
and message 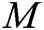 as input to run this algorithm with, and then outputs the signature
as input to run this algorithm with, and then outputs the signature 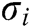 of
of 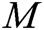 .
.
User-Encrypt: User  usually executes this algorithm after the User-Sign algorithm. User
usually executes this algorithm after the User-Sign algorithm. User 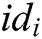 inputs the public parameters
inputs the public parameters  , the signature
, the signature 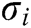 of
of  , and the public keys of the receivers, and then outputs the signcryption message
, and the public keys of the receivers, and then outputs the signcryption message 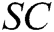 of
of 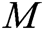 .
.
Verify: To verify the signature  of
of 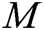 , other users take the signer’s identity
, other users take the signer’s identity 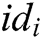 ,
,  and
and 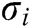 as input to carry out this algorithm. If the signature
as input to carry out this algorithm. If the signature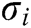 is valid, it returns
is valid, it returns  , otherwise returns
, otherwise returns 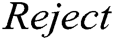 .
.
Receiver-Decrypt: Only the receivers picked by the user can run the algorithm to decrypt 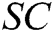 . Any one of the receivers inputs public parameter
. Any one of the receivers inputs public parameter  ,
, 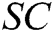 , and the user’s secret key to the algorithm, and then obtains
, and the user’s secret key to the algorithm, and then obtains 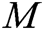 and the sharer’s
and the sharer’s 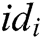 .
.
Definition 1 and Definition 2 respectively introduce the two security attributes of the adapted signcryption scheme: unforgeability and confidentiality.
Definition 1: Suppose F is a forger, ℧ is defined as the MA-IBSC scheme for multiple receivers. The game between F and Challenger C is described as follows:
Global Setup: Challenger C takes a security parameter 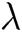 as input, runs global setup algorithm, then generates
as input, runs global setup algorithm, then generates  and transmits it to F.
and transmits it to F.
Authority Setup: Challenger C runs authority setup algorithm to output secret key 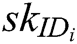 for each authority
for each authority 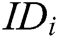 , where
, where 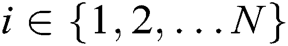 . Then Forger F outputs his/her target identity
. Then Forger F outputs his/her target identity  .
.
Queries: Forger F performs the following four queries to Challenger C:
- Secret key queries: F asks C for the secret key of some authorities 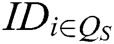 , where
, where 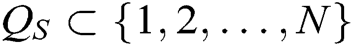 represents the index set of corrupt authorities, and then Challenger C outputs
represents the index set of corrupt authorities, and then Challenger C outputs  to F.
to F.
- Key generation queries: When C receives the private key query about identity 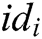 , C runs the key generation algorithm and returns
, C runs the key generation algorithm and returns  to F.
to F.
- User-sign queries: When C receives the signature query about message 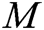 and identity
and identity 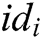 , C returns
, C returns 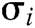 to F.
to F.
- encrypt queries: To forge a signcryption, the user-encrypt query always follows user-sign query. When C receives the encryption query about 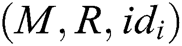 , where
, where 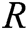 represents the identity set of the receivers, namely,
represents the identity set of the receivers, namely, 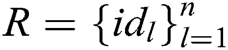 , then C calculates signcryption
, then C calculates signcryption  and returns it to F.
and returns it to F.
Forgery: Forger F finally outputs a new signcryption 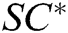 and the public key pair
and the public key pair 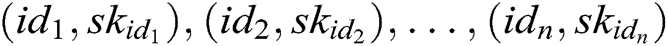 of
of 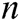 receivers. If
receivers. If  is the signcryption of
is the signcryption of 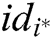 to the message
to the message  and can be correctly decrypted and verified by receivers in set
and can be correctly decrypted and verified by receivers in set 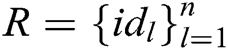 , then
, then  is a valid signcryption and F wins the game. The limitations here are described below. F cannot query the
is a valid signcryption and F wins the game. The limitations here are described below. F cannot query the  with identity
with identity 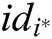 through the key generation query, and
through the key generation query, and  cannot be generated by the User-Sign and User-Encrypt algorithm.
cannot be generated by the User-Sign and User-Encrypt algorithm.
Definition 2: Suppose that A is an adversary, ℧ is defined as the MA-IBSC scheme for multiple receivers. The game between Adversary A and Challenger C is introduced as follows:
Global Setup: Challenger C takes a security parameter  as input, runs global setup algorithm, and then generates
as input, runs global setup algorithm, and then generates  and transmits it to A.
and transmits it to A.
Authority Setup: Challenger C runs authority setup algorithm to output secret key 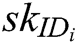 for each authority
for each authority 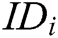 , where
, where 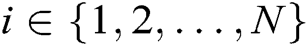 . Adversary A outputs target identities
. Adversary A outputs target identities 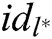 of
of 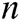 receivers, where
receivers, where 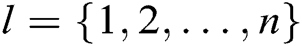 .
.
Phase 1: Adversary A performs the following five queries to Challenger C:
- Secret key queries: A asks C for the secret key of some authorities  , where
, where 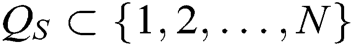 represents the index set of corrupt authorities, and then Challenger C outputs
represents the index set of corrupt authorities, and then Challenger C outputs  to A.
to A.
- Key generation queries: When C receives the private key query about identity 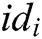 , C runs the key generation algorithm and returns
, C runs the key generation algorithm and returns 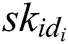 to A.
to A.
- User-sign queries: When C receives the signature query about message  and identity
and identity  , where
, where 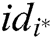 is the user being attacked, then C returns
is the user being attacked, then C returns 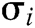 to A.
to A.
- User-encrypt queries: The user-encrypt query always follows the user-sign query. When C receives the encryption query about 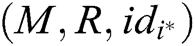 , where
, where 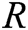 represents the identity set of the receivers, namely
represents the identity set of the receivers, namely 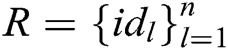 , then C calculates signcryption
, then C calculates signcryption  and returns to A.
and returns to A.
- Receiver-Decrypt-and-Verify queries: When C receives the decryption and verify query together about 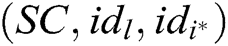 , where
, where 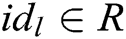 , if
, if 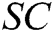 is a valid singcryption, then C decrypts it, verifies
is a valid singcryption, then C decrypts it, verifies 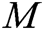 , and returns
, and returns 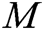 to A.
to A.
Challenge: A outputs a target plaintext pair 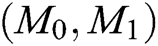 and a private key
and a private key 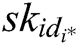 . When Challenger C receives
. When Challenger C receives 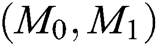 and
and  , C randomly selects a message
, C randomly selects a message 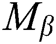 , where
, where 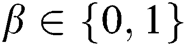 , then generates the target signcryption
, then generates the target signcryption 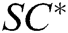 based on
based on 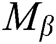 ,
,  and
and 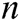 target receivers
target receivers 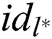 , where
, where 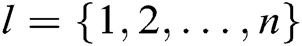 , and finally returns
, and finally returns 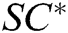 to A.
to A.
Phase 2: A makes multiple queries as those in Phase 1. The limitations here are described below. A cannot ask 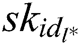 of
of 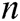 target receivers
target receivers 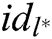 , where
, where 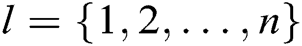 during the key generation query, and A cannot ask
during the key generation query, and A cannot ask during Receiver-Decrypt-and-Verify query.
during Receiver-Decrypt-and-Verify query.
Guess: In the end, A outputs its guess  and wins the game if
and wins the game if 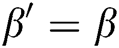 .
.
3 EHRs System Model in Blockchain
In this section, the EHRs system model in blockchain is introduced in detail. The model combines the EHRs system with the MA-IBSC scheme for multiple receivers, realizes the sharing of EHRs in the blockchain, and ensures the privacy and validity of EHRs. The system roles, EHRs storage mode, authentication cases, and the application of the signcryption scheme are introduced below.
There are three main roles in EHRs system in the blockchain: EHRs server, authority, and user.
EHRs Server: The EHRs server is mainly responsible for generating public parameters  in EHRS system initialization, and distributing corresponding identity for each authority and each user in the system.
in EHRS system initialization, and distributing corresponding identity for each authority and each user in the system.
Authority: The authorities include all medical departments: hospitals, pharmacies, health insurance companies, medical research institutes and so on. As the bookkeeping nodes in the blockchain, they package a set of transactions that are broadcast on the network and upload them to the new block created by them through the DPoS consensus mechanism.
User: As ordinary nodes in the blockchain, users primarily create new transactions and publish them to the network. Users include patients, medical workers and common people. Patients create their own EHRs after treatment, and then adopt MA-IBSC scheme to share their private EHRs with other designated users in the blockchain.
EHRs of patients are generally private data and cannot be directly uploaded to the blockchain for sharing. Therefore, we adopt the on-chain and off-chain storage mode and only upload the address of the stored EHRs to the blockchain. The EHRs are signcrypted and stored in the off-blockchain database of each node, and the decryption permission is set at the same time. This storage mode enables patient’s EHRs to be safely shared among the users that the patient designates.
As shown in Fig. 1, when a patient creates his/her own new EHRs after diagnosis or treatment, he/she uses his/her secret key and the public keys of users, whom he/she wants to share the data with, to signcrypt the EHRs, and stores the signcrypted data in his/her off-blockchain database. Then he/she signs the address of the stored EHRs and publishes it to the blockchain.
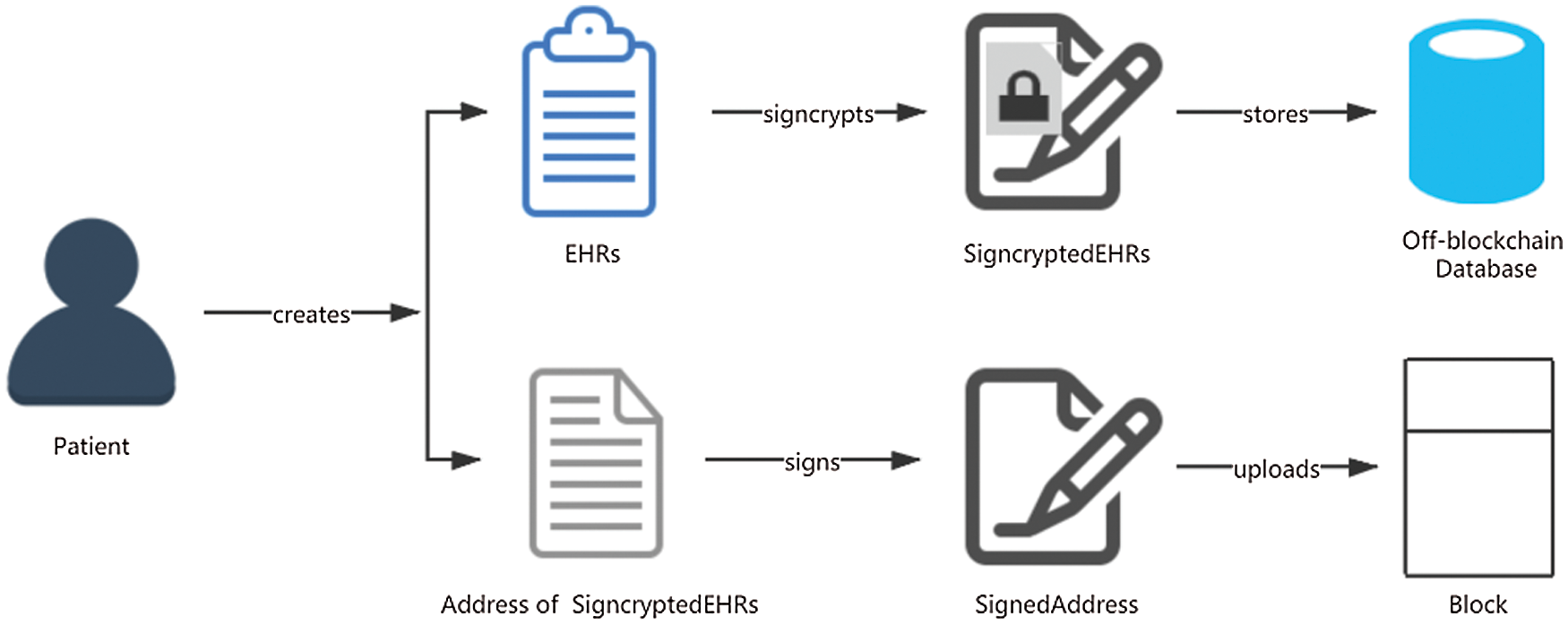
Figure 1: Storage Mode of EHRs in Blockchain
To guarantee that the EHRs shared by the patient and the storage address of the EHRs broadcast by the patient in the blockchain are real, it is necessary to perform authentication. Authentication is mainly performed by verifying the signature of the sharer. Based on the system model and EHRs storage mode, authentication can be mainly classified into the following two cases:
- Case 1 (Signature Authentication): Only the address of the stored EHRs is uploaded to the blockchain. Therefore, the patient needs to sign it with his/her own secret key, and other users can verify the authenticity and validity of the address.
- Case 2 (Signcryption Authentication): All users can retrieve the patient’s signcrypted EHRs with the address stored in the blockchain. However, only the users (such as doctors, family members, and friends) authorized by the patient can decrypt the EHRs with their secret key, and then verify the signature of the patient to ensure the authenticity of the patient’s identity and the EHRs.
3.4 Application of the Sigcryption Scheme
For the purposes of realizing the signcryption of EHRs and the two authentication cases, we describe the relationships between the system roles and the MA-IBSC scheme for multiple receivers below.
First, the EHRs server runs the Global Setup algorithm to generate the public parameters of the system. Next, each authority performs Authority Setup algorithm to produce its own secret key and then cooperates with other authorities to generate the master secret key and the master public key of the system. After that, with the identity of each user in the system, each authority runs the KenGen algorithm and jointly distribute the secret key to the user. After receiving the secret key, the patient uses User-Sign algorithm to sign his/her own EHRs, executes User-Encrypt algorithm immediately, encrypts the signed EHRs with the public keys of the receivers whom he/she wants to share the data with. In this way, the decryption permission is set for these designated receivers. After storing the signcrypted EHRs in the off-blockchain database, the patient executes the User-Sign algorithm again and broadcasts the signed storage address of EHRs. All other nodes (authorities or users) can verify the validity of the address given by the patient by executing the Verify algorithm. Then, for a period of time, the bookkeeping node packs the storage addresses of EHRs signed by some patients, and uploads them to a new block, which is connected by the hash value of the previous block to form a blockchain. The data structure of blockchain is shown in Fig. 2.
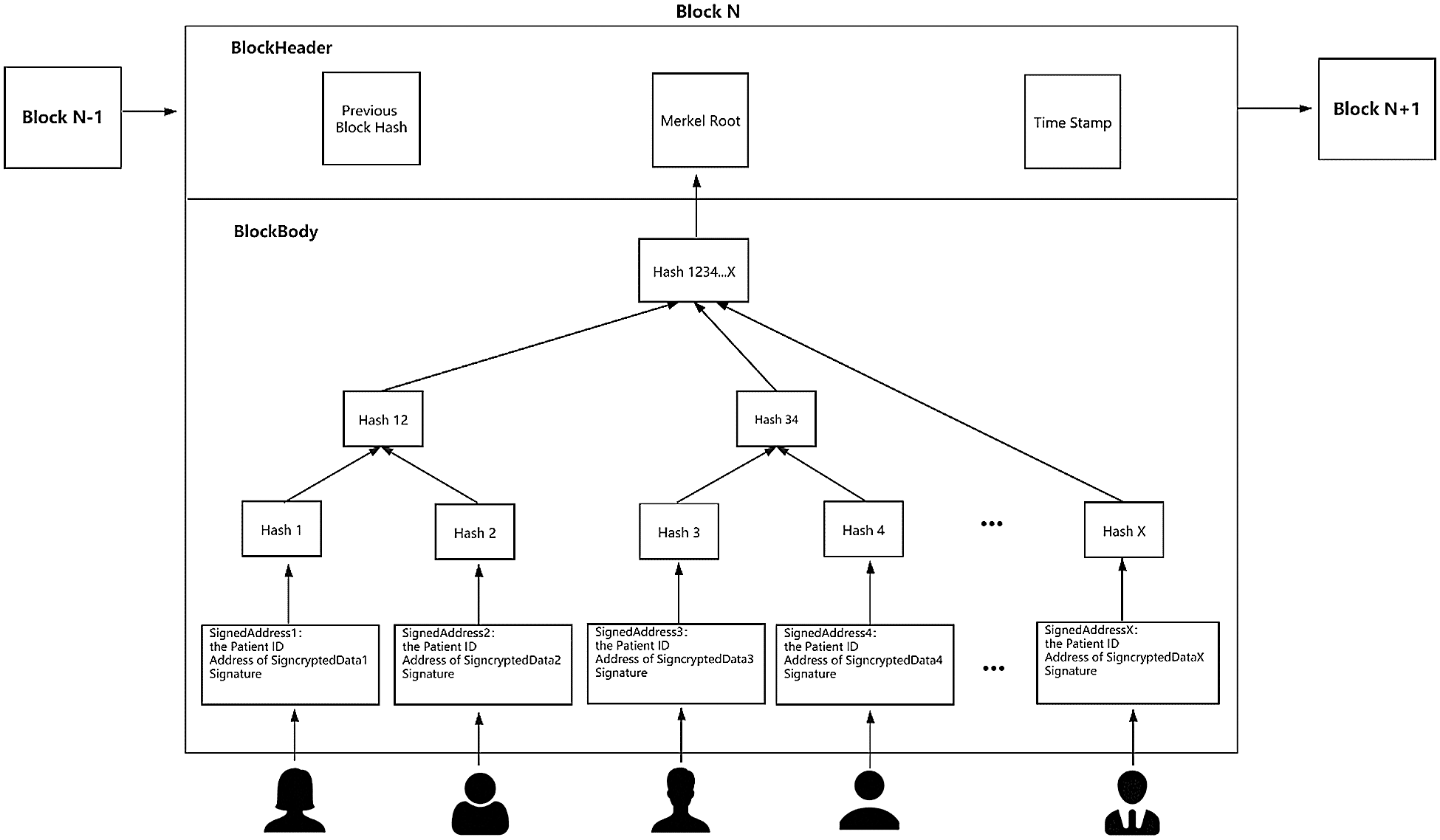
Figure 2: Data Structure of Blockchain in EHRs System
When other users want to access the patient’s EHRs, they retrieve the patient’s signcrypted data in the off-blockchain database through the storage address on the blockchain and then run the Receiver-Decrypt algorithm. Only receivers with the decryption permission set by the patient can decrypt the signcrypted EHRs with their secret keys, and then run the Verify algorithm to ensure that the real EHRs are obtained.
4 Proposed Signcryption Scheme
Based on the EHRs system of blockchain, we propose an identity-based signcryption with multiple authorities (MA-IBSC) scheme for multiple receivers. In the scheme, users are issued their secret keys from 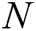 authorities. In addition, a user can send the same signcryption information to multiple receivers. The anonymity of the receivers is realized by Lagrange interpolation.
authorities. In addition, a user can send the same signcryption information to multiple receivers. The anonymity of the receivers is realized by Lagrange interpolation.
The detailed MA-IBSC scheme for multiple receivers is introduced bellow:
Global Setup: The EHRs server chooses two suitable multiplicative cyclic groups  and
and 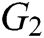 with a prime order
with a prime order 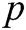 , equipped with a bilinear map
, equipped with a bilinear map  . Assuming that
. Assuming that  is a random generator of
is a random generator of 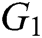 , an element
, an element 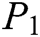 in
in 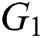 is randomly selected. There are four strong collision-resistant hash functions
is randomly selected. There are four strong collision-resistant hash functions  ,
,  ,
, 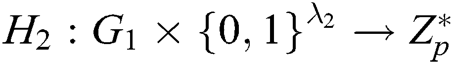 , and
, and 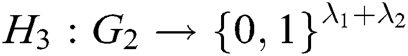 , where
, where  and
and 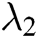 represent the length of each user’s identity and the length of message, respectively. Suppose that there are
represent the length of each user’s identity and the length of message, respectively. Suppose that there are 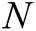 authorities in the system. The public parameters of the system are
authorities in the system. The public parameters of the system are 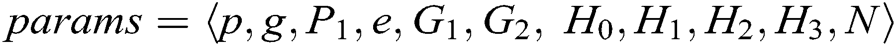 .
.
Authority Setup: Each authority runs this algorithm with the input of public parameters 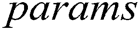 and identity
and identity 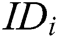 , where
, where 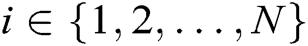 . The two phases of generating master secret key
. The two phases of generating master secret key  , master public key
, master public key 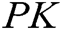 and authority’s secret key
and authority’s secret key  , where
, where 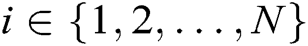 , are described as follows:
, are described as follows:
- Phase 1 (generation of the master secret key of the system and the secret key of each authority):
1) First, each authority  randomly selects a polynomial
randomly selects a polynomial  of
of  degree over
degree over  :
:
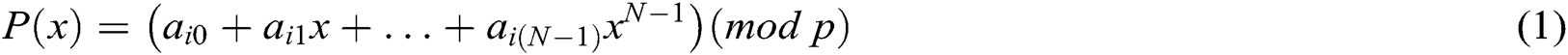
To hide the polynomial coefficients, 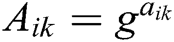 is calculated and broadcast, where
is calculated and broadcast, where 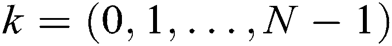 . Second, it calculates secret shares
. Second, it calculates secret shares  , where
, where  . Finally, it secretly sends
. Finally, it secretly sends  to
to  for
for .
.
2) After receiving the secret share 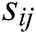 from
from  , each authority
, each authority 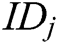 verifies whether the equation
verifies whether the equation 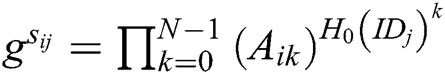 holds. If it holds, the secret share
holds. If it holds, the secret share  is valid and the sender
is valid and the sender  is considered to be honest. If not,
is considered to be honest. If not,  broadcasts a complaint against
broadcasts a complaint against 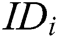 . Then, to prove its honesty,
. Then, to prove its honesty, 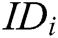 needs to keep broadcasting the secret shares
needs to keep broadcasting the secret shares 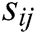 until the equation holds.
until the equation holds.
3) After the above interactions, 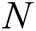 authorities jointly generate the master secret key
authorities jointly generate the master secret key  . If the number of corrupt authorities is less than
. If the number of corrupt authorities is less than  , they cannot recover
, they cannot recover  . The secret key of each authority
. The secret key of each authority  is the constant term of its randomly selected polynomial, namely,
is the constant term of its randomly selected polynomial, namely, 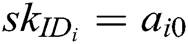 , where
, where 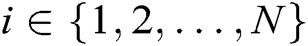 .
.
- Phase 2 (generation of the master public key of system): In Phase 1, each authority has broadcast a publicly verifiable value 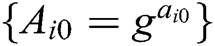 , where
, where 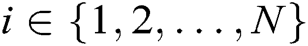 . Thus, the master public key
. Thus, the master public key 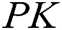 is calculated as:
is calculated as:
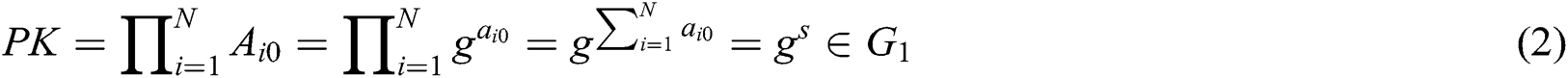
Finally, each authority adds parameters  and
and  to
to 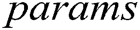 , which is finally expressed as:
, which is finally expressed as:
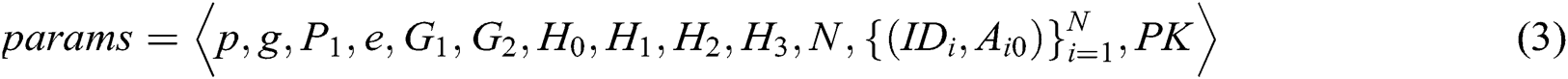
KeyGen: When a user with his/her identity 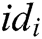 registers in the EHRs system of blockchain, he/she obtains his/her public key
registers in the EHRs system of blockchain, he/she obtains his/her public key 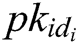 and secret key
and secret key 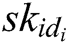 from
from 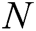 authorities. The process consists of the following three phases.
authorities. The process consists of the following three phases.
- Phase 1 (generation of the public key and partial secret key): First, every authority 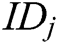 , where
, where 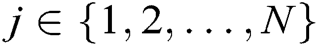 , calculates the user’s public key
, calculates the user’s public key 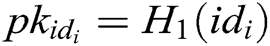 with his/her identity
with his/her identity 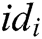 , then calculates partial secret key
, then calculates partial secret key 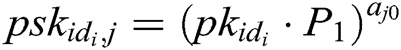 and secretly sends it to
and secretly sends it to  .
.
- Phase 2 (verification of the partial secret key): After receiving the 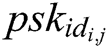 from authority
from authority  ,
, 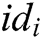 verifies whether the equation
verifies whether the equation  holds. If it holds, the partial secret key is valid. If not, the authority
holds. If it holds, the partial secret key is valid. If not, the authority 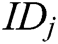 needs to transmit the partial secret key again until the equation holds.
needs to transmit the partial secret key again until the equation holds.
- Phase 3 (generation of the secret key): Through the above interactions, user 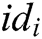 receives all partial secret keys from
receives all partial secret keys from 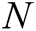 authorities, and then calculates his/her secret key
authorities, and then calculates his/her secret key 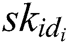 as:
as:
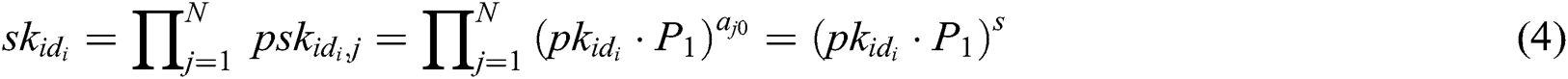
User-Sign: To sign a message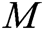 , user (mainly refers to the patient user in the system)
, user (mainly refers to the patient user in the system)  selects a random integer
selects a random integer 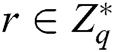 , and then calculates
, and then calculates 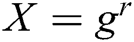 ,
, 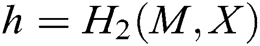 and
and 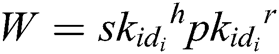 . The signature
. The signature 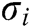 of message
of message  is
is 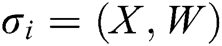 .
.
User-Encrypt: To complete the signcryption of 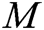 , this algorithm is usually used after the User-Sign algorithm. Encryption is mainly divided into the following six steps. First, user
, this algorithm is usually used after the User-Sign algorithm. Encryption is mainly divided into the following six steps. First, user 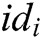 calculates
calculates 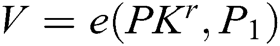 ,
, 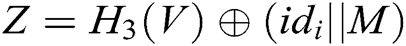 . Second, he/she selects other users whom he/she wants to share message
. Second, he/she selects other users whom he/she wants to share message 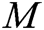 with, counts the number
with, counts the number 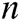 of these receivers, calculates
of these receivers, calculates  and
and  based on the identity
based on the identity 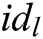 of the
of the 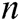 receivers, where
receivers, where 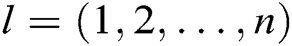 , and then gets
, and then gets 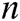 sets of data:
sets of data: 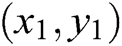 ,
,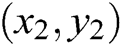 ,
,  ,
,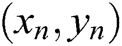 . Third,
. Third, 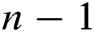 degree polynomial
degree polynomial 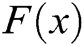 is constructed by Lagrange interpolation, so that
is constructed by Lagrange interpolation, so that 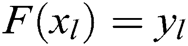 , where
, where 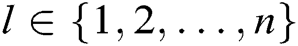 . Fourth, for
. Fourth, for  , the user
, the user  calculates
calculates
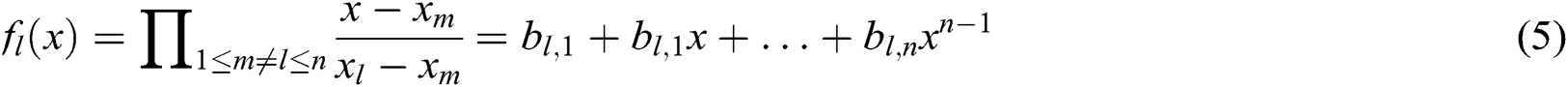
After that, for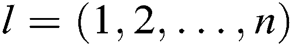 ,
, 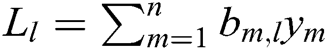 is calculated. Finally, the signcryption of
is calculated. Finally, the signcryption of 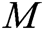 is expressed as:
is expressed as:

As you can see, the identity information of receivers is not directly displayed in the 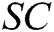 .
.
Verify: To verify the validity of signature 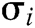 from user
from user 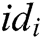 , first, other users calculate
, first, other users calculate 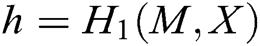 , and then verify whether the equation
, and then verify whether the equation 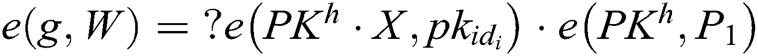 holds or not. If it holds, the signature from
holds or not. If it holds, the signature from 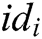 is valid and it returns
is valid and it returns 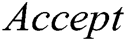 . If not, it returns
. If not, it returns 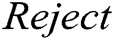 .
.
Receiver-Decrypt: Only the receiver with identity 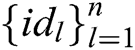 designated by sharer
designated by sharer  has the right to decrypt the signcryption
has the right to decrypt the signcryption  and obtain message
and obtain message  . The receiver
. The receiver 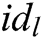 takes
takes 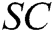 ,
,  , his/her identity
, his/her identity 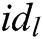 and secret key
and secret key 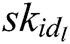 as inputs to run this algorithm. He/she first calculates
as inputs to run this algorithm. He/she first calculates 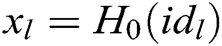 ,
,  , and
, and 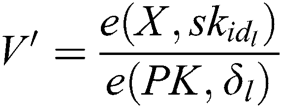 and then gets the message
and then gets the message 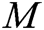 and the identity
and the identity 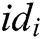 of the signer through the following calculation:
of the signer through the following calculation:

Correctness:
1) The correctness of signature 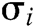 from user
from user  is derived from the following equation:
is derived from the following equation:
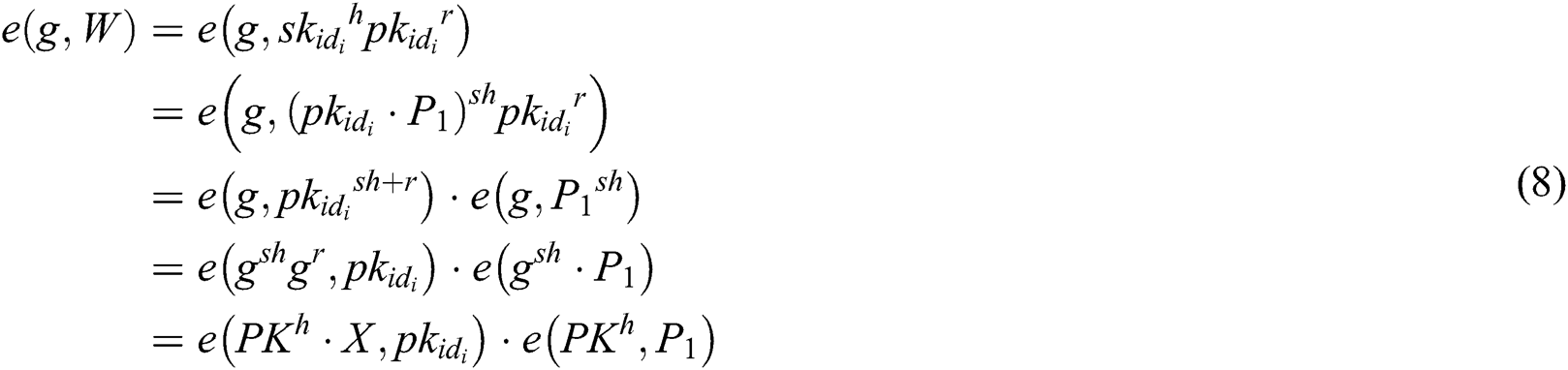
2) When 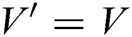 , message
, message  of the user
of the user 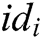 can be obtained. For each
can be obtained. For each 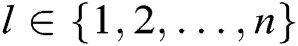 , there is
, there is 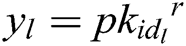 . According to Lagrange interpolation, we can calculate:
. According to Lagrange interpolation, we can calculate:

Thus, the correctness of decryption is derived from the following two equations:

and

5 Security Analysis and Performance Evaluation
In this section, Theorem 1 and Theorem 2 respectively prove the unforgeability and confidentiality of signcryption.
The master secret key 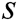 is randomly generated by
is randomly generated by  authorities by the distributed key generation and no one knows the real value of
authorities by the distributed key generation and no one knows the real value of  , so
, so 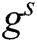 cannot be used as an instance of CDH problem. Here, we set
cannot be used as an instance of CDH problem. Here, we set 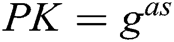 , where
, where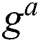 is a CDH instance.
is a CDH instance. 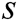 is still generated by all authorities randomly and unknown to others,
is still generated by all authorities randomly and unknown to others, 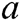 and
and 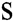 are independent of each other. For any PPT adversary, even if he/she corrupts
are independent of each other. For any PPT adversary, even if he/she corrupts 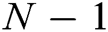 authorities, he/she cannot recover the value
authorities, he/she cannot recover the value 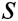 . Therefore, for the PPT adversary,
. Therefore, for the PPT adversary, 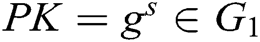 and
and 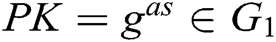 are indistinguishable.
are indistinguishable.
Theorem 1: In the random oracle model, if there is a probabilistic polynomial time (PPT) adversary F, who can win the Definition 1 game in Section 2.5 with a non-negligible advantage 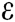 within time
within time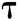 , then there is an algorithm C that can solve the CDH problem with the advantage
, then there is an algorithm C that can solve the CDH problem with the advantage  within time
within time 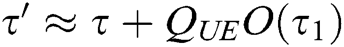 , where
, where 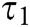 is the running time of
is the running time of 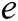 . (PPT adversary can make
. (PPT adversary can make  secret key quires,
secret key quires,  key generation quires,
key generation quires, 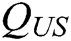 user-sign quires,
user-sign quires, 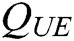 user-encrypt quires and
user-encrypt quires and 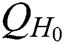 ,
,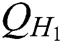 ,
,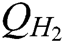 ,
, 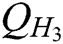 hash function
hash function 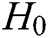 ,
, 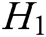 ,
,  ,
, quires at most).
quires at most).
Proof: The following shows how algorithm C uses F to solve the CDH problem with probability  within time
within time 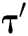 .
.
First, C gets an instance  of CDH problem, whose goal is to calculate
of CDH problem, whose goal is to calculate  . C simulates a challenger to play the following game with F.
. C simulates a challenger to play the following game with F.
Global Setup: Challenger C executes global setup algorithm, inputs parameter  , outputs public parameter
, outputs public parameter  and sends it to F.
and sends it to F.
Authority Setup: C represents all authorities to run the authority setup algorithm and generate secret key 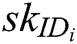 for each authority
for each authority 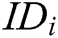 , where
, where  , so only C knows the real value
, so only C knows the real value 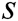 of the master secret key. However, C sets the master secret key as
of the master secret key. However, C sets the master secret key as  , and sets the public key as
, and sets the public key as 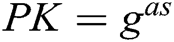 . Because
. Because 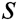 and
and  are unknown to F,
are unknown to F, 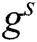 and
and 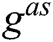 are indistinguishable to F. Finally, C adds parameters
are indistinguishable to F. Finally, C adds parameters  and
and 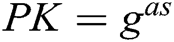 to
to 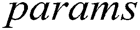 . F can obtain
. F can obtain 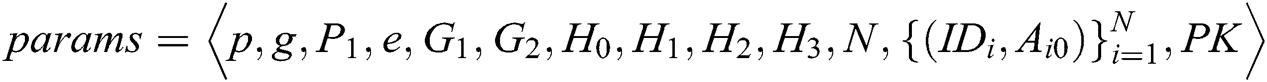 from C. After receiving the
from C. After receiving the 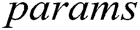 , F outputs the target identity
, F outputs the target identity  .
.
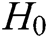 ,
, 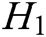 ,
,  , and
, and 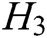 are random oracle models controlled by C. The query results of
are random oracle models controlled by C. The query results of 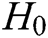 ,
, 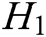 ,
, 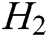 , and
, and 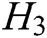 are stored in
are stored in 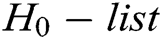 ,
,  ,
, 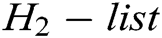 , and
, and 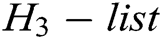 respectively.
respectively.
Queries: Forger F performs some queries to Challenger C:
- 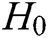 queries: C enters an identity
queries: C enters an identity 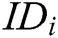 or
or 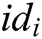 into
into 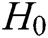 . If there is
. If there is 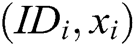 or
or 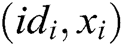 in the
in the 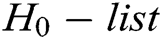 , returns
, returns 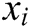 , otherwise C performs the following steps:
, otherwise C performs the following steps:
1) Randomly selects an integer 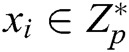 ;
;
2) Saves 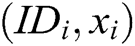 or
or 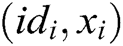 to
to  ;
;
3) Returns 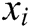 .
.
- 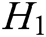 queries: C enters an identity
queries: C enters an identity 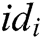 into
into . If there is
. If there is 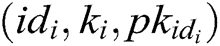 in the
in the  , returns
, returns 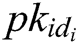 , otherwise C performs the following steps:
, otherwise C performs the following steps:
1) Randomly selects an integer 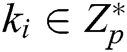 ;
;
2) If 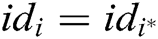 , (where
, (where 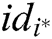 is C random guess of the identity that F will attack) calculates
is C random guess of the identity that F will attack) calculates 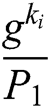 , otherwise calculates
, otherwise calculates  ;
;
3) Saves 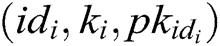 to
to  ;
;
4) Returns  .
.
- 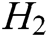 queries: C enters an array
queries: C enters an array 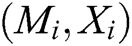 into
into 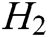 . If there is
. If there is 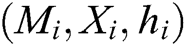 in the
in the  , returns
, returns  , otherwise C performs the following steps:
, otherwise C performs the following steps:
1) Randomly selects an integer 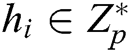 ;
;
2) Saves 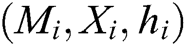 to
to 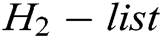 ;
;
3) Returns 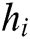 .
.
- 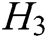 queries: C enters an element
queries: C enters an element 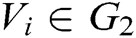 into
into  . If there is
. If there is 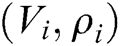 in the
in the 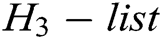 , returns
, returns  otherwise C performs the following steps:
otherwise C performs the following steps:
1) Randomly selects a character string  ;
;
2) Saves 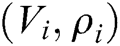 to
to 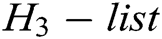 ;
;
3) Returns 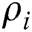 .
.
- Secret key queries: F requests secret keys 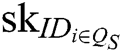 of authority
of authority 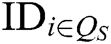 , where
, where 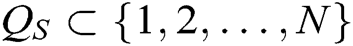 represents the index set of corrupt authorities. Because C generates the secret keys of all authorities , C can answer the queries from F.
represents the index set of corrupt authorities. Because C generates the secret keys of all authorities , C can answer the queries from F.
- Key generation queries: F asks C about the secret key 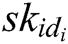 of the identity
of the identity  . If
. If 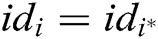 , C does not answer this query and terminate the game. Otherwise, C looks for
, C does not answer this query and terminate the game. Otherwise, C looks for 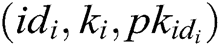 in
in 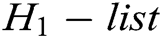 , calculates
, calculates 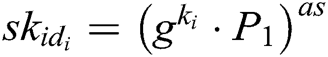 , and then returns it to F.
, and then returns it to F.
- User-sign queries: F asks C for the signature 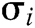 of a tuple
of a tuple  . If
. If 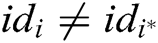 , C will get the correct
, C will get the correct 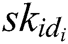 from key generation queries, and then calculates the signature
from key generation queries, and then calculates the signature 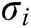 and transmits it to F. If
and transmits it to F. If 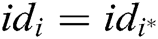 , C cannot obtain
, C cannot obtain  from key generation queries to calculate the signature directly. However, C can answer F’s query through the following steps: 1) C randomly selects
from key generation queries to calculate the signature directly. However, C can answer F’s query through the following steps: 1) C randomly selects 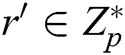 and calculates
and calculates 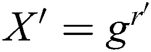 . 2) C finds
. 2) C finds 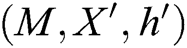 in
in 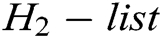 list and gets
list and gets 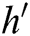 . 3) C finds
. 3) C finds  in
in  (if it cannot be found, C chooses
(if it cannot be found, C chooses 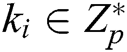 , then calculates
, then calculates  and stores
and stores 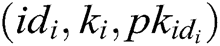 in
in 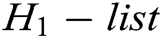 ). 4) C calculates
). 4) C calculates 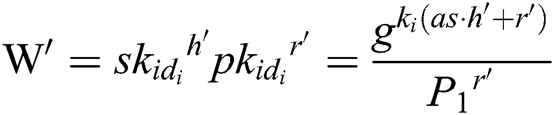 , and then gets
, and then gets  and returns it to F.
and returns it to F.
- User-encrypt queries: To forge a signcryption, the query is executed after the user-sign query. When C receives the encryption query about 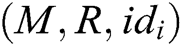 , where
, where  and
and 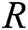 represents a receiver set
represents a receiver set 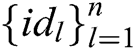 (
(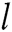 represents the identity of receivers and
represents the identity of receivers and  represents the number of receivers), C answers F through the following steps: 1) C calculates
represents the number of receivers), C answers F through the following steps: 1) C calculates  , and then finds
, and then finds  in the
in the  . 2) C calculates
. 2) C calculates ; 3) C finds
; 3) C finds  in the H0 – list, calculates
in the H0 – list, calculates 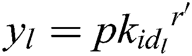 and gets
and gets  , where
, where 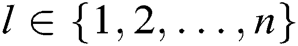 . 4) C gets the signcryption
. 4) C gets the signcryption 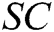 and sends it to F.
and sends it to F.
Forgery: F generates the target signcryption:
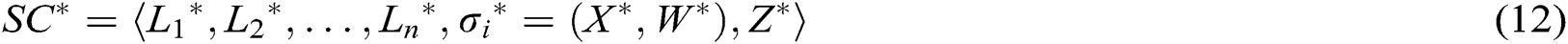
If the forgery is successful, the following equation holds:
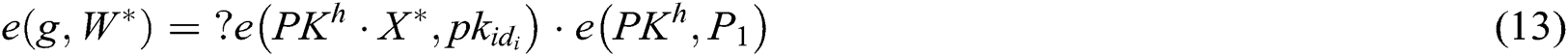
Define 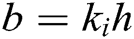 , then
, then 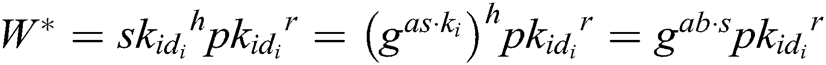 . Therefore, we can get the solution of CDH problem
. Therefore, we can get the solution of CDH problem  .
.
In the general signcryption query, as most  queries are conducted, the probability that C fails to answer a signcryption query is not greater than
queries are conducted, the probability that C fails to answer a signcryption query is not greater than 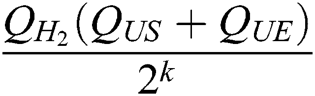 . Therefore, C can get the advantage
. Therefore, C can get the advantage  and
and  , where
, where  is the running time of
is the running time of 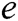 . From the above proof and CDH problem, we can see that this scheme satisfies the unforgeability of signcryption.
. From the above proof and CDH problem, we can see that this scheme satisfies the unforgeability of signcryption.
Theorem 2: In the random oracle model, if there is a probabilistic polynomial time (PPT) adversary A, who can win the Definition 2 game in Section 2.5 with a non-negligible advantage 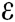 within time
within time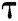 , then there is an algorithm C that can solve the BCDH problem with the advantage
, then there is an algorithm C that can solve the BCDH problem with the advantage  within time
within time 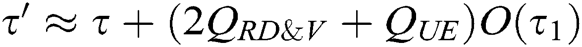 , where
, where  is the running time of
is the running time of 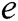 . (PPT adversary can make
. (PPT adversary can make 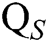 secret key quires,
secret key quires, 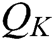 key generation quires,
key generation quires,  user-sign quires,
user-sign quires,  user-encrypt quires,
user-encrypt quires, 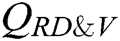 receiver-decrypt-and-verify quires and
receiver-decrypt-and-verify quires and 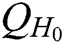 ,
,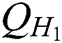 ,
, , and
, and 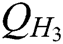 hash function
hash function 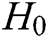 ,
,  ,
, 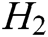 , and
, and 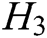 quires at most).
quires at most).
Proof: The following shows how algorithm C uses A to solve the BCDH problem with probability 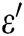 within time
within time 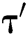 .
.
First, C gets an instance  of BCDH problem, whose goal is to calculate
of BCDH problem, whose goal is to calculate 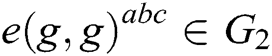 . C simulates a challenger to play the following game with A.
. C simulates a challenger to play the following game with A.
Global Setup: Challenger C executes global setup algorithm, inputs parameter 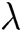 , outputs public parameter
, outputs public parameter 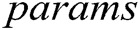 and sends it to F.
and sends it to F.
Authority Setup: C represents all authorities to run authority setup algorithm and generate secret key 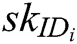 for each authority
for each authority 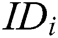 , where
, where 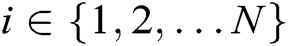 . Similarly, C sets
. Similarly, C sets  instead of
instead of 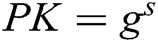 , where
, where  and
and 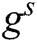 are indistinguishable to A. Finally, C adds parameters
are indistinguishable to A. Finally, C adds parameters  and
and 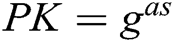 to
to  . A can obtain
. A can obtain 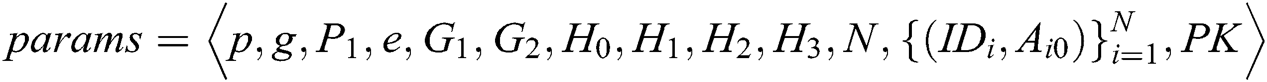 from C. After receiving the
from C. After receiving the 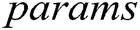 , A outputs target identities
, A outputs target identities 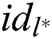 of
of 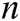 receivers, where
receivers, where 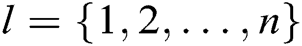 .
.
Phase 1: Adversary A performs the following five queries to Challenger C:
- Secret key queries: A requests secret keys 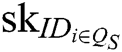 of authority
of authority 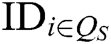 , where
, where 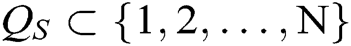 represents the index set of corrupt authorities. Because C generates the secret keys of all authorities , C can answer the queries from A.
represents the index set of corrupt authorities. Because C generates the secret keys of all authorities , C can answer the queries from A.
- Key generation queries: A asks C about the secret key 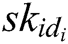 of the identity
of the identity  . If
. If 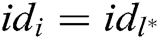 , where
, where 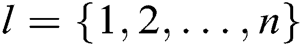 , C does not answer this query and terminate the game. Otherwise, C looks for
, C does not answer this query and terminate the game. Otherwise, C looks for 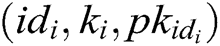 in
in  , then calculates
, then calculates 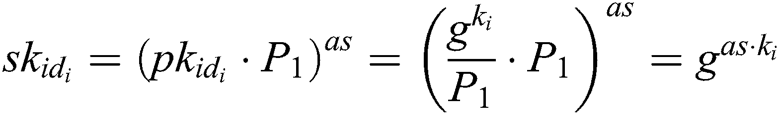 , and returns it to A.
, and returns it to A.
- User-sign queries: A asks C about the signature 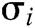 of a tuple
of a tuple 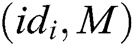 , where
, where 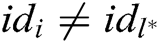 (
(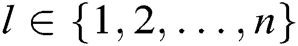 ). C answers A through the following calculations: 1) C randomly selects
). C answers A through the following calculations: 1) C randomly selects 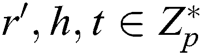 , calculates
, calculates  ,
,  ,
,  , and gets
, and gets  . 2) C finds
. 2) C finds 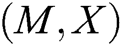 in
in 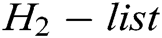 so that it does not appear in
so that it does not appear in 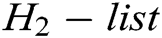 . Otherwise, C reselects
. Otherwise, C reselects 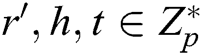 , repeats the above calculation step, and then adds eligible
, repeats the above calculation step, and then adds eligible 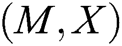 to
to  . 3) C gets
. 3) C gets 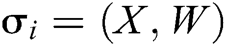 of
of 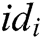 and returns it to A.
and returns it to A.
- User-encrypt queries: To form a complete signcryption, the query is executed after the user-sign query. When C receives the encryption query about 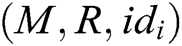 , where
, where 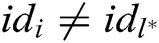 and
and 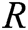 represents a set of
represents a set of  receivers
receivers 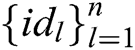 , C answer A through the following steps: 1) C calculates
, C answer A through the following steps: 1) C calculates 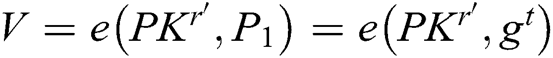 , and then finds
, and then finds  in the
in the 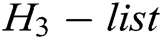 . 2) C calculates
. 2) C calculates . 3) C finds
. 3) C finds 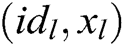 in the
in the  , calculates
, calculates 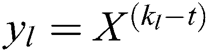 and gets
and gets 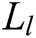 , where
, where 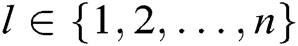 . 4) C gets the signcryption
. 4) C gets the signcryption 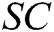 and sends it to A.
and sends it to A.
- Receiver-Decrypt-and-Verify queries: When C receives the decrypt-and-verify query about a signcryption 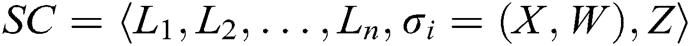 and an identity
and an identity  , where
, where 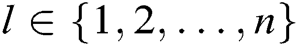 , C answers A through the following steps: 1) C finds
, C answers A through the following steps: 1) C finds 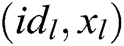 in the
in the 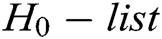 and calculates
and calculates 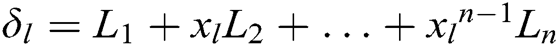 . 2) C finds
. 2) C finds 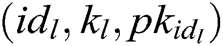 in the
in the 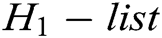 , then calculates
, then calculates 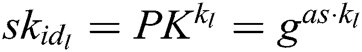 and
and 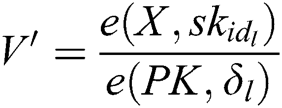 , so C can obtain
, so C can obtain 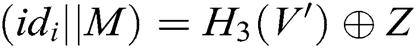 . 3) C finds
. 3) C finds 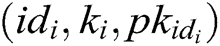 in
in 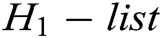 and gets
and gets 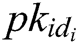 . 4) C verifies that
. 4) C verifies that  holds. If it holds,
holds. If it holds, 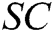 is a valid signcryption and
is a valid signcryption and 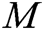 is returned to A.
is returned to A.
Challenge: A selects a target plaintext pair 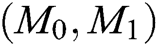 and identity
and identity 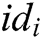 of the same signer and encryptor. When Challenger C receives
of the same signer and encryptor. When Challenger C receives 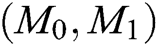 and
and 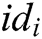 , C randomly selects a message
, C randomly selects a message 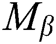 to signcrypt, where
to signcrypt, where 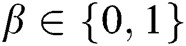 . The signcryption calculation is as follows: 1) C finds
. The signcryption calculation is as follows: 1) C finds 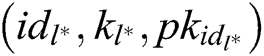 in
in 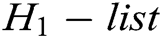 , where
, where 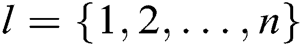 , and then obtains their
, and then obtains their 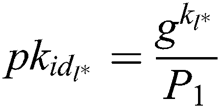 . 2) C calculates
. 2) C calculates  and gets
and gets 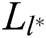 , where
, where  . 3) C generates the target signcryption
. 3) C generates the target signcryption  , where
, where 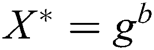 ,
,  ,
, 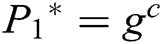 ,
, 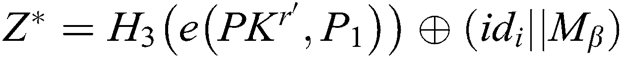 , and returns
, and returns 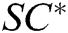 to A.
to A.
Phase 2: A makes multiple queries as those in Phase 1. Note that A cannot ask 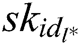 of
of 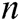 target receivers
target receivers 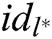 , where
, where 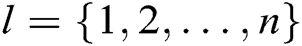 during the key generation query, or
during the key generation query, or  during Receiver-Decrypt-and-Verify query.
during Receiver-Decrypt-and-Verify query.
Guess: In the end, A outputs its guess  . If
. If 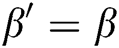 , C selects
, C selects 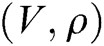 from
from 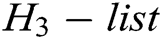 and outputs
and outputs 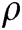 as the solution of BCDH problem.
as the solution of BCDH problem.
Analysis: In User-sign and User-encrypt quires, since 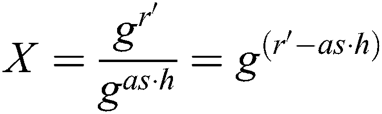 , there is
, there is 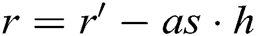 , and
, and 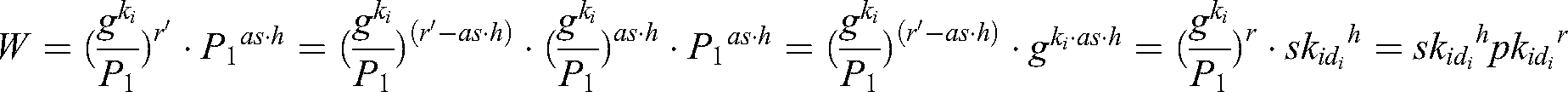 . Because
. Because 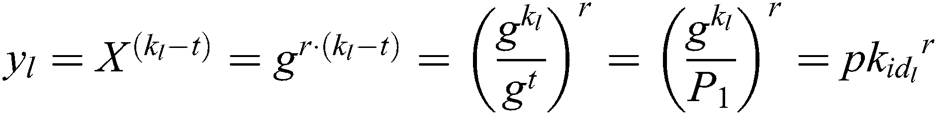 , where
, where 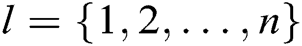 ,
,  can be calculated and the target signcryption can be realized.
can be calculated and the target signcryption can be realized.
During the challenge process, C sets 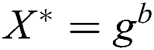 and
and 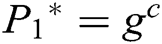 . After knowing
. After knowing  , C can get
, C can get 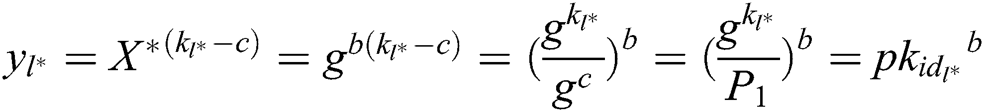 , and then get
, and then get 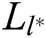 by Lagrange interpolation function. Therefore,
by Lagrange interpolation function. Therefore,  is the same as described in the actual attack process. If A’s guess is correct, A needs to ask the random oracle function
is the same as described in the actual attack process. If A’s guess is correct, A needs to ask the random oracle function 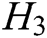 to get
to get 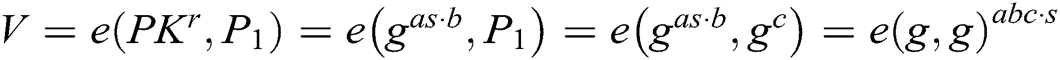 , Therefore, we can get the solution of BCDH problem
, Therefore, we can get the solution of BCDH problem 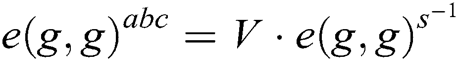 .
.
In the attack phase, A performs 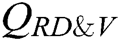 receiver-decrypt-and-verify quires. C selects
receiver-decrypt-and-verify quires. C selects 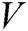 randomly from
randomly from 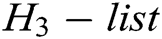 to calculate
to calculate  as the result of BCDH problem. Therefore, C can get the advantage
as the result of BCDH problem. Therefore, C can get the advantage  , and
, and 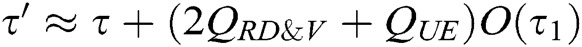 , where
, where 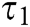 is the running time of
is the running time of  . From the above proof and BCDH problem, we can see that this scheme satisfies the confidentiality of signcryption.
. From the above proof and BCDH problem, we can see that this scheme satisfies the confidentiality of signcryption.
In this paper, we mainly evaluate the performance from signcryption efficiency and signcryption attributes.
In order to explore the signcryption efficiency, we mainly analyze its computing cost and communication traffic (i.e., length of signcryption). Tab. 1 shows the comparison results of the signcryption efficiency between the proposed scheme and prvious schemes.
Table 1: Comparison of the Signcryption Efficiency

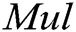 represents multiplication operation in
represents multiplication operation in 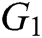 ;
; 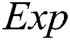 represents exponential operation in
represents exponential operation in 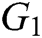 ;
; 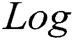 represents logical operation;
represents logical operation;  represents bilinear operation in
represents bilinear operation in 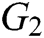 ;
;  represents the hash operation in the signature and encryption step;
represents the hash operation in the signature and encryption step;  represents the number of parameters;
represents the number of parameters; 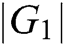 represents the length of elements in
represents the length of elements in 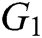 ;
; 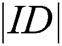 represents the length of identity information;
represents the length of identity information; 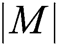 represents the length of plaintext message;
represents the length of plaintext message; 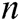 represents the number of receivers.
represents the number of receivers.
Tab. 2 shows the comparison results of signcryption attributes between the proposed scheme and previous schemes.
Table 2: Comparison of the Signcryption Attributes

Compared with previous schemes, the proposed scheme has less 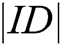 length and relatively moderate communication traffic in terms of signcryption efficiency. In order to ensure that the identities of receivers are not exposed in the signcrypted message, our scheme uses Lagrange interpolation to realize the anonymity of receivers. Lagrange interpolation involves many multiplications and exponential operations, so it increases the computing cost and affects the efficiency. However, the Lagrange formula can be calculated before the signcryption, so the operation in the signcryption step can be greatly reduced.
length and relatively moderate communication traffic in terms of signcryption efficiency. In order to ensure that the identities of receivers are not exposed in the signcrypted message, our scheme uses Lagrange interpolation to realize the anonymity of receivers. Lagrange interpolation involves many multiplications and exponential operations, so it increases the computing cost and affects the efficiency. However, the Lagrange formula can be calculated before the signcryption, so the operation in the signcryption step can be greatly reduced.
In terms of signcryption attributes, the signcryption scheme proposed in this paper satisfies unforgeability and confidentiality under a random oracle model. Compared with other schemes, the proposed scheme is more suitable for multiple receivers and can guarantee the anonymity of receivers. Importantly, the distributed key generation is realized by multiple authorities and can resist collusion attacks.
In order to allow patients to control their own EHRs initiative and share EHRs safely in blockchain, in this paper, we introduced multiple authorities into the identity-based signcryption scheme, and constructed a detailed MA-IBSC scheme for multiple receivers. The MA-IBSC scheme can not only resist the collusion attack of at most N-1 corrupted authorities, but also share the same signcryption message with multiple designated receivers. At the same time, the identity information of these receivers is anonymous. Under the assumptions of CDH and BCDH, it is proved that the proposed scheme is secure, that is, it satisfies unforgeability and confidentiality of signcryption.
Funding Statement: This work was supported by the National Key Research and Development Project of China (Grant No. 2017YFB0802302), the Science and Technology Support Project of Sichuan Province (Grant Nos. 2016FZ0112, 2017GZ0314, and 2018GZ0204), the Academic and Technical Leaders Training Funding Support Projects of Sichuan Province (Grant No. 2016120080102643), the Application Foundation Project of Sichuan Province (Grant No. 2017JY0168), and the Science and Technology Project of Chengdu (Grant Nos. 2017-RK00-00103-ZF, and 2016-HM01-00217-SF).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. L. Z. Xiong and Y. Q. Shi. (2018). “On the privacy-preserving outsourcing scheme of reversible data hiding over encrypted image data in cloud computing,” Computers, Materials & Continua, vol. 55, no. 3, pp. 523–539. [Google Scholar]
2. U. Premarathne, A. Abuadbba, L. Khalil, Z. Tari and A. Zomaya. (2016). “Hybrid cryptographic access control for cloud-based EHR systems,” IEEE Cloud Computing, vol. 3, no. 4, pp. 58–64. [Google Scholar]
3. G. Ramu. (2018). “A secure cloud framework to share EHRs using modified CP-ABE and the attribute bloom filter,” Education and Information Technologies, vol. 23, no. 5, pp. 2213–2233. [Google Scholar]
4. Z. Deng, Y. Ren, Y. Liu, X. Yin, Z. Shen et al. (2019). , “Blockchain-based trusted electronic records preservation in cloud storage,” Computers, Materials & Continua, vol. 58, no. 1, pp. 135–151. [Google Scholar]
5. S. Nakamoto. (2008). “Bitcoin: A peer-to-peer electronic cash system,” . [Online]. Available: https://nakamotoinstitute.org/bitcoin. [Google Scholar]
6. P. B. Nichol. (2016). “Blockchain applications for healthcare: Blockchain opportunities are changing healthcare globally-innovative leaders see the change,” . [Online]. Available: http://www.cio.com/article/3042603/innovation/blockchain-applications/for-healthcare.html. [Google Scholar]
7. M. Crosby and V. Kalyanaraman. (2015). Blockchain Technology: Beyond Bitcoin. Berkeley, USA: Applied Innovation Review, issue no. 2. [Google Scholar]
8. A. Roehrs, C. A. da Costa and R. da Rosa Righi. (2017). “OmniPHR: A distributed architecture model to integrate personal health records,” Journal of Biomedical Informatics, vol. 71, pp. 70–81. [Google Scholar]
9. W. J. Gordon and C. Catalini. (2018). “Blockchain technology for healthcare: Facilitating the transition to patient-driven interoperability,” Computational and Structural Biotechnology Journal, vol. 16, pp. 224–230. [Google Scholar]
10. A. A. Omar, S. Rahman, A. Basu and S. Kiyomoto. (2017). “MediBchain: A blockchain based privacy preserving platform for healthcare data,” in International Conference on Security, Privacy and Anonymity in Computation, Communication and Storage, Cham, Switzerland: Springer, pp. 534–543. [Google Scholar]
11. S. Badr, I. Gomaa and E. Abd-Elrahman. (2018). “Multi-tier blockchain framework for IoT-EHRs system,” Procedia Computer Science, vol. 141, pp. 159–166. [Google Scholar]
12. L. X. Chen, W. K. Lee, C. C. Chang, K. K. R. Choo and N. Zhang. (2019). “Blockchain based searchable encryption for electronic health record sharing,” Future Generation Computer Systems, vol. 95, pp. 420–429. [Google Scholar]
13. X. Jiang, M. Z. Liu, C. Yang, Y. H. Liu and R. L. Wang. (2019). “A blockchain-based authentication protocol for WLAN mesh security access,” Computers, Materials & Continua, vol. 58, no. 1, pp. 45–59. [Google Scholar]
14. F. Tang, S. Ma, Y. Xiang and C. L. Lin. (2019). “An efficient authentication scheme for blockchain-based electronic health records,” IEEE Access, vol. 7, pp. 41678–41689. [Google Scholar]
15. R. Guo, H. Shi, Q. Zhao and D. Zheng. (2018). “Secure attribute-based signature scheme with multiple authorities for blockchain in electronic health records systems,” IEEE Access, vol. 6, pp. 11676–11686. [Google Scholar]
16. Y. Sun, R. Zhang, X. Wang, K. Gao and L. Liu. (2018). “A decentralizing attribute-based signature for healthcare blockchain,” in 27th International Conference on Computer Communication and Networks (ICCCNHangzhou, China, pp. 1–9. [Google Scholar]
17. Y. Zheng. (1997). “Digital signcryption or how to achieve cost (signature & encryption),” in CRYPTO '97: Proceedings of the 17th Annual International Cryptology Conference on Advances in Cryptology, B. S. Kaliski, CA, USA, Berlin, Heidelberg: Springer-Verlag, pp. 165–179. [Google Scholar]
18. J. Malone-Lee. (2002). “Identity-based signcryption,” in Cryptology ePrint Archive, Report 2002/098, . [Online]. Available: http://eprint.iacr.org/2002/098.pdf. [Google Scholar]
19. A. Karati and G. P. Biswas. (2016). “A practical identity based signcryption scheme from bilinear pairing,” in International Conference on Advances in Computing, Communications and Informatics, Jaipur, India, pp. 832–836. [Google Scholar]
20. C. X. Zhou, Y. Zhang and L. M. Wang. (2018). “A provable secure identity-based generalized proxy signcryption scheme,” International Journal of Network Security, vol. 20, no. 6, pp. 1183–1193. [Google Scholar]
21. S. Duan and Z. Cao. (2006). “Efficient and provably secure multi receiver identity based signcryption,” in Australasian Conference on Information Security & Privacy, Australia, pp. 195–206. [Google Scholar]
22. S. S. D. Selvi, S. S. Vivek and R. Srinivasan. (2009). “An efficient identity-based signcryption scheme for multiple receivers,” in Proceedings of the 4th International Workshop on Security: Advances in Information and Computer Security, Berlin: Springer, pp. 71–88. [Google Scholar]
23. B. Zhang and Q. L. Xu. (2010). “An ID-based anonymous signcryption scheme for multiple receivers secure in the standard model,” in Proceedings of the 2010 International Conference on Advances in Computer Science and Information Technology, Berlin: Springer, vol. 20, pp. 15–27. [Google Scholar]
24. X. Wang, J. Shu, W. Zheng, L. L. Liu and X. Fan. (2014). “New multi-receiver ID-based ring signcryption scheme,” in Unifying Electrical Engineering and Electronics Engineering. X. Song, VA, New York, USA: Springer, pp. 2251–2257. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |