Computer Systems Science & Engineering DOI:10.32604/csse.2021.014476
Article

On Computer Implementation for Comparison of Inverse Numerical Schemes for Non-Linear Equations

Mudassir Shams1,*, Naila Rafiq2, Nazir Ahmad Mir1,2, Babar Ahmad3, Saqib Abbasi1 and Mutee-Ur-Rehman Kayani1

1Department of Mathematics and Statistics, Riphah International University, I-14, Islamabad, 44000, Pakistan
2Department of Mathematics, NUML, Islamabad, Pakistan
3Department of Mathematics, Comsats University, Islamabad, 44000, Pakistan
*Corresponding Author: Mudassir Shams. Email: mudassir4shams@gmail.com
Received: 22 September 2020; Accepted: 24 November 2020

Abstract: In this research article, we interrogate two new modifications in inverse Weierstrass iterative method for estimating all roots of non-linear equation simultaneously. These modifications enables us to accelerate the convergence order of inverse Weierstrass method from 2 to 3. Convergence analysis proves that the orders of convergence of the two newly constructed inverse methods are 3. Using computer algebra system Mathematica, we find the lower bound of the convergence order and verify it theoretically. Dynamical planes of the inverse simultaneous methods and classical iterative methods are generated using MATLAB (R2011b), to present the global convergence properties of inverse simultaneous iterative methods as compared to classical methods. Some non-linear models are taken from Physics, Chemistry and engineering to demonstrate the performance and efficiency of the newly constructed methods. Computational CPU time, and residual graphs of the methods are provided to present the dominance behavior of our newly constructed methods as compared to existing inverse and classical simultaneous iterative methods in the literature.

Keywords: Non-linear equation; inverse iterative method; simultaneous method; basins of attraction; lower bound of convergence

1  Introduction

A large number of physical and theoretical problems arise in various fields of mathematical, physical and engineering sciences which can be formulated as a non-linear equation:

The most primitive and popular iterative technique for approximating single root of Eq. (1) is Newton’s method [1] (abbreviated as NM) having local quadratic convergence.

In the year 2016, Nedzhibov et al. [2] presented inverse method (abbreviated as INM) corresponding to method Eq. (2) given as:

In the last few years, lot of work has been done on those numerical iterative methods which approximate single root at a time. Besides these methods in literature, there is another class of derivative free iterative schemes which approximate all roots of Eq. (1) simultaneously. These methods are very popular due to their global convergence and parallel implementation on computer (see, e.g., Weierstrass’ [3], Cholakov et al. [4], Ivanov [5], Kyncheva [6], Mir et al. [7], Proinov [8], Shams et al. [9], Farmer [10] and reference cited there in [11–13]).

Among derivative free simultaneous methods, Weierstrass-Dochive method (abbreviated as WDK) is the most attractive method given by:

where

is Weierstrass’ Correction, Eq. (4) has local quadratic convergence.

G.H Nedzibove presented two new modifications of Eq. (4) namely, inverse WDK and modified inverse WDK as:

First modification (abbreviated as INHB):

where is Vietas formula for monic polynomial.

Second modification (abbreviated as INHH):

The main aim of this research article is to accelerate the convergence order of Eqs. (5) and (6) from 2 to 3. The programs written in CAS-Mathematica are presented to find the lower bound of the convergence order of both the new and the existing inverse simultaneous methods and verify the local convergence theoretically. We take some engineering applications as numerical test examples to show the convergence behavior of simultaneous iterative schemes. Computational efficiency, dynamical planes, basins of attraction and residual graphs are presented to demonstrate the dominance performance of our newly constructed methods over existing methods in the literature of same convergence order.

2  Construction of Simultaneous Methods

Here, we propose the following methods by replacing by in Eqs. (5) and (6) i.e.,

and

where 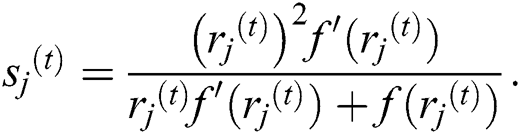Newly proposed inverse simultaneous methods Eqs. (7) and (8) are abbreviated as IWKM1 and IWKM2 respectively.

2.1 Convergence Frame Work

In this section, we prove third order convergence of the methods IWKM1 and IWKM2.

Let 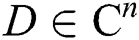be an open convex subset, 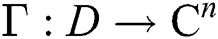and u-times differentiable operators 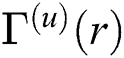, 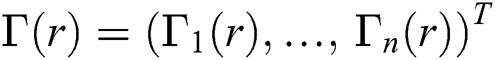be continuous and the sequence 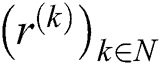be defined by ,

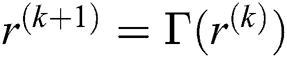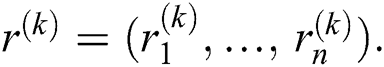
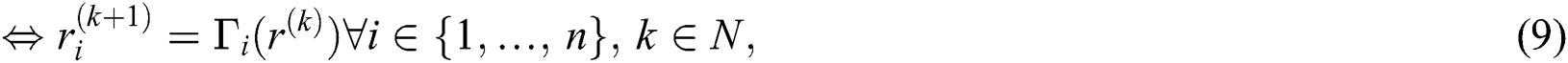
where norm in 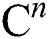be defined by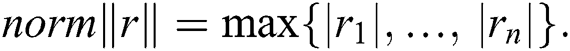

Theorem 1 [2]: Let 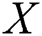, 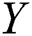be normed spaces. Take an open convex subset D of X for a u-times Frēchet differential Operator 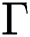, i.e., 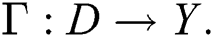Then, for any x,y :

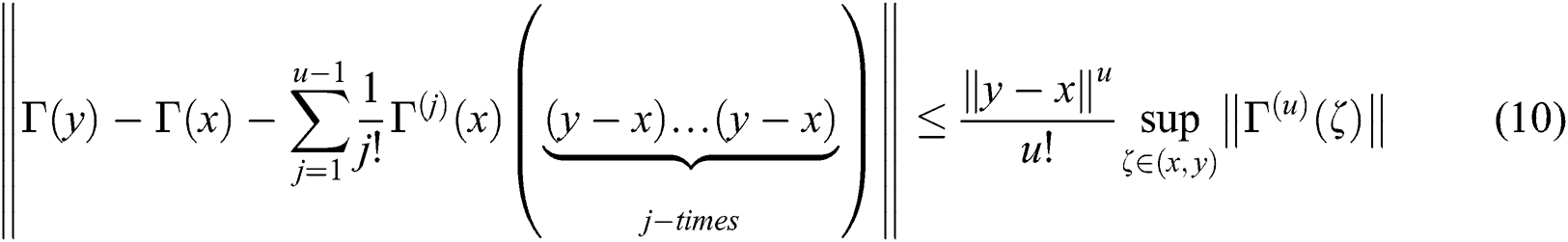
Using Theorem 1, we have:

Theorem 2: Let 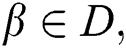if

then there exists, 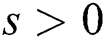such that for any 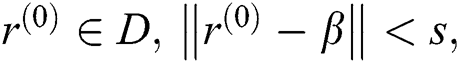the sequence 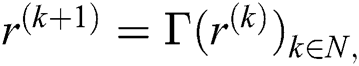converges to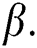

Proof: Let 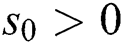be such that

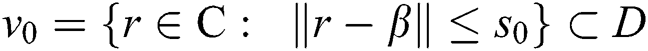
and C 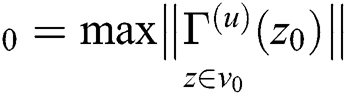then, there exists, 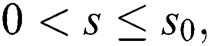such that

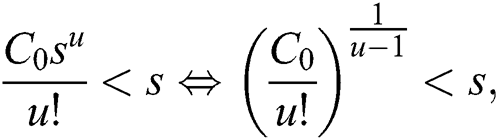
where If r 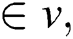then (ii) and Theorem 1 implies:

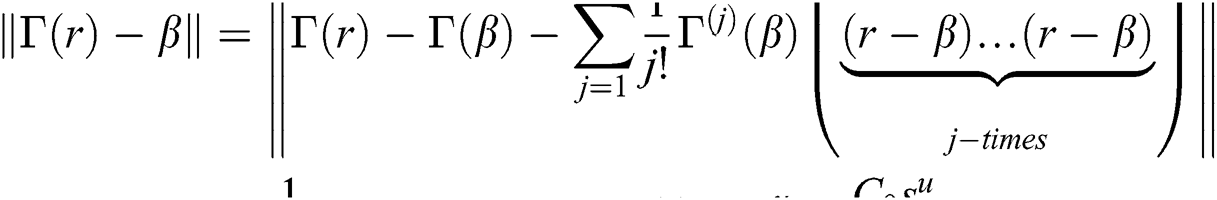
Thus, 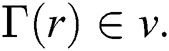Using above relation for 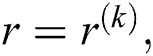we have:

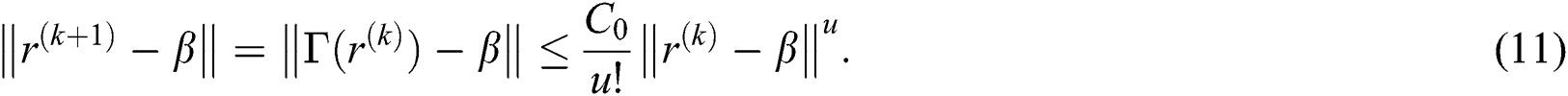
Using Eq. (11), recursively, we have:

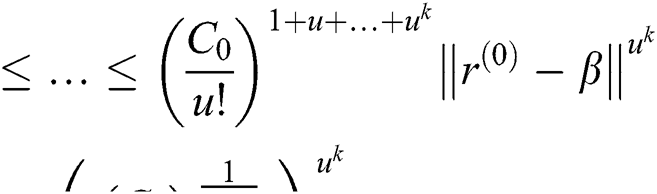
Thus, from last inequality, the convergence order of 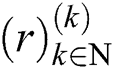is at least 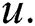Now, consider IWKM1 as a vector function, i.e., 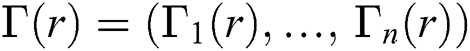, where

For a fixed point 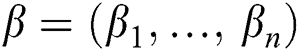, it is not difficult to prove 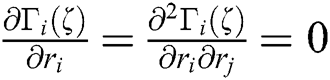and higher order partial derivative is not equal to zero. Thus, IWKM1 has at least third order convergence.

Theorem 3: Let be simple roots of Eq. (1) and for sufficiently close initial distinct estimations of the roots respectively, IWKM2 then has convergence order 3.

Proof: Let 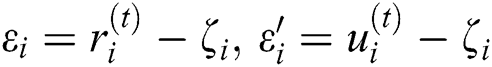be the errors in 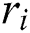and 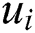respectively. From the first-step of IWKM2, we have:

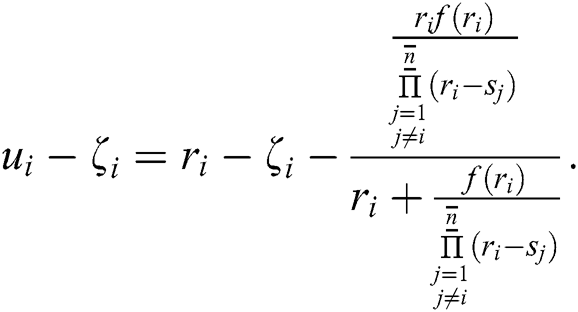
Thus, we get:

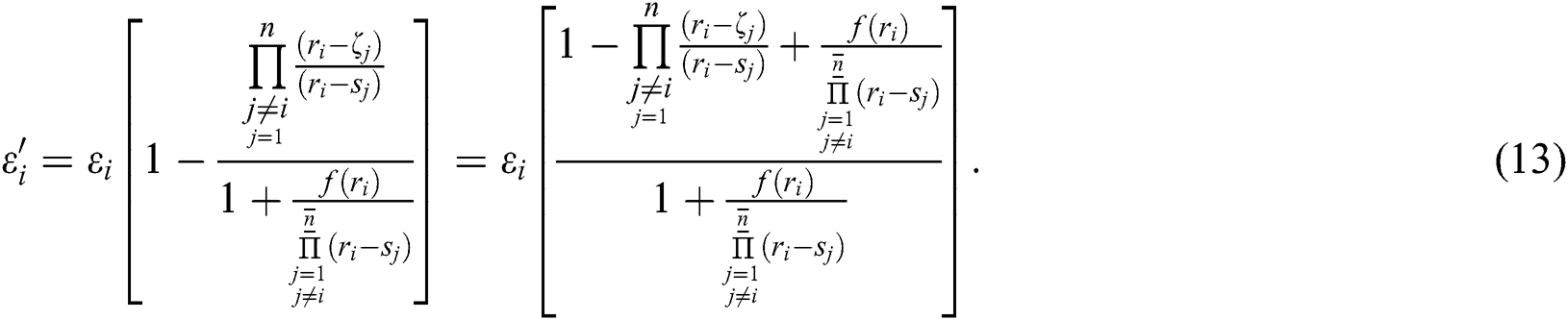
Using the expression 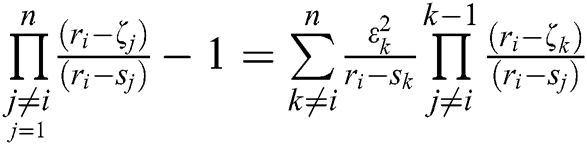[2] in Eq. (13), we have:

If we assume all error are of the same order, i.e., 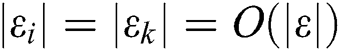, then

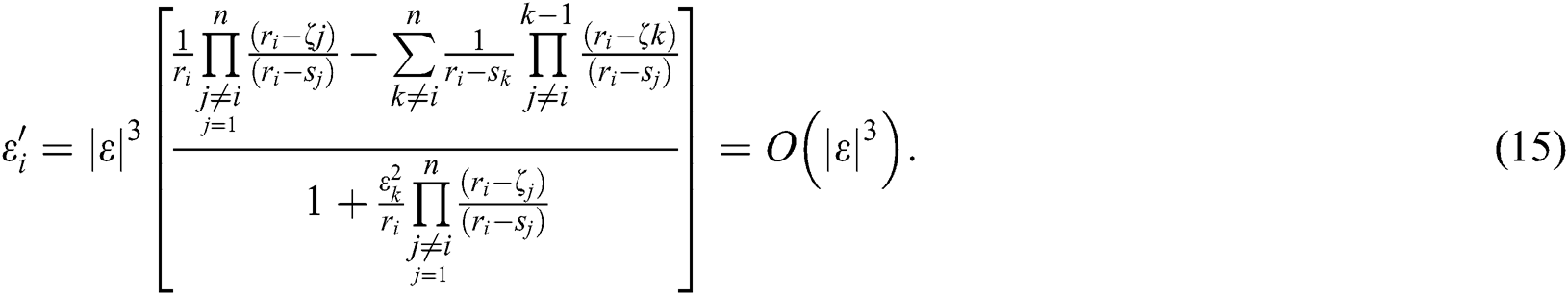
Hence, from Eq. (15), third order convergence is proved.

2.2 Using CAS for Verification of Convergence Order

Consider

and the first components of 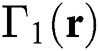iterative scheme to find roots of Eq. (16), 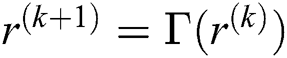simultaneously. In order to verify conditions of Theorem 2, we have to express the differential of an operator 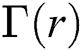in terms of their partial derivate of its component as .

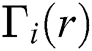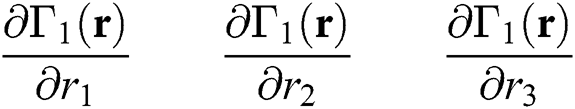
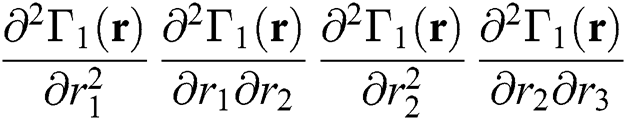
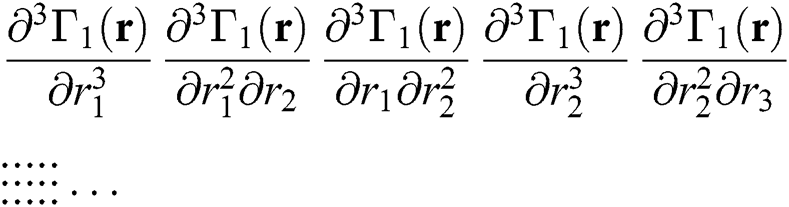
and so on.

The lower bound of the convergence is obtained until the first non-zero element of row is found. The Mathematica codes are given for each of the considered methods as:

Weierstrass-Dochive Method WDK

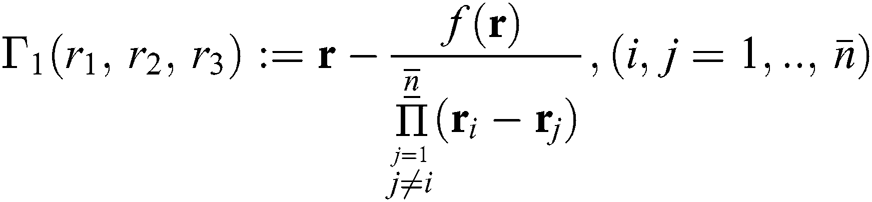
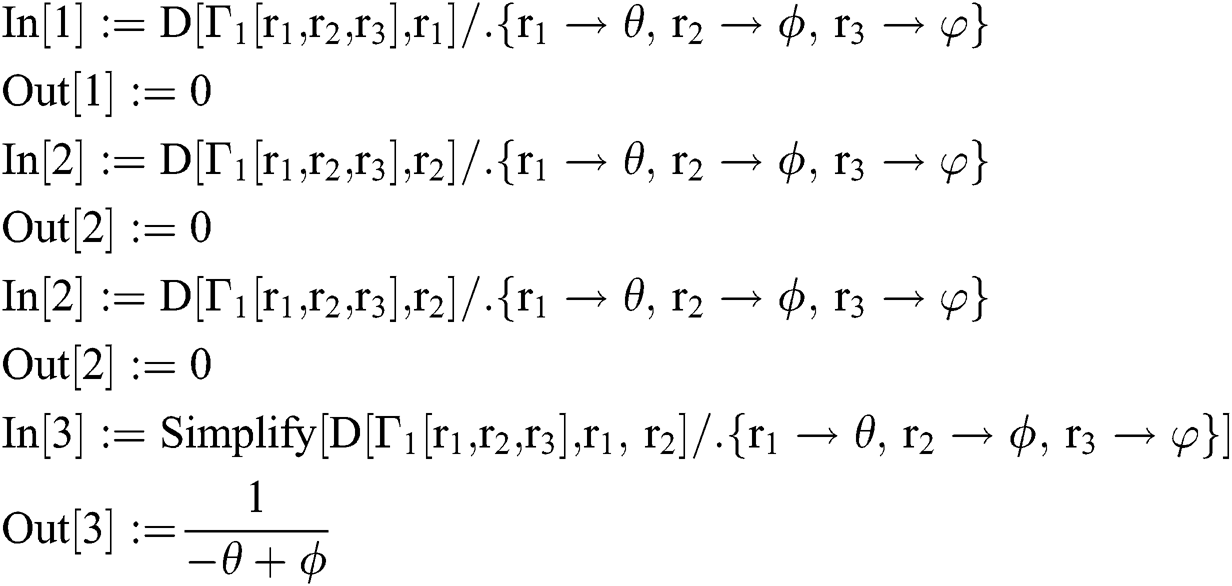
Modified Inverse Weierstrass Method-INHH

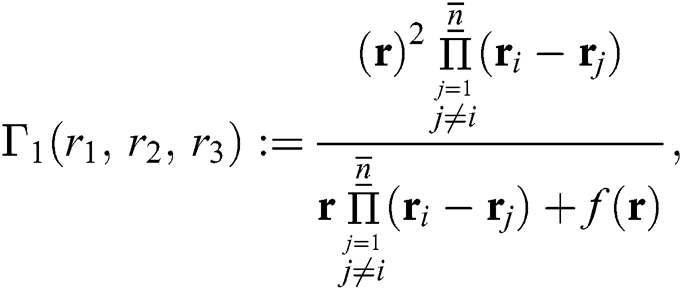
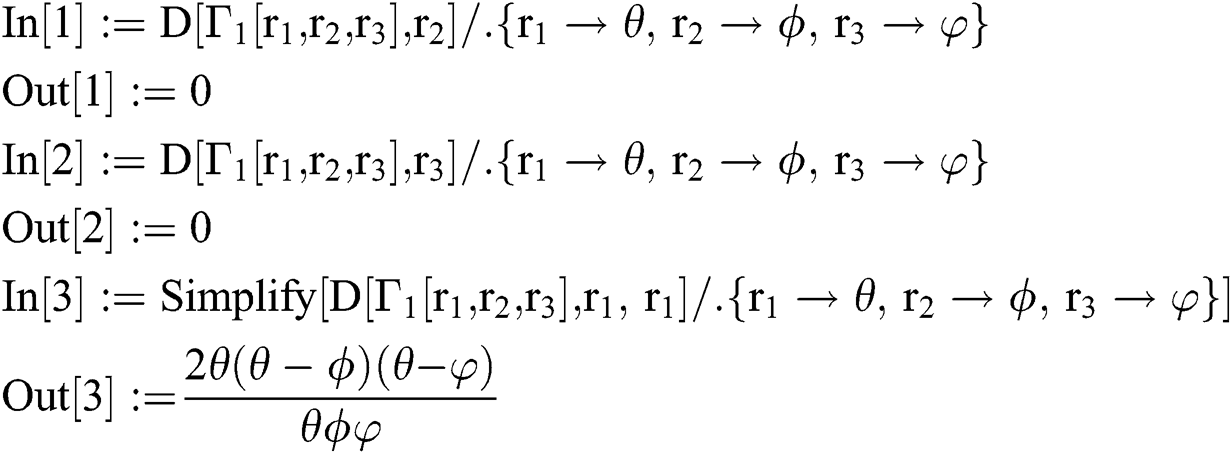
Inverse Weierstrass Method - INHB

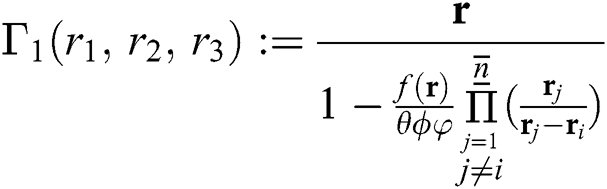
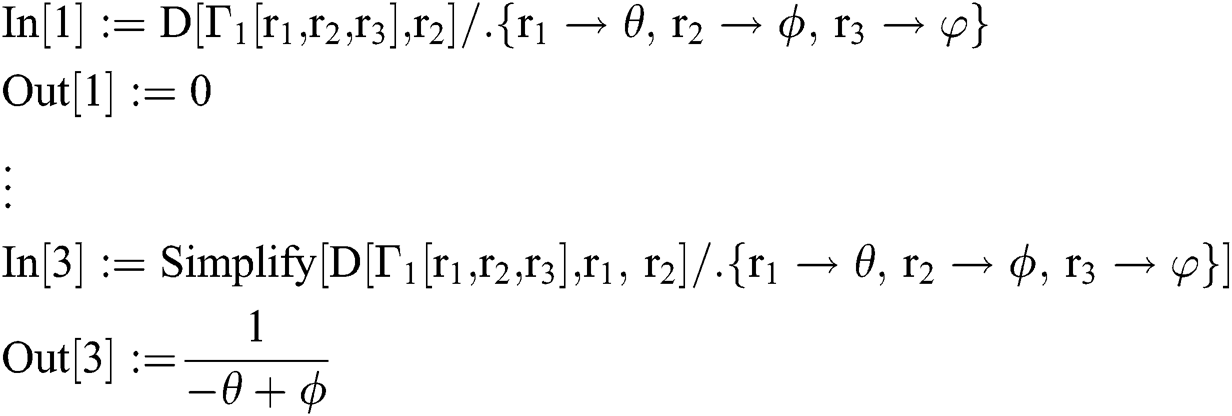
IWKM1 Method

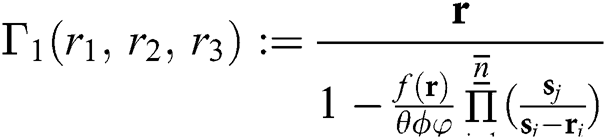, where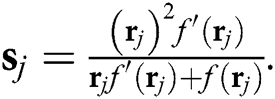

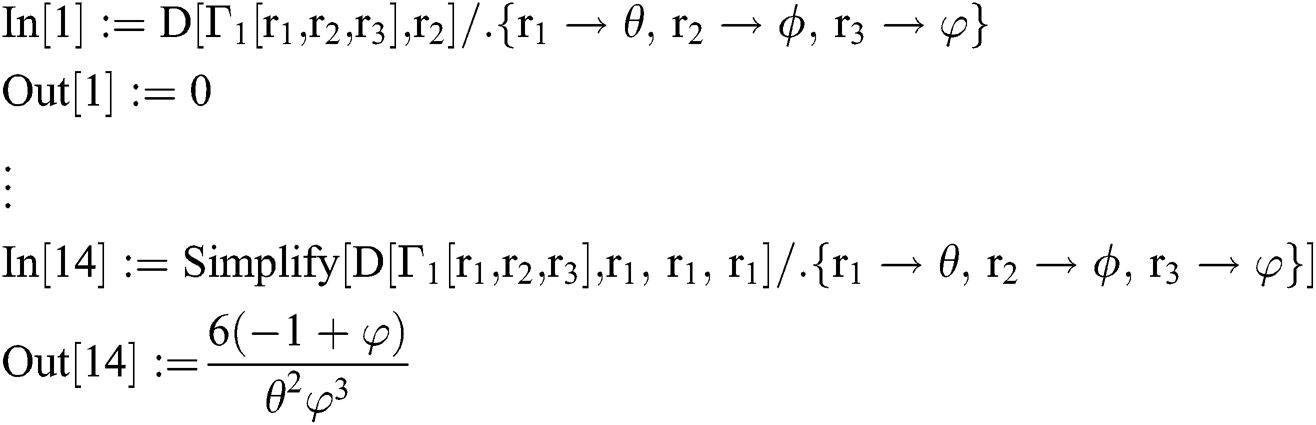
IWKM2 Method

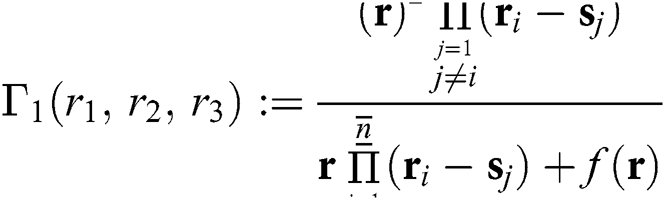, where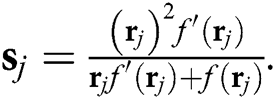

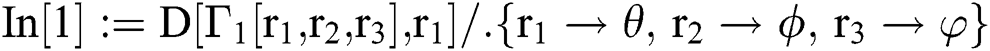
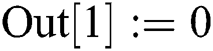
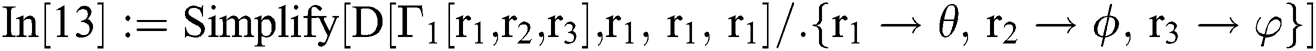
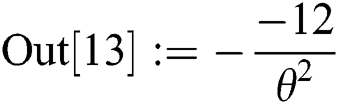
3  Basins of Attraction

To provoke the basins of attraction of iterative schemes NM, INM, WDK, INHB, INHH, IWKM1, IWKM2 for the roots of non-linear equation, we execute the real and imaginary parts of the starting approximations represented as two axes over a mesh of in complex plane. We use 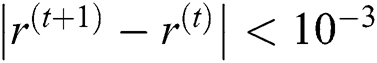as a stopping criteria or maximum number of iterations as 5 due to wider convergence region of simultaneous methods. We allow different colors to mark to which root the iterative schemes converge and black in other cases. Color brightness in basins shows less number of iterations. For the generation of basins of attraction, we consider a non-linear polynomial equation .

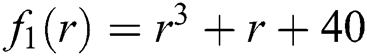Figure 1: Basin of attraction of iterative method NM for polynomial equation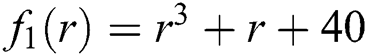

Figure 2: Basin of attraction of iterative method INM for polynomial equation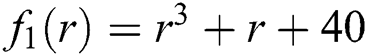

Figure 3: Basin of attraction of iterative method WDK for polynomial equation

Figure 4: Basin of attraction of iterative method INHB for polynomial equation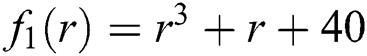

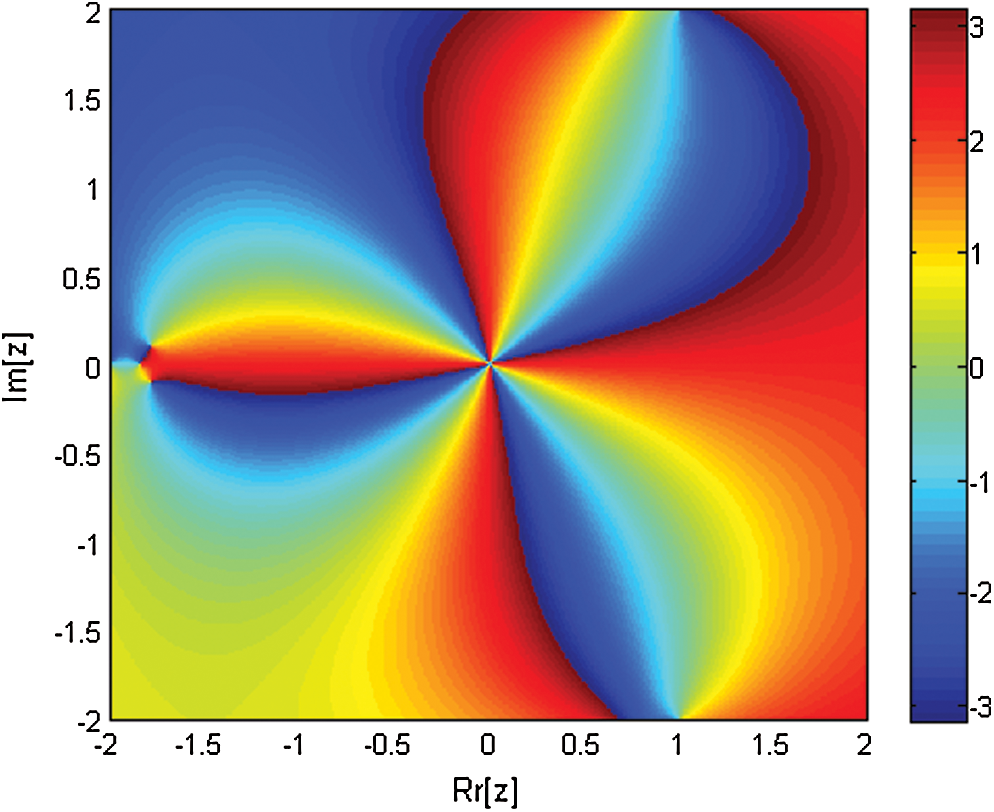
Figure 5: Basin of attraction of iterative method INHH for polynomial equation

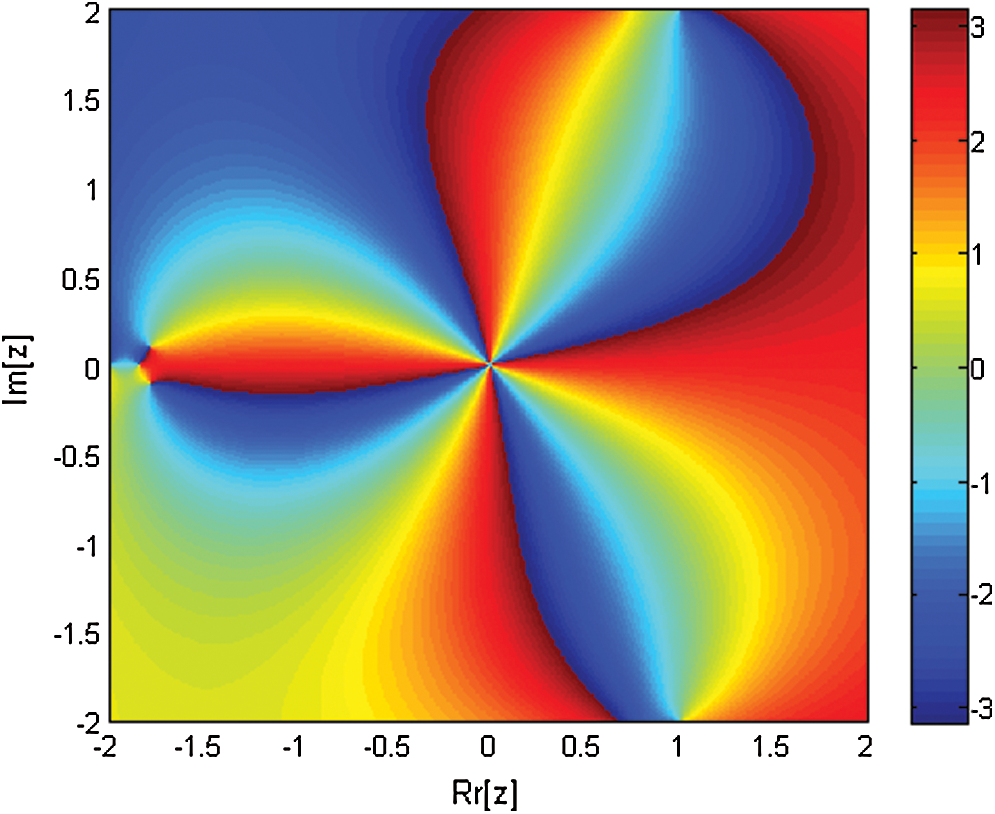
Figure 6: Basin of attraction of iterative method IWKM1 for polynomial equation

Figure 7: Basin of attraction of iterative method IWKM2 for polynomial equation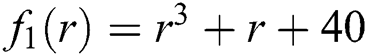

Table 1: Elapsed time in seconds

The basins of attraction of single root finding iterative schemes NM and INM are shown in Figs. 1 and 2. The basins of attraction of simultaneous iterative schemes WDK, INHB, INHH, IWKM1 and IWKM2 are presented in Figs. 3–6 and Fig. 7 respectively. The elapsed time from Tab. 1 and brightness in color in Figs. 6 and 7 show the dominance behavior of IWKM1 and IWKM2 as compared to NM, INM, WDK, INHB and INHH respectively.

4  Numerical Results

Some non-linear models from engineering and applied sciences are considered to illustrate the performance and efficiency of WDK, INHB, INHH, IWKM1 and IWKM2. All calculations are done with 64 digits floating point arithmetic. The following stopping criteria are used to terminate the computer program:

,

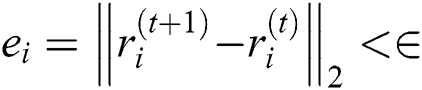where 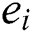represents the absolute error and . In Tabs. 2–4, CO represents convergence order of iterative simultaneous schemes.

Example 1 [14]: Fractional Conversion

As described in [14,15],

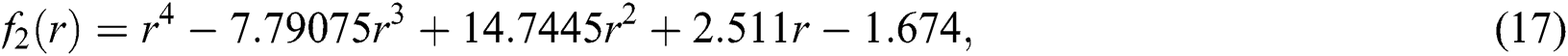
is the fractional conversion of nitrogen, hydrogen feed at 250 atm and 227k.

The exact roots of Eq. (17) are:

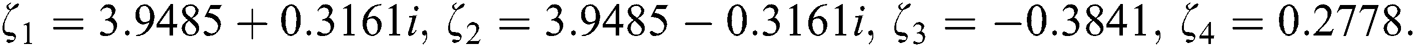
The initial calculated values of Eq. (17) have been taken as:

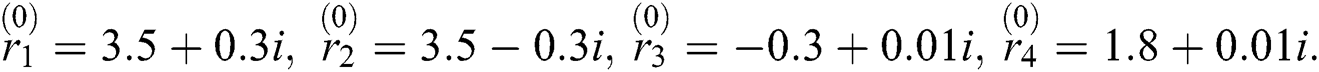
Table 2: Simultaneous determination of all roots of

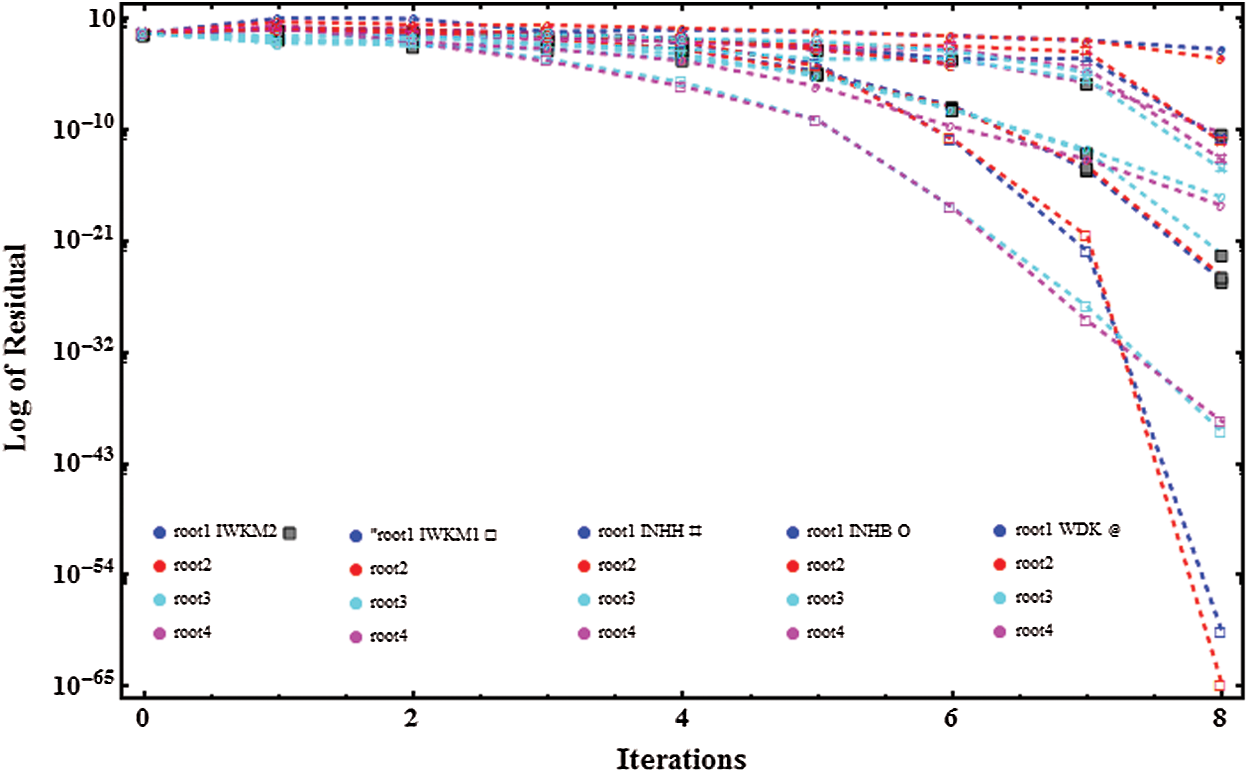
Figure 8: Residual graphs of WDK, INHB, INHH, IWKM1 and IWKM2 for non-linear function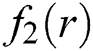

Example 2 [16]: Beam Designing Model

Problem of beam positioning [16], results a non-linear function as:

The exact roots of Eq. (18) are:

The initial calculated values of Eq. (18) have been taken as:

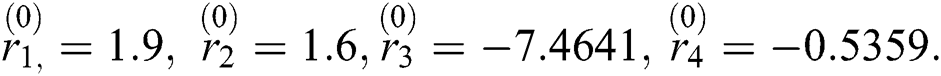
Table 3: Simultaneous determination of all roots of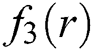

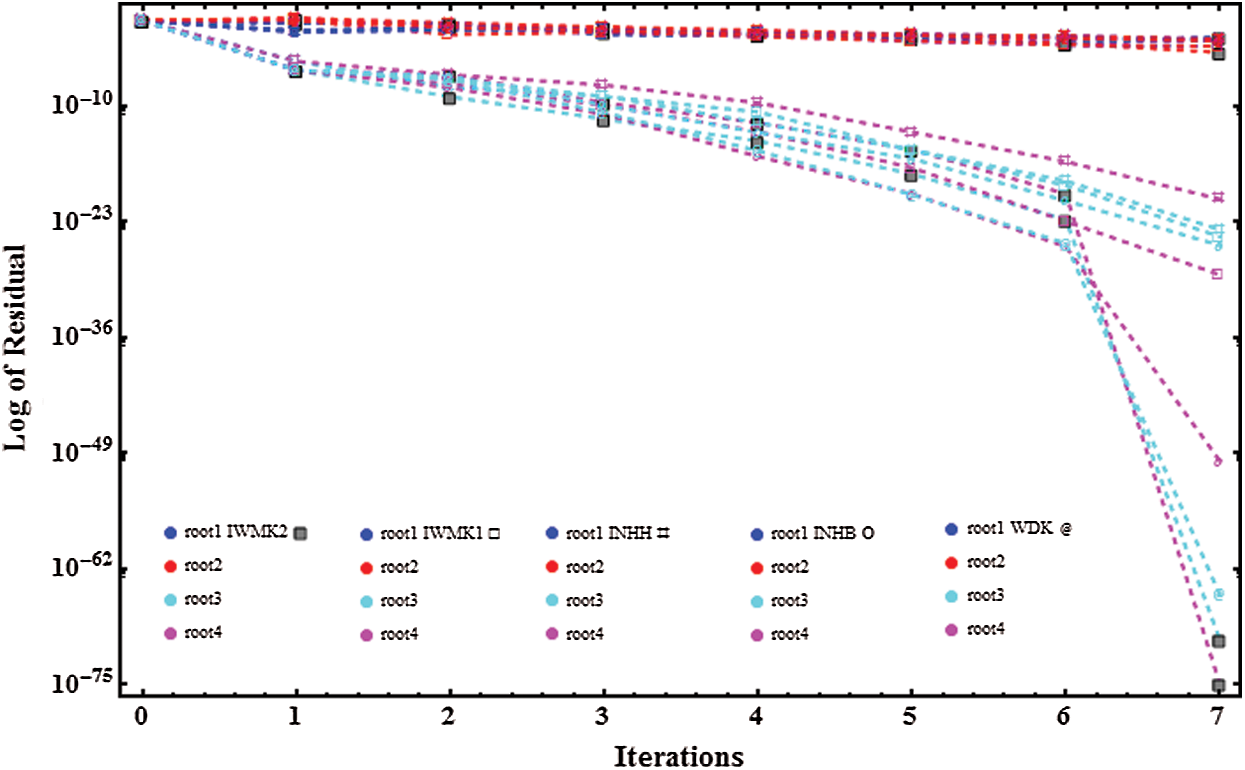
Figure 9: Residual graphs of WDK, INHB, INHH, IWKM1 and IWKM2 for non-linear function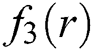

Example 3 [17]: Predator-Prey Model

In Predator-Prey model, predation rate is denoted by

where r is number of aphids as preys [17] and lady bugs as a predator. Obeying the Malthusian Model, the growth rate of aphids is defined as 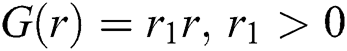. To find the solution of the problem, we take the aphid density for which 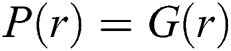implies

Taking k = 30 (aphids eaten rate), a = 20 (number of aphids) and 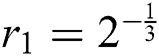(rate per hour) in Eq. (20), we get:

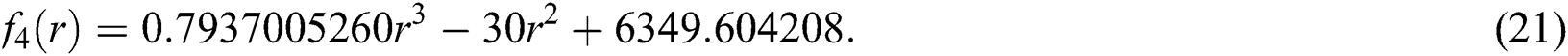
The exact roots of Eq. (21) are:

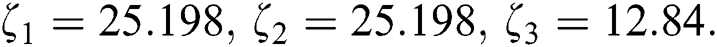
The initial estimates for are taken as:

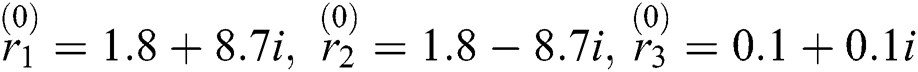
Table 4: Simultaneous determination of all roots of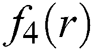

Figure 10: Residual graphs of WDK, INHB, INHH, IWKM1 and IWKM2 for non-linear function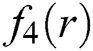

5  Conclusion

Here, we have developed two new inverse simultaneous methods of order three for determining all the roots of non-linear equations simultaneously. It must be pointed out that so far there exists an inverse simultaneous iterative scheme of order two only in the literature. We have made here comparison with the methods INHB, INHH and with classical Weierstrass-Dochive method WDK all of order two. The dynamical behavior/basins of attractions of iterative methods IWKM1, IWKM2 are also discussed here to show the global convergence behavior. Single root finding methods may have divergence region. From Tabs. 1–4 and Figs. 1–10, we observe that our numerical results are much better in terms of absolute error, number of iterations, CPU time and lapsed time of dynamical planes.

Funding Statement: The author(s) received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  V. K. Kyncheva, V. V. Yotov and S. I. Ivanov. (2017). “Convergence of Newton, Halley and Chebyshev iterative methods as methods for simultaneous determination of multiple polynomial zeros,” Applied Numerical Mathematics, vol. 112, pp. 146–154. [Google Scholar]

 2.  G. H. Nedzhibov. (2016). “Convergence of the modified inverse Weierstrass method for simultaneous approximation of polynomial zeros,” Communications in Numerical Analysis, vol. 16, no. 1, pp. 74–80. [Google Scholar]

 3.  P. D. Proinov and M. D. Petkova. (2014). “A new semilocal convergence theorem for the Weierstrass method for finding zeros of a polynomial simultaneously,” Journal of Complexity, vol. 30, no. 3, pp. 366–380. [Google Scholar]

 4.  S. I. Cholakov. (2019). “Local and semilocal convergence of Wang-Zheng’s method for simultaneous finding polynomial zeros,” Symmetry, vol. 736, pp. 15. [Google Scholar]

 5.  S. I. Ivanov. (2017). “A unified semilocal convergence analysis of a family of iterative algorithms for computing all zeros of a polynomial simultaneously,” Numerical Algorithms, vol. 75, no. 4, pp. 1193–1204. [Google Scholar]

 6.  V. K. Kyncheva, V. V. Yotov and S. I. Ivanov. (2017). “Convergence of Newton, Halley and Chebyshev iterative methods as methods for simultaneous determination of multiple polynomial zeros,” Applied Numerical Mathematics, vol. 112, pp. 146–154. [Google Scholar]

 7.  N. A. Mir, M. Shams, N. Rafiq, S. Akram and M. Rizwan. (2020). “Derivative free iterative simultaneous method for finding distinct roots of polynomial equation,” Alexandria Engineering Journal, vol. 59, no. 3, pp. 1629–1636. [Google Scholar]

 8.  P. D. Proinov and M. T. Vasileva. (2016). “On a family of Weierstrass-type root-finding methods with accelerated convergence,” Applied Mathematics and Computation, vol. 273, pp. 957–968. [Google Scholar]

 9.  M. Shams, N. A. Mir, N. Rafiq, A. O. Almatroud and S. A. Akram. (2020). “On dynamics of iterative technique for nonlinear equation with application in engineering,” Mathematical Problems in Engineering, vol. 2020, pp. 17. [Google Scholar]

10. M. R. Farmer. (2014). “Computing the zeros of polynomials using the divide and conquer approach,” Ph.D. thesis. Department of Computer Science and Information Systems, Birkbeck, University of London. [Google Scholar]

11. N. A. Mir, R. Muneer and I. Jabeen. (2011). “Some families of two-step simultaneous methods for determining zeros of non-linear equations,” ISRN Applied Mathematics, vol. 2011, pp. 1–11. [Google Scholar]

12. P. D. Proinov and M. T. Vasileva. (2019). “On the convergence of high-order Gargantini-Farmer-Loizou type iterative methods for simultaneous approximation of polynomial zeros,” Applied Mathematics and Computation, vol. 361, pp. 202–214. [Google Scholar]

13. N. A. Mir, M. Shams, S. Akram and R. Ahmed. (2020). “On the family of simultaneous method for finding distinct as well as multiple roots of nonlinear equation,” Punjab University Journal of Mathematics, vol. 52, no. 6, pp. 31–44. [Google Scholar]

14. M. Ivanov. (1989). “An improved memory method for the solution of a nonlinear equation,” Chemical Engineering Science, vol. 44, no. 7, pp. 1495–1501. [Google Scholar]

15. Y. M. Chu, N. Rafiq, M. Shams, S. Akram, N. A. Mir et al., “Computer methodologies for the comparison of some efficient derivative free simultaneous iterative methods for finding roots of non-linear equations,” Computers, Materials & Continua, vol. 66, no. 1, pp. 275–290, 2021. [Google Scholar]

16. N. Rafiq, S. Akram, N. A. Mir and M. Shams. (2020). “Study of dynamical behavior and stability of iterative methods for nonlinear equation with application in engineering,” Mathematical Problems in Engineering, vol. 2020, pp. 20. [Google Scholar]

17. S. C. Chapra. (2010). Applied Numerical Methods with MATLAB® for Engineers and Scientists. 6th edition. New York: McGraw Hill. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.