DOI:10.32604/csse.2021.014896

| Computer Systems Science & Engineering DOI:10.32604/csse.2021.014896 |  |
| Article |
Comparative Study of Valency-Based Topological Descriptor for Hexagon Star Network
1Department of Mathematics, College of Science, Jazan University, New Campus, Jazan, 2097, Saudi Arabia
2College of Computer Science & Information Technology Jazan University, Jazan, Saudi Arabia
3Department of Mathematics, COMSATS University Islamabad, Lahore Campus, Lahore, 54000, Pakistan
*Corresponding Author: Ali Ahmad. Email: ahmadsms@gmail.com
Received: 25 October 2020; Accepted: 13 November 2020
Abstract: A class of graph invariants referred to today as topological indices are inefficient progressively acknowledged by scientific experts and others to be integral assets in the depiction of structural phenomena. The structure of an interconnection network can be represented by a graph. In the network, vertices represent the processor nodes and edges represent the links between the processor nodes. Graph invariants play a vital feature in graph theory and distinguish the structural properties of graphs and networks. A topological descriptor is a numerical total related to a structure that portray the topology of structure and is invariant under structure automorphism. There are various uses of graph theory in the field of basic science. The main notable utilization of a topological descriptor in science was by Wiener in the investigation of paraffin breaking points. In this paper we study the topological descriptor of a newly design hexagon star network. More preciously, we have computed variation of the Randi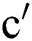
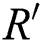 , fourth Zagreb
, fourth Zagreb 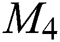 , fifth Zagreb
, fifth Zagreb 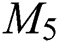 , geometric-arithmetic
, geometric-arithmetic 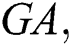 atom-bond connectivity
atom-bond connectivity 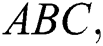 harmonic
harmonic 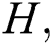 symmetric division degree
symmetric division degree 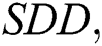 first redefined Zagreb, second redefined Zagreb, third redefined Zagreb, augmented Zagreb
first redefined Zagreb, second redefined Zagreb, third redefined Zagreb, augmented Zagreb 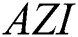 , Albertson
, Albertson 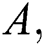 Irregularity measures, Reformulated Zagreb, and forgotten topological descriptors for hexagon star network. In the analysis of the quantitative structure property relationships (QSPRs) and the quantitative structure activity relationships (QSARs), graph invariants are important tools to approximate and predicate the properties of the biological and chemical compounds. We also gave the numerical and graphical representations comparisons of our different results.
Irregularity measures, Reformulated Zagreb, and forgotten topological descriptors for hexagon star network. In the analysis of the quantitative structure property relationships (QSPRs) and the quantitative structure activity relationships (QSARs), graph invariants are important tools to approximate and predicate the properties of the biological and chemical compounds. We also gave the numerical and graphical representations comparisons of our different results.
Keywords: Topological indices; degree-based index; hexagon star network
Cheminformatics is another field of modern sciences that connects chemistry, math, and other fields of science. Quantitative structure-activity relationship (QSAR) and Quantitative structure-activity relationship (QSPR) are the principle parts of cheminformatics which are useful to contemplate the physico-chemical properties of networks. A topological descriptor (TD) is a numerical total related to a structure that portray the topology of the structure and is invariant under structure automorphism. There are various uses of graph theory in the field of basic science. The main notable utilization of a TD in science was by Wiener in the investigation of paraffin breaking points [1]. From that point forward, to clarify physico-chemical properties, different TDs have been presented.
Topological descriptors (TD) are commonly partitioned into three sorts: degree, distance and spectrum based. The structures of networks can be scientifically demonstrated by a figure. The vertex represents the processor hub and an edge describes the links among processors. The topology of the figure of a network chooses the way by which any two vertices are linked by an edge. The topology of a network system can be used to obtained specific properties without a lot of stretches. The width is resolved as the most extreme separation between any two hubs in the system. The quantity of connections associated with a hub decides the level of that hub. If this number is the equivalent for all hubs in the system, the system is called regular.
TD can be effortlessly processed by utilizing the ideas of atomic topology (AT), an order dependent on the graph theory. Actually, AT has demonstrated to be a fantastic apparatus for quick and exact estimation of numerous physicochemical as well as biological properties [2,3]. So as to compute topological indices, basics of AT are utilized where chemical compound is changed over into a graph, considering the atoms and bonds are represented by vertices and edges of a graph. The basic definitions and notations are taken from the book [4]. The number of vertices adjacent to the vertex 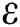 is the degree of
is the degree of 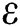 , denoted as
, denoted as 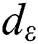 .
.
TD which are obtained through the connectivity of two-dimensional structures, deliver significant connections to various properties of these structures via QSAR/QSPR resulting from the topological networks of these structures [5]. Since last few years, numerous researchers conducted for the expansion of TD because of their significance [6–9]. For detail study of TD see [10–21].
In this section, we define some degree based topological indices 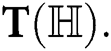

• 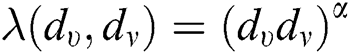 , represents
, represents 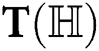 as the general, second, and second modified Randi
as the general, second, and second modified Randi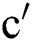 indices if
indices if 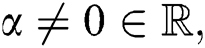
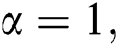 and
and 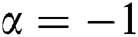 respectively.
respectively.
• 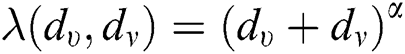 , represents
, represents 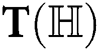 as the general sum connectivity, sum connectivity, Zagreb and hyper Zagreb indices, if
as the general sum connectivity, sum connectivity, Zagreb and hyper Zagreb indices, if 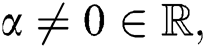
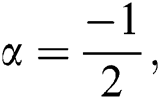
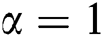 and
and 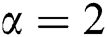 respectively.
respectively.
• If 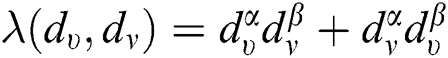 , then
, then 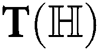 represents generalized Zagreb index.
represents generalized Zagreb index.
Similarly, if
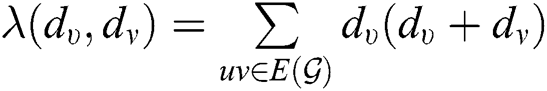 ,
, 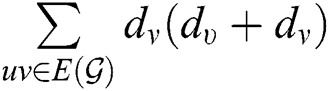 ,
, 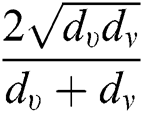 ,
, 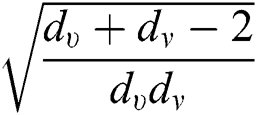 ,
, 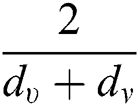 ,
, 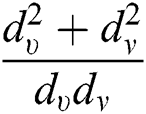 ,
, 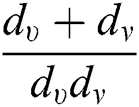 ,
, 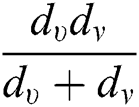 ,
, 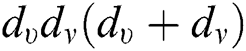 ,
, 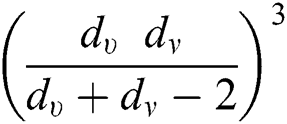 ,
, 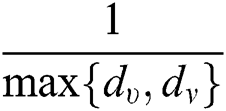 ,
, 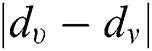 ,
, 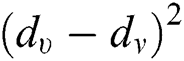 ,
, 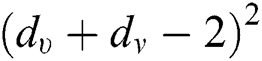 ,
, 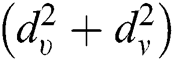 , we obtained fourth Zagreb
, we obtained fourth Zagreb 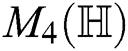 , fifth Zagreb
, fifth Zagreb 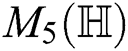 , geometric-arithmetic
, geometric-arithmetic 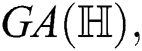 atom-bond connectivity
atom-bond connectivity 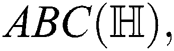 harmonic
harmonic 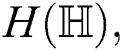 symmetric division degree
symmetric division degree 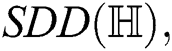 first redefined Zagreb, second redefined Zagreb, third redefined Zagreb, augmented Zagreb
first redefined Zagreb, second redefined Zagreb, third redefined Zagreb, augmented Zagreb 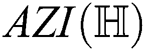 , variation of the Randi
, variation of the Randi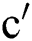
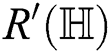 , Albertson
, Albertson 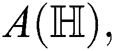 IRM
IRM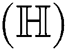 irregularity measures, Reformulated Zagreb, and forgotten topological indices respectively.
irregularity measures, Reformulated Zagreb, and forgotten topological indices respectively.
Interconnection systems are significant in PC systems administration and used to change information between the PC and processer. In the most recent couple of years, numerous specialists structured the new interconnection systems. In an equal PC framework, interconnection organize is accustomed to expanding the exhibition. In diagram hypothesis, organize is spoken to as a chart. In this articulation, the processer spoke to by vertex and association between the units spoke to by edges. From the topology of a system, we can decide certain properties. The level of a hub is characterized as the all outnumber of connections associated with that hub. The system is supposed to be regular if each hub in the system has the same degree. In this paper, we define a new interconnection network hexagon star network. This network is a composition of triangles around a hexagon, as shown in Fig. 1.
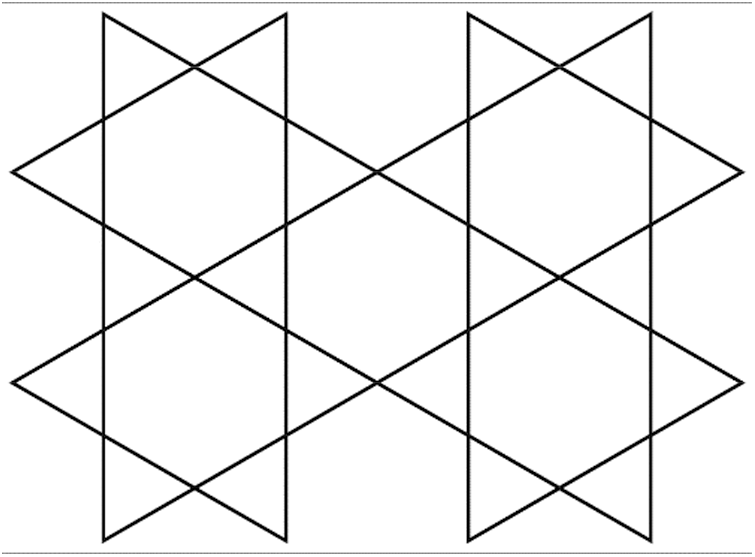
Figure 1: The hexagon star network sheet for 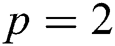 ,
, 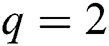
In this section, we give results, which are used to obtained any degree-based topological descriptors. We obtained exact results of degree-based TD for hexagon star network sheet  . Vetrík [22] introduced a new method to calculate the topological indices and also in [23], we follow the same technique in this paper. Now, we presents a formula, which can be used to obtain any degree based TD.
. Vetrík [22] introduced a new method to calculate the topological indices and also in [23], we follow the same technique in this paper. Now, we presents a formula, which can be used to obtain any degree based TD.
Lemma 4.1 Let  be a hexagon star network. Then
be a hexagon star network. Then 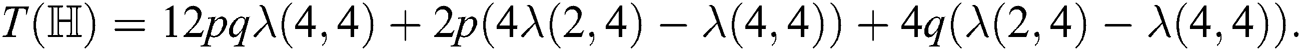
Proof. The graph  contains
contains 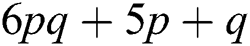 vertices and
vertices and 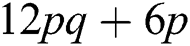 edges. Each vertex of
edges. Each vertex of  has degree 2 or 4, vertices of
has degree 2 or 4, vertices of 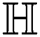 can be partitioned according to their degrees. Let
can be partitioned according to their degrees. Let
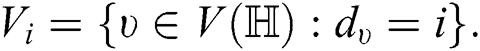
This means that the set 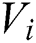 contains the vertices of degree
contains the vertices of degree 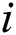 . The set of vertices with respect to their degrees are as follows:
. The set of vertices with respect to their degrees are as follows:
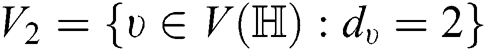
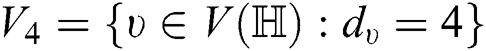
Since,  and
and 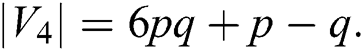 We partite the edges of
We partite the edges of 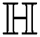 into sets based on degrees of its end vertices. Let
into sets based on degrees of its end vertices. Let
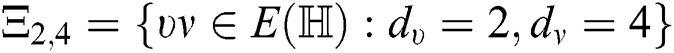
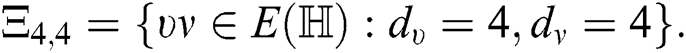
Note that 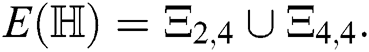 The number of edges incident to one vertex of degree 2 and other vertex of degree 4 is
The number of edges incident to one vertex of degree 2 and other vertex of degree 4 is 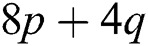 , so
, so 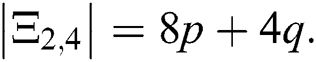 Now, the remaining number of edges are those edges which are incident to two vertices of degree 4, i.e.,
Now, the remaining number of edges are those edges which are incident to two vertices of degree 4, i.e., 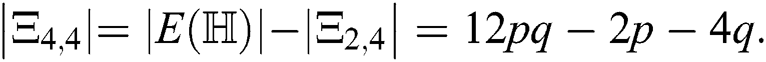
Hence,
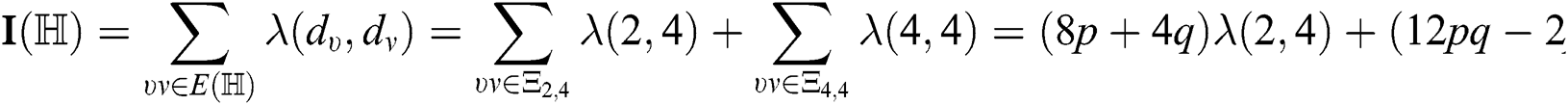
After simplification, we get
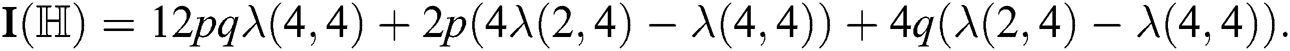
Now we obtained the well-known degree based TD of hexagon star network in the following theorem.
Theorem 4.2 For the hexagon star network 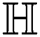 , we have
, we have
the general Randic′ index of 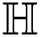 is,
is,
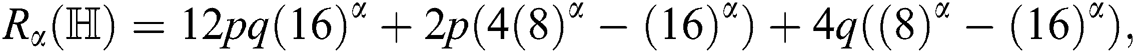
the Randi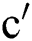 index of
index of 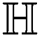 is
is
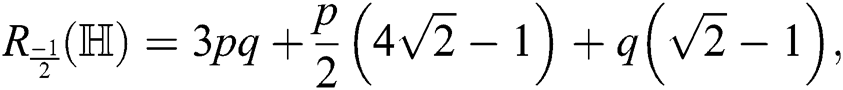
the second Zagreb index of 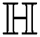 is
is
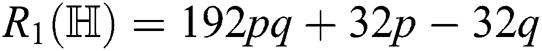
the second Zagreb index of 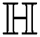 is
is
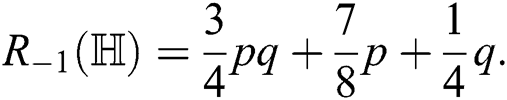
Proof. For 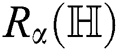 which is the general Randi
which is the general Randi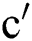 indices of
indices of  , we have
, we have 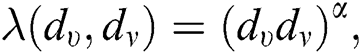 therefore
therefore 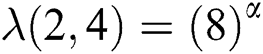 and
and 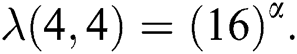 Thus by Lemma 4.1,
Thus by Lemma 4.1,
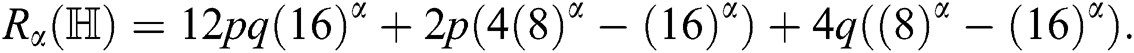
For 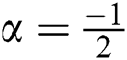 , the Randic′ index
, the Randic′ index
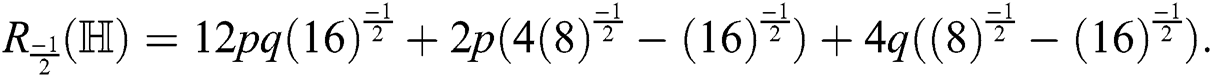
After simplification, we get
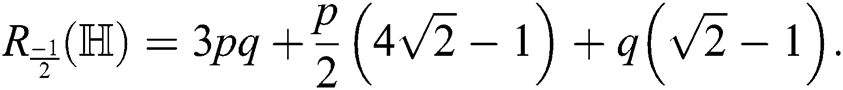
For 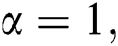 the second Zagreb index is
the second Zagreb index is
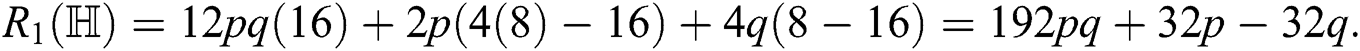
For 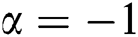 , the second modified Zagreb index is
, the second modified Zagreb index is
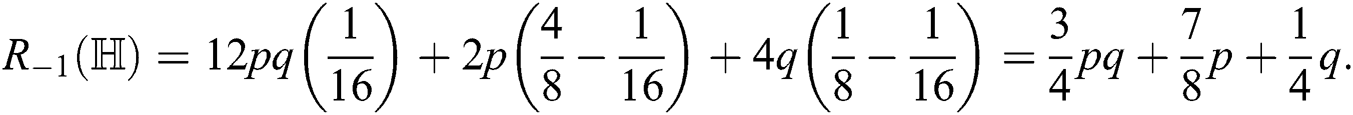
Table 1: Numerical representation of Theorem 4.2
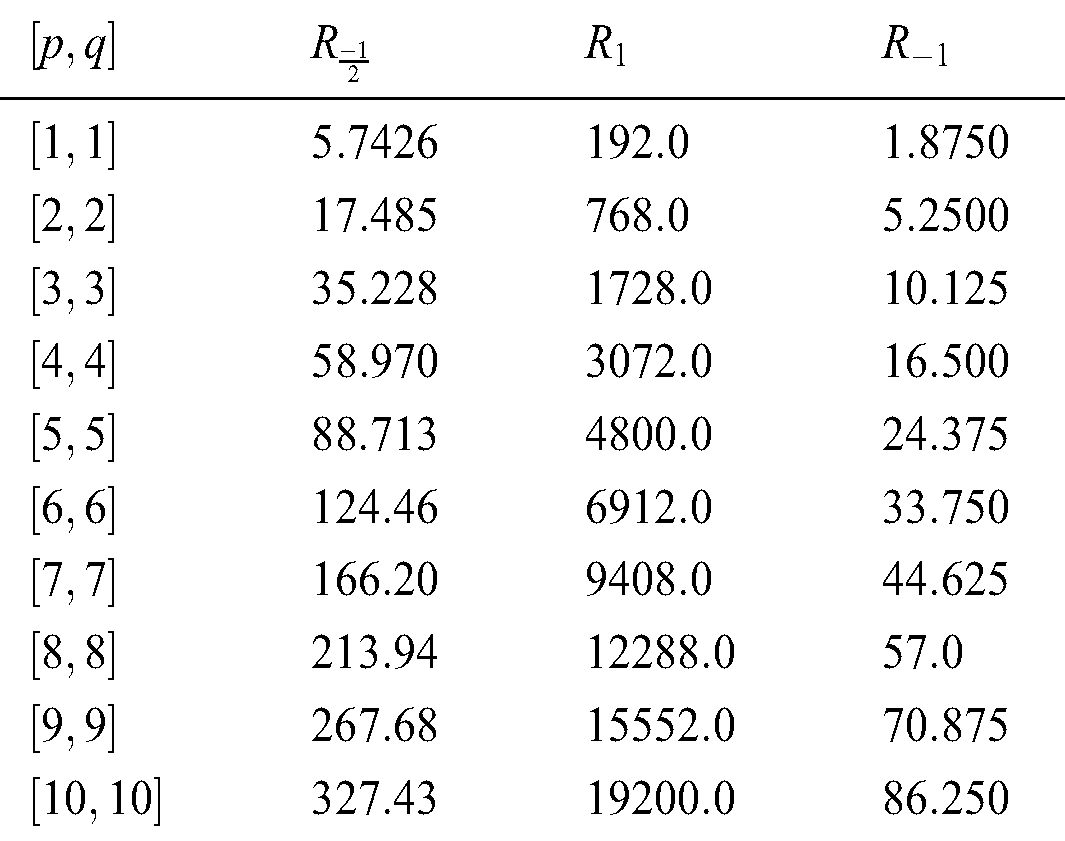
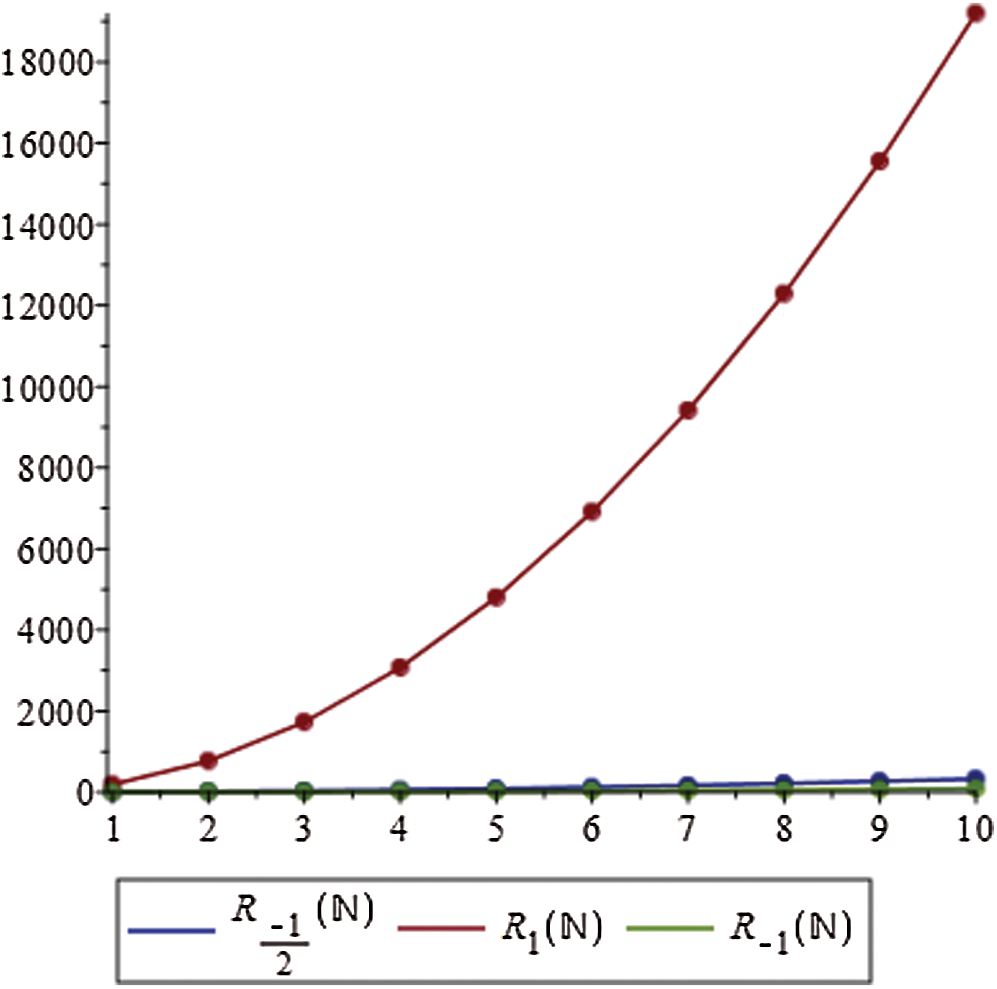
Figure 2: Graphical comparison of Theorem 4.2
We gave graphical comparison of Theorem 4.2 in Fig. 2 and numerical values Tab. 1.
In the next theorem, we determined general sum-connectivity index, first Zagreb index and hyper-Zagreb index of the hexagon star network  .
.
Theorem 4.3 For the hexagon star network  , we have
, we have
the general sum-connectivity index of  is
is
the sum-connectivity index of  is
is
the first Zagreb index of  is
is
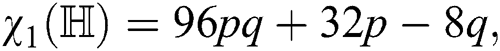
the hyper-Zagreb index of  is
is
Proof. For 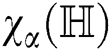 which is the general sum-connectivity index of
which is the general sum-connectivity index of 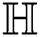 , we have
, we have 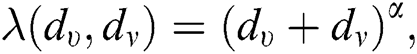 therefore
therefore 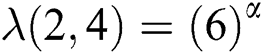 and
and 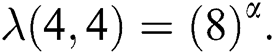 Thus by Lemma 4.1,
Thus by Lemma 4.1,
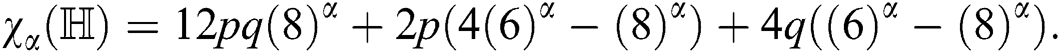
For 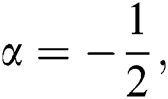 sum-connectivity index of
sum-connectivity index of 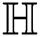
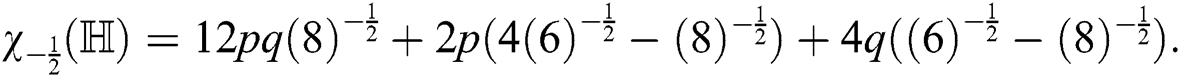
After simplification, we get
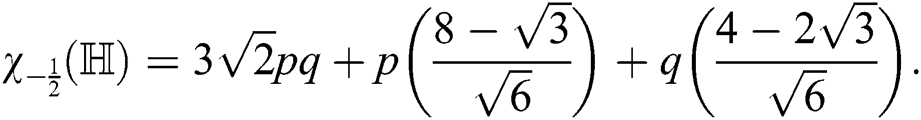
For 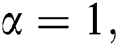 the first Zagreb index is
the first Zagreb index is
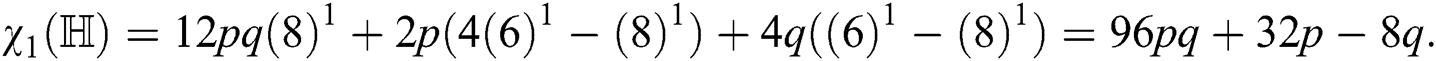
For 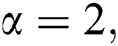 the hyper-Zagreb index is
the hyper-Zagreb index is
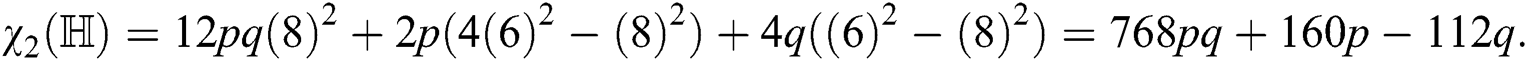
Table 2: Numerical representation of Theorem 4.3
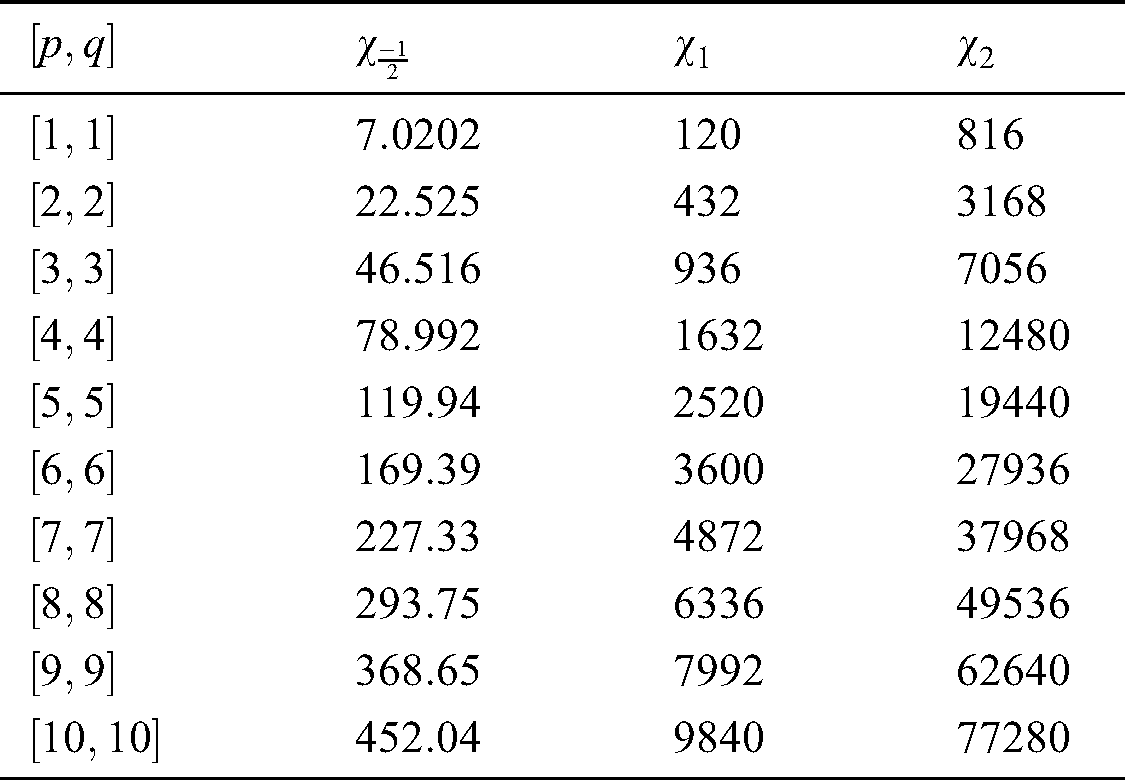
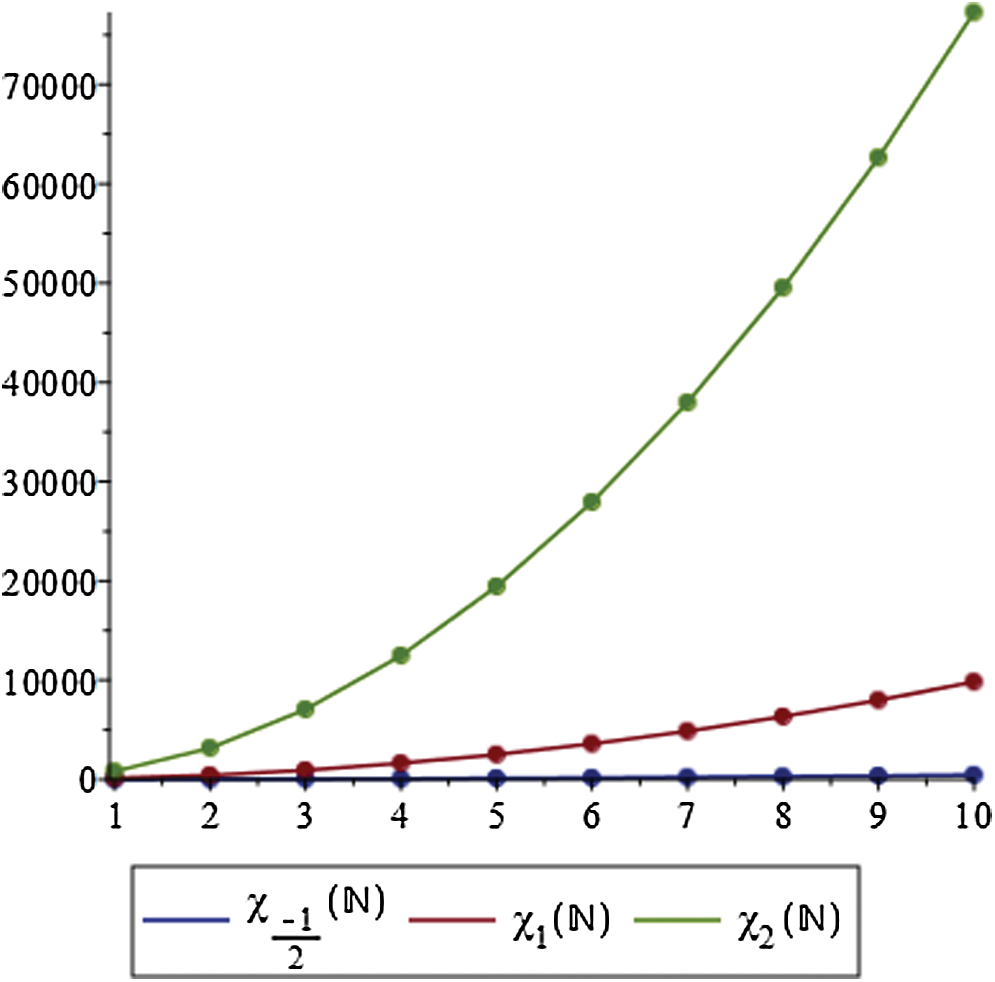
Figure 3: Graphical comparison of Theorem 4.3
We gave graphical comparison of Theorem 4.3 in Fig. 3 and numerical values Tab. 2.
Theorem 4.4 For the hexagon star network 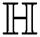 , we have
, we have
the geometric-arithmetic index of 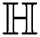 ,
,
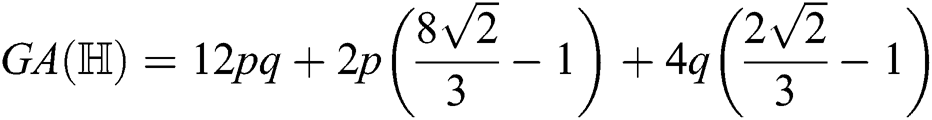
the atom-bond connectivity index of  ,
,
the augmented Zagreb index of  ,
,
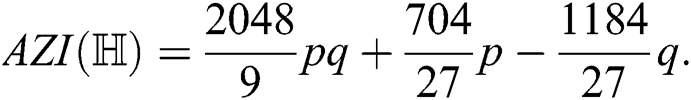
Proof. For  which is the geometric-arithmetic index of
which is the geometric-arithmetic index of  , we have
, we have 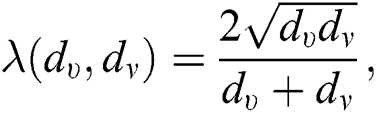 therefore
therefore 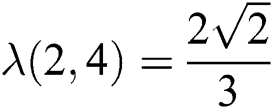 and
and 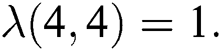 Thus by Lemma 4.1,
Thus by Lemma 4.1,
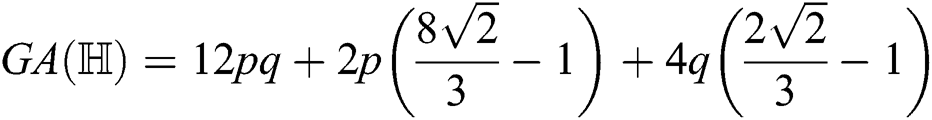
For 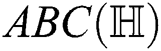 which is the atom-bond connectivity index of
which is the atom-bond connectivity index of  , we have
, we have 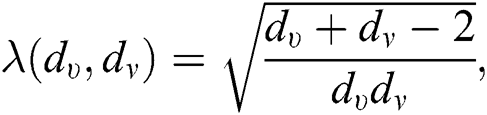 therefore
therefore 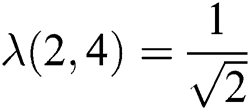 and
and 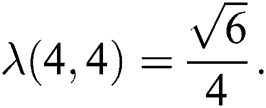 Thus by Lemma 4.1,
Thus by Lemma 4.1,
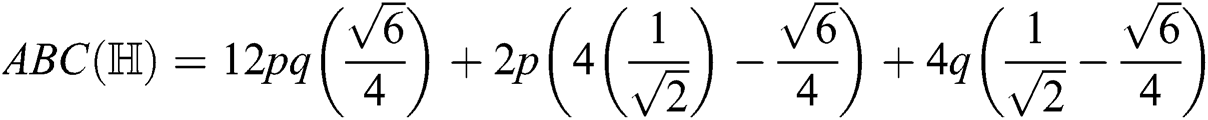
After simplification, we get
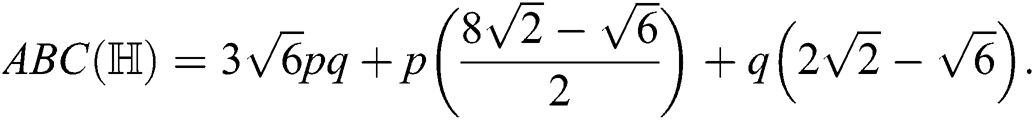
For 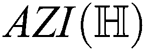 which is the augmented Zagreb index of
which is the augmented Zagreb index of 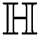 , we have
, we have 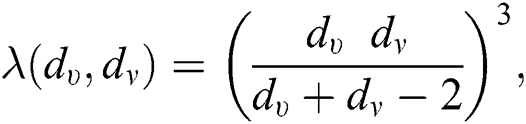 therefore
therefore 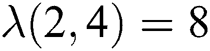 and
and 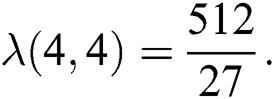 Thus by Lemma 4.1,
Thus by Lemma 4.1,
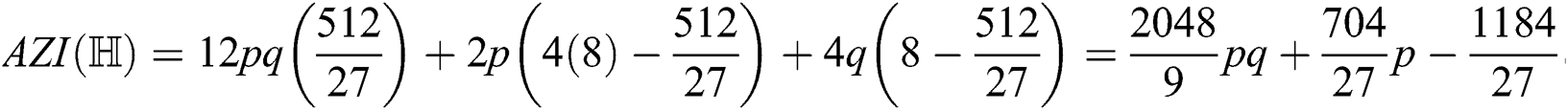
Table 3: Numerical representation of Theorem 4.4.
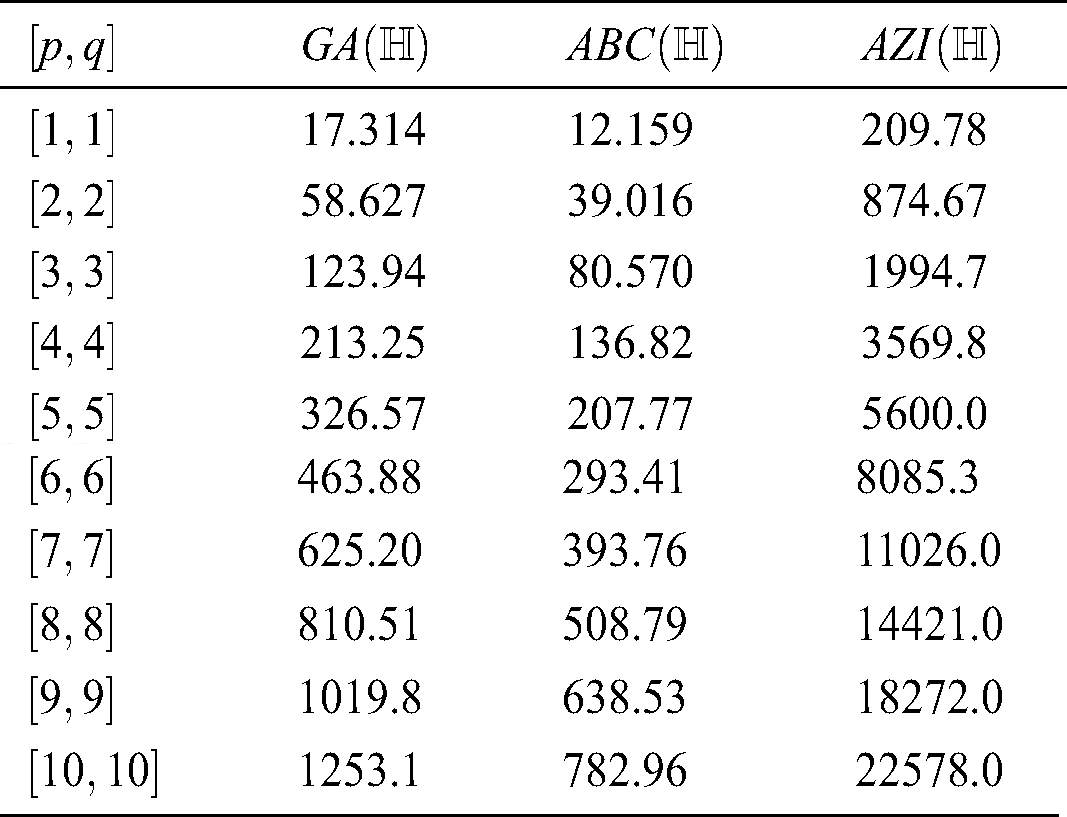
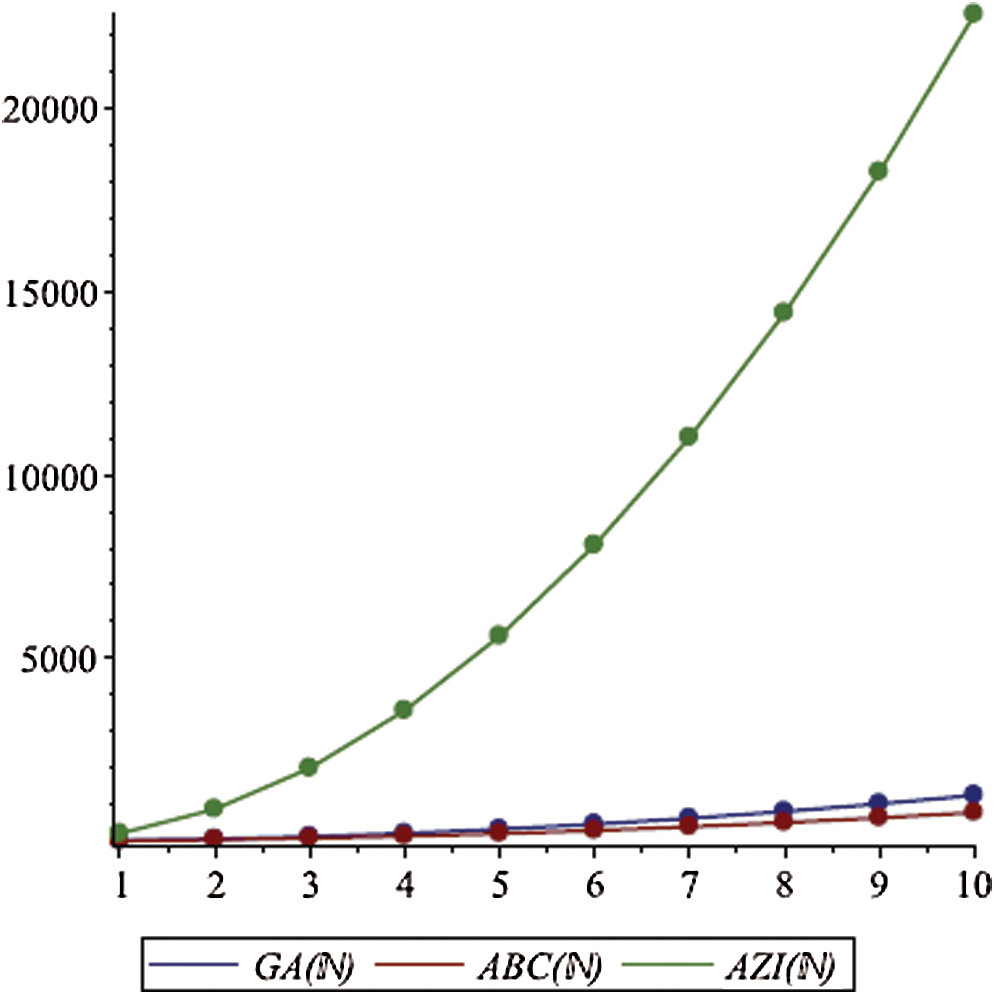
Figure 4: Graphical comparison of Theorem 4.4
We gave graphical comparison of Theorem 4.4 in Fig. 4 and numerical values Tab. 3.
Theorem 4.5 For the hexagon star network 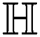 , we have
, we have
the symmetric division degree index of 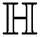 ,
,
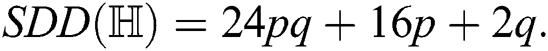
the Albertson index of 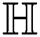 ,
,
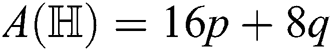
the harmonic index of 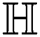
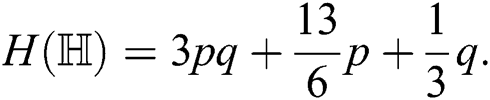
Proof. For  which is the symmetric division degree index of
which is the symmetric division degree index of  , we have
, we have 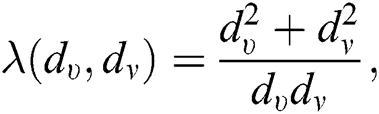 therefore
therefore 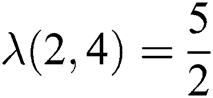 and
and 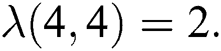 Thus by Lemma 4.1,
Thus by Lemma 4.1, 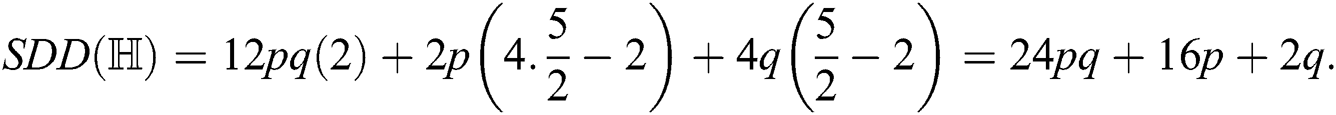
For  which is the Albertson index of
which is the Albertson index of 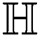 , we have
, we have 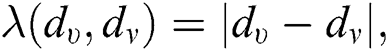 therefore
therefore 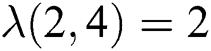 and
and 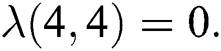 Thus by Lemma 4.1,
Thus by Lemma 4.1,
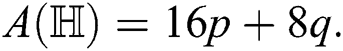
For 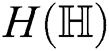 which is the harmonic index of
which is the harmonic index of 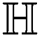 , we have
, we have 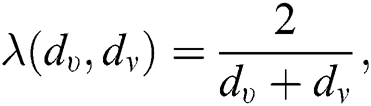 therefore
therefore 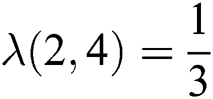 and
and 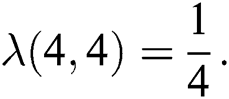 Thus by Lemma 4.1,
Thus by Lemma 4.1,
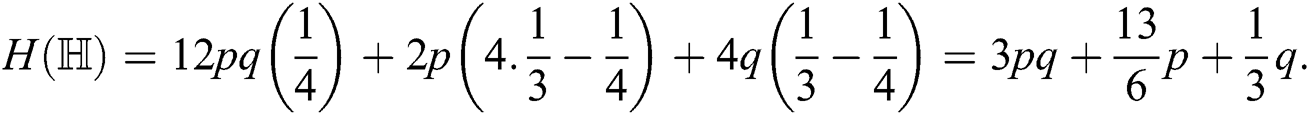
Table 4: Numerical representation of Theorem 4.5
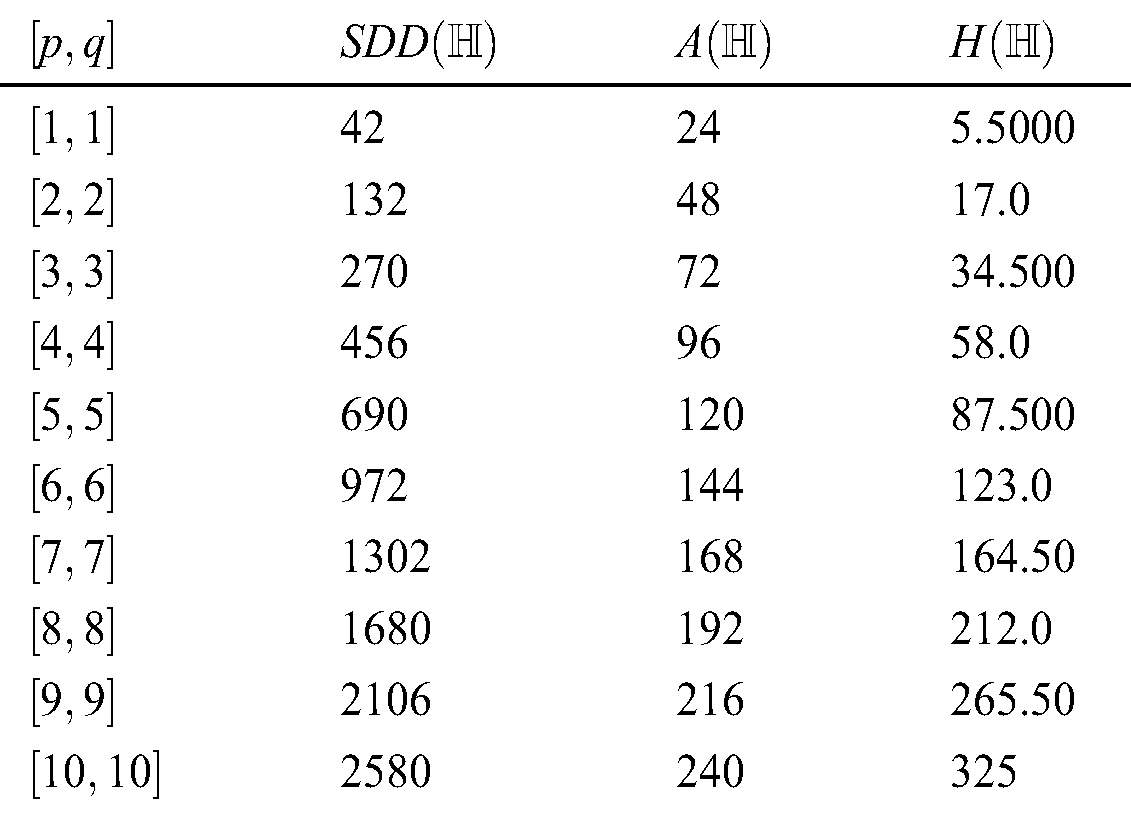
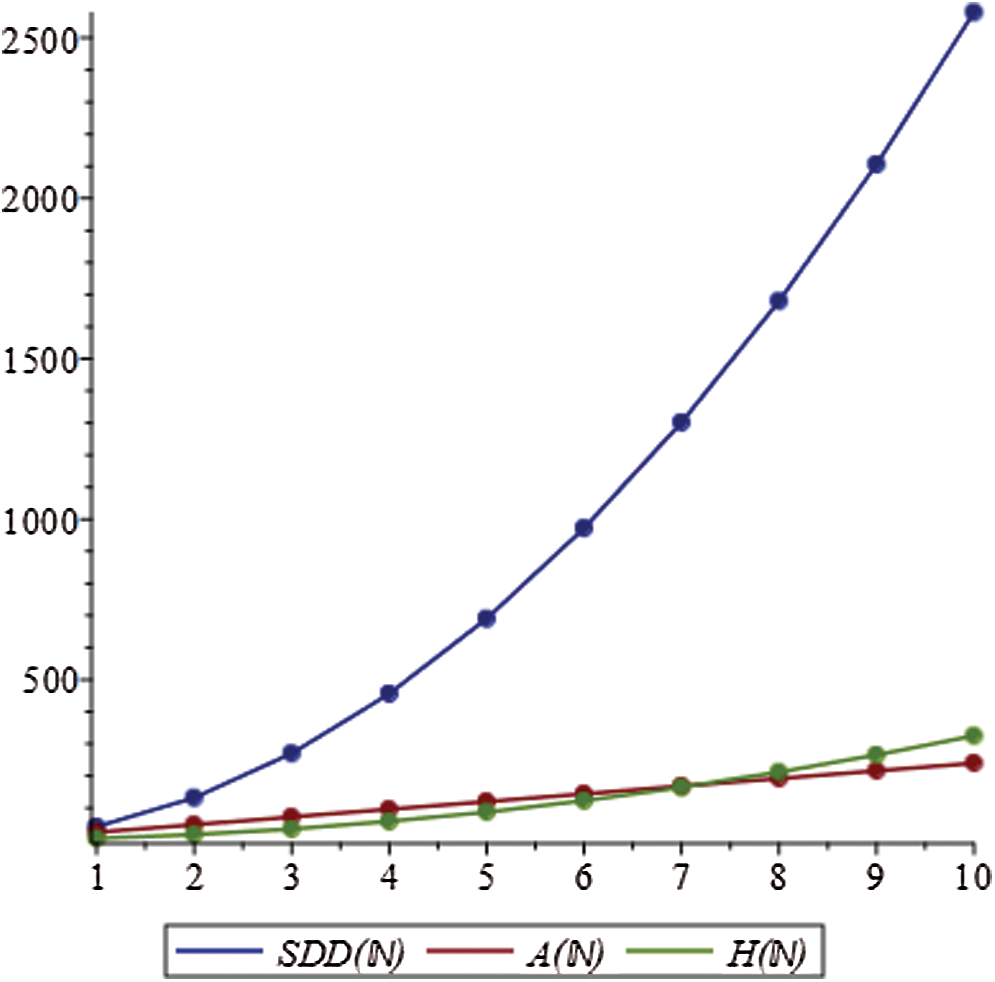
Figure 5: Graphical comparison of Theorem 4.5
We gave graphical comparison of Theorem 4.5 in Fig. 5 and numerical values Tab. 4.
Theorem 4.6 For the hexagon star network 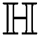 , we have
, we have
the first redefined Zagreb index of 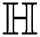 ,
,
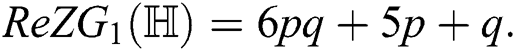
the second redefined Zagreb index of 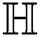 ,
,
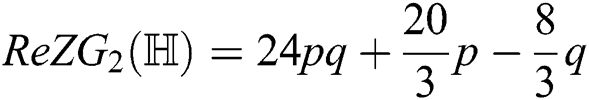
the third redefined Zagreb index of 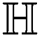
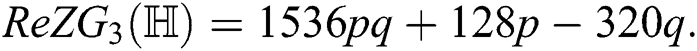
Proof. For 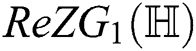 which is the first redefined Zagreb index of
which is the first redefined Zagreb index of 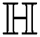 , we have
, we have 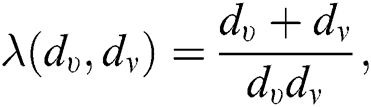 therefore
therefore 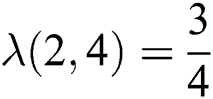 and
and 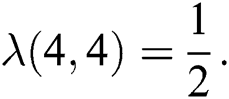 Thus by Lemma 4.1,
Thus by Lemma 4.1,
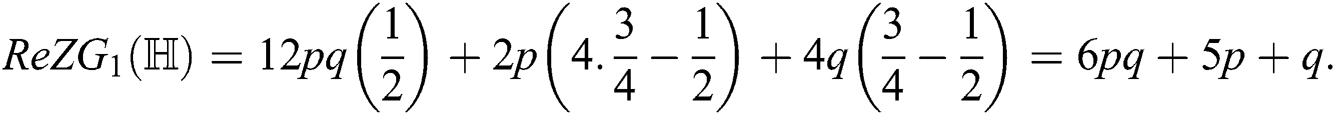
For 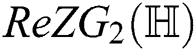 which is the second redefined Zagreb index of
which is the second redefined Zagreb index of  , we have
, we have 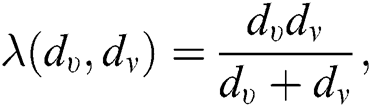 therefore
therefore 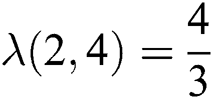 and
and 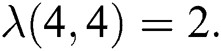 Thus by Lemma 4.1,
Thus by Lemma 4.1,
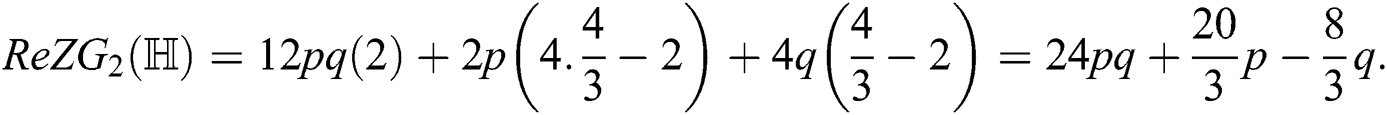
For  which is the third redefined Zagreb index of
which is the third redefined Zagreb index of  , we have
, we have 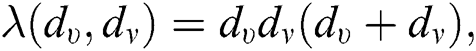 therefore
therefore 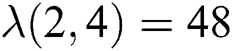 and
and 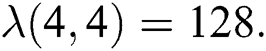 Thus by Lemma 4.1,
Thus by Lemma 4.1,
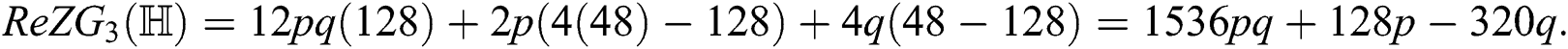
Table 5: Numerical representation of Theorem 4.6
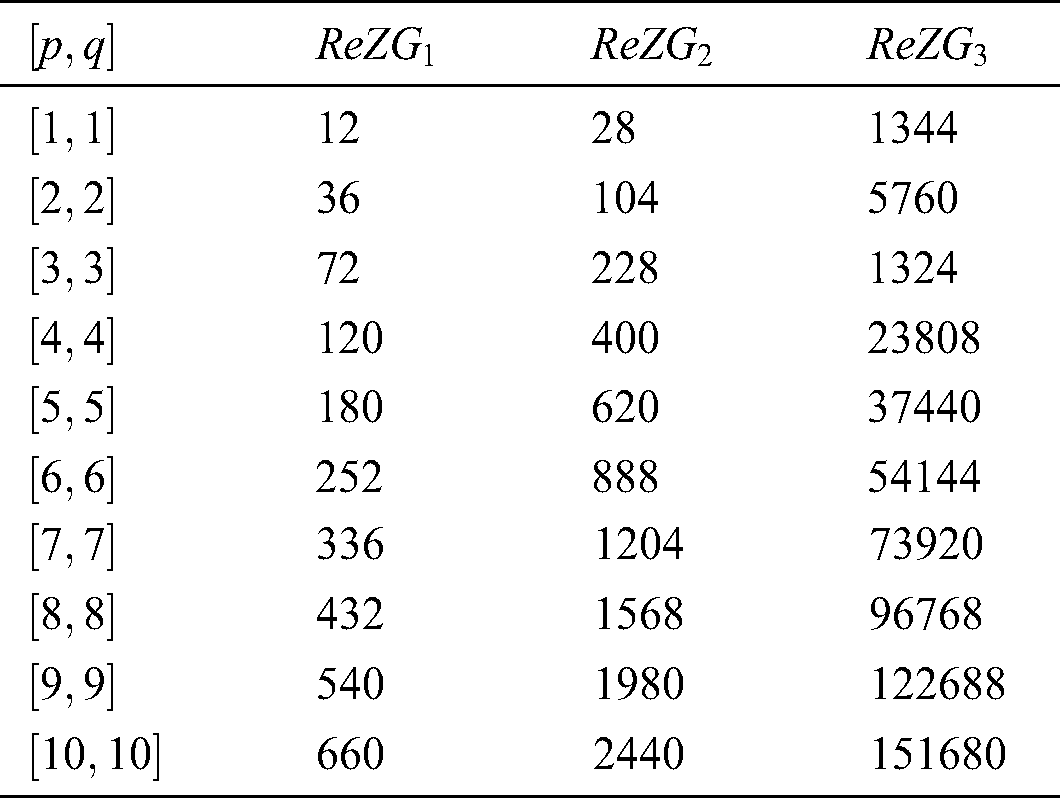
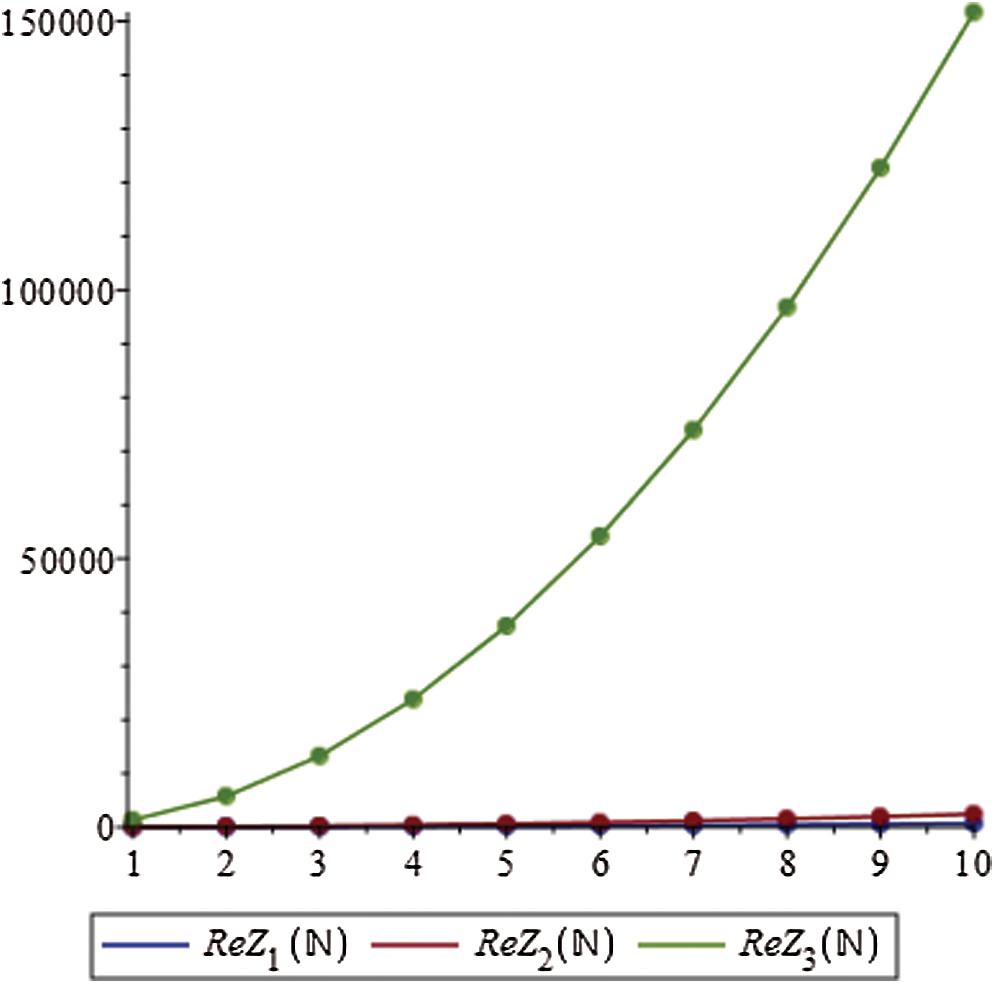
Figure 6: Graphical comparison of Theorem 4.6
We gave graphical comparison of Theorem 4.6 in Fig. 6 and numerical values Tab. 5.
Theorem 4.7 For the hexagon star network 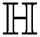 , we have
, we have
the Randi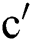 index of
index of 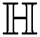 ,
,
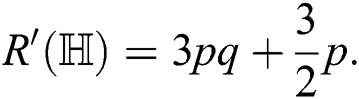
the Reformulated Zagreb index of  ,
,
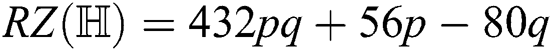
the forgotten index of 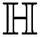
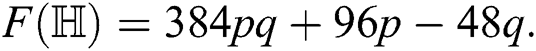
the irregularity measures of 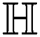
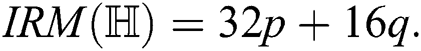
Proof. For 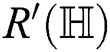 which is the Randi
which is the Randi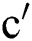 index of
index of 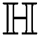 , we have
, we have  therefore
therefore  and
and  Thus by Lemma 4.1,
Thus by Lemma 4.1,
For 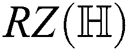 which is the Reformulated Zagreb index of
which is the Reformulated Zagreb index of 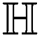 , we have
, we have 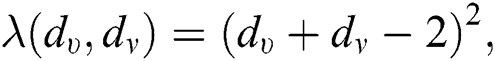 therefore
therefore 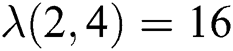 and
and 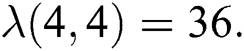 Thus by Lemma 4.1,
Thus by Lemma 4.1,
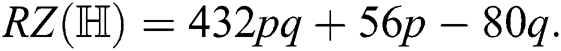
For  which is the forgotten index of
which is the forgotten index of  , we have
, we have 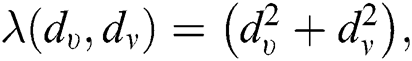 therefore
therefore 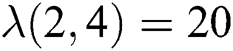 and
and 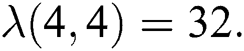 Thus by Lemma 4.1,
Thus by Lemma 4.1,
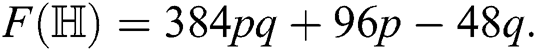
For 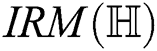 which is the irregularity measures of
which is the irregularity measures of 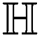 , we have
, we have 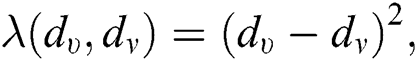 therefore
therefore 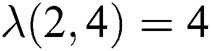 and
and 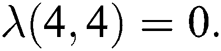 Thus by Lemma 4.1,
Thus by Lemma 4.1,
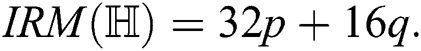
The study of graphs and networks through topological descriptors is important to understand their underlying topologies. Such investigations have a wide range of applications in cheminformatics, bioinformatics and biomedicine fields, where various graph invariants based assessments are used to deal with several challenging schemes. In the analysis of the quantitative structure property relationships (QSPRs) and the quantitative structureactivity relationships (QSARs), graph invariants are important tools to approximate and predicate the properties of the biological and chemical compounds. In this paper, we study the valency-based topological descriptor for hexagon star network.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. H. Wiener. (1947). “Structural determination of paraffin boiling points,” Journal of the American Chemical Society, vol. 69, no. 1, pp. 17–20.
2. J. Galvez, M. Galvez-Llompart, R. Zanni and R. Garcia-Domenech. (2013). “Molecular topology dissimilar similarities,” Drug Discovery Today Technologies, vol. 10, pp. 475–481.
3. O. Sporns. (2018). “Graph theory methods: applications in brain networks,” Dialogues in Clinical Neuroscience, vol. 20, no. 2, pp. 111–120.
4. K. H. Rosen. (2018). Discrete Mathematics and Its Applications, 8th edition, McGraw-Hill Education.
5. S. C. Basak, D. Mills and M. M. Mumtaz. (2007). “Quantitative structure-activity relationship (QSAR) study of dermal absorption using theoretical molecular descriptors,” SAR and QSAR in Environmental Research, vol. 18, no. 1–2, pp. 45–55.
6. M. Arockiaraj, S. Klavžar, J. Clement, S. Mushtaq and K. Balasubramanian, “Edge distance-based topological indices of strength-weighted graphs and their application to coronoid systems, carbon nanocones and SiO2 nanostructures,” Molecular Informatics, 2019. [Online]. https://doi.org/10.1002/minf.201900039.
7. M. repnjak and N. Tratnik. (2017). “The Szeged index and the Wiener index of partial cubes with applications to chemical graphs,” Applied Mathematics and Computation, vol. 309, pp. 324–333.
8. E. Estrada. (2017). “The ABC matrix,” Journal of Mathematical Chemistry, vol. 55, no. 4, pp. 1021–1033.
9. B. Furtula, K. C. Das and I. Gutman. (2018). “Comparative analysis of symmetric division deg index as potentially useful molecular descriptor,” International Journal of Quantum Chemistry, vol. 118, no. 17, e25659.
10. T. Vetrík. (2018). “Degree-based topological indices of hexagonal nanotubes,” Journal of Applied Mathematics and Computing, vol. 58, no. 1-2, pp. 111–124. [Google Scholar]
11. A. Ahmad. (2018). “On the degree based topological indices of benzene ring embedded in P-type-surface in 2D network,” Hacettepe Journal of Mathematics and Statistics, vol. 47, no. 1, pp. 9–18. [Google Scholar]
12. F. M. Brückler, T. Doslic’, A. Graovac and I. Gutman. (2011). “On a class of distance-based molecular structure descriptors,” Chemical Physics Letters, vol. 503, no. 4-6, pp. 336–338. [Google Scholar]
13. H. Gonzalez-Diaz, S. Vilar, L. Santana and E. Uriarte. (2007). “Medicinal chemistry and bioinformatics-current trends in drugs discovery with networks topological indices,” Current Topics in Medicinal Chemistry, vol. 7, no. 10, pp. 1015–1029. [Google Scholar]
14. M. C. Wasson, J. Lyu, T. Islamoglu and O. K. Farha. (2019). “Linker competition within a metal-organic framework for topological insights,” Inorganic Chemistry, vol. 58, no. 2, pp. 1513–1517. [Google Scholar]
15. G. Hong, Z. Gu, M. Javaid, M. H. Awais and M. K. Siddiqui. (2020). “Degree-based topological invariants of metal-organic networks,” IEEE Access, vol. 8, pp. 68288–68300. [Google Scholar]
16. M. R. Farahani. (2012). “Some connectivity indices and Zagreb index of polyhex nanotubes,” Acta Chimica Slovenica, vol. 59, no. 4, pp. 779–783. [Google Scholar]
17. M. Ajmal, W. Nazeer, M. Munir, S. M. Kang and Y. C. Kwun. (2017). “Some algebraic polynomials and topological indices of generalized prism and toroidal polyhex networks,” Symmetry, vol. 9, no. 1, pp. 5. [Google Scholar]
18. M. K. Siddiqui, M. Imran and A. Ahmad. (2016). “On Zagreb indices, Zagreb polynomials of some nanostar dendrimers,” Applied Mathematics and Computation, vol. 280, pp. 132–139. [Google Scholar]
19. M. R. Farahani, W. Gao, M. R. R. Kanna, R. P. Kumar and J. B. Liu. (2016). “General Randić, sum-connectivity, hyper-Zagreb and harmonic indices, and harmonic polynomial of molecular graphs,” Advances in Physical Chemistry, . [Online]. https://doi.org/10.1155/2016/2315949. [Google Scholar]
20. N. A. Koam A. and Ahmad A. (2020). “Polynomials of degree-based indices for three dimensional mesh network,” Computers, Materials & Continua, vol. 65, no. 2, pp. 1271–1282. [Google Scholar]
21. M. Baca, J. Horváthová, M. Mokrišová and A. Suhányiová. (2015). “On topological indices of fullerenes,” Applied Mathematics and Computation, vol. 251, pp. 154–161. [Google Scholar]
22. T. Vetrík. (2019). “Polynomials of degree-based indices for hexagonal nanotubes, Scientific Bulletin-University Politehnica of Bucharest,” Series B, vol. 81, no. 1, pp. 109–120. [Google Scholar]
23. A. Ahmad. (2020). “Topological properties of sodium chloride, Scientific Bulletin-University Politehnica of Bucharest,” Series B, vol. 82, no. 1, pp. 35–46. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |