DOI:10.32604/csse.2021.014460

| Computer Systems Science & Engineering DOI:10.32604/csse.2021.014460 |  |
| Article |
Clustering Collision Power Attack on RSA-CRT
1School of Cybersecurity, Chengdu University of Information Technology, Chengdu, 610225, China
2International Business Machines Corporation (IBM), New York, 10041 NY 212, USA
*Corresponding Author: Wunan Wan. Email: nan_wwn@cuit.edu.cn
Received: 22 September 2020; Accepted: 23 October 2020
Abstract: In this paper, we propose two new attack algorithms on RSA implementations with CRT (Chinese remainder theorem). To improve the attack efficiency considerably, a clustering collision power attack on RSA with CRT is introduced via chosen-message pairs. This attack method is that the key parameters dp and dq are segmented by byte, and the modular multiplication collisions are identified by k-means clustering. The exponents dp and dq were recovered by 12 power traces of six groups of the specific message pairs, and the exponent d was obtained. We also propose a second order clustering collision power analysis attack against RSA implementation with CRT, which applies double blinding exponentiation. To reduce noise and artificial participation, we analyze the power points of interest by preprocessing and k-means clustering with horizontal correlation collisions. Thus, we recovered approximately 91% of the secret exponents manipulated with a single power curve on RSA-CRT with countermeasures of double blinding methods.
Keywords: Collision attack; power analysis attack; chosen-message attack; module exponentiation; RSA-CRT
Currently, most smart cards use the RSA algorithm to realize digital signature and identity authentication [1]. However, the implementation of RSA requires high power consumption, high execution time and computational power, and the execution time of RSA is 100 times slower than that of DES [2]. In 1982, Quisquate et al. [3] proposed a fast variant algorithm based on the CRT, which can greatly improve the performances of RSA in both running times and memory requirements. Thus, RSA implementations using CRT (RSA-CRT) are widely used in smart cards and embedded devices to ensure system security. However, cryptographic devices have been subject to side channel attack techniques since Kocher first introduced a power analysis attack based on execution time measurements in 1996 Kocher [4]. Side channel attacks (SCAs) have attracted the attention of many researchers, and many SCA attacks against RSA-CRT cryptosystems have been proposed, such as simple power analysis (SPA) [5,6], differential power analysis (DPA) [7–9], and template attack [10].
In 2000, a timing attack against RSA-CRT was first proposed if the Montgomery algorithms were used for squaring and multiplication operations [11]. In 2002, Boer first presented a DPA attack against RSA-CRT [7], namely, modular reduction on equidistant data (MRED), by choosing ciphertexts of equidistant data, in which an additional modular reduction is performed at the end of the operation according to the input data. However, a basic precondition of the MRED attack is that the attacker is required to have the possibility of choosing messages. Subsequently, several improved DPA attacks based on MRED have been proposed [8]. In 2009, Witteman [12] proposed a DPA on RSA-CRT without requiring any knowledge of the input message. This attack can retrieve both primes and private keys by splitting intermediate results during the reorganization process. DPA attacks on RSA-CRT of the Montgomery domain were developed [13,14]. In 2018, Kaedi et al. [15] presented a DPA attack on the modular reduction in RSA-CRT, named non-equidistant plaintext on modular reduction (NEMR). This attack requires choosing nonequidistant plaintext and has a lower level of accessibility than a chosen equidistant plaintext attack by Boer et al. Several SPA attacks on RSA-CRT have been presented. Novka [5] described the SPA with adaptively chosen messages when the Garner’s algorithm implemented the CRT in 2002. Pouque et al. [6] improved the Novak’s attack with a combination of grid technology and SPA. The collision power analysis against RSA was proposed by using the two related input messages “X” and “-X”, “X” and “X2” or the particular input data of “N-1”, where N is the modulus [16–19], and pointed out that these methods were equally effective for RSA-CRT Yen et al. [17].
To prevent these attacks, hardware protections and software countermeasures have been published, and the exponent and message blinding methods are the main countermeasures. In the exponent blinding method [20–22], the exponent is randomized or split, and consequently, subsequent exponentiation operations handle different exponential data. For message blinding methods [23–25], the message is multiplied by a random value, and this blinded message is then used in exponentiation algorithms.
However, advance attacks have recently emerged. Witteman et al. [26] presented the correlation power analysis (CPA) attack on the square and multiply always algorithm by cross-correlating measurements of consecutive operations sharing the same input values. Kim et al. [27] showed that correlation analysis can be used to retrieve the secret key for RSA derivatives of a message blinding countermeasure. Clavier noted that horizontal correlation attacks (HCAs) were effective in attacking almost all message blinding countermeasures [28–30]. Akalp et al. [31] proposed two correlation attacks on a Montgomery ladder implementation of the RSA algorithm. The cross correlation technique was introduced in Wan et al. [32], and the secret exponent with message blinding can be recovered by using this attack.
With the development of machine learning techniques [33–39], machine learning can provide efficient pattern recognition and feature extraction algorithms. Carbone et al. presented several successful profiled SCAs based on deep learning for RSA and pointed out the need for dedicated countermeasures [40]. Differential cluster analysis (DCA) as an extension to DPA was proposed in Batina et al. [41]. Cluster collision attacks presented by Chen are very efficient via two traces of execution on chosen inputs [42]. Heyszl et al. [43] introduced a clustering single execution attack for an elliptic curve scalar multiplication. In Perin et al. [44], explored and developed an attack by combining the fuzzy k-means algorithm for an RNS-based implementation of the RSA. Subsequently, improving nonprofiled attacks based on clustering by applying principal component analysis (PCA) against elliptic curve digital signature algorithm (ECDSA) was proposed [45]. In Wan et al. [46], a clustering correlation power analysis was described against double blinding exponentiation.
SCA attacks on RSA-CRT with no countermeasures can be currently divided into two main types: attacks on the modular reduction step and attacks on the recombination step. Most DPA attacks against RSA-CRT are based on MRED attacks. The attacker chooses a large number of input data related to the prime numbers p and q in the modular reduction step. The proposed collision SPA attacks have been shown to be valid for RSA-CRT in theory by Yen et al. However, searching for collisions of modular multiplication is difficult due to noise in real environments. Moreover, Yen's collision attack takes place bit by bit, and if the 1-bit inference is an error, the subsequent bit will be affected. High-order correlation power analyses are effective for the blinding countermeasures of exponentiation according to the previous analysis; similarly, much noise leads to lower attack accuracy. Clustering is generally useful in SCAs. Clustering algorithms can provide a straightforward way to increase the signal-to-noise ratio (SNR) of the exploited leakage for side channel measurements. Therefore, we take advantage of the cluster classification K-mean algorithm to exploit leakage and to recover secret exponents for RSA-CRT. The cluster classifications are used at each phase to recover the entire exponent.
Our main contributions are listed as follows:
1) We put forward the innovative idea of clustering collision power attack based on exponent segment by byte on RSA-CRT with none countermeasures. The new attack method improves the utilization of valid information, and reduces the noise and artificial participation. The experimental results prove that the attack ration is more efficient on RSA-CRT in the IC (integrated circuit) card.
2) A new cluster collision power attack against double blinding exponentiation is proposed. We demonstrate how to find the points of interest using preprocessing and k-means clustering with only one execution power curve. The experimental results show that the new attack can enhance the attack efficiency compared with other CPA methods. The approximately 91% exponent was broken via a single power curve.
The rest of this paper is organized as follows. Section 2 introduces the relevant knowledge. Section 3 presents the clustering collision power attack against RSA-CRT of none countermeasures. Section 4 gives the new attack against countermeasures of double blinding exponentiation in RSA-CRT. Experimental results are reported in Section 5. Finally, the conclusions are proposed in Section 6.
In a standard RSA algorithm, 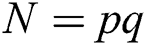 denotes the n-bit public modulus, where the bits of two large prime numbers p and q are required to be equal, satisfying
denotes the n-bit public modulus, where the bits of two large prime numbers p and q are required to be equal, satisfying 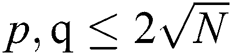 . d is the secret private key and e is the public key, where
. d is the secret private key and e is the public key, where 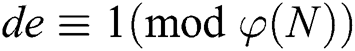 and
and 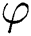 denotes Euler’s totient function, where
denotes Euler’s totient function, where 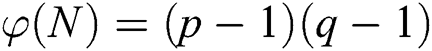 . RSA signature and verification are modular exponentiation. Let M be a message to sign. A signature for M is
. RSA signature and verification are modular exponentiation. Let M be a message to sign. A signature for M is 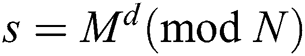 , and a verification is
, and a verification is 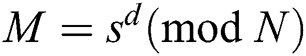 .
.
As we know, the Chinese remainder theorem is a technique used to optimize RSA exponentiation. A detailed description of this algorithm can be found in [21]. In Algorithm 1, we describe the RSA signature generation using Garner’s algorithm in [1].
Algorithm 1: RSA-CRT signature implementation

In a CRT implementation, the signer first precomputes the reduced secret exponent values 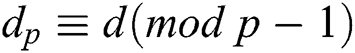 ,
,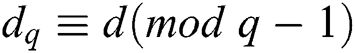 ,
, 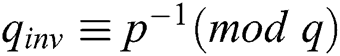 and subsequently uses Algorithm 1 to compute the signature s. This algorithm does not require any reduction modulo N, but instead uses reductions modulo on the factors p and q. The size of p and q is approximately half the size of N, so CRT exponentiation is nearly four times faster than direct exponentiation [1].
and subsequently uses Algorithm 1 to compute the signature s. This algorithm does not require any reduction modulo N, but instead uses reductions modulo on the factors p and q. The size of p and q is approximately half the size of N, so CRT exponentiation is nearly four times faster than direct exponentiation [1].
2.2 Binary Modular Exponentiation Algorithm
Modular exponentiation is one of the most important arithmetic operations of the RSA-CRT algorithm. The Montgomery modular multiplication algorithm is the best approach on minimizing the computation cost of modular multiplication [7].
We define the modulus n as a k-bit integer, i.e., 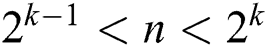 ,
, 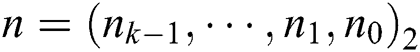 and we let
and we let 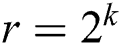 , and
, and 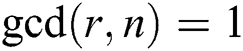 . The Montgomery product is defined as the n-residue:
. The Montgomery product is defined as the n-residue:
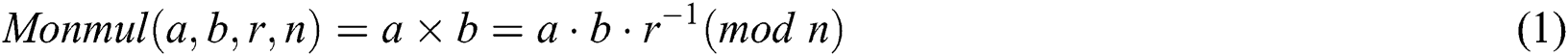
Algorithm 2 gives the Montgomery exponentiation algorithm, which performs multiplication and squaring operations in according with the bit pattern of the exponent. This is aleft-to-right binary method that starts at the exponent's MSB (most significant bit), and is thus called the L-R binary algorithm.
Algorithm 2: Montgomery binary modular exponentiation (L-R)

2.3 Exponent and Message Blinding Modular Exponentiation Algorithm
The exponent blinding method and the message blinding method can also be regarded as effective countermeasures for modular exponentiation algorithms. There are generally two type exponent blinding countermeasures in present [20–25]. Ha et al. [24] proposed a modular exponentiation protection method for double masking by using a random number r to blind the message and the exponent split. As is illustrated Algorithm 3, it is assumed that the length of m, r, or 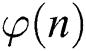 is k-bit. Let the exponent d to be split t and s, where
is k-bit. Let the exponent d to be split t and s, where 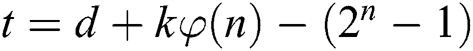 ,
, 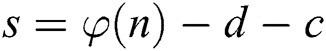 . And the message m is masked by random number r, the parameter c is a very small random value such that
. And the message m is masked by random number r, the parameter c is a very small random value such that 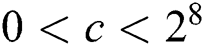 .
.
Algorithm 3: Montgomery exponentiation based on double masking

Algorithm 3 always executes square and multiplication in turn, and is therefore resistant to the SPA attacks of attempting to recover the key by identifying the different modular operations. And it is also resistant to DPA and the first order CPA, even if an attacker could distinguish the square and multiply operations, this would not lead to key computer. Therefore, the leakage model of Algorithm 3 will be given in following section in this paper.
3 New Cluster Collision Attack against RSA-CRT Based on Chosen-Message Pair
In this subsection, we propose a chosen-message clustering collision power attack against Algorithm 2 based on exponent segment by byte for RSA-CRT. In the scheme, the information leakage of loaded data was integrated into the information leakage of loaded data using a chosen-message pair, and the attack accuracy per byte of the secret exponent do not affect each other. The utilization of valid information is improved, and the noise and artificial participation are reduced by cluster analysis.
3.1 Choosing the Message Pairs for Secret Exponents in RSA-CRT
Two modular exponentiations 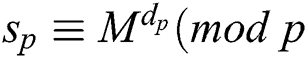 ) and
) and 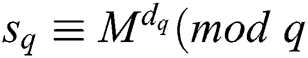 ) appear in Algorithm 1 for RSA-CRT. According to Fermat's theorem, the public key parameter modulus
) appear in Algorithm 1 for RSA-CRT. According to Fermat's theorem, the public key parameter modulus 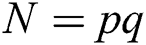 , and thus formula (3) exists:
, and thus formula (3) exists:

Although p and q are unknown, the modulus N is given, and we can perform a different collision attack that uses the chosen-message pair “X” and “N-X”, where the message “X” is random. The secret exponents 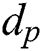 and
and 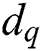 can be obtained by Yen’s attack, and then exponent d can be calculated.
can be obtained by Yen’s attack, and then exponent d can be calculated.
3.2 Power Leakage Model of Modular Multiplication Using a Chosen-Message Pair
The power consumption mainly depends on the operations and data of running cryptographic algorithms in cryptographic devices. In addition to these two dependent components, the existence of noise in the power traces is inevitable in a real attack environment. The total power consumption of the cryptosystem can be determined as follows:

where 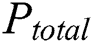 is the total power,
is the total power, 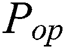 is the operation-dependent power consumption,
is the operation-dependent power consumption, 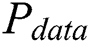 is the data-dependent power consumption,
is the data-dependent power consumption, 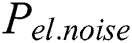 denotes the power resulting from the electronic noise in the hardware, and
denotes the power resulting from the electronic noise in the hardware, and 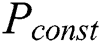 is some constant power consumption, depending on the technical implementation.
is some constant power consumption, depending on the technical implementation.
Every power point of power traces can be modeled by formula (3). Every modular multiplication has the same operations, thus 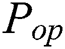 of each point is roughly the same, and
of each point is roughly the same, and 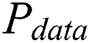 depends on two operands of the multiplication. If two modular multiplications have two operands in common, referred to as “collision”,
depends on two operands of the multiplication. If two modular multiplications have two operands in common, referred to as “collision”, 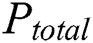 is exactly the same in theory. Therefore, in turn, we can infer a collision relationship between modular multiplication operands according to the similarity of power consumption, as illustrated in Tab. 1.
is exactly the same in theory. Therefore, in turn, we can infer a collision relationship between modular multiplication operands according to the similarity of power consumption, as illustrated in Tab. 1.
Table 1: Collision relation of power consumption

If two multiplications 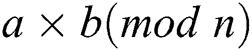 and
and 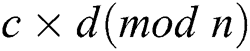 were performed, we can distinguish a collision relation between two operands by quantifying the similarity of the power trace for the two modular operations. Therefore, Yen’s attack uses the message pair “X” and “–X ” for Algorithm 2 [17]. The secret exponent is inferred by detecting collisions of the squaring operations in two power traces.
were performed, we can distinguish a collision relation between two operands by quantifying the similarity of the power trace for the two modular operations. Therefore, Yen’s attack uses the message pair “X” and “–X ” for Algorithm 2 [17]. The secret exponent is inferred by detecting collisions of the squaring operations in two power traces.
Fig. 1 shows Yen’s attack against Algorithm 2. When the key bit 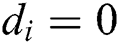 , two squaring modular multiplications have the operand in common, and a “collision” between power traces can be observed. Therefore, if the differential value of two power traces is low for modular multiplication, we can infer that this and the former modular multiplication are “squaring” in theory, and the key bit of the former modular multiplication is “0”.
, two squaring modular multiplications have the operand in common, and a “collision” between power traces can be observed. Therefore, if the differential value of two power traces is low for modular multiplication, we can infer that this and the former modular multiplication are “squaring” in theory, and the key bit of the former modular multiplication is “0”.
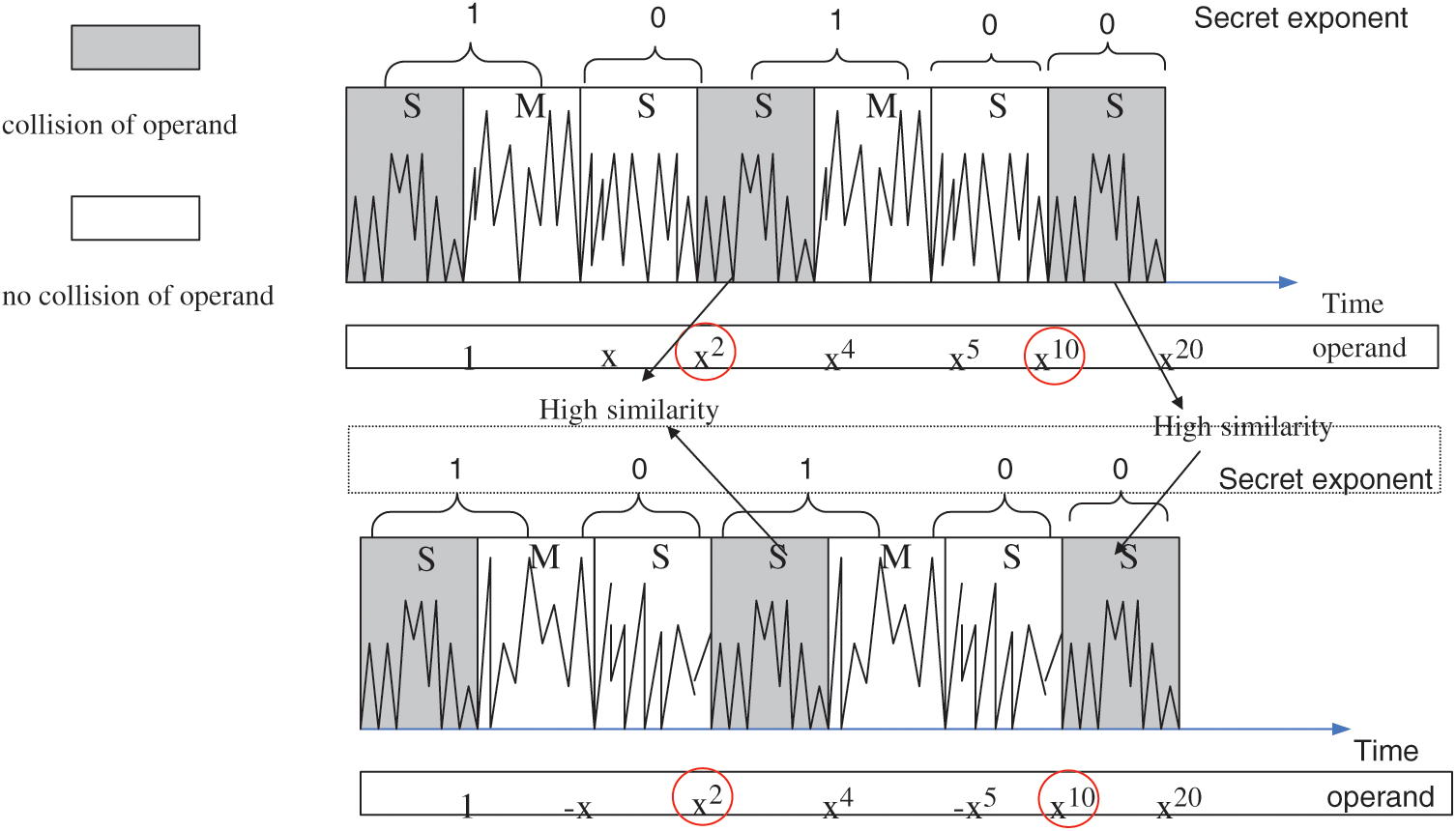
Figure 1: Yen’s collision attack
3.3 Feature Analysis and Preprocessing of Power Traces
Each power trace of modular exponentiation is mainly composed of modular multiplication (“square(S)” and “multiplication (M)”) and loads the operand (“L”) between two modular multiplications. The power voltage of modular multiplication is high, as denoted 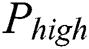 , and the power voltage of load data is low, as denoted by
, and the power voltage of load data is low, as denoted by 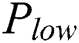 . The power trace of modular multiplication can be extracted from the power trace, as shown in Fig. 3. Another choice, for the cipher chip is the MCU-coprocessor structure, and the number of bit processing data is 8 bits, i.e., the exponent is loaded by byte. Every byte exponent needs to increase the operation in load data, and thus there are two types of low power characteristics between modular multiplication operations, as denoted by
. The power trace of modular multiplication can be extracted from the power trace, as shown in Fig. 3. Another choice, for the cipher chip is the MCU-coprocessor structure, and the number of bit processing data is 8 bits, i.e., the exponent is loaded by byte. Every byte exponent needs to increase the operation in load data, and thus there are two types of low power characteristics between modular multiplication operations, as denoted by 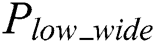 and
and 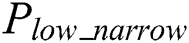 in Fig. 2.
in Fig. 2.
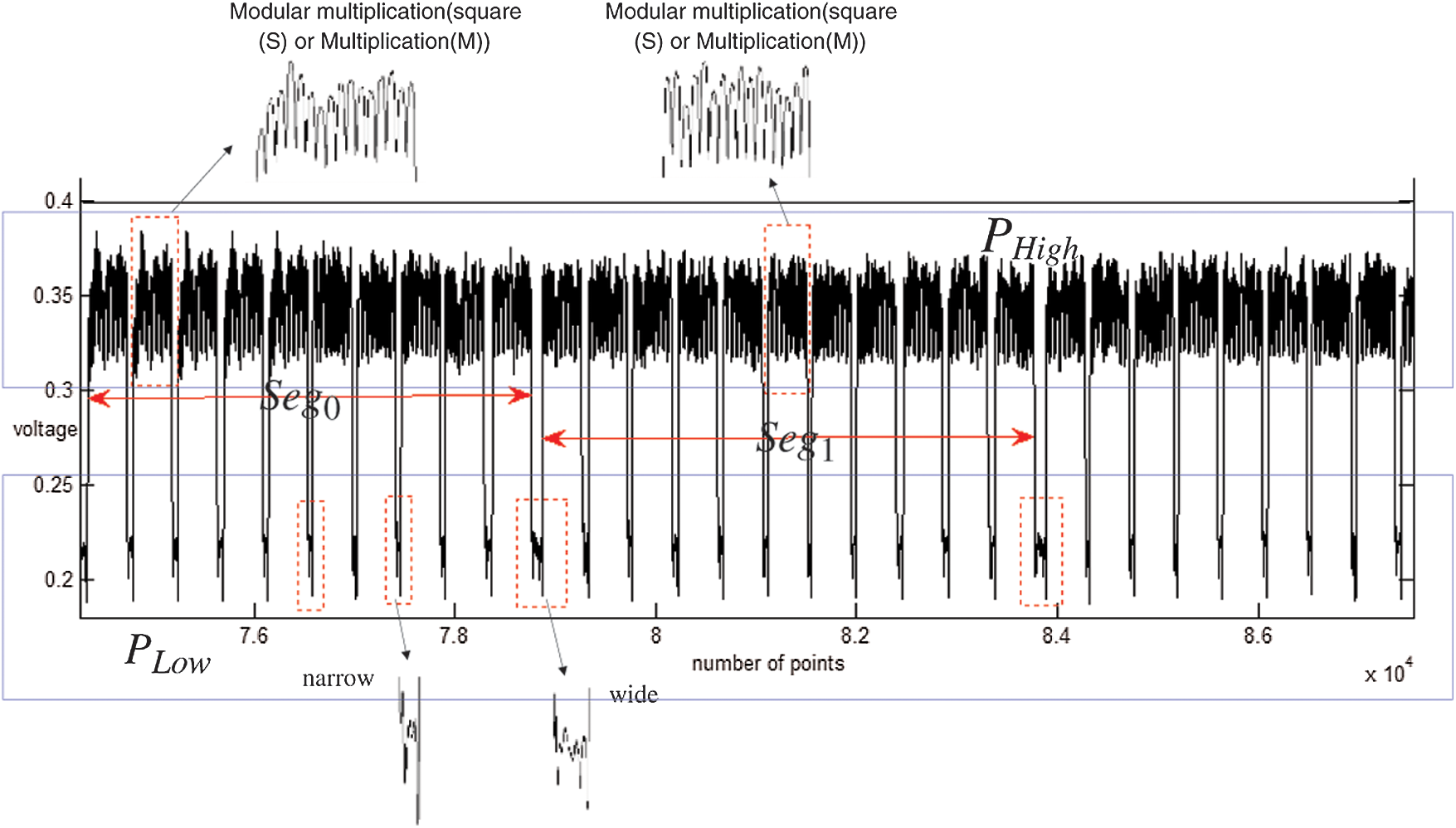
Figure 2: Power characteristics of modular exponentiation operations

Figure 3: Power traces of the multiplication
The power trace of modular exponentiation is segmented according to the power characteristic 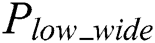 by byte of the secret private key. Every segment includes only modular multiplication while ignoring the load on the operand, as depicted in Fig. 3.
by byte of the secret private key. Every segment includes only modular multiplication while ignoring the load on the operand, as depicted in Fig. 3.
We extract the signals of modular multiplication related to Step 3 and Step 5 in Algorithm 2 from each power trace and begin with a definition.
Definition 1: A power trace with a z-byte private key with z segments of modular multiplication is denoted as follows:

where every segment includes 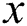 modular multiplication operations,
modular multiplication operations, 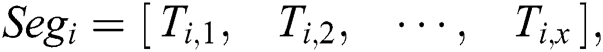
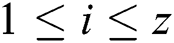 , and
, and 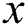 is the dynamic change between 8 and 16. If a modular multiplication has w power points, the power trace of a modular multiplication,
is the dynamic change between 8 and 16. If a modular multiplication has w power points, the power trace of a modular multiplication, 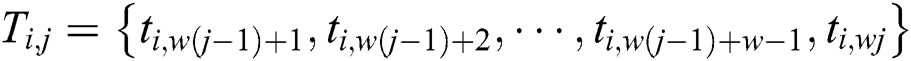 .
.
The attacker inputs u pairs of message “X” and “N-X”, the same modulus N and the same secret key d into RSA-CRT cryptosystem devices, and executes Algorithm 1. We can collect u pairs of power traces. We define that 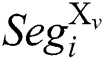 is a segment of the power trace with input message “X”, and
is a segment of the power trace with input message “X”, and 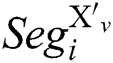 is a segment of the power trace with input message "N-X", where
is a segment of the power trace with input message "N-X", where 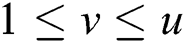 ,
, 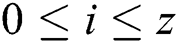 . The segment differential is performed between
. The segment differential is performed between 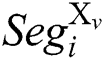 and
and 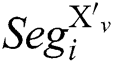 , and we can obtain a new difference segment, which is defined as follows:
, and we can obtain a new difference segment, which is defined as follows:

Therefore, we can obtain a new difference segment matrix:
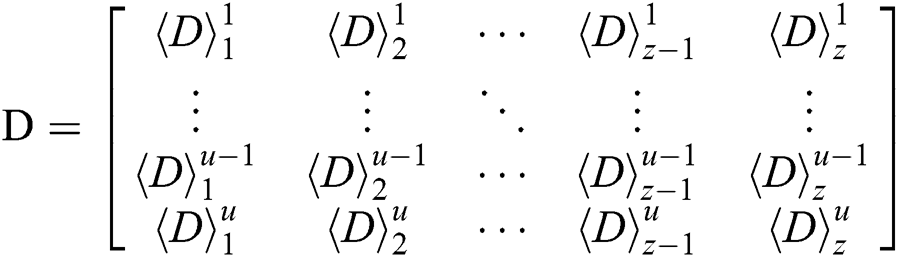
Where 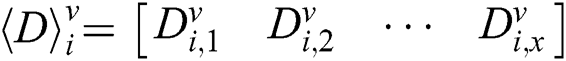
In a practical environment, due to noise, random time delay and random clock, it is difficult to distinguish collisions directly according to the difference segment 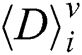 directly. We will give the collision cluster classification of modular in the next subsection.
directly. We will give the collision cluster classification of modular in the next subsection.
3.4 Collision Cluster Classification of Modular Multiplication Operations
Each segment 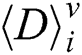 has x difference values of modular multiplication operations for a 1-byte secret exponent. For noise, we compute the area of each modular multiplication difference and sum the difference areas with u input message pairs. We can obtain the difference area sum of modular multiplication in every segment:
has x difference values of modular multiplication operations for a 1-byte secret exponent. For noise, we compute the area of each modular multiplication difference and sum the difference areas with u input message pairs. We can obtain the difference area sum of modular multiplication in every segment:

where 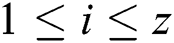 ,
, 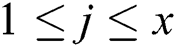 ,
, 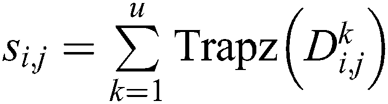
Thus, 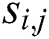 can be classified into two classes (collision and noncollision) as a data set
can be classified into two classes (collision and noncollision) as a data set 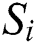 by applying the k-means algorithm. Here, we summarize the classification process [34,35,46]:
by applying the k-means algorithm. Here, we summarize the classification process [34,35,46]:
1. The data set 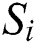 consists of
consists of 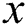 samples
samples 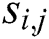 , where
, where 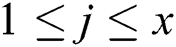 ,
,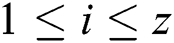 .
.
2. Set the two cluster centers 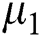 and
and 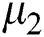 randomly.
randomly.
3. For each sample 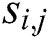 of the data set
of the data set 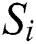 , computer the Euclidean distance
, computer the Euclidean distance 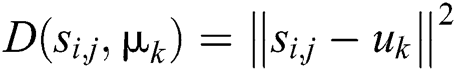 , where
, where 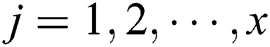 ,
, 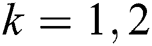 . Classify samples
. Classify samples 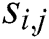 according to the nearest
according to the nearest 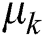 . If
. If 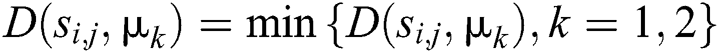 , then
, then 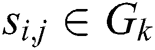 ,
,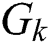 is a class cluster.
is a class cluster.
4. Recompute the two cluster centers 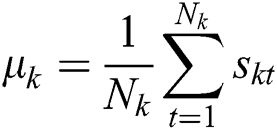 , where
, where 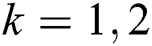 , t is a new number in a new cluster, and
, t is a new number in a new cluster, and 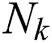 represents the number of samples.
represents the number of samples.
5. Computer the deviation: 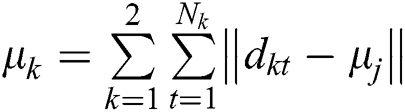 .
.
6. Convergence the judgment: if J Convergence, then continue; else return to Step 3.
7. Recompute each cluster center 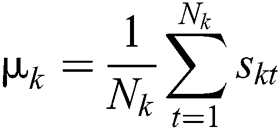 , where
, where 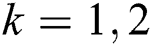 .
.
The steps are repeated z times, and all segments are classified. We can obtain two classes (“collision” and “noncollision”) and denote the vector 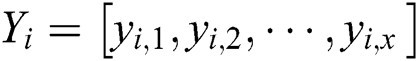 , where if
, where if 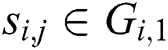 , then let
, then let 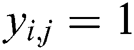 (“collision”), else
(“collision”), else 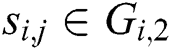 , then let
, then let 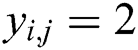 (“noncollision”). Fig. 4 shows that all segments can be classified in our practical experiments. The red band denots “noncollision”, and the blue band indicates “collision”.
(“noncollision”). Fig. 4 shows that all segments can be classified in our practical experiments. The red band denots “noncollision”, and the blue band indicates “collision”.
Figure 4: Classification of modular multiplications
3.5 Recovering the Secret Exponent
Moreover, Yen’s collision attack is bit by bit, and the subsequent secret key bit may be affected if the 1-bit inference is an error. Therefore, in the case, the existing collision attacks could not be used to make the squaring operations distinction in Algorithm 2.
We can conclude the secret key 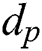 by byte by segment classification cluster
by byte by segment classification cluster 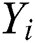 for Algorithm 4.
for Algorithm 4.
Algorithm 4: Recovering the secret exponent 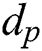

According to Algorithm 4, we know the secret parameter 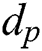 , and the modulus N is given. Thus,
, and the modulus N is given. Thus, 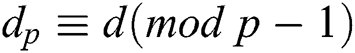 ,
,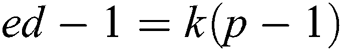 ,
, 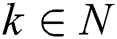 and
and 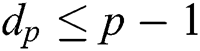 , we can compute
, we can compute

where 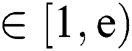 ,
, 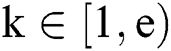 , the public key parameter e is a small integer(generally 65537), we can obtain a large prime number p by exhausting the k value, and then we can obtain the key d.
, the public key parameter e is a small integer(generally 65537), we can obtain a large prime number p by exhausting the k value, and then we can obtain the key d.
4 Cluster Collision Power Analysis against Double Blinding Exponentiation
In this subsection, a new cluster collision power attack against double blinding exponentiation is proposed by a single power trace. The proposed attack shows how to find the points of interest by using preprocessing and k-means clustering with only one execution power curve, and the attack accuracy can be improved. The new attack requires three phases: trace preprocessing, identification of points of interest and distinguishing the multiplications by using k-means clustering.
4.1 Power Leakage Model of Modular Multiplication-Based Correlation
The Pearson correlation coefficient of power curves can map the relation between operands [26]. For two multiplications 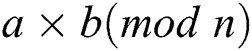 and
and 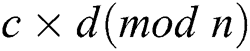 , if the operands
, if the operands  and
and 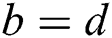 , the correlation coefficient between power traces of two multiplications is approximately 1 in theory. If the operands
, the correlation coefficient between power traces of two multiplications is approximately 1 in theory. If the operands 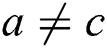 and
and 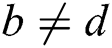 , the correlation coefficient is almost 0. If the operands
, the correlation coefficient is almost 0. If the operands  and
and 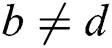 or
or  and
and 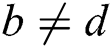 , the correlation coefficient is almost 0.5. Therefore, the correlation coefficients can be divided into three types of: high, medium and low, which we denote as
, the correlation coefficient is almost 0.5. Therefore, the correlation coefficients can be divided into three types of: high, medium and low, which we denote as 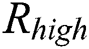 ,
, 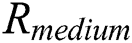 , and
, and 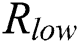 respectively. We can divide the relations of the four operands into three categories according to the correlation coefficient (see Tab. 2).
respectively. We can divide the relations of the four operands into three categories according to the correlation coefficient (see Tab. 2).
Table 2: Relation between operands and power consumption

According to Tab. 2, we can identify the relation of the operands by the relation of power consumption of two modular operations with two operations 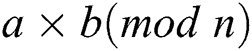 and
and 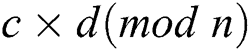 in theory. We analyzed the power trace of Algorithm 3, mainly including “square (S)” of step 4 and “multiplication (M)” of step 5. The power traces of Step 4 and Step 5 can be extracted as shown in Fig. 5.
in theory. We analyzed the power trace of Algorithm 3, mainly including “square (S)” of step 4 and “multiplication (M)” of step 5. The power traces of Step 4 and Step 5 can be extracted as shown in Fig. 5.
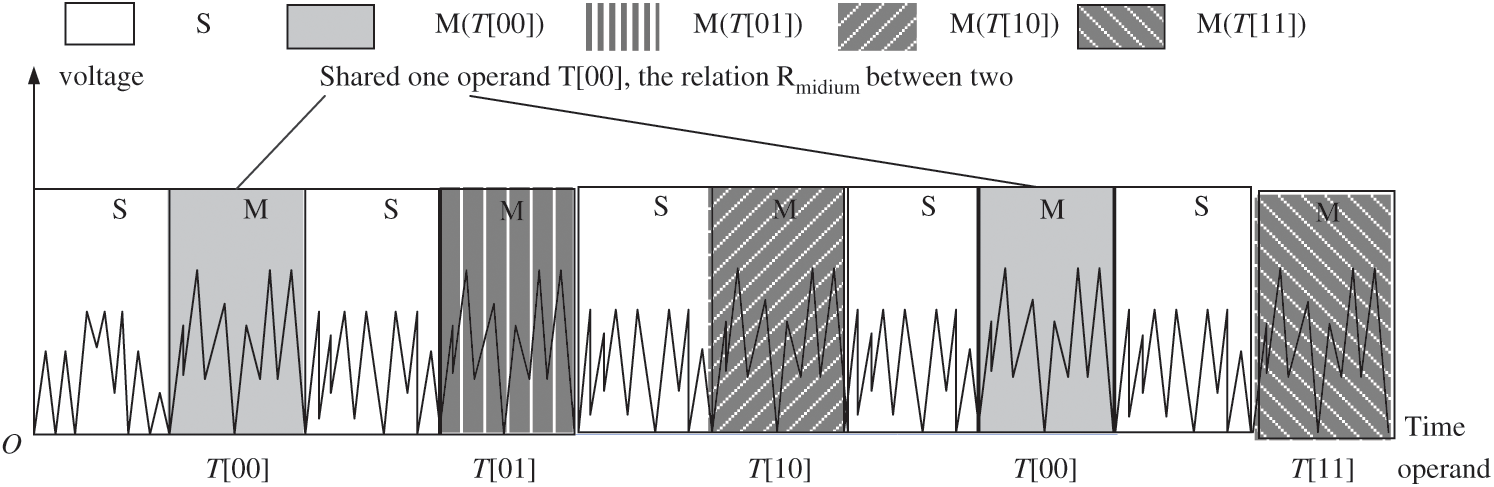
Figure 5: The power trace of step 4 and step 5 in Algorithm 3
We know that the multiplication operation of Step 5 is 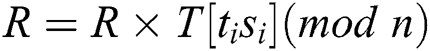 , where “
, where “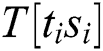 ” are only four types of
” are only four types of 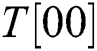 ,
, 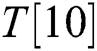 ,
, 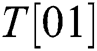 , T [11], and “R” is dynamic. We can infer whether “
, T [11], and “R” is dynamic. We can infer whether “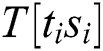 ” of the two multiplication operations is the same according to the correlation coefficient.
” of the two multiplication operations is the same according to the correlation coefficient. 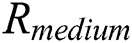 . All “multiplication” of Step 5 can be classified into four cluster sets. Therefore, we can deduce t and s from the correct cluster sets of
. All “multiplication” of Step 5 can be classified into four cluster sets. Therefore, we can deduce t and s from the correct cluster sets of 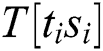 , and the secret exponent
, and the secret exponent 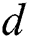 can be recovered using t and s. The correct classification of all multiplication operations in Step 5 is the key to breaking the secret exponent
can be recovered using t and s. The correct classification of all multiplication operations in Step 5 is the key to breaking the secret exponent 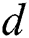 .
.
4.2 Preprocessing of Power Traces
The attacker inputs the k-bit message m, the k-bit modulus n and the k-bit secret key d into cryptosystem devices and executes Algorithm 3. We can collect power traces with the randomized message and the secret key d. Each power trace is sliced in l operations of Step 4 (“square (S)”) and Step 5 (“multiplication (M)”) and we load the operands 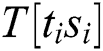 from Step 4 to Step 5. In Algorithm 3, the power consumption
from Step 4 to Step 5. In Algorithm 3, the power consumption  of the operand
of the operand 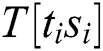 has “multiplication (M)” and “load (L)”, as depicted in Fig. 6.
has “multiplication (M)” and “load (L)”, as depicted in Fig. 6.
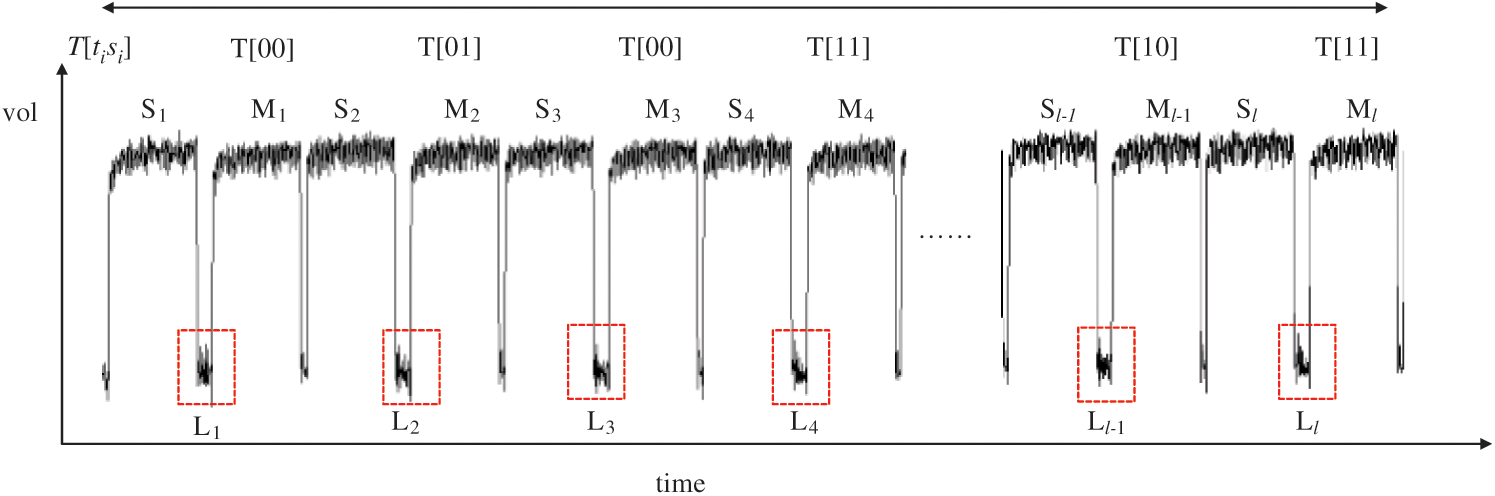
Figure 6: Power traces of the multiplication of Algorithm 3
First, we construct a new power trace while ignoring “Square(S)”, which can be extracted, and concatenate the signals of “multiplication (M)” and “load (L)” related to step 5 from the power traces. We define that the new power curve is related to the operands 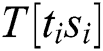 while ignoring “square(S)”.
while ignoring “square(S)”.
Definition 2: A new power curve with l multiplication and load operations is presented by a matrix T:

where 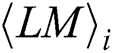 represents the power points of the ith multiplication and loads the operand
represents the power points of the ith multiplication and loads the operand 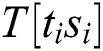 , and
, and 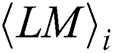 has w power points and is defined as
has w power points and is defined as 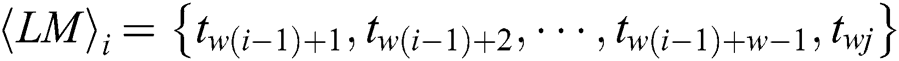 .
.
After power trace preprocessing, the attack enters the second phase, which consists of finding the points of interest.
4.3 Finding the Points of Interest Based on Cluster
For noise, we can redefine the power consumption 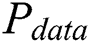 of each
of each 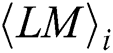 as follows:
as follows:

where 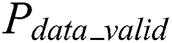 represents the data directly dependent on the power consumption of the operand
represents the data directly dependent on the power consumption of the operand 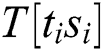 and
and 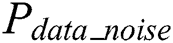 is the other dependent power consumption. Thus, w power points can be divided into two groups for
is the other dependent power consumption. Thus, w power points can be divided into two groups for 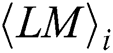 . One group is related power points of the operand
. One group is related power points of the operand 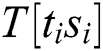 , and the other group is the power points of noise.
, and the other group is the power points of noise.
We compute the variance value of every column of the matrix T and obtain the vector of variances 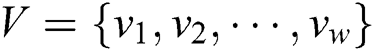 , where
, where 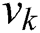 is the variance of the kth column. The magnitude of variance can be considered as the degree of dependence of the operand
is the variance of the kth column. The magnitude of variance can be considered as the degree of dependence of the operand 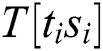 . The variance set can be classified into two classes (interest and uninterest) by the k-means algorithm. Finally, the attacker can find power points of interest with the operand
. The variance set can be classified into two classes (interest and uninterest) by the k-means algorithm. Finally, the attacker can find power points of interest with the operand 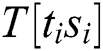 in each
in each 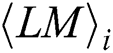 , as shown Fig. 7. In our practical experiments, each
, as shown Fig. 7. In our practical experiments, each 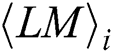 has 241 power points and 16 interesting power points. The index set consists of power point subscripts of interest, and is defined as
has 241 power points and 16 interesting power points. The index set consists of power point subscripts of interest, and is defined as 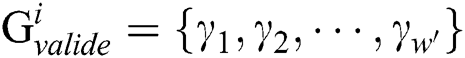 , where
, where 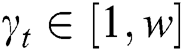 ,
, 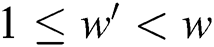 , and
, and 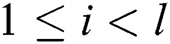 .
.
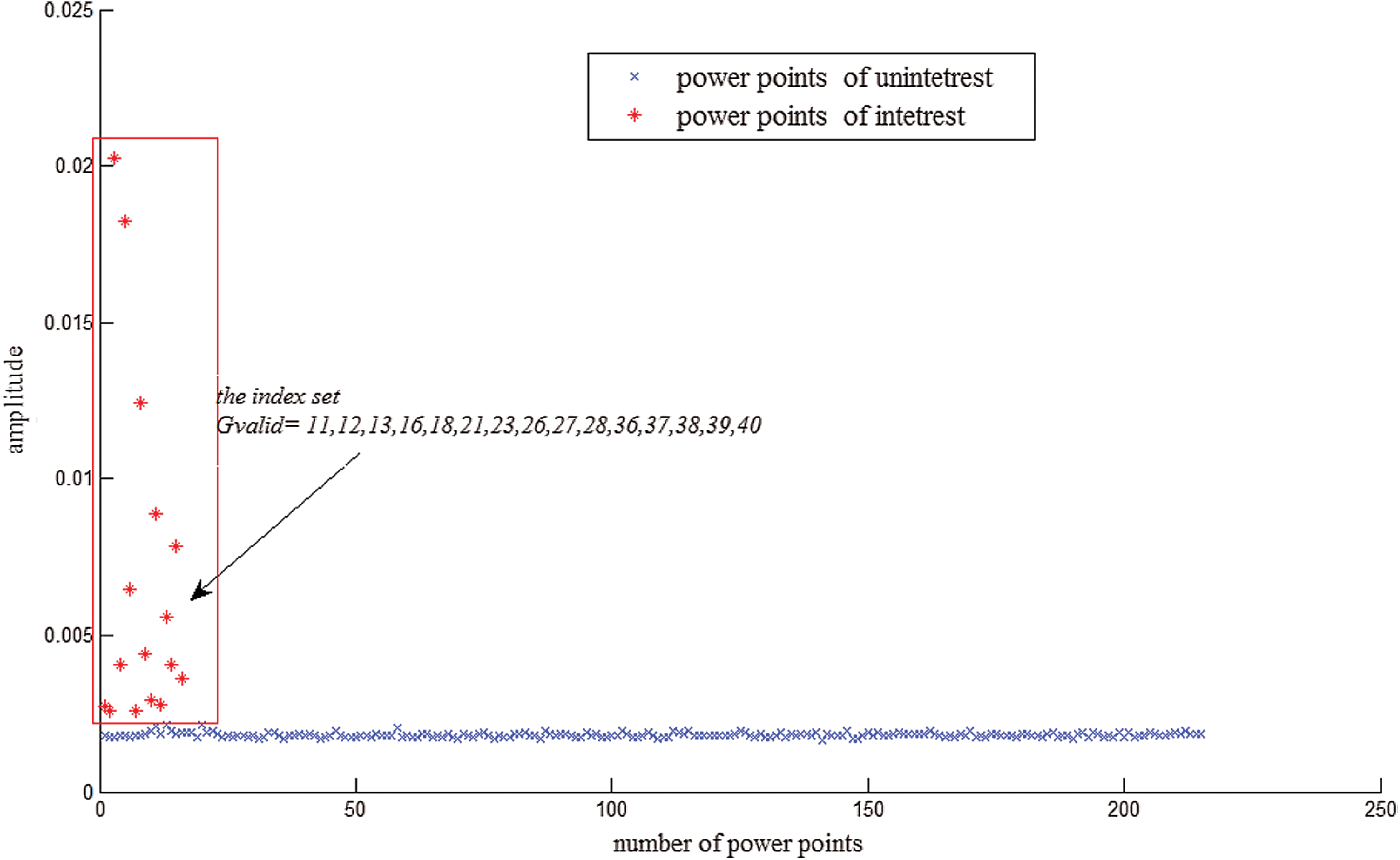
Figure 7: The classification of w power points in every multiplication
4.4 Cluster Classification of Multiplication
According to the indices set 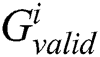 , we can find the power points of the operand
, we can find the power points of the operand 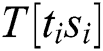 in each
in each 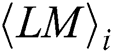 and reconstruct a matrix T’ with only interest power points.
and reconstruct a matrix T’ with only interest power points.
Definition 3: The matrix T’ has l multiplication and load operations with only interest power points:
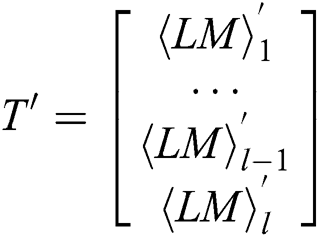
where 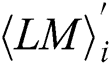 represents the power points of the ith multiplication and loads the operand
represents the power points of the ith multiplication and loads the operand 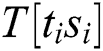 with only interest power points.
with only interest power points. 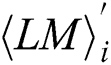 has w' power points, and
has w' power points, and 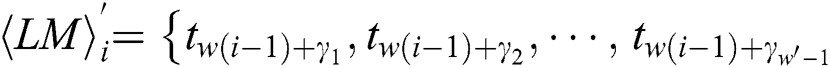 ,
, 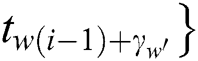 ,
, 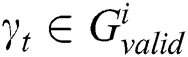 .
.
We compute the correlation coefficient between the fixed row 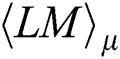 and every row of the matrix
and every row of the matrix 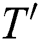 , where
, where 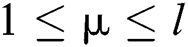 , and obtain a matrix
, and obtain a matrix 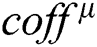
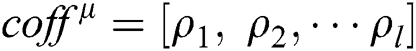
where 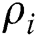 is the Pearson correlation coefficient value of the same position between the fixed
is the Pearson correlation coefficient value of the same position between the fixed 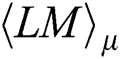 and the other
and the other 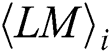 and is calculated as:
and is calculated as:
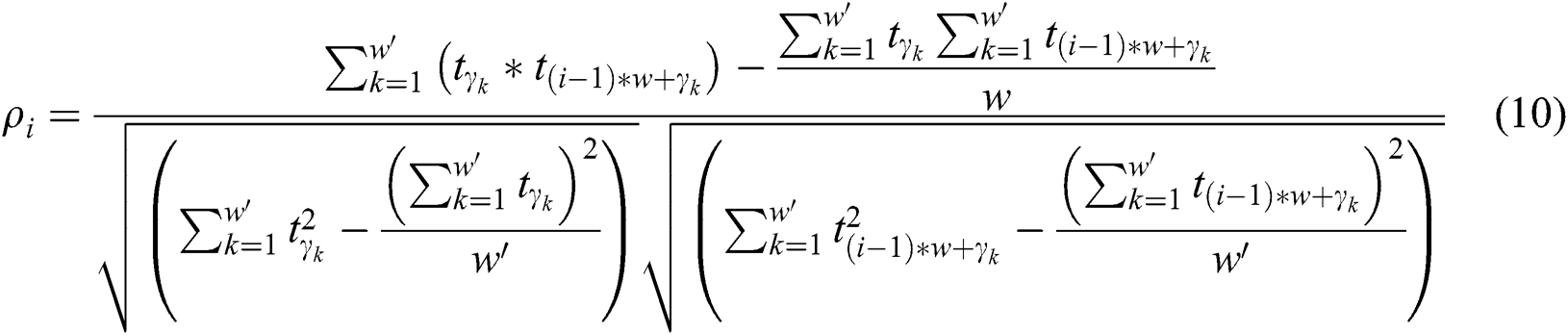
Next, the data set 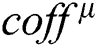 can be divided into two groups by k-means. One group shares one operand
can be divided into two groups by k-means. One group shares one operand 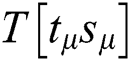 . The other group includes no shared operands. Fig. 8 shows that 511 modular multiplications can be classified in our practical experiment, and the red class represents the shared operands of the first modular multiplication.
. The other group includes no shared operands. Fig. 8 shows that 511 modular multiplications can be classified in our practical experiment, and the red class represents the shared operands of the first modular multiplication.
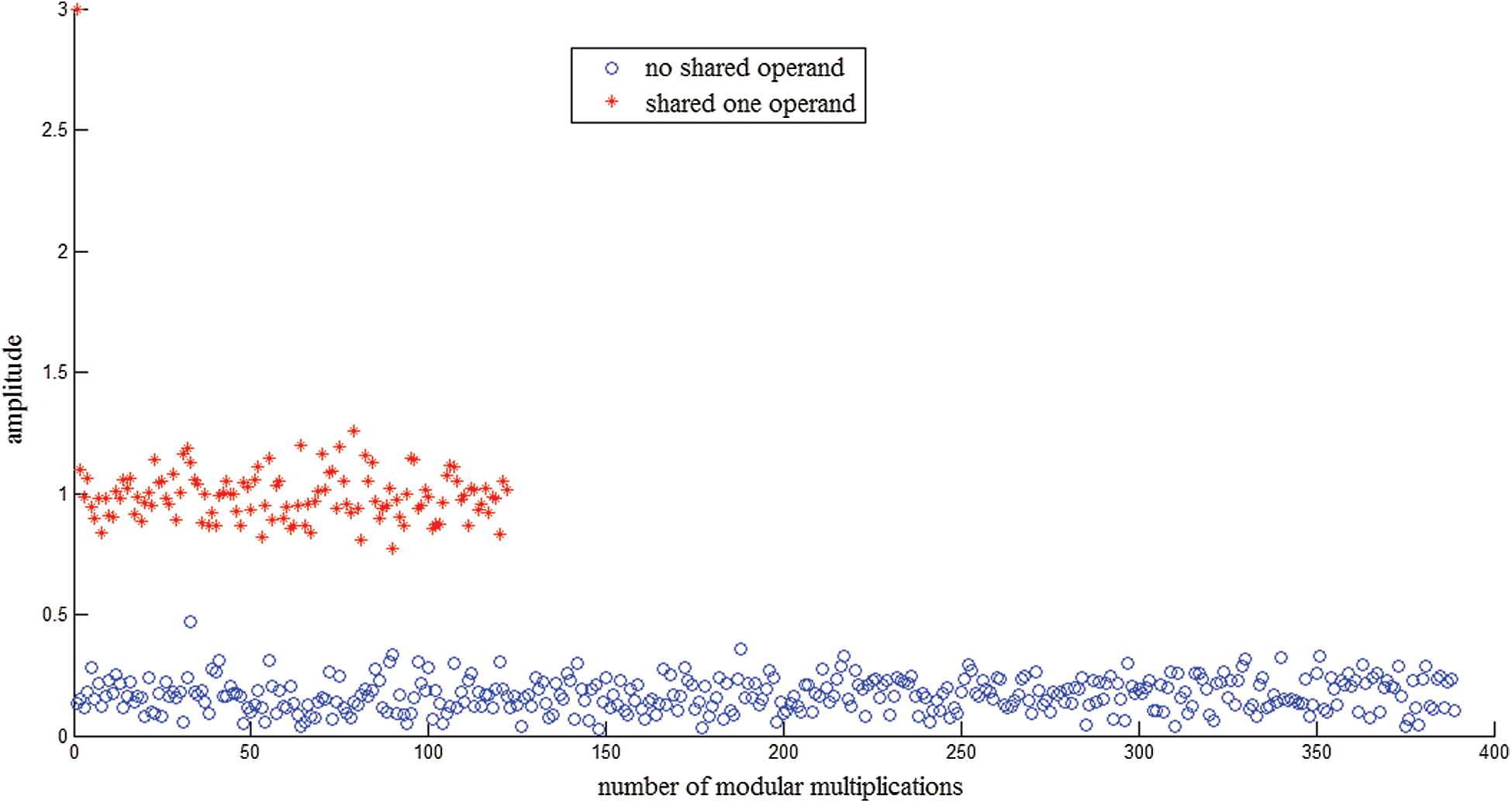
Figure 8: Classification of l modular multiplications
Finally, by repeating all processes four times, l modular multiplications can be divided into four groups, and each group can be guessed as T [00], T [01], T [10], or T [11]. Thus, there are 16 possibilities s and t. The correct power exponent d is calculated by using s and t.
Observers carried out experiments to test the crypto chip in the smartcard, and the hardware composition of the power analysis platform is shown in Fig. 9. In the platform, the oscilloscope can collect the voltage signal (power trace) from the two ends of the resistance connected to the FPGA board when Algorithm 1, Algorithm 2 and Algorithm 3 are run in the crypto chip.
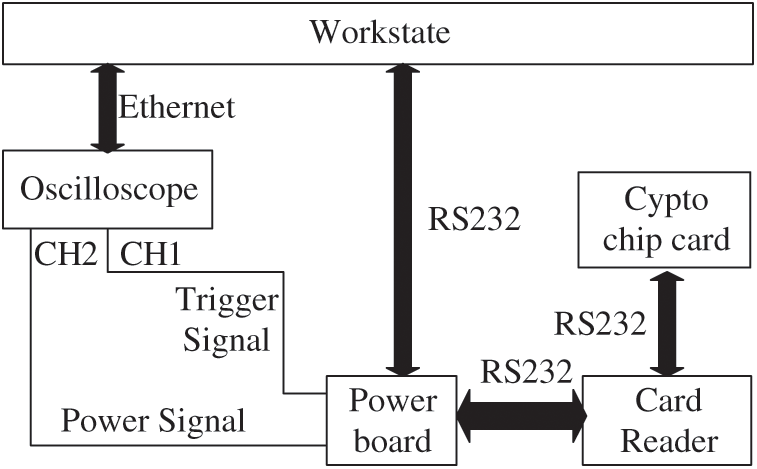
Figure 9: Power analysis platform
5.1 Experimental Results for Algorithm 2
For the attack against Algorithm 2, the input parameters of the smart card are 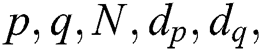
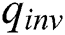 , and 1000 different plaintext “X” and “N-X” plaintext pairs are randomly generated and inputted. The sampling frequency of the oscilloscope is 25 MHz, and 2 power curves are collected for each plaintext using an oscilloscope. The 2000 power curves of RSA-CRT are collected, as shown in Fig. 10.
, and 1000 different plaintext “X” and “N-X” plaintext pairs are randomly generated and inputted. The sampling frequency of the oscilloscope is 25 MHz, and 2 power curves are collected for each plaintext using an oscilloscope. The 2000 power curves of RSA-CRT are collected, as shown in Fig. 10.
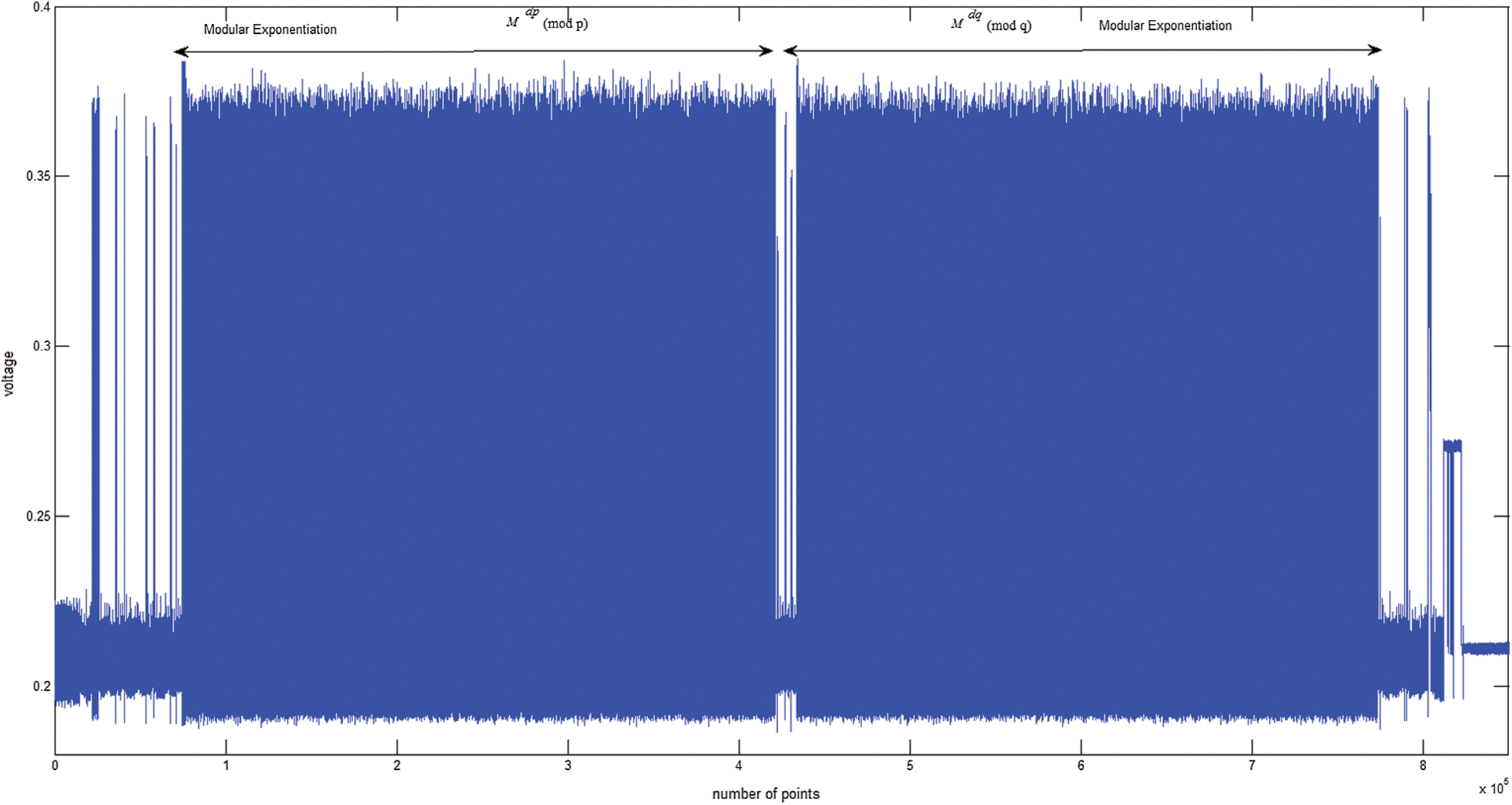
Figure 10: Power trace of Algorithm 2 in RSA-CRT
As mentioned in the previous section, we used the proposed attack against Algorithm 2 with input of the same exponent d and modulus N and compared the attack accuracy rate with Yen’s attack in [17], as shown in Fig. 11. The accuracy of Yen’s attack fluctuates greatly from top to bottom, and the highest accuracy is approximately 91%. However, the accuracy of the attack proposed in this paper is higher than that of Yen’s attack. The fluctuation of the range of Yen’s attack accuracy is mainly due to Yen's collision attack occurring bit by bit. If the 1-bit inference is an error, the subsequent bit is affected. The bit error affects only the 8-bit attack for our scheme based on the exponent segment by byte. In addition, different modes of the collision classification sets can affect the attack accuracy, as shown in Fig. 11. The attack rates of differential sum and variance are approximately 93% and 94%, respectively, which cannot reach 100%. The attack accuracy of the differential area is the highest, and six pairs of messages can recover the secret 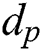 . Thus, we can deduce the secret exponent d by exhausting k.
. Thus, we can deduce the secret exponent d by exhausting k.
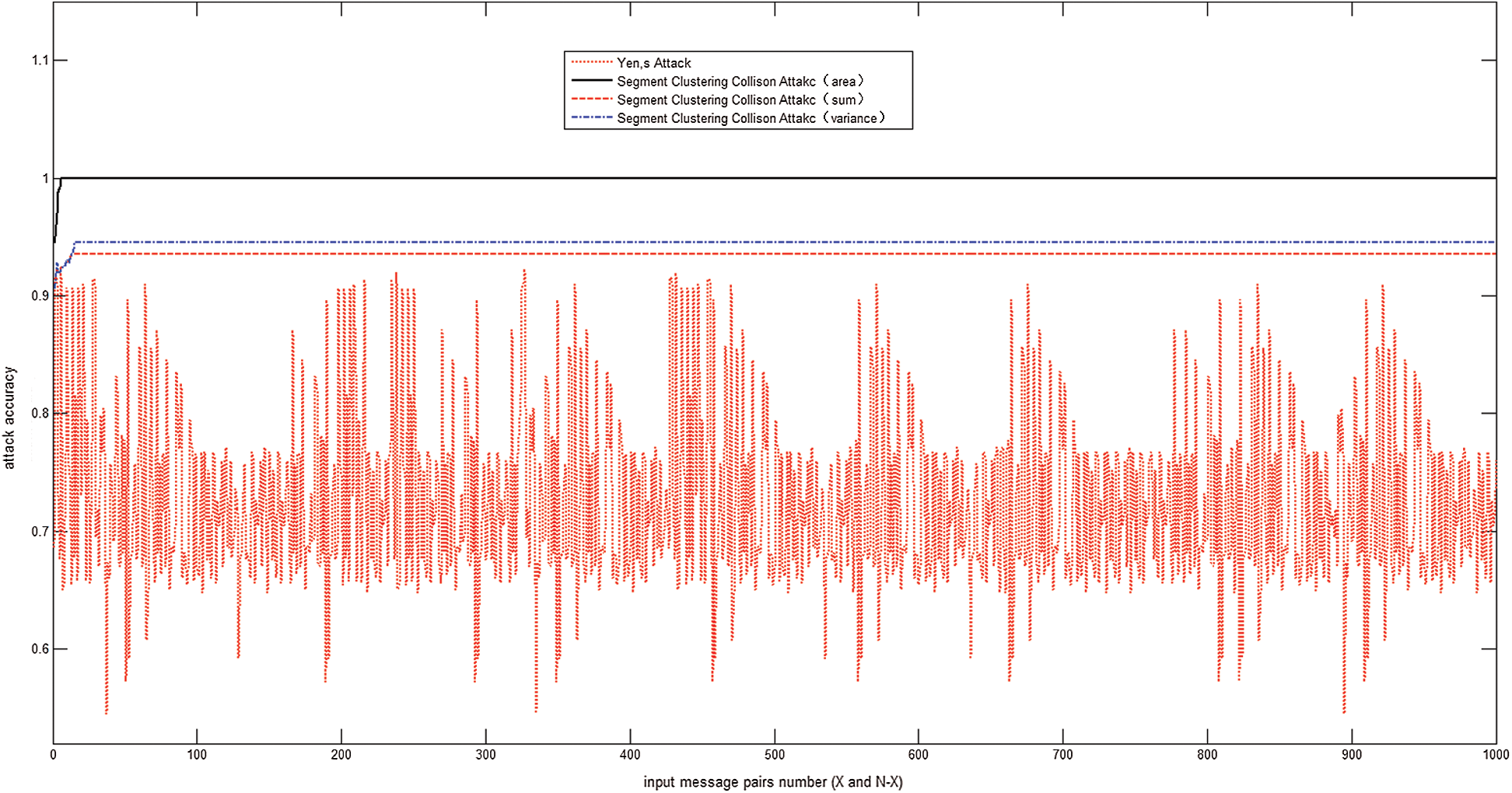
Figure 11: Attack accuracy rate of the proposed collision power attack
5.2 Experimental Results for Algorithm 3
For the attack on Algorithm 3, the input parameters of the smart card are 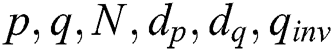 . The double blinding countermeasures on the modular exponentiation algorithm are used in Algorithm 3. Therefore, the random message is sent to the chip. The corresponding power traces are collected using an oscilloscope. Traces are gathered at 1 MHz/sec and 2.5 MHz/sec sampling rates by an active probe. As mentioned in Section 4.2, we used the proposed attack against Algorithm 3 with only one power trace by comparing with the proposed algorithm in [30,31,46], see Tab. 3.
. The double blinding countermeasures on the modular exponentiation algorithm are used in Algorithm 3. Therefore, the random message is sent to the chip. The corresponding power traces are collected using an oscilloscope. Traces are gathered at 1 MHz/sec and 2.5 MHz/sec sampling rates by an active probe. As mentioned in Section 4.2, we used the proposed attack against Algorithm 3 with only one power trace by comparing with the proposed algorithm in [30,31,46], see Tab. 3.
Table 3: Contrast of attack results

The data from Tab. 3 illustrate that the attack results of all attack methods are related to the sampling rate, which means that a larger sampling rate can obtain a high accuracy. The attack accuracy rate converges to approximately 91% using a proposed clustering attack method proposed in this paper when only one power curve is used. The attack accuracy rate is not up to 100% correct because some valid information may be removed due to only one power curve. The attack accuracy rates are less than 70% using the first-order attack method proposed in [30,31] because all power points participate in calculation correlation and the denoising result is bad. The highest attack accuracy is approximately 75% by using the second-order attack method proposed in [46] is approximately 75%.
In this paper, a new cluster collision attack based on exponent segment by byte is proposed for RSA-CRT with no countermeasures. By inputting multiple groups of specific “X” and “N-X” message pairs and combining the information leakage of loaded data, the power exponents 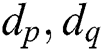 are successfully recovered, and the secret exponents d can be obtained. This paper demonstrated and analyzed the effectiveness of the new cluster correlation collision attack against double blinding exponentiation in a real attack environment. Through this experiment, it was observed that the utilization of valid information is improved and the noise and artificial participation are reduced by using the cluster classifications at each phase to recover the entire exponent. The new cluster correlation collision attack is effective in theory for modular exponential algorithms with randomized blinding countermeasures because only one power curve is used. Therefore, in the next study, we will analyze the new modular exponential algorithms, and report the experimental results. The attack accuracy rate converges to approximately 91% but is not 100%. We plan to develop better SCAs by combining fuzzy cluster methods in the future and unsupervised learning methods in deep learning.
are successfully recovered, and the secret exponents d can be obtained. This paper demonstrated and analyzed the effectiveness of the new cluster correlation collision attack against double blinding exponentiation in a real attack environment. Through this experiment, it was observed that the utilization of valid information is improved and the noise and artificial participation are reduced by using the cluster classifications at each phase to recover the entire exponent. The new cluster correlation collision attack is effective in theory for modular exponential algorithms with randomized blinding countermeasures because only one power curve is used. Therefore, in the next study, we will analyze the new modular exponential algorithms, and report the experimental results. The attack accuracy rate converges to approximately 91% but is not 100%. We plan to develop better SCAs by combining fuzzy cluster methods in the future and unsupervised learning methods in deep learning.
With the development of quantum computing, we are currently researching the side channel attack against the McEliece algorithm. We will also study the important issue of SCAs of postquantum cryptography (PQC).
Acknowledgement: The authors would like to thank the reviewers for their detailed reviews and constructive comments, which have helped improve the quality of this paper.
Funding Statement: This work is supported by the National Key R&D Program of China (No. 2017YFB0802300), the Key Research and Development Project of Sichuan Province (No. 2020YFG0307, No. 2018TJPT0012), the Key Research and Development Project of Chengdu (No. 2019-YF05-02028-GX).
Conflicts of Interest: We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.
References
1. M. S. Raniyal, I. Woungang and S. K. Dhurandher. (2018). “An RSA-based user authentication scheme for smart-homes using smart card,” in Proc. ISDDC, Lecture Notes in Computer Science (LNCS 11317Vancouver, BC, Canada, vol. 11317, pp. 16–29.
2. C. P. Ge, Z. Liu, J. Xia and L. M. Fang. (2019). “Revocable identity-based broadcast proxy re-encryption for data sharing in clouds,” IEEE Transactions on Dependable and Secure Computing, vol. 99, pp. 1.
3. J. J. Quisquater and C. Couvreur. (1982). “Fast decipherment algorithm for RSA public-key crypto system,” Electronics Letters, vol. 18, no. 21, pp. 905–907.
4. P. Kocher. (1996). “Timing attacks on implementations of Diffie-Hellman, RSA, DSS, and other systems,” in Proc. CRYPTO’96, California, USA: Springer, pp. 104–113.
5. R. Novak. (2002). “SPA-based adaptive chosen-ciphertext attack on RSA implementation,” in Proc. PKC, Lecture Notes in Computer Science (LNCS 2274Paris, France, vol. 2274, pp. 252–262.
6. P. A. Pouque, G. Martinet and G. Poupard. (2003). “Attacking unbalanced RSA-CRT using SPA,” in Proc. CHES, Lecture Notes in Computer Science (LNCS 2779Cologne, Germany, vol. 2779, pp. 254–268.
7. B. D. Boer, K. Lemke and G. Wicke. (2003). “A DPA attack against the modular reducation within a CRT implementation of RSA,” in Proc. CHES, Lecture Notes in Computer Science (LNCS 2523California, USA, vol. 2523, pp. 228–243.
8. P. Kocher, J. Jaffe and B. Jun. (2011). “Introduction to differential power analysis,” Journal of Cryptographic Engineering, vol. 1, no. 1, pp. 5–27.
9. S. W. Zhang, X. Y. Yang, W. D. Zhong and Y. J. Sun. (2018). “A highly effective DPA attack method based on genetic algorithm,” Computers, Materials & Continua, vol. 56, no. 2, pp. 325–338.
10. S. Xu, X. J. Lu and K. Y. Zhang. (2018). “Similar operation template attack on RSA-CRT as a case study,” Science China (Information Sciences), vol. 61, no. 3, 032111. [Google Scholar]
11. W. Schindler. (2000). “A timing attack against RSA with the Chinese remainder theorem,” in Proc. CHES, Lecture Notes in Computer Science (LNCS 1965vol. 1965, pp. 109–124. [Google Scholar]
12. M. Witteman. (2009). “A DPA attack on RSA in CRT mode,” . [Online]. Available: https:www.riscure.comarchive_DPA_attack_on_RSA_in_CRT_mode.pdf. [Google Scholar]
13. Z. J. Li, R. H. Shi, J. X. Wang, C. Li, H. B. Li et al. (2016). , “DPA-based adaptive chosen-message attack on CRT-RSA,” Journal of Cryptologic Research, vol. 3, no. 2, pp. 201–210. [Google Scholar]
14. Z. J. Li, Q. Peng, R. H. Shi, C. Li, Z. P. Ma et al. (2016). , “Chosen plaintext attack on CRT-RSA,” Journal of Cryptologic Research, vol. 3, no. 5, pp. 447–461. [Google Scholar]
15. S. Kaedi, M. Doostari and M. B. Ghaznavi-Ghoushchi. (2018). “NEMR: A nonequidistant DPA attack proof of modular reduction in a CRT implementation of RSA,” Journal of Circuits, Systems and Computers, vol. 27, no. 12, pp. 1850191. [Google Scholar]
16. A. P. Fouque and F. F.Valette. (2003). “The doubling attack-why upwards is better than downawards,” in Proc. CHES, Lecture Notes in Computer Science (LNCS 2779Cologne, Germany, vol. 2779, pp. 269–280. [Google Scholar]
17. S. M. Yen, W. C. Lien, S. J. Moon and J. C. Ha. (2005). “Power analysis by exploiting chosen message and internal collisions vulnerability of checking mechanism for RSA decryption,” in Proc. Mycrypt’05, Kuala Lumpur, Malaysia, pp. 183–195. [Google Scholar]
18. S. M. Yen, L. C. Ko, S. J. Moon and J. Ha. (2006). “Relative doubling attack against Montgomery ladder,” in Proc. ICISC, Lecture Notes in Computer Science (LNCS 3935Seoul, Korea, vol. 3935, pp. 117–128. [Google Scholar]
19. N. Homma, A. Miyamoto, T. Aoki and A. Shamir. (2010). “Comparative power analysis of modular exponentiation algorithms,” IEEE Transactions on Computer, vol. 59, no. 6, pp. 795–807. [Google Scholar]
20. J. S. Coron. (2009). “Resistance against differential power analysis for elliptic curve crypto systems,” in Proc. CHES, Lecture Notes in Computer Science (LNCS 1717MA, USA, vol. 1717, pp. 292–302. [Google Scholar]
21. C. Kim, J. Ha, S. H. Kim, S. Kim, S. M. Yen et al. (2004). , “A secure and practical CRT-based RSA to resist side channel attacks,” in Proc. ICCSA, Lecture Notes in Computer Science (LNCS 3043Assisi, Italy, vol. 3043, pp. 150–158. [Google Scholar]
22. H. J. Mahanta and A. K. Kan. (2017). “Securing RSA against power analysis attacks through non-uniform exponent partitioning with randomization,” IET Information Security, vol. 12, pp. 1–9. [Google Scholar]
23. H. Mamiya, A. Miyaji and H. Morimoto. (2004). “Efficient countermeasure against RPA, DPA, and SPA,” in Proc. CHES, Lecture Notes in Computer Science (LNCS 3156MA, USA, vol. 3156, pp. 343–356. [Google Scholar]
24. J. C. Ha, C. H. Jun and J. H. Park. (2008). “A new CRT-RSA scheme resistant to power analysis and fault attack,” in Proc. ICCHIT, Busan, South Korea, pp. 351–356. [Google Scholar]
25. M. Barman and H. J. Mahanta. (2019). “A randomised scheme for secured modular exponentiation against power analysis attacks,” Cyber-Physical Systems, vol. 5, no. 4, pp. 209–230. [Google Scholar]
26. M. F. Witteman, J. G. J. van Woudenberg and F. Menarini. (2011). “Defeating RSA multiply always and message blinding counter measures,” in Proc. Topics in Cryptology C CT-RSA 2011, Lecture Notes in Computer Science (LNCS 6558vol. 6558, pp. 77–88. [Google Scholar]
27. H. S. Kim, T. H. Kim, J. C. Yoon and S. H. Hong. (2010). “Practical second-order correlation power analysis on the message blinding method and its novel counter-measure for RSA,” ETRI Journal, vol. 3, no. 1, pp. 102–108. [Google Scholar]
28. C. Clavier, B. Feix, G. Gagnerot and V. Verneuil. (2010). “Horizontal correlation analysis on exponentiation,” in Proc. ICICS 2010, Lecture Notes in Computer Science (LNCS 6476Barcelona, Spain, vol. 6476, pp. 46–61. [Google Scholar]
29. S. Bauer. (2012). “Attacking exponent blinding in RSA without CRT,” in Proc. COSADE, Lecture Notes in Computer Science (LNCS 7275), Darmstadt, Germany, vol. 7275, pp. 82–88. [Google Scholar]
30. A. Bauer, E. Jaulmes and E. Prouff. (2013). “Horizontal and vertical side channel attacks against secure RSA implementations,” in Proc. COSADE, Lecture Notes in Computer Science (LNCS 7779), San Francisco, CA, USA, vol. 7779, pp. 1–17. [Google Scholar]
31. K. E. Akalp and A. Tangel. (2016). “Correlation template matching CPA method,” Electronics Letters, vol. 52, no. 15, pp. 1306–1308. [Google Scholar]
32. W. N. Wan, W. Yang and J. Chen. (2015). “An optimized cross correlation power attack of message blinding exponentiation algorithms,” China Communication, vol. 12, no. 6, pp. 22–32. [Google Scholar]
33. L. Fang, C. Yin, L. Zhou, Y. Li, C. Su et al. (2020). , “A physiological and behavioral feature authentication scheme for medical cloud based on fuzzy-rough core vector machine,” Information Sciences, vol. 507, pp. 143–160. [Google Scholar]
34. J. Wang, Y. Gao, W. Liu, W. B. Wu and S. J. Lim. (2019). “An asynchronous clustering and mobile data gathering schema based on timer mechanism in wireless sensor networks,” Computers, Materials & Continua, vol. 58, no. 3, pp. 711–725. [Google Scholar]
35. Z. Liu, B. Xiang, Y. Q. Song, H. Lu and Q. F. Liu. (2019). “An improved unsupervised image segmentation method based on multi-objective particle, swarm optimization clustering algorithm,” Computers, Materials & Continua, vol. 58, no. 2, pp. 451–461. [Google Scholar]
36. R. H. Meng, Q. Cui and C. H. Yuan. (2018). “A survey of image information hiding survey of image information hiding algorithms based on deep learning,” Computer Modeling in Engineering & Sciences, vol. 117, no. 3, pp. 425–454. [Google Scholar]
37. S. F. Ren, G. R. Chen, T. G. Li, Q. J. Chen and S. F. Li. (2018). “A deep learning-based computational algorithm for identifying damage load condition: An artificial intelligence inverse problem solution for failure analysis,” Computer Modeling in Engineering & Sciences, vol. 117, no. 3, pp. 287–307.
38. M. Ardashir and K. Okyay. (2019). “A novel general type-2 fuzzy controller for fractional-order multi-agent systems under unknown time-varying topology,” Journal of the Franklin Institute, vol. 356, no. 10, pp. 5151–5171.
39. B. Bhushan and G. Sahoo. (2020). “ISFC-BLS (Intelligent and secured fuzzy clustering algorithm using balanced load sub-cluster formation) in WSN environment,” Wireless Personal Communications, vol. 111, no. 3, pp. 1667–1694. [Google Scholar]
40. M. Carbone, V. Conin, M. A. Cornelie, F. Dassance, G. Dufresne et al. (2019). , “Deep learning to evaluate secure RSA implementations,” Embedded Syst, vol. 2019, no. 2, pp. 132–161. [Google Scholar]
41. L. Batina, B. Gierlichs and K. Lemke-Rust. (2009). “Differential cluster analysis,” in Proc. CHES, Lecture Notes in Computer Science (LNCS 5747), Lausanne, Switzerland, vol. 5747, pp. 112–127. [Google Scholar]
42. A. D. Chen, S. Xu, Y. Chen and Z. G. Qin. (2013). “Collision based on chosen message sample power clustering attack algorithm,” China Communications, vol. 5, pp. 114–119. [Google Scholar]
43. J. Heyszl, A. Ibing, S. Mangard, F. D. Santis and G. Sigl. (2014). “Clustering algorithms for non-profiled single-execution attacks on exponentiations,” in Proc. Smart Card Research and Advanced Applications, Lecture Notes in Computer Science (LNCS 8419), Berlin, Germany, vol. 8419, pp. 79–93. [Google Scholar]
44. G. Perin, L. Imbert, L. Torres and P. Maurine. (2014). “Attacking randomized exponentiations using unsupervised learning,” in Proc. COSADE, Lecture Notes in Computer Science (LNCS 8622), Paris, France, vol. 8622, pp. 144–160. [Google Scholar]
45. S. Robert, H. Johann, K. Martin and S. Georg. (2015). “Improving Non-profiled attacks on exponentiations based on clustering and extracting leakage from multi-channel high resolution EM measurements,” in Proc. COSADE, Lecture Notes in Computer Science (LNCS 9064Berlin, Germany, vol. 9064, pp. 3–19. [Google Scholar]
46. W. N. Wan, J. Chen and S. B. Zhang. (2019). “A Cluster Correlation power analysis against double blinding exponentiation,” Journal of Information Security and Applications, vol. 48, no. 10, pp. 1–8. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |