DOI:10.32604/csse.2021.014181
| Computer Systems Science & Engineering DOI:10.32604/csse.2021.014181 | |
| Article |
Three-Dimensional Measurement Using Structured Light Based on Deep Learning
1School of Mechanical Engineering, North China University of Water Conservancy and Hydroelectric Power, Zhengzhou, 450045, China
2Department of Computer Engineering, National Institute of Technology, Kurukshetra, 136119, India
3Department of Computer Science and Information Engineering, Asia University, 41449, Taiwan
*Corresponding Author: Tao Zhang. Email: ztncwu@126.com
Received: 04 September 2020; Accepted: 13 November 2020
Abstract: Three-dimensional (3D) reconstruction using structured light projection has the characteristics of non-contact, high precision, easy operation, and strong real-time performance. However, for actual measurement, projection modulated images are disturbed by electronic noise or other interference, which reduces the precision of the measurement system. To solve this problem, a 3D measurement algorithm of structured light based on deep learning is proposed. The end-to-end multi-convolution neural network model is designed to separately extract the coarse- and fine-layer features of a 3D image. The point-cloud model is obtained by nonlinear regression. The weighting coefficient loss function is introduced to the multi-convolution neural network, and the point-cloud data are continuously optimized to obtain the 3D reconstruction model. To verify the effectiveness of the method, image datasets of different 3D gypsum models were collected, trained, and tested using the above method. Experimental results show that the algorithm effectively eliminates external light environmental interference, avoids the influence of object shape, and achieves higher stability and precision. The proposed method is proved to be effective for regular objects.
Keywords: 3D reconstruction; structured light; deep learning; feature extraction
Three-dimensional (3D) reconstruction technology in vision is an important area of research [1,2] in the computer field. It uses a vision test system to collect two-dimensional image information of objects, analyze image features, and process the acquired data to generate a point cloud. Finally, 3D reconstruction is used. The emergence of 3D imaging technology has transcended the limitations of traditional 2D imaging systems to enhance our understanding of the world.
The structural light method is one of the main research directions to have sprung from 3D reconstruction technology [3,4]. Its traditional form is based on the method of projecting an encoded image onto a depth image formed on the surface of a 3D object and recovering the depth information through an algorithm [5,6]. However, such algorithms have major problems related to stability, real-time performance, and reliability. Deep learning is a feature-learning method that transforms low-level raw data to higher-level expressions through simple nonlinear models [7]. In deep-learning studies, 3D reconstruction methods based on structured light have been proposed, mainly including structural light center extraction, image feature extraction, and real-time algorithms. Guo et al. [8] researched a multi-scale convolution parallel approach using an end-to-end depth learning method to extract the line structure light center. The first network was used for target detection, which in turn was used to extract the image feature area of interest and detect the line structure light. A second network of line structure light centers was obtained using the second network and a sparse algorithm. Li [9] selected the appropriate sensor for secondary development and obtained point-cloud data, which were processed using point-cloud filtering and segmentation algorithms to obtain a pure target point cloud and map it to a normalized depth image of size 227 × 227. Li used the Caffe deep-learning framework, replaced the classifier with regression, and iteratively trained the data with the weight as a label. A deep learning regression model was obtained to accurately measure weight. Liu [10] used a depth convolutional neural network (CNN) and conditional generative adversarial network (CGAN) to estimate depth information from a single image, and converted the depth map to a point cloud on the NYUD V2 dataset to achieve 3D reconstruction. Hong et al. [11] and Xu et al. [12] researched the application of deep learning to different fields, and improved the performance of the CNN that was used. Zhu et al. [13] combined deconvolution with a feature pyramid network to propose an extraction feature based on the heat map of a solder joint identification network, and used the pyramid strategy to map the features of different scales into the feature-point heat map to obtain the solder joint’s exact location. An algorithm based on self-supervised deep learning with strong robustness was proposed to effectively auto-map the feature points of 2D faces into 3D space to realize 3D face reconstruction [14]. Wang [15] combined the deep-learning GoogleNet framework with image knowledge to reconstruct a 3D human body model, using skeleton extraction technology to predefine feature points to assist the positioning of human feature points, increasing the robustness of anthropometric measurements.
The 3D reconstruction algorithm using structured light based on deep learning is an improvement on a traditional algorithm, but problems exist, such as the generalization ability and accuracy of the network model. Therefore, it is necessary to increase the reconstruction resolution, improve the network structure, improve the reconstruction effect, and widen the use of deep learning. Aiming to solve these problems, the convolution operation is used to extract the features of the 3D image, and the different convolution kernels are used for multi-scale parallel feature extraction to obtain the fine-layer features. Through the continuous deepening of the number of network layers, the abstraction of feature information is increased to improve the ability of feature information to describe the target. The coarse- and thin-layer features are connected and convoluted, and nonlinear regression is used to obtain the reconstruction model.
2.1 3D Reconstruction Technology Based on Structured Light
The principle of 3D measurement [7] is shown in Fig. 1. P is the position of the optical center of the projector, C is the position of the camera center, the curved surface represents the object surface, L is the distance from the charge-coupled-device camera to the bottom of the experimental platform, and d is the distance between the camera center and the projection center of the projector in the horizontal direction. When the object is not placed, the light intersects with the object at point A in the plane. After the object is placed, the propagation direction of the beam changes, and the extension line of the reflected light intersects with the plane at point B. According to trigonometry, we have the following equation:
where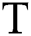 
is a stripe grating, and 
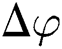is a phase change due to height information.
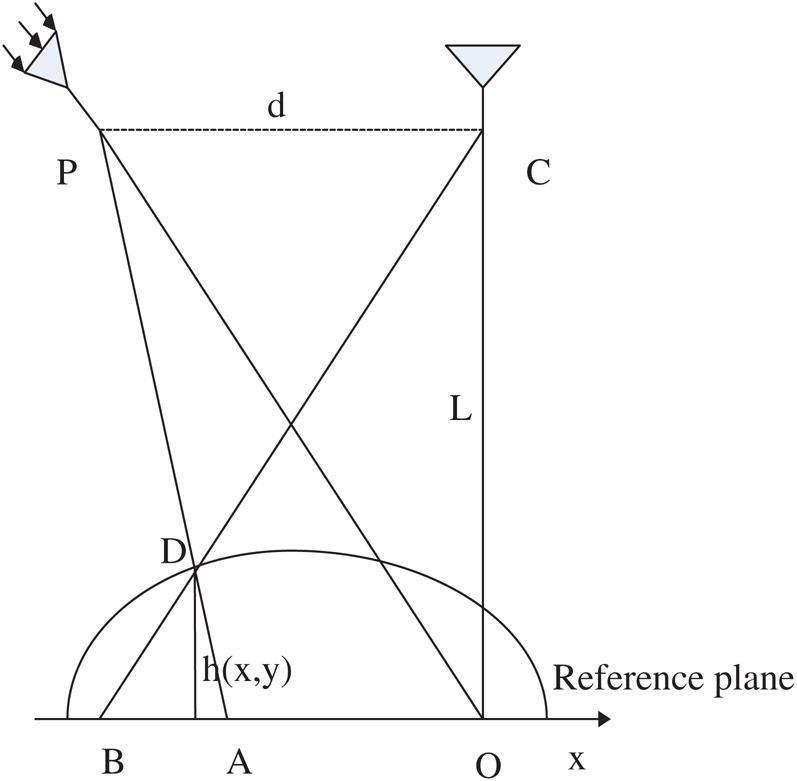
Figure 1: 3D measurement principle of structured light
Due to the measurement environment, image equipment, and measured objects, the measurement results cannot be expressed by a simple linear formula. The collected raster image is expressed as follows:
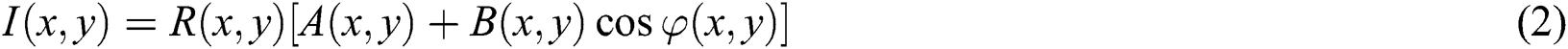
The phase-shifting method can more accurately obtain the phase value. One-quarter of the grating period is moved each time, so the phase-shifting amount is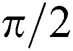 
. The four acquired fringes are:
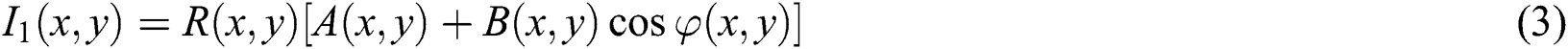
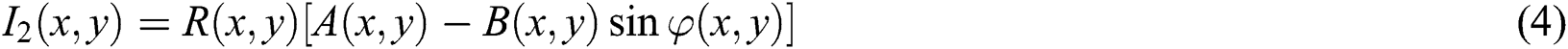
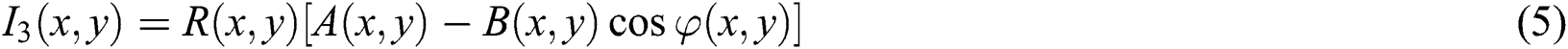
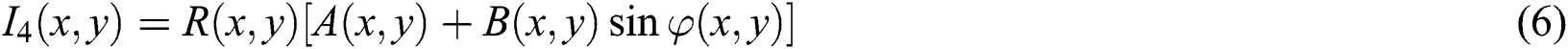
The phase can be calculated as
To accurately obtain the 3D size of the object requires us to determine the corresponding relationship between the phase of the projection image in the 2D coordinate system and the position of the 3D coordinate system, i.e., to determine the scale factor between the object and the image. Using a square calibration board, the relative relationship between the camera and reference plane is established according to the number of corresponding pixel points and the geometric characteristics of the image. The scale relationship between the real object and image is calculated by the size of the calibration board and the number of corresponding pixel points in the image.
2.2 Convolutional Neural Network
As a typical deep-learning method, a CNN [16] is a feedforward neural network with convolution computation and a depth structure. It is essentially a multilayer perceptron, which adopts local connection and weight sharing. It reduces the number of weights of the traditional neural network, making it easy to optimize, and it reduces the complexity of the model and the risk of overfitting.
A CNN has obvious advantages in image processing. It can directly take the image as input of the network, avoiding the complex process of feature extraction and data reconstruction in a traditional image-processing algorithm. The basic CNN usually consists of a convolution layer and a pooling layer. In the convolution layer, the different features of the input image are extracted by the sliding of the convolution kernel. The output vector is decided and excited by the activation function, and the network scale is simplified by the pooling layer to reduce the computational complexity, so as to achieve compression of the input characteristic map.
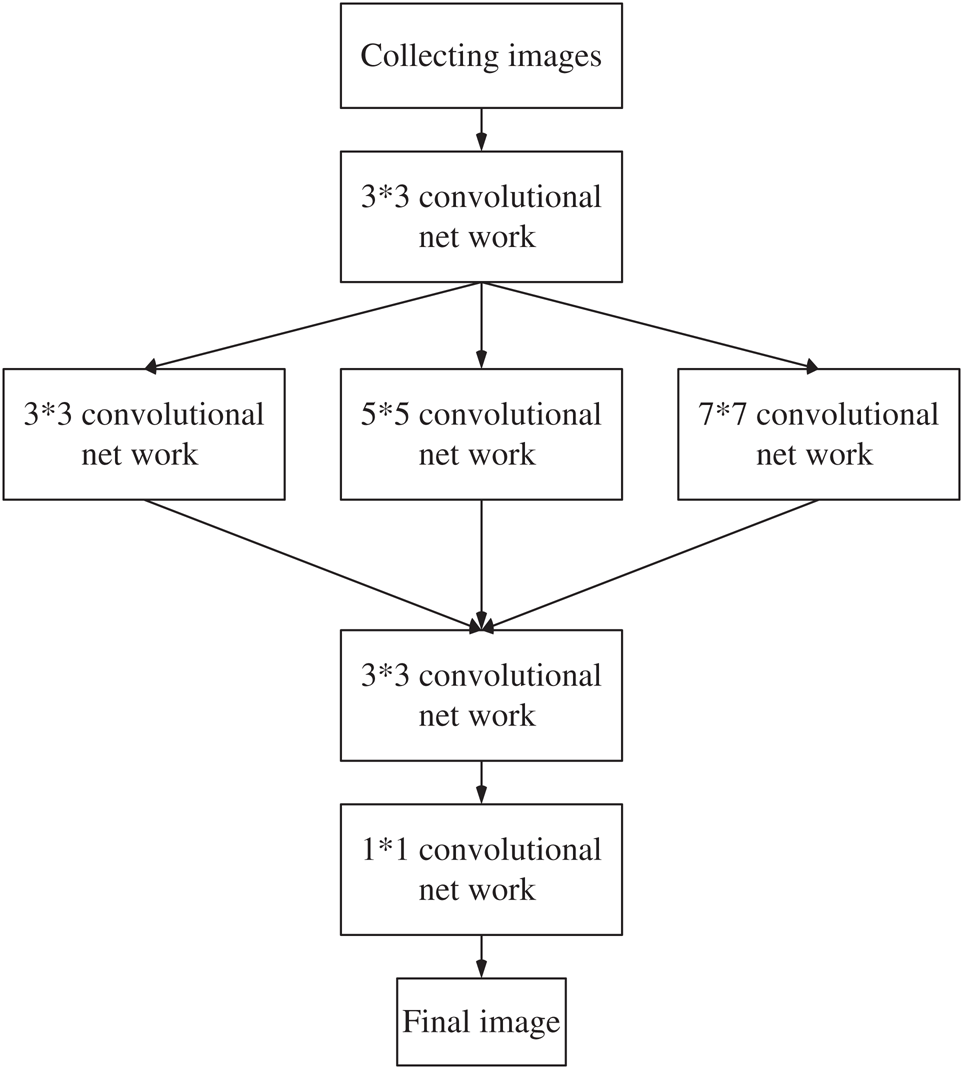
Figure 2: Schematic of CNN
In the multi-scale CNN model, as shown in Fig. 2, coarse-layer feature-extraction includes two convolutional layers, which extract the features of the 3D object, such as the edge and the corner points. To reduce the parameters and simplify the model, the number of convolution kernels per layer in the two convolutional layers is set to 10, and the size is 3 × 3. Multiple 3 × 3 convolution kernels replace the traditional 5 × 5 and 7 × 7 convolution kernels, so the CNN can extract more shallow information of 3D images, and can reduce the complexity of convolution operations. A zero-padding operation is used for convolution to ensure that the feature map is consistent with the original image size after convolution. The 10 convolution kernels of each layer perform convolution operations on input images by local connection and weight sharing to realize feature learning. The convolution formula of the coarse layer is
where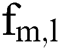 
and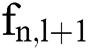 
represent the characteristic maps of the (l + 1)th convolutional layer input and output, respectively; 
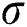is the activation function; k is the convolution kernel; and b is the bias term. The traditional neural network sigmoid activation function has a gradient divergence problem due to the differential chain law in backpropagation. To calculate the differentiation of each weight, when the backpropagation passes through multiple sigmoid functions, the weight will have little effect on the loss function, which is not conducive to optimization of the weight. A parametric rectified linear unit (PReLU) activation function is used to select the activation function σ. Compared to the sigmoid function, the PReLU function has the advantages of faster convergence and a small slope in the negative region, which can mitigate the gradient divergence problem to some extent, as shown in Fig. 3.
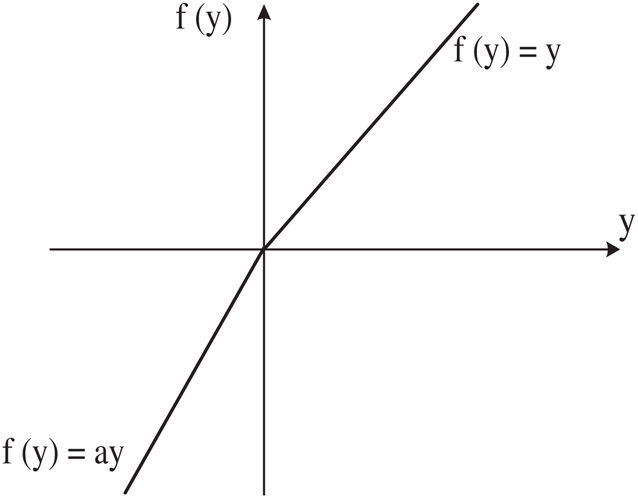
Figure 3: Activation function
The PReLU function is expressed as
where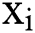 
is the input signal for the positive interval of the ith layer, and 
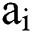is the weight coefficient of the negative interval of the ith layer, which is a learnable parameter in the PReLU function.
After the first two convolution layers, feature extraction is used to retrieve the thick-layer features, such as the edge of the input image. The image also contains numerous deep details, such as texture and other deep information, but the deep information, which only relies on simple feature extraction, is not available. Hence we propose a multi-scale convolutional network model to further extract the detailed information of the 3D image. In the third layer of the network, three sets of filters, of size 3 × 3, 5 × 5, and 7 × 7, are used for parallel convolution. The convolution kernels perform parallel feature extraction to extract the fine-layer features of the input image, and the convolution calculation uses zero padding.
The multi-scale convolution formula of the fine layer is
where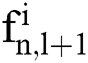 
is the nth feature maps output by different multi-scale convolution operations for the (l + 1)th convolutional layer, 
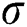is the activation function, and 
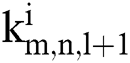is the mth sets of different-size convolution kernels with multi-scale convolution. Five feature maps are obtained after each set of convolution kernel operations, and the feature maps obtained by each group are combined to obtain 15 feature maps.
To achieve a better reconstruction effect, the calculated point-cloud data must be fine, and the individual coarse- or thin-layer features cannot realize this. Hence it is necessary to extract more comprehensive image feature information. First, features extracted by different-scale convolution kernels are connected. To obtain these detailed features, a small network consisting of two consecutive 3 × 3 convolutional layers is used instead of a single 5 × 5 or 7 × 7 convolutional layer stacking method. This greatly reduces the parameters of the multi-convolution kernel, better optimizes the calculation time, increases the network capacity, and enhances the feature-extraction capability of the activation function. The coarse-layer features obtained by feature extraction and the fine-layer features extracted by multi-scale extraction are connected and convolved, so the obtained feature map contains both the coarse-layer features of the 3D image and more details to avoid loss of information during subsequent processing. In the process of mapping 3D structured light images and point-cloud images, since the feature map has multiple channels before the output and the model finally needs a single-channel point-cloud map, the last layer is nonlinear, and the final output is produced by a 1 × 1 convolution kernel and a PReLU activation function.
The CNN model is used to obtain the mapping relationship between the 3D image and the depth image through deep learning. During the training process, the parameters must be updated continuously to achieve the optimal result. It is important to choose the correct loss function. A good one can provide a better convergence direction and obtain better results. Common loss functions [17] include log loss, absolute value loss, and square loss functions. We use the BerHu function,
where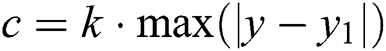 
, y is the point-cloud tag data, and 
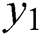is the predictive data for deep learning. The function takes c as the limit and makes a first-order differential jump at the critical point. When the predicted value exceeds the critical value, the gradient is rapidly reduced while ensuring a large residual error. When the predicted value is less than the critical value, the prediction result is kept close to the label data, and the gradient slow-down speed can be maintained, which significantly improves the convergence performance of the network. The output result is filtered before the loss function is calculated, and pixel points with missing depth-information values in the real depth map are removed to avoid interference of irrelevant information. Training incorporates backpropagation and a 0.9 momentum gradient-descent method to minimize the loss value. The input image has a batch size of 100, initial learning rate of 0.001, decay after every 10 rounds, attenuation rate of 0.99, and iteration count of 100.
4 Experiment and Analysis of Results
The 3D shape measurement experiment system, shown in Fig. 4, consisted of a projector, camera, and computer. The projector used a BenQ es6299 photo sensor with a highest resolution of 1920 × 1200, and a VGA interface to connect with a notebook computer. MATLAB (MathWorks, USA) was used to write a program to project stripe images onto a 3D object through the projector. A Canon EOS550D digital camera collected images of objects with stripes. The deep learning network implementation was based on a TensorFlow framework. The training data were taken from the laboratory, and the size of each picture was 1920 × 1200.
Figure 4: Experimental environment
To verify the performance of the proposed algorithm in 3D reconstruction, the image-acquisition process with structured light, as shown in Fig. 5, was used. A dataset for different locations of multiple objects was established, each sampled from a different angle. Of the generated data, 70% was used as a training set and 30% as a test set. Caffe was selected as the deep learning framework, and the algorithm was implemented in MATLAB. Stochastic gradient descent was chosen as the optimizer, and the learning rate of neural network regression decayed exponentially.
Figure 5: Image with stripe structured light
The reconstruction results of the 3D image are shown in Fig. 6. For the 3D reconstruction of four selected objects, the basic contour can be obtained. The measured effect of the object size parallel to the incident angle of the lens is very good, and the boundary between the object and background is better searched. Compared with other objects, the cone is not occluded. The reconstruction effect of the cone is better than others. For a beveled cylinder, the size of the stripe projected on the slope will influence the accuracy of measurement, because the larger the stripe the less obvious the inclined lines. The reconstruction of the slope of the beveled cylinder is affected by the angle, and it is necessary to estimate the images with different angles to ensure accuracy. Since the shooting position is on top of the subject, the outline of the image exhibits some wrinkling and is not smooth. This is mainly because the illumination angle during the acquisition process cannot guarantee uniform sampling of the object, especially in the cuboid shape and cylinder.
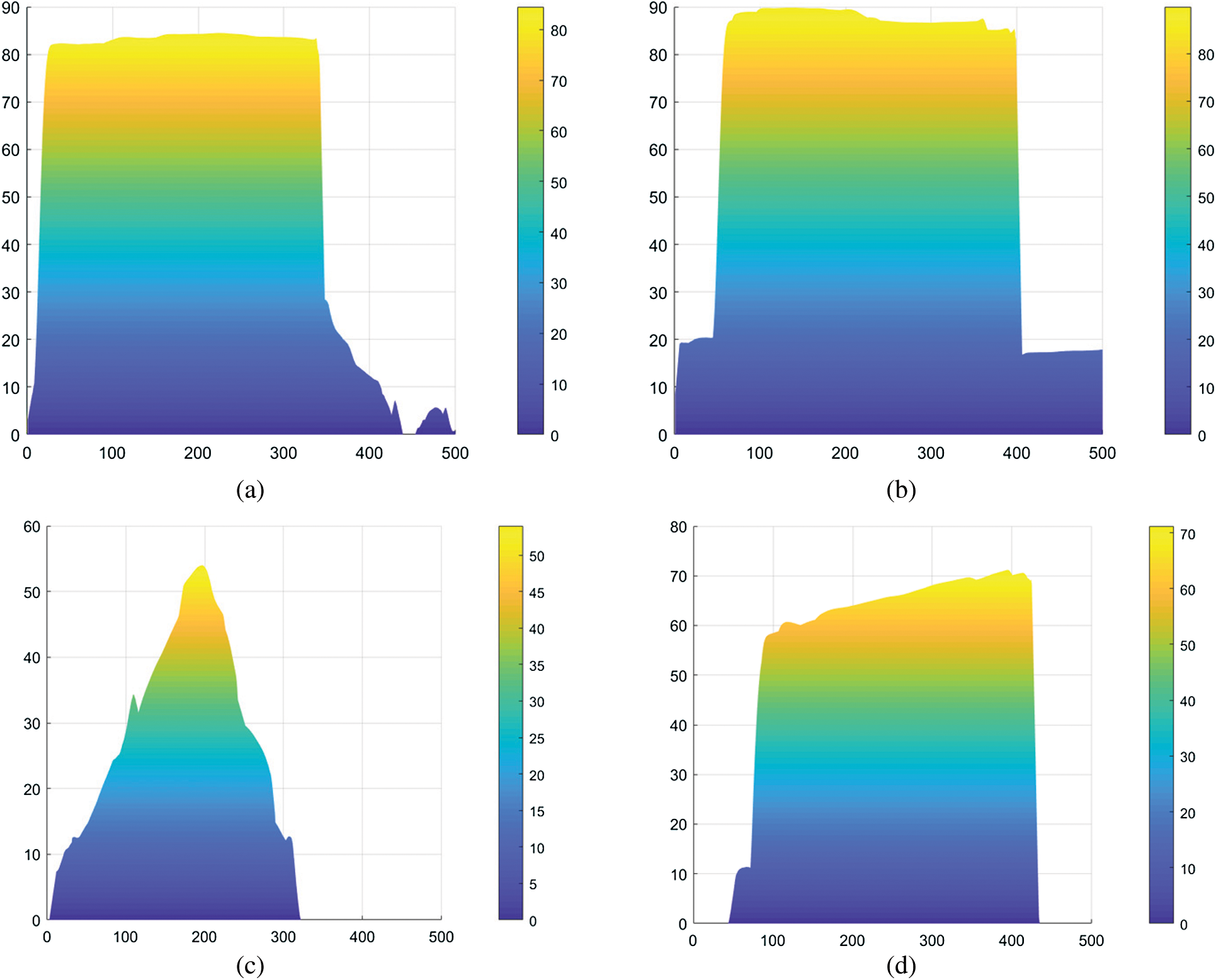
Figure 6: 3D reconstruction results (a) cuboid (b) cylinder (c) cone (d) beveled cylinder
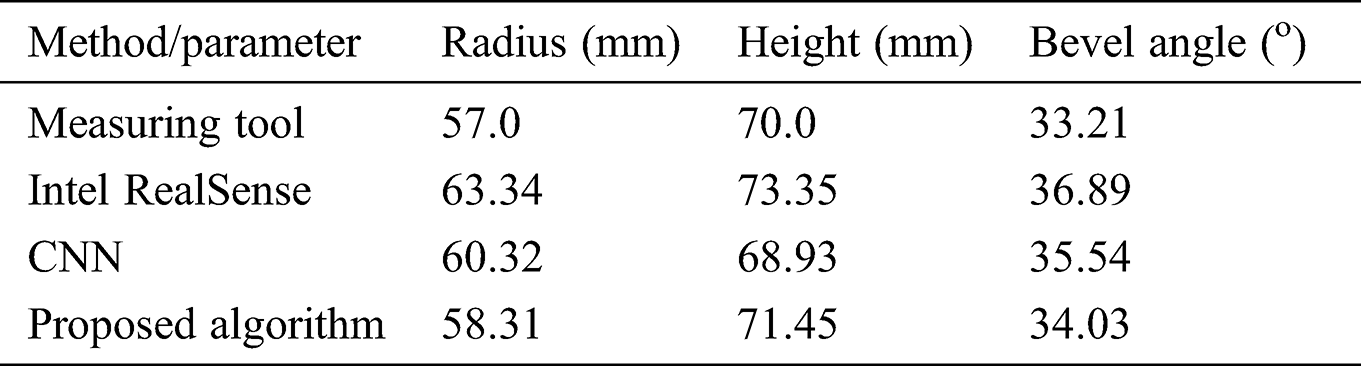
To further verify the performance of the proposed algorithm, a measurement tool, an Intel RealSense depth camera, a traditional CNN algorithm, and the proposed algorithm were used to reconstruct the image. Taking the beveled cylinder as an example, the data analysis of the experimental results is shown in Tab. 1. The size errors of the radius, height, and bevel angle of the object, measured by the proposed algorithm, are 0.52%, 2.07%, and 2.43%, respectively. Compared with the Intel RealSense depth camera and CNN neural network, the accuracy is improved significantly.
Table 1: Measurement data of different methods
A 3D reconstruction algorithm based on deep learning was proposed. An end-to-end full CNN model was designed, the coarse-layer features of the 3D image were obtained by a convolutional layer operation, and the fine-layer features were obtained through multi-scale convolution kernel operation mapping. The two features were connected and fused, and the trained model was obtained through nonlinear regression to obtain the 3D image point-cloud model. Analysis of experimental data indicated that 3D reconstruction based on the deep-learning CNN model showed great improvement in accuracy and could be applied to actual measurement, providing a reference for the subsequent processing of 3D reconstruction. Although certain results were achieved, several problems must be addressed: (1) The algorithm improves matching accuracy, but it has a certain impact on the calculation speed, and the real-time effect is not good; (2) The measured object is a regular object and cannot have wide adaptability, so the next step is reconstruction of complex objects and adaptability to the environment.
Acknowledgement: We thank LetPub (www.letpub.com) for its linguistic assistance during the preparation of this manuscript.
Funding Statement: This work is funded by Scientific and Technological Projects of Henan Province under Grant 182102210065, and Key Scientific Research Projects of Henan Universities under Grant 15A413015.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Y. Qu, J. Huang and X. Zhang. (2018). “Rapid 3D reconstruction for image sequence acquired from UAV camera,” Sensors, vol. 18, no. 2, pp. 225–244. [Google Scholar]
2. D. Y. Lee, S. A. Park and S. J. Lee. (2016). “Segmental tracheal reconstruction by 3D-printed scaffold: Pivotal role of asymmetrically porous membrane,” Laryngoscope, vol. 126, no. 9, pp. E304–E309. [Google Scholar]
3. D. Scharstein and R. Szeliski. (2003). “High-accuracy stereo depth maps using structured light,” in Proc. of IEEE Computer Society Conf. on Computer Vision and Pattern Recognition, Madison, Wisconsin, USA, pp. 195–202. [Google Scholar]
4. M. Pollefeys and L. G. Van. (1999). “Stratified self-calibration with the modulus constraint,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 21, no. 8, pp. 707–724. [Google Scholar]
5. M. O. Toole, J. Mather and K. N. Kutulakos. (2016). “3D shape and indirect appearance by structured light transport,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 38, no. 7, pp. 1298–1312. [Google Scholar]
6. X. Y. Su, Q. C. Zhang and W. J. Chen. (2014). “Three-dimensional image based on structured illumination,” Chinese Journal of Lasers, vol. 41, no. 2, pp. 9–18. [Google Scholar]
7. C. Y. Le, Y. Bengio and G. Hinton. (2015). “Deep learning,” Nature, vol. 521, no. 7553, pp. 436–444. [Google Scholar]
8. Y. R. Guo, J. Yang and W. A. Song. (2019). “Method for extracting line structured light center in complex environment,” Computer Engineering and Design, vol. 40, no. 4, pp. 1133–1138+1144. [Google Scholar]
9. D. F. Li. (2017). “Research and application of three-dimensional object measurement based on CNN,” M.S. dissertation, Harbin Engineering University, China. [Google Scholar]
10. L. Q. Liu. (2019). “Research on 3D reconstruction in vision based on deep learning,” M.S. dissertation, North China University of Technology, China. [Google Scholar]
11. X. D. Hong, X. Zheng, J. Y. Xia, L. Wei and W. Xu. (2019). “Cross-lingual non-ferrous metals related news recognition method based on CNN with a limited bi-Lingual dictionary,” Computers, Materials & Continua, vol. 58, no. 2, pp. 379–389. [Google Scholar]
12. F. Xu, X. f. Zhang, Z. H. Xin and A. Yang. (2019). “Investigation on the Chinese text sentiment analysis based on convolutional neural networks in deep learning,” Computers, Materials & Continua, vol. 58, no. 3, pp. 697–709. [Google Scholar]
13. Q. D. Zhu, Y. K. Wang and W. Zhu. (2019). “Intelligent recognition algorithm design of solder joints based on structured light,” Transactions of the China Welding Institution, vol. 40, no. 7, pp. 82–87+99+164-165. [Google Scholar]
14. C. P. Liu, B. Wu and Z. Yang. (2019). “Face representation and 3d reconstruction based on self-supervised deep learning,” Transducer and Microsystem Technologies, vol. 38, no. 9, pp. 126–128+133. [Google Scholar]
15. J. F. Wang. (2018). “Three dimensional body measurement based on CNNs and body silhouette,” M.S. dissertation, Zhejiang University, China. [Google Scholar]
16. Y. C. Guo, C. Li and Q. Liu. (2019). “(RN)-N-2: A novel deep learning architecture for rain removal from single image,” Computers, Materials & Continua, vol. 58, no. 3, pp. 829–843. [Google Scholar]
17. T. T. Bi, Y. Liu and D. D. Weng. (2018). “Overview of single image depth estimation based on supervised learning,” Journal of Computer-Aided Design & Computer Graphics, vol. 30, no. 9, pp. 1383–1393. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |