An Efficient and Secure Data Audit Scheme for Cloud-Based EHRs with Recoverable and Batch Auditing

1  Introduction

In the era of big data, a vast amount of sensitive information is being stored on cloud servers, and the associated data security issues in cloud storage have become increasingly prominent. In the cloud storage environment, the security measures provided by a single service provider are insufficient. Although cloud storage services are provided by major internet companies, absolute security cannot be guaranteed. Furthermore, in the event of data loss or corruption, companies may try to conceal the issue in order to protect their reputation and minimize potential losses. This highlights a critical issue: once users upload their data, they lose control over the original data, leading to a lack of trust in cloud storage. In electronic healthcare systems, Electronic Health Records (EHRs) are used to document users’ health data and identify their health status. Due to the large number of patients, some medical institutions store EHRs on cloud servers to reduce the pressure on local storage. However, since EHRs contain sensitive patient information, users must verify the integrity of their EHRs while ensuring their privacy is protected. Data integrity auditing can verify users’ data.

Generally, a cloud storage auditing protocol involves three entities: the user, the auditor, and the cloud server. Based on the security parameters, the user initializes the system and generates the system parameters. Subsequently, the user signs each block with a private key to obtain the block’s tags. The cloud server stores the data and the corresponding tags, while the user deletes all locally stored data and the generated tags. The auditor sends an audit request to the cloud server. The cloud server must return valid proof to the auditor. The auditor then verifies the proof.

1.1 Our Contribution

A practical data audit scheme has garnered significant interest from researchers because of its broad practical utility. Recently, Zhou et al. [1] proposed a practical data audit scheme with retrievability. Their solution can achieve many excellent features, such as retrievability, indistinguishable privacy preservation, and dynamic updates. Nevertheless, it has come to our attention that a malicious cloud server has the capability to fabricate the labels of data blocks. Thus, even if a malicious cloud server were to remove all externally stored data, it could still present falsified evidence of having outsourced the data. Based on the scheme of Zhou et al., we provide data owners with a data audit scheme for cloud-based EHRs with recoverable and batch auditing. Our scheme can resist forgery attacks.

Specifically, we observed that during the auditing phase, a malicious cloud server, using public information, outsourced data, and auxiliary information related to the data at its disposal, can forge proof. This means that when the auditor verifies the validity of the proof, the forged proof provided by the malicious cloud server can still satisfy the verification equation. To address this, we redesigned the auditing phase by incorporating random masking techniques and hash functions. Moreover, the evidence provided by the cloud server must undergo stricter verification equations by the auditor. By combining random masking techniques and hash functions, our algorithm can resist both proof forgery attacks and replay audit attacks. Additionally, our scheme supports batch auditing, enabling the auditor to audit more data in the same amount of time. For users, this means they can monitor data dynamics in real time and quickly detect any data corruption.

1.2 Organization

In Section 2, we present recent work on cloud auditing protocols. In Section 3, we review Zhou et al.’s practical data audit scheme and introduce attacks against their algorithm. We introduce the system model, threat model, design goals, and preliminary knowledge in Section 4. In Section 5, we present a data audit scheme for cloud-based EHRs with recoverable and batch auditing. In Section 6, we provide formal proof of the security of the signature algorithm and the auditing scheme. Additionally, we demonstrate the privacy protection of the scheme and its ability to resist malicious attackers. In Section 7, we conduct a comparative analysis with other schemes. In Section 8, we present the conclusion of our paper.

2  Related Work

In 2007, Ateniese et al. [2] introduced the Provable Data Possession (PDP) scheme, enabling users to securely store data on untrusted servers. Users have the capability to verify the integrity of the original data. However, this scheme only supports static auditing. During that same year, Juels et al. [3] presented the “Proofs of Retrievability” (POR) scheme, which utilizes sampling and erasure code techniques in cloud servers to ensure the retrievability and possession of data files. The scheme is capable of validating the integrity of stored data files and restoring data in the presence of sporadic errors. However, this scheme supports only a limited number of verifications. Both schemes verify data integrity, but the POR scheme incorporates erasure code techniques for data recovery. As the amount of stored data grows, users’ auditing tasks become increasingly burdensome. To solve this challenge, Wang et al. [4] proposed a publicly verifiable dynamic auditing scheme, which leverages Third Party Auditors (TPAs) to validate the integrity of dynamically stored data in the cloud. Cui et al. [5] improved the efficiency of auditing and user revocation by leveraging TPA, reducing many time-consuming operations. Wang et al. [6] also proposed a PDP protocol that supports third-party verification, implementing blind auditing and leveraging homomorphic signatures to aggregate data labels for batch auditing. For batch auditing, Huang et al. [7] implemented batch auditing for multiple files to reduce computational overhead. However, this scheme is vulnerable to malicious TPAs. Li et al. [8] designed a certificateless public auditing scheme that supports batch auditing, in which only designated auditors can verify the data.

To support dynamic updates of cloud data, Erway et al. [9] were the first to propose an integrity auditing scheme for dynamic data. To address the significant computational overhead generated during updates, Tian et al. [10] introduced the Dynamic Hash Table (DHT) for updating cloud data; however, their approach raises concerns about data confidentiality. Yuan et al. [11] designed a novel framework to support provable data possession schemes for dynamic multi-replica data. Bai et al. [12] and Zhou et al. [13] leveraged blockchain technology to enable dynamic updates on cloud data. However, their efficiency is constrained by the blockchain consensus protocol. Recently, Zhou et al. [14] implemented a dynamic multi-replica cloud auditing scheme using the Leaves Merkle Hash Tree (LMHT), which demonstrates improved performance in data deletion. Yu et al. [15] found that a malicious TPA could obtain sensitive information through replay audit attacks, posing significant privacy concerns. Shah et al. [16] proposed a public auditing scheme capable of resisting malicious TPA attacks. However, this scheme limits the number of audits and is restricted to encrypted files.

Numerous public auditing schemes [17,18–21], built upon Public Key Infrastructure (PKI), face the key limitation of expensive certificate management. Wang et al.’s identity-based PDP scheme [22] eliminates the need for certificate management. In the literature, an identity-based auditing scheme [23] has also been proposed. In their work, Wang et al. [23] tasked the auditor with creating tags and encrypting the file. Both PKI-based and identity-based auditing schemes face several challenges. Wang et al. [24] introduced a certificate-driven auditing approach that leverages bilinear pairings for verification in both private and public validation processes. The scheme supports both private and public verification, with private verification incurring lower computational costs than public verification. Shen et al. [25] proposed a certificateless PDP scheme for cloud-based electronic health records, enabling the restoration of corrupted data. In 2023, Zhou et al. [1] introduced a practical data auditing scheme. The auditing process is fast and efficient. However, Zhou et al.’s scheme [1] is vulnerable to evidence fabrication by adversaries. Our scheme retains the advantages of the original scheme while enhancing security. Importantly, our scheme addresses security flaws, offering improved security and resistance against forged evidence attacks.

3  Analysis Zhou et al.’s Scheme

Zhou et al. proposed an auditing scheme that ensures retrievability and privacy preservation [1]. In this section, we first review Zhou et al.’s scheme. Then, we identify the security weaknesses in its construction.

3.1 Review of Zhou et al.’s Scheme

Leveraging the Invertible Bloom Filter (IBF), Zhou et al. proposed a data auditing scheme. Due to the properties of the IBF, in the event of data corruption, users can utilize the remaining blocks to recover the damaged data blocks. Additionally, the scheme achieves indistinguishable privacy protection, even in the face of replay audit attacks.

The scheme proposed by Zhou et al. employs the notation summarized in Table 1.

: The user executes the algorithm by selecting random element in G, independent hash functions , and a random number in . Then, the user computes , stores its private key and sends the public key to the cloud server (CS) and the third party auditor (TPA).

The user executes the algorithm by splitting the M into data blocks . For , it sequentially computes and the homomorphic verification label (HVL) . Meanwhile, based on and , the user initializes IBF and computes the IBF for data recovery. The identifier (ID) sequence used to update the data is represented as , and the HVL sequence for block verification is represented as . The user computes , where . The user stores locally and sends the to the CS.

The CS computes R based on M and verifies the SIG. When the verification is successful, the CS responds with .

The user modifies a block after the -th data block. It computes ID value , generates , and creates , where or . The user then sends a modify request or to the CS.

For the modify request , the CS computes and verifies .

(1)

If the verification Eq. (1) holds true, the CS modifies the M and the HVL , then computes the signature for . The CS outputs or . Otherwise, if the equation does not hold, the CS outputs . Based on , the user modifies the IBF by running the algorithm . At the same time, the user also updates the ID and R.

The TPA randomly selects two random numbers and in . Based on the required confidence level, the TPA selects a number and outputs .

The CS randomly selects a number in . Based on the , for , the CS uses the public pseudorandom permutation (PRP) and the pseudorandom function (PRF) to compute and , respectively. For , it then computes the aggregated HVL , and calculates , where . The CS outputs the proof .

Based on , for each , the TPA uses the public PRP and PRF to compute and , respectively. Denoted the subset of indices , the TPA verifies the proof P as follows:

(2)

If the Eq. (2) holds, it outputs 1; otherwise, it outputs 0. The TPA returns the result to the user.

When the TPA detects data corruption, the user uses two algorithms to restore the corrupted data. The user sends parameters to the CS for generating the IBF. We assume that data blocks are corrupted, and the sequence of noncorrupted data blocks is denoted as . For , where , based on the parameters , the CS generates a new IBF and then sends it to the user. Based on the IBF B and the IBF , the user retrieves the corrupted data blocks.

3.2 Attack

We observe that when the CS executes the polynomial time algorithm , it is possible to forge a proof P based on the public information available, outsourced data, and auxiliary information related to the data. Specifically, a malicious CS first computes based on the data M, obtains , , and then verifies the signature SIG. Next, in the update phase, the malicious CS computes the updated block’s and . It executes the algorithm and randomly selects from the group , then computes and based on the challenge . For , it computes and sets . The proof is then sent to the TPA.

In this way, when the TPA executes the algorithm to verify the validity of the proof , the proof provided by the malicious CS passes Eq. (2). This works because

The malicious CS does not need to store the data M and HVLs . It only needs to store the sequence , significantly reducing storage requirements. The malicious CS has both the incentive and the ability to forge data storage proofs, and the forged proof will not be detected by the TPA. Furthermore, during the update phase, the malicious CS can still interact with the user normally, verify the signature , and output the response message . Since the output from the algorithm is always 1, the TPA cannot detect data corruption.

Finally, the malicious CS is able to successfully attack Zhou et al.’s scheme by only storing the sequence , without storing the data M and HVLs . This allows the malicious CS to bypass the intended security measures perfectly.

4  Definition and Preliminary

4.1 System Model

We propose a data auditing scheme with recoverability and batch auditing capabilities for EHRs. Our scheme is designed for patients and healthcare institutions, enabling patients to outsource their electronic health records to cloud services. If the data is found to be corrupted or lost, patients can recover it, ensuring the integrity and availability of the electronic health records. The TPA can perform batch audits on the patients’ EHRs. Our scheme’s system comprises five entities: data owners, sensors, data users, a third-party auditor, and a cloud server. The system model of our scheme is illustrated in Fig. 1.

•   Sensors: Comprising wearable devices, embedded sensors, and body area sensors, they collect real-time health data from patients, such as heart rate, blood glucose levels, and physical activity status. As a result, sensors are considered trusted entities.

•   Data Owner (DO): The data owner, who is always a patient, generates EHRs using sensors and other data collection devices. Once the data is collected, the patient encrypts and transmits it to the cloud server. The patient can dynamically update the data stored on the cloud server and recover it if the data is found to be corrupted or lost. The data owner is regarded as a trusted entity.

•   Cloud Server (CS): The CS provides storage and computational resources for the medical data of data owners. When the third-party auditor issues an audit request, the CS generates a proof in response. However, due to unforeseen circumstances, the stored data may become corrupted, and in an effort to protect its reputation, the CS may forge a proof. As a result, the CS is regarded as a semi-trusted entity.

•   Third Party Auditor (TPA): The TPA is authorized by the data owner to periodically audit the medical data stored in the cloud. However, the TPA may exhibit curiosity, such as by conducting repeated audits on the same data to gain additional insights. As a result, the TPA is regarded as a semi-trusted entity.

•   Data User (DU): The DU is a user authorized by the DO to access the relevant EHR. Typically, the DU is the patient’s attending physician. During medical visits, the DO can grant key authorization to the DU, enabling them to download the encrypted EHR from the CS and decrypt it. The DU is regarded as a trusted entity.

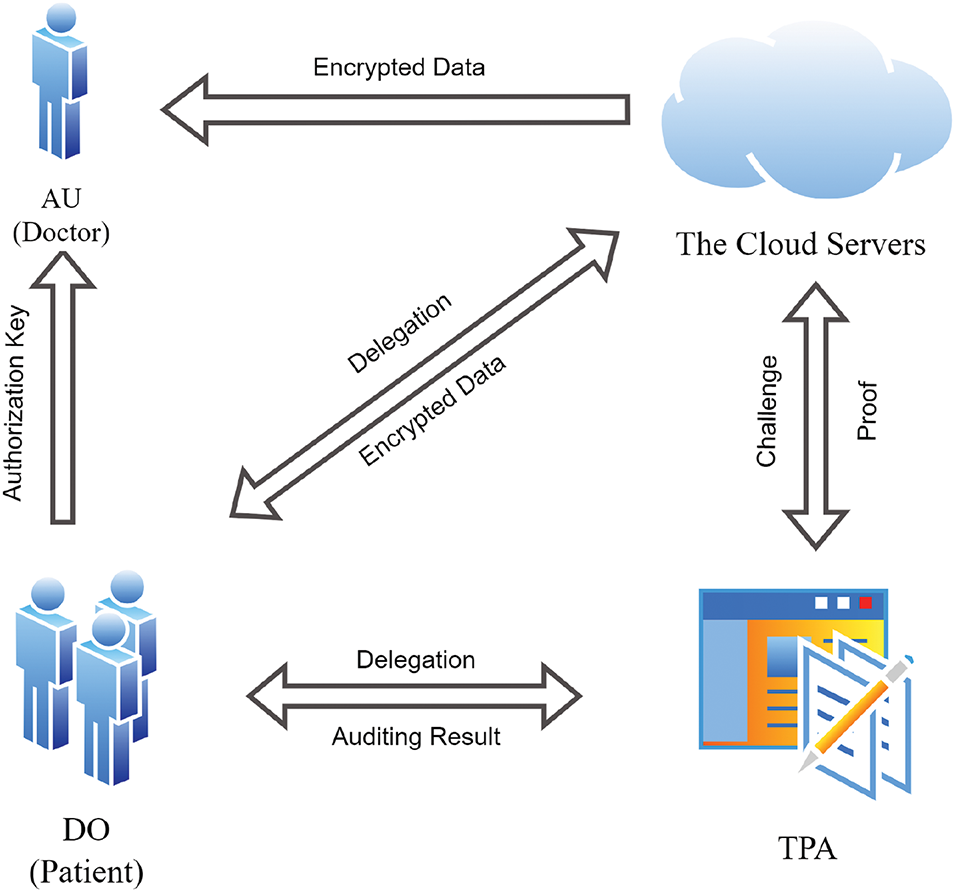
Figure 1: System model

The system leverages wearable devices, embedded sensors, and body-area sensors to collect real-time health data from patients, such as heart rate, blood sugar levels, and exercise status. This data is used to generate EHRs for the patients. Due to limitations in storage and computational resources, patients encrypt the data and transmit it to the cloud server, where dynamic update algorithms ensure timely updates to the health data. The CS stores the patients’ EHRs and generates data possession proofs in response to audit requests from the TPA. When doctors request access, the CS provides the relevant electronic health records. Authorized by the data owner, the TPA periodically sends audit requests to verify the integrity, accuracy, and privacy of the EHRs stored in the cloud. If the auditing algorithm fails, the TPA promptly notifies the patient of data corruption or loss. In such cases, the patient can utilize a data recovery algorithm to restore the damaged data. When seeking medical treatment, the patient provides the doctor with the decryption key. The doctor then downloads and decrypts the EHR from the CS to facilitate accurate diagnosis and treatment.

This system model integrates medical IoT, cloud computing, and privacy protection technologies to deliver an efficient, transparent, and secure collaborative framework for patients, doctors, and data auditors in complex healthcare environments.

4.2 Threat Model

In our threat model, the cloud server is considered untrustworthy and may behave maliciously. The cloud server may attempt to forge valid proofs to conceal data loss and preserve its reputation. The TPA is assumed to be curious. While it performs public verification of outsourced data integrity under user authorization and honestly participates in the auditing protocol, it may attempt to infer sensitive data information. We assume that the DO and DU will not compromise the scheme.

We classify potential adversaries into two categories:

Type I Adversary (): A malicious CS that possesses the data and corresponding tags. It has knowledge of the system’s public parameters and other public information. The generates evidence messages in an attempt to pass the verification equation, thereby concealing activities such as data modification, loss, or deletion.

Type II Adversary (): A curious TPA that may launch replay auditing attacks to infer sensitive data. By conducting repeated audits on the same data block, the TPA attempts to deduce its content.

It is important to note that both the CS and the auditor are considered ’semi-trusted,’ and their behavior may not always align with real-world scenarios. A malicious cloud server, having access to the data and tags, can generate forged proofs. A malicious auditor may exploit mathematical techniques to launch replay audit attacks and infer the content of the data. As a result, we treat both the CS and the TPA as untrusted entities. To address the issue of untrusted entities, we enhance the security of the signature algorithm to mitigate malicious cloud servers and strengthen the auditing algorithm to counteract malicious auditors. This ensures the integrity and privacy of the data while enhancing the reliability of the auditing process.

4.3 Design Goals

We aim to design a data auditing scheme with recoverability and batch auditing capabilities for EHR systems. The scheme not only enables data recovery but also facilitates batch auditing. Additionally, the scheme ensures correctness, privacy protection, and resistance to forgery attacks.

To ensure effective integrity auditing of outsourced data within the threat model, our scheme must fulfill the following objectives:

Functionality: Support for Dynamic Updates: Since the EHR of the DO may be updated dynamically, the data auditing scheme must support dynamic auditing. Data Recoverability: To enhance data availability, the scheme should enable the DO to recover corrupted data through data recovery operations, thereby improving data security. Batch Auditing: The auditor should deliver audit results to multiple data owners simultaneously. This ensures that the DO can promptly monitor the status of their EHR. In the event of a batch audit failure, a normal audit identifies the specific data owner’s EHR that is compromised and recovery algorithms can be applied to restore the corrupted data.

Security: Privacy Protection: The DO should encrypt their EHR data to safeguard the privacy of their medical information. During the auditing process, the auditor should neither require access to nor be able to retrieve the user’s stored data. Furthermore, the auditor must not infer any sensitive information about the user from the response messages.

Efficiency: Lightweight: To ensure the scheme is suitable for resource-constrained devices, the design should minimize communication overhead and computational costs during data auditing.

4.4 Invertible Bloom Filter

We use an IBF to compute data differences and improve IBF for recovering data blocks in cases of corruption. We first initialize the IBF as an empty table with cells, where is the maximum number of corrupted data blocks. Let denote independent hash functions. For a given data block in the , we map it to different hash values, . Each cell in the IBF contains three fields: , and . represents the number of data blocks mapped to the cell. represents the XOR of all data blocks mapped to the cell. represents the product of the hashes of all data blocks mapped to the cell. Here, is used to generate the hash value for each data block. The fields and are both initialized to zero, while is initialized to the generator of G. To process the IBF, we set or to handle the data blocks.

1. Encoding: Given a data , the client initializes the IBF B. For each data block , it uses independent hash functions to generate different hash indices. For each hash index, it XORs (Exclusive OR) with the , multiplies with , and increments the by 1.

2. Decoding: Given two data and along with their respective IBFs and , the client computes the difference IBF , where it XORs , multiplies and subtracts . A cell in is considered a pure cell if it satisfies the following two conditions: and . The decoding process terminates when no longer contains pure cells, indicating that the corrupted or differing data blocks between and have been successfully recovered.

4.5 and Algorithms

To recover corrupted data, we set or to process the IBF and propose the Algorithm 1 and Algorithm 2 . We execute the algorithm times to generate the IBF for the data . When data corruption occurs, the IBF is generated for the remaining data blocks using the same algorithm. Based on and we use the algorithm to compute the IBF which allows the recovery of corrupted data blocks. A cell in is considered a pure cell if it satisfies the following two conditions: and . The decoding process terminates when no longer contains pure cells, indicating that the corrupted or differing data blocks between and have been successfully recovered.

5  Our Scheme

In this section, we propose a secure cloud-based EHR data auditing scheme designed to prevent data leakage. The scheme also incorporates an improved IBF to facilitate the recovery of corrupted data. In large-scale EHR systems, the DO collects real-time health data through sensors and uploads it to the CS. Our scheme comprises two components: Normal Audit and Batch Audit.

: The TPA performs a data possession challenge on the EHR stored in the cloud and verifies the response proof. If data corruption is detected, the scheme initiates the data recovery phase. The data owner provides the necessary parameters to enable the CS to generate a new IBF. The corrupted data is then recovered using the newly generated IBF and the locally retained IBF.

: The batch auditing function provides timely audit results to multiple data owners, enhances the real-time performance and efficiency of auditing, and enables data owners to promptly monitor the status of their EHR. If the batch audit fails, a normal audit is conducted to identify the specific data owner’s EHR data that is compromised and the recovery algorithm is applied to restore the corrupted data.

5.1 Construction of Our Scheme

In this section, we propose a more secure and privacy-preserving cloud auditing scheme. We adopt the same notation as Zhou et al.’s scheme [1]. The procedures of our scheme are illustrated in Fig. 2.

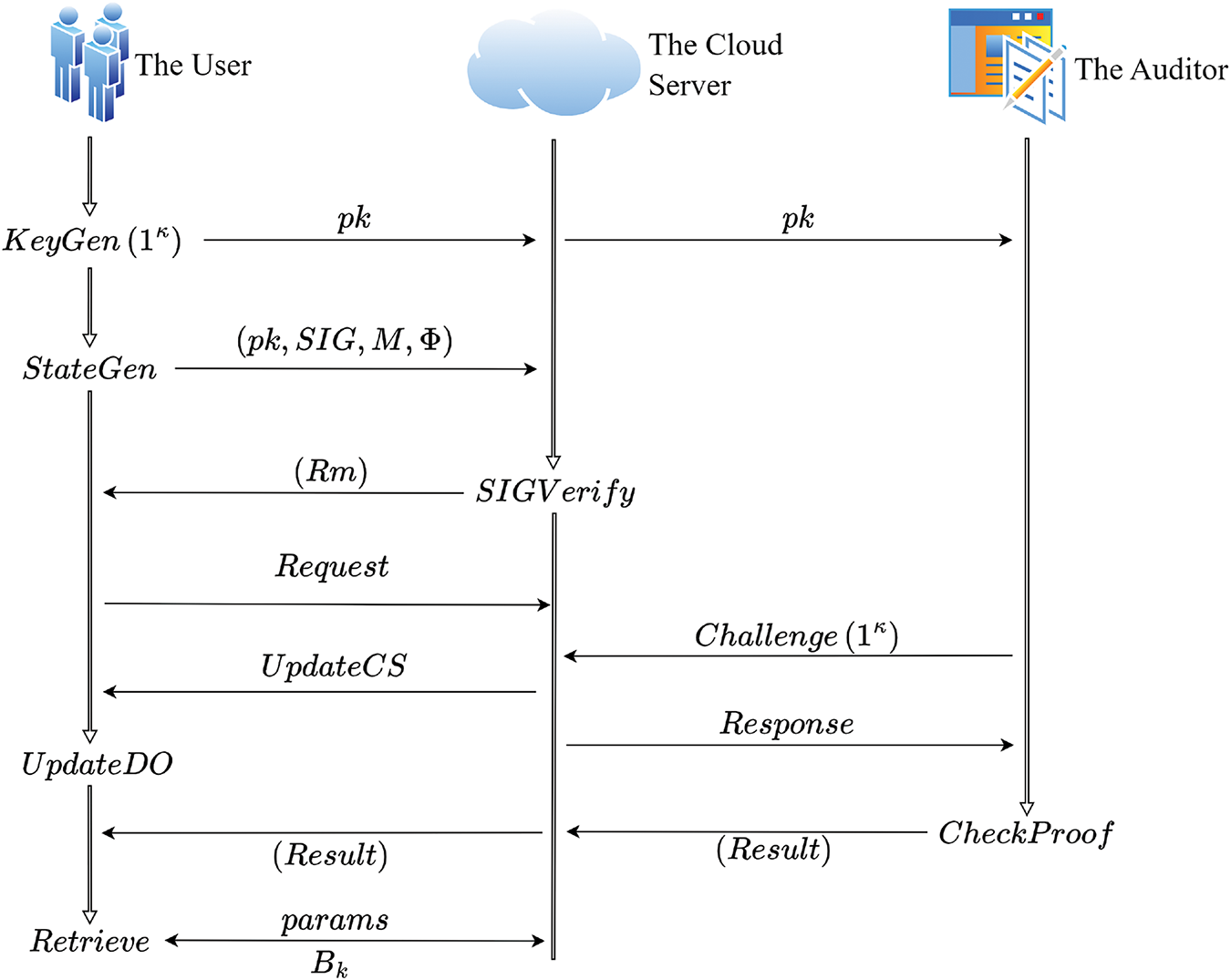
Figure 2: Procedures of our scheme

The DO executes the algorithm by selecting a random number in G, independent hash functions , and a random element in . Then, the DO computes , stores its private key and sends the public key to the CS and the TPA.

The DO executes the algorithm by splitting the M into . For , it sequentially computes and the label . Meanwhile, based on and , the DO initializes the IBF and computes the IBF . The ID sequence used to update the data is represented as , and the HVL sequence for block verification is represented as . The DO computes to record the operation, where . The DO stores locally and sends the to the CS.

The CS computes R based on the M and verifies the SIG. When the signature verification is successful, the CS responds with , where is the CS’s signature.

The DO inserts a block after the -th data block, which is the insert operation . It computes a new ID value , generates a new , and creates a new , where . The DO then sends an update request to the CS. Additionally, the DO deletes the -th data block, which is the delete operation . It computes a new , where . The DO then sends the update request . Through both the insert and delete operations, the DO also supports modifying the data.

For the insert request , the CS computes and verifies .

(3)

If Eq. (3) holds true, the CS updates the data M and the corresponding HVL , then computes the for . The CS outputs a response message . Otherwise, if the equation does not hold, the CS outputs . Similarly, for the delete request and ID, the CS computes and verifies . If the equation holds true, the CS updates the data M and the corresponding HVL , then computes the for . The CS outputs . Otherwise, if the equation does not hold, the CS outputs .

For the insert operation, based on and , the DO runs the to update the IBF. For the delete operation, based on and , the DO updates the IBF by running the algorithm . At the same time, the DO also updates the ID and R.

The TPA randomly selects two random numbers and in . Based on the required confidence level, the TPA selects a number and outputs .

: The CS randomly selects a number in . Based on the , for , the CS uses the PRP and the PRF to compute and , respectively. For , it then computes the aggregated HVL , and calculates , where , . The CS outputs the proof .

Based on , for each , the TPA uses the public PRP and PRF to compute and , respectively. Denoted the subset of indices , the TPA verifies the proof P as follows:

(4)

If Eq. (4) holds, it outputs 1; otherwise, it outputs 0. TPA returns the result.

When the TPA detects data corruption, the DO uses two algorithms (, ) to restore the corrupted data. The DO sends parameters to the CS for generating the IBF. We assume that data blocks are corrupted, and the sequence of noncorrupted data blocks is denoted as . For , where , based on the parameters , the CS runs the algorithm times to generate a new IBF and then sends it to the DO. The DO uses the algorithm, inputting the IBFB and the IBF , to retrieve the corrupted data blocks.

Batch Audit:

To deliver timely audit results for multiple users, we introduce the batch auditing feature. In the event of a batch audit error, the normal audit is employed to identify the specific user and the problematic data block. Subsequently, the data recovery algorithm is applied to restore the corrupted data. If an error is detected during the batch audit, the need for separate audits for each user is minimized by isolating the issue to the specific user and data block, enabling faster response and recovery. The scheme facilitates batch auditing of cloud data for multiple data owners.

Let randomly select as private key and compute as public key. The DOs split their data into . For each data block, the DO sequentially computes and the HVL . Meanwhile, based on and , the DO initializes the IBF and computes IBF . The ID sequence used to update the data is represented as . The DO stores locally and transmits to the CS.

The TPA selects two random numbers and from the group and sends the to the CS. The TPA and CS utilize public PRP and PRF to compute and , respectively. Upon receiving the challenge indices, the CS computes the aggregated HVL and calculates , where , . The CS then sends the proof to the TPA. Denoted the subset of indices , the TPA verifies the proof P.

(5)

If Eq. (5) holds, it confirms that the user’s data is intact. In this case, the TPA proceeds to perform batch auditing. Otherwise, the TPA conducts a standard audit to identify the specific DO and the data block that is compromised. The damaged data is then recovered using the recovery algorithm described in the following section.

When the TPA detects data corruption, the DO uses two algorithms (, ) to restore the corrupted data. The DO sends parameters to the CS for generating the IBF. We assume that data blocks are corrupted, and the sequence of noncorrupted data blocks is denoted as . For , where , based on the parameters , the CS runs the algorithm times to generate a new IBF and then sends it to the DO. The DO uses the algorithm, inputting the IBF B and the IBF , to retrieve the corrupted data blocks.

5.2 Correctness Analysis

The correctness of Eq. (4) is derived as follows:

The correctness of Eq. (5) is derived as follows:

6  Security Proof

In this section, we present the security proof of our scheme from two aspects: (1) the unforgeability of the auditing scheme and (2) the resistance to type I adversary and type II adversary as defined in Section 4.

Theorem 1. Our signature algorithm is existentially unforgeable under adaptive chosen-message attacks (EUF-CMA).

Specifically, assume there exists an EUF-CMA adversary that can break the signature algorithm with an advantage of . Then, there must exist an adversary capable of solving the Computational Diffie-Hellman (CDH) problem with an advantage of at least .

Proof. The following proves that the signature algorithm can be reduced to the CDH problem. The adversary , given , uses (which attacks the signature algorithm) as a subroutine, with the goal of computing . In the actual proof, aims to hide the problem instance within the simulation.

The reduction process is as follows:

(1) sends the generator and the public key to .

(2) Hash Query (up to Query): constructs a list , initially empty, where each element is a tuple of the form . When makes its -th query, the response is as follows:

(1) If the list already contains corresponding to , responds with the value .

(2) Otherwise, randomly chooses a value . If , it computes . Otherwise, it computes . It uses as the response and stores the tuple in the list .

(3) Tag Query (up to Query): When requests the signature for the message , let . Denote the queried value for the -th Hsah query as . answers the query. If , there exists a tuple in the list . It computes the signature and responds to with . This works because . If , it aborts the simulation.

(4) Output: The adversary eventually outputs , where and are the forged proof. If , aborts the simulation. Otherwise, outputs as to the problem. This works because .              □

Theorem 2. Assume the hash function H is a random oracle. If the CDH assumption holds, then our scheme is existentially unforgeable under an adaptive chosen message attack.

Proof. Assume there is a challenger , who has a CDH instance . To output , interacts with the adversary .

Setup. The sends the generator and to the adversary .

Query. The responds to the adversary ’s adaptive Hash query and signature query as follows:

Hash query. The constructs a list , initially empty, where each element is a tuple of the form . When submits a data for a hash query, checks whether exists in . If it exists, the hash value is returned; otherwise, randomly choses , computes as the return value, and inserts the tuple into .

Signature query. The constructs a list , initially empty, where each element is a tuple of the form . When submits a data for a signature query, checks whether exists in . If it exists, the is returned; otherwise, computes . This works because . inserts the tuple into .

Forgery. Finally, under the challenge , forges a proof . Moreover, can pass the TPA’s verification, and at least one data has not been submitted for a signature query, where . The challenger searches the list and finds , where . In this case, the challenger obtains

(6)

Moreover, the challenger possesses the valid proof and obtains

(7)

Based on Eqs. (6) and (7), the challenger obtains

In this way, gets , because . Thus, the challenger computes from , , and , thereby solving the CDH problem.□

Theorem 3. Our scheme is resistant to malicious TPA attacks, thereby ensuring privacy protection. A malicious TPA cannot obtain the actual data from the proof provided by the CS.

Proof. We use random masking techniques to ensure data privacy and security. The CS introduces random numbers to protect data security. In our scheme, is the proof generated by the CS. First, the CS aggregates the challenged data blocks into . By using a random number , is blinded into , where . Here, is a random value chosen by the CS in the group and is kept secret from other entities. In this way, the malicious TPA is unable to perform a replay audit attack to extract the challenge data blocks from the blinded . Second, the CS generates different data possession proofs for each challenge . Since the CS selects a new random number each time it generates a proof, even for the same challenge, the generated will be different. As a result, the actual data information will not be leaked to the malicious TPA.□

Theorem 4. Our scheme is resistant to forgery attacks as described in Section 3.

Proof. In algorithm, we compute the homomorphic verification label (HVL) , and calculate , where , . The malicious CS is unable to forge the proof P based on the public information, outsourced data, and auxiliary information related to the data. The malicious CS can compute based on the dataM to obtain . It can then compute based on the challenge , as well as . However, the malicious cloud cannot forge , because in the equation.

is in the exponent of , and it is not combined with as a single entity in the proof. Unless the malicious cloud can solve the discrete logarithm problem to make , it cannot successfully forge P. Similarly, for R, the malicious cloud may also attempt forgery. However, before forging, it must first know , which is only generated after R is determined. Therefore, the malicious cloud cannot forget R. If the malicious cloud attempts to forge the proof P, the TPA will immediately detect that the proof is fraudulent.

□

7  Performance Analysis

7.1 Functional Comparison

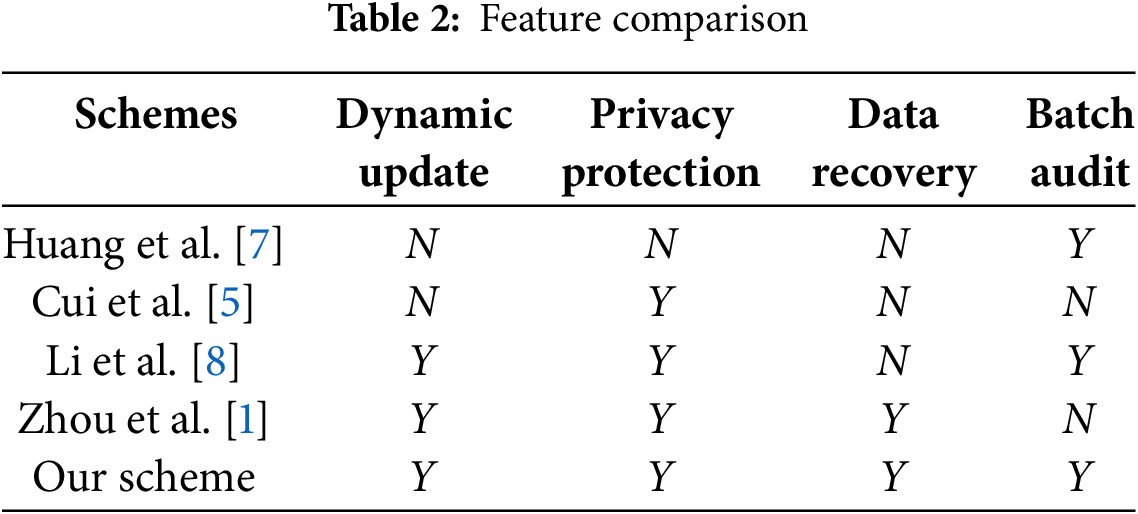
We compared our scheme with schemes [5,7,8], and [1] in terms of functionality. As shown in Table 2, our scheme supports features such as dynamic updates, privacy protection, data recovery, and batch auditing. In contrast, none of the schemes [7,5,8], or [1] simultaneously satisfy all these functional requirements. Scheme [7] only supports batch auditing, while scheme [5] only supports privacy protection. Scheme [8] does not support data recovery for corrupted data, and scheme [1] does not support batch auditing. Our scheme overcomes these limitations and provides comprehensive functionality.

7.2 Computational Cost

We compare the computational costs of each phase with schemes [5,7,8], and [1]. The notations in our scheme are described in Table 3. In our scheme, the data owner generates homomorphic verification labels before outsourcing the data. In Table 4, the computational cost for generating labels is , where represents the cost of exponentiation in G, represents the cost of multiplication in G, and H represents the cost of a hash function mapping to G. The TPA first generates a challenge and sends it to the CS. Upon receiving the challenge, the CS generates the verification proof. The computational cost of generating the challenge index is negligible and thus omitted. The computational cost of generating the verification proof is , where represents the cost of multiplication in the , represents the cost of addition in the , and denotes the number of challenged data blocks. In the phase, the TPA spends to check the integrity of the data, where P represents the cost of a bilinear pairing operation. Similarly, during batch auditing, the TPA spends , where is the number of users.

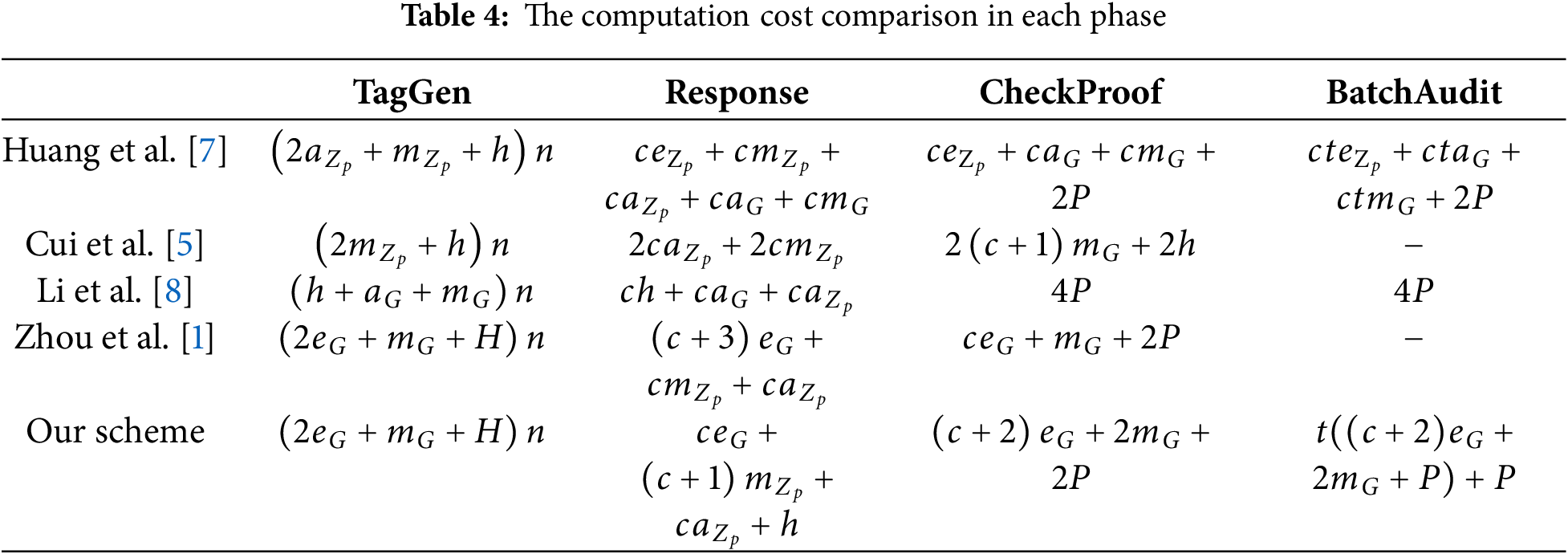
Table 4 shows that our scheme has the same computational cost as scheme [1] for generating homomorphic verification labels. For the algorithm, compared to scheme [1], our scheme introduces an additional but reduces . This leads to a reduction in overall computational cost. For the algorithm, our scheme increases the computational cost for proof verification to an acceptable level. Assuming the TPA audits the data of users, our scheme only requires a computational cost of , while scheme [1] incurs a higher computational cost of , as bilinear pairing operation P is very time-consuming.

Compared to scheme [7], our scheme requires roughly the same computational cost in the and phases but incurs higher computational costs during the batch auditing phase. Additionally, in the verification label generation phase, our scheme’s computational cost is slightly higher than that of scheme [7].

7.3 Experimental Results

In this section, we analyze our scheme in terms of communication overhead and computational cost. Our experiments were conducted on a computer equipped with I7-9750H 2.60 GHz processor and 8 GB of memory. We implemented our scheme using the JAVA programming language and the JPBC cryptographic library. In the experiments, we selected a 512-bit base field size and a 160-bit size element in .

Here, represents the number of data blocks uploaded by the user, and represents the number of data blocks challenged by TPA. We use a 2 MB file as the outsourced file and divide it into 50, 100, 150, 200, 250, 300, 350, 400, 450, and 500 blocks. For the setting of challenge blocks, based on [2], we know that a constant number of 460 blocks need to be challenged with confidence. When the number of data blocks exceeds 460, we set the number of challenge blocks to 460. When the number of data blocks is less than 460, we set the number of challenge blocks to .

We perform a simulation of our scheme on the computer. In Fig. 3a, we can see the runtime of each phase for scheme [1], and in Fig. 3b, we can observe the runtime of each phase for our scheme. Since we only modifies the and algorithms, the overall computational cost of the () algorithm shows little difference between the two schemes.

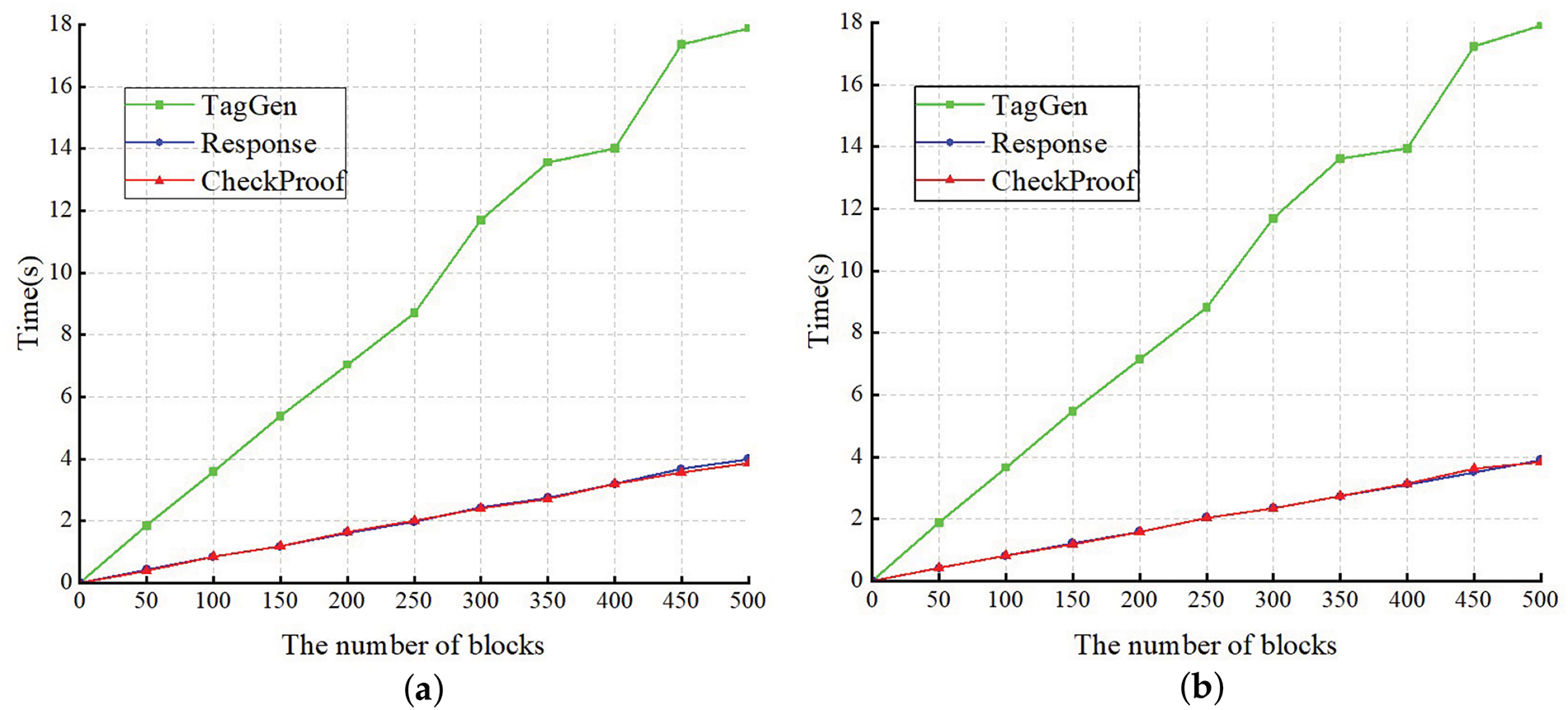
Figure 3: (a) Computation cost of the original scheme; (b) Computation cost of our scheme

In Fig. 4a, we compare the runtime of the phase between our scheme and scheme [1]. The runtime of our scheme is approximately the same as that of scheme [1]. The runtime of the phase increases as the number of data blocks increases. Furthermore, since we did not modify the algorithm in the phase, the runtime remains essentially the same.

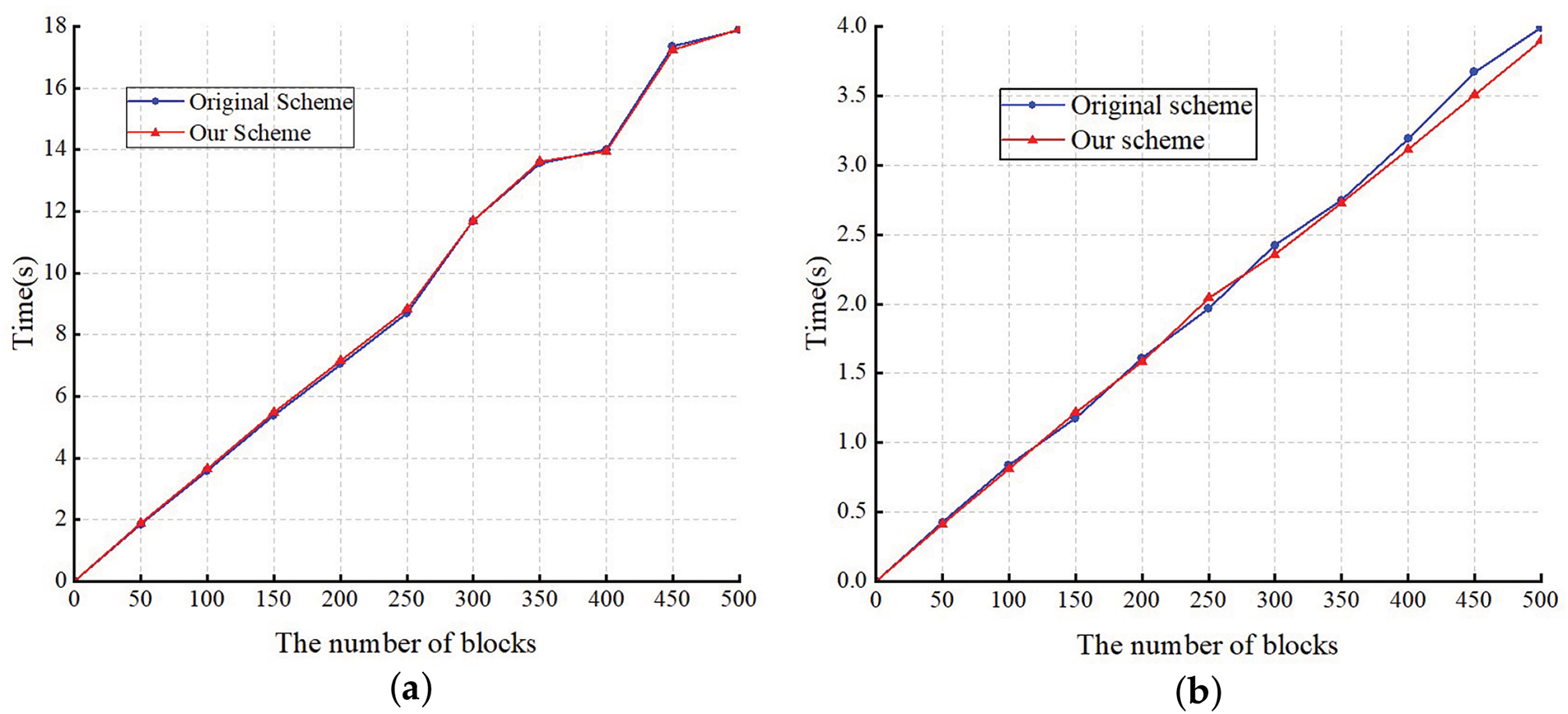
Figure 4: (a) Computational cost comparison in the TagGen phase; (b) Computational cost comparison in the Response phase

In Fig. 4b, we compare the runtime of the phase between our scheme and scheme [1]. Although we add a few operations in this phase, the impact on the overall overhead is minimal. The computational cost of both schemes increases with the number of data blocks.

In Fig. 5a, we compare the runtime of the phase. In practice, we add two exponentiation operations in G and one multiplication operation in G. However, based on the experimental results, the impact on performance is minimal. Consequently, despite the differences in the verification equations between the two schemes, their computational overhead is nearly identical.

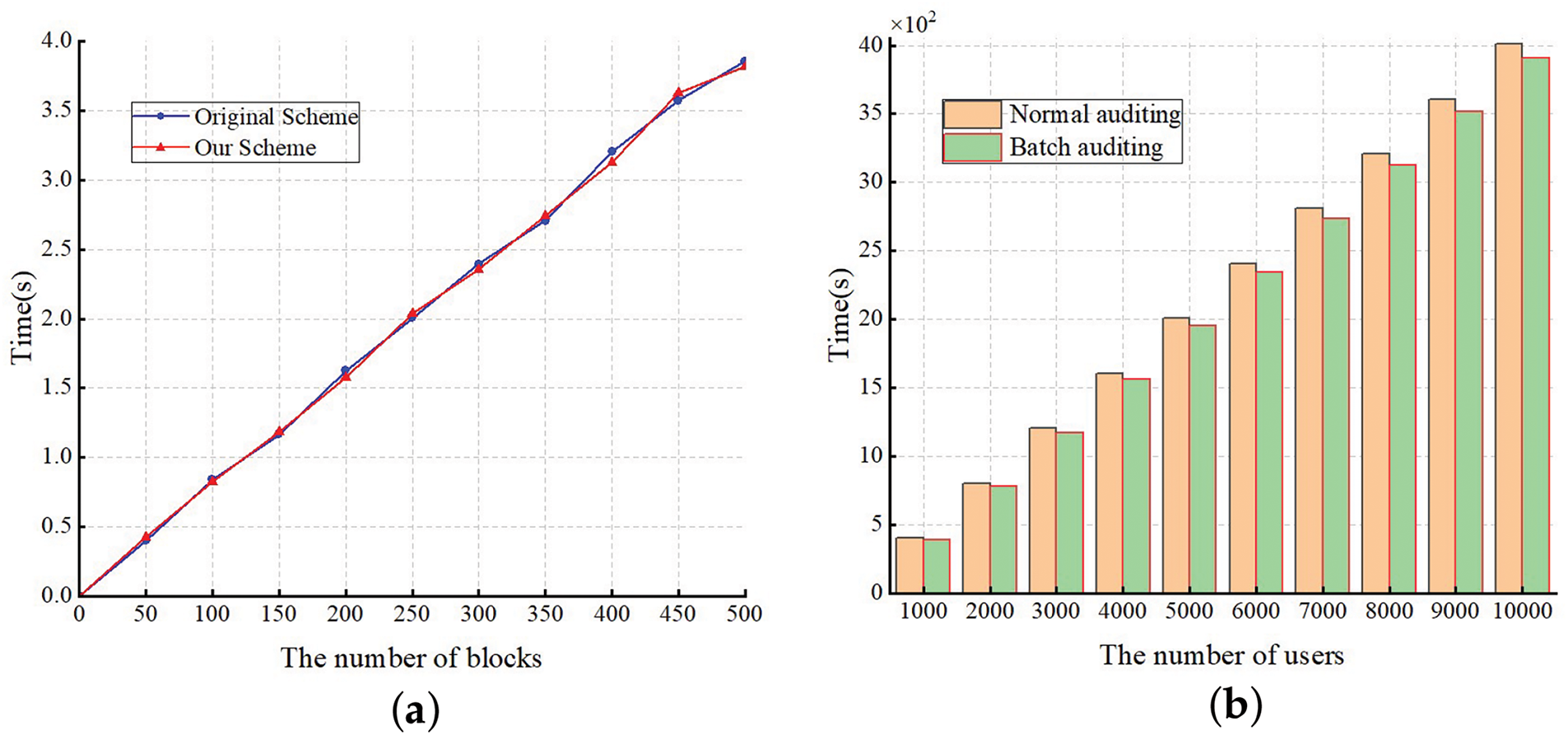
Figure 5: (a) Computational cost comparison in the CheckProof phase; (b) Comparison of normal auditing and batch auditing

In Fig. 5b, we evaluate the computational cost of auditing 0 to 10,000 different users simultaneously. The results in Fig. 5b demonstrate that the computational cost increases with the number of users. As the number of users increases, the advantages of batch auditing become more pronounced. Specifically, for 10,000 users, batch auditing reduces the computational cost by 101 s compared to normal auditing. Our scheme supports batch auditing, allowing the TPA to audit a larger volume of data in the same timeframe. For users, this enables timely monitoring of data status and rapid detection of data corruption.

For larger datasets, we implemented our auditing scheme across varying file sizes. As shown in Fig. 6, the signature time increases proportionally with the file size. It is worth noting that the proof generation and verification times exhibit minimal variation, as c is set to 460. Comparing Fig. 6a and b, we observe that although our scheme introduces additional computations during the auditing phase, the computational overhead remains minimal. Simultaneously, the scheme ensures enhanced security.

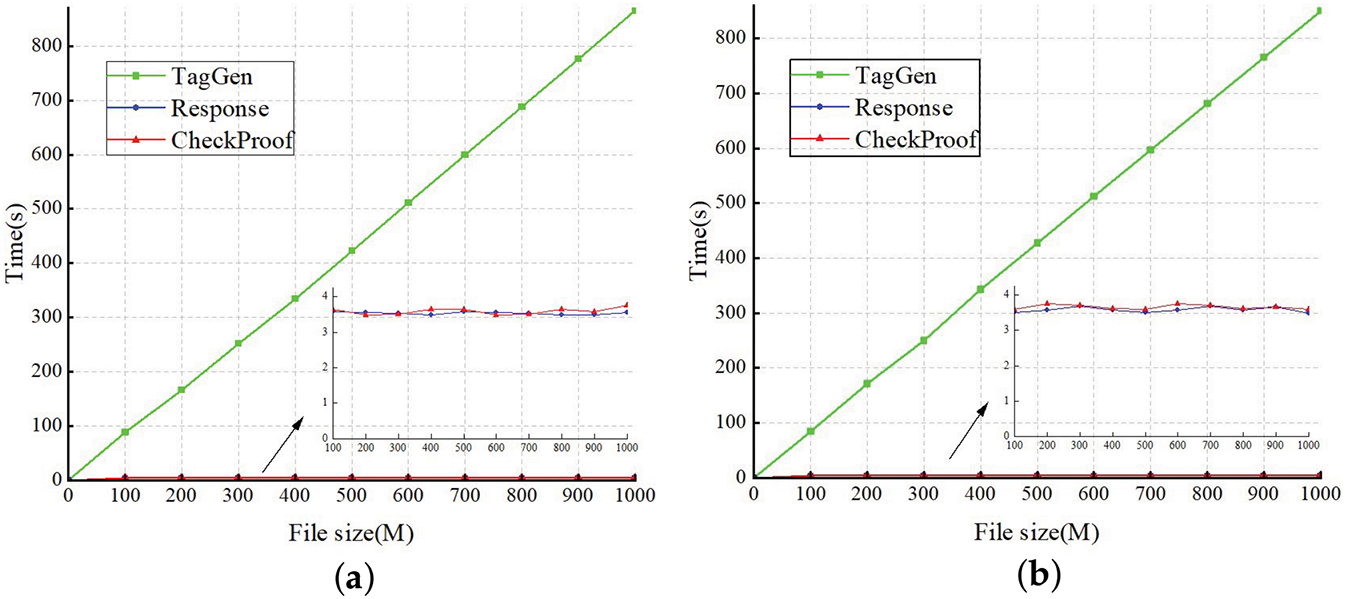
Figure 6: (a) Computation cost of the original scheme with different file sizes; (b) Computation cost of our scheme with different file sizes

8  Conclusion

To ensure the security of users’ data, Zhou et al. proposed a practical data auditing scheme. However, certain security issues have been identified during the auditing process. After identifying the issues in the original scheme, we propose an auditing scheme with recoverability and batch auditing capabilities to address these challenges. Our scheme incorporates masking techniques to enhance the auditing phase, ensuring secure data storage at a reduced cost. Additionally, we utilize an improved IBF to efficiently recover damaged data in the event of corruption. The security analysis demonstrates enhanced security, while the performance analysis reveals only a marginal increase in computational overhead. Most importantly, our scheme supports batch auditing, enabling the TPA to audit a larger volume of data within the same timeframe and allowing users to monitor data dynamics and rapidly detect data corruption.

Acknowledgement: The authors are grateful to all the editors and anonymous reviewers for their comments and suggestions.

Funding Statement: This work is supported by National Natural Science Foundation of China (No. 62172436). Additionally, it is supported by Natural Science Foundation of Shaanxi Province (No. 2023-JC-YB-584) and Engineering University of PAP’s Funding for Scientific Research Innovation Team and Key Researcher (No. KYGG202011).

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Yuanhang Zhang and Xu An Wang; methodology, Xu An Wang and Weiwei Jiang; validation, Mingyu Zhou; resources, Xiaoxuan Xu; data curation, Hao Liu; writing—original draft preparation, Yuanhang Zhang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Xu An Wang, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Zhou Z, Luo X, Wang Y, Mao J, Luo F, Bai Y, et al. A practical data audit scheme with retrievability and indistinguishable privacy-preserving for vehicular cloud computing. IEEE Transact Vehic Technol. 2023;72(12):16592–606. doi:10.1109/TVT.2023.3295953. [Google Scholar] [CrossRef]

2. Ateniese G, Burns R, Curtmola R, Herring J, Kissner L, Peterson Z, et al. Provable data possession at untrusted stores. In: Proceedings of the 14th ACM Conference on Computer and Communications Security; 2007; New York, NY, USA. p. 598–609. doi:10.1145/1315245.1315318. [Google Scholar] [CrossRef]

3. Juels A, Kaliski BS. Pors: proofs of retrievability for large files. In: CCS ’07. New York, NY, USA: Association for Computing Machinery; 2007. p. 584–97. doi:10.1145/1315245.1315317. [Google Scholar] [CrossRef]

4. Wang Q, Wang C, Li J, Ren K, Lou W. Enabling public verifiability and data dynamics for storage security in cloud computing. Vol. 5789. In: Computer security–ESORICS 2009. Lecture notes in computer science. Berlin/Heidelberg; Germany: Springer; 2009. p. 355–70. [Google Scholar]

5. Cui M, Han D, Wang J, Li K-C, Chang C-C. ARFV: an efficient shared data auditing scheme supporting revocation for fog-assisted vehicular ad-hoc networks. IEEE Transact Vehic Technol. 2020;69(12):15815–27. doi:10.1109/TVT.2020.3036631. [Google Scholar] [CrossRef]

6. Wang C, Chow SSM, Wang Q, Ren K, Lou W. Privacy-preserving public auditing for secure cloud storage. IEEE Transact Comput. 2013;62(2):362–75. doi:10.1109/TC.2011.245. [Google Scholar] [CrossRef]

7. Huang L, Zhou J, Zhang G, Zhang M. Certificateless public verification for data storage and sharing in the cloud. Chinese J Elect. 2020;29(4):639–47. doi:10.1049/cje.2020.05.007. [Google Scholar] [CrossRef]

8. Li R, Wang XA, Yang H, Niu K, Tang D, Yang X. Efficient certificateless public integrity auditing of cloud data with designated verifier for batch audit. J King Saud Univ-Comput Inf Sci. 2022;34(10, Part A):8079–89. doi:10.1016/j.jksuci.2022.07.020. [Google Scholar] [CrossRef]

9. Erway C, Küpçü A, Papamanthou C, Tamassia R. Dynamic provable data possession. ACM Trans Inf Syst Secur. 2015 Apr;17(4):1–29. doi:10.1145/2699909. [Google Scholar] [CrossRef]

10. Tian H, Chen Y, Chang CC, Jiang H, Huang Y, Chen Y, et al. Dynamic-hash-table based public auditing for secure cloud storage. IEEE Transact Serv Comput. 2017;10(5):701–14. doi:10.1109/TSC.2015.2512589. [Google Scholar] [CrossRef]

11. Yuan Y, Zhang J, Xu W. Dynamic multiple-replica provable data possession in cloud storage system. IEEE Access. 2020;8:120778–84. doi:10.1109/ACCESS.2020.3006278. [Google Scholar] [CrossRef]

12. Bai Y, Zhou Z, Luo X, Wang X, Liu F, Xu Y. A cloud data integrity verification scheme based on blockchain. In: 2021 IEEE SmartWorld, Ubiquitous Intelligence & Computing, Advanced & Trusted Computing, Scalable Computing & Communications, Internet of People and Smart City Innovation (SmartWorld/SCALCOM/UIC/ATC/IOP/SCI); Atlanta, GA, USA; 2021. p. 357–63. doi:10.1109/SWC50871.2021.00055. [Google Scholar] [CrossRef]

13. Zhou Z, Luo X, Bai Y, Wang X, Liu F, Liu G, et al. A scalable blockchain-based integrity verification scheme. Wirel Commun Mob Comput. 2022;2022(1):7830508. doi:10.1155/2022/7830508. [Google Scholar] [CrossRef]

14. Zhou H, Shen W, Liu J. Certificate-based multi-copy cloud storage auditing supporting data dynamics. Comput Secur. 2025;148(3):104096. doi:10.1016/j.cose.2024.104096. [Google Scholar] [CrossRef]

15. Yu Y, Au MH, Ateniese G, Huang X, Susilo W, Dai Y, et al. Identity-based remote data integrity checking with perfect data privacy preserving for cloud storage. IEEE Transact Inform Foren Secur. 2017;12(4):767–78. doi:10.1109/TIFS.2016.2615853. [Google Scholar] [CrossRef]

16. Shah MA, Swaminathan R, Baker M. Privacy-preserving audit and extraction of digital contents. Cryptology ePrint Archive. 2008; [cited 2025 Jan 20]. Available from: https://eprint.iacr.org/2008/186. [Google Scholar]

17. Shacham H, Waters B. Compact proofs of retrievability. J Cryptol. 2013;26(3):442–83. doi:10.1007/s00145-012-9129-2. [Google Scholar] [CrossRef]

18. Yan H, Li J, Zhang Y. Remote data checking with a designated verifier in cloud storage. IEEE Syst J. 2020;14(2):1788–97. doi:10.1109/JSYST.2019.2918022. [Google Scholar] [CrossRef]

19. Yu J, Ren K, Wang C, Varadharajan V. Enabling cloud storage auditing with key-exposure resistance. IEEE Transact Inform Foren Secur. 2015;10(6):1167–79. doi:10.1109/TIFS.2015.2400425. [Google Scholar] [CrossRef]

20. Yang K, Jia X. An efficient and secure dynamic auditing protocol for data storage in cloud computing. IEEE Transact Paral Distrib Syst. 2013;24(9):1717–26. doi:10.1109/TPDS.2012.278. [Google Scholar] [CrossRef]

21. Shen J, Shen J, Chen X, Huang X, Susilo W. An efficient public auditing protocol with novel dynamic structure for cloud data. IEEE Transact Inform Forens Secur. 2017;12(10):2402–15. doi:10.1109/TIFS.2017.2705620. [Google Scholar] [CrossRef]

22. Wang H, Wu Q, Qin B, Domingo-Ferrer J. Identity-based remote data possession checking in public clouds. IET Information Security. 2014;8(2):114–21. doi:10.1049/iet-ifs.2012.0271. [Google Scholar] [CrossRef]

23. Wang H, He D, Tang S. Identity-based proxy-oriented data uploading and remote data integrity checking in public cloud. IEEE Transact Inform Forens Secur. 2016;11(6):1165–76. doi:10.1109/TIFS.2016.2520886. [Google Scholar] [CrossRef]

24. Wang F, Xu L, Choo KKR, Zhang Y, Wang H, Li J. Lightweight certificate-based public/private auditing scheme based on bilinear pairing for cloud storage. IEEE Access. 2020;8:2258–71. doi:10.1109/ACCESS.2019.2960853. [Google Scholar] [CrossRef]

25. Shen J, Zeng P, Choo KKR, Li C. A certificateless provable data possession scheme for cloud-based EHRs. IEEE Transact Inform Forens Secur. 2023;18:1156–68. doi:10.1109/TIFS.2023.3236451. [Google Scholar] [CrossRef]