A DFE²-SPCE Method for Multiscale Parametric Analysis of Heterogenous Piezoelectric Materials and Structures

1  Introduction

Advanced industrial applications requiring multifunctional structures or components have prompted the emergence of smart materials. These materials exhibit remarkable mechanical responses to various external stimuli, including fluctuations in temperature, variations in pressure, electrical fields, and magnetic influences [1–4]. Piezoelectric ceramics, as a type of smart material, are widely used in the fabrication of transducers, actuators, and sensors. These components serve various purposes, including health monitoring and the control of structural deformations [5–7]. Accurately and efficiently evaluating the interdependent electrical and mechanical properties of piezoelectric ceramics and their associated structures is essential for guiding their design, optimization, and fabrication in various engineering applications. However, this task is challenging due to the complex interplay of material parameters—such as elasticity, piezoelectric behavior, and dielectric properties—along with geometric factors, all of which significantly influence the mechanical performance of macroscopic piezoelectric systems [8–10]. Traditionally, empirical tests combined with theoretical analyses have been used to evaluate piezoelectric ceramics’ electromechanical properties, particularly under relatively uncomplicated loading conditions [11–13]. Nevertheless, these techniques fall short of accurately capturing the coupled electromechanical responses under complex loading conditions typical of industrial applications. This limitation mainly arises from the constraints imposed by experimental methodologies and theoretical assumptions [14]. Aiming to tackle these obstacles, growing research attention has been dedicated to finite element (FE) simulations facilitated by widely used commercial codes like ABAQUS [15]. To simulate the behavior of piezoelectric ceramics or structures using the finite element method (FEM) [16–20], it is essential to develop a FE model that captures all relevant features and patterns inherent to the material or structural system [21]. For piezoelectric ceramics or structural systems with multiscale characteristics and micro-patterns, many finite elements are required to build a comprehensive FE model that can represent both microscopic and macroscopic features. However, the significant computational cost associated with such many finite elements makes direct FEM simulation of these multiscale piezoelectric ceramics and structures impractical [22–24]. Consequently, performing direct numerical simulations (DNS) for these multiscale systems becomes nearly an impossibility. Therefore, it proves crucial to develop precise and computationally efficient multilevel techniques enabling co-simulation of micro-scale and macro-scale responses in piezoelectric ceramics [25]. To address this need, Fang et al. [26] conducted an extensive investigation into various methodologies for analyzing ferroelectric and piezoelectric behaviors. Lv et al. [27] suggested a layered multiscale method using multiscale FEM to model the thermo-electro-mechanical coupled of smart materials with different piezoelectric microstructures. These methodologies were categorized into three classes: macroscopic, mesoscopic, and atomic-scale techniques. Jafari et al. [28] explored the representative volume element (RVE) to investigate the mechanical and electrical properties of nanocomposites containing piezoelectric nanotubes. Maruccio et al. [29] introduced the computational homogenization approach designed to characterize the nonlinear constitutive behavior observed in piezoelectric shells. Fu et al. [30] proposed a multiscale computational method that is very effective for heterogeneous piezoelectric ceramics geometrically nonlinear analysis. Recent studies have investigated meshless methods, such as the spectral element method (SEM), to reduce computational costs in dynamic analyses of piezoelectric materials [31,32].

As one of the aforementioned multiscale modeling methodologies, the finite element squared (FE2) technique was originally formulated by Feyel [33]. The FE2 methodology uses the Hill-Mandel homogenization principle to infer from a multiscale material’s or structural system’s micro-scale RVE its macro-scale properties [34–36]. In the FE2 method, The micro-scale RVE and the macro-scale FE model form the two iterative loops. The macro-scale model’s kinematic field is transferred into the corresponding micro-scale RVEs for simulations. The effective mechanical properties are then obtained by homogenizing the simulation results, and they are then returned to the macro-scale model [37–40]. This method facilitates the simultaneous simulation of multiscale materials and structures’ macro- and micro-scale behaviors. However, it presents challenges in numerical implementation due to the need for control scripts to facilitate data exchange between the macro- and micro-scale models. Moreover, these control scripts are often problem-specific, limiting their transferability to different applications.

Tan [41] introduced the DFE2 method, which offers a streamlined approach for integrating two-scale FE computations into a single computation. This is accomplished by applying multiple points constraints (MPCs), which are obtained from the Hill-Mandel condition and the energy equilibrium equation of FEM. The use of MPCs, commonly found in various commercial FE software, significantly enhances the accessibility and straightforwardness of implementing the DFE2 method [42]. Consequently, this method has found widespread application in addressing a diverse range of multiscale problems. In one example, Zhi et al. [43] used the DFE2 method to analyze the heterogeneous materials’ dynamic and thermodynamic responses. The DFE2 method eliminates the need for exhaustive macro-to-micro iterative loops, reducing computational costs compared to DNS while maintaining predictive accuracy for heterogeneous material behaviors.

Most studies on the numerical analysis of piezoelectric problems primarily focus on the deterministic parameters of the materials under examination [44,45]. However, in real-world engineering scenarios, highly uncertain input parameters are often encountered, and the limitations of parameter estimation in models can lead to flawed decisions when addressing certain engineering challenges. Uncertainty quantification in engineering aims to derive the statistical properties of the system’s response by evaluating the uncertainty associated with the input parameters. Various methods, including Monte Carlo simulations (MCs) [46–50], stochastic spectral methods [51,52], and perturbation techniques [53], are commonly employed to analyze uncertainty. These approaches typically assess the statistical characteristics, such as the mean and standard deviation, of the system’s response. With the growing demands for modeling, the complexity of the simulation model increases, leading to longer computation times for uncertainty quantification and reduced efficiency. This presents challenges for traditional MCs, which require a large number of samples and model evaluations to address complex problems [54]. To overcome these challenges, surrogate models provide an alternative to complex analytical or computational models. By using basic polynomial functions to establish input-output relationships, surrogate models enable the generation of necessary model evaluations at a reasonable computational cost, overcoming the limitations of conventional approaches [55,56].

Polynomial chaos expansions (PCE) [57] are effective for uncertainty quantification and reliability analysis, but their complexity grows exponentially with system dimensionality or polynomial degree, resulting in the “curse of dimensionality.” To address this, SPCE reduces the number of terms by exploiting sparsity, maintaining accuracy while improving computational efficiency for high-dimensional problems. SPCE techniques use various algorithms to identify and retain only the most significant terms in the polynomial expansion. The SPCE model alleviates the computational burden associated with traditional MCs by reducing the required sample size while preserving accuracy. Methods such as least angle regression (LAR) [58], stepwise regression [59], and Bayesian approaches [60] have been proposed to construct sparse expansions efficiently. These methods can be adaptive, as they iteratively select important terms and improve computational efficiency without sacrificing accuracy. In addition, greedy algorithms [61] and diffeomorphic modulation under observable response-preserving homotopy (D-MORPH) regression [62] have been explored to optimize the selection of basis terms. Recent advancements in SPCE have extended its application to stochastic finite element analysis [63], sensitivity analysis [60], and reliability assessment [64]. These approaches have demonstrated that SPCE can significantly reduce computational costs while maintaining robust performance across a wide range of engineering applications. The efficacy of SPCE has been benchmarked in several studies [65], highlighting its potential for handling complex systems with uncertainty.

Despite significant advancements in multiscale modeling, existing methods for the analysis of piezoelectric materials face critical limitations. DNS requires immense computational resources, making them impractical for large-scale or complex systems. Current approaches struggle to efficiently account for uncertainties in piezoelectric and elastic properties, which are critical for practical engineering applications. Additionally, many existing models fail to accurately represent coupled electromechanical behaviors in heterogeneous multiscale systems. To address these deficiencies, this study proposes an integrated framework that combines the computational efficiency of the DFE2 method with the flexibility of SPCE. This approach ensures significant reductions in computational cost, the accurate modeling of stochastic parameter variations, and an enhanced capability to represent electromechanical coupling in multiscale piezoelectric materials. As proposed by Li et al. [66], the piezoelectric DFE2 method enables accurate and efficient multiscale simulations while accounting for stochastic disturbances in piezoelectric parameters. When integrated with the SPCE method, it significantly improves computational efficiency and accuracy, providing a robust solution for uncertainty analysis in multiscale piezoelectric systems.

2  Brief Introduction of the Piezoelectric DFE2 Method

Li et al. [66] successfully extended the theory of the DFE2 method to piezoelectric problems and is briefly introduced as follows.

The electromechanical coupling of the piezoelectric material and structure with random input parameters can be described as:

(1)

and

(2)

where the stress resulting from mechanical deformation is denoted as for the strain tensor , and for the electric gradient tensor . Similarly, the gradient tensor and the electric displacement vectors are represented as and , respectively. The strain tensor , the gradient tensor , the variable represents displacement and corresponds to electric potential.

Consider a multiscale piezoelectric material or structure, such as the fiber-reinforced composite in Fig. 1. The density of electric enthalpy evaluated can be formulated as:

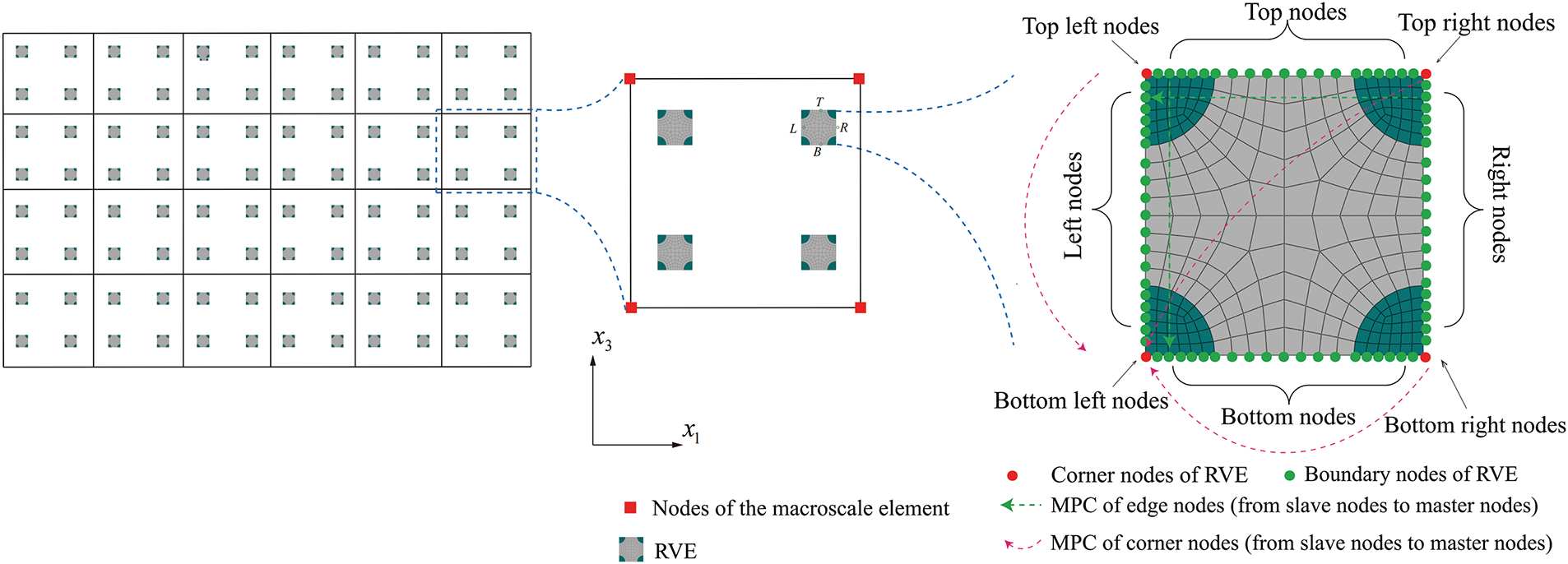
Figure 1: The application of periodic boundary conditions through the MPC method entails integrating a single macroscale FE with RVEs positioned at the Gauss quadrature points [66]

(3)

Energy equilibrium between the macro-scale and meso-scale requires that the macro-scale electric enthalpy equals the volumetric mean of the electric enthalpy evaluated at the meso-scale, i.e.,

(4)

where the symbol represents volume-averaged quantities and denotes the volume of the RVE (A small-scale material sample assumed to statistically represent the entire heterogeneous material in multiscale simulations.).

To satisfy the energy equilibrium and kinematic constraints between the macro- and meso-scales, one needs to prescribe periodic boundary conditions to the meso-scale RVEs as follows (see Fig. 1 for reference):

(5)

where refer to the upper, left, right, and lower edges of the RVE, respectively. Periodic boundary conditions were enforced by linking corresponding slave and master nodes along opposite edges of the RVE using MPCs available in ABAQUS. This ensures the continuity of the electric potential and the displacement across the RVE boundaries.

Enforcing the Hill-Mandel condition also requires scaling of the meso-scale RVEs such that:

(6)

which indicates that the volume of RVE at the Gaussian point needs to be scaled to . This can be easily done by scaling the RVE’s thickness for 2D cases. More details about the piezoelectric DFE2 method refer to [66].

From the theory reviewed above, it can be seen that the meso-scale material properties such as elastic constants , piezoelectric constants and dielectric constants dominates the macro-scale piezoelectric responses, while this study was focused on the effect of and .

3  Parametric Analysis via a Combination of the DFE2 and SPCE Methods

To conduct a parametric analysis of multiscale piezoelectric materials and structures, a large number (thousands or more) of data points is required to account for the randomness (or uncertainties) in various properties. Performing such many simulations is impractical, even though the DFE2 method significantly reduces computational cost. To address this issue, the DFE2 method was combined with the SPCE method.

As a widely used method for stochastic finite element analysis, the SPCE method constructs a surrogate model to facilitate uncertainty quantification analyses using a sparse representation of polynomial basis functions that are orthogonal with respect to the distribution of the random vector. To implement the SPCE method for the parametric study of the effect of meso-scale material properties on the macro-scale response of heterogeneous piezoelectric materials and structures, one can assume that the meso-scale material properties vary randomly within a defined range for the parametric analysis. In this work, only the meso-scale elastic constants and piezoelectric constants are considered, and thus they are assumed to be random and denoted as $ if the multiscale piezoelectric material or structure consists of meso-scale parental materials where . According to the SPCE method, the response (such as macro-scale electric potential, electric potential gradient, stress, or logarithmic strain components) of the multiscale piezoelectric material or structure can be expressed using a sparse set of orthogonal polynomials, as shown below:

(7)

where represents multivariate orthogonal polynomials, and denotes the corresponding coefficient for each polynomial. The index set contains all non-zero or significant polynomial chaos terms, emphasizing the sparsity of the expansion. In SPCE, a sparse subset of these polynomials is used, significantly reducing the computational complexity while maintaining accuracy in representing the response . The polynomial order determines the highest-degree terms retained in the expansion. In this study, we chose to explore the trade-off between computational cost and fitting precision. Lower orders (e.g., ) provide a coarse approximation with minimal computational effort, while higher orders (e.g., ) improve the fitting of nonlinear responses but increase computational demand. Stepwise regression was selected as the primary method for feature selection in the SPCE model due to its balance between computational efficiency and accuracy. This method iteratively adds or removes predictors based on predefined criteria (e.g., values), ensuring that the final model retains only the most relevant terms while avoiding overfitting. In comparison to alternative sparse modeling techniques, such as LAR or Bayesian methods:

1.    LAR: While effective for high-dimensional data, LAR tends to be computationally intensive for large-scale nonlinear problems and may overestimate the importance of collinear variables;

2.    Bayesian methods: These provide probabilistic interpretations and can handle uncertainty better, but they often require prior knowledge, are computationally expensive, and may lack scalability in high-dimensional settings.

The multivariate orthogonal polynomials can be obtained using the cumulative product of univariate orthogonal polynomials:

(8)

where denotes univariate polynomials of the random input parameters in . In SPCE, a sparse subset of these multivariate orthogonal polynomials is chosen based on their significance, thereby reducing computational complexity while maintaining the accuracy of the response representation.

Several sample points are needed to determine the coefficients . This is done by conducting a series of piezoelectric DFE2 simulations whereby the parameters and responses are denoted by and , respectively. Every DFE2 simulation results in a sample point , and thus sample points can be obtained. As detailed in [67], coefficients can then be calculated as:

(9)

where is a vector consisting of all coefficients and is a vector consisting of the responses of sample points.

(10)

(11)

In this work, the random parameters, i.e., , are assumed to follow a Gaussian distribution which can be described using the following probability density function (PDF):

(12)

(13)

where is the random variable, is the mean (expected value), is the standard deviation, and is the variance. COV stands for coefficient of variation, a relative measure of data dispersion.

In SPCE, Gaussian distribution corresponds to Hermite orthogonal polynomials . Hence,

(14)

where represents the floor function, and denotes random parameters.

In SPCE, a sparse subset of these Hermite polynomials is chosen based on their significance, thereby reducing computational complexity while maintaining the accuracy of the response representation.

The Hermite orthogonal polynomials can also be expressed using the following recurrence relation, with the first five Hermite orthogonal polynomials displayed in Fig. 2:

(15)

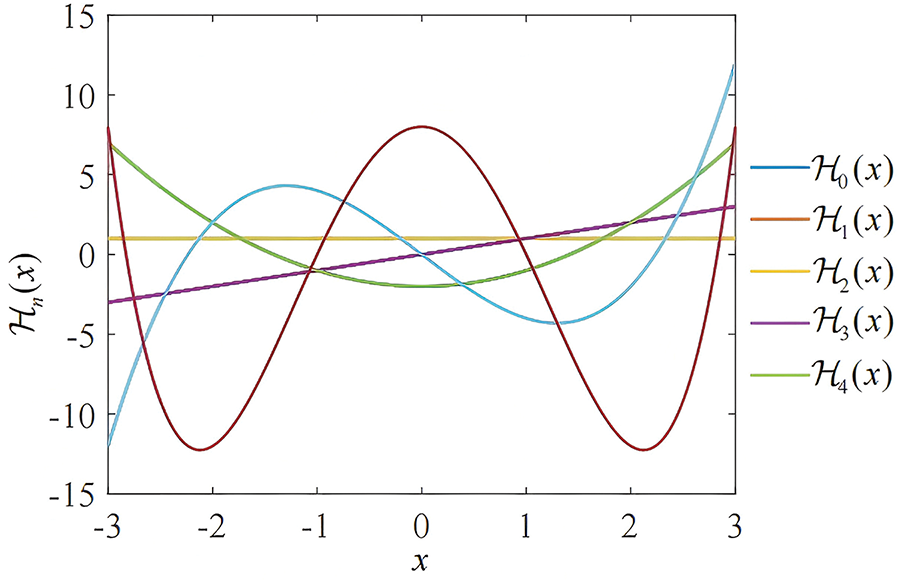
Figure 2: The first five polynomials of Hermite orthogonal polynomials

In SPCE, a sparse subset of these Hermite polynomials is chosen based on their significance, thereby reducing computational complexity while maintaining the accuracy of the response representation.

To evaluate the accuracy of the SPCE model established above, a parameter, namely the coefficient of variation (CV), is typically defined using the relative root mean square deviation (RRMSE):

(16)

where denotes the response in the sample points generated via the DFE2 simulations, and represents the response predicted by the SPCE model.

The multiscale parametric analysis, namely the effect of meso-scale material properties on macro-scale behavior, can be summarized in the following steps:

1.    Generate a series of random values for meso-scale properties for the multiscale piezoelectric material or structure;

2.    Obtain the corresponding macro-scale responses using DFE2 simulations, and thus get sample points ;

3.    Use Eqs. (9) to (15) to establish the SPCE model that can accurately approximate the relationship between the meso-scale properties and macro-scale responses ;

4.    Analyze the effect of the meso-scale properties on the macro-scale responses based on the SPCE model.

Hence, this combination of the DFE2 and SPCE methods enables the analysis of the effect of meso-scale parameters on the macro-scale responses of multiscale materials and structures using a limited number of DFE2 simulation results. Furthermore, the expected value and standard deviation of the response predicted by the SPCE model are crucial for estimating the performance of structures, accounting for the randomness of meso-scale parameters. The SPCE model, which utilizes PCE to approximate system responses, requires feature selection methods capable of efficiently handling nonlinear dependencies while preserving model interpretability. Stepwise regression satisfies these requirements by iteratively selecting the most significant terms, enabling it to scale effectively to higher-order polynomial terms in SPCE. Its computational simplicity and widespread availability in statistical software make it a practical choice for engineering applications, particularly when real-time model updates or limited computational resources are factors to consider.

4  Accuracy and Efficiency of the DFE2 Method

Uncertainty analysis using SPCE requires a series of data, which is generated through multiscale analysis based on the DFE2 method in this work. Therefore, it is essential to first validate the accuracy and efficiency of the DFE2 method. To achieve this, a complex piezoelectric composite was modeled using the DFE2 method and DNS. The geometric nonlinearity and piezoelectric plane strain elements [68] were employed for all numerical simulations. Details of the numerical implementation can be found in [66].

A composite piezoelectric panel with a thickness of , shaped like a rhombus with its base parallel to the x-axis, was simulated using DFE analysis. This panel comprises 120 smaller rhombus-shaped composite panels aligned horizontally. A tensile displacement load was applied to the right edge, while the left edge was constrained to have zero horizontal displacement. The bottom edge was set to zero electric potential, and a vertical displacement constraint was applied to the top edge, as displayed in Fig. 3a. Fig. 3b provides a magnified view of a selected region from Fig. 3a, showing the periodic arrangement of the composite elements, which is further enlarged in Fig. 3c to depict a detailed model with a 0.1 mm diameter central circular hole within a 0.2 mm rhombus. Subsequently, an RVE was established at each macro-element integration point. The RVE comprises a piezoelectric composite model featuring a central circular hole with a diameter of 0.1 mm and an enclosing rhombus with a side length of 0.2 mm, as displayed in Fig. 3d–f. The thickness of all RVEs was adjusted in accordance with Eq. (6). Periodic boundary conditions were applied to the edge nodes and of the RVE (see Fig. 3f), where the node corresponds to , and corresponds to . Further details are available in Li et al.’s paper [66].

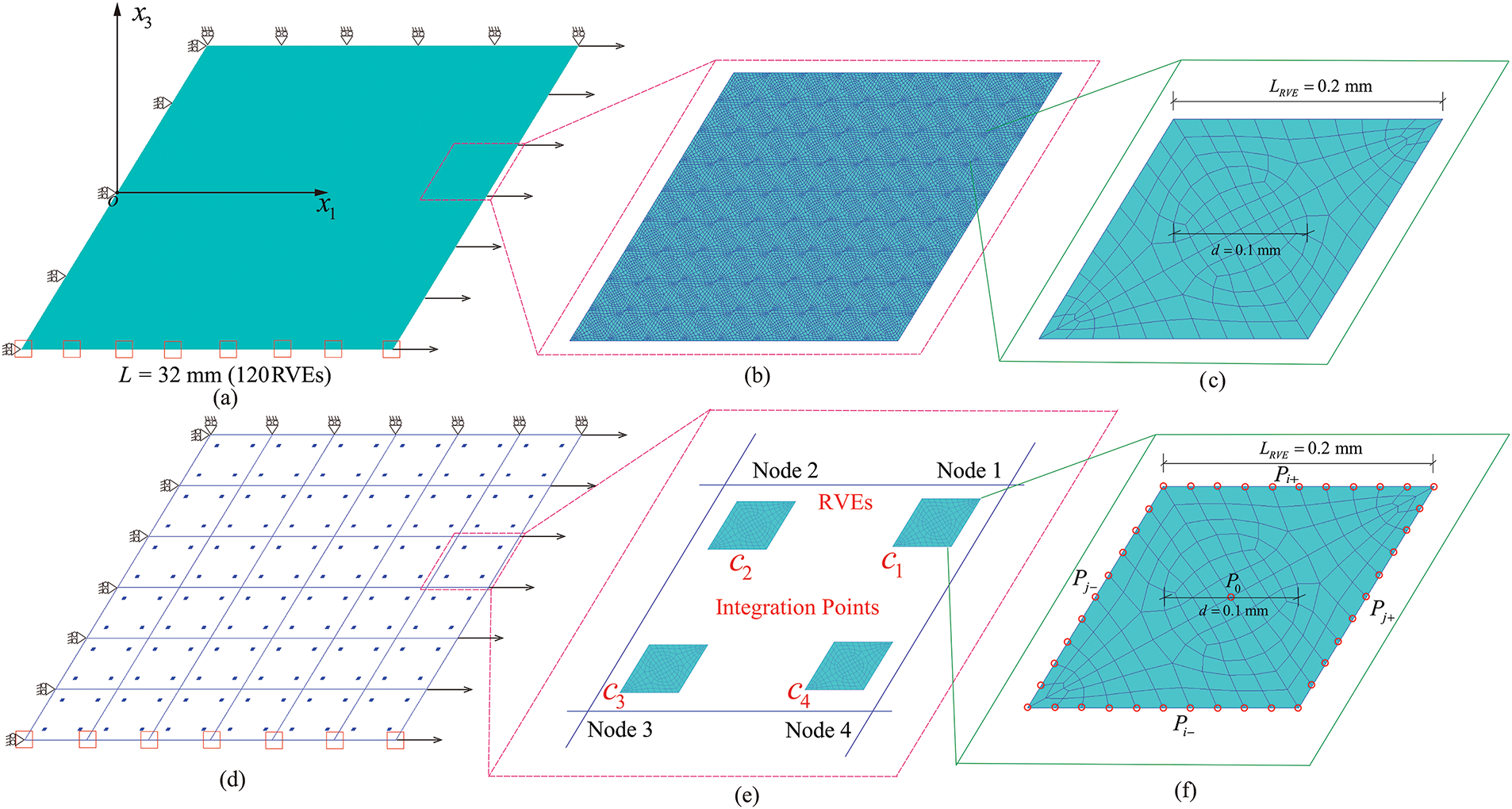
Figure 3: The composite piezoelectric panel is shown schematically: (a) boundary conditions of composite piezoelectric plates, (b) a detailed local enlargement of the DNS is shown, (c) the internal mesh division of the DNS is depicted, (d) the corresponding DFE2 model of the composite piezoelectric panel consists of macro-scale elements, with each RVE’s thickness scaled by a factor of 25 as per Eq. (6), (e) the RVEs located at the Gauss integration points are illustrated, (f) the periodic boundary conditions (PBCs) of the RVE are outlined

The panel comprises PZT-5H as the matrix and PZT-8 as the fiber phase, as illustrated in Fig. 4a. The material properties of these phases are provided in Table 1. The panel’s left edge was fixed horizontally, while a displacement of 1.2 mm was applied to the right edge. The lower edge’s electric potential is zero, and the top edge remains vertically fixed. Both the meso-scale RVE and the macro-scale panel were discretized using CPE4E elements (see Fig. 4b). The boundary conditions described in Eq. (5) were applied to the multiscale model, and Eq. (6) was employed to compute the RVE thickness, , for the CPE4E elements.

Figure 4: The effect of mesh size at macro-and meso-scales on the simulation outcomes for the composite piezoelectric panel is investigated, (a) composite RVE of the PZT-5H matrix with PZT-8 inclusion, (b) DFE2 model with varying mesh sizes, (c) the modeling results for meso-scale RVEs with elements of different sizes, (d) the modeling results for macro-scale RVEs with elements of different sizes

where the dimensions of the macro-element, denoted as , , and , represent the length, width, and thickness, respectively. Additionally, and indicate the length and width of the RVE. The piezoelectric composites were divided into elements along the length and width directions, as illustrated in Fig. 4d. Consequently, and are derived.

The DFE2 simulations were performed using various meso-element sizes: = 0.043, 0.02, and 0.013 mm (as illustrated in Fig. 4b). These simulations aimed to investigate the impact of meso-element size on the simulation outcomes. The electric potential-displacement curves in Fig. 4c indicate negligible variation when the meso-element size is reduced below 0.02 mm. Additionally, simulations with varying numbers of macro-elements were conducted to examine the effect of macro-element size on the DFE2 results (i.e., = 3 = 2, = 6 = 4, and = 10 = 6). As the number of macro-elements increased to , the results from DFE2 simulations (see Fig. 4d) converged with those obtained from DNS. To balance computational accuracy and efficiency, subsequent DFE2 simulations adopted a macro-element mesh. RVEs were discretized using an element size of = 0.02 mm at the meso-scale (as illustrated in Fig. 4b). The same meso-element size ( = 0.02 mm) was also used for meshing the DNS model.

The electric potential and displacement outlines of certain unit cells at points F and E, as found by both the DNS and DFE2 methods, are shown in Fig. 5a,b. The results indicate favorable agreement between DNS and DFE2 simulations, demonstrating the capability of the proposed DFE2 approach to accurately capture the coupled electromechanical response of piezoelectric composites. Additionally, the RVE’s electric potential and displacement outlines at points F and E (illustrated in Fig. 5) derived from DNS and DFE2 methods show a maximum discrepancy of 2.2%. This minor difference can be attributed to slight variations in element size and aspect ratio between the macro- and meso-scale models. Despite these discrepancies, the errors remain within acceptable bounds for most engineering applications, confirming that the DFE2 method delivers both accurate and computationally efficient predictions.

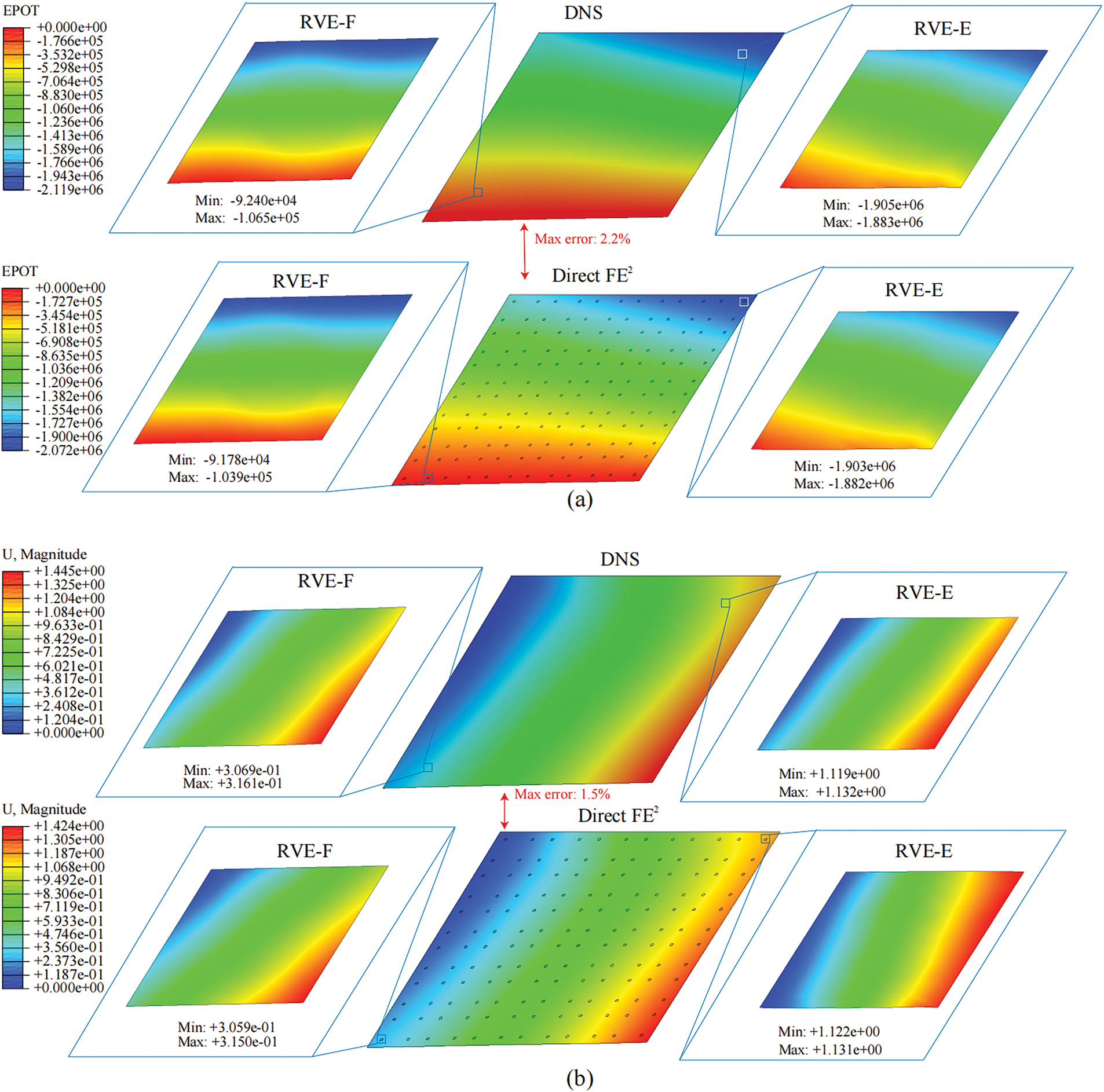
Figure 5: The displacement magnitude and electric potential distribution at points F and E for the chosen cells in the DFE2 and DNS models are shown: (a) distribution of displacement magnitude, (b) distribution of electric potential

Both the DFE2 simulations and DNS were performed on the same computer, equipped with an Intel Core i7-8700 CPU and 64 GB of RAM. For the composite piezoelectric panel, the computational times were 16 s for the DFE2 method and 385 s for DNS. The significant reduction in computational time, combined with the favorable accuracy of the DFE2 method, establishes it as a promising tool for generating a sufficiently large dataset. This capability facilitates large-scale uncertainty quantification and optimization using the SPCE method. To further validate the accuracy and efficiency of the DFE2 method, we reference the findings from [66], which applied the DFE2 method to multiscale material and structural analysis. The DFE2 and DNS approaches differed by less than 3% at most. Furthermore, the efficiency in the computation of the DFE2 method was shown to be approximately 10 times higher than that of DNS, consistent with the results in this study. This comparison provides additional context and supports the robustness of our results.

5  Multiscale Parametric Analysis: Results and Discussion

In this section, the influence of meso-scale parameters on the macro-scale electromechanical responses of the composite piezoelectric panel is analyzed using the combined DFE2 and SPCE methods, as outlined in Section 4. Both univariate and bivariate analyses are performed. For the univariate analysis, one of the two parameters in was treated as a random variable, while all other parameters were assigned fixed values as listed in Table 1. A Gaussian distribution was used to generate 100 random values for the selected parameter. Subsequently, 100 DFE2 simulations were performed to evaluate the piezoelectric responses. The random meso-scale parameters considered were . In the bivariate analysis, the same parameters were treated as random variables, with a COV set to 0.2. The model’s elastic constants () and piezoelectric parameters () were varied 50 times each, resulting in a total of 2500 parameter combinations. Subsequently, 2500 DFE2 simulations were performed to compute the piezoelectric responses, following the same setup detailed in Section 5.

The macro-scale responses of interest in this study include the electric potential and displacement magnitude at the selected points E (36.54, 7.65) and F (6.89, −9.14) in Fig. 5, i.e., . SPCE models were constructed using the sample points obtained through the methods introduced in Section 4. For the univariate analysis, two types of SPCE models, i.e., and , were established, while for the bivariate analysis, only one type of SPCE model, i.e., , was needed. The results of the univariate and bivariate analyses are discussed in the following sections.

5.1 Univariate Analysis

Fig. 6a,b illustrates the displacement magnitude of the composite piezoelectric panel, as predicted by the univariate SPCE models and . It is observed that as the elastic constant and piezoelectric constant increase, the corresponding displacement exhibits a nonlinear growth trend. Additionally, the polynomial order has a significant impact on the fitting precision. When , the SPCE model captures the general trend but fails to accurately represent localized nonlinearities. When , the SPCE model accurately captures the displacement response trend with minimal error, indicating that this order provides an optimal balance between accuracy and computational efficiency. When , the highest accuracy is achieved, especially for strongly nonlinear responses, though at the expense of increased computational effort. This trend indicates that higher-order SPCE models provide superior fitting precision, particularly in capturing the nonlinear responses of complex materials and accurately modeling multiphysics coupling problems.

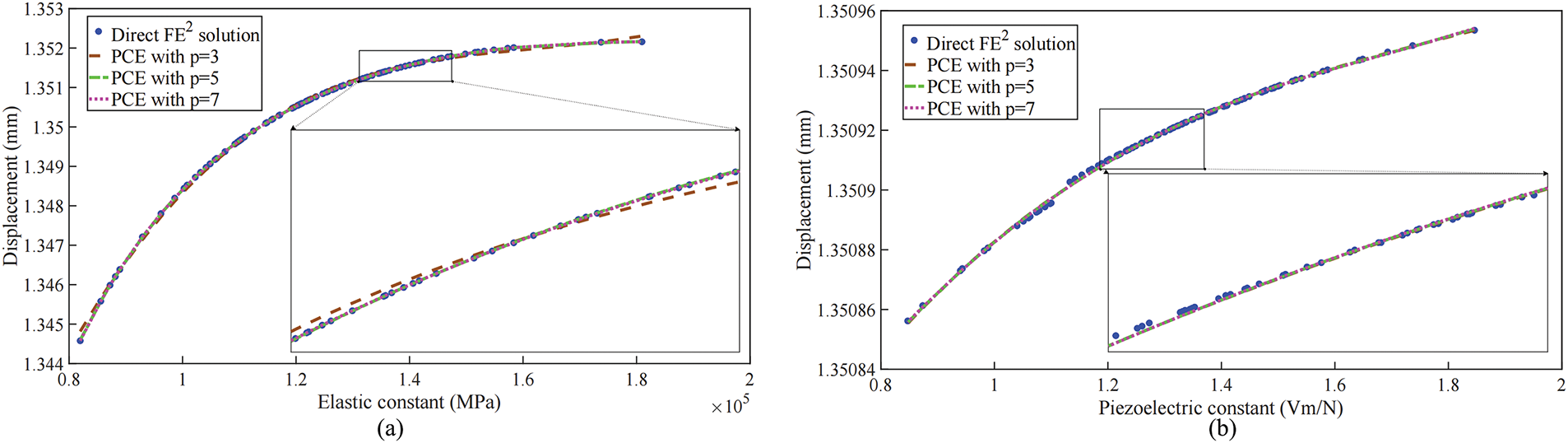
Figure 6: Results obtained from the univariate SPCE model and for the composite piezoelectric panel (dots represent sample points obtained from DFE2 simulations, while dashed lines indicate the results from SPCE models using different orders ): (a) displacement magnitude corresponding to variations in elastic constants, (b) displacement magnitude corresponding to variations in piezoelectric constants

Fig. 7a,b depicts the influence of the meso-scale elastic constant and the piezoelectric constant on the macroscopic electric potential response . Fig. 7a reveals a clear linear relationship between the elastic constant and the electric potential , which can be attributed to the assumption of linear elasticity in the meso-scale material. As increases, a decreasing trend in the electric potential is evident, due to the interaction between the electric potential and the elastic strain energy. Conversely, Fig. 7b demonstrates an increasing trend in the electric potential with rising , attributed to the coupling between the electric potential , the electric field, and polarization effects. The variations in are more pronounced with changes in the piezoelectric constant than in the elastic constant. This is primarily because the piezoelectric effect directly influences the charge distribution and polarization response, rendering the electric potential more sensitive to these changes.

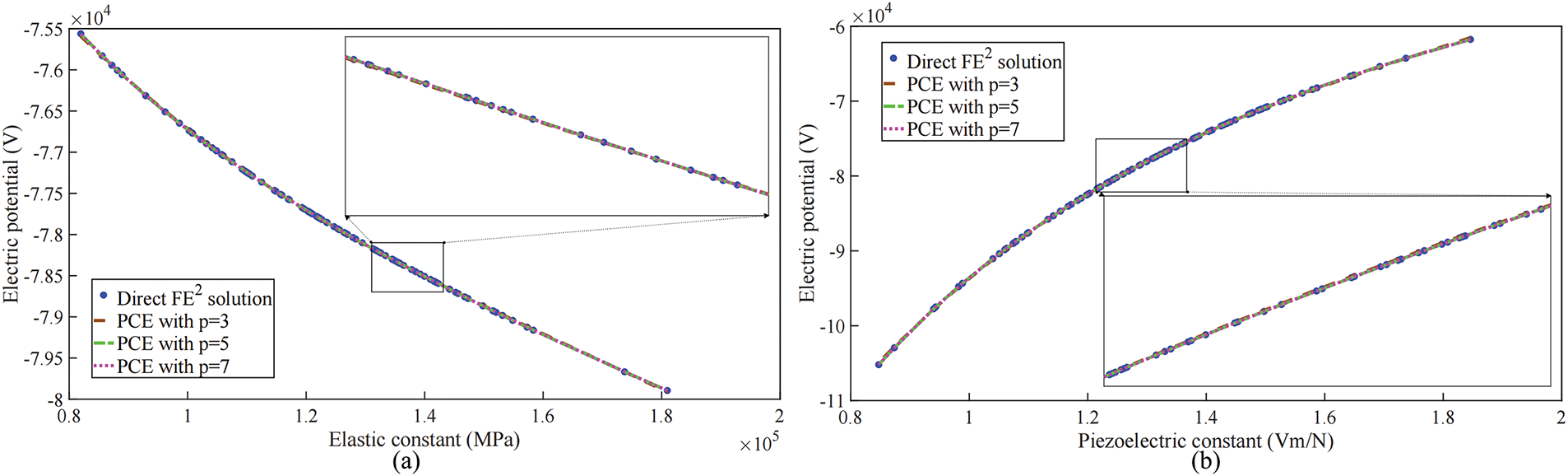
Figure 7: Results obtained from the univariate SPCE model and for the composite piezoelectric panel: (a) electric potential corresponding to variations in elastic constants, (b) electric potential corresponding to variations in piezoelectric constants

5.2 Bivariate Analysis

The bivariate SPCE model , with the order , corresponds to two macro-scale responses (i.e., and ). Numerical validation confirms that the model accurately captures the complex nonlinear relationships in predicting these two macro-scale responses, showcasing strong accuracy and stability [61].

Fig. 8a,b illustrates the coupled effects of the mesoscale elastic constant and the piezoelectric constant on two macro-scale responses: displacement and electric potential . The results indicate that both displacement and electric potential are predominantly influenced by the piezoelectric constant, with minimal contribution from the elastic constant. This phenomenon can likely be attributed to the tensile load applied to the panel, where variations in displacement are primarily governed by the piezoelectric effect, while changes in the elastic constant have a limited impact on both displacement and electric potential.

Figure 8: Results obtained from the bivariate SPCE model for the composite piezoelectric panel (dots represent sample points obtained from DFE2 simulations, while surfaces represent the results from the SPCE model): (a) displacement magnitude corresponding to variations in both elastic and piezoelectric constants, (b) electric potential corresponding to variations in both elastic and piezoelectric constants

6  Conclusion

A novel framework for multiscale parametric analysis of heterogeneous piezoelectric materials and structures, incorporating random meso-scale properties, is proposed. This approach employs the piezoelectric DFE2 method to facilitate concurrent multiscale simulations. The simulation data are subsequently utilized to construct univariate and bivariate SPCE models for parametric analysis across different scales.

To validate the methodology, a composite piezoelectric panel was analyzed as a case study, treating meso-scale elastic constants and piezoelectric constants as random variables. The SPCE models effectively captured the influence of these meso-scale parameters on the macroscopic responses (displacement) and (electric charge) of the panel. The results demonstrate a favorable balance between computational efficiency, scalability, and accuracy, underscoring the framework’s potential for optimizing piezoelectric energy harvesting devices. This is particularly significant in scenarios where computational efficiency and precision are critical for evaluating performance under varying operational conditions.

Acknowledgement: I would like to express my sincere gratitude to Dr. Shuai Li and Dr. Pei Li for their invaluable assistance and support throughout the process of completing this thesis. Their guidance, insightful feedback, and encouragement were instrumental in shaping this work. I greatly appreciate their willingness to share their knowledge and expertise, which significantly contributed to the success of this research. Thank you both for your continuous support and dedication.

Funding Statement: This work was supported by the Zhumadian 2023 Major Science and Technology Special Project (Grant No. ZMDSZDZX2023002) and the Postgraduate Education Reform and Quality Improvement Project of Henan Province (Grant No. YJS2023JD52).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Xiaohui Yuan, Qingxiang Pei; data collection: Fan Li; analysis and interpretation of results: Xiaohui Yuan, Haojie Lian, Qingxiang Pei; draft manuscript preparation: Fan Li, Ziheng Fei. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, X Yuan, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Aabid A, Raheman MA, Ibrahim YE, Anjum A, Hrairi M, Parveez B, et al. A systematic review of piezoelectric materials and energy harvesters for industrial applications. Sensors. 2021;21(12):4145. doi:10.3390/s21124145. [Google Scholar] [PubMed] [CrossRef]

2. Abuzaid A, Hrairi M, Shaik Dawood M. Survey of active structural control and repair using piezoelectric patches. Actuators. 2015;4(2):77–98. doi:10.3390/act4020077. [Google Scholar] [CrossRef]

3. He D, Li W, Vaziri V, Aphale SS. Thermo-electro-mechanical vibration analysis for piezoelectric plates under two-parameter elastic foundation with general boundary conditions. Int J Eng Sci. 2024;201(3):104057. doi:10.1016/j.ijengsci.2024.104057. [Google Scholar] [CrossRef]

4. He D, Wang Q, Zhong R, Qin B. A unified analysis model of FGM double-layered submarine type coupled structure with spectral geometry method. Ocean Eng. 2023;267:113213. doi:10.1016/j.oceaneng.2022.113213. [Google Scholar] [CrossRef]

5. Hooper TE, Roscow JI, Mathieson A, Khanbareh H, Goetzee-Barral AJ, Bell AJ. High voltage coefficient piezoelectric materials and their applications. J Eur Ceram Soc. 2021;41(13):6115–29. doi:10.1016/j.jeurceramsoc.2021.06.022. [Google Scholar] [CrossRef]

6. Watson BHIII, Brova MJ, Fanton M, Meyer RJJr, Messing GL. Textured Mn-doped PIN-PMN-PT ceramics: harnessing intrinsic piezoelectricity for high-power transducer applications. J Eur Ceram Soc. 2021;41(2):1270–9. doi:10.1016/j.jeurceramsoc.2020.07.071. [Google Scholar] [CrossRef]

7. Micheal A, Bahei-El-Din YA. Implementation of multiscale mechanisms in finite element analysis of active composite structures. J Compos Mater. 2022;56(13):2129–44. doi:10.1177/00219983221082492. [Google Scholar] [CrossRef]

8. Lv N, Zhong C, Wang L. Bending vibration characteristics of the piezoelectric composite double laminated vibrator. Ceram Int. 2021;47(22):31259–67. doi:10.1016/j.ceramint.2021.07.302. [Google Scholar] [CrossRef]

9. Liu Z, Bian P-L, Qu Y, Huang W, Chen L, Chen J, et al. A Galerkin approach for analysing coupling effects in the piezoelectric semiconducting beams. Eur J Mech A-Solid. 2024;103(6):105145. doi:10.1016/j.euromechsol.2023.105145. [Google Scholar] [CrossRef]

10. Jia H, Yang S, Zhu W, Li F, Wang L. Improved piezoelectric properties of Pb(Mg1/3Nb2/3)O3-PbTiO3 textured ferroelectric ceramics via Sm-doping method. J Alloys Compd. 2021;881:160666. doi:10.1016/j.jallcom.2021.160666. [Google Scholar] [CrossRef]

11. Chen P, Liu J, Zhang H, Chu B. Increase of capacitance of thick dielectrics by fringe effect. IEEE Trans Dielectr Electr Insul. 2019;26(5):1716–9. doi:10.1109/TDEI.2019.008291. [Google Scholar] [CrossRef]

12. Chen P, Zhou W, Zhang H, Pan Q, Zhang X, Chu B. Large thermal-electrical response and rectifying conduction behavior in asymmetrically reduced ferroelectric ceramics. ACS Appl Electron Mater. 2019;1(4):478–84. doi:10.1021/acsaelm.8b00107. [Google Scholar] [CrossRef]

13. Chen P, Yi K, Liu J, Hou Y, Chu B. Effects of density inhomogeneity in green body on the structure and properties of ferroelectric ceramics. J Mater Sci-Mater El. 2021;32(12):16554–64. doi:10.1007/s10854-021-06211-y. [Google Scholar] [CrossRef]

14. Haertling GH. Ferroelectric ceramics: history and technology. J Am Ceram Soc. 1999;82(4):797–818. doi:10.1111/j.1151-2916.1999.tb01840.x. [Google Scholar] [CrossRef]

15. MacKrell A. Multiscale composite analysis in Abaqus: theory and motivations. Plast Compos. 2017;61(3):153–6. doi:10.1016/j.repl.2016.01.003. [Google Scholar] [CrossRef]

16. Chen L, Lian H, Pei Q, Meng Z, Jiang S, Dong H-W, et al. FEM-BEM analysis of acoustic interaction with submerged thin-shell structures under seabed reflection conditions. Ocean Eng. 2024;309(1):118554. doi:10.1016/j.oceaneng.2024.118554. [Google Scholar] [CrossRef]

17. Chen L, Lian H, Liu Z, Gong Y, Zheng C, Bordas S. Bi-material topology optimization for fully coupled structural-acoustic systems with isogeometric FEM-BEM. Eng Anal Boundary Elem. 2022;135(1):182–95. doi:10.1016/j.enganabound.2021.11.005. [Google Scholar] [CrossRef]

18. Chen L, Zhao J, Lian H, Yu B, Atroshchenko E, Li P. A BEM broadband topology optimization strategy based on Taylor expansion and SOAR method—application to 2D acoustic scattering problems. Int J Numer Methods Eng. 2023;124(23):5151–82. doi:10.1002/nme.7345. [Google Scholar] [CrossRef]

19. Lu C, Chen L, Luo J, Chen H. Acoustic shape optimization based on isogeometric boundary element method with subdivision surfaces. Eng Anal Boundary Elem. 2023;146:951–65. doi:10.1016/j.enganabound.2022.11.010. [Google Scholar] [CrossRef]

20. Chen L, Pei Q, Fei Z, Zhou Z, Hu Z. Deep-neural-network-based framework for the accelerating uncertainty quantification of a structural-acoustic fully coupled system in a shallow sea. Eng Anal Boundary Elem. 2025;171(4):106112. doi:10.1016/j.enganabound.2024.106112. [Google Scholar] [CrossRef]

21. Bishay PL, Dong L, Atluri SN. Multi-physics computational grains (MPCGs) for direct numerical simulation (DNS) of piezoelectric composite/porous materials and structures. Comput Mech. 2014;54(5):1129–39. doi:10.1007/s00466-014-1044-y. [Google Scholar] [CrossRef]

22. Otero J, Castillero J, Ramos R. Homogenization of heterogeneous piezoelectric medium. Mech Res Commun. 1997;24(1):75–84. doi:10.1016/S0093-6413(96)00081-X. [Google Scholar] [CrossRef]

23. Lenglet E, Hladky-Hennion A-C, Debus J-C. Numerical homogenization techniques applied to piezoelectric composites. J Acoust Soc Am. 2003;113(2):826–33. doi:10.1121/1.1537710. [Google Scholar] [PubMed] [CrossRef]

24. Ammosov D, Vasilyeva M, Nasedkin A, Efendiev Y. Generalized multiscale finite element method for piezoelectric problem in heterogeneous media. Eng Anal Boundary Elem. 2022;135(12):12–25. doi:10.1016/j.enganabound.2021.09.014. [Google Scholar] [CrossRef]

25. Fish J, Wagner GJ, Keten S. Mesoscopic and multiscale modelling in materials. Nat Mater. 2021;20(6):774–86. doi:10.1038/s41563-020-00913-0. [Google Scholar] [PubMed] [CrossRef]

26. Fang D, Li F, Liu B, Zhang Y, Hong J, Guo X. Advances in developing electromechanically coupled computational methods for piezoelectrics/ferroelectrics at multiscale. Appl Mech Rev. 2013;65(6):060802. doi:10.1115/1.4025633. [Google Scholar] [CrossRef]

27. Lv J, Yang K, Zhang H, Yang D, Huang Y. A hierarchical multiscale approach for predicting thermo-electro-mechanical behavior of heterogeneous piezoelectric smart materials. Comput Mater Sci. 2014;87:88–99. doi:10.1016/j.commatsci.2014.01.059. [Google Scholar] [CrossRef]

28. Jafari A, Khatibi AA, Mashhadi MM. Comprehensive investigation on hierarchical multiscale homogenization using representative volume element for piezoelectric nanocomposites. Compos Part B-Eng. 2011;42(3):553–61. doi:10.1016/j.compositesb.2010.10.010. [Google Scholar] [CrossRef]

29. Maruccio C, De Lorenzis L, Persano L, Pisignano D. Computational homogenization of fibrous piezoelectric materials. Comput Mech. 2015;55(5):983–98. doi:10.1007/s00466-015-1147-0. [Google Scholar] [CrossRef]

30. Fu P, Liu H, Chu X. An efficient multiscale computational formulation for geometric nonlinear analysis of heterogeneous piezoelectric composite. Compos Struct. 2017;167(2):191–206. doi:10.1016/j.compstruct.2017.02.005. [Google Scholar] [CrossRef]

31. Motlagh PL, Bediz B, Alan S, Kefal A. Analysis of smart laminated composites integrated with piezoelectric patches using spectral element method and lamination parameters. J Sound Vib. 2023;567(1):118063. doi:10.1016/j.jsv.2023.118063. [Google Scholar] [CrossRef]

32. Hu G, Tang L, Yang Y, Yu D, Zi Y. High-fidelity dynamics of piezoelectric covered metamaterial timoshenko beams using the spectral element method. Smart Mater Struct. 2023;32(9):095023. doi:10.1088/1361-665X/aceba5. [Google Scholar] [CrossRef]

33. Feyel F. Multiscale FE2 elastoviscoplastic analysis of composite structures. Comput Mater Sci. 1999;16(1–4):344–54. doi:10.1016/S0927-0256(99)00077-4. [Google Scholar] [CrossRef]

34. Feyel F. A multilevel finite element method (FE2) to describe the response of highly non-linear structures using generalized continua. Comput Methods Appl Mech Eng. 2003;192(28–30):3233–44. doi:10.1016/S0045-7825(03)00348-7. [Google Scholar] [CrossRef]

35. Terada K, Kikuchi N. A class of general algorithms for multi-scale analyses of heterogeneous media. Comput Methods Appl Mech Eng. 2001;190(40–41):5427–64. doi:10.1016/S0045-7825(01)00179-7. [Google Scholar] [CrossRef]

36. Feyel F, Chaboche J-L. Multi-scale non-linear FE2 analysis of composite structures: damage and fiber size effects. Revue Européenne Des éléments Finis. 2001;10(2–4):449–72. doi:10.1080/12506559.2001.11869262. [Google Scholar] [CrossRef]

37. Papadopoulos V, Tavlaki M. The impact of interfacial properties on the macroscopic performance of carbon nanotube composites. A FE2-based multiscale study. Compos Struct. 2016;136(12):582–92. doi:10.1016/j.compstruct.2015.10.025. [Google Scholar] [CrossRef]

38. Tikarrouchine E, Chatzigeorgiou G, Praud F, Piotrowski B, Chemisky Y, Meraghni F. Three-dimensional FE2 method for the simulation of non-linear, rate-dependent response of composite structures. Compos Struct. 2018;193(8):165–79. doi:10.1016/j.compstruct.2018.03.072. [Google Scholar] [CrossRef]

39. Herwig T, Wagner W. On a robust FE2 model for delamination analysis in composite structures. Compos Struct. 2018;201:597–607. doi:10.1016/j.compstruct.2018.06.033. [Google Scholar] [CrossRef]

40. Xu R, Hui Y, Hu H, Huang Q, Zahrouni H, Zineb TB, et al. A Fourier-related FE2 multiscale model for instability phenomena of long fiber reinforced materials. Compos Struct. 2019;211(9):530–9. doi:10.1016/j.compstruct.2018.12.028. [Google Scholar] [CrossRef]

41. Tan VBC, Raju K, Lee HP. Direct FE2 for concurrent multilevel modelling of heterogeneous structures. Comput Methods Appl Mech Eng. 2020;360:112694. doi:10.1016/j.cma.2019.112694. [Google Scholar] [CrossRef]

42. Chen W, Tan VBC, Zeng X, Li P. FE2 methodology for discrete cohesive crack propagation in heterogenous materials. Eng Fract Mech. 2022;269(8):108537. doi:10.1016/j.engfracmech.2022.108537. [Google Scholar] [CrossRef]

43. Zhi J, Raju K, Tay T-E, Tan VBC. Transient multi-scale analysis with micro-inertia effects using Direct FE 2 method. Comput Mech. 2021;67(6):1645–60. doi:10.1007/s00466-021-02012-6. [Google Scholar] [CrossRef]

44. Vinyas M, Nischith G, Loja M, Ebrahimi F, Duc N. Numerical analysis of the vibration response of skew magneto-electro-elastic plates based on the higher-order shear deformation theory. Compos Struct. 2019;214(3):132–42. doi:10.1016/j.compstruct.2019.02.010. [Google Scholar] [CrossRef]

45. Zhao Q, Liu Y, Wang L, Yang H, Cao D. Design method for piezoelectric cantilever beam structure under low frequency condition. Int J Pavement Res Technol. 2018;11(2):153–9. doi:10.1016/j.ijprt.2017.08.001. [Google Scholar] [CrossRef]

46. Shen X, Du C, Jiang S, Sun L, Chen L. Enhancing deep neural networks for multivariate uncertainty analysis of cracked structures by POD-RBF. Theor Appl Fract Mech. 2023;125(51–52):103925. doi:10.1016/j.tafmec.2023.103925. [Google Scholar] [CrossRef]

47. Shen X, Du C, Jiang S, Zhang P, Chen L. Multivariate uncertainty analysis of fracture problems through model order reduction accelerated SBFEM. Appl Math Modell. 2024;125(3–4):218–40. doi:10.1016/j.apm.2023.08.040. [Google Scholar] [CrossRef]

48. Lian H, Li X, Qu Y, Du J, Meng Z, Liu J, et al. Bayesian uncertainty analysis for underwater 3D reconstruction with neural radiance fields. Appl Math Modell. 2025;138(1):115806. doi:10.1016/j.apm.2024.115806. [Google Scholar] [CrossRef]

49. Qu Y, Zhou Z, Chen L, Lian H, Li X, Hu Z, et al. Uncertainty quantification of vibro-acoustic coupling problems for robotic manta ray models based on deep learning. Ocean Eng. 2024;299(1553):117388. doi:10.1016/j.oceaneng.2024.117388. [Google Scholar] [CrossRef]

50. Chen L, Lian H, Xu Y, Li S, Liu Z, Atroshchenko E, et al. Generalized isogeometric boundary element method for uncertainty analysis of time-harmonic wave propagation in infinite domains. Appl Math Modell. 2023;114(39–41):360–78. doi:10.1016/j.apm.2022.09.030. [Google Scholar] [CrossRef]

51. Honda R. Stochastic BEM with spectral approach in elastostatic and elastodynamic problems with geometrical uncertainty. Eng Anal Boundary Elem. 2005;29(5):415–27. doi:10.1016/j.enganabound.2005.01.007. [Google Scholar] [CrossRef]

52. Liu WK, Belytschko T, Mani A. Random field finite elements. Int J Numeri Methods Eng. 1986;23(10):1831–45. doi:10.1002/nme.1620231004. [Google Scholar] [CrossRef]

53. Chen L, Huo R, Lian H, Yu B, Zhang M, Natarajan S, et al. Uncertainty quantification of 3D acoustic shape sensitivities with generalized nth-order perturbation boundary element methods. Comput Methods Appl Mech Eng. 2025;433(4):117464. doi:10.1016/j.cma.2024.117464. [Google Scholar] [CrossRef]

54. Zhang B-Y, Ni Y-Q. A hybrid sequential sampling strategy for sparse polynomial chaos expansion based on compressive sampling and Bayesian experimental design. Comput Methods Appl Mech Eng. 2021;386(2):114130. doi:10.1016/j.cma.2021.114130. [Google Scholar] [CrossRef]

55. Kersaudy P, Sudret B, Varsier N, Picon O, Wiart J. A new surrogate modeling technique combining Kriging and polynomial chaos expansions-Application to uncertainty analysis in computational dosimetry. J Comput Phys. 2015;286(1):103–17. doi:10.1016/j.jcp.2015.01.034. [Google Scholar] [CrossRef]

56. Novak L, Novak D. Polynomial chaos expansion for surrogate modelling: theory and software. Beton-und Stahlbetonbau. 2018;113(S2):27–32. doi:10.1002/best.201800048. [Google Scholar] [CrossRef]

57. Cao G, Yu B, Chen L, Yao W. Isogeometric dual reciprocity BEM for solving non-Fourier transient heat transfer problems in FGMs with uncertainty analysis. Int J Heat Mass Transfer. 2023;203(6):123783. doi:10.1016/j.ijheatmasstransfer.2022.123783. [Google Scholar] [CrossRef]

58. Blatman G, Sudret B. Adaptive sparse polynomial chaos expansion based on least angle regression. J Comput Phys. 2011;230(6):2345–67. doi:10.1016/j.jcp.2010.12.021. [Google Scholar] [CrossRef]

59. Abraham S, Raisee M, Ghorbaniasl G, Contino F, Lacor C. A robust and efficient stepwise regression method for building sparse polynomial chaos expansions. J Comput Phys. 2017;332(1):461–74. doi:10.1016/j.jcp.2016.12.015. [Google Scholar] [CrossRef]

60. Shao Q, Younes A, Fahs M, Mara TA. Bayesian sparse polynomial chaos expansion for global sensitivity analysis. Comput Methods Appl Mech Eng. 2017;318(11):474–96. doi:10.1016/j.cma.2017.01.033. [Google Scholar] [CrossRef]

61. Baptista R, Stolbunov V, Nair PB. Some greedy algorithms for sparse polynomial chaos expansions. J Comput Phys. 2019;387(5):303–25. doi:10.1016/j.jcp.2019.01.035. [Google Scholar] [CrossRef]

62. Cheng K, Lu Z. Sparse polynomial chaos expansion based on D-MORPH regression. Appl Math Comput. 2018;323(2):17–30. doi:10.1016/j.amc.2017.11.044. [Google Scholar] [CrossRef]

63. Blatman G, Sudret B. An adaptive algorithm to build up sparse polynomial chaos expansions for stochastic finite element analysis. Probab Eng Mech. 2010;25(2):183–97. doi:10.1016/j.probengmech.2009.10.003. [Google Scholar] [CrossRef]

64. Zhou Y, Lu Z, Yun W. Active sparse polynomial chaos expansion for system reliability analysis. Reliab Eng Syst Saf. 2020;202(4):107025. doi:10.1016/j.ress.2020.107025. [Google Scholar] [CrossRef]

65. Lüthen N, Marelli S, Sudret B. Sparse polynomial chaos expansions: literature survey and benchmark. SIAM-ASA J Uncertain. 2021;9(2):593–649. [Google Scholar]

66. Li H, Chen L, Zhi G, Meng L, Lian H, Liu Z, et al. A direct FE2 method for concurrent multilevel modeling of piezoelectric materials and structures. Comput Methods Appl Mech Eng. 2024;420(12):116696. doi:10.1016/j.cma.2023.116696. [Google Scholar] [CrossRef]

67. Hauseux P, Hale JS, Bordas SP. Accelerating Monte Carlo estimation with derivatives of high-level finite element models. Comput Methods Appl Mech Eng. 2017;318(3):917–36. doi:10.1016/j.cma.2017.01.041. [Google Scholar] [CrossRef]

68. Abaqus Analysis User’s Guide (6.14). Abaqus. 2013. [Google Scholar]

69. Yang J. Mechanics of piezoelectric structures. Singapore: World Scientific; 2006. [Google Scholar]