FedCPS: A Dual Optimization Model for Federated Learning Based on Clustering and Personalization Strategy

1  Introduction

In many modern applications, such as image recognition, speech recognition, cloud computing, and recommendation systems, distributed computing has become an essential calculation mode [1]. Federated learning is a distributed machine learning framework that trains a global model while protecting client privacy. This approach is particularly suitable for applications with distributed data storage and privacy-sensitive scenarios and is gaining significant attention in increasingly complex network environments.

However, data heterogeneity among clients, meaning the inconsistency in data distribution, poses a significant challenge for federated learning [2]. Data heterogeneity can lead to inefficient model training and even reduce the final model’s accuracy and generalization capability. In recent years, researchers have explored how clustering techniques can address this challenge [3–5]. Clustering methods, by grouping clients with similar data distributions, can effectively mitigate the impact of data heterogeneity, thereby improving model training efficiency and accuracy to a certain extent [6–8]. This approach ensures model robustness across data types and accelerates training.

Currently, with the proliferation of smart devices in daily life, personalized federated learning has become an important research direction [9–11]. Personalization techniques aim to adjust the federated learning model to better adapt to the unique data characteristics of each client, providing more accurate and user-specific services. This not only enhances user experience but also addresses the issue of performance degradation caused by differences in data distribution across devices. However, achieving effective personalized federated learning is not an easy task. System heterogeneity and data scarcity are significant challenges in personalized learning [12]. FedFGCR [13] introduces a novel federated learning framework based on fine-grained classifier reconstruction within a federated meta-learning paradigm to effectively address data heterogeneity. This approach demonstrates excellent advantages in complex data environments. For the issue of data scarcity, the inclusion of new clients or infrequent clients often leads to the emergence of few-shot clients. The insufficient amount of local data on these clients may fail to support effective local model training, resulting in overfitting issues. This, in turn, adversely affects the model’s generalization ability and accuracy.

To overcome these challenges, this paper proposes a collaborative optimization strategy that combines clustering and personalization in a complementary manner. By alternating between clustering to identify groups of clients with similar data distributions and personalization to fine-tune the model to each client’s specific characteristics, our approach mitigates both the issues of data heterogeneity and scarcity. This dual optimization framework aims to improve the global model’s generalization while enhancing personalization for individual clients, ultimately achieving better accuracy and robustness in diverse data environments. This strategy considers the performance of the global model while accommodating the needs of personalized training. During the alternating iterations, the clustering method provides a global framework to integrate information from various clients, while the personalization method makes adjustments at the local level, balancing the training needs of global and local perspectives. The clustering method groups users into clusters based on similarity, reducing the impact of data heterogeneity on training. By minimizing the loss function, each client’s cluster membership is identified, and each cluster model is optimized in a distributed setting. Clients with similar data share information during training, improving model accuracy within each cluster. Few-shot clients benefit from cluster models obtained through clustering tasks, as these incorporate similar features from other cluster members but remain underfitted relative to clients’ limited local data. Building on this, we introduce personalized tasks at the client level to further adjust each client’s local model, enabling it to better adapt to the local data distribution.

During local updates, we incorporate a regularization term to control the degree of deviation between the client’s local model and the cluster model through a regularization coefficient. For few-shot clients, the cluster model serves as an initialization model for local training to prevent overfitting, which would occur quickly if a simple initialization model were used. However, directly using the cluster model may make it challenging to adapt to the local data of few-shot clients. Therefore, we introduce a personalization task to fine-tune the cluster model parameters, producing a personalized local model. By leveraging similarity, we mitigate the impact of data heterogeneity, ensuring that few-shot clients can rely on a cluster model to avoid overfitting issues caused by insufficient data.

At the same time, considering the communication cost issue arising from an increased number of communication rounds, we integrated weight-sharing techniques with FedCPS. When training neural network models, the weights of the initial layers are shared across all clusters, enabling the use of all available data to learn robust representations. Additionally, FedCPS enhances client privacy protection in federated learning systems while providing personalized predictions. The primary tasks of data processing and model computation are performed locally by the clients. The raw data will not be transmitted to the central server or other clients. FedCPS can be viewed as a method in which clients independently perform local training based on cluster models established through decentralized clustering. We compared FedCPS with existing methods under the same data heterogeneity environment and achieved superior results. The following contributions are summarized:

(1)   We adopt a decentralized clustering-based federated learning approach instead of one-time centralized clustering. Clients only need to identify their cluster membership locally to complete clustering tasks. FedCPS distributes computational tasks to edge devices in the training network, thereby reducing the computational burden on the central server.

(2)   Similarly, due to the existence of few-shot clients, we have developed a personalized task scheme. By introducing a regularization term, we can control the differences between the local model and the cluster model, and at the same time solve the overfitting problem that is highly likely to occur for few-shot clients. In the experiment in Section 5, under the existence of few-shot clients, the degree of influence on other methods is approximately 5–6 times that of FedCPS.

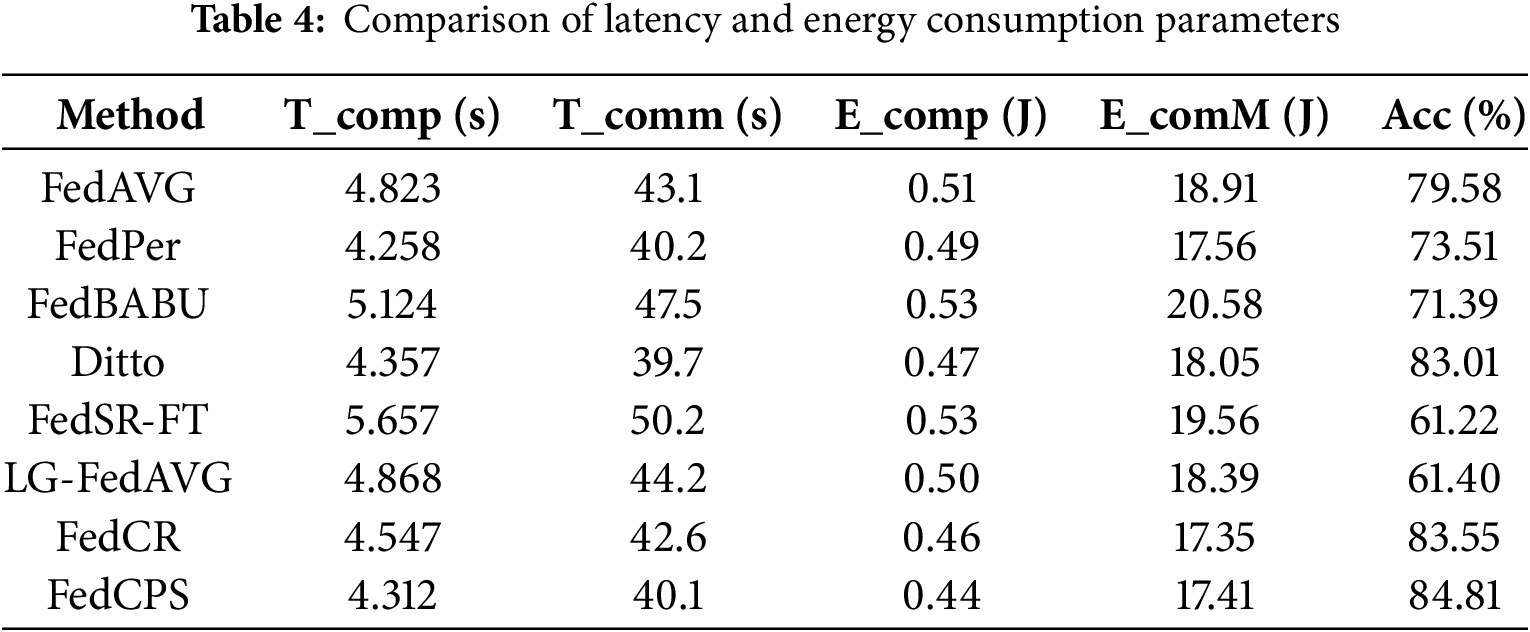
(3)   Next, the use of the weight-sharing technique reduces the communication cost to a certain extent. The central server only needs to send different versions of all subsets of weights according to the number of clusters, as well as a single copy of the shared layer, instead of sending the entire model to all clients. In the experiments in Section 5, we compared the latency and energy consumption parameters of different methods. FedCPS only increased the latency and energy consumption by approximately 0.02%.

(4)   Finally, we propose a collaborative optimization strategy that alternates between clustering and personalization. Based on clustering using the similarity of clients to obtain cluster models, we introduce local personalized training to adapt to the local data of clients. After multiple iterations, the cluster models meet the similarity requirements of cluster members while the local personalized models also fit their data better. Experiments in Section 5 show that, in the same non-iid environment, our method achieves an average test accuracy improvement of 0.81%–2.96%.

2  Related Works

2.1 Personalized Federated Learning Method

The goal of personalized federated learning (PFL) is to train user-specific models that adapt to their personal data. Personalized federated learning methods based on multitask learning [14,15] categorize each client into different tasks, simultaneously addressing multiple related tasks. While multitasking learning methods [16–18] offer many advantages in federated learning, they also face challenges such as task selection, task interference, and resource allocation. Based on meta-learning methods for personalized federated learning [19–21], local fine-tuning techniques are used to rapidly adapt the global model to each client’s personalized model. Zhang et al. [13] proposed a novel federated learning framework called FedFGCR based on fine-grained classifier reconstruction for federated meta-learning. It designed an adaptive interpolation strategy based on meta-learning, introduced a new regularization term, and proposed a fine-grained classifier to enhance the personalized diagnostic ability.

Lee et al. [22] investigate federated meta-learning issues in learning personalized strategies, using meta-networks to induce batch normalization and learning rate parameters based on local data statistics for each client. Model blending approaches in federated learning [8,23] aim to merge the global model with personalized models, where each device learns a hybrid model consisting of both the global model and its own local model.

Methods of personalized federated learning based on hierarchical personalization [9,24] aim for all clients to share a base layer while having different personalized top layers based on their respective data distributions. Federated learning methods based on transfer learning [10,25] involve retraining parts or all parameters of the globally trained model on local data. Federated learning approaches based on knowledge distillation [26–28] transfer the knowledge or mapping relationships contained in a large model (Teacher) to a smaller model (Student), fundamentally a form of transfer learning.

Wu et al. [29] used Gaussian Mixture Models (GMM) to effectively fit the input data distributions among different clients. Zhang et al. [30] introduced a regularizer to local clients, minimizing the difference between local and global Conditional Mutual Information (CMI), thereby encouraging clients to learn and utilize shared representations. Ye et al. [31] comprised collaboration modules based on pairwise model similarity and server dataset size inference, facilitating fine-grained cooperation. Optimizing local collaboration modules with assistance from client-aggregated models to enhance personalized modules, adaptable to various levels of data heterogeneity and model poisoning attacks. Wang et al. [32] utilized heterogeneous model recombination to achieve personalized federated learning, treating the personalization of heterogeneous models as a server-side model-matching optimization task. Bao et al. [33] introduce a novel setup called Testing-Time Personalized Federated Learning (TTPFL), where clients locally adjust the global model in an unsupervised manner during testing, without relying on any labeled data. Based on data augmentation, PFL methods [34] distribute a small amount of uniformly distributed global data from the cloud to edge clients, mitigating the impact of non-IID data on model performance.

Most existing personalized federated learning methods do not consider the factor of experimental data scarcity. The non-iid datasets used in most methods ensure that each client receives different types but the same amount of data, thus minimizing the impact of data scarcity. However, due to the diversity of clients targeted by federated learning, few-shot clients should also be included in training and able to develop personalized local models suited to their data. Addressing this issue, this paper proposes a personalized federated learning algorithm called FedCPS, building upon existing PFL methods, tailored specifically for few-shot clients.

2.2 Cluster Federated Learning Method

Due to the heterogeneity of data in federated learning, the data owned by different clients participating in training often varies significantly. The introduction of clustered federated learning (CFL) aims to leverage commonalities among client data by clustering clients into groups for training. The model disregards multi-task optimization and uses cosine similarity between client gradient updates to classify categories, employing a node binary classification approach where k − 1 correct binary splits can generate k clusters. Ghosh et al. [4] propose that clients identify their cluster identities while participating in global model clustering, ultimately allowing users to join clusters suitable for their datasets. Additionally, Sattler et al. [5] introduce a novel Federated Multi-Task Learning (FMTL) framework, which utilizes the geometric properties of FL loss surfaces to group client populations with jointly trainable data distributions.

Common clustered federated learning algorithms are divided into hard clustering and soft clustering. The training goal of hard clustering is to identify clusters, partition them, and jointly train a model for the clients in each cluster. For example, Duan et al. [35] complete partitioning by calculating the cosine similarity of clients and checking their gradient norms. Blumenberg et al. [36] calculate the loss generated by each client model on its local data and assign it to the cluster with the lowest loss. IFCA [4], similar to the aforementioned methods, has high requirements for initialization and client data distribution. Unlike traditional hard clustering, soft clustering does not assign each data point to a single cluster but rather to a probability distribution across all clusters. The training objective of soft clustering is typically to optimize a loss function by maximizing the association of data points with cluster centers. Acar et al. [20] proposed a soft clustering method based on multi-task learning, allowing for mixed client data distributions. They introduced the FedEM algorithm, which performs local updates for each cluster in every round, consuming significant training time. Building on this, Ruan et al. [37] achieve efficient training by requiring only a portion of clients to return gradients for an optimization task in each round. It employs proximal local updates and adds a regularization term to the local objective.

Hard clustering trains a single global model for all clients within each cluster. However, in the real world, it is impossible for multiple clients to have identical data distributions; there will always be differences. More often, data follows a mixture of multiple distributions. Compared to hard clustering, soft clustering typically requires more computational resources and time because each sample’s membership to every cluster needs to be calculated. Consequently, training on large-scale datasets can become very expensive. Additionally, the results of soft clustering can be difficult to interpret, as each sample can belong to multiple clusters, leading to fuzzy cluster boundaries. This makes it complex to interpret and understand the clustering results.

In the clustering process, the inconsistency in data distribution and volume among clients can lead to the marginalization of some clients’ data or have a limited impact on the final clustering results. This variability in data distribution and magnitude can not only cause biases in the clustering results but also increase inconsistencies between clustering outcomes, thereby affecting the training effectiveness and final application of the model. Therefore, a well-designed clustering strategy that takes into account the data characteristics and volume of each participant is crucial for optimizing the performance and broad applicability of federated learning models. In traditional federated learning soft and hard clustering methods, all clients within each cluster collaboratively train a unified global model.

However, in real-world scenarios, the data distribution among different clients is often diverse, and it is rare for data to be completely identical. More commonly, data distribution exhibits various mixed forms. Therefore, adopting a partially personalized model approach and flexibly adjusting soft and hard clustering is crucial. By introducing shared layers and personalized layers in the model and assigning weights to them accordingly, we can achieve more refined personalization adjustments both between and within clusters.

In this mechanism, when the differences between clusters are significant, the weight of the personalized layer is relatively higher to account for their specific characteristics. Within a cluster, because the differences between clients are relatively smaller and usually limited to certain specific features, the weight of the personalized layer can be appropriately reduced. For instance, the difference between two clusters, one preferring cats and the other preferring dogs, is significant. However, within the cat-preferring cluster, the differences might only pertain to preferences for black cats vs. yellow cats.

In this paper, we use the decentralized clustering method to estimate the cluster identities of users and optimize the cluster model parameters simultaneously, aiming to achieve efficient clustering in a distributed environment while avoiding reliance on centralized clustering algorithms. The central server plays a coordinating and integrating role throughout the process. In each iteration, it broadcasts the current model parameters to a subset of worker nodes (clients), then collects the information returned by the worker nodes and updates the model parameters based on this information. The central server does not directly participate in determining the cluster identities but guides the entire system to develop towards optimizing the model parameters through interaction with the worker nodes. Each worker node not only has local data but also possesses certain computing capabilities. They perform local computations based on the model parameters provided by the central server, including estimating cluster identities and participating in the optimization process of model parameters. The worker nodes perform these operations independently of each other, but their computational results are aggregated and integrated through the central server, thus affecting the update direction of the entire model. The notations used in this paper are presented in Table 1.

3  FedCPS Task Description

3.1 Clustering Task

In the context of federated learning, the problem of data heterogeneity is prominent, especially in the personalized tasks of few-shot clients. Traditional federated learning usually focuses on adapting a single global model to all local data within the network. However, in the context where there are few-shot clients, this approach has obvious drawbacks, that is, it is prone to the overfitting problem in the locally trained models. To effectively address this challenge, we introduce the decentralized clustering method. The key to using the clustering method lies in identifying the commonalities and differences among clients and then clustering the clients reasonably. Clients with similar characteristics are grouped into the same cluster, enabling each cluster to maintain its own characteristics while being distinguished from other clusters, thus effectively solving the data heterogeneity problem.

3.1.1 Estimated Cluster Identity

As shown in Eq. (1), in each iteration, each client utilizes the current model parameters received from the central server (, where is the number of clusters) and estimates the cluster identity it belongs to by minimizing the local loss function . This step enables each node to preliminarily determine the cluster it may belong to based on the performance of the current model on the local data, which is the foundation for subsequent optimization.

(1)

3.1.2 Optimization Model Parameters

After determining the cluster identity estimates, the clients and the central server work together to optimize the model parameters of each cluster. The worker nodes perform corresponding local computations and return the results to the central server, and then the central server updates the cluster model parameters based on this information. This step aims to optimize the model of each cluster in a distributed manner by leveraging the local data and computing resources of the clients so that the model can better adapt to the data distribution within each cluster.

3.2 Personal Local Update (PLU)

As shown in Algorithm 1, FedCPS executes a PLU operation after client authentication. The local objective function is designed to learn a model using only the data from the client . To accomplish this, we introduce a regularization term that encourages the personalized local model of client to be close to the cluster’s global model. The optimization problem for the model of each cluster is given by the following equation:

(2)

The objective proposed in Eq. (2) is to minimize the cluster loss function, allowing each client to compute a unique solution that minimizes the loss function. After completing their cluster estimation, clients participate in updating the cluster model. Due to issues of data heterogeneity and scarcity, malicious nodes within a cluster can potentially corrupt the cluster model, thereby further degrading the training of the global model. Thus, simply applying the global model to each heterogeneous device might yield poor results. Similarly, benign nodes relying solely on their limited local data might fail to train a satisfactory model. Therefore, we adopt a local update method where each client completes its update task locally and then returns the model and gradient computation results to the server. The returned model includes both a personalized layer adapted to the client’s own data and a cluster-shared layer.

In Section 5.2, we illustrate through experiments the changes in the values of few-shot clients and other clients during the training process. The less data there is, the smaller the , and the more reliance on the cluster model; for other clients, becomes larger and larger. The optimal value of λ is calculated by Eq. (3). Among them, is related to the change of gradients, is the number of local samples, and controls the correlation of data among devices. When the number of local samples is large enough, will gradually decrease. When a device has a sufficient amount of local data, the model is more inclined to rely on local information for training, because the local data is sufficient to support the model to learn effective feature representations and there is no need to rely on the cluster model. A decrease in means that the penalty strength of the regularization term is weakened, and the client can deviate from the cluster model to adapt to the local data. At this time, the personalized model can better capture the details of the local data, thus achieving better performance on the local data.

(3)

Conversely, when the number of local samples decreases, will gradually increase, strengthening the penalty of the regularization term, meaning that the model should rely more on the cluster model. This is because in the case of a small amount of data, using local data for training while deviating from the cluster model is likely to lead to overfitting problems. By increasing the value and fine-tuning the cluster model parameters locally, the generalization ability of the model can be improved while maintaining personalization, reducing the risk of overfitting.

3.3 Personalized Task

In the context of personalized tasks, the personalized approach we propose offers higher fairness and robustness. This work addresses the training results for few-shot clients. Under the influence of clustering, few-shot clients, after participating in the clustering task, will train a model that better suits their data on a cluster model with low-dimensional shared layers and high-dimensional representation layers. This will be demonstrated in the experimental section later. The goal of this optimization is to mitigate the issue where few-shot clients are unable to obtain a model suitable for their data when participating in training due to the limitations of solely personalized approaches.

Few-shot clients only need to participate in the gradient update training within their assigned cluster, which involves local personalized updates, while simultaneously estimating their cluster identity. Generally, to avoid overfitting, few-shot clients will train with personalized hyperparameters that are relatively large, meaning they are closer to the cluster’s global model. By increasing the penalty of the regularization term, we reduce the gap between the few-shot clients’ models and the cluster’s global model. This ensures that the training of each client within the cluster is not affected, and the global model remains unaffected. Consequently, few-shot clients can avoid overfitting and obtain a cluster model, thereby ensuring overall training performance.

3.4 Personal Layers (PL)

Our local personalized model adopts a layered structure approach. By considering the deep learning model as consisting of a base layer and a personalized layer, we can layer the client’s local model accordingly. All clients belonging to the same current cluster share a set of base layers with identical weights, while each client retains their unique personalized layer. This method extends the original scope of federated learning, which involves training a global model and essentially replicating it across all client devices. It is well-known that most algorithms may not converge when training on pathological and highly heterogeneous data partitions.

4  FedCPS Design

4.1 Framework Overview

The FedCPS process is illustrated in Fig. 1. To address personalization issues and reduce the impact of few-shot clients on overall training accuracy, our personalized federated learning framework alternates between clustering and personalization methods to train the model. By adding a regularization term to constrain the gap between the client model and the cluster model and setting hyperparameters to control the degree of personalization of the local model, we achieve improved performance.

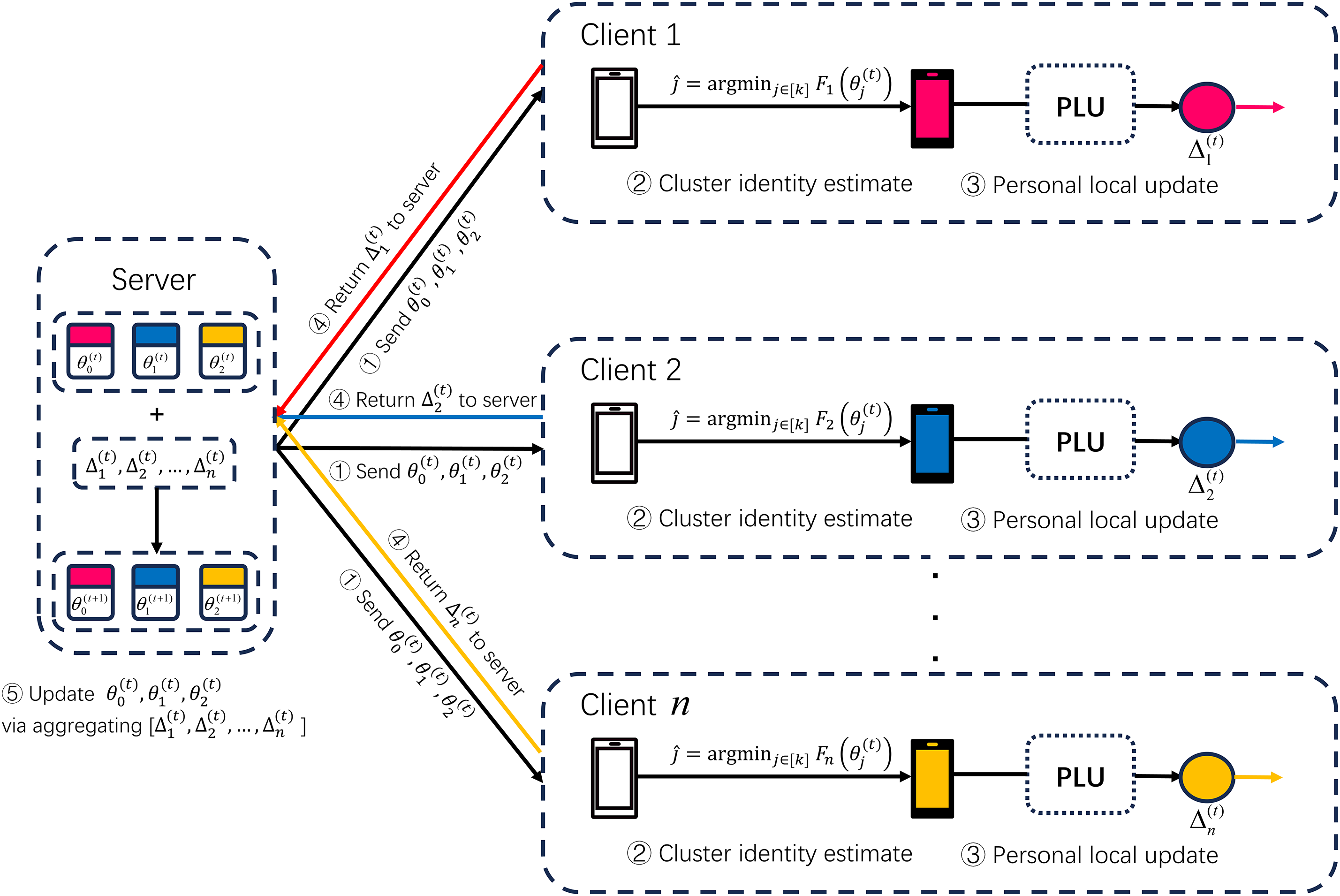
Figure 1: The framework of FedCPS. i. The server broadcasts the cluster model; ii. The client performs cluster identity recognition; iii. The client performs local updates; iv. The gradients are computed and returned to the server; v. The server updates the cluster model based on the received gradients from the clients

The client receives the model from the server, then locally computes its estimated cluster identity, performs PLU operations, updates gradients locally, and returns the results. The server uses these results to synchronize and update the corresponding cluster model, and then proceeds with the next round of iterative training. Additionally, if integrated with edge computing, these clusters can be deployed on intermediate devices like edge servers. The entire framework involves three types of models: global model, cluster model, and local model. FedCPS also includes multiple clients, such as smartphones, computers, and Internet of Things (IoT) devices. Communication between clients and clusters is one-to-one, employing synchronization mechanisms to ensure that clients possess the most current models.

FedCPS uses a decentralized method to estimate the cluster identities of clients. In each iteration, each client estimates the cluster identity it belongs to by calculating the local empirical loss function based on the received current model parameters, rather than relying on the central server for centralized clustering calculations. This approach avoids the high computational complexity brought about by traditional centralized clustering algorithms when dealing with a large number of clients because the central server does not need to perform global clustering analysis on the data of all clients. Instead, clients themselves make preliminary clustering judgments based on local information, thereby significantly reducing the computational burden.

At the same time, in order to solve the problem of increased communication costs, FedCPS uses weight-sharing technology (detailed in Section 4.4) to share low dimensional basic layer weights among all clusters. The central server only needs to send different versions of all weight subsets and one copy of the low dimensional basic layer, instead of sending models to all clients. In addition, when the central server observes that the cluster identities of all clients are stable, that is, their cluster identity estimates have not changed in several parallel iterations, the central server can stop sending models to each client and simply send the model corresponding to each client’s cluster identity estimate.

4.2 Implementation Process

FedCPS differs from the method of clustering first and then personalizing, which can sometimes lead to clients not finding clusters that truly fit their characteristics. Instead, we opt for an alternating approach using both clustering and personalization. After clients achieve their clustering objectives, they execute local updates for personalization. Each participating client utilizes a regularization parameter to constrain their regularization term, adaptively adjusting λ during each training round to control the degree of personalization in their local model. This approach ensures robustness and flexibility in completing clustering tasks, followed by personalized tasks after each round of clustering adjustments.

The specific implementation process of FedCPS is shown in Fig. 1. Combining with Algorithm 2 in Section 4.3, we will introduce the algorithm flow of FedCPS in detail.

Initialization. The algorithm starts from initial model parameters , where is the number of clusters.

Central Server. In the -th iteration, the central server selects a random subset (where is the number of worker nodes) of worker nodes and broadcasts the current model parameters to these nodes.

Clients. Each worker node receives the model parameter broadcast by the central server and estimates its cluster identity using the local empirical loss function . Use one-hot encoding to identify one’s own cluster identity. Then perform personalized local update and execute the PLU operation. As shown in Algorithm 1 in Section 3.1, we introduce regularization in the local update, where is the local objective of the client , is the cluster model obtained by client after completing cluster identity estimation, and controls the trade-off between the local and cluster models. When = 0, PLU degenerates into training a completely independent local model. At this time, each client trains only according to its own data, without considering the information of the cluster model, achieving the highest degree of personalization. In this case, the model may show good adaptability on the training data, but due to the lack of cluster information, it may lack generalization ability, especially when the local data is limited.

As gradually increases, the personalized model will gradually approach the cluster model. This means that the model will consider more cluster information during the training process, thereby improving the generalization ability to a certain extent. A larger enables the model to learn more general feature representations when facing data from different devices, reducing performance fluctuations caused by data differences between devices, that is, reducing the variance of performance differences between devices. After the client completes the PLU operation, it returns the local update result to the server. Subsequently, the central server collects the information returned by the worker nodes to update the cluster model.

In a non-iid data environment, our algorithm demonstrates its advantages. Due to the inevitability of data scarcity, training few-shot clients can impact the overall training accuracy. In our approach, we employ weight-sharing techniques in updating cluster models. Few-shot clients receive models that combine a low-dimensional shared representation layer with a high-dimensional representation layer trained collectively by clients within the cluster. This integration addresses the issue of overfitting due to insufficient data. Additionally, the central server only needs to send different versions of high-dimensional representation layer model parameters each time, along with one copy of the shared layer, instead of sending models to all clients individually.

During the clustering process, in each iteration round, cluster undergoes changes. Here, we use to represent the estimated cluster identity of client after iterations.

(4)

As shown in Eq. (4), represents the subset of data samples for client , used to estimate the clustering identity of client -th iteration. This shows that our algorithm uses fresh data samples in each iteration. Moreover, in each iteration, we use different data subsets to obtain cumulative estimates and compute gradients. This effectively eliminates interdependencies between clustering estimation and gradient computation.

(5)

As shown in Eq. (5), represents the result of the local execution of PLU gradient update operations by clients belonging to . The cluster model aggregates the computed gradients from all clients in the list, and updates it as the initial model for the + 1-th iteration of cluster .

Based on completing clustering tasks, each client determines the cluster identity that best matches the local data features through identity assessment. The server distributes the cluster model to each client, incorporating personalization on top of clustering, considering that each client possesses different data. This involves adding a regularization term to the cluster objective function and setting hyperparameters to control the regularization’s impact on personalization. As clients personalize based on the cluster model, it maximally preserves commonalities among clients. Therefore, our personalization task aims to fully leverage client uniqueness. Each client needs to achieve high levels of personalization, adjusting the distance between the local model and the cluster model gradually based on the trained parameter , while controlling the value of to prevent overfitting.

In PLU operations, we augment the local objective function on the client side with a regularization term, using the hyperparameter to balance between the personalized local model and the cluster model . The choice of hyperparameter directly affects the degree of deviation between the personalized model and the cluster model. A higher deviation indicates a higher degree of personalization for the local model , meaning it diverges more from the standardized cluster model . For few-shot clients, opting for a value closer to the global model can effectively mitigate overfitting issues caused by data scarcity.

4.3 Personalization

As shown in Algorithm 2, we add a regularization term to the objective function and set a hyperparameter to control the influence of this regularization term on the local personalized model. On this basis, we divide clients into different clusters through clustering identity recognition. Each cluster’s internal members perform personalization operations locally, training on the cluster model using local data. This approach allows them to inherit the characteristics of the cluster model and obtain a personalized local model that better fits their own data.

As shown in Eq. (6), server initializes cluster model parameters , .

(6)

In the -th iteration of FedCPS, a random subset of clients is selected, and the model is broadcast to the clients in . Each client uses the local loss function and the received model parameters to perform computations. They confirm their identity , by choosing the model parameters that minimize the loss. The client cluster identity may change as the iterations progress. After obtaining the estimated identity through one-hot encoding, clients need to fit their personalized model locally, executing PLU. Client solves the regularized local objective through multiple iterations.

The hyperparameter affects the difference between the local personalized model and the cluster model. The larger the , the closer the personalized model is to the cluster model; the smaller the , the more the personalized model deviates from the cluster model, achieving a higher degree of personalization. Each client adjusts the value of to find a suitable personalized model between the local model and the cluster model and returns the gradient update result to the server. After all clients complete the local update operations, the server updates the cluster model in real time based on the local gradient update results sent by each client. Once each cluster has completed its update, we do not perform model averaging of the cluster models ; instead, we use multi-task weight sharing techniques to fully leverage the commonalities among clusters, thereby reducing communication costs and computational complexity.

When performing global model updates, common features from the low-dimensional representation layers of the cluster models are extracted as the shared layer to avoid overfitting for few-shot clients. The high-dimensional representation layers address the distribution differences between different clusters. By iteratively executing the FedCPS algorithm, the high-dimensional features of each cluster become increasingly distinct, and clients’ estimated identification will be more accurate and stable.

4.4 Personal Layers

For the model , we denote the number of basic and personalized layers for each client by the positive integers and , respectively. We use to represent the weight matrices of the basic layers, with the corresponding vector-valued activation functions . Since the weight matrices of the basic layers may have different dimensions, the tuple is denoted by the symbol , using tensor notation. Similarly, for the personalized layer weight matrices of the -th client device, we denote them as , with the corresponding vector-valued activation functions represented as . is the same as .

As shown in Eq. (7), The implicit uniqueness of the vector-valued activation functions’ dimensions ensures that the domain dimensions and the range of the activation functions are uniquely defined to satisfy the forward propagation/inference operations for any input data point on client .

(7)

For any input data point on the -th client, for convenience, we represent this forward propagation operation as . Therefore, we implicitly assume that the weight tensor captures all aspects of personalization on the -th client.

5  Experiment

5.1 Experimental Setup

5.1.1 Experimental Environment

Our experiments were conducted on a system running Windows 11, equipped with a 12th Gen Intel (R) Core (TM) i7-12700 processor, featuring 12 cores and 20 logical processors. The system has 16 GB of RAM. We used Python 3.10 and PyTorch for the experiments, conducted in PyCharm 2021.

5.1.2 Datasets

In the experimental section, we utilized four widely used datasets within the realm of federated learning: MNIST, FMNIST, CIFAR10 and CIFAR100. The MNIST and FMNIST datasets each contain approximately 70,000 image samples, divided into a training set (60,000 images) and a test set (10,000 images). The distribution of numbers in the MNIST dataset is relatively uniform, which makes it convenient for researchers to test the performance of algorithms in an ideal data environment, for example, to test basic indicators such as the convergence speed and accuracy of the model. Fashion-MNIST (FMNIST) consists of images of ten different types of fashion items, and the classification task is more challenging. Using FMNIST in federated learning can test the performance of algorithms when dealing with more complex data features. CIFAR10 is a small dataset for identifying universal objects, curated by Alex Krizhevsky and Ilya Sutskever, students of Hinton. It includes 10 categories of RGB color images, each with a size of 32Ã32 pixels, comprising 50,000 training images and 10,000 test images. The data complexity in CIFAR10 is moderate. It is neither as simple as MNIST nor as difficult to handle as some large and complex datasets. It is suitable to be used as a transitional test dataset in research to evaluate the performance of algorithms when dealing with complex image data. The CIFAR100 dataset contains 100 classes. Each class has 600 color images of size 32Ã32 pixels, with 500 images for training and 100 images for testing. Using CIFAR100 in federated learning can test the limit performance of algorithms when dealing with a large number of categories and complex image data. When these datasets are assigned to participating clients for training, some clients will have a small amount of data, thereby simulating an experimental environment with few-shot clients. The data obtained by each client is randomly divided into equal proportion datasets, consisting of 60% training set, 20% test set, and 20% validation set.

Our non-iid_1 data setting is as follows: For the MNIST [38], FMNIST [39], and CIFAR10 [40] datasets, which have fewer label categories, each participating training client is randomly assigned 5 classes, while few-shot clients are randomly assigned 2 classes. For the CIFAR100 [41] dataset, each client is randomly assigned 15 classes, and few-shot clients are randomly assigned 5 classes. The amount of data in each class is the same.

non-iid_2. Each client has an uncertain number of classes, and the data within each class varies widely by setting client sample labels according to the Dirichlet distribution. In the non-iid_2 setting, each client has about four classes that consume 70% of data and misses one or two classes with Dirichlet parameter 0.6 for MNIST, FMNIST, CIFAR10 and CIFAR100 (and Dirichlet parameter 0.4 for CIFAR100). All data is split into 70% training set and 30% test set. The test set and the training set have the same data distribution.

As shown in Table 2, we compared the test performance of the FedCPS method with other methods under non-iid data settings, including FedAvg [42], FedPer [43], LG-FedAvg [44], FedBABU [45], Ditto [19], FedSR-FT [46] (FedSR with local fine-tuning), and FedCR [30]. For the convenience of comparing the experimental results, we specifically introduce several personalized federated learning algorithms. FedPer is a personalized federated learning method with a base layer + personalization layer for the federal training of deep feedforward neural networks. It can cope with the adverse effects brought about by statistical heterogeneity. FedBABU only updates the main part of the model during the federal training process (the head is randomly initialized and never updated) and fine-tunes the head for personalization during the evaluation process. Ditto has developed a scalable solver to address the issues of robustness against data and model poisoning attacks and fairness measured by the consistency of performance among various devices. FedCR introduces a regularizer in the local-client update. The aim is to minimize the difference between the local and global conditional mutual information (CMI), thus encouraging the clients to learn and utilize common representation. Additionally, we compared the impact on training accuracy in a regular non-iid experimental environment by controlling the proportion of few-shot clients among the total participating training clients.

5.2 Experimental Result

5.2.1 Accuracy Test

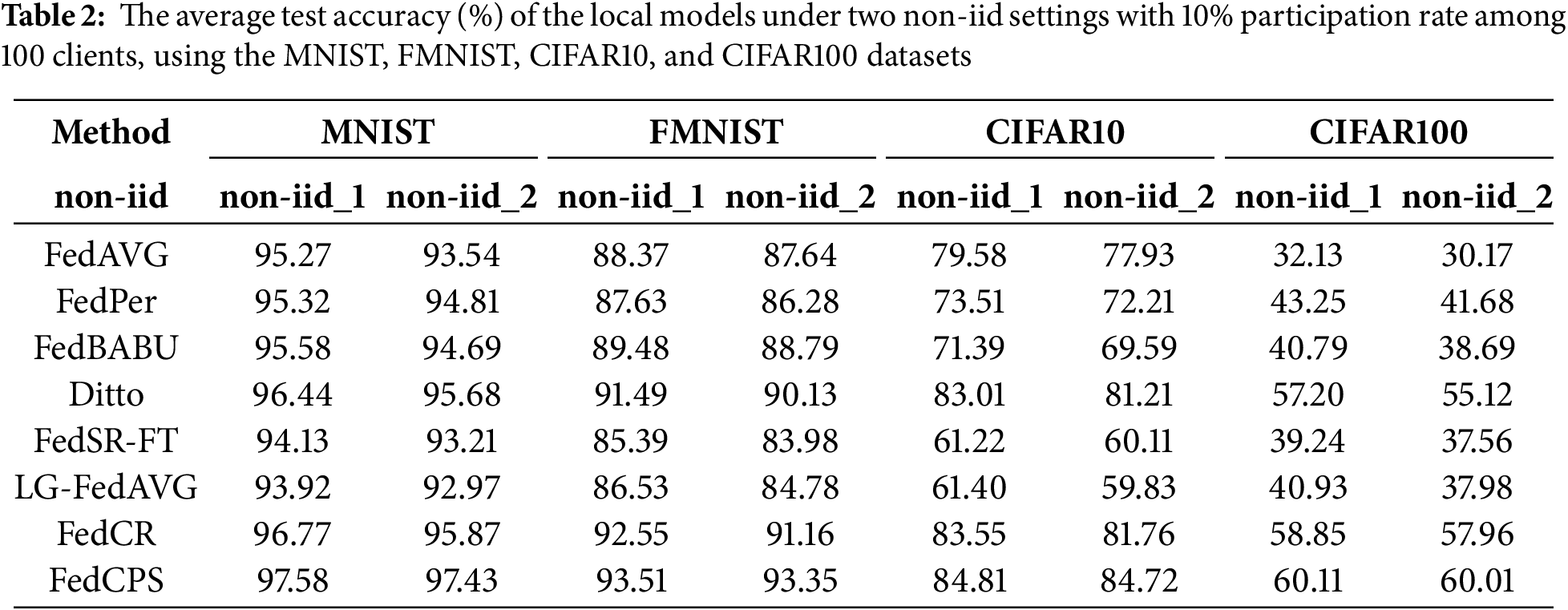
As shown in Fig. 2, the experimental results show that under the same non-iid data setting, FedCPS achieves a higher test accuracy compared to other methods. In Fig. 2a, we used the MNIST dataset and set the number of communication rounds to 500. The experimental results showed that the test accuracy of FedCPS is 0.81% higher than that of FedCR. In Fig. 2b, when performing 250 rounds of communication on FMNIST and reaching convergence, its average test accuracy is 0.96% higher than that of FedCR. MNIST and FMNIST provide relatively simple and structured data, which helps to evaluate the performance of models in basic image classification tasks. In Fig. 2c,d, FedCPS demonstrates better advantages in more complex data environments. We conducted 500 rounds of communication on CIFAR10 and CIFAR100 and reached convergence, with the average test accuracy increased by 1.26% compared to FedCR respectively. For data environments involving more categories and more complex image features, FedCPS has more advantages in high-difficulty tasks.

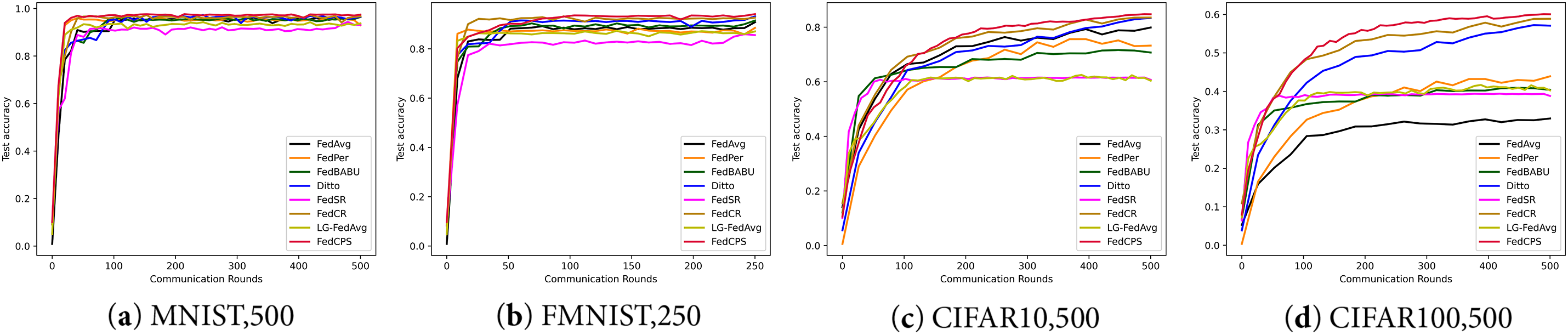
Figure 2: The comparison of average test accuracy for clients across different datasets and communication rounds: (a) MNIST dataset with 500 communication rounds; (b) FMNIST dataset with 250 communication rounds; (c) CIFAR10 dataset with 500 communication rounds; (d) CIFAR100 dataset with 500 communication rounds

To further validate FedCPS’s advantages in complex data environments, we used the non-iid_2 setting for MNIST, FMNIST, CIFAR10 and CIFAR100 datasets. The experimental results are shown in Table 2. The complex non-iid_2 environment has an impact on the average accuracy, and existing methods are all affected to varying degrees. FedCPS performs well on the CIFAR10 dataset, with an average test accuracy 2.96% higher than that of FedCR. Our strategy of decentralized clustering and personalized collaborative optimization enables the model to not only adapt to local data but also maintain the generalization ability for data from other clients, showing better advantages in more complex environments.

5.2.2 Data Scarcity Experiment

By setting the proportions of few-shot clients to 10%, 20%, 30%, 40% and 50%, we followed a random sampling principle for client selection in each round. This means that in any given round, a larger number of few-shot clients might be selected, or alternatively, a larger number of regular non-iid clients might be selected.

In our experiments, we used to represent the proportion of few-shot clients among all clients. A larger indicates a more pronounced data scarcity in the experimental environment. We set different values and calculated the average test accuracy on the CIFAR10 dataset to show the impact of data scarcity on model training. The experimental results are shown in Table 3. When = 10%, it can be observed that compared with the non-iid_1 setting, the accuracy of FedCPS decreases by 0.21%, while the accuracy of FedBABU decreases by as much as 2.14%. The difference in the environment under this setting compared to non-iid_1 is not significant, and the advantages of our method are not manifested. When we continue to increase to 30%, the accuracy of FedCPS decreases by 2.22%, and the accuracy of FedPer decreases by 6.8%, with the decreasing amplitude being approximately three times that of FedCPS. As more and more few-shot clients participate in the training, the existing methods will encounter the problem of overfitting of the local models of few-shot clients during training, thus affecting the average test accuracy and causing it to decline. When reaches 50%, the accuracy of FedCPS decreases by 3. 17%, and the accuracy of FedBABU decreases by as much as 10.02%. Few-shot clients have a great impact on the training ability of this method. The increase in few-shot clients does not have a significant impact on the FedCPS method. Due to the strong generalization ability of the cluster model, few-shot clients obtain the cluster model and use local data to train and adjust the model parameters, so that the local model can achieve a personalized effect on the basis of having generalization ability.

5.2.3 The Value of

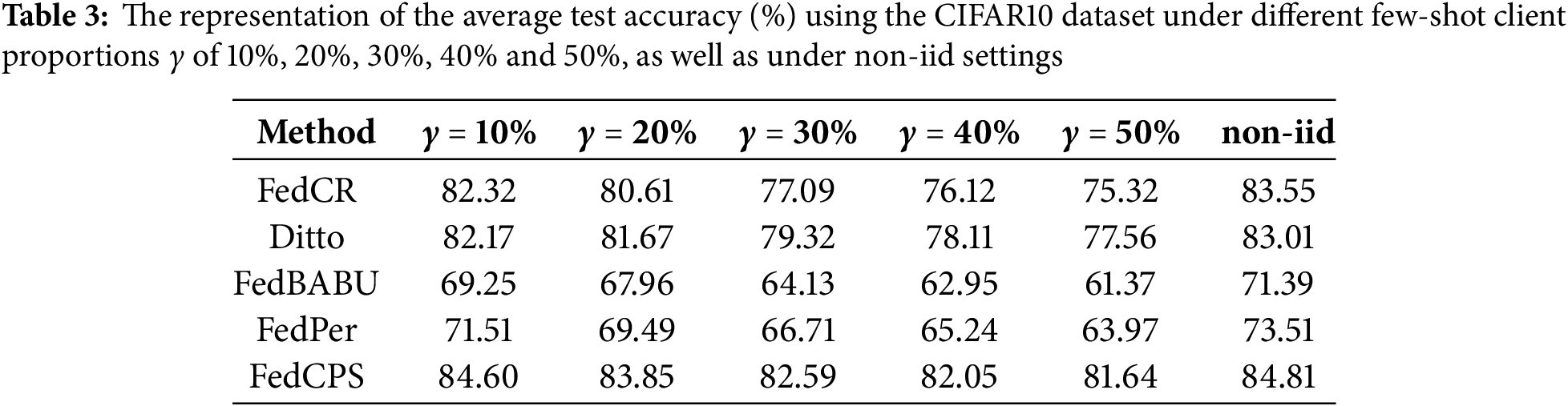
As shown in Fig. 3, we tracked and recorded the average value of for few-shot clients and other clients during the training process on the CIFAR10 dataset. We can clearly see that as the number of communication rounds increases, the value for few-shot clients will gradually increase, while the value for other clients will gradually decrease. As we mentioned in Section 3.2, few-shot clients will encounter the overfitting problem when training with local data. Increasing the value is equivalent to increasing the penalty strength of the regularization term and reducing the degree of deviation of the local model from the cluster model. They can obtain a personalized local model by fine-tuning the parameters of the cluster model with local data. On the contrary, other clients have a sufficient number of samples, so they reduce the value to deviate from the cluster model and train a personalized model that fits their local data better.

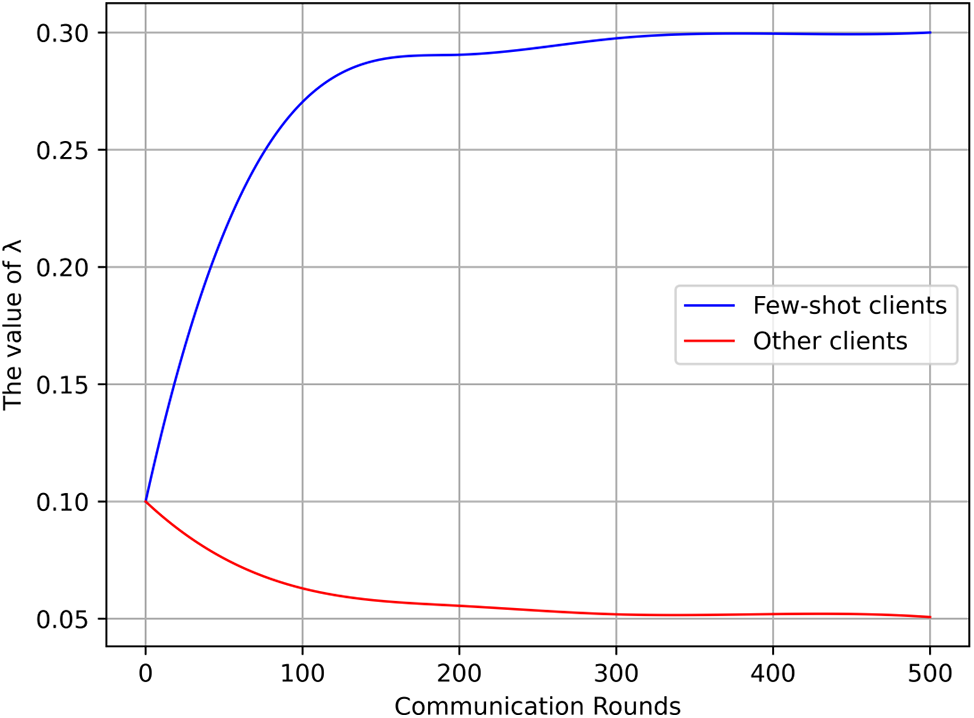
Figure 3: The change in the average value of for few-shot clients and other clients

5.2.4 Communication Cost

To evaluate the system performance of the FedCPS framework, we conducted experiments in the complex CIFAR10 dataset, and the detailed results are shown in Table 4. FedCPS only increased the latency and energy consumption by approximately 0.02% compared to other methods. Although our method increases the number of computations and communications, we combine the weight sharing technique to reduce the network load per communication. Meanwhile, in each round of communication, the central server will choose the number of cluster models to be sent to clients, which reduces the number of communication rounds to a certain extent. Specifically, the low dimensional base layer is shared among clusters, and the central server only needs to send different versions of all weight subsets and one copy of the low-dimensional base layer instead of sending models to all clients. In addition, when the central server observes that the cluster identities of all clients are stable, that is, their cluster identity estimates have not changed in several parallel iterations, then the central server can stop sending models to each client and can simply send the model corresponding to the cluster identity estimate of each client.

5.2.5 Analysis of Scalability

FedCPS maintains its scalability and stability through various mechanisms and characteristics when the number of clients increases or the dataset expands, so that it is not affected or the negative impacts brought by these factors are reduced. The experimental results are shown in Table 5. During the execution of the algorithm, a strategy of randomly selecting participating devices is usually adopted. This random selection method enables different clients to have the opportunity to participate in the calculation in different iterations, achieving a kind of dynamic load balancing. Even if the number of clients increases, the system will not experience performance degradation due to some clients being overly busy or idle. In addition, FedCPS gradually optimizes the model parameters through multiple iterations. When the dataset expands, this iterative update method helps the model gradually adapt to large-scale data. As the number of iterations increases, the model parameters can converge to a stable solution.

With the advancement and development of artificial intelligence, the number of clients participating in federated learning and the data that need to be trained will increase exponentially. The increasingly large number of clients and datasets will significantly affect the scalability and maintainability of algorithms. We will conduct further research and make improvements in our future work.

5.2.6 Personal Layers

As shown in Fig. 4, we compared the differences in training between the method with the personalized layer added and the original method through experiments. We set equal to 2, meaning that in each local model, the personalized layer contains 2 model blocks, while the rest are basic layers. In Fig. 4a, we use the CIFAR10 dataset for training, FedCPS with personalized layers reaches convergence around the 470th communication round, 20 communication rounds earlier than the method without personalized layers. In Fig. 4b, we use the CIFAR100 dataset for training, FedCPS with personalized layers reaches convergence around the 480th communication round, 10 communication rounds earlier than the method without personalized layers. During the training process, the server sends different versions of the high-dimensional representation layer model parameters, as well as a single copy of the shared layer, rather than sending models to all clients. This approach helps reduce the server’s communication costs to some extent. On the other hand, the use of personalized layers accelerates the convergence speed of the model, enabling more precise personalized models to be trained locally while improving overall training efficiency.

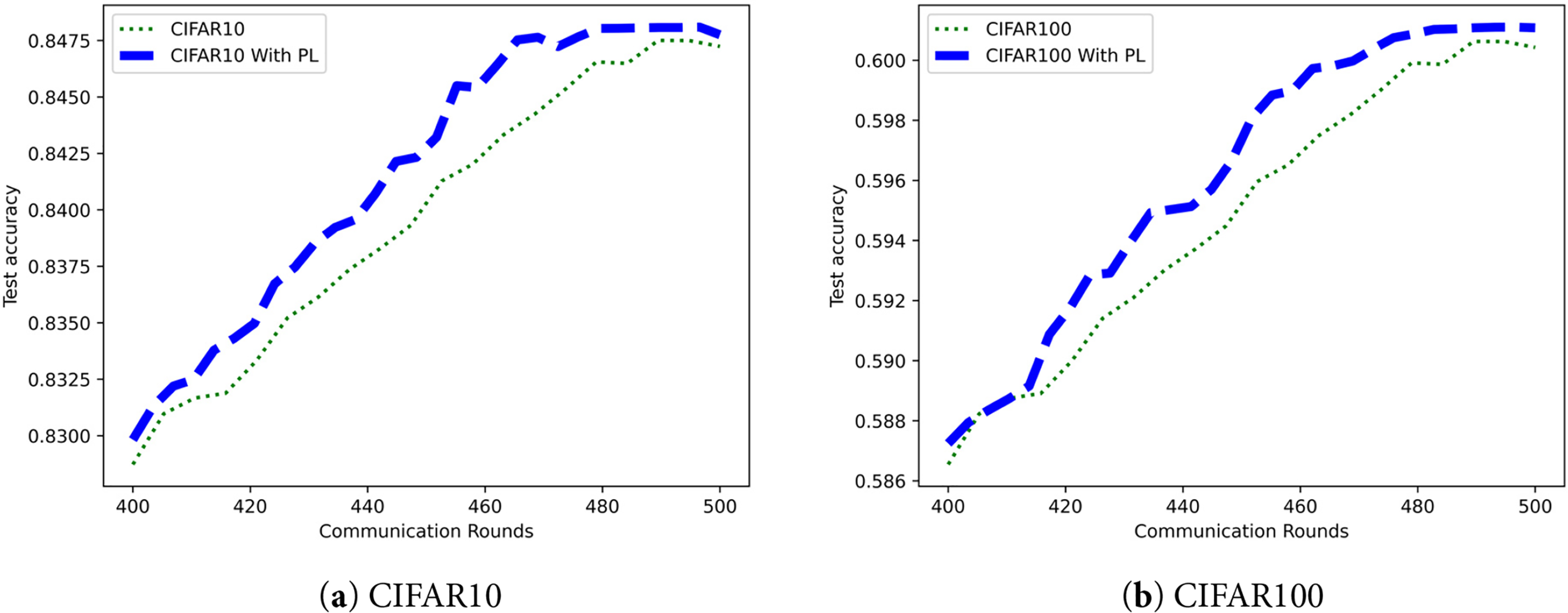
Figure 4: Comparison of convergence after adding local personalization layers: (a) CIFAR10 dataset; (b) CIFAR100 dataset

5.2.7 The Value of

We regarded the number of clusters as a hyperparameter and ran experiments on the CIFAR10 dataset with different values of . As we emphasized in Section 2, FedCPS employs a decentralized clustering method instead of running centralized clustering, thus reducing the computational cost of the central server. The experimental results are shown in Table 6. As we can observe, when the value of k increases, there is only a 0.08%–0.1% decrease in the average test accuracy rate (excluding the floating values). When = 3 or > 3, the change in the accuracy rate tends to stabilize. Regardless of how the value of is set, compared with the situation when = 1 (where there is only one cluster, which is equivalent to global training), there is a significant improvement in the average test accuracy rate.

In addition, we have drawn the t-SNE visualization of FedCPS on the CIFAR10 dataset. We observed that FedCPS is robust to the choice of the number of clusters . The x-axis and y-axis in the t-SNE visualization do not have specific physical meanings; they merely represent the positions of the dimensionality-reduced data points in a two-dimensional space. The distances between points reflect the similarity of samples in the original high-dimensional space: the closer the points, the more similar the samples; the farther apart the points, the greater the difference. The orientation and specific positions of the images may vary, but the relative relationships between the data points remain unchanged. The algorithm results for = 2 (Fig. 5) and = 3 (Fig. 6) are similar. In Figs. 5a and 6a, the clustering effect is not obvious at the 100th epoch, and clients cannot accurately perform cluster identity recognition. In Figs. 5b and 6b, the clustering results become clearer at the 300th epoch, with only a small number of clients failing to accurately complete the clustering identity recognition. In Figs. 5c and 6c, the clustering task is completed at the 500th epoch, and each client accurately performs cluster identity recognition. We noticed that when > 3 (Fig. 7), FedCPS would automatically identify 3 clusters while the remaining clusters would be empty. In Fig. 7a, the clustering results are chaotic at the 100th epoch, with most clients failing to accurately complete the clustering identity recognition. In Fig. 7b, the clustering boundaries representing the four different categories become clearer at the 300th epoch, with only a small number of clients failing to accurately complete the clustering identity recognition. In Fig. 7c, the clustering boundaries become clearer at the 500th epoch, and the clients are automatically divided into three clusters. This indicates the applicability of FedCPS in practical problems where the cluster structure is ambiguous and the number of clusters is unknown.

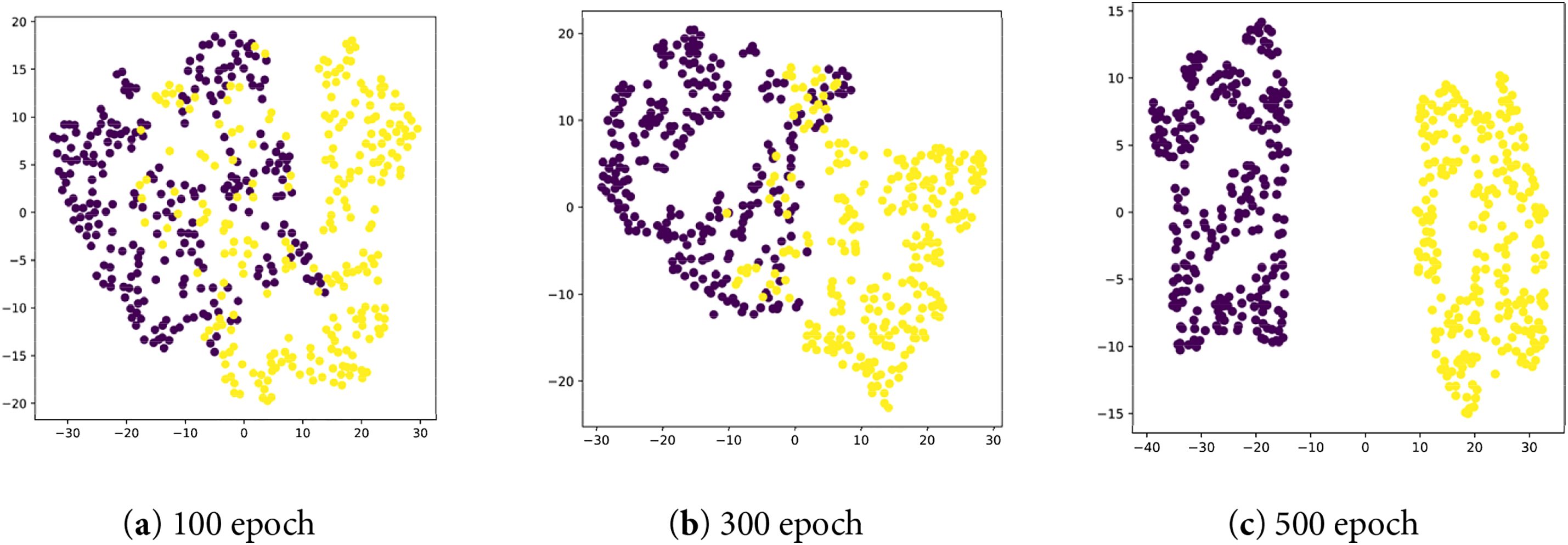
Figure 5: The t-SNE visualization of FedCPS on the CIFAR10 dataset when k = 2: (a) clustering situation at the 100th epoch; (b) clustering situation at the 300th epoch; (c) clustering situation at the 500th epoch

Figure 6: The t-SNE visualization of FedCPS on the CIFAR10 dataset when k = 3: (a) clustering situation at the 100th epoch; (b) clustering situation at the 300th epoch; (c) clustering situation at the 500th epoch

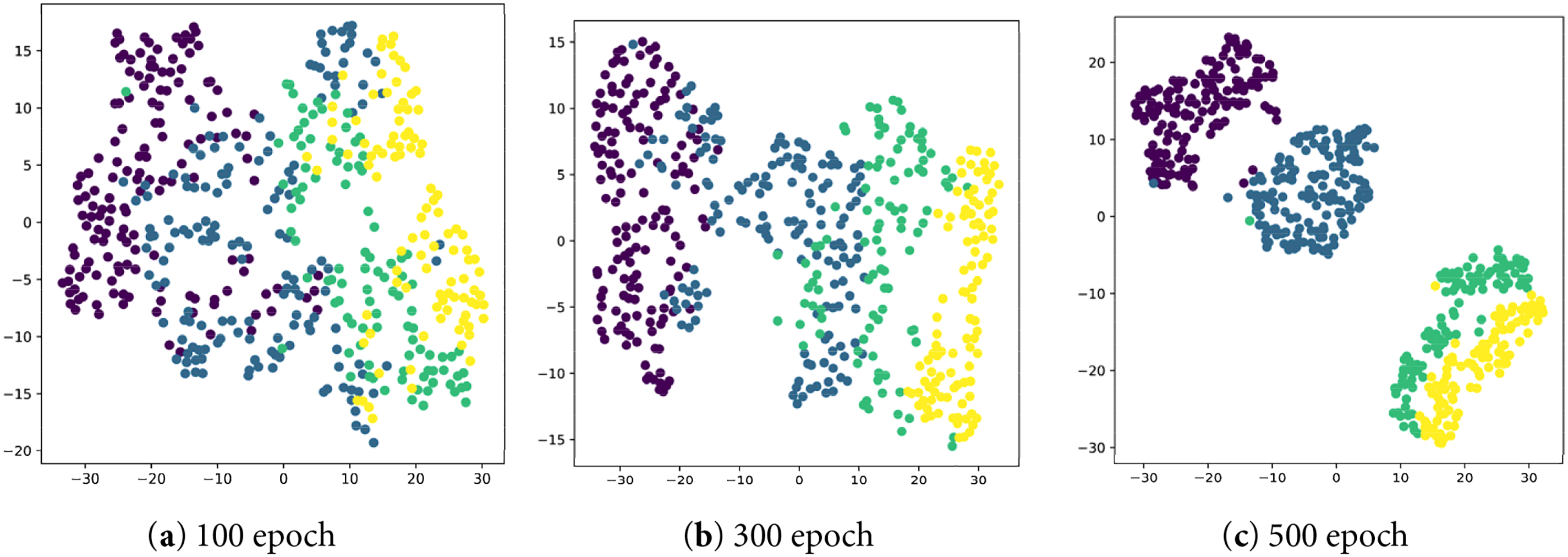
Figure 7: The t-SNE visualization of FedCPS on the CIFAR10 dataset when k = 4: (a) clustering situation at the 100th epoch; (b) clustering situation at the 300th epoch; (c) clustering situation at the 500th epoch

6  Conclusion and Future Work

In this paper, we propose the FedCPS method. We adopt a decentralized clustering approach where clients complete cluster identity recognition locally and there is no need for centralized clustering algorithms. Meanwhile, personalization is introduced to enable the participating clients to obtain personalized local models. Through the regularization term, we effectively balance the degree of deviation between the local model and the cluster model. The PLU operation allows clients to focus on improving their local personalized models while fulfilling cluster tasks. In this way, clients can use local data to train personalized models and avoid the occurrence of overfitting problems. Extensive experiments demonstrate the effectiveness of FedCPS. In our future work, we will focus on training lighter models on the client side to reduce communication costs and optimize our algorithms to decrease the number of communications. Meanwhile, we will concentrate on integrating the latest privacy protection technologies to defend against attacks on the server or the client.

Acknowledgement: The authors would like to thank the highly respected editor and reviewers for their valuable suggestions for improving the article.

Funding Statement: This work was supported by the Foundation of President of Hebei University (XZJJ202303).

Author Contributions: Zhen Yang: Conceptualization, Methodolgy, Software, Visualization, Writing—original draft. Yifan Liu: Supervision, Writing—review & editing, Data curation. Fan Feng: Supervision, Data curation. Yi Liu: Supervision, Data curation. Zhenpeng Liu: Supervision, Writing—review & editing, Data curation. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets generated and/or analyzed during the current study are available from the corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Wu Q, He K, Chen X. Personalized federated learning for intelligent IoT applications: a cloud-edge based framework. IEEE Open J Comput Soc. 2020;1:35–44. doi:10.1109/OJCS.2020.2993259. [Google Scholar] [PubMed] [CrossRef]

2. Kulkarni V, Kulkarni M, Pant A. Survey of personalization techniques for federated learning. In: Proceedings of the 2020 Fourth World Conference on Smart Trends in Systems, Security and Sustainability (WorldS4); 2020 Jul 27–28; London, UK. p. 794–7. doi:10.1109/WorldS450073.2020.9210355. [Google Scholar] [CrossRef]

3. Shu J, Yang T, Liao X, Chen F, Xiao Y, Yang K, et al. Clustered federated multitask learning on non-IID data with enhanced privacy. IEEE Internet Things J. 2023;10(4):3453–67. doi:10.1109/JIOT.2022.3228893. [Google Scholar] [CrossRef]

4. Ghosh A, Chung J, Yin D, Ramchandran K, Ghosh A, Chung J, et al. An efficient framework for clustered federated learning. In: Larochelle H, Ranzato M, Hadsell R, Balcan MF, Lin H, editors. Advances in Neural Information Processing Systems. Proceedings of the 33rd Annual Conference on Neural Information Processing Systems; 2020 Dec 6–12; Vancouver, BC, Canada. p. 19586–97. [Google Scholar]

5. Sattler F, Müller KR, Samek W. Clustered federated learning: model-agnostic distributed multitask optimization under privacy constraints. IEEE Trans Neural Netw Learn Syst. 2021;32(8):3710–22. doi:10.1109/TNNLS.2020.3015958. [Google Scholar] [PubMed] [CrossRef]

6. Sattler F, Muller KR, Wiegand T, Samek W. On the Byzantine robustness of clustered federated learning. In: Proceedings of the 2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); 2020 May 4–8; Barcelona, Spain. p. 8861–5. doi:10.1109/icassp40776.2020.9054676. [Google Scholar] [CrossRef]

7. Nguyen DC, Ding M, Pathirana PN, Seneviratne A, Li J, Vincent Poor H. Federated learning for Internet of Things: a comprehensive survey. IEEE Commun Surv Tutor. 2021;23(3):1622–58. doi:10.1109/COMST.2021.3075439. [Google Scholar] [CrossRef]

8. Matsuda K, Sasaki Y, Xiao C, Onizuka M. FedMe: federated learning via model exchange. In: Proceedings of the 2022 SIAM International Conference on Data Mining (SDM); 2022 Apr 28–30; Alexandria, VA, USA. p. 459–67. doi:10.1137/1.9781611977172.52 [Google Scholar] [CrossRef]

9. Ma X, Zhang J, Guo S, Xu W. Layer-wised model aggregation for personalized federated learning. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2022 Jun 18–24; New Orleans, LA, USA. p. 10082–91. [Google Scholar]

10. Fallah A, Mokhtari A, Ozdaglar A. Personalized federated learning with theoretical guarantees: a model-agnostic meta-learning approach. In: Larochelle H, Ranzato M, Hadsell R, Balcan MF, Lin H, editors. Advances in Neural Information Processing Systems. Proceedings of the 33rd Annual Conference on Neural Information Processing Systems; 2020 Dec 6–12; Vancouver, BC, Canada. p. 3557–68. [Google Scholar]

11. Shamsian A, Navon A, Fetaya E, Chechik G. Personalized federated learning using hypernetworks. In: Meila M, Zhang T, editors. Proceedings of the 38th International Conference on Machine Learning; 2021 Jul 18–24; Red Hook, NY, USA: Curran Associates Inc. p. 9489–502. [Google Scholar]

12. Chen D, Yao L, Gao D, Ding B, Li Y, Chen D, et al. Efficient personalized federated learning via sparse model-adaptation. In: Krause A, Brunskill E, Cho K, Engelhardt B, Sabato S, Scarlett J, editors. Proceedings of the 40th International Conference on Machine Learning; 2023 Jul 23–29; Honolulu, HI, USA. p. 5234–56. [Google Scholar]

13. Zhang X, Li C, Han C, Li S, Feng Y, Wang H, et al. A personalized federated meta-learning method for intelligent and privacy-preserving fault diagnosis. Adv Eng Inform. 2024;62:102781. doi:10.1016/j.aei.2024.102781. [Google Scholar] [CrossRef]

14. Vanhaesebrouck P, Bellet A, Tommasi M. Decentralized collaborative learning of personalized models over networks. In: Singh A, Zhu J, editors. Proceedings of the 20th International Conference on Artificial Intelligence and Statistics; 2017 Apr 20–22; Fort Lauderdale, FL, USA. p. 509–17. [Google Scholar]

15. Zantedeschi V, Bellet A, Tommasi M. Fully decentralized joint learning of personalized models and collaboration graphs. In: Chiappa S, Calandra R, editors. Proceedings of the Twenty Third International Conference on Artificial Intelligence and Statistics; 2020 Aug 26–28; Palermo, Sicily, Italy. p. 864–74. [Google Scholar]

16. Huang Y, Chu L, Zhou Z, Wang L, Liu J, Pei J, et al. Personalized cross-silo federated learning on non-IID data. Proc AAAI Conf Artif Intell. 2021;35(9):7865–73. doi:10.1609/aaai.v35i9.16960. [Google Scholar] [CrossRef]

17. Li T, Hu SY, Beirami A, Smith V. Fair and robust federated learning through personalization. In: Meila M, Zhang T, editors. Proceedings of the 38th International Conference on Machine Learning; 2021 Jul 18–24; Red Hook, NY, USA: Curran Associates Inc. p. 6357–68. [Google Scholar]

18. Marfoq O, Neglia G, Bellet A, Kameni L, Vidal R, Marfoq O, et al. Federated multi-task learning under a mixture of distributions. In: Ranzato M, Beygelzimer A, Dauphin Y, Liang PS, Wortman Vaughan J, editors. Advances in Neural Information Processing Systems. Proceedings of the 34th Annual Conference on Neural Information Processing Systems; 2020 Dec 6–12; Vancouver, BC, Canada. p. 15434–47. [Google Scholar]

19. Yang L, Huang J, Lin W, Cao J. Personalized federated learning on non-IID data via group-based meta-learning. ACM Trans Knowl Discov Data. 2023;17(4):1–20. doi:10.1145/3558005. [Google Scholar] [CrossRef]

20. Acar DAE, Zhao Y, Zhu RZ, Matas R, Mattina M, Whatmough P, et al. Debiasing model updates for improving personalized federated training. In: Meila M, Zhang T, editors. Proceedings of the 38th International Conference on Machine Learning. 2021 Jul 18–24; Red Hook, NY, USA: Curran Associates Inc. p. 21–31. [Google Scholar]

21. Khodak M, Balcan MF, Talwalkar A. Adaptive gradient-based meta-learning methods. In: Advances in Neural Information Processing Systems: Proceedings of the 33rd International Conference on Neural Information Processing Systems; 2019 Dec 8–14. Vancouver, BC, Canada. Red Hook, NY, USA: Curran Associates Inc. p. 532–43. [Google Scholar]

22. Lee R, Kim M, Li D, Qiu XC, Hospedales T, Huszár F, et al. FedL2P: federated learning to personalize. In: Proceedings of the 37th International Conference on Neural Information Processing Systems (NIPS’23); 2024 Dec 10–16. New Orleans, LA, USA. Red Hook, NY, USA: Curran Associates Inc. p. 653–71. [Google Scholar]

23. Zhang J, Hua Y, Wang H, Song T, Xue Z, Ma R, et al. FedALA: adaptive local aggregation for personalized federated learning. Proc AAAI Conf Artif Intell. 2023;37(9):11237–44. doi:10.1609/aaai.v37i9.26330. [Google Scholar] [CrossRef]

24. Collins L, Hassani H, Mokhtari A, Shakkottai S. Exploiting shared representations for personalized federated learning. In: Meila M, Zhang T, editors. Proceedings of the 38th International Conference on Machine Learning; 2021 Jul 18–24. Red Hook, NY, USA: Curran Associates Inc. p. 2089–99. [Google Scholar]

25. Ozkara K, Singh N, Data D, Diggavi S. QuPeD: quantized personalization via distillation with applications to federated learning. In: Proceedings of the 35th International Conference on Neural Information Processing Systems; 2021 Dec 6–14; Red Hook, NY, USA: Curran Associates Inc. p. 277–89. [Google Scholar]

26. Zhou S, Wang Y, Chen D, Chen J, Wang X, Wang C, et al. Distilling holistic knowledge with graph neural networks. In: Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV); 2021 Oct 10–17; Montreal, QC, Canada. p. 10367–76. [Google Scholar]

27. Chen P, Liu S, Zhao H, Jia J. Distilling knowledge via knowledge review. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2021 Jun 20–25; Nashville, TN, USA. p. 5006–15. [Google Scholar]

28. Ahn JH, Simeone O, Kang J. Wireless federated distillation for distributed edge learning with heterogeneous data. In: Proceedings of the 2019 IEEE 30th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC); 2019 Sep 8–11; Istanbul, Turkey. p. 1–6. [Google Scholar]

29. Wu Y, Zhang S, Yu W, Liu Y, Gu Q, Zhou D, et al. Personalized federated learning under mixture of distributions. In: Krause A, Brunskill E, Cho K, Engelhardt B, Sabato S, Scarlett J, editors. Proceedings of the 40th International Conference on Machine Learning; 2023 Jul 23–29; Honolulu, HI, USA. p. 37860–79. [Google Scholar]

30. Zhang H, Li CL, Dai WR, Zou JN, Xiong HK. FedCR: personalized federated learning based on across-client common representation with conditional mutual information regularization. In: Krause A, Brunskill E, Cho K, Engelhardt B, Sabato S, Scarlett J, editors. Proceedings of the 40th International Conference on Machine Learning; 2023 Jul 23–29; Honolulu, HI, USA. p. 41314–30. [Google Scholar]

31. Ye R, Ni Z, Wu F, Chen S, Wang Y, Ye R, et al. Personalized federated learning with inferred collaboration graphs. In: Krause A, Brunskill E, Cho K, Engelhardt B, Sabato S, Scarlett J, editors. Proceedings of the 40th International Conference on Machine Learning; 2023 Jul 23–29; Honolulu, HI, USA. p. 39801–17. [Google Scholar]

32. Wang J, Yang X, Cui S, Che L, Lyu L, Xu D, et al. Towards personalized federated learning via heterogeneous model reassembly. In: Proceedings of the 37th International Conference on Neural Information Processing Systems; 2023 Dec 10–16; New Orleans, LA, USA. p. 29515–31. [Google Scholar]

33. Bao W, Wei T, Wang H, He J, Bao W, Wei T, et al. Adaptive test-time personalization for federated learning. In: Proceedings of the 37th International Conference on Neural Information Processing Systems; 2023 Dec 10–16; New Orleans, LA, USA. p. 77882–914. [Google Scholar]

34. Zhu H, Xu J, Liu S, Jin Y. Federated learning on non-IID data: a survey. Neurocomputing. 2021;465(4–2):371–90. doi:10.1016/j.neucom.2021.07.098. [Google Scholar] [CrossRef]

35. Duan M, Liu D, Ji X, Liu R, Liang L, Chen X, et al. FedGroup: efficient federated learning via decomposed similarity-based clustering. In: 2021 IEEE Intl Conf on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing, Sustainable Computing & Communications, Social Computing & Networking (ISPA/BDCloud/SocialCom/SustainCom); 2021 Sep 30–Oct 3; New York, NY, USA. p. 228–37. doi:10.1109/ISPA-BDCloud-SocialCom-SustainCom52081.2021.00042. [Google Scholar] [CrossRef]

36. Blumenberg L, Ruggles KV. Hypercluster: a flexible tool for parallelized unsupervised clustering optimization. BMC Bioinform. 2020;21(1):428. doi:10.1186/s12859-020-03774-1. [Google Scholar] [PubMed] [CrossRef]

37. Ruan Y, Joe-Wong C. FedSoft: soft clustered federated learning with proximal local updating. Proc AAAI Conf Artif Intell. 2022;36(7):8124–31. doi:10.1609/aaai.v36i7.20785. [Google Scholar] [CrossRef]

38. Deng L. The MNIST database of handwritten digit images for machine learning research [best of the web]. IEEE Signal Process Mag. 2012;29(6):141–2. doi:10.1109/MSP.2012.2211477. [Google Scholar] [CrossRef]

39. Xiao H, Rasul K, Vollgraf R. Fashion-MNIST: a novel image dataset for benchmarking machine learning algorithms. arXiv:1708.07747. 2017. [Google Scholar]

40. Krizhevsky A, Hinton G. Learning multiple layers of features from tiny images. Toronto, ON, Canada: University of Toronto; 2009. [Google Scholar]

41. Krizhevsky A, Sutskever I, Hinton GE. ImageNet classification with deep convolutional neural networks. In: Pereira F, Burges CJ, Bottou L, Weinberger KQ, editors. 26th Annual Conference on Neural Information Processing Systems 2012; 2012 Dec 3–6; Lake Tahoe, NV, USA. doi:10.1145/306538. [Google Scholar] [CrossRef]

42. McMahan B, Moore E, Ramage D, Hampson S, Arcas BA. Communication-efficient learning of deep networks from decentralized data. In: Singh A, Zhu J, editors. Proceedings of the 20th International Conference on Artificial Intelligence and Statistics; 2017 Apr 20–22; Fort Lauderdale, FL, USA. p. 1273–82. [Google Scholar]

43. Arivazhagan MG, Aggarwal V, Singh AK, Choudhary S. Federated learning with personalization layers. arXiv:1912.00818. 2019. [Google Scholar]

44. Liang PP, Liu T, Liu Z, Allen NB, Auerbach RP, Brent D, et al. Think locally, act globally: federated learning with local and global representations. arXiv:2001.01523. 2020. [Google Scholar]

45. Oh J, Kim S, Yun SY. FedBABU: towards enhanced representation for federated image classification. arXiv:2106.06042. 2021. [Google Scholar]

46. Nguyen AT, Torr PHS, Lim SN. FedSR: a simple and effective domain generalization method for federated learning. In: Proceedings of the 36th International Conference on Neural Information Processing Systems; 2022 Nov 28–Dec 9; New Orleans, LA, USA. p. 38831–43. [Google Scholar]