Phasmatodea Population Evolution Algorithm Based on Spiral Mechanism and Its Application to Data Clustering

1  Introduction

Clustering represents a method of unsupervised learning, and the original purpose of cluster analysis is to put physical objects with similar characteristics in people’s lives together, grouping the samples in a dataset in such a way that the similarity of the samples in the same group is maximized and the similarity of the samples in different groups is minimized [1]. In the field of data analysis, clustering analysis, as one of the most representative methods, has been studied in depth by researchers. Traditional clustering methods primarily consist of partition-based, hierarchical [2], grid-based [3], and model-based algorithms [4], among others. In addition, there are density-based clustering algorithms [5]. The division-based c lustering is currently among the most commonly used clustering techniques, and its core idea is: for the dataset containing N samples, the clusters are defined in advance to be L in number, and then the whole dataset is divided into L clusters by successively optimizing a certain objective as the division criterion until the end of the iteration.

Of these, the K-means algorithm is the most widely used partitioning method in practical applications [6,7]. Therefore, it is extensively applied in pattern recognition, data processing, model classification and other fields. With the progress of technology and the increased demand for large-scale data processing, the application of K-means algorithm also shows a trend of continuous expansion. Meanwhile, as clustering algorithms are studied more extensively, providing new possibilities for more efficient and accurate processing of various data types. Therefore, the K-means algorithm still holds an important position in today’s data analysis field and is constantly evolving and developing, providing powerful tools and support for solving practical problems [8].

However, K-means has some limitations when performing clustering optimization, such as its results depend on the initial conditions, leading to locally optimal solutions. To address the challenge of local optima, a lot of research has been done in clustering. Researchers have increasingly turned their attention to harnessing the inherent principles of the natural world for computational purposes through the advancement of meta-heuristic algorithms. In the context of life sciences, they began to explore the swarm intelligence behavior exhibited by living organisms (e.g., chromosomes) and animal populations. This collective intelligence phenomenon has garnered interest from numerous scholars globally [9,10]. Drawing inspiration from the intelligence and behaviors found in nature, these algorithms offer innovative approaches to tackling complex problems [11].

Typical metaheuristic algorithms include Genetic Algorithm (GA) [12,13], Coyote Optimization Algorithm (COA) [14], Cuckoo Search (CS) [15], Differential Evolution (DE) [16,17], Harmony Search (HS) [18], Biogeography-Based Optimization (BBO) [19], Particle Swarm Optimization (PSO) [20–22], Grey Wolf Optimizer (GWO) [23,24], Whale Optimization Algorithm (WOA) [25,26], Butterfly Optimization Algorithm (BOA) [27], Archimedes Optimization Algorithm (AOA) [28], Harris Hawks Optimization (HHO) [29] and Ant Colony Optimization (ACO) [30,31]. These algorithms collectively fall under the umbrella term Swarm Intelligence Optimization Algorithm (SIOA). SIOA has many advantages, including easy to find potential solutions, simple parameter tuning, easy to implement, and more effective information exchange between individuals. However, there is no single SIOA that is universally effective for all optimization challenges, as each has its own strengths and weaknesses. Therefore, many researchers have worked on proposing a large number of novel SIOAs and improving the existing algorithms [32]. These improvements include hybridization of algorithms, optimization of parameter tuning strategies, and personalized algorithms designed for specific problems. The goal of these efforts is to continuously expand the applicability of SIOA to better address different types of optimization challenges and to promote the application and development of optimization algorithms in practice.

The Phasmatodea Population Evolution Algorithm (PPE) proposed by Song et al. [33] was inspired by evolutionary features observed in Phasmatodea populations. Since the algorithm was proposed, researchers have successfully applied it to a number of fields, demonstrating its competitiveness. For example, the PPE has been utilized to optimize downlink power allocation in fifth-generation heterogeneous networks, and it has also been applied to task scheduling optimization in cloud computing environments. These experimental findings indicate that the PPE population evolution algorithm holds significant promise [34,35].

We integrate PPE with K-means for optimization.This fusion can effectively utilize advantages such as the more powerful global search capability of PPE to boost the performance of K-means in global search. However, PPE also suffers from the challenge of being prone to local optimal solutions. Therefore, in this paper, we will further optimize PPE and apply it to the K-means clustering optimization problem. To address these issues, in this study, a Phasmatodea population evolution algorithm with a spiral mechanism (SPPE) is designed, and SPPE also incorporates a balancing factor, which achieves good results in data clustering. The primary contributions outlined in this paper include:

1. To bolster the local search capability and foster population diversity, we integrated the Variable Neighborhood Search factor into our approach.

2. A position update model is introduced, featuring a novel position update formula and a spiral function designed to enhance the exploration capabilities of PPE.

3. Based on the fitness value, a proposed balancing factor is added to the PPE through the information guidance strategy although it can enhance the development efficiency of the PPE.

4. SPPE is evaluated against various algorithms on CEC2013, and the results demonstrate that SPPE performs well on most functions.

5. In the data clustering application, SPPE is assessed alongside several clustering techniques, and the experimental findings indicate that SPPE surpasses the other methods.

The subsequent sections of the paper are structured as follows: Section 2 presents related work, while Section 3 provides an exposition on the traditional PPE algorithm. Section 4 outlines the SPPE algorithm and CEC2013 experiments in detail. Section 5 conducts clustering experiments and compares them with existing methods to evaluate the performance of the SPPE algorithm. Section 6 gives conclusions.

2  Related Work

K-means partitions the dataset into mutually exclusive clusters based on specific criteria, making the data objects within the same cluster more similar. Assume initial clustering centers in the sample set , where represents the number of samples. The cluster centers are represented as and denotes the distance between different data objects and the cluster centers, calculated using the Euclidean distance.

(1)

where indicates the dimension of the data sample, denotes the data sample, is the value in the -th dimension of .

The termination condition for K-means iteration is typically that the points in each cluster remain unchanged. Additionally, the new cluster centroid is determined by averaging all the points within the cluster, it can be judged according to the change of Sum of Square Errors (SSE), which is commonly used in mathematics as shown in Eq. (2):

(2)

Given that the position of the data object point remains constant, if the cluster center also remains unchanged, the SSE value will not vary, indicating that the iteration can be concluded.

To overcome the limitations of K-means, extensive research has been conducted on clustering techniques. A DE method based on one-step K-mean clustering to cope with unconstrained global optimization problems, called clustering-based DE, was proposed by Cai et al. [36]. By fully leveraging the population information, one-step K-means clustering substantially enhances the performance of DE. Nayak et al. [37] introduced FA-K-means, a firefly-inspired K-means algorithm. The approach leverages the firefly algorithm’s global search ability to perform efficient cluster analysis. The Enhanced Shuffled Bat Algorithm (EShBAT), developed by Chaudhary et al. [38], is an improved variant of the Bat Algorithm. A key feature of EShBAT is that it divides the bat population into independent groups called memeplexes, where each group evolves independently using the Bat Algorithm, and it has achieved success in numerical optimization tasks. This study introduces a hybrid algorithm called HESB that combines K-means, K-medoids and EShBAT. This creates a diverse initial population for EShBAT, resulting in an effective clustering algorithm.

Huang [39] proposed a novel method for color image quantization that utilizes the Artificial Bee Colony (ABC) algorithm to choose N colors from M available options for the initial palette, followed by an accelerated K-means lgorithm. Additionally, a sampling process is introduced to reduce the computation time. García et al. [40] proposed a method called K-means combined with the Cuckoo Search algorithm. This method utilizes K-means for discretizing solutions and employs the CS algorithm for optimizing in the continuous domain. Pal et al. [41] combined the Black Hole for data clustering with K-means to achieve better results. The method utilizes some optimization outcomes from K-means to initialize a portion of the population, while the remaining portion is initialized randomly.

3  Principle of PPE

The PPE algorithm originated from the observation and study of the survival characteristics of Phasmatodea populations in natural environments and their population dynamics. In the PPE algorithm, the Phasmatodea population is defined as having two key attributes: population growth rate and population quantity. Its primary aim is to address the challenge of finding a globally optimal solution within a multidimensional space, where the optimal position of the Phasmatodea population is regarded as a candidate for the global optimum. The application of this algorithm benefits from a more profound understanding of the ecological properties of biological populations.

The representation of a Phasmatodea population in n-dimensional space is given by the expression , where each dimension represents a natural characteristic of that population of Phasmatodea. Generate populations using Eq. (3).

(3)

Two of the most significant attributes of Phasmatodea populations that best reflect their outcomes as influenced by environmental and other factors are the growth rate and the population quantity . Firstly, takes values between 0 and 4, and secondly, is determined using the following formula:

(4)

where denotes the number of Phasmatodea populations. The evolutionary trend in PPE is mainly guided by the first L historical optimal solutions, which are stored into .

(5)

The formula for adjusting the position of the Phasmatodea population is as follows:

(6)

(7)

If the population shows improvement after updating its position compared to before, the population’s can be divided into three parts. First, the population will approach the nearest historical optimal solution, which reflects the self-determination property of the Phasmatodea population. Second, the population will maintain a relatively stable trend through path-dependent effects. Finally, the population may adjust the trend through mutation.

(8)

(9)

(10)

(11)

(12)

When the distance between and is below the G, the geographic locations of these two populations collide, which in turn triggers competition between the populations. In this case, the population’s and values are:

(13)

(14)

The core mechanism of PPE is built upon this foundation. First, convergent evolution emphasizes how environmental constraints guide populations toward locally optimal solutions, balancing local and global search. Second, path dependence highlights the influence of historical decisions on evolutionary trends, enabling efficient adaptation to changing environments while preserving successful past trajectories. Third, population mutation helps escape local optima, enhancing adaptability in dynamic or multi-modal landscapes. Fourth, the population size and competition model illustrates how resource limitations and competition drive diversity and improve performance, particularly in multi-modal optimization. Together, these mechanisms enable PPEA to balance exploration and exploitation dynamically, offering a robust framework for solving complex, high-dimensional, and dynamic optimization problems.

4  Improved PPE Algorithm: SPPE

4.1 Variable Neighborhood Search

Hansen et al. [42] proposed the Variable Neighborhood Search (VNS) algorithm, which initially defines a set of neighborhoods that are considered potential good solutions. The core concept of VNS is to systematically modify the neighborhood structures of multiple solutions during the local search process. Under the condition of identical initial solutions, this process deepens and broadens the search space, thus improving the effectiveness of the local search. VNS focuses on locking the superior solutions in the solution space quickly by the fast transformation between different neighborhood structures.

By integrating the VNS strategy, SPPE systematically alters the neighborhood structures during the local search process. This enables the algorithm to lock high-quality solutions quickly and enhances its ability to perform deep searches in locally optimal regions. Such systematic modification of search patterns is a unique addition that sets SPPE apart from traditional metaheuristic algorithms.

In the PPE algorithm, when a particle falls into a local optimal solution, in order to search for the particle in a wider neighborhood, we need to extend the search for the direction of movement of the particle to find a more superior direction. Incorporating the key features of VNS into the PPE results in a powerful PPE algorithm. Another feature of the PPE algorithm with the introduction of VNS is to re-initialize the search for the locally optimal neighborhood. The pseudocode of the VNS algorithm is shown in Algorithm 1.

represents the -th neighborhood structure of . By exploring broader neighborhoods when stuck in local optima, the algorithm intensifies the search when a better solution is found and diversifies the search when local exploration is exhausted. This systematic adjustment ensures robustness, enabling the algorithm to escape from local optima and discover globally superior solutions.

4.2 Spiral Mechanism

The second stage of PPE remains close to only the nearest optimal solution even when convergent evolution is ineffective. In this approach, position updates rely solely on previous movement direction. This will hinder the algorithm’s convergence speed, so we propose adopting a spiral search mechanism. Unlike conventional search strategies that often rely on linear or random exploration, the spiral mechanism introduces a dynamic and expansive search trajectory. This approach allows the algorithm to explore the solution space more effectively, avoiding duplicate paths and improving global search capabilities. The spiral mechanism also helps maintain population diversity, which is crucial for escaping local optima.

This mechanism offers a broader range of exploration opportunities for the Phasmatodea, enabling it to better adjust its position through multiple search paths. Simultaneously, this mechanism fully utilizes the top k best positions from the existing Phasmatodea population, thereby enhancing the capability to discover the global solution throughout the optimization process. The spiral mechanism leverages a logarithmic spiral model to ensure diverse exploration paths. The position update formula is:

(15)

(16)

(17)

where is the spiral shape constant, which is set to a value of 1 and represents the spiral exploration factor. denotes the path coefficient, which is a random number in . The exponential term allows the search radius to expand or contract dynamically, providing a fine balance between exploration and exploitation. Meanwhile, the cosine term ensures variability in the search direction, enabling broader coverage of the solution space and improving the global search performance.

Individuals of Phasmatodea use a spiral advance strategy during search. Unlike straight lines, spiral advancement uses a straight line as the central axis, which makes the individual move in a spiral when moving towards the target individual. This strategy minimizes the possibility of generating duplicate individuals. The integration of a spiral mechanism into the position updating process enhances the Phasmatodea’s ability to explore unknown regions, effectively improving the algorithm’s global search performance.

4.3 Balancing Factor

We use the value of the fitness function to form a balancing factor, and this dynamic adjustment strategy enhances the algorithm’s search effectiveness and efficiency across various search stages. This way, the SPPE will become more flexible, which can improve the algorithm’s search efficiency. The balancing factor dynamically adjusts the exploration and exploitation tendencies of the algorithm based on fitness values. This mechanism ensures a more adaptive search process, allowing SPPE to maintain a fine balance between global and local optimization. It improves convergence speed and enhances the algorithm’s robustness in different stages of the search.

(18)

Ensures that individuals with better fitness have a stronger influence during population updates. This mechanism reduces the premature convergence common in other algorithms by preventing excessive exploitation of local optima. The updated population parameter:

(19)

The population quantity incorporates this balancing factor to maintain diversity while focusing on promising areas of the search space. This balance between exploration and exploitation enhances the convergence rate while maintaining sufficient diversity to avoid stagnation in suboptimal regions. Introducing a balance factor into the process of updating the population quantity helps to fully utilize effective information within the population and enhancing its ability to escape local optimal solutions. Through this approach, significant improvements in optimization speed and accuracy can be achieved. Algorithm 2 outlines the pseudocode of the SPPE algorithm.

4.4 Complexity Analysis

The time complexity of the algorithm mainly depends on population initialization and iterative optimization. The population initialization time complexity of the SPPE algorithm is , where is the population size, and is the dimension of the solution space. In each iteration, the SPPE algorithm includes four key steps: population position updating in the PPE algorithm, the spiral mechanism, VNS, and balancing factor updates.

Among them, the population position updating and spiral mechanism both involve position updates, with a time complexity of ; the balancing factor update only requires simple arithmetic operations, resulting in a time complexity of . The VNS involves checking multiple neighborhood structure. Assuming the number of neighborhood structures is , the overall complexity of VNS is . In SPPE, the probability of triggering VNS in each iteration is 0.7, and three neighborhood structures are used (), so the complexity of VNS is .

In summary, the total time complexity of each SPPE iteration is . Considering the algorithm runs for I iterations, the total time complexity is . This complexity is equivalent to the standard PPE algorithm’s time complexity of .

To further demonstrate the computational performance of SPPE, we analyzed its runtime under the same experimental conditions and compared it with other algorithms. The runtime results (in seconds) are as follows: SPPE: 490.20, PPE: 420.19, PSO: 130.38, HHO: 560.90, GWO: 140.67, AOA: 145.80, GA: 207.3, BOA: 422.86. Although the runtime of SPPE is slightly higher than its predecessor PPE due to the additional computational costs of the spiral mechanism and VNS, SPPE still demonstrates competitiveness compared to other algorithms. For instance, SPPE outperforms HHO in terms of runtime while offering better robustness and convergence. Although algorithms like PSO, GWO, and GA have shorter runtimes, SPPE’s enhanced optimization capability proves that the moderate increase in computational cost is justified.

Similar to PPE, SPPE’s space complexity is determined by population storage () and historical best positions (). Auxiliary components like the spiral mechanism, VNS, and balancing factor require space. Thus, the total space complexity of SPPE is .

In conclusion, compared to PPE, SPPE achieves significant improvements in robustness and convergence while maintaining a time complexity of . Additionally, its computational cost is comparable to other popular algorithms, making it an efficient solution for complex optimization problems.

4.5 Experiments and Data Evaluation

In this section, Our experimental tests performed on a computer with an operating system of Windows 11 and software of MATLAB R2022a are tested using 28 benchmark functions from the CEC2013. Additionally, a more intuitive comparison of the algorithms was conducted through curve analysis of the fitness values. We compared the SPPE algorithm with the PPE algorithm, AOA algorithm, PSO algorithm, HHO algorithm, GWO algorithm, GA algorithm, and BOA algorithm. The parameter configurations for these algorithms are shown in Table 1.

To ensure fairness, each algorithm was subjected to 1000 function iterations with a total of 30 independent function runs, and the solution space range was set to [−100, 100]. We evaluated the algorithms in 10, 30, and 50 dimensions, recording the mean and variance of their results. Additionally, we conducted the Friedman test and obtained the Friedman rankings, which are displayed in Tables 2–4. In these tables, the bold data values represent the best results in each function. Observing the tables reveals SPPE’s outstanding performance across all dimensions, with its efficacy progressively enhancing as the dimensions expand. We conducted a Wilcoxon rank-sum test at a significance level of 0.05 to compare the optimization results of SPPE with those of other algorithms. In the table, a “+” indicates that the results of the SPPE algorithm outperform those of its comparison algorithms, “=” signifies that the results are similar, and “−” indicates that the SPPE algorithm’s results are inferior to those of its comparison algorithms. The results in the table indicate that the SPPE algorithm has a significant advantage in seeking optimal solutions compared to other algorithms, outperforming most of them. From the results presented in Tables 2–4, it can be observed that, in most cases, there is a statistically significant difference between the SPPE algorithm and the competing algorithms in the Wilcoxon signed-rank test. Furthermore, when such significant differences exist, the SPPE algorithm demonstrates a clear statistical advantage over the competing algorithms. This further validates the effectiveness of the SPPE’s improvement strategies and its superiority under various test conditions.

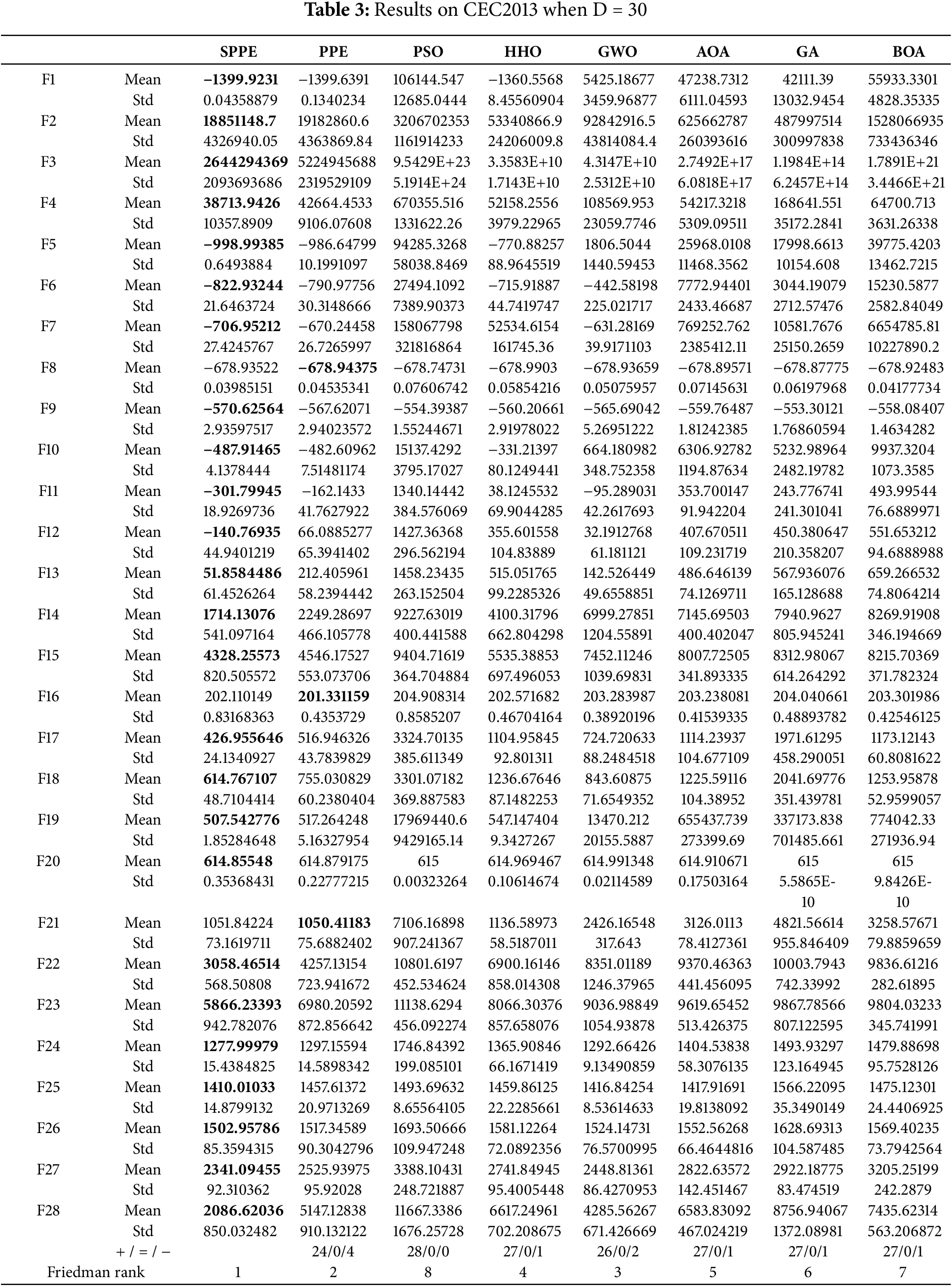
Finally, we illustrate the convergence curves of the SPPE and other algorithms in Figs. 1 and 2 for a dimensionality of 50. It is clear that the SPPE algorithm demonstrates superior convergence in F1, F6, F10, F12, F21, F27, and F28 compared to the other algorithms, as it reaches the optimal value more rapidly. The substantial advantage exhibited by the SPPE algorithm over the others underscores its superior capability in exploring and evading local optima. In functions F9, F15, F22, and F23, while SPPE may not initially surpass PPE and GWO, its curve continues to decline while PPE converges. This suggests that SPPE retains significant potential in the later stages of algorithmic exploration. In summary, SPPE’s capability to avoid local optima and effectively find the global optimum has seen significant enhancement following the implemented improvements.

Figure 1: Partial convergence curves of CEC2013 unimodal functions and basic multimodal functions

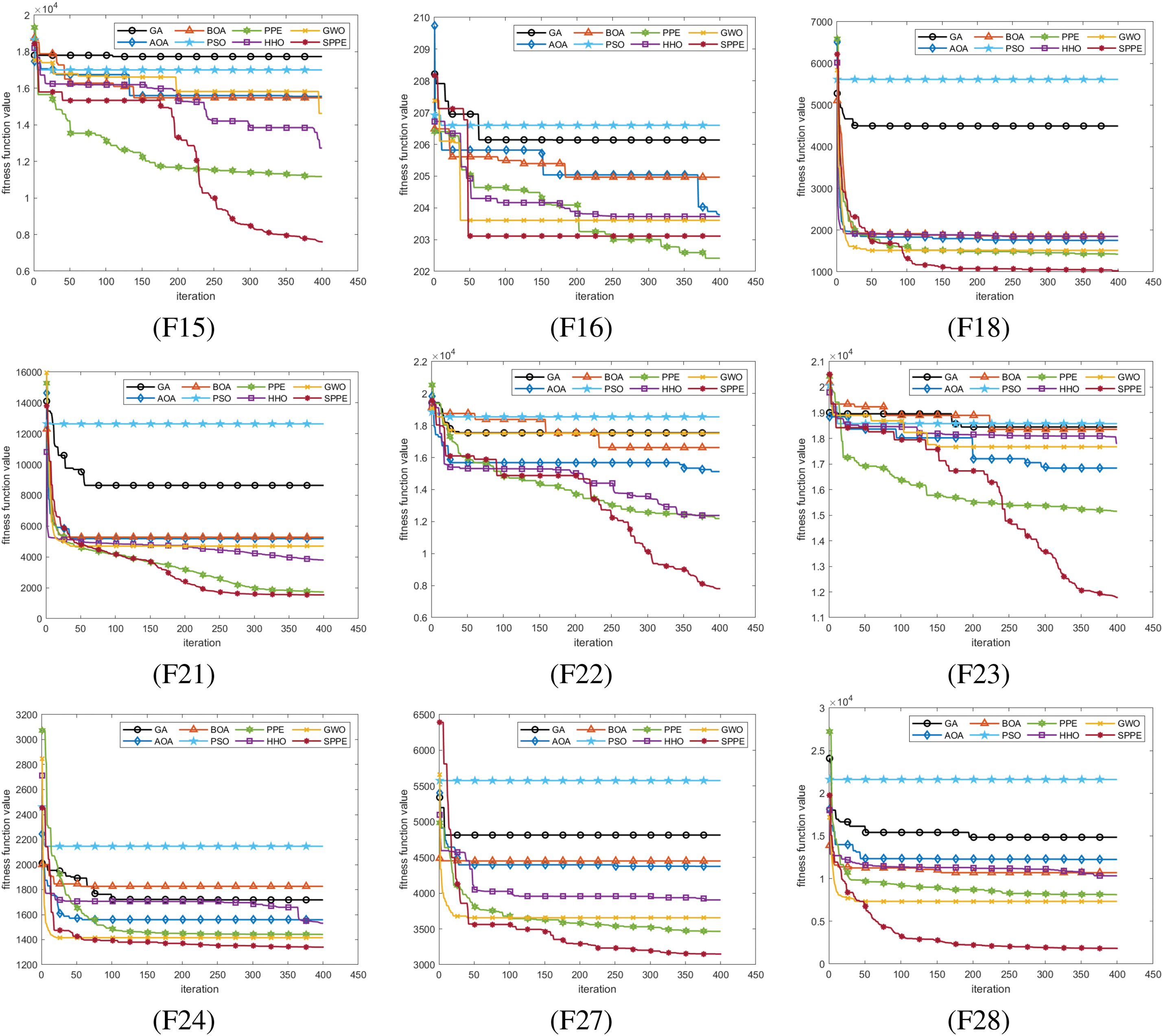
Figure 2: Partial convergence curves of CEC2013 basic multimodal functions and composition functions

4.6 Ablation Study

In order to verify the effectiveness and impact of the improved strategy proposed in this paper on the performance improvement of PPE algorithm, we conducted the following experiments: SPPE represents the PPE algorithm that combines multiple strategies, while SPPE1, SPPE2, and SPPE3 represent the PPE algorithm that uses spiral mechanism, VNS, and balancing factor to optimize a single strategy, respectively. Through these ablation experiments, we aim to evaluate the specific effects of each improvement strategy on the performance of PPE algorithms. The results are shown in Table 5. From the comprehensive evaluation of mean and standard deviation, the three single-strategy optimized PPE algorithms perform significantly better than the original PPE algorithm in 25 out of 28 functions, which indicates that the proposed improvement strategies effectively enhance the performance of the algorithms.

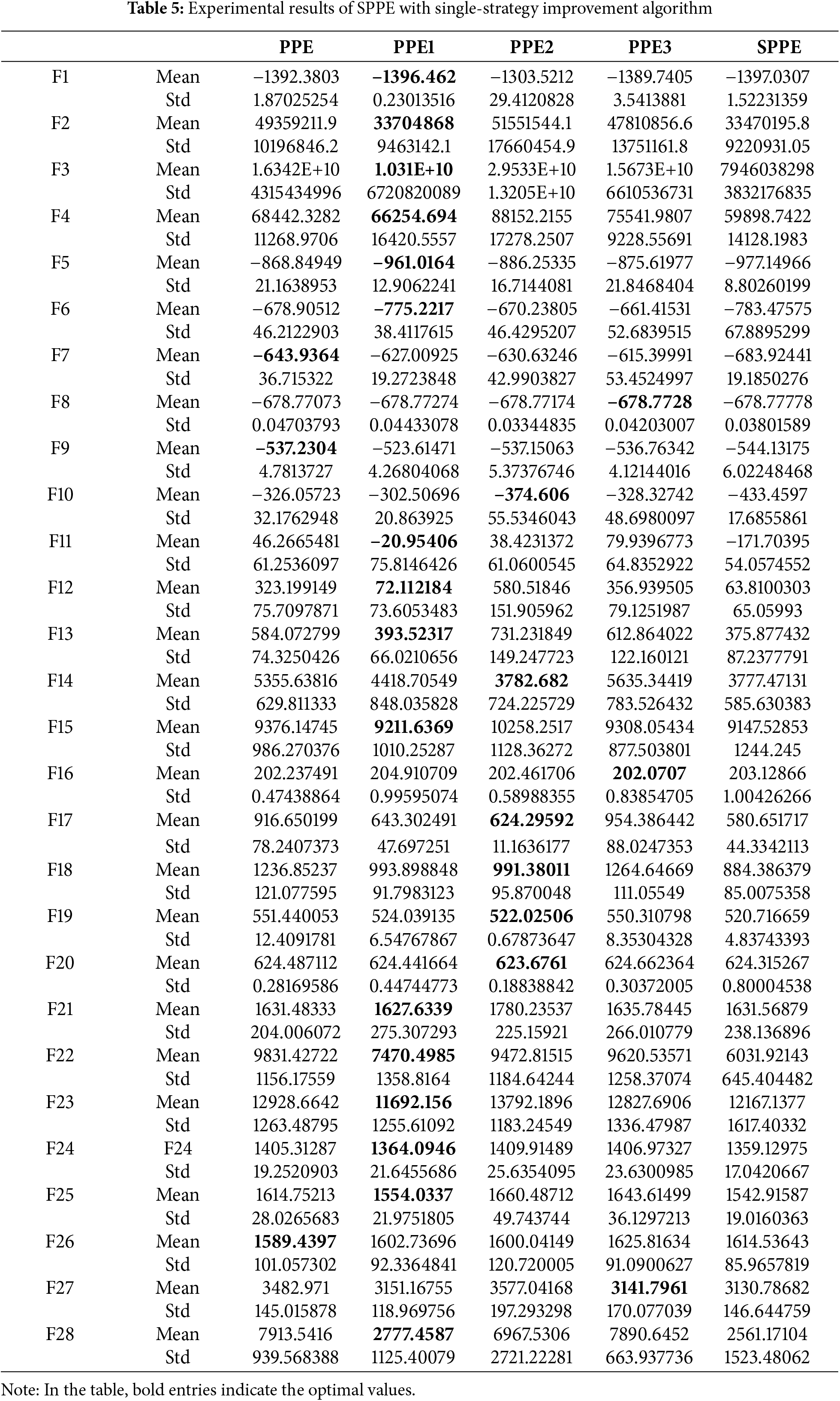
On unimodal functions and composition functions, SPPE1 reaches the optimal solution among the 4 algorithms, which is superior to other single-strategy optimization PPE algorithms and similar to the data obtained by the SPPE algorithm. This indicates that the spiral mechanism optimization strategy has significant effect in improving the performance of the algorithm on single peaked functions, especially in enhancing the algorithm’s ability to find the optimal solution.

On basic multimodal functions, SPPE2 and SPPE3 perform comparably on functions F7 F10, but on other functions, the notation of SPPE2 outperforms most of the other PPE algorithms optimized by a single strategy. Therefore, this verifies that the VNS optimization strategy is significantly effective in improving the algorithm’s global exploration and local exploitation.

The experimental data of SPPE3 on functions F8, F16, F27 outperforms other improved algorithms. Although SPPE3 has no obvious shortcomings in improving the algorithm’s optimization searching ability or local exploitation ability compared to SPPE1 and SPPE3, it helps to balance the algorithm’s performance in a comprehensive way.

In the above experimental data, the SPPE algorithm is less than or equal to other improved algorithms except in 4 functions. It shows that the fusion of multiple strategies makes the PPE optimization algorithm combine the advantages of each improvement strategy to improve the performance of the algorithm, and rely on the effect of different strategies to neutralize the shortcomings of each improvement strategy, avoiding the influence of the shortcomings of the improvement strategy on the algorithm.

5  SPPE Applied to Data Clustering

5.1 SPPE-K-Means

To address the dependency of K-means on the initial cluster centers, we propose an improved K-means algorithm that leverages the rapid convergence of the SPPE algorithm and its capability to efficiently find the global optimal solution. The SPPE algorithm optimizes the position of Phasmatodea through iterative updates, and using the final optimal solution as the clustering center, instead of the clustering center obtained by the traditional algorithm after random initialization which has uncertain factors. To validate the clustering performance of SPPE in this paper, classic datasets from the UCI repository including Wine, Iris, Zoo, Glass, Pima, Ionosphere, and Vehicle were selected for experimentation. The dataset’s comprehensive information is provided in Table 6.

5.2 Analysis of Clustering Experiment Results

In this simulation experiment, GA, PSO, GWO, PPE, HHO, AOA, BOA and SPPE are introduced for comparison, and the algorithms are iterated for 100 times and run independently for 10 times, and the experimental findings are presented in Tables 7–9.

In this paper, we utilize Within-Cluster Sum of Squares (WCSS), Silhouette Coefficient (Sc) and the Davies-Bouldin Index (DBI). Sc is used to evaluate the goodness of clustering effect, DBI index is used as a metric to evaluate the performance of clustering algorithms, and WCSS is a widely used method of evaluating the effectiveness of clustering.

(20)

where represents the set of all samples in the -th cluster. The smaller the WCSS, the better the clustering performance of the algorithm. Sc combines the tightness within a cluster and its separation from other clusters. The value of Silhouette Coefficient ranges from −1 to 1, the closer to 1, the better the clustering result.

(21)

The average distance value of a sample to other points in the same cluster is and is the average distance value of a sample to samples in different clusters closest to it. The DBI index assesses the closeness between clusters and the proximity of sample points within clusters once the clustering process is finished.

(22)

(23)

where denotes the number of clusters, signifies the average distance from all samples in the -th cluster to its center, indicates the number of samples in the -th cluster, and is the distance between the centroids of the -th and the -th clusters. The DBI index represents the ratio of the tightness within clusters to the separation between clusters. A higher level of tightness within clusters, coupled with greater separation between them, indicates a more effective clustering outcome.

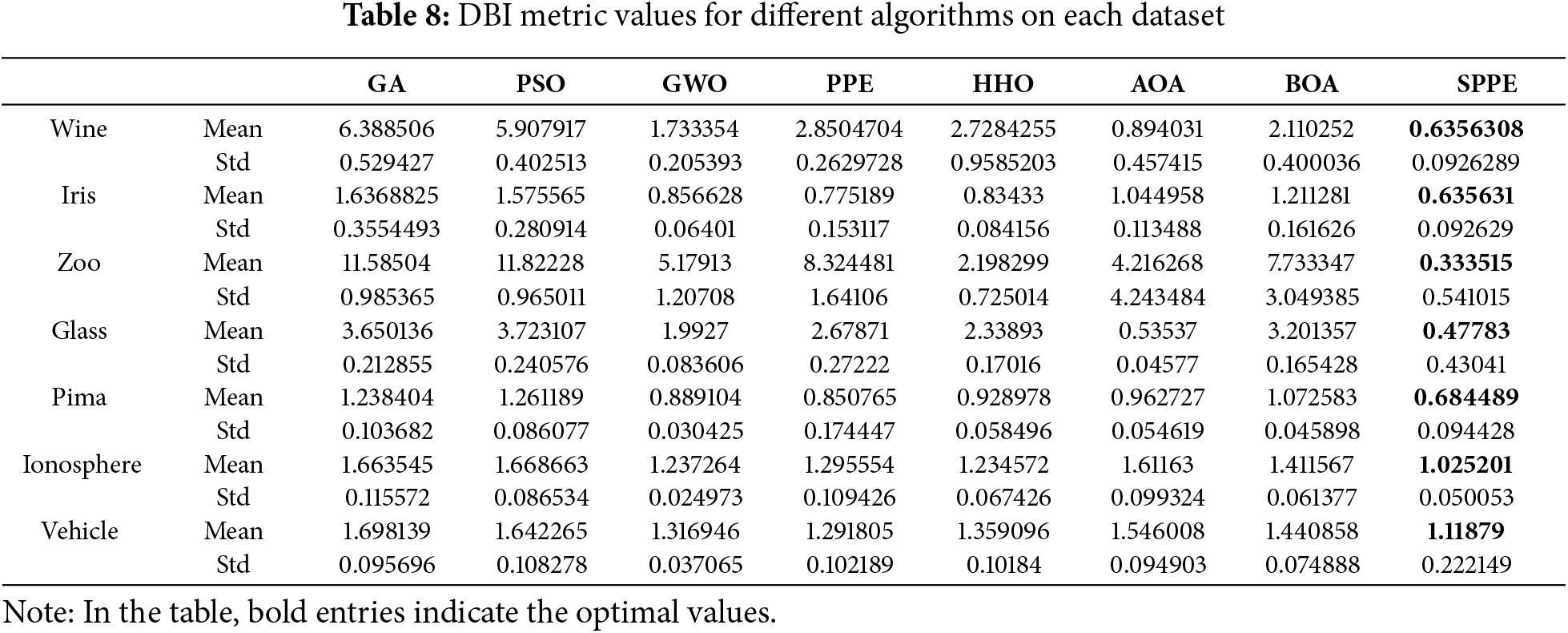
Table 7 displays the WCSS indicator values of the algorithms on each dataset. On the Zoo dataset, the results of SPPE are not as good as those of the HHO algorithm. However, in datasets such as Iris and Wine where data separation is not distinct, the WCSS results of SPPE-K-means clustering algorithm are improved. Meanwhile, on complex datasets like Pima and Glass, the clustering performance of SPPE-K-means is notably superior to other algorithms. This supports the effectiveness of the enhanced algorithm presented. Table 8 displays the DBI metric values for the algorithm across the datasets. On each dataset, the results of SPPE consistently yield the minimum value, indicating that incorporating the SPPE algorithm into K-means improves its clustering effectiveness. This result verifies that the SPPE-K-means algorithm has a good clustering effect on these seven datasets, effectively reduces the dependence of K-means on the initial clustering centers, and shows that K-means combined with the SPPE algorithm can improve its clustering effect. The Sc results, as shown in Table 9, indicate that the SPPE algorithm outperforms other algorithms on most datasets, except for the Pima dataset. This demonstrates that the intra-cluster samples are tightly distributed, and the clustering performance is significant, providing a strong basis for evaluating the clustering effectiveness. In summary, the SPPE algorithm can be effectively used in the field of clustering analysis and has strong applicability.

6  Conclusion and Future Work

The SPPE-based K-means algorithm proposed in this paper, which obtains optimized cluster centers, addresses the issue of K-means’ significant dependency on the initial cluster centers. Firstly, VNS is introduced to quickly lock the high quality solutions. Secondly, by integrating the proposed spiral factor updating formula, individual search space is expanded, enhancing global search capability, thereby improving search efficiency and convergence speed. Finally, the balancing factor fully utilizes the effective information from the Phasmatodea population, making the SPPE algorithm more flexible, enhancing its exploration capabilities, and establishing a more balanced SPPE algorithm for exploration and exploitation.

Subsequently, we carried out extensive experiments on the SPPE algorithm with the CEC2013 benchmark functions. The experimental findings indicate that the SPPE algorithm offers notable benefits regarding performance and greatly enhances convergence. In addition, we also conducted clustering experiments based on the UCI dataset. The experimental findings indicate that K-means clustering, when based on the SPPE algorithm, demonstrates enhanced optimization capability and offers greater clustering stability.

Future research can focus on optimizing SPPE’s performance by developing adaptive parameter adjustment methods to dynamically optimize key parameters (e.g., spiral mechanism, balancing factor) based on problem characteristics, enhancing adaptability. Additionally, as SPPE’s computational complexity grows with population size and problem dimensionality, future studies will explore parallelization strategies, such as GPU acceleration or distributed frameworks, to improve scalability and efficiency for large-scale problems. These efforts will further enhance SPPE’s robustness, efficiency, and practical application value.

While this study demonstrates the effectiveness of SPPE in data clustering, future research will explore its application to more complex tasks. SPPE can be applied to image segmentation, dividing images into meaningful regions based on features like pixel intensity or texture, and is well-suited for non-convex, high-dimensional search spaces. It could also analyze high-dimensional biological data, such as gene expression or protein interaction networks, to uncover meaningful patterns. These applications will further validate SPPE’s utility across diverse and complex domains, enhancing its relevance in both theory and practice.

Acknowledgement: The authors are grateful to editor and reviewers for their valuable comments.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Jeng-Shyang Pan and Mengfei Zhang; data collection: Jeng-Shyang Pan, Mengfei Zhang and Xingsi Xue; analysis and interpretation of results: Mengfei Zhang, Shu-Chuan Chu and Václav Snášel; draft manuscript preparation: Xingsi Xue and Václav Snášel. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are availale within the article. The original dataset can be found at: https://archive.ics.uci.edu/datasets (accessed on 26 December 2024).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Saxena A, Prasad M, Gupta A, Bharill N, Patel OP, Tiwari A, et al. A review of clustering techniques and developments. Neurocomputing. 2017;267(10):664–81. doi:10.1016/j.neucom.2017.06.053. [Google Scholar] [CrossRef]

2. Murtagh F, Contreras P. Algorithms for hierarchical clustering: an overview. Wiley Interdiscip Rev: Data Min Knowl Discov. 2012;2(1):86–97. doi:10.1002/widm.53. [Google Scholar] [CrossRef]

3. Starczewski A, Scherer MM, KsiaŻek W, Debski M, Wang L. A novel grid-based clustering algorithm. J Artif Intell Soft Comput Res. 2021;11(4):319–30. doi:10.2478/jaiscr-2021-0019. [Google Scholar] [CrossRef]

4. Cheam A, Marbac M, McNicholas P. Model-based clustering for spatiotemporal data on air quality monitoring. Environmetrics. 2017;28(3):e2437. doi:10.1002/env.2437. [Google Scholar] [CrossRef]

5. Kriegel HP, Kröger P, Sander J, Zimek A. Density-based clustering. Wiley Interdiscip Rev: Data Mining Knowl Discov. 2011;1(3):231–40. doi:10.1002/widm.30. [Google Scholar] [CrossRef]

6. Ahmed M, Seraj R, Islam SMS. The k-means algorithm: a comprehensive survey and performance evaluation. Electronics. 2020;9(8):1295. [Google Scholar]

7. Sinaga KP, Yang MS. Unsupervised K-means clustering algorithm. IEEE Access. 2020;8:80716–27. [Google Scholar]

8. Poggiali A, Berti A, Bernasconi A, Del Corso GM, Guidotti R. Quantum clustering with k-Means: a hybrid approach. Theor Comput Sci. 2024;992:114466. [Google Scholar]

9. Zhang C, Ouyang D, Ning J. An artificial bee colony approach for clustering. Expert Syst Appl. 2010;37(7):4761–7. [Google Scholar]

10. Zhang X, Lin Q, Mao W, Liu S, Dou Z, Liu G. Hybrid Particle Swarm and Grey Wolf Optimizer and its application to clustering optimization. Appl Soft Comput. 2021;101:107061. [Google Scholar]

11. Sharma V, Tripathi AK. A systematic review of meta-heuristic algorithms in IoT based application. Array. 2022;14(1):100164. doi:10.1016/j.array.2022.100164. [Google Scholar] [CrossRef]

12. Vasconcelos J, Ramirez JA, Takahashi R, Saldanha R. Improvements in genetic algorithms. IEEE Trans Magn. 2001;37(5):3414–7. doi:10.1109/20.952626. [Google Scholar] [CrossRef]

13. Whitley D. A genetic algorithm tutorial. Stat Comput. 1994;4(2):65–85. doi:10.1007/BF00175354. [Google Scholar] [CrossRef]

14. de Souza RCT, de Macedo CA, dos Santos Coelho L, Pierezan J, Mariani VC. Binary coyote optimization algorithm for feature selection. Pattern Recognit. 2020;107(5):107470. doi:10.1016/j.patcog.2020.107470. [Google Scholar] [CrossRef]

15. Mareli M, Twala B. An adaptive Cuckoo search algorithm for optimisation. Appl Comput Inform. 2018;14(2):107–15. doi:10.1016/j.aci.2017.09.001. [Google Scholar] [CrossRef]

16. Das S, Mullick SS, Suganthan PN. Recent advances in differential evolution-an updated survey. Swarm Evol Comput. 2016;27:1–30. [Google Scholar]

17. Opara KR, Arabas J. Differential evolution: a survey of theoretical analyses. Swarm Evol Comput. 2019;44:546–58. [Google Scholar]

18. Alia OM, Mandava R. The variants of the harmony search algorithm: an overview. Artif Intell Rev. 2011;36:49–68. [Google Scholar]

19. Ma H. An analysis of the equilibrium of migration models for biogeography-based optimization. Inf Sci. 2010;180(18):3444–64. [Google Scholar]

20. Kennedy J, Eberhart R. Particle swarm optimization. In: Proceedings of ICNN’95-International Conference on Neural Networks; 1995; Perth, WA, Australia: IEEE. Vol. 4, p. 1942–8. [Google Scholar]

21. Wang D, Tan D, Liu L. Particle swarm optimization algorithm: an overview. Soft Comput. 2018;22(2):387–408. doi:10.1007/s00500-016-2474-6. [Google Scholar] [CrossRef]

22. Wu D, Jiang N, Du W, Tang K, Cao X. Particle swarm optimization with moving particles on scale-free networks. IEEE Trans Netw Sci Eng. 2018;7(1):497–506. doi:10.1109/TNSE.2018.2854884. [Google Scholar] [CrossRef]

23. Gupta S, Deep K. A novel random walk grey wolf optimizer. Swarm Evol Comput. 2019;44(4):101–12. doi:10.1016/j.swevo.2018.01.001. [Google Scholar] [CrossRef]

24. Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Adv Eng Softw. 2014;69:46–61. doi:10.1016/j.advengsoft.2013.12.007. [Google Scholar] [CrossRef]

25. Mirjalili S, Lewis A. The whale optimization algorithm. Adv Eng Softw. 2016;95(12):51–67. doi:10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]

26. Yang W, Xia K, Fan S, Wang L, Li T, Zhang J, et al. A multi-strategy whale optimization algorithm and its application. Eng Appl Artif Intell. 2022;108:104558. doi:10.1016/j.engappai.2021.104558. [Google Scholar] [CrossRef]

27. Arora S, Singh S. Butterfly optimization algorithm: a novel approach for global optimization. Soft Comput. 2019;23:715–34. doi:10.1007/s00500-018-3102-4. [Google Scholar] [CrossRef]

28. Hashim FA, Hussain K, Houssein EH, Mabrouk MS, Al-Atabany W. Archimedes optimization algorithm: a new metaheuristic algorithm for solving optimization problems. Appl Intell. 2021;51:1531–51. doi:10.1007/s10489-020-01893-z. [Google Scholar] [CrossRef]

29. Alabool HM, Alarabiat D, Abualigah L, Heidari AA. Harris hawks optimization: a comprehensive review of recent variants and applications. Neural Comput Appl. 2021;33:8939–80. doi:10.1007/s00521-021-05720-5. [Google Scholar] [CrossRef]

30. Dorigo M, Blum C. Ant colony optimization theory: a survey. Theor Comput Sci. 2005;344(2–3):243–78. doi:10.1016/j.tcs.2005.05.020. [Google Scholar] [CrossRef]

31. Parpinelli RS, Lopes HS, Freitas AA. Data mining with an ant colony optimization algorithm. IEEE Trans Evol Comput. 2002;6(4):321–32. doi:10.1109/TEVC.2002.802452. [Google Scholar] [CrossRef]

32. Mavrovouniotis M, Li C, Yang S. A survey of swarm intelligence for dynamic optimization: algorithms and applications. Swarm Evol Comput. 2017;33:1–17. doi:10.1016/j.swevo.2016.12.005. [Google Scholar] [CrossRef]

33. Song PC, Chu SC, Pan JS, Yang H. Simplified Phasmatodea population evolution algorithm for optimization. Complex Intell Syst. 2022;8(4):2749–67. doi:10.1007/s40747-021-00402-0. [Google Scholar] [CrossRef]

34. Pan JS, Song PC, Pan CA, Abraham A. The phasmatodea population evolution algorithm and its application in 5G heterogeneous network downlink power allocation problem. J Internet Technol. 2021;22(6):1199–213. doi:10.53106/160792642021112206001. [Google Scholar] [CrossRef]

35. Zhang AN, Chu SC, Song PC, Wang H, Pan JS. Task scheduling in cloud computing environment using advanced phasmatodea population evolution algorithms. Electronics. 2022;11(9):1451. doi:10.3390/electronics11091451. [Google Scholar] [CrossRef]

36. Cai Z, Gong W, Ling CX, Zhang H. A clustering-based differential evolution for global optimization. Appl Soft Comput. 2011;11(1):1363–79. doi:10.1016/j.asoc.2010.04.008. [Google Scholar] [CrossRef]

37. Nayak J, Naik B, Behera H. Cluster analysis using firefly-based K-means Algorithm: a combined approach. In: Computational Intelligence in Data Mining: Proceedings of the International Conference on CIDM; 2016 Oct 10–11; Singapore: Springer; 2017. p. 55–64. [Google Scholar]

38. Chaudhary R, Banati H. Hybrid enhanced shuffled bat algorithm for data clustering. Int J Adv Intell Paradig. 2020;17(3–4):323–41. doi:10.1504/IJAIP.2020.109513. [Google Scholar] [CrossRef]

39. Huang SC. Color image quantization based on the artificial bee colony and accelerated K-means algorithms. Symmetry. 2020;12(8):1222. doi:10.3390/sym12081222. [Google Scholar] [CrossRef]

40. García J, Yepes V, Martí JV. A hybrid k-means cuckoo search algorithm applied to the counterfort retaining walls problem. Mathematics. 2020;8(4):555. doi:10.3390/math8040555. [Google Scholar] [CrossRef]

41. Pal SS, Pal S. Black hole and k-means hybrid clustering algorithm. In: Computational Intelligence in Data Mining: Proceedings of the International Conference on ICCIDM 2018; 2020; Singapore: Springer; p. 403–13. [Google Scholar]

42. Hansen P, Mladenović N, Brimberg J, Pérez JAM. Variable neighborhood search. Cham: Springer; 2019. [Google Scholar]