A Federated Learning Incentive Mechanism for Dynamic Client Participation: Unbiased Deep Learning Models

1  Introduction

Due to the growing security issues, there is a growing emphasis on developing more secure training methods for deep learning [1,2]. Federated learning (FL), as a successful privacy-preserving paradigm, enables multiple clients to jointly train deep learning models without uploading their own raw data under the coordination of the central server [3]. In FL, training occurs through multiple rounds of global iterations, where clients utilize their local datasets to train local models or gradients, subsequently uploading them to the central server for each training round. The distinct advantages of FL have sparked its adoption in various fields such as healthcare, agriculture, and blockchain applications [4]. Each client retains control over its local data, enabling independent decisions regarding participation in FL training. However, owing to associated participation costs like training and communication expenses, the server must offer appropriate compensation to incentivize self-interested clients to engage in the collaborative training process [5].

However, the FL training process typically involves numerous global iterations, posing challenges in designing efficient incentive mechanisms. First, in large-scale distributed scenarios, clients typically exhibit heterogeneous local resources and independent activity. While assuming unlimited resources and disregarding the straggler effect could enable full client participation, this scenario fails to align with the reality of limited resources. This limitation hampers the execution of many studies that rely on full client participation and constant availability [6–8]. Second, clients may disconnect due to unexpected circumstances during training, i.e., the client’s state may change dynamically [9]. Despite clients’ efforts to minimize disconnections, this incurs additional local costs. Waiting for all clients to respond in dropout situations can seriously impede training efficiency. Although some studies suggest partial client participation to enhance the training process, they presuppose that the server can accurately identify participating clients in each round, which is an ideal assumption [10,11]. Third, client-local datasets are often non-IID [12–14]. Partial local datasets may fail to represent the true data distribution globally, potentially introducing biases during training with dynamic client participation [15].

Despite the clarity of the above considerations, there remain significant challenges in designing an efficient incentive mechanism for unbiased FL. First, how do we effectively incentivize clients to train an unbiased global model under conditions of a limited budget and dynamically changing client status? Encouraging full client participation under a limited budget poses a dilemma for the server. Although existing researchers propose sampling methods to ensure unbiased models, most are applicable only in scenarios where clients are always available [16,17]. Although studies like [18,19] delve into optimization methods for independent client sampling, they assume unconditional client participation in FL. Due to system heterogeneity, clients often face varying local costs during model training, leading to diverse participation preferences [20]. However, without insights into clients’ participation preferences and communication conditions, appropriately rewarding clients becomes challenging. This can result in budget inefficiencies and a decline in client participation levels.

To address the above challenges, we propose a contract-based dynamic participation incentive for unbiased FedeRated LEarning, called ENTIRE. ENTIRE can provide personalized payments to clients with varying participation preferences to compensate for their local costs while ensuring an unbiased deep-learning model. Specifically, we first investigate the impact of randomly independent participation from arbitrary clients on the convergence bounds of FL under non-convex loss functions. Subsequently, we design a set of optimal contracts for clients with heterogeneous participation preferences under different budget constraints and incomplete information models to maximize model performance. Furthermore, we find that when the server’s budget is sufficient, it is adequate to design a single optimal contract to incentivize full participation from all categories of clients. Our main contributions can be summarized as follows:

(1) Methodologically, we propose ENTIRE, a dynamic participation incentive mechanism for unbiased FL aimed at mitigating model bias arising due to dynamic client participation. It encourages all clients to participate in FL by offering independent participation levels and appropriate economic compensation. By customizing personalized participation levels for clients and optimizing reward allocation for contracts, we enhance the model performance under incomplete information.

(2) Theoretically, we establish the FL convergence bound when clients have independent participation levels, which guides the optimization of both model performance and reward allocation. This convergence bound applies to a more general assumption of non-convex loss functions. Furthermore, we derive the optimal contract design under varying budget conditions, enabling ENTIRE to ensure optimal model performance even when the server has an arbitrary budget.

(3) Experimentally, we performed extensive experiments on three real datasets and compared ENTIRE to three state-of-the-art baselines. For the same budget, ENTIRE achieves a 12.9% performance improvement compared to other methods and differs in accuracy by only 0.9% from a model trained with the full participation of all clients. Furthermore, the results show that our approach is equally applicable to the IID scenario.

The remainder of this paper is organized as follows. Section 2 provides a summary of related work. Then, in Section 3, we introduce the system model and define the design goals of ENTIRE through convergence analysis. Section 4 describes the design of optimal contracts under an incomplete information model and varying budget conditions. Subsequently, in Section 5, we provide a comprehensive performance evaluation of ENTIRE through experiments. Finally, we conclude the full paper in Section 6.

2  Related Work

The training process in FL entails communication links between a central server and numerous decentralized clients. This large-scale distributed training scenario is prone to client dropout, which seriously hampers the efficiency of model training. Therefore, the classical FedAvg algorithm usually performs multiple local iterations on a randomly selected subset of clients to update the model [21].

Various FL algorithms have been proposed to improve training efficiency. For example, in [22], the model convergence rate was improved by compressing local model updates and designing client scheduling and resource allocation strategies. A stochastic optimization problem linking resource allocation with client scheduling and training loss was presented in [23] and solved using the Lyapunov method. The work in [24] utilized layered computing resources to reduce the end clients’ workload and explored task offloading from edge to end. These approaches focused on the resource allocation issue among clients to optimize the training process from the server’s perspective, neglecting client incentives and assuming clients are consistently available during training. In contrast, our work compensates for heterogeneous clients’ local costs during training and considers the possibility of client dropouts.

To incentivize clients to participate and improve training efficiency, certain approaches have focused on selectively incentivizing specific high-value clients to engage in FL training. The work in [25] designed a Stackelberg-based incentive mechanism, where the server and clients collaboratively determined the participating client set to incentivize maximal data contribution. In [26], a contractual and coalitional game-based incentive mechanism was introduced to motivate the participation of clients with high contributions. A reverse auction-based incentive mechanism to select a more cost-effective set of clients for training was designed in [27]. Although these methods can expedite training efficiency and reduce costs to some extent, selecting only a subset of clients for training with an imbalanced data distribution may introduce bias during the training process, leading to a decline in model performance. Instead, we ensure an unbiased global model while allowing dynamic client participation.

Considering the non-IID data and the independent availability of clients, the work in [28] delved into incentivizing all clients to engage in FL with varying participation probabilities. However, their convergence analysis for unbiased models only was limited to convex functions and applicable solely in scenarios with complete information. Furthermore, their approach still results in clients with negative utility when the server’s budget was insufficient, and failed to motivate all clients to participate. In contrast, our study establishes convergence outcomes under a broader non-convex framework. Moreover, we can incentivize the involvement of all clients and ensure unbiased training models across diverse budget constraints and incomplete information scenarios.

3  System Model and Problem Formulation

In this section, we describe the system model and formulate the optimal participation contract design problem for incomplete information scenarios based on the results of convergence analysis.

3.1 System Model

We consider an FL scenario with a central server and a set of clients. Each client has a local loss function associated with the model parameter . Specifically, each client optimizes a shared model to minimize the loss function using its local dataset. The goal of an FL system is to enable clients to collaboratively train a shared model to minimize the global loss function [29]:

(1)

Note that we use average rather than weighted average here, due to we consider the weights as part of the local loss function. In large-scale distributed scenarios, FL typically employs the client sampling method for model training [30]. However, each client in FL serves as a decision maker, choosing its own participation level instead of using the server’s predetermined sampling probabilities. Consequently, each training round involves a random subset of clients, which can introduce significant biases into the global model without an appropriate aggregation rule [18]. To ensure an unbiased global model, we implement an aggregation rule akin to [31], which guarantees that Here, represents the local model of client in round , and indicates the subset of clients participating in round t. Furthermore, we describe the local training process as a small batch of stochastic gradient descent, denoted as , which may consist of the global model after multiple local iterations. The specific training process is summarized in Algorithm 1, which differs from vanilla FL only in client sampling and model aggregation. The comprehensive system process is depicted in Fig. 1, with the server required to establish agreements with clients concerning participation levels and rewards.

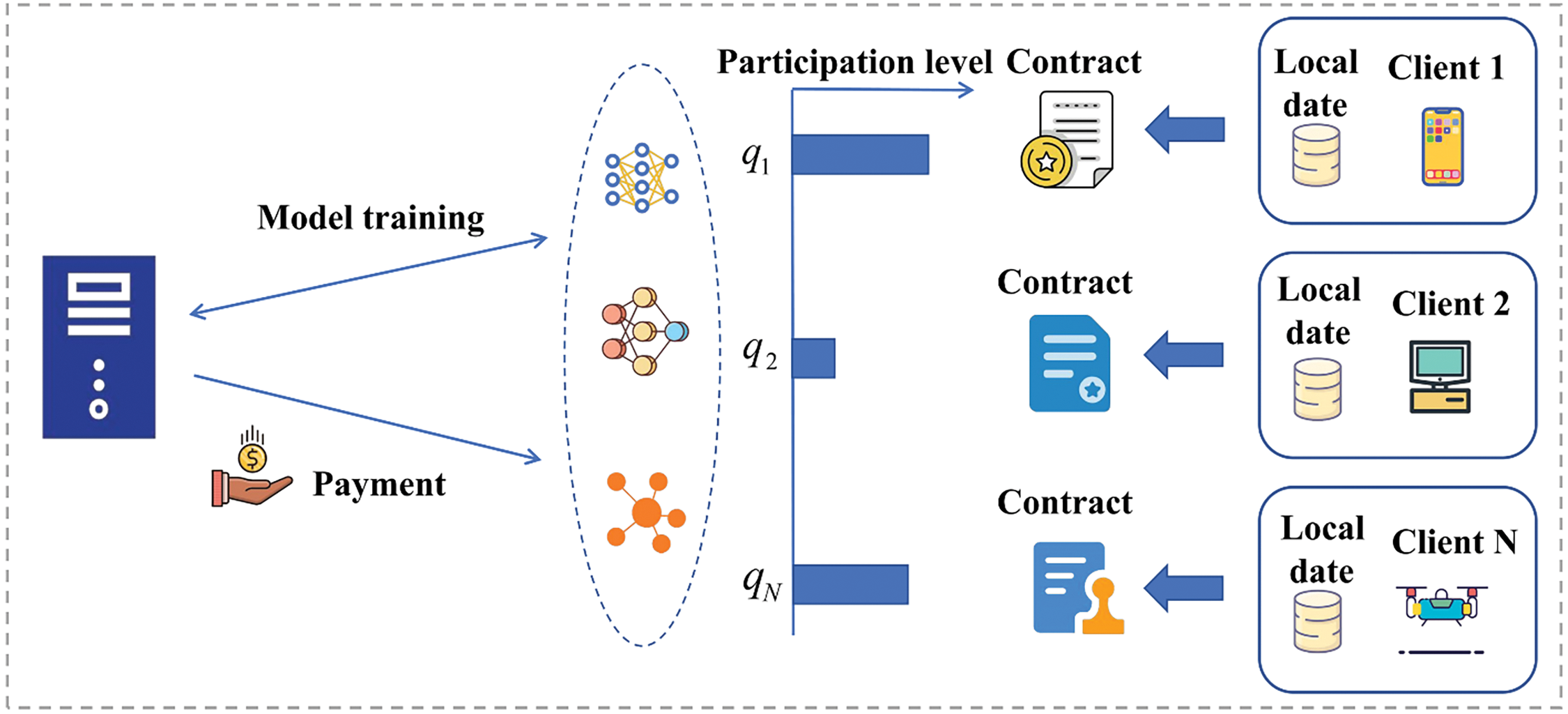
Figure 1: The server and clients sign different participation contracts. Clients and the server conduct training according to the participation levels specified in the contract and allocate rewards accordingly

3.2 System Model

The server needs to incentivize clients to join FL at a high participation level to train an efficient global model. In this part, we construct the upper bound on the convergence of Algorithm 1 with non-convex loss functions to relate the global model performance to the client participation level. To establish the theory boundary on convergence, we introduce the following common assumptions from existing work [19,32].

Assumption 1 (β-Lipschitz Continuous Gradient). There exists a constant β, such that the difference between the local gradient and satisfies for any and .

Assumption 2 (Unbiased Stochastic Gradient with Bounded Variance). The stochastic local gradient satisfies and .

Assumption 3 (Bounded Local and Global Variance). The difference between the local gradient and the global gradient satisfies .

The main convergence result is given in the following theorem:

Theorem 1. The difference between the local gradient and the global gradient satisfies . With Assumption 1–3, given and learning rate , after global rounds, Algorithm 1 ensures that

(2)

Proof. With the smoothness assumption, taking the expectation of over the randomness, we have

(3)

The term can be bounded as:

(4)

where follows Jensen’s inequality, and follows the fact that and Assumption 2. Add a zero term to , we have

(5)

(6)

(7)

Taking the total expectation collapsing the above in equality, we obtain

(8)

Averaging overall t, we can obtain the final result as Eq. (2). This completes the proof. □

The convergence bound in Theorem 1 applies to any varying number of participating clients per round. Furthermore, this upper bound suggests that to guarantee an unbiased global model, all clients need to be incentivized to participate in FL. Because may lead to non-convergence, which also explains why incentivizing only a subset of clients may not converge to a globally optimal solution. The key factor controlling the convergence upper bound is , which reaches its minimum when , i.e., full participation of all clients. To obtain a high-performance global model, clients need to adopt high participation levels. However, increasing the participation level implies a higher cost, which requires a reasonable incentive mechanism to reconcile the conflict between the server and clients.

3.3 Problem Formulation

Without loss of generality, we assume that in incomplete information scenarios, clients can be categorized into different types based on their participation preferences. Sorting the different types in ascending order, we get , . A larger value of with represents a greater local overhead cost for the client to participate in training. In addition, the cost to a client is related to the participation level it chooses. Intuitively, a higher participation level means that clients participate in each round with a higher probability (more training rounds), which leads to higher costs. The utility of a client in type is defined as the difference between the rewards offered by the server and its participation cost, calculated as

(9)

where implies full client participation. captures the sensitivity of clients to rewards. When is small, clients focus more on their participation preferences and less on the rewards offered by the server. In our work, we mainly consider the design of incentive mechanism based on the client participation level, and is only used to observe the impact of different values on our system.

In incomplete information scenarios, the type of client’s participation preference is private information and unavailable. The server can only estimate the distribution of from historical data, and we use to denote the probability that a client belongs to type , which means that . As shown in Fig. 1, our goal is to design the optimal contracts for each type of client, i.e., , guaranteeing an unbiased global model and maximizing model performance with a limited budget. Each client selects a contractual item, engages in training at the specified participation level, and receives corresponding rewards. We formally define this engagement as a participation contract:

Definition 1 (PC). A participation contract is represented as a 2-tuple , i.e., a participation level requirement rule , and a payment determination rule .

: is responsible for determining the participation level that clients belonging to type should employ in model training, i.e., .

: determines the reward that should be given to clients belonging to type and participation level , i.e., .

In order to encourage clients to reveal their types truthfully in information asymmetry, we need to introduce the following three fundamental properties, namely budget feasibility (BF), individual rationality (IR), and incentive compatibility (IC).

Definition 2 (BF). A set of PCs satisfies BF if the rewards to be paid to all clients do not exceed the budget , i.e., .

Definition 3 (IR). A set of PCs satisfies IR if they provide non-negative utility to the corresponding type of clients, i.e., , .

Definition 4 (IC). A set of PCs satisfies IC if a client can maximize its utility only by honestly choosing the contract that corresponds to its type, i.e., , .

The server needs to design a set of optimal PCs that satisfy the above properties to maximize model performance, which can be formalized as

(10)

Note that in cases of complete information, the server knows the type to which each client belongs, so only a single contract needs to be sent to each client. However, in the case of incomplete information, where the type of any client is unknown, the server needs to send all the contracts to clients for selection.

4  The Set of Optimal Participation Contracts Design

In this section, we study the optimal PC design problem for different budget levels and provide key insights to distinguish between the different scenarios.

4.1 Optimal Contract Design under Insufficient Budget

When the server lacks the budget to incentivize all clients to fully participate, we assert that the participation level constraint proves more restrictive than the budget-feasibility (BF) constraint. This is because to ensure IC property, the server can only guarantee partial low client types achieve full participation, while it cannot incentivize the others to increase their participation levels with an entire budget. To solve this problem, the key idea of our method is to separate the two constraints by considering varying budget scenarios. We assume the server’s budget cannot support any client type for full participation, allowing us to omit the participation level constraint and allocate the entire budget accordingly. Under the remaining constraints, we outline the essential conditions needed to guarantee an optimal set of PCs in the following proposition:

Proposition 1. A set of feasible PCs must meet the following necessary and sufficient conditions:

(11)

Proof. The first two equations are relaxations of the BF and IR constraints, where the latter effectively reduces IR constraints to one. We can prove this by the IC property of the feasible PCs. Recall that we have sorted clients’ types in ascending order, i.e., . According to Definition 4, we have

(12)

Thus, we only need to guarantee to satisfy the IR constraints for any type of client. Moreover, assuming that there exists an optimal PC such that , we can always raise to reduce the convergence upper bound up to . Similarly, if the set of PCs satisfies , the server can choose a larger up to . Note that this approach is only applicable to insufficient budget cases, otherwise the server will not be able to incentivize the client with the entire budget due to the IC and participation level constraints. For example, when , the server cannot make by raising . The above analysis indicates that only the highest type of clients can achieve zero utility. This is because the server does not know the type of each client, and it needs to incentivize clients in the form of positive utility, encouraging them to reveal their true type.

The third and fourth inequalities are about the participation level and reward monotonicity. We use IC constraints to prove the monotonicities of the set of optimal PCs. According to IC property, we have and . Take the sum of both sides of the two inequalities, we have . Thus, if , then for . Furthermore, according to the first inequality, we also have . Since and , we have . Similarly, by the second inequality, we can prove necessity. Therefore, if a set of PCs satisfies the IC property, they spontaneously satisfy these two monotonicities.

For the fifth inequality, we show that IC constraints can be simplified to IC constraints in Eq. (11). We first prove that if local downward incentive compatibility (LDIC) is satisfied, i.e., , then hold for .

Suppose , . If the LDIC holds, we have

(13)

Note that , which we can easily obtain . Thus, we have , for . Additionally, if local upward incentive compatibility (LUIC) holds, i.e., , we can obtain , for by a similar proof. Similar to the approach of simplifying BF and IR constraints, for a set of optimal PCs, we have . Because we can always find a larger participation level to achieve better model performance until the equal sign holds. Notice that by the monotonicity, we also have

(14)

Therefore, in order for the optimal contract to satisfy the IC property, we only need to ensure that . At this point, we have completed the IC constraints simplification. □

According to Proposition 1, we can reduce the complexity of the problem by simplifying BF, IR, and IC constraints. Now, we formally rewrite the problem as follows:

(15)

By solving , we can summarize the set of optimal PCs as the following theorem.

Theorem 2. In the incomplete information scenario, the set of optimal PCs is given by

(16)

where , for , and .

Proof. According to the last two constraints of , we have

(17)

Following the same procedure, we obtain

(18)

where , for . Adding up the rewards of all clients, we have

(19)

Let , we have

(20)

So far, we have simplified the constraint conditions of into one. Since is convex, we can use the KKT condition to find the optimal set of PCs. The corresponding Lagrangian dual function is

(21)

where is the Lagrange multiplier. By solving the first-order condition, we have . Substitute the result into Eq. (20), we have

(22)

Using Eqs. (18) and (22) with some simple transformations, we complete this proof. □

4.2 Optimal Contract Design under Sufficient Budget

Recall that the previous analysis builds on the premise that the budget is inadequate to incentivize full participation by any client type, i.e., . In this part, we explore two scenarios: one where the server’s budget can support full participation by a subset of clients, and another where the server’s budget is adequate for full participation by all clients. We consolidate the optimal set of PCs for both scenarios in the following theorem:

Theorem 3. In the incomplete information scenario, and when the server’s budget is sufficient, the set of optimal PCs is given as

(23)

Proof. According to the monotonicity of the participation level of the set of optimal PCs, we can easily get that when the server’s budget is not enough to incentivize all clients to fully participate, only the clients with the lowest type can satisfy full participation. Thus, we have

(24)

Bringing the above results into Eq. (16), we can obtain the optimal set of PCs.

For the case where the server has sufficient budget to incentivize full participation by all clients, we only need to design one PC term. This is because when all clients are fully participated, the clients belonging to the highest type have the largest participation costs, i.e., the optimal PC term only needs to be able to compensate for the type clients’ costs. In this case, we have an . Furthermore, we can calculate the budget to satisfy at least . This completes the proof. □

5  Experiments

In this section, we perform an extensive experimental evaluation of ENTIRE on three real-world datasets and compare it to three baselines.

5.1 Experiment Setup

FL Setup. Similarly to [28,31], we consider the FL scenario with a central server and clients. Besides, we assume that clients’ participation preferences can be divided into types, and satisfy for . All clients are randomly distributed among the ten participant groups, the reward sensitivity parameter is satisfied , and the total budget for the server satisfies .

Datasets & Models. We use non-convex deep learning models on two datasets, i.e., a multi-layer perceptron (MLP) on the MNIST dataset and Fashion-MNIST (FMNIST) dataset. We sort and slice the datasets by label to ensure that each client’s local dataset meets non-IID requirements. In this case, most clients will only have data of one class (out of all the 10 classes). Additionally, we train a convolutional neural network (CNN) on the CIFAR-10 dataset to test the performance of our method in IID scenarios. For the training parameters, we use SGD batch size 30 and local epoch 2.

Baselines. (1) CC: A contract-based incentive mechanism under complete information, i.e., the server knows each client’s participation preference. It is unnecessary to consider IC property when designing optimal participation contracts. (2) UC: A contract-based incentive mechanism with a uniform contract, i.e., the server makes the same contract for all client types, and only clients with non-negative utility choose to accept the contract [33]. (3) SG: A Stackerberg game-based incentive mechanism, i.e., the server distributes rewards proportionally based on the participation level selected by the clients, and each client aims to maximize their own utility [28].

5.2 Experimental Results

We compare the design of optimal PCs for complete and incomplete information scenarios, i.e., CC and ENTIRE. For CC, the server knows the type of each client, and therefore only needs to send one corresponding contract to each client. The optimal set of contracts for the full information scenario is given as

(25)

Fig. 2 demonstrates that ENTIRE satisfies monotonicity, IR, and IC simultaneously. In Fig. 2a, the participation levels assigned by CC and ENTIRE for various client types are displayed. Clients with higher types opt for lower participation levels. This decision is driven by the server’s strategy to maximize model performance within a constrained budget by favoring smaller client types in more training rounds due to their lower participation costs. Conversely, under the same budget constraints, ENTIRE designates a reduced participation level for each client type compared to CC. This adjustment is necessary in an environment of incomplete information, where the server lacks specific knowledge about individual client types and must motivate lower client types with positive utility (Fig. 2b).

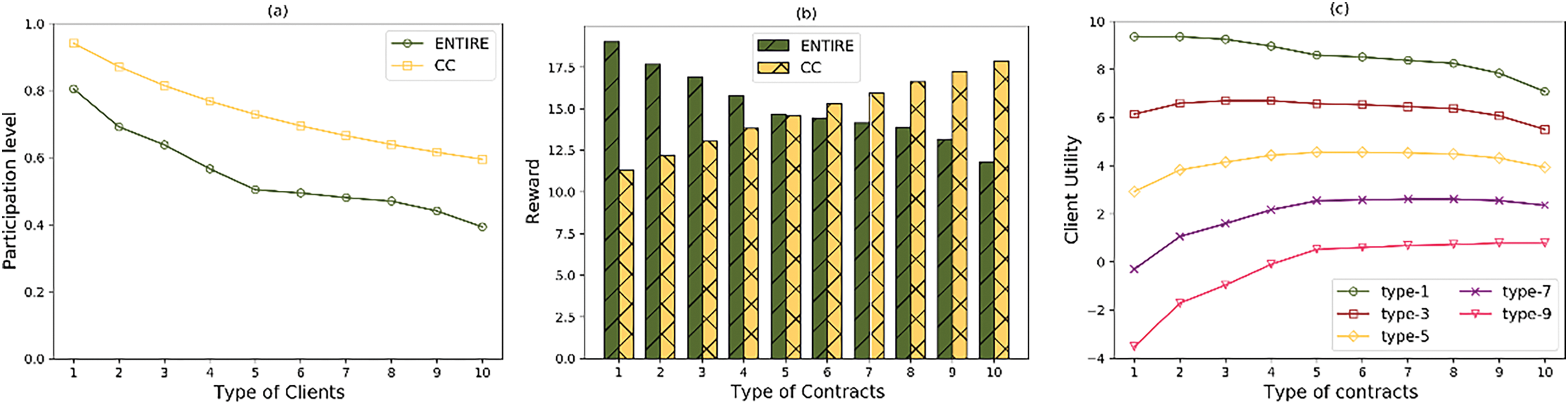
Figure 2: Contract properties: (a) Participation level monotonicity; (b) Reward monotonicity; (c) IR & IC

illustrates the rewards specified by ENTIRE and CC for each contract type. ENTIRE satisfies the monotonicity of rewards in Proposition 1, whereas CC exhibits the opposite behavior. This aligns with the reasoning in Fig. 2a, where the server can guarantee zero utility for all client types in the complete information scenario, but can only ensure that the highest type client achieves zero utility in the incomplete information case. Fig. 2c shows that any client type can only obtain maximum utility by choosing its corresponding type of PC, which satisfies the IC property. In addition, each client has a non-negative utility in choosing its corresponding contract, which satisfies the IR property.

Table 1 illustrates the effect of system parameters on participation levels and rewards specified by ENTIRE. Regarding the reward sensitivity factor, as its value rises, clients prioritize the rewards offered by the server, leading to a selection of higher participation levels. However, since the total reward remains constant, the server’s reward for different contract types does not fluctuate. This indicates that heightened client reward sensitivity facilitates model training at a consistent budget level. Moreover, with an increase in the total server budget, both participation levels and rewards for each client type increase gradually. At a budget of , type-1 clients achieve full participation. To maintain the monotonicity of the PCs, contracts remain unchanged until the budget reaches , at which stage full participation is attained for all client types, resulting in identical PCs for all clients.

Fig. 3 illustrates the model performance of three methods on different datasets. ENTIRE demonstrates the optimal model performance in Fig. 3a,b, as it ensures that all clients participate in the model training, resulting in an unbiased global model. On the contrary, UC and SG only ensure that a fixed subset of clients joins FL at the same participation level. Although this may lead to a faster convergence rate, due to the lack of training data (especially in extreme non-IID cases), the global model cannot converge to the degree of full client participation.

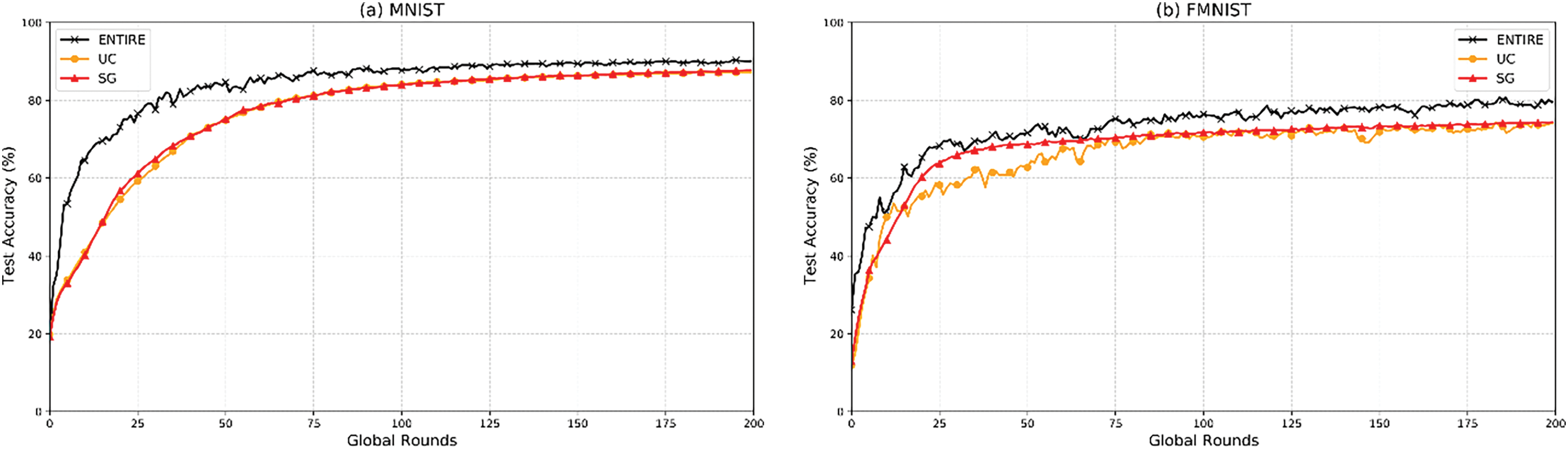
Figure 3: Model performance on different datasets: (a) MNIST dataset with three methods; (b) FMNIST dataset with three methods

Fig. 4 depicts the effect of varying budgets on model performance. In Fig. 4a, both the convergence rate and performance of the global model improve as the budget increases. With , the training process exhibits significant fluctuations due to lower participation levels across all client types. As the budget escalates from to , the final global model performance remains relatively consistent, but training fluctuations decrease as full client participation is achieved . This highlights that our aggregation strategy enables the model to converge towards full client participation. Furthermore, we show the performance of ENTIRE with IID setting in Fig. 4b. Increasing budget increase enhances model performance significantly at lower budgets but shows slower accuracy improvements at higher budgets. The main difference is that the training accuracy fluctuates less in the IID setting, which suggests that our conclusions can be applied to the IID scenario as well.

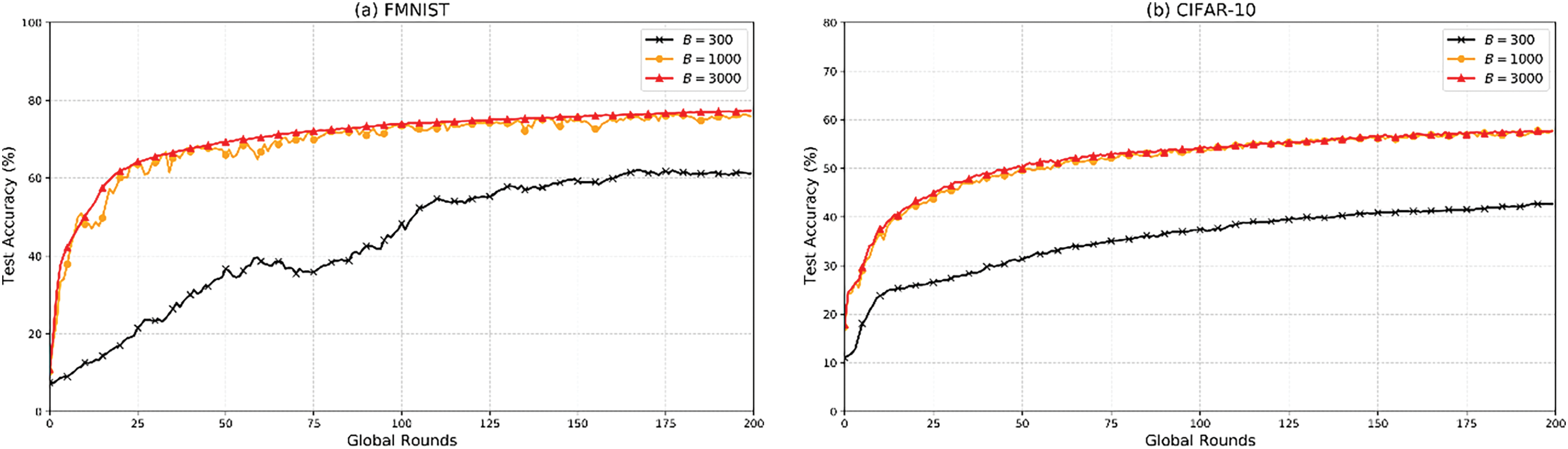
Figure 4: Model performance for different : (a) non-IID with FMNIST; (b) IID with CIFAR-10

6  Conclusion

In this paper, we proposed ENTIRE, a dynamic participation incentive mechanism for unbiased FL, which was able to guarantee an unbiased FL model in scenarios with asymmetric information, and appropriately compensated clients with differing participation costs. First, the impact of clients’ participation levels on the model performance was explored by rigorously deriving a non-convex convergence bound with random client participation. Second, a set of optimal PCs was derived based on the convergence bound to maximize the model performance. Third, the practicality and efficacy of ENTIRE were validated through extensive experiments, showcasing ENTIRE was also applicable to IID scenarios. Note that although ENTIRE uses the FL framework, it still has privacy concerns. Future considerations involve integrating differential privacy to enhance client privacy protection, but this requires sacrificing some model performance. The privacy-utility trade-off under independent client participation is the pivotal direction for future research.

Acknowledgement: We would like to extend our sincere appreciation to the editor and reviewers for their valuable feedback and constructive comments, which greatly improved the quality of this paper.

Funding Statement: This work was supported by the National Natural Science Foundation of China (Nos. 62072411, 62372343, 62402352, 62403500); the Key Research and Development Program of Hubei Province (No. 2023BEB024); the Open Fund of Key Laboratory of Social Computing and Cognitive Intelligence (Dalian University of Technology), Ministry of Education (No. SCCI2024TB02).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Jianfeng Lu, Tao Huang; data collection: Shuqin Cao, Bing Li; analysis and interpretation of results: Yuanai Xie, Shuqin Cao; draft manuscript preparation: Jianfeng Lu and Tao Huang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are openly available in https://yann.lecun.com/exdb/mnist/ (accessed on 02 January 2025), https://tensorflow.google.cn/datasets/catalog/fashion_mnist (accessed on 02 January 2025), and http://www.cs.toronto.edu/~kriz/cifar.html (accessed on 02 January 2025).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Tang D, Yan Y, Zhang Z, Chen J, Qin Z. Performance and features: mitigating the low-rate TCP-targeted DoS attack via SDN. IEEE J Sel Areas Commun. 2022;40(1):428–44. doi:10.1109/JSAC.2021.3126053. [Google Scholar] [CrossRef]

2. Tang D, Wang S, Liu B, Jin W, Zhang J. GASF-IPP: detection and mitigation of LDoS attack in SDN. IEEE Trans Serv Comput. 2023;16(5):3373–84. doi:10.1109/TSC.2023.3266757. [Google Scholar] [CrossRef]

3. McMahan B, Moore E, Ramage D, Hampson S, Arcas BAY. Communication-efficient learning of deep networks form decentralized data. Paper presented at: 20th International Conference on Artificial Intelligence and Statistics; 2017 Apr 20–22; Fort Lauderdale, FL, USA. [Google Scholar]

4. Liu H, Lu J, Wang X, Wang C, Jia R, Li M. FedUP: bridging fairness and efficiency in cross-silo federated learning. IEEE Trans Serv Commput. 2024;17(6):3672–84. doi:10.1109/TSC.2024.3489437. [Google Scholar] [CrossRef]

5. Lu J, Liu H, Jia R, Zhang Z, Wang X, Wang J. Incentivizing proportional fairness for multi-task allocation in crowdsensing. IEEE Trans Serv Comput. 2024;17(3):990–1000. doi:10.1109/TSC.2023.3325636. [Google Scholar] [CrossRef]

6. Tang M, Wong VWS. An incentive mechanism for cross-silo federated learning: a public goods perspective. Paper presented at: 40th IEEE Conference on Computer Communications; 2021 May 10–13; Vancouver, BC, Canada. [Google Scholar]

7. Huang C, Zhang H, Liu X. Incentivizing data contribution in cross-silo federated learning. 2022. doi: 10.48550/ARXIV.2203.03885. [Google Scholar] [CrossRef]

8. Lu J, Chen Y, Cao S, Chen L, Wang W, Xin Y. LEAP: optimization hierarchical federated learning on non-IID data with coalition formation game. Paper presented at: 33th International Joint Conference on Artificial Intelligence; 2024 Aug 3–9; Jeju, Republic of Korea. [Google Scholar]

9. Hu M, Wu D, Zhou Y, Chen X, Chen M. Incentive-aware autonomous client participation in federated learning. IEEE Trans Parallel Distrib Syst. 2022;33(10):2612–27. doi:10.1109/TPDS.2022.3148113. [Google Scholar] [CrossRef]

10. Ding N, Fang Z, Huang J. Optimal contract design for efficient federated learning with multi-dimensional private information. IEEE J Sel Areas Commun. 2021;39(1):186–200. doi:10.1109/JSAC.2020.3036944. [Google Scholar] [CrossRef]

11. Huang G, Wu Q, Sun P, Ma Q, Chen X. Collaboration in federated learning with differential privacy: a stackerberg game analysis. IEEE Trans Parallel Distrib Syst. 2024;35(3):455–69. doi:10.1109/TPDS.2024.3354713. [Google Scholar] [CrossRef]

12. Wang H, Jia Y, Zhang M, Hu Q, Ren H, Sun P, et al. FedDSE: distribution-aware sub-model extraction for federated learning over resource-constrained devices. Paper presented at: ACM on Web Conference 2024; 2024 May 13–17; Singapore. [Google Scholar]

13. Wang H, Zheng P, Han X, Xu W, Li R, Zhang T. FedNLR: federated learning with neuron-wise learning rates. Paper presented at: 30th ACM Conference on Knowledge Discovery and Data Mining; 2024 Aug 25–29; Barcelona, Spain. [Google Scholar]

14. Lu J, Liu H, Jia R, Wang J, Sun L, Wan S. Toward personalized federated learning via group collaboration in IIoT. IEEE Trans Ind Inform. 2023;19(8):8923–32. doi:10.1109/TII.2022.3223234. [Google Scholar] [CrossRef]

15. Wang H, Xu H, Li Y, Xu Y, Li R, Zhang T. FedCDA: federated learning with cross-rounds divergence-aware aggregation. Paper presented at: 12th International Conference on Learning Representations; 2024 May 7–11; Vienna, Austria. [Google Scholar]

16. Cho YJ, Wang J, Joshi G. Towards understanding biased client selection in federated learning. Paper presented at: 25th International Conference on Artificial Intelligence and Statistics; 2022 Mar 28–30. [Google Scholar]

17. Luo B, Xiao W, Wang S, Huang J, Tassiulas L. Adaptive heterogeneous client sampling for federated learning over wireless networks. IEEE Trans Mob Comput. 2024;23(10):9663–77. doi:10.1109/TMC.2024.3368473. [Google Scholar] [CrossRef]

18. Chen W, Horváth S, Richtárik P. Optimal client sampling for federated learning. Trans Mach Learn Res. 2022. [Google Scholar]

19. Yang H, Fang M, Liu J. Achieving linear speedup with partial worker participation in non-IID federated learning. Paper presented at: 9th International Conference on Learning Representations; 2021 May 3–7; Virtual Event, Austria. [Google Scholar]

20. Le THT, Tran NH, Tun KY, Nguyen MNH, Pandey SR, Han Z, et al. An incentive mechanism for federated learning in wireless cellular networks: an auction approach. IEEE Trans Wirel Commun. 2021;20(8):4874–87. doi:10.1109/TWC.2021.3062708. [Google Scholar] [CrossRef]

21. Bonawitz KA, Eichner H, Grieskamp W, Huba D, Ingerman A, Ivanov V, et al. Towards federated learning at scale: system design. Paper presented at: 2th Conference on Machine Learning and Systems; 2019 Mar 31–Apr 2; Stanford, CA, USA. [Google Scholar]

22. Amiri MM, Gündüz D, Kulkarni SR, Poor HV. Convergence of update aware device scheduling for federated learning at the wireless edge. Trans Wirel Commun. 2021;20(6):3643–58. doi:10.1109/TWC.2021.3052681. [Google Scholar] [CrossRef]

23. Wadu MM, Samarakoon S, Bennis M. Joint client scheduling and resource allocation under channel uncertainty in federated learning. IEEE Trans Commun. 2021;69(9):5962–74. doi:10.1109/TCOMM.2021.3088528. [Google Scholar] [CrossRef]

24. Guo Y, Liu F, Zhou T, Cai Z, Xiao N. Privacy vs. efficiency: achieving both through adaptive hierarchical federated learning. IEEE Trans Parallel Distrib Syst. 2023;34(4):1331–42. doi:10.1109/TPDS.2023.3244198. [Google Scholar] [CrossRef]

25. Huang G, Chen X, Ouyang T, Ma Q, Chen L, Zhang J. Collaboration in participant-centric federated learning: a game-theoretical perspective. IEEE Trans Mob Comput. 2023;22(11):6311–26. doi:10.1109/TMC.2022.3194198. [Google Scholar] [CrossRef]

26. Lim WYB, Xiong Z, Miao C, Niyato D, Yang Q, Leung C, et al. Hierarchical incentive mechanism design for federated machine learning in mobile networks IEEE. Internet Things J. 2020;7(10):9575–88. doi:10.1109/JIOT.2020.2985694. [Google Scholar] [CrossRef]

27. Sun P, Chen X, Liao G, Huang J. A profit-maximizing model marketplace with differentially private federated learning. Paper presented at: 41th IEEE Conference on Computer Communications; 2022 May 2–5; London, UK. [Google Scholar]

28. Luo B, Feng Y, Wang S, Huang J, Tassiulas L. Incentive mechanism design for unbiased federated learning with randomized client participation. Paper presented at: 43th IEEE International Conference on Distributed Computing Systems; 2023 Jul 18–21; Hong Kong, China. [Google Scholar]

29. Kairous P, McMahan HB, Avent B, Bellet A, Bennis M, Bhagoji AN, et al. Advances and open problems in federated learning. Found Trends Mach Learn. 2021;14(1–2):1–210. doi:10.1561/2200000083. [Google Scholar] [CrossRef]

30. Zhang H, Li Z, Gong Z, Siew M, Wong CJ, Azouze RE. Poster: optimal variance-reduced client sampling for multiple models federated learning. Paper presented at: 44th IEEE International Conference on Distributed Computing Systems; 2024 Jul 23–26; Jersey City, NJ, USA. [Google Scholar]

31. Wang S, Perazzone JB, Ji M, Chan KS. Federated learning with flexible control. Paper presented at: 42th IEEE Conference on Computer Communications; 2023 May 17–20; New York, NY, USA. [Google Scholar]

32. Reddi SJ, Charles Z, Zaheer M, Garrett Z, Rush K, Konečný J, et al. Adaptive federated optimization. Paper presented at: 9th International Conference on Learning Representations; 2021 May 3–7; Austria. [Google Scholar]

33. Jiang L, Chen B, Xie S, Maharjan S, Zhang Y. Incentivizing resource cooperation for blockchain empowered wireless power transfer in UAV networks. IEEE Trans Veh Technol. 2020;69(12):15828–41. doi:10.1109/TVT.2020.3036056. [Google Scholar] [CrossRef]