Weighted Attribute Based Conditional Proxy Re-Encryption in the Cloud

1  Introduction

Proxy re-encryption (PRE) refers to a cryptographic system with secure ciphertext transformation, where the agent acts as an intermediary for the ciphertext transformation, allowing the user to obtain the intended ciphertext. At the same time, in the process of ciphertext transformation, the agent can neither obtain the plaintext information nor the encryption key of the DO, so the agent can carry out ciphertext transformation in an untrustworthy environment. However, the disadvantage of the traditional PRE is that if the agent has the correct key for the DO, the agent can change all the ciphertexts of the DO to be decrypted by the user directly. The more granular delegation of decryption permissions that are required in a lot of application scenarios is not satisfied by this.

It was not until 2009 that Weng et al. [1] introduced the idea of Conditional proxy re-encryption (CPRE) to address this issue. This approach allows the DO to define a condition during the encryption process, which is then used to construct ciphertext with a transformation condition that can only be satisfied if the agent has a re-encryption key that satisfies that condition. The introduction of CPRE limits the ability of the agent to re-encrypt data, limiting it to transforming the partially satisfied ciphertexts of the DO even when the agent possesses the re-encryption key. Subsequently, various attribute-based conditional proxy re-encryption (AB-CPRE) schemes emerged to restrict the user’s decryption rights further. In the AB-CPRE scheme, the access structure will be used as a condition to restrict the agent from transforming the ciphertext. This optimizes the CPRE scheme in conjunction with the granular access control structure of attribute-based encryption (ABE), which provides a more granular delegation of decryption permissions than before.

The AB-CPRE scheme currently in use assumes that two users with identical attributes have the same access rights. For instance, an access policy should be set so that only physicians over 45 years old can access encrypted files. However, the physician attribute may comprise ‘director physician’, ‘associate director physician’, ‘house physician’, ‘doctor in charge of a case’. If we were to allow the director physician, associate director physician, or house physician over 45 years old to access the file, we would have to add three of the four sub-attributes divided under the physician attribute to the access structure. This access policy is {{“Director Physician” OR “Associate Director Physician” OR “house physician”} AND “Age > 45”}. Considering all possible situations will inevitably lead to a greater number of characteristics in the management system, making the access structure more complicated. The current AB-CPRE adopts the same access structure as its predecessor, treating attribute characteristics at the same level without hierarchical classification based on importance.

According to the needs of the actual situation, each attribute of the user is given a weight according to its own importance so that the user gets a set of weighted attributes. Assign weights of 4, 3, 2, and 1 to ‘director physician’, ‘associate director physician’, ‘house physician’, ‘doctor in charge of a case’, respectively. If a weighted access policy is constructed, it can only satisfy the above three cases. This weighted access policy is {“Physician {2}” AND “Age > 45”}, where “Physician {2}” indicates that the node requirement can only be satisfied if the user’s attribute weight is not less than 2. As shown in Fig. 1, the improved weighted access tree is simpler, and the effect is more pronounced as the user attributes are divided into more levels.

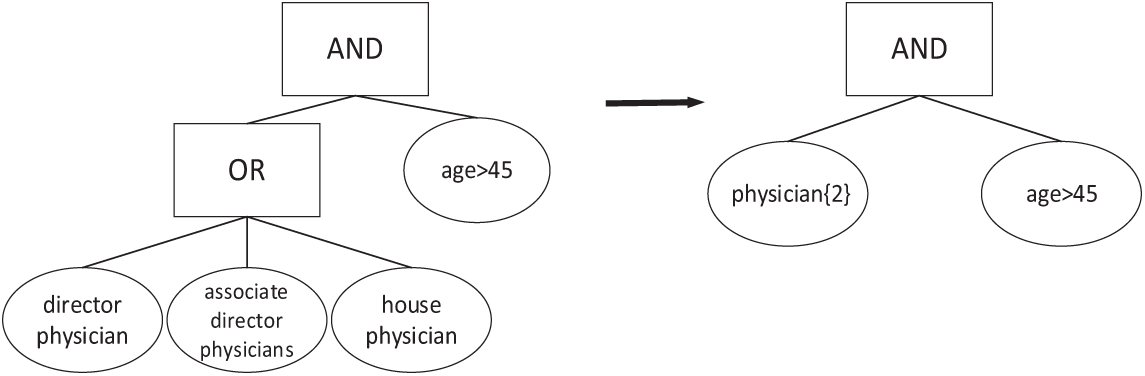
Figure 1: Comparison of access policy

By assigning appropriate weights to the attributes, the identity characteristics of each user are further refined, and the agent can more accurately restrict the user’s decryption rights through the weighted access policy. At the same time, setting a weighted access policy can further simplify the access structure. Therefore, in order to granular delegation of decryption permissions for AB-CPRE, it is meaningful to propose a weighted attribute-based conditional proxy re-encryption (WAB-CPRE) scheme at this stage.

1.1 Related Work

Blaze et al. [2] first presented the idea of PRE, who created a scheme that was fundamentally comparable to the ElGamal encryption method [3] by using a public-key cryptography algorithm with straightforward proxies. As PRE is slowly becoming an important cryptographic primitive in secure cloud computing and cloud storage, PRE is required to support a more granular delegation of decryption permissions for practical applications at this stage. Weng et al. [1] presented the idea of CPRE for the first time and proved that the scheme satisfies CCA security. However, early CPRE schemes used simple keywords or “AND” joins of multiple keywords as conditions for re-encryption by the agent, but these CPRE schemes are still somewhat unsatisfactory for the granular delegation of decryption permissions required by practical examples.

An AB-CPRE system was initially presented by Zhao et al. [4] in 2010. It allows attribute-based management of decryption delegation by allowing access structures and attribute sets to be established. The scheme embeds access structure in the re-encryption key, the collection of attributes into the ciphertext, for the first time realizing granular conditions than the keyword. A new AB-CPRE technique was suggested by Yang et al. [5], who also showed how useful the scheme is for cloud deployment. This scheme uses a ciphertext policy to realize AB-CPRE, which is more natural and flexible compared to the literature [4]. An identity-based CPRE will be presented by Yao et al. [6] in 2021. It solves the problem that the traditional PRE scheme focuses on access authorization and ignores key updates and ciphertext evolution. Subsequently, a granular certificateless CPRE scheme without pairings was proposed by Yang et al. [7]. It not only solves the problem of the traditional certificates CPRE scheme that does not support one-to-many transformations but also improves the efficiency of the scheme through the without pairings approach.

In 2023, Tang et al. [8] proposed an attribute-based verifiable CPRE scheme, which is based on homomorphic signatures, and introduced a verification server so that the re-encrypted ciphertext can be verified by a verification server. The scheme can determine whether the original ciphertext has been correctly transformed and thus can effectively detect the agent’s illegal activities. First, in 2024, a single-hop directly revocable AB-CPRE was proposed based on standard LWE assumptions [9], which provides more flexible access control while allowing the delegate to dynamically authorize and revoke a user’s decryption privileges.

However, none of the existing AB-CPRE schemes describe the importance of attributes, but in reality, the access rights of different users with the same attribute may not be the same. Liu et al. [10] generalized the traditional ABE and proposed a weighted ABE scheme by performing weighting operations on attributes according to their importance. Only when the ciphertext contains a set of attributes with different weights that satisfy the access structure can the user decrypt the ciphertext. However, this scheme is only an improvement of the traditional ABE, and there is no function for a semi-trusted agent to securely transfer the decryption right of its ciphertext. Therefore, this scheme, compared to the scheme [10], in addition to supporting the delegation of decryption rights, also has a more fine-grained delegation of decryption rights than the current AB-CPRE. Meanwhile, this program supports the direct revocation of user access rights, which solves the complex revocation work of traditional attribute-based encryption. High user-side efficiency is also a major advantage of this scheme, which enables users to decrypt access to data on cloud services on resource-constrained devices.

1.2 Contribution

A WAB-CPRE scheme will be presented in conjunction with Liu et al. [10] approach to achieve a more flexible and granular delegation of decryption permissions in a cloud computing environment. The following are the principal contributions:

•   By introducing the concept of weighted attributes, the user’s identity characteristics are refined, and the decryption delegation of the AB-CPRE scheme is fine-grained. Assigning weights to each user’s attributes according to the degree of importance can relieve the number of system attributes and ease the server management burden. The effect of this simplification is more pronounced when the user hierarchizes more attributes or has more levels at which each attribute is hierarchized.

•   In conjunction with CPRE technology, a weighted access tree will be set up to control user access rights. The cloud service provider (CSP) can successfully transform the ciphertext decryption permission to the user as long as the user’s collection of weighted attributes satisfies the weighted access structure set by the DO.

•   By assigning the re-encryption procedures to the server, outsourcing techniques help the DO cut down on computational and communication expenses. At the same time, the scheme supports the direct revocation of the user’s decryption right, eliminating the tedious procedure of updating the ciphertext data and distributing re-encryption keys in the original revocation function.

•   The security of the CPA is accomplished under decision -Expanded Bilinear Diffie-Hellman exponent (-Expanded DBDH) assumptions. To illustrate the greater user-side computing and communication efficiency of the proposed method, simulation experiments are carried out in addition to a comparison and analysis of its functionality and performance.

1.3 Organization

The remainder of the document is arranged as follows: Section 2 focuses on basic preparatory knowledge. Section 3 gives the algorithm definition and security model, and the application scenarios are specifically analyzed at the end of this section. Section 4 details the specific construction and security analysis. Then, in Section 4, the performance analysis is made by comparing the scheme with the existing schemes. Lastly, Section 6 provides the paper’s conclusion.

2  Preliminaries

2.1 Access Structure

Definition 1: If there are participants, let be a collection of participants. The set is monotone if : , then , where the access structure is a nonempty subset of , . Assume that there is an authorized subset of set and that there are illegal sets for the other sets that are not in .

2.2 Weighted Access Tree

In the WAB-CPRE scheme, the DO uses a collection of descriptive weighted attributes to structure the associated re-encryption key. DO specifies the desired for the message and creates the ciphertext under . When a collection of descriptive weighted attributes satisfies , the CSP successfully transforms the ciphertext and transmits it to the user. We name , which contains both leaf and non-leaf nodes, as its weighted access tree. The non-leaf node consists of the number of sub-nodes and the threshold , where . When and are set to “AND” and “OR” gates, the leaf node represents a weighted attribute, and the of its parent node is increased by 1 if the user’s weight for that attribute is satisfied. The function can be called on the parent of node , while the function can extract the weighted attribute connected to the leaf node. Assign a unique index value to each child node of a non-leaf node in order from 1 to , and the function is used to represent the index value of that child node.

2.3 Satisfying a Weighted Access Tree

is defined as a weighted access tree with root . Define a collection of attributes satisfies as . We define a recursive algorithm to compute the value of . The of a non-leaf node returns 1, and a specific number of its leaf nodes must be required to all have a of 1. If is a leaf node, the value of is 1 when the weight of the attribute attribute in is not less than the weight of the attribute of the leaf node, that is, .

2.4 The Decisional -Expanded BDHE Assumption

We introduce the paper [11] constructing the decision -Expanded Bilinear Diffie-Hellman Exponent problem. The chosen randomly and is a generating element of the cyclic group . Assume that an opponent is provided

Define random tuple and tuple , where is chosen independently from . Let Algorithm B have an advantage in solving the decision -Expanded BDHE in is .

Definition 2: The assumption of decision -Expanded BDHE is valid if no algorithm is able to obtain a non-negligible advantage in polynomial time when addressing the problem.

3  Definition and Application

3.1 Algorithm Definition

: After inputting the master entity’s security parameters and attribute universe , this algorithm produces the scheme’s public parameters, and the public parameters are published by the master entity.

: The algorithm outputs the key pairs , for the user .

: Given an access tree input the message that you want to encrypt and the DO’s public key . The algorithm generates ciphertext .

: After inputting the private key of the DO and a collection of weighted attributes and public key of the user . Subsequently, the algorithm outputs associated with the set of weighted attributes.

: The algorithm is performed by the CSP. Enter the ciphertext and the user’s re-encryption key . If the collection of weighted attributes satisfies the weighted access structure , the algorithm sends the ciphertext to the user.

: The decryption algorithm takes the key and the converted ciphertext as input, which produces the plaintext if is a working decryption key.

3.2 Security Model Definition

Init. The adversary chooses and declares a weighted access structure .

Setup. Challenger executes the algorithm and outputs and then performs the algorithm to obtain the key pairs . Finally, sends the output to .

Phase 1. Using a different collection of weight attributes , respectively, adversary asks challenger for the re-encryption keys. Subsequently, challenger responds by executing the algorithm to distribute the key pairs a for adversary and by using the algorithm to create a re-encryption key for . Finally, the key pairs and are returned to the adversary.

Challenge. Two challenge messages of identical length, and , are sent by the adversary. The challenger tosses a coin at random and encrypts the message by running an algorithm under a weighted access structure and submits the ciphertext to .

Phase 2. Using a different collection of weight attributes again, adversary asks the challenger for the re-encryption keys. As in phase 1, the challenger returns and to the adversary if satisfies ; otherwise, and are returned to the adversary.

Guess. A guess about is output by the adversary.

Definition 3: A WAB-CPRE scheme satisfies CPA security if, for any PPT adversary , there exists a negligible function such that , which defines ’s advantage in this game to be .

3.3 Application Scenario

The system model of the WAB-CPRE scheme includes four entities: the data owner (DO), the user, the cloud service provider (CSP), and the key generation center (KGC). Using the hospital employee system as an example, we can better demonstrate the system model by designating the DO Alice and the user Bob as the medical staff and the hospital administration, respectively. Assuming that the collection of weighted attributes of the healthcare worker meets the weighted access structure set by the hospital administrator, Fig. 2a shows the data sharing procedure from the hospital administrator (Alice) to the healthcare worker (Bob), and Fig. 2b illustrates the multiple operations involved between the various entities.

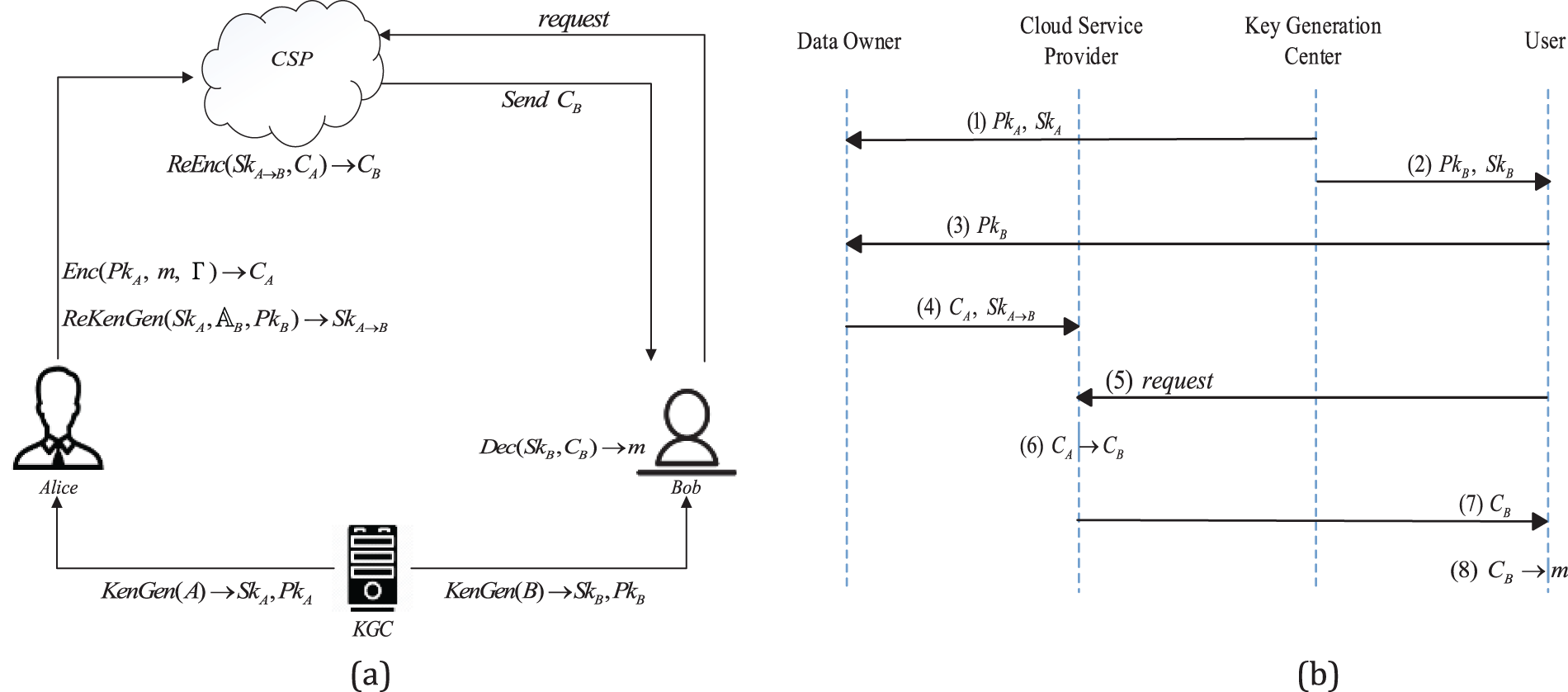
Figure 2: System model and workflow

First, Alice sets the access rights for each file according to the roles of the accessors and delivers the encrypted ciphertext to the CSP. Subsequently, Alice assigns re-encryption keys to healthcare workers (which includes Bob) at different position levels in each department and uploads them to the CSP. The CSP stores a large amount of received ciphertext data and keys in two separate tables. Bob notifies the CSP of his requirement for access to the pertinent files by sending a request. The CSP extracts the appropriate ciphertext file and Bob’s re-encryption key from a lookup table and performs the algorithm. If Bob’s collection of attributes meets the weighted access structure, the CSP successfully transforms the ciphertext and transmits it to Bob. At last, Bob runs the algorithm to decrypt and extract the plaintext data.

The system takes advantage of cloud services by outsourcing large amounts of data and complex calculations to a CSP, which acts as a semi-trusted platform and will not extract any information from the uploaded data. Having the correct re-encryption key is an important condition for CSP to securely translate decryption permissions. When a healthcare worker leaves the hospital or joins the staff, there is no revocation of the role attribute in the system, but rather the revocation of the old healthcare worker’s access rights and the granting of the new healthcare worker’s access rights. Therefore, when a healthcare worker leaves and joins the staff, the system can remove or add the re-encryption key for that healthcare worker directly from the cloud.

4  Construction and Security Analysis

4.1 The Construction

: First, the security parameter and the attribute domain are input for the algorithm. Define a bilinear map , where and are cyclic groups of prime order , and is chosen as the generators of , a hash function . The scheme assigns a maximum weight of to each attribute separately. The random number is generated for and published (Table 1 shows the meaning of each symbol in this scheme):

: The key generation center first selects for user randomly and computes , then outputs user’s key pairs , .

, .

: The DO inputs the public key , the message , and the weighted access tree . Let be the collection of leaf nodes of a weighted access tree . Each leaf node represents an attribute that has a weight value of , where . For , the encryption algorithm randomly generates . Generates the secret value of the root node and generates a polynomial of order such that . Then, a order polynomial is generated for all child nodes of the root node , setting finally until all leaf nodes are assigned the unique secret value . The function , which indicates the attributes connected to that leaf node , is defined exclusively in cases when is a leaf node.

First, set and .

Then let , when , for set:

when , for set:

Finally, output ciphertext:

: The algorithm starts by picking a random number for pick , where ( denotes the magnitude of the weight of the weighted attribute ).

Firstly, set

Secondly, for , when set:

when set:

Finally, output the re-encryption key:

: First, define a recursive algorithm , where is a node of the tree . ① In the case where is a leaf node, then define and give the following definition: If , then ; otherwise, let . Then, run the recursive algorithm to find the specific value of .

First, when set:

Second, when set:

Finally, if is satisfied, then and let .

② In the case where is a non-leaf node, the recursive algorithm is called. Let be the set of of size not less than , where is a leaf node of and . Then if there isn’t such a collection, otherwise:

③ If is the root node, then .

At last compute and , then outputs the re-encrypted ciphertext as .

: The user performs the decryption algorithm. After entering a valid private key and the re-encrypted ciphertext , the following computation is performed to obtain the plaintext message:

4.2 Security Analysis

There are two separate situations to take into account. ① The first case is when none of the collection of attributes satisfies the . Adversary would receive the key pairs and the re-encryption key that challenger provided to the user. ② The second case is when at least one of the attribute collections satisfies the weighted access structure . Therefore, the challenger returns the user’s public keys and to .

Assume, for the first example, that there is a polynomial-time whose advantage in attacking the selective access tree model in this scheme is . The security model for this case is the same as in the paper [10]. The following describes in detail the parameterization, ciphertext generation, and re-encryption key request of adversary by simulator during the simulation process. The simulation process is shown below:

Definition 4: Assume that the decisional -Expanded BDHE assumption is valid. Then, given a challenge access tree , no adversary with polynomial time could selectively compromise our system.

First, challenger chooses two cyclic groups, and , where is the generator of . flips an arbitrary binary coin . When , sets ; when , the challenger sets , where is chosen independently from .

Init. selects and declares a weighted access structure .

Setup. Choose random indices , and is the weight value of attribute , ( is attribute universe). The challenger uses an empty table in order to mimic the hash function . When asks a query that has never been asked before, computes and adds a table entry to the table, returning to . The challenger chooses a random identity and executes the algorithm to obtain key pairs , where is defined and parameterized:

Phase 1. Adversary makes a key query to the challenger. implicitly setting and executes the algorithm using a random user identity and generates the key pairs for adversary . For , define a set , where .

When , set

When , set

Challenge. When starts to create a challenge ciphertext, it is necessary first to establish the individual node polynomials of the access tree . If the collection does not satisfy , then . To access all sub-nodes of the tree , define and compute . Ultimately, polynomials for the remaining nodes are recursively created.

When is a sub-node of that satisfies the collection of weighted attributes, the value of can be calculated. The simulator subsequently runs the recursive algorithm to generate a polynomial for that node. If the node is an unsatisfiable child node, the value of can be computed by interpolation algorithm. The simulator then runs the recursive algorithm to generate a polynomial for the node. At last, the value of for each leaf node is output, .

Let . Two equal-length challenge messages and , are submitted by adversary , and the challenger tosses a coin, .

When , it set:

If is a correct Expanded BDHE tuple, then is the ciphertext encrypted by . If not, then is a random element in , and will not have access to valid information about .

Guess. will provide a guess . Judge the output according to the following rules: If , the simulator outputs 1. If not, the simulator outputs 0.

When the simulator outputs 1, the simulation attack view of adversary is the same as the actual attack view, so that we can get . On the other hand, if the simulator returns 0, then the message is concealed from , where is a random selection from . As a result, the simulator is able to play that game with a non-negligible advantage.

For the second scenario, the collection of weighted attributes of the key query performed by all satisfy the challenge weighted access structure . Thus, can obtain the transformed ciphertext. A detailed description of the proposed scheme’s security game under the CPA follows.

Init. selects and declares a weighted access structure .

Setup. As in the same case, challenger sets the public parameters and sends them to . Subsequently, selects a random identity and executes the algorithm to obtain the public and private key .

Phase 1. The adversary performs a re-encryption key lookup operation by providing a weighted attribute set to the challenger (This weighted attribute set satisfies the weighted access structure ). For the weighted access structure received by the challenger for the th time, first randomly chooses and generates the private key of . Subsequently, select , where , and return , , to .

Challenge. Challenger chooses , where . Then, the challenger distributes secret values according to declared by so that each leaf node of is assigned a unique secret value. Finally, after sends two challenge messages , chooses , and computes to return the ciphertext to .

Phase 2. The challenger keeps answering A’s questions on re-encryption key generation.

Guess. A guess about is output by the adversary .

We will cite a game [12] where the challenged ciphertext is either or , where . The adversary has to guess which is correct. Next, we prove with likelihood that A’s guess is in the simulation. Adversary has an advantage of at most given , since the challenge message is independent of the encrypted message.

When requests the group oracles, we require to obtain values only from the simulation. Here we consider an oracle query as a rational function and queries only in the variables . Since the adversary’s two different formal rational functions , will have an accidental collision caused by the random choice of variables, the condition is set that no collision of this kind occurs in any of the groups , . A collision occurs if and only if for different rational functions and of the query satisfy . Note that the total degree of is in our case at most 5, the likelihood of this event, according to the Schwartz-Zippel Lemma [13,14], is . By a union bound, the probability of a collision occurring is maximized to so that it can be calculated that there is a probability that no accidental collision will occur.

Conditional on the absence of collisions, if the challenger sets , we must show that the opponents’ views are identically distributed. In particular, under the above setup conditions, the only way to make an adversary’s viewpoint different is two queries , in such that but . However, that case will not occur since only is computed from the element in . Thus, for some constant , one must have . When we provide a query a to the adversary, the adversary will never be able to construct a query for as long as there is no accidental collision, which contradicts the above theory, thus proving the theorem.

4.3 Correctness Analysis

This subsection demonstrates the correctness of the scheme. First, this subsection shows the process of DO decrypting the original ciphertext using the original key . Secondly, a correctness proof of the evolution of the ciphertext from the original ciphertext to is given. Finally, evidence of the correctness of the evolved ciphertext in the decryption process is presented.

(1)   Decryption of original ciphertext : The original encrypted message and the public-private key pair obtained by the DO are , and respectively. The decryption of original ciphertext is given as follows:

(2)   The agent acquires the evolved ciphertext : Upload the original ciphertext and the re-encryption key to the cloud server. Only the process of calculating is given below, and is the same as the original ciphertext:

(3)   Decryption of delegated ciphertext :When the user wants to access the ciphertext , the agent will use the re-encryption key of user to obtain the evolved ciphertext . Subsequently, the user decrypts it using his private key and the obtained from the agent. The derivation process is as follows:

5  Performance Analysis

5.1 Performance Comparison

As shown in Table 2, it demonstrates the functionality and performance comparison of the proposed scheme with Xiong’s scheme [16], Yao’s scheme [6,15,17]. Let and denote the computation time of signature verification, ciphertext verification, multiplication operation, modular exponentiation, and pairing, respectively.

Firstly, Table 2 shows the comparison of two key features, namely “whether to support weighting of attributes” and “whether to support direct revocation by the user.” In real-application scenarios, CSP usually requires fine-grained data sharing and efficient user revocation. Therefore, the two functions in Table 2 are important in cloud storage services today, and only the proposed scheme supports both functions. Second, the proposed scheme has high efficiency on the user side because the complex pairing operation in the previous decryption algorithms is replaced by the re-encryption algorithm, which is implemented by the CSP. The length of the ciphertext obtained at the user side is only 2 . As shown in Table 2, decryption requires only power and multiplication operations, making the decryption cost much lower than other related schemes.

In summary, compared with other relative schemes, the proposed scheme has the smallest re-encrypted ciphertext size, which effectively enhances the communication efficiency on the user side, and adds additional functions such as weighting of attributes and attribute revocation so that the proposed scheme has a far wider range in the realm of health care.

5.2 Experimental Results

In this paper, the experimental environment is IntelliJ IDEA Community Edition 2023, and Java Pairing Based Cryptography Library and elliptic curves chosen as class curves of over the domain. It runs on a computer with parameters of 2.30 GHz Inter(R) Core (TM) i7-12700H, 16.0 GB of RAM, and operating system Windows 11.

The time consumed in running the decryption algorithm 100 times in the simulation experiment is listed as shown in Fig. 3a. The maximum time required to decrypt the ciphertext is 8.9 ms, and the minimum is 6.03 ms. The time consumed for user decryption is kept in the range of 6–9 ms and does not grow with the magnitude of user attributes. In addition, we perform communication overhead tests of the scheme’s decryption algorithm on a smartphone with a 2.4 GHz CPU and 8 GB RAM. The experimental results demonstrate that the communication overhead for the user is 2 , which is about 0.8 kb in the implementation.

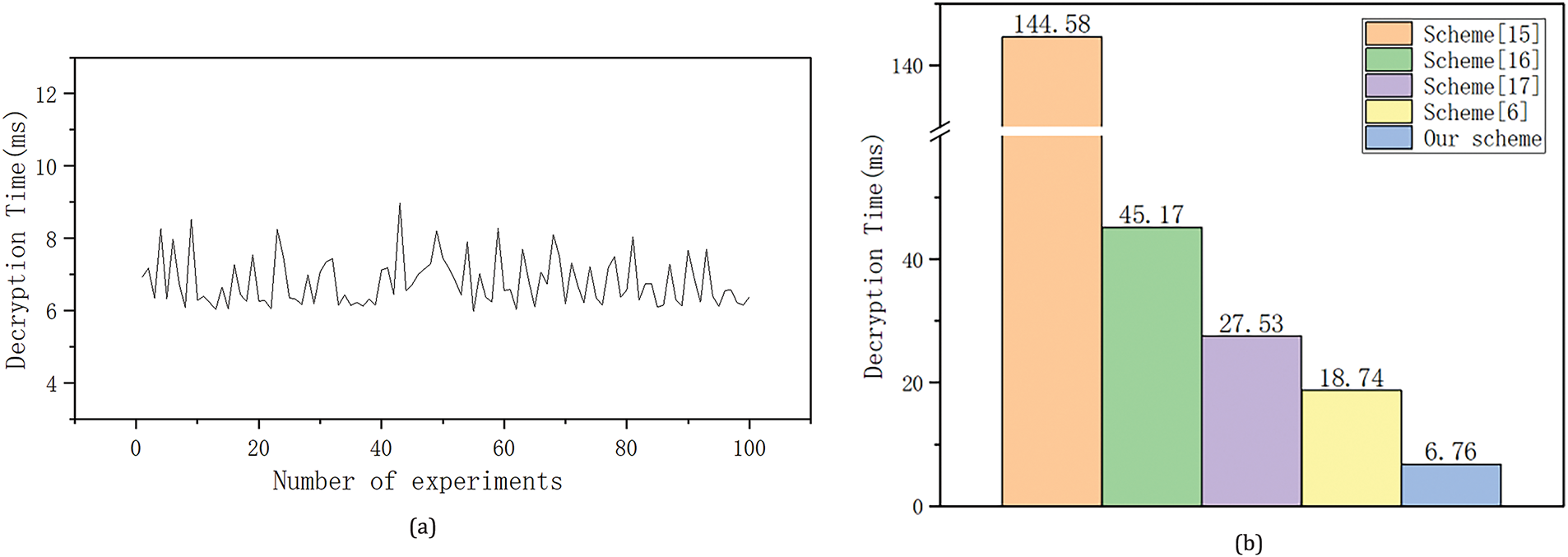
Figure 3: (a) Decryption time cost; (b) Comparison of decryption time cost [6,15–17]

We use the average of one hundred decryption times as the decryption time for this scheme. As can be seen in Fig. 3b, the proposed scheme has the least user decryption time overhead compared to other schemes. Although this scheme is constructed based on bilinear mapping, the decryption algorithm does not have a pairing operation with high overhead. Therefore, the proposed scheme has less computation and communication overhead on the user side, making it feasible for users to access cloud servers with resource-constrained devices.

6  Conclusion

In order to make cloud servers satisfy as high as possible access control mechanisms, a WAB-CPRE scheme is proposed. By combining weighted attribute-based encryption, the proposed scheme provides more granularity and a more flexible access structure for decryption. The scheme also supports CSP in performing direct revocation of user access rights, and there is no computational cost to achieve revocation. In addition, the user side of the scheme has low computational and communication overhead, enabling users to access cloud service data even in device-constrained environments. In the future, our motivation is to construct a more effective CPRE scheme where the DO can directly revoke a user’s weighted attributes.

Acknowledgement: Thanks to my tutor for careful guidance and the help of my classmates.

Funding Statement: Programs for Science and Technology Development of Henan Province, grant number 242102210152. The Fundamental Research Funds for the Universities of Henan Province, grant number NSFRF240620. Key Scientific Research Project of Henan Higher Education Institutions, grant number 24A520015. Henan Key Laboratory of Network Cryptography Technology, grant number LNCT2022-A11.

Author Contributions: Xixi Yan: the main idea, conceptualization and methodology. Jing Zhang: The framework was built, the encryption scheme was written, the security proof was derived, and the experimental analysis and test were carried out. Pengyu Cheng: Integration and analysis of experimental data. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Weng J, Deng RH, Ding X, Chu CK, Lai J. Conditional proxy re-encryption secure against chosen-ciphertext attack. In: Proceedings of the 4th International Symposium on Information, Computer, and Communications Security; 2009; Sydney Australia: ACM. p. 322–32. doi:10.1145/1533057.1533100. [Google Scholar] [CrossRef]

2. Blaze M, Bleumer G, Strauss M. Divertible protocols and atomic proxy cryptography. In: Advances in cryptology-EUROCRYPT’98. Berlin, Heidelberg; 1998. p. 127–44. [Google Scholar]

3. Elgamal T. A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Trans Inf Theory. 1985;31(4):469–72. doi:10.1109/TIT.1985.1057074. [Google Scholar] [CrossRef]

4. Zhao J, Feng D, Zhang Z. Attribute-based conditional proxy re-encryption with chosen-ciphertext security. In: 2010 IEEE Global Telecommunications Conference GLOBECOM 2010; 2010 Dec 6–10; Miami, FL, USA: IEEE; 2010. p. 1–6. doi:10.1109/GLOCOM.2010.5684045. [Google Scholar] [CrossRef]

5. Yang Y, Zhu H, Lu H, Weng J, Zhang Y, Choo KR. Cloud based data sharing with fine-grained proxy re-encryption. Pervasive Mob Comput. 2016;28(1):122–34. doi:10.1016/j.pmcj.2015.06.017. [Google Scholar] [CrossRef]

6. Yao S, Dayot RVJ, Kim HJ, Ra IH. A novel revocable and identity-based conditional proxy re-encryption scheme with ciphertext evolution for secure cloud data sharing. IEEE Access. 2021;9:42801–16. doi:10.1109/ACCESS.2021.3064863. [Google Scholar] [CrossRef]

7. Yang H, Li L, Yang C. A fine-grained certificateless conditional proxy broadcast re-encryption scheme without pairing. In: 2022 IEEE 10th Joint International Information Technology and Artificial Intelligence Conference (ITAIC); 2022 Jun 17–19; Chongqing, China: IEEE; 2022. p. 1414–23. doi:10.1109/ITAIC54216.2022.9836814 [Google Scholar] [CrossRef]

8. Tang Y, Jin M, Meng H, Yang L, Zheng C. Attribute-based verifiable conditional proxy re-encryption scheme. Entropy. 2023;25(5):822. doi:10.3390/e25050822. [Google Scholar] [PubMed] [CrossRef]

9. Wang Y, Wang M. Improved AB-CPREs with revocability and HRA security under LWE. IET Inf Secur. 2024;2024(1):4333883. doi:10.1049/2024/4333883. [Google Scholar] [CrossRef]

10. Liu X, Ma J, Xiong J, Li Q, Ma J. Ciphertext-policy weighted attribute based encryption for fine-grained access control. In: 2013 5th International Conference on Intelligent Networking and Collaborative Systems; 2013 Sep 9–11; Xi’an, China: IEEE; 2013. p. 51–7. doi:10.1109/INCoS.2013.18. [Google Scholar] [CrossRef]

11. Waters B. Functional encryption for regular languages. In: Annual International Cryptology Conference; 2012; Berlin/Heidelberg: Springer; p. 218–35. [Google Scholar]

12. Bethencourt J, Sahai A, Waters B. Ciphertext-policy attribute-based encryption. In: 2007 IEEE Symposium on Security and Privacy (SP ‘07); 2007 May 20–23; Berkeley, CA, USA: IEEE; 2007. p. 321–34. doi:10.1109/SP.2007.11. [Google Scholar] [CrossRef]

13. Schwartz JT. Fast probabilistic algorithms for verification of polynomial identities. J ACM. 1980;27(4):701–17. doi:10.1145/322217.322225. [Google Scholar] [CrossRef]

14. Zippel R. Probabilistic algorithms for sparse polynomials. In: Proceedings of the International Symposiumon on Symbolic and Algebraic Computation; 1979; Berlin/Heidelberg: Springer. p. 216–26. [Google Scholar]

15. Yao S, Dayot RVJ, Ra IH, Xu L, Mei Z, Shi J. An identity-based proxy re-encryption scheme with single-hop conditional delegation and multi-hop ciphertext evolution for secure cloud data sharing. IEEE Trans Inf Forensics Secur. 2023;18(2):3833–48. doi:10.1109/TIFS.2023.3282577. [Google Scholar] [CrossRef]

16. Xiong H, Wang Y, Li W, Chen CM. Flexible, efficient, and secure access delegation in cloud computing. ACM Trans Manage Inf Syst. 2019;10(1):1–20. doi:10.1145/3318212. [Google Scholar] [CrossRef]

17. Yao S, Sankar R, Ra IH. A collusion-resistant identity-based proxy reencryption scheme with ciphertext evolution for secure cloud sharing. Secur Commun Netw. 2020;2020:8833693. doi:10.1155/2020/8833693. [Google Scholar] [CrossRef]