A Low-Collision and Efficient Grasping Method for Manipulator Based on Safe Reinforcement Learning

1  Introduction

With robots showing advantages of great accuracy and efficiency in performing various tedious and repetitive jobs, they are widely used in industrial manufacturing [1,2], space exploration [3,4], medical services [5,6], and other related fields. In practical robotic applications, ensuring the safety of system operations is the primary principle. However, potential collision risks are inevitably present in the complex and unknown environments, such as industrial settings. On the one hand, accidental collisions may result in damage to both the workpieces and the robots, even putting the operator’s life in jeopardy. On the other hand, frequent collisions can decrease production efficiency and increase equipment maintenance and repair costs, which is harmful to the long-term development of enterprises. Achieving task completion with high safety and efficiency remains a critical research challenge in modern robotics.

As one of the most basic operations in robotic manipulation tasks, grasping has been highly valued by researchers. Song et al. [7] proposed a 6-Degrees-of-Freedom (DOF) closed-loop capturing algorithm based on motion view rendering for dynamic objects and accelerated the training process through self-collected manual demonstration data. Xiong et al. [8] combined with 3D visual perception, introduced an active obstacle avoidance policy that separated the target from obstacles, thereby significantly enhancing the fruit-picking performance. Inspired by deep learning, Lundell et al. [9] presented a generative sampling method for collision-free grasping in cluttered scenes, achieving high-quality multi-finger grasping, and the runtime speed was more than 4 times faster than the baselines. Similarly, Morrison et al. [10] realized fast closed-loop capture by processing depth images. Wang et al. [11] extended the end-to-end hierarchical learning framework to 6D object grasping in chaotic scenes based on partial point cloud observation, thereby improving both the success rate and efficiency. In robot grasping research, most of the work tends to identify target objects and separate them from obstacles using precise image analysis, facilitating efficient grasping in chaotic scenes. However, in high-risk application scenarios, it is necessary for the manipulator to avoid contact with obstacles. Therefore, this paper concentrates on handling obstacle avoidance constraints in the grasping task.

Traditional obstacle avoidance methods for robots typically rely on sensors such as vision and touch. These methods are combined with various planning algorithms to achieve tasks. Early planning involved predefined trajectories through both online and offline programming [12], which required reprogramming for even small task changes, resulting in a lack of flexibility [13]. Then, planning methods based on graph search gained popularity due to their stability and accuracy. However, their low efficiency limits their application to low-dimensional spaces. Khatib [14] proposed a robot planning method based on artificial potential field (APF). Although APF is insensitive to dimension, constructing a repulsive potential field in a complicated setting remains challenging. In addition, APF is difficult to jump out of the local optimum [15]. Many researchers prefer sample-based planning methods in complex environments [16–18], such as Rapidly-Exploring Random Tree (RRT) and Probabilistic Roadmap (PRM). However, this method cannot guarantee finding the optimal solution within a limited time, and the trajectory planned in high-dimensional space is could be more suboptimal [19]. Another popular method for manipulator obstacle avoidance is model predictive control (MPC). Considering obstacle avoidance constraints, Tika et al. [20] developed the MPC algorithm optimized for time, applied to dual manipulator pick-and-place tasks in shared spaces, but it may fall into the local minimum. Traditional obstacle avoidance methods require accurate environment modeling and complex planning algorithms. With the increase in planning dimensions, this non-learning method is limited.

Given the fast growth of artificial intelligence, the rise of deep reinforcement learning (DRL) has caused a wave of research on robotics and its related fields. Bai et al. [15] overcame training difficulties in high-precision planning tasks by combining APF, Soft Actor-Critic (SAC), and curriculum learning, and the task success rate reached 80% with a position accuracy of 0.01 m. Ying et al. [21] described multi-process robot tasks as continuous trajectory segments chronologically and designed corresponding reward functions. Similarly, Kim et al. [22] designed a reward function that considered position and energy constraints based on task decomposition. To achieve the shortest path and stable end-effector, Kuo et al. [23] discussed a method combining fuzzy control and Deep Deterministic Policy Gradient (DDPG) for grasping. However, setting accurate fuzzy rules and membership functions is a difficult task. Hu et al. [24] focused on grasping living objects by decomposing the grasping process into two stages and used inverse reinforcement learning to design intensive reward functions for each stage. Li et al. [25] designed the reward function in detail, considering end-effector constraints, and adopted the DDPG algorithm to control the free-floating space dual-arm robot for grasping rotating objects. To resolve the sparse reward issue in obstacle-rich environments, Bing et al. [26] proposed a graph-based solution using curriculum-guided hindsight experience replay (CHER), significantly improving the sample efficiency and task success rate. Reinforcement learning (RL) has shown bright prospects in robot control. However, this practice of only maximizing the expected reward can cause a series of problems and even catastrophic losses [27] when agents are deployed in the real world. Therefore, these unsafe behaviors need to be restricted to achieve safe exploration. Most RL-based work implements constraints by setting negative rewards in the reward function, limiting the action space, or terminating training directly when encountering unsafe actions or states. Unfortunately, designing a reward function that accounts for all constraints is complex and time-consuming, and even setting a negative reward may drown out the punishment in the reward. In addition, limiting the action space can cause the optimal solution to be missed. These cause the agent to be unable to balance the performance and safety constraints.

Over the past few years, safe reinforcement learning (Safe RL) has become a new way to ensure the safety of agents and environments during both training and deployment. Safe RL aims to maximize the cumulative reward while satisfying constraints, offering broad application potential in autonomous driving [28], robot control [29], and power system optimization [30]. Zhao et al. [31] suggested a multi-agent RL algorithm under security constraints to improve grid voltage stability in power generation. Wang et al. [32] constructed the cost function for base movement in the motion planning system of the space manipulator and applied the penalty method and Lagrange method to balance the trade-off between objectives and constraints. Thananjeyan et al. [27] provided a recoverable RL methodology, which combined with offline demonstration data, implemented a recovery policy after filtering dangerous actions from the original policy. Zhang et al. [33] combined traditional impedance control and Safe RL for contact-rich robot operation tasks, activated recovery strategies in the face of constraints violation, and limited contact forces to ensure system safety. Others also set the contact force as a constraint condition [34,35]. The activation of this recovery policy depends on the value function, and the security during learning is hard to guarantee. Based on precise dynamical models, safety Control Barrier Functions (CBFs) are constructed by Lyapunov-like CBFs [36], making the learning process more stable and safer. Methods based on the safety layer directly guarantee the system’s safety [37]. In [38], OptLayer imposes constraints on the actions predicted by the neural network, transforming unsafe actions into the closest ones that satisfy the constraints, ensuring that only safe actions are executed. Another high-security approach is Constrained Policy Optimization [39]. However, it is sensitive to initial parameter settings and faces computational challenges. The Trust Region Policy Optimization method indirectly improves learning safety by stabilizing policies [40]. Meng et al. [41] further utilized off-policy data to ensure the monotonic improvement of the policy, though the algorithm lacks flexibility.

To address the above challenges and enhance the safety of the manipulator during grasping tasks, a manipulator grasping method based on Safe RL is suggested. It combines RL and the Lagrange method to deal with safety constraints related to obstacles in the environment promptly. The main contributions of this paper are as follows:

1)   The manipulator grasping is modeled as a Constrained Markov Decision Process (CMDP), and a Safe RL method based on the Lagrange multiplier and dynamic weighted mechanism is proposed to solve it.

2)   A composite reward function related to the pose of the manipulator is designed, enabling the end-effector to adjust dynamically based on orientation errors, thus achieving effective grasping with an accurate pose while avoiding obstacles.

3)   A risky grasping environment for the manipulator is developed in the simulation, and extensive experiments prove that the suggested method outperforms the advanced baselines.

2  System Framework

Fig. 1 illustrates the proposed framework of manipulator grasping based on Safe RL, aimed at improving system safety by minimizing possible risks during the grasping task. Traditional RL often relies on complex, manually designed reward functions to avoid collisions. In this study, safety constraints related to collision events and a dynamic weighted mechanism are introduced into the policy, limiting cumulative costs within an acceptable range to reduce unsafe operations. A saddle-point optimization problem with no constraints is derived from the original constrained optimization problem using the Lagrange multiplier, which can deal with the constrained grasping task simply and efficiently. The safety constraint is integrated into the Proximal Policy Optimization (PPO) framework by Lagrange multiplier, and then the objective and constraint are dynamically weighted. The dynamic weighted Lagrange PPO (DWL-PPO) algorithm designed to solve the problem with constraints is thus constructed. Agent learning is a closed-loop feedback process. Agent continuously interacts with the environment to update the policy network and then influences its own behavior.

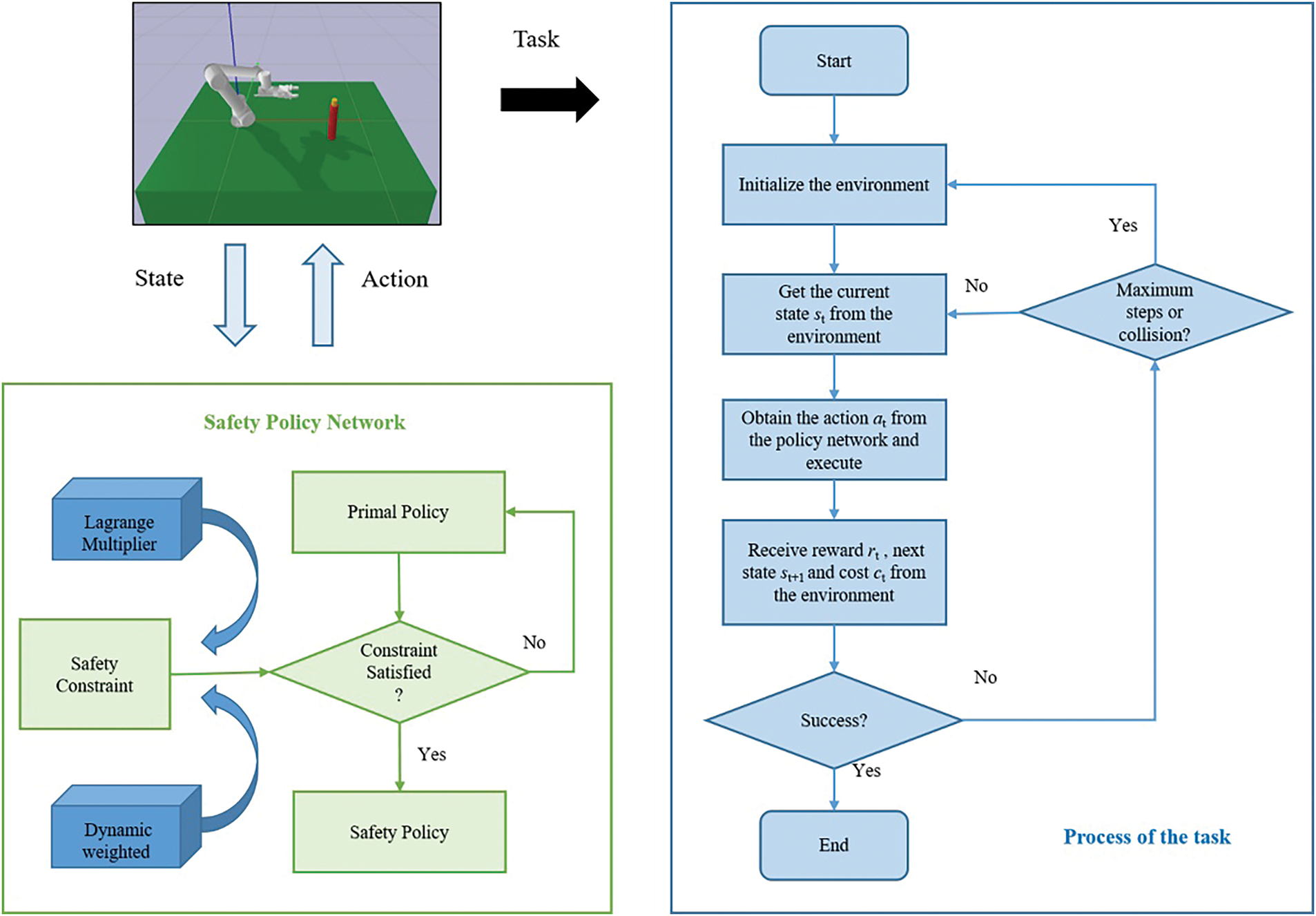
Figure 1: Grasping framework of the manipulator based on Safe RL. The security requirements of the system are converted into policy constraints. By introducing the Lagrange multiplier, the relationship between RL and constraint optimization is established, and the optimal policy can be found under the premise of no or less violation of safety constraints. A dynamic weighted mechanism is used to further balance the attention to objective and constraint

At the beginning of training, the environment is initialized. The agent obtains the current state of the environment, selects a safe action through the policy network, and executes it. The corresponding reward, the next state, and the cost associated with increased risk are returned from the environment to optimize the policy network. Orientation control of the end-effector is introduced into the reward function. This can guide the agent to gradually learn the behavior policy that is in line with the task goal, ensuring that the grasping operation is performed with an appropriate attitude. The cost arises from collision events. Through adjustment of the Lagrange multiplier, the final cost is kept within the predefined safety threshold. Then, the dynamic weight coefficient is introduced to make a secondary balance between reward and cost. In the current episode, the agent can gradually learn the optimal action that satisfies the constraints and can complete the task by employing numerous interactions with the surroundings. Once the task termination condition is met, the current episode ends, and the agent enters a new episode. The task is considered complete when the target object is successfully captured. In the set environment, the role of DPL-PPO is to ensure that the manipulator achieves the mission objective while maintaining safety by reducing collisions. The Safe RL method based on the Lagrange multiplier provides an effective solution to balance task performance and safety in manipulator control. The following section offers an extensive description of it.

3  Methodology

3.1 Problem Statement

The robotic grasping discussed in this paper takes place in an environment with potential collision risks, which implies that the security of this system ought to be ensured during the process. While RL performs well in complex and unknown environments, intrinsic security is difficult to guarantee. System safety can be improved by introducing additional constraints into RL, but the computational complexity goes up unfortunately. Therefore, the proposed method must not only achieve optimal task performance but also ensure reliability in terms of safety. The purpose of this paper is to develop an efficient and safe robotic grasping policy suitable for the environment with obstacles, overcoming the difficulty that performance and safety cannot be guaranteed simultaneously during task execution.

3.2 Constrained Markov Decision Process

Manipulator control can be modeled as a CMDP, which is an extension of the standard Markov decision process (MDP). CMDP consists of a six-tuple (S, A, P, R, γ, C). Where S is the finite set of states, A is the finite set of actions, P represents the state transition function, R represents the reward function, is the discount factor, and C is the constraint set different from standard MDP. Safe RL aims to seek out an optimal policy that maximizes the desired cumulative reward during the training process, subject to the constraints. In this paper, a Safe RL environment is developed to train an agent to perform grasping operations. The core components of this environment include the state space S, the action space A, the reward function R, and the safety constraint C, which are described in detail below.

3.2.1 State Space S

The state space is the basis of the perception and decision of the agent in the environment. The state information can completely describe the relative relationship between the manipulator and the target as well as the posture of the manipulator, which is composed of the following three parts:

(1) Joint Angle

The state representation is built by obtaining the current angles of each joint of the manipulator. The information is normalized to ensure that it falls within the range of [−1, 1]. To facilitate subsequent learning and decision-making, mapping it to the range [0, 1].

(2) Tool Center Point (TCP)

The position of TCP in the world coordinate system is another key state information. The three-dimensional coordinates of TCP are normalized to a range between [0, 1].

(3) Target position

The position of the target to be grasped in the world coordinate system is also included in the state space. Its three-dimensional coordinates are also normalized to the range of [0, 1] so that the agent can accurately judge its spatial relationship with the target object.

Thus, the state is specified as

(1)

where is the angle vector of each joint of the current manipulator, and represent the current position vectors of TCP and the target in the world coordinate system respectively.

3.2.2 Action Space A

The action space defines the actions that can be carried out in the surroundings for the agent. Since the actions output by the network are continuous, and each action corresponds to a pose, the increase in dimension will cause a significant computation burden. Instead of [42] still using inverse kinematics, a trajectory generation method based on safe RL is constructed without inverse kinematics. It can directly control the joint angle by establishing a mapping from the state space to the joint space, avoiding complex modeling and dependence on the solution of inverse kinematics. Each action is normalized to the range of [−1, 1], and the agent adjusts the pose of the manipulator by selecting the appropriate action.

Thus, the action is defined as

(2)

where represents the angle increment of the jth joint of the current manipulator.

3.2.3 Reward Function R

In Safe RL, the agent action is also guided by the reward function, and the design of the reward function directly affects the completion of the task and the convergence speed of the algorithm. In obstacle avoidance grasping task, the reward function should include the following three aspects:

(1) Positional reward

The Euclidean distance d between the end-effector and the target is an important basis for calculating the reward. When d is less than the given threshold , the actuator is judged to have reached the target position, and a high reward is given to motivate the agent to complete the task. Otherwise, the reward decays based on an exponential function of distance. The specific form is

(3)

where is a positive constant. In this paper, and .

(2) Orientation reward

In most tasks using RL for manipulator control, the reward function only involves position control [15,25,43]. However, only considering the position deviation of the end-effector is easy to cause failure, and unreasonable grasping posture will affect the execution of subsequent work. Therefore, the orientation control of the end-effector is taken into account to construct a compound reward function suitable for the grasping task under constraints. The orientation of the end-effector is expressed visually by Tait–Bryan angles. The orientation reward is calculated by evaluating the degree of deviation from the orientation. The specific form is

(4)

where , , and are roll, pitch and yaw angles. , , and are the weight coefficients.

(3) Collision penalty

To ensure safety, a negative reward will be applied to the agent instantly when the operation collapses due to dangerous behaviors such as collision (including self-collision of the manipulator and collision with the environment). The specific form is

(5)

Therefore, the final reward function can be expressed as

(6)

3.2.4 Safety Constraint C

The introduction of constraints helps to optimize the policy while considering the risk of adverse events. To reduce the occurrence of potential collision events in the environment, the corresponding cost will be accumulated when the collision occurs. The cost function can be defined as

(7)

where represents the cost of collision between the end-effector and the target, and the actuator may collide with the target if it is too close to the target. includes the manipulator collision with external obstacles and the self-collision cost. In this paper, and .

Through the cost mechanism, the agent learns behaviors to comply with long-term safety requirements during optimization.

3.3 Lagrange Method

In Safe RL, the original objective is to find the optimal feasible policy that maximizes the expected cumulative reward.

(8)

where is the immediate reward the agent receives for choosing the action in the state .

Some unsafe behaviors are restricted by introducing constraints in the solution process for decision-making tasks with strict security requirements. The cost constraint function is defined as

(9)

where is the expected cumulative discount cost of violating the constraint in the state action trajectory under the policy, represents the cost generated by executing the action, and is the maximum cost value allowed by setting.

For the agent, the original objective function and cost function are convex, and solving the convex optimization problem is a considerable challenge. The Lagrange method is a common method to solve such problems. Its key idea is to introduce the Lagrange multiplier to transform the constrained optimization problem into an unconstrained optimization problem with a penalty term. It implicitly expresses the penalty on the original objective function. The constructed Lagrange function is expressed as

(10)

where is the lagrange multiplier.

The objective function changes as follows:

(11)

Under the influence of , the cost becomes increasingly important for the policy and tends to be within the threshold. The rule for updating the Lagrange multiplier is

(12)

where is the Lagrange learning rate.

The dual problem can then be solved using RL. At each iteration, the policy is optimized, and the Lagrange multiplier is adjusted alternately by the policy gradient method until the optimal solution is found. To avoid over-dependence on and stabilize the training process, the constructed Lagrange function is further adjusted. Eq. (10) is redefined as

(13)

where is the dynamic weight coefficient.

The dynamic weighted mechanism can further adjust the relative importance between rewards and constraints. Initially, the model pays more attention to constraint compliance in an unknown environment. As exploration progresses, it gradually shifts its focus to return. is defined as

(14)

where and are the initial and final weight coefficients, is the maximum steps.

3.4 DWL-PPO Algorithm for Safe RL

PPO [44] is a standard RL algorithm based on policy gradient. The importance sampling and the clipping mechanism are introduced to improve sample utilization and stabilize the policy update process. The formula for policy to update is expressed as

(15)

where is the advantage function, is the current policy, is the old policy, is the clip range.

The DWL-PPO algorithm is a specialized implementation based on PPO. Its core is to add the treatment of constraint to the optimization objective. In DWL-PPO, the Lagrange multiplier is used to adjust the influence of the constraint on the objective, and then the dynamic weighted method is adopted to balance the trade-off between reward and constraint further. The DWL-PPO algorithm introduces a cost function to reduce the possibility of collision events when the policy is updated. The increase in cost reflects the occurrence of a collision, serving as a penalty for the agent. At each iteration, the algorithm optimizes the policy based on the reward and evaluates the cost according to the current constraint compliance. Specifically, according to Eqs. (13) and (15), the policy update formula is expressed as

(16)

At the same time, the algorithm calculates whether the current policy violates the constraint and uses the Lagrange multiplier and dynamic weighted mechanism to adjust the proportion of reward and cost. This ensures that the agent gradually learns to perform the task within a safe range. Under the guidance of the DWL-PPO algorithm, the agent will continuously learn the behavior that maximizes the reward while obeying the safety constraint, such as avoiding collisions, thereby improving the task success rate. Based on Eq. (12), DWL-PPO dynamically adjusts the emphasis on cost during the task. Thus, in the policy optimization process, the cost is strictly controlled to ensure the safety of the manipulator when grasping.

4  Experiment

4.1 Experiment Setup

To evaluate the effectiveness of the proposed method, an experimental platform is created based on the PyBullet (v 3.2.6) simulation environment. As shown in Fig. 2, the grasping experiment is performed using a 6-DOF FR5 manipulator. The target is a small yellow cylinder, while the large red cylinder and the table are obstacles. The target is in direct contact with the obstacles, which is prone to collision problems. The objective of the agent is to grasp the target object (random position) from any pose without violating the collision constraint. In this case, the agent may fail to complete the task by adopting a conservative policy, and unreasonable punishments may be ignored. Therefore, it needs to learn a feasible policy satisfying both security constraints and task objectives. When the agent violates the constraint, the current training episode will be terminated early to improve the training efficiency.

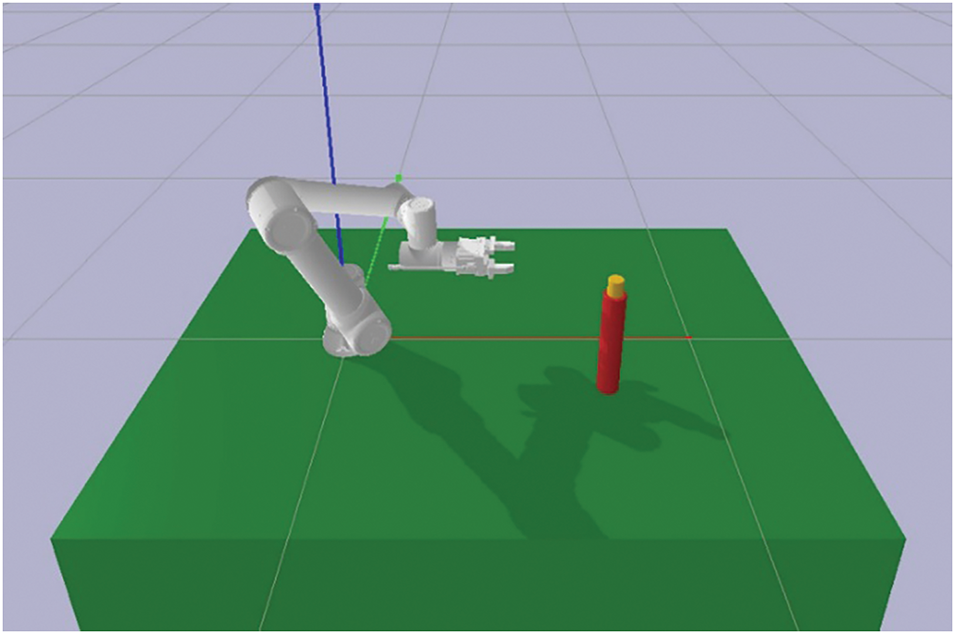
Figure 2: The simulation environment of the manipulator grasping task. The manipulator needs to grasp the small yellow cylinder without self-collision or collision with the table and the red cylinder

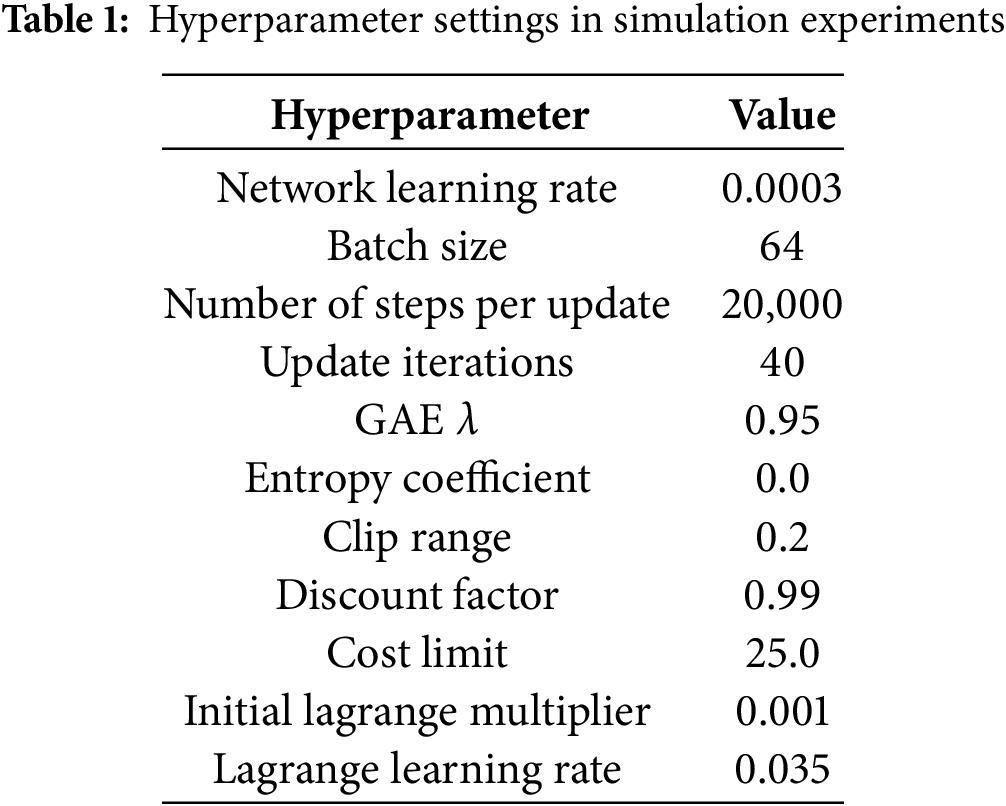
Training is performed on a computer equipped with an Intel(R) Xeon(R) Gold 5218R CPU @ 2.10 GHz and an NVIDIA GeForce RTX 4090. The experimental program is based on Python (v 3.10.13), Cuda (v 12.2), and Pytorch (v 2.1.1+cu121). The learning rate is 0.0003 for both actor and critic networks, the hidden layer size is [64, 64], the activation function is the tanh function, and the Adam optimizer is utilized to update the network parameters and Lagrange multiplier. Table 1 describes the hyperparameter Settings in the simulation experiment in detail.

4.2 Simulation Experiments

The purpose of the following simulation experiments is to compare the performance differences between the proposed method and the baselines in terms of safety and efficiency. Five advanced RL methods, including PPO [45], SAC [43], DDPG [46], and Twin Delayed Deep Deterministic Policy Gradient (TD3) [47], and OptLayer [38], are used as baselines. OptLayer imposes hard constraints to ensure safety. OptLayer, combined with the standard PPO algorithm, includes joint velocity, joint position, and distance-related obstacle avoidance constraints. PPO belongs to the on-policy algorithm, while SAC, DDPG, and TD3 are off-policy. SAC is based on random policy, whereas DDPG and TD3 are based on deterministic policy. Unless otherwise stated, the reward function settings for the baselines are consistent with the proposed method.

Each method is run 10 times with different random seeds using the same hyperparameters. The number of training episodes per round is 100, and the maximum number of steps is 100. At the start of each episode, the initial pose of the manipulator and the position of the target object are randomly generated, and then the grasp is performed. Task termination conditions include successful grasping, constraint violation, and reaching the maximum number of steps. The safe grasping problem discussed in this paper evaluates the performance based on the reward, cost, and convergence of the algorithm.

Fig. 3 displays the cumulative reward curves of each method during the training process. It is clear that the DWL-PPO (ours) algorithm rapidly increases the reward to 1000 after about 20 episodes, with only minor fluctuations afterward, indicating that the algorithm has high stability and can successfully complete the task in the later stage. The OptLayer method needs about 80 episodes to converge, which is slower. The PPO algorithm performs similarly to ours, but the reward increases more slowly, reaching the success reward after about 70 episodes. It means the traditional PPO algorithm requires more episodes to reach convergence than the method combining the Lagrange multiplier. Although the PPO algorithm converges eventually, the TD3, SAC, and DDPG methods fail to converge to the target value within 100 episodes. Their reward curves show a slow upward trend, often around negative rewards, indicating that the three methods cannot effectively complete the grasping task under the safety constraint. Although OptLayer imposes hard constraints that strictly ensure safety, the additional quadratic programs solution brings high computational complexity. It is also sensitive to the design of constraint functions.

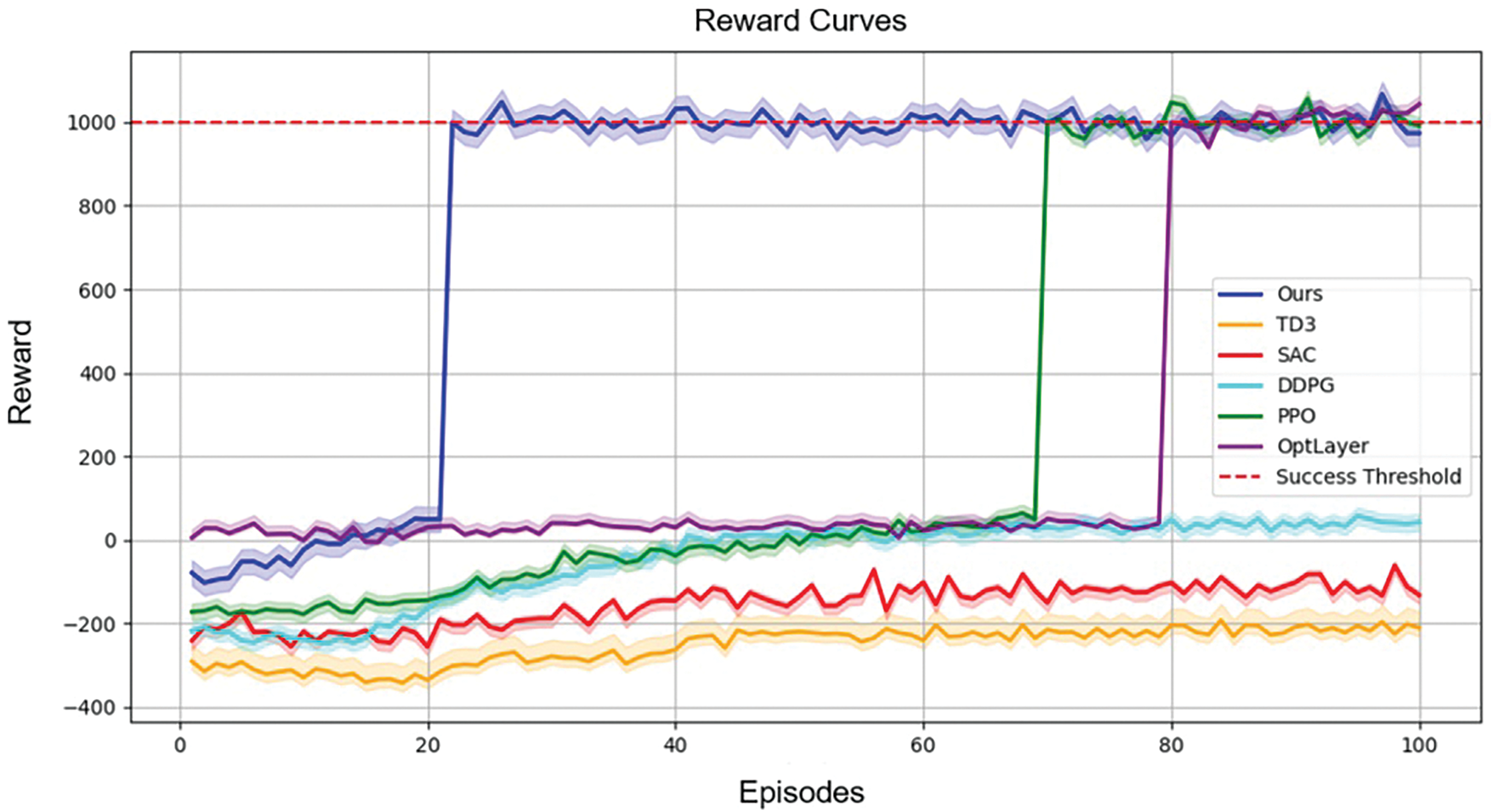
Figure 3: Reward curves: The solid line is the average of 10 runs of each method. The red dotted line represents the success reward, the blue represents ours, the purple represents the OptLayer, the green represents the traditional PPO, the orange represents the TD3, the red represents the SAC, and the turquoise represents the DDPG. The faster the reward curve converges, the larger the value, and the narrower the shadow, the better the method

Fig. 4 illustrates the cost curves of each method during training. Our method incurs a small cost before 20 episodes, after which it drops to near zero. It represents that our method can quickly learn a safety policy and achieve a good trade-off between task performance and security. In contrast, the PPO algorithm generates a higher cost early in training, approaching zero after about 70 episodes. This indicates that PPO brings a higher collision risk in the early stage, negatively impacting task performance, while our method learns to obey safety constraints faster than PPO. TD3, SAC, and DDPG performed similarly to PPO before 30 episodes. After that, TD3 and SAC produce higher costs (more than 200), and the curve fluctuates greatly. This means these two algorithms frequently violate safety constraints during training and fail to stabilize the cost below the safety threshold. DDPG performs slightly better than TD3 and SAC, but the cost remains high (more than 100), which indicates that DDPG also struggles to comply with constraints in the task.

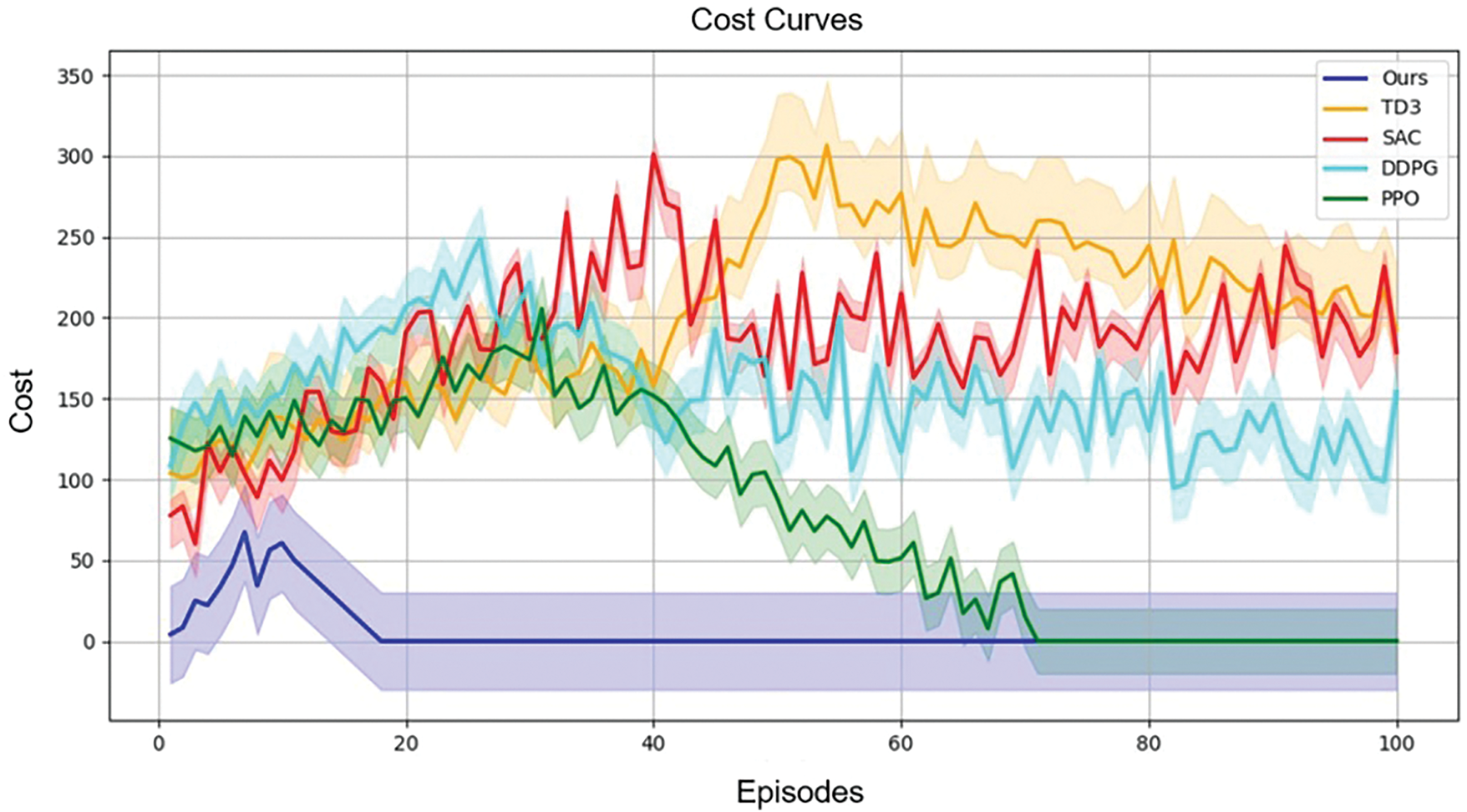
Figure 4: Cost curves: The solid line is the average of 10 runs of each method. The blue represents ours, the green represents the traditional PPO, the orange represents the TD3, the red represents the SAC, and the turquoise represents the DDPG. The faster the cost curve converges, the smaller the value, and the narrower the shadow, the better the method

Table 2 visually shows the performance differences between the methods. In contrast to the baselines, the proposed method has obvious advantages in the final reward, the final cost, and the number of episodes required for convergence. Our method achieves higher efficiency and a good trade-off between task performance and safety.

To present the completion of the task more clearly, a successful episode is chosen at random to plot the position and orientation errors of the end-effector relative to the target, as shown in Fig. 5. Observably, the end-effector reaches the target pose within the error tolerance, successfully completing the grasp operation.

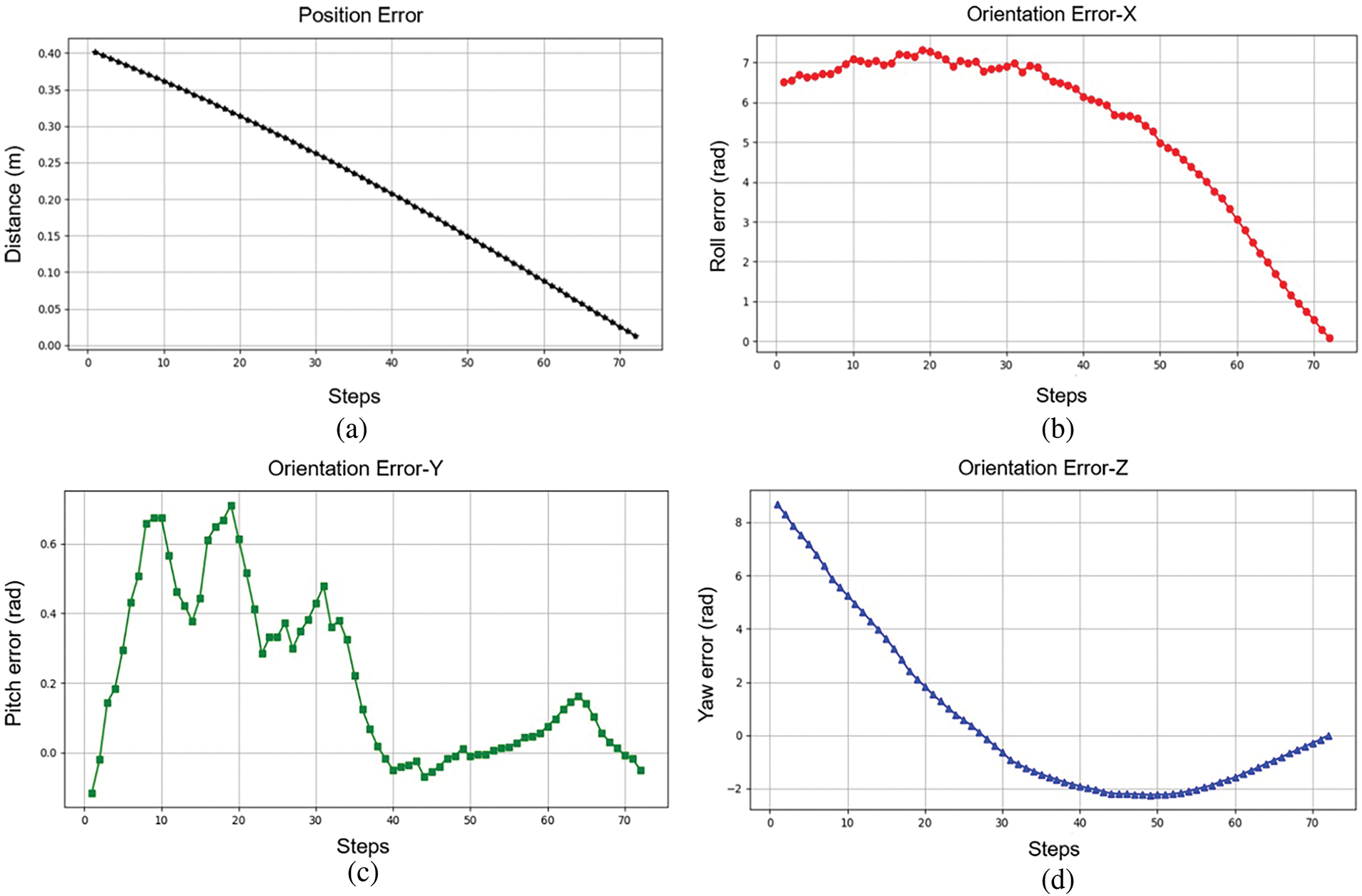
Figure 5: Position error and orientation error between the end-effector and the target: (a) position error; (b), (c), and (d) represent orientation errors in the x, y, and z axes, respectively. Grasping is implemented when the distance is less than 0.015 m. The end-effector reaches the target attitude at about 74 steps

Fig. 6 completely portrays the successful grasping process of the manipulator. The possible collision behavior is constrained in the grasping process, and the proposed method can complete the task under the condition of obeying the safety constraints.

Figure 6: Successful grasping process: (a) initializing the manipulator posture and target position; (b) adjustment of the manipulator posture; (c) reaching the target position under safety constraints; (d) completing the grasp

5  Discussion

A brief discussion is given to highlight the benefits and limitations of the proposed method compared with other methods. The PPO algorithm combined with the Lagrange multiplier and dynamic weighted mechanism is better than the baselines. It pays more attention to the trade-off between tasks and constraints. In a simple obstacle environment, the DWL-PPO algorithm achieves the target reward in the shortest episode. The cost caused by collision events is effectively limited to the safety threshold, almost zero, making the algorithm more efficient and safer. However, the algorithm still incurs a cost of around 50 in the early stage, as the Lagrange multiplier takes time to continuously optimize. In contrast, the TD3, SAC, and DDPG algorithms (without constraints) fail to converge within 100 episodes, resulting in huge costs, which shows that complex constraint problems cannot be dealt with only by a simple reward function. OptLayer performs well in obeying the constraints but converges slowly due to high computational complexity. Our method achieves efficient management of safety constraints with lower computational complexity.

In the DWL-PPO algorithm, the Lagrange multiplier is effectively used to enforce safety constraints. However, determining the Lagrange multiplier presents a huge computational challenge when dealing with more complex nonlinear constraints and dynamic environments. The Noether theorem offers a potential solution to the difficulty of explicitly solving for the Lagrange multiplier under complex constraints. Similarly, Wu et al. [48] derived the Euler-Lagrange equation in Samuelson’s variational principle without using the Lagrange multiplier, employing a direct variational approach based on variational iterations. Integrating these techniques into our approach is expected to enhance the algorithm’s ability to handle complex constraints. This provides a broader range of solutions for real-world applications.

6  Conclusion and Future Work

In this study, an obstacle avoidance control method based on Safe RL is offered for grasping tasks. The grasping task is modeled as a CMDP, and the safety constraint is integrated into the PPO framework using a Lagrange multiplier and dynamic weighted mechanism to construct the DWL-PPO algorithm. Risky actions are constrained by the DWL-PPO algorithm. Additionally, a composite reward function is designed to control the orientation of the end-effector accurately, enabling the manipulator to grasp with a proper attitude. Simulation experiments demonstrate that the suggested approach balances compliance with the safety constraint and task completion well and is superior to the baselines. Compared with advanced RL methods, the proposed method effectively reduces the possibility of collision and converges quickly. In the future, the introduction of hard constraints will enhance the feasibility of our method in practical applications. The trained model will be extended to the real world, and the proposed method is expected to be expanded to more different task scenarios to improve the generalization and robustness. Microelectromechanical Systems (MEMS) technology will be employed in physical systems to further optimize our approach by acquiring real-time sensor data. MEMS gyroscopes will effectively improve the grasping attitude accuracy of the end-effector, and MEMS actuators are essential for finer and more stable operations. This will contribute to more accurate, safer, and efficient grasping tasks.

Acknowledgement: The researchers are grateful to family and friends for their emotional support.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: The authors confirm contribution to the paper as follows: research conception: Qinglei Zhang, Jianguo Duan and Jiyun Qin; methodology: Bai Hu; software: Bai Hu; results visualization and analysis: Bai Hu; draft manuscript preparation: Bai Hu; supervision: Qinglei Zhang, Jiyun Qin, Jianguo Duan and Ying Zhou. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Liu Q, Liu Z, Xiong B, Xu W, Liu Y. Deep reinforcement learning-based safe interaction for industrial human-robot collaboration using intrinsic reward function. Adv Eng Inform. 2021;49(12):101360. doi:10.1016/j.aei.2021.101360. [Google Scholar] [CrossRef]

2. Maldonado-Ramirez A, Rios-Cabrera R, Lopez-Juarez I. A visual path-following learning approach for industrial robots using DRL. Robot Comput Integr Manuf. 2021;71(6419):102130. doi:10.1016/j.rcim.2021.102130. [Google Scholar] [CrossRef]

3. Wu YH, Yu ZC, Li CY, He MJ, Hua B, Chen ZM. Reinforcement learning in dual-arm trajectory planning for a free-floating space robot. Aerosp Sci Technol. 2020;98(1):105657. doi:10.1016/j.ast.2019.105657. [Google Scholar] [CrossRef]

4. Liu YC, Yan W, Zhang T, Yu CX, Tu HY. Trajectory tracking for a dual-arm free-floating space robot with a class of general nonsingular predefined-time terminal sliding mode. IEEE Trans Syst Man Cybern-Syst. 2022;52(5):3273–86. doi:10.1109/TSMC.2021.3064898. [Google Scholar] [CrossRef]

5. Hwang M, Kwon D-S. Strong continuum manipulator for flexible endoscopic surgery. IEEE/ASME Trans Mechatron. 2019;24(5):2193–203. doi:10.1109/TMECH.2019.2932378. [Google Scholar] [CrossRef]

6. Liu Y, Wang Y, Wang C, Wang X, Zhang X, Yang Y, et al. Comparison of short-term outcomes of robotic-assisted radical colon cancer surgery using the kangduo surgical robotic system and the da vinci si robotic system: a prospective cohort study. Int J Surg. 2024;110(3):1511–8. doi:10.1097/JS9.0000000000000976. [Google Scholar] [PubMed] [CrossRef]

7. Song S, Zeng A, Lee J, Funkhouser T. Grasping in the wild: learning 6DoF closed-loop grasping from low-cost demonstrations. IEEE Robot Autom Lett. 2020;5(3):4978–85. doi:10.1109/LRA.2020.3004787. [Google Scholar] [CrossRef]

8. Xiong Y, Ge Y, From PJ. An obstacle separation method for robotic picking of fruits in clusters. Comput Electron Agric. 2020;175(6):105397. doi:10.1016/j.compag.2020.105397. [Google Scholar] [CrossRef]

9. Lundell J, Verdoja F, Kyrki V. DDGC: generative deep dexterous grasping in clutter. IEEE Robot Autom Lett. 2021;6(4):6899–906. doi:10.1109/LRA.2021.3096239. [Google Scholar] [CrossRef]

10. Morrison D, Corke P, Leitner J. Learning robust, real-time, reactive robotic grasping. Int J Rob Res. 2020;39(2–3):183–201. doi:10.1177/0278364919859066. [Google Scholar] [CrossRef]

11. Wang L, Meng X, Xiang Y, Fox D. Hierarchical policies for cluttered-scene grasping with latent plans. IEEE Robot Autom Lett. 2022;7(2):2883–90. doi:10.1109/LRA.2022.3143198. [Google Scholar] [CrossRef]

12. Billard A, Kragic D. Trends and challenges in robot manipulation. Science. 2019;364(6446):eaat8414. doi:10.1126/science.aat8414. [Google Scholar] [PubMed] [CrossRef]

13. Lobbezoo A, Qian Y, Kwon H-J. Reinforcement learning for pick and place operations in robotics: a survey. Robotics. 2021;10(3):105. doi:10.3390/robotics10030105. [Google Scholar] [CrossRef]

14. Khatib O. Real-time obstacle avoidance for manipulators and mobile robots. Int J Rob Res. 1986;5(1):90–8. doi:10.1177/027836498600500106. [Google Scholar] [CrossRef]

15. Bai C, Zhang J, Guo J, Patrick Yue C. Adaptive hybrid optimization learning-based accurate motion planning of multi-joint arm. IEEE Trans Neural Netw Learn Syst. 2023;34(9):5440–51. doi:10.1109/TNNLS.2023.3262109. [Google Scholar] [PubMed] [CrossRef]

16. Salzman O, Halperin D. Asymptotically near-optimal RRT for fast, high-quality motion planning. IEEE Trans Robot. 2016;32(3):473–83. doi:10.1109/TRO.2016.2539377. [Google Scholar] [CrossRef]

17. Jang K, Baek J, Park S, Park J. Motion planning for closed-chain constraints based on probabilistic roadmap with improved connectivity. IEEE/ASME Trans Mechatron. 2022;27(4):2035–43. doi:10.1109/TMECH.2022.3175260. [Google Scholar] [CrossRef]

18. Jiang X, Wang Z, Dong C. A path planning algorithm based on improved RRT sampling region. Comput Mater Contin. 2024;80(3):4303–23. doi:10.32604/cmc.2024.054640. [Google Scholar] [CrossRef]

19. Marcucci T, Petersen M, von Wrangel D, Tedrake R. Motion planning around obstacles with convex optimization. Sci Robot. 2023;8(84):eadf7843. doi:10.1126/scirobotics.adf7843. [Google Scholar] [PubMed] [CrossRef]

20. Tika A, Bajcinca N. Predictive control of cooperative robots sharing common workspace. IEEE Trans Contr Syst Technol. 2024;32(2):456–71. doi:10.1109/TCST.2023.3331525. [Google Scholar] [CrossRef]

21. Ying F, Liu H, Jiang R, Yin X. Trajectory generation for multiprocess robotic tasks based on nested dual-memory deep deterministic policy gradient. IEEE/ASME Trans Mechatron. 2022;27(6):4643–53. [Google Scholar]

22. Kim B, Kwon G, Park C, Kwon NK. The task decomposition and dedicated reward-system-based reinforcement learning algorithm for pick-and-place. Biomimetics. 2023;8(2):240. [Google Scholar] [PubMed]

23. Kuo PH, Hu J, Lin ST, Hsu PW. Fuzzy deep deterministic policy gradient-based motion controller for humanoid robot. Int J Fuzzy Syst. 2022;24(5):2476–92. [Google Scholar]

24. Hu Z, Zheng Y, Pan J. Grasping living objects with adversarial behaviors using inverse reinforcement learning. IEEE Trans Robot. 2023;39(2):1151–63. [Google Scholar]

25. Li Y, Hao X, She Y, Li S, Yu M. Constrained motion planning of free-float dual-arm space manipulator via deep reinforcement learning. Aerosp Sci Technol. 2021;109(4):106446. doi:10.1016/j.ast.2020.106446. [Google Scholar] [CrossRef]

26. Bing Z, Zhou H, Li R, Su X, Morin FO, Huang K, et al. Solving robotic manipulation with sparse reward reinforcement learning via graph-based diversity and proximity. IEEE Trans Ind Electron. 2022;70(3):2759–69. doi:10.1109/TIE.2022.3172754. [Google Scholar] [CrossRef]

27. Thananjeyan B, Balakrishna A, Nair S, Luo M, Srinivasan K, Hwang M, et al. Recovery rl: safe reinforcement learning with learned recovery zones. IEEE Robot Autom Lett. 2021;6(3):4915–22. doi:10.1109/LRA.2021.3070252. [Google Scholar] [CrossRef]

28. Zhang L, Zhang R, Wu T, Weng R, Han M, Zhao Y. Safe reinforcement learning with stability guarantee for motion planning of autonomous vehicles. IEEE Trans Neural Netw Learn Syst. 2021;32(12):5435–44. doi:10.1109/TNNLS.2021.3084685. [Google Scholar] [PubMed] [CrossRef]

29. García J, Shafie D. Teaching a humanoid robot to walk faster through safe reinforcement learning. Eng Appl Artif Intell. 2020;88(1):103360. doi:10.1016/j.engappai.2019.103360. [Google Scholar] [CrossRef]

30. Du Y, Wu D. Deep reinforcement learning from demonstrations to assist service restoration in islanded microgrids. IEEE Trans Sustain Energy. 2022;13(2):1062–72. doi:10.1109/TSTE.2022.3148236. [Google Scholar] [CrossRef]

31. Zhao Y, Zhong H, Lim CC. Safety-constrained multi-agent reinforcement learning for power quality control in distributed renewable energy networks. Comput Mater Contin. 2024;79(1):449–71. doi:10.32604/cmc.2024.048771. [Google Scholar] [CrossRef]

32. Wang S, Cao Y, Zheng X, Zhang T. A learning system for motion planning of free-float dual-arm space manipulator towards non-cooperative object. Aerosp Sci Technol. 2022;131(6):107980. doi:10.1016/j.ast.2022.107980. [Google Scholar] [CrossRef]

33. Zhang H, Solak G, Lahr GJG, Ajoudani A. SRL-VIC: a variable stiffness-based safe reinforcement learning for contact-rich robotic tasks. IEEE Robot Autom Lett. 2024;9(6):5631–8. doi:10.1109/LRA.2024.3396368. [Google Scholar] [CrossRef]

34. Duan A, Yang C, Zhao J, Huo S, Zhou P, Ma W, et al. Safe learning by constraint-aware policy optimization for robotic ultrasound imaging. IEEE Trans Autom Sci Eng. 2024;22(1):2349–60. doi:10.1109/TASE.2024.3378915. [Google Scholar] [CrossRef]

35. Beltran-Hernandez CC, Petit D, Ramirez-Alpizar IG, Nishi T, Kikuchi S, Matsubara T, et al. Learning force control for contact-rich manipulation tasks with rigid position-controlled robots. IEEE Robot Autom Lett. 2020;5(4):5709–16. doi:10.1109/LRA.2020.3010739. [Google Scholar] [CrossRef]

36. Cohen MH, Belta C. Safe exploration in model-based reinforcement learning using control barrier functions. Automatica. 2023;147(8):110684. doi:10.1016/j.automatica.2022.110684. [Google Scholar] [CrossRef]

37. Gu S, Yang L, Du Y, Chen G, Walter F, Wang J, et al. A review of safe reinforcement learning: methods, theories, and applications. IEEE Trans Pattern Anal Mach Intell. 2024;46(12):11216–35. doi:10.1109/TPAMI.2024.3457538. [Google Scholar] [PubMed] [CrossRef]

38. Pham TH, De Magistris G, Tachibana R. OptLayer—practical constrained optimization for deep reinforcement learning in the real world. In: 2018 IEEE International Conference on Robotics and Automation (ICRA); 2018 May 21–25; Brisbane, Australia: IEEE. p. 6236–43. doi:10.1109/ICRA.2018.8460547 [Google Scholar] [CrossRef]

39. Achiam J, Held D, Tamar A, Abbeel P. Constrained policy optimization. In: The 34th International Conference on Machine Learning; 2017 Aug 6–11;Sydney, Australia:PMLR. p. 22–31. [Google Scholar]

40. Schulman J. Trust region policy optimization. arXiv:150205477. 2015. [Google Scholar]

41. Meng W, Zheng Q, Shi Y, Pan G. An off-policy trust region policy optimization method with monotonic improvement guarantee for deep reinforcement learning. IEEE Trans Neural Netw Learn Syst. 2021;33(5):2223–35. doi:10.1109/TNNLS.2020.3044196. [Google Scholar] [PubMed] [CrossRef]

42. Yang X, Ji Z, Wu J, Lai Y-K, Wei C, Liu G, et al. Hierarchical reinforcement learning with universal policies for multistep robotic manipulation. IEEE Trans Neural Netw Learn Syst. 2021;33(9):4727–41. doi:10.1109/TNNLS.2021.3059912. [Google Scholar] [PubMed] [CrossRef]

43. Chen P, Pei J, Lu W, Li M. A deep reinforcement learning based method for real-time path planning and dynamic obstacle avoidance. Neurocomputing. 2022;497(8):64–75. doi:10.1016/j.neucom.2022.05.006. [Google Scholar] [CrossRef]

44. Schulman J, Wolski F, Dhariwal P, Radford A, Klimov O. Proximal policy optimization algorithms. arXiv:170706347. 2017. [Google Scholar]

45. Zhang J, Zhang Z, Han S, Lü S. Proximal policy optimization via enhanced exploration efficiency. Inf Sci. 2022;609:750–65. [Google Scholar]

46. Zhong J, Wang T, Cheng L. Collision-free path planning for welding manipulator via hybrid algorithm of deep reinforcement learning and inverse kinematics. Complex Intell Syst. 2022;8(3):1899–912. doi:10.1007/s40747-021-00366-1. [Google Scholar] [CrossRef]

47. Fan Y, Dong H, Zhao X, Denissenko P. Path-following control of unmanned underwater vehicle based on an improved TD3 deep reinforcement learning. IEEE Trans Contr Syst Technol. 2024;32(5):1904–19. doi:10.1109/TCST.2024.3377876. [Google Scholar] [CrossRef]

48. Wu Y, He JH. A remark on Samuelson’s variational principle in economics. Appl Math Lett. 2018;84(4):143–7. doi:10.1016/j.aml.2018.05.008. [Google Scholar] [CrossRef]