 Open Access
Open Access
ARTICLE
Efficient Bit-Plane Based Medical Image Cryptosystem Using Novel and Robust Sine-Cosine Chaotic Map
1 Department of Electrical and Electronic Engineering, College of Technology (COT), University of Buea, Buea, P.O. Box 63, Cameroon
2 Department of Software Engineering, College of Engineering, University of Business and Technology, Jeddah, 22246, Saudi Arabia
3 Department of Computer Engineering, Jamia Millia Islamia, New Delhi, 110025, India
4 Department of Computer Science, School of Engineering, Computing and Design, Dar Al-Hekma University, Jeddah, 22246, Saudi Arabia
* Corresponding Author: Musheer Ahmad. Email:
Computers, Materials & Continua 2025, 83(1), 917-933. https://doi.org/10.32604/cmc.2025.059640
Received 14 October 2024; Accepted 05 February 2025; Issue published 26 March 2025
Abstract
This paper presents a high-security medical image encryption method that leverages a novel and robust sine-cosine map. The map demonstrates remarkable chaotic dynamics over a wide range of parameters. We employ nonlinear analytical tools to thoroughly investigate the dynamics of the chaotic map, which allows us to select optimal parameter configurations for the encryption process. Our findings indicate that the proposed sine-cosine map is capable of generating a rich variety of chaotic attractors, an essential characteristic for effective encryption. The encryption technique is based on bit-plane decomposition, wherein a plain image is divided into distinct bit planes. These planes are organized into two matrices: one containing the most significant bit planes and the other housing the least significant ones. The subsequent phases of chaotic confusion and diffusion utilize these matrices to enhance security. An auxiliary matrix is then generated, comprising the combined bit planes that yield the final encrypted image. Experimental results demonstrate that our proposed technique achieves a commendable level of security for safeguarding sensitive patient information in medical images. As a result, image quality is evaluated using the Structural Similarity Index (SSIM), yielding values close to zero for encrypted images and approaching one for decrypted images. Additionally, the entropy values of the encrypted images are near 8, with a Number of Pixel Change Rate (NPCR) and Unified Average Change Intensity (UACI) exceeding 99.50% and 33%, respectively. Furthermore, quantitative assessments of occlusion attacks, along with comparisons to leading algorithms, validate the integrity and efficacy of our medical image encryption approach.Keywords
In the aftermath of the epidemic, there has been a notable shift toward digitalization in the medical field, leading to an increase in the volume of medical data and images. The advent of new communication and smart wearable technologies has further reinforced this trend. These technologies facilitate the transmission and storage of personal patient data and medical images via wireless body networks [1]. These data are instrumental in clinical practice, disease diagnosis, and treatment planning. However, the digitization of medical information also brings about significant security concerns, as the widespread sharing of data makes them vulnerable to threats and breaches [2]. Therefore, it is imperative to ensure the confidentiality and integrity of medical images. Implementing image encryption is a key security measure to mitigate the risks of unauthorized access and data exposure. Consequently, there is an urgent need for rigorous investigation and advancements in the field of cryptography applied in medicine [3]. Some of these cryptographic methods are based on keys generated by maps, among which the logistic map is able to exhibit chaotic behavior for a suitable value of the control parameter. Engineers have created and used many chaotic maps for image encryption. The work in [4] introduced a quantum chaotic map. It studied its features and merged the map’s random number sequences into a DNA sequence to suggest a secure encryption solution. For picture encryption, researchers used a particle swarm optimization technique and a novel modular integrated logistic exponential map to get the optimum key [5]. Before the engineering application, the dynamical features of the new map are examined using nonlinear analytic tools, including the Lyapunov exponent graph and the test 0–1 graph. The 2D Henon map, DNA sequence, and cyclic chaos three-cell chaotic map were used to encrypt images in [6]. Entropy analysis, correlation coefficients, and differential attacks verified their algorithm’s robustness. The dynamics of a one-dimensional map using sine and cosine functions were studied in [7]. The model’s dynamical properties are examined using a bifurcation diagram and the graph of the greatest Lyapunov exponents. Then, the method mixes the map’s random numbers with a random DNA operation. Similarly, literature [8] introduced a 1D piecewise quadratic polynomial chaotic map. After showing that the model can exhibit chaotic dynamics suited for cryptography across a wide range of parameters, it built an S-box from the produced random number. The security analysis proved the strategy worked.
A new generative adversarial network (GAN) was created to secure medical photos in [9]. Their system was robust and strong, using 2D chaotic maps, hash tables, and deep learning (DL). Finally, they verified their result using a popular encryption method. Based on WBAN technology, adaptive DNA encryption, and multi-chaotic maps, they created a secure encryption method [10]. To assess resilience, brute force, statistical, differential, and noise analysis were used. A new medical image encryption method using message queuing telemetry transfer was proposed [11]. The analysis metrics showed that the suggested system could transmit real-time medical images across WI-FI and the Internet. A logistic map was used to construct an upgraded variable dimension map [12]. Their full-and semi-full encryption approach is better for medical image encryption, they say. Analysis of their results showed that semi-full encryption mode had good security performance and reduced execution time, while complete encryption mode had superior security and acceptable execution time. Medical image encryption may assist many engineering applications [13–15].
Some encryption schemes use image compression before encryption. Srinivasu et al. [16] demonstrated the secure compression of 2D medical images, achieving a 58% reduction in size while maintaining image quality. The approximated entropy indicated robustness for secure storage. Another study [17] introduced an adaptive sparse basis compressive sensing model using singular value decomposition and random number sequences from a Hopfield neural network, demonstrating resilience against security attacks and balanced compressibility. Additionally, a robust image encryption scheme utilizing hyperchaotic maps and parallel compression sensing was proposed, with simulations revealing enhanced security and efficiency [18]. These findings suggest that integrating compression with random number sequences can improve encryption effectiveness, leading this study to adopt a discrete system for its computational advantages.
The literature survey conducted for this study indicates that both continuous and discrete nonlinear dynamical systems can be employed for the generation of the random sequences of numbers required for image encryption [3–6]. Nevertheless, high-dimensional systems can be readily generated; however, they require a greater investment of computational resources. In contrast, the maps are capable of exhibiting chaotic dynamics over a broad range of parameters, as evidenced by the findings in [3–6], where a high-dimensional map and a memristive map with a limited range of chaotic dynamics were employed. In light of the aforementioned, this work’s contribution to the field can be seen in two key areas: firstly, in terms of the model’s simplicity and the chaotic dynamics exhibited across a wide range of parameters, the chaotic dynamical behavior exhibited by this map is known as a robust chaos rarely found in such types of systems; secondly, in terms of the security and robustness of the encryption algorithm, the analysis metric showed the superiority of the proposed method in contrast to some recent literatures [4–6]. The low dimensionality of our introduced map is of particular importance for practical implementation since the low memory size of the microcontroller will be used for the storage of the encryption algorithm; therefore, more microcontroller memory will be exploited for the transmission protocol.
Unique properties, like approximately 70% 0 bits, distinguish medical images from classic graphics that clearly disseminate information [19]. Even if the higher bit planes in the original representation look similar, picture encryption methods that focus on them are vulnerable because the lower bit planes contain vital information [20]. A minor pixel modification has little effect on encryption. Permutation and replacement encryption is reduced by the high 0-bit rate. To overcome 0 bits in medical images, a high-performance image encryption solution is urgently needed. This work proposes a medical image encryption technique based on sine-cosine maps, which exploits the plane bit decomposition to effectively manage the abundance of 0 bits and overcome this challenge. The uniqueness of this cryptosystem stems from two key features: the unique sine-cosine map’s capacity to produce a diverse array of chaotic sequences for a given set of parameters and the incorporation of both the most and least significant bit planes of the image into a single auxiliary matrix to facilitate confusion and diffusion. The main contributions of this investigation include:
• The introduction of a new sine-cosine map that has the ability to generate a wide range of chaotic sequences for a given set of system parameters.
• The medical image encryption technique highlights the performance of bit plane decomposition in the confusion and diffusion process. It is important to remember that medical images mainly consist of 0 bits, which are better managed in low-bit planes.
• The proposed cryptosystem is flexible, accommodates images of different sizes, and is therefore suitable for many applications without prior processing of the images.
• This technique is a pixel-loss-free system throughout the entire encryption/decryption process, ensuring image quality, as pixel loss or alteration may lead to poor medical interpretation and therefore poor diagnosis.
The subsequent parts of this paper are organized as follows: Section 2 presents the new sine-cosine map, as well as its intrinsic properties. Section 3 builds the cryptosystem. Its application to medical image encryption is also discussed, and the model’s performances are analyzed in Sections 4 and 5. Related discussions of the work are provided in Section 6. The paper ends in Section 7 with a conclusion that summarizes the work.
2 Novel Chaotic Map and Its Properties
In Eq. (1), a new simple sine-cosine map is proposed that aims to generate a high level of complexity. In order to assure a certain level of simplicity, only one tunable parameter is considered during its design.
{xn+1=a(cos(xn))2−sin(2yn)yn+1=xn(1)
The ability to use a model such as Eq. (1) in engineering applications such as image encryption passes through a suitable mastery of its dynamical properties, including the stability of the equilibria as well as the varieties of bifurcations that can occur in the model. In Eq.(1), xn and yn represent the state variable of the system at the instant n while xn+1 and yn+1 represent the state equation at the instant n+1. For the determination of the equilibrium points, all the instants are considered as n+1=n=0. By solving Eq. (2), the equilibrium point of the introduced map is obtained, referencing the work of [21].
{x0=a(cos(x0))2−sin(2y0)y0=x0(2)
After some algebraic manipulations, Eq. (3) is obtained.
x0−a(cos(x0))2+sin(2x0)=0(3)
By solving Eq. (3), the couple of equilibria (x0,y0) where x0=y0 is obtained as it can be seen in the second column of Table 1. The Jacobian matrix derived from Eq. (1) is presented in Eq. (4). The third column of Table 1 provides the model’s eigenvalues and their stability for certain discrete values of the parameter. The model introduced in Eq.(1) is a new type of sine-cosine map involving only one tuneable parameter. Intensive computer simulations demonstrated that an increase of that control parameter enabled the augmentation of the equilibrium points of the model, therefore enabling the generation of complicated dynamics with the size of the attractor growing with the control parameter. It should be emphasized that the maps with such types of behavior are rarely reported in the literature. In order to explore the dynamical behavior of the considered model, three main tools are used. The bifurcation diagram and the corresponding largest Lyapunov exponent are the two main tools. They enable a global exploration of the dynamical behavior of the model for a wide range of variations of the control parameter. The third tool, the phase portrait, allows you to provide specific information about the model’s behavior for a discrete value of the control parameter. Fig. 1 shows the bifurcation diagrams in the first row and the largest Lyapunov exponents in the second row. The main diagrams in Fig. 1 report the model’s behavior, which varies from periodic to chaotic, and also depict enlargements of the diagrams. It shows that the model has a type of robust chaotic dynamic that can be used for image encryption.
J=[−2cos(x0)sin(x0)−2cos(2y0)10](4)
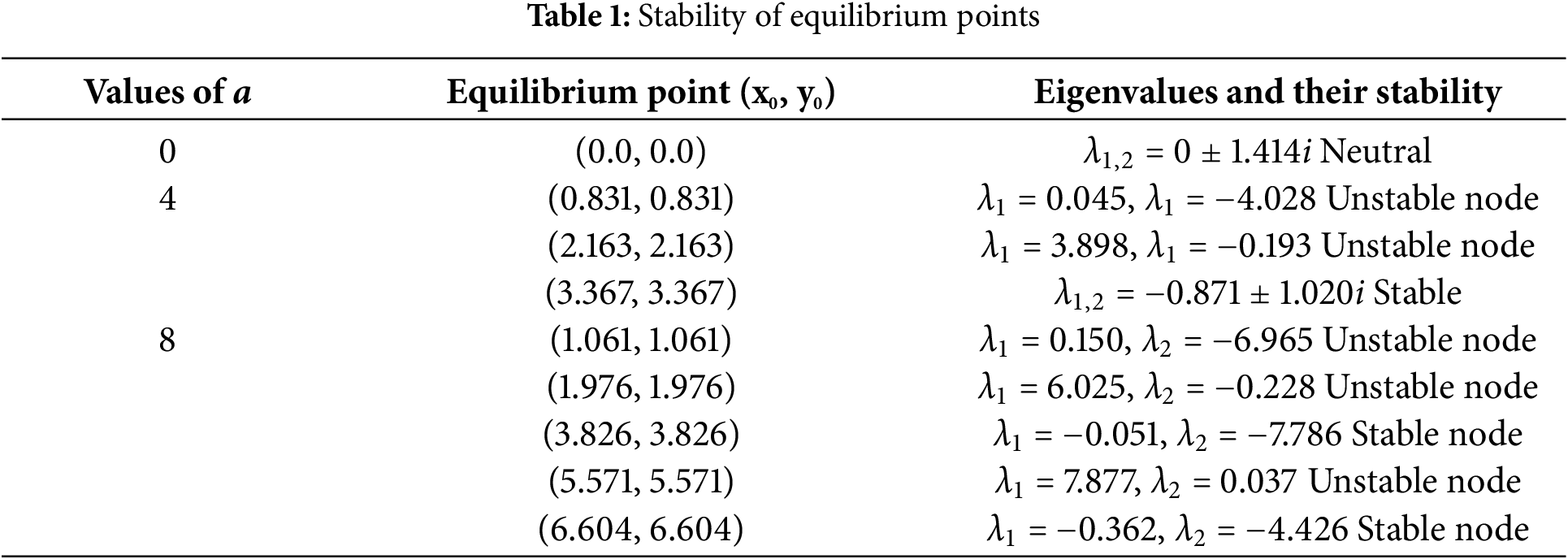
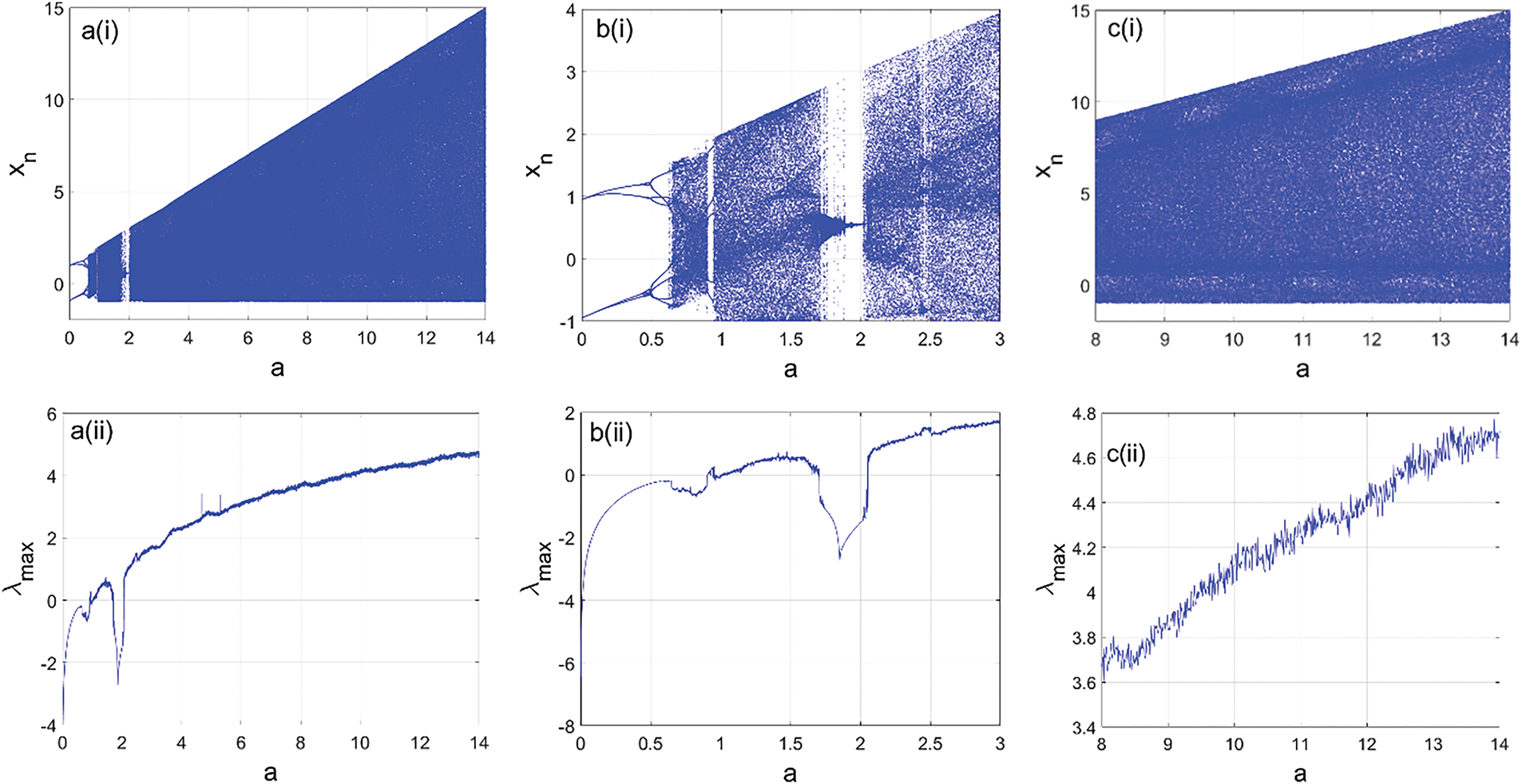
Figure 1: Bifurcation diagrams of the proposed map showing the local maxima of the state variable xn, under the variation of the control parameter a as presented in a(i), b(i), c(i) with their corresponding lagest lyapunov exponents as shown in a(ii), b(ii), c(ii)
Form the expression det(J−λId)=0, the characteristic equation is given as
λ2+2acos(x0)sin(x0)λ+2cos(2y0)=0(5)
Those varieties of dynamical behavior exhibited by the model are supported using the phase portraits of Fig. 2. Furthermore, it’s important to remember that the use of chaotic maps in cryptography stems from their capacity to produce intricate and unpredictable numerical sequences, serving as keys for both encryption and decryption. These sequences are difficult to predict or reproduce, making them ideal for secure communication [22,23].
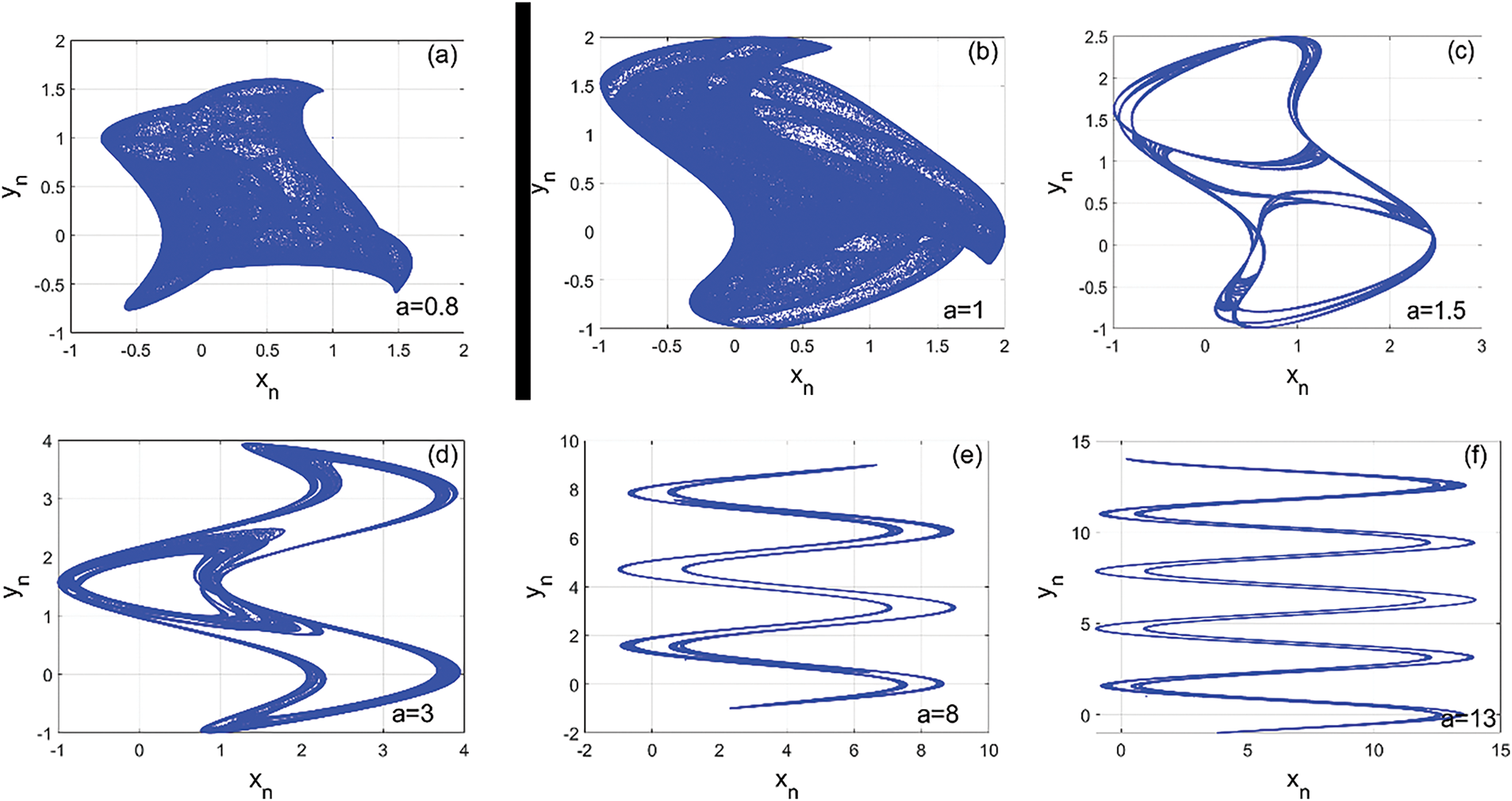
Figure 2: Phase portraits, showing the varieties of the dynamical behaviors obtained from the model the diverse value of the control parameter a as reported in (a)–(f)
The encryption technique proposed in this work has several features that are sought after in cryptosystem design. The chaotic sequence is generated from a discrete 2D map. This class of chaotic systems is unique in that it produces a wide range of chaotic behaviors, as shown by the bifurcation diagrams and maximum exponent graphs in Fig. 1. Another special feature of this technique is the use of information extracted from bitplans to enhance security. In addition, part of the chaotic key is used in the diffusion phase and another part in the confusion phase. This secret key separation technique strengthens the confidentiality and integrity of the cryptosystem. Fig. 3 shows a block diagram of the proposed technique, which consists of three main stages. The first is the decomposition of the image into bitplanes, which is a kind of initialization of the technique. This decomposition/combination of bitplanes is closely related to the original or encrypted image. The other two stages are diffusion and chaotic confusion.
Figure 3: Block diagram of the proposed encryption technique, illustrating the various steps followed from the original to the encrypted image
3.1 Image Bitplane Decomposition
The plain (original) image, labeled P, is a grayscale image of size MN. Since the images used in this cryptosystem are grayscale, they can be represented by a unique 8-bit binary sequence, where the decimal value of each pixel is between 0 and 256. The Binary Bitplane Decomposition (BBD) used in this work can decompose a grayscale image into 8 binary planes, as shown in Fig. 4. Thus, a decimal number A can be represented via BBD by a binary sequence given by Eq. (6):
A=7∑k=02kbk=b0+2b1+22b2+…+27b7(6)
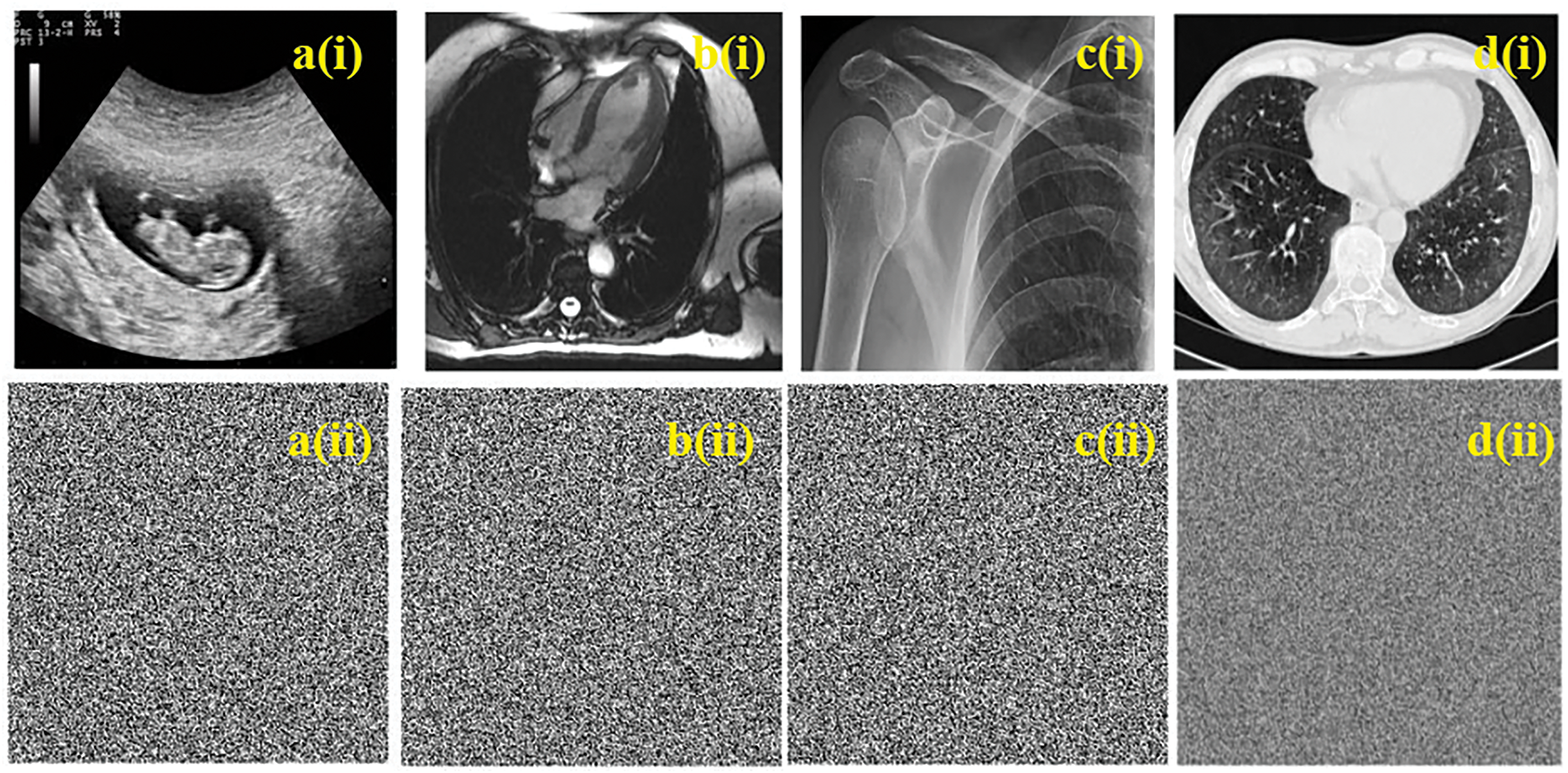
Figure 4: Simulation results of proposed cryptosystem for given images. a(i), b(i), c(i), and d(i) which are original images; a(ii), b(ii), c(ii), and d(ii) which are ciphered images
where bk represents the kth bitplane with k=[0,1,2,…,7]. The bits of the original image are extracted one by one from the first to the 8th bit noted b0 to b7 according to the following Eq. (7):
{b0=mod(I,2),bk=mod(floor(I/2k),2),k=1to7(7)
where I is the binary sequence of the original image. It is important to point out that the upper bitplanes (the first ones from the high bit) carry more information about the image than the lower bitplanes (up to the low bit). The bitplane image for the 7th significant bit must contain more information than bitplane 0. For the rest of the process, two matrices are created that can contain the bitplanes. These matrices, called M1 and M2, each contain half of the previously obtained bitplanes and are associated with the initial conditions in the diffusion and confusion stages.
Step 1: Generation of the secrete key
Using the initial conditions x0, y0, the chaotic sequence is generated by map (1) through Eq.(8). The chaotic key is obtained by concatenating the sequences X and Y of Eq. (9).
{X=mod(floor(x(n)×1014),256)Y=mod(floor(y(n)×1014),256)(8)
Key=[X,Y](9)
Step 2: Diffusion operation
For this diffusion phase, the Key1 sequence containing the X-sequence is used with the M2 bitplane matrix consisting of the four most significant bitplanes used in the XOR operation by the following Eq. (10):
d(i)=b(i)⊕Key1⊕S2(10)
with S2=∑Li=1M2(i) the sequence consisting of the sum of the elements of the matrix M2 and L the size of M2 (L = 4MN).
Stage 1: Initialization
As in the diffusion phase, the second element of the chaotic key2, which contains the sequence Y, is used and linked to the M1 matrix of least significant bitplanes (S1=∑Li=1M1(i)). Since the selected bitplanes contain the least significant information in the image, they are a good candidate for this confusion phase.
Step 2: Global bit scrambling
In this step, key1, sequence S1, and diffusion sequence d(i) are used to globally scramble the image bits by the following expressions Eq. (11):
c(i)=d(Key2(S1))(11)
Step 3: Combining the bitplanes and encrypted image
In this step, the sequences c(i) and d(i) from the diffusion and confusion steps are combined by concatenation as in Eq. (12).
Q(i)=[d(i),c(i)](12)
The sequence c(i) is converted into a matrix A of dimension M × N, then two other matrices A1 and A2 are created from A of the same dimension but containing half the information. Four bitplanes are extracted from each matrix A1 and A2, which are then combined to obtain an encrypted image Q(i) with M × N dimensions.
Decryption is the reverse process of encryption, but special caution is required with bitplanes. In fact, in both the encryption and decryption processes, there is a need to start with the decomposition of bit planes and end with the combination of these bit planes. In principle, the reconstruction of the original image from the encrypted image using the proposed technique is as follows:
• Decompose the encrypted image into bitplanes.
• Split the bitplans into two matrices of equal size, one consisting of the first four bitplans and the other of the last four.
• The first matrix and part of the chaotic key (from the variable yn) are used to obtain the confusion sequence.
• The sequence from the confusion phase combined with the other part of the chaotic key (from the variable xn) and the other bitplane matrix to obtain the diffusion sequence.
• Finally, the original image is restored by combining the bitplanes from the diffusion phase.
Experiments and analysis of the nonlinear dynamics and the proposed cryptosystem are performed on an Intel(R) Core(TM) i7-3630QM CPU @ 2.40 GHz (8 CPUs), ~2.4 GHz, and 12 GB RAM. The basic software used for the analyses is the MATLAB R2024a environment, running on the 64-bit Windows 11 Professional operating system. The selected test images were taken from the web and publicly available databases known as Radiopaedia. These images are of medical type (X-ray, CT scan, sonography, and MR scan) and of different resolutions, whose description is given in Table 2. The system parameters used to obtain the secret key are a=1, x(1)=1, y(1)=1 of the chaotic behavior shown in Fig. 2. Fig. 4 presents an experiment whose images are of all types of medical images used, namely child sonography (1st column), heart MRI scan (2nd column), shoulder X-ray (3rd column), and brain CT scan (4th column). The first line of Fig. 4 presents the original images (a(i), b(i), c(i), and d(i)) and the second line presents the encrypted images (a(ii), b(ii), c(ii), and d(ii)). From this figure, the visual inspection confirms that the proposed technique has successfully encrypted the selected images.
5 Performance Analysis of Proposed Cryptosystem
To validate an encryption technique, it must be attacked through a series of tests, and the response to these attacks will validate or invalidate the proposed technique. In this way, statistical, differential, robustness, and other attacks are applied.
The Structural Similarity Index (SSIM) is a quantitative metric employed to assess the similarity between two images. It is worth mentioning that SSIM was developed in [23] and is related to the perceived quality of the human visual system (HVS). Thus, SSIM is a better candidate for extracting structural information from visual inspection. The structural similarity index consists of three components: luminance, contrast, and structure between a reference image and a test image, given by Eq. (13):
SSIM(g,h)=l(g,h)⋅c(g,h)⋅s(g,h)=(2μgμh+c1)(2σgσh+c2)(covgh+c3)(μ2g+μ2h+c1)(σ2g+σ2h+c2)(σgσh+c3)(13)
where μg is the mean of g; μh is the mean of h; σg is the variance of g; σh is the variance of h; ci are constants defined by c1=(k1L)2, c2=(k2L)2, and c3=c22. L represents the value of the image pixels. For medical images, L = 255 (8-bit coded images). By default, k1=0.01 and k2=0.03. The term l(g,h) is the luminance function, which determines the closeness of the mean luminance of the two images. The term c(g,h) is the contrast comparison function, which determines the closeness of the contrasts of the images. The term s(g,h) is the structure comparison function, which determines the correlation coefficient from two images g and h. SSIM values are between −1 and +1. An SSIM of +1 indicates that the two images are similar or identical. A value of 0 means there is no correlation between the two images. An SSIM value of −1 indicates that the two images are very different.
Another metric for evaluating image quality is Peak Signal to Noise Ratio (PSNR). It is used as a measure of reconstruction quality in image compression and noise reduction [22]. Given an 8-bit grayscale reference image g, as in this case, and a test image h, both of size M × N, the PSNR (dB) between g and h is given by Eqs. (14) and (15). It can be assumed that the PSNR value approaches infinity as the MSE approaches zero; this shows that a higher PSNR value means higher image quality. At the other end of the scale, a low PSNR value indicates large numerical differences between images. The SSIM and PSNR metrics of the images considered in Table 2 are evaluated and presented in Table 3. Between the original image and the decrypted image, the SSIM value is 1, indicating the success of the decryption process. PSNR has an infinite value because the original image is digitally identical to the decrypted image. SSIM and PSNR are also evaluated between original and encrypted images. Low SSIM values close to zero indicate a good difference between the two images. Likewise, the PSNR obtained has low values, which justifies the result obtained for the SSIM analysis.
PSNR(g,h)=10log102552MSE(g,h)(14)
MSE(g,h)=1M×NM∑i=1N∑j=1(g(i,j)−h(i,j))2(15)
A histogram is a graphical representation of the distribution of pixel intensities in an image. Through a histogram, all numerical values of each pixel in an image can be visually observed. Thus, the histogram of a sharp, clear, or original image should have a distinct distribution, representing sharp peaks that are distinct from each other.
The correlation coefficient is one of the metrics used to evaluate the effectiveness of an encryption technique. It determines the correlation value between two adjacent pixels in an image. Mathematically, the correlation coefficient is calculated using Eq. (16).
Cx,y=cov(xp,yp)√D(xp)D(yp)(16)
where xp and yp are two adjacent pixel values, S the number of selected pixel pairs, Cx,y is the correlation coefficient. The correlation coefficient is calculated for each of the medical images in Table 2 and presented in Table 4. It can be observed that the correlation values for all the considered encrypted images are close to zero, indicating that the proposed encryption technique is secure against statistical attacks.

The histogram and graphical representation of the correlations between adjacent pixels of the images in Fig. 4 (child sonography (1st column), heart MRI scan (2nd column), shoulder X-ray (3rd column), and brain CT scan (4th column)) are shown in Fig. 5. Lines 1 and 2 show the histograms and correlations between the corresponding adjacent pixels of the original images, respectively. The histograms and correlations of the corresponding encrypted images are shown in lines 3 and 4, respectively. It can be seen that the histograms of the original images are distinct and proportional, while those of the encrypted images are subject to a uniform distribution. The same observation can be made in the correlations, with a strong connection between adjacent pixels in the original images and a total disorder between adjacent pixels in the encrypted images. This uniform but disordered distribution of the histograms and correlations of the encrypted images across an image shows the security and effectiveness of encryption against statistical attacks.
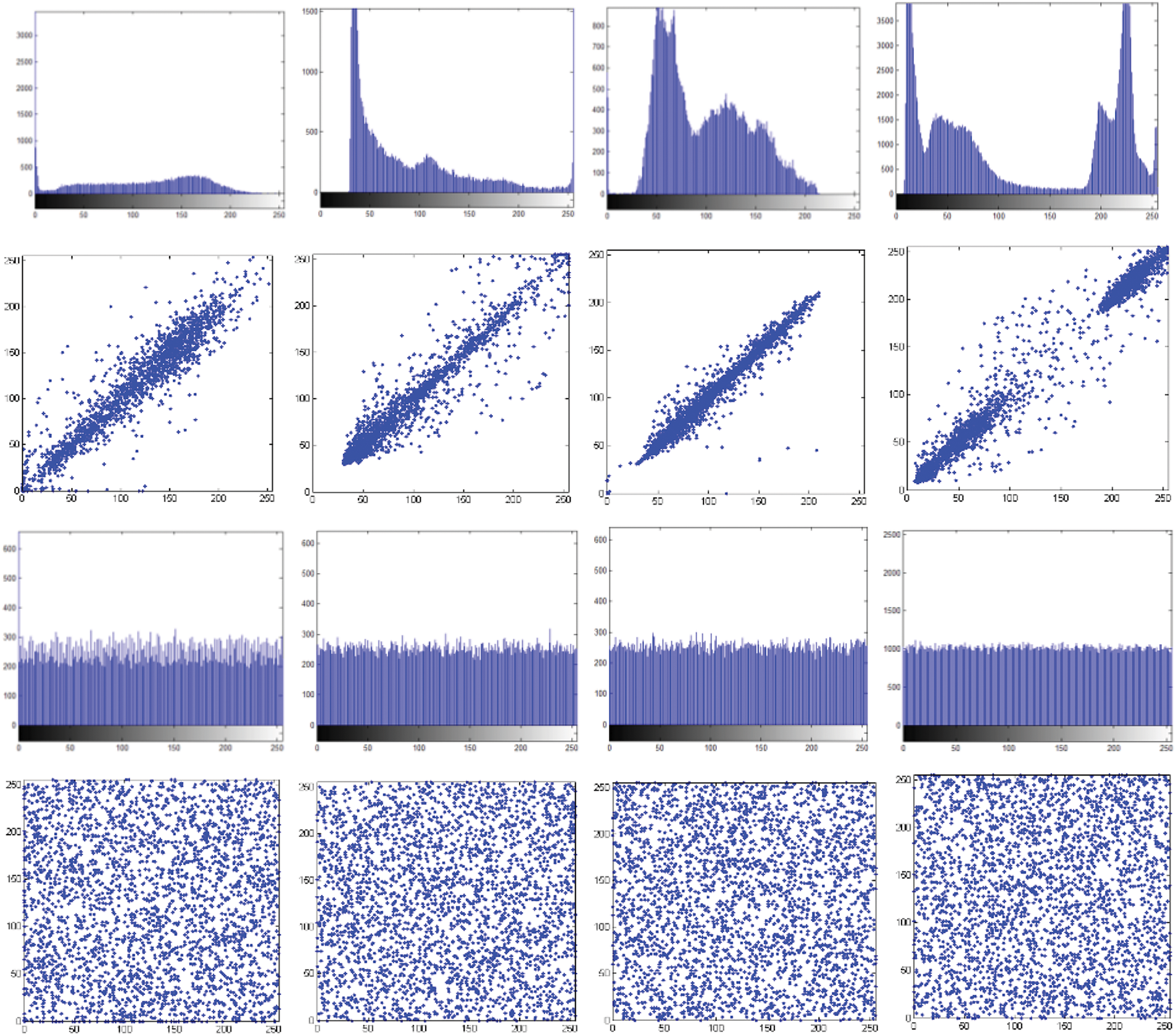
Figure 5: Histogram and correlation between original and encrypted images
Information entropy indicates the degree of uniformity, randomness, and unpredictability of the state of a system. At minimal values of the entropy of the encrypted image, the cryptosystem is vulnerable, and the larger the value of the entropy, the more disordered the state of the system and the more difficult an attack is. The information entropy is evaluated by Eq. (17):
H(x)=255∑i=0P(xi)log21P(xi)(17)
where P(xi) is the existence probability of the event xi where the current pixel value is i. For a K-bit image, the information entropy H is H=K. This indicates that the information contained in the image is completely random, and it is difficult to decipher the existing information. Since the experiment uses 8-bit grayscale medical images, the maximum value of the entropy information of the cryptosystem must be close to 8. The entropy of the original medical images in Table 2 and the corresponding encrypted images using the proposed technique are shown in Table 5. It can be seen that the entropy of the information in the encrypted images is close to 8, which confirms H=K theory, indicating that the information contained in these images has strong disorder.
The resistance of a cryptosystem to differential attacks is generally assessed using NPCR (number of pixel change rate) and UACI (unified average change intensity). The ideal values for NPCR and UACI are 0.996094 and 0.334635, respectively [24,25]. These two metrics are obtained from the following equations Eq. (18):
{NPCR=∑i,jD(i,j)M×NUACI=∑i,j|E1(i,j)−E2(i,j)|255(18)
The image size is denoted by M×N, and the pixel values of the two considered images at coordinates (i,j) are represented by E1(i,j)and E2(i,j), respectively. Table 5 shows the NPCR and UACI values obtained. As a result, all of these values are above the ideal values. This confirms that the proposed encryption technique is very sensitive to small pixel changes in the image and can withstand differential attacks.
5.5 Robustness to Occlusion Attacks
Images are generally subject to various attacks during transmission and sometimes storage. These attacks range from modification, occlusion, or shearing with the aim of causing the loss of image information. When an encrypted image is attacked by occlusion, the robust cryptosystem must be able to recover important information from the original image. To test the robustness of the proposed technique to shear attacks, the encrypted child sonography image was cropped by 1/16, 1/4, and 1/2, respectively. The corresponding visual result for the child sonography image is depicted in Fig. 6. In addition, the PSNR values of all the test recovered and encrypted images are listed in Table 6. From this table, it can be seen that the PSNR of the recovered image is higher than that of the encrypted image, regardless of the loss fraction data, which ensures the robustness of the cryptosystem to occlusion attacks.
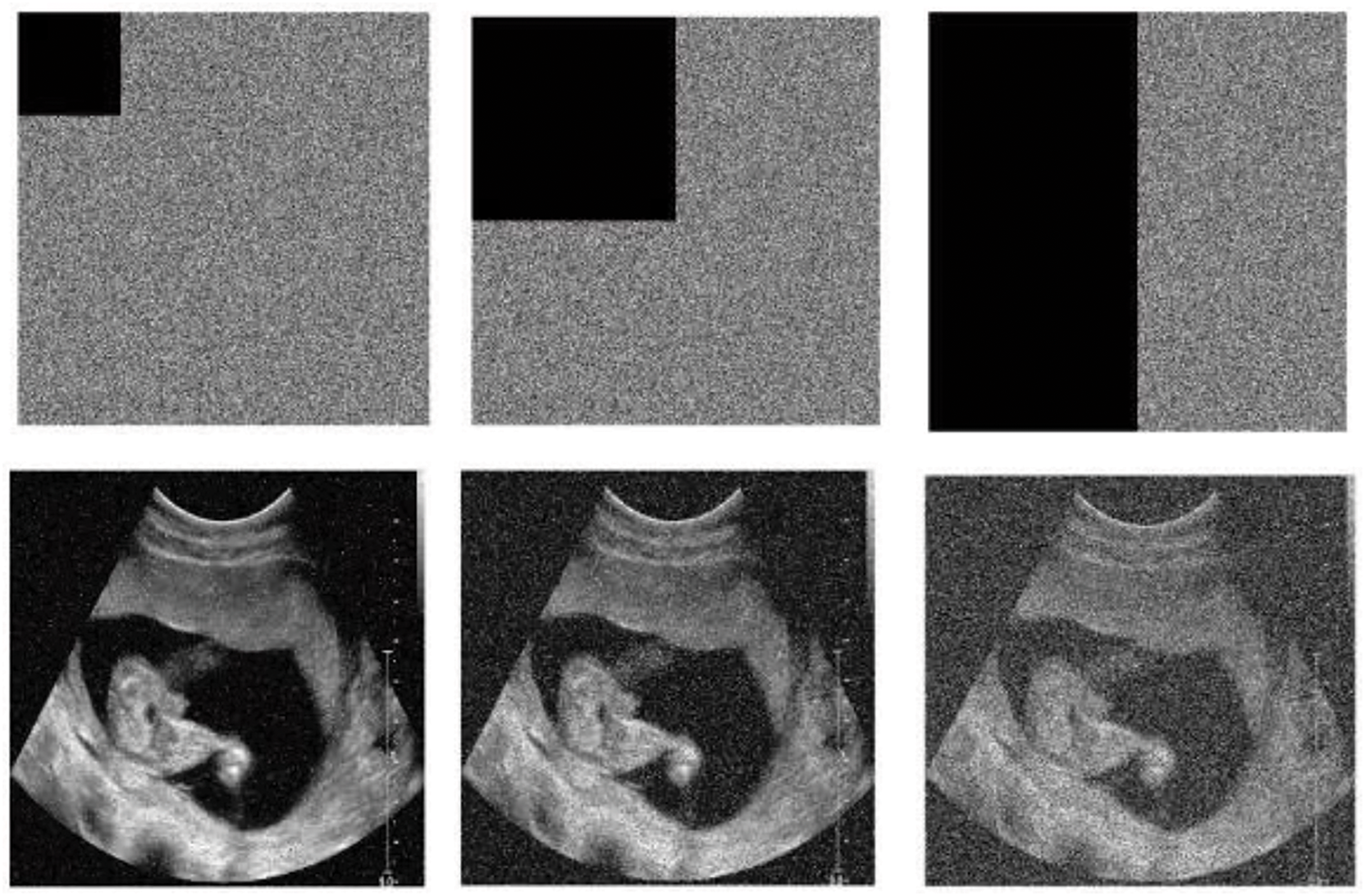
Figure 6: Occlusion attack results for child sonography image
5.6 Comparison Analysis with Other Techniques
The performance of the proposed encryption technique is locally validated through analysis and performed attacks (statistical, differential, entropy, noise, and occlusion attacks). To increase credibility, the performance of this technique is compared with other approaches that use the same analyzes, and the results obtained confirm the best security performance. Comparison results for correlation coefficients, NPCR, UACI, and entropy analysis are shown in Table 7 with chest X-ray image. The values obtained with the proposed technique are better compared to some selected techniques and show good performance. For more competitive reasons, the PSNR values between the plain and recovered images of occlusion attacks obtained in this work for the chest X-ray image are compared with some existing techniques and presented in Table 8. The results show that the proposed technique outperforms the competing algorithms in terms of resistance to occlusion attacks. As the results show, the proposed method performs better against noise attacks than existing algorithms. This sufficiently shows that the proposed technique is robust against noise attacks.
The sensitive digital medical pictures, like CT and ultrasound scans, can now be transmitted across open networks thanks to substantial advancements in medical technology, including wireless body area networks, e-health, smart health, and telemedicine. Medical images play a crucial role in eHealthcare systems by accurately assessing patient conditions and facilitating healthcare providers’ intuitive discussion of treatment options. Individuals’ privacy is represented by a variety of diagnostic images, and there could be serious consequences if they are disclosed without authorization. In other words, because of inadequate transmission security and storage flaws, these photos inherently contain extremely sensitive information, and any abuse or illegal access could jeopardize patient privacy and have serious medical repercussions [10,11,13]. Chaotic systems, which are recognized for their pseudo-randomness and sensitivity to beginning conditions, are increasingly being used for picture encryption [25,26]. This is done in order to overcome the problem that has been identified. The implementation of traditional N-dimensional chaotic maps is simpler than that of continuous systems, and updated versions of these maps keep their advantages while expanding the chaotic parameter space. The complexity of high-dimensional systems is increased, but they also require a greater amount of processing resources. Utilizing a unique sine-cosine map that possesses strong chaotic dynamics across a large parameter range, the suggested approach for high-security medical image encryption includes the utilization of this map. Two reasons contribute to the significance of this approach: first, it is straightforward, and second, it demonstrates a resilient chaos that is not typically seen in systems of this kind. Furthermore, when compared to the most recent research, the encryption technique that has been provided displays higher security and robustness. When it comes to actual implementation, the low dimensionality of the sine-cosine map is particularly useful. This is because it enables optimal utilization of microcontroller memory for both encryption and transmission protocols.
In this paper, a new cryptosystem based on chaos and bit-plane decomposition for medical images has been proposed. The chaotic sequence used in the encryption process was generated from a new sine-cosine map, which has the property of exhibiting chaotic dynamics for a wide range of parameters. It emerges that the map can present a stable or unstable node from the eigenvalue analysis. Using non-linear tools such as bifurcation diagrams and their associated graph of the largest Lyapunov exponent and a phase portrait, the robust chaotic dynamics of the model have been provided. One of the special features of the proposed technique is that the single image is divided into bit-planes, which are arranged in two matrices containing the most significant bit-planes and the least significant bit-planes. These matrices have been used in chaotic confusion and diffusion phases. Finally, another auxiliary matrix was created, containing in turn the bit planes that are combined to obtain the encrypted image. Experiments and analyses were successfully carried out using common attacks such as statistical, differential, entropy, occlusion, and noise attacks, demonstrating the effectiveness of the proposed cryptosystem.
Acknowledgement: The authors would like to appreciate the anonymous reviewers and editors for their valuable feedback, suggestions, and comments on this work which greatly improved the work.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: Zeric Tabekoueng Njitacke; Data collection: Zeric Tabekoueng Njitacke; Analysis and interpretation of results: Musheer Ahmad and Louai A. Maghrabi; Draft manuscript preparation: Zeric Tabekoueng Njitacke and Louai A. Maghrabi; Supervision, Methodology, Conceptualization, Formal analysis, Writing—review & editing: Musheer Ahmad and Turki Althaqafi. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data is available with the corresponding author and can be shared on request. The test images are publicly available database Radiopaedia.org at the following links: https://radiopaedia.org/articles/radiograph-1?lang=us (last accessed on 04 February 2025). https://radiopaedia.org/articles/chest-radiograph?lang=us (last accessed on 04 February 2025).
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Zhou SK, Greenspan H, Davatzikos C, Duncan JS, Van Ginneken B, Madabhushi A, et al. A review of deep learning in medical imaging: imaging traits, technology trends, case studies with progress highlights, and future promises. Proc IEEE. 2021;109(5):820–38. doi:10.1109/JPROC.2021.3054390. [Google Scholar] [PubMed] [CrossRef]
2. Thirupathi Rao N, Bhattacharyya D, Neal S. An extensive discussion on utilization of data security and big data models for resolving healthcare problems. In: Multi-chaos, fractal and multi-fractional artificial intelligence of different complex systems. Academic Press; 2022. p. 311–24. [Google Scholar]
3. Anupama CSS, Alsini R, Supriya N, Laxmi Lydia E, Kadry S, Yeo SS, et al. Wind driven optimization-based medical image encryption for blockchain-enabled Internet of Things environment. Comput Mater Contin. 2022;73(2):3219–33. doi:10.32604/cmc.2022.030267. [Google Scholar] [CrossRef]
4. Wen H, Lin Y. Cryptanalysis of an image encryption algorithm using quantum chaotic map and DNA coding. Expert Syst Appl. 2024;237:121514. doi:10.1016/j.eswa.2023.121514. [Google Scholar] [CrossRef]
5. Kocak O, Erkan U, Toktas A, Gao S. PSO-based image encryption scheme using modular integrated logistic exponential map. Expert Syst Appl. 2024;237:121452. doi:10.1016/j.eswa.2023.121452. [Google Scholar] [CrossRef]
6. SaberiKamarposhti M, Sahlabadi M, Lin CC, Muniyand RC. Using 2D Hénon map, cycling chaos and DNA sequence for new secure color image encryption algorithm. Arab J Sci Eng. 2024;49(3):4125–37. doi:10.1007/s13369-023-08298-3. [Google Scholar] [CrossRef]
7. Liang Q, Zhu C. A new one-dimensional chaotic map for image encryption scheme based on random DNA coding. Opt Laser Technol. 2023;160:109033. doi:10.1016/j.optlastec.2022.109033. [Google Scholar] [CrossRef]
8. Zhu S, Deng X, Zhang W, Zhu C. Secure image encryption scheme based on a new robust chaotic map and strong S-box. Math Comput Simul. 2023;207:322–46. doi:10.1016/j.matcom.2022.12.025. [Google Scholar] [CrossRef]
9. Kumar P, Rahman M, Namasudra S, Moparthi NR. Enhancing security of medical images using deep learning, chaotic map, and hash table. Mob Netw Appl. 2023. doi:10.1007/s11036-023-02158-y. [Google Scholar] [CrossRef]
10. Abdelfatah RI, Saqr HM, Nasr ME. An efficient medical image encryption scheme for (WBAN) based on adaptive DNA and modern multi chaotic map. Multimed Tools Appl. 2023;82(14):22213–27. doi:10.1007/s11042-022-13343-8. [Google Scholar] [CrossRef]
11. Trujillo-Toledo DA, López-Bonilla OR, García-Guerrero EE, Esqueda-Elizondo JJ, Cárdenas-Valdez JR, Tamayo-Pérez UJ, et al. Real-time medical image encryption for H-IoT applications using improved sequences from chaotic maps. Integration. 2023;90:131–45. doi:10.1016/j.vlsi.2023.01.008. [Google Scholar] [CrossRef]
12. Zhang B, Rahmatullah B, Wang SL, Almutairi HM, Xiao Y, Liu X, et al. A variable dimensional chaotic map-based medical image encryption algorithm with multi-mode. Med Biol Eng Comput. 2023;61(11):2971–3002. doi:10.1007/s11517-023-02874-3. [Google Scholar] [PubMed] [CrossRef]
13. El-Shafai W, Khallaf F, El-Rabaie EM, El-Samie FEA. Proposed 3D chaos-based medical image cryptosystem for secure cloud-IoMT eHealth communication services. J Ambient Intell Humaniz Comput. 2024;15(1):1–28. doi:10.1007/s12652-022-03832-x. [Google Scholar] [CrossRef]
14. Zhang B, Rahmatullah B, Wang SL, Liu Z. A plain-image correlative semi-selective medical image encryption algorithm using enhanced 2D-logistic map. Multimed Tools Appl. 2023;82(10):15735–62. doi:10.1007/s11042-022-13744-9. [Google Scholar] [PubMed] [CrossRef]
15. Kumar D, Sudha VK, Ranjithkumar R. A one-round medical image encryption algorithm based on a combined chaotic key generator. Med Biol Eng Comput. 2023;61(1):205–27. doi:10.1007/s11517-022-02703-z. [Google Scholar] [PubMed] [CrossRef]
16. Srinivasu PN, Norwawi N, Amiripalli SS, Deepalakshmi P. Secured compression for 2D medical images through the manifold and fuzzy trapezoidal correlation function. Gazi Univ J Sci. 2022;35(4):1372–91. doi:10.35378/gujs.884880. [Google Scholar] [CrossRef]
17. Jiang D, Tsafack N, Boulila W, Ahmad J, Barba-Franco JJ. ASB-CS: adaptive sparse basis compressive sensing model and its application to medical image encryption. Expert Syst Appl. 2024;236:121378. doi:10.1016/j.eswa.2023.121378. [Google Scholar] [CrossRef]
18. Gao Y, Liu J, Chen S. Image encryption algorithms based on two-dimensional discrete hyperchaotic systems and parallel compressive sensing. Multimed Tools Appl. 2024;83(19):57139–61. doi:10.1007/s11042-023-17745-0. [Google Scholar] [CrossRef]
19. Chen JX, Zhu ZL, Fu C, Zhang LB, Zhang Y. An image encryption scheme using nonlinear inter-pixel computing and swapping based permutation approach. Commun Nonlinear Sci Numer Simul. 2015;23(1–3):294–310. doi:10.1016/j.cnsns.2014.11.021. [Google Scholar] [CrossRef]
20. Zhang YQ, Wang XY. Analysis and improvement of a chaos-based symmetric image encryption scheme using a bit-level permutation. Nonlinear Dyn. 2014;77(3):687–98. doi:10.1007/s11071-014-1331-3. [Google Scholar] [CrossRef]
21. Tsafack N, Sankar S, Abd-El-Atty B, Kengne J, Jithin KC, Belazi A, et al. A new chaotic map with dynamic analysis and encryption application in Internet of health things. IEEE Access. 2020;8:137731–44. doi:10.1109/ACCESS.2020.3010794. [Google Scholar] [CrossRef]
22. Kocarev L. Chaos-based cryptography: a brief overview. IEEE Circuits Syst Mag. 2002;1(3):6–21. doi:10.1109/7384.963463. [Google Scholar] [CrossRef]
23. Mislovaty R, Klein E, Kanter I, Kinzel W. Public channel cryptography by synchronization of neural networks and chaotic maps. Phys Rev Lett. 2003;91(11):118701. doi:10.1103/PhysRevLett.91.118701. [Google Scholar] [PubMed] [CrossRef]
24. Nanfak A, de Dieu Nkapkop J, Mvogo Ngono J, Tabekoueng Njitacke Z, Lessouga Etoundi CM, Effa JY. Enhanced chaos-based image compression-encryption algorithm utilizing 2D compressive sensing and genetic algorithm optimization. Multimed Tools Appl. 2024. doi:10.1007/s11042-024-20469-4. [Google Scholar] [CrossRef]
25. Le Z, Li Q, Chen H, Cai S, Xiong X, Huang L. Medical image encryption system based on a simultaneous permutation and diffusion framework utilizing a new chaotic map. Phys Scr. 2024;99(5):055249. doi:10.1088/1402-4896/ad3bf4. [Google Scholar] [CrossRef]
26. Xiong J, Ji’e M, Wang L, Duan S. Fully chaotic medical image encryption scheme based on dynamic DNA and block rotation. Phys Scr. 2023;98(7):075234. doi:10.1088/1402-4896/acde1e. [Google Scholar] [CrossRef]
27. Belazi A, Talha M, Kharbech S, Xiang W. Novel medical image encryption scheme based on chaos and DNA encoding. IEEE Access. 2019;7:36667–81. doi:10.1109/ACCESS.2019.2906292. [Google Scholar] [CrossRef]
28. Kumar S, Sharma D. Image scrambling encryption using chaotic map and genetic algorithm: a hybrid approach for enhanced security. Nonlinear Dyn. 2024;112(14):12537–64. doi:10.1007/s11071-024-09670-0. [Google Scholar] [CrossRef]
29. Cun Q, Tong X, Wang Z, Zhang M. A new chaotic image encryption algorithm based on dynamic DNA coding and RNA computing. Vis Comput. 2023;39(12):6589–608. doi:10.1007/s00371-022-02750-5. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF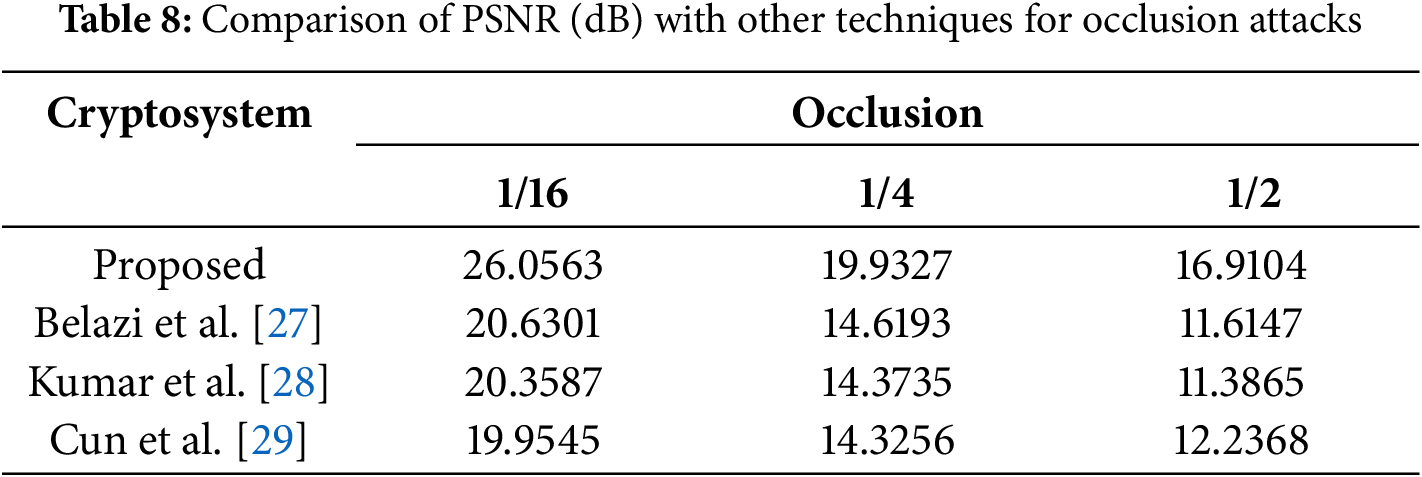
 Downloads
Downloads
 Citation Tools
Citation Tools
