Optimization of Dimensional Factors Using AI Technique Affecting Solar Dryer Efficiency for Drying Agricultural Materials

1  Introduction

The need for energy in industrial and agricultural industries has grown along with the global population. Around 90% of the energy used worldwide by the year 2100 has to come from renewable energy sources, such as solar energy, which is an abundant and clean energy source [1]. Also, there has been a high population growth and food supply which are caused by agricultural food losses after harvesting and quality degradation. Innovative processing methods have been applied to preserve the quality, extend the shelf life, and avoid product loss in marine and agricultural products. A long-standing method for drying agricultural goods such as potatoes, tomatoes, bananas, etc., is solar drying [2]. It was discovered that about a third of the energy used worldwide is consumed by the food sector. In addition, the processing of food accounts for about 26% of all greenhouse gas emissions. Because the majority of foods—roughly 34% of all goods worldwide—need to have at least some portion of their product dried at some point during processing, drying is an energy-intensive unit activity within this industry [3]. A clean, renewable energy source that has the potential to replace traditional fossil fuels is the use of solar radiation for drying operations. Open sun drying (OSD) is the term used to describe the conventional sunlight method for drying. However, since the product will be exposed to many environmental factors (such as rain, dirt, insects, etc.), several drawbacks will affect its quality [4].

It is anticipated that the solar constant, or extraterrestrial total solar irradiance per unit area is measured at one astronomical unit from the sun on a surface perpendicular to the rays [5]. This will fluctuate from 1412 W/m2 in early January to 1321 W/m2 in July due to the Earth’s changing distance from the sun. Approximately 165 petawatts (PW) of solar energy are absorbed by the Earth’s surface. This energy is reflected into space which is about 30% of its total value, 47% is converted to low-temperature heat (water evaporation), 23% is turned to wind energy, and 0.5% is transferred to wave kinetic energy [6,7]. Tropical regions are known for being popular with sun drying due to the abundant solar energy available there, the ease of design and installation, and the resulting effectiveness. With few exceptions, most countries of the developing world are located in climatic zones receiving reasonably higher insolation than the world average figure which varies from 1600 to 2200 kWh/m2/year [8]. The main classification of solar drying system is mentioned in Fig. 1. According to the utilization of solar power, the drying system is classified into two groups; open sun drying (OSD) and controlled solar drying [9].

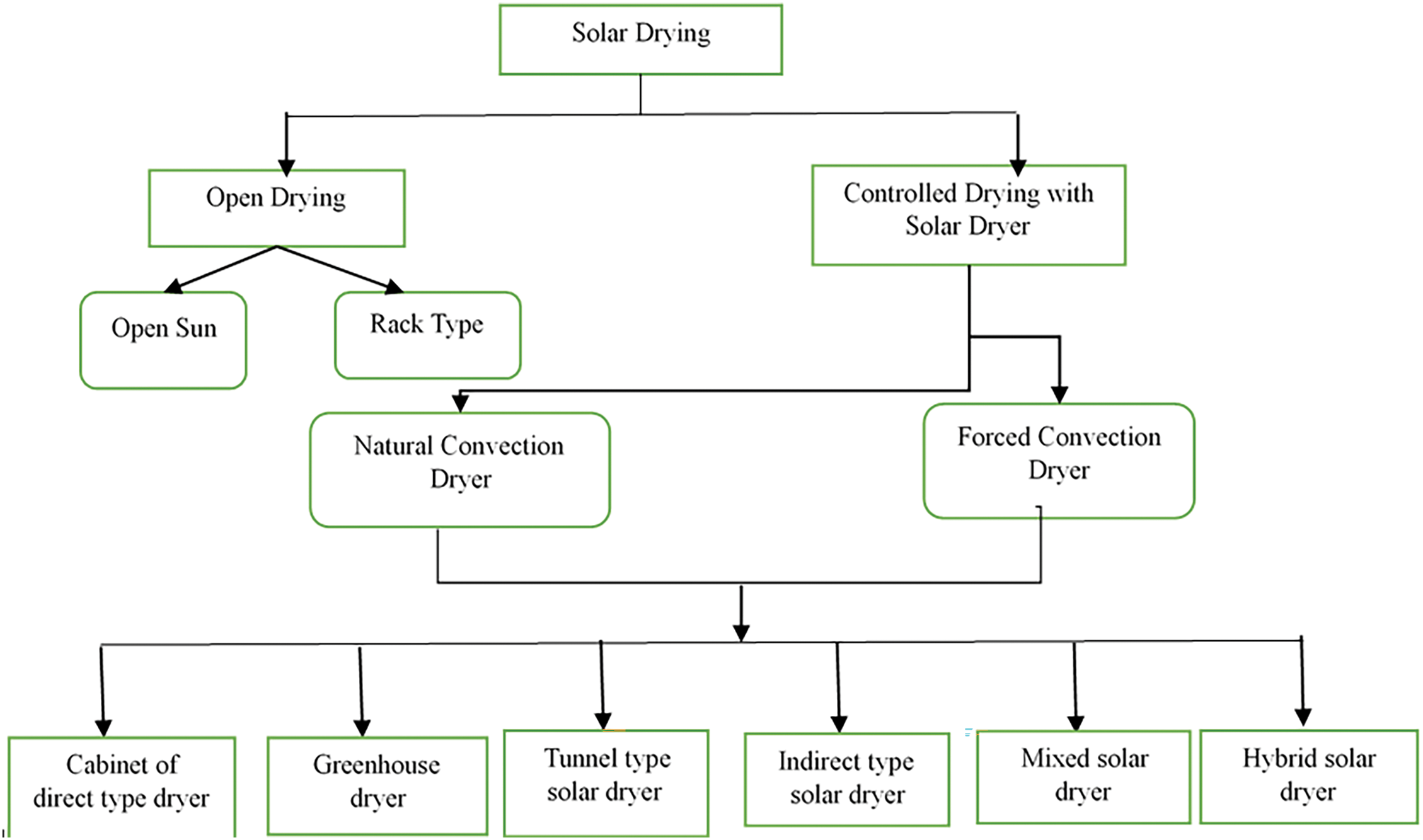
Figure 1: Classification of the solar dryer system

The technique to be selected depends on the food, otherwise, it may lead to inadequate drying which can potentially cause the agricultural goods to expire completely [10]. There are essentially two strategies for drying: artificial and natural. The first process of natural drying involves subjecting the materials to direct sunlight and wind conditions. Alongside harvesting and threshing, it is the most inexpensive and popular method of drying crops. It has been recognized, nonetheless, that natural drying techniques have drawbacks, including lengthy drying times, insect infestations, a tendency to lag behind industrialized agricultural production, dependence on weather conditions, uneven drying, contamination risk, lack of temperature control, slow drying process, and space requirements.

Hence, the context of large-scale mechanization and the disadvantages of natural drying stimulated the development of artificial drying, which employs artificial devices with heat supply for material drying regardless of the ambient conditions [11]. AI helps to optimize the design of solar dryers developed in Computational Fluid Dynamics (CFD) since it improves their performance and efficiency and automates them. AI systems, or artificial intelligence, use predictive modeling to evaluate weather data and forecast levels of solar radiation with a high enough degree of precision to enable improved planning and real-time drying process fine-tuning [12]. Examining factors that expose important essential qualities in the areas of moisture content, temperature distributions, and airflow, aids in optimizing the design and helps identify the best feasible configurations. AI-powered automation systems may maintain an eye on and control important variables like drying time, moisture ratio (MR), drying rate (DR), temperature, and airflow.

Consequently, less labor is required, and the drying process is more consistent [13]. AI methods such as Artifical Neural Network (ANN), Support Vector Machine (SVM), Deep Neural Network (DNN), etc., could assist with energy efficiency by reducing waste energy use and optimizing the amount of solar radiation that is accessible. It will also make it possible to adapt optimal material selection and structural designs best suited to increase solar input and retain heat [14]. Its smooth drying conditions allow it to retain consistent and uniform product quality. Even better, it can identify problems and forecast when maintenance will be needed, extending the solar dryers’ lifespan and reliability. AI typically enhances the sun drying process, making it safer, more efficient, and condition-adaptive, a literature describing the key benfits is mentioned in Table 1.

In view of the recent advancement in Artificial Intelligence, an inverse artificial neural network (ANNi) with genetic algorithm (GA) optimization was used to evaluate the hybrid design of an active indirect sun dryer for plantain and taro. This model is exceptionally efficient; in its 4.3-s calculation time, it produced a highly precise velocity forecast with only 0.83% error [17]. The DNN, on the other hand, was able to predict the irradiance of the sun with respectable R2 values between 70% and 73%. An innovative solar dryer that features a modified peanut drying chamber outperformed the conventional tunnel drier in terms of drying performance in terms of peanuts. The best model was found to be the Random Tree followed by the ensemble model with an R2 of 0.9972 for the MR predictions [19]. Finally, infrared-assisted hybrid solar dryers were tested on stevia leaves; in this scenario, it was discovered the ANN model delivered the greatest value regarding the accuracy in terms of moisture ratio prediction with a coefficient of determination R2 = 0.9995, which is again symbolic of AI’s potential to enhance solar drying technologies [21]. The study conducted on Infrared-Assisted Air Impingement Dryer for Apple drying explored the use of a Multi-Objective Genetic Algorithm (MOGA) in hybridization with Back-Propagation Artificial Neural Network (BP-ANN) which resulted in an exergy efficiency of 62.23% [22]. A Genetic Algorithm-Optimized Artificial Neural Network (GA-ANN) has also been brought to use for predicting the irradiation levels of Algeria for studying the drying characteristics in that region. GA-ANN achieved an R2 of 0.9005 [23]. For the Solar-Biomass Hybrid Greenhouse Dryer Elitist Non-Dominated Sorting Genetic Algorithm (NSGA-II) was applied to maximize exergy efficiency and optimize drying air temperature. The solar-biomass mode achieved the highest exergy efficiency (80.21% ± 14.26%) in this algorithm. Genetic Algorithms rely on crossover and mutation operations to explore the solution space, which can be relatively slow to converge. HT_SOGT combines swarm optimization with a Gradient Tree component, which leverages predictive adjustments to guide the optimization process more effectively From all the literature, it can be concluded that the dryer efficiency and drying time (DT) are highly dependent on the environmental conditions and sun’s exposure at a certain region where the setup is installed. The dryer input parameters are chosen from the work [24] which are then analyzed for the input conditions of the Bhopal region. Fig. 2 depicts the temperature variation of the region [25].

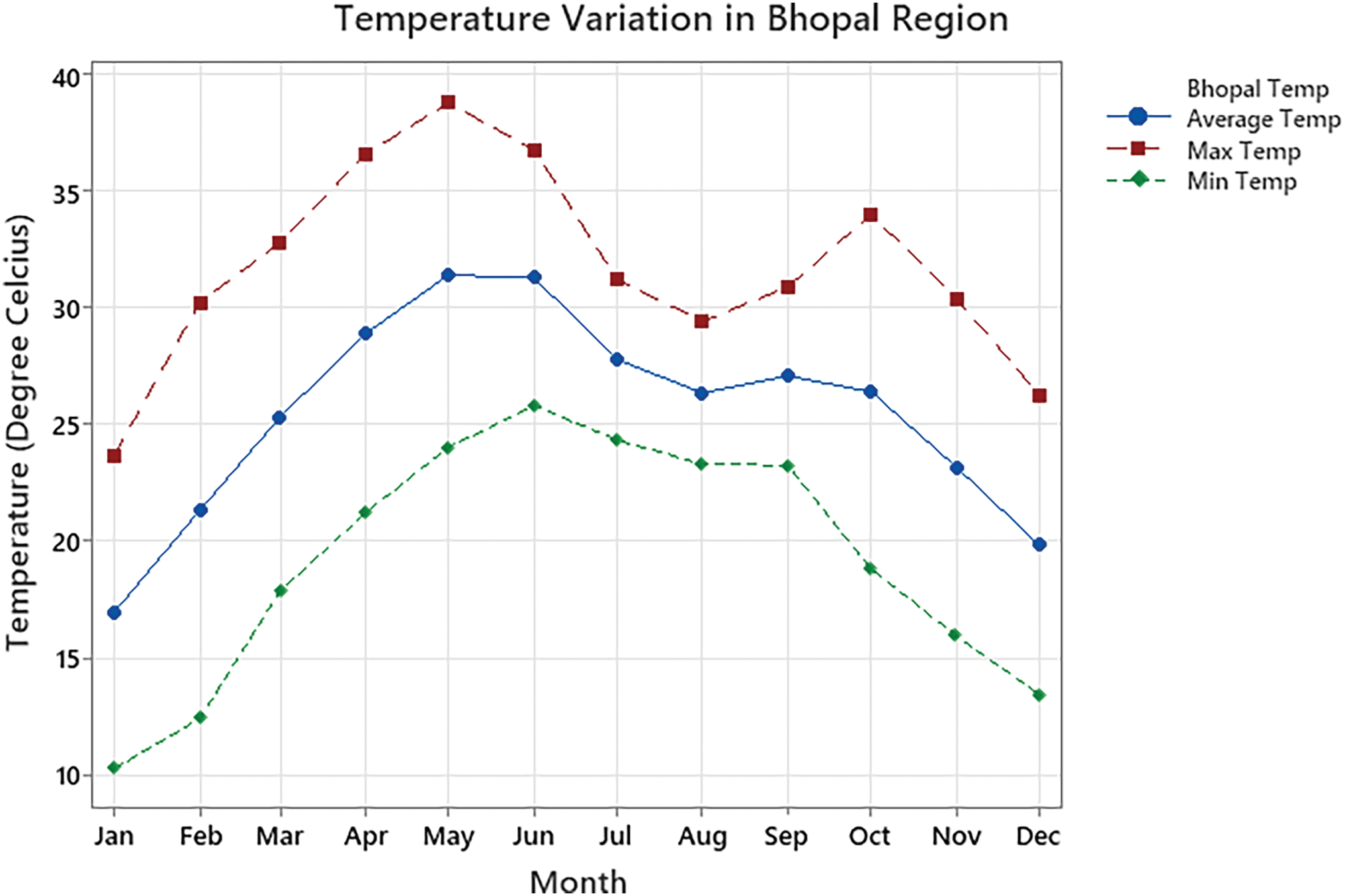
Figure 2: Temperature variation of Bhopal throughout the year

Traditional optimization approaches (e.g., genetic algorithms (GA) [26], particle swarm optimization) are commonly applied in dryer design, but they often lack the predictive accuracy and adaptability needed for real-world applications having a common model designed that will focus on optimizing the geometrical dimensions of the dryer, they are rather focused on optimizing the process by controlling the airflow and temperature on an existing design [27,28]. By applying HT_SOGT, this research introduces a novel approach that combines swarm optimization with gradient tree learning, leading to superior accuracy in predicting optimal dryer dimensions. This innovative approach could be a significant advancement in the field, as it allows for both the exploration and exploitation of parameter spaces, resulting in more efficient and reliable designs suitable for different input conditions.

The irradiation for the Bhopal region as mentioned in Fig. 3 is evaluated by calculating the solar declination angle (δ) for ζ=23.450 inclination of solar collector as per the latitude of this region, which is formulated as:

δd=23.450×sin⁡(3600×(N−81)365)(1)

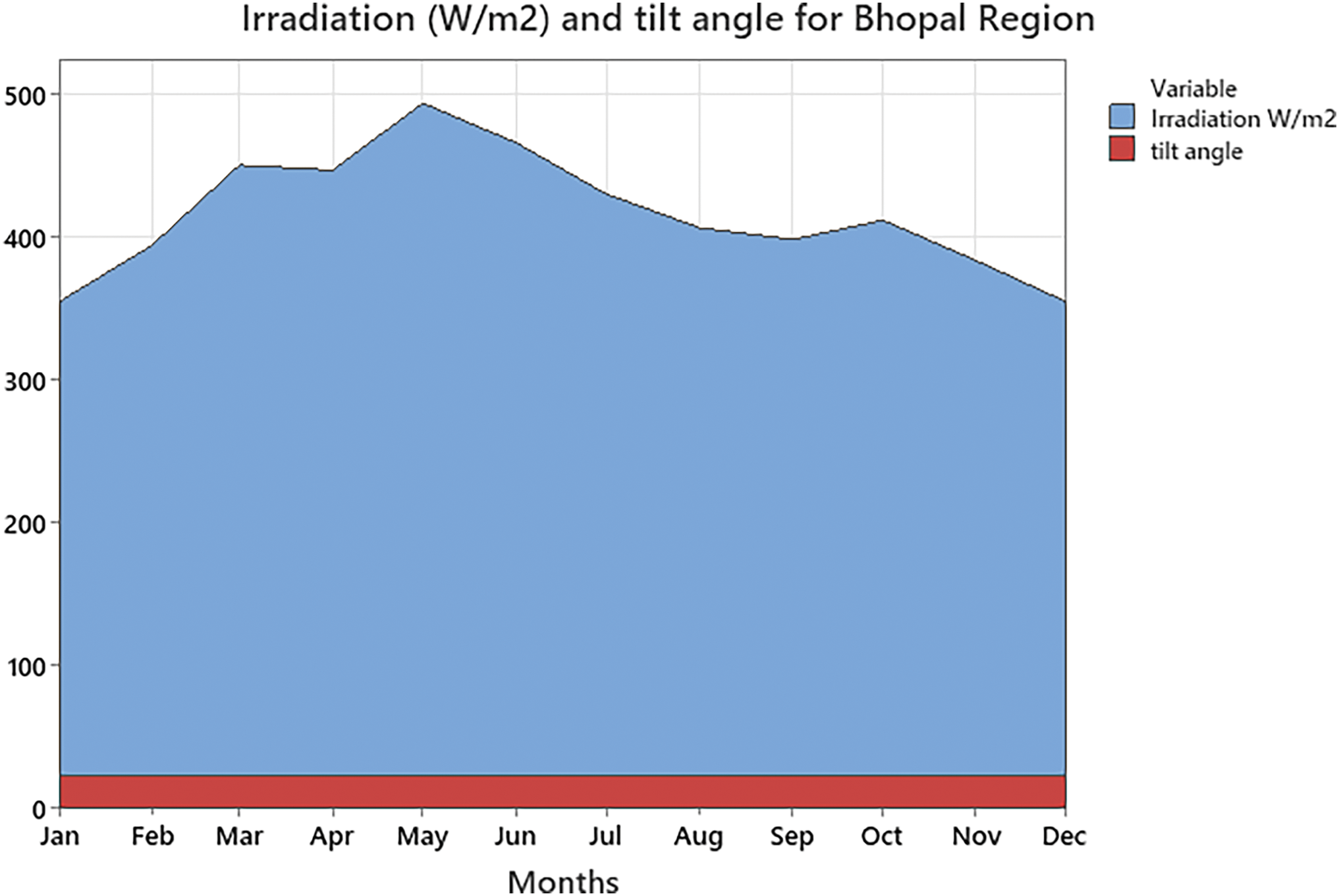
Figure 3: Irradiation levels of the Bhopal, M.P, India

N is the mean day of the months which are taken as 17 January, 16 February, 16 March, 15 April, 16 May, 17 June, 17 July, 16 August, 15 September, October, 14 November & 10 December. The sunset hour angle is calculated as:

ha=cos−1⁡(−tan⁡ζ×tan⁡δd)(2)

The ha Sunset hour angle in degree is the angle when the sun sets and helps calculate the total amount of solar radiation received during the entire daylight period. The irradiation level is then evaluated as Ib in W/m2.

Ib=3600×24πIsc[1.0+0.033cos⁡(360n365)](cos⁡ζcos⁡δdcos⁡ha)(3)

Isc is defined as the solar constant which is 1361 W/m2. This research work aims to predict the optimum drying parameters of the solar dryer that is intended to achieve better drying efficiency (ηdr) throughout the year according to the environmental conditions of the Bhopal region using artificial intelligence (AI) based optimization algorithm. The suggested geometry is compared against the previous design for DT and ηdr. Mathematical evaluations have been used to generate the data set for optimization under varying irradiation levels, different collector areas, and variable chimney dimensions.

After carefully considering the parameters of the experimental region, the dryer specifications described have been selected as the optimum design that is to be developed according to Bhopal environmental condition. Since the changes in the environmental factors can change the drying efficiency of the dryer, prior estimation of the performance of the dryer is done by mathematical modeling. After this, the optimum size of the effective drying area is predicted making use of hyper-tuned swarm optimization with gradient tree (HT_SOGT) predictive modeling.

2  Mathematical Approach for Solar Dryer Design Considerations

The solar dryer system is composed of a solar air collector and a drying chamber, each with distinct specifications designed for optimal drying efficiency whose dimensional parameters are taken by [24] and represented by Fig. 4. The solar air collector is set at an inclination angle of 23.03 degrees, utilizing an absorber made from iron with a matte black finish for maximum heat absorption. The absorber has a thickness of 0.2 cm, and the glass cover, which spans an area of 0.57 m2, has a thickness of 0.4 cm. The rear of the collector is insulated with 4 cm thick polystyrene, enclosed by two wooden plates, covering a total insulation area of 0.858 m2 to minimize heat loss. The lux meter of accuracy ±3% has been used with a temperature sensor of −200°C to 1300°C range for noting the inlet and outlet reading. For measuring the mass, a weighing scale of up to 10 kg has been used.

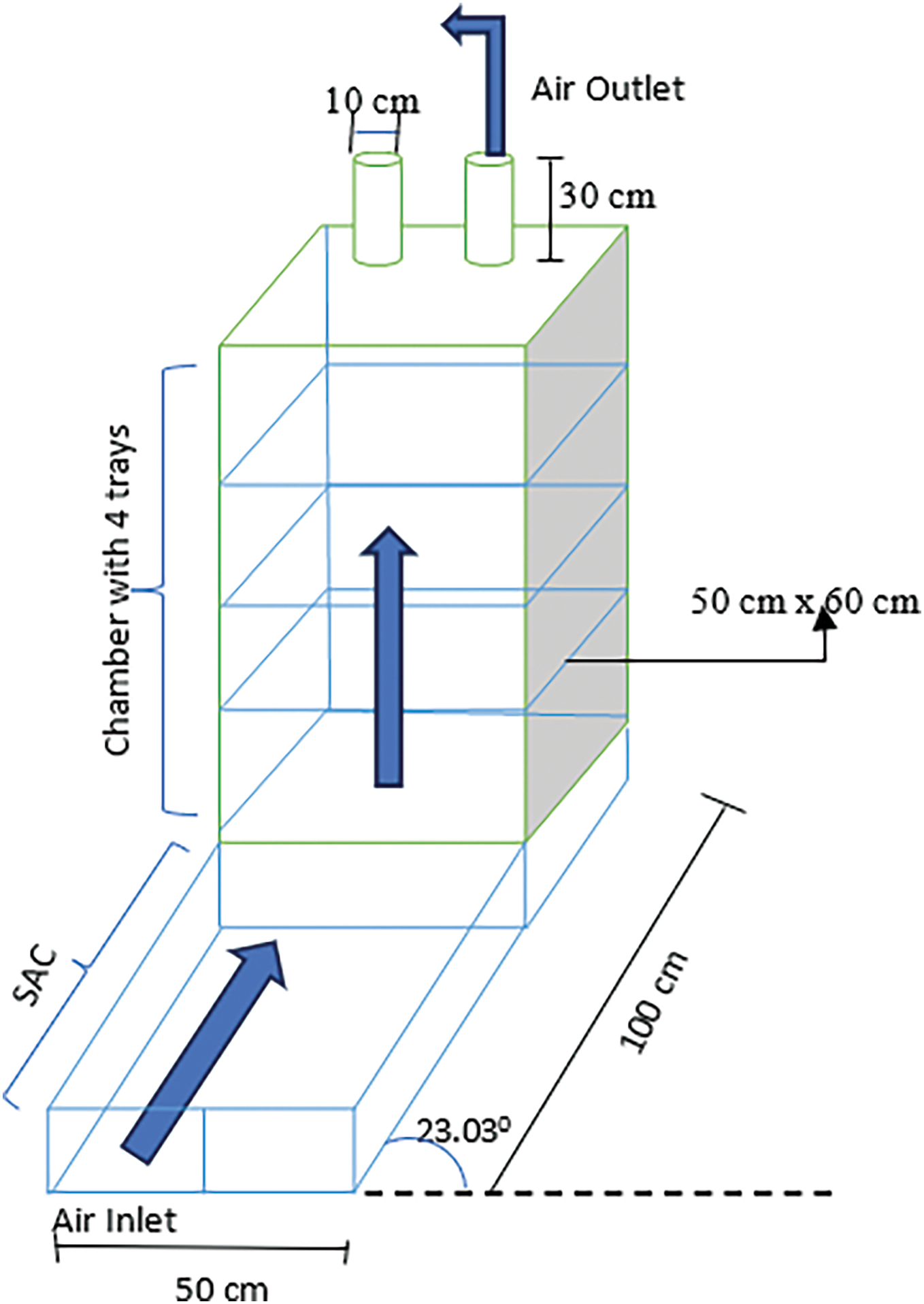
Figure 4: Chamber dimension details for banana drying

The drying chamber is made of wood and measures 50 cm in width, 60 cm in depth, and 100 cm in height. It contains four trays made of iron mesh, with 20 cm spacing between each tray to allow for adequate air circulation during the drying process. The chamber is ventilated by two PVC chimneys, each with a diameter of 10 cm and a height of 30 cm, facilitating efficient airflow. As per the references studied the standard range for the final moisture content of the dried banana chips is between 15% to 30% which will ensure durability of products while maintaining the nutritional content of the final product. The design has a drying surface area for a single tray which is the product of the chamber’s width and depth because all four trays are anticipated to completely use the drying chamber’s cross-sectional area and because the material spreads throughout each tray’s whole surface. The per-tray drying area is represented as ap in m2 in having length lp taken as 50 cm and breadth bp taken as 60 cm. Since each tray adds to the overall drying capacity, the total drying surface area denoted as at is therefore four times larger than the area of a single tray.

ap=lp×bp=50×60cm2=300010,000cm2=0.3m2(4)

at=4×ap=4×0.3m2=1.2m2(5)

dr=k×at×ΔT(6)

dt=Mi−Mfdr= DT(7)

ηd=mw×hfgac×Ib×dt(8)

The dryer efficiency (ηd) mentioned in the paper is typically calculated using Eq. (8). The ac is the collector area of the dryer designed which is 0.57 m2, Ib is the available irradiation on the collector surface in W/m2, mw mass of the water removed from the banana slices in kg, ΔT represents the change in temperature inside the dryer at °C and k is the drying coefficient of the dryer. hfg latent heat of vaporization of water 2.45 × 106 J/kg.

The bananas have dimensions of similar slices with a thickness of L = 4 ± 1 mm and a diameter of D = [3.5; 4] ± 0.2 cm. According to the study, the initial mass of the banana slices being dried was 549.76 g, and after the drying process, the final mass was reduced to 138.41 g the mass of the water being removed was 411.35 g. The mw is used as 0.41135 kg.

The steps of working involved in designing a dryer with optimized parameters have been shown in Fig. 5. Bhopal region experiences significant climatic variability throughout the year, with a marked reduction in solar dryer efficiency during the rainy season. Therefore, the dryer dimensions must be optimized to ensure reliable performance during periods of low solar radiation while maximizing efficiency during peak solar availability in the summer months. This adaptive design approach accounts for seasonal fluctuations, enabling the dryer to operate effectively under diverse environmental conditions. Therefore, a model is designed to specifically identify the accurate dryer dimensions for such conditions taking input from the irradiation levels, and temperature variations of the region. The methodology helps design an efficient dryer from scratch by leveraging AI to predict the most effective dimensions and parameters. The approach is highly scalable, enabling users to adapt the methodology to any geographical location with available climatic and product data.

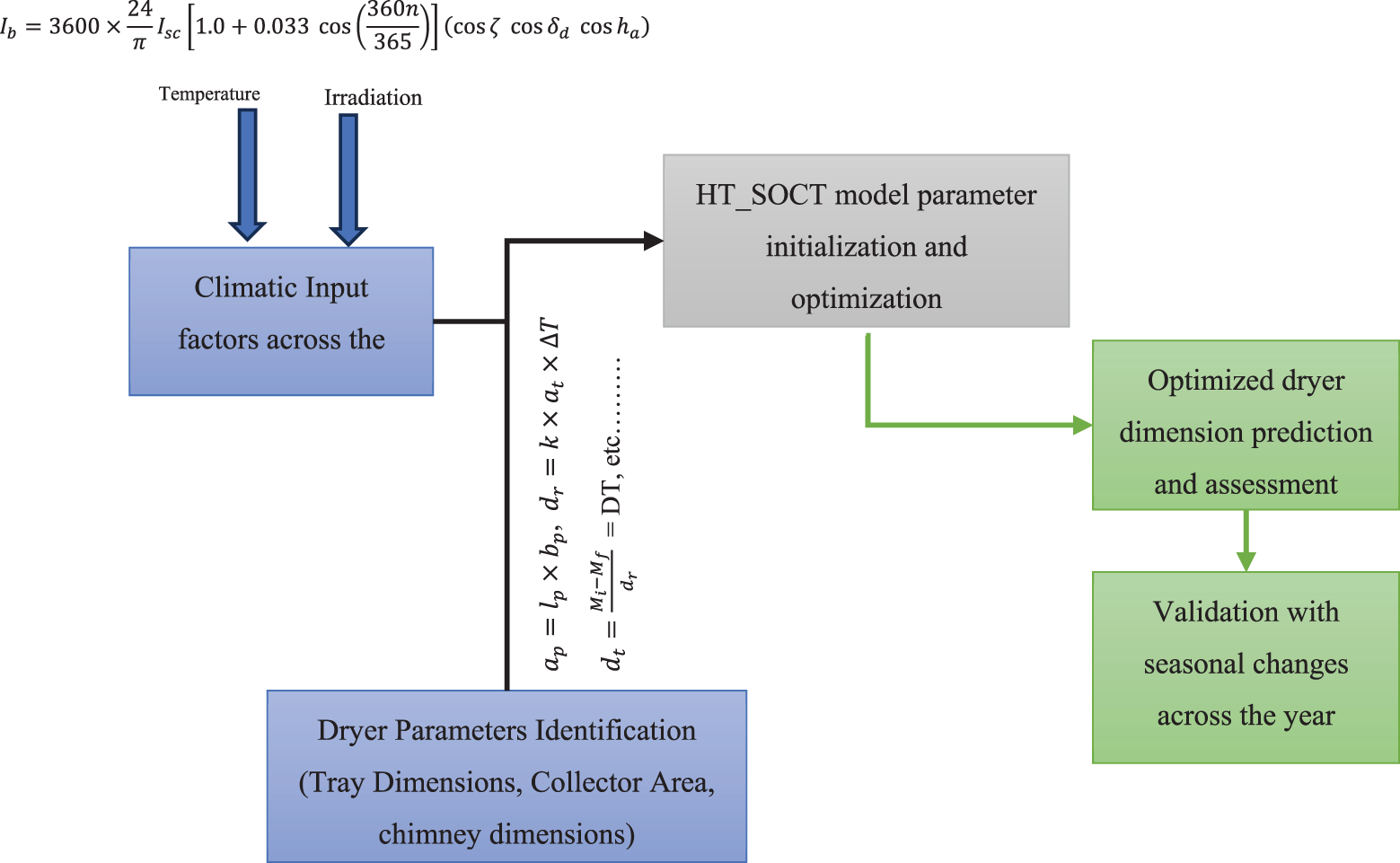
Figure 5: Process flow diagram of the model designing

3  Geometry Optimization and Prediction Modelling

Artificial Intelligence (AI) methods offer significant advantages in predicting the optimal dimensions of a dryer for various drying processes. Predicting these dimensions involves understanding complex, non-linear relationships between the physical properties of the product to be dried, environmental conditions (temperature, humidity), and operational constraints (airflow, drying rate). Traditional methods of calculating dryer dimensions often rely on empirical formulas or trial-and-error, but AI methods, including machine learning (ML) and optimization techniques, allow for more precise, data-driven predictions that are adaptive to changes in input conditions. The Gradient Tree Boosting model predicts the drying time by learning complex relationships between temperature, effective drying area, efficiency, collector area, irradiation level, number of trays in the dryer chimney height, and drying time. The PSO algorithm fine-tunes the GTB model’s hyperparameters, such as the number of trees, learning rate, and tree depth, to minimize the error in predicting drying time.

The objective of the PSO-GTB hybrid is to find the set of hyperparameters that minimizes the prediction error for drying time while accounting for complex environmental interactions. For optimizing dryer performance, an initial grid search is useful to set ranges for key parameters in both the swarm optimization and gradient tree components. Once ranges are established, random search allows for faster, more targeted tuning by randomly sampling values within the selected hyperparameter ranges.

A differentiable loss function is minimized through gradient descent in the function space.

n^it=n^i(t−1)+α.treet(xi)(9)

The gradient tree descent algorithm produces the variable n^it for tth iteration when the sample of the dryer parameters is xi. The variable α is the learning rate of the decision tree model where treet(xi) represents the tth tree output for sample xi. The objective function (Of) typically consists of a loss function and a regularization term to prevent overfitting in the algorithm:

Of=∑i=1mL(ni,n^i)+∑t=1Tε(treet)(10)

dr=k(AT,at).(Mi(t)−Meq)(11)

ε(treet) represents the regularization term to prevent overfitting in the Of. The L(ni,n^i) is the loss function in the learning method, also represented as:

L(ni,n^i)=12(ni−n^i)2(12)

The tree-building method involves residual building represented as ri(t) for any sample i.

ri(t)=−∂L(ni,n^i(t−1))∂n^i(t−1)(13)

xi(t+1)=xi(t)+vi(t+1)(14)

where the hyperparameters of particle i at step tth iteration is represented by xi(t) = [αi(t),Ti(t),dmax,i(t),nmin,i(t)] and vi(t+1) is the particle velocity at (t+1) of particle i.

vi(t+1)=ω.vi(t)+c1.r1.(pi(t)−xi(t))+c2.r2(g(t)−xi(t))(15)

ω of the equation, c1, c2 learning coefficients of the swarm intelligence, r1, r2 are the degree of randomization, where the pi(t) best particle position and g(t) is the global best position of the swarm intelligence. The fitness function for the optimization of the solar dryer is defined as:

Fit=1n∑i=1m(ni−n^i(xi))2(16)

Fig. 6 shows the diversity of the swarm (standard deviation of particle positions) over time. Swarm diversity measures how spread out the particles are in the search space. High diversity means that particles are spread across a wide area, promoting exploration. Low diversity suggests that the particles are converging, focusing on a specific region of the search space. HT_SOGT uses swarm optimization which has a computational complexity of O (N.I) where N is defined as the population size, and I is the number of iterations. The addition of a gradient tree model increases complexity but adds predictive accuracy, helping to fine-tune solutions more effectively. However, the Gradient Boosting Machine operates with a complexity of O (D. NlogN), where D is the depth of the trees. In combination with swarm optimization, the computational cost increases but is controlled due to the efficiency of swarm algorithms in reducing solution space exploration over successive generations. By leveraging swarm-based exploration with gradient tree adjustments, it avoids exhaustive search processes, making it relatively more computationally efficient for high-dimensional parameter spaces. The HT_SOGT model benefits from parallel processing capabilities, especially in swarm optimization stages where population members can evaluate solutions independently. This allows runtime reductions when implemented on multi-core processors, GPU clusters, or cloud computing environments. The HT_SOGT model achieves convergence within 150 iterations. HT_SOGT minimizes computational costs while maintaining high optimization performance, making it a competitive choice among numerical methods in the field.

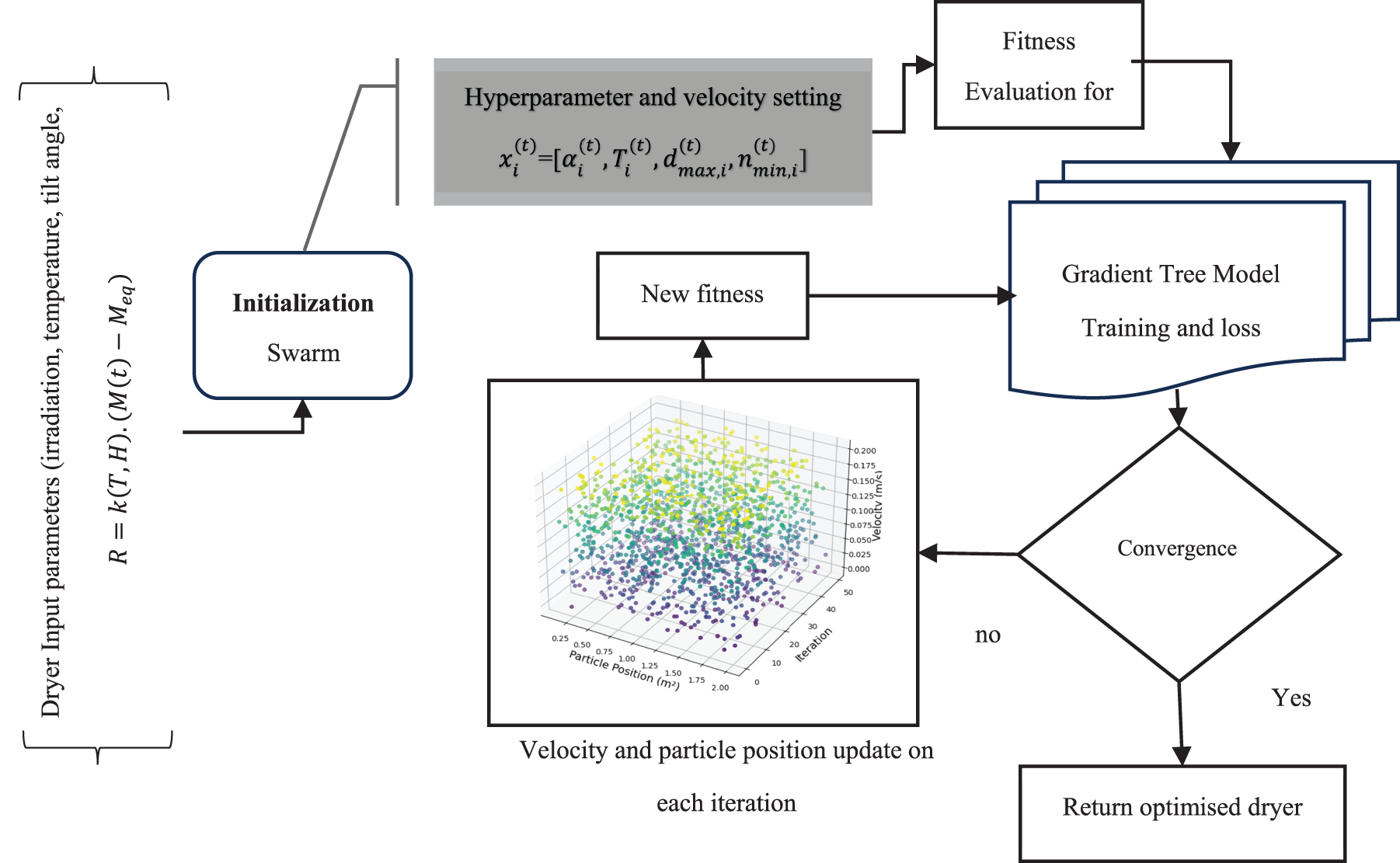
Figure 6: Hyper-tuned swarm optimization with gradient tree (HT_SOGT) algorithm for optimized dryer design prediction

In each iteration i, the PSO algorithm searches for the optimal effective drying area that minimizes drying time, given the temperature conditions as shown in Fig. 7. The variability in the global best position indicates that the algorithm is dynamically adjusting the drying area at, trying different configurations as described in Table 2. This adjustment is necessary because the ideal drying area likely depends on the temperature ΔT. For example, at higher temperatures, the drying rate may increase, and the area can be reduced while maintaining the desired drying speed. Conversely, lower temperatures might require a larger area to maintain the drying efficiency. The variations in diversity suggest that the algorithm is alternating between periods of exploration and exploitation. When the diversity is high, the algorithm explores many different configurations, perhaps testing the effects of large changes in drying area or temperature. When diversity decreases, the algorithm focuses on fine-tuning around a promising solution. The dryer parameters suggest shall have the at in the range of 1.35 to 1.5 m2 with the number of trays 3. Considering the fact that an increase in the area would involve extra purchase of the material, the further the testing is performed using 1.35 m2 as it would involve economic benefits.

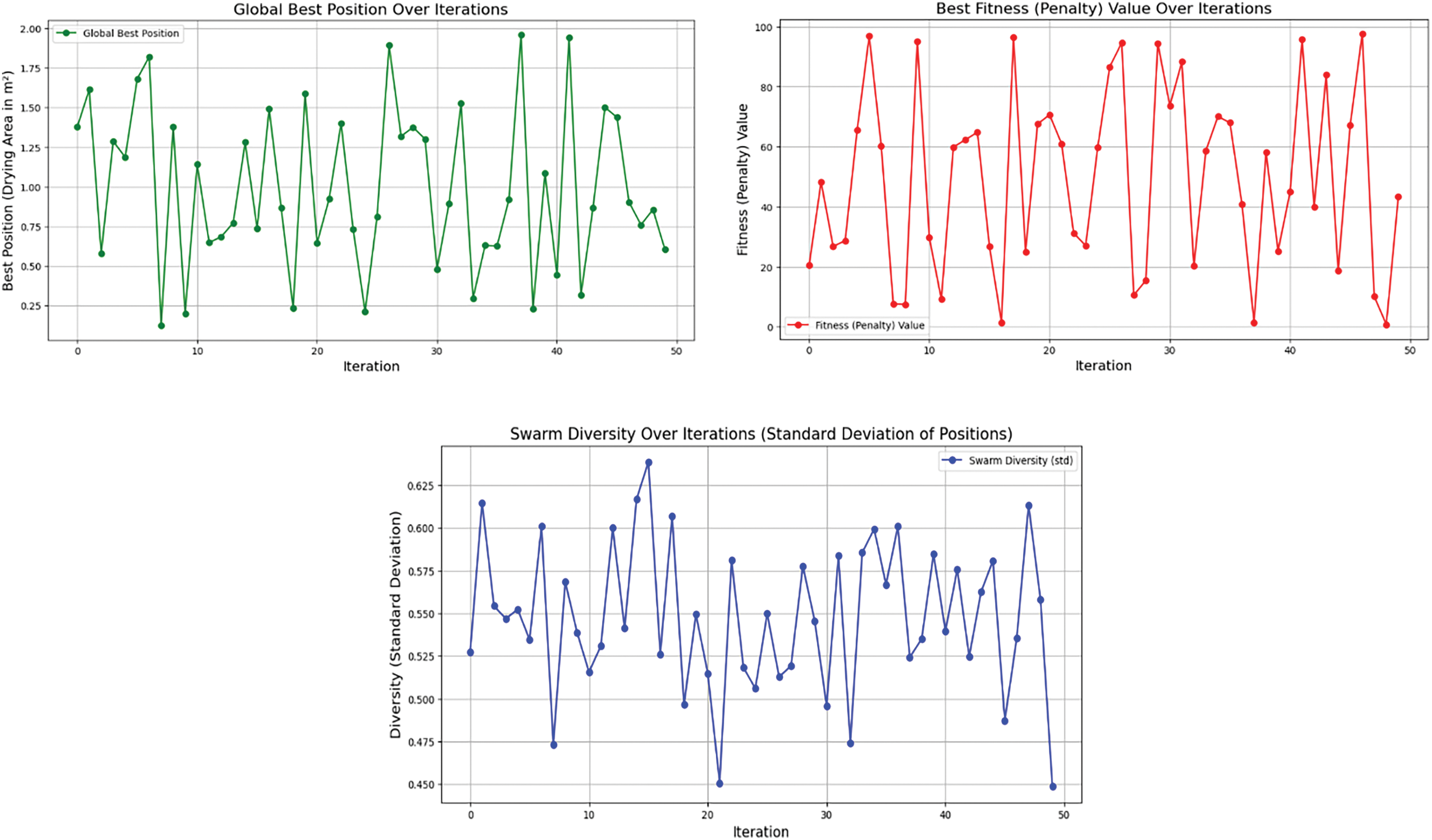
Figure 7: Algorithm flow and iteration steps for dryer dimension prediction

The ambient temperature in Bhopal ranges from 16.985°C to 31.4°C, covering the typical seasonal fluctuations in the area. During colder months, such as in winter when the ambient temperature is around 17°C–21°C, the dryer with the predicted drying area of 1.35 m2 manages to raise the temperature inside the drying chamber to 39°C–44.5°C as shown in Fig. 8. During the peak summer months, with ambient temperatures reaching 31.4°C, the solar dryer achieves its highest efficiency, with outlet temperatures rising to 66.2°C with the proposed drying area. This demonstrates the system’s effectiveness during the hottest months, ensuring rapid and efficient drying processes. Even in slightly cooler late summer periods, with ambient temperatures around 27°C–28°C, the dryer maintains high performance, reaching outlet temperatures around 62°C–63°C.

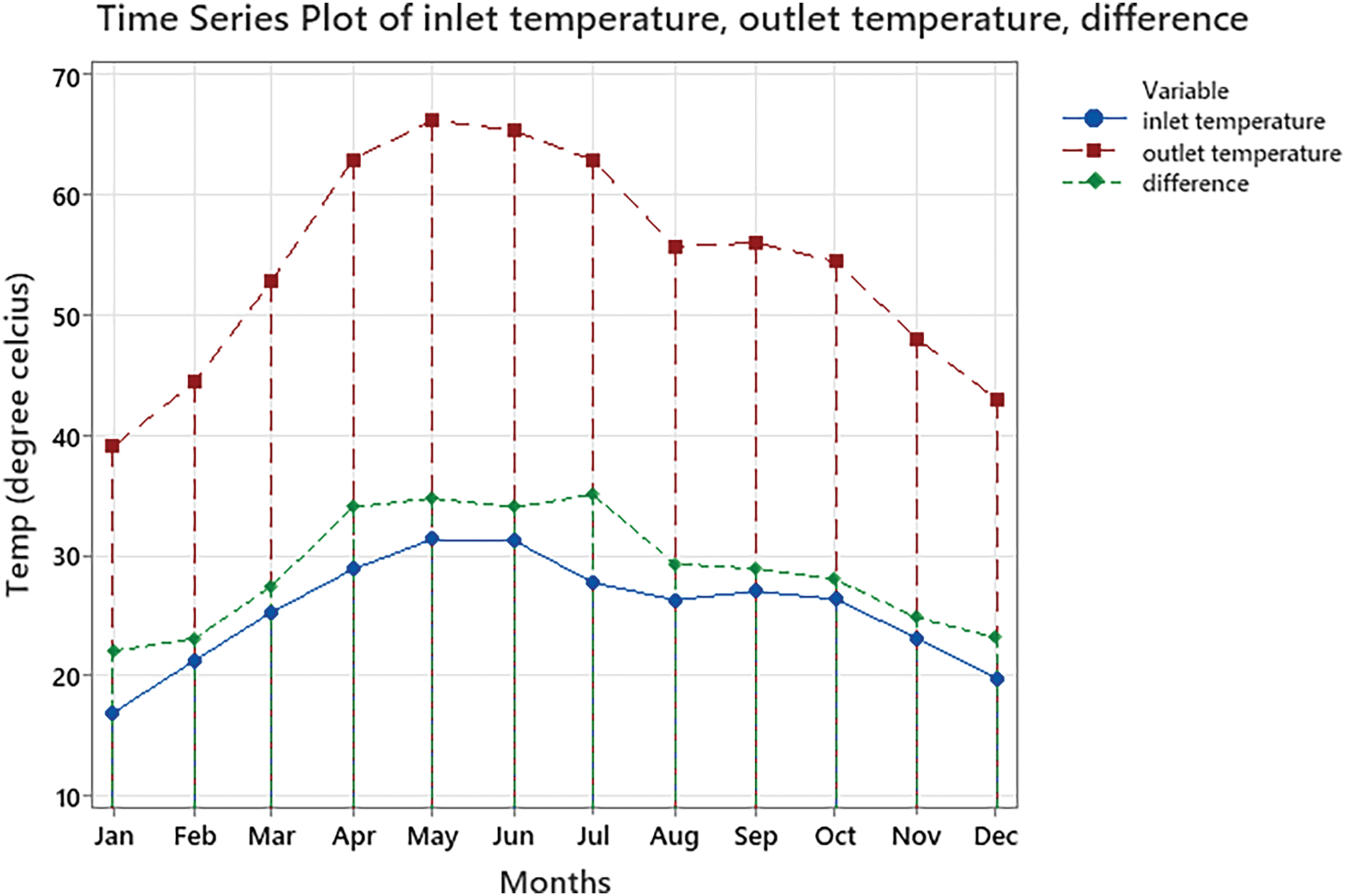
Figure 8: Temperature difference across the inlet and outlet of the dryer

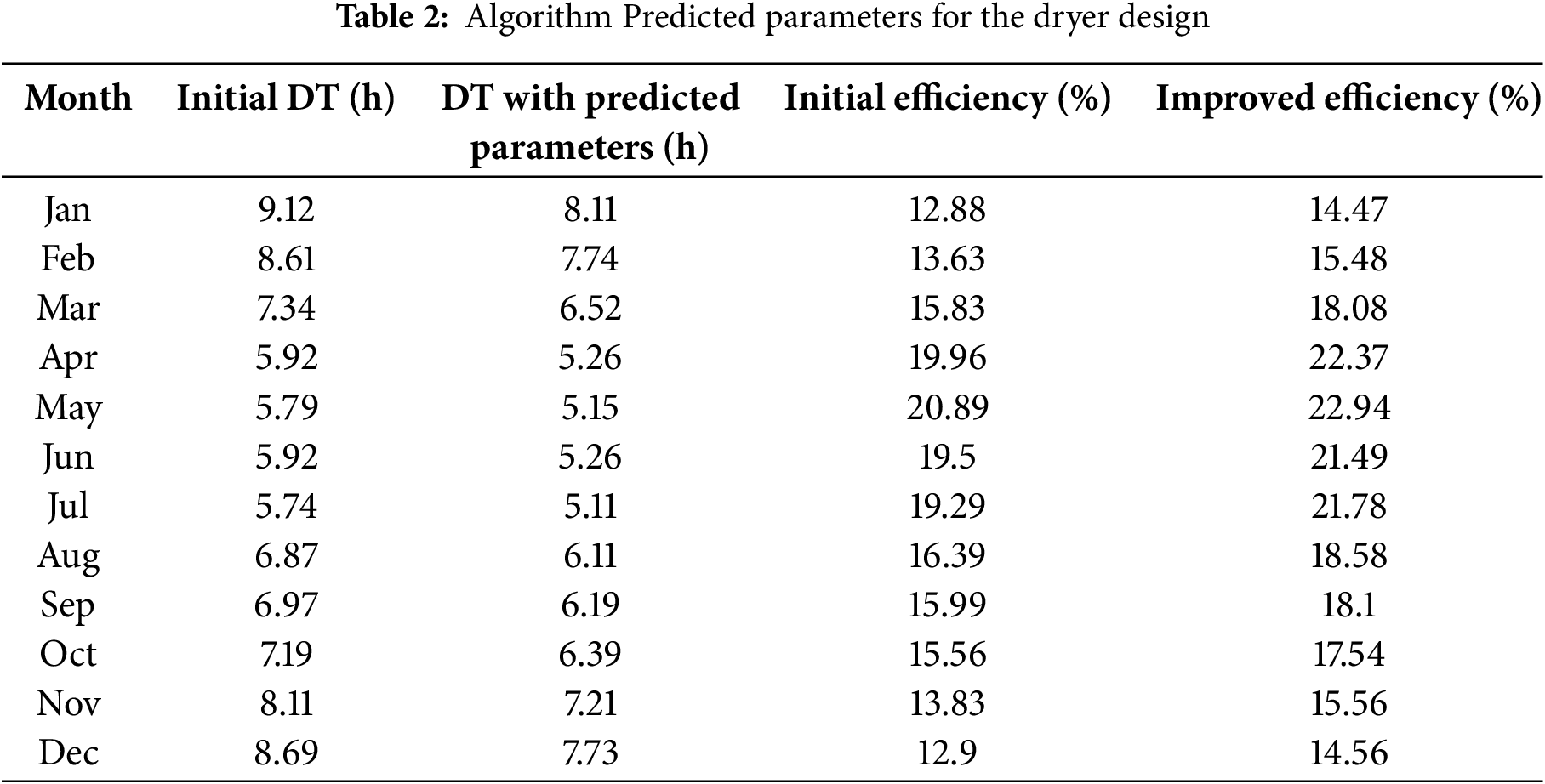
During the winter months (January, February, and December), the dryer with the predicted drying area of 1.35 m2 exhibits its slowest drying times and lowest efficiency as shown in Fig. 9. In January, the drying time is 9.12 h with an efficiency of 12.88%, while in February and December, drying times are 8.61 and 8.69 h, respectively, with efficiency hovering around 13%. Even after optimizing the drying area to 1.35 m2, drying times remain relatively slow (7.73–8.11 h), though efficiency improves slightly to 14%–15%. As temperatures rise in March, April, and May, the performance of the dryer improves significantly. In March, the drying time drops to 7.34 h with 15.83% efficiency, and further to 5.92 h in April and 5.79 h in May. Efficiency also peaks in these months, reaching over 20%. After optimization, drying times improve even more, dropping to around 5.15–6.52 h, while efficiency increases to over 22%, especially in April and May. June and July have the fastest drying times before optimization, both close to 5.74–5.92 h, with efficiency at around 19%. The optimized area reduces drying times further to approximately 5.11–5.26 h, and efficiency improves to over 21%. The drying times remain relatively slow (7.73–8.11 h) in the cold months of Dec to Jan, though efficiency improves slightly to 14%–15%.

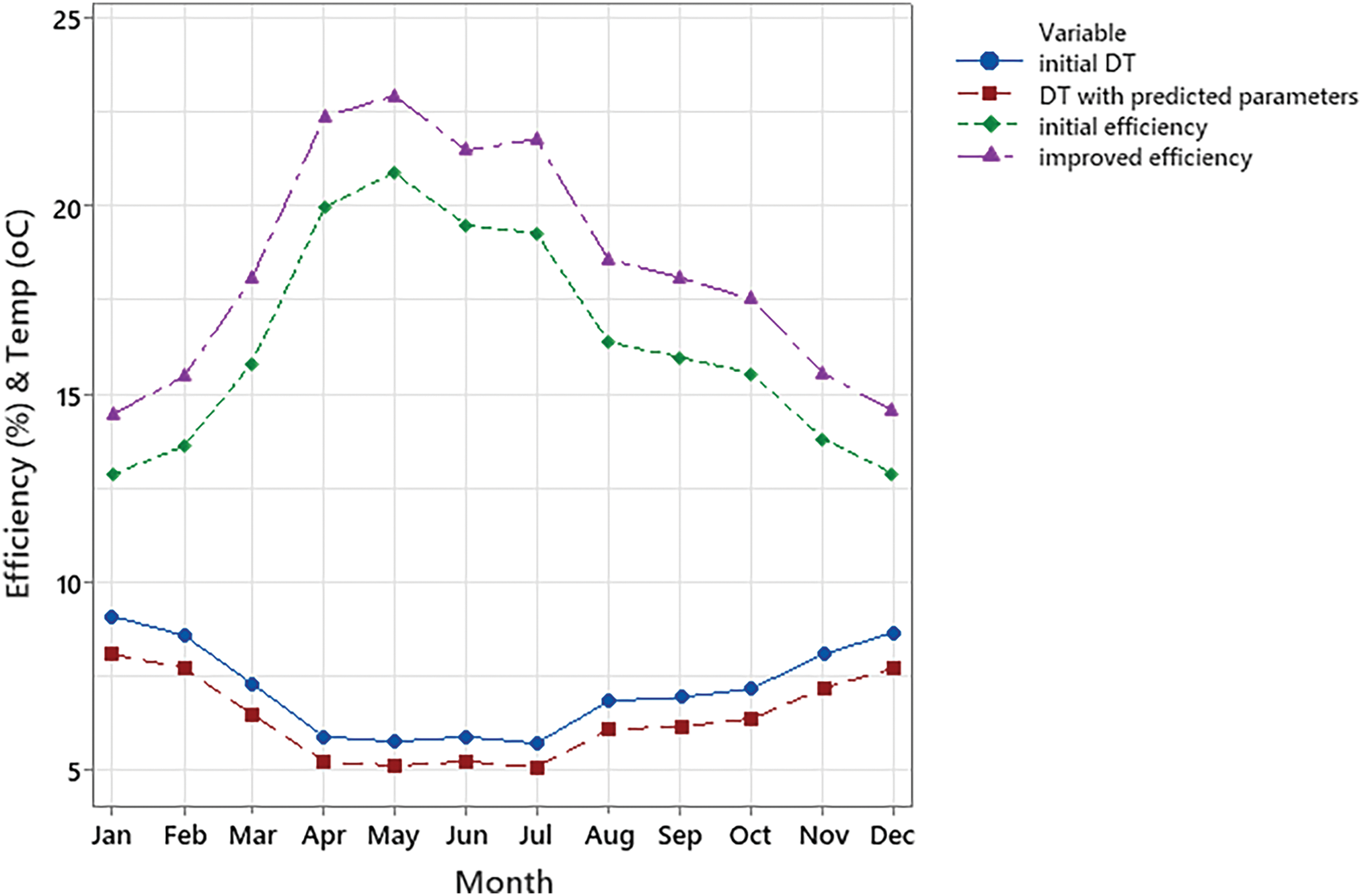
Figure 9: Dryer change in drying time and efficiency with predicted dryer dimensions

The dryer geometrical predictions are being made considering the climatic conditions such as temperature, and solar radiation that influence the drying time in the Bhopal region whose benefits are highlighted in Table 3. The AI model has the flexibility to change these parameters according to a different location which can then serve as an input to the HT_SOGT model. This reliability in design will ensure optimized dryer systems tailored to local requirements. Since it predicts the best design, this data-driven approach minimizes initial costs, speeds up deployment, and provides long-term stability, making it an attractive choice for both large-scale facilities and smaller operations.

4  Conclusion

The efficient operation of dryers at variable input conditions throughout the year is crucial in the food processing industry for improving efficiency and reducing operational costs. In order to achieve this, the geometrical design of the dryer to be installed at a location can be primarily subjected to optimization algorithms to predict the most efficient and reliable dimensions that are most suited for the geographical conditions of that area. The work has used the predictive method of Hyper Tuned Swarm Optimization with Gradient Tree (HT_SOGT) modeling having fast convergence and the optimal size for the effective drying area has been predicted to be 1.35 m2 for maximum efficiency across seasonal variations in the Bhopal region, India, while considering an economic solution. The prediction constraint was given to achieve optimized dryer dimensions that are targeted to achieve a drying time of approximately 7 h throughout the year. The predicted geometry improved the efficiency of the dryer to 21% from the 19% in the previous geometry during all the seasons of the year. The designed AI model can minutely study the environmental aspects of a region and suggest an optimized dryer design that will operate efficiently under such circumstances therefore this model can be used to predict industrial dryer specifications suitable for pharmaceutical drying processes where precision is critical or textile drying other than food processing industries.

Acknowledgement: The authors express their gratitude to the University Institute of Technology (UIT-RGPV), Bhopal, for providing the resources and facilities necessary to conduct this research. Special thanks are extended to the Department of Mechanical Engineering for their technical support and guidance. The authors also acknowledge the invaluable insights and suggestions from colleagues that greatly contributed to the improvement of this study.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design with analysis and interpretation of results: Ravindra Kumar Ray; draft manuscript preparation: Ravindra Kumar Ray; proof reading and editing: A.C. Tiwari. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Ravindra Kumar Ray, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Sethi CK, Acharya SK, Patnaik PP. Investigation on solar drying characteristics of ginger (Zingiber officinale) in a reflector-attached solar air heater and thermal energy storage system using nanomaterials. J Sol Energy Eng. 2023;145(6):061005. doi:10.1115/1.4062195. [Google Scholar] [CrossRef]

2. Nukulwar MR, Tungikar VB. Recent development of the solar dryer integrated with thermal energy storage and auxiliary units. Therm Sci Eng Progress. 2022;29:101192. doi:10.1016/j.tsep.2021.101192. [Google Scholar] [CrossRef]

3. Ortiz-Rodríguez NM, Condorí M, Durán G, García-Valladares O. Solar drying technologies: a review and future research directions with a focus on agroindustrial applications in medium and large scale. Appl Therm Eng. 2022;215(3):118993. doi:10.1016/j.applthermaleng.2022.118993. [Google Scholar] [CrossRef]

4. Ramirez C, Palacio M, Carmona M. Reduced model and comparative analysis of the thermal performance of indirect solar dryer with and without PCM. Energies. 2020;13(20):5508. doi:10.3390/en13205508. [Google Scholar] [CrossRef]

5. Yang D, Wang W, Gueymard CA, Hong T, Kleissl J, Huang J, et al. A review of solar forecasting, its dependence on atmospheric sciences and implications for grid integration: towards carbon neutrality. Renew Sustain Energy Rev. 2022;161:112348. doi:10.1016/j.rser.2022.112348. [Google Scholar] [CrossRef]

6. Kumar A, Singh KU, Singh MK, Kushwaha AKS, Kumar A, Mahato S. Design and fabrication of solar dryer system for food preservation of vegetables or fruit. J Food Qual. 2022;22:6564933. doi:10.1155/2022/6564933. [Google Scholar] [CrossRef]

7. Fernandes L, Fernandes JR, Tavares PB. Design of a friendly solar food dryer for domestic over-production. Solar. 2022;2(4):495–508. doi:10.3390/solar2040029. [Google Scholar] [CrossRef]

8. Mohana Y, Mohanapriya R, Anukiruthika T, Yoha KS, Moses JA, Anandharamakrishnan C. Solar dryers for food applications: concepts, designs, and recent advances. Sol Energy. 2020;208:321–44. doi:10.1016/j.solener.2020.07.098. [Google Scholar] [CrossRef]

9. Lingayat AB, Chandramohan VP, Raju VRK, Meda V. A review on indirect type solar dryers for agricultural crops-Dryer setup, its performance, energy storage and important highlights. Appl Energy. 2020;258(3):114005. doi:10.1016/j.apenergy.2019.114005. [Google Scholar] [CrossRef]

10. Gunathilake DMCC, Senanayaka DP, Adiletta G, Senadeera W. Drying of agricultural crops. In: Advances in agricultural machinery and technologies. Boca Raton, FL, USA: CRC Press; 2018. p. 331–65. doi:10.1201/9781351132398-14. [Google Scholar] [CrossRef]

11. Yao Y, Pang YX, Manickam S, Lester E, Wu T, Pang CH. A review study on recent advances in solar drying: mechanisms, challenges and perspectives. Sol Energy Mater Sol Cells. 2022;248(12):111979. doi:10.1016/j.solmat.2022.111979. [Google Scholar] [CrossRef]

12. Tiwari GN, Singh RK, Sinha ASK, Singh AK. Study of performance of the flexible (Al-based) N-PVT-TEC collectors in different configurations. ASME J Sol Energy Eng. 2023 Dec;145(6):061003. doi:10.1115/1.4062171. [Google Scholar] [CrossRef]

13. Castillo Téllez M, Pilatowsky Figueroa I, Castillo Téllez B, López Vidaña EC, López Ortiz A. Solar drying of Stevia (Rebaudiana Bertoni) leaves using direct and indirect technologies. Sol Energy. 2018;159(4):898–907. doi:10.1016/j.solener.2017.11.031. [Google Scholar] [CrossRef]

14. Arunkumar PM, Balaji N, Madhankumar S, Mohanraj T. Prediction of red chilli drying performance in solar dryer with natural energy storage element using machine learning models. J Energy Storage. 2024;101:113825. doi:10.1016/j.est.2024.113825. [Google Scholar] [CrossRef]

15. Das M, Alic E, Akpinar EK. Detailed analysis of mass transfer in solar food dryer with different methods. Int Commun Heat Mass Transf. 2021;128:105600. doi:10.1016/j.icheatmasstransfer.2021.105600. [Google Scholar] [CrossRef]

16. Cetina-Quiñones AJ, Santamaria-Bonfil G, Medina-Esquivel RA, Bassam A. Techno-economic analysis of an indirect solar dryer with thermal energy storage: an approach with machine learning algorithms for decision making. Therm Sci Eng Progress. 2023;45(2):102131. doi:10.1016/j.tsep.2023.102131. [Google Scholar] [CrossRef]

17. Nukulwar MR, Tungikar VB. A review on performance evaluation of solar dryer and its material for drying agricultural products. Mat Today: Proc. 2021;46(4):345–9. doi:10.1016/j.matpr.2020.08.354. [Google Scholar] [CrossRef]

18. Brahma B, Wadhvani R. Solar irradiance forecasting based on deep learning methodologies and multi-site data. Symmetry. 2020;12(11):1830. doi:10.3390/sym12111830. [Google Scholar] [CrossRef]

19. Hürdoğan E, Çerçi KN, Saydam DB, Ozalp C. Experimental and modeling study of peanut drying in a solar dryer with a novel type of a drying chamber. Energy Sour, Part A: Recov Utiliz Environ Effects. 2021;44(2):5586–609. doi:10.1080/15567036.2021.1974126. [Google Scholar] [CrossRef]

20. Gupta A, Das B, Arslan E, Das M, Kosan M, Can OF. Artificial neural networks based computational and experimental evaluation of thermal and drying performance of partially covered PVT solar dryer. Process Saf Environ Prot. 2024;183(2):1170–85. doi:10.1016/j.psep.2024.01.068. [Google Scholar] [CrossRef]

21. Bakhshipour A, Zareiforoush H, Bagheri I. Mathematical and intelligent modeling of stevia (Stevia Rebaudiana) leaves drying in an infrared-assisted continuous hybrid solar dryer. Food Sci Nutrit. 2021;9(1):532–43. doi:10.1002/fsn3.2022. [Google Scholar] [PubMed] [CrossRef]

22. Parida C, Sahoo PK, Nasir R, Waseem LA, Tariq A, Aslam M, et al. Exergy assessment of infrared assisted air impingement dryer using response surface methodology, Back Propagation-Artificial Neural Network, and multi-objective genetic algorithm. Case Stud Therm Eng. 2024;53:103936. doi:10.1016/j.csite.2023.103936. [Google Scholar] [CrossRef]

23. Halima D, Djelloul B, Mehdi G, Camel T, Ali B, Bouchra B. Solar radiation estimation based on a new combined approach of artificial neural networks (ANN) and genetic algorithms (GA) in South Algeria. Comput Mater Contin. 2024;79(3):4725–40. doi:10.32604/cmc.2024.051002. [Google Scholar] [CrossRef]

24. Ennissioui J, El Rhafiki T. Experimental study of a natural convection indirect solar dryer. Heliyon. 2023;9(11):e21299. doi:10.1016/j.heliyon.2023.e21299. [Google Scholar] [PubMed] [CrossRef]

25. [cited 2021 Aug 30]. Available from: https://www.meteoblue.com/en/weather/week/bhopal_india_1275841. [Google Scholar]

26. Kiburi FG, Ronoh EK, Kanali CL, Kituu GM, Ajwang PO. Exergetic optimisation of a solar-biomass hybrid greenhouse dryer in drying banana slices. Int J Exergy. 2023;41(1):41–59. doi:10.1504/IJEX.2023.130940. [Google Scholar] [CrossRef]

27. Paramasivam P, Dzida M, Osman SM, Le DTN, Cao DN, Truong TH, et al. Development of advanced machine learning for prognostic analysis of drying parameters for banana slices using indirect solar dryer. Case Stud Therm Eng. 2024;60:104743. doi:10.1016/j.csite.2024.104743. [Google Scholar] [CrossRef]

28. Bhardwaj AK, Kumar R, Kumar S, Goel B, Chauhan R. Energy and exergy analyses of drying medicinal herb in a novel forced convection solar dryer integrated with SHSM and PCM. Sustain Energy Technol Assess. 2021;45(4):101119. doi:10.1016/j.seta.2021.101119. [Google Scholar] [CrossRef]

29. Daliran A, Taki M, Marzban A, Rahnama M, Farhadi R. Experimental evaluation and modeling the mass and temperature of dried mint in greenhouse solar dryer; Application of machine learning method. Case Stud Therm Eng. 2023;47(4):103048. doi:10.1016/j.csite.2023.103048. [Google Scholar] [CrossRef]

30. Tlatelpa Becerro A, Rico Martínez R, López-Vidaña EC, Montiel Palacios E, Torres Segundo C, Gadea Pacheco JL. Dynamic behavior forecast of an experimental indirect solar dryer using an artificial neural network. AgriEngineering. 2023;5(4):2423–38. doi:10.3390/agriengineering5040149. [Google Scholar] [CrossRef]

31. Moheno-Barrueta M, Tzuc OM, Martínez-Pereyra G, Cardoso-Fernández V, Rojas-Blanco L, Ramírez-Morales E, et al. Experimental evaluation and theoretical optimization of an indirect solar dryer with forced ventilation under tropical climate by an inverse artificial neural network. Appl Sci. 2021;11(16):7616. doi:10.3390/app11167616. [Google Scholar] [CrossRef]