 Open Access
Open Access
ARTICLE
Reliable Task Offloading for 6G-Based IoT Applications
1 Department of Computer Software Engineering, National University of Science and Technology (NUST), Islamabad, 44000, Pakistan
2 Department of Electrical and Computer Engineering, COMSATS University Islamabad, Islamabad, 45550, Pakistan
3 Information Systems Department, College of Computer and Information Sciences, Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh, 11432, Saudi Arabia
* Corresponding Author: Mohammed Alkhathami. Email:
(This article belongs to the Special Issue: Distributed Computing with Applications to IoT and BlockChain)
Computers, Materials & Continua 2025, 82(2), 2255-2274. https://doi.org/10.32604/cmc.2025.061254
Received 20 November 2024; Accepted 31 December 2024; Issue published 17 February 2025
Abstract
Fog computing is a key enabling technology of 6G systems as it provides quick and reliable computing, and data storage services which are required for several 6G applications. Artificial Intelligence (AI) algorithms will be an integral part of 6G systems and efficient task offloading techniques using fog computing will improve their performance and reliability. In this paper, the focus is on the scenario of Partial Offloading of a Task to Multiple Helpers (POMH) in which larger tasks are divided into smaller subtasks and processed in parallel, hence expediting task completion. However, using POMH presents challenges such as breaking tasks into subtasks and scaling these subtasks based on many interdependent factors to ensure that all subtasks of a task finish simultaneously, preventing resource wastage. Additionally, applying matching theory to POMH scenarios results in dynamic preference profiles of helping devices due to changing subtask sizes, resulting in a difficult-to-solve, externalities problem. This paper introduces a novel many-to-one matching-based algorithm, designed to address the externalities problem and optimize resource allocation within POMH scenarios. Additionally, we propose a new time-efficient preference profiling technique that further enhances time optimization in POMH scenarios. The performance of the proposed technique is thoroughly evaluated in comparison to alternate baseline schemes, revealing many advantages of the proposed approach. The simulation findings indisputably show that the proposed matching-based offloading technique outperforms existing methodologies in the literature, yielding a remarkable 52 reduction in task latency, particularly under high workloads.Keywords
The Internet of Things (IoT) is a profound and transformative phenomenon that seamlessly connects physical devices with the digital world. It assigns everyday devices with remarkable capabilities, leading to enhanced convenience, efficiency, and resource management across different industries [1]. The imapct of IoT is evident in automated smart homes and wearable health devices that have become common in our lives. Advancements in technologies like 6G, edge computing, and artificial intelligence (AI) drive IoT’s progress, enabling transformative applications in healthcare, environmental conservation, and autonomous vehicles. As IoT continues to evolve, its diverse implications on human life will thrive, shaping a future marked by profound interconnectedness and unprecedented intelligence [2].
The IoT ecosystem benefits from cloud computing, efficiently providing processing, storage, and other services. This is particularly advantageous in speeding up AI algorithms by processing their operations quickly, resulting in quicker application-related decision-making. Thus, reliability and trust in AI algorithms can be enhanced by using cloud-assisted computing solutions. However, cloud computing might not always meet the stringent real-time demands of IoT applications. To address this, fog computing has surfaced as a strategic solution, extending cloud services to the network edge and leveraging local resources near IoT devices for faster data processing [3]. Fog devices play a crucial role in reducing data transfer time and volume, enabling quicker response times and lower latency for critical applications [4]. Rather than replacing cloud computing, fog computing complements it by focusing on the “device” side, bridging the gap between cloud and edge devices. It significantly enriches IoT scenarios by providing critical resources, including computation, storage, and networking capabilities in proximity [5].
In the fog computing environment, effective task offloading from IoT devices to fog devices remains a significant challenge. Qualitative parameters like cost, computation time, energy consumption, and adherence to task deadlines must be carefully considered to optimise task assignment. As the IoT ecosystem expands, fog computing’s strategic role contributes to seamless connectivity and intelligent data processing, enhancing transformative applications in various domains.
Partial Offloading to Multiple Helpers (POMH) is an effective way to optimally utilize the computing resources of available devices [6]. POMH enables collaboration among different computing devices, allowing them to pool their resources and compute tasks collectively that might exceed their capacities. By subdividing a task into subtasks and offloading them to multiple fog nodes simultaneously, POMH achieves parallel task computation and efficiently optimizes task latency for faster completion [7]. However, implementing POMH involves critical decisions related to task splitting and offloading, requiring coordination among multiple stakeholders.
Matching theory is highly regarded for its simplicity and low computation complexity [8,9] and finds extensive application in fog computing for many resource allocation problems [10]. When matching theory is applied for resource allocation in the POMH scenario, it faces a notorious externalities matching problem. This problem arises due to the dynamic and fluctuating subtask sizes of a task, leading to continuous changes in preference profiles of the assisting fog devices. In such scenarios, assisting fog devices constantly adjust their preferences for the tasks, forming and breaking matching pairs in an ongoing loop [11]. Consequently, the intricacies involved have led to relatively limited research in this domain, highlighting the need for further exploration to address the complex externalities problem effectively.
In previous work [12], the externalities matching problem for resource allocation in the POMH scenario is solved using the novel Stable Matching Update Algorithm (SMUA). However, the findings show that devising preference profiling techniques for assisting fog devices with continuously changing preferences is a highly complex task to achieve the desired objective function. To optimize resource allocation further, we propose the “Time Improvement Scheme,” which is more time-efficient than the technique in [12], though it involves a trade-off with fairness.
The summarized contributions of this paper are:
1. The resource allocation problem is formulated as a many-to-one matching to achieve time efficiency by enabling multiple devices to compute a task simultaneously.
2. A novel many-to-one Stable Matching Update Algorithm with a new profiling technique to enhance time efficiency in the POMH scenario is proposed. Furthermore, the proposed technique also efficiently resolves the externalities problem in POMH-based task offloading scenarios.
The subsequent sections of this paper are organized as follows. Section 2 delves into prior research concerning POMH. In Section 3, we present the system model and formulate the problem at hand. The proposed solution, centered around the matching technique, is elucidated in Section 4. An evaluation of the technique’s performance is conducted in Section 5. Finally, Section 6 concludes the paper by summarizing the results obtained.
This section discusses two categories of related works on POMH-based task offloading scenarios: non-matching-based and matching-based approaches. The summary of the previous research work is shown in Table 1.
2.1 Non-Matching Based Approaches
Chen et al. [13] used a heuristic technique to process a task simultaneously at the device, edge, and cloud server, achieving significant reductions in time and energy consumption for Mobile Edge Computing (MEC) systems. Chen et al. [14] investigated a collaborative mobile computing system, dividing tasks into subtasks and processing them simultaneously on distributed mobile devices. They used a graph theory-based heuristic to optimize time and energy efficiency. Deb et al. [15] studied fog computing with task offloading to multiple neighboring fog nodes for simultaneous computation of tasks. They employed directed acyclic task graphs to achieve efficient offloading, leading to reduced task completion time and energy consumption.
Liu et al. [16] considered a fog computing network comprising Helper Nodes (HNs) and Task Nodes (TNs) to achieve time efficiency. They gathered global information through task advertisements from TNs and proposals from HNs. By formulating the task splitting as a Generalized Nash Equilibrium Problem (GNEP), they balanced task ratios to achieve similar finish times. Bozorgchenani et al. [17] proposed POMH policies for fog computing, optimizing energy or time efficiency through task offloading to fog nodes or access points with high residual power, using a heuristic technique.
Feng et al. [18] performed partial task offloading in a Cellular Vehicle-to-Everything system. They distributed tasks to both Road Side Units (RSUs) and neighboring vehicles based on successful transmission probabilities, achieving time efficiency through a heuristic approach. Lakew et al. [19] explored aerial access IoT networks with multiple unmanned aerial vehicles (UAVs) to achieve energy efficiency by computing tasks simultaneously. They utilized a learning technique based on Markov decision processes (MDP) for task optimization. Baek et al. [20] studied the online partial offloading and task scheduling problem for achieving energy efficiency. They controlled both transmission and CPU energy consumption by employing an online Deep Recurrent Reinforcement Learning (DRRL) approach.
Thai et al. [21] studied Collaborative Cloud-Edge Computing with a three-layered architecture. Tasks can be offloaded to multiple helping devices within the same layer and higher layers. The authors utilized a branch-and-bound algorithm based on graph theory to iteratively solve sub-problems and achieve the optimal solution. Tran-Dang et al. [22] did POMH-based task offloading in a fog-cloud system, using both horizontal and vertical task offloading to neighboring fog devices and the cloud. They introduced an adaptive task offloading mechanism with a heuristic algorithm to balance task ratios and reduce computation time.
Zu et al. [23] investigated POMH-based task offloading in a fog computing system involving HNs and TNs. They utilized a many-to-one matching technique to minimize energy consumption. However, they did not consider externalities arising from changes in preference profiles due to varying subtask sizes. The resizing of subtasks was performed based on the assigned matches after the process.
Tran-Dang et al. [24] investigated POMH-based task offloading in a fog computing system, aiming for time efficiency. They used a many-to-one matching technique and considered interference at the HNs as a source of externalities. The authors formulated a TN preference list based on the time efficiency provided collectively by a group of HNs, rather than considering individual HNs. The authors employed swap matching between TNs and groups of HNs to avoid explicitly addressing the externalities problem during the matching process.
In [12], the focus is on POMH-based task offloading utilizing a many-to-one matching technique to minimize task latency. This study specifically tackles the externalities problem that arises from changes in task sizes during the matching process. A matching update algorithm is proposed to effectively handle externalities and generate a stable matching assignment. This paper builds on [12] and introduces a new preference profiling technique, demonstrating higher time efficiency.
3 System Model & Problem Formulation
This paper considers a fog computing network with a centralized architecture, where the Fog Node Controller (FNC) makes all resource allocation decisions as shown in Fig. 1. The notations used in the paper are shown in Table 2.

Figure 1: System model

Fog nodes in the network can be categorized into three categories; Task Nodes (TNs), which require additional computation resources to efficiently complete their tasks; Helper Nodes (HNs), capable of performing a part of the TN tasks concurrently with their tasks; and Busy Nodes (BNs), occupied with their computations.
The set of HNs, denoted as H, consists of
The subtask size is expressed as a percentage
When a task
A task
3.1.1 Time for Local Computation of Task
If the computation resources (CPU cycles) of
3.1.2 Time for Computing Offloaded Subtasks
To compute a subtask at HN
Here,
This paper uses fog nodes with a single antenna, limiting its transmission capability to only one other fog node at a time. This arrangement does not pose any problem for the HNs since they only have to receive a single subtask. On the contrary, each TN needs to transmit up to
In this paper, HNs perform concurrent computation of received TN subtasks alongside their tasks, which eliminates the wait time for a subtask at HN. As a result, HNs can immediately start processing the subtask upon receiving it. If
The output size is considered to be negligible in this paper, and as a result, we neglect result download latency [25].
From Eqs. (3), (6), and (7), the time used in computing
Task
Eq. (9) emphasizes the need to complete all subtasks simultaneously; otherwise, the valuable computation resources of HNs that finish their subtasks early would be wasted. The ideal required scenario is:
By balancing task offloading percentages
This paper focuses on the scenario where HNs have limited spare computation resources and aim to assist neighboring TNs in computing their tasks in a time-efficient manner. To enhance network-level time efficiency, we propose a POMH strategy, where multiple HNs collaborate to complete a TN task faster. The optimization problem is formulated as follows:
Problem (P1):
Constraint (12a) ensures that all TN tasks are completed within their specified deadline time
The problem presented in this paper belongs to the class of combinatorial optimization problems, which are notoriously known to be NP-hard [26]. As the number of TNs and HNs grows, finding an optimal solution becomes increasingly difficult. Additionally, each device’s goal to maximize its benefit may lead to an unstable outcome, making it challenging to achieve a stable matching assignment.
Matching theory is a mathematical optimization technique known for its low computation complexity and ease of use. It efficiently matches resources with users while considering their preferences and constraints [27]. Categorizing devices into resource-demanding and resource-lending sets forms mutually beneficial associations, leading to optimized resource-user pairings based on individual objectives.
In the POMH scenario, subtask sizes are continuously adjusted to ensure the same completion time for all subtasks of the task
To address this problem, we propose a two-step approach. In the first step, we use the standard Deferred Acceptance Algorithm (DAA) [28] to obtain a stable matching assignment without considering subtask changes, thereby avoiding externalities. For the second step, we propose the Stable Matching Update Algorithm (SMUA) [12] which is based on the work of Ma [29]. SMUA allows HNs to reconsider their matches of the first step based on the actual size of the subtask they will perform. The underlying assumption in SMUA is that only a few players are likely to change their partners during the updating of the stable matching assignment. This approach significantly reduces the search space, allowing for a quick and efficient discovery of a stable matching decision. SMUA effectively resolves the externalities problem, leading to more efficient resource allocation.
4.1.1 Definition 1 (Matching Assignment)
The matching assignment is a two-sided problem where players from sets
Condition (13a) indicates that each HN is allowed to have a maximum of one match with tasks in the task set
4.1.2 Definition 2 (Preference Profile and Preference List)
“The preference relations
A preference profile indicates how each player in one set prefers the players in the other set based on a utility function, which quantifies how well a player’s objective is met. Players create preference lists by ranking others according to utility values. Players can have fixed or dynamic preference lists. Fixed lists lead to stable outcomes, while dynamic lists adapt to changing factors, introducing uncertainty. Dynamic preference lists create externalities, requiring special arrangements for stable matching.
Preference of Tasks: TNs use fixed priority lists with the transmission rate
Preference of HNs: In this paper, two HN preference profiling techniques are used for the two resource allocation steps. In the first step, HNs use task computation time
In the second step, the matching assignment is updated to address externalities, and HNs adjust their matches based on the actual subtask sizes.
In this paper, we propose the “Time Improvement” profiling technique for time-efficient task allocation. Previously, we developed the “Percentage Improvement in Time” profiling technique [12], which was time-efficient and fair. However, the new “Time Improvement” profiling technique may involve a trade-off with fairness compared to the previous approach. The “Time Improvement” profiling technique calculates the time saved by an HN when assisting a task, compared to not helping at all. It uses the difference in time between both scenarios to prioritize tasks that benefit most from HN assistance, optimizing time efficiency in the POMH scenario.
where,
4.1.3 Definition 3 (Quota of Players)
Quota refers to the maximum number of matches allowed for a player with players from the opposite set [31]. In this paper, HNs can have a maximum of one match with a TN task, while a TN task can have a maximum of
4.1.4 Definition 4 (Block Pair)
A pair (a, b) is considered a block pair for a matching assignment
This implies that the pair (a, b) is a block pair when player a is not matched with player b in
4.1.5 Definition 5 (Stable Matching Assignment)
A matching assignment
In matching assignments, the aim is stability rather than optimality, ensuring that no agents have an incentive to change their current matched partners. Stability requires the absence of blocking pairs in the matched pairs.
4.2 Two-Step Resource Allocation Scheme for Externalities
To efficiently address externalities, this paper employs a two-step approach. First, a stable matching assignment is determined based on players’ initial preferences, maintaining their preference order throughout the matching process. Next, the assignment is updated in the second step to handle potential block pairs using the SMUA method, as described below.
4.2.1 Step 1 (Stable Matching Assignments without Considering Changes in Subtask Sizes)
In this paper, all algorithms run at the FNC. The utility function for TN tasks is based on the transmission rate. The FNC uses known distances between fog nodes in the static network and periodically updated Channel State Information (CSI) sent by all fog devices to calculate transmission rates. Using these transmission rates, the FNC determines the preference list of all TN tasks. This preference list remains the same for both steps of resource allocation.
On the other hand, the FNC prepares the preference list for HNs based on the method described for HN preference profiling in the first step. The FNC then uses the DAA [28] to find an initial stable matching assignment without considering the changes in subtask sizes.
SMUA effectively resolves externalities in matching by updating the initial stable assignment from step 1. This update process resolves any blocking pairs that arise due to the current matches of the TN tasks. This approach ensures a more optimal and stable matching outcome in a shorter timeframe, making it an efficient solution to the externalities problem. The update process is outlined below:
SMUA employs a “stability update room” as shown in Fig. 2 to update matches of a TN task one by one. A TN task is randomly selected, and its current matches enter the room, while the rest of the HNs queue outside the room, following the sequence

Figure 2: SMUA employing stability update room
HNs in the queue enter the room one by one. The preference of each incoming HN with the selected TN task is evaluated to determine if it can be accepted, considering the preference of the TN task’s current matches and quota limitations. If the incoming HN is ineligible for acceptance, it promptly exits the room. However, if it meets the criteria for acceptance, it undergoes further evaluation and processing.
If the incoming HN has no match, it will immediately decide to pair with the selected TN task. However, if the HN already has a match, it will calculate its utility function for both its current match and the potential match with the selected TN task to determine the priority order for the two matches. If the existing match has higher priority, the HN keeps its original match and exits the room. Otherwise, it switches its match to the TN task and stays inside the room.
When a TN task receives a new HN match, it evaluates its total number of matches in comparison to its quota
The process is iteratively repeated until all blocking pairs are resolved and the initial pairing at the start of the iteration remains unchanged throughout the loop.
The proposed SUA is an update mechanism to resolve block pairs in an existing stable matching assignment. As a result, it always gives stable matching assignments.
DAA used to find the initial stable matching assignment has a time complexity of

The performance of the proposed profiling technique is evaluated through simulation scenarios in MATLAB. These scenarios include different workload conditions to assess how well the technique performs and adapts in various situations. The results are then compared against other established baseline schemes to assess the degree of improvement achieved. The key parameters used in the simulations are summarized in Table 3.
We consider a network with
The fog nodes are evenly distributed within an area of 60 m × 60 m. This distribution ensures that each TN has 8 to 10 neighboring HNs within an efficient communication range of 30 meters. These nearby HNs are readily available to assist the TNs with their tasks whenever needed. All fog nodes are connected wirelessly, with each node equipped with a single antenna. They have a dedicated active uplink channel of 5 MB and a transmission power of 100 mW. However, due to the limitation of a single antenna, subtasks have to wait for their turn to be transmitted to their respective HNs, which introduces a sequence time constraint in the task offloading process, impacting the overall task offloading latency. The noise power is set as
For easy referencing, we will name the results of our proposed profiling technique as SMUA-T. We compare the proposed approach with the following baseline schemes:
1. Our work at [12] (SMUA),
2. Tran et al. [24] (DISCO),
3. Zu et al. [23] (SMETO).
The baseline schemes are closely related to the proposed SMUA-T technique. SMUA-T introduces a new, more time-efficient profiling technique compared to our previous work in SMUA [12]. All baseline schemes employ the many-to-one matching technique to map HN resources to TN tasks. While both SMUA-T and SMUA consider externalities arising from changes in subtask size, DISCO focuses on interferences at HNs as the source of externalities. SMUA-T and SMUA address these externalities, whereas DISCO utilizes a swap-matching algorithm to avoid considering externalities during the matching process. On the other hand, SMETO completely ignores their existence. Notably, SMUA-T, SMUA, and DISCO aim to optimize time, while SMETO prioritizes energy efficiency in the task-offloading process.
We evaluate the performance of all schemes based on three parameters: delay reduction ratio (
5.1 Results with SMUA-T and SMUA
The delay reduction ratio experienced by all baseline schemes with TN task quota

Figure 3: Delay reduction ratio, q = 3
Our other preference profiling technique, SMUA, is both time-efficient and fair, prioritizing fairness over time efficiency. Despite having a lower delay reduction ratio compared to SMUA-T, it still achieves a significant delay reduction compared to all other baseline schemes. DISCO prioritizes time efficiency, leading to a higher delay reduction ratio compared to SMRETO, which focuses on energy efficiency. The results demonstrate how each scheme’s specific objective impacts its performance, with DISCO excelling in delay reduction ratios over SMRETO delays.
The results in Fig. 4 show the average task latency achieved by all baseline schemes, indicating their time efficiency. This metric serves as an extension of the delay reduction ratio and offers further insights into the performance of each scheme concerning task completion time. SMUA-T stands out as the most time-efficient scheme, delivering the lowest average task latency across all workload scenarios, while SMUA, employing different preference profiling but a similar resource allocation method, also demonstrates commendable performance in reducing task latency, albeit with slightly higher average task latency values compared to SMUA-T. On the other hand, DISCO, designed primarily for time efficiency, performs well in reducing task latency but exhibits higher average task latency values than SMUA and SMUA-T. SMRETO, which is aimed at achieving energy efficiency, has the poorest average task latency among all the schemes evaluated.
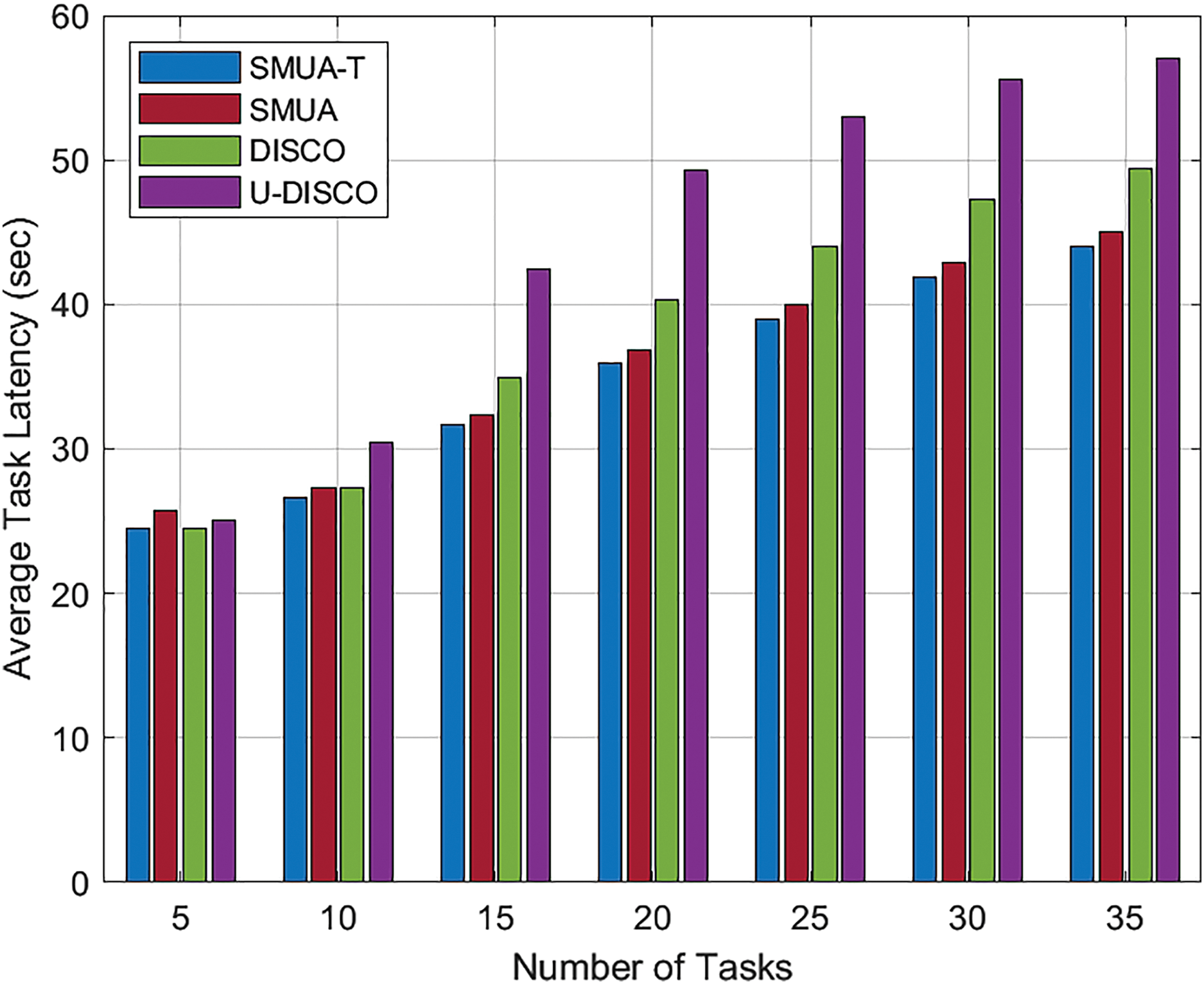
Figure 4: Average task latency, q = 3
Fig. 5 illustrates the number of TN tasks that couldn’t find any matches from the available HNs. This evaluation criterion provides valuable insights into the fairness of the schemes used based on the ability to serve the maximum number of TN tasks. In an ideal fair scheme, one would expect 30 HNs to be able to serve 30 TN tasks, making this observation particularly interesting.
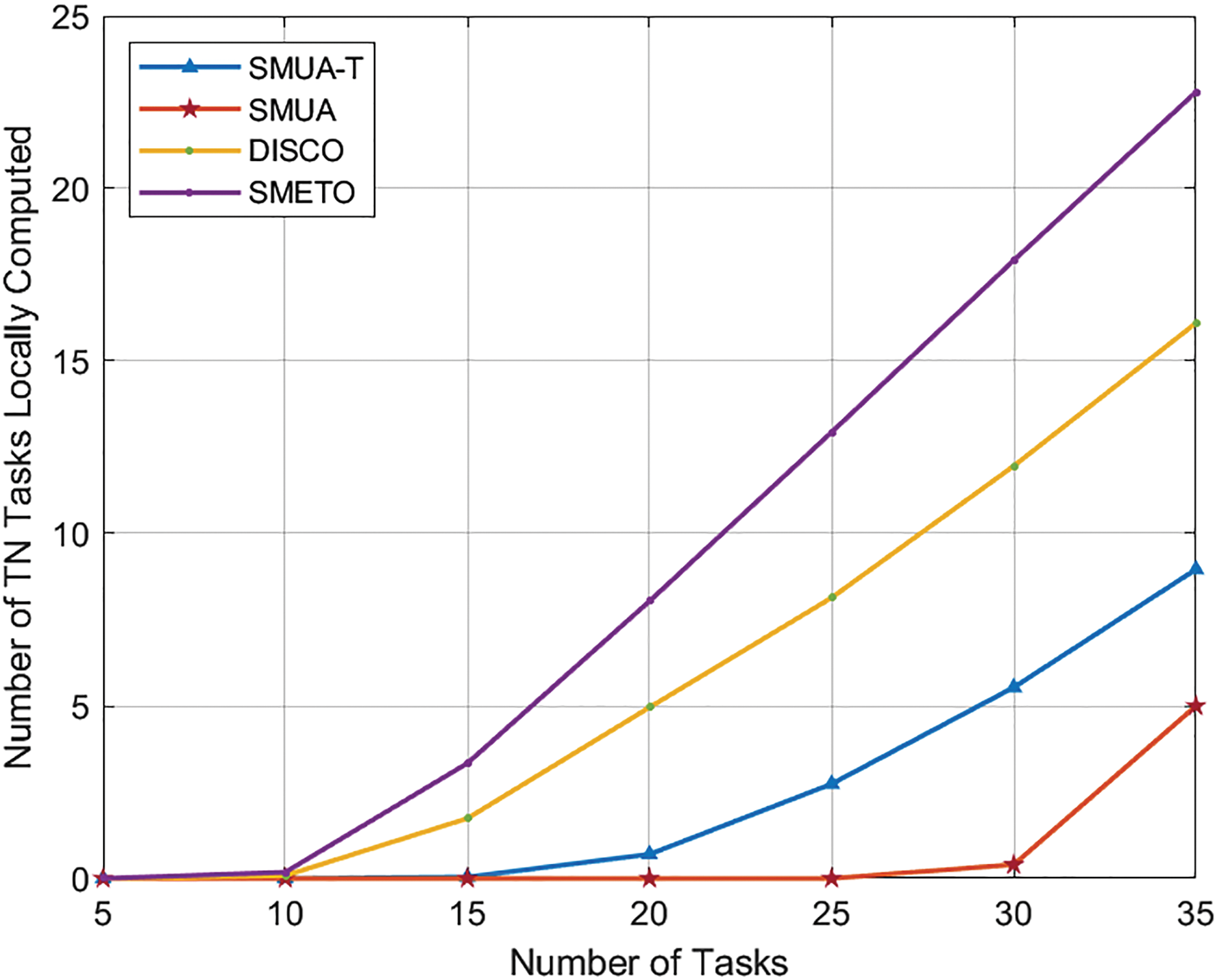
Figure 5: TN tasks not served. q = 3
These results demonstrate that our preference profiling techniques, SMUA and SMUA-T, are the fairest among all baseline schemes. However, SMUA-T sacrifices some fairness to achieve better time efficiency, as can be seen in Fig. 3. These results support our claim that our preference profiling techniques effectively achieve their set objectives while also avoiding convergence towards TN tasks with more matches in a greedy pursuit of their objectives. The results reveal that DISCO and SMETO leave many TN tasks unserved. However, it’s important to note that their preference profiling was not designed with fairness in their resource allocation. Instead, these schemes prioritize other optimization criteria that could be advantageous in specific scenarios.
5.2 Results with SMUA-T Step1 and SMUA Step1
The initial matching assignments in step 1 lack stability, as they overlook the real preference profiles of HNs, especially about the sizes of the subtasks they will compute. However, comparing these initial unstable outcomes with other baseline schemes can provide valuable insights into the preference profiling techniques of “Time Improvement” and “Percentage Time Improvement.”
In Fig. 6, looking at the delay reduction ratio, we can see that DISCO performs the best under very low workloads, followed closely by SMETO. However, SMUA-T Step1 and SMUA Step1 show the lowest performance levels. Interestingly, as the workload increases, SMUA-T Step1 takes the lead as the most effective scheme. Notably, DISCO, designed for time efficiency, remains efficient, closely trailing behind SMUA-T Step1. SMUA Step 1, which aims for both time efficiency and fairness, follows suit in performance. In contrast, SMETO prioritizes energy efficiency and displays the lowest time efficiency among the schemes.
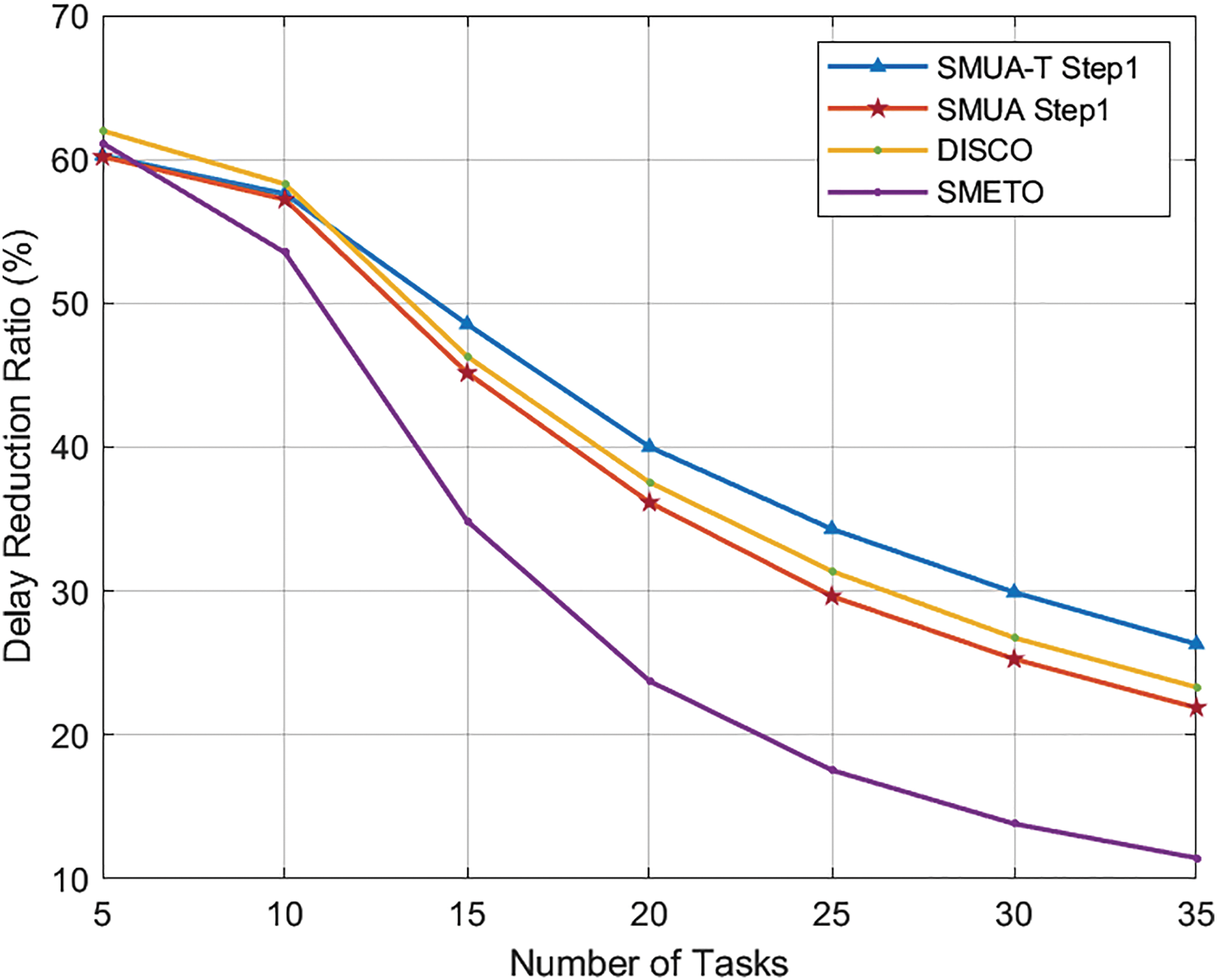
Figure 6: Delay reduction ratio, q = 3
Transitioning to the average task latency results in Fig. 7, we witness a continuation of the consistent trend observed in the delay reduction ratio outcomes from Fig. 6. DISCO stands out in very low workload scenarios, while SMUA-T Step1 takes the lead as the workload intensifies. Notably, the innovative “Time Improvement” profiling technique proposed in this paper consistently demonstrates impressive time efficiency, even when externalities are not resolved. Importantly, the results become even more pronounced and time-efficient when externalities are addressed, as illustrated in Figs. 3 and 4. This emphasizes the robustness of the “Time Improvement” profiling technique in elevating time-related performance metrics across diverse operational scenarios.
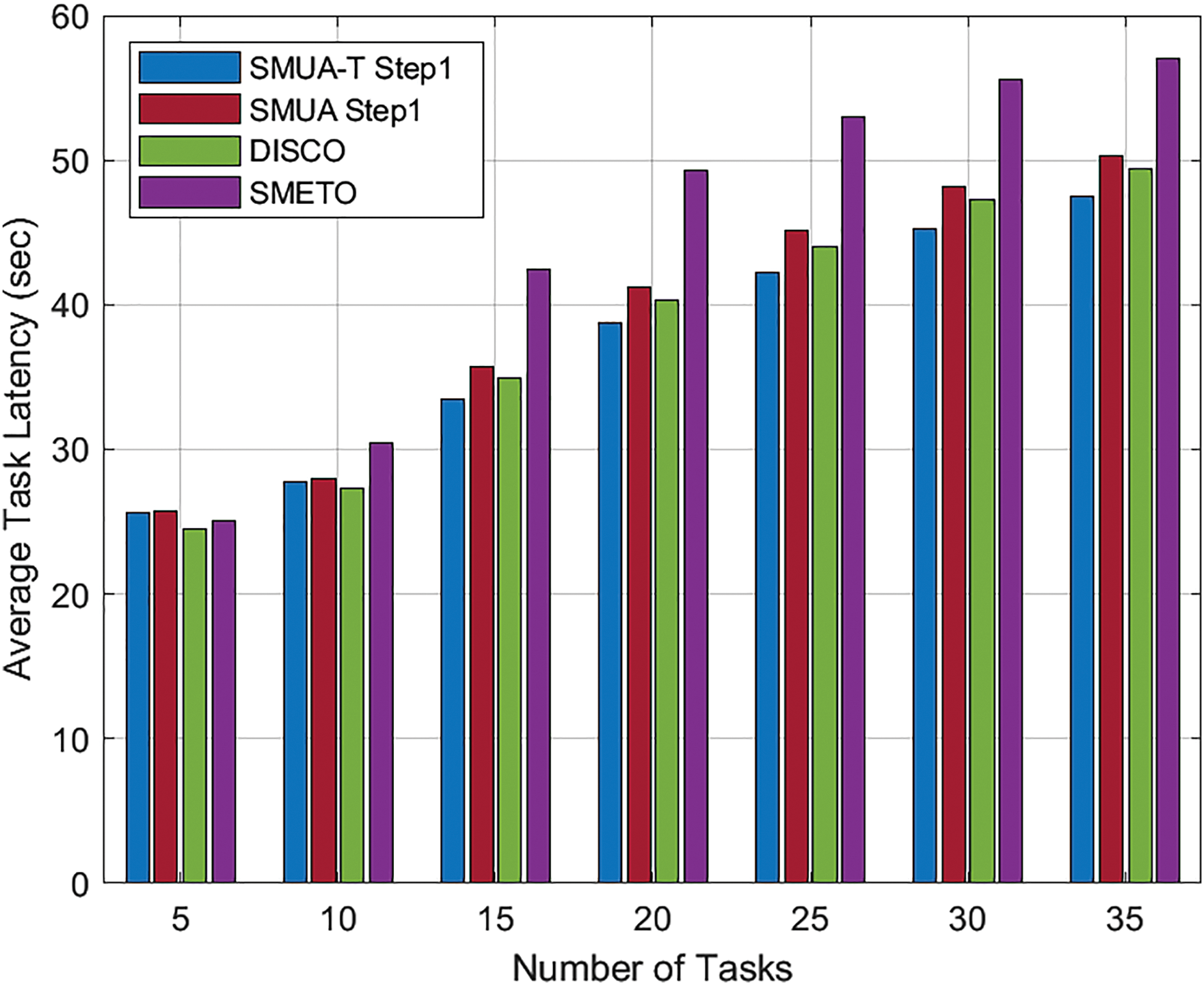
Figure 7: Average task latency, q = 3
Analyzing the count of TN tasks unable to find suitable matches from the pool of available HNs, as depicted in Fig. 8, reveals an intriguing facet of the comparison. It’s noteworthy that DISCO, despite leaving a considerable number of TN tasks unserved, still emerges as the fairest among the schemes. Surprisingly, the results unveil that SMETO, SMUA-T Step1, and SMUA Step1 all yield an identical level of fairness in this context. This observation emphasizes a crucial point: the “Time Improvement” and “Percentage Time Improvement” profiling techniques attain fairness only after resolving the externalities. In the absence of resolving these externalities, the effectiveness of these proposed profiling techniques in achieving fairness is limited.
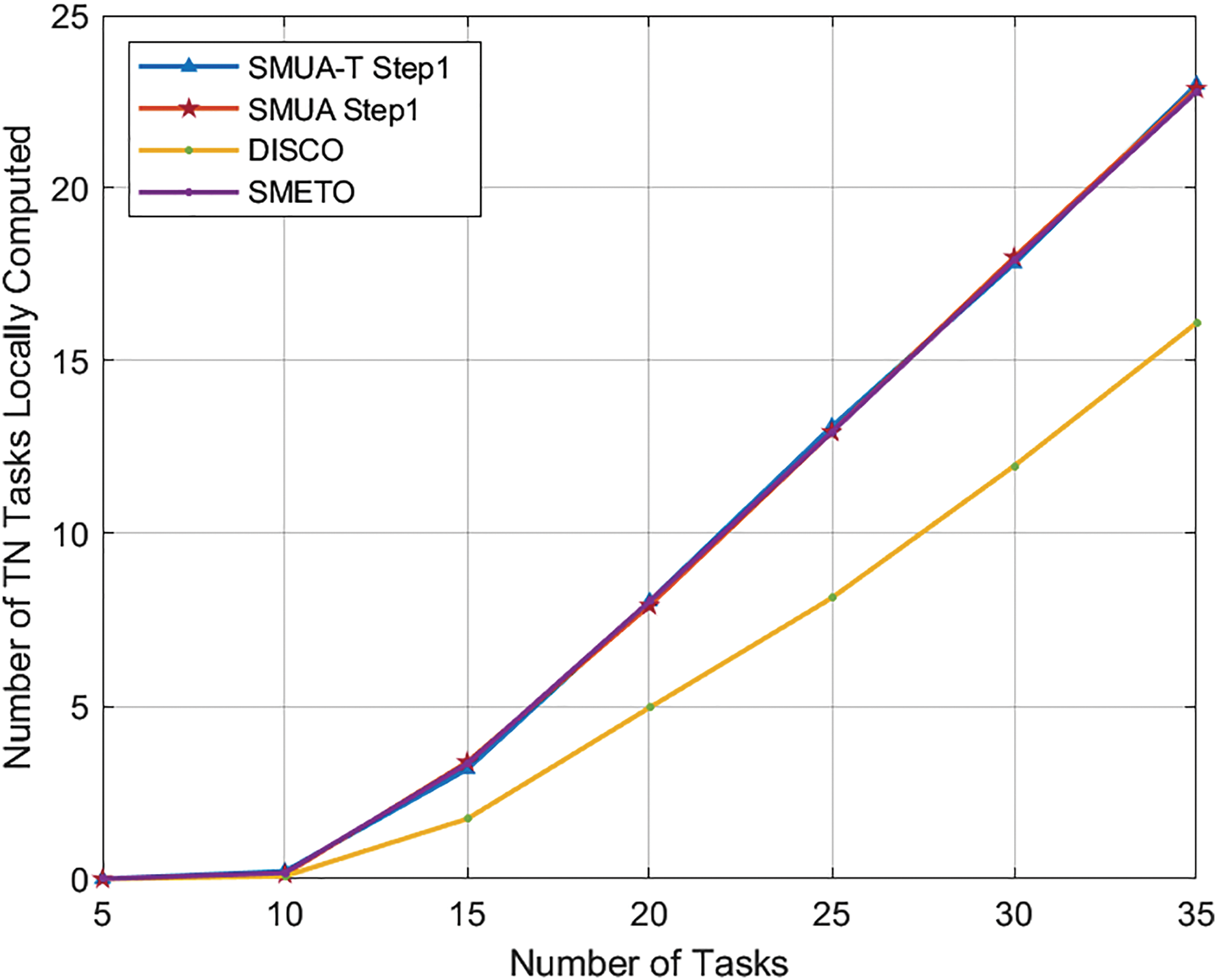
Figure 8: TN tasks not served. q = 3
The work in this paper proposes a task computation technique for 6G networks is proposed. The idea is to use parallel task offloading with many-to-one matching for allocating resources of fog computing nodes. The novel aspect of the developed technique is a new preference profiling technique that improves the time efficiency of the task computation which is necessary for 6G applications. Analysis of the proposed technique based on simulations shows improved task delay at different network densities. Moreover, this work also highlights the importance of using externalities-based solutions when using matching-based allocation of computing resources in the POMH-based task offloading scenario. Developing new and improved preference profiling techniques to consider multiple objectives in light of externalities remains an essential and interesting challenge for future work. Such advancements can lead to fairer and more efficient resource allocation outcomes in dynamic environments. In the future, we will further explore the performance of the proposed technique as the network size is increased. Moreover, we will also consider different type IoT workloads and develop machine learning techniques for dynamic task offloading.
Acknowledgement: This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-RP23082).
Funding Statement: This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-RP23082).
Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Usman Mahmood Malik, Muhammad Awais Javed, Ahmad Naseem Alvi and Mohammed Alkhathami; writing—original draft preparation, Usman Mahmood Malik and Muhammad Awais Javed; writing—review and editing, Ahmad Naseem Alvi and Mohammed Alkhathami. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: All related data is available in the manuscript.
Ethics Approval: Not applicable.
Conflicts of interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Javed MA, Nguyen TN, Mirza J, Ahmed J, Ali B. Reliable communications for cybertwin driven 6G IoVs using intelligent reflecting surfaces. IEEE Trans Indust Inf. 2022;18(11):7454–62. doi:10.1109/TII.2022.3151773. [Google Scholar] [CrossRef]
2. Malik UM, Javed MA, Zeadally S, Su I. Energy efficient fog computing for 6G enabled massive IoT: recent trends and future opportunities. IEEE Internet Things J. 2021;9(16):14572–94. doi:10.1109/JIOT.2021.3068056. [Google Scholar] [CrossRef]
3. Amshavalli RS, Kalaivani J. A comprehensive survey on role of fog computing and need for semantic technology in modern computing platform. In: 2023 7th International Conference on Intelligent Computing and Control Systems (ICICCS); 2023; Tamil Nadu, India. p. 719–25. [Google Scholar]
4. Kar B, Yahya W, Lin YD, Ali A. Offloading using traditional optimization and machine learning in federated cloud-edge–fog systems: a survey. IEEE Commun Surv Tutor. 2023;25(2):1199–226. doi:10.1109/COMST.2023.3239579. [Google Scholar] [CrossRef]
5. Hosseinzadeh M, Azhir E, Lansky J, Mildeova S, Ahmed OH, Malik MH, et al. Task scheduling mechanisms for fog computing: a systematic survey. IEEE Access. 2023;11:50994–1017. doi:10.1109/ACCESS.2023.3277826. [Google Scholar] [CrossRef]
6. Zhang G, Shen F, Liu Z, Yang Y, Wang K, Zhou M. FEMTO: fair and energy-minimized task offloading for fog-enabled IoT networks. IEEE Internet Things J. 2019;6(3):4388–400. doi:10.1109/JIOT.2018.2887229. [Google Scholar] [CrossRef]
7. Liang Z, Liu Y, Lok TM, Huang K. Multiuser computation offloading and downloading for edge computing with virtualization. IEEE Trans Wireless Commun. 2019;18(9):4298–311. doi:10.1109/TWC.2019.2922613. [Google Scholar] [CrossRef]
8. Jiang W, Han H, Zhang Y, He M, Gu W. Matching games in satellite-terrestrial integrated networks: who to match and how to match?. In: Proceedings of the 2023 9th International Conference on Communication and Information Processing, ICCIP ’23; New York, NY, USA: Association for Computing Machinery; 2024. p. 284–8. doi:10.1145/3638884.3638927. [Google Scholar] [CrossRef]
9. Raveendran N, Zhang H, Song L, Wang LC, Hong CS, Han Z. Pricing and resource allocation optimization for IoT fog computing and NFV: an EPEC and matching based perspective. IEEE Trans Mob Comput. 2022;21:1349–61. [Google Scholar]
10. Zhang Q, Xiao M, Xu Y. Task offloading in fog: a matching-driven multi-user multi-armed bandit approach. In: 2022 18th International Conference on Mobility, Sensing and Networking (MSN); Guangzhou, China; 2022. p. 213–7. [Google Scholar]
11. Alimudin A, Ishida Y. Matching-updating mechanism: a solution for the stable marriage problem with dynamic preferences. Entropy. 2022;24:263. doi:10.3390/e24020263. [Google Scholar] [PubMed] [CrossRef]
12. Malik UM, Javed MA, Frnda J, Rozhon J, Khan WU. Efficient matching-based parallel task offloading in IoT networks. Sensors. 2022;22(18):1–22. [Google Scholar]
13. Chen Q, Meng W, Quek TQS, Chen S. Multi-tier hybrid offloading for computation-aware IoT applications in civil aircraft-augmented SAGIN. IEEE J Sel Areas Commun. 2023;41(2):399–417. doi:10.1109/JSAC.2022.3227031. [Google Scholar] [CrossRef]
14. Chen R, Wang X. Maximization of value of service for mobile collaborative computing through situation-aware task offloading. IEEE Trans Mob Comput. 2023;22(2):1049–65. doi:10.1109/TMC.2021.3086687. [Google Scholar] [CrossRef]
15. Deb PK, Misra S, Mukherjee A. Latency-aware horizontal computation offloading for parallel processing in fog-enabled IoT. IEEE Syst J. 2021;16(2):2537–254. doi:10.1109/JSYST.2021.3085566. [Google Scholar] [CrossRef]
16. Liu Z, Yang Y, Wang K, Shao Z, Zhang J. POST: parallel offloading of splittable tasks in heterogeneous fog networks. IEEE Internet Things J. 2020;7(4):3170–83. doi:10.1109/JIOT.2020.2965566. [Google Scholar] [CrossRef]
17. Bozorgchenani A, Tarchi D, Corazza G. An energy and delay-efficient partial offloading technique for fog computing architectures. In: GLOBECOM 2017–2017 IEEE Global Communications Conference; 2017; Singapore. p. 1–6. [Google Scholar]
18. Feng W, Lin S, Zhang N, Wang G, Ai B, Cai L. Joint C-V2X based offloading and resource allocation in multi-tier vehicular edge computing system. IEEE J Sel Areas Commun. 2023;41(2):432–45. doi:10.1109/JSAC.2022.3227081. [Google Scholar] [CrossRef]
19. Lakew DS, Tran AT, Dao NN, Cho S. Intelligent offloading and resource allocation in heterogeneous aerial access IoT networks. IEEE Internet Things J. 2023;10(7):5704–18. doi:10.1109/JIOT.2022.3161571. [Google Scholar] [CrossRef]
20. Baek J, Kaddoum G. Online partial offloading and task scheduling in SDN-Fog networks with deep recurrent reinforcement learning. IEEE Internet Things J. 2022;9(13):11578–89. doi:10.1109/JIOT.2021.3130474. [Google Scholar] [CrossRef]
21. Thai MT, Lin YD, Lai YC, Chien HT. Workload and capacity optimization for cloud-edge computing systems with vertical and horizontal offloading. IEEE Trans Netw Serv Manag. 2020;17(1):227–38. doi:10.1109/TNSM.2019.2937342. [Google Scholar] [CrossRef]
22. Tran-Dang H, Kim D-S. FRATO: fog resource based adaptive task offloading for delay-minimizing IoT service provisioning. IEEE Trans Parallel Distr Syst. 2021;32(10):2491–508. doi:10.1109/TPDS.2021.3067654. [Google Scholar] [CrossRef]
23. Zu Y, Shen F, Yan F, Shen L, Qin F, Yang R. SMETO: stable matching for energy-minimized task offloading in cloud-fog networks. In: 2019 IEEE 90th Vehicular Technology Conference (VTC2019-Fall). Honolulu, HI, USA; 2019. p. 1–5. [Google Scholar]
24. Tran-Dang H, Kim D-S. Distributed computation offloading framework for fog computing networks. J Commun Netw. 2023;25(1):121–31. doi:10.23919/JCN.2022.000058. [Google Scholar] [CrossRef]
25. Lyu X, Tian H, Sengul C, Zhang P. Multiuser joint task offloading and resource optimization in proximate clouds. IEEE Trans Veh Technol. 2017;66(4):3435–47. doi:10.1109/TVT.2016.2593486. [Google Scholar] [CrossRef]
26. Bertsimas D, Tsitsiklis JN. Introduction to linear optimization. MA: Athena Scientific Belmont; 1997. Vol. 6. [Google Scholar]
27. Chiti F, Fantacci R, Picano B. A matching theory framework for tasks offloading in fog computing for IoT systems. IEEE Internet Things J. 2018;5(6):5089–96. doi:10.1109/JIOT.2018.2871251. [Google Scholar] [CrossRef]
28. Roth AE. Deferred acceptance algorithms: history, theory, practice, and open questions. National Bureau Econ Res. 2008;36:13225. [Google Scholar]
29. Ma J. On randomized matching mechanisms. Econ Theory. 1996;8(2):377–81. doi:10.1007/BF01211824. [Google Scholar] [CrossRef]
30. Wu H, Zhang J, Cai Z, Ni Q, Zhou T, Yu J, et al. Resolving multi-task competition for constrained resources in dispersed computing: a bilateral matching game. IEEE Internet Things J. 2021;8(23):16972–83. doi:10.1109/JIOT.2021.3075673. [Google Scholar] [CrossRef]
31. Malik UM, Javed MA. Ambient intelligence assisted fog computing for industrial IoT applications. Comput Commun. 2022;196:117–28. doi:10.1016/j.comcom.2022.09.024. [Google Scholar] [CrossRef]
32. Tran-Dang H, Kim DS. A survey on matching theory for distributed computation offloading in IoT-Fog-cloud systems: perspectives and open issues. IEEE Access. 2022;10:118353–69. doi:10.1109/ACCESS.2022.3219427. [Google Scholar] [CrossRef]
33. Malik UM, Javed MA, Frnda J, Nedoma J. SMRETO: stable matching for reliable and efficient task offloading in fog-enabled IoT networks. IEEE Access. 2022;10:111579–90. doi:10.1109/ACCESS.2022.3215555. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF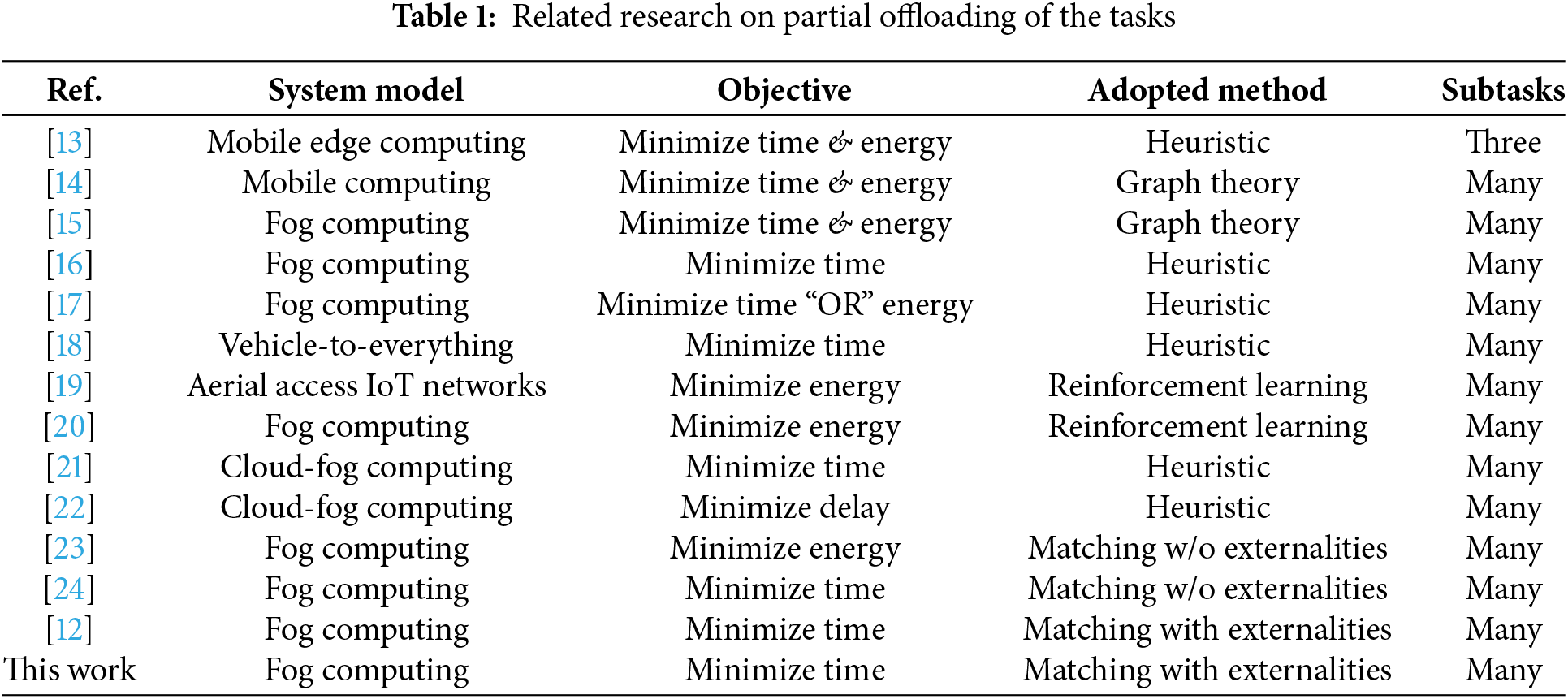
 Downloads
Downloads
 Citation Tools
Citation Tools