Dynamic Task Offloading Scheme for Edge Computing via Meta-Reinforcement Learning

1  Introduction

Cloud computing, as a centralized computing model, provides powerful computing and storage capabilities through remote data centers and is widely adopted [1,2]. Edge computing, as a paradigm of cloud computing, provides distributed computing services at the network’s edge, addressing the growing need for real-time processing and large datasets in various application scenarios [3–6]. Mobile Edge Computing (MEC) deploys server at the network edge to handle intensive computing and data processing tasks, effectively reducing backhaul link load and minimizing service delays [7–9]. However, diverse terminal devices and task types bring challenges to task offloading decision. How to allocate tasks reasonably to achieve efficient utilization of computing resources has become a very urgent challenge.

The early research mainly focused on the static optimization of task offloading decision, and determined the task allocation strategy by offline methods. However, these methods are often unable to adapt to the dynamic network environment and task characteristics. Literature [10] proposes a scheme based on heuristic algorithm to construct offloading strategy, but the proposed scheme relies too much on the expert strategy of MEC system, adapting a specific heuristic algorithm to the dynamic MEC landscape, influenced by the growing complexity of MEC applications and architecture, can be challenging, and it is impossible to adapt the learning strategy to different network environments. Literature [11] introduced a strategy calculation offloading algorithm utilizing a double-depth Q-network (DKN). This algorithm learns the optimal strategy without prior knowledge of network dynamics, but the scheme could not adapt to the new network environment. Literature [12] introduced an offloading algorithm using deep meta reinforcement learning. This algorithm utilizes multiple parallel deep neural networks (DNN) and Q learning to make precise decisions, swiftly adapting to dynamic environments to obtain the optimal offloading strategy, but this scheme does not consider the analysis of each detailed index in edge calculation. Hence, a multi-objective optimization meta-reinforcement learning algorithm is needed to adapt to diverse network environments and simultaneously optimize time delay and energy consumption.

This paper suggests an adaptive task offloading scheme for edge computing to address dynamic environment task offloading challenges, utilizing the concept of meta-strategy. A novel approach is introduced, leveraging the MRL algorithm by combining it with a seq2seq neural network. This innovative method focuses on learning a meta-offload strategy applicable to all User Equipment (UE), enabling the rapid derivation of efficient strategies for individual UEs through the integration of meta-strategy and local data. To assess the dynamic task offloading meta-reinforcement learning (DTOML)’s performance in dynamic scenarios, diverse situations are considered, involving heterogeneous users with distinct mobile application preferences represented as DAGs varying in height, width, and task numbers. Additionally, the transmission rate is adjusted based on the proximity of UEs to MEC hosts. We explore how to use machine learning and decision optimization algorithms to adaptively adjust the task allocation strategy by learning historical data and monitoring network status in real time. We will design and implement a meta-strategy model, and learn and update the strategy by analyzing the task characteristics and network status, so as to provide the best task processing performance.

In view of these observations, we propose a meta-strategy-based dynamic task offloading scheme for distributed edge computing (DTOML), which establishes an offloading decision through DAG, then establishes different network environment models through multiple MDPs, and then learns and updates the offloading strategy through seq2seq network to adapt to the dynamic network environment and task requirements. Finally, the NSGA-II is employed to optimize task scheduling by jointly addressing delay and energy consumption. Our approach demonstrates reduced latency and energy consumption compared to alternative schemes.

In addition, this scheme has good application value. First, it can be used in the traffic management system. Through edge computing task offloading, traffic flow can be analyzed in real time, congestion can be predicted, and traffic signals can be dynamically adjusted to improve urban traffic efficiency. Secondly, it can be used in the intelligent driving system. Through edge computing task offloading, it can quickly process the perception data of the vehicle’s surrounding environment, support the auto drive system to make decisions, and improve safety and reaction speed.

The main contributions are as follows:

(1)   This paper proposes a dynamic task offloading scheme for edge computing based on MRL. By modeling the task offloading decision as a DAG, different edge computing network environments are modeled by using multiple markov decision processes (MDP), and the “outer loop” training of offloading strategy is carried out by using Proximal Policy Optimization (PPO) strategy gradient method in deep reinforcement learning.

(2)   To further improve the self-adaptability of task offloading scheme, introduces seq2seq network to carry out self-adaptive “inner-loop” training of offloading strategy. By analyzing historical data and real-time network status, the seq2seq network can adaptively learn and update offloading strategies in response to dynamic changes in the network environment and task requirements.

(3)   Aiming at two important indexes, time delay and energy consumption, this paper adopts multi-objective optimization algorithm for joint optimization. By weighing the relationship between the two, a set of balanced offloading strategies is found.

The overall structure is as follows: The Section 2 expounds the related work of this paper; In Section 3, the edge calculation model is put forward and the problems studied are expounded. In Section 4, an adaptive task offloading scheme for distributed edge computing based on meta-strategy is proposed. In Section 5, the performance is evaluated. Finally, we conclude our paper in Section 6.

2  Related Work

This section describes the related work on edge computing, meta-reinforcement learning and multi-objective optimization.

2.1 Edge Computation

In recent years, people have recognized edge computing as an emerging network paradigm. It alleviates the strain caused by the unprecedented surge in traffic and computing demand by offering cloud services at the network edge. The surge of mobile devices for emerging applications such as healthcare, media recognition, intelligent transportation systems (ITS), and drones is driving the rapid advancement and optimization of edge computing technology [13].

MEC plays a crucial role in task offloading, specifically in computing offloading. In order to find the best strategy, Al-Shuwaili et al. [14] proposed a scheme to model the related tasks that organize the mobile application as a DAG, but did not solve the key problem that the offloading of the DAG model with minimum delay in MEC system depends on tasks. To solve the resource allocation problem in MEC systems, Lyu et al. [15] proposed a resource allocation scheme of Stackelberg game model with multi-leaders and multi-followers. Edge nodes can set the price of edge computing resources according to other nodes’ strategies and predict users’ behaviors. Then, end users can choose their own optimal strategy according to the value strategy of edge nodes, but it still does not solve the problem that the offloading strategy cannot adapt to various network environments. To solve the problem that the offloading strategy cannot adapt to various network environments, Wang et al. [16] introduced a task offloading approach using meta-reinforcement learning, enabling rapid adaptation to new environments with minimal gradient updates and samples, and the learning agent interacts with different network environments to train an offloading strategy that can quickly adapt to new environments, unfortunately, this method only optimizes time delay. To solve the problem of geographical dispersion of edge computing, Hu et al. [17] proposed an adaptive scheduling method to deal with dynamic real-time computing requests, reducing the complexity of decentralization work to minimize the energy consumption, while this method only optimizes the energy consumption.

Additionally, Dong et al. [18] proposed an algorithm based on quantum particle swarm optimization (QPSO) to minimize energy consumption. Liu et al. [19] introduced a multi-master multi-slave bi-level game model based on task offloading and pricing strategies for edge computing in vehicular networks. Jeremiah et al. [20] achieved edge node collaboration by integrating digital twin technology (DT).

2.2 Meta-Reinforcement Learning

DRL integrates reinforcement learning (RL) with DNNs, offering a promising solution to the mentioned challenges. DRL excels at addressing intricate problems through trial-and-error learning, even in the absence of a precise environmental model [21–23]. In order to realize an efficient task offloading, Zhu et al. [24] introduced a scheme to formalize the offloading problem, framing it as an optimization challenge involving energy and time based on users’ experience. The strategy is derived using deep Q learning (DQN), but it did not consider the adaptability of the strategy to different network environments. The aforementioned solutions lack adaptability to unforeseen disturbances or unknown scenarios (e.g., a new environment). Their low sample efficiency and the requirement for extensive retraining hinder their ability to cope with changes in applications, tasks, or data rates. Consequently, they spend a considerable amount of time learning new strategies for the updated environment.

Meta-reinforcement learning accelerates the learning of new tasks by leveraging past experiences in a sequence of learning tasks [25,26], and strives to acquire strategies by leveraging prior experience, effectively tackling new tasks with minimal interaction in the environment. The application of MRL to address the computational offloading issue yields evident advantages. We can rapidly acquire tailored strategies for novel mobile users based on local data and meta-strategies. To address the challenge of the offloading strategy’s lack of adaptability to the evolving network environment, Botvinick et al. [27] introduced the “inner loop” and “outer loop” training approach for acquiring the optimal offloading strategy. The “outer loop” leverages its experience across various task contexts to iteratively fine-tune the parameters of the meta-strategy controlling the “inner loop.” Utilizing the meta-strategy, the “inner loop” can rapidly adjust to new tasks with minimal gradient updates. However, this approach does not explicitly consider its applicability in the edge computing environment. To solve the problem of how to choose the most suitable neural network architecture among many types of deep learning architectures and how to optimize the superparameter of the selected neural network, Thar et al. [28] proposed a deep learning model deployment scheme based on meta-reinforcement learning to build a suitable model for self-prediction of content popularity, and proposed a feedback mechanism to find a prediction model, but it did not compare its performance with the latest meta-reinforcement learning algorithm scheme. Merging deep learning for perception with reinforcement learning for decision-making, and meta-learning’s rapid environmental adaptation, an offloading strategy can be efficiently derived in dynamic environments. However, this approach solely focuses on offloading efficiency without delving into a comprehensive analysis of various detailed metrics in edge computing. To solve the problem of computing task scheduling in heterogeneous cellular systems, Niu et al. [29] proposed a multi-agent element PPO algorithm extended to non-stationary heterogeneous edge computing systems, so as to quickly adapt the control strategy learning to non-stationary, but this method does not involve the joint optimization of multiple task indicators. To minimize processing delays and energy consumption in a collaborative edge computing system with multiple users and sites, Avgeris et al. [30] proposed a two-stage mechanism based on reinforcement learning. In the first stage, mobile devices (MDs) autonomously decide whether to offload tasks to edge sites (ES) through an iterative reinforcement learning mechanism, thereby reducing energy consumption for compute-intensive tasks. In the second stage, if some ES are overloaded, task collaboration offloading between sites is implemented using DQN, transferring tasks to less loaded sites. However, this method also does not consider the joint optimization of multiple task metrics and relies on an offline-trained DQN model, which may lack adaptability in dynamic network environments. To address the impact of dynamic changes in the MEC on the generalization ability of task offloading algorithms, Li et al. [31] proposed a MRL algorithm, can adapting faster to new environments, And dynamically adjust the priority of the sampling task during the training process to improve the sampling efficiency of the task, but this algorithm also does not involve how to balance and optimize multiple task indicators for task offloading. Hence, this paper presents a dynamic method with meta-reinforcement learning. The method integrates a directed acyclic graph, multiple Markov strategies, adaptive training network, and a multi-objective optimization algorithm to address the mentioned challenges.

In summary, while the current MRL-based offloading strategies demonstrate many advantages, they still have some limitations. Firstly, many existing MRL methods focus on a single performance metric, lacking a comprehensive consideration of multi-objective optimization, which restricts their applicability in complex environments. Secondly, many MRL methods rely on prior experience for policy learning, but in dynamically changing environments, the initial experience may not sufficiently cover all situations, leading to suboptimal performance in new tasks or environments. Additionally, some MRL algorithms exhibit poor adaptability when faced with complex tasks, and their update frequency and adaptability may not meet the demands of rapidly changing network environments.

2.3 Multi-Objective Optimization

Multi-objective optimization algorithm is to make multiple objectives to be optimized as best as possible at the same time under given constraints, and the solution is usually a set of equilibrium solutions [32–36]. To enhance the estimation accuracy of range vector jump technology, Verma et al. [36] suggested using NSGA-II algorithm to solve the selected multi-class combinatorial optimization problem, and elaborated the multi-class combinatorial optimization problem in detail. To reduce the positioning error, Wang et al. [37] proposed a localization algorithm based on NSGA-II, however, the experimental part of this scheme lacks effectiveness verification for dynamically changing topological structures. To solve the joint optimization of reservoir operation problem and benchmark problem, Liu et al. [38] proposed a new bi-objective algorithm based on NSGA-II algorithm, and then tested its performance in the bi-objective optimization through benchmark problem and reservoir operation problem, but did not apply it to practical problems, such as edge computing. To solve the task offloading problem under 6G networks, Long et al. [39] proposed an algorithm based on the “end-to-end cloud” architecture. However, this algorithm does not consider completely dispersed network environments, But it is validated in a collaborative network environment with edge clouds. To solve the workflow offloading problem in multi-objective optimization, Pan et al. [40] proposed a clustering evolutionary algorithm to minimize the cost and energy consumption. However, the optimization effect of this algorithm is not significantly improved.

Based on the above research, this paper proposes a distributed edge computing adaptive task offloading solution (DTOML) based on a meta-strategy. This solution establishes offloading decisions through DAG, builds different network environment models using multiple MDPs, and subsequently employs a seq2seq network to learn and update offloading strategies, adapting to the dynamically changing network environment and task demands. Seq2seq networks have been widely applied in previous works, including in natural language processing [41] and time series prediction [42], particularly excelling in problems that require handling continuous data or multi-step decision-making. In reinforcement learning, seq2seq helps RL agents generate suitable action sequences [43], effectively addressing multi-step task planning and the decomposition of complex tasks. Finally, the NSGA-II algorithm is used to jointly optimize the delay and energy consumption during the task scheduling process. The NSGA-II algorithm has demonstrated outstanding performance in previous multi-objective optimization problems, particularly in scenarios such as communication networks, resource allocation, and multi-objective task scheduling [44]. It effectively balances multiple conflicting optimization objectives and shows high efficiency and stability in solving task offloading problems. Compared with other solutions, this approach achieves lower latency and reduced energy consumption.

3  System Model and Overview of the Problem

3.1 System Overview

As shown in Fig. 1, we consider two scenarios: an increase in the number of users and a decrease in the number of users. We consider three network environments, namely, environments A, B and C, and each environment is composed of multiple user equipments. When increasing, environment A becomes environment B; and, when decreasing, environment B becomes environment C. For network environment A, its composition is expressed as: . In time slot , the device generates a set of tasks, which are expressed as: , is the total number of tasks of device in network environment A, the each device’s task generation process can be represented by a Poisson process. The size of task is denoted by , the CPU cycle per second required for computing task is denoted by . For task , device can offload it to device or process it locally. The addition of new devices will cause changes in the network structure, and network environment A will become network environment B.

Figure 1: System model diagram

For network environment B, its composition is expressed by . The device generates a set of tasks, which are expressed as: , is the total number of tasks of device in network environment B. In network environment B, the departure of existing edge devices will lead to network environment B being transformed into another new network environment C. For network environment C, its composition is expressed as: . The device generates a set of tasks, which are expressed as: , here is the total number of tasks of device in network environment C. A dynamic network environment is built through the entry and exit of devices, constructing three different network environments A, B, and C with different numbers of devices. The main symbol descriptions involved in this paper are shown in Table 1.

3.2 Communication and Computing Model

In distributed computing offloading, end-to-end delay includes local processing delay, uplink transmission delay, downlink transmission delay and remote processing delay.

If the task is executed locally, the delay of processing the task is only the local execution delay , which is calculated by the following formula:

(1)

where is the CPU cycle required for computing task , is the computing power of the UE. denoted the energy consumption when task is processed and calculated locally, which is calculated by the following formula:

(2)

If the task is offloaded, the UE need to send the task to the MEC host through wireless transmission channel, and the transformation delay of the task is calculated by the following formula:

(3)

where is the size of -th subtask of . The transmission rate of wireless uplink channel is denoted as . Then, the MEC terminal executes the receiving party of , and the delay executing the task at the MEC terminal is calculated by the following formula:

(4)

where is the computing power of the MEC device. Finally, the execution result of the task is returned to the UE, and the reception delay of the task is calculated by the following formula:

(5)

where denotes the size of the result of processing , the transmission rate of the downlink is denoted as .

The energy consumption offloading the task includes two parts:

(1)    of the task in the transmission process, including the transmission energy consumption of the task in the uplink and the reception energy consumption in the downlink, namely: .

(2)   The calculation energy consumption at the edge devices.

Therefore, the energy consumption offloading the task can be calculated by the following formula:

(6)

3.3 Problem Description

We consider that the task offloading decision is a DAG offloading plan, that is, , where the set of offloading tasks is denoted as A and the dependency between tasks is denoted by D. For example, means that task is the parent task of task . Subject to dependencies, subtasks must wait until all their parent tasks are finished.

If the task is processed locally at the UE side, the start execution time of the task depends on the completion time of its parent task and the available time of the UE. The completion time of task on the UE side is calculated by:

(7)

(8)

where the resource available time of task on the UE is denoted as , the completion time of the parent of on the UE side, the completion time of parent task on downlink is denoted as , the delay of task on UE side is denoted by , the resource available time of task on the UE is denoted as , the completion time of task on UE is denoted as .

Therefore, the energy consumption of task in local processing is calculated by the following formula:

(9)

If task is offloaded to the MEC host, then can only initiate data transmission after completing its parent tasks and ensuring the availability of the uplink channel. Therefore, the completion time on the wireless uplink can be calculated by the following formula:

(10)

(11)

where the resource availability time of task on uplink channel is denoted as , the delay of task on uplink channel is denoted as , the resource availability time of task on uplink channel is denoted as , the transmission time of task on uplink channel is denoted by .

The completion time of task on MEC terminal is calculated by the following formula:

(12)

(13)

where denotes the resource availability time of task on MEC side, the transmission time of task on uplink channel is denoted as , the transmission time of parent task of task on MEC side is denoted as , the delay of task at MEC end is denoted as , the resource availability time of task on MEC side is denoted as , the completion time of task on MEC side is denoted as , and the completion time of task on MEC side is denoted by .

The transmission time of task on the wireless downlink channel is calculated by the following formula:

(14)

(15)

where the resource availability time of task on downlink channel is denoted by , the delay of task on the downlink is denoted by .

The total energy consumption when task is offloaded is calculated by the following formula:

(16)

The total delay and energy consumption are calculated using the following formulas, respectively:

(17)

(18)

where the exit the collection of tasks is denoted as , that is, the set of task that has been completed.

The ultimate goal of this article is to find a fast and effective offloading plan for DAG, which minimizes the total time delay and total energy consumption of the entire system. Therefore, we describe the task offloading process as a multi-objective optimization problem with two objective functions. The total delay of Eq. (17) and energy consumption of Eq. (18) are reduced to the equilibrium minimum by adding a weight factor , so as to obtain the total target value Q, that is: the minimization of the total delay denoted as in Eq. (17) and the total energy consumption denoted as in Eq. (18) is achieved by introducing a weight factor . This optimization process aims to balance both metrics to reach an equilibrium state, ultimately resulting in the minimization of the overall objective function denoted as Q. Mathematically, this can be expressed as:

(19)

(20)

(21)

(22)

(23)

Due to the latency and energy consumption in problem P1, which are closely related to drones and users, and will increase with the increase of users and drones, the action and state space of the offloading strategy will grow exponentially, making it an NP hard problem that cannot be solved by traditional methods. Therefore, this paper proposes the DTOML algorithm to solve this problem.

4  Meta-Policy-Based Distributed Edge Computing Adaptive Task Offloading Scheme (DTOML)

In this section, a scheme based on meta-strategy (DTOML) is introduced. Firstly, an overview of the scheme is provided, and then the scheme is described in detail.

4.1 Overview of Algorithm

The DTOML algorithm is divided into two training cycles: the “inner loop” training of task-specific strategy at UE end and the “outer loop” training of meta-strategy at MEC end.

Fig. 2 shows the architecture of integrating DTOML into an MEC system. User level encompasses diverse user equipment (UE), edge level involves MEC provides edge computing services, with edge hosts offering services and cloud servers at the remote level, as detailed below:

(1)   At the user layer: the parser operating at the user level, transforms applications into a DAG. The local trainer handles the “inner loop” training by receiving the parsed DAG as training data from the parser. The trained policy network parameters are transmitted to the MEC host. After the training process is completed, the uninstallation scheduler makes uninstallation decisions based on policy network inference. On the other hand, any tasks that are offloaded are transmitted to the MEC host for further processing.

(2)   At the edge layer: The MEC platform utilizes modules for global training services and remote execution services. The global training service handles “outer-loop” training by exchanging policy network parameters with User Equipment (UE). The remote execution service manages tasks offloaded from the UE, assigns them to the appropriate cloud, and returns the results to the UE.

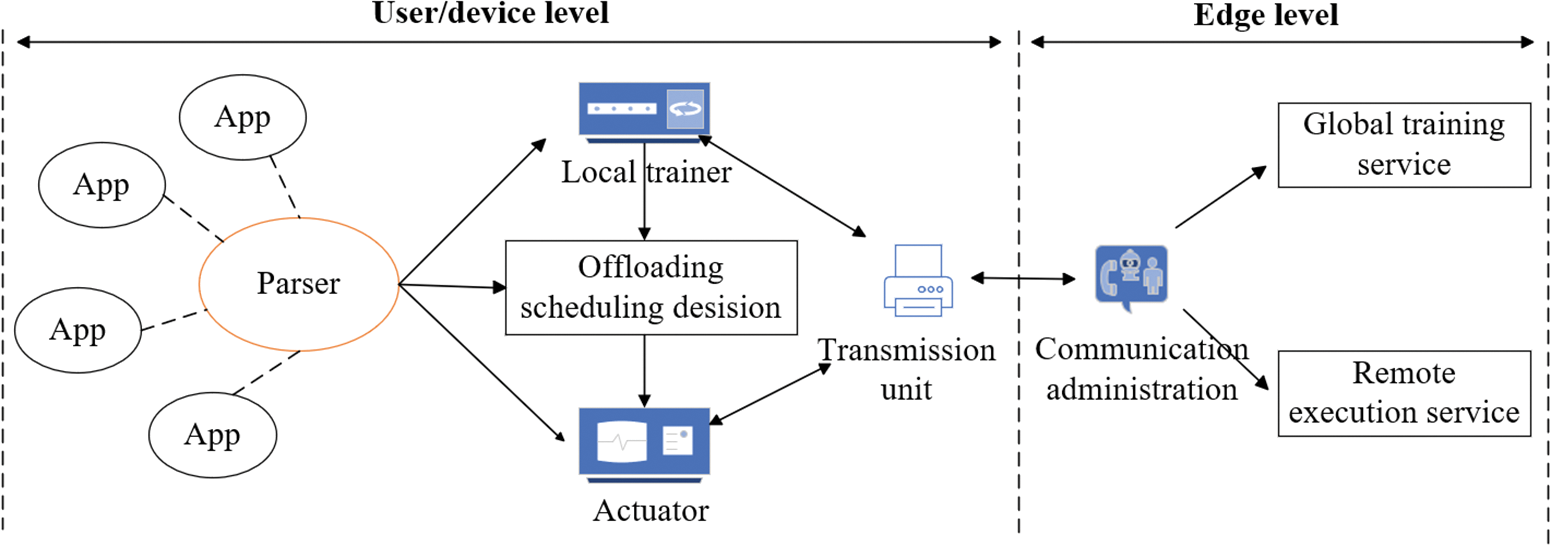
Figure 2: Edge computing system architecture

Next, we’ll outline the DTOML algorithm’s training process in the MEC system, depicted in Fig. 3. This process comprises four steps:

(1)   Initial parameter download: UE retrieves meta-policy parameters from MEC host.

(2)   UE-side inner-loop training: Performing “inner-loop” training on each UE using meta-strategy and local data to acquire task-specific strategy. Simultaneously, UE uploads task-specific strategy parameters to the MEC host.

(3)   MEC-side outer-loop training: MEC host conducts “outer-loop” training based on collected task-specific strategy parameters, generates a new meta-strategy, and initiates a new training round. Once a stable meta-strategy is achieved, it learns the task-specific strategy of new UEs through “inner-loop” training. Algorithm details will be explained in Section 4.3.

(4)   Target optimization: Based on the specific task strategy of the learned new UE, use the NSGA-II algorithm to jointly optimize the delay and energy consumption.

Figure 3: The algorithm structure diagram of the design

4.2 Multiple MDP Modeling

To address the computation offloading challenge within diverse MEC environments, in this paper, we formulat the computation offloading process as multiple MDPs. The overall learning process is bifurcated into two segments: efficaciously acquiring meta-strategies across all MDPs and rapidly learning a strategy for a MDP by leveraging meta-strategies. The definitions of each element in MDPs are as follows:

(1)   State S: When scheduling task , the task delay is critically dependent on several factors, including the task configuration file (which encompasses the necessary CPU cycles and data size), the DAG topology, the transmission rate, and MEC resources. The MEC resource status, in particular, plays a pivotal role in the offloading decisions made prior to time . Thus, we characterize the status by combining the coding DAG with offloading plan: , among them, consists of task embedding sequence, and is the offloading plan of the first tasks and subtasks.

(2)   Action A: Task scheduling involves making binary decisions, defining the action space as . In this context, the indicates that the task will be executed on the UE, while the signifies that the task will be offloaded.

(3)   Reward R: The reward function is defined as: .

4.3 Inner Ring Training and Outer Ring Training

DTOML and gradient-based MRL algorithm share similar algorithm structure, and the scheme consists of two training cycles. The objective function is defined based on near-end strategy optimization (PPO). Compared with other strategy gradient methods, PPO has better exploration ability and training stability. Initially, each sampled learning task undergoes training as an “inner loop.” Following the completion of the “inner loop” training, the meta-strategy parameter is updated using the gradient ascent method through Adam (Adaptive Moment Estimation) to achieve outer loop training. In this scheme, the inner loop training and outer loop training complement each other to update parameters and obtain the optimal strategy. The inner loop training is mainly based on meta policies and local data to run “inner loop” training on each UE to obtain task specific policies, while the outer loop training is to perform “outer loop” training on the collected task specific policy parameters, generate new meta policies, pass them back to the inner loop, and start a new round of training until they are optimal.

4.3.1 “Inner Ring” Training Based on PPO Strategy Gradient Method

For a learning task , initialize the policy parameters and target policy , generate trajectory through sample policy sampling, then calculate the optimization objective function , and update the policy parameters through the optimization objective function . During multiple periods, update the sample policy sampling to avoid large-scale updates, and finally repeat the training until convergence, achieving optimization of task specific policies. The objective function for each inner loop training based on PPO is defined as the follows:

(24)

where the objective function of the PPO algorithm is denoted as , the optimization objectives is denoted as , the hyperparameters of the value function term in balanced optimization objectives is denoted as , the value function is denoted as , the generated trajectory is denoted as , the parameters of the strategy is denoted as .

The pseudocode for inner loop training based on PPO is shown in Algorithm 1.

4.3.2 “Outer Loop” Training Based on Seq2seq Network

The seq2sequence network mainly consists of an encoder and a decoder. Additionally, it incorporates an attention mechanism, enabling the decoder to focus on distinct segments of the encoder input sequence during each step of output generation. This helps mitigate information loss inherent in seq2sequence networks.

According to PPO algorithm and the objective function of inner-loop training, the objective function of each outer-loop training is defined as the following formula:

(25)

where the objective function of the outer loop is denoted by , the expected value under the given learning task, task sampling distribution and policy distribution is denoted as , the sampling distribution of learning task is denoted as , the strategy for learning tasks is denoted as , the strategy distribution for given trajectory and optimized strategy parameters is denoted as .

The network structure diagram of seq2seq is shown in Fig. 4. The seq2seq network mainly includes the following parts: (1) Input sequence encoding: The encoder is composed of an RNN, which is used to gradually process the input task sequence and finally output a context vector that compresses the information of the input sequence. (2) Context vector generation: The final hidden state of the encoder is used as a context vector to represent the features of the input sequence. This vector will be used in the decoder. (3) Output sequence decoding: The context vector is passed into the decoder, which is also an RNN that gradually generates the output sequence. The decoder generates an output at each step, which is the offloading decision for each task.

Figure 4: Network structure diagram of seq2seq

4.4 Joint Optimization Algorithm Based on NSGA-II Algorithm

The NSGA-II algorithm has the advantages of efficiently handling multi-objective problems and maintaining diversity of solutions. It can not only find Pareto optimal solutions through non dominated sorting, but also balance multiple objectives simultaneously. We also use the crowding distance mechanism to maintain the diversity of solutions on the Pareto front. This ensures that the optimization process can explore a wide range of potential solutions, rather than just converging to a single solution point. Therefore, this algorithm was chosen for further optimization. Using the time delay and energy consumption during task scheduling with the adaptive scheduling strategy as input for the NSGA-II algorithm, efficient joint optimization results can be swiftly achieved through operations like selection, crossover, mutation, and rapid non-dominated sorting. The NSGA-II algorithm’s joint optimization process unfolds as follows:

(1)   Initially creating a population of size N using random generation, followed by non-dominant sorting.

(2)   From the second generation onwards, merging the parent population and offspring population for efficient non-dominant sorting.

(3)   Generate new offspring population through the basic operation of genetic algorithm, until the constraint condition of the algorithm is met, that is, the iteration number of the algorithm is less than the maximum iteration number .

Algorithm 2 is pseudocode for the NSGA-II algorithm.

5  Performance Evaluation

Basic Environment Setting

This paper is conducted in Python 3.7 simulation environment. The number of users is 10–50, the effective distance of wireless communication is 60–100 m, the data size of a single task is 2000–10,000 kB, the CPU cycle provided to each user is 8–12 MHz, and the transmission rate is determined by Shannon formula.

Fig. 5 shows the variation of task offloading latency and energy consumption with the number of gradient update steps in a 2 2 network environment (network environment A) with five algorithm schemes. Fig. 5a can be observed that during the entire gradient step size update process, the proposed DTOML scheme has lower task offloading latency than the Greedy scheme [16], RL scheme [27], and DRL scheme [16] in a 2 2 network environment. Fig. 5b can be observed that the proposed DTOML scheme has lower task offloading energy consumption than the Greedy scheme [16], RL scheme [27], PSO scheme, and DRL scheme [16] in a 2 2 network environment throughout the entire gradient step size update process. Due to the fact that the Greedy, RL, PSO, DRL, and DTOML schemes update their strategies through parameter optimization iterations with increasing gradient update steps, the poor performance of the Greedy algorithm results in a stable trend in the target value with increasing gradient steps. In contrast, the target value in the RL scheme, DRL scheme, and DTOML scheme all show a decreasing trend. DTOML scheme and DRL scheme are obviously superior to Greedy scheme, PSO scheme and RL scheme, because both of them are model learning and updating strategies based on pre training, but the optimization effect of DTOML algorithm is the best.

Figure 5: The impact of gradient update steps on task offloading latency and energy consumption in a 2 2 network environment (network environment A). (a) Latency. (b) Energy consumption

Fig. 6 shows the variation of task offloading latency and energy consumption with gradient update steps for five algorithm schemes in a 4 4 network environment (network environment B). From Fig. 6a, it can be observed that the proposed DTOML scheme has lower task offloading latency than the Greedy scheme and RL scheme in a 4 4 network environment throughout the entire gradient update process. When the gradient update step size is small, there is almost no difference in task offloading latency between the DTOML scheme and the DRL scheme. As the gradient update step size increases, the task offloading latency of the DTOML scheme is lower than that of the DRL scheme, exhibiting better performance. From Fig. 6b, it can be observed that the proposed DTOML scheme has lower task offloading energy consumption than the Greedy scheme, RL scheme, and DRL scheme in a 4 4 network environment throughout the entire gradient update process. Due to the fact that the Greedy scheme, PSO scheme, RL scheme, DRL scheme, and DTOML scheme all update their strategies through parameter optimization iterations as the gradient update step size increases, the poor performance of the Greedy scheme results in a stable trend in target value as the gradient step size is updated. On the other hand, the RL scheme and DTOML scheme show a decreasing trend in target value, while the DRL scheme performs worse as it changes from a 2 2 network environment to a more complex 4 4 network environment, causing the trend of task offloading latency to fluctuate up and down. The DTOML scheme and DRL scheme are obviously superior to Greedy scheme, PSO scheme and RL scheme, because both DTOML and DRL are model learning and updating strategies based on pre training, but DTOML has the best optimization effect, because DTOML scheme achieves the results that target value are lower than Greedy scheme, RL scheme, PSO scheme and DRL scheme by optimizing parameter update efficiency, collaborative learning effect and network transmission overhead.

Figure 6: The impact of gradient update steps on task offloading latency and energy consumption in a 4 4 network environment (network environment A). (a) Latency. (b) Energy consumption

Fig. 7 shows the variation of task offloading latency and energy consumption with gradient update steps for five algorithm schemes in a 3 3 network environment (network environment C). From Fig. 7a, it can be observed that during the entire gradient update process, the proposed DTOML scheme has a lower task offloading latency than the Greedy scheme, PSO scheme and RL scheme in a 3 3 network environment. When the gradient update step size is small, the task offloading delay of the DTOML scheme is higher than that of the DRL scheme, and as the gradient update step size increases, the task offloading delay of the DTOML scheme is lower than that of the DRL scheme, exhibiting better performance. From Fig. 7b, it can be observed that during the entire gradient update process, the proposed DTOML scheme has lower task offloading energy consumption than the Greedy scheme, PSO scheme, RL scheme, and DRL scheme in a 3 3 network environment. When the gradient update step size is small, the task offloading energy consumption of the DTOML scheme is higher than that of the DRL scheme, and as the gradient update step size increases, the task offloading energy consumption of the DTOML scheme is lower than that of the DRL scheme, exhibiting better performance.

Figure 7: The impact of gradient update steps on task offloading latency and energy consumption in a 3 3 network environment (network environment A). (a) Latency. (b) Energy consumption

Due to the fact that the Greedy scheme, RL scheme, PSO scheme, DRL scheme, and DTOML scheme update their strategies through parameter optimization iterations with increasing gradient update step size, the performance of the Greedy algorithm is poor as the gradient step size is updated, resulting in a stable trend in target value. When the network environment changes from 4 4 to 3 3, the performance of the DRL scheme improves, causing the trend of task offloading latency to fluctuate up and down. The DTOML scheme and DRL scheme are obviously superior to Greedy scheme and RL scheme, because both DTOML and DRL are model learning and updating strategies based on pre training, but the optimization effect of DTOML is the best, because DTOML scheme achieves the effect that target value are lower than Greedy scheme, RL scheme and DRL scheme by optimizing parameter update efficiency, collaborative learning effect and network transmission overhead. The three different network environments A, B, and C are formed by the dynamic changes in the network environment caused by the entry and exit of edge devices. According to Figs. 5–7, it can be observed that the proposed DTOML scheme has lower task offloading latency and energy consumption compared to the Greedy scheme, RL scheme, PSO scheme and DRL scheme. This indicates that the proposed DTOML scheme always ensures better adaptability in different network environments (A, B, C).

5.1.1 Influence of Transmission Rate

Learning the offloading strategy for each transmission rate is considered a separate learning task, and the trained meta strategy is evaluated at transmission rates of 6, 9, and 12 Mbps. From Fig. 8a,c,e, it can be observed that as the channel transmission rate increases, the overall task offloading delay shows a downward trend. That is, when the rate is 9 Mbps, the task offloading delay is generally smaller than when the rate is 6 Mbps, and when the rate is 12 Mbps, the task offloading delay is basically smaller than when the rate is 9 Mbps. As shown in Fig. 8a, when the rate is 6 Mbps, it can be seen from the trend of the task offloading delay of the five algorithm schemes with the number of gradient update steps that the proposed DTOML scheme has a higher task offloading delay than the DRL scheme at the initial gradient update step, and a lower task offloading delay than the Greedy scheme, RL scheme, and DRL scheme at other gradient update steps. From Fig. 8c,e, it can be observed that when the channel transmission rate increases from 6 to 9 and 12 Mbps, even in the initial update steps, the DTOML scheme achieves the lowest task offloading delay among the five algorithm schemes. This proves that the proposed DTOML scheme has better delay optimization ability than the Greedy scheme, PSO scheme, RL scheme, and DRL scheme.

Figure 8: The influence of different transmission rates on task offload delay and energy consumption

5.1.2 Impact of the Number of Tasks

From Fig. 8b,d,f, it can be observed that as the channel transmission rate increases, the overall energy consumption of task offloading shows an upward trend. That is, when the channel transmission rate is 9 Mbps, the energy consumption of task offloading is generally higher than that when the channel transmission rate is 6 Mbps, and when the channel transmission rate is 12 Mbps, the energy consumption of task offloading is basically higher than that when the channel transmission rate is 9 Mbps. The trend of task offloading energy consumption with gradient step updates for the five algorithm schemes shows that although the task offloading energy consumption increases with the increase of gradient update steps, the proposed DTOML scheme consistently has lower task offloading energy consumption than the Greedy scheme, RL scheme, PSO scheme and DRL scheme, demonstrating good performance. From Fig. 8d,f, it can be observed that when the channel transmission rate increases from 6 to 9 and 12 Mbps, the DTOML scheme also has the lowest task offloading energy consumption among the five algorithm schemes. This proves that the proposed DTOML scheme has better energy optimization ability than the Greedy scheme, RL scheme, PSO scheme and DRL scheme.

Fig. 9 shows the variation of task offloading latency and energy consumption with gradient update steps for five algorithm schemes under different task quantities. From Fig. 9a,c,e, it can be observed that as the number of tasks increases, the overall trend of task offloading delay shows an increasing trend, that is, the task offloading delay when the quantity is 40 is greater than that when the quantity is 30, and the task offloading delay when the quantity is 50 is greater than that when the quantity is 40. As shown in Fig. 9a, the trend of task offloading delay of the five algorithm schemes with the update of gradient steps can be observed that during the entire update process of gradient steps, the DTOML scheme proposed has a lower task offloading delay than the Greedy scheme when the quantity is 30. The DTOML scheme proposed has a higher task offloading delay than the DRL scheme at the initial gradient update steps, but at other gradient update steps, the DTOML scheme has a lower task offloading delay than the Greedy scheme, RL scheme, PSO scheme and DRL scheme. From Fig. 9a,c,e, it can be observed that when the quantity increases from 30 to 50, the task offloading delay of the DTOML scheme is only slightly higher than the other three schemes at the initial update step. As the gradient update step increases, the task offloading delay of the DTOML scheme is lower than the other three schemes, proving that the proposed DTOML scheme has better delay optimization ability than the Greedy scheme, RL scheme, PSO scheme and DRL scheme.

Figure 9: The impact of different task quantities on task offloading latency and energy consumption

From Fig. 9b,d,f, it can be observed that as the number of tasks increases, the overall energy consumption of task offloading shows an upward trend. The trend of task offloading energy consumption with gradient step updates for the five algorithm schemes shows that although the task offloading energy consumption increases with the increase of gradient update steps, the proposed DTOML scheme has overall lower task offloading energy consumption than the Greedy scheme, RL scheme, and DRL scheme, demonstrating good performance. From Fig. 9d,f, it can be observed that when the quantity increases from 30 to 40 and 50, the DTOML scheme is also the scheme with the lowest overall task offloading energy consumption among the five algorithm schemes. This proves that the proposed DTOML scheme has better energy optimization ability than the Greedy scheme, RL scheme, PSO scheme and DRL scheme.

The scheme proposed in this article obtains task specific strategies through inner loop training of PPO algorithm. Compared with reinforcement learning, particle swarm optimization and other algorithms, it has the advantages of handling high-dimensional state space and adapting to dynamic environments that reinforcement learning, particle swarm optimization and other algorithms do not have. In addition, this scheme models multiple Markov decision processes (MDPs), processes sequence data through seq2seq network, and uses NSGA-II algorithm for Pareto optimization, which can more comprehensively capture the dynamic features of different tasks and environments. It has stronger accuracy, effectiveness, adaptability, and flexibility than deep reinforcement learning algorithms, and can better reduce energy consumption and latency while ensuring performance, and improve overall system efficiency.

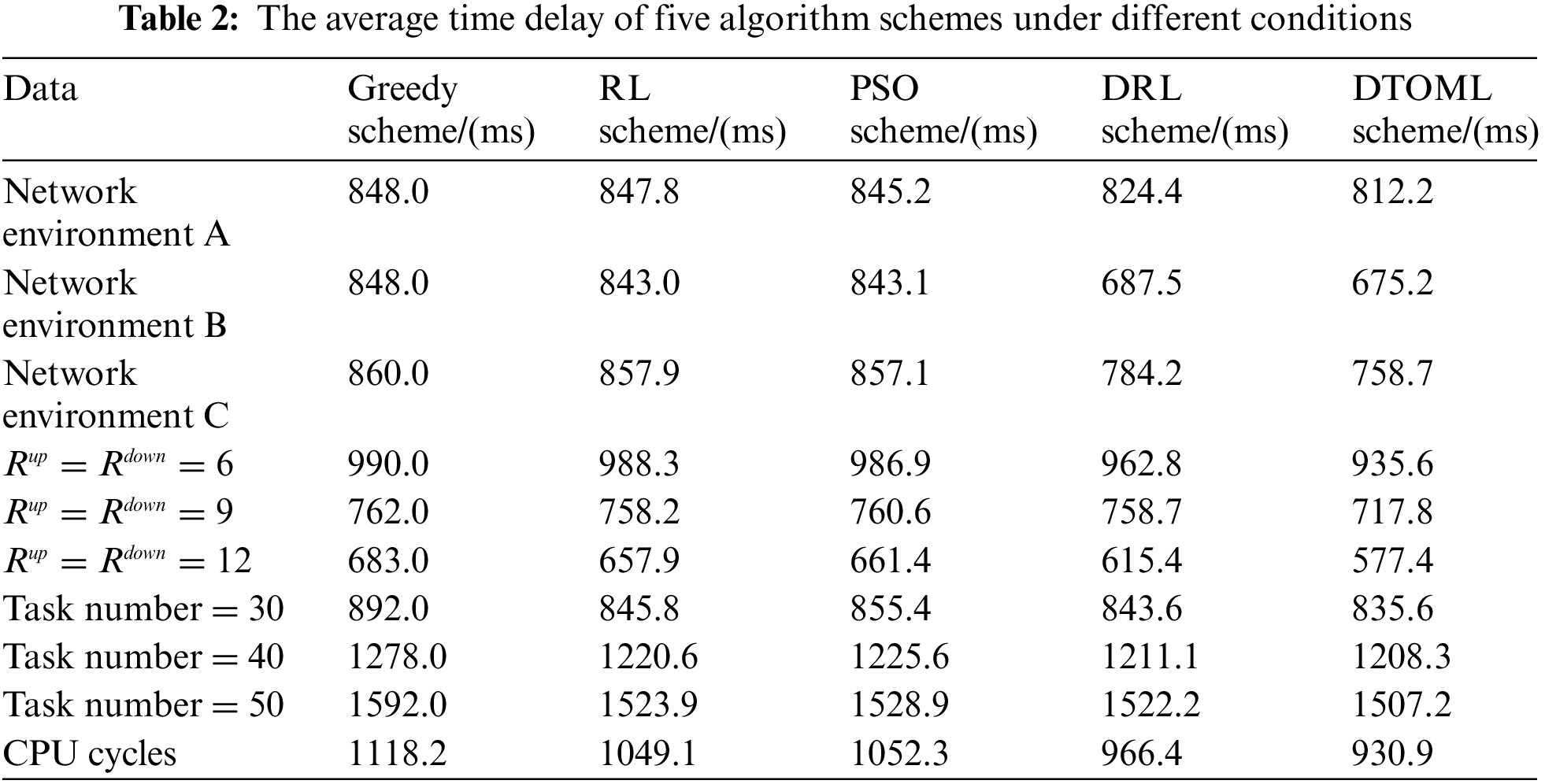
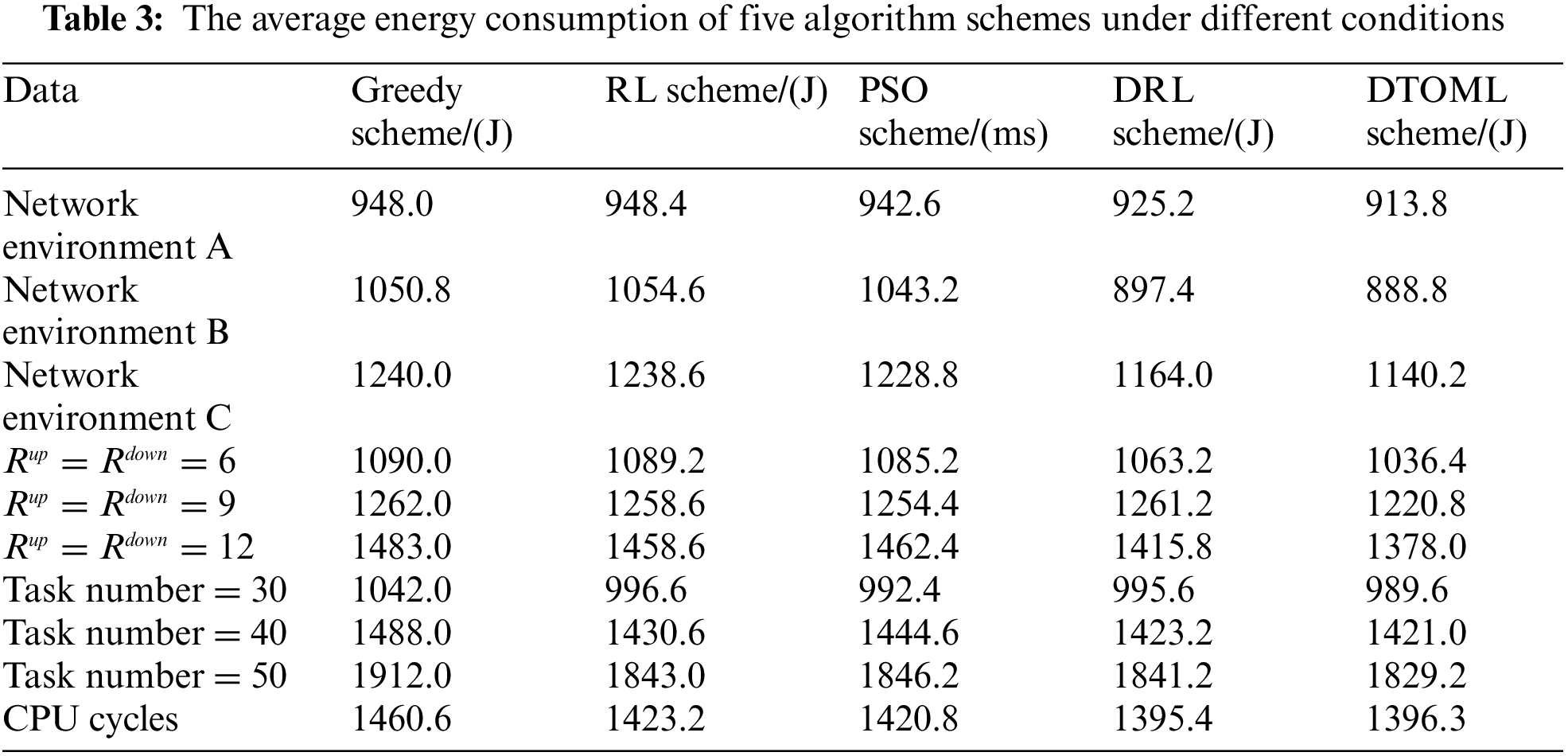
Tables 2 and 3 compare the average task offloading latency and energy consumption of five algorithm schemes under different network environments, channel transmission rates, and task volumes. It can be observed that under different comparison indicators, the proposed DTOML scheme has lower average latency and energy consumption compared to the Greedy scheme, RL scheme, and DRL scheme. In different network environments, the lower the average latency and energy consumption of task offloading in the DTOML scheme, the better its adaptability. At different channel transmission rates and task volumes, the lower the average task offloading delay and average energy consumption of the DTOML scheme, the better the joint optimization ability.

From Fig. 10, it can be observed that as the number of CPU cycles allocated to each user increases, the time delay and energy consumption of each algorithm gradually decrease, but the decrease in time delay will be more pronounced. This is because as the allocated CPU cycles increase, there are more available computing resources, and tasks are processed faster, resulting in an obvious reduction in time delay. The system energy consumption includes two parts: transmission and computation energy consumption. Although more computing resources are allocated, the task offloading process involves two processes: transmission and computation, both of which consume energy. Therefore, the reduction in energy consumption is not as significant.

Figure 10: The impact of the CPU cycle for each user on task offloading latency and energy consumption. (a) Latency. (b) Energy consumption

6  Conclusion

In this paper, to solve the problem that the learning task offloading strategy cannot have good adaptability in different network environments, a distributed edge computing adaptive task offloading scheme based on MRL is proposed, which simultaneously realizes the joint optimization of delay and energy consumption in edge computing networks. In this paper, we first establish various network environment models and formulate the task offloading strategy using DAGs. Subsequently, we employ meta reinforcement learning MDP and seq2seq for adaptive training of task scheduling strategies. To jointly optimize delay and energy consumption, we integrate the NSGA-II algorithm. Simulation results reveal that the proposed distributed edge computing adaptive task offloading scheme (DTOML), which utilizes a meta strategy, exhibits remarkable advantages across various network environments, transmission rates, and task sequences. From the average values in Tables 2 and 3, it can be observed that our algorithm performs the best. In comparison to other edge computing adaptive task offloading schemes, the DTOML achieves a 21% reduction in delay and a 19% reduction in energy consumption.

For more dynamic or resource constrained environments, the number and layers of neurons in the PPO actor network and critic network during inner loop training can be increased to enhance the model’s expressive power. In the future, multi-agent collaborative offloading strategy will be further studied to enable multiple edge computing nodes to work in coordination and further improve the efficiency and robustness of the overall system.

Acknowledgement: The authors gratefully acknowledge the helpful comments and suggestions of the reviewers and editors, which have improved the presentation.

Funding Statement: This research was funded by the Fundamental Research Funds for the Central Universities (J2023-024, J2023-027).

Author Contributions: Conceptualization, Jiajia Liu and Jianhua Liu; methodology, Jiajia Liu and Jianhua Liu; validation, Jiajia Liu, Peng Xie, Wei Li, Bo Tang and Jianhua Liu; investigation, Jiajia Liu, Peng Xie and Wei Li; writing—original draft preparation, Wei Li and Jianhua Liu; writing—review and editing, Jiajia Liu, Peng Xie, Wei Li, Bo Tang and Jianhua Liu; supervision, Jiajia Liu and Jianhua Liu; project administration, Jianhua Liu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. M. -R. Ra, A. Sheth, L. Mummert, P. Pillai, D. Wetherall and R. Govindan, “Odessa: Enabling interactive perception applications on mobile devices,” Commun. Biol., pp. 43–56, 2011. doi: 10.1145/1999995.2000000. [Google Scholar] [CrossRef]

2. Z. Liu et al., “PPRU: A privacy-preserving reputation updating scheme for cloud-assisted vehicular networks,” IEEE Trans. Vehicular Technol., pp. 1–16, 2023. doi: 10.1109/TVT.2023.3340723. [Google Scholar] [CrossRef]

3. D. Sabella et al., “Developing software for multi-access edge computing,” ETSI White Paper, vol. 20, pp. 1–38, 2019. Accessed: Aug. 26, 2024. [Online]. Available: https://www.etsi.org. [Google Scholar]

4. J. B. da Costa et al., “Mobility-aware vehicular cloud formation mechanism for vehicular edge computing environments,” Ad Hoc Netw., vol. 151, no. 1, 2023, Art. no. 103300. doi: 10.1016/j.adhoc.2023.103300. [Google Scholar] [CrossRef]

5. Z. Liu et al., “PPTM: A privacy-preserving trust management scheme for emergency message dissemination in space–air–ground-integrated vehicular networks,” IEEE Internet Things J., vol. 9, no. 8, pp. 5943–5956, 2022. doi: 10.1109/JIOT.2021.3060751. [Google Scholar] [CrossRef]

6. Q. Tang, C. Dai, Z. Yu, D. Cao, and J. Wang, “An UAV and EV based mobile edge computing system for total delay minimization,” Comput. Commun., vol. 212, no. 1, pp. 104–115, 2023. doi: 10.1016/j.comcom.2023.09.025. [Google Scholar] [CrossRef]

7. J. Liu, Z. Wu, J. Liu, and X. Tu, “Distributed location-aware task offloading in multi-UAVs enabled edge computing,” IEEE Access, vol. 10, no. 2, pp. 72416–72428, 2022. doi: 10.1109/ACCESS.2022.3189682. [Google Scholar] [CrossRef]

8. J. Liu, P. Xie, J. Liu, and X. Tu, “Task offloading and trajectory optimization in UAV networks: A deep reinforcement learning method based on SAC and A-star,” Comput. Model. Eng. Sci., vol. 141, no. 2, pp. 1243–1273, 2024. doi: 10.32604/cmes.2024.054002. [Google Scholar] [CrossRef]

9. J. Liu, Z. Wu, J. Liu, and Y. Zou, “Cost research of internet of things service architecture for random mobile users based on edge computing,” Int. J. Web Inf. Syst., vol. 18, no. 4, pp. 217–235, 2022. doi: 10.1108/IJWIS-02-2022-0039. [Google Scholar] [CrossRef]

10. X. Lin, Y. Wang, Q. Xie, and M. Pedram, “Task scheduling with dynamic voltage and frequency scaling for energy minimization in the mobile cloud computing environment,” IEEE Trans. Serv. Comput., vol. 8, no. 2, pp. 175–186, 2015. doi: 10.1109/TSC.2014.2381227. [Google Scholar] [CrossRef]

11. X. Chen, H. Zhang, C. Wu, S. Mao, Y. Ji and M. Bennis, “Optimized computation offloading performance in virtual edge computing systems via deep reinforcement learning,” IEEE Internet Things J., vol. 6, no. 3, pp. 4005–4018, 2019. doi: 10.1109/JIOT.2018.2876279. [Google Scholar] [CrossRef]

12. G. Qu, H. Wu, R. Li, and P. Jiao, “DMRO: A deep meta reinforcement learning-based task offloading framework for edge-cloud computing,” IEEE Trans. Netw. Serv. Manag., vol. 18, no. 3, pp. 3448–3459, 2021. doi: 10.1109/TNSM.2021.3087258. [Google Scholar] [CrossRef]

13. S. Dong et al., “Task offloading strategies for mobile edge computing: A survey,” Comput. Netw., vol. 254, no. 6, 2024, Art. no. 110791. doi: 10.1016/j.comnet.2024.110791. [Google Scholar] [CrossRef]

14. A. Al-Shuwaili and O. Simeone, “Energy-efficient resource allocation for mobile edge computing-based augmented reality applications,” IEEE Wirel. Commun. Lett., vol. 6, no. 3, pp. 398–401, 2017. doi: 10.1109/LWC.2017.2696539. [Google Scholar] [CrossRef]

15. T. Lyu, H. Xu, and Z. Han, “Multi-leader multi-follower stackelberg game based resource allocation in multi-access edge computing,” in ICC 2022–IEEE Int. Conf. Commun., 2022, pp. 4306–4311. doi: 10.1109/ICC45855.2022.9838425. [Google Scholar] [CrossRef]

16. J. Wang, J. Hu, G. Min, A. Y. Zomaya, and N. Georgalas, “Fast adaptive task offloading in edge computing based on meta reinforcement learning,” IEEE Trans. Parallel Distrib. Syst., vol. 32, no. 1, pp. 242–253, 2021. doi: 10.1109/TPDS.2020.3014896. [Google Scholar] [CrossRef]

17. B. Hu, Y. Shi, and Z. Cao, “Adaptive energy-minimized scheduling of real-time applications in vehicular edge computing,” IEEE Trans. Ind. Inform., vol. 19, no. 5, pp. 6895–6906, 2023. doi: 10.1109/TII.2022.3207754. [Google Scholar] [CrossRef]

18. S. Dong, Y. Xia, and J. Kamruzzaman, “Quantum particle swarm optimization for task offloading in mobile edge computing,” IEEE Trans. Ind. Inform., vol. 19, no. 8, pp. 9113–9122, 2023. doi: 10.1109/TII.2022.3225313. [Google Scholar] [CrossRef]

19. J. Liu, J. Wei, R. Luo, G. Yuan, J. Liu and X. Tu, “Computation offloading in edge computing for internet of vehicles via game theory,” Comput. Mater. Contin., vol. 81, no. 1, pp. 1337–1361, 2024. doi: 10.32604/cmc.2024.056286. [Google Scholar] [CrossRef]

20. S. R. Jeremiah, L. T. Yang, and J. H. Park, “Digital twin-assisted resource allocation framework based on edge collaboration for vehicular edge computing,” Future Gener. Comput. Syst., vol. 150, no. 3, pp. 243–254, 2024. doi: 10.1016/j.future.2023.09.001. [Google Scholar] [CrossRef]

21. H. Wu, W. J. Knottenbelt, and K. Wolter, “An efficient application partitioning algorithm in mobile environments,” IEEE Trans. Parallel Distrib. Syst., vol. 30, no. 7, pp. 1464–1480, 2019. doi: 10.1109/TPDS.2019.2891695. [Google Scholar] [CrossRef]

22. D. Silver et al., “Mastering the game of go without human knowledge,” Nature, vol. 550, no. 7676, pp. 354–359, 2017. doi: 10.1038/nature24270. [Google Scholar] [PubMed] [CrossRef]

23. T. P. Lillicrap et al., “Continuous control with deep reinforcement learning,” 2015. doi: 10.48550/arXiv.1509.02971. [Google Scholar] [CrossRef]

24. A. Zhu et al., “Computation offloading for workflow in mobile edge computing based on deep Q-learning,” in 2019 28th Wirel. Opt. Commun. Conf. (WOCC), 2019, pp. 1–5. doi: 10.1109/WOCC.2019.8770689. [Google Scholar] [CrossRef]

25. J. Vanschoren, “Meta-learning: A survey,” 2018. doi: 10.48550/arXiv.1810.03548. [Google Scholar] [CrossRef]

26. H. Fu, H. Tang, J. Hao, W. Liu, and C. Chen, “MGHRL: Meta goal-generation for hierarchical reinforcement learning,” 2019. doi: 10.48550/arXiv.1909.13607. [Google Scholar] [CrossRef]

27. M. Botvinick, S. Ritter, J. X. Wang, Z. Kurth-Nelson, C. Blundell and D. Hassabis, “Reinforcement learning, fast and slow,” Trends Cogn. Sci., vol. 23, no. 5, pp. 408–422, 2019. doi: 10.1016/j.tics.2019.02.006. [Google Scholar] [PubMed] [CrossRef]

28. K. Thar, T. Z. Oo, Z. Han, and C. S. Hong, “Meta-learning-based deep learning model deployment scheme for edge caching,” in 2019 15th Int. Conf. Netw. Serv. Manag. (CNSM), 2019, pp. 1–6. doi: 10.23919/CNSM46954.2019.9012733. [Google Scholar] [CrossRef]

29. L. Niu et al., “Multiagent meta-reinforcement learning for optimized task scheduling in heterogeneous edge computing systems,” IEEE Internet Things J., vol. 10, no. 12, pp. 10519–10531, 2023. doi: 10.1109/JIOT.2023.3241222. [Google Scholar] [CrossRef]

30. M. Avgeris, M. Mechennef, A. Leivadeas, and I. Lambadaris, “A two-stage cooperative reinforcement learning scheme for energy-aware computational offloading,” in 2023 IEEE 24th Int. Conf. High Performance Switching Routing (HPSR), 2023, pp. 179–184. doi: 10.1109/HPSR57248.2023.10147932. [Google Scholar] [CrossRef]

31. Y. Li, J. Li, Z. Lv, H. Li, Y. Wang and Z. Xu, “GASTO: A fast adaptive graph learning framework for edge computing empowered task offloading,” IEEE Trans. Netw. Serv. Manag., vol. 20, no. 2, pp. 932–944, 2023. doi: 10.1109/TNSM.2023.3250395. [Google Scholar] [CrossRef]

32. H. Xie, D. Ding, L. Zhao, K. Kang, and Q. Liu, “A two-stage preference driven multi-objective evolutionary algorithm for workflow scheduling in the cloud,” Expert. Syst. Appl., vol. 238, no. 18, 2024, Art. no. 122009. doi: 10.1016/j.eswa.2023.122009. [Google Scholar] [CrossRef]

33. P. L. Manikowski, D. J. Walker, and M. J. Craven, “Multi-objective optimisation of the benchmark wind farm layout problem,” J. Mar. Sci. Eng., vol. 9, no. 12, 2021. doi: 10.3390/jmse9121376. [Google Scholar] [CrossRef]

34. N. Panagant, N. Pholdee, S. Bureerat, A. R. Yildiz, and S. Mirjalili, “A comparative study of recent multi-objective metaheuristics for solving constrained truss optimisation problems,” Arch. Computat. Methods Eng., vol. 28, no. 5, pp. 4031–4047, 2021. doi: 10.1007/s11831-021-09531-8. [Google Scholar] [CrossRef]

35. M. Chen and Z. Jun, “Research on layered microgrid operation optimization based on NSGA-II algorithm,” in 2018 Int. Conf. Power Syst. Technol. (POWERCON), IEEE, 2018, pp. 2149–2156. doi: 10.1109/POWERCON.2018.8602169. [Google Scholar] [CrossRef]

36. S. Verma, M. Pant, and V. Snasel, “A comprehensive review on NSGA-II for multi-objective combinatorial optimization problems,” IEEE Access, vol. 9, pp. 57757–57791, 2021. doi: 10.1109/ACCESS.2021.3070634. [Google Scholar] [CrossRef]

37. P. Wang, F. Xue, H. Li, Z. Cui, L. Xie and J. Chen, “A multi-objective DV-hop localization algorithm based on NSGA-II in internet of things,” Mathematics, vol. 7, no. 2, 2019, Art. no. 184. doi: 10.3390/math7020184. [Google Scholar] [CrossRef]

38. D. Liu, Q. Huang, Y. Yang, D. Liu, and X. Wei, “Bi-objective algorithm based on NSGA-II framework to optimize reservoirs operation,” J. Hydrol., vol. 585, no. 3, 2020, Art. no. 124830. doi: 10.1016/j.jhydrol.2020.124830. [Google Scholar] [CrossRef]

39. S. Long, Y. Zhang, Q. Deng, T. Pei, J. Ouyang and Z. Xia, “An efficient task offloading approach based on multi-objective evolutionary algorithm in cloud-edge collaborative environment,” IEEE Trans. Netw. Sci. Eng., vol. 10, no. 2, pp. 645–657, 2022. doi: 10.1109/TNSE.2022.3217085. [Google Scholar] [CrossRef]

40. L. Pan, X. Liu, Z. Jia, J. Xu, and X. Li, “A multi-objective clustering evolutionary algorithm for multi-workflow computation offloading in mobile edge computing,” IEEE Trans. Cloud Comput., vol. 11, no. 2, pp. 1334–1351, 2021. doi: 10.1109/TCC.2021.3132175. [Google Scholar] [CrossRef]

41. K. Palasundram, N. Mohd Sharef, K. A. Kasmiran, and A. Azman, “Enhancements to the sequence-to-sequence-based natural answer generation models,” IEEE Access, vol. 8, pp. 45738–45752, 2020. doi: 10.1109/ACCESS.2020.2978551. [Google Scholar] [CrossRef]

42. Z. Masood, R. Gantassi, and Y. A. Choi, “A multi-step time-series clustering-based seq2seq lstm learning for a single household electricity load forecasting,” Energies, vol. 15, no. 7, 2022, Art. no. 2623. doi: 10.3390/en15072623. [Google Scholar] [CrossRef]

43. Y. Keneshloo, T. Shi, N. Ramakrishnan, and C. K. Reddy, “Deep reinforcement learning for sequence-to-sequence models,” IEEE Trans. Neural Netw. Learn. Syst., vol. 31, no. 7, pp. 2469–2489, 2020. doi: 10.1109/TNNLS.2019.2929141. [Google Scholar] [PubMed] [CrossRef]

44. H. Ma, Y. Zhang, S. Sun, and Y. Shan, “A comprehensive survey on NSGA-II for multi-objective optimization and applications,” Artif. Intell. Rev., vol. 56, no. 12, pp. 15217–15270, 2023. doi: 10.1007/s10462-023-10526-z. [Google Scholar] [CrossRef]