Innovative Approaches to Task Scheduling in Cloud Computing Environments Using an Advanced Willow Catkin Optimization Algorithm

1  Introduction

1.1 Research Background

Cloud computing plays a pivotal role in various fields, offering a ubiquitous resource base where users can readily access cloud services on demand [1]. The “pay-as-you-go” model, characteristic of web-based applications, is employed in cloud computing to facilitate large-scale sharing of resources, including software and hardware [2]. Cloud computing systems utilize distributed technology and virtualization to enhance flexibility and resource utilization, thereby addressing diverse user requirements. Cloud service providers [3] assume responsibility for hardware and software maintenance and updates, while users need only specify their business requirements. Additionally, users circumvent the substantial expenses typically associated with constructing and maintaining extensive IT infrastructure.

Cloud computing operates on the principle of providing computing resources on demand through virtualization technologies. Task scheduling [4–6] plays a crucial role in this process, as it manages the allocation of computing tasks to virtual machines (VMs) for optimized resource utilization and system performance. The importance of task scheduling lies in its ability to ensure efficient task completion while minimizing costs and execution time and maintaining system load balance. However, current task scheduling faces numerous challenges, including finding an optimal balance between cost management, task execution efficiency, and load balancing to meet increasing computational demands.

1.2 Research Objective

The task scheduling problem in distributed systems [7,8] is generally considered a complex combinatorial optimization challenge, classified as a Non-deterministic Polynomial (NP)-hard problem [9]. Meta-heuristic algorithms [10,11] constitute a comprehensive framework for optimization methods and have demonstrated significant advantages in addressing complex objective optimization problems, particularly in resource allocation, task scheduling, and performance optimization. Population intelligence optimization algorithms [12–14], a subset of meta-heuristic algorithms, identify solutions by simulating group behavior or individual interactions. Examples of such techniques include Particle Swarm Optimization (PSO) [15–17], Ant Colony Optimization (ACO) [18], Genetic Algorithm (GA) [19,20], Tumbleweed Algorithm (TA) [21], Cat Swarm Optimization (CSO) [22,23], Artificial Bee Colony (ABC) [24], and Willow Catkin Optimization (WCO) [25].

The WCO algorithm is a meta-heuristic optimization technique designed to address complex optimization challenges by simulating the natural process of willow seed dispersal and aggregation in wind currents. This algorithm explores the solution space by emulating the diffusion and aggregation patterns of willow seeds in nature. However, the WCO algorithm exhibits certain limitations, particularly in its global search capability and convergence speed, both of which are comparatively slow. Additionally, the algorithm is prone to being trapped in local optima, which poses a significant challenge in identifying the optimal solution for complex problems.

To address these challenges, an improved Advanced Willow Catkin Optimization (AWCO) algorithm is developed in this study. This novel algorithm enhances global search capability by incorporating a reverse learning strategy and employs sinusoidal mapping to expedite convergence. AWCO substantially improves resource utilization efficiency in cloud computing task scheduling through optimized task allocation processes. The algorithm simulates willow diffusion and aggregation dynamics by initializing a set of candidate solutions, integrating these with a reverse learning strategy for global search, and swiftly identifying optimal task allocation schemes. In applications, AWCO assigns the most suitable VMs to each task, ensuring task completion with optimal resource consumption and minimal time. Simultaneously, AWCO accelerates algorithm convergence through sinusoidal mapping, effectively avoids local optima, and ultimately achieves load balancing and improved system performance in task scheduling.

1.3 Contributions and Structure of the Paper

This paper makes the following contributions:

•   The AWCO algorithm is introduced as an innovative optimization approach. The proposed reverse learning strategy is incorporated into the individual evolution process of WCO, thereby enhancing the algorithm’s capacity for exploration and exploitation, as well as its global search capability and convergence speed.

•   The sinusoidal mapping strategy is integrated into the individual position updating process to minimize the distance between individuals and the optimal solution, thereby enhancing the algorithm’s performance.

•   The AWCO algorithm is evaluated using 30 test functions from the CEC2014 dataset and is benchmarked against various alternative algorithms, including GA, bat algorithm (BA), and PSO. The experimental results demonstrate that AWCO exhibits superior performance.

•   To assess the efficacy of the proposed algorithm, it is applied to task scheduling in cloud computing environments. The experimental results indicate that, compared to similar algorithms in two heterogeneous cloud environments, the enhanced algorithm improves resource utilization for task scheduling.

Section 2 offers a comprehensive review of existing scheduling models and techniques utilized in cloud computing environments. Section 3 introduces the proposed scheduling system, followed by Section 4, which provides an in-depth examination of the WCO algorithm. Section 5 elucidates the improvements made to the WCO algorithm and illustrates the implementation of AWCO for task scheduling purposes. Section 6 presents the experimental outcomes and their subsequent performance analysis, while Section 7 concludes with a summary of the paper’s key findings and contributions.

2  Related Work

2.1 Task Scheduling Models

The diverse requirements of tasks and the intricacies of cloud environments have led to the development of numerous models for task scheduling in cloud computing. Among these, scheduling methods based on mathematical models are the most precise, typically employing mathematical optimization techniques such as linear programming, integer programming, and dynamic programming to determine the optimal task allocation scheme. These models represent the objectives and constraints of task scheduling through explicit mathematical formulas. For instance, the model proposed by Alguliyev et al. [26] ensures the efficient allocation of mobile users’ tasks to appropriate cloud resources. This is accomplished by defining a set of mathematical variables and constraints that minimize task processing time, reduce network latency, and lower the energy consumption of mobile devices. However, the computational complexity of these models increases significantly as the problem size grows. To address the challenges posed by large-scale task scheduling problems in cloud computing environments more effectively, meta-heuristic algorithms are adopted.

Moreover, load-balancing task scheduling models aim to ensure a relatively balanced load across computing nodes in cloud computing systems. Fang et al. [27] proposed a two-tier scheduling mechanism for efficient task execution in cloud computing environments. This approach initially assigns tasks to VMs, followed by mapping these VMs to physical resources. However, unlike the model presented in this study, these conventional methods typically focus solely on balanced task distribution without considering factors such as the optimization of task execution time and cost.

2.2 Task Scheduling Strategy

Task scheduling policies in cloud computing environments play a crucial role in efficient task allocation and scheduling to cloud computing resources, aiming to optimize system performance and resource utilization. These policies typically consider various factors, including time, cost, makespan [28], reliability, availability, throughput, and resource utilization, to ensure the reliable and cost-effective execution of tasks within a cloud environment. Common task scheduling techniques, such as dynamic priority scheduling [29] and hierarchical scheduling [30], are frequently employed for task optimization in cloud computing. Additionally, meta-heuristic algorithms are utilized to address cloud task scheduling challenges [31,32]. These algorithms offer advantages such as conducting more comprehensive searches, accommodating complex objective optimization problems, avoiding local optima, and improving resource utilization.

Task scheduling algorithms in these environments include those based on GA, PSO, and ACO. GAs in task scheduling identify optimal solutions by simulating natural selection and evolution processes. Changtian et al. [33] characterized independent task scheduling as a two-objective minimization problem, optimizing completion time and energy consumption. Sheng et al. [34] noted that most task scheduling algorithms prioritized overall task completion duration over individual task completion time and proposed a Template-Based Genetic Algorithm (TBGA) with user Quality of Service (QoS) constraints. Pirozmand et al. [35] emphasized that scheduling and associated energy consumption posed significant challenges for cloud computing systems and proposed a two-step hybrid scheduling approach. The PSO algorithm in task scheduling identifies optimal solutions by simulating collaborative and informational transfer dynamics observed in bird flocks or fish schools. Mansouri et al. [36] developed a new task scheduling algorithm, FMPSO, employing advanced PSO techniques and fuzzy systems. Task scheduling based on the ACO algorithm simulates ant colony behavior to solve task allocation and scheduling problems. Moon et al. [37] proposed an innovative ACO algorithm, SACO, for cloud computing task scheduling. Experimental findings confirmed SACO’s ability to maximize cloud server utilization while solving the NP-hard issue. In contrast, AWCO demonstrates enhanced global search capabilities and dynamic adaptability in task scheduling. By simulating willow diffusion and aggregation processes, AWCO accelerates convergence speed, avoids local optima, and achieves efficient resource utilization and balanced system load.

3  Task Scheduling System

3.1 Model Design

In a cloud computing environment, the task scheduling algorithm initiates the assignment of tasks to VMs upon their addition to the task queue by the task manager. Fig. 1 illustrates a representative example of task scheduling in a cloud computing system. Presently, task scheduling in cloud computing faces significant challenges, primarily in intelligently allocating tasks to processors for cost-effectiveness, load balancing, and reduced makespan. To address the limitations of current research on task scheduling algorithms in cloud computing, this study proposes an enhanced task scheduling method utilizing an enhanced version of the Advanced Phasmatodea Population Evolution (APPE) algorithm [38].

Figure 1: Task scheduling model for cloud computing environment

Each task is characterized by two attributes: the number of tasks designated as n and the number of machine language instructions in millions required for task execution represented by variable len. VMs possess five attributes: m, MIPS, RAM, bandwidth, and storage. The m attribute represents the number of available VMs, while MIPS indicates the average speed at which a VM processes single-word fixed-point instructions. The RAM attribute refers to the VM’s memory capacity, the bandwidth attribute represents the network bandwidth of a VM, and the storage attribute denotes a VM’s storage capacity. Several key factors primarily influence the load profile of a VM. The system employs sequential task execution through task queues and scheduling algorithms, whereby each assignment is completed linearly on the VM.

3.2 Formulation of the Objective Function

This article aims to assess the performance of task scheduling in makespan, cost-effectiveness, and load balancing.

Consider a scenario where a cloud user submits a task queue, denoted as Task, comprising tasks T1, T2, …, up to Tn (30 ≤ n ≤ 300). Testing low and high task counts demonstrates the algorithm’s adaptability to varying task quantities. Additionally, a set of VMs is defined as VM = {VM1, VM2, ..., VMm}, where VMj corresponds to the j-th VM. We introduce the variable EXT, represented as EXT = {EXTij}n × m, to signify the expected execution time. This metric indicates the time required for task i to be processed on VMj and is calculated using the following Eq. (1):

(1)

The variable T_length, consisting of elements len1, len2, ..., and lenn, represents the duration of the i-th task, denoted as leni. MIPSj denotes the execution rate of VMj. Consequently, EXTij signifies the estimated time required to complete task i on VMj, considering various factors such as task length and potentially relevant parameters.

(a)   Cost:

The cost of a VM encompasses multiple factors, including the utilization of CPU, memory, and storage resources, as well as the operational duration of the VM. These costs are typically billed on a usage-per-unit-of-time basis. The calculation formula is presented in Eq. (2):

(2)

where costj denotes the hourly cost of the jth VM, influenced by MIPS, RAM, bandwidth, and storage in this environment. Let RUN = {RUNij}n × m, where RUNij is a binary indicator (1 or 0) representing whether task i is executed on VM j. Specifically, RUNij = 1 indicates task i is assigned to VM j, while RUNij = 0 implies otherwise.

(b)   Makespan:

In the context of task scheduling, Makespan represents a critical performance metric for the total time required to complete the entire set of tasks, which reflects the efficiency and productivity of task scheduling. Consequently, minimizing Makespan is commonly considered an optimization objective in the development of scheduling algorithms. The calculation formula is presented in Eq. (3):

(3)

(c)   Load:

The significance of load in task scheduling is exemplified by the system’s selection of suitable nodes for task execution. A node with a higher load may result in increased task execution time. Consequently, task scheduling algorithms typically consider node load and select nodes with the lowest load to execute tasks, aiming to maintain system efficiency and optimize performance. The calculation formula is provided in Eq. (4):

(4)

where m is the number of VMs, loadj denotes the load of the jth VM, denotes the overall VMs’ average load, and VTj denotes the running time of the jth VM, as described in Eqs. (5)–(7). Specifically, MIPS is used to calculate the task execution time of a VM; RAM and storage impose constraints on the number and size of tasks a VM can host; and bandwidth is utilized to simulate the task transmission time over the network, reflecting network latency’s impact on task completion time. Consequently, the resource constraints of the VM directly influence task allocation and execution, ensuring that the processing capacity of the VM is not exceeded during scheduling [39].

(5)

(6)

(7)

where α, β, γ, and δ are the four parameters.

Based on these performance indicators, the expression of the fitness function is given in Eq. (8):

(8)

where a1, a2, and a3 are three weights that satisfy a1 + a2 + a3 = 1. The value of each weight can be adjusted according to specific task requirements. The objective of task scheduling is to minimize the value of the fitness function.

4  WCO Algorithm

The WCO algorithm simulates the dispersal of willow seeds, also referred to as willow flakes, as they are carried by the wind. This process is primarily influenced by two factors: wind speed and wind direction. As the willow flakes descend, they tend to cluster together, potentially adhering to one another when in close proximity. Furthermore, the algorithm reflects the gradual decrease in the dispersal range of willow seeds, representing a transition from an exploration phase to an exploitation phase in the optimization process.

4.1 Initialization Phase

The algorithm’s initialization phase involves generating random seeds and distributing them across the solution space. This space can be represented by a matrix with N rows and D columns, where N signifies the total population size, and D represents the dimensionality of each individual. In this matrix, each row corresponds to a single individual, while each column represents a specific attribute of that individual. The WCO process commences with this random population in the willow tree, generating the initial random population using the following Eq. (9):

(9)

Here, the random number r is within the range [0, 1], xi denotes a D-dimensional solution, and the solution space is bounded by an upper limit UB and a lower limit LB.

4.2 Search Phase

During the search phase, following the descent of willow catkins from the willow tree, each flake is influenced by two primary factors: wind speed and direction. If individuals update their positions too closely to one another during the iterative process, they will be blown closer together by the wind. To measure the distance between individuals, the distance between the current individual and the global optimal solution, denoted by di, is calculated. An adhesion-prone radius R is introduced; if the distance di between individuals exceeds R, they are less likely to stick together, and Eq. (10) is applied to determine the stochastic wind speed and direction. Conversely, if di is less than or equal to R, indicating a higher probability of adhesion, Eq. (11) is employed. The weights are then computed according to Eqs. (12) and (13).

(10)

(11)

(12)

(13)

where pg represents the current global optimal solution, the symbol signifies the Euclidean distance between xi and pg, DW denotes the weight of the distance between pg and xi in each dimension relative to the total distance, while μ is a random number generated within the range of 0.4 to 0.6.

By incorporating the randomly generated wind speed ws and wind direction wd into Eq. (14), we can determine the direction and distance of an individual’s movement during each iterative update.

(14)

The individual update process can be accomplished by decomposing the wind’s direction and speed into components u and v. We employ Eq. (15) to execute the individual update.

(15)

where xi represents the current position of the individual, and a is a parameter that governs the transition from exploration to exploitation during the individual’s iterative process.

(16)

Here, t represents the current number of iterations, T denotes the maximum number of iterations allowed, and c is a constant fixed at 2.

5  AWCO Algorithm

The update mechanism in WCO primarily relies on local information despite its efforts to guide updates toward the global optimum in each generation. However, an update mechanism lacking global search capabilities may struggle with complex optimization problems. The proposed reverse learning strategy addresses this limitation by considering both the current and inverse solutions, thereby expanding the search space coverage and exploring a wider range of potential solutions. Additionally, improvements to the WCO algorithm’s convergence speed are essential. The incorporation of sinusoidal mapping in the initialization phase and position update formula aims to enhance the algorithm’s ability to identify the optimal solution.

5.1 Improvement Methods

5.1.1 Sinusoidal Mapping for Enhanced Population Initialization

Sine chaotic mapping [40] is a chaotic system derived from sinusoidal functions, which is characterized by high dynamic randomness that produces a nonlinear and unpredictable output sequence. The nonlinear properties of this mapping increase the algorithm’s complexity, particularly in scenarios where avoiding locally optimal solutions is crucial. Implementing sine chaotic mapping in the algorithm enables a more thorough exploration of the search space. Its irregular trajectory allows for the traversal of each potential solution and enhances the algorithm’s convergence, thus facilitating more efficient identification of the global optimum solution. The mathematical formulation of this mapping is presented in the following Eq. (17):

(17)

The sinusoidal mapping’s value domain is defined as the interval [−1, 1]. In Eq. (17), a represents a real number within the interval (0, 4], zk denotes the mapping sequence of the k-th individual, while zk+1 represents the mapping sequence of the (k+1)-th individual.

The parameter a plays a crucial role in determining the randomness of sinusoidal mapping. To identify the optimal value of a, this study conducts a comparative experiment using CEC2014, with the results presented in Table 1. The algorithms yielding the optimal results are highlighted in bold. The comparison reveals that when a is set to 4, the algorithm achieves the highest number of optimal outcomes. Consequently, this paper adopts a value of 4 for a.

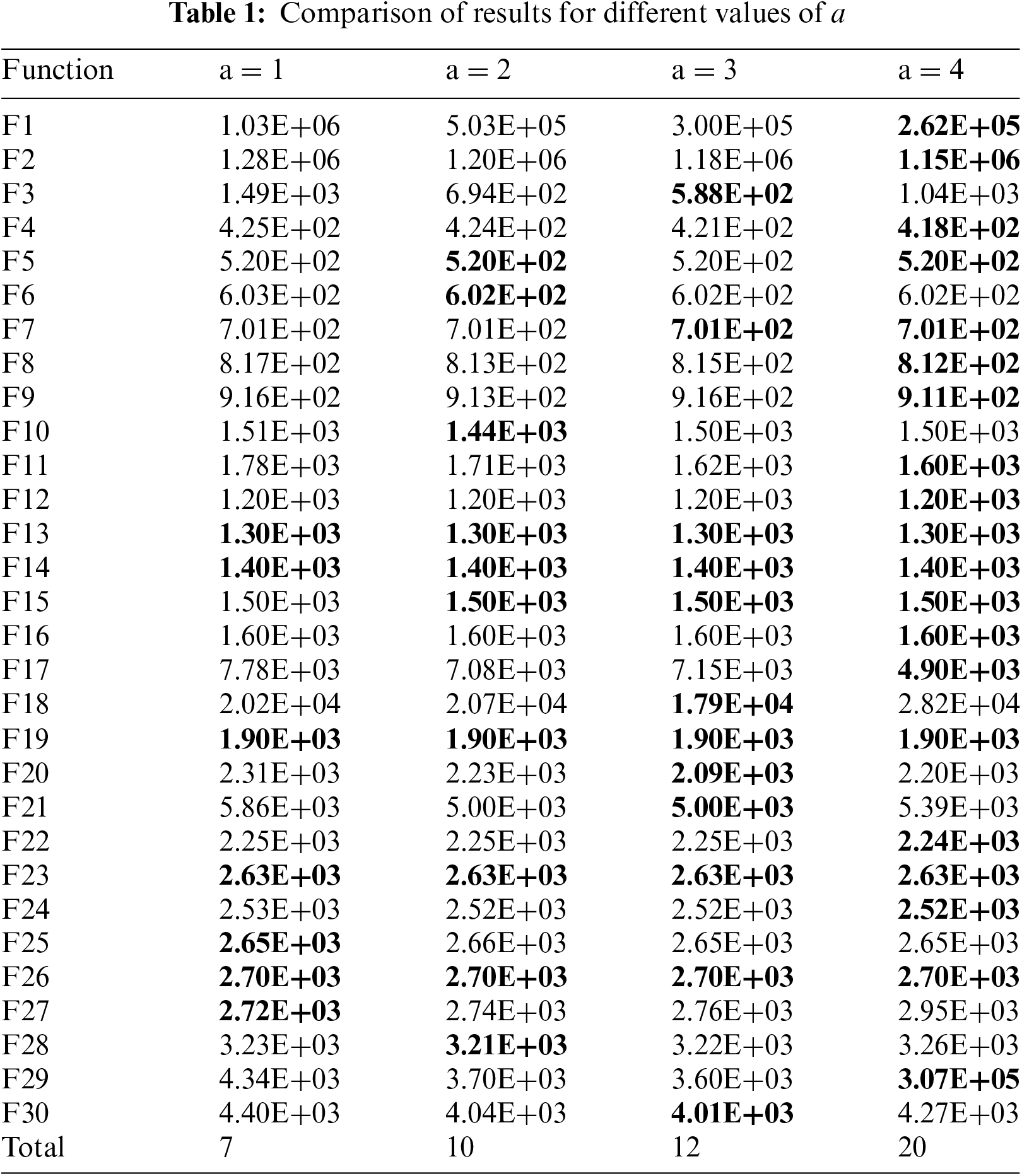
Consequently, the initialization formula is modified as follows:

(18)

where z represents the sequence of sinusoidal mappings.

5.1.2 Sinusoidal Mapping for Improved Position Update Formula

In the original algorithm, the component vectors of wind in the position update formula are generated using pseudo-random numbers to create d-dimensional vectors. However, pseudo-random number generators may not provide adequate randomness and distribution. To address this limitation, this study employs sinusoidal mapping as an alternative to pseudo-random numbers for position updates. The enhanced formula is presented in Eq. (19):

(19)

5.1.3 Quasi-Opposition-Based Learning (QOBL) Strategy

QOBL [41] builds upon the concept of Opposition-Based Learning (OBL) [42], aiming to enhance the search process efficiency and global optimization performance. Unlike conventional OBL, QOBL implements a more flexible adversarial strategy. Instead of merely adopting elements from the inverse solution, it incorporates perturbations or variations of adversarial elements. This approach facilitates a more adaptable exploration of the search space, thereby strengthening the algorithm’s ability to conduct global searches and avoid entrapment in local optima.

Consider x as a point in the d-dimensional space, represented by the vector x = (x1, x2, …, xd), where each component xj is a real number within the interval [aj, bj], with aj and bj being constants. The inverse solution is defined in d-dimensions and is expressed by the following Eqs. (20)–(22):

(20)

(21)

(22)

where represents a uniform random number between Mj and , signifies the inverse solution of xj, and denotes the proposed inverse solution of xj.

If the termination condition is not met, each individual’s fitness value is evaluated after each position update. Subsequently, the lowest-performing 10% of individuals are selected for the proposed reverse learning process. Following this, individuals with superior fitness values are incorporated into the population.

The AWCO pseudo-code is presented in Algorithm 1 below for reference.

5.2 AWCO-Based Task Scheduling

The primary aim of task scheduling is to allocate specific tasks to VMs. In this context, the dimension d signifies the number of tasks, while n represents both the number of solutions and the population size within the algorithm. Each individual in the population corresponds to a potential solution. The optimal solution, which represents the most efficient resource allocation plan, is determined through the application of a fitness function.

To determine the initial globally optimal solution, the population must first be initialized, followed by solving the fitness function to ascertain the fitness value. Subsequently, the position of each generation of individuals is updated using the willow position, and the global optimal solution is refined. This process continues, with fitness values recalculated until the termination condition is met. The final globally optimal solution represents the ideal scheduling plan.

In cloud computing environments, tasks often present diverse priorities, variable execution time, and fluctuating resource requirements during the execution phase. Many conventional scheduling algorithms tend to converge on local optimal solutions, leading to suboptimal resource utilization and inefficient task execution. AWCO addresses these limitations by overcoming the constraints of conventional algorithms. It demonstrates an enhanced ability to approximate optimal solutions efficiently. These improvements enable AWCO to effectively tackle task scheduling challenges in cloud computing environments. Consequently, AWCO facilitates the optimization of resource utilization, reduces task completion time, and enhances overall system performance.

6  Experiments

This section provides a preliminary evaluation of the AWCO algorithm’s performance on CEC2014, comparing it with other established algorithms such as the GA, BA [43,44], Sinusoidal Cosine Algorithm (SCA) [45], TA, PSO, Rafflesia Optimization Algorithm (ROA) [46], and WCO. Following this comparison, AWCO’s performance is assessed in two distinct heterogeneous cloud environments.

6.1 Experimental Setup

The CEC2014 benchmark function set, established by the 2014 IEEE Congress on Evolutionary Computation, consists of a series of test functions. These functions have been utilized to assess and compare the performance of various optimization algorithms, particularly those related to evolutionary computation and meta-heuristic algorithms. The test suite encompasses 30 test functions, including single-peaked (F1–F3), multi-peaked (F4–F16), mixed-peaked (F17–F22), and combinatorial-peaked (F23–F30) ones. This diversity aims to assess the algorithms’ performance and adaptability across various problem types. This study presents an analysis of the comparative effectiveness of several algorithms, with particular emphasis on contrasting the AWCO algorithm with the original algorithm. The comparison involved executing each benchmark function 20 times. Each iteration was performed using CEC2014 with function dimensions of 10, 30, and 50, culminating in a total of 50,000 function evaluations.

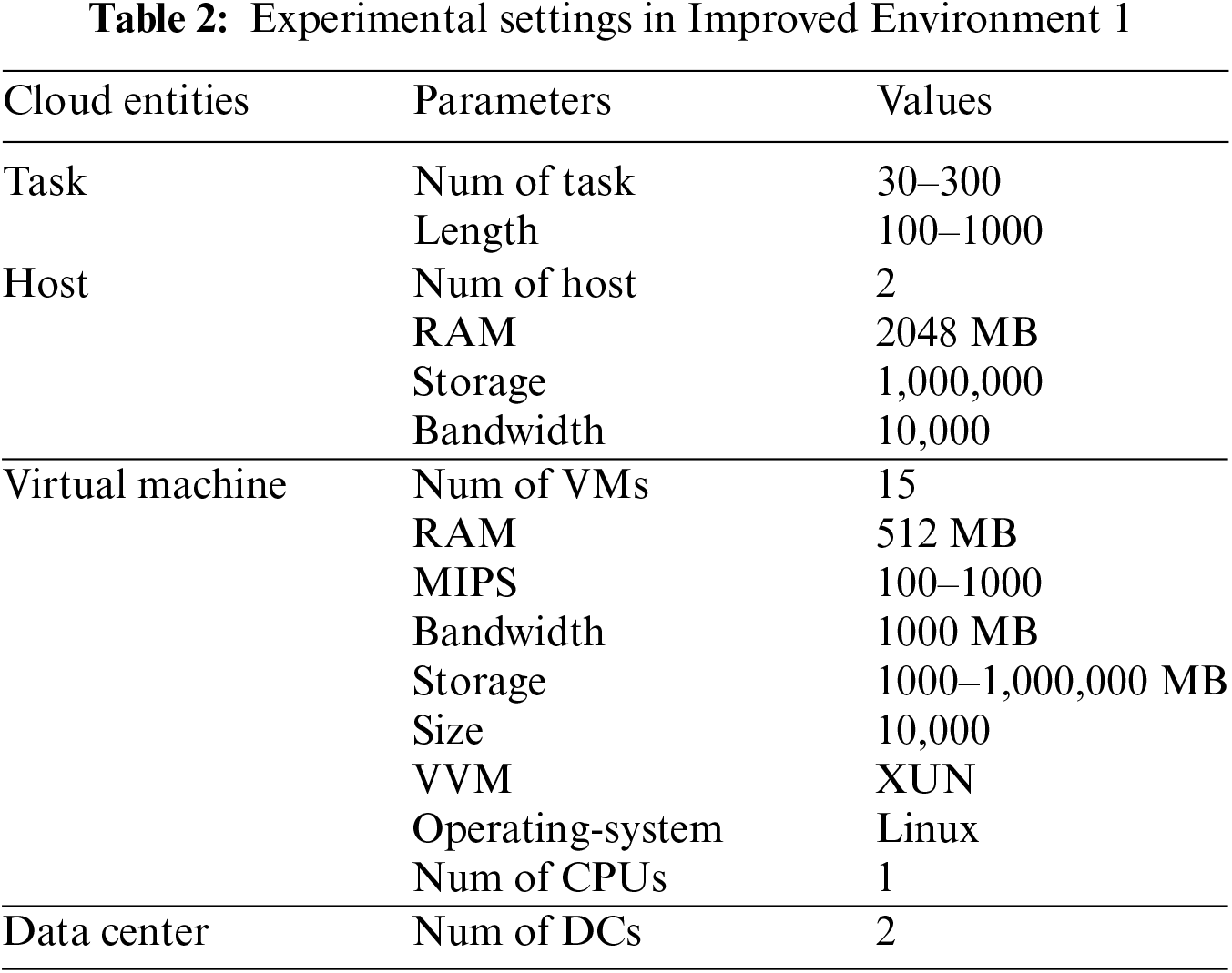
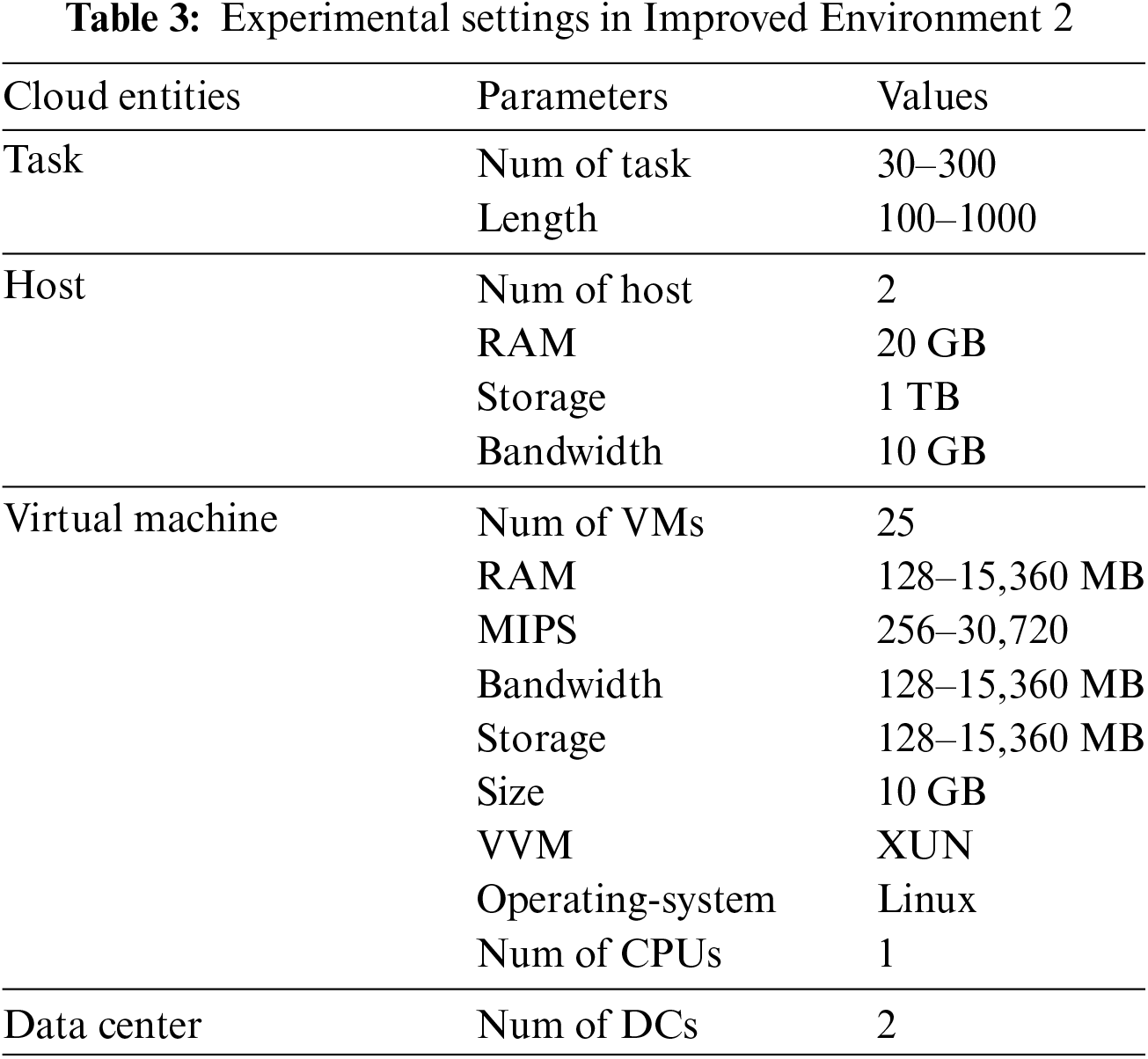
Following comprehensive simulations of the CEC2014 test functions, practical application tests were conducted on the AWCO algorithm in an enhanced mixed cloud environment. This approach facilitated a comparison with other algorithms, including WCO, PSO, GA, BA, SCA, TA, and APPE. To ensure a fair comparison, identical initial conditions were maintained, with the population size and iteration times set to 100. The performance of the two independent heterogeneous environment evaluation algorithms was enhanced. In the initial improved environment (hereinafter referred to as Improved Environment 1), the MIPS and storage capacity values of the VMs were distinct, while the remaining factors remained constant. In the second improved environment (hereinafter referred to as Improved Environment 2), a random number generator was employed to select values for RAM, MIPS, bandwidth, and storage of the VMs, which were then assigned to specific ranges. The relevant parameters are presented in Tables 2 and 3. The costs associated with resource utilization were determined by the specifications delineated for the VMs. The resulting calculations yielded the following costs: $0.12, $0.13, $0.17, $0.48, $0.52, and $0.96 per hour [47].

6.2 Comparison Results of CEC2014 Benchmark Test Suite

Table 4 employs the following notations: “+” indicates superior performance of AWCO compared to other algorithms, “−” denotes inferior performance, and “=” signifies comparable performance. The AWCO algorithm demonstrates superior performance across all functions when compared to GA, SCA, TA, and WCO. Furthermore, it outperforms BA and ROA in 29 functions and PSO in 26 functions. AWCO exhibits superior performance in all single-peak functions, attributable to its implementation of sinusoidal mapping for position updates. The AWCO algorithm only shows marginal inferiority to PSO regarding F27. Additionally, AWCO demonstrates superior performance in the remaining mixed-peak and combinatorial functions, which often comprise multiple local and global optimal solutions. The QOBL strategy employed by AWCO effectively navigates around local optima, showcasing robust global search capabilities. Moreover, AWCO demonstrates an effective balance between exploration and exploitation processes, enabling thorough exploration of unvisited regions while accurately searching for optimal solutions near local optima.

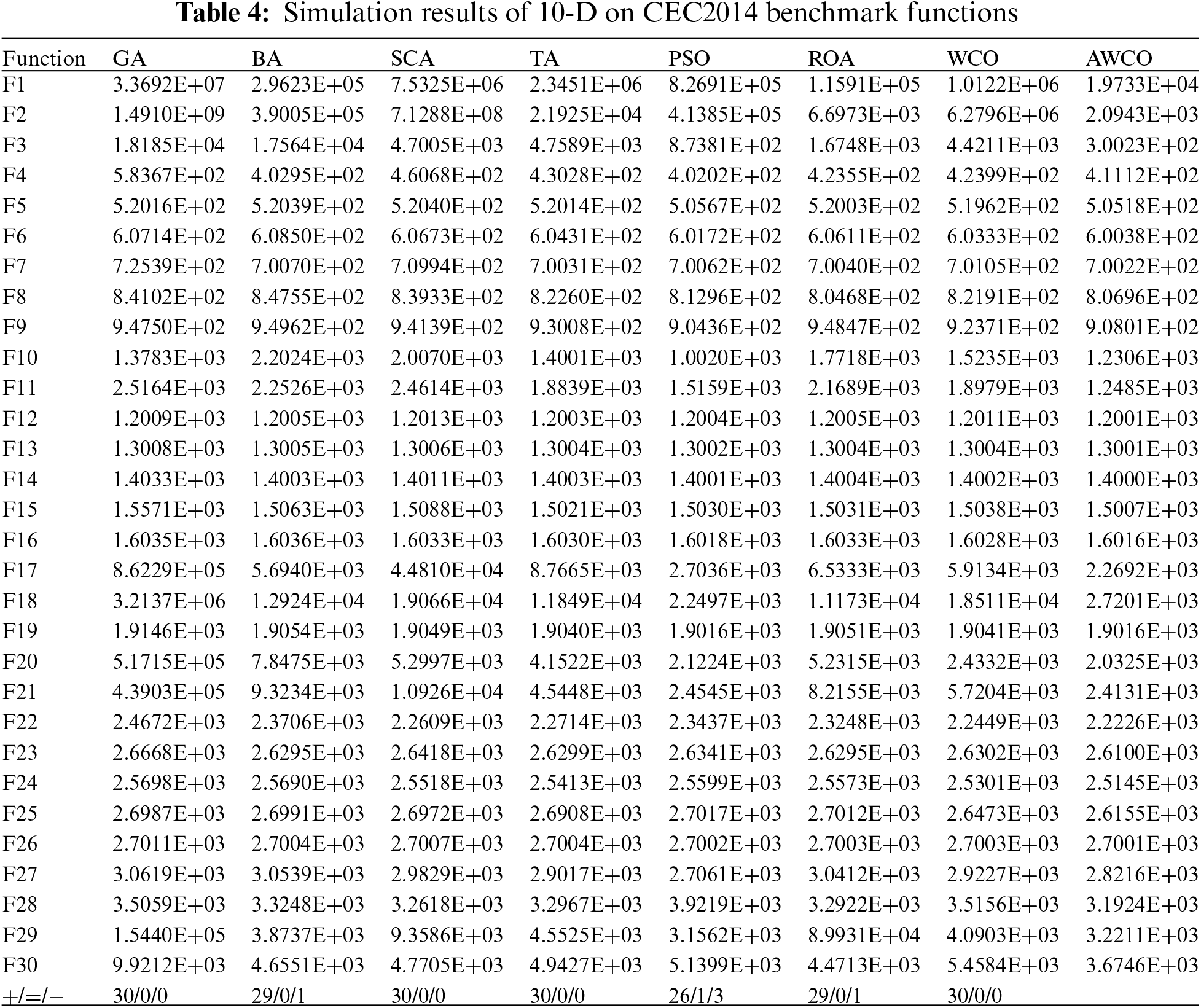
Table 5 presents a comparative analysis of the algorithms across 30 dimensions. The data in the table demonstrates that the AWCO algorithm outperforms GA, SCA, TA, and WCO in various scenarios, including single-peak, multi-peak, and mixed-peak problems. The results indicate the algorithm’s robustness in handling diverse problem types, from simple single-peak problems to multi-peak problems with multiple local optima and mixed-peak problems with complex structures. Moreover, AWCO exhibits enhanced performance compared to BA and ROA in single-peak and mixed-peak scenarios. In the mixed-peak function, AWCO slightly underperforms PSO in F22 but surpasses the other algorithms in the remaining cases. These findings suggest that as problem dimensionality increases, AWCO demonstrates a superior ability to avoid local optima, making it more suitable for complex optimization problems.

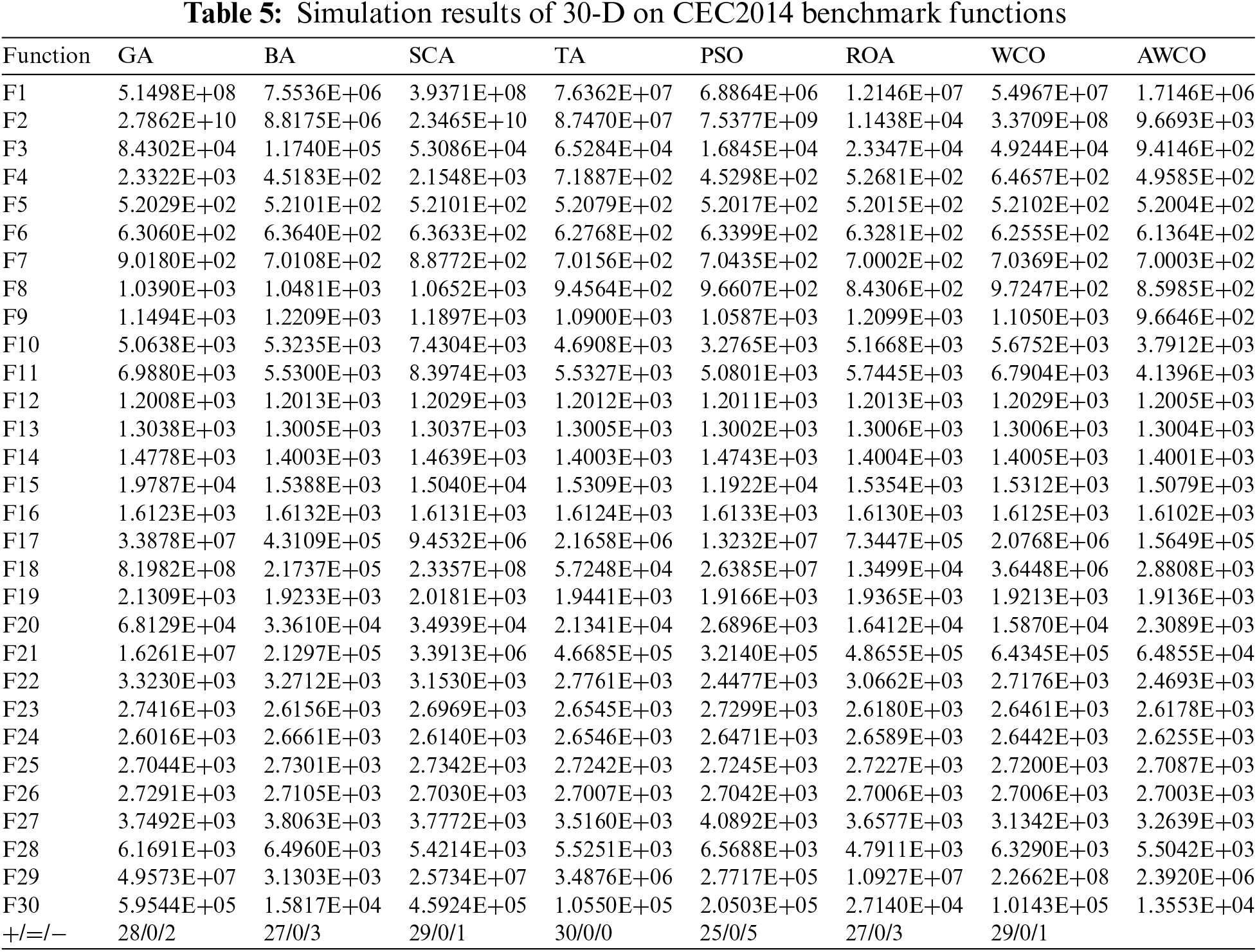
Table 6 presents a comparative analysis of the algorithms across 50 dimensions. Among the 50 dimensions, AWCO exhibits 28 test functions with superior performance when compared to SCA, 26 test functions surpassing GA and TA, and 25 test functions outperforming WCO. These results indicate that the AWCO algorithm demonstrates effective global search capabilities. Except for F12 and F16, which show performance characteristics similar to those of SCA, all functions exhibit superior performance in AWCO compared to SCA. Moreover, AWCO outperforms the remaining algorithms by a margin exceeding 80% in high-dimensional problems, suggesting its proficiency in navigating high-dimensional spaces. High-dimensional problems typically present complex search spaces with numerous local optima. AWCO employs the QOBL strategy to maintain population diversity throughout the search process, preventing solution space reduction due to over-aggregation and ensuring adequate exploration capabilities in high-dimensional problems. The commendable performance of AWCO demonstrates its ability to efficiently navigate these complex spaces, avoiding the pitfalls of local optima. AWCO outperforms other classical algorithms on most test functions, thus exhibiting robustness and consistency.

To further demonstrate the superior performance of AWCO, we conducted convergence performance tests on 30 benchmark functions in CEC2014, including convergence graphs of 10-D, 30-D, and 50-D. Each dimension was tested on functions exhibiting single, multiple, mixed, and combined peaks, enabling a comprehensive evaluation of AWCO’s convergence and robustness. Fig. 2 illustrates the convergence performance of AWCO on the 10-D dataset. Compared to other algorithms such as GA, WCO, and SCA, the results show that AWCO exhibits superior performance, particularly for multiple and combined peaks. This is attributed to AWCO’s utilization of a reverse learning strategy to identify the optimal solution, allowing it to converge to the global optimal solution more rapidly.

Figure 2: Convergence graph of CEC2014 benchmark functions on 10-D

Fig. 3 illustrates the convergence performance of AWCO on 30-D. AWCO demonstrates superior performance compared to alternative algorithms, particularly in processing data related to functions with multiple and combined peaks. The AWCO algorithm converges notably faster than other algorithms for most functions. AWCO’s ability to achieve low fitness values with limited evaluations highlights its exceptional global search capability and efficiency in identifying optimal solutions. The graph displays several fitness curves, with AWCO’s curve being the most prominent, especially in the early stages. The sinusoidal mapping enables a more uniform initial population distribution across the solution space, facilitating rapid identification of high-quality solutions in the algorithm’s initial phase. The AWCO curve exhibits minimal fluctuation, indicating stability throughout the optimization process and reduced susceptibility to significant performance variations.

Figure 3: Convergence graph of CEC2014 benchmark functions on 30-D

Fig. 4 illustrates the convergence performance of AWCO on the 50-dimensional data set. While the performance of many algorithms may deteriorate with increasing dimensionality, AWCO consistently demonstrates superior convergence and achieves lower fitness values more quickly than other algorithms for most functions. This suggests that AWCO possesses enhanced global search capabilities and convergence speed when addressing high-dimensional problems. Although increased dimensionality typically results in performance fluctuations for many algorithms, AWCO’s fitness curves remain smooth with minimal variations, indicating its robustness is well-preserved even in high-dimensional problems. This stability is attributed to the sinusoidal mapping, which enhances the stochastic nature of positional updates while maintaining a uniform distribution of population initialization, thus providing a robust foundation for the algorithm’s exploration from the outset. AWCO’s superiority in various aspects renders it a noteworthy and applicable algorithm.

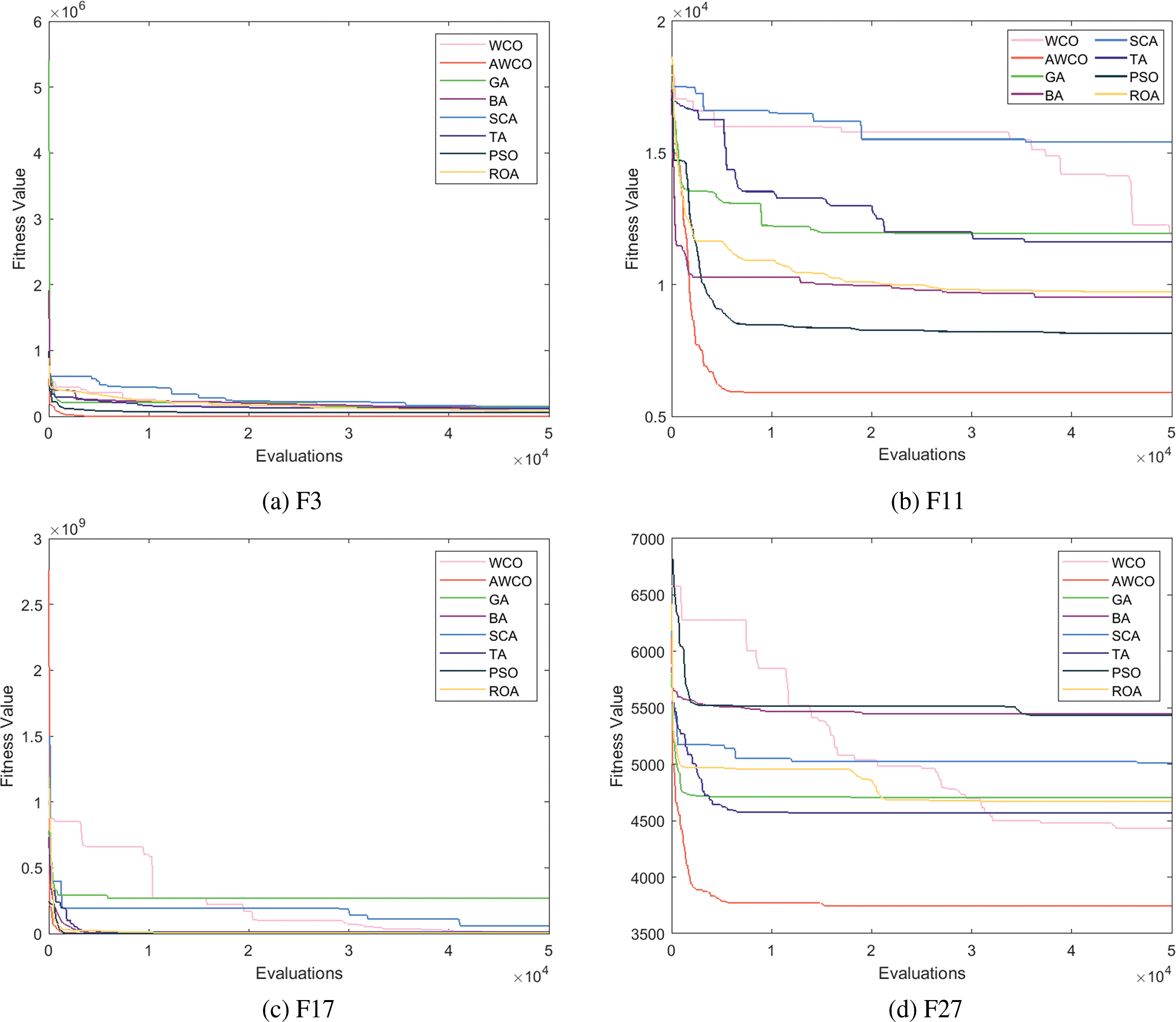
Figure 4: Convergence graph of CEC2014 benchmark functions on 50-D

6.3 Experimental Results of Task Scheduling in Improved Heterogeneous Cloud Environments

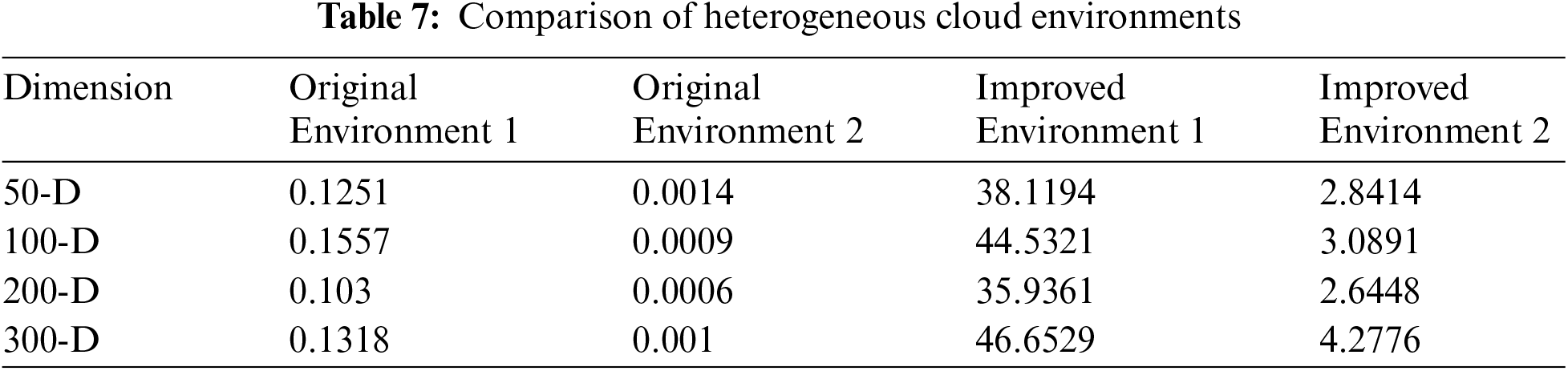
The APPE algorithm was employed to evaluate the performance of both the original and improved heterogeneous cloud environments, and the results are presented in Table 7. The objective function values of Improved Environments 1 and 2 are significantly lower than those of the original environments, indicating that the improved environments are more conducive to optimization and demonstrate superior performance across all dimensions. This suggests that in these improved environments, the optimization algorithm can identify outcomes more closely aligned with the global optimal solution. Since the goal is to minimize the objective function value, the lower values in the improved environments indicate greater efficiency. In dimensions ranging from 50-D to 300-D, the improved environments (1 and 2) consistently exhibit lower objective function values, demonstrating that the enhanced cloud environments maintain their optimization capability for high-dimensional problems.

To rigorously evaluate the effectiveness of the AWCO algorithm, 30 trials were conducted for each of the following algorithms: WCO, PSO, GA, BA, SCA, TA, and APPE. These trials were performed in the improved heterogeneous cloud environment, and the resulting averages were compared across dimensions of 30-D, 50-D, 100-D, 200-D, and 300-D, where the dimension refers to the task volume. The comparative analysis of these averages is presented in Tables 8 and 9. The data in these tables indicate that AWCO consistently demonstrates the lowest mean value compared to other algorithms, suggesting superior efficiency and global search capability in optimizing cloud-based tasks. Furthermore, the values in Table 9 (Improved Environment 2) are generally lower than those in Table 8 (Improved Environment 1), particularly at smaller dimensions (30-D and 50-D). This implies more effective task allocation management in the context of enhanced load capacity. In this environment, the reduced average values across all algorithms indicate improved efficiency in resource management and task scheduling.

At elevated task counts (e.g., 200-D and 300-D tasks), the mean value of AWCO is significantly lower than that of the other algorithms. This suggests that AWCO not only performs optimally with low task volumes but also demonstrates notable adaptability and robustness in high-volume task scenarios. The sinusoidal mapping strategy and QOBL approach contribute to the algorithm’s enhanced flexibility within the solution space. The dynamic adjustment of task scheduling, based on feedback during the search process, enables the algorithm to utilize high-quality solutions more efficiently while maintaining the ability to explore new solutions.

Figs. 5 and 6 illustrate the convergence of the algorithm in both improved environments with varying task volumes. The convergence plots demonstrate three scenarios: low, medium, and high task volumes. The BA, TA, and APPE algorithms exhibit greater consistency across all task volumes, although they do not perform as well as the AWCO algorithm under high task volumes. The AWCO algorithm demonstrates superior performance under varying task volumes, particularly in high task volumes, where it shows higher convergence speeds and final convergence values. While the other algorithms may perform better under specific task volumes, they generally do not match the effectiveness of the AWCO algorithm. A comparison of the AWCO algorithm with the other algorithms reveals its notable advantage in terms of convergence speed and capacity to handle different task volumes and heterogeneous environments. This indicates that the AWCO algorithm is more efficient and robust than similar algorithms for task scheduling. Moreover, AWCO not only demonstrates notable performance under a single task volume but also exhibits adaptability in diverse heterogeneous environments. This positions the AWCO algorithm as an effective tool for addressing task scheduling challenges and a reliable solution for task allocation in complex environments.

Figure 5: Comparison of convergence for different tasks in Improved Environment 1

Figure 6: Comparison of convergence for different tasks in Improved Environment 2

To effectively demonstrate the efficacy of the AWCO algorithm in cloud environments, experiments were conducted to analyze the makespan, cost, and load. Figs. 7 and 8 illustrate the experiments conducted in homogeneous (Improved Environment 1) and heterogeneous (Improved Environment 2) cloud environments, respectively. The number of tasks varied between 30 and 300, with a step size of 90. The experimental results presented in Fig. 7 demonstrate that the AWCO algorithm exhibits notable superiority over the other meta-heuristic algorithms in terms of cost, completion time, and load as the number of tasks increases. The ability to achieve the lowest cost, shortest completion time, and most effective load balancing is of great significance in task scheduling. This is attributed to the AWCO algorithm’s effective exploration and development capabilities, enabling it to identify more suitable solutions for task allocation. The experimental results in Fig. 8 are analogous to those in Fig. 7, with the AWCO algorithm again demonstrating advantages over the other algorithms. In the heterogeneous Improved Environment 2, the completion time is reduced in comparison to the cost. This is because a greater number of VMs can be assigned to the tasks, thereby improving efficiency.

Figure 7: Comparison of makespan, cost, and load balancing level of each algorithm for different task volumes in Improved Environment 1

Figure 8: Comparison of makespan, cost, and load balancing level of each algorithm for different task volumes in Improved Environment 2

7  Conclusions

To enhance global search capability, this study implements the QOBL strategy in the proposed AWCO algorithm, which proves effective in achieving the desired outcome. Additionally, the incorporation of chaotic mapping improves the convergence rate, strengthens its exploration and exploitation capabilities, and facilitates rapid and accurate identification of the optimal solution. In the CEC2014 benchmark functions, the AWCO algorithm demonstrates superior performance compared to the original WCO algorithm, effectively addressing the latter’s convergence and instability issues. Moreover, it yields favorable results in task scheduling within cloud computing environments. These improvements offer a more viable and reliable solution for the practical implementation of WCO.

While AWCO demonstrates effectiveness in solving task scheduling problems, it may not be the optimal solution for highly complex and multimodal issues. In such scenarios, AWCO might struggle to efficiently escape local optima, potentially limiting its global search capabilities. To address these limitations, future research should focus on incorporating an adaptive mechanism to dynamically adjust AWCO parameters and enhance its ability to navigate complex problem spaces. Although this study has provided valuable insights into the task scheduling algorithm’s efficacy, it primarily emphasizes algorithmic optimization and has not fully examined the impacts of cloud and data center dynamics on task scheduling in cloud computing environments. This includes crucial factors such as dynamic resource management, data transmission overheads, and energy consumption optimization. Future investigations could integrate cloud computing infrastructure characteristics with a more comprehensive analysis of data center resource fluctuations and network environment dynamics. This approach would better align with task scheduling requirements in real-world cloud computing scenarios, thereby improving the algorithm’s practicality and efficiency.

Acknowledgement: The authors would like to express their gratitude to all the anonymous reviewers and the editorial team for their valuable feedback and suggestions.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Jeng-Shyang Pan, Na Yu; data collection: Na Yu; analysis and interpretation of results: An-Ning Zhang; draft manuscript preparation: Shu-Chuan Chu, Bin Yan, Junzo Watada. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Shu-Chuan Chu, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. R. Kaewpuang, D. Niyato, P. Wang, and E. Hossain, “A framework for cooperative resource management in mobile cloud computing,” IEEE J. Sel. Areas Commun., vol. 31, no. 12, pp. 2685–2700, 2013. doi: 10.1109/JSAC.2013.131209. [Google Scholar] [CrossRef]

2. J. Huang, W. Susilo, F. Guo, G. Wu, Z. Zhao and Q. Huang, “An anonymous authentication system for pay-as-you-go cloud computing,” IEEE Trans. Dependable Secure Comput., vol. 19, no. 2, pp. 1280–1291, 2020. doi: 10.1109/TDSC.2020.3007633. [Google Scholar] [CrossRef]

3. B. Calder et al., “Windows azure storage: A highly available cloud storage service with strong consistency,” in Proc. Twenty-Third ACM Symp. Oper. Syst. Princ., Cascais, Portugal, 2011, pp. 143–157. [Google Scholar]

4. A. Arunarani, D. Manjula, and V. Sugumaran, “Task scheduling techniques in cloud computing: A literature survey,” Future Gener. Comput. Syst., vol. 91, no. 4, pp. 407–415, 2019. doi: 10.1016/j.future.2018.09.014. [Google Scholar] [CrossRef]

5. E. H. Houssein, A. G. Gad, Y. M. Wazery, and P. N. Suganthan, “Task scheduling in cloud computing based on meta-heuristics: Review, taxonomy, open challenges, and future trends,” Swarm Evol. Comput., vol. 62, no. 3, 2021, Art. no. 100841. doi: 10.1016/j.swevo.2021.100841. [Google Scholar] [CrossRef]

6. N. Mansouri et al., “An efficient task scheduling based on seagull optimization algorithm for heterogeneous cloud computing platforms,” Int. J. Eng., vol. 35, no. 2, pp. 433–450, 2022. doi: 10.5829/IJE.2022.35.02B.20. [Google Scholar] [CrossRef]

7. K. Efe, “Heuristic models of task assignment scheduling in distributed systems,” Computer, vol. 15, no. 6, pp. 50–56, 1982. doi: 10.1109/MC.1982.1654050. [Google Scholar] [CrossRef]

8. J. Huang, C. Lin, and B. Cheng, “Energy efficient speed scaling and task scheduling for distributed computing systems,” Chin. J. Electron., vol. 24, no. 3, pp. 468–473, 2015. doi: 10.1049/cje.2015.07.005. [Google Scholar] [CrossRef]

9. D. S. Hochba, “Approximation algorithms for np-hard problems,” ACM Sigact News, vol. 28, no. 2, pp. 40–52, 1997. doi: 10.1145/261342.571216. [Google Scholar] [CrossRef]

10. Z. Beheshti and S. M. H. Shamsuddin, “A review of population-based meta-heuristic algorithms,” Int. J. Adv. Soft Comput. Appl., vol. 5, no. 1, pp. 1–35, 2013. [Google Scholar]

11. M. Hubálovská, Š. Hubálovský, and P. Hubálovský, “Botox optimization algorithm: A new human-based metaheuristic algorithm for solving optimization problems,” Biomimetics, vol. 9, no. 3, 2024, Art. no. 137. doi: 10.3390/biomimetics9030137. [Google Scholar] [PubMed] [CrossRef]

12. M. Mavrovouniotis, C. Li, and S. Yang, “A survey of swarm intelligence for dynamic optimization: Algorithms and applications,” Swarm Evol. Comput., vol. 33, no. 11, pp. 1–17, 2017. doi: 10.1016/j.swevo.2016.12.005. [Google Scholar] [CrossRef]

13. H. Ma, S. Shen, M. Yu, Z. Yang, M. Fei and H. Zhou, “Multi-population techniques in nature inspired optimization algorithms: A comprehensive survey,” Swarm Evol. Comput., vol. 44, no. 10, pp. 365–387, 2019. doi: 10.1016/j.swevo.2018.04.011. [Google Scholar] [CrossRef]

14. J. Tang, G. Liu, and Q. Pan, “A review on representative swarm intelligence algorithms for solving optimization problems: Applications and trends,” IEEE/CAA J. Automatica Sinica, vol. 8, no. 10, pp. 1627–1643, 2021. doi: 10.1109/JAS.2021.1004129. [Google Scholar] [CrossRef]

15. F. Marini and B. Walczak, “Particle swarm optimization (PSO). A tutorial,” Chemometr. Intell. Lab. Syst., vol. 149, pp. 153–165, 2015. doi: 10.1016/j.chemolab.2015.08.020. [Google Scholar] [CrossRef]

16. C. -L. Huang and J. -F. Dun, “A distributed PSO-SVM hybrid system with feature selection and parameter optimization,” Appl. Soft Comput., vol. 8, no. 4, pp. 1381–1391, 2008. doi: 10.1016/j.asoc.2007.10.007. [Google Scholar] [CrossRef]

17. A. R. Jordehi, “Enhanced leader PSO (ELPSOA new PSO variant for solving global optimisation problems,” Appl. Soft Comput., vol. 26, pp. 401–417, 2015. doi: 10.1016/j.asoc.2014.10.026. [Google Scholar] [CrossRef]

18. M. Dorigo and C. Blum, “Ant colony optimization theory: A survey,” Theor. Comput. Sci., vol. 344, no. 2–3, pp. 243–278, 2005. doi: 10.1016/j.tcs.2005.05.020. [Google Scholar] [CrossRef]

19. J. H. Holland, “Genetic algorithms,” Sci. Am., vol. 267, no. 1, pp. 66–73, 1992. doi: 10.1145/114055.114056. [Google Scholar] [CrossRef]

20. J. Vasconcelos, J. A. Ramirez, R. Takahashi, and R. Saldanha, “Improvements in genetic algorithms,” IEEE Trans. Magn., vol. 37, no. 5, pp. 3414–3417, 2001. doi: 10.1109/20.952626. [Google Scholar] [CrossRef]

21. Q. -Y Yang, S. -C. Chu, A. Liang, and J. -S. Pan, “Tumbleweed algorithm and its application for solving location problem of logistics distribution center,” in Genet. Evol. Comput.: Proc. Fourteenth Int. Conf. Genet. Evol. Comput., Jilin, China, Springer, 2022, pp. 641–652. [Google Scholar]

22. A. Seyyedabbasi and F. Kiani, “Sand cat swarm optimization: A nature-inspired algorithm to solve global optimization problems,” Eng. Comput., vol. 39, no. 4, pp. 2627–2651, 2023. doi: 10.1007/s00366-022-01604-x. [Google Scholar] [CrossRef]

23. Y. Kumar and P. K. Singh, “Improved cat swarm optimization algorithm for solving global optimization problems and its application to clustering,” Appl. Intell., vol. 48, no. 9, pp. 2681–2697, 2018. doi: 10.1007/s10489-017-1096-8. [Google Scholar] [CrossRef]

24. Y. He, X. Xue, and S. Zhang, “Using artificial bee colony algorithm for optimizing ontology alignment,” J. Inf. Hiding Multim. Signal Process, vol. 8, no. 4, pp. 766–773, 2017. [Google Scholar]

25. J. -S. Pan, S. -Q. Zhang, S. -C. Chu, H. -M. Yang, and B. Yan, “Willow catkin optimization algorithm applied in the TDOA-FDOA joint location problem,” Entropy, vol. 25, no. 1, 2023, Art. no. 171. doi: 10.3390/e25010171. [Google Scholar] [PubMed] [CrossRef]

26. R. M. Alguliyev and R. G. Alakbarov, “Integer programming models for task scheduling and resource allocation in mobile cloud computing,” Int. J. Comput. Netw. Inform. Security, vol. 15, no. 5, pp. 13–16, 2023. doi: 10.5815/ijcnis.2023.05.02. [Google Scholar] [CrossRef]

27. Y. Fang, F. Wang, and J. Ge, “A task scheduling algorithm based on load balancing in cloud computing,” in Web Inf. Syst. Min.: Int. Conf., WISM 2010, Sanya, China, Springer, 2010, pp. 271–277. [Google Scholar]

28. S. Gupta et al., “Efficient prioritization and processor selection schemes for heft algorithm: A makespan optimizer for task scheduling in cloud environment,” Electronics, vol. 11, no. 16, 2022, Art. no. 2557. doi: 10.3390/electronics11162557. [Google Scholar] [CrossRef]

29. C. S. Pawar and R. B. Wagh, “Priority based dynamic resource allocation in cloud computing,” in 2012 Int. Symp. Cloud Serv. Comput., Mangalore, India, IEEE, 2012, pp. 1–6. [Google Scholar]

30. Z. Wu, X. Liu, Z. Ni, D. Yuan, and Y. Yang, “A market-oriented hierarchical scheduling strategy in cloud workflow systems,” J. Supercomput., vol. 63, no. 1, pp. 256–293, 2013. doi: 10.1007/s11227-011-0578-4. [Google Scholar] [CrossRef]

31. M. Chhabra and S. Basheer, “Recent task scheduling-based heuristic and meta-heuristics methods in cloud computing: A review,” in 2022 5th Int. Conf. Contemp. Comput. Inf. (IC3I), Uttar Pradesh, India, IEEE, 2022, pp. 2236–2242. [Google Scholar]

32. X. Chen et al., “A woa-based optimization approach for task scheduling in cloud computing systems,” IEEE Syst. J., vol. 14, no. 3, pp. 3117–3128, 2020. doi: 10.1109/JSYST.2019.2960088. [Google Scholar] [CrossRef]

33. Y. Changtian and Y. Jiong, “Energy-aware genetic algorithms for task scheduling in cloud computing,” in 2012 Seventh China Grid Annu. Conf., Beijing, China, IEEE, 2012, pp. 43–48. [Google Scholar]

34. X. Sheng and Q. Li, “Template-based genetic algorithm for qos-aware task scheduling in cloud computing,” in 2016 Int. Conf. Adv. Cloud Big Data (CBD), Chengdu, China, IEEE, 2016, pp. 25–30. [Google Scholar]

35. P. Pirozmand, A. A. R. Hosseinabadi, M. Farrokhzad, M. Sadeghilalimi, S. Mirkamali and A. Slowik, “Multi-objective hybrid genetic algorithm for task scheduling problem in cloud computing,” Neural Comput. Appl., vol. 33, no. 19, pp. 13075–13088, 2021. doi: 10.1007/s00521-021-06002-w. [Google Scholar] [CrossRef]

36. N. Mansouri, B. M. H. Zade, and M. M. Javidi, “Hybrid task scheduling strategy for cloud computing by modified particle swarm optimization and fuzzy theory,” Comput. Ind. Eng., vol. 130, no. 5, pp. 597–633, 2019. doi: 10.1016/j.cie.2019.03.006. [Google Scholar] [CrossRef]

37. Y. Moon, H. Yu, J. -M. Gil, and J. Lim, “A slave ants based ant colony optimization algorithm for task scheduling in cloud computing environments,” Hum. Centric Comput. Inf. Sci., vol. 7, no. 1, pp. 1–10, 2017. doi: 10.1186/s13673-017-0109-2. [Google Scholar] [CrossRef]

38. A. -N. Zhang, S. -C. Chu, P. -C. Song, H. Wang, and J. -S. Pan, “Task scheduling in cloud computing environment using advanced phasmatodea population evolution algorithms,” Electronics, vol. 11, no. 9, 2022, Art. no. 1451. doi: 10.3390/electronics11091451. [Google Scholar] [CrossRef]

39. L. Tang et al., “Online and offline based load balance algorithm in cloud computing,” Knowl. Based Syst., vol. 138, no. 4, pp. 91–104, 2017. doi: 10.1016/j.knosys.2017.09.040. [Google Scholar] [CrossRef]

40. F. B. Demir, T. Tuncer, and A. F. Kocamaz, “A chaotic optimization method based on logistic-sine map for numerical function optimization,” Neural Comput. Appl., vol. 32, no. 17, pp. 14227–14239, 2020. doi: 10.1007/s00521-020-04815-9. [Google Scholar] [CrossRef]

41. S. Zhao, Y. Wu, S. Tan, J. Wu, Z. Cui and Y. -G. Wang, “QQLMPA: A quasi-opposition learning and q-learning based marine predators algorithm,” Expert. Syst. Appl., vol. 213, no. 190, 2023, Art. no. 119246. doi: 10.1016/j.eswa.2022.119246. [Google Scholar] [CrossRef]

42. Y. Wang, W. Wang, I. Ahmad, and E. Tag-Eldin, “Multi-objective quantum-inspired seagull optimization algorithm,” Electronics, vol. 11, no. 12, 2022, Art. no. 1834. doi: 10.3390/electronics11121834. [Google Scholar] [CrossRef]

43. A. Alharbi, W. Alosaimi, H. Alyami, H. T. Rauf, and R. Damaševičius, “Botnet attack detection using local global best bat algorithm for industrial internet of things,” Electronics, vol. 10, no. 11, 2021, Art. no. 1341. doi: 10.3390/electronics10111341. [Google Scholar] [CrossRef]

44. X. Cai, X. -Z Gao, and Y. Xue, “Improved bat algorithm with optimal forage strategy and random disturbance strategy,” Int. J. Bioinspired Comput., vol. 8, no. 4, pp. 205–214, 2016. doi: 10.1504/IJBIC.2016.078666 [Google Scholar] [CrossRef]

45. N. Neggaz, A. A. Ewees, M. Abd Elaziz, and M. Mafarja, “Boosting salp swarm algorithm by sine cosine algorithm and disrupt operator for feature selection,” Expert Syst. Appl., vol. 145, no. 1181, 2020, Art. no. 113103. doi: 10.1016/j.eswa.2019.113103. [Google Scholar] [CrossRef]

46. J. -S. Pan, Z. Fu, C. -C. Hu, P. -W. Tsai, and S. -C. Chu, “Rafflesia optimization algorithm applied in the logistics distribution centers location problem,” J. Internet Technol., vol. 23, no. 7, pp. 1541–1555, 2022. doi: 10.53106/160792642022122307009. [Google Scholar] [CrossRef]

47. S. H. H. Madni, M. S. Abd Latiff, M. Abdullahi, S. M. Abdulhamid, and M. J. Usman, “Performance comparison of heuristic algorithms for task scheduling in iaas cloud computing environment,” PLoS One, vol. 12, no. 5, 2017, Art. no. e0176321. doi: 10.1371/journal.pone.0176321. [Google Scholar] [PubMed] [CrossRef]