An Improved Chaotic Quantum Multi-Objective Harris Hawks Optimization Algorithm for Emergency Centers Site Selection Decision Problem

1  Introduction

Various major urban emergencies have frequently occurred worldwide in recent years, causing significant casualties and property damage [1]. Emergency resource distribution centers (hereafter referred to as “Centers”) are facilities specifically designed to store disaster relief supplies and are responsible for a series of activities, including the storage and distribution of emergency resources [2,3]. Numerous scholars have researched the site selection problem of emergency resources and proposed various site selection models [4–6]. Kacprzyk et al. [7] employed fuzzy multi-attribute group decision-making and Associated Triangular Fuzzy Probability Averaging (As-TFPA) aggregation operators to solve a two-stage multi-objective site selection model for emergency facilities. Huang et al. [8] developed a multi-objective planning model for the site selection and allocation of cruise emergency supplies, and used the Non-dominated Sorting Genetic Algorithm II (NSGA-II) to solve the model. de Veluz et al. [9] proposed a scenario-based multi-objective site selection and routing model, and used a multi-objective particle swarm optimization algorithm to solve the model. Although existing studies have achieved significant results in emergency resource site selection, some limitations remain [10]. Most studies assume that site selection decision problems (SSDPs) are conducted in deterministic environments. However, in real-world scenarios, factors influencing emergency center site selection, such as facility capacity and operational costs, are often uncertain, making it difficult for existing models to address these uncertainties effectively. As a result, fuzzy theory has gradually been applied to tackle these uncertainty issues and has proven its effectiveness in various decision-making environments [11,12]. In previous studies on constructing site selection decision models (SSDMs), scholars have predominantly focused on economic and time-related factors. However, in real-world scenarios, the degree of urgency in demand at each Disaster-Affected Site (hereafter referred to as “Site”) should be incorporated into the SSDM, as the situations at different Sites vary [13]. The SSDP for Emergency Centers is a Non-deterministic Polynomial (NP)-Hard problem, and intelligent optimization algorithms can find satisfactory solutions quickly [14]. The Harris Hawks Optimization (HHO) algorithm is a swarm intelligence optimization algorithm based on the cooperative hunting strategy of Harris Hawks [15]. The HHO algorithm, known for its simplicity, fast convergence, and minimal control parameters [16,17], is widely used in path planning and image processing. However, its application to SSDP still needs to be explored. Therefore, this study proposes an improved Chaotic Quantum Harris Hawks Optimization algorithm (CQ-MOHHO) to address the Centers’ SSDPs in uncertain environments [18,19].

This study introduces a multi-objective, multi-constraint optimization modeling framework combined with the CQ-MOHHO algorithm, effectively addressing the uncertainty and complexity of emergency center site selection. This approach enhances the practical applicability of the model. First, the study employed triangular fuzzy numbers to describe the uncertain decision information in the SSDP for Emergency Centers. Subsequently, key parameters such as the degree of urgency in demand at Sites were incorporated into the mathematical model, leading to the establishment of a triangular fuzzy multi-objective SSDM for Emergency Centers with three primary objectives: urgency cost, economic cost, and transportation distance cost. Next, using the defuzzification definition and the Graded Mean Integration Representation (GMIR) method, the triangular fuzzy multi-objective mathematical model was converted into a precise multi-objective mathematical model that is easier to solve. This study proposes an improved Chaotic Quantum Multi-Objective Harris Hawks Optimization (CQ-MOHHO) algorithm to solve the model above. In addition, the effectiveness of the proposed model and the CQ-MOHHO algorithm was validated through case analysis, with comparisons against Multi-Objective Harris Hawks Optimization (MOHHO), NSGA-II, and Multi-Objective Grey Wolf Optimizer (MOGWO) demonstrating its feasibility and superiority. Furthermore, the algorithm’s performance was evaluated using Zitzler-Deb-Thiele (ZDT) test functions and Generational Distance (GD), Hypervolume (HV), and Inverted Generational Distance (IGD) metrics confirming its superior global search capability, faster convergence, and higher solution quality.

The organization of this study is as follows. Section 2 presents the basic concepts of triangular fuzzy numbers and defuzzification methods. Section 3 describes the problem formulation and model construction for the SSDP of Emergency Centers. Section 4 introduces the proposed CQ-MOHHO algorithm and the steps for solving the model. Section 5 presents a case study and discusses the performance comparison between the CQ-MOHHO algorithm and other algorithms. Section 6 presents the conclusions.

2  Basic Concepts

2.1 Basic Concepts of Triangular Fuzzy Numbers

In the site selection decision model (SSDM) for Emergency Centers, some parameters are difficult to obtain precise values for, and fuzzy number theory can effectively address this issue. This study uses triangular fuzzy numbers to represent the uncertain parameters in the SSDM for Emergency Centers.

Definition 1: Let be a triangular fuzzy number, and its membership function is shown in Eq. (1), where and are the lower and upper limits of the triangular fuzzy number, respectively, is the most likely value, and [20].

Definition 2: Let and be two triangular fuzzy numbers, whose mathematical operation rules are shown in Eqs. (2) to (5) [21].

(1)

(2)

(3)

(4)

(5)

Definition 3: Let and be two triangular fuzzy numbers. The ordinal relationship between and is defined as: (a) If and only if , then ; (b) If and only if , then ; (c) If and only if , then [22].

2.2 Defuzzification Method of Triangular Fuzzy Numbers

The majority of current intelligent optimization algorithms are specifically developed to tackle mathematical models that incorporate exact parameters. Hence, it is imperative to employ a defuzzification approach to transform the fuzzy parameters in the SSDM for Emergency Centers into precise parameters for the solution. Following defuzzification, the parameters can accurately represent their inherent uncertainty and ensure the model’s effective solution. According to the Graded Mean Integration Representation (GMIR) theory [23], Definition 4 shows how to turn triangular fuzzy parameters into precise parameters.

Definition 4: Let be a triangular fuzzy number. The method of converting into a precise number is shown in Eq. (6), where is any positive integer [24].

(6)

3  Site Selection Decision Model for Emergency Centers

3.1 Problem Description and Model Assumptions

This study considers a scenario involving candidate Emergency Centers and Sites, aiming to select of the candidate locations to open as Emergency Centers to meet the emergency resource needs of all Sites [25]. The SSDM for Emergency Centers requires determining the optimal number and locations of Emergency Centers to open and planning the Sites to be served by each open Emergency Center and their emergency resource distribution quantities under the given objectives and constraints. In this model, the number of Emergency Centers to be opened is an optimization variable, and the decision is made by minimizing urgency, economic, and transportation distance costs. Model assumptions are as follows: (a) The final selected centers can only be chosen from known candidate Emergency Center locations. (b) Each Emergency Center can serve all Sites in its coverage area with its maximum storage capacity. (c) One Emergency Center serves each Site. (d) Traffic accidents and extreme weather delays are ignored. (e) The Emergency Center to Site distance is assumed to be the vehicle travel path length. Table 1 lists SSDM symbols and meanings.

3.2 Construction of Multi-Objective SSDM for Emergency Centers

This section constructs a Triangular Fuzzy Multi-Objective SSDM (Model M4-1) and a Precise Multi-Objective SSDM (Model M4-2) separately for the Emergency Center site selection problem.

(1) The Triangular Fuzzy Multi-Objective SSDM

The Model M4-1 is a triangular fuzzy multi-objective SSDM for Emergency Centers. Urgency, economic, and transportation distance costs are fully considered in the model. Eqs. (7)–(9) show Model M4-1’s three objective functions. Eqs. (10)–(15) represent model constraints.

Model M4-1:

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

The first objective function represents the minimization of urgency cost (). To better quantify each Site’s urgency level and time sensitivity, the urgency coefficient of demand and the unit material time penalty cost are introduced, as shown in Eq. (7). The second objective function is the minimization of economic cost (), which includes the material delivery cost and the operating cost of the Emergency Center, as shown in Eq. (8). The third objective function aims to minimize the total transportation distance cost () from Emergency Center to its corresponding Sites on the premise that the needs of all Sites are met, as shown in Eq. (9). The first set of constraints indicates that if an Emergency Center serves a Site, then the corresponding candidate Emergency Center must be selected, as shown in Eq. (10). The second set of constraints ensures that the demand of each Site must be met, as shown in Eq. (11). The third set of constraints requires that the storage capacity of each Emergency Center must accommodate the distribution quantity to its corresponding Sites, as shown in Eq. (12). The fourth set of constraints states that the emergency resource distribution quantities, as decision variables, should take non-negative values, as shown in Eq. (13). The fifth and sixth sets of constraints are 0–1 binary decision variables, as shown in Eqs. (14) and (15). represents the selection of candidate Emergency Centers. When equals 1, it indicates that the candidate Emergency Center is selected. When equals 1, it indicates that the Emergency Center serves the Site .

(2) The Precise Multi-Objective SSDM

The meaning of Model M4-2’s objective functions and constraints are the same as Model M4-1, including the selection of Emergency Centers and the assignment of Sites. The meaning of Model M4-2’s objective functions and constraints are the same as Model M4-1. According to Definition 2–Definition 4, Eq. (6) can convert Model M4-1’s triangular fuzzy parameters into precise parameters (set k = 2 in this study). Eqs. (16)–(18) show Model M4-2’s three objective functions, and Eqs. (19)–(24) show its constraints.

Model M4-2:

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

According to Definition 3, the constraints in Model M4-2 that are in the form of fuzzy triplets can be converted into precise constraints, meaning that Eqs. (20)–(22) can be transformed into Eqs. (25)–(27).

(25)

(26)

(27)

4  Solving the Emergency Centers SSDM Using the CQ-MOHHO Algorithm

4.1 The Harris Hawks Optimization Algorithm

The Harris Hawks Optimization (HHO) algorithm, introduced by Heidari and Mirjalili in 2019, is a bio-inspired method based on the predatory behavior of Harris Hawks [26]. As a global optimization approach, it solves constrained problems [27]. The HHO algorithm operates through three phases: exploration, transition, and exploitation.

(1) Exploration Phase. Different strategies are selected using a random number , as shown in Eq. (28). Where represents the position of the Harris Hawk at the iteration, represents the current prey’s position, represents the center position of the Harris Hawk group, and are random numbers generated within the interval (0, 1). and are the upper and lower bounds of the variable range, respectively [28].

(28)

(2) Transition Phase. Harris Hawks switch between different predatory behaviors based on the prey’s escape energy, which is calculated as shown in Eq. (29). Where represents the prey’s escape energy, is the initial energy of the prey, is the current iteration, and is the maximum iteration [29].

(29)

(3) Exploitation Phase. When the prey’s escape energy is less than 1, the Harris Hawk group compares the value and a random number within the range (0, 1) against the value 0.5, adopting an appropriate siege strategy [30]. These strategies are categorized into the following four types, see Fig. 1.

Figure 1: Spatial diagrams of the four strategies in the HHO algorithm

(a) Soft Siege. When and , the prey’s escape energy is relatively high, and the position update formula for the Harris Hawks is shown in Eq. (30). Where represents the difference between the prey’s position and the Harris Hawk’s position at the iteration; indicates the prey’s jumping ability, which is a random number within the range (0, 2).

(30)

(b) Hard Siege. When and , the prey’s escape energy is relatively low, and the position update formula for the Harris Hawks is shown in Eq. (31).

(31)

(c) Progressive Rapid Dive Soft Siege. When and , the Harris Hawks initially adopt a soft siege strategy. If the ambush is successful, they update the fitness value and execute strategy ; otherwise, they switch to a random walk strategy . If the random walk strategy fails, they return to their original position, with the position update formula shown in Eq. (32). represents a random vector of dimension , and stands for the Levy function.

(32)

(d) Progressive Rapid Dive Hard Siege. When and , the Harris Hawks initially adopt a hard siege strategy. If the ambush is successful, their position is updated based on the mean value , and they execute strategy ; otherwise, they switch to a random walk strategy . If the random walk strategy fails, they return to their original position, with the position update formula shown in Eq. (33).

(33)

4.2 Improvement Strategies of the CQ-MOHHO Algorithm

The traditional HHO algorithm performs well in single-objective optimization but struggles in complex multi-objective problems, frequently lacking the ability to balance competing objectives. The Multi-Objective Harris Hawks Optimization (MOHHO) algorithm addresses this, but it may still exhibit local optima due to limited population diversity. In order to enhance performance, this study proposes the CQ-MOHHO algorithm, which incorporates chaotic mapping and quantum optimization strategies.

(1) Chaotic Mapping Improvement Strategy

As a nonlinear dynamic system, chaos mapping offers good randomness and broad coverage of the solution space, helping prevent premature convergence. Effective population initialization is crucial, ensuring a uniform distribution of position vectors and avoiding duplication common in random methods. This study integrates logistic chaotic mapping into the MOHHO algorithm to enhance population initialization, improving the quality of the initial population. Eq. (34) presents the logistic chaotic mapping [31].

(34)

The population generated using Logistic chaotic mapping can have its position initialized according to Eq. (35). Here, represents the initial population position matrix of the decision variable for the individual. denotes the chaotic sequence matrix, where is the population size and is the dimension of the decision variables.

(35)

(2) Quantum Optimization Improvement Strategy

This study introduces a quantum optimization strategy based on the uncertainty principle in quantum mechanics [32]. Quantum optimization is applied during the MOHHO algorithm’s local search when to track each Harris Hawk’s position. Individuals follow quantum mechanics’ motion rules, potentially moving to any location in the search space. The quantum mechanical motion rules are obtained by applying the probabilistic distribution characteristics of quantum states and the position and momentum uncertainty principle, which allows individuals to be randomly distributed across the search space according to the quantum state function, thereby enhancing global exploration capability [33]. Using the Monte Carlo method, each individual’s positions are observed times per iteration, with fitter individuals replacing others to improve escape from local optima. is set to 6 to reduce computational costs [34]. Fig. 2 illustrates this strategy.

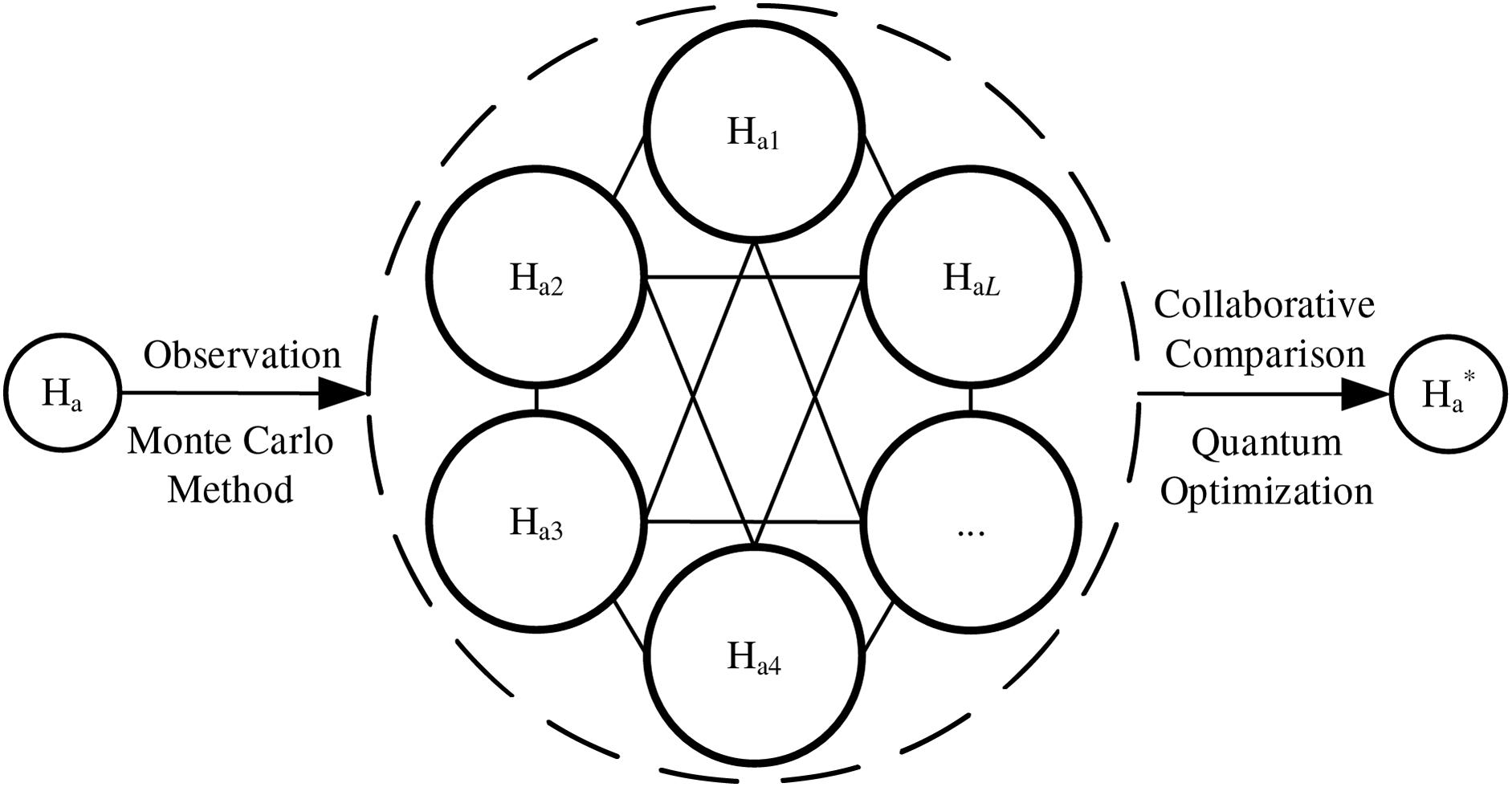
Figure 2: Schematic diagram of the quantum optimization strategy for Harris Hawk individuals

In the MOHHO algorithm, when the prey’s escape energy , a quantum improvement is applied to the Harris Hawk individuals in the population. The specific approach involves observing the Harris Hawk individual in population to obtain six positions: . After quantum processing, a new individual is obtained (the same operation is applied to population as to population ). After completing one iteration, populations and generate the optimal prey positions and . These positions are then collaboratively processed to yield the prey position , superior to both and across all objectives, representing the quantum-improved prey position. This quantum improvement strategy, which integrates the uncertainty principle of quantum mechanics, significantly enhances the optimization accuracy and convergence speed of the MOHHO algorithm. It strengthens the global search capability and increases the likelihood of escaping local optima while finding the optimal balance among multiple objectives, thereby improving overall optimization performance.

4.3 Algorithm Steps of the CQ-MOHHO Algorithm

The steps of the improved CQ-MOHHO algorithm are as follows:

Step 1: Generate the initial population using logistic chaotic mapping, where the population dimension is , the number of Harris Hawk individuals is , and the maximum number of iterations is .

Step 2: Initialize the external set P to store the dominant solutions. Divide the initial population evenly into population and , and assign them the prey escape energies and , respectively.

Step 3: Start the algorithm iteration, evaluate the objective function values of each individual in the population, and update the non-dominated solutions in the external set to ensure the non-dominance and diversity of .

Step 4: For each population, if the energy , the Harris Hawks update their positions according to Eq. (28). When , quantum local optimization is performed, observing each individual L times using the Monte Carlo method to find precise positions, with the best value replacing the original position. Based on the random number , individuals select a strategy from the four exploitation phase strategies, as defined by Eqs. (30) to (33) t to update their positions.

Step 5: Collaboratively process prey positions from different populations, using the Pareto front to update global positions. The non-dominated solution set is selected based on multi-objective optimization values to update the global optimal solution. The specific steps are as follows:

Step 5-1: Calculate the objective function values for each individual in different populations.

Step 5-2: Construct the Pareto front based on the objective function values and select the non-dominated solution set.

Step 5-3: Update the non-dominated solution set of the current Pareto front into the external set .

Step 6: Update the Harris Hawk population, prey escape energy , and the fitness values of the external set .

Step 7: Check whether the termination conditions of the algorithm are met. In this study, two termination conditions are set: (1) the number of iterations reaches the maximum set value (e.g., 100 iterations); (2) the change in the non-dominated solution set in the external archive is less than a preset threshold over multiple consecutive iterations, indicating that the solution set has stabilized. If either condition is satisfied, the algorithm stops and proceeds to Step 8; otherwise, it continues to repeat Steps 4–7.

Step 8: Output the global prey positions and their corresponding non-dominated solution set. Use the non-dominated solution set in the external set as the global optimal solution set.

The improved CQ-MOHHO algorithm enhances population diversity during initialization and improves local search. It balances global and local search more effectively, accelerates convergence, and increases the likelihood of finding the global optimal solutions.

4.4 Solving the Emergency Centers SSDM Based on the CQ-MOHHO Algorithm

This study proposes solving the Emergency Centers SSDM based on the improved CQ-MOHHO algorithm, and the framework diagram is shown in Fig. 3. The overall steps for solving the model are as follows:

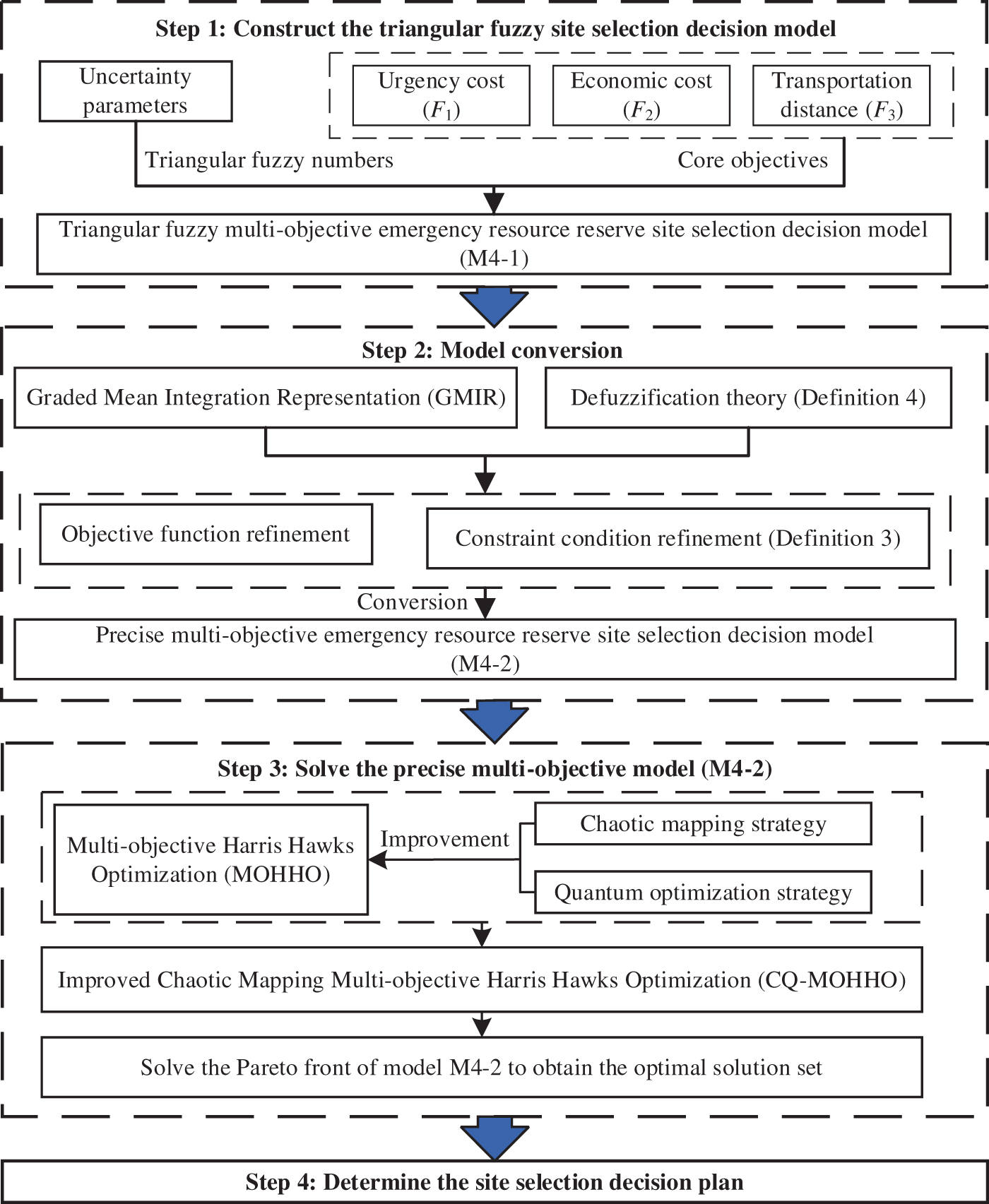
Figure 3: Framework diagram of the solution method for the SSDM

Step 1: Construct the triangular fuzzy multi-objective SSDM M4-1 for Emergency Centers.

Step 2: Convert the model M4-1 into the precise multi-objective SSDM M4-2.

Step 3: Propose the improved CQ-MOHHO algorithm to solve the Pareto front of the precise multi-objective SSDM M4-2.

Step 4: Balance the three core objectives to select the ideal solution set, in order to determine the final site selection decision plan.

5  Case Study

This section takes the site selection of Emergency Centers after an earthquake in City W as a background. The Emergency Centers SSDM is solved, and the performance of the solving algorithm is tested and evaluated.

5.1 Case Background and Experimental Data

After the sudden earthquake in City W, 20 Sites required emergency resources. It is known that there are 9 candidate Emergency Centers available locally. The City W plans to select several Emergency Centers from these nine candidate locations to ensure that the material needs of the 20 Sites are met under the objectives of minimizing urgency cost, economic cost, and transportation distance cost.

This study obtained the latitude and longitude information of each candidate Emergency Center and Site using GIS and Google Maps, as shown in Table 2. It is assumed that the distance calculated from the latitudes and longitudes of and is equivalent to the transportation distance , the transport vehicle speed is , and the fuzzy delivery time can be calculated using the formula . Based on case and expert evaluation data, this study sets the unit transportation cost per distance at ten thousand yuan and the time cost coefficient at . In this case, to better account for uncertainty factors such as resource demand following the earthquake, operating costs, storage capacity, and unit material time penalty costs, these variables are represented as triangular fuzzy numbers. The experimental data are presented in Tables 3 to 6. Due to space constraints, only a portion of the experimental data is presented. The full dataset will be uploaded as an attachment.

5.2 Experimental Environment and Case Study Results

All algorithms were tested using Matlab 2021a on a 64-bit Windows 10 system. Experiments show that the algorithm achieved excellent average results and runtime performance with 100 Pareto front size, 200 population size, and 100 iterations.

This study addresses the multi-objective SSDM using the improved CQ-MOHHO algorithm, generating Pareto front solutions from the case data. Tables 7 and 8 present key results. In Table 7, Best 1, Best 2, and Best 3 represent the optimal solutions for urgency, economic, and transportation distance costs, respectively. The ideal solution has the highest crowding degree on the Pareto front, while the worst solution has the highest crowding degree in the lowest-ranked non-dominated set. Table 8 details the site selection plan for the ideal solution, including selected Emergency Centers, served Sites, and emergency resource distribution. Fig. 4 provides a schematic of the selected Emergency Centers and Sites.

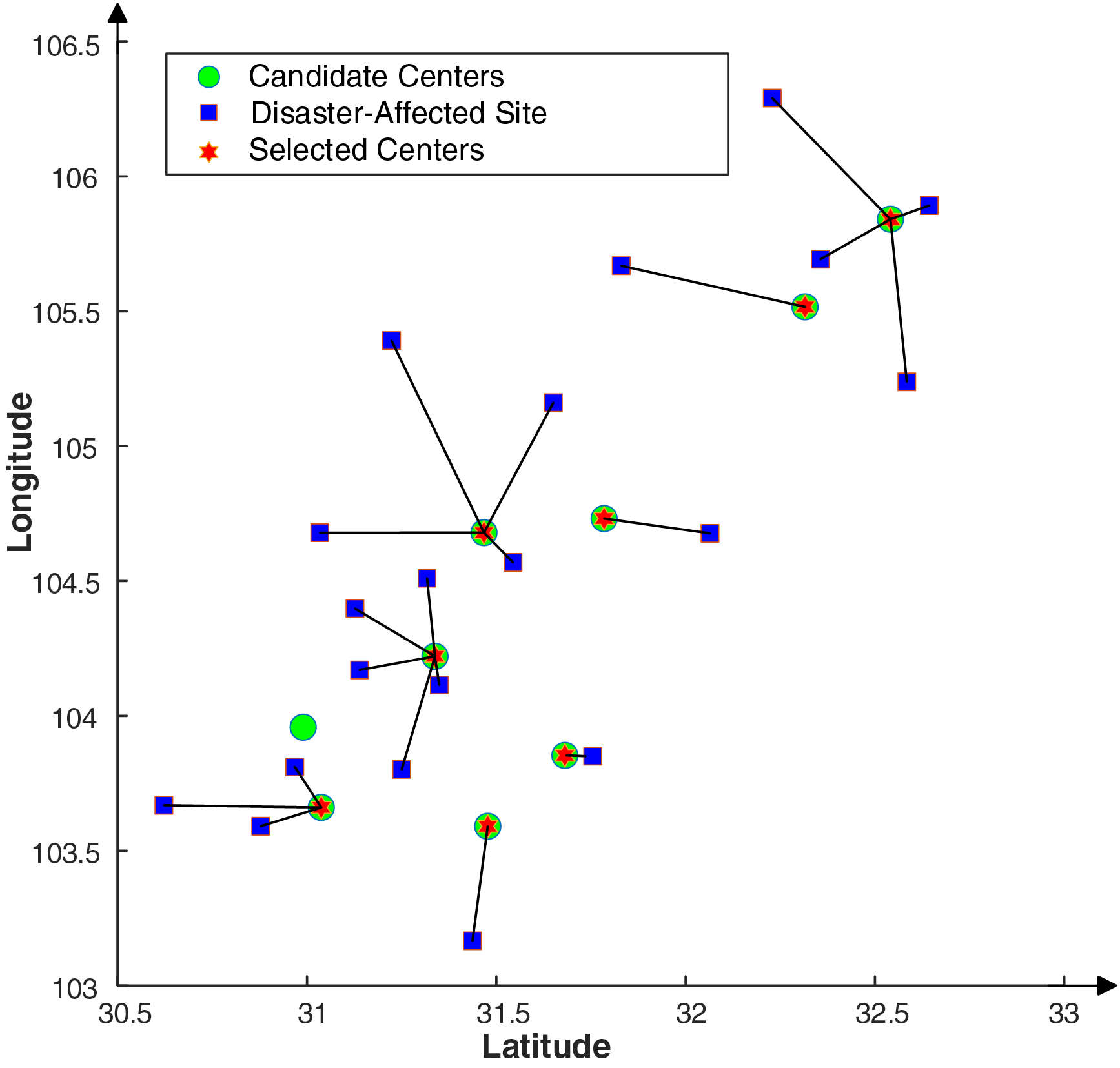
Figure 4: Schematic diagram of the selected centers and corresponding served sites

5.3 Algorithm Comparison and Discussion

To validate the superiority of the CQ-MOHHO algorithm for solving SSDM, experiments were conducted in the same environment as those with the Nondominated Sorting Genetic Algorithm II (NSGA-II) [35], MOHHO [36], and the Multi-Objective Grey Wolf Optimization (MOGWO) [37]. The CQ-MOHHO algorithm enhances the MOHHO by integrating chaotic mapping and quantum behavior strategies, significantly enhancing the balance between global search capability and local refinement. It offers faster convergence and higher accuracy, effectively avoiding local optima, and performs exceptionally well in complex, large-scale multi-objective optimization problems. The algorithm efficiently explores complex search spaces, precisely balances conflicting objectives, and generates diverse, high-quality solutions, providing decision-makers with a broad range of options. In contrast, NSGA-II, a classic genetic algorithm-based approach, is simple and stable, maintaining solution diversity, but it struggles with high-dimensional problems and has longer computation times. The MOHHO algorithm, inspired by Harris hawks’ hunting behavior, exhibits strong global search ability but is prone to local optima and is sensitive to parameters. MOGWO, based on grey wolf hunting, is simple and easy to implement but underperforms in complex multi-objective problems, often getting trapped in local optima and poorly balancing conflicting objectives.

The urgency cost (), economic cost (), and transportation distance cost () were calculated for all non-dominated solutions, and the Pareto front solutions are shown in Fig. 5. Fig. 6a–c compares the convergence of four different algorithms across the three objectives.

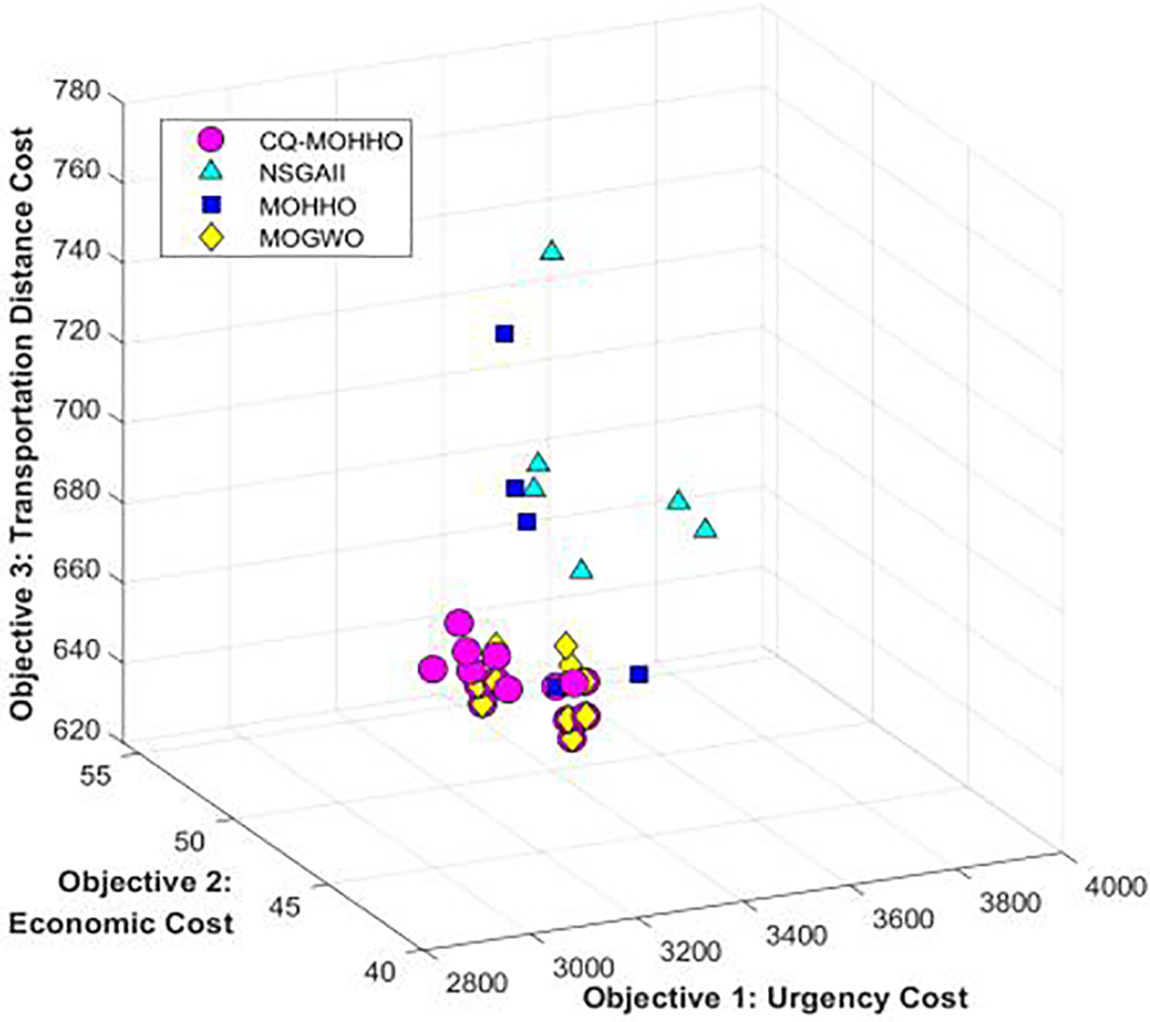
Figure 5: Pareto front surfaces obtained by four algorithms

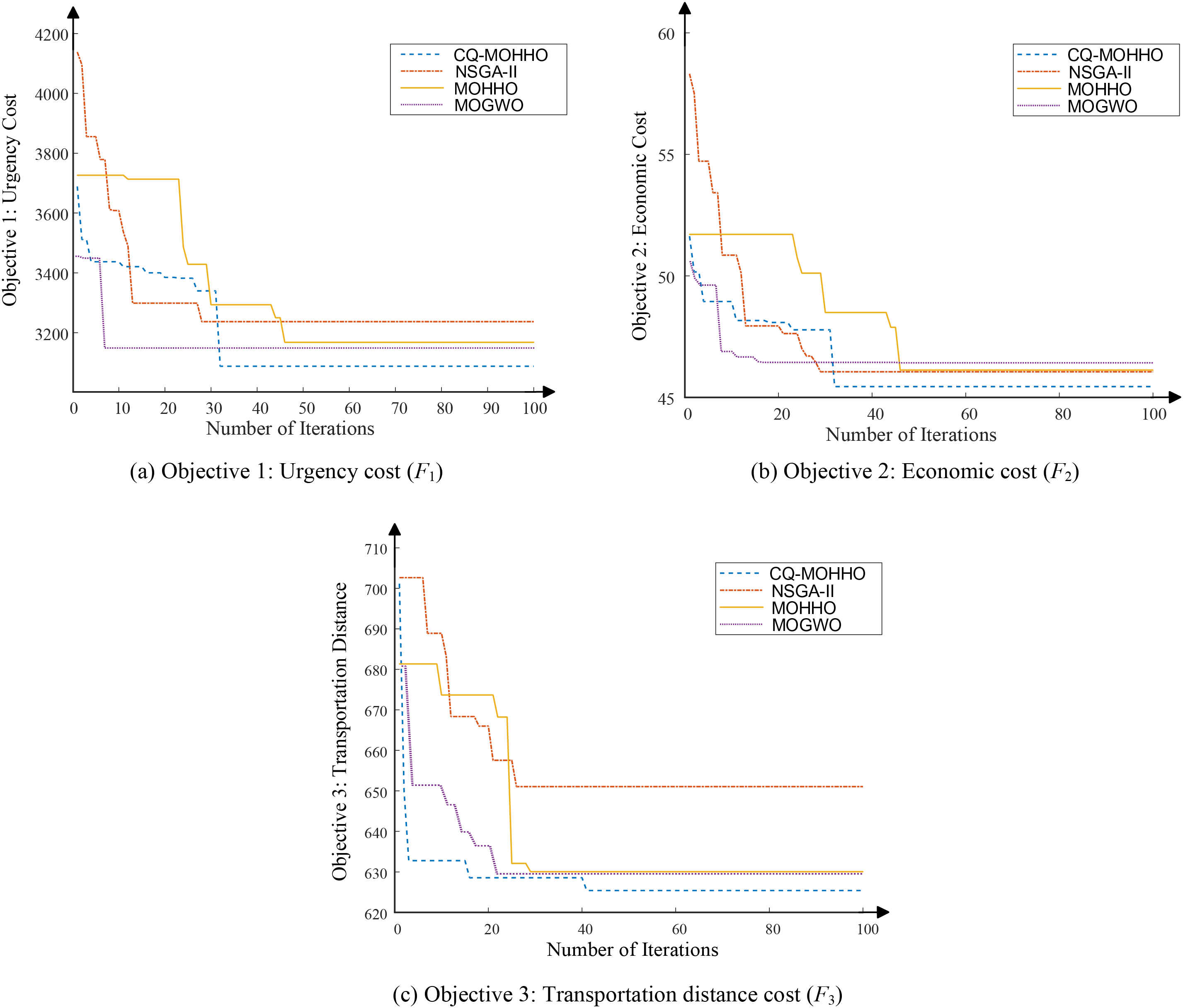
Figure 6: Convergence comparison of the four algorithms

Fig. 5 shows that the CQ-MOHHO algorithm outperforms NSGA-II, MOHHO, and MOGWO in the non-dominated solution set. CQ-MOHHO solutions are closer to the optimal Pareto front, with broader distribution in the objective optimization region and concentration in lower-value regions, indicating stronger global search and higher solution quality. In contrast, other algorithms are confined to higher-value regions. Combined with additional results, CQ-MOHHO generates more and higher-quality Pareto optimal solutions. Fig. 6 further demonstrates CQ-MOHHO’s superior initialization, faster convergence, and better final solution quality, confirming its effectiveness in solving complex multi-objective optimization problems. The experimental results show that CQ-MOHHO outperforms the other three algorithms in optimizing the key objectives –.

To better evaluate the solution performance of the improved CQ-MOHHO algorithm, this section selects the ZDT series of test functions widely used in multi-objective optimization, including ZDT1, ZDT2, and ZDT3 [38]. These test functions cover various complex types, such as convex, concave, continuous, and discontinuous functions. Generational Distance (GD), Hypervolume (HV), and Inverted Generational Distance (IGD) were chosen as evaluation metrics [39]. A performance comparison was conducted between the improved CQ-MOHHO algorithm and the MOHHO, NSGA-II, and MOGWO algorithms. The test results are shown in Tables 9–11. The Pareto fronts obtained by the four algorithms on the ZDT1, ZDT2, and ZDT3 test functions are illustrated in Fig. 7.

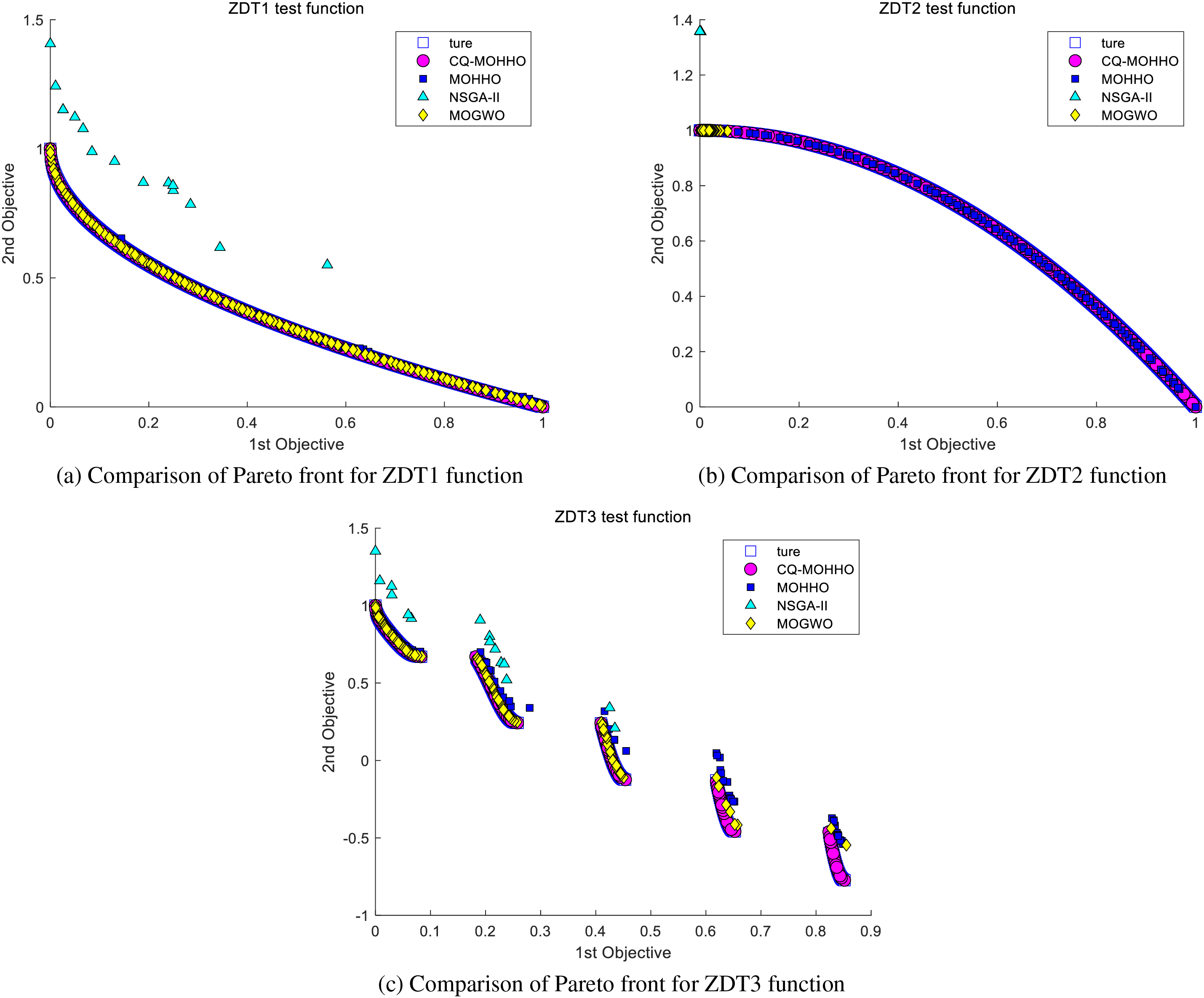
Figure 7: Comparison of Pareto fronts for ZDT1, ZDT2, and ZDT3 functions

As shown in Tables 9–11 and Fig. 7, the CQ-MOHHO algorithm demonstrates superior global search capability, stronger convergence, and higher solution set quality across the GD, HV, and IGD metrics. This fully validates the advantages of CQ-MOHHO in the field of multi-objective optimization. The CQ-MOHHO algorithm exhibits clear superiority across different test functions, particularly in solving multi-objective optimization problems, where it generates solution sets that are closer to the true Pareto front. Additionally, it excels in terms of solution diversity and distribution.

6  Conclusion

This study proposed an improved Chaotic Quantum Harris Hawks Optimization (CQ-MOHHO) algorithm to address the site selection problem of Emergency Centers under multi-objective and multi-constraint conditions, particularly in uncertain environments. Initially, a fuzzy multi-objective SSDM was developed using triangular fuzzy numbers, which was then transformed into a deterministic model via defuzzification and GMIR theory. Subsequently, the CQ-MOHHO algorithm enhanced global search and convergence performance by incorporating chaotic mapping and quantum optimization strategies. Comparative experiments with NSGA-II, MOHHO, and MOGWO validated CQ-MOHHO’s superiority in generating Pareto optimal solution sets. Moreover, further performance evaluation using ZDT1, ZDT2, and ZDT3 test functions, along with comparisons through GD, HV, and IGD metrics, confirmed CQ-MOHHO’s superior global search capability, faster convergence, and higher solution quality. The results demonstrated that CQ-MOHHO effectively solved complex multi-objective SSDMs, offering strong global exploration and high solution accuracy. Thus, the SSDM and CQ-MOHHO algorithms developed in this study demonstrated significant practical potential, providing an efficient and reliable solution for the site selection of Emergency Centers during major urban emergencies.

Although the CQ-MOHHO algorithm performs excellently in multi-objective site selection problems, it may face challenges related to computational complexity and parameter tuning in real-world applications. To ensure the effective implementation of the algorithm in emergency management, it is recommended that practitioners conduct parameter sensitivity analysis prior to application and adjust the model settings based on actual needs. Future research could incorporate more complex fuzzy numbers, such as interval Pythagorean fuzzy numbers or probabilistic dual hesitant fuzzy numbers, to enhance the model’s ability to handle uncertainty. Additionally, the robustness and scalability of the model should be further explored in more application scenarios, such as logistics and supply chain optimization. Conducting large-scale experiments with real-world data and developing intelligent decision support tools will help enhance the practical value of the algorithm.

Acknowledgement: The authors would like to acknowledge the support provided by the China Aerospace Academy of Systems Science and Engineering. They also thank the anonymous reviewers and journal editors for their valuable insights and feedback.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Yuting Zhu; data collection: Yuting Zhu, Wenyu Zhang; analysis and interpretation of results: Yuting Zhu, Hainan Wang; participated in editing of the manuscript: Haining Wang, Junjie Hou, Meng Wang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data is available upon request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. G. Shen, L. Zhou, X. Xue, and Y. Zhou, “The risk impacts of global natural and technological disasters,” Socioecon Plann. Sci., vol. 88, no. 5552, Aug. 2023, Art. no. 101653. doi: 10.1016/j.seps.2023.101653. [Google Scholar] [CrossRef]

2. M. Aghajani, S. Torabi, and N. Altay, “Resilient relief supply planning using an integrated procurement-warehousing model under supply disruption, OMEGA-Int,” J. Manag. Sci., vol. 118, no. 5, Jul. 2023, Art. no. 102871. doi: 10.1016/j.omega.2023.102871. [Google Scholar] [CrossRef]

3. N. Nickdoost, H. Jalloul, and J. Choi, “An integrated framework for temporary disaster debris management sites selection and debris collection logistics planning using geographic information systems and agent-based modeling,” Int. J. Disaster Risk Reduct., vol. 80, no. 5, Oct. 2022, Art. no. 103215. doi: 10.1016/j.ijdrr.2022.103215. [Google Scholar] [CrossRef]

4. M. Sarikaya, M. Yanalak, and H. Karaman, “Site selection of natural gas emergency response team centers in Istanbul metropolitan area based on GIS and FAHP,” ISPRS Int. J. GEO-Inf., vol. 11, no. 11, Nov. 2022, Art. no. 571. doi: 10.3390/ijgi11110571. [Google Scholar] [CrossRef]

5. R. Zhang, J. Li, and Y. Shang, “Multi-level site selection of mobile emergency logistics considering safety stocks,” Appl. Sci., vol. 13, no. 20, Oct. 2023, Art. no. 11245. doi: 10.3390/app132011245. [Google Scholar] [CrossRef]

6. L. Fei, X. Liu, and C. Zhang, “An evidential linguistic ELECTRE method for selection of emergency shelter sites,” Artif. Intell. Rev., vol. 57, no. 4, Mar. 2024, Art. no. 81. doi: 10.1007/s10462-024-10709-2. [Google Scholar] [CrossRef]

7. J. Kacprzyk, G. Sirbiladze, and G. Tsulaia, “Associated fuzzy probabilities in MADM with interacting attributes: Application in multi-objective facility location selection problem,” Int. J. Inf. Technol. Decis. Mak., vol. 21, no. 4, pp. 1155–1188, Jul. 2022. doi: 10.1142/S0219622022500146. [Google Scholar] [CrossRef]

8. L. Huang, Y. Tan, J. Ye, and X. Guan, “Coordinated location-allocation of cruise ship emergency supplies under public health emergencies,” Electron Res. Arch., vol. 31, no. 4, pp. 1804–1821, Apr. 2023. doi: 10.3934/era.2023093. [Google Scholar] [CrossRef]

9. M. de Veluz et al., “Scenario-based multi-objective location-routing model for pre-disaster planning: A philippine case study,” Sustainability, vol. 15, no. 6, Mar. 2023, Art. no. 4882. doi: 10.3390/su15064882. [Google Scholar] [CrossRef]

10. Y. Hosseini, R. Mohammadi, and T. Yang, “Resource-based seismic resilience optimization of the blocked urban road network in emergency response phase considering uncertainties,” Int. J. Disaster Risk Reduct., vol. 85, no. 12, Feb. 2023, Art. no. 103496. doi: 10.1016/j.ijdrr.2022.103496. [Google Scholar] [CrossRef]

11. W. Zhang and Y. Zhu, “The probabilistic dual hesitant fuzzy multi-attribute decision-making method based on cumulative prospect theory and its application,” Axioms, vol. 12, no. 10, Oct. 2023, Art. no. 925. doi: 10.3390/axioms12100925. [Google Scholar] [CrossRef]

12. Y. Zhu, W. Zhang, J. Hou, and R. Zhang, “The large-scale group consensus multi-attribute decision-making method based on probabilistic dual hesitant fuzzy sets,” Math. Biosci. Eng., vol. 21, no. 3, pp. 3944–3966, Feb. 2024. doi: 10.3934/mbe.2024175. [Google Scholar] [PubMed] [CrossRef]

13. A. Mukhopadhyay et al., “A review of incident prediction, resource allocation, and dispatch models for emergency management,” Accid. Anal. Prev., vol. 165, no. 1, Feb. 2022, Art. no. 106501. doi: 10.1016/j.aap.2021.106501. [Google Scholar] [PubMed] [CrossRef]

14. E. Chappidi, A. Singh, and R. Mallipeddi, “Intelligent optimization algorithms for disruptive anti-covering location problem,” presented at the Distrib. Comput. Intell. Technol., ICDCIT, Bhubaneswar, India, 2023, vol. 13776, pp. 165–180. doi: 10.1007/978-3-031-24848-1_12. [Google Scholar] [CrossRef]

15. M. Shehab et al., “Harris hawks optimization algorithm: Variants and applications,” Arch. Comput. Methods Eng., vol. 29, no. 7, pp. 5579–5603, Nov. 2022. doi: 10.1007/s11831-022-09780-1. [Google Scholar] [CrossRef]

16. A. Anwaar, A. Ashraf, W. Bangyal, and M. Iqbal, “Genetic algorithms: Brief review on genetic algorithms for global optimization problems,” presented at the 2022 Human-Cent. Cognit. Syst., HCCS, Shanghai, China, Dec 17–18, 2022, pp. 80–85. doi: 10.1109/HCCS55241.2022.10090327. [Google Scholar] [CrossRef]

17. A. Chen, H. Tan, and Y. Zhu, “Ant colony optimization algorithm and its application,” presented at the 2nd Int. Conf. Appl. Math. Modell. Intell. Comput. (CAMMIC 2022Mar. 25–27, 2022 doi: 10.1117/12.2639584. [Google Scholar] [CrossRef]

18. C. Zhu, Y. Zhang, X. Pan, Q. Chen, and Q. Fu, “Improved Harris Hawks optimization algorithm based on quantum correction and Nelder-Mead simplex method,” Math. Biosci. Eng., vol. 19, no. 8, pp. 7606–7648, Jun. 2022. doi: 10.3934/mbe.2022358. [Google Scholar] [PubMed] [CrossRef]

19. D. Dhawale, V. Kamboj, and P. Anand, “An improved Chaotic Harris Hawks Optimizer for solving numerical and engineering optimization problems,” Eng. Comput., vol. 39, no. 2, pp. 1183–1228, Apr. 2023. doi: 10.1007/s00366-021-01487-4. [Google Scholar] [CrossRef]

20. A. Shyamal and M. Pal, “Triangular fuzzy matrices,” Iran J. Fuzzy Syst., vol. 4, no. 1, pp. 75–87, Apr. 2007. [Google Scholar]

21. A. Syropoulos, “On triangular multisets and triangular fuzzy multisets,” Mathematics, vol. 10, no. 5, Mar. 2022, Art. no. 726. doi: 10.3390/math10050726. [Google Scholar] [CrossRef]

22. H. Garg, C. Sugapriya, S. Rajeswari, D. Nagarajan, and A. Alburaikan, “A model for returnable container inventory with restoring strategy using the triangular fuzzy numbers,” Soft Comput., vol. 28, no. 4, pp. 2811–2822, Feb. 2024. doi: 10.1007/s00500-023-09539-1. [Google Scholar] [CrossRef]

23. S. Kusumadewi, H. Wahyuningsih, and E. Wahyuni, “Graded mean integration representation and intuitionistic fuzzy weighted arithmetic mean for similarity measures in case-based reasoning,” Int. J. Fuzzy Syst., vol. 26, no. 6, pp. 1802–1826, Apr. 2024. doi: 10.1007/s40815-024-01704-4. [Google Scholar] [CrossRef]

24. B. Kumar, S. Paikray, and H. Dutta, “Cost optimization model for items having fuzzy demand and deterioration with two-warehouse facility under the trade credit financing,” AIMS Math., vol. 5, no. 2, pp. 1603–1620, Mar. 2020. doi: 10.3934/math.2020109. [Google Scholar] [CrossRef]

25. X. Ju et al., “Method for site selection of relief supply warehouses in earthquakes with Ms ≥ 7—a case study of western Yunnan, China,” Nat. Hazards, vol. 116, no. 3, pp. 3495–3520, Apr. 2023. doi: 10.1007/s11069-023-05821-5. [Google Scholar] [CrossRef]

26. A. Heidari, S. Mirjalili, H. Faris, I. Aljarah, M. Mafarja and H. Chen, “Harris Hawks optimization: Algorithm and applications,” Future Gener. Comput. Syst., vol. 97, pp. 849–872, Aug. 2019. doi: 10.1016/j.future.2019.02.028. [Google Scholar] [CrossRef]

27. M. Mao and D. Gui, “Enhanced adaptive-convergence in Harris’ Hawks optimization algorithm,” Artif. Intell. Rev., vol. 57, no. 7, Jun. 2024, Art. no. 164. doi: 10.1007/s10462-024-10802-6. [Google Scholar] [CrossRef]

28. A. Kaveh, P. Rahmani, and A. D. Eslamlou, “An efficient hybrid approach based on Harris Hawks optimization and imperialist competitive algorithm for structural optimization,” Eng. Comput., vol. 38, no. Suppl 2, pp. 1555–1583, Jun, 2022. doi: 10.1007/s00366-020-01258-7. [Google Scholar] [CrossRef]

29. C. W. Qu, W. He, X. G. Peng, and X. N. Peng, “Harris Hawks optimization with information exchange,” Appl. Math. Model., vol. 84, no. 1, pp. 52–75, Aug. 2020. doi: 10.1016/j.apm.2020.03.024. [Google Scholar] [CrossRef]

30. H. L. Yu et al., “Laplace crossover and random replacement strategy boosted Harris Hawks optimization: Performance optimization and analysis,” J. Comput. Des. Eng., vol. 9, no. 5, pp. 1879–1916, Oct. 14, 2022. doi: 10.1093/jcde/qwac085. [Google Scholar] [CrossRef]

31. H. Gezici and H. Livatyalı, “Chaotic Harris hawks optimization algorithm,” J. Comput. Des. Eng., vol. 9, no. 1, pp. 216–245, Feb. 2022. doi: 10.1093/jcde/qwab082. [Google Scholar] [CrossRef]

32. V. Rugveth and K. Khatter, “Sensitivity analysis on gaussian quantum-behaved particle swarm optimization control parameters,” Soft Comput., vol. 27, no. 13, pp. 8759–8774, Jul. 2023. doi: 10.1007/s00500-023-08011-4. [Google Scholar] [CrossRef]

33. O. Klein, “The quantum theory and five-dimensional relativity theory,” Z. Phys., vol. 37, no. 12, pp. 895–906, Jul. 1926. doi: 10.1007/BF01397481. [Google Scholar] [CrossRef]

34. Y. Li and Q. Qian, “Harris Hawks optimization algorithm based on multi group and collaborative quantization,” Control Decis., vol. 39, no. 7, pp. 2169–2176, Apr. 2024. doi: 10.13195/j.kzyjc.2022.2076. [Google Scholar] [CrossRef]

35. L. Zhong, W. Li, K. Gao, L. He, and Y. Zhou, “An improved NSGAII for Integrated container scheduling problems with two transshipment routes,” IEEE Trans. Intell. Transp. Syst., vol. 25, no. 10, pp. 14586–14599, Apr. 2024. doi: 10.1109/TITS.2024.3388468. [Google Scholar] [CrossRef]

36. M. Kou, K. Zhang, W. Zhang, J. Ma, J. Ren and G. Wang, “Application research of combined model based on VMD and MOHHO in precipitable water vapor prediction,” Atmospheric Res., vol. 292, no. 1, Sep. 2023, Art. no. 106841. doi: 10.1016/j.atmosres.2023.106841. [Google Scholar] [CrossRef]

37. A. Torabi, F. Yosefvand, S. Shabanlou, A. Rajabi, and B. Yaghoubi, “Optimization of integrated operation of surface and groundwater resources using multi-objective grey wolf optimizer (MOGWO) algorithm,” Water Resour. Manag., vol. 38, no. 6, pp. 2079–2099, Apr. 2024. doi: 10.1007/s11269-024-03744-9. [Google Scholar] [CrossRef]

38. T. Cao, H. Pham, and V. Truong, “An efficient algorithm for multi-objective structural optimization problems using an improved pbest-based differential evolution algorithm,” Adv. Eng. Softw., vol. 197, no. 4, Nov. 2024, Art. no. 103752. doi: 10.1016/j.advengsoft.2024.103752. [Google Scholar] [CrossRef]

39. M. Noori, R. Sahbudin, A. Sali, and F. Hashim, “Multi-objective multi-exemplar particle swarm optimization algorithm with local awareness,” IEEE Access, vol. 12, pp. 125809–125834, 2024. doi: 10.1109/ACCESS.2024.3426104. [Google Scholar] [CrossRef]