Patterns in Heuristic Optimization Algorithms: A Comprehensive Analysis

1  Introduction

1.1 Background and Motivation

Optimization problems arise in various fields such as engineering, economics, and computer science. Finding the optimal solution to these problems is often difficult and time-consuming, especially when the problem involves a large search space or multiple objectives [1–4]. As these problems become increasingly complex, finding optimal or near-optimal solutions through traditional deterministic methods has proven to be both time-consuming and computationally infeasible [5,6]. This has led to the broad adoption of heuristic optimization algorithms, which are specifically designed to explore large and complex search spaces efficiently. These algorithms effectively balance the need to search for new solutions (exploration) with the focus on refining known, promising solutions (exploitation) [7,8]. However, despite their effectiveness, the design of these algorithms remains a challenging task, often requiring a deep understanding of both the problem domain and the algorithmic strategies involved [2,9].

To address this challenge, researchers developed heuristic optimization algorithms, which are designed to find high-quality solutions efficiently by balancing exploration of the search space and exploitation of promising solutions [7,8,10]. While heuristic optimization algorithms have been successful in solving many complex optimization problems, the design of these algorithms remains a challenging task [11,12].

One approach to designing effective heuristic optimization algorithms is to identify the common patterns that are essential to their effectiveness [13,14]. These patterns can provide guidance on how to design new algorithms and improve the performance of existing ones [6,15].

This research is driven by the need for an analysis of common patterns in heuristic optimization algorithms, as these patterns play a crucial role in enhancing algorithmic efficiency and effectiveness across various complex optimization tasks. The goal is to provide a structured understanding of these patterns, not only in terms of their functions but also in how they influence the search process to achieve optimal solutions. This analysis aims to bridge gaps in the existing literature by offering a framework that highlights the underlying principles guiding the design and adaptation of heuristic algorithms. We identify core patterns—such as initialization, local search, diversity maintenance, adaptation, and stochasticity—that recur across different algorithmic families. For each pattern, we provide specific motivations behind its use, the techniques employed for its implementation, and the measurable impact it has on the search dynamics and final outcomes of the algorithms. By examining these components, we aim to contribute new insights that can guide the development of more adaptive, resilient, and high-performing heuristic optimization algorithms tailored to a variety of complex optimization problems.

1.2 Previous Studies

Previous research efforts on analyzing search patterns and styles in heuristic optimization algorithms have been focused on identifying and analyzing individual algorithms or families of algorithms, such as evolutionary algorithms, swarm intelligence algorithms, and simulated annealing, among others [16,17]. For instance, some studies have analyzed the impact of different search operators, such as mutation, crossover, and selection, on the performance of evolutionary algorithms [18,19]. Others have focused on identifying the key parameters and settings that affect the behavior and performance of swarm intelligence algorithms, such as the number of agents, the size of the search space, and the communication topology [20,21]. There have been efforts to classify heuristic optimization algorithms based on their search patterns or styles. For example, some studies have classified algorithms as either exploration-based or exploitation-based, depending on whether they prioritize exploring new areas of the search space or exploiting known solutions [22,23]. Other studies have classified algorithms as either global or local, depending on whether they focus on finding the global optimum or a good local optimum [24,25].

The behavior of individuals in nature can be mapped to search operators in optimization algorithms, and that the learning process between individuals can be translated to the learning process between different solutions in optimization [26,27]. They also emphasize the importance of competition, which can be translated to competing for the best fitness value in optimization [28,29]. Their approach is aimed at leveraging the insights from natural systems to develop effective optimization algorithms [30,31].

Recent studies have explored the integration of heuristic optimization algorithms with machine learning techniques, particularly reinforcement learning methods like Q-learning and Deep Q-Networks (DQN). This hybridization leverages the strengths of both approaches: heuristic optimization as ability to effectively search complex spaces and machine learning as capability to adaptively learn and make decisions based on accumulated knowledge. For example, Q-learning, a model-free reinforcement learning algorithm, has been successfully combined with heuristic optimization patterns to dynamically adjust search strategies in response to changing environments, showing promise in applications like resource allocation and scheduling [32]. DQN, which uses deep neural networks to approximate Q-values, has been integrated with heuristic algorithms to enhance the balance between exploration and exploitation in large search spaces [33]. Recent research demonstrates that combining DQN with optimization patterns like local search and adaptive mechanisms can significantly improve convergence rates and solution quality, especially in dynamic and high-dimensional problem spaces [34]. These advances highlight the potential of combining reinforcement learning with heuristic patterns to address increasingly complex optimization challenges, positioning hybrid approaches as a promising direction for future developments in adaptive optimization algorithms.

These previous research efforts have provided valuable insights into the behavior and performance of heuristic optimization algorithms and have helped to inform the design of new algorithms [35,36]. However, there is still a need for more comprehensive and systematic analyses of heuristic optimization patterns.

1.3 Research Objective and Scope

The objective of this research paper is to analyze and explore the common patterns in heuristic optimization algorithms. The paper aims to provide a comprehensive understanding of these patterns, including their motivation, implementation, and impact on the search process. The scope of this paper includes a comprehensive review of the literature on heuristic optimization algorithms, with a focus on the identification and analysis of common patterns. We will examine the impact of these patterns on the search process, including their contributions to the efficiency and effectiveness of the algorithms. We also apply these patterns to three case studies: Krill Herd optimisation (KHO), Red Fox Optimisation (RFO) and Coronavirus Herd Immunity Optimizer (CHIO) algorithms. Through these case studies, we analyze how the patterns are implemented in the algorithms and how they contribute to their performance.

1.4 Novelty and Contributions

The novelty and contributions of this paper are:

•   A comprehensive analysis of heuristic optimization algorithms by examining common patterns across different algorithms. This analysis allows for a better understanding of the strengths and limitations of different optimization algorithms.

•   A detailed description of how common patterns, such as initialization, local search, diversity maintenance, adaptation, stochasticity, population-based search, memory-based search, and hybridization, are implemented in KHO, RFO and CHIO algorithms. This analysis provides a deeper understanding of the inner workings of these algorithms.

2  Identification and Description of Patterns in Heuristic Optimization Algorithms

2.1 Pattern Description Scheme

The pattern description scheme in heuristic optimization algorithms is inspired by the need to systematically capture and convey the core principles, techniques, and impacts of recurring strategies used in solving complex optimization problems [36,37]. In essence, the pattern description scheme draws inspiration from software engineering, where design patterns are utilized to describe general reusable solutions to common problems [38,39]. In the context of heuristic optimization, patterns are identified and documented to provide a framework that guides the design and implementation of optimization algorithms across various domains [40]. An inspiration for this scheme comes from the field of artificial intelligence and machine learning, where the behavior of algorithms is often analyzed and refined through the understanding of underlying patterns [41,42]. By identifying and categorizing these patterns, researchers and practitioners can better understand the strengths and weaknesses of different heuristic approaches [17]. This understanding facilitates the development of more robust and efficient algorithms, as the patterns provide a blueprint for solving specific types of optimization problems [43]. These patterns offer a way to encapsulate best practices, enabling the transfer of knowledge and experience across different applications and domains [44].

The scheme is also inspired by the concept of modularity in algorithm design, where complex systems are broken down into smaller, manageable components or modules [45,46]. In heuristic optimization, each pattern can be seen as a modular component that addresses a particular aspect of the optimization process, such as initialization, local search, or diversity maintenance [47,48]. By isolating and documenting these components, the pattern description scheme allows for the flexible combination and adaptation of patterns to suit the needs of specific optimization tasks. This modular approach not only enhances the reusability of algorithms but also fosters innovation by enabling the exploration of new combinations of patterns [49].

Another inspiration for the pattern description scheme is the need for clarity and consistency in the communication of algorithmic strategies [50,51]. The scheme provides a standardized way to describe the motivation, implementation, and impact of each pattern, ensuring that the information is accessible and understandable to both researchers and practitioners [52]. This standardization is important in the context of interdisciplinary collaboration, where different fields may employ varied terminologies and approaches. By offering a common language for describing heuristic optimization patterns, the scheme promotes the exchange of ideas and techniques across disciplines, leading to the advancement of the field as a whole [53].

Finally, the pattern description scheme is inspired by the ongoing evolution of heuristic optimization algorithms and the recognition that these algorithms must continually adapt to new challenges and technological advancements [54]. As optimization problems become more complex and diverse, the need for a dynamic and adaptable framework for algorithm design becomes increasingly important [55]. The pattern description scheme addresses this need by providing a structured yet flexible approach to documenting and applying optimization patterns, allowing for the continuous refinement and expansion of heuristic strategies in response to emerging trends and challenges in the field [56].

Here we propose a heuristic optimisation algorithm pattern description scheme that could be used to describe common behaviours of heuristic optimization algorithms:

•   Pattern name: A descriptive name for the pattern

•   Motivation: A brief explanation of the problem that the pattern is intended to solve

•   Impact: A description of how the pattern affects the search process

•   Form: A formal definition of the pattern, if possible

•   Algorithm: A detailed pseudocode description of the pattern

•   Variants: Any variants or modifications of the pattern that have been proposed or implemented

•   Examples: Examples of the pattern in use in specific heuristic optimization algorithms or problems

•   References: Citations to relevant literature on the pattern and its use in heuristic optimization.

2.2 Identification and Outlook of Patterns

The identification of patterns in heuristic optimization algorithms was achieved through a comprehensive and systematic review of the existing literature, coupled with a detailed analysis of various optimization algorithms across multiple domains. The process began by examining a broad range of heuristic optimization techniques, including evolutionary algorithms, swarm intelligence methods, simulated annealing, and other nature-inspired approaches. By scrutinizing the underlying mechanisms of these algorithms, the study aimed to uncover recurring strategies and structures that contribute to their effectiveness. The initial phase of the research focused on gathering a wide array of scholarly articles, technical reports, and case studies that describe the design, implementation, and application of heuristic optimization algorithms. Once the relevant literature was collected, the researchers employed a pattern recognition methodology to distill common elements from the diverse set of algorithms. This involved breaking down each algorithm into its constituent components and analyzing the roles these components play in the search process.

Based on the above process, the following patterns were identified:

•   Initialization pattern: Many heuristic optimization algorithms begin by initializing the solution randomly or using some other heuristic. This allows the algorithm to explore a wide range of solutions and avoid getting stuck in local optima [57].

•   Local Search pattern: Heuristic optimization algorithms often use local search techniques to improve the quality of the solutions. Local search involves making small changes to the current solution and evaluating the new solution. If the new solution is better, it replaces the current solution. Local search can be repeated multiple times to further improve the solution [58].

•   Diversity Maintenance pattern: Maintaining diversity in the population of solutions is important in many heuristic optimization algorithms. This is because diversity helps the algorithm explore a wider range of solutions and avoid premature convergence. Techniques such as niching and crowding are commonly used to maintain diversity [59].

•   Adaptation pattern: Many heuristic optimization algorithms adapt their search strategy based on the performance of the solutions found so far. For example, if the algorithm is finding good solutions quickly, it may increase the intensity of the search. Conversely, if the algorithm is struggling to find good solutions, it may decrease the intensity of the search to explore a wider range of solutions [60].

•   Stochasticity pattern: Heuristic optimization algorithms often introduce some degree of stochasticity in the search process. This can help the algorithm explore a wider range of solutions and avoid getting stuck in local optima. Examples of stochastic techniques include randomization of the search direction, random perturbations of the solutions, and random selection of solutions for further evaluation [61].

•   In population-based search pattern, multiple candidate solutions are maintained simultaneously and evolve over time. The population can be updated using techniques such as mutation, crossover, and selection. Population-based search pattern is effective in problems with complex landscapes or multiple optima [62].

•   Memory-based search pattern involves storing information about the search process to guide future search. This can be done by maintaining a history of previous solutions or by using a memory-based search technique such as tabu search or simulated annealing [63].

•   Hybridization pattern involves combining two or more different optimization algorithms to create a new algorithm [64]. This can lead to improved performance by combining the strengths of different algorithms. For example, a genetic algorithm may be combined with a local search algorithm to create a hybrid algorithm that benefits from both global and local search [65].

•   Constraint handling pattern: Many optimization problems have constraints that must be satisfied. Constraint handling techniques can be used to ensure that the solutions generated by the algorithm are feasible and satisfy the constraints [66].

•   Fitness landscape analysis pattern: The fitness landscape of an optimization problem refers to the relationship between the fitness of a solution and the values of its parameters. Fitness landscape analysis techniques can be used to gain insight into the properties of the fitness landscape and design more effective optimization algorithms [67].

These patterns are not exhaustive, and different heuristic optimization algorithms may use different combinations of these patterns or other patterns altogether. However, these patterns are common in many heuristic optimization algorithms and provide a useful starting point for understanding the search process.

3  Common Patterns in Heuristic Optimization Algorithms

3.1 Initialization Pattern

3.1.1 Motivation

The motivation behind the Initialization pattern in heuristic optimization algorithms is to generate a diverse set of initial solutions for the optimization process. The initial solutions serve as the starting point for the search process, and they can have a significant impact on the quality of the final solution [57,68]. Random initialization is a commonly used approach in heuristic optimization algorithms. It generates solutions by randomly selecting values for each variable within the defined search space [69]. Other initialization techniques may also be used, such as constructing solutions using domain-specific knowledge or heuristics [70]. The goal of the Initialization pattern is to ensure that the search process is not biased towards a specific region of the search space and to increase the chances of finding a high-quality solution [71]. By generating a diverse set of initial solutions, the algorithm can explore a wider range of solutions and avoid getting stuck in local optima [72].

3.1.2 Implementation

The Initialization pattern is a commonly used pattern in heuristic optimization algorithms. It is used to initialize the search process by generating an initial solution or population of solutions.

The Initialization pattern can be described in pseudocode in Algorithm 1.

This algorithm initializes the search process by generating a set of N random solutions and evaluating their quality. The best solution is then used as the initial solution for the optimization algorithm. The exact method of generating the initial solution(s) can vary depending on the specific optimization problem and the heuristic algorithm being used. The goal of the Initialization pattern is to provide a starting point for the search process that allows the algorithm to explore a wide range of solutions and avoid getting stuck in local optima. This approach allows the algorithm to explore a diverse set of candidate solutions and avoid getting stuck in local optima. The algorithm can be modified to use different initialization strategies, such as using a heuristic to generate the initial solution or using a set of previously known good solutions as a starting point.

3.1.3 Impact on Search Process

The Initialization pattern (Fig. 1) has a significant impact on the search process of a heuristic optimization algorithm. Since the algorithm starts with a randomly generated or heuristic-based initial solution, the quality of the initial solution has a direct impact on the quality of the final solution obtained by the algorithm. If the initialization generates a good initial solution, the algorithm may converge quickly to a high-quality solution. On the other hand, if the initialization generates a poor initial solution, the algorithm may take a longer time to converge or may even get stuck in a suboptimal solution. Therefore, a well-designed initialization strategy can significantly improve the performance of a heuristic optimization algorithm.

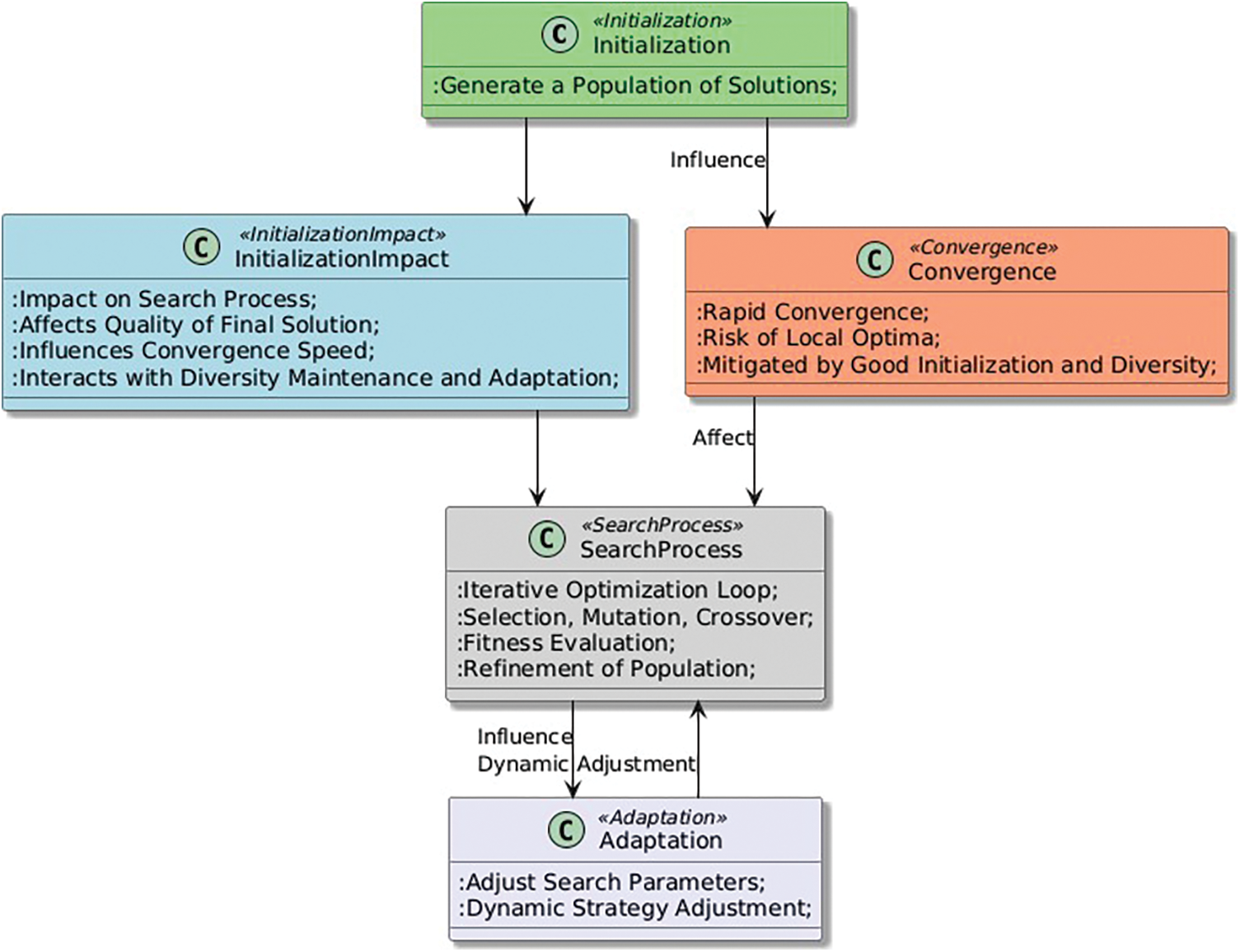
Figure 1: Initialization pattern

The initialization pattern is also important for ensuring diversity in the population of solutions. A good initialization strategy should generate diverse initial solutions to ensure that the algorithm explores a wide range of solutions and avoids getting stuck in local optima.

3.2 Local Search Pattern

3.2.1 Motivation

The Local Search pattern focuses on refining existing solutions by exploring their immediate neighborhoods [73]. The primary motivation behind this pattern is to enhance the quality of solutions by making incremental improvements [74]. In many optimization problems, particularly those with a large search space, it can be computationally expensive to evaluate every possible solution. Therefore, the Local Search pattern offers a practical strategy by allowing the algorithm to start with an initial solution and iteratively explore nearby solutions to find better alternatives [75]. Local Search is particularly valuable in scenarios where solutions are densely packed, and small adjustments can yield significant improvements. The approach leverages the idea that the optimal solution is likely to be located close to a good starting point [76]. This is especially true for problems characterized by a smooth fitness landscape, where small changes in the solution can result in better outcomes. The Local Search pattern can help mitigate the risk of becoming trapped in local optima by enabling the algorithm to explore various neighborhoods around the current solution [77]. By adopting a systematic search strategy that includes mechanisms to escape local optima, such as allowing for random jumps to less explored areas of the search space, the algorithm can improve its chances of converging to a global optimum [78]. Therefore, the algorithm can effectively navigate the search space, often leading to high-quality solutions without the need for exhaustive searches.

3.2.2 Implementation

The Local Search pattern is a heuristic optimization pattern that aims to improve a given solution by iteratively exploring its neighborhood solutions. It can be described by Algorithm 2. In this pattern, the initial solution is first set as the current solution . Then, the algorithm iterates over each neighbor solution of , which can be obtained by making small modifications to . For example, in a continuous optimization problem, a neighbor solution can be obtained by adding a small random value to each variable of . In a discrete optimization problem, a neighbor solution can be obtained by swapping the values of two variables. If a neighbor solution has better fitness than the current best solution , then s′ is updated to n. This process is repeated until no better neighbor solution is found, at which point the algorithm returns the improved solution .

The Local Search pattern can be applied as a standalone optimization method or can be used as a subroutine in more complex optimization algorithms. It is particularly effective in optimizing problems with a relatively smooth fitness landscape. Here is the pseudocode for the Local Search pattern:

Here, the procedure LocalSearch takes an initial solution and iteratively searches its neighborhood for a better solution. It uses a Boolean variable improved to keep track of whether any improvement was made in each iteration. It repeatedly loops over all the neighbors of and checks if a neighbor has a lower objective function value than . If so, is considered an improvement over , and is updated to . The loop continues until no improvement is found, at which point the procedure returns the current best solution x.

3.2.3 Impact on Search Process

The Local Search pattern can have a significant impact on the search process in heuristic optimization algorithms. By performing local search around a candidate solution, the algorithm can refine and improve the solution by exploring the neighborhood of the current solution (Fig. 2). This can help to avoid getting stuck in local optima and to improve the overall quality of the solutions found. The impact of the Local Search pattern can vary depending on the specifics of the algorithm and the problem being solved. In some cases, local search may be crucial for finding high-quality solutions, while in other cases it may be less important or even detrimental to the search process. Overall, the Local Search pattern can be a powerful tool for improving the effectiveness and efficiency of heuristic optimization algorithms.

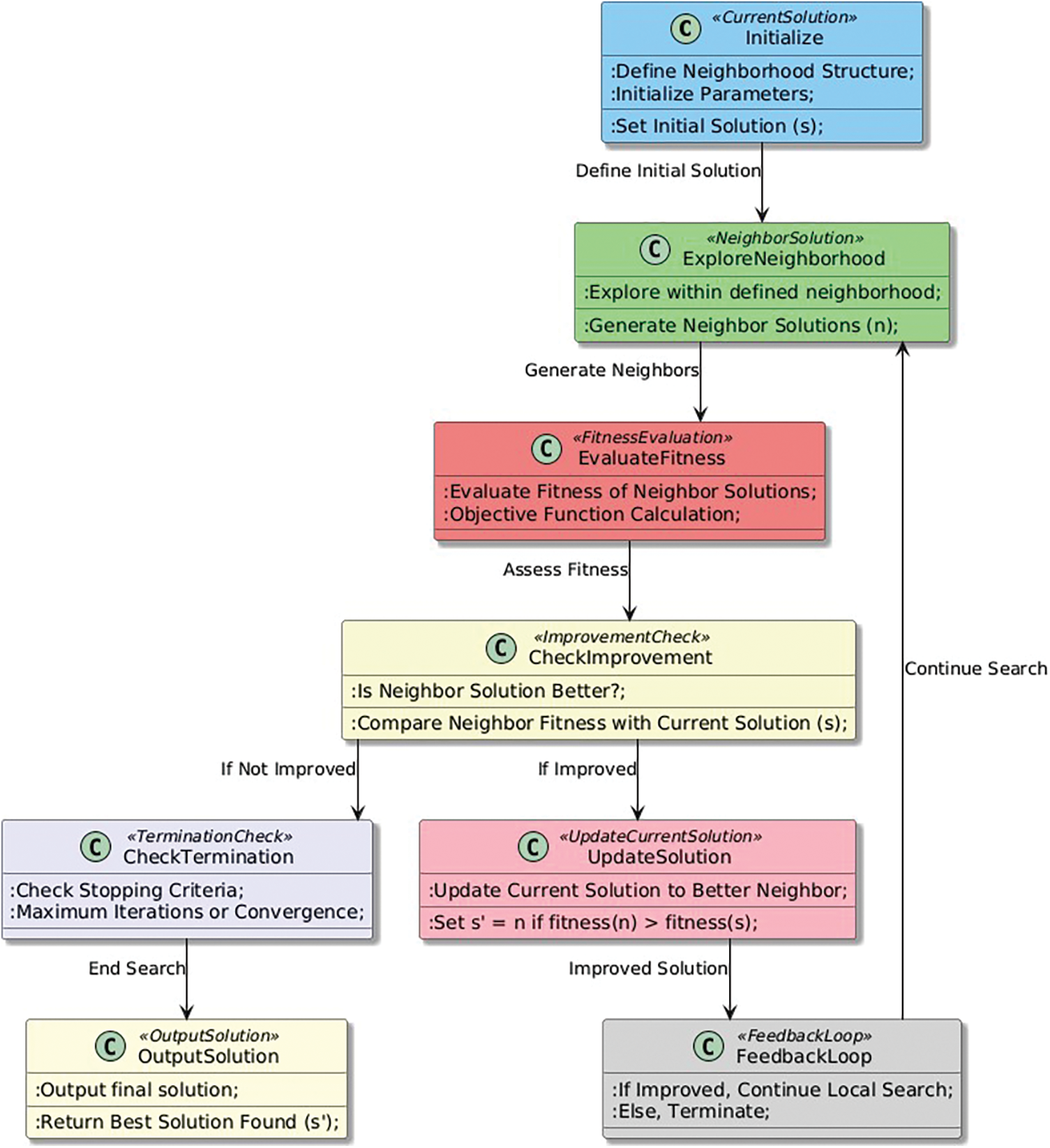
Figure 2: Local Search pattern

3.3 Diversity Maintenance Pattern

3.3.1 Motivation

The motivation behind the Diversity Maintenance pattern in heuristic optimization algorithms is to prevent premature convergence to suboptimal solutions and to ensure that the algorithm explores a wide range of solutions in the search space [79,80]. Without diversity maintenance, the algorithm may quickly converge to a local optimum or a small subset of the solution space, which can limit the quality of the solutions that are found [81,82]. By maintaining diversity in the population of solutions, the algorithm can continue to explore different regions of the solution space and avoid getting stuck in local optima [83,84].

Diversity maintenance can also help the algorithm to identify multiple optimal solutions, rather than just a single global optimum. This is particularly important in multi-objective optimization problems, where there may be multiple solutions that are optimal in different ways [83,85].

The motivation behind the Diversity Maintenance pattern is to improve the quality and robustness of the solutions found by heuristic optimization algorithms, and to enable the algorithm to explore a wide range of solutions in the search space [86,87].

3.3.2 Implementation

The Diversity Maintenance pattern refers to the practice of maintaining diversity in the population of solutions throughout the optimization process. This is typically achieved by ensuring that the population contains solutions that are not only high quality, but also diverse in terms of their characteristics or attributes. Formally, diversity maintenance can be defined as a constraint that is imposed on the optimization algorithm to ensure that the population of solutions does not converge too quickly towards a single optimal solution. This can be achieved by introducing mechanisms that promote exploration of different regions of the solution space, such as:

•   Niching: This involves partitioning the population into subgroups or niches, where each niche represents a different region of the solution space. Solutions are then evaluated based on their fitness within their respective niches, and only the fittest solutions from each niche are allowed to reproduce and create the next generation.

•   Crowding: This involves selecting a subset of the population that represents the diversity of solutions and removing solutions that are too similar to each other. This ensures that the population is not dominated by a few highly similar solutions.

•   Fitness sharing: This involves reducing the fitness of a solution based on its similarity to other solutions in the population. This encourages the population to explore different regions of the solution space and prevents the population from converging too quickly.

Here is an example algorithm for Diversity Maintenance pattern in pseudocode given as Algorithm 3.

In this algorithm, the Diversity Maintenance pattern is implemented by applying a diversity maintenance technique to the remaining solutions in the population . The specific technique used will depend on the algorithm being used, but could include methods such as niching or crowding. The algorithm starts by initializing the population and evaluating the fitness of each solution. The algorithm then enters a loop where it iteratively improves the population by generating new solutions, evaluating their fitness, and adding them to the population while also removing solutions with low fitness. In addition to this basic optimization process, the algorithm also includes a step where a diversity maintenance technique is applied to the population. This helps to ensure that the population of solutions remains diverse, even as the algorithm converges towards a solution. The algorithm continues until a stopping criterion is met, such as reaching a maximum number of iterations or achieving a desired level of solution quality. At this point, the best solution found by the algorithm is returned as the output.

3.3.3 Impact on Search Process

The impact of the Diversity Maintenance pattern on the search process in heuristic optimization algorithms is significant. By maintaining diversity in the population of solutions, the algorithm is able to explore a wider range of solutions and avoid getting stuck in local optima. This can lead to better quality solutions and a more robust search process. Diversity maintenance can also help the algorithm to identify multiple optimal solutions, rather than just a single global optimum. This is particularly important in multi-objective optimization problems, where there may be multiple solutions that are optimal in different ways. However, maintaining diversity in the population of solutions can also have some drawbacks. For example, it can increase the computational complexity of the algorithm, as more solutions need to be evaluated and stored. Maintaining diversity can also make it more difficult for the algorithm to converge to a high-quality solution, as the search process is more exploratory and less focused.

The impact of the Diversity Maintenance pattern on the search process depends on the specific implementation of the algorithm and the characteristics of the optimization problem being solved. In general, however, maintaining diversity is an important strategy for improving the quality and robustness of heuristic optimization algorithms.

Diversity maintenance (Fig. 3) is an important pattern in heuristic optimization algorithms because it allows the algorithm to explore a wider range of solutions and avoid premature convergence to suboptimal solutions. By maintaining diversity, the algorithm can continue to search for better solutions even after it has found a good solution, which can lead to further improvements in the quality of the solutions.

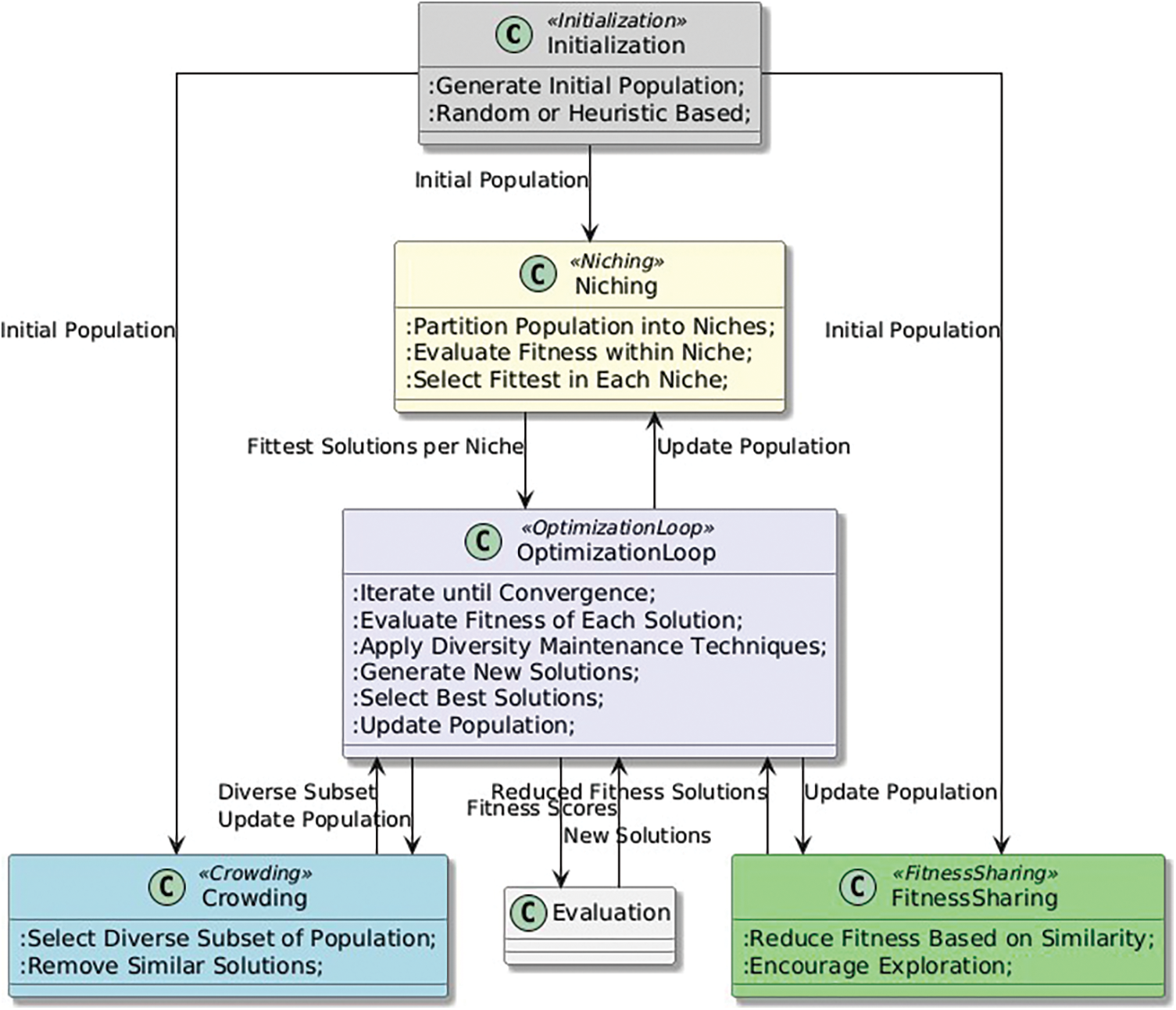
Figure 3: Diversity Maintenance pattern

3.4 Adaptation Pattern

3.4.1 Motivation

The motivation behind the Adaptation pattern in heuristic optimization is to improve the efficiency and effectiveness of the search process by dynamically adjusting the search strategy based on the performance of the algorithm [88,89]. In traditional heuristic optimization algorithms, the search strategy is fixed throughout the search process, which can limit the algorithm’s ability to find good solutions [90]. By adapting the search strategy, the algorithm can focus on promising areas of the search space and avoid wasting time exploring areas that are unlikely to yield good solutions [91,92]. For example, if the algorithm is finding good solutions quickly, it may increase the intensity of the search by using more aggressive operators or focusing on a smaller region of the search space [93]. Conversely, if the algorithm is struggling to find good solutions, it may decrease the intensity of the search to explore a wider range of solutions [94]. Adaptation can also help the algorithm overcome challenges such as changing problem landscapes or noisy objective functions [95]. By monitoring the performance of the algorithm and adjusting the search strategy accordingly, the algorithm can quickly adapt to these challenges and continue to search for good solutions [96]. The motivation behind the Adaptation pattern is to make heuristic optimization algorithms more flexible, robust, and efficient by dynamically adjusting the search strategy based on the problem and the performance of the algorithm [97].

3.4.2 Implementation

The Adaptation pattern is not an algorithm by itself but rather a general approach to adjust the behavior of a heuristic optimization algorithm during its execution. Specific adaptation mechanisms must be defined and implemented for each particular algorithm.

However, we can provide a general overview of the Adaptation pattern:

1.    Define a set of parameters or settings that control the behavior of the algorithm.

2.    Monitor the performance of the algorithm as it searches for a solution.

3.    Use performance information to adjust the parameters or settings in order to improve the algorithm’s performance.

4.    Repeat Steps 2 and 3 until a satisfactory solution is found or a stopping criterion is met.

The specific adaptation mechanisms can vary widely depending on the algorithm and the problem being solved. Some examples of adaptation mechanisms include:

•   Changing the search space or the search direction based on the current state of the search.

•   Adjusting the step size or the mutation rate in a local search algorithm.

•   Increasing or decreasing the population size in a population-based algorithm.

•   Adjusting the probability distribution used to generate new solutions.

•   Changing the selection mechanism used to choose the next solution to evaluate.

The goal of the Adaptation pattern is to allow the algorithm to dynamically adjust its behavior to the problem being solved and the progress it has made so far, to improve its performance and find better solutions.

In Algorithm 4, the Adaptation pattern is implemented by periodically updating the algorithm parameters based on the performance of the solutions found so far. The adaptation interval determines how often the parameters are updated. In addition to adaptation, the algorithm also includes initialization, evaluation, and heuristic search operators. The best solution found is tracked and returned as the output of the algorithm.

3.4.3 Impact on Search Process

The Adaptation pattern is a commonly used heuristic optimization pattern (Fig. 4) that allows the algorithm to dynamically adjust its search strategy based on the performance of the solutions found. This pattern is motivated by the fact that different problems require different search strategies, and a fixed search strategy may not be effective for all problems. By adapting the search strategy, the algorithm can more effectively explore the search space and find better solutions. The impact of the Adaptation pattern on the search process can be significant. By dynamically adjusting the search strategy, the algorithm can avoid getting stuck in local optima and explore a wider range of solutions. This can lead to better performance and faster convergence to good solutions. Adaptation can help the algorithm maintain diversity in the population of solutions, which is important for avoiding premature convergence. Adaptation can also introduce additional complexity into the algorithm, particularly if the adaptation mechanism is not well-designed. Careful consideration must be given to the design of the adaptation mechanism to ensure that it is effective and does not introduce unintended side effects.

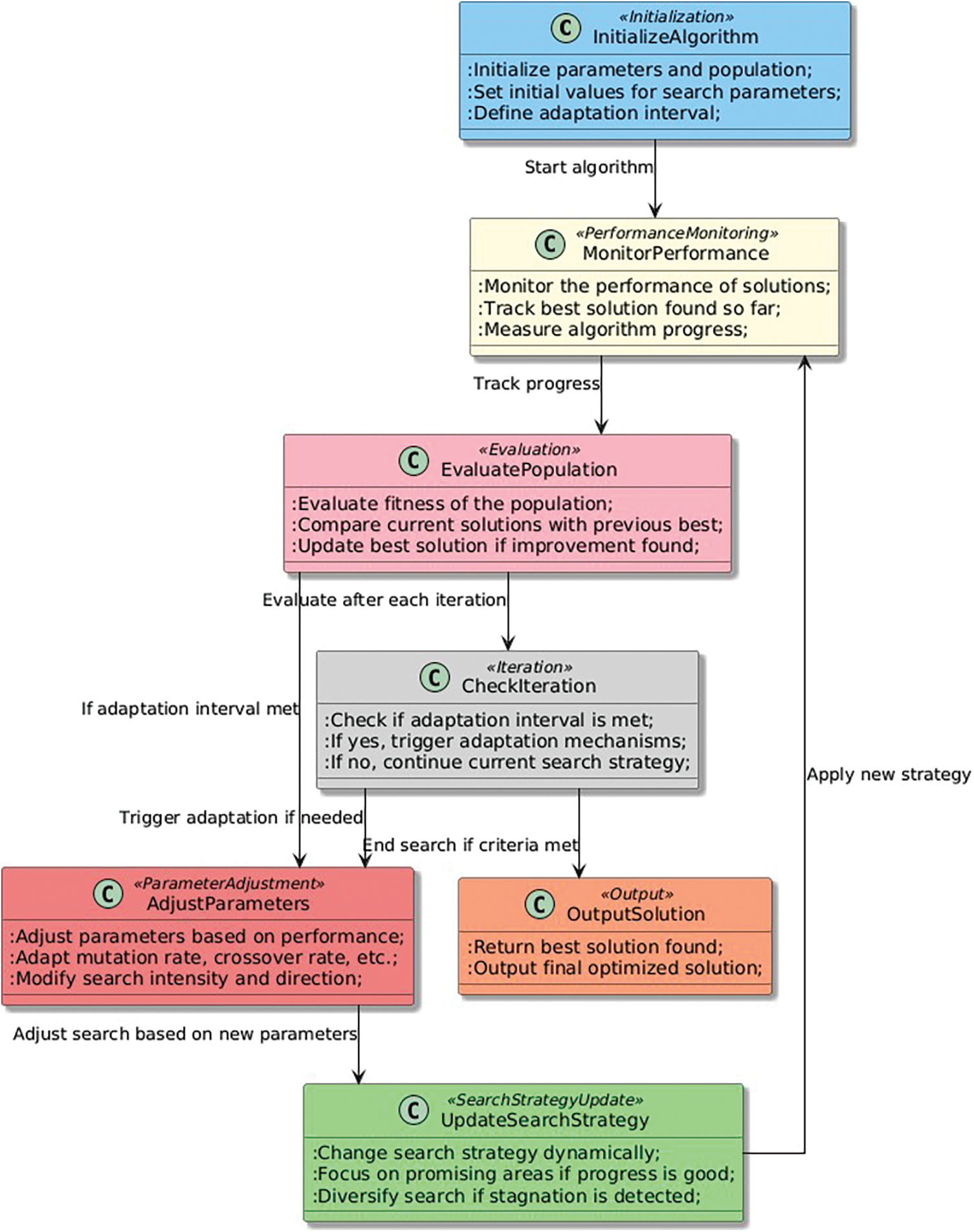
Figure 4: Adaptation pattern

3.5 Stochasticity

3.5.1 Motivation

The motivation behind the Stochasticity pattern in heuristic optimization patterns is to introduce randomness or probabilistic decisions in the search process. This pattern is used in heuristic optimization algorithms to avoid being trapped in local optima and explore the solution space more effectively [98,99]. Stochasticity allows the algorithm to take risks and try new search directions, which can lead to the discovery of better solutions [100]. In addition, stochasticity can help the algorithm escape from plateaus or other regions of the search space where the objective function is flat or nearly constant [101,102]. By introducing stochasticity, the algorithm can sample a wider range of solutions and make progress towards better solutions [103,104].

3.5.2 Implementation

The Stochasticity pattern (Algorithm 5) is a heuristic optimization pattern that involves introducing some degree of randomness or chance in the search process. This can help the algorithm explore a wider range of solutions and avoid getting stuck in local optima. The degree of randomness introduced can vary from completely random search to partially randomized search, where only certain aspects of the search process are randomized. In addition to random perturbation, other stochastic techniques such as randomization of the search direction and random selection of solutions for further evaluation can be used to introduce randomness in the search process.

In this algorithm, we start by initializing the solution, and then we repeatedly generate random perturbations to the solution and evaluate the new solutions. If a new solution is found that is better than the current solution, we update the solution. This introduces stochasticity into the search process, as the random perturbations allow the algorithm to explore a wider range of solutions.

3.5.3 Impact on Search Process

The Stochasticity pattern (Fig. 5) has a significant impact on the search process in heuristic optimization algorithms. By introducing randomness and probability into the search process, it helps the algorithm explore a wider range of solutions and avoid getting stuck in local optima. Stochastic techniques can be used in various parts of the algorithm, such as the initialization, the generation of new solutions, the selection of solutions for further evaluation, and the local search process. For example, in the initialization phase, the solutions can be generated randomly, with a certain probability of each solution being selected. In the generation of new solutions, stochastic techniques can be used to add randomness to the search direction or to perturb the current solution randomly. In the selection of solutions for further evaluation, random selection can be used to avoid bias towards certain solutions. In the local search process, stochastic techniques can be used to add noise to the search direction or to perturb the current solution randomly. This can help the algorithm explore a wider range of solutions and avoid getting stuck in local optima.

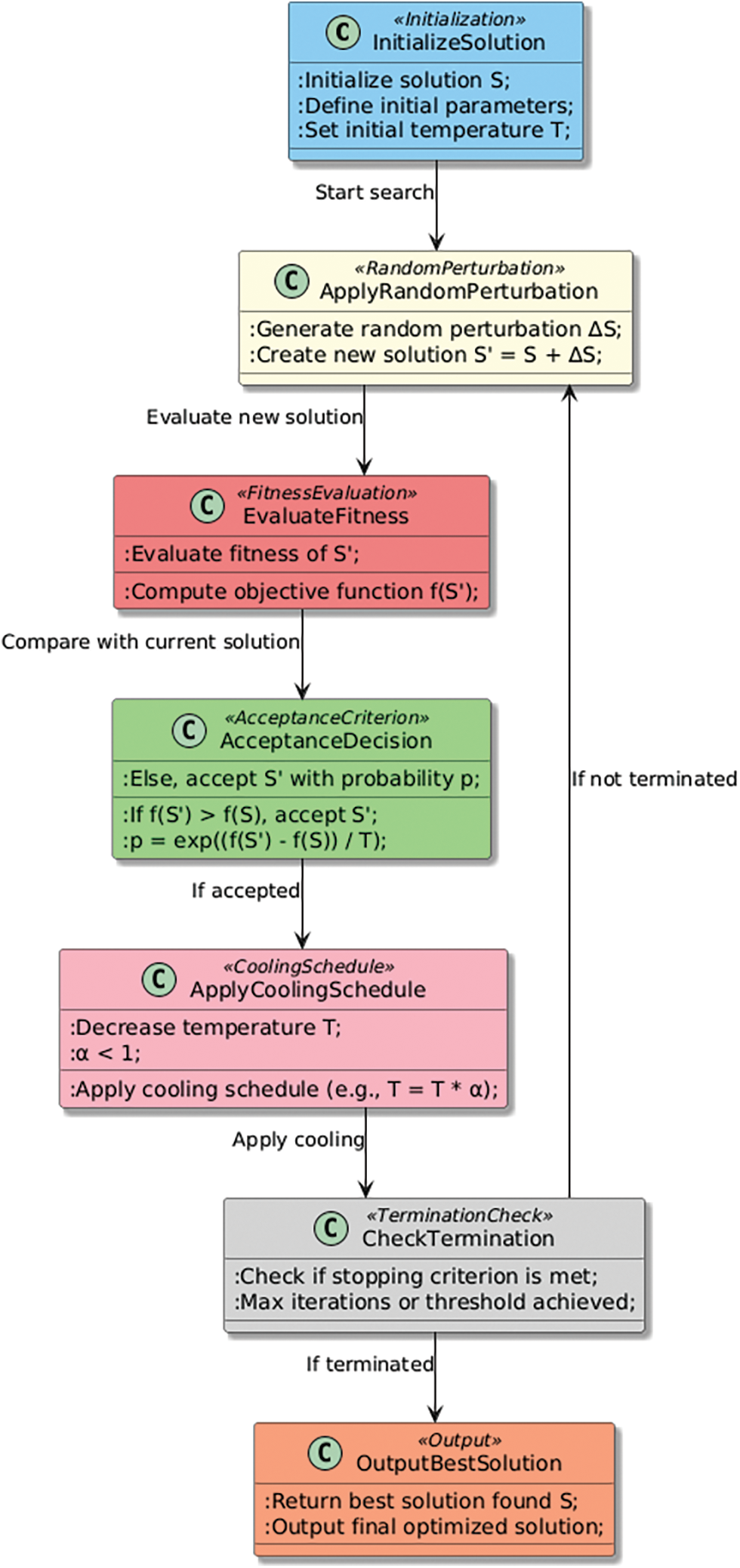
Figure 5: Stochasticity pattern

The Stochasticity pattern plays an important role in balancing exploration and exploitation in the search process, which is crucial for finding high-quality solutions in heuristic optimization algorithms.

3.6 Population-Based Search

3.6.1 Motivation

The Population-based search pattern aims to enhance the optimization process by leveraging the collective knowledge and experiences of a group of candidate solutions. In many optimization scenarios, the optimal solution is not readily apparent and can be challenging to locate through a single search method. By employing a population-based approach, the algorithm can explore a more extensive search space and potentially discover superior solutions compared to single-solution strategies [105,106]. This approach also helps prevent premature convergence by maintaining diversity among the solutions [107,108].

3.6.2 Implementation

Population-based search is a prevalent pattern in heuristic optimization algorithms [65]. The core concept is to maintain a population of candidate solutions and utilize the interactions between these solutions to guide the search toward optimal outcomes [106]. Typically, the population is initialized either randomly or through heuristic methods, with the search process focusing on iteratively improving the quality of the solutions within the population [57]. During each iteration, the algorithm generates a new set of candidate solutions by applying various search operators, such as mutation, crossover, and selection, to the existing population. These new solutions are evaluated based on their fitness, which informs the subsequent update of the population. The design of the search operators is crucial, as it fosters diversity within the population, thereby reducing the risk of the algorithm getting trapped in local optima.

Population-based search can be enhanced by incorporating adaptive mechanisms that modify the parameters of the search operators in response to the algorithm’s performance [109]. For instance, if the algorithm shows signs of rapid convergence, the mutation rate may be increased to encourage further exploration [110]. This pattern has been successfully applied across various heuristic optimization frameworks, including genetic algorithms, particle swarm optimization, and differential evolution, among others [111]. The population-based search pattern can be described as follows:

1: Initialize population P with N random solutions

2: Evaluate fitness of each solution in P

3: Set generation counter g = 1

4: while g ≤ G do

5:    Select parents from P using a selection strategy

6:    Generate offspring by applying genetic operators to parents

7:    Evaluate fitness of offspring

8:    Merge P and offspring into a combined population Q

9:    Select new population P from Q using a selection strategy

10:  Evaluate fitness of new population P

11:   g = g + 1

12: end while

13: Return best solution found in P

In this algorithm, the population of solutions is represented by the variable P, which is initialized with N random solutions in Line 1. The fitness of each solution in P is evaluated in Line 2. The algorithm then enters a loop that iterates for a maximum G generations (Lines 4–12). In each generation, the algorithm selects parents from the population using a selection strategy (Line 5). The parents are used to generate offspring by applying genetic operators such as mutation and crossover (Line 6). The fitness of the offspring is evaluated (Line 7). The offspring are then merged with the original population into a combined population Q (Line 8). The new population P is selected from Q using a selection strategy (Line 9), and the fitness of the new population is evaluated (Line 10). The generation counter g is incremented (Line 11), and the algorithm proceeds to the next generation until the maximum number of generations is reached. Finally, the best solution found in P is returned as the output of the algorithm (Line 13).

3.6.3 Impact on Search Process

The population-based search pattern (Fig. 6) can have a significant impact on the search process in heuristic optimization algorithms. By maintaining a diverse population of solutions and allowing for interaction between individuals, population-based search can help the algorithm explore a wider range of solutions and avoid getting stuck in local optima. This pattern can also help the algorithm converge more quickly to high-quality solutions by sharing information between individuals.

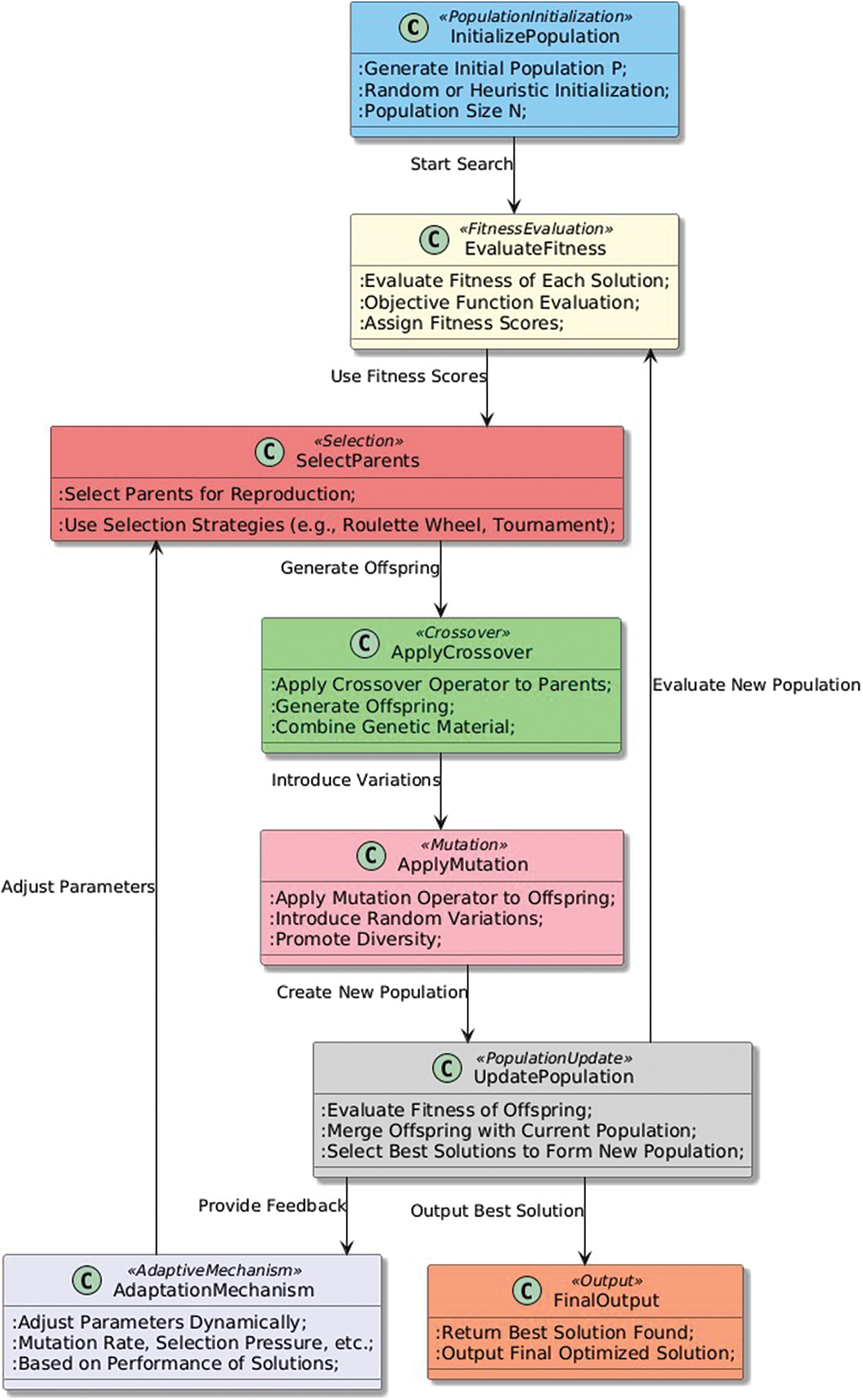
Figure 6: Population-based search pattern

The use of the population-based search can also make the algorithm more robust to changes in the problem landscape. If the problem landscape changes during the search process, some individuals in the population may become less fit or even become completely invalid solutions. However, the use of a diverse population can help ensure that the algorithm is still able to find high-quality solutions by exploring alternative regions of the search space. Therefore, the population-based search pattern can have a positive impact on the search process by promoting diversity, sharing information between individuals, and improving the robustness of the algorithm.

3.7 Memory-Based Search

3.7.1 Motivation

The motivation behind the Memory-based search pattern is to improve the search process by using information from previous iterations to guide the search towards promising regions of the solution space. By maintaining a memory of the best solutions found so far, the algorithm can avoid revisiting unpromising areas and focus on exploring areas that are likely to yield better solutions [112,113]. This can lead to faster convergence and improved quality of the solutions [114]. Memory-based search is particularly useful in problems where the objective function is noisy or where the search space is large and complex [115,116].

3.7.2 Implementation

Memory-based search pattern involves storing information about previous solutions and using it to guide the search towards better solutions. The main motivation behind this pattern is that good solutions often have similar characteristics and are in similar regions of the search space. By using information about previous solutions, the algorithm can avoid exploring unpromising regions of the search space and focus on the areas that are more likely to contain good solutions.

The implementation of the Memory-based search pattern typically involves maintaining a memory of the best solutions found so far, as well as the corresponding regions of the search space. This memory can be used in various ways, such as:

•   Intensification: If the algorithm finds a new solution that is similar to a previously discovered good solution, it can intensify the search in the corresponding region of the search space. This can be done by increasing the local search intensity, or by using specialized search operators that are tailored to the characteristics of the region.

•   Diversification: If the algorithm is struggling to find new good solutions, it can use the memory to diversify the search. This can be done by selecting solutions from the memory that are dissimilar to the current solution and exploring the corresponding regions of the search space.

•   Restart: If the algorithm gets stuck in a local optima, it can use the memory to perform a restart. This involves selecting a solution from the memory and using it as the starting point for a new search.

The pseudocode for the Memory-based search pattern is presented in Algorithm 6.

In this algorithm, the memory M stores a set of previously generated solutions. The algorithm begins by initializing the memory and a current solution S. Then, it generates a candidate solution Sc and compares its objective function value to that of the current solution S. If Sc has a lower objective function value, it replaces S and adds S to the memory. Otherwise, it adds Sc to the memory. After each iteration, the algorithm selects a solution from the memory and updates the current solution S to the selected solution. This helps the algorithm maintain a diverse set of solutions and avoid getting stuck in local optima. The algorithm continues until a termination criterion is met, such as a maximum number of iterations or a sufficient improvement in the objective function value. Finally, the algorithm returns the best solution found during the search process.

3.7.3 Impact on Search Process

The Memory-based search pattern (Fig. 7) in heuristic optimization algorithms involves utilizing the information obtained from previous searches to guide the search towards better solutions. This pattern is motivated by the fact that previous search experiences can provide valuable insights into the search space and help avoid revisiting unpromising areas.

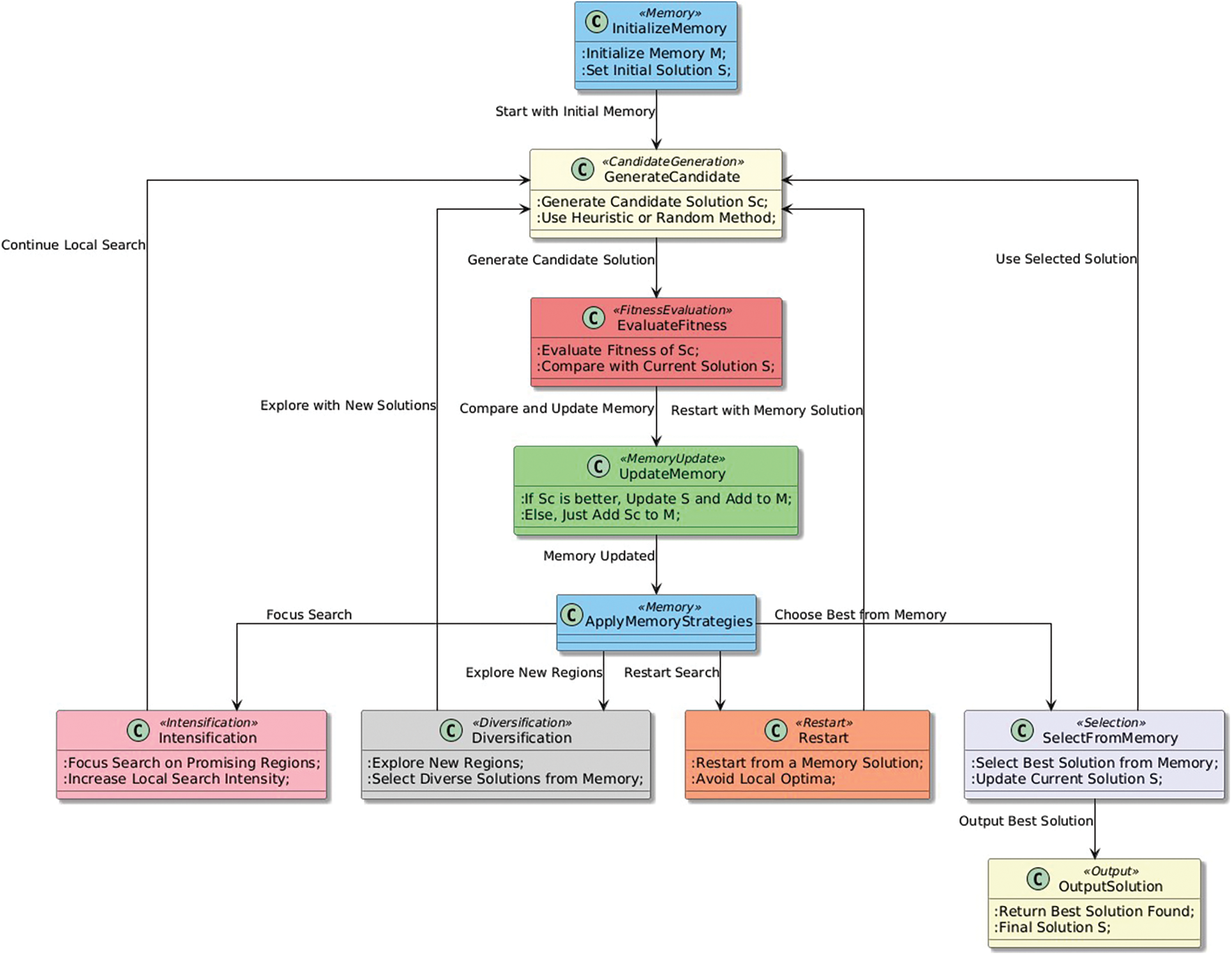
Figure 7: Memory-based search pattern

By incorporating memory-based search, the algorithm is able to learn from past experiences and use this information to guide the search towards promising regions of the search space. This can significantly improve the efficiency and effectiveness of the search process, as the algorithm is able to avoid repeating unsuccessful search paths and focus on promising areas. Memory-based search can help the algorithm escape local optima and find better solutions. By storing information about previous search experiences, the algorithm is able to remember promising solutions that were previously found and explore the search space around them in more detail.

The Memory-based search pattern can be combined with other patterns, such as population-based search and hybridization, to further improve the search performance. Memory-based search can have a significant impact on the search process by improving the efficiency, effectiveness, and robustness of the algorithm.

3.8 Hybridization

3.8.1 Motivation

The motivation behind the hybridization pattern in heuristic optimization algorithms is to leverage the strengths of different algorithms or techniques and overcome their weaknesses to achieve better results. In many cases, a single algorithm or technique may not be sufficient to solve complex optimization problems, or may become trapped in local optima and fail to find the global optimum [117,118]. By combining two or more algorithms or techniques, the hybrid algorithm can benefit from their complementary strengths and overcome their weaknesses. For example, one algorithm may be good at global exploration but slow to converge, while another algorithm may be good at local exploitation but prone to getting stuck in local optima. By combining these two algorithms, the hybrid algorithm can explore a wider range of solutions and quickly converge to good solutions [119,120]. Another motivation behind the hybridization pattern is to enhance the robustness of the optimization process. By using multiple algorithms or techniques, the hybrid algorithm is less vulnerable to the performance fluctuations of individual algorithms or techniques. This is particularly important in noisy or dynamic optimization problems where the quality of the solutions may change over time [121,122].

The motivation behind the hybridization pattern is to improve the effectiveness and efficiency of the optimization process by combining different algorithms or techniques in a synergistic way [123,124].

3.8.2 Implementation

The hybridization pattern is a pattern in heuristic optimization algorithms where two or more different algorithms or techniques are combined to improve the overall performance of the optimization process. The motivation behind this pattern is to leverage the strengths of each individual algorithm or technique to overcome their weaknesses and achieve better results. The hybridization pattern involves combining two or more algorithms or techniques to form a new algorithm or technique that incorporates the strengths of each individual component. The combination can be done in various ways, such as running the individual algorithms sequentially, running them in parallel, or alternating between them at different stages of the optimization process.

The hybridization pattern can be used in a variety of contexts, such as combining different optimization algorithms, combining optimization algorithms with machine learning techniques, or combining optimization algorithms with mathematical programming techniques. The choice of algorithms or techniques to combine depends on the problem being solved and the characteristics of the individual algorithms or techniques. The impact of the hybridization pattern on the search process can be significant, as it allows for a more diverse and robust exploration of the search space. By combining different algorithms or techniques, the hybrid algorithm is able to benefit from the strengths of each individual component and overcome their weaknesses, resulting in improved convergence, solution quality, and efficiency.

Algorithm 7 presents the Hybridization pattern. In this algorithm, we first initialize the population P using some heuristic or randomization technique. Then, we repeat a cycle of operations until a stopping criterion is met. During each cycle, we first apply local search to a subset of the solutions in P to improve their quality. Then, we apply crossover and mutation operators to the solutions in P to generate new solutions. We evaluate the fitness of the new solutions and select the best solutions from P and the new solutions to form the next generation. Finally, we return the best solution found during the search.

3.8.3 Impact on Search Process

The Hybridization pattern (Fig. 8) combines different optimization techniques to enhance the search process. The use of local search can help to refine promising solutions, while the use of crossover and mutation can introduce diversity and explore new areas of the search space. By combining these techniques, the Hybridization pattern can be more effective at finding high-quality solutions than any single technique alone.

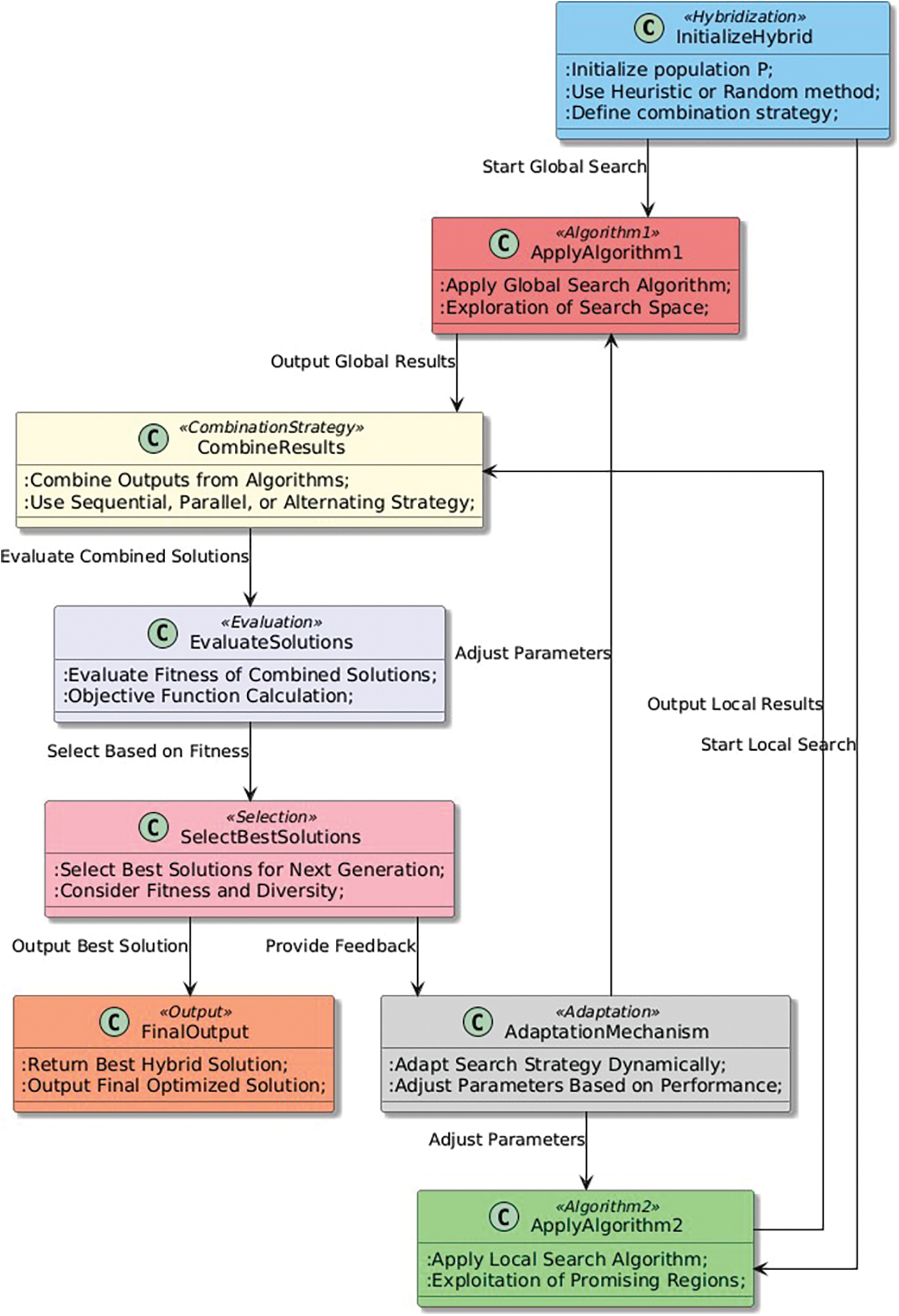
Figure 8: Hybridization pattern

The impact of hybridization on the search process can be significant. By combining different optimization algorithms or techniques, hybridization can improve the exploration and exploitation of the search space, leading to better-quality solutions. Hybridization can also help overcome the limitations or weaknesses of individual algorithms. For example, one algorithm may be good at exploring the search space but may struggle to converge to a good solution, while another algorithm may be good at exploitation but may get stuck in local optima. By combining these algorithms, the hybrid algorithm can leverage the strengths of both and overcome their weaknesses. The Hybridization pattern can also enable the use of complementary search strategies. For instance, a population-based search algorithm may be combined with a memory-based search algorithm, where the population-based algorithm explores the search space globally, and the memory-based algorithm exploits the promising regions found by the population-based algorithm. The impact of hybridization on the search process can be highly positive, leading to improved quality of solutions, faster convergence, and better exploration of the search space.

3.9 Constraint Handling

3.9.1 Motivation

The Constraint Handling pattern is motivated by the fact that many real-world optimization problems involve constraints that need to be satisfied. These constraints could be hard constraints that must be satisfied for a solution to be valid, or soft constraints that represent preferences that should be optimized while satisfying the hard constraints [125,126]. In such cases, it is important for optimization algorithms to take these constraints into account during the search process to ensure that the solutions found are feasible and acceptable [127,128]. The Constraint Handling pattern provides a systematic approach for incorporating constraints into the search process, and can improve the quality of solutions and efficiency of the search process [129,130].

3.9.2 Implementation

The Constraint Handling pattern is a set of techniques used in heuristic optimization algorithms to handle constraints imposed by the problem. The pattern typically involves handling constraints in a way that ensures feasible solutions are generated, and unfeasible solutions are either discarded or repaired.

The Constraint Handling pattern can be described by Algorithm 8. This algorithm iteratively solves a constrained subproblem that minimizes the objective function subject to the violated constraints at the current solution. The algorithm terminates when all constraints are satisfied, or the maximum number of iterations is reached. The function returns the value of the i-th constraint function at , and the constraints are considered violated if their value is greater than zero.

The Constraint Handling pattern (Fig. 9) can be used in conjunction with other heuristic optimization patterns to improve the search process, such as Initialization, Local Search, and Diversity Maintenance. By ensuring that feasible solutions are generated, the Constraint Handling pattern can help to guide the search towards better solutions, while avoiding infeasible regions of the search space.

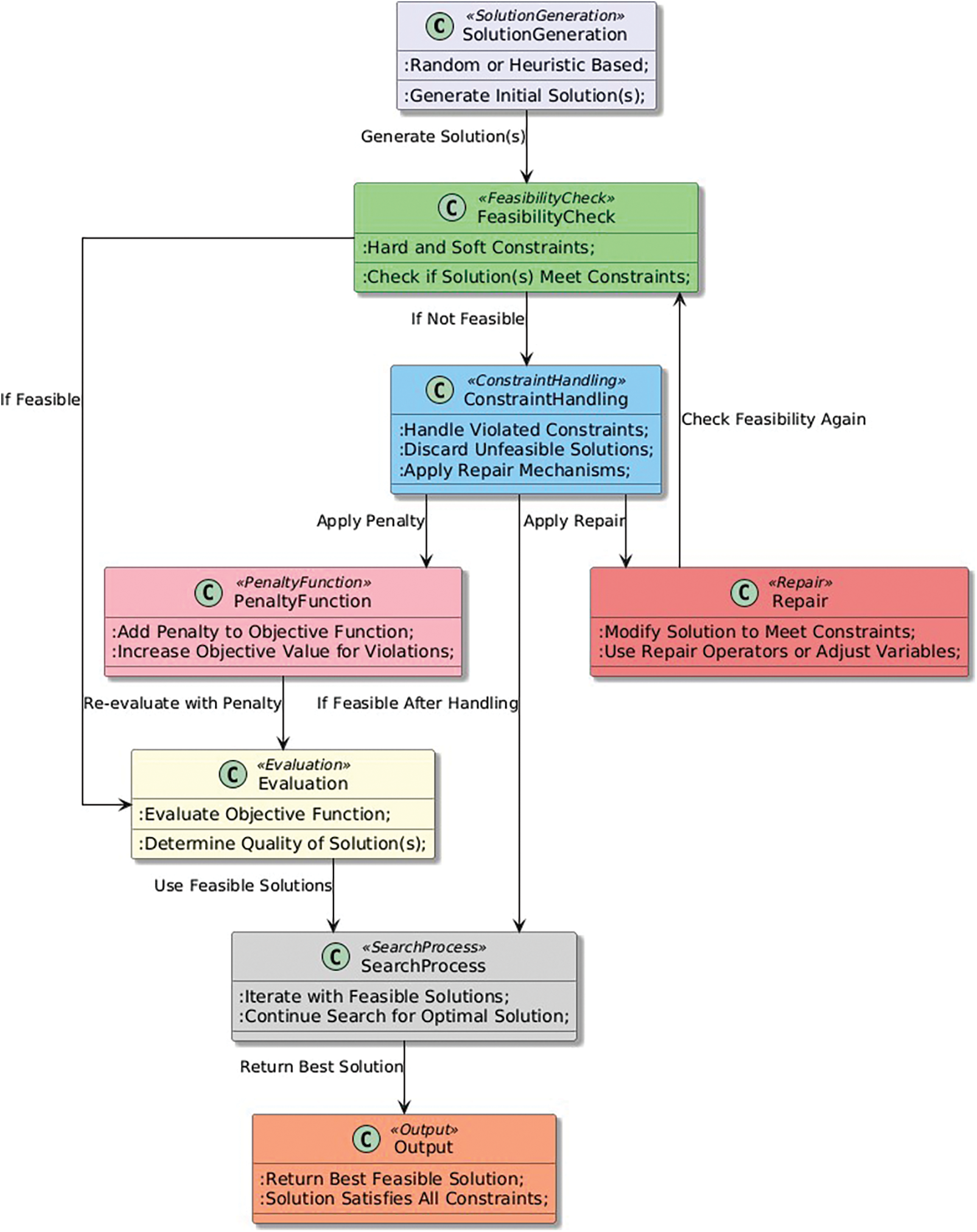
Figure 9: Constraint Handling pattern

3.9.3 Impact on Search Process

The Constraint Handling pattern is aimed at improving the search process of optimization algorithms in constrained optimization problems. By incorporating constraints into the optimization process, this pattern ensures that the solutions generated by the algorithm satisfy the constraints imposed by the problem.

The impact of the Constraint Handling pattern on the search process can be significant, especially in constrained optimization problems. By incorporating the constraints, the algorithm is able to generate feasible solutions, thereby reducing the search space and improving the efficiency of the search process. By ensuring that the solutions generated satisfy the constraints, the algorithm is able to produce high-quality solutions that are likely to be acceptable in practice. The impact of the Constraint Handling pattern on the search process may depend on the specific approach used to handle the constraints. Different methods, such as penalty functions, feasibility-based methods, and constraint handling techniques based on evolutionary algorithms, have been proposed in the literature, and their effectiveness may vary depending on the problem characteristics and the algorithm being used. Therefore, careful consideration and selection of the appropriate constraint handling approach is important for achieving optimal performance in constrained optimization problems.

3.10 Fitness Landscape Analysis

3.10.1 Motivation

The motivation behind the Fitness Landscape Analysis pattern is to gain insights into the problem structure and characteristics of the fitness landscape of a given optimization problem. The fitness landscape is a visualization of the relationship between the objective function and the search space, and it provides information on how difficult the optimization problem is and what search strategies might be effective [131,132]. By analyzing the fitness landscape, researchers can gain valuable knowledge that can be used to design better optimization algorithms or adapt existing ones to improve their performance on specific problem instances [133,134]. The fitness landscape analysis can also be used to guide the selection of appropriate operators and parameters for an optimization algorithm [135,136].

3.10.2 Implementation

The Fitness landscape pattern describes the analysis of the problem’s fitness landscape to gain insight into the problem structure and search process. The fitness landscape refers to the mapping of the search space onto the fitness or objective function values. This pattern is motivated by the idea that understanding the problem’s fitness landscape can lead to the development of more effective search algorithms.

A fitness landscape is a function that maps a set of candidate solutions to fitness value. More formally, let be the set of all possible solutions to an optimization problem, and let be the fitness function that assigns a real-valued fitness score to each solution . The fitness landscape is then defined as the mapping that maps each solution to a vector , where is the number of solutions that are at a Hamming distance of from .

The fitness landscape captures not only the fitness score of each solution, but also the structure of the search space, by counting the number of neighboring solutions at different distances. This information can be used to guide the search process, by identifying regions of the search space that are likely to contain good solutions, or by characterizing the overall topology of the search space.

The fitness landscape pattern can be described as Algorithm as follows:

1.    Input: Problem instance P.

2.    Output: Analysis of the fitness landscape.

3.    Generate a set of representative solutions from the search space.

4.    Evaluate the fitness function for each of the representative solutions.

5.    Analyze the fitness values of the representative solutions to identify the characteristics of the fitness landscape, such as the number and location of local optima, the degree of ruggedness, and the presence of plateaus or ridges.

6.    Use the insights gained from the fitness landscape analysis to inform the design of the search algorithm, such as selecting appropriate search operators or tuning the algorithm parameters.

The fitness landscape pattern (Fig. 10) does not provide a specific algorithm for solving the optimization problem but rather a framework for analyzing the problem structure to guide the development of more effective search algorithms.

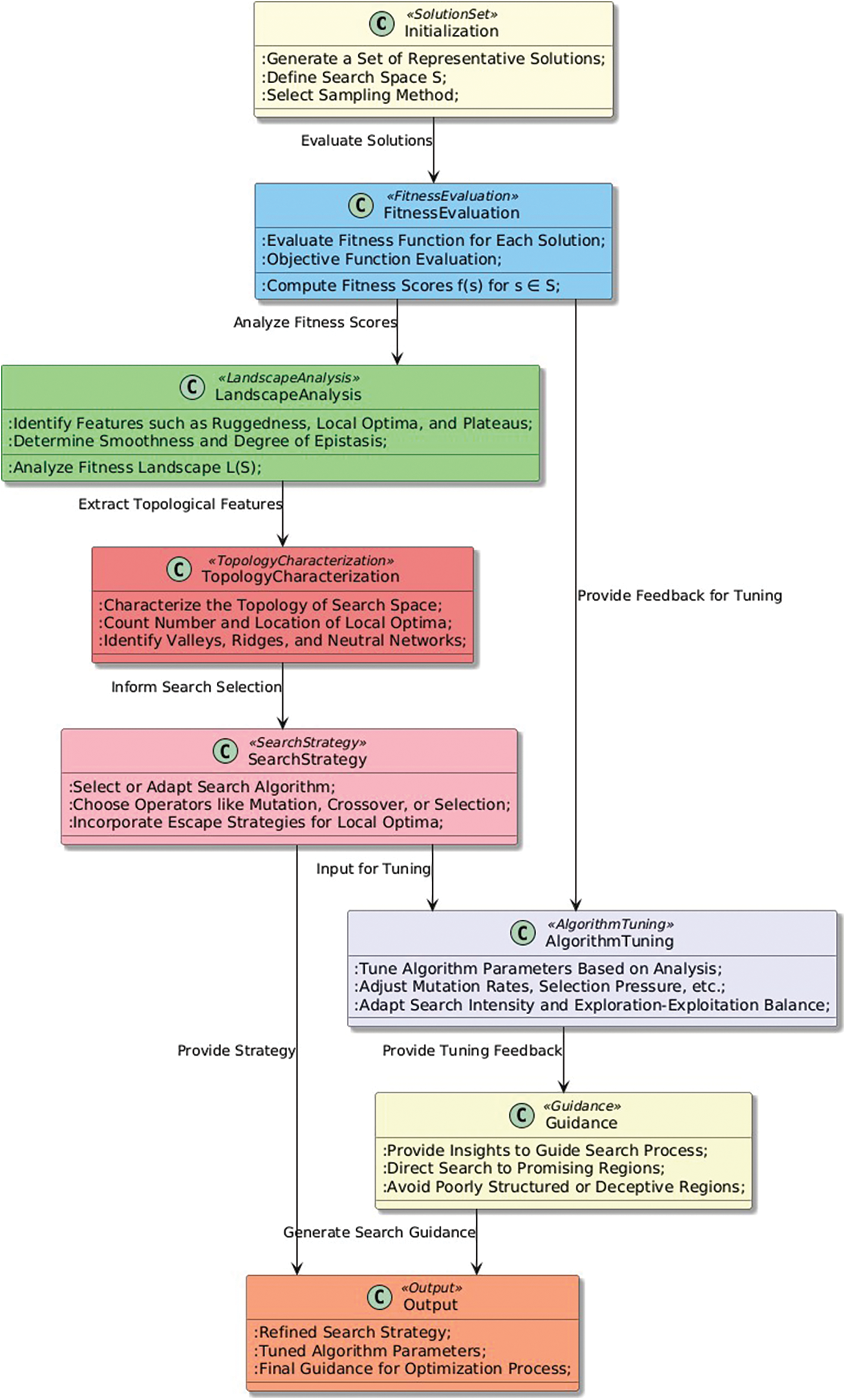
Figure 10: Fitness landscape analysis pattern

3.10.3 Impact on Search Process

The Fitness landscape analysis pattern has a significant impact on the search process in heuristic optimization. By analyzing the fitness landscape, it is possible to gain insights into the characteristics of the search space, such as the presence of local optima, the smoothness of the landscape, and the degree of epistasis. This information can be used to guide the design of the search algorithm and to make informed decisions about the search strategy. For example, if the fitness landscape is found to be rugged with many local optima, it may be necessary to employ a search algorithm that is able to escape local optima, such as a metaheuristic that uses population-based search. On the other hand, if the landscape is found to be relatively smooth, a simpler optimization algorithm such as gradient descent may be sufficient.

The Fitness landscape analysis pattern can improve the efficiency and effectiveness of the search process by providing valuable information about the search space that can be used to tailor the search algorithm to the specific problem at hand.

4  Case Studies

4.1 Overview of Heuristic Optimization Algorithms

Heuristic optimization algorithms are computational methods used to find approximate solutions to complex optimization problems. These problems often involve finding the optimal solution to a problem with a large number of variables and constraints, and in many cases, the solution space is too vast to search exhaustively [137,138]. Heuristic optimization algorithms are based on the principles of natural systems, such as evolution, swarm behavior, and survival of the fittest. These algorithms are designed to strike a balance between exploration of the search space and exploitation of promising solutions [139]. In other words, these algorithms try to find the optimal solution by exploring as much of the search space as possible while also exploiting the most promising areas of the search space [117].

There are many types of heuristic optimization algorithms, including genetic algorithms, particle swarm optimization, simulated annealing, ant colony optimization, and differential evolution. Each algorithm has its own strengths and weaknesses and is designed to solve specific types of problems [140,141].

The general workflow of heuristic optimization algorithms can be described as follows. First, the algorithm initializes the search process by creating a population of potential solutions. These solutions are randomly generated and are represented as a set of variables or decision variables [142]. The next step is to evaluate the fitness of each solution by calculating the objective function value. The objective function is the function that the algorithm is trying to optimize [143]. After the fitness evaluation, the algorithm applies various operators to the population, such as mutation, crossover, and selection, to create new solutions. These operators are designed to mimic the principles of natural selection and evolution [144].

The newly generated solutions are then evaluated using the objective function, and the process continues until the stopping criteria are met. The stopping criteria can be a maximum number of iterations, reaching a predefined fitness level, or running out of computational resources [145].

The motivation for using Krill Herd Optimization (KHO), Red Fox Optimization (RFO), and Coronavirus Herd Immunity Optimizer (CHIO) as case studies in this paper lies in their representation of diverse and innovative approaches within the field of heuristic optimization, each inspired by different natural processes. KHO is based on the biological principles of krill herding behavior, emphasizing global search through environmental sensing and local search through individual movements, making it a prime example of a bio-inspired algorithm. RFO, inspired by the hunting strategies of red foxes, offers a distinct approach that combines exploration and exploitation in a dynamic search space. RFO has been applied in medical imaging [146]. CHIO, modeled on the concept of herd immunity from epidemiology, introduces a unique mechanism of solution propagation and immune response, showcasing how heuristic optimization can be creatively adapted from various scientific domains. CHIO has been used for various optimization problems, including power scheduling [147]. By analyzing these diverse algorithms, the study aims to illustrate the applicability and effectiveness of common optimization patterns across different problem-solving paradigms, thereby enriching the understanding of heuristic optimization design.

4.2 Krill Herd Optimisation (KHO)

4.2.1 Description of KHO

Krill Herd Optimization (KHO) is a swarm intelligence-based heuristic optimization algorithm that mimics the behavior of a krill herd [148]. The Krill Herd Optimization (KHO) algorithm is given in Algorithm 9. It models the movement and behavior of the krill in the herd. The KHO algorithm (Algorithm 9) models the collective behavior of the krill herd to guide the search for the optimal solution to the optimization problem. By adjusting the parameters in the equations, such as the step size and weighting coefficients, the KHO algorithm can be tailored to different optimization problems and solution spaces.

4.2.2 Patterns of KHO

KHO combines elements of swarm intelligence, evolutionary algorithms, and local search to find high-quality solutions to optimization problems. Here are some of the key patterns implemented in KHO:

•   Initialization pattern: In KHO, the initial population of solutions is generated randomly, with each krill (i.e., solution) represented as a vector of decision variables.

•   Local Search pattern: KHO uses a local search mechanism called krill neighborhood search (KNS) to improve the quality of the solutions. KNS selects a subset of the krill in the population and performs a local search around each krill to improve its fitness. The best solution found in this local search is then added to the population.

•   Diversity Maintenance pattern: KHO uses a diversity maintenance mechanism called krill movement to maintain diversity in the population. Krill movement involves randomly perturbing the position of each krill in the population to encourage exploration of different regions of the search space.

•   Adaptation pattern: KHO includes several adaptive mechanisms to adjust the search strategy based on the performance of the algorithm. For example, the step size used in krill movement is adjusted based on the convergence rate of the algorithm.

•   Stochasticity pattern: KHO includes stochastic elements in several parts of the algorithm. For example, the krill movement mechanism introduces random perturbations to the position of each krill. The selection of krill for KNS is performed randomly.

Overall, KHO combines these patterns to create a search process that involves both exploration of the search space and exploitation of promising solutions. By combining swarm intelligence, evolutionary algorithms, and local search, KHO is able to efficiently search large and complex search spaces and find high-quality solutions to a wide range of optimization problems.

4.3 Red Fox Optimisation (RFO)

4.3.1 Description of RFO

Red Fox Optimization (RFO) is a metaheuristic optimization algorithm inspired by the hunting behavior of red foxes [149]. The RFO algorithm is based on the idea of dividing the search process into three phases: the red fox movement phase, the pouncing behavior phase, and the searching behavior phase. In each phase, candidate solutions in the population are updated based on the positions of other solutions or the leader red fox. RFO has been shown to be effective in solving a wide range of optimization problems, including engineering design, feature selection, and image processing, among others.

The RFO algorithm consists of the following steps:

1.    Initialization: Initialize the population of candidate solutions x1, x2, , xN randomly within the search space.

2.    Red fox movement: Each candidate solution xi is updated based on the position of the leader red fox L as follows:

(1)

       where dL,i is the Euclidean distance between the leader L and candidate solution xi, r1,i is a random vector, α1 and β1 are the movement step sizes.

3.    Pouncing behavior: The pouncing behavior updates the position of each candidate solution based on the positions of other candidate solutions within a certain radius rp around them:

(2)

       where S is the set of candidate solutions within the radius rp of candidate solution xi, di,S is the Euclidean distance between candidate solution xi and the centroid of the solutions in S, r2,i is a random vector, α2 and β2 are the movement step sizes.

4.    Searching behavior: The searching behavior updates the position of each candidate solution based on its distance to the best candidate solution G in the population:

(3)

       where di,G is the Euclidean distance between candidate solution xi and the global best solution G, r3,i is a random vector, α3 and β3 are the movement step sizes.

5.    Update population: Calculate the fitness values of the new candidate solutions, and replace the worst solutions in the population with the new solutions if they have better fitness values.

6.    Termination: Terminate the algorithm if a stopping criterion is met (e.g., maximum number of iterations, target fitness value, etc.).

The algorithm for Red Fox Optimization (RFO) is presented in Algorithm 10.

4.3.2 Patterns of RFO

RFO incorporates several patterns commonly observed in heuristic optimization algorithms. Here is how some of these patterns are implemented in RFO:

•   Initialization pattern: RFO begins by randomly generating a population of candidate solutions. The population size is user-defined and typically ranges from 10 to 50.

•   Local Search pattern: RFO uses a local search technique called ‘local roaming’ to improve the quality of the solutions. In local roaming, a random subset of solutions is selected from the population, and each solution is randomly perturbed. If the perturbed solution is better than the original solution, it replaces the original solution in the population. Local roaming is performed a user-defined number of times.

•   Diversity Maintenance pattern: RFO maintains diversity in the population using a technique called ‘predator-prey interaction’. In this technique, each solution in the population is assigned a prey index and a predator index. Solutions with similar prey indices are encouraged to move towards each other, while solutions with similar predator indices are encouraged to move away from each other. This helps to maintain diversity in the population.

•   Adaptation pattern: RFO adapts its search strategy by dynamically adjusting the values of several parameters based on the performance of the solutions found so far. For example, if the algorithm is finding good solutions quickly, it may increase the intensity of the search. Conversely, if the algorithm is struggling to find good solutions, it may decrease the intensity of the search to explore a wider range of solutions.

•   Stochasticity pattern: RFO introduces stochasticity in several ways. Firstly, the local roaming step involves randomly perturbing the solutions. Secondly, the predator-prey interaction technique uses random values to assign prey and predator indices. Thirdly, the algorithm uses a random number generator to make certain decisions, such as which solutions to update.

•   Population-based search pattern: RFO is a population-based search algorithm. The population of candidate solutions is updated using a technique called ‘hunting’. In hunting, each solution in the population is assigned a hunting distance. Solutions with shorter hunting distances are more likely to be selected for further search. A user-defined number of solutions are selected for hunting, and their hunting distances are updated based on their performance.

•   Memory-based search pattern: RFO does not explicitly use a memory-based search technique, but it does maintain a history of the best solution found so far. This history is used to determine when to terminate the search.

The patterns used in RFO are designed to help the foxes explore the search space efficiently and to converge towards promising regions. By mimicking the hunting behavior of red foxes, RFO is able to leverage these patterns to effectively optimize a wide range of computational problems.

4.4 Coronavirus Herd Immunity Optimizer (CHIO)

4.4.1 Description of CHIO

Coronavirus Herd Immunity Optimizer (CHIO) is a nature-inspired heuristic optimization algorithm [150]. The algorithm is inspired by the herd immunity phenomenon in epidemiology and aims to find the optimal solution to a given optimization problem by simulating the process of herd immunity. The algorithm uses a combination of two strategies, namely, immunity and infection, to generate new candidate solutions and gradually converge towards the global optimum. The CHIO algorithm has been applied to a variety of optimization problems and has shown promising results in terms of efficiency and effectiveness. The CHIO algorithm aims to simulate the herd immunity phenomenon by dividing the population of candidate solutions into three categories: susceptible, infected, and immune.

Let f(x) be the objective function to be optimized, where x is the candidate solution vector. The CHIO algorithm can be described mathematically as follows:

1.    Initialize the population of candidate solutions P = x1, x2, , xn randomly.

2.    Define the initial values of the parameters, including the infection rate β, the recoveryrate γ, the immunity rate α, and the maximum number of iterations Tmax.

3.    Evaluate the fitness of each candidate solution in P using the objective function f(x).

4.    Sort the candidate solutions in P based on their fitness values in descending order.

5.    Initialize the infected and immune populations I and U as empty sets.

6.    Set the infection status of each candidate solution in P as susceptible.

7.    Randomly select a candidate solution xi from P and infect it.

8.    Update the infection status of the remaining candidate solutions in P based on their  distance to xi and the infection rate β.

9.    Evaluate the fitness of the newly infected candidate solutions and add them to I.

10.   Update the infection status of the candidate solutions in I based on the recovery rate γ and the immunity rate α.

11.   Evaluate the fitness of the newly immune candidate solutions and add them to U.

12.   Select the best candidate solution x∗ from P ∪ I ∪ U based on their fitness values.

13.   Terminate the algorithm if the maximum number of iterations Tmax is reached or a  stopping criterion is met; otherwise, go to Step 7.

14.   Return the best candidate solution x∗.

The CHIO algorithm (Algorithm 11) simulates the herd immunity phenomenon by updating the infection status of candidate solutions based on their proximity to the infected and the infection rate. The recovery and immunity rates are used to update the infection status of the infected candidate solutions, which eventually become immune and help to improve the quality of the solutions. The CHIO algorithm has shown promising results in solving various complex optimization problems.

4.4.2 Patterns of CHIO

The Coronavirus Herd Immunity Optimizer (CHIO) algorithm is a metaheuristic optimization algorithm that aims to find optimal solutions to complex optimization problems by simulating the process of herd immunity. The CHIO algorithm incorporates several heuristic optimization patterns to enhance its performance and improve the quality of solutions as follows:

•   Initialization pattern: CHIO initializes a population of candidate solutions randomly in the search space.

•   Local Search pattern: CHIO employs a local search operator to exploit the promising regions of the search space. Specifically, the algorithm uses a mutation operator that generates new solutions by making small perturbations to the current solutions.

•   Diversity Maintenance pattern: CHIO maintains diversity in the population by employing a niching operator that identifies and preserves different clusters of solutions.

•   Stochasticity pattern: CHIO introduces stochasticity in the search process by incorporating a probabilistic update rule for selecting the new candidate solutions.

•   Population-based search pattern: CHIO employs a population-based search strategy to explore the search space efficiently. The algorithm updates the population by selecting the best solutions from the current population and the newly generated solutions.

•   Adaptation pattern: CHIO adapts its search strategy by adjusting the algorithm parameters dynamically based on the current state of the search. Specifically, the algorithm increases the mutation rate and niching radius when the search progress slows down.

4.5 Key Findings

For each of the three algorithms in your study–Krill Herd Optimization (KHO), Red Fox Optimization (RFO), and Coronavirus Herd Immunity Optimizer (CHIO)–different optimization patterns show varying impacts on their performance and results:

•   For KHO, the Diversity Maintenance pattern has a significant impact on the results. This algorithm leverages krill movement mechanisms to maintain diversity in the population, thereby avoiding premature convergence and enhancing exploration in complex search spaces. The diversity pattern allows KHO to adapt dynamically to varying optimization landscapes, making it particularly effective in locating high-quality solutions across diverse environments.

•   For RFO, the local search pattern is especially impactful due to its reliance on local roaming and predatorprey interactions to refine candidate solutions iteratively. By simulating red fox hunting behavior, this pattern improves solution quality within the immediate neighborhood of high-potential solutions, significantly enhancing the algorithm as exploitation capabilities. This pattern is crucial for RFO’s convergence efficiency, as it maximizes solution refinement in high-density regions of the search space.

•   For CHIO, the adaptation pattern has the most notable effect. CHIO uses this pattern by adjusting mutation rates and niching radii based on the current state of the search, which helps maintain balance between exploration and exploitation. This dynamic adaptation supports CHIO as ability to adjust search intensity according to the population as progress, improving its effectiveness in navigating complex optimization landscapes.

4.6 Computational Complexity of Patterns

The computational complexity of the patterns is given in Table 1.

5  Discussion and Conclusion

The paper provides a comprehensive analysis of heuristic optimization patterns in various algorithms. Heuristic optimization patterns provide a useful framework for designing new heuristic optimization algorithms. By following these patterns, researchers can build upon existing knowledge and design algorithms that are more likely to be effective and efficient. One implication of heuristic optimization patterns is that they can guide the selection of appropriate components for an algorithm. For example, if a problem is known to have many local optima, an algorithm designer may choose to incorporate a local search pattern to help the algorithm escape these optima. If the problem is known to have a rugged fitness landscape, the designer may choose to incorporate a diverse maintenance pattern to promote exploration of the search space. Another implication is that the patterns can be combined in various ways to create hybrid algorithms. For example, an algorithm may incorporate both local search and population-based search patterns to leverage the strengths of both approaches. The patterns can also inform the parameter-tuning process for heuristic optimization algorithms. By understanding the impact of different patterns on the search process, algorithm designers can better tune the parameters to balance exploration and exploitation and improve the overall performance of the algorithm.

The limitations of this study are as follows:

•   The study mainly focused on nature-inspired heuristic optimization algorithms and did not cover other types of optimization algorithms such as mathematical programming or evolutionary algorithms.

•   The study is limited to the patterns identified in the literature up to 2021, and there may be additional patterns that have not yet been discovered.

•   The study did not include a comparison of the effectiveness of different patterns or their combinations in solving specific problems.

Further research could focus on identifying new patterns in heuristic optimization algorithms that have not yet been discovered. The effectiveness of different patterns or combinations of patterns could be compared using a variety of benchmarks and real-world problems. Future research also could investigate the use of machine learning techniques to identify the most effective patterns for a given problem; the transferability of patterns between different types of optimization algorithms and domains; and the integration of multiple patterns into a single algorithm to enhance the overall performance of heuristic optimization algorithms.

Acknowledgement: None.

Funding Statement: The author received no specific funding for this study.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The author declares no conflicts of interest to report regarding the present study.

References

1. G. Li, F. Shuang, P. Zhao, and C. Le, “An improved butterfly optimization algorithm for engineering design problems using the cross-entropy method,” Symmetry, vol. 11, no. 8, 2019, Art. no. 1049. doi: 10.3390/sym11081049. [Google Scholar] [CrossRef]

2. S. Barshandeh and M. Haghzadeh, “A new hybrid chaotic atom search optimization based on tree-seed algorithm and levy flight for solving optimization problems,” Eng. Comput., vol. 37, no. 4, pp. 3079–3122, 2021. doi: 10.1007/s00366-020-00994-0. [Google Scholar] [CrossRef]

3. T. Kundu and H. Garg, “A hybrid ITLHHO algorithm for numerical and engineering optimization problems,” Int. J. Intell. Syst., vol. 37, no. 7, pp. 3900–3980, 2021. doi: 10.1002/int.22707. [Google Scholar] [CrossRef]

4. C. Liu et al., “Improved multi-search strategy A* algorithm to solve three-dimensional pipe routing design,” Expert. Syst. Appl., vol. 240, Apr. 2024, Art. no. 122313. doi: 10.1016/j.eswa.2023.122313. [Google Scholar] [CrossRef]

5. A. Kaveh and A. Zolghadr, “Comparison of nine meta-heuristic algorithms for optimal design of truss structures with frequency constraints,” Adv. Eng. Softw., vol. 76, no. 12, pp. 9–30, 2014. doi: 10.1016/j.advengsoft.2014.05.012. [Google Scholar] [CrossRef]

6. A. Sobester, S. J. Leary, and A. Keane, “On the design of optimization strategies based on global response surface approximation models,” J. Glob. Optim., vol. 33, no. 1, pp. 31–59, 2005. doi: 10.1007/s10898-004-6733-1. [Google Scholar] [CrossRef]

7. L. Lin and M. Gen, “Auto-tuning strategy for evolutionary algorithms: Balancing between exploration and exploitation,” Soft Comput., vol. 13, no. 2, pp. 157–168, 2008. doi: 10.1007/s00500-008-0303-2. [Google Scholar] [CrossRef]

8. V. Punnathanam and P. Kotecha, “Yin-yang-pair optimization: A novel lightweight optimization algorithm,” Eng Appl. Artif. Intell., vol. 54, pp. 62–79, 2016. doi: 10.1016/j.engappai.2016.04.004. [Google Scholar] [CrossRef]

9. A. Zhang, G. Sun, J. Ren, X. Li, Z. Wang and X. Jia, “A dynamic neighborhood learning-based gravitational search algorithm,” IEEE Trans. Cybern., vol. 48, no. 1, pp. 436–447, 2018. doi: 10.1109/TCYB.2016.2641986. [Google Scholar] [PubMed] [CrossRef]

10. R. Tao, Z. Meng, and H. Zhou, “A self-adaptive strategy based firefly algorithm for constrained engineering design problems,” Appl. Soft Comput., vol. 107, 2021, Art. no. 107417. doi: 10.1016/j.asoc.2021.107417. [Google Scholar] [CrossRef]

11. S. Aras, E. Gedikli, and H. Kahraman, “A novel stochastic fractal search algorithm with fitness-distance balance for global numerical optimization,” Swarm Evol. Comput., vol. 61, 2020, Art. no. 100821. doi: 10.1016/j.swevo.2020.100821. [Google Scholar] [CrossRef]

12. N. Guedria, “Improved accelerated PSO algorithm for mechanical engineering optimization problems,” Appl. Soft Comput., vol. 40, no. 9, pp. 455–467, 2016. doi: 10.1016/j.asoc.2015.10.048. [Google Scholar] [CrossRef]

13. P. B. Reverdy, R. C. Wilson, P. Holmes, and N. E. Leonard, “Towards optimization of a human-inspired heuristic for solving explore-exploit problems,” in 2012 IEEE 51st IEEE Conf. Decis. Cont. (CDC), 2012, pp. 2820–2825. [Google Scholar]

14. E. Burke et al., “Iterated local search vs. hyper-heuristics: Towards general-purpose search algorithms,” in IEEE Cong. Evolution. Comput., 2010, pp. 1–8. [Google Scholar]

15. C. Yu et al., “Quantum-like mutation-induced dragonfly-inspired optimization approach,” Math. Comput. Simul., vol. 178, no. 9, pp. 259–289, 2020. doi: 10.1016/j.matcom.2020.06.012. [Google Scholar] [CrossRef]

16. H. Youssef, S. M. Sait, and H. Adiche, “Evolutionary algorithms, simulated annealing and tabu search: A comparative study,” Eng. Appl. Artif. Intell., vol. 14, no. 2, pp. 167–181, 2001. doi: 10.1016/S0952-1976(00)00065-8. [Google Scholar] [CrossRef]

17. O. Bozorg-Haddad, M. Solgi, and H. Loaiciga, Meta-Heuristic and Evolutionary Algorithms for Engineering Optimization. USA: John Wiley & Sons, Inc., 2017. [Google Scholar]

18. R. Guha et al., “Deluge based genetic algorithm for feature selection,” Evol. Intell., vol. 14, no. 2, pp. 357–367, 2019. doi: 10.1007/s12065-019-00218-5. [Google Scholar] [CrossRef]

19. L. D. Afonso, V. Mariani, and L. Coelho, “Modified imperialist competitive algorithm based on attraction and repulsion concepts for reliability-redundancy optimization,” Expert. Syst. Appl., vol. 40, no. 9, pp. 3794–3802, 2013. doi: 10.1016/j.eswa.2012.12.093. [Google Scholar] [CrossRef]

20. S. L. Tilahun, “Balancing the degree of exploration and exploitation of swarm intelligence using parallel computing,” Int. J. Artif. Intell. Tools., vol. 28, 2019, Art. no. 1950014. doi: 10.1142/S0218213019500143. [Google Scholar] [CrossRef]

21. E. Mirsadeghi and S. Khodayifar, “Hybridizing particle swarm optimization with simulated annealing and differential evolution,” Cluster Comput., vol. 24, no. 2, pp. 1135–1163, 2020. doi: 10.1007/s10586-020-03179-y. [Google Scholar] [CrossRef]

22. W. Chen, C. Dai, and Y. Zheng, “Two population-based heuristic search algorithms and their applications,” in N. Mansour, Ed. Search Algorithms and Applications, 2011. doi: 10.5772/16060. [Google Scholar] [CrossRef]

23. B. Dahiya, S. Rani, and P. Singh, “A hybrid artificial grasshopper optimization (HAGOA) meta-heuristic approach: A hybrid optimizer for discover the global optimum in given search space,” Int. J. Mathem., Eng. Manag. Sci., vol. 4, no. 2, pp. 471–488, 2019. doi: 10.33889/IJMEMS.2019.4.2-039. [Google Scholar] [CrossRef]

24. M. Vargas-MartÃnez, N. Rangel-Valdez, E. Fernandez, C. Gomez-Santillan and M. L. MoralesRodrÃguez, “Performance analysis of multi-objective simulated annealing based on decomposition,” Math. Comput. Appl., vol. 28, no. 2, p. 38, 2023. [Google Scholar]

25. F. C. C. Mei, S. Phon-Amnuaisuk, and M. Y. Alias, “Metaheuristic methods in hybrid flow shop scheduling problem,” Expert Syst. Appl., vol. 38, pp. 10787–10793, 2011. [Google Scholar]

26. M. Sharma and P. Kaur, “A comprehensive analysis of nature-inspired meta-heuristic techniques for feature selection problem,” Arch. Comput. Methods Eng., vol. 28, no. 3, pp. 1103–1127, 2020. doi: 10.1007/s11831-020-09412-6. [Google Scholar] [CrossRef]

27. F. L. de Sousa, F. Ramos, R. L. Galski, and I. Muraoka, “Generalized external optimization: A new meta-heuristic inspired by a model of natural evolution,” in L. Nunes de Castro, F. J. Von Zuben, Eds. Recent Developments in Biologically Inspired Computing, 2005, pp. 41–60. doi: 10.4018/978-1-59140-312-8.ch003. [Google Scholar] [CrossRef]

28. S. Debnath, W. Arif, and S. Baishya, “Buyer inspired meta-heuristic optimization algorithm,” Open Comput. Sci., vol. 10, no. 1, pp. 194–219, 2020. doi: 10.1515/comp-2020-0101. [Google Scholar] [CrossRef]

29. H. A. A. Nomer, A. W. Mohamed, and A. Yousef, “GSK-RL: Adaptive gaining-sharing knowledge algorithm using reinforcement learning,” in 2021 3rd Novel Intell. Lead. Emerg. Sci. Conf. (NILES), 2021, pp. 169–174. [Google Scholar]

30. A. M. F. Fard, M. Hajiaghaei-Keshteli, and R. Tavakkoli-Moghaddam, “Red deer algorithm (RDAA new nature-inspired meta-heuristic,” Soft Comput., vol. 24, no. 19, pp. 14637–14665, 2020. doi: 10.1007/s00500-020-04812-z. [Google Scholar] [CrossRef]

31. M. A. El-aziz, A. Ewees, N. Neggaz, R. Ibrahim, M. A. Al-qaness and S. Lu, “Cooperative metaheuristic algorithms for global optimization problems,” Expert. Syst. Appl., vol. 176, 2021, Art. no. 114788. doi: 10.1016/j.eswa.2021.114788. [Google Scholar] [CrossRef]

32. T. N. Huynh, D. T. T. Do, and J. Lee, “Q-learning-based parameter control in differential evolution for structural optimization,” Appl. Soft Comput., vol. 107, 2021, Art. no. 107464. doi: 10.1016/j.asoc.2021.107464. [Google Scholar] [CrossRef]

33. A. D. Martinez, E. Osaba, J. Ser, and F. Herrera, “Simultaneously evolving deep reinforcement learning models using multifactorial optimization,” in 2020 IEEE Cong. Evolution. Comput. (CEC), 2020, pp. 1–8. [Google Scholar]

34. Y. Chen, L. Cheng, and T. Wang, “Deep reinforcement learning for QoS-aware IoT service composition: The PD3QND approach,” in 2023 IEEE 14th Int. Conf. Softw. Eng. Serv. Sci. (ICSESS), 2023, pp. 38–41. [Google Scholar]

35. G. Albeanu, H. Madsen, and F. Popentiu-Vladicescu, “Learning from nature: Nature-inspired algorithms,” in 12th Int. Scientif. Conf. eLearn. Softw. Edu., Bucharest, Romania, 2016, vol. 2, pp. 477–482. [Google Scholar]

36. S. Salcedo-Sanz, “Modern meta-heuristics based on nonlinear physics processes: A review of models and design procedures,” Phys. Rep., vol. 655, no. 3, pp. 1–70, 2016. doi: 10.1016/j.physrep.2016.08.001. [Google Scholar] [CrossRef]

37. S. Pickin and Á. Manjarrés, “Describing AI analysis patterns with UML,” In: A. Evans, S. Kent, B. Selic, Eds. ≪UML≫ 2000—The Unified Modeling Language. Berlin, Heidelberg: Springer, 2000, vol. 1939. pp. 466–481. doi: 10.1007/3-540-40011-7_34. [Google Scholar] [CrossRef]

38. N. Tsantalis, A. Chatzigeorgiou, G. Stephanides, and S. T. Halkidis, “Design pattern detection using similarity scoring,” IEEE Trans. Softw. Eng., vol. 32, no. 11, pp. 1–9, 2006. doi: 10.1109/TSE.2006.112. [Google Scholar] [CrossRef]

39. A. Felner, R. Korf, and S. Hanan, “Additive pattern database heuristics,” 2004, arXiv:1107.0050. [Google Scholar]

40. V. Hayyolalam and A. Kazem, “Black widow optimization algorithm: A novel meta-heuristic approach for solving engineering optimization problems,” Eng Appl. Artif. Intell., vol. 87, 2020, Art. no. 103249. doi: 10.1016/j.engappai.2019.103249. [Google Scholar] [CrossRef]

41. K. Krawiec and J. Swan, “Pattern-guided genetic programming,” in Proc. 15th Annual Conf. Gen. Evolution. Comput., 2013, pp. 949–956. [Google Scholar]

42. G. Navarro and R. Baeza-Yates, “Improving an algorithm for approximate pattern matching,” Algorithmica, vol. 30, no. 4, pp. 473–502, 2001. doi: 10.1007/s00453-001-0034-6. [Google Scholar] [CrossRef]

43. S. Franco, A. Torralba, L. H. S. Lelis, and M. Barley, “On creating complementary pattern databases,” in Proc. Int. Joint Conf. Artif. Intell., 2017, pp. 4302–4309. [Google Scholar]

44. S. Edelkamp, “Automated creation of pattern database search heuristics,” in Model Checking and Artificial Intelligence. Berlin, Heidelberg: Springer, 2007, pp. 35–50. [Google Scholar]

45. D. Vermetten, F. Caraffini, A. V. Kononova, and T. Back, “Modular differential evolution,” in Proc. Gen. Evolution. Comput. Conf., 2023. [Google Scholar]

46. H. G. Wahdan, H. M. Abdelslam, and S. Kassem, “An efficient optimization algorithm for modular product design,” J. Européen des Systèmes Automatisés, vol. 54, pp. 195–207, 2021. [Google Scholar]

47. Z. Xiang, J. Li, B. Xia, J. Li, K. Yang and Z. Yang, “Module partition of complex products based on multi-relational networks,” in 2022 8th Int. Conf. Big Data Inform. Analyt. (BigDIA), 2022, pp. 88–94. [Google Scholar]

48. B. Gonzalez, F. Valdez, P. Melin, and G. Prado-Arechiga, “A Gravitational search algorithm for optimization of modular neural networks in pattern recognition,” In: O. Castillo, P. Melin, Eds. Fuzzy Logic Augmentation of Nature-Inspired Optimization Metaheuristics. Cham: Springer, 2015, vol. 574, pp. 127–137. doi: 10.1007/978-3-319-10960-2_8. [Google Scholar] [CrossRef]

49. V. Kreng and T. -P. Lee, “Modular product design with grouping genetic algorithm a case study,” Comput. Ind. Eng., vol. 46, no. 3, pp. 443–460, 2004. doi: 10.1016/j.cie.2004.01.007. [Google Scholar] [CrossRef]

50. A. Arenas, J. Duch, A. Fernandez, and S. Gomez, “Size reduction of complex networks preserving modularity,” New J. Phys., vol. 9, 2007, Art. no. 176. doi: 10.1088/1367-2630/9/6/176. [Google Scholar] [CrossRef]

51. J. Stork, A. E. Eiben, and T. Bartz-Beielstein, “A new taxonomy of global optimization algorithms,” Nat. Comput., vol. 21, no. 2, pp. 219–242, 2022. doi: 10.1007/s11047-020-09820-4. [Google Scholar] [CrossRef]

52. L. Mu, V. Sugumaran, and F. Wang, “A hybrid genetic algorithm for software architecture remodularization,” Inf. Syst. Front., vol. 22, no. 5, pp. 1133–1161, 2020. doi: 10.1007/s10796-019-09906-0. [Google Scholar] [CrossRef]

53. M. Tyburec, J. Zeman, M. Doškář, M. Kružík, and M. Lepš, “Modular-topology optimization with wang tilings: An application to truss structures,” Struct. Multidiscipl. Optim., vol. 63, no. 3, pp. 1099–1117, 2020. doi: 10.1007/s00158-020-02744-8. [Google Scholar] [CrossRef]

54. D. Vermetten, F. Caraffini, B. van Stein, and A. V. Kononova, “Using structural bias to analyse the behaviour of modular CMA-ES,” in Proc. Genet. Evolution. Comput. Conf. Compan., 2022. [Google Scholar]

55. I. M. Ali, H. Turan, R. Chakrabortty, S. Elsawah, and M. Ryan, “An integrated differential evolutionbased heuristic method for product family design problem,” in 2021 IEEE Cong. Evolution. Comput. (CEC), 2021, pp. 25–32. [Google Scholar]

56. M. Newman, “Modularity and community structure in networks,” Proc. Nat. Acad. Sci., vol. 103, no. 23, pp. 8577–8582, 2006. doi: 10.1073/pnas.0601602103. [Google Scholar] [PubMed] [CrossRef]

57. J. Agushaka and A. Ezugwu, “Initialisation approaches for population-based metaheuristic algorithms: A comprehensive review,” Appl. Sci., vol. 12, no. 2, 2022, Art. no. 896. doi: 10.3390/app12020896. [Google Scholar] [CrossRef]

58. O. Kramer, “Iterated local search with Powell’s method: A memetic algorithm for continuous global optimization,” Memetic Comput., vol. 2, no. 1, pp. 69–83, 2010. doi: 10.1007/s12293-010-0032-9. [Google Scholar] [CrossRef]

59. G. Wu, R. Mallipeddi, and P. Suganthan, “Ensemble strategies for population-based optimization algorithms a survey,” Swarm Evol. Comput., vol. 44, pp. 695–711, 2019. [Google Scholar]

60. A. Ghosh, S. Das, A. Chowdhury, and R. Giri, “An improved differential evolution algorithm with fitness-based adaptation of the control parameters,” Inf. Sci., vol. 181, no. 18, pp. 3749–3765, 2011. doi: 10.1016/j.ins.2011.03.010. [Google Scholar] [CrossRef]

61. P. Lehre and P. S. Oliveto, “Theoretical analysis of stochastic search algorithms,” In: R. Martí, P. Pardalos, M. Resende, Eds. Handbook of Heuristics. Cham: Springer, 2017, pp. 849–884. doi: 10.1007/978-3-319-07124-4_35. [Google Scholar] [CrossRef]

62. E. Haq, I. Ahmad, A. Hussain, and I. Almanjahie, “A novel selection approach for genetic algorithms for global optimization of multimodal continuous functions,” Comput. Intell. Neurosci., vol. 2019, no. 1, pp. 1–14, 2019. doi: 10.1155/2019/8640218. [Google Scholar] [PubMed] [CrossRef]

63. V. V. D. Melo and G. Iacca, “A CMA-ES-based 2-stage memetic framework for solving constrained optimization problems,” in 2014 IEEE Symp. Found. Comput. Intell. (FOCI), 2014, pp. 143–150. [Google Scholar]

64. R. Damasevicius and R. Maskeliunas, “Agent state flipping based hybridization of heuristic optimization algorithms: A case of bat algorithm and krill herd hybrid algorithm,” Algorithms, vol. 14, no. 12, 2021, Art. no. 358. doi: 10.3390/a14120358. [Google Scholar] [CrossRef]

65. M. Oszust, G. Sroka, and K. Cymerys, “A hybridization approach with predicted solution candidates for improving population-based optimization algorithms,” Inf. Sci., vol. 574, no. 3, pp. 133–161, 2021. doi: 10.1016/j.ins.2021.04.082. [Google Scholar] [CrossRef]

66. E. K. da Silva, H. Barbosa, and A. C. C. Lemonge, “An adaptive constraint handling technique for differential evolution with dynamic use of variants in engineering optimization,” Optim. Eng., vol. 12, no. 1–2, pp. 31–54, 2011. doi: 10.1007/s11081-010-9114-2. [Google Scholar] [CrossRef]

67. R. Pasti, F. V. Zuben, R. D. Maia, and L. Castro, “Heuristics to avoid redundant solutions on populationbased multimodal continuous optimization,” in 2011 IEEE Cong. Evolution. Comput. (CEC), 2011, pp. 2321–2328. [Google Scholar]

68. Q. Li, S. -Y. Liu, and X. -S. Yang, “Influence of initialization on the performance of metaheuristic optimizers,” Appl. Soft Comput., vol. 91, 2020, Art. no. 106193. doi: 10.1016/j.asoc.2020.106193. [Google Scholar] [CrossRef]

69. B. Doerr and C. Doerr, “The impact of random initialization on the runtime of randomized search heuristics,” Algorithmica, vol. 75, no. 3, pp. 529–553, 2014. doi: 10.1007/s00453-015-0019-5. [Google Scholar] [CrossRef]

70. C. Li, X. Chu, Y. Chen, and L. Xing, “A knowledge-based technique for initializing a genetic algorithm,” J. Intell. Fuzzy Syst., vol. 31, no. 2, pp. 1145–1152, 2016. doi: 10.3233/JIFS-169043. [Google Scholar] [CrossRef]

71. A. Ashraf et al., “Studying the impact of initialization for population-based algorithms with low-discrepancy sequences,” Appl. Sci., vol. 11, no. 17, 2021, Art. no. 8190. doi: 10.3390/app11178190. [Google Scholar] [CrossRef]

72. M. Ali, M. Pant, and A. Abraham, “Unconventional initialization methods for differential evolution,” Appl. Math. Comput., vol. 219, no. 9, pp. 4474–4494, 2013. doi: 10.1016/j.amc.2012.10.053. [Google Scholar] [CrossRef]

73. X. Gillard and P. Schaus, “Large neighborhood search with decision diagrams,” in Proc. IJCAI, 2022, pp. 4754–4760. [Google Scholar]

74. G. Ospina and R. D. Landtsheer, “Towards distributed local search through neighborhood combinators,” in Proc. ICORES, 2021, pp. 248–255. [Google Scholar]

75. H. F. Amaral, S. Urrutia, and L. M. Hvattum, “Delayed improvement local search,” J. Heuristics, vol. 27, no. 5, pp. 923–950, 2021. doi: 10.1007/s10732-021-09479-9. [Google Scholar] [CrossRef]

76. P. Chen, H. Wan, S. Cai, J. Li, and H. Chen, “Local search with dynamic-threshold configuration checking and incremental neighborhood updating for maximum k-plex problem,” in Proc. AAAI, 2020, pp. 2343–2350. [Google Scholar]

77. H. N. K. Al-Behadili, “Improved firefly algorithm with variable neighborhood search for data clustering,” Baghdad Sci. J., vol. 19, no. 2, 2021, Art. no. 0409. doi: 10.21123/bsj.2022.19.2.0409. [Google Scholar] [CrossRef]

78. J. G. C. Costa, Y. Mei, and M. Zhang, “Guided local search with an adaptive neighbourhood size heuristic for large scale vehicle routing problems,” in Proc. Gen. Evolution. Comput. Conf., 2022. [Google Scholar]

79. M. Gouvea, A. Fausto, and P. Ribeiro Araujo, “Diversity-based adaptive evolutionary algorithms,” IntechOpen, 2010. doi: 10.5772/8046. [Google Scholar] [CrossRef]

80. G. Ruan, G. Yu, J. Zheng, J. Zou, and S. Yang, “The effect of diversity maintenance on prediction in dynamic multi-objective optimization,” Appl. Soft Comput., vol. 58, no. 2, pp. 631–647, 2017. doi: 10.1016/j.asoc.2017.05.008. [Google Scholar] [CrossRef]

81. X. Gao, S. Song, and J. Dong, “An elite-guided evolutionary algorithm for large-scale multi-objective optimization,” in 2023 IEEE Cong. Evolution. Comput. (CEC), 2023, pp. 1–8. [Google Scholar]

82. B. Qu and P. Suganthan, “Multi-objective differential evolution with diversity enhancement,” J. Zhejiang Univ.-Sci. C, vol. 11, no. 7, pp. 538–543, 2010. doi: 10.1631/jzus.C0910481. [Google Scholar] [CrossRef]

83. W. Tong, S. Chowdhury, and A. Messac, “A multi-objective mixed-discrete particle swarm optimization with multi-domain diversity preservation,” Struct. Multidiscipl. Optim., vol. 53, no. 3, pp. 471–488, 2016. doi: 10.1007/s00158-015-1319-8. [Google Scholar] [CrossRef]

84. S. Cheng, H. Zhan, and Z. Shu, “An innovative hybrid multi-objective particle swarm optimization with or without constraints handling,” Appl. Soft Comput., vol. 47, no. 3, pp. 370–388, 2016. doi: 10.1016/j.asoc.2016.06.012. [Google Scholar] [CrossRef]

85. P. Ammaruekarat and P. Meesad, “A multi-objective memetic algorithm based on chaos optimization,” Appl. Mech. Mater., vol. 130–134, pp. 725–729, 2011. doi: 10.4028/www.scientific.net/AMM.130-134.725. [Google Scholar] [CrossRef]

86. C. Segura, C. Coello, E. Segredo, G. Miranda, and C. Leon, “Improving the diversity preservation of multi-objective approaches used for single-objective optimization,” in 2013 IEEE Cong. Evolution. Comput. (CEC), 2013, pp. 3198–3205. [Google Scholar]

87. H. Jia, X. Peng, W. Song, C. Lang, Z. Xing and K. Sun, “Multiverse optimization algorithm based on Lévyflight improvement for multithreshold color image segmentation,” IEEE Access, vol. 7, pp. 32805–32844, 2019. doi: 10.1109/ACCESS.2019.2903345. [Google Scholar] [CrossRef]

88. V. A. Tatsis and K. Parsopoulos, “Dynamic parameter adaptation in metaheuristics using gradient approximation and line search,” Appl. Soft Comput., vol. 74, no. 2, pp. 368–384, 2019. doi: 10.1016/j.asoc.2018.09.034. [Google Scholar] [CrossRef]

89. X. He, Z. Zheng, Z. Chen, and Y. Zhou, “Adaptive evolution strategies for stochastic zeroth-order optimization,” IEEE Trans. Emerg. Top. Comput. Intell., vol. 6, no. 5, pp. 1271–1285, 2022. doi: 10.1109/TETCI.2022.3146330. [Google Scholar] [CrossRef]

90. D. Arnold and H. Beyer, “Performance analysis of evolutionary optimization with cumulative step length adaptation,” IEEE Trans. Automat. Contr., vol. 49, no. 4, pp. 617–622, 2004. doi: 10.1109/TAC.2004.825637. [Google Scholar] [CrossRef]

91. H. Kim and M. Liou, “Adaptive directional local search strategy for hybrid evolutionary multiobjective optimization,” Appl. Soft Comput., vol. 19, no. 2, pp. 290–311, 2014. doi: 10.1016/j.asoc.2014.02.019. [Google Scholar] [CrossRef]

92. J. Cui, L. Wu, X. Huang, D. Xu, C. Liu and W. Xiao, “Multi-strategy adaptable ant colony optimization algorithm and its application in robot path planning,” Knowl.-Based Syst., vol. 288, Mar. 2024, Art. no. 111459. doi: 10.1016/j.knosys.2024.111459. [Google Scholar] [CrossRef]

93. B. Zeng and Y. Dong, “An improved harmony search based energy-efficient routing algorithm for wireless sensor networks,” Appl. Soft Comput., vol. 41, no. 4, pp. 135–147, 2016. doi: 10.1016/j.asoc.2015.12.028. [Google Scholar] [CrossRef]

94. V. Zakharov and A. Mugaiskikh, “Dynamic adaptation of genetic algorithm for solving routing problems on large scale systems,” Adv. Syst. Sci. Appl., vol. 20, pp. 32–43, 2020. [Google Scholar]

95. D. Arnold and H. Beyer, “A comparison of evolution strategies with other direct search methods in the presence of noise,” Comput. Optim. Appl., vol. 24, no. 1, pp. 135–159, 2003. doi: 10.1023/A:1021810301763. [Google Scholar] [CrossRef]

96. V. V. D. Melo and G. Iacca, “A modified covariance matrix adaptation evolution strategy with adaptive penalty function and restart for constrained optimization,” Expert. Syst. Appl., vol. 41, no. 16, pp. 7077–7094, 2014. doi: 10.1016/j.eswa.2014.06.032. [Google Scholar] [CrossRef]

97. J. E. Smith, “Self-adaptation in evolutionary algorithms for combinatorial optimisation,” In: C. Cotta, M. Sevaux, K. Sörensen, Eds. Adaptive and Multilevel Metaheuristics. Berlin, Heidelberg: Springer, 2008, vol. 136. pp. 31–57. doi: 10.1007/978-3-540-79438-7_2. [Google Scholar] [CrossRef]

98. K. Hamacher, “Hybridization of stochastic tunneling with (quasi)-infinite time-horizon tabu search,” In: M. Blesa Aguilera, C. Blum, H. Gambini Santos, P. Pinacho-Davidson, J. Godoy del Campo, Eds. Hybrid Metaheuristics. Cham: Springer, 2018, vol 11299. #x2013;135. doi: 10.1007/978-3-030-05983-5_9. [Google Scholar] [CrossRef]

99. N. Thomaidis and V. Vassiliadis, “Stochastic convergence analysis of metaheuristic optimisation techniques,” In: C. Borgelt, M. Gil, J. Sousa, M. Verleysen, Eds. Towards Advanced Data Analysis by Combining Soft Computing and Statistics. Berlin, Heidelberg: Springer, 2013, vol. 285. pp. 343–357. doi: 10.1007/978-3-642-30278-7_27. [Google Scholar] [CrossRef]

100. J. -H. Wu, R. Kalyanam, and R. Givan, “Stochastic enforced hill-climbing,” J. Artif. Intell. Res., vol. 31, pp. 396–403, 2008. [Google Scholar]

101. A. M. Sutton, A. Howe, and L. D. Whitley, “Estimating bounds on expected plateau size in maxsat problems,” In: T. Stützle, M. Birattari, H. H. Hoos, Eds. Engineering Stochastic Local Search Algorithms. Designing, Implementing and Analyzing Effective Heuristics. Berlin, Heidelberg: Springer, 2009, vol. 5752. pp. 31–45. doi: 10.1007/978-3-642-03751-1_3. [Google Scholar] [CrossRef]

102. B. C. Lam and H. Leung, “Progressive stochastic search for solving constraint satisfaction problems,” in 15th IEEE Int. Conf. Tools with Artif. Intell., 2003, pp. 487–491. [Google Scholar]

103. J. V. Deshmukh, X. Jin, J. Kapinski, and O. Maler, “Stochastic local search for falsification of hybrid systems,” In: B. Finkbeiner, G. Pu, L. Zhang, Eds. Automated Technology for Verification and Analysis. Cham: Springer, 2015, vol. 9364. pp. 500–517. doi: 10.1007/978-3-319-24953-7_35. [Google Scholar] [CrossRef]

104. S. Ye, K. Zhou, A. Zain, F. Wang, and Y. Yusoff, “A modified harmony search algorithm and its applications in weighted fuzzy production rule extraction,” Front. Inform. Technol. Electron. Eng., vol. 24, no. 11, pp. 1574–1590, 2023. doi: 10.1631/FITEE.2200334. [Google Scholar] [CrossRef]

105. Q. Lei, T. Y. Xiao, and S. J. Song, “Multi-population bayesian optimization algorithm using cooperated pattern search strategy,” in 2006 Chin. Cont. Conf., 2006, pp. 1454–1459. [Google Scholar]

106. A. A. Bidgoli and S. Rahnamayan, “A collective intelligence strategy for enhancing population-based optimization algorithms,” in 2020 IEEE Cong. Evolution. Comput. (CEC), 2020, pp. 1–9. [Google Scholar]

107. M. Bhattacharya, “Exploiting landscape information to avoid premature convergence in evolutionary search,” in 2006 IEEE Int. Conf. Evolution. Comput., 2006, pp. 560–564. [Google Scholar]

108. J. C. Castillo and C. Segura, “Differential evolution with enhanced diversity maintenance,” Optim. Lett., vol. 14, pp. 1471–1490, 2019. [Google Scholar]

109. S. -F. Ding, W. Li, and Y. Huang, “Particle swarm optimization algorithm with dual population adaptive mutation,” in 2022 IEEE 21st Int. Conf. Cognit. Inform. Cognit. Comput. (ICCI*CC), 2022, pp. 168–174. [Google Scholar]

110. K. Wang, Y. Zhu, G. Li, J. Wang, and Z. Liu, “Test case generation method based on particle swarm optimization algorithm,” SPIE Proc., vol. 12721, no. 8, pp. 127–211, 2023. doi: 10.1117/12.2683538. [Google Scholar] [CrossRef]

111. H. Zhu, Y. Hu, and W. dong Zhu, “A dynamic adaptive particle swarm optimization and genetic algorithm for different constrained engineering design optimization problems,” Adv. Mech. Eng., vol. 11, no. 3, 2019. doi: 10.1177/1687814018824930. [Google Scholar] [CrossRef]

112. A. Ahmadi, “Memory-based adaptive partitioning (MAP) of search space for the enhancement of convergence in pareto-based multi-objective evolutionary algorithms,” Appl. Soft Comput., vol. 41, no. 2, pp. 400–417, 2016. doi: 10.1016/j.asoc.2016.01.029. [Google Scholar] [CrossRef]

113. H. Yun, M. H. Ha, and R. McKay, “VLR: A memory-based optimization heuristic,” in Parallel Problem Solving from Nature–PPSN XIII, 2014, pp. 151–160. doi: 10.1007/978-3-319-10762-2_15. [Google Scholar] [CrossRef]

114. S. Jiang, Y. Wang, and Z. Ji, “Convergence analysis and performance of an improved gravitational search algorithm,” Appl. Soft Comput., vol. 24, no. 1, pp. 363–384, 2014. doi: 10.1016/j.asoc.2014.07.016. [Google Scholar] [CrossRef]

115. H. S. Alamri and K. Z. Zamli, “PMT: Opposition-based learning technique for enhancing meta-heuristic performance,” IEEE Access, vol. 7, pp. 97653–97672, 2019. doi: 10.1109/ACCESS.2019.2925088. [Google Scholar] [CrossRef]

116. M. Ahmadi and Z. Seif, “A convergence algorithm for function optimization,” in 2016 Future Technol. Conf. (FTC), 2016, pp. 137–139. [Google Scholar]

117. C. Blum, J. Puchinger, G. Raidl, and A. Roli, “Hybrid metaheuristics in combinatorial optimization: A survey,” Appl. Soft Comput., vol. 11, no. 6, pp. 4135–4151, 2011. doi: 10.1016/j.asoc.2011.02.032. [Google Scholar] [CrossRef]

118. R. Nand, K. Chaudhary, and B. Sharma, “Stepping ahead based hybridization of meta-heuristic model for solving global optimization problems,” in 2020 IEEE Cong. Evolution. Comput. (CEC), 2020, pp. 1–8. [Google Scholar]

119. A. M. Ibrahim and M. Tawhid, “A hybridization of differential evolution and monarch butterfly optimization for solving systems of nonlinear equations,” J. Comput. Des. Eng., vol. 6, pp. 354–367, 2018. [Google Scholar]

120. T. Ledlow, Z. J. Kiyak, and R. Hartfield, “Missile system design using a hybrid evolving swarm algorithm,” in 2014 IEEE Aerospace Conf., 2014, pp. 1–8. [Google Scholar]

121. H. H. Doulabi, P. Jaillet, G. Pesant, and L. -M. Rousseau, “Exploiting the structure of two-stage robust optimization models with exponential scenarios,” INFORMS J. Comput., vol. 33, no. 1, pp. 143–162, 2020. doi: 10.1287/ijoc.2019.0928. [Google Scholar] [CrossRef]

122. H. Chong, H. Yap, S. C. Tan, K. S. Yap, and S. Wong, “Advances of metaheuristic algorithms in training neural networks for industrial applications,” Soft Comput., vol. 25, no. 16, pp. 11209–11233, 2021. doi: 10.1007/s00500-021-05886-z. [Google Scholar] [CrossRef]

123. H. -J. Yi and I. Kim, “Differential evolutionary cuckoo-search-integrated tabu-adaptive pattern search (decs-tapsA novel multihybrid variant of swarm intelligence and evolutionary algorithm in architectural design optimization and automation,” J. Comput. Des. Eng., vol. 9, no. 5, pp. 2103–2133, 2022. doi: 10.1093/jcde/qwac100. [Google Scholar] [CrossRef]

124. R. Thangaraj, M. Pant, A. Abraham, and P. Bouvry, “Particle swarm optimization: Hybridization perspectives and experimental illustrations,” Appl. Math. Comput., vol. 217, no. 12, pp. 5208–5226, 2011. doi: 10.1016/j.amc.2010.12.053. [Google Scholar] [CrossRef]

125. P. -S. Chen and Z. Zeng, “Developing two heuristic algorithms with metaheuristic algorithms to improve solutions of optimization problems with soft and hard constraints: An application to nurse rostering problems,” Appl. Soft Comput., vol. 93, 2020, Art. no. 106336. doi: 10.1016/j.asoc.2020.106336. [Google Scholar] [CrossRef]

126. E. Tsang and N. Jin, “Incentive method to handle constraints in evolutionary algorithms with a case study,” in Lecture Notes in Computer Science, 2006, pp. 133–144. [Google Scholar]

127. J. Li, E. Burke, T. Curtois, S. Petrovic, and R. Qu, “The falling tide algorithm: A new multi-objective approach for complex workforce scheduling,” Omega, vol. 40, no. 3, pp. 283–293, 2012. doi: 10.1016/j.omega.2011.05.004. [Google Scholar] [CrossRef]

128. E. C. Freuder, R. Heffernan, R. Wallace, and N. Wilson, “Lexicographically-ordered constraint satisfaction problems,” Constraints, vol. 15, no. 1, pp. 1–28, 2009. doi: 10.1007/s10601-009-9069-0. [Google Scholar] [CrossRef]

129. M. Wijaya, “Two stages best first search algorithm using hard and soft constraints heuristic for course timetabling,” Rev. D’Intelligence Artif., vol. 34, no. 4, pp. 413–418, 2020. doi: 10.18280/ria.340405. [Google Scholar] [CrossRef]

130. M. Al-Betar, A. Khader, and O. Muslih, “A multiswap algorithm for the university course timetabling problem,” in 2012 Int. Conf. Comput. Inform. Sci. (ICCIS), 2012, pp. 301–306. [Google Scholar]

131. N. D. Jana, J. Sil, and S. Das, “Continuous fitness landscape analysis using a chaos-based random walk algorithm,” Soft Comput., vol. 22, no. 3, pp. 921–948, 2018. doi: 10.1007/s00500-016-2397-2. [Google Scholar] [CrossRef]

132. Y. Wang and K. Li, “A Levy flight-inspired random walk algorithm for continuous fitness landscape analysis,” Int. J. Cogn. Informatics Nat. Intell., vol. 17, pp. 1–18, 2023. doi: 10.4018/IJCINI. [Google Scholar] [CrossRef]

133. K. AlYahya and J. Rowe, “Landscape analysis of a class of NP-hard binary packing problems,” Evol. Comput., vol. 27, no. 1, pp. 47–73, 2019. doi: 10.1162/evco_a_00237. [Google Scholar] [PubMed] [CrossRef]

134. M. D. Karatas, O. Akman, and J. Fieldsend, “Towards population-based fitness landscape analysis using local optima networks,” in Proc. Gen. Evolution. Comput. Conf. Compan., 2021. [Google Scholar]

135. P. Merz and B. Freisleben, “Fitness landscape analysis and memetic algorithms for the quadratic assignment problem,” IEEE Trans. Evol. Comput., vol. 4, no. 4, pp. 337–352, 2000. doi: 10.1109/4235.887234. [Google Scholar] [CrossRef]

136. M. Martins, M. El Yafrani, M. Delgado, and R. Lüders, “Multi-layer local optima networks for the analysis of advanced local search-based algorithms,” in Proc. 2020 Gen. Evolution. Comput. Conf., 2020. [Google Scholar]

137. K. -L. Du and M. Swamy, Search and Optimization by Metaheuristics: Techniques and Algorithms Inspired by Nature. Springer, 2016. [Google Scholar]

138. M. W. U. Kabir, N. Sakib, S. M. Chowdhury, and M. S. Alam, “A novel adaptive bat algorithm to control explorations and exploitations for continuous optimization problems,” Int. J. Comput. Appl., vol. 94, pp. 15–20, 2014. [Google Scholar]

139. G. Raidl et al., “Applications of evolutionary computing,” in Applications of Evolutionary Computing, 2004, pp. 1–2. [Google Scholar]

140. S. Pant, D. Anand, A. Kishor, and S. B. Singh, “A particle swarm algorithm for optimization of complex system reliability,” Int. J. Performability Eng., vol. 11, no. 1, pp. 33–42, 2015. [Google Scholar]

141. Y-C. Liang, and J. R. Cuevas Juarez, “A novel metaheuristic for continuous optimization problems: Virus optimization algorithm,” Eng. Optim., vol. 48, no. 1, pp. 73–93, 2016. doi: 10.1080/0305215X.2014.994868. [Google Scholar] [CrossRef]

142. S. Jadon, R. Tiwari, H. Sharma, and J. C. Bansal, “Hybrid artificial bee colony algorithm with differential evolution,” Appl. Soft Comput., vol. 58, no. 1, pp. 11–24, 2017. doi: 10.1016/j.asoc.2017.04.018. [Google Scholar] [CrossRef]

143. R. Wiener, “Ant colony system optimization,” J. Object Technol., vol. 8, no. 6, pp. 39–58, 2009. doi: 10.5381/jot.2009.8.6.c4. [Google Scholar] [CrossRef]

144. S. Rather and P. Bala, “Hybridization of constriction coefficient-based particle swarm optimization and chaotic gravitational search algorithm for solving engineering design problems,” in Applied Soft Computing and Communication Networks. Singapore: Springer, 2019, pp. 95–115. [Google Scholar]

145. F. Ferrandi, P. Lanzi, C. Pilato, D. Sciuto, and A. Tumeo, “Ant colony heuristic for mapping and scheduling tasks and communications on heterogeneous embedded systems,” IEEE Trans. Comput. Aided Des. Integr. Circuits Syst., vol. 29, no. 6, pp. 911–924, 2010. doi: 10.1109/TCAD.2010.2048354. [Google Scholar] [CrossRef]

146. A. Jaszcz, D. Polap, and R. Damasevicius, “Lung X-ray image segmentation using heuristic red fox optimization algorithm,” Scient. Programm., 2022. doi: 10.1155/2022/4494139. [Google Scholar] [CrossRef]

147. S. N. Makhadmeh et al., “A modified coronavirus herd immunity optimizer for the power scheduling problem,” Mathematics, vol. 10, no. 3, 2022, Art. no. 315. doi: 10.3390/math10030315. [Google Scholar] [CrossRef]

148. A. H. Gandomi and A. H. Alavi, “Krill herd: A new bio-inspired optimization algorithm,” Commun. Nonlinear Sci. Numer. Simul., vol. 17, no. 12, pp. 4831–4845, 2012. doi: 10.1016/j.cnsns.2012.05.010. [Google Scholar] [CrossRef]

149. D. Połap, and M. Woźniak, “Red fox optimization algorithm,” Expert. Syst. Appl., vol. 166, 2021, Art. no. 114107. doi: 10.1016/j.eswa.2020.114107. [Google Scholar] [CrossRef]

150. M. A. Al-Betar, Z. A. A. Alyasseri, M. A. Awadallah, and I. Abu Doush, “Coronavirus herd immunity optimizer (CHIO),” Neural Comput. Appl., vol. 33, no. 10, pp. 5011–5042, 2021. doi: 10.1007/s00521-020-05296-6. [Google Scholar] [PubMed] [CrossRef]