 Open Access
Open Access
ARTICLE
Evolutionary Particle Swarm Optimization Algorithm Based on Collective Prediction for Deployment of Base Stations
1 School of Computer Science and Technology, Zhejiang Normal University, Jinhua, 321004, China
2 School of Future Technologies, Jiangxi Institute of Applied Science and Technology, Nanchang, 330000, China
3 School of Computing and Artificial Intelligence, Southwestern University of Finance and Economics, Chengdu, 611130, China
* Corresponding Author: Taiyong Li. Email:
(This article belongs to the Special Issue: Particle Swarm Optimization: Advances and Applications)
Computers, Materials & Continua 2025, 82(1), 345-369. https://doi.org/10.32604/cmc.2024.060335
Received 29 October 2024; Accepted 05 December 2024; Issue published 03 January 2025
Abstract
The wireless signals emitted by base stations serve as a vital link connecting people in today’s society and have been occupying an increasingly important role in real life. The development of the Internet of Things (IoT) relies on the support of base stations, which provide a solid foundation for achieving a more intelligent way of living. In a specific area, achieving higher signal coverage with fewer base stations has become an urgent problem. Therefore, this article focuses on the effective coverage area of base station signals and proposes a novel Evolutionary Particle Swarm Optimization (EPSO) algorithm based on collective prediction, referred to herein as ECPPSO. Introducing a new strategy called neighbor-based evolution prediction (NEP) addresses the issue of premature convergence often encountered by PSO. ECPPSO also employs a strengthening evolution (SE) strategy to enhance the algorithm’s global search capability and efficiency, ensuring enhanced robustness and a faster convergence speed when solving complex optimization problems. To better adapt to the actual communication needs of base stations, this article conducts simulation experiments by changing the number of base stations. The experimental results demonstrate that under the condition of 50 or more base stations, ECPPSO consistently achieves the best coverage rate exceeding 95%, peaking at 99.4400% when the number of base stations reaches 80. These results validate the optimization capability of the ECPPSO algorithm, proving its feasibility and effectiveness. Further ablative experiments and comparisons with other algorithms highlight the advantages of ECPPSO.Keywords
Nomenclature
| AIS | Artificial Immune System |
| CLPSO | Comprehensive learning particle swarm optimization algorithm |
| EPSO | Evolutionary Particle Swarm Optimization |
| FLC | Fuzzy logic control |
| GIS | Geographic Information System |
| IoT | Internet of Things |
| NEP | Neighbor-based evolution prediction |
| OLPSO | Orthogonal learning particle swarm optimization |
| PSO | Particle Swarm Optimization |
| SE | Strengthening evolution |
| SSA | Sparrow search algorithm |
| AR | Augmented Reality |
| VR | Virtual Reality |
In current highly interconnected world, base stations play an indispensable role as the link connecting us all. From the bustling streets of urban centers to the remote pathways of rural areas, base stations have always supported our communication and connectivity needs. Whether facilitating collaboration between businesses or facilitating personal interactions, base stations are fundamental. The unimpeded communication network provides convenient conditions for business activities, information exchange and technological innovation, and promotes the development of economy.
With the rise of the IoT [1], the importance of base stations is further underscored. An increasing number of devices require connectivity to the internet, and base stations serve as the bridge between these devices and the internet. From smart cities to smart homes, from intelligent transportation to telemedicine, the development of the IoT relies on the support of base stations, which provide a solid foundation for realizing a smarter way of life [2].
The quality of signals emitted by base stations, which are used to build wireless communication networks, is crucial as it directly determines users’ network experience [3]. At present, the 5G network signals emitted by base stations have been widely adopted, spreading across streets and alleys. The performance of 5G has improved significantly compared to the previous 3G and 4G networks, meeting the needs of the majority of people [4,5]. However, the 5G network also faces some problems and challenges [6], so the 6G technology is proposed to make up for the defects of the 5G network, and it is already in the stage of research and development [7,8].
Compared with 5G network, the 6G communication network offers more pronounced advantages [9–11]. 6G networks are expected to be even faster than 5G. According to predictions, the download speed of 6G could reach up to 1 TB per second. This means that users will be able to download and share large files more quickly and enjoy higher-quality streaming content and real-time gaming experiences. 6G networks will further reduce latency, which refers to the delay in data transmission. This will make real-time interactive applications such as Augmented Reality (AR), Virtual Reality (VR), remote healthcare, and autonomous driving more feasible, providing a smoother user experience. 6G will provide higher network capacity, supporting a larger number of devices to connect simultaneously. This is crucial for the growth of IoT devices and the development of smart cities, as these devices require ample bandwidth and stable connections. 6G is expected to have a wider effective coverage area, including remote and sparsely populated areas. This will enable people around the world to enjoy high-speed and stable network connections. Security will be a major focus for 6G networks, adopting advanced encryption technologies and authentication mechanisms to ensure the privacy and security of user data.
Various factors affect network signals within a specific area, including but not limited to distance and obstacles, signal frequency, electromagnetic interference, weather conditions, network congestion and device performance [12,13]. In mobile communication networks or the IoT, base stations act as nodes, while the connections between nodes represent communication links [14]. In networks associated with base stations, common network structure models can be used to describe the connectivity between base stations, the distribution of communication links, and the overall performance of the network [15]. For example, random network models, small-world network models, scale-free network models, hierarchical network models, and modular network models [16]. These network structure models can help analyze and optimize the structure, performance, and reliability of base station networks in associated scenarios, thereby improving the operational efficiency and user experience of wireless communication systems [17].
Certainly, it’s inevitable that base stations face a myriad of challenges if they are to deliver satisfactory results [18–20]. As the demand for mobile communication continues to increase, base stations need to handle a greater volume of data transmission. However, spectrum resources are finite, posing difficulties for base stations in providing higher rates and broader coverage. The construction costs of base stations are relatively high, particularly in urban areas, where land leasing and infrastructure development require substantial capital. Furthermore, the deployment of base stations necessitates a certain amount of space, presenting challenges in locating suitable sites within urban environments. Base stations require continuous power supply to ensure the continuity of communication services, resulting in significant energy consumption. Concurrently, the construction and operation of base stations can have environmental implications, such as electromagnetic radiation and visual pollution. The ongoing evolution of communication technologies demands timely updates and upgrades of base station equipment to meet new technical requirements, which also necessitates substantial funding and technical support. Base stations’ communication signals may be susceptible to interference or attacks, potentially jeopardizing the stability and security of communication services. Moreover, the deployment and operation of base stations may give rise to privacy concerns, such as the leakage and monitoring of personal communication data.
In recent years, meta-heuristic algorithms have been widely used to solve various complex problems such as computationally expensive simulation model [21] and structural optimization [22], among many others, with their high efficiency, robustness and fast convergence rate [23]. Among them, the particle swarm optimization (PSO) is one of the most popular algorithms in the meta-heuristic algorithms, which has been widely used in several fields due to its simplicity, easy implementation and fast convergence [24–26]. The concept behind the PSO algorithm draws inspiration from the collective behavior observed in bird flocks during foraging. In PSO, solutions are represented as particles navigating through a search space, mirroring the dynamic interactions within bird flocks. Within a flock, each bird maintains a specific velocity and position while engaging with nearby peers. As birds seek sustenance, they adapt their speed and trajectory based on the movements of neighboring birds, gradually homing in on food sources. Similarly, every particle in PSO represents a potential solution within the solution space, characterized by three key attributes: position, velocity, and individual best solution (pBest). Concurrently, the collective group shares a global best solution (gBest). By leveraging both individual experiences and collective experience, particles dynamically adapt their speed and position, collectively navigating the solution space towards optimal solutions.
The deployment of a limited number of base stations in specific areas presents a unique challenge. It necessitates maximizing signal coverage across the entire city while ensuring adequate signal supply to high-demand areas such as gyms, residential zones, and major commercial centers [27]. Optimizing the placement of base stations can lead to cost savings, resource efficiency, enhanced regional signal stability, and improved utilization of signal resources. To address the challenges of base station deployment, researchers have employed various techniques including greedy algorithms, genetic algorithms, branch and bound algorithms, particle swarm optimization algorithms, clustering algorithms, and other methodologies [28]. Under the consideration of the contraction effect, Wang et al. integrated the Artificial Immune System (AIS) and Geographic Information System (GIS) to achieve superior comprehensive performance in the global optimization of base station deployment [29]. This innovative approach offers a valuable solution for the planning of 5G base stations in densely constructed areas. Ayati et al. proposed a mobile base station mobility control strategy for wireless sensor networks, which combined the PSO algorithm, fuzzy logic node clustering, fuzzy clustering head selection, and fuzzy logic control (FLC) for base station mobility, significantly improving the lifespan of mobile base station wireless sensor network [30].
In order to enhance the effective coverage area under a specific number of base stations in a particular region, this paper has made improvements to the Particle Swarm Optimization (PSO) algorithm, ECPPSO, and applied it to the aforementioned optimization problem. This algorithm addresses two critical issues of the original PSO: premature convergence and limited global search capability. Firstly, it introduces the NEP strategy to alleviate the problem of premature convergence. Secondly, the ECPPSO algorithm employs a refined SE strategy to counteract the possibility of individuals falling into local optimal traps. The proposed algorithm was then applied in a base station layout experiment and compared with variations of PSO and sparrow search algorithm (SSA). By varying the number of base stations, the experiments demonstrated the ECPPSO’s superior optimization efficiency in addressing the effective coverage area of base station deployment, further validating the effectiveness and competitiveness of the proposed algorithm. The specific contributions and innovations are as follows:
• The NEP strategy was introduced in the PSO to predict the most correct direction of evolution for each individual to accelerate convergence and reduce uncertainty.
• By adjusting the SE strategy, selective evolutionary operations were conducted to optimize individuals with poor performance in the population, thereby enhancing the overall fitness level of the population. This approach has led to a more efficient and accurate resolution of optimization problems.
• The proposed algorithm was compared with variations of PSO and SSA by varying the number of base stations.
The subsequent sections of the paper will be organized as follows: Section 2 will introduce the proposed model. Section 3 will present and analyze the ECPPSO algorithm. Section 4 will demonstrate the results of the base station layout experiments and provide an analysis of the obtained results. Finally, Section 5 will conclude the main research findings of this paper and propose future research directions.
This section discusses the issue of signal effective coverage, using the effective coverage area of the signal as a criterion to test the algorithm.
The paper assumes that there are NM base stations with negligible volume, each with the same signal transmission radius R and capability. Furthermore, the signal strength is assumed to be independent of distance, so the signal transmission range of any base station forms a circular region with the base station as the center and R as the radius. This set of base stations can be denoted as S = {S1, S2,…,SNM}, and let (xi, yi) represent the two-dimensional spatial coordinate of Si in set S.
Assuming that these NM base stations are placed in a rectangular area of length L meters and a width of W meters, the total area is L * W square meters. Therefore, this rectangle area can be divided into small rectangles, each with an area of 1 * 1 and represented by the center point of each small rectangle. The set of these central points can be classified as
If a certain central point is effectively covered by the signal emitted from any base station, then the entire small rectangular area is considered effectively covered, meaning that the signal from the base station effectively covers a specific small area. This is the concept of signal effective coverage mentioned at the beginning of this section. By comparing the Euclidean distance D(si, mj) between the central point and the base station location with the signal transmission radius R of the base station, it can be determined whether the small rectangular area is effectively covered. This process can be described by the following Eqs. (1) and (2):
where
S(M) drepresents the effective coverage area of base station signals within the entire region M.
However, the position of the base station is not fixed. This article achieves the maximum effective coverage area by changing the placement of the base station.
In this section, the original PSO is outlined and the motivation, principle and pseudocode of the proposed algorithm are illustrated.
3.1 The Traditional PSO Algorithm
The traditional PSO algorithm, proposed by Eberhart and Kennedy in 1995, is a global optimization algorithm based on swarm intelligence. This algorithm effectively solves complex optimization problems by simulating social behaviors such as foraging in bird flocks. The PSO algorithm not only considers the social interactions of biological populations but also integrates the cognitive and learning abilities of each individual, thus forming an efficient search strategy.
In the PSO algorithm, each candidate solution in the search space is abstracted as a particle, with each particle possessing two attributes: velocity and position. The velocity determines the direction and step size of the particle’s movement in the search space, while the position represents the current location of the particle in the search space.
The core idea of the particle swarm optimization algorithm is to start from a set of random solutions (i.e., particles) and gradually approach the optimal solution through collaboration and information sharing among particles during the iterative process. During the algorithm’s iteration, each particle tracks two “extremes” to update its velocity and position: the first extreme is the best solution found by the particle individually so far, known as the personal best (pBest), which represents the particle’s search experience and historical best position; the second extreme is the best solution found by the entire particle swarm so far, known as the global best (gBest), which represents the collective search experience and best position of the entire population.
During each iteration process, once each particle acquires the crucial information of individual best (pBest) and global best (gBest), they will adjust their velocity and position according to Eqs. (4) and (5) in order to further explore the optimal solution in the search space:
where t represents the current iteration count,
The PSO algorithm, as a population-based optimization strategy relying on collective intelligence, has demonstrated significant advantages in various fields due to its simplicity, intuitiveness, ease of implementation, and efficient convergence speed. However, as the application domains continue to expand and problem complexity increases, the challenges faced by the PSO algorithm in solving complex optimization problems are becoming increasingly apparent. These challenges not only limit the application scope of the PSO algorithm but also demand higher performance from it.
In the process of in-depth research into the PSO algorithm, researchers have identified several limitations of this algorithm when addressing complex optimization problems. On the one hand, the PSO algorithm is prone to premature convergence, leading to rapid convergence to a local optimum in the early stages of the search, while neglecting the existence of the global optimum. This limitation stems from the close information sharing mechanism among particles in the algorithm, which causes the particle swarm to prematurely converge and lose diversity. On the other hand, when facing complex and dynamic search spaces, the global search capability of the PSO algorithm is often restricted. The algorithm may be at risk of being trapped in a local optimum and finding it difficult to escape, or it may lose direction during the search process, resulting in a slowdown in convergence rate and even failure to converge. This is mainly because the particles in the algorithm typically tend to follow the search path of the current best particle. However, in complex search spaces, there may be multiple local optima, and the algorithm may explore only one and then stop the search. This “short-sighted” behavior prevents the algorithm from discovering the global optimum, leading to performance loss. In addition, the convergence speed and stability of the PSO algorithm also exhibit deficiencies in certain scenarios, further limiting its application in complex optimization problems.
In order to overcome the aforementioned limitations of the PSO algorithm and expand its application scope, researchers have begun to improve the algorithm from multiple dimensions. Firstly, in order to enhance the diversity of the population and avoid premature convergence, researchers have attempted to introduce different parameter adjustment strategies, diversity maintenance mechanisms, and cross-mutation operations. Yang et al. introduced an acceleration coefficient based on the Singer map, where fluctuating acceleration coefficients made particle movement more disorderly, effectively helping particles reduce the probability of entering local optima [31]. Chen et al. employed the chaotic grouping mechanism (CGM) to partition the entire population into multiple subgroups, and then utilized the dynamic regrouping strategy (DRS) to guide the reorganization of the population, enabling the population to initiate the exploration of a new configuration. This approach improved the quality of population grouping during the search process and enhanced the population’s learning diversity [32]. Molaei et al. drew inspiration from genetic algorithms to propose a novel variant of PSO with an enhanced learning strategy and crossover operator, significantly elevating the algorithm’s search precision [33]. These strategies contributed to maintaining diversity among particles, enabling the algorithm to explore a wider search space.
Furthermore, to enhance the algorithm’s global search capability and locate the global optimum, researchers have focused on improving the algorithm’s overall search performance. They have adopted various multi-population strategies or introduced new search strategies, enabling the algorithm to conduct parallel searches within different regions, thereby increasing the probability of finding the global optimum. Zhao et al. proposed an elite-ordinary synergistic particle swarm optimization, where elite members and ordinary members were classified based on particle fitness. Elite individuals achieved high-level global exploration through self-learning, while ordinary particles performed auxiliary local searches around elite individuals [34]. Zhang et al. established three elite archives to store particles at different levels, and designed six learning strategies to aid the particles in their evolutionary learning process [35]. Inspired by conditional integration in automatic control, Xiang et al. proposed a method for adaptive learning of search directions. This method utilized the linear combination of a particle’s past momentum and the current search direction to achieve particle updates [36]. Xu et al. constructed a strategy pool for an existing PSO variant, selecting the optimal combination of learning strategies each time and effectively enhancing the performance of PSO [37].
Undeniably, these well-designed improved PSO variants possessed superior global search capabilities and stability compared to the original PSO. However, when tackling complex optimization problems, their robustness, convergence speed, and ability to escape local optima were still suboptimal. In order to overcome the inherent limitations of particle swarm optimization, this paper proposes a novel Evolutionary Particle Swarm Optimization algorithm based on collective prediction, named ECPPSO, aiming to significantly enhance the overall performance of the algorithm. The ECPPSO algorithm focuses on addressing two core issues of PSO: firstly, it employs the NEP strategy to tackle the problem of premature convergence in PSO by predicting the future positions of individuals using historical information, combining multi-individual predictions to guide evolution, reducing errors, and making full use of population diversity. Secondly, to address the issue of early entrapment in local optima or late-stage low fitness, the algorithm utilizes the SE strategy to evolve low-fitness individuals multiple times, enhancing the algorithm’s global search capabilities and search efficiency, while ensuring that the algorithm possesses stronger robustness and higher convergence speed when solving complex optimization problems.
The algorithm primarily focuses on improving two key issues of the original PSO. Firstly, to alleviate the problem of premature convergence, this paper introduces the NEP strategy. This strategy was initially proposed by Zhao et al. in the SEDE-PS (strengthening evolution-based differential evolution with prediction strategy) algorithm, aiming to predict the future positions of individuals and guide the direction of evolution [38]. In this study, this strategy is applied to PSO by combining predictive information from multiple individuals to reduce the errors associated with individual predictions and fully utilize population diversity information to guide the search.
Furthermore, to address the potential local optima traps that individuals may encounter, the ECPPSO algorithm adopts a unique SE strategy. This strategy also originates from the research of Zhao et al., used for multiple evolutionary operations in the SEDE-PS algorithm [38]. In this study, this strategy is adjusted and applied to PSO, guiding the lower-fitness individuals to escape local optima and evolve towards higher fitness through carefully designed multiple evolutionary operations.
According to the description of Eq. (4),
To overcome this limitation, this paper introduces the NEP strategy. The core idea of the NEP strategy is to use the historical evolutionary information of each particle to predict its future position and to guide the individual’s evolutionary direction through the predictive information from multiple individuals. Specifically, it involves recording and analyzing the particle’s movement trajectory and speed in past iterations, and using a predictive vector to estimate the particle’s potential position in the next iteration. In the NEP strategy, the velocity learning strategy for individual particles is updated as shown in Eqs. (6) and (7):
where w are the inertial weights,
By accumulating the historical evolutionary trends of individuals, the vector
However, as the number of evolutionary generations increases, the later predictive vectors may gradually increase. This may cause particles to make overly aggressive movements in the later stages of the search space, which is not conducive to fine-grained search and finding the global optimum. To address this issue, a dynamic adjustment mechanism is introduced in this paper to limit the size of the predictive vector, thereby changing the velocity learning strategy for individual particles as shown in Eqs. (8) and (9):
where, t represents the current generation and is used to balance the evolutionary trend.
Due to the existence of errors in individual predictions, multiple neighboring individuals are chosen to generate the prediction vectors. However, because individual predictions often contain a certain degree of error and uncertainty, in order to improve the accuracy of predictions, this paper chooses to comprehensively consider the information from multiple neighboring individuals to generate prediction vectors. By integrating the prediction results of these neighboring individuals, the collective intelligence can be fully utilized, reducing the bias brought about by individual predictions, and thus obtaining more robust and reliable prediction results. Therefore, the prediction vector generated by multiple neighboring individuals can be obtained through Eq. (10):
where
Fig. 1 demonstrates the role of the NEP strategy in improving the accuracy of the solution.

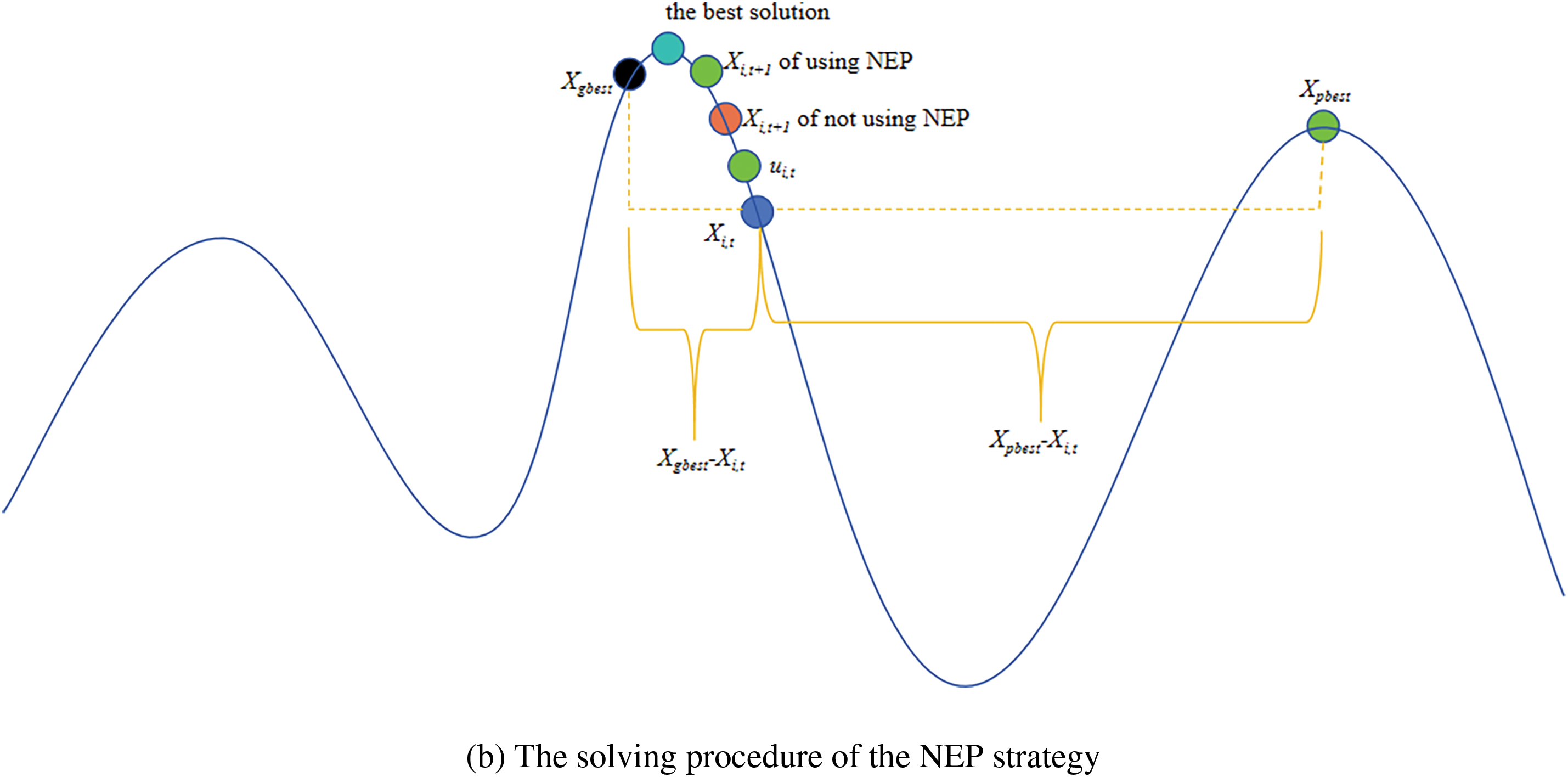
Figure 1: Comparison and effect diagram of the NEP strategy
The NEP strategy not only considers the predictive information of individual particles, but also integrates the predictive information of multiple neighboring particles to collectively guide the evolution direction of individuals. This collective intelligence approach can reduce the potential errors from individual particle predictions and fully utilize the historical information and search experiences of different individuals in the population. By implementing the NEP strategy, the PSO algorithm can more robustly handle complex and changing search spaces, reduce the risk of premature convergence, and improve solution accuracy. Additionally, this population-based predictive approach also helps the algorithm to better explore local areas, thus discovering superior global solutions. Therefore, the NEP strategy provides an effective way to improve the PSO algorithm’s performance in solving optimization problems.
The detailed flow of the NEP strategy is presented in Algorithm 1.

After adopting the NEP strategy, the exploration process sometimes encounters individuals that prematurely converge to lower levels or become trapped in local optimal states, as well as individuals with significantly lower fitness levels than the population’s average optimal fitness in the later stages. These individuals waste evaluation resources due to repeated evaluations. To address this issue, this paper introduces the SE strategy to improve the NEP strategy.
The core idea of the SE strategy is to perform multiple evolutionary operations on poorly performing individuals in the population without evaluating their fitness temporarily. After these individuals undergo evolutionary transformations through the SE strategy, the newly generated individuals are directly selected for the next generation to avoid wasting resources due to repeated evaluations.
Specifically, we first rank individuals based on their fitness and select the bottom G% of individuals in terms of fitness ranking as the target group for the SE strategy. For these individuals, traditional fitness evaluations are no longer conducted. Instead, the SE strategy is directly applied to perform multiple evolutionary operations, guiding the individuals toward directions of higher fitness using the velocity learning modes described by Eqs. (12) and (13). This approach guides these initially poor-performing individuals to move toward better solution spaces, gradually approaching or even surpassing the average optimal fitness level in the population, thereby improving the overall fitness level of the entire population.
where
With the continuous application of SE strategy, multiple evolution will also make the prediction vector larger and reduce the exploration ability of the algorithm in the search space. To balance this trend, this paper also introduces a control parameter
where d is the dimension of the problem.
The SE strategy is an advanced improvement over the NEP strategy, specifically addressing the issues of local optima and wastage of computational resources. The SE strategy does not completely abandon fitness evaluation but rather selectively applies it at specific stages and under certain conditions. The core idea of this strategy is to concentrate limited computational resources on those individuals that are most likely to improve the overall population fitness, thereby enhancing the efficiency and effectiveness of the entire optimization process. Through selective evolutionary operations, the SE strategy can optimize the performance of individuals with lower fitness within the population, thereby elevating the overall fitness level of the population and enabling more efficient and accurate resolution of optimization problems.
The detailed flow of the SE strategy is shown in Algorithm 2.

3.4 Procedure of ECPPSO Algorithm
First, the particles are arranged in ascending order to determine the position of the particles in the group: if the particle is ranked high, the group prediction vector is generated according to Algorithm 1, and update the speed and location information of the particles according to the corresponding formula; if the particles are located G% after the group, the particles will generate the predicted evolution vector according to Algorithm 2, and update their own speed and position, so that these originally poor individuals can move to a better solution space, thus improving the fitness level of the whole population. The specific pseudo-code is shown in Algorithm 3.

The algorithm presented in this paper incorporates both NEP and SE strategies and aims to address specific optimization problems. In order to get insight into the performance and efficiency of the algorithm, this block will conduct a detailed analysis of the computational complexity of its key components, where the dimension of the setting problem is D and the total number of particles is N.
First, the algorithm ranks particles by their fitness values and selects the top N*G% particles with better fitness values as the basis for the next generation. The complexity of the sequencing operation is mainly determined by the number of particles N, so the computational complexity at this stage is O (NlogN). Secondly, the algorithm will choose whether to execute the NEP strategy or the SE strategy according to the ranking situation of the particles. The NEP strategy requires traversing the entire population to find the index of the particle with the fitness value closest to the current particle’s fitness value. The computational complexity is O (N), while the SE strategy only involves the current particle information, so the computational complexity is O (1), so the computational complexity of this stage is O (N).
Next, the algorithm calculates the fitness value of each particle, which is a key step in evaluating the quality of the particle. Since the fitness value of N particles needs to be calculated, and the computational complexity of each particle does not increase significantly with increasing particle dimension D, the computational complexity at this stage is also O (N). In conclusion, considering the computational complexity of the main steps of particle sorting, NEP strategy, SE policy, and fitness values, it is concluded that the overall computational complexity of the proposed algorithm here in each generation is O (NlogN).
4 Experiment and Analysis of Base Station Layout
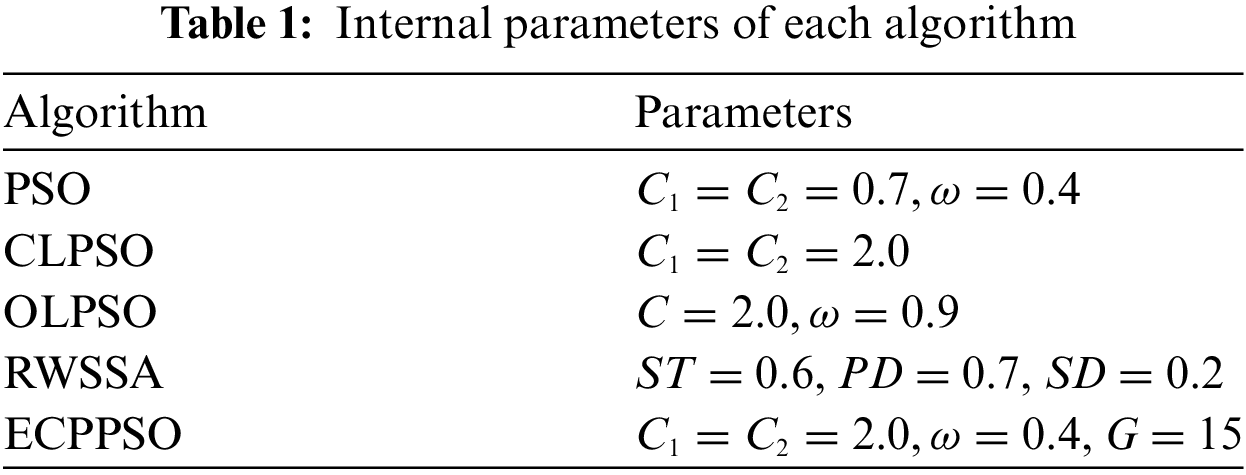
In this section, the optimization capability of each algorithm is discussed by the coverage effect under different numbers of base stations. The internal parameters of each algorithm used in this article are shown in Table 1.
4.1 Base Station Experiments at Different Numbers
In order to comprehensively evaluate the system performance stability of ECPPSO under different base station configurations, while considering the feasibility and rationality of practical applications, this paper selected four relatively reasonable numbers of base stations, 50, 60, 70, and 80, as experimental scenarios for practical applications. This paper will layout the base stations in the number of 50, 60, 70, 80, and compare comprehensive learning particle swarm optimization algorithm (CLPSO) [39], orthogonal learning particle swarm optimization (OLPSO) [40], sparrow search algorithm with random walk strategy (RWSSA) [41] and PSO, among which RWSSA is an effective algorithm in the base station layout in recent years. CLPSO and OLPSO are the more mainstream algorithms in PSO variant.
The population size of each algorithm is 50, the maximum number of evaluations is N * 1000, the L and W of the overall area are set to 50, and the radius of the signal transmission R is set to 5. The parameters of each algorithm are set as follows. Each algorithm is run independently for 20 times, and the best value, average value, and standard deviation of the effective coverage ratio of base station signals (i.e., the ratio between the area effectively covered by the base station signals and the total area L * W, which is specifically denoted as S(M)/(L * W)) in each algorithm are counted, and then the optimal base station deployment map for each algorithm with different numbers of base stations is given. On the other hand, the Wilcoxon test was conducted to assess the performance difference between each algorithm and ECPPSO, with a significant level set as 0.05. A p-value less than 0.05 indicates a statistically significant difference performance between the two algorithms, while the performance is comparable. At the same time, the Friedman test is also used to calculate the comprehensive ranking of each algorithm under the number of different base stations, to test the comprehensive optimization ability of each algorithm. The specific optimization results are shown in Table 2, the deployment effect is shown in Figs. 2–5, and the box plot of the data of 20 runs is shown in Fig. 6. The experimental environment is Windows 11, the processor is 11th Gen Intel (R) Core (TM) i5-11500 @ 2.70 GHz, and the language environment is pycharm.
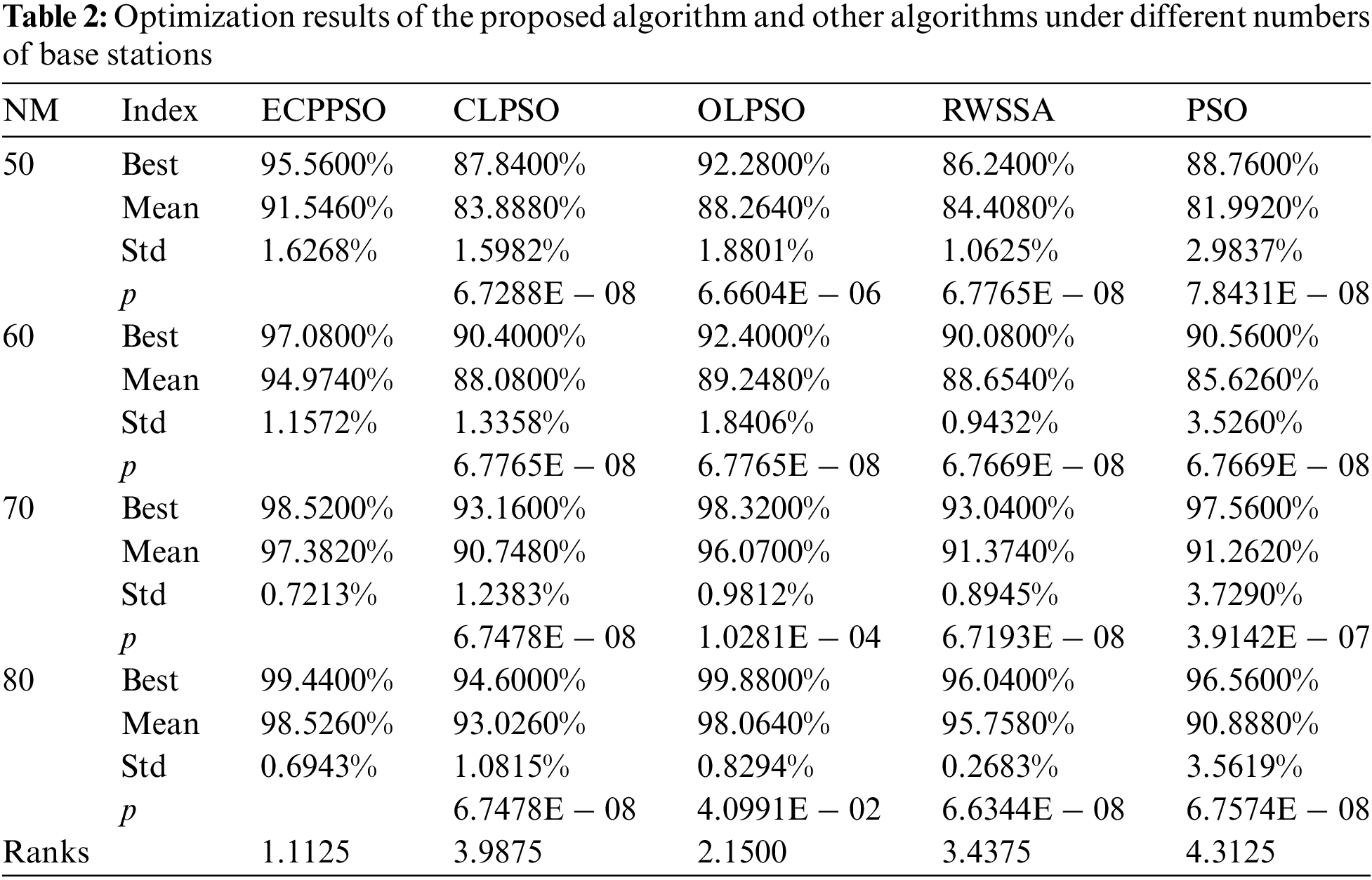
Figure 2: Deployment of base stations under 50 base stations
Figure 3: Deployment of base stations under 60 base stations
Figure 4: Deployment of base stations under 70 base stations
Figure 5: Deployment of base stations under 80 base stations
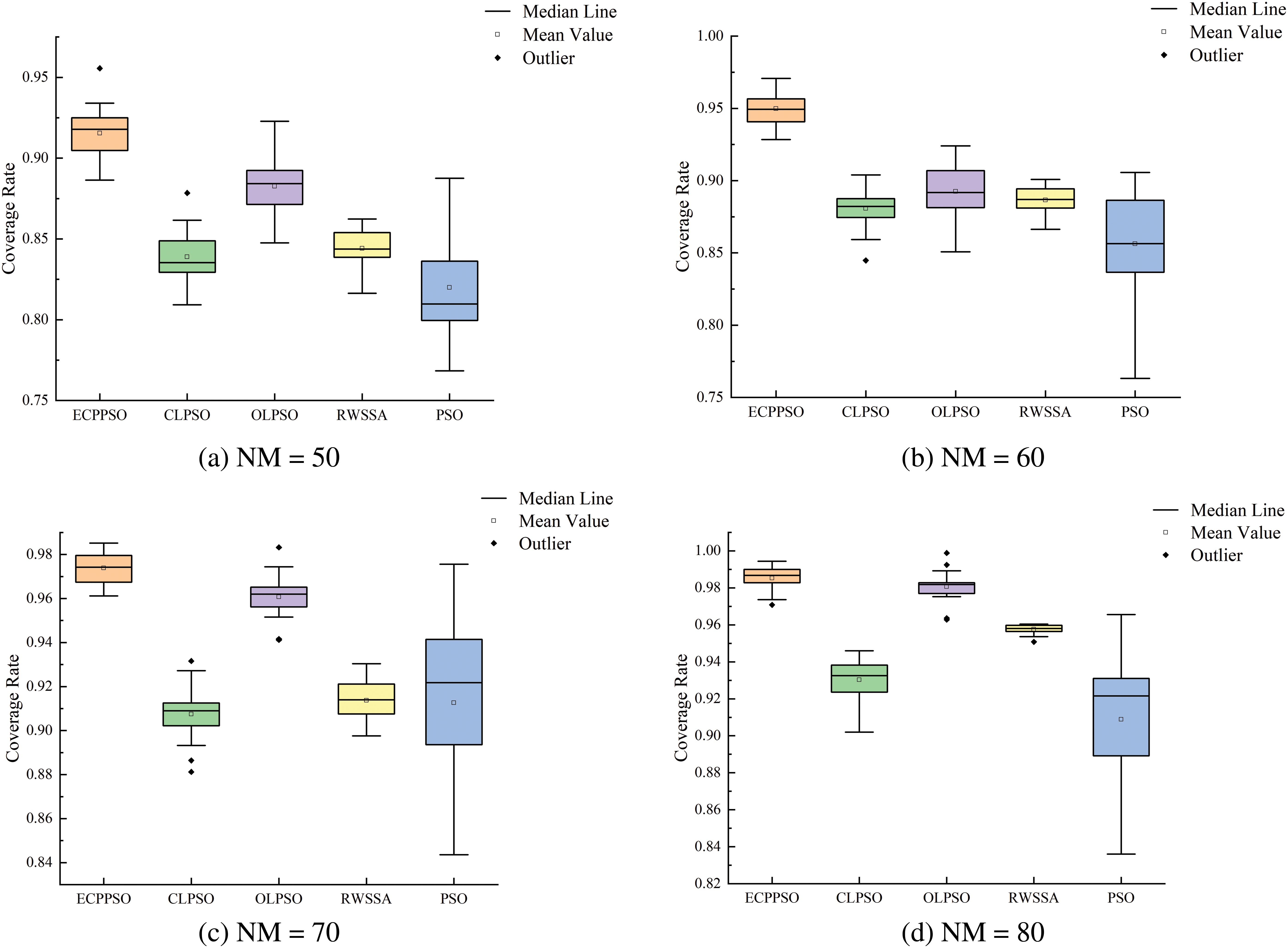
Figure 6: Results of 20 runs of each algorithm
According to the data in Table 2, the ECPPSO, CLPSO, OLPSO, RWSSA, and PSO algorithms were compared under the scenarios of testing 50, 60, 70, and 80 random locations. In these scenarios, the coverage rate and average coverage rate of ECPPSO were significantly superior to other algorithms, with the best coverage rates reaching 95.5600%, 97.0800%, and 98.5200%, respectively. Although the standard deviation of ECPPSO was not the smallest among all algorithms, its performance remained relatively stable. Even in the case of 80 random locations, while the coverage rate of ECPPSO was not the highest among all algorithms, it still approached the highest level, and its average coverage rate remained optimal among all algorithms. Additionally, the relatively small standard deviation of ECPPSO demonstrated the stability of the algorithm. The data in the last row of the table also showed that ECPPSO ranked highest, followed by OLPSO, RWSSA, CLPSO, and traditional PSO as the last. Through the visual comparisons in Figs. 2 to 5, it is evident that ECPPSO exhibited outstanding performance in terms of coverage rate, surpassing most of the improved algorithms, especially outperforming the PSO algorithm by a large margin. Furthermore, the standard deviation of ECPPSO was significantly smaller than that of PSO, further proving the stability and superiority of ECPPSO in performance. In summary, ECPPSO demonstrated good performance and robustness in base station deployment problems, particularly in complex environments, making its deployment strategy feasible.
Moreover, Boxplot in Fig. 6 also demonstrated the good data stability and high coverage rate of ECPPSO. In the boxplot, the higher position of the box represents a higher coverage rate, and the smaller area represents the stability of the algorithm. In subfigures (a), (b), (c), and (d), the height of the box representing ECPPSO was higher than those of other algorithm boxes, and in the case of 60 random locations, it was significantly superior to other algorithms in both stability and coverage rate. This further validates the robustness and superiority of the ECPPSO algorithm.
In order to further see the advantages and efficiency of each algorithm in base station planning, the average convergence effect of each algorithm under 20 runs is shown in this section, as shown in Fig. 7.
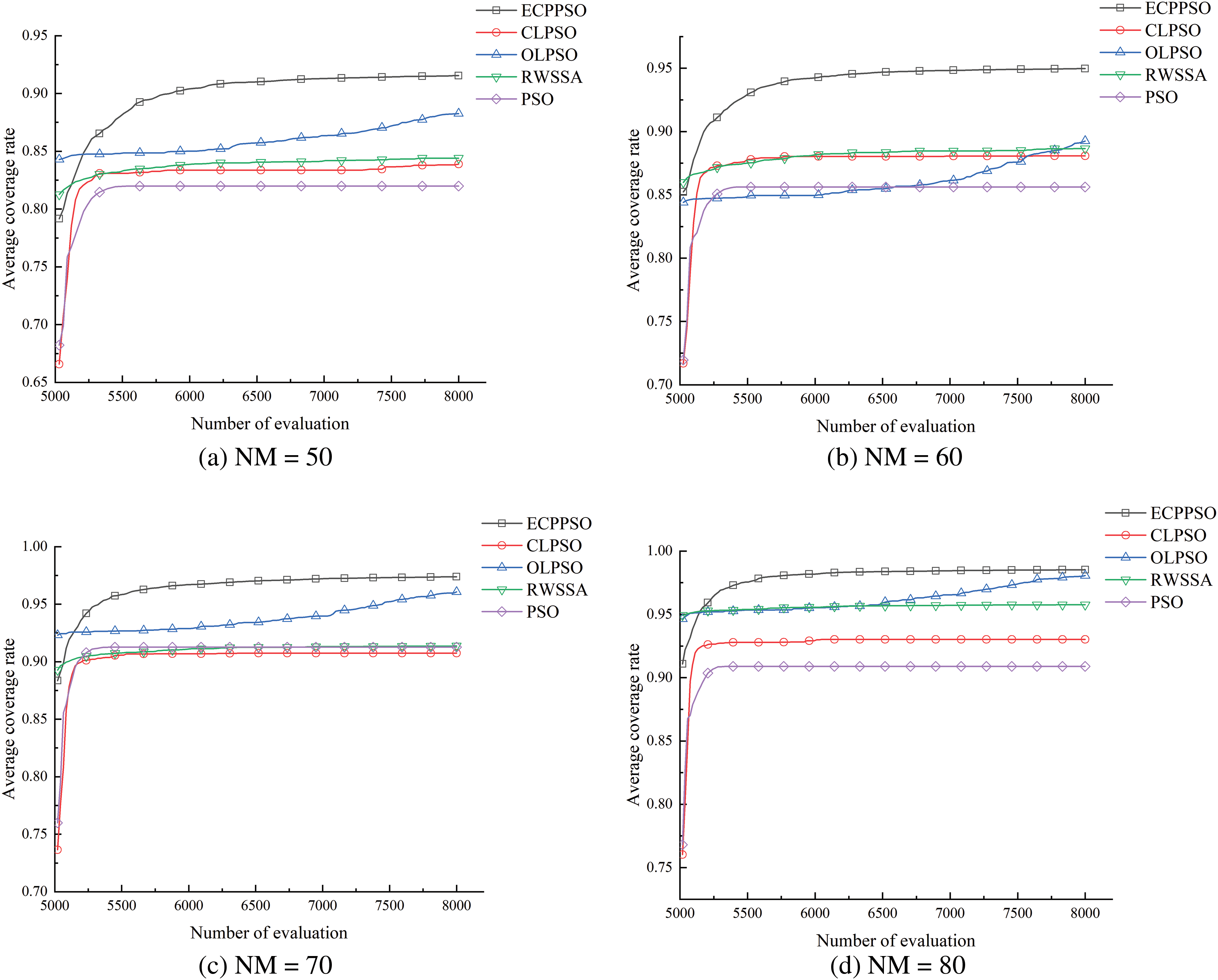
Figure 7: Average convergence effect of each algorithm
To accurately demonstrate the convergence consistency of algorithms in the base station deployment problem, Fig. 7 presents the average convergence curves of 5 algorithms over 20 independent runs for visual comparison.
From Fig. 7, it is evident that ECPPSO achieves an average coverage rate of 90% or higher across different numbers of base stations. For the cases of NM = 50, NM = 60, and NM = 70, the average coverage rate of ECPPSO far surpasses that of the other three algorithms, excluding OLPSO. Although the convergence accuracy of OLPSO approaches that of ECPPSO when NM = 70 and 80, the convergence speed of OLPSO is significantly lower than that of ECPPSO. With an increase in the number of base stations, the average coverage rate of ECPPSO continues to rise, reaching close to 98% at NM = 80, while PSO only achieves around 90%. In terms of convergence speed and accuracy, ECPPSO exhibits a significant advantage over PSO. The convergence performance of PSO is notably inferior to that of ECPPSO, further highlighting the optimization efficiency of ECPPSO in the base station deployment problem. It is evident that ECPPSO achieves outstanding convergence accuracy and demonstrates faster convergence speed, indicating a clear advantage. This showcases the excellent optimization efficiency of ECPPSO in addressing the effective coverage area in base station deployment, validating its effectiveness in solving complex base station deployment problems and further emphasizing its efficacy.
To further validate the effectiveness of the individual strategies within ECPPSO, we conducted an ablation experiment by introducing the NEP strategy or SE strategy separately into the PSO algorithm, denoted as PSO-1 and PSO-2, respectively. The same experimental settings were applied, and the specific optimization results are shown in Table 3.
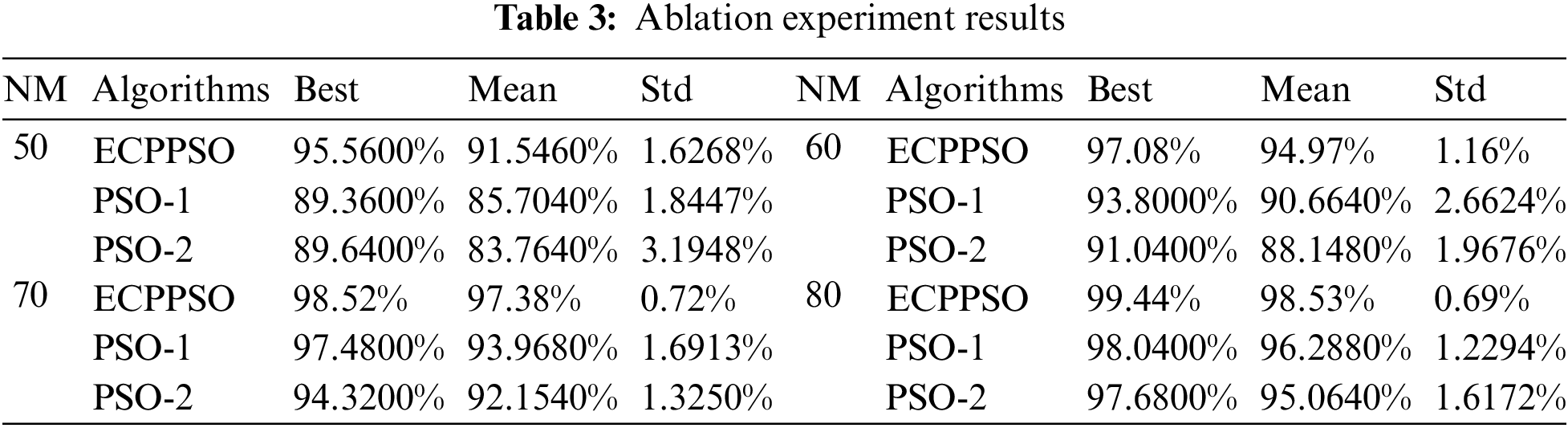
As depicted in Table 3, when considering 50 random locations, ECPPSO achieved the highest coverage rate, followed by PSO-2, while PSO-1 exhibited the lowest coverage rate. In terms of average coverage rate, ECPPSO demonstrated the best performance, while PSO-2 showed the lowest average coverage rate. Furthermore, ECPPSO exhibited the smallest variance compared to PSO-1 and PSO-2, indicating its stable optimization performance. These results signify the excellent optimization effectiveness of the ECPPSO algorithm, along with its ability to maintain good stability.
When the number of random locations increased to 60 and 70, ECPPSO maintained its leading position in terms of coverage rate, followed by PSO-1, with PSO-2 exhibiting the lowest coverage rate. In terms of average coverage rate, ECPPSO continued to outperform the other algorithms, while PSO-2 showed the lowest average coverage rate. It is worth noting that although the variance of ECPPSO remained the smallest, at this point, the variance of PSO-2 was lower than that of PSO-1. This further demonstrates that while the NEP strategy and SE strategy can produce certain optimization effects when used individually, their combination yields the best results, highlighting the superiority of the ECPPSO algorithm.
In the scenario with 80 random locations, ECPPSO still achieved the highest coverage rate, followed by PSO-1 and then PSO-2. In terms of average coverage rate, ECPPSO significantly outperformed the other two algorithms. Additionally, the variance of ECPPSO was much smaller than that of PSO-1 and PSO-2, further validating its stability and superiority. Even when using only the NEP strategy or SE strategy for optimization, the coverage rates already exceeded 95%. However, the combined use of both strategies in the ECPPSO algorithm resulted in a coverage rate as high as 99.44%. Furthermore, the average coverage rate of the PSO-1 algorithm reached 96.2880%, while that of the PSO-2 algorithm reached 95.0640%. In contrast, ECPPSO achieved a coverage rate of 98.53%. This fully demonstrates the effectiveness of the NEP strategy and SE strategy within the PSO algorithm, especially when used in combination. Once again, this emphasizes the superiority and rationality of the ECPPSO algorithm.
The wireless signals emitted by base stations have become the linchpin of communication and connectivity in today’s society, playing an increasingly crucial role in real-life applications. With the rapid development of the IoT, the importance of base stations has become even more pronounced as they not only facilitate communication between individuals but also provide essential support for realizing smarter and more convenient lifestyles. The applications of IoT encompass various fields such as smart homes, smart cities, intelligent transportation, all of which heavily rely on the support and coverage provided by base stations. Therefore, it is vital that signals emitted by base stations cover specific areas as comprehensively as possible.
This article focuses on the goal of achieving extensive coverage with minimal base stations, with a particular emphasis on the effective coverage area of base station signals. It proposes an innovative algorithm based on the concept of collective prediction. This algorithm introduces new strategies such as the NEP and SE to address the issue of premature convergence often encountered in traditional particle swarm optimization algorithms. Moreover, it aims to enhance the algorithm’s global search capability and search efficiency, ensuring robustness and faster convergence speed when dealing with complex optimization problems.
In addressing scenarios with different numbers of base stations, the article conducts experiments and analyses the proposed algorithm through base station layout. Through simulation experiments, it is observed that ECPPSO outperforms other algorithms, significantly enhancing the performance of PSO. ECPPSO demonstrates outstanding convergence accuracy and faster convergence speed, presenting clear advantages. The algorithm displays excellent optimization efficiency in solving the problem of effective coverage area in base station deployment, further validating its effectiveness.
However, this article does not consider the three-dimensional layout of base stations and solely focuses on the effective coverage area of base station signals in a two-dimensional scenario. Additionally, the model used is idealized and does not account for the relationship between signal strength and distance from the signal source. In reality, signals emitted by base stations exist in three dimensions, forming irregular spheres expanding outward from the signal source due to various factors, including obstruction from tall buildings and interference from other sources. Future research directions for the algorithm will focus on more complex situations, such as establishing a three-dimensional model, considering the impact of signal strength and distance from the signal source, and incorporating constraints related to signal range and other factors like obstructions. Furthermore, it is essential to integrate the proposed algorithm with strategies or algorithms that yield superior performance to achieve more satisfactory results.
It is noted that rural areas are geographically remote, with a wide geographical scope and relatively low economic development, resulting in fewer base stations being available for deployment. It is desirable for every household to be covered by signals emitted by base stations, making the research proposed in this article relevant in such circumstances. Additionally, in addition to considering the effective coverage area of base station signals, it is also important to consider signal strength. Poor signals are likely to cause dissatisfaction among individuals, as demonstrated in scenarios such as concert venues where the demand for wireless signals reaches tens of thousands, resulting in weak or nonexistent signals becoming commonplace. Therefore, enhancing the signal strength in specific areas is also a future research direction for the team.
Acknowledgement: I express my sincere gratitude to all individuals who have contributed to this paper. Their dedication and insights have been invaluable in shaping the outcome of this work.
Funding Statement: This work is supported by the National Natural Science Foundation of China (Nos. 62272418, 62102058), Basic Public Welfare Research Program of Zhejiang Province (No. LGG18E050011), the Major Open Project of Key Laboratory for Advanced Design and Intelligent Computing of the Ministry of Education under Grant ADIC2023ZD001, National Undergraduate Training Program on Innovation and Entrepreneurship (No. 202410345054).
Author Contributions: Study conception and design: Jiaying Shen and Donglin Zhu; draft manuscript preparation: Yujia Liu, Leyi Wang, Jialing Hu and Zhaolong Ouyang; supervision: Taiyong Li and Changjun Zhou. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data used to support the findings of this study are available from the corresponding author upon request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Z. Ma, M. Xiao, Y. Xiao, Z. Pang, H. V. Poor and B. Vucetic, “High-reliability and low-latency wireless communication for internet of things: Challenges, fundamentals, and enabling technologies,” IEEE Internet Things J., vol. 6, no. 5, pp. 7946–7970, 2019. doi: 10.1109/JIOT.2019.2907245. [Google Scholar] [CrossRef]
2. L. Chettri and R. Bera, “A comprehensive survey on Internet of Things (IoT) toward 5G wireless systems,” IEEE Internet Things J., vol. 7, no. 1, pp. 16–32, 2019. doi: 10.1109/JIOT.2019.2948888. [Google Scholar] [CrossRef]
3. D. Xu et al., “Understanding operational 5G: A first measurement study on its coverage, performance and energy consumption,” in Proc. Annual Conf. ACM Special Interest Group Data Commun. Appl. Technol. Architec. Protoc. Comput. Commun., 2020, pp. 479–494. doi: 10.1145/3387514.3405882. [Google Scholar] [CrossRef]
4. W. Chen, X. Lin, J. Lee, A. Toskala, S. Sun and C. F. Chiasserini, “5G-advanced toward 6G: Past, present, and future,” IEEE J. Sel. Areas Commun., vol. 41, no. 6, pp. 1592–1619, 2023. doi: 10.1109/JSAC.2023.3274037. [Google Scholar] [CrossRef]
5. M. J. Shehab, I. Kassem, A. A. Kutty, M. Kucukvar, N. Onat and T. Khattab, “5G networks towards smart and sustainable cities: A review of recent developments, applications and future perspectives,” IEEE Access, vol. 10, pp. 2987–3006, 2021. doi: 10.1109/ACCESS.2021.3139436. [Google Scholar] [CrossRef]
6. M. Shafi et al., “5G: A tutorial overview of standards, trials, challenges, deployment, and practice,” IEEE J. Sel. Areas Commun., vol. 35, no. 6, pp. 1201–1221, 2017. doi: 10.1109/JSAC.2017.2692307. [Google Scholar] [CrossRef]
7. S. Dang, O. Amin, B. Shihada, and M. -S. Alouini, “What should 6G be?” Nature Electron., vol. 3, pp. 20–29, 2020. doi: 10.1038/s41928-019-0355-6. [Google Scholar] [CrossRef]
8. W. Saad, M. Bennis, and M. Chen, “A vision of 6G wireless systems: Applications, trends, technologies, and open research problems,” IEEE Netw., vol. 34, no. 3, pp. 134–142, 2019. doi: 10.1109/MNET.001.1900287. [Google Scholar] [CrossRef]
9. M. Z. Chowdhury, M. Shahjalal, S. Ahmed, and Y. M. Jang, “6G wireless communication systems: Applications, requirements, technologies, challenges, and research directions,” IEEE Open J. Commun. Soc., vol. 1, pp. 957–975, 2020. doi: 10.1109/OJCOMS.2020.3010270. [Google Scholar] [CrossRef]
10. Z. Zhang et al., “6G wireless networks: Vision, requirements, architecture, and key technologies,” IEEE Vehicular Technol. Mag., vol. 14, no. 3, pp. 28–41, 2019. doi: 10.1109/MVT.2019.2921208. [Google Scholar] [CrossRef]
11. M. Giordani, M. Polese, M. Mezzavilla, S. Rangan, and M. Zorzi, “Toward 6G networks: Use cases and technologies,” IEEE Commun. Mag., vol. 58, no. 3, pp. 55–61, 2020. doi: 10.1109/MCOM.001.1900411. [Google Scholar] [CrossRef]
12. N. Naderializadeh, M. A. Maddah-Ali, and A. S. Avestimehr, “Cache-aided interference management in wireless cellular networks,” IEEE Trans. Commun., vol. 67, no. 5, pp. 3376–3387, 2019. doi: 10.1109/TCOMM.2019.2893669. [Google Scholar] [CrossRef]
13. S. Rangan, T. S. Rappaport, and E. Erkip, “Millimeter wave cellular wireless networks: Potentials and challenges,” Proc. IEEE, vol. 102, no. 3, pp. 366–385, 2014. doi: 10.1109/JPROC.2014.2299397. [Google Scholar] [CrossRef]
14. J. Qiao, X. S. Shen, J. W. Mark, Q. Shen, Y. He and L. Lei, “Enabling device-to-device communications in millimeter-wave 5G cellular networks,” IEEE Commun. Mag., vol. 53, no. 1, pp. 209–215, 2015. doi: 10.1109/MCOM.2015.7010536. [Google Scholar] [CrossRef]
15. P. K. Agyapong, M. Iwamura, D. Staehle, W. Kiess, and A. Benjebbour, “Design considerations for a 5G network architecture,” IEEE Commun. Mag., vol. 52, no. 11, pp. 65–75, 2014. doi: 10.1109/MCOM.2014.6957145. [Google Scholar] [CrossRef]
16. E. Bertilsson, O. Gustafsson, and E. G. Larsson, “A modular base station architecture for massive MIMO with antenna and user scalability per processing node,” in 2018 52nd Asilomar Conf. Sign. Syst. Comput., IEEE, 2018, pp. 1649–1653. [Google Scholar]
17. S. Sun, T. S. Rappaport, M. Shafi, P. Tang, J. Zhang and P. J. Smith, “Propagation models and performance evaluation for 5G millimeter-wave bands,” IEEE Trans. Vehicular Technol., vol. 67, no. 9, pp. 8422–8439, 2018. doi: 10.1109/TVT.2018.2848208. [Google Scholar] [CrossRef]
18. M. Feng, S. Mao, and T. Jiang, “Base station ON-OFF switching in 5G wireless networks: Approaches and challenges,” IEEE Wirel. Commun., vol. 24, no. 4, pp. 46–54, 2017. doi: 10.1109/MWC.2017.1600353. [Google Scholar] [CrossRef]
19. D. Muirhead, M. A. Imran, and K. Arshad, “A survey of the challenges, opportunities and use of multiple antennas in current and future 5G small cell base stations,” IEEE Access, vol. 4, pp. 2952–2964, 2016. doi: 10.1109/ACCESS.2016.2569483. [Google Scholar] [CrossRef]
20. M. Farasat, D. N. Thalakotuna, Z. Hu, and Y. Yang, “A review on 5G sub-6 GHz base station antenna design challenges,” Electronics, vol. 10, no. 16, 2021, Art. no. 2000. doi: 10.3390/electronics10162000. [Google Scholar] [CrossRef]
21. A. Kangrang, S. Compliew, and W. Chaiyapoom, “Heuristic algorithm with simulation model for searching optimal reservoir rule curves,” Am. J. Appl. Sci., vol. 6, no. 2, 2009, Art. no. 263. [Google Scholar]
22. T. Dede and Y. Ayvaz, “Combined size and shape optimization of structures with a new meta-heuristic algorithm,” Appl. Soft Comput., vol. 2015, no. 28, pp. 250–258, 2015. doi: 10.1016/j.asoc.2014.12.007. [Google Scholar] [CrossRef]
23. E. Osaba et al., “A tutorial on the design, experimentation and application of metaheuristic algorithms to real-world optimization problems,” Swarm Evol. Comput., vol. 64, 2021, Art. no. 100888. doi: 10.1016/J.SWEVO.2021.100888. [Google Scholar] [CrossRef]
24. J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Proc. ICNN’95-Int. Conf. Neural Netw., IEEE, 1995, vol. 4, pp. 1942–1948. doi: 10.1109/ICNN.1995.488968. [Google Scholar] [CrossRef]
25. A. G. Gad, “Particle swarm optimization algorithm and its applications: A systematic review,” Arch. Comput. Methods Eng., vol. 30, no. 5, pp. 3471, 2022. doi: 10.1007/s11831-022-09762-3. [Google Scholar] [CrossRef]
26. T. M. Shami et al., “Particle swarm optimization: A comprehensive survey,” IEEE Access, vol. 10, no. 4, pp. 10031–10061, 2022. doi: 10.1109/ACCESS.2022.3142859. [Google Scholar] [CrossRef]
27. T. Bai and R. W. Heath, “Coverage and rate analysis for millimeter-wave cellular networks,” IEEE Transac. Wireless Commun., vol. 14, no. 2, pp. 1100–1114, 2015. doi: 10.1109/TWC.2014.2364267. [Google Scholar] [CrossRef]
28. S. Abdollahzadeh and N. Navimipour, “Deployment strategies in the wireless sensor network: A comprehensive review,” Comput. Commun., vol. 91–92, no. 1, pp. 1–16, 2016. doi: 10.1016/j.comcom.2016.06.003. [Google Scholar] [CrossRef]
29. Q. Wang, X. Zhao, Z. Lv, X. Ma, R. Zhang and Y. Lin, “Optimizing the ultra-dense 5G base stations in urban outdoor areas: Coupling GIS and heuristic optimization,” Sustain. Cities Soc., vol. 63, no. 4, 2020, Art. no. 102445. doi: 10.1016/j.scs.2020.102445. [Google Scholar] [CrossRef]
30. M. Ayati and M. Pasha-Zanousi, “Fuzzy PSO-based algorithm for controlling base station movements in a wireless sensor network,” Turkish J. Electrical Eng. Comput. Sci., vol. 24, pp. 5068–5077, 2016. doi: 10.3906/elk-1411-118. [Google Scholar] [CrossRef]
31. J. Yang, J. Yu, and C. Huang, “Adaptive multistrategy ensemble particle swarm optimization with Signal-to-Noise ratio distance metric,” Inf. Sci., vol. 612, pp. 1066–1094, 2022. doi: 10.1016/j.ins.2022.07.165. [Google Scholar] [CrossRef]
32. K. Chen, B. Xue, M. Zhang, and F. Zhou, “Novel chaotic grouping particle swarm optimization with a dynamic regrouping strategy for solving numerical optimization tasks,” Knowl. Based Syst., vol. 194, no. 1, 2020, Art. no. 105568. doi: 10.1016/j.knosys.2020.105568. [Google Scholar] [CrossRef]
33. S. Molaei, H. Moazen, S. Najjar-Ghabel, and L. Farzinvash, “Particle swarm optimization with an enhanced learning strategy and crossover operator,” Knowl. Based Syst., vol. 215, 2021, Art. no. 106768. doi: 10.1016/j.knosys.2021.106768. [Google Scholar] [CrossRef]
34. S. Zhao and D. Wang, “Elite-ordinary synergistic particle swarm optimization,” Inf. Sci., vol. 609, pp. 1567–1587, 2022. doi: 10.1016/j.ins.2022.07.131. [Google Scholar] [CrossRef]
35. Y. Zhang, “Elite archives-driven particle swarm optimization for large scale numerical optimization and its engineering applications,” Swarm Evol. Comput., vol. 76, 2023, Art. no. 101212. doi: 10.1016/j.swevo.2022.101212. [Google Scholar] [CrossRef]
36. X. Shao et al., “An adaptive integral separated proportional-integral controller based strategy for particle swarm optimization,” Knowl. Based Syst., vol. 195, no. 3, 2020, Art. no. 105696. doi: 10.1016/j.knosys.2020.105696. [Google Scholar] [CrossRef]
37. H. Q. Xu et al., “A strategy learning framework for particle swarm optimization algorithm,” Inf. Sci., vol. 619, pp. 126–152, 2023. doi: 10.1016/j.ins.2022.10.069. [Google Scholar] [CrossRef]
38. H. Zhao, L. Tang, J. Li, and J. Liu, “Strengthening evolution-based differential evolution with prediction strategy for multimodal optimization and its application in multi-robot task allocation,” Appl. Soft Comput., vol. 139, 2023, Art. no. 110218. doi: 10.1016/j.asoc.2023.110218. [Google Scholar] [CrossRef]
39. Y. Cao, H. Zhang, W. Li, M. Zhou, Y. Zhang and W. A. Chaovalitwongse, “Comprehensive learning particle swarm optimization algorithm with local search for multimodal functions,” IEEE Trans. Evol. Comput., vol. 23, no. 4, pp. 718–731, 2019. doi: 10.1109/TEVC.2018.2885075. [Google Scholar] [CrossRef]
40. Z. H. Zhan, J. Zhang, and O. Liu, “Orthogonal learning particle swarm optimization,” in Proc. 11th Annual Conf. Genet. Evol. Comput., 2009, pp. 1763–1764. doi: 10.1145/1569901.1570147. [Google Scholar] [CrossRef]
41. Z. Chang, Q. Gu, C. Lu, Y. Zhang, S. Ruan and S. Jiang, “5G private network deployment optimization based on RWSSA in open-pit mine,” IEEE Trans. Ind. Inform., vol. 18, no. 8, pp. 5466–5476, 2021. doi: 10.1109/TII.2021.3132041. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools