Toward Analytical Homogenized Relaxation Modulus for Fibrous Composite Material with Reduced Order Homogenization Method

1  Introduction

Fiber-reinforced composites offer advantages such as lightweight properties, high strength, extended maintenance intervals, and corrosion resistance, making them widely used in the aerospace and automotive industries [1–5]. Thermosetting or thermoplastic matrices with cylindrical microstructures exhibit transversely isotropic viscoelastic behavior, as documented in the literature [6,7]. The overall mechanical behavior of fibrous composites is analyzed using multiscale methods. These methods provide detailed insights into the underlying mechanisms, enabling material performance optimization and guiding innovative material design.

Initially, homogenization methods for viscoelastic composites were based on the correspondence principle. Micromechanical theoretical schemes developed for elastic composites were extended to viscoelastic composites to estimate their effective elastic moduli in the Laplace domain. Various approaches, including mean-field homogenization methods [8–10], the asymptotic homogenization method [11–13], the variational principle [14,15], and the sequential linearization approach [16], have been employed to simulate viscoelastic composites. Results obtained in the Laplace domain are then transformed back to the time domain to determine the effective response of the viscoelastic materials. However, performing an analytical inverse transform is usually too complex, so the macroscopic response in the time domain can only be obtained through numerical inversion [12] or approximate inversion methods [17], which can be costly and less accurate.

To overcome the limitations of the Laplace transformation, various homogenization methods have been developed to operate directly in the time domain [18–20]. Mean-field homogenization methods, initially formulated for linear elastic composite materials, have since been extended to address nonlinear behaviors, such as elastoplastic [21,22] and viscoelastic [23] responses, among others. These extensions are typically implemented by linearizing local constitutive laws incrementally, an approach necessitated by the Eshelby problem’s assumption that mechanical interactions within phases are purely elastic. Additionally, stress and strain fields within each phase are approximated as phase averages, treating them as homogeneous. However, in nonlinear problems, where stress and strain distributions are inherently non-uniform across phases, this approximation can lead to an over-stiffness issue. To address this challenge, techniques such as the isotropization method [24] and higher-order theories [25] have been proposed. Bleiler et al. [26] introduced a tangent second-order homogenization method to estimate the effective mechanical response of fibrous composites with hyperelastic, anisotropic, and incompressible phases. Furthermore, Barral et al. [27] advanced the Mori-Tanaka method by incorporating a modified transformation field analysis (TFA) approach first proposed by Dvorak and his coworkers [28] and introducing a specialized coating between fibers and the matrix, effectively mitigating over-stiffness in the analysis of fiber-reinforced composites. In the TFA method, the inelastic strains are considered as given eigenstrains. This method assumes that eigenstrains in each phase of the composite are piecewise constant, this lower-order approximation can lead to inaccurate solutions for overall properties. To overcome the problem, Michel et al. [29,30] have introduced the nonuniform transformation field analysis, where full field calculations take place and the plastic behavior is traced with the help of several plastic modes. Strategies such as subdividing each phase into numerous partitions, using asymptotically consistent eigenstrain fields have also been employed [31].

The asymptotic homogenization method is a mathematically rigorous methodology developed by Sanchez-Palencia [32], Bensoussan and Alain [33]. Compare to the Mean-field homogenization method, it effectively captures the interactions between different phases within composite materials, enabling more precise predictions of their overall performance. It has been proved that the considered fields converge towards the homogeneous macroscopic solution as the micro-structural parameter tends to 0. The classic asymptotic homogenization method can obtain the linear homogenized modulus by solving a linear unit cell problem with given phase material elastic properties. Thus, one can use the homogenized elastic properties in a macroscopic simulation without downscaling or upscaling between the macro- and meso-scales. In this manner, the linear homogenization process is named as “off-line” process. However, if material nonlinearities at the mesoscale are considered, a unit cell problem must be solved at every integration point of all the macroscopic elements during each macroscopic Newton-Raphson iteration. Additionally, the unit cell problem itself requires a Newton-Raphson iterative process due to material nonlinearities. This repeating process is known as the “on-line” process since it depends on the “on-the-fly” kinematic measurements at the macro-scale, significantly increasing the computational cost. Yu et al. [34] used the asymptotic homogenization method to solve thermo-viscoelastic problems, considering both multiple spatial and temporal scales. Zhai et al. [18] developed a time-domain asymptotic homogenization method based on the integral form of the Kelvin–Voigt viscoelastic model and used it for woven fabric composites.

Multiscale computational techniques based on the finite element method such as , offer the possibility of computing the macro-structural response of heterogeneous materials with an arbitrary microscopic geometry and constitutive behavior. A scheme based on the discrete homogenization method are developed to predict the effective mechanical properties of 3D dry textiles [35]. Recently, the isogeometric analysis method (IGA), proposed by Hughes and his coworkers [36,37], has been incorporated into computational homogenization [38–40]. The method aims to unify the representation of geometric models and mesh models by directly employing the spline functions as the shape functions. The errors produced by geometric approximations inherent in conventional finite-element and finite-volume techniques could be greatly reduced because the same model is used for both modeling and analysis. Cylindrically orthotropic [41] and viscoelasticity [42] are considered for fiber-reinforced composites using IGH methods.

To decrease computational costs at the meso-scale without significantly compromising solution accuracy, the reduced-order-homogenization (ROH) multiscale method was developed, combining the asymptotic homogenization method with transformation field analysis (TFA) [43,44]. The ROH method was first used in composite plasticity and failure analysis [43,45], and higher-order ROH methods have been developed for three-scale nonlinear problems [46–49]. In this paper, a two-phase model with the assumption of one partition per phase is employed for fiber-reinforced composites. Due to the unique structure of the fiber-reinforced unit cell, analytical transformation influence functions can be derived. Based on ROH theory, an analytical homogenization constitutive model for unidirectional fibrous composites is proposed, eliminating the need for computational homogenization. As demonstrated in the following section, the proposed model does not exhibit significant over-stiffness and helps reduce computational time.

This paper is organized as follows. In Section 2, we introduce the analytical viscoelastic fibrous composites constitutive model based on the ROH homogenization method. Special cases where the fiber volume fraction approaches zero are considered to confirm the model’s consistency under extreme conditions. We investigate the impact of material parameters of each component on the relaxation times of the homogenized viscoelastic material. Additionally, numerical implementation specifics for the proposed model are detailed in this section. Section 3 presents numerical verifications of the proposed model through three sets of numerical examples: unit cell tests, three-point beam bending tests, and torsion tests. Experimental results from the literature are used to validate the proposed constitutive model. Conclusions are provided in Section 4.

2  Methodology

In this section, we introduce an analytical framework to determine homogenized viscoelastic material properties for the fibrous composite material based on the so-called reduced order homogenization (ROH) method. Here we assume the fiber phase follows transversely isotropic symmetry and keeps elastic that

(1)

On the other hand, the matrix phase is viscoelastic and described by the standard solid model [50], and the stress response is written as the following form:

(2)

where

(3a)

(3b)

Here is the equilibrium Young’s modulus of the matrix phase, and is the corresponding Poisson’s ratio. is the isotropic relaxation modulus. Finally, the fourth-order tensors and are defined as

(4)

respectively. Here the quantities associated with the fiber and the matrix phase are marked with superscription and , respectively.

Our goal is to obtain an analytical homogeneous relaxation tensor that

(5)

based on given material properties of the fiber and the matrix phase without computational homogenization process, where , are the macroscopic stress and strain tensor, respectively, is homogenized linear elastic stiffness tensor, and denotes the convolution of function and . Here the macroscopic properties are marked with superscription .

2.1 Reduced Order Homogenization (ROH) for Fibrous Composite Material

The reduced-order homogenization (ROH) method is based on two key assumptions: 1) It is possible to distinguish between two length scales associated with macroscopic and microscopic phenomena; 2) The microstructure is sufficiently regular to be considered periodic; 3) The material within the same partition maintains a consistent status throughout, which reduces computational costs at the meso-scale. A complete derivation of the ROH method would be too extensive for this section, so we will present only the essential formulas. For a detailed explanation of the methodology, please refer to reference [44]. The fibrous composite material consists of the fiber and matrix phases. We introduce eigenstrains defined as [44]

(6)

where is the elastic compliance tensor. The ROH aims to solve the following system of nonlinear equations [44]:

(7a)

(7b)

where and are the elastic strain influence functions, , , and are the eigenstrain influence functions, and is the macroscopic strain tensor.

Since the fiber phase keeps elastic, we can obtain directly. The eigenstrains of the matrix phase are given as

(8)

by the standard solid model defined in Eq. (2), with consideration of material isotropy Eqs. (3a) and (3b), and define . Here we define

(9)

By linear elastic stiffness tensor of the fiber phase and the matrix phase given in Eqs. (1) and (9), respectively, we can first obtain the homogenized elastic stiffness tensor that

(10)

where and are the volume fraction for the fiber and the matrix phase, respectively. The macro-scopic averaged stress then is given by volumetric averaging of phase stresses that

(11)

(12)

Usually, the fibrous composite material is assumed to satisfy the transversely isotropic symmetry so that the linear elastic stiffness tensor can be written with Hill’s constants , , , , and [51], with the fibers aligned along the longitudinal axis:

(13)

The fiber phase also is transversely isotropic, where its Hill’s constants are written as , , , , and . For fibrous composite material, the following universal connections are satisfied [51]:

(14)

where and are the Lamé constants of the matrix phase.

2.2 Analytical Influence Functions for Fibrous Composite Material

The elastic strain and eigenstrain influence functions are usually evaluated by solving a number of finite element problems over the given fibrous unit cell [44]. In this manuscript, we aim to provide an analytical method to evaluate those functions with given linear homogenized stiffness tensor , which can be estimated by Mori-Tanaka or self-consistent method [51].

First of all, the elastic strain influence functions satisfy the following constraint that [44]

(15)

One can obtain the elastic strain influence functions by Eqs. (10) and (15) [44]:

(16a)

(16b)

In other words, for a two-phase unit cell, as long as is given, the elastic strain influence functions can be obtained directly.

Next, we continue to evaluate the eigenstrain influence functions. Define the following supportive tensors:

(17)

and

(18)

(19)

(20a)

(20b)

However, and are not used since .

Due to the symmetry of fibrous unit cell, one can use only non-zero parameters to define one influence tensor. For the linear strain influence tensors, we have ()

(21)

and for the eigenstrain influence tensors, we also have ()

(22)

From Eqs. (21) and (22), we can quickly obtain the following results:

(23)

which means the axial strains of the matrix and the fiber phases are the same and equals to the macroscopic axial strain .

2.3 Viscoelastic Model for the Fibrous Composite Material

In this section, we propose a homogenized viscoelastic model with the analytical elastic strain and eigenstrain influence functions. Substituting Eqs. (8) into (7b) with yields

(24)

where is not considered due to Eq. (23). In the rest of this section, we derive system of ordinary differential equations (ODEs) for with . First, taking the derivative of Eq. (24) with respect to time yields

(25)

Thus we obtain

(26)

Next, substituting Eqs. (26) into (24) yields

(27)

By solving the system of ordinary differential equations in Eq. (27), we obtain the matrix phase strain , where . The detailed derivation is provided in Appendix A. The solutions for the normal strains and can be expressed as

(28a)

(28b)

The solutions for the shear strains

(29a)

(29b)

(29c)

respectively. With

(30)

here are characteristic relaxation times for the fibrous composite materials.

So far, we are able to find the matrix phase strain by the macroscopic strain and the corresponding strain rate . In order to obtain an analytical result for macroscopic stress defined in Eq. (11), we continue to derive the eigenstrain of the matrix phase. For , we can directly obtain

(31)

by considering Eq. (23). For the rest components, expand Eq. (7b) into

(32a)

(32b)

(32c)

(32d)

Finally, one can introduce a fourth-order tensor to represent the eigenstrain as the following:

(33)

First, from Eq. (31), we can obtain the components corresponding to that

(34)

From Eqs. (28a) and (28b), we obtain

(35a)

(35b)

(35c)

(35d)

In addition, from Eq. (29b) and (29c), we obtain

(35e)

and all other components of are zero. In summary, the components of the eigenstrain are written as the following:

(36)

Substituting Eqs. (33) into (11) yields

(37)

2.4 Model Consistency in an Extreme Case

In this section, we exam the homogenized viscoelastic properties of the fibrous composite material by letting and . Under this situation, the homogenized viscoelastic properties should approach the viscoelastic response of pure matrix phase as well.

By setting , one obtains through Eq. (10) and . In addition, we have by Eq. (12). The value of does not have any meaning. Similarly, by Eq. (18), we obtain and thus leads to by Eq. (20a). This result guarantees that , by Eq. (30).

Considering the aforementioned conditions, we can obtain from Eqs. (23), (28a) and (29a), by applying , , . Finally, one can obtain and

(38)

which traces back to the pure matrix case.

2.5 Influence of Component Parameters on Homogenization Relaxation Times

In this section, we analytically calculate the homogenization relaxation times using known component parameters, investigating how fiber and matrix properties influence the overall viscoelastic response. It is important to note that relaxation time is closely related to material viscosity. A smaller viscosity results in a shorter relaxation time. When viscosity () approaches zero, the material behaves like an inviscid fluid, whereas when it approaches infinity, the material behaves like an elastic solid. We observe that changes in component parameters lead to variations in the homogenization relaxation times, with certain parameters exerting more significant influence compared to others.

We first investigate the influence of fiber parameters on homogenized relaxation times. Parameters are chosen as detailed in Table 1, with one parameter varied within specified ranges. Fig. 1a illustrates the impact of fiber volume fraction on viscoelastic behavior: as the fiber fraction increases, the relaxation times also increase, indicating that, in our research, fibrous composites with higher fiber content tend to exhibit more solid-like characteristics in the homogenized state. It is noteworthy that relaxation time associated with the fiber direction is always equal to the matrix relaxation time, as indicated by Eq. (36), implying that the viscoelastic behavior in this direction is solely influenced by matrix components, while viscoelastic behavior in other directions is influenced by both fiber and matrix components. Fig. 1b demonstrates how homogenized relaxation time varies with changes in , revealing that has a limited impact on viscosity behavior. A slight decrease in homogenized relaxation time is observed with increasing .

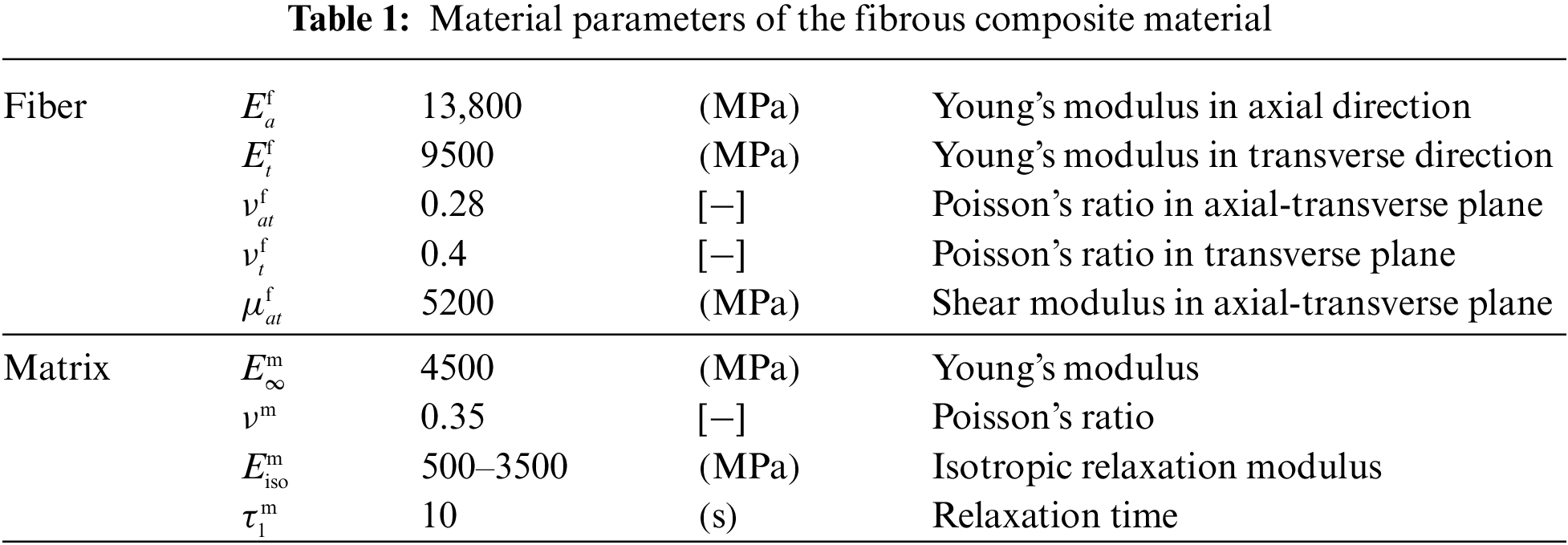
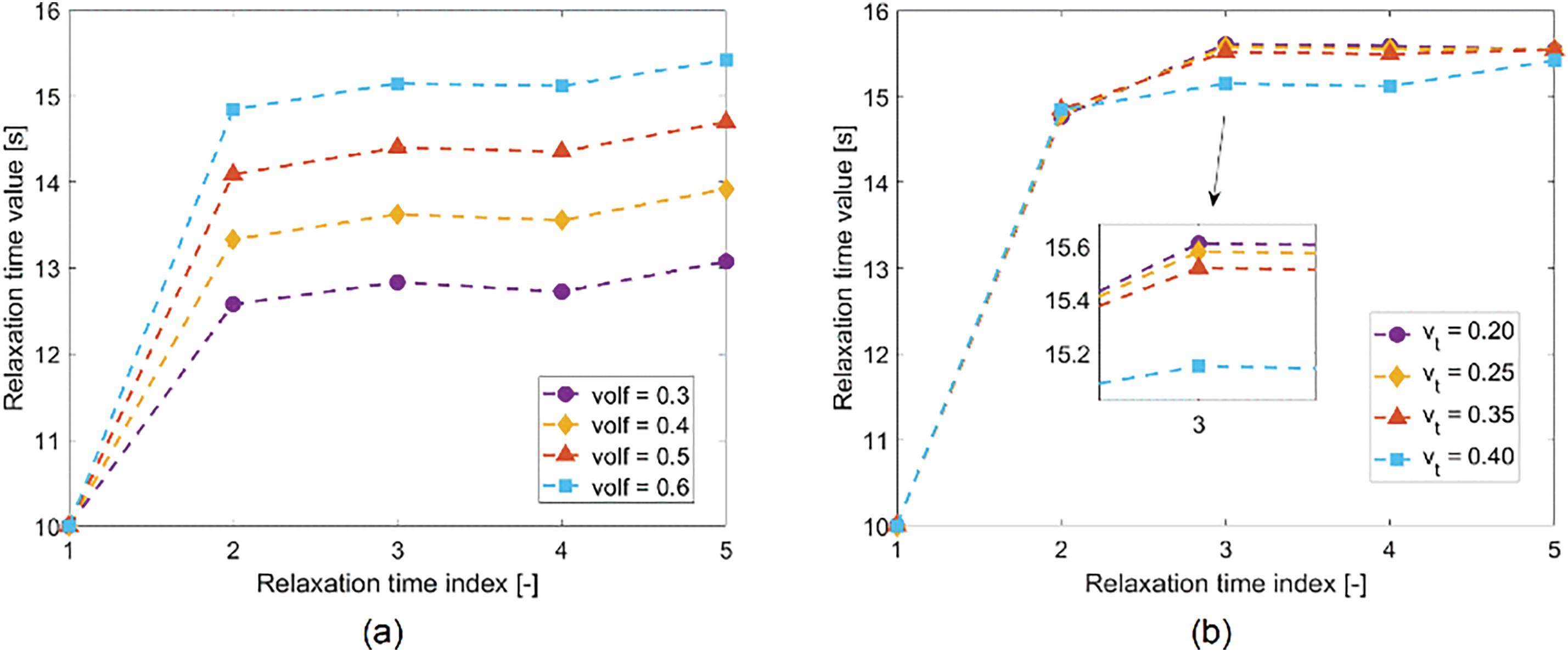
Figure 1: Influence of fiber parameters on homogenized relaxation times: (a) Fiber volume; (b) Poisson ratio in the transverse plane

Next, we explore the influence of matrix parameters on homogenized relaxation times. As shown in Fig. 2a, an increase in leads to higher homogenized relaxation times due to the corresponding increase in viscosity. Similarly, Fig. 2b demonstrates that higher results in increased homogenization relaxation times, paralleling the trend observed in Fig. 1a. Fig. 2c indicates that has minimal impact on viscosity behavior, albeit showing a slight increase with higher .

Figure 2: Influence of matrix parameters on homogenized relaxation times: (a) Relaxation modulus ; (b) Elastic modulus ; (c) Poisson ratio

2.6 Numerical Algorithm

In this section, we briefly introduce the numerical algorithm for the homogenized viscoelastic model of fibrous composite material. In finite element analysis, we update material stress as well as consistent tangent modulus over one increment . The stress at , namely, is given as

(39)

again is the homogeneous relaxation tensor. The second term in the right-hand-side of Eq. (39) is given by the classic integration form:

(40)

The numerical integration scheme is the same as the classic viscoelastic stress update procedure. For example:

(41a)

(41b)

With , and the incremental strain at component.

From the convolution form in Eq. (36), define the following state variables:

(42)

From (41a) and (41b), we can obtain

(43)

and

(44)

Similar equations can be derived for . Thus, Eq. (36) can be written with the aforementioned state variables that

(45)

In addition, one can derive so that the consistent tangent material modulus is given as

(46)

Specifically,

(47)

3  Numerical Examples and Validation

In this section, we propose several groups of numerical examples to verify and validate the proposed analytical homogenized viscoelastic model for fibrous composite materials. The numerical examples and validation are organized as follows: In Section 3.1, unit cell tests under uniaxial tension and pure shear conditions are performed to demonstrate consistency between FEM and the proposed homogenized model under a uniform strain field. In Sections 3.2 and 3.3, we introduce pure bending beam experiments and torsion experiments to further investigate the ability of the proposed homogenized method. In Section 3.4, theoretical predictions are compared with experimental results from the literature to validate prediction accuracy. All simulations are conducted using the commercial FEM software ABAQUS/Standard 2022 with a user material subroutine (UMAT).

3.1 Unit Cell Tests

We first verify the accuracy of the homogenized viscoelastic model using a uniform strain field problem. We explicitly construct a unit cell of the fibrous composite material for the direct numerical simulation (DNS), where the fiber is transversely isotropic elastic and the matrix follows the standard solid model, as depicted in Fig. 3. The size of the unit cell is set as , , and . By applying periodic boundary conditions and a macroscopic strain history, we obtain the corresponding averaged stress history. For comparison, we construct a one-element model associated with the homogenized viscoelastic constitutive model and apply the same strain history. Table 1 lists the parameters for both the fiber and the matrix phases.

Figure 3: Unit cell model with size of , ,

Various numerical tests are proposed with different fiber volume fractions: and different relaxation moduli: . For each unit cell problem, we perform three uniaxial tension tests in the -, -, and -direction, and three pure shear tests in the -, -, and - planes, where refers to the axial direction of the fiber. In order to capture the viscoelastic response, we apply a loading-holding-unloading curve for the prescribed macroscopic strain, as depicted in Fig. 4. In the unit cell problem, we use the loading rate defined in Fig. 4a. For pure bending and torsion tests, the loading rate is defined as in Fig. 4b for a clearer observation of the viscoelastic response.

Figure 4: Loading rates: (a) Unit cell test; (b) Pure bending and torsion tests

A group of DNS simulations is depicted in Fig. 5, while the corresponding group of one-element simulation using the proposed homogenized viscoelastic constitutive model is depicted in Fig. 6. Clearly, the DNS results provide more detail but at a higher computational cost. To avoid redundancy, not all simulation results will be displayed. Figs. 7 and 8 show comparison of strain-stress responses between the DNS and the homogenized model (HM for short) for and . Note that the x-direction of the material coordinate system coincides with the z-direction of the overall coordinate system. Figs. 7c and 8c show that the composite response is fiber-dominated in this direction, while in other directions, the response is matrix-dominated. A more significant viscoelastic response is observed as increases. All the results show good agreement between the homogenized model and the DNS simulations.

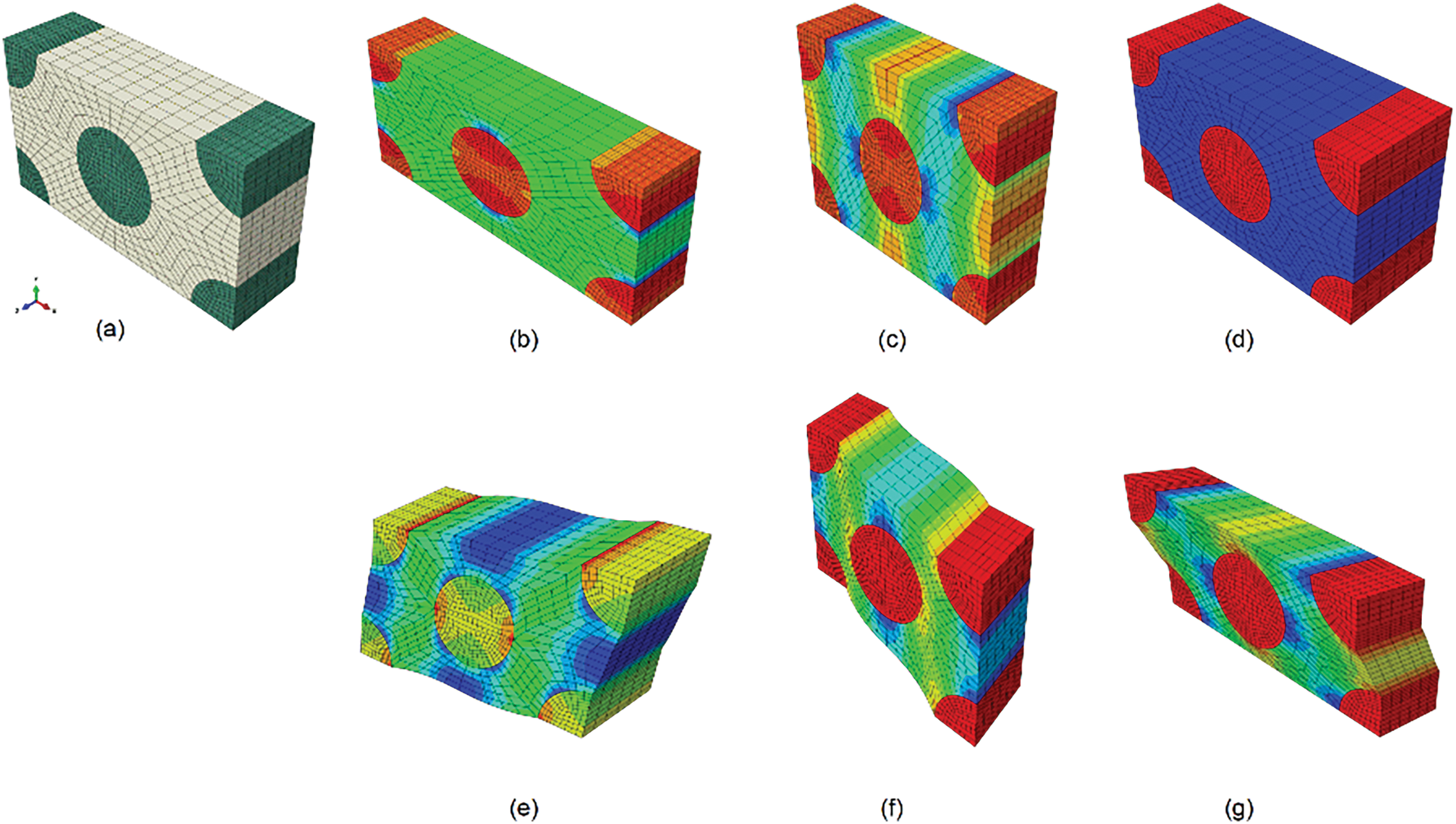
Figure 5: Demonstrations of DNS model and six loading cases: (a) Honeycomb unit cell; (b) uniaxial tension test in x-direction; (c) uniaxial tension test in y-direction; (d) uniaxial tension test in z-direction; (e) pure shear test in xy plane; (f) pure shear test in xz plane; (g) pure shear test in yz plane

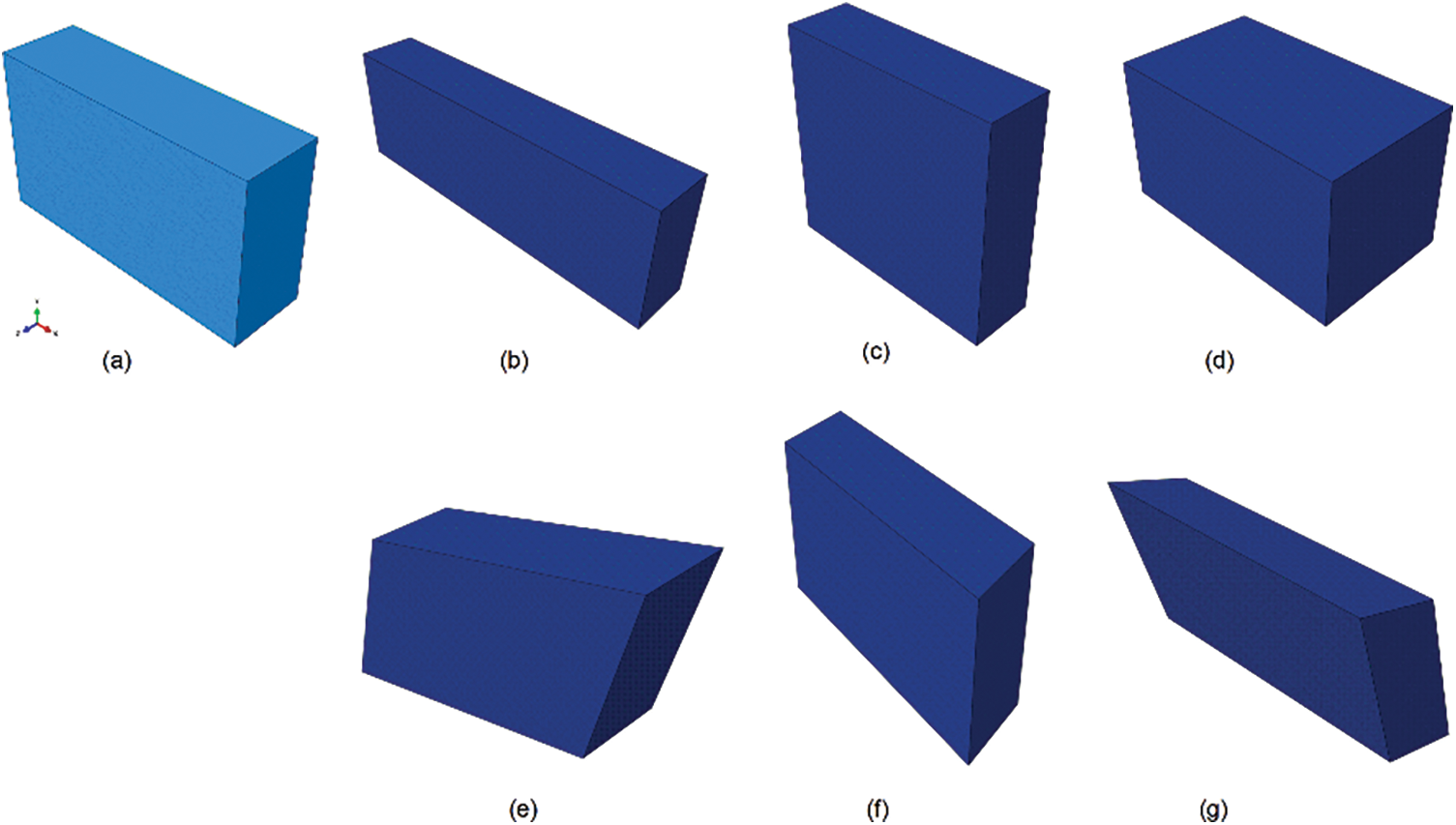
Figure 6: Demonstrations of homogenized model and six loading cases: (a) One-element model; (b) uniaxial tension test in x-direction; (c) uniaxial tension test in y-direction; (d) uniaxial tension test in z-direction; (e) pure shear test in xy plane; (f) pure shear test in xz plane; (g) pure shear test in yz plane

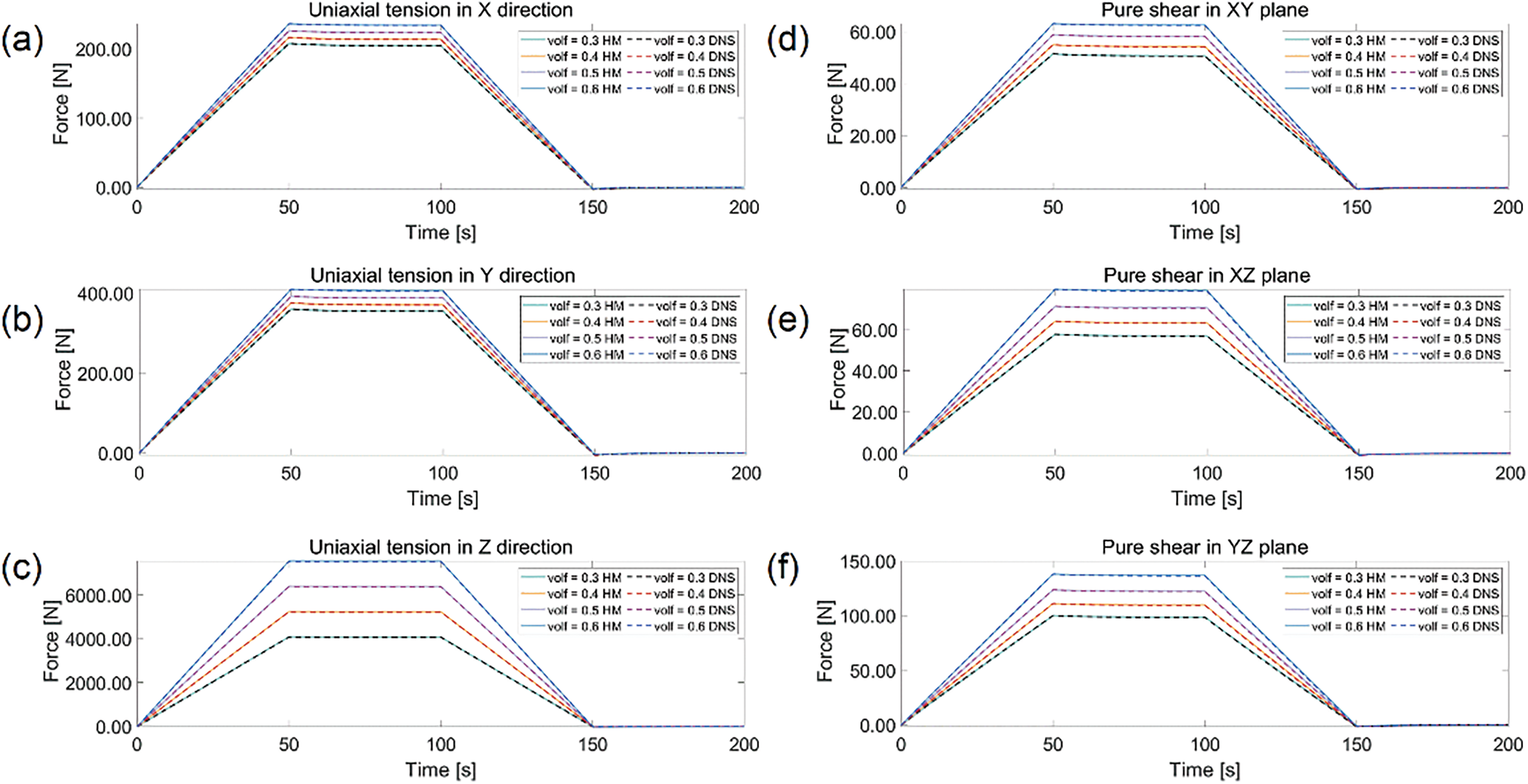
Figure 7: Relaxation curves under different fiber volume ratios with : uniaxial tension test in (a) x-direction; (b) y-direction; (c) z-direction; pure shear test in (d) xy plane; (e) xz plane; (f) yz plane

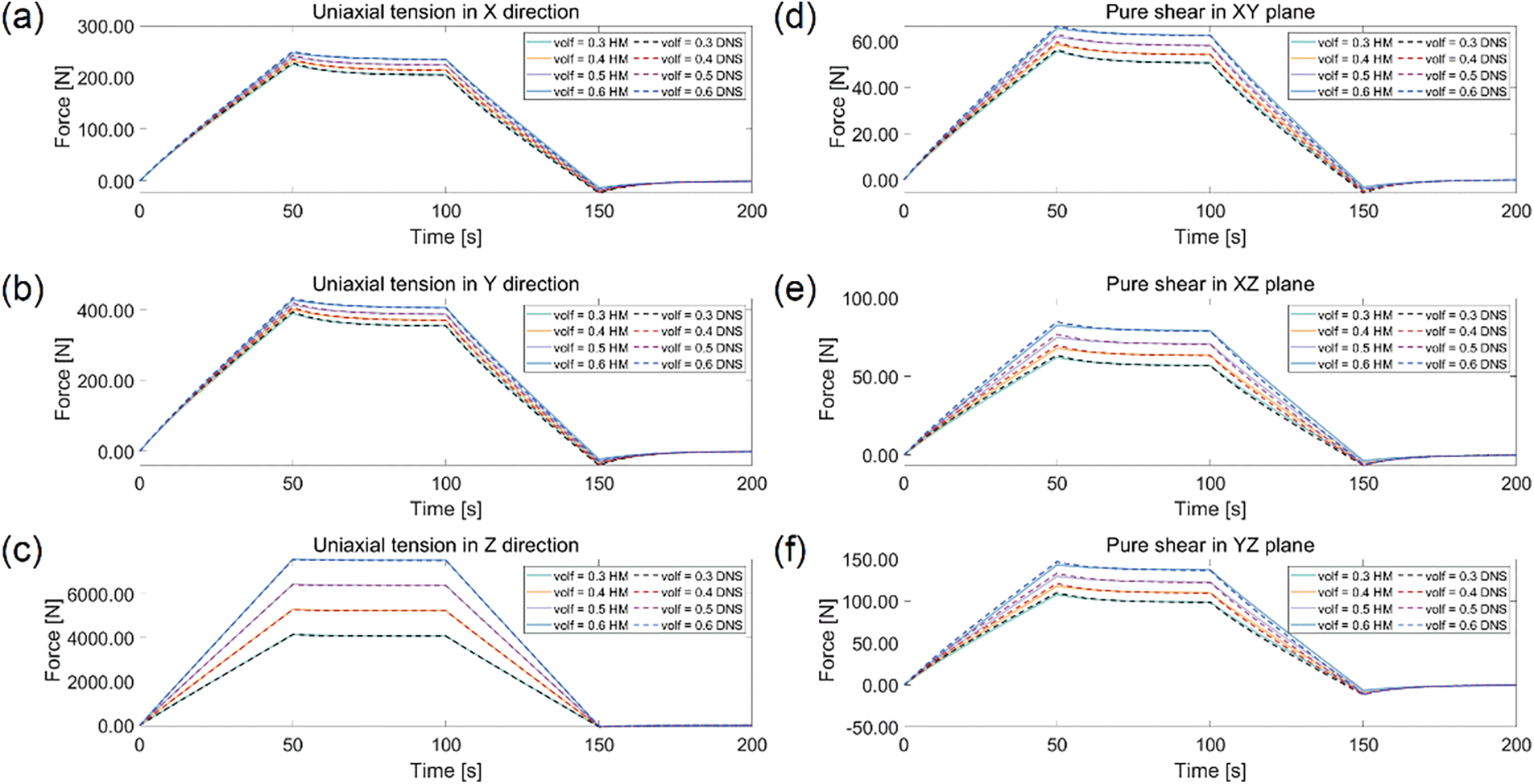
Figure 8: Relaxation curves under different fiber volume ratios with : uniaxial tension test in (a) x-direction; (b) y-direction; (c) z-direction; pure shear test in (d) xy plane; (e) xz plane; (f) yz plane

3.2 Pure Bending Tests

The unit cell tests verify the homogenized viscoelastic model under uniform strain fields. To extend this validation to non-uniform strain fields, we propose a series of pure bending tests with geometric setups and boundary conditions outlined in Fig. 9. The size of beam is . The applied moment follows the loading rate defined in Fig. 4b, with a maximum value of . Both direct numerical simulation (DNS) and homogenized models, as illustrated in Fig. 10, are employed to compare numerical efficiency and accuracy. The results are presented in Fig. 11. It is observed that the stress concentration effect cannot be effectively captured due to the piecewise constant eigenstrain assumption. This approach sacrifices some detail for the sake of efficiency.

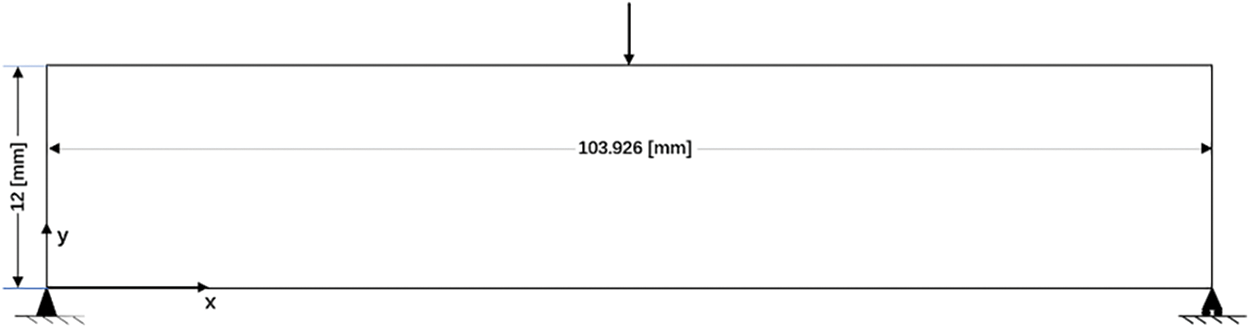
Figure 9: Geometric setup of pure bending beam and boundary conditions

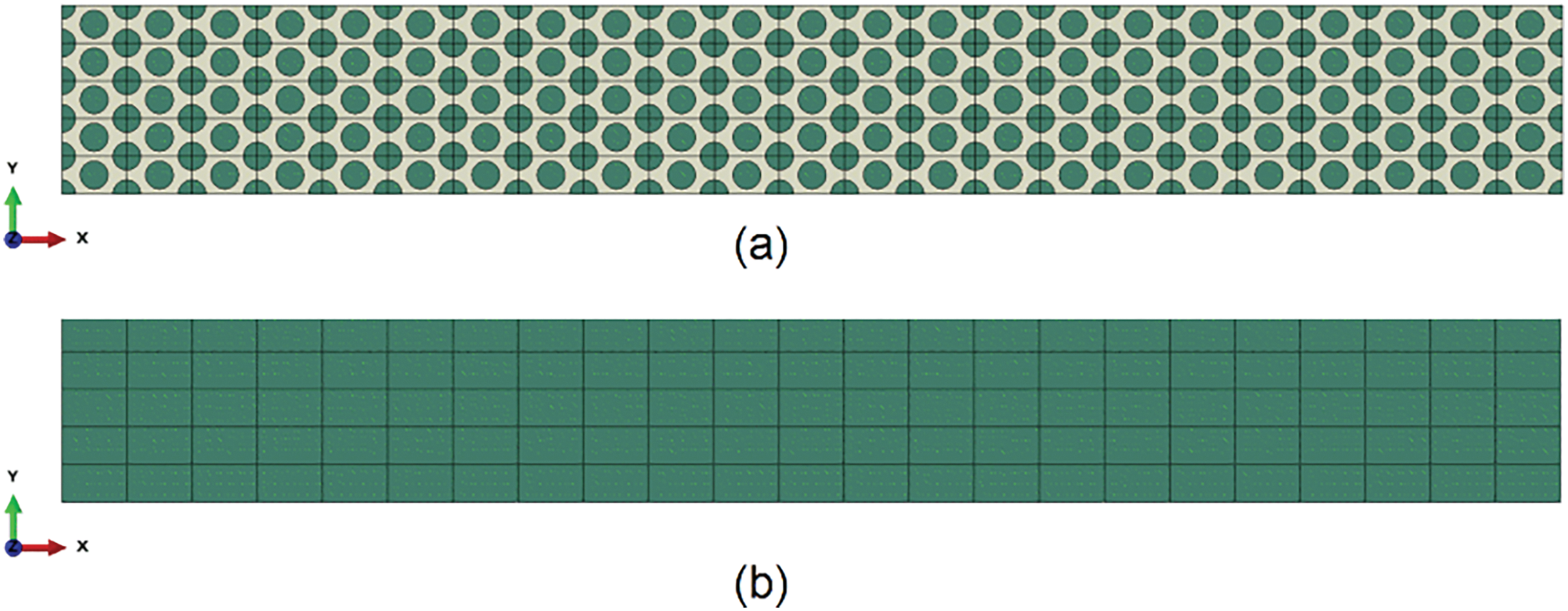
Figure 10: Pure bending beam models: (a) DNS; (b) homogenized model

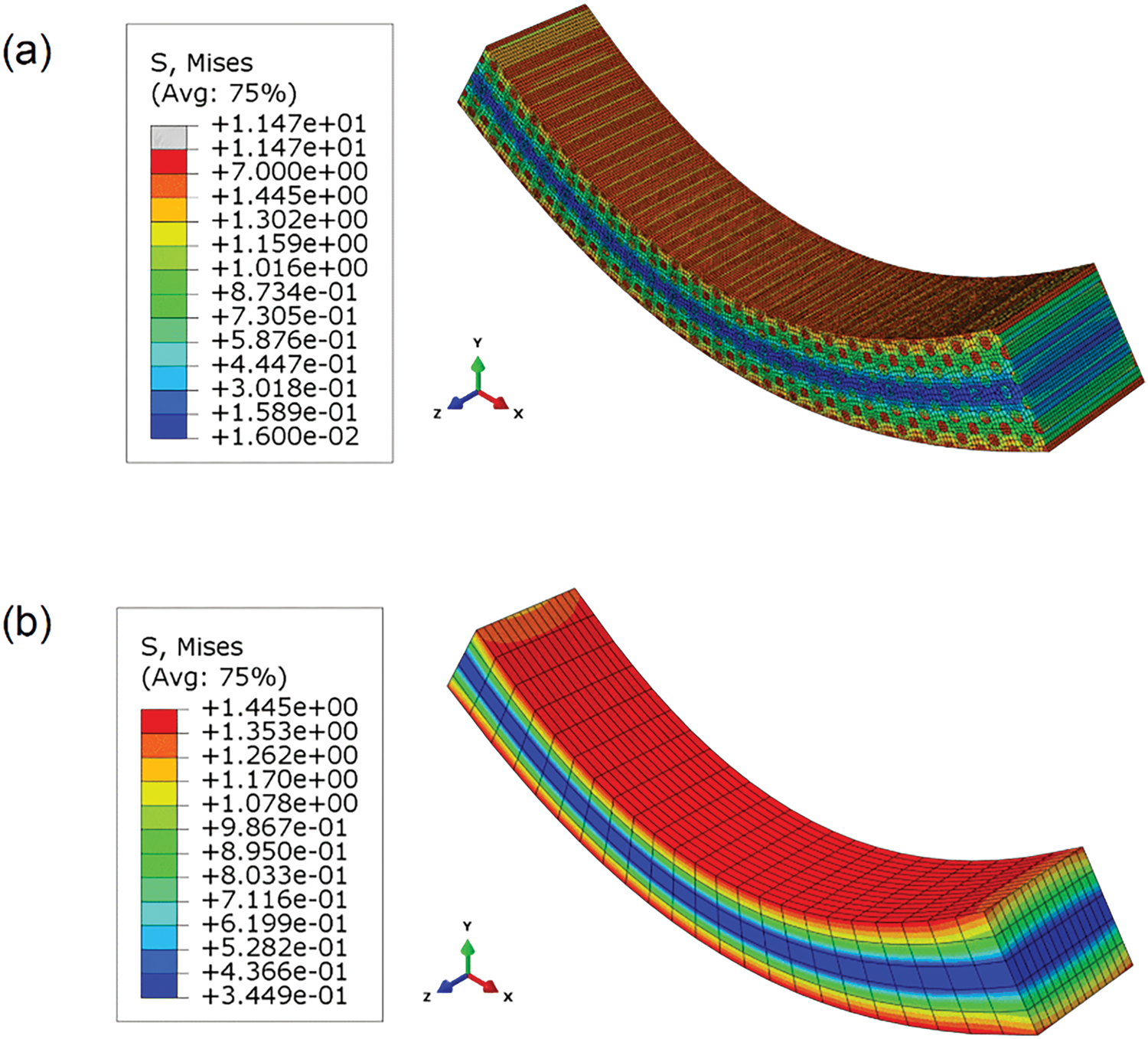
Figure 11: Pure bending beam simulation result demonstrations: (a) DNS; (b) homogenized model

We tested different fiber volume fractions, , with the matrix relaxation moduli set to . The results of the homogenized model and the reference results for comparison are shown in Fig. 12. We used the displacement at to estimate the relative displacement error between the DNS and homogenized models, as depicted in Fig. 13. The proposed method demonstrates good consistency with the DNS method, with relative errors below . It is also noteworthy that the DNS method takes approximately , while the homogenized model requires only . The simulation is significantly faster than DNS, and the overall response remains highly accurate.

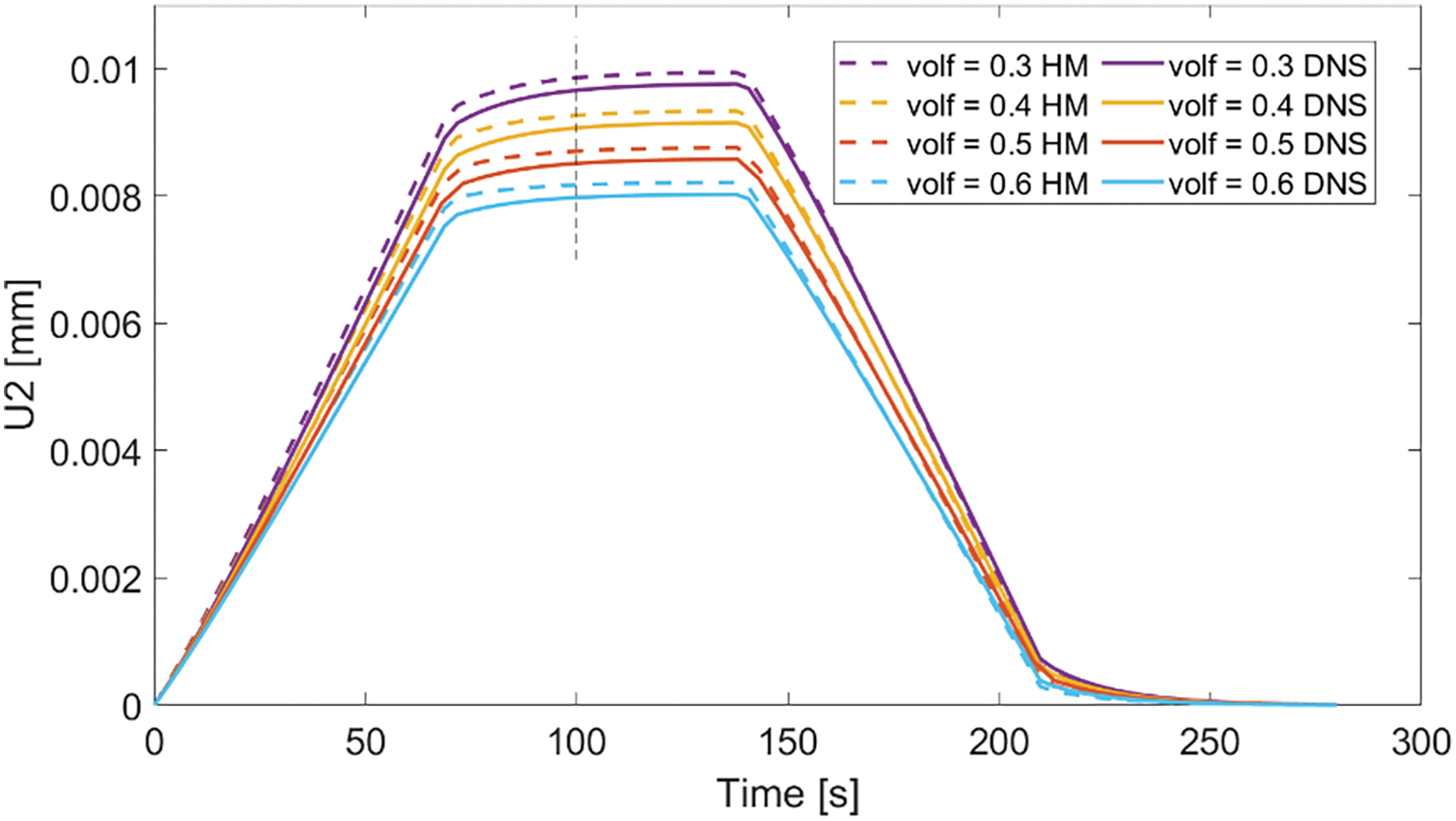
Figure 12: Pure bending beam experiment under different fiber volume fractions: DNS and homogenized model result comparison with

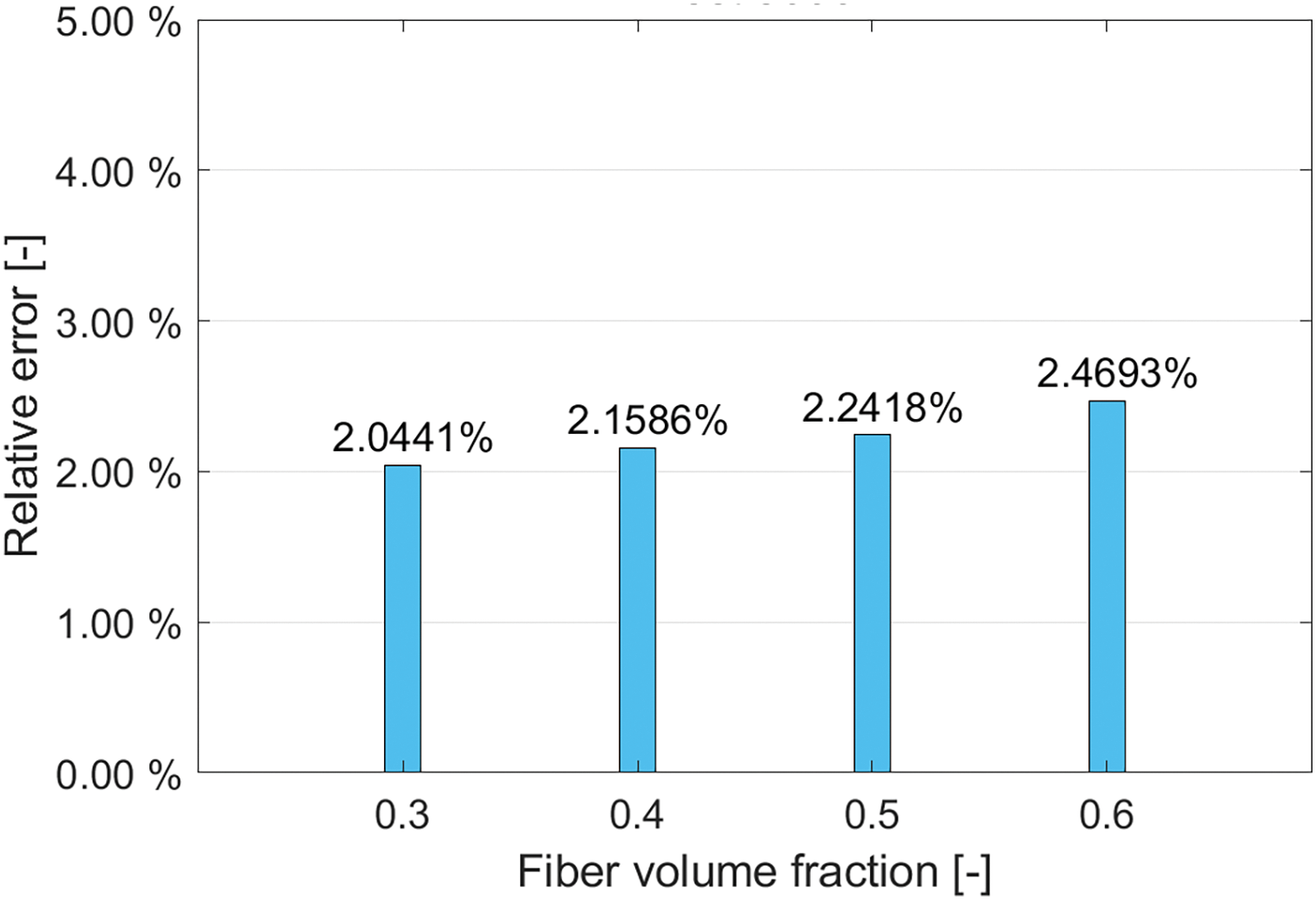
Figure 13: Pure bending beam tests under different fiber volume fractions: displacement relative error between DNS and homogenized model result with

3.3 Torsion Tests

In this section, the beam used for the pure bending tests is employed to conduct torsion tests. We select viscoelastic parameters as and investigate creep behavior under four sets of fiber volume fractions: . The left boundary of the beam is fixed, and a moment of is applied to the right boundary with the loading rate shown in Fig. 4b. The simulation results for both the DNS and homogenized models are demonstrated in Fig. 14. The comparison of relaxation curves is depicted in Fig. 15. It is evident from the analysis that the discrepancy between the two curves is minimal, suggesting that the proposed model effectively captures torsional deformation.

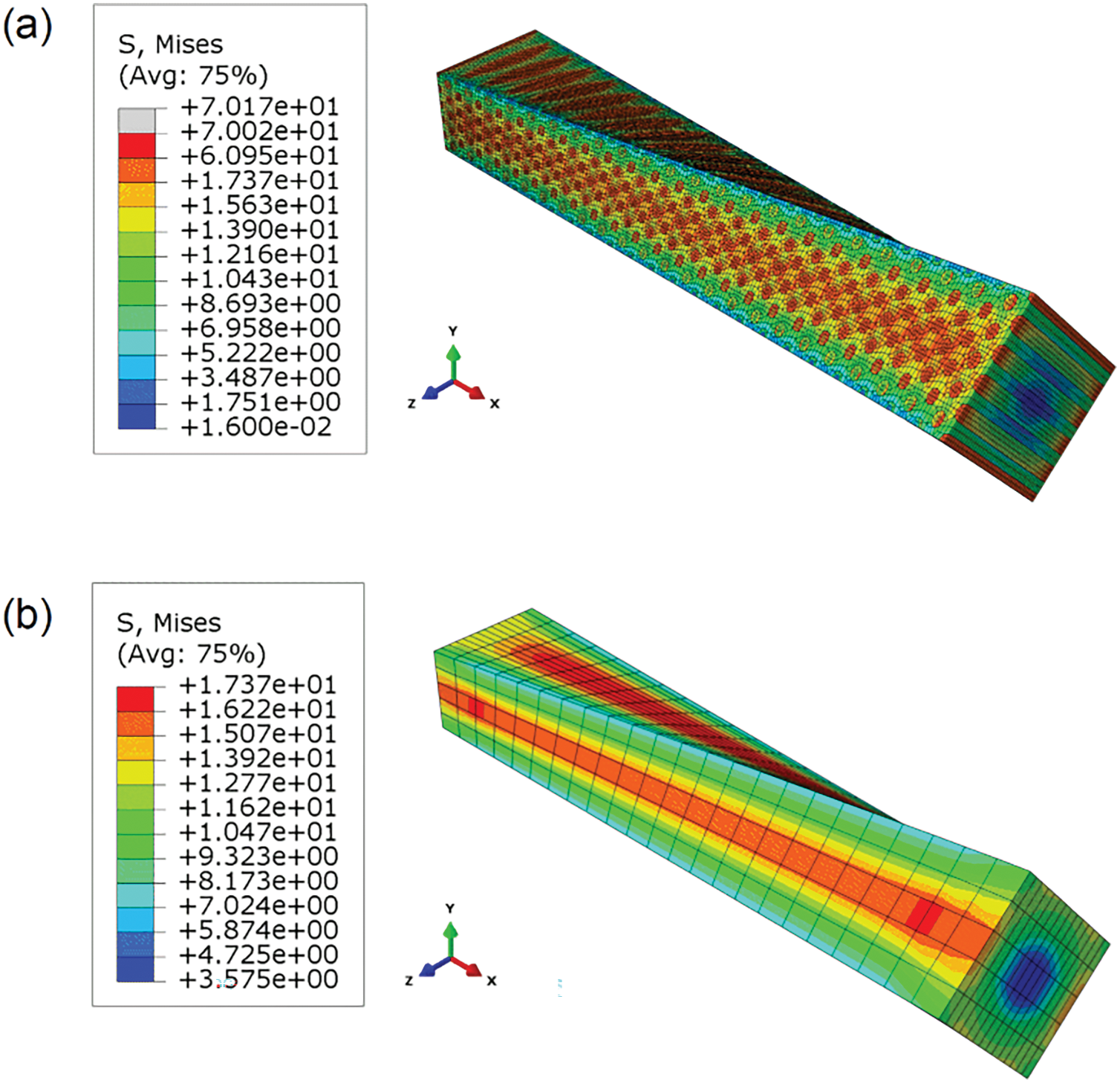
Figure 14: Beam torsion simulation result demonstrations: (a) DNS; (b) homogenized model

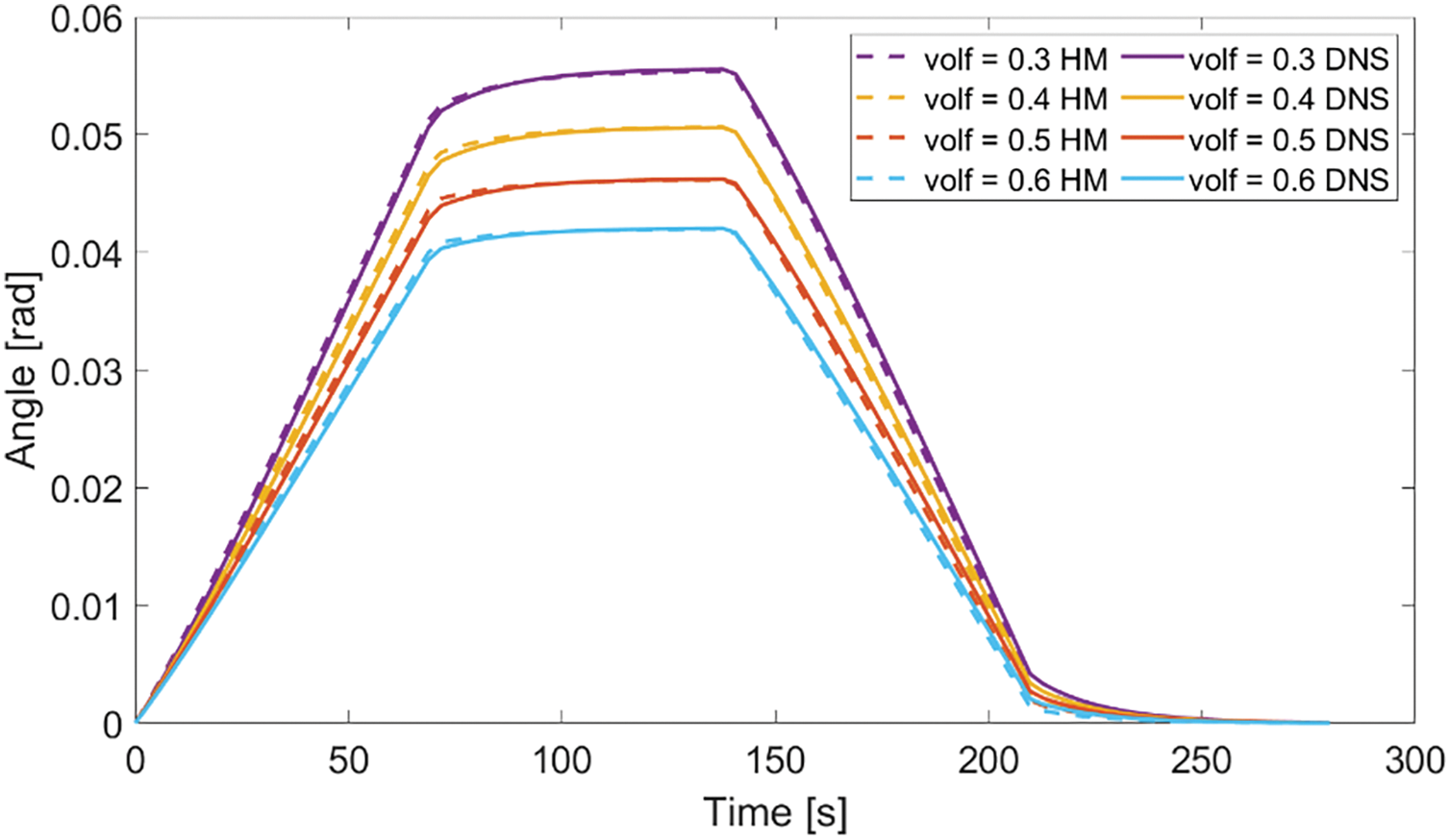
Figure 15: Beam torsion experiment under different fiber volume fractions, DNS and homogenized model result comparison with

3.4 Experiment Validation

We obtained experimental data from a paper published by Thiruppukuzhi et al. [52] and referenced another paper by Chen et al. [53]. In the first paper, Thiruppukuzhi et al. conducted experiments using S2-glass/8553-40 epoxy fiber-reinforced composite with a fiber volume fraction of . They performed a series of off-axial tensile tests at three strain rates: , , , and four off-axial tensile directions: , , , and . The combination of loading strain rate and off-axis tensile direction in the experiment is shown in Table 2, where markers represent the experiments conducted under the corresponding combinations. The setup of off-axial tensile tests is illustrated in Fig. 16. The specimen dimensions are as described in the original experiment, and we set . We simulate the actual experimental boundary conditions by clamping the two ends of the specimen with fixtures, resulting in an over-constrained setup. Symmetric boundary conditions are applied in the z-direction to represent the specimen’s real-life thickness.

Figure 16: Setup of off-axial tensile tests

The elastic material parameters of both the fiber and matrix are identified inversely using experimental data of composite materials under two sets of conditions: and . The viscoelastic material parameters for the matrix are determined using experimental data with the following test conditions:, , and . Table 3 presents the material parameters of the fiber and matrix obtained by fitting the experimental data. Fig. 17 shows the homogenized model results and experimental data along the directions under a loading strain rate of . The simulation results along the and directions also show good agreement with the experimental data, indicating that the parameters are a good fit. The Von Mises stress contour plots for the homogenized models along the four directions are shown in Fig. 18. Theoretical predictions begin to diverge from experimental results due to significant nonlinearity induced by plasticity or damage at relatively large strains.

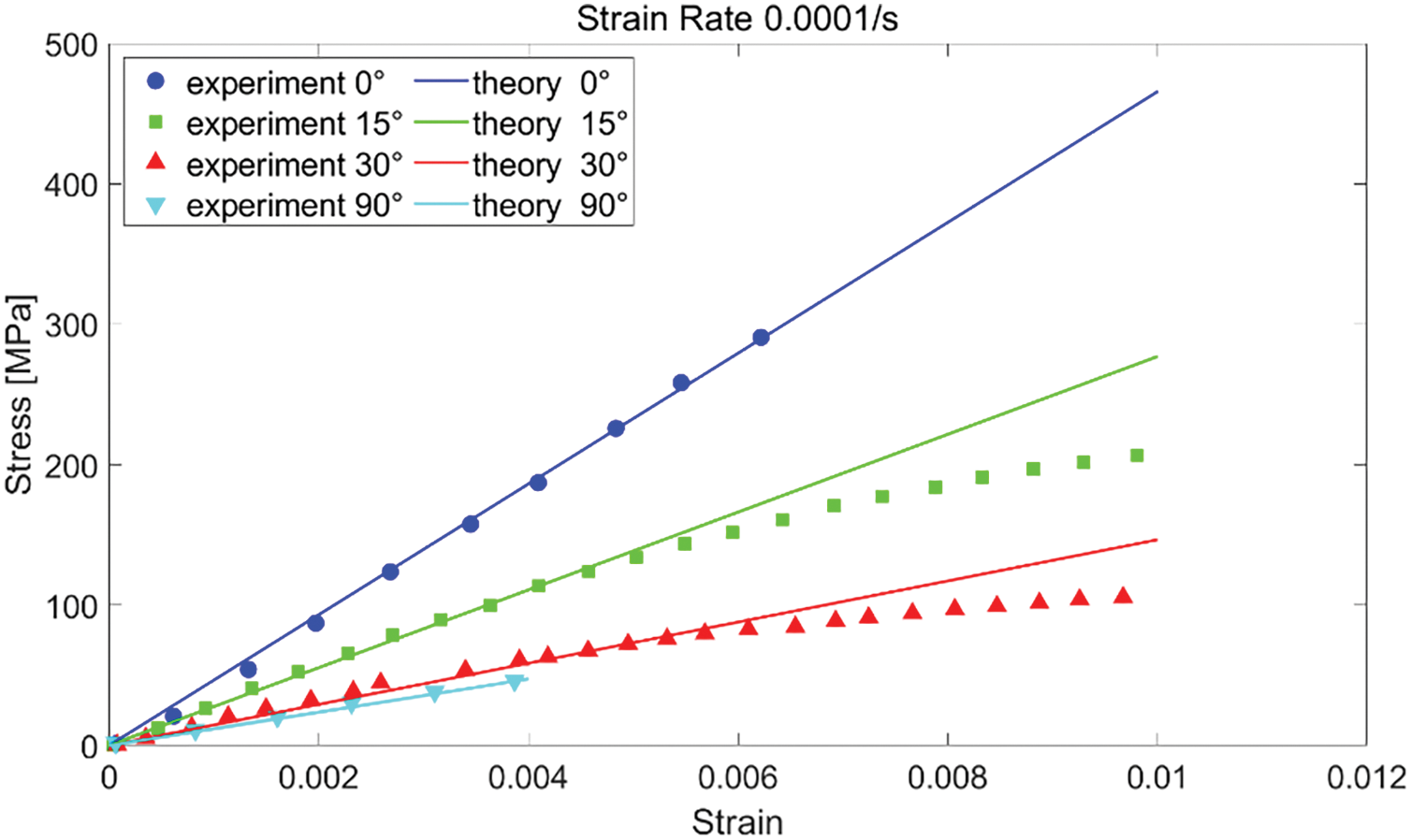
Figure 17: Strain-stress curves obtained from experiment results and homogenized model predictions for four off-axis tensile directions , , , and , loading strain rate

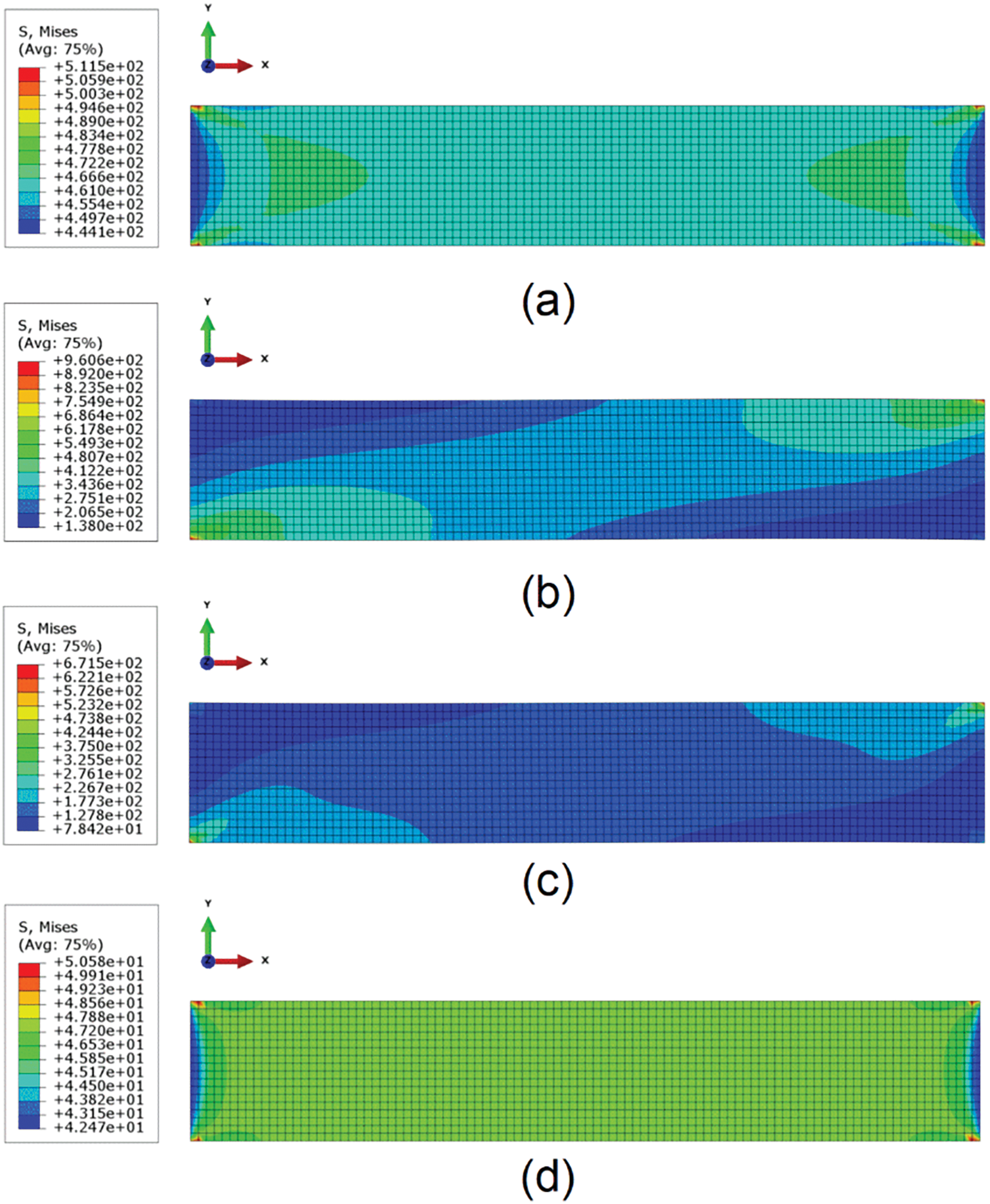
Figure 18: Von Mises stress cloud for homogenized models of four off-axis tensile directions: (a) ; (b) ; (c) ; (d) , loading strain rate

Figs. 19 and 20 present the homogenized model results and experimental data along directions under loading strain rates of and , respectively. The corresponding Von Mises stress contour plots for the homogenized models are shown in Figs. 21 and 22. The experimental data along were used to fit the viscoelastic parameters, while the data along were used to validate the accuracy of the proposed homogenized model. From Figs. 19 and 20, the simulation results along exhibit good consistency with experimental data, indicating that our homogenized model can provide reasonable predictions for fibrous composite materials with viscoelastic effects.

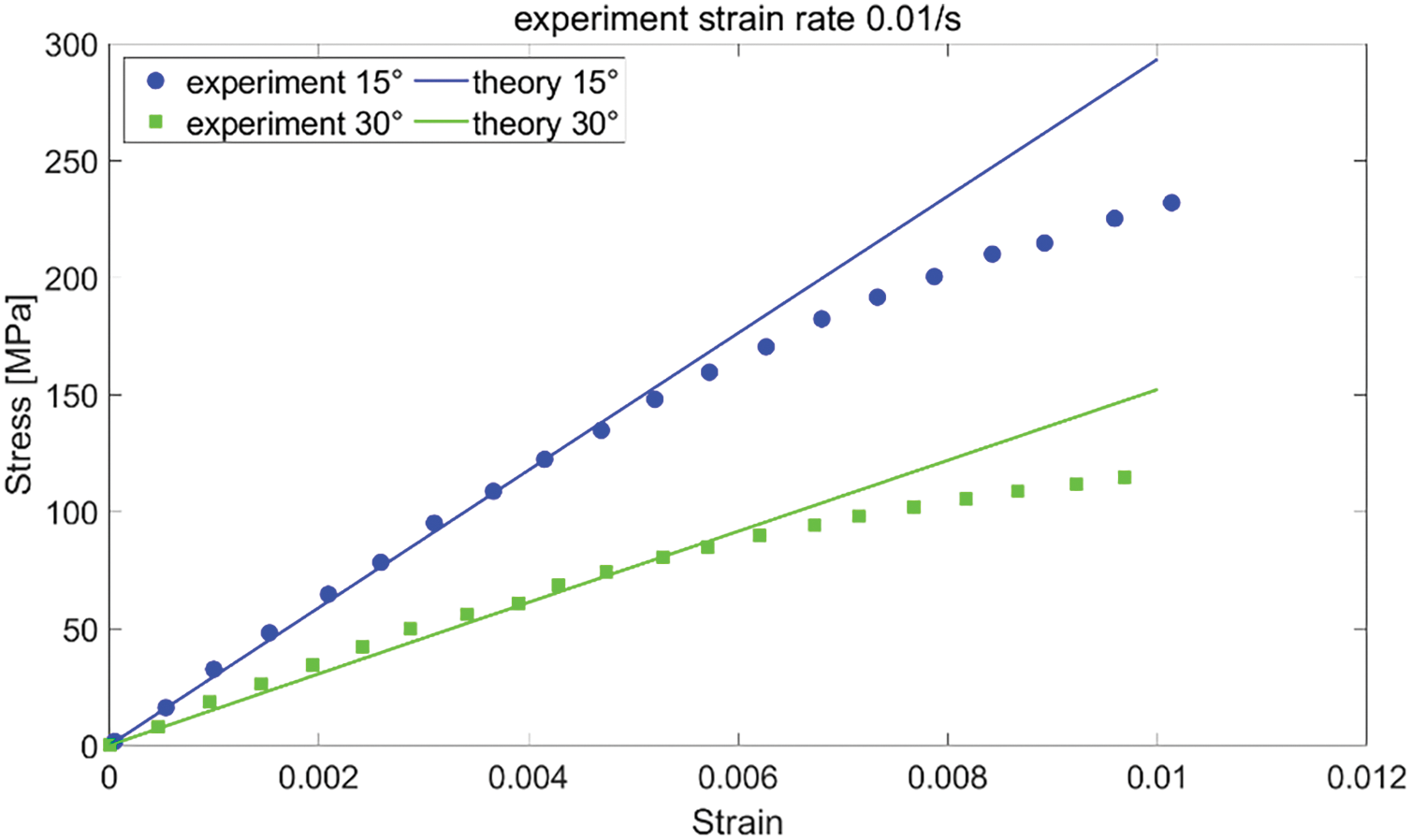
Figure 19: Strain-stress curves obtained from experiment results and homogenized model predictions for two off-axis tensile directions , , loading strain rate

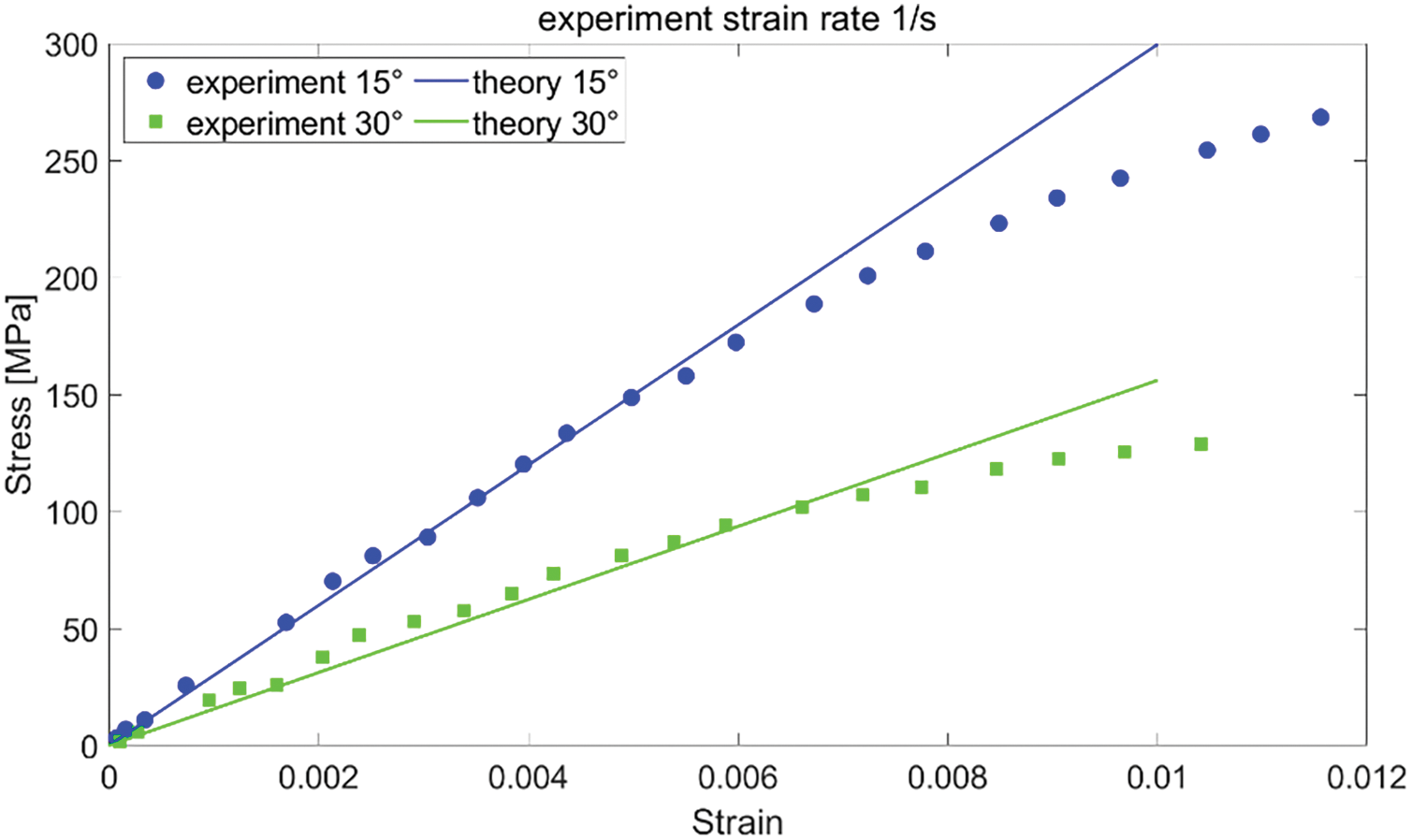
Figure 20: Strain-stress curves obtained from experiment results and homogenized model predictions for two off-axis tensile directions , , loading strain rate

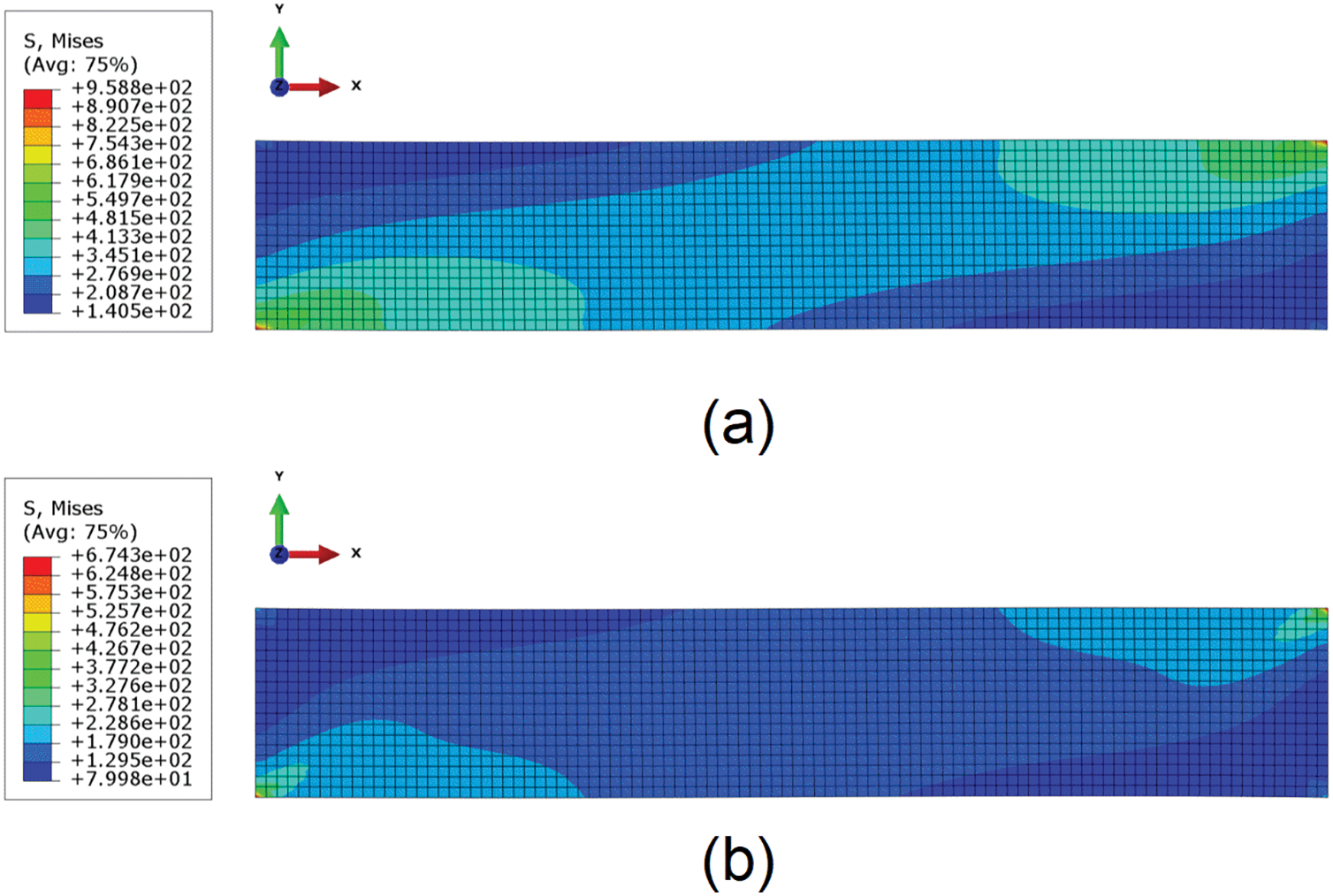
Figure 21: Von Mises stress contour plot for homogenized models of two off-axis tensile directions: (a) ; (b) , loading strain rate

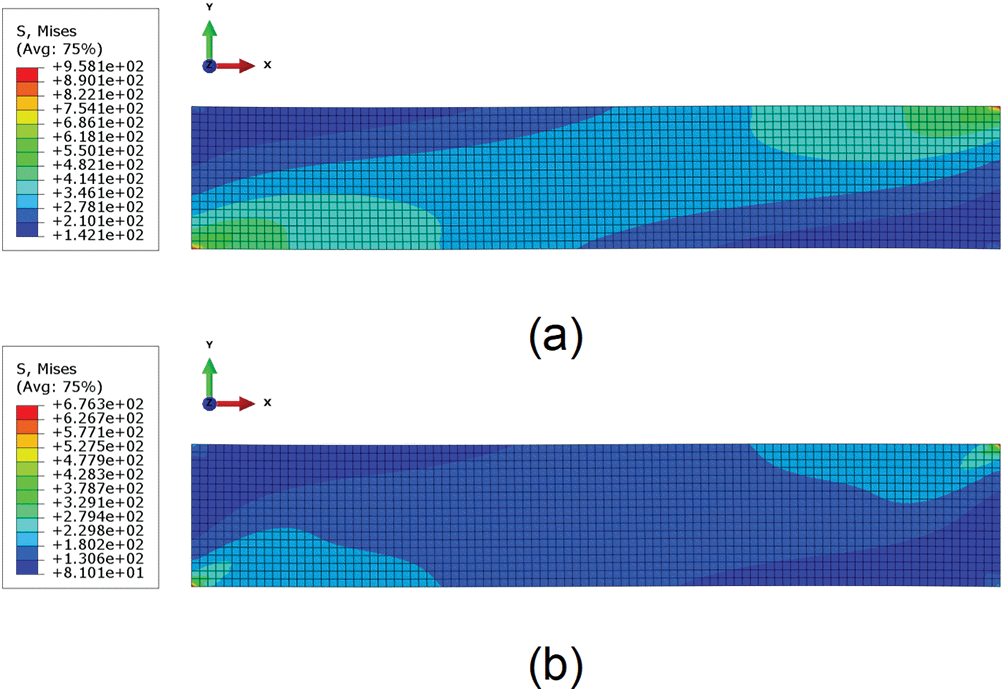
Figure 22: Von Mises stress contour plot for homogenized models of two off-axis tensile directions: (a) ; (b) , loading strain rate

4  Conclusion

In this manuscript, we propose an analytical homogenized viscoelastic model for fibrous composite materials using the reduced-order homogenization (ROH) method. Compared to numerical homogenization methods, our analytical model significantly reduces simulation costs while providing accurate predictions of the overall mechanical behavior. However, some deviations in local stress are observed, attributable to the one-partition-per-phase assumption. We model the fiber phase as transversely isotropic elastic, while the matrix phase follows a standard solid model. This approach allows for the analytical determination of effective moduli and relaxation times in fibrous composites. As the fiber volume fraction approaches zero, our homogenized viscoelastic model simplifies to a pure viscoelastic model. We verify our model through numerical unit cell tests, pure bending beam tests, and torsion tests, demonstrating its accuracy and computational efficiency compared to direct numerical simulations. Experimental validations further confirm the reliability of our approach.

Acknowledgement: The authors would like to acknowledge the support of the National Key R&D Program of China and the National Natural Science Foundation of China. The research is also supported by Peking University for this publication.

Funding Statement: Financial support by the National Key R&D Program of China (Grant No. 2023YFA1008901) and the National Natural Science Foundation of China (Grant Nos. 11988102, 12172009) is gratefully acknowledged. The research is also supported by “The Fundamental Research Funds for the Central Universities, Peking University”.

Author Contributions: The authors confirm contribution to the paper as follows: Huilin Jia contributed to the formula derivation, and simulation. Shanqiao Huang assisted in offering methodology and revising the manuscript. Zifeng Yuan contributed to the initial idea, the overall structure and final editing of the manuscript. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on request from the authors.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Z. Guo et al., “3D printing of curvilinear fiber reinforced variable stiffness composite structures: A review,” Compos. Part B Eng., vol. 272, no. 1, 2024, Art. no. 112039. doi: 10.1016/j.compositesb.2024.112039. [Google Scholar] [CrossRef]

2. P. Aduwenye, B. W. Chong, P. Gujar, and X. Shi, “Mechanical roperties and durability of carbon fiber reinforced cementitious composites: A review,” Constr. Build. Mater., vol. 452, 2024, Art. no. 138822. doi: 10.1016/j.conbuildmat.2024.138822. [Google Scholar] [CrossRef]

3. Z. Li, B. Wang, P. Hao, K. Du, Z. Mao and T. Li, “Multi-scale numerical calculations for the interphase mechanical properties of carbon fiber reinforced thermoplastic composites,” Compos. Sci. Technol., vol. 260, 2025, Art. no. 110982. doi: 10.1016/j.compscitech.2024.110982. [Google Scholar] [CrossRef]

4. M. Mohammed et al., “A review on the advancement of renewable natural fiber hybrid composites: Prospects, challenges, and industrial applications,” J. Renew. Mater., vol. 12, pp. 1237–1290, 2024. doi: 10.32604/jrm.2024.051201. [Google Scholar] [CrossRef]

5. H. Awais, Y. Nawab, A. Amjad, A. Anjang, H. M. Akil and M. S. Z. Abidin, “Environmental benign natural fibre reinforced thermoplastic composites: A review,” Compos. Part C Open Access, vol. 4, 2021, Art. no. 100082. doi: 10.1016/j.jcomc.2020.100082. [Google Scholar] [CrossRef]

6. B. Nedjar, “A time dependent model for unidirectional fibre-reinforced composites with viscoelastic matrices,” Int. J. Solids Struct., vol. 48, no. 16–17, pp. 2333–2339, 2011. doi: 10.1016/j.ijsolstr.2011.04.007. [Google Scholar] [CrossRef]

7. U. Hofer, M. Luger, R. Traxl, and R. Lackner, “Closed-form expressions for effective viscoelastic properties of fiber-reinforced composites considering fractional matrix behavior,” Mech. Mater., vol. 127, pp. 14–25, 2018. doi: 10.1016/j.mechmat.2018.08.005. [Google Scholar] [CrossRef]

8. Q. Chen, G. Chatzigeorgiou, and F. Meraghni, “Extended mean-field homogenization of viscoelastic-viscoplastic polymer composites undergoing hybrid progressive degradation induced by interface debonding and matrix ductile damage,” Int. J. Solids Struct., vol. 210–211, pp. 1–17, 2021. doi: 10.1016/j.ijsolstr.2020.11.017. [Google Scholar] [CrossRef]

9. C. A. Suarez-Afanador, N. Lahellec, and M. I. Idiart, “Mean-field descriptions for the viscoelastic response of thermorheologically complex reinforced solids,” Eur. J. Mech. A Solids, vol. 98, 2023, Art. no. 104859. doi: 10.1016/j.euromechsol.2022.104859. [Google Scholar] [CrossRef]

10. P. Lenz and R. Mahnken, “Multiscale simulation of polymer curing of composites combined mean-field homogenisation methods at large strains,” Int. J. Solids Struct., vol. 290, no. 2, 2024, Art. no. 112642. doi: 10.1016/j.ijsolstr.2023.112642. [Google Scholar] [CrossRef]

11. Q. Li, W. Chen, S. Liu, and J. Wang, “A novel implementation of asymptotic homogenization for viscoelastic composites with periodic microstructures,” Compos. Struct., vol. 208, no. 1–3, pp. 276–286, 2019. doi: 10.1016/j.compstruct.2018.09.056. [Google Scholar] [CrossRef]

12. Y. -M. Yi, S. -H. Park, and S. -K. Youn, “Asymptotic homogenization of viscoelastic composites with periodic microstructures,” Int. J. Solids Struct., vol. 35, no. 17, pp. 2039–2055, 1998. doi: 10.1016/S0020-7683(97)00166-2. [Google Scholar] [CrossRef]

13. I. V. Andrianov, V. V. Danishevs’kyy, and D. Weichert, “Homogenization of viscoelastic-matrix fibrous composites with square-lattice reinforcement,” Arch. Appl. Mech., vol. 81, no. 12, pp. 1903–1913, 2011. doi: 10.1007/s00419-011-0526-z. [Google Scholar] [CrossRef]

14. C. Badulescu, N. Lahellec, and P. Suquet, “Field statistics in linear viscoelastic composites and polycrystals,” Eur. J. Mech. A Solids, vol. 49, pp. 329–344, 2015. doi: 10.1016/j.euromechsol.2014.07.012. [Google Scholar] [CrossRef]

15. G. Debotton and L. Tevet-Deree, “The response of a fiber-reinforced composite with a viscoelastic matrix phase,” J. Compos. Mater., vol. 38, no. 14, pp. 1255–1277, 2004. doi: 10.1177/0021998304042732. [Google Scholar] [CrossRef]

16. K. Kowalczyk-Gajewska and H. Petryk, “Sequential linearization method for viscous/elastic heterogeneous materials,” Eur. J. Mech. A Solids, vol. 30, no. 5, pp. 650–664, 2011. doi: 10.1016/j.euromechsol.2011.04.002. [Google Scholar] [CrossRef]

17. R. Brenner, R. Masson, O. Castelnau, and A. Zaoui, “A quasi-elastic affine formulation for the homogenised behaviour of nonlinear viscoelastic polycrystals and composites,” Eur. J. Mech. A Solids, vol. 21, no. 6, pp. 943–960, 2002. doi: 10.1016/S0997-7538(02)01247-0. [Google Scholar] [CrossRef]

18. H. Zhai, T. Bai, Q. Wu, N. Yoshikawa, K. Xiong and C. Chen, “Time-domain asymptotic homogenization for linear-viscoelastic composites: Mathematical formulae and finite element implementation,” Compos. Part C Open Access, vol. 8, 2022, Art. no. 100248. doi: 10.1016/j.jcomc.2022.100248. [Google Scholar] [CrossRef]

19. Y. Liu, F. P. V. der Meer, L. J. Sluys, and J. T. Fan, “A numerical homogenization scheme used for derivation of a homogenized viscoelastic-viscoplastic model for the transverse response of fiber-reinforced polymer composites,” Compos. Struct., vol. 252, no. 1, 2020, Art. no. 112690. doi: 10.1016/j.compstruct.2020.112690. [Google Scholar] [CrossRef]

20. A. Carini, F. Genna, and F. Levi, “Time domain analytical bounds to the homogenized viscous kernels of linear viscoelastic composites,” Eur. J. Mech. A Solids, vol. 102, no. 6, 2023, Art. no. 105108. doi: 10.1016/j.euromechsol.2023.105108. [Google Scholar] [CrossRef]

21. C. Mareau, V. Favier, B. Weber, A. Galtier, and M. Berveiller, “Micromechanical modeling of the interactions between the microstructure and the dissipative deformation mechanisms in steels under cyclic loading,” Int. J. Plast., vol. 32–33, pp. 106–120, 2012. doi: 10.1016/j.ijplas.2011.12.004. [Google Scholar] [CrossRef]

22. M. Zecevic and M. Knezevic, “Latent hardening within the elasto-plastic self-consistent polycrystal homogenization to enable the prediction of anisotropy of AA6022-T4 sheets,” Int. J. Plast., vol. 105, pp. 141–163, 2018. doi: 10.1016/j.ijplas.2018.02.007. [Google Scholar] [CrossRef]

23. Y. Rémond, “Constitutive modelling of viscoelastic unloading of short glass fibre-reinforced polyethylene,” Compos. Sci. Technol., vol. 65, no. 3–4, pp. 421–428, 2005. doi: 10.1016/j.compscitech.2004.09.010. [Google Scholar] [CrossRef]

24. O. Pierard and I. Doghri, “Study of various estimates of the macroscopic tangent operator in the incremental homogenization of elastoplastic composites,” Int. J. Multiscale Comput. Eng., vol. 4, no. 4, pp. 521–543, 2006. doi: 10.1615/IntJMultCompEng.v4.i4.80. [Google Scholar] [CrossRef]

25. P. Suquet, “Overall properties of nonlinear composites: A modified secant moduli theory and its link with Ponte Castañeda’s nonlinear variational procedure,” Comptes Rendus Académie Sci. Sér. II Mécanique Phys. Chim. Astron., vol. 320, pp. 563–571, 1995. [Google Scholar]

26. C. Bleiler, P. P. Castañeda, and O. Röhrle, “Tangent second-order homogenisation estimates for incompressible hyperelastic composites with fibrous microstructures and anisotropic phases,” J. Mech. Phys. Solids, vol. 147, no. 4, 2021, Art. no. 104251. doi: 10.1016/j.jmps.2020.104251. [Google Scholar] [CrossRef]

27. M. Barral, G. Chatzigeorgiou, F. Meraghni, and R. Léon, “Homogenization using modified Mori-Tanaka and TFA framework for elastoplastic-viscoelastic-viscoplastic composites: Theory and numerical validation,” Int. J. Plast., vol. 127, no. 2–3, p. 102632, 2020. doi: 10.1016/j.ijplas.2019.11.011. [Google Scholar] [CrossRef]

28. G. J. Dvorak and Y. Benveniste, “On transformation strains and uniform fields in multiphase elastic media,” Proc. R Soc. Lond A, vol. 437, no. 1900, pp. 291–310, 1992. doi: 10.1098/rspa.1992.0062. [Google Scholar] [CrossRef]

29. J. C. Michel and P. Suquet, “Nonuniform transformation field analysis,” Int. J. Solids Struct., vol. 40, no. 25, pp. 6937–6955, 2003. doi: 10.1016/S0020-7683(03)00346-9. [Google Scholar] [CrossRef]

30. J. C. Michel and P. Suquet, “Computational analysis of nonlinear composite structures using the nonuniform transformation field analysis,” Comput. Methods Appl. Mech. Eng., vol. 193, no. 48–51, pp. 5477–5502, 2004. doi: 10.1016/j.cma.2003.12.071. [Google Scholar] [CrossRef]

31. J. Fish, V. Filonova, and Z. Yuan, “Hybrid impotent-incompatible eigenstrain based homogenization,” Int. J. Numer. Methods Eng., vol. 95, no. 1, pp. 1–32, 2013. doi: 10.1002/nme.4473. [Google Scholar] [CrossRef]

32. E. Sanchez-Palencia, Non-Homogeneous Media and Vibration Theory. Berlin, Heidelberg: Springer, 1980, vol. 127. doi: 10.1007/3-540-10000-8. [Google Scholar] [CrossRef]

33. G. Papanicolau, A. Bensoussan, and J. L. Lions, Asymptotic Analysis for Periodic Structures. New York, USA: Elsvier North-Holland, 1978. [Google Scholar]

34. Q. Yu and J. Fish, “Multiscale asymptotic homogenization for multiphysics problems with multiple spatial and temporal scales: A coupled thermo-viscoelastic example problem,” Int. J. Solids Struct., vol. 39, no. 26, pp. 6429–6452, 2002. doi: 10.1016/S0020-7683(02)00255-X. [Google Scholar] [CrossRef]

35. Y. Rahali, M. Assidi, I. Goda, A. Zghal, and J. F. Ganghoffer, “Computation of the effective mechanical properties including nonclassical moduli of 2.5D and 3D interlocks by micromechanical approaches,” Compos. Part B Eng., vol. 98, no. 10, pp. 194–212, 2016. doi: 10.1016/j.compositesb.2016.04.066. [Google Scholar] [CrossRef]

36. T. J. R. Hughes, J. A. Cottrell, and Y. Bazilevs, “Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement,” Comput. Methods Appl. Mech. Eng., vol. 194, no. 39–41, pp. 4135–4195, 2005. doi: 10.1016/j.cma.2004.10.008. [Google Scholar] [CrossRef]

37. J. A. Cottrell, T. J. Hughes, and Y. Bazilevs, Isogeometric Analysis: Toward Integration of CAD and FEA. The Atrium, Southern Gate, Chichester, West Sussex, UK: John Wiley & Sons, 2009. [Google Scholar]

38. S. Matsubara, S. -N. Nishi, and K. Terada, “On the treatments of heterogeneities and periodic boundary conditions for isogeometric homogenization analysis,” Int. J. Numer. Methods Eng., vol. 109, no. 11, pp. 1523–1548, 2017. doi: 10.1002/nme.5328. [Google Scholar] [CrossRef]

39. R. Alberdi, G. Zhang, and K. Khandelwal, “A framework for implementation of RVE-based multiscale models in computational homogenization using isogeometric analysis,” Int. J. Numer. Methods Eng., vol. 114, no. 9, pp. 1018–1051, 2018. doi: 10.1002/nme.5775. [Google Scholar] [CrossRef]

40. F. Schmidt, M. Krüger, M. -A. Keip, and C. Hesch, “Computational homogenization of higher-order continua,” Int. J. Numer. Methods Eng., vol. 123, no. 11, pp. 2499–2529, 2022. doi: 10.1002/nme.6948. [Google Scholar] [CrossRef]

41. X. Du, Q. Chen, G. Chatzigeorgiou, F. Meraghni, G. Zhao and X. Chen, “Nitsche’s method enhanced isogeometric homogenization of unidirectional composites with cylindrically orthotropic carbon/graphite fibers,” Compos. Sci. Technol., vol. 256, no. 3, 2024, Art. no. 110787. doi: 10.1016/j.compscitech.2024.110787. [Google Scholar] [CrossRef]

42. Q. Chen, X. Du, W. Wang, G. Chatzigeorgiou, F. Meraghni and G. Zhao, “Isogeometric homogenization of viscoelastic polymer composites via correspondence principle,” Compos. Struct., vol. 323, 2023, Art. no. 117475. doi: 10.1016/j.compstruct.2023.117475. [Google Scholar] [CrossRef]

43. C. Oskay and J. Fish, “Eigendeformation-based reduced order homogenization for failure analysis of heterogeneous materials,” Comput. Methods Appl. Mech. Eng., vol. 196, no. 7, pp. 1216–1243, 2007. doi: 10.1016/j.cma.2006.08.015. [Google Scholar] [CrossRef]

44. J. Fish, Practical Multiscaling. The Atrium, Southern Gate, Chichester, West Sussex, UK: John Wiley & Sons, 2014. [Google Scholar]

45. J. Fish, K. Shek, M. Pandheeradi, and M. S. Shephard, “Computational plasticity for composite structures based on mathematical homogenization: Theory and practice,” Comput. Methods Appl. Mech. Eng., vol. 148, no. 1-2, pp. 53–73, 1997. doi: 10.1016/S0045-7825(97)00030-3. [Google Scholar] [CrossRef]

46. Z. Yuan and J. Fish, “Multiple scale eigendeformation-based reduced order homogenization,” Comput. Methods Appl. Mech. Eng., vol. 198, no. 21–26, pp. 2016–2038, 2009. doi: 10.1016/j.cma.2008.12.038. [Google Scholar] [CrossRef]

47. J. Fish, Z. Yang, and Z. Yuan, “A second-order reduced asymptotic homogenization approach for nonlinear periodic heterogeneous materials,” Int. J. Numer. Methods Eng., vol. 119, no. 6, pp. 469–489, 2019. doi: 10.1002/nme.6058. [Google Scholar] [CrossRef]

48. Z. Yang, Y. Liu, Y. Sun, Y. Jing, and Q. Ma, “A novel second-order reduced homogenization approach for nonlinear thermo-mechanical problems of axisymmetric structures with periodic micro-configurations,” Comput. Methods Appl. Mech. Eng., vol. 368, no. 3, 2020, Art. no. 113126. doi: 10.1016/j.cma.2020.113126. [Google Scholar] [CrossRef]

49. Z. Yang, Y. Sun, Y. Liu, and Q. Ma, “A second-order reduced multiscale approach for non-linear axisymmetric structures with periodic configurations,” Appl. Math. Model., vol. 88, no. 3, pp. 791–809, 2020. doi: 10.1016/j.apm.2020.07.009. [Google Scholar] [CrossRef]

50. J. C. Simo and T. J. Hughes, Computational Inelasticity. New York, USA: Springer Science & Business Media, 2006. [Google Scholar]

51. G. Dvorak, Micromechanics of Composite Materials. New York, USA: Springer Science & Business Media, 2012. [Google Scholar]

52. S. V. Thiruppukuzhi and C. T. Sun, “Models for the strain-rate-dependent behavior of polymer composites,” Compos Sci. Technol., vol. 61, no. 1, pp. 1–12, 2001. doi: 10.1016/S0266-3538(00)00133-0. [Google Scholar] [CrossRef]

53. Y. Chen, Z. Zhao, D. Li, Z. Guo, and L. Dong, “Constitutive modeling for linear viscoelastic fiber-reinforced composites,” Compos. Struct., vol. 263, 2021, Art. no. 113679. doi: 10.1016/j.compstruct.2021.113679. [Google Scholar] [CrossRef]

Appendix A

In this section, we solve the ODE equation system in Eq. (27) to obtain the matrix phase strains. With the reduced 1-index defined in Eq. (22), we can rewrite Eq. (27) into the following system of ODEs:

(A1a)

and

(A1b)

(A1c)

(A1d)

(A2)

Here are characteristic relaxation times for the fibrous composite materials.

For the coupled ODEs defined in Eq. (A1a), notice that

(A3)

Define the following two strains:

(A4)

and the corresponding ODEs become:

(A5)

The solution of Eqs. (A5) can be written as

(A6a)

(A6b)

Substituting Eqs. (A6a) and (A6b) into (A4) yields the solution that

(A7a)

(A7b)

The shearing response Eqs. (A1b)–(A1d), can be solved similarly. Taking Eq. (A1b) as an example. Rewrite Eq. (A1b) into

(A8)

so that the solution can be given by the convolution form:

(A9a)

Similarly, the solutions of (A1c) and (A1d) are written with convolution form that

(A9b)

(A9c)

respectively.