CSRWA: Covert and Severe Attacks Resistant Watermarking Algorithm

1  Introduction

Watermarking involves embedding secret messages within a cover media, such as an image, to maintain copyright protection or preserve authentication [1,2]. In this process, imperceptibility (minimizing cover image degradation due to watermark embedding) and robustness (the ability of the watermark to withstand intentional or unintentional signal processing) are the two most important requirements for a watermark [3–5]. The signal processing operations may be necessary to eliminate noise and unwanted interleaved communication signals [6].

When adding a watermark, it’s crucial to consider the Human Visual System (HVS) to ensure that the watermark is not noticeable. This means that the intensity of the watermark should be adjusted based on the significance of each area according to the HVS. Using fixed intensity levels for the watermark can result in poor quality, as it will be added with the same intensity in every area regardless of its visual significance. Therefore, it’s important to make this adjustment to enhance the watermark’s invisibility [7,8].

The HVS is less sensitive to changes in high textures, contrast, and high-intensity regions. For this, the Just Noticeable Distortion (JND) model in [9] considers the various aspects of the HVS, such as contrast sensitivity function, luminance adaptation, and contrast masking, Eq. (1). Such a JND model can help determine the most suitable embedding strength factors based on these aspects, enabling the desired imperceptibility level [10].

TJNDk(x,y)=Tbasek⋅FLAk(x,y)⋅FCMk(x,y),(1)

where TJNDK(x,y) is the JND threshold for the kth block, Tbasek is the base threshold based on the spatial CSF for kth block, the modulation factor is LA factor FLAk(x,y) and the CM factor FCMk(x,y). x, y are the indices (x = 0, 1, 2, …, 7, y = 0, 1, 2, …, 7) in a block.

When choosing the embedding strength for a watermark, it’s important to consider its non-proportional relationship to imperceptibility. It’s widely known that embedding a watermark in the frequency domain, using specific frequency coefficients, can provide greater robustness than using the spatial domain [8]. Therefore, using the Discrete Cosine Transform (DCT) as an energy representation, combined with a Dither Modulation (DM) watermarking algorithm, which is one of the most robust watermarking algorithms, can significantly increase the watermark’s robustness. Such a hybrid algorithm may withstand conventional and unconventional modifications or attacks [11].

For an attack to be considered powerful, it must defeat the most powerful watermarking algorithms, whatever the watermark’s robustness and appearance are, without much-watermarked image fidelity degradation. Denoising Convolution Neural Network (DnCNN) attacks usually treat watermarks as noise, which is dealt with through image denoising. However, this method is only effective for Gaussian-distributed noise. A marginal difference between Gaussian-distributed noise and watermark distribution leads to less accurate watermark removal performance [12]. The ability of an adversarial network to remove different types of noise, including watermarks, depends on training it with a diverse set of inputs from a specific class. When trained in this way, it becomes difficult for most watermarking algorithms to resist. This paper will investigate a DCT-based DM watermarking algorithm that is enhanced with suitable step size adjustment using JND models to assess its imperceptibility and robustness against various types of conventional and severe attacks (such as volumetric, histogram equalization, and DnCNN).

Our motivation is to boost the DM watermarking algorithm as one of the most robust algorithms by utilizing the DCT transform. The ease of this transform energy spectrum representation facilitates the selection of the proper watermark embedding strength regarding imperceptibility and robustness considerations. Also, spanning the embedded watermark energy across frequency spectrum terms can grant more control over the watermark requirements. The wider the spanning, the more learning time and samples will be needed for the DnCNN to learn patterns in such a complicated and confused environment. Such a spanning is perceptually guided through two JND models for determining the watermark embedding strength and spreading out this strength respectively. Last but not least, the relative stability of the relation between the Direct Current coefficient (DC) and the Alternating Current (ACs) coefficients, such as the ‘DC/ACs’ ratio before and after some attacks, will be employed to gain robustness against such attacks.

The contributions that have been gained in this work can be summarized as follows:

•   Implementing severe covert attack capable of destroying the watermarks with as little fidelity degradation as possible of the attacked watermarked image.

•   Developing a watermarking algorithm with relative resistance capabilities against such attacks and conventional severe attacks.

•   Supporting the proposed method with JND models to adapt the amount of embedding strength and spread this energy across a wider band based on HVS concepts.

The paper is organized as follows: Section 1 introduces the subject principles. Section 2 reviews the related work. Section 3 concerns all the materials and methods utilized. Section 4 gives details of the watermarking algorithm proposal. Section 5 shows the experiments and results. Section 6 concludes with conclusions and recommendations for future work.

2  Related Works

As a crucial matter, robust watermarking is essential to ensure digital content protection. Traditional and non-traditional (AI-based) approaches have been used to develop watermarking schemes that meet these requirements. Invariant signal features under various signal processing operations supported by incorporating neural network capabilities, as in [13], can be used as a base to enhance watermarking algorithms’ robustness performance. Such robustness can be further boosted by utilizing blind watermarking algorithms based on quantization techniques [14]. However, attackers can exploit these same schemes to launch attacks and remove watermarks to violate copyright protection [15]. Volumetric scaling and histogram equalization, which are two of the most used image processing operations, can be easily maliciously exploited by attackers as two forms of the formal approach attacks. Such attacks can cause watermark destruction due to their high impact on the cover image’s pixel modification and, consequently, the embedded watermark. To be robust to volumetric scaling, the proposed algorithm [16] adopted a small modification to the Watson model, which makes slacks scale linearly. Consequently, the quantization step sizes are scaled using the same scaling factor that the signal underwent during the embedding to perform Quantization Index Modulation (QIM) decoding correctly. To address the previously discussed issues, a robust JND model in the DCT domain is introduced in [17]. This model can estimate the specific JND threshold for each pixel. A logarithmic function is also applied to the DC value, and an optimal quantization step is derived based on different block types.

Using deep neural networks (DNN) has led to increased attacks against image watermarks. Unlike traditional attacks, these attacks are particularly harmful and have less obvious effects. They can cause significant damage to watermarks without significantly degrading the quality of the cover image. Understanding these types of attacks can help in developing more resilient watermarking algorithms.

To successfully attack a robust watermarking scheme, the attack should be comprehensive and flexible enough to be effective, regardless of the watermarking algorithm used or the availability of information about it. Real covert communication scenarios make it harder for the attacker to succeed than when complete information about the watermarking algorithm and image distribution is already available [12]. An attack known as a black box attack assumes that the attacker has only a watermarked image and does not know the watermarking algorithm used. To investigate its effectiveness, this type of attack must be validated against various algorithms’ watermarked images through a cross-validation test [15]. Such a black box scenario should not be a barrier to designing a successful watermark-removing attack. Therefore, a DNN denoiser can be considered a candidate solution for designing watermark removal attacks in such a scenario. The idea comes from the fact that the watermarks are also considered as one form of the images’ noise. For a more general attack, introducing various noise levels as inputs to be presented in parallel with the watermarked images to the network to be trained can satisfy such generality [18]. By introducing some noise to the training data, the network learns to recognize and remove different forms of noise [19]. In black box scenarios, finding a general distribution function for use as an image watermarking pair generator is crucial. With the unavailability of any knowledge about the watermarking algorithm used, the general distribution functions can be derived using a model based on the common features of the widely used robust watermarking algorithms [12]. Such a model aims to estimate the latent watermark features and satisfy the Minimum Mean Square Error (MMSE) when mapping between the watermarking pair [12].

In addition to cross-validation, an attack should be tested against the most robust watermarking algorithms. It is well-known that robustness can be achieved by using the frequency domain. Various kinds of research have shown that the transform coefficients usually modified to achieve the watermark robustness. For this, the low and middle frequencies are used for watermark embedding due to their stability against various processing operations. The changes made to these coefficients are indeed spread across the entire set of other transform domain terms, with most of the changes concentrated in the low and middle coefficients and minimal changes in the high-frequency coefficients. Therefore, in such scenarios, a watermarked image of a corresponding cover image can be simulated by changing the low, mid, and high-frequency coefficients to produce cover and watermarked image pairs as a training dataset [12].

In [20], a Fully Convolutional Neural Network (FCNN) deep architecture with an improved training process and performance is proposed as a denoising attack to deal with and remove the watermark as image noise with less watermarked image structure degradation. In [19], a new watermarking attack scheme called Fast and Covert Watermarking Attack Network in Wavelet Domain (Wavelet-FCWAN) has been developed using deep learning. The scheme uses noise filling as a pre-processing step for the watermarked image. This image is then transformed into sub-images using wavelet transform operation. The wavelet-transformed sub-images are then input in parallel into the Wavelet-FCWAN along with the noise level map. When used as an attack, the network can then be quickly trained as a denoiser capable of ensuring the visual quality of the cover image details. In [18], A new method called FFDNet has been developed to quickly and effectively reduce noise, using the same notion of noise level maps. It produces good results when the input noise level matches the actual noise, striking a balance between noise reduction and detail preservation. The method has been tested on synthetic images with Additive White Gaussian Noise (AWGN). An adversarial attack scheme, proposed in [15], demonstrates effectiveness against popular watermark embedding schemes. Different datasets were generated, as in [11], to train Convolutional Neural Network (CNN) models for attacking watermarked images based on varying levels of knowledge about the watermarking algorithm.

The challenge of making a watermarking algorithm robust enough to withstand attacks comes at the cost of reducing its imperceptibility, which is a conflicting requirement. This is why JND models are useful for finding a balance. These models use elements such as contrast sensitivity function, luminance adaptation, and contrast masking to adjust the embedding strength based on the details of the region [17]. In [21], a study has found that the strength of embedded energy should not be concentrated in a single block, but instead, it should be spread across a wider zone. To achieve this, the researchers developed the Spread Transform Zone Modulation (STZM) technique, which uses the DCT transform. They examined the texture energy within each block, as well as the regularity between neighboring blocks in horizontal, vertical, and diagonal directions. The difference between the corresponding horizontal, vertical, and diagonal vectors in the neighbors with the selected block was then modulated based on the watermark bit. The energy was controlled by an adequate JND threshold suitable for each directional vector. In a study referenced in [22], a method for watermarking colored images was proposed. This method uses a quaternion just-noticeable-difference (QJND) model to embed the watermark. A colored contrast masking factor is added to the three commonly used frequency-based JND factors to adjust the quantization step size for the DM scheme. In [23], a network architecture similar to U-Net was trained to serve as a robust watermark embedding and extraction system for colored images. The system utilizes a JND for each color channel instead of mean square error (MSE) as a loss function. This decision was made due to the incompatibility of MSE with the principles of the human visual system. In [24], the step size of the Spread Transform Dither Modulation (STDM) was adaptive, based on their developed JND model. This model utilized the first, second, and fourth AC coefficients of the DCT for the JND calculation. These coefficients were selected because the first nine AC coefficients, in zig-zag order, contain most of the energy of the entire block features.

In this paper, we plan to use the DnCNN denoising attack as a test system for our proposed watermarking algorithm. This is because the DnCNN can recognize different watermark pattern appearances. Our training dataset is generated based on two assumptions. The first assumption is that the well-known DM watermarking algorithm, which can produce robust watermarks, will be used for both the watermarking process and to generate training images for the DnCNN. This will serve as a challenge for our proposed watermarking algorithm, as the images will simulate the hardest noise forms for the network to treat. The second assumption is that random Gaussian noise will give the generated training watermarked images various latent watermark appearances.

Our proposed JND model considers sensitivity, LA (Luminance Adaptation), and intra- and inter-block contrast masking factors to ensure the watermark’s imperceptibility. The factors are based on psychological experiments on the HVS. Furthermore, the sensitivity table of the DCT-based Watson model will be used to distribute the watermark’s energy across the DCT coefficients of the watermarked image.

3  Methods and Materials

The next sections discuss the key principles used to develop the proposed Covert and Severe Attacks Resistant Watermarking Algorithm (CSRWA). These methods aim to balance robustness and imperceptibility, which the algorithm is expected to provide. The following sections also cover image denoising as a potential attack for removing the watermark. They also address the tools used to maintain the tradeoff mentioned above, even when facing such attacks, as well as other severe attacks or common image processing operations.

3.1 DnCNN Attack for Watermark Removal

The ability of an attack to defeat the most resilient watermarking algorithms can provide a good indication of its effectiveness and universality against many other similar or less robust algorithms. Therefore, when planning the design of a harmful attack, one should consider employing non-traditional approaches, such as using Convolutional Neural Networks (CNN) as a denoiser (Dn) to attack the most robust watermarking algorithms.

Many watermarking algorithms embed watermarks in the low-frequency terms of the transform domain, while denoisers typically focus on removing noise from the high-frequency terms of images. However, because watermarks are considered a noise embedded in frequencies other than the higher ones, they cannot be removed using denoising alone. To address this, adding complementary noise to the watermarked image before applying the denoiser can help remove these watermarks, as they are present in some high-frequency terms. Adding this complementary noise is important, as denoising an image without it can lead to undesirable fidelity consequences [19]. The fidelity of the predicted image is affected in proportion to the level of the added noise [18]. Configurations such as network depth, filter numbers and sizes, pooling, and batch normalization are crucial for determining prediction accuracy and time consumption.

3.2 Transform Domain Quantization for Robustness

The QIM-based watermarking algorithm family is known for its robustness against various attacks. One well-known algorithm in this family is the DM algorithm, which we used in our experiments to embed binary watermark image bits. We can use the cover image’s DCT frequency terms to enhance robustness, choosing either low or high-frequency terms for higher or lesser robustness, respectively. We can then embed and extract these bits by quantizing selected DCT terms. The Eqs. (2)–(5) for DCT and Eq. (6) for DM are provided below [25].

For M×N image f(x,y)(x=0,1,2,…,M−1,y=0,1,2,…,N−1) 2-D DCT is given as follows:

C(u,v)=αuαv∑x=0M−1∑y=0N−1f(x,y)cosπ(2x+1)u2M×cosπ(2y+1)v2N(2)

where M and N is the row, and the column size of f x, y, u, and v are the horizontal and vertical frequency (u=0,1,2,…,M−1,v=0,1,2,…,N−1) and C(u,v) is DCT coefficient of image f(x,y).

αu={1/M,u=02/M,1≤u<M−1(3)

αv={1/N,v=02/N,1≤v<N−1(4)

DCT coefficients of an image include one DC coefficient and some alternating current (AC) coefficients with different frequencies. From Eq. (5), the DC coefficient can be obtained as:

DC=C(0,0)=1MN∑x=0M−1∑y=0N−1f(x,y)(5)

The DM quantization formula is given in Eq. (6).

yn(xn,mn)=Q(xn+d(n,mn),Δ)−d(n,mn)(6)

Where the dithers are driven utilizing Eq. (7).

d[n,1]={d[n,0]+Δ2,d[n,0]<0,d[n,0]−Δ2,d[n,0]>0,n=1,2,…,L(7)

The basic quantization process is done utilizing the formula of Eq. (8) below [26].

s=Qm(x,Δ)=round(xΔ)Δ+(−1)m+1∗Δ4,where m∈{0,1}(8)

3.3 JND Model for Imperceptibility

To ensure robustness, it’s important to choose a high step size value while balancing it with the need for imperceptibility of the watermark. This can be achieved by determining a suitable threshold for the allowable change in each cover frequency term before any noticeable distortion occurs. To strike the right balance, a JND model based on Weber’s law for luminance adaptation, combined with the contrast of both inter and intra-cover image blocks, is utilized to control the step size. Additionally, a Watson-based JND model is employed to enhance watermark imperceptibility and regulate the distribution of the watermark energy across the cover image blocks’ DCT terms. This is to avoid noticeable watermark patterns that could be detected during the DnCNN training and noise removal phases.

3.3.1 Weber-Based JND Model

The German physician and psychologist Ernst Weber stated that HVS sensitivity to the signal change has a constant non-proportional relation to the background luminance. Thus, according to Weber’s law of Eq. (9), the allowed JND for a signal increasing with the background luminance.

JND=ΔL=(|Ly−Lx|)=constant∗Lx(9)

where Lx, andLy are the background and foreground luminance values, respectively.

Thus, the smallest allowed signal’s luminance changes before getting a noticeable distortion is proportionally related to the background luminance.

Since the digital image processing operations are done utilizing pixel intensities, which are non-linearly related to the luminance values due to the Gamma correction (Eq. (10)), a recent measure metric (LA-SSIM) has been developed to reflect Weber’s law utilizing pixel intensity values [27] (Eqs. (11) and (12)). The JND model for this metric can be used to determine the suitable embedding strength thresholds for the imperceptibility considerations in the pixel domain.

Lx=α+β.μxy(10)

Lx+ΔL=α+β.μXY(1+Δμ/μx)y(11)

JND(μx)=Δμ=a1.μxa2+a3.μx+a4(12)

where α, β, and γ are model parameters of a Gamma correction function ,μx is the background pixel intensity value. According to Taylor series, a1 = −2.655, a2 = 0.9259, a3 = 1.709 and a4 = 21.73.

3.3.2 Watson-Based JND Model

As another JND model, Watson’s model employed the same three common factors of Eq. (1) to estimate a change threshold for every 8×8 image block’s DCT transform individual term. The sensitivity of each block’s DCT coefficient to the change before producing one JND, which was derived by Ahumada and Peterson as a DCT-based frequency sensitivity, Fig. 1, is used as a base for the subsequent calculations of the luminance (Eq. (13)) and contrast masking (Eq. (14)) [28].

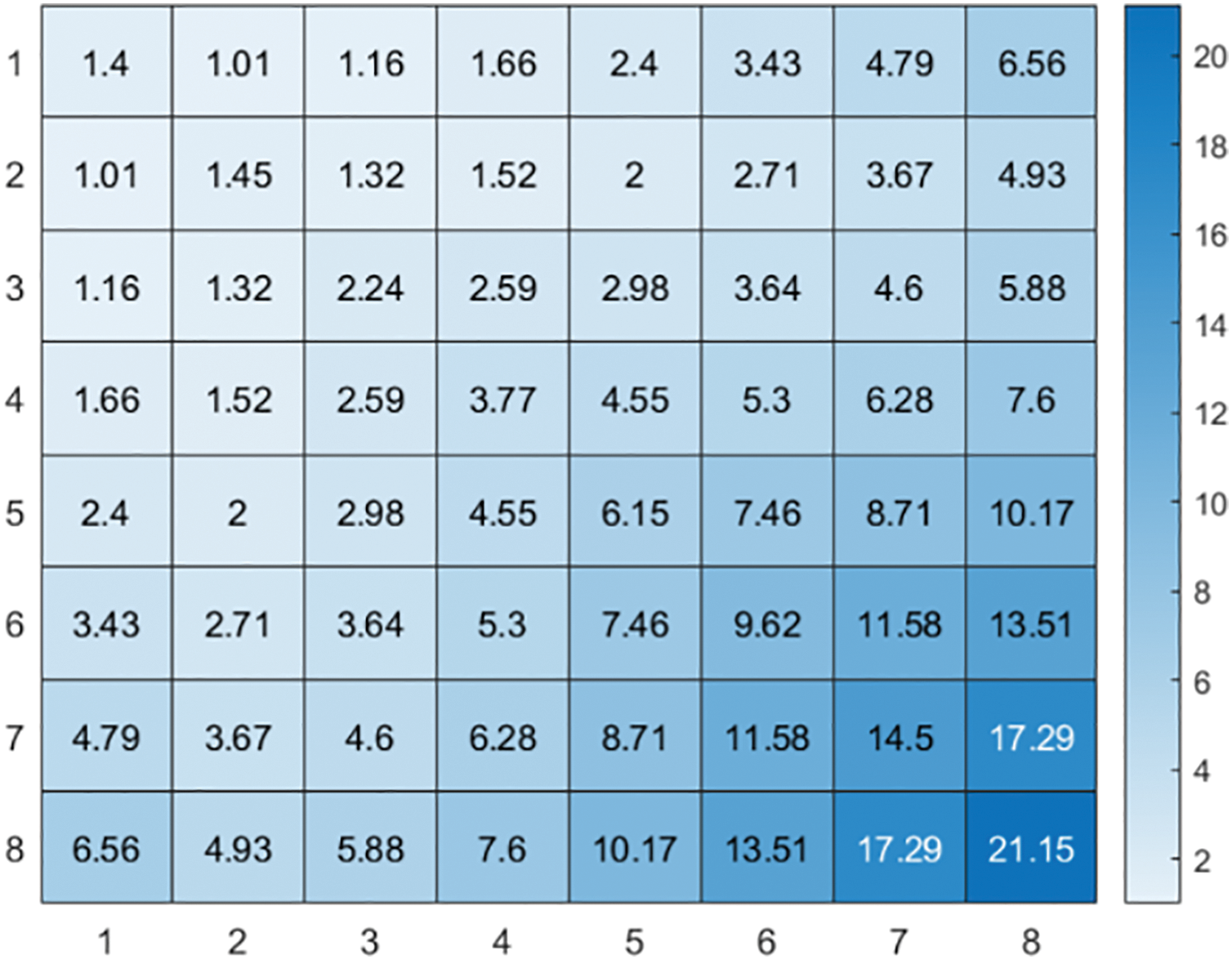
Figure 1: Sensitivity thresholds, namely JND of the corresponding 8×8 block’s DCT coefficients

tL[i,j,k]=t[i,j](C0[0,0,K]/C0,0)αT(13)

where T is a constant with a suggested value of 0.649, C0[0,0,K] is the DC coefficient of the kth block in the original image, and C0,0 is the average of the DC coefficients in the image.

S[i,j,k]=max{tL[i,j,k],|C0[i,j,k]|w[i,j]tL[i,j,k]1−w[i,j]}(14)

where w[i,j] is a constant between 0 and 1 and may differ for each frequency coefficient. Watson uses a value of w[i,j]=0.7 for all i,j.

4  Proposed Work

Fig. 2 involves training a DnCNN on pairs of training images, including cover and watermarked images generated using a similar approach as the watermarking algorithm. This approach enables the DnCNN model to learn various watermark patterns, presenting approximately white-box scenarios as a challenge for our proposed CSRWA. The trained DnCNN is then used to perform a denoising attack without leaving evidence, as it can remove the embedded watermarks while maintaining the fidelity of the cover image. The watermarking algorithm is designed to withstand such an attack.

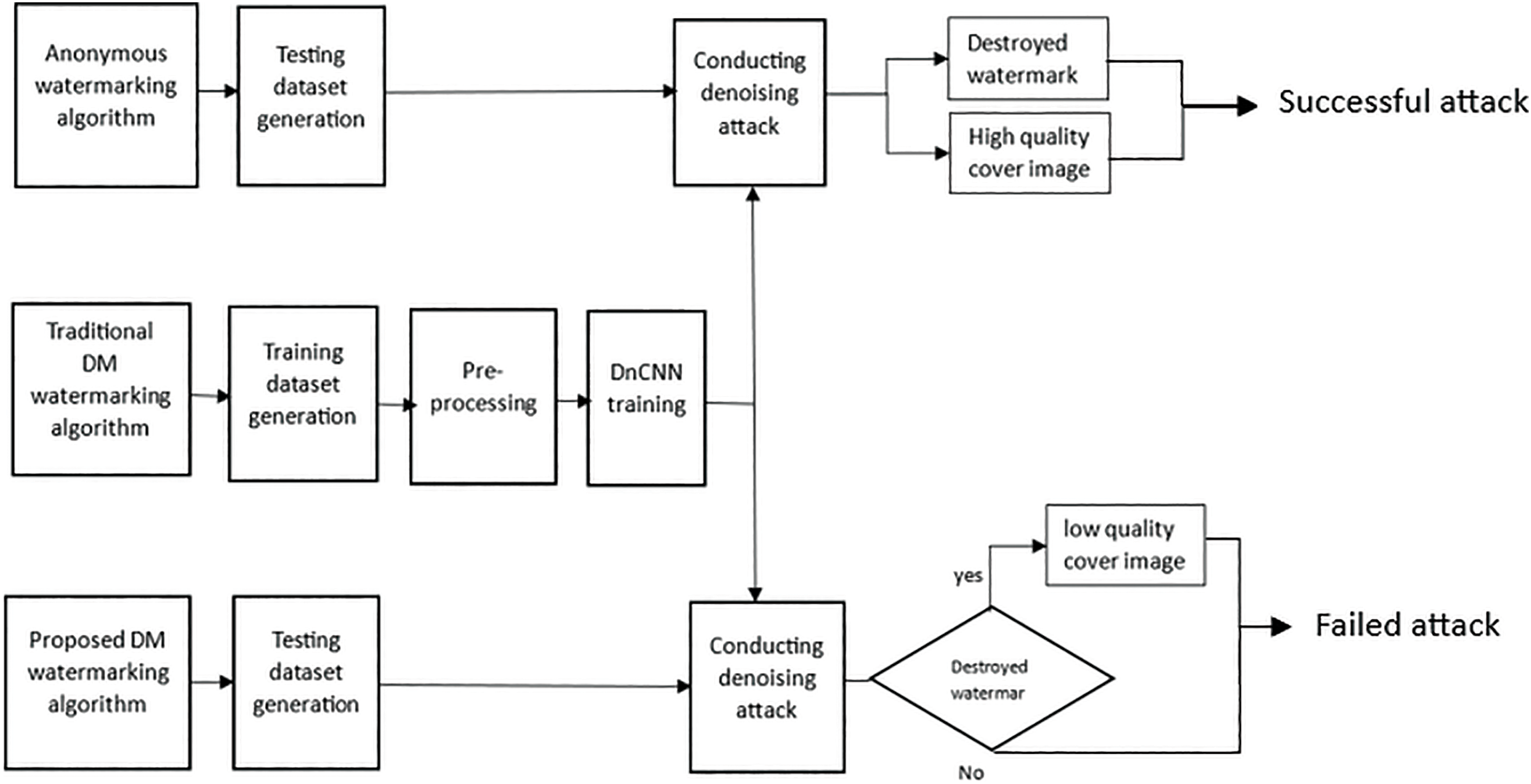
Figure 2: An emulation for the conditions where a DnCNN can achieve a successful attack when facing watermarking algorithms other than the proposed one. An attack can be regarded as successful when it destroys the watermark without much noticeable impact on the cover image fidelity. Our proposed watermarking algorithm can resist or at least enforce the attack to leave a noticeable impact in extreme attack cases

4.1 The Procedure of the DnCNN Attack

The DnCNN attack can be characterized as a covert attack due to its malicious behavior, which involves destroying the watermark while having minimal impact on the imperceptibility of the cover image. This makes the attack relatively undetectable, as the alterations are hardly noticeable. Its effectiveness stems from a well-structured design incorporating multiple convolutional layers, allowing the model to adjust its parameters throughout the training process for specific tasks. The model is trained on diverse samples that accurately represent real-world noise patterns, which include watermarks as a type of noise. To achieve the best results, the following training steps should be followed:

Step 1: To account for different levels of robustness and shapes of the watermark within the image, we will use the traditional DM watermarking algorithm. This algorithm is known for its high level of robustness compared to other algorithms, and it will utilize the DCT transform and a specific step size value calculated for each image block. To balance the watermark requirements, our proposed algorithm uses a direct-to-alternate currents relationship for the quantization process. We rely on this relationship for quantization due to its stability against volumetric scaling and histogram equalization. See Fig. 3 for more details.

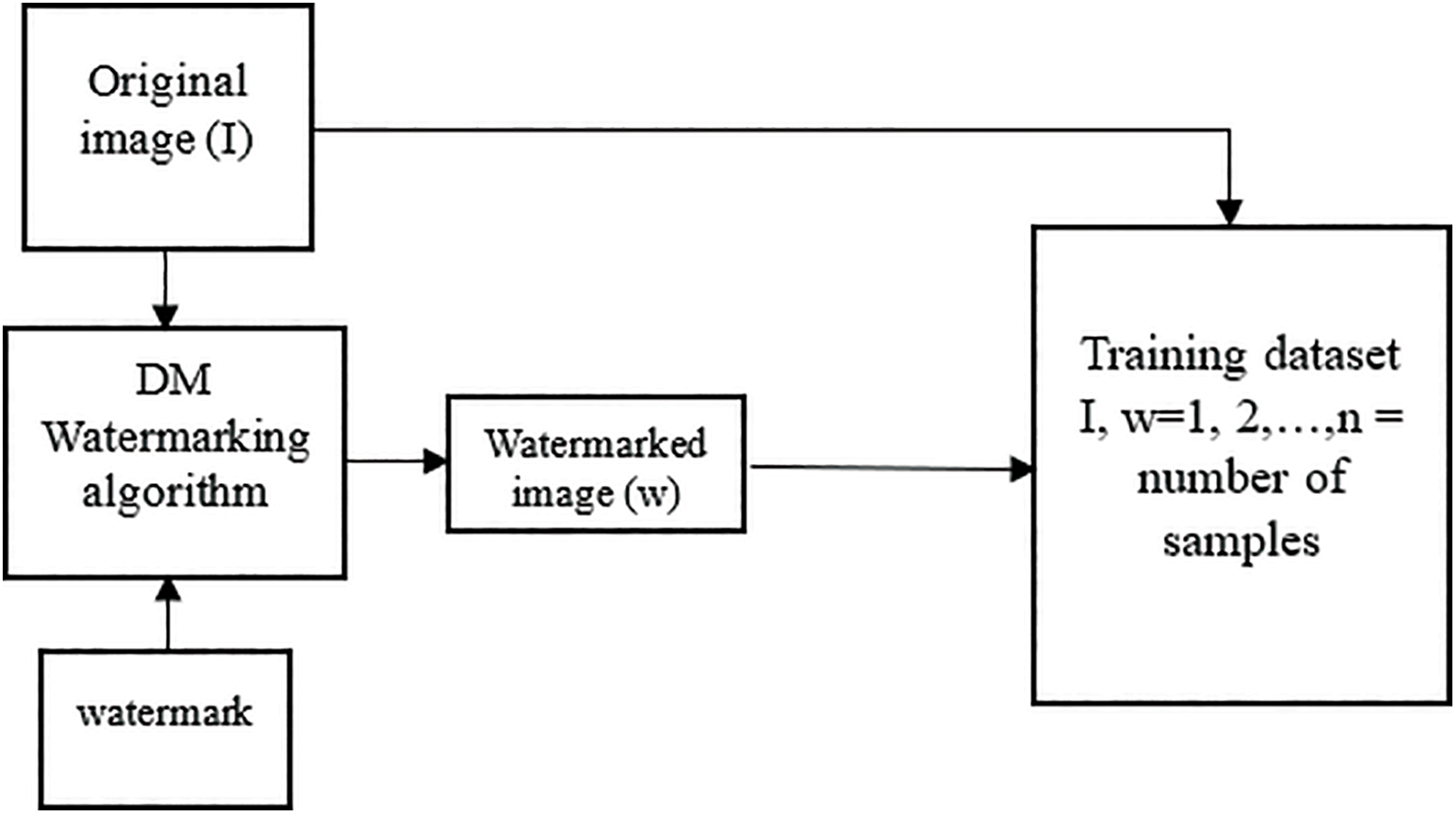
Figure 3: The training dataset generation with multiple embedding strengths (Δ) utilizing one of the most robust algorithm families (DM) with an aim for providing a comprehensive view of the various robust embedding map forms of the input data

As shown in Fig. 3, we intentionally utilized the DM algorithm to enhance the resilience of the embedded watermark. Any potential attacks must be prepared to confront and overcome such robust watermark scenarios. Furthermore, the range of step sizes enhances the ability of the DnCNN to be trained to handle the different appearances of the watermark embedding map for each image.

Step 2: The resulting training set from Step 1 undergoes pre-processing to introduce more randomness for embedding watermarks. This aims to provide the DnCNN with diverse knowledge from a wide range of embedded watermark appearances (Fig. 4).

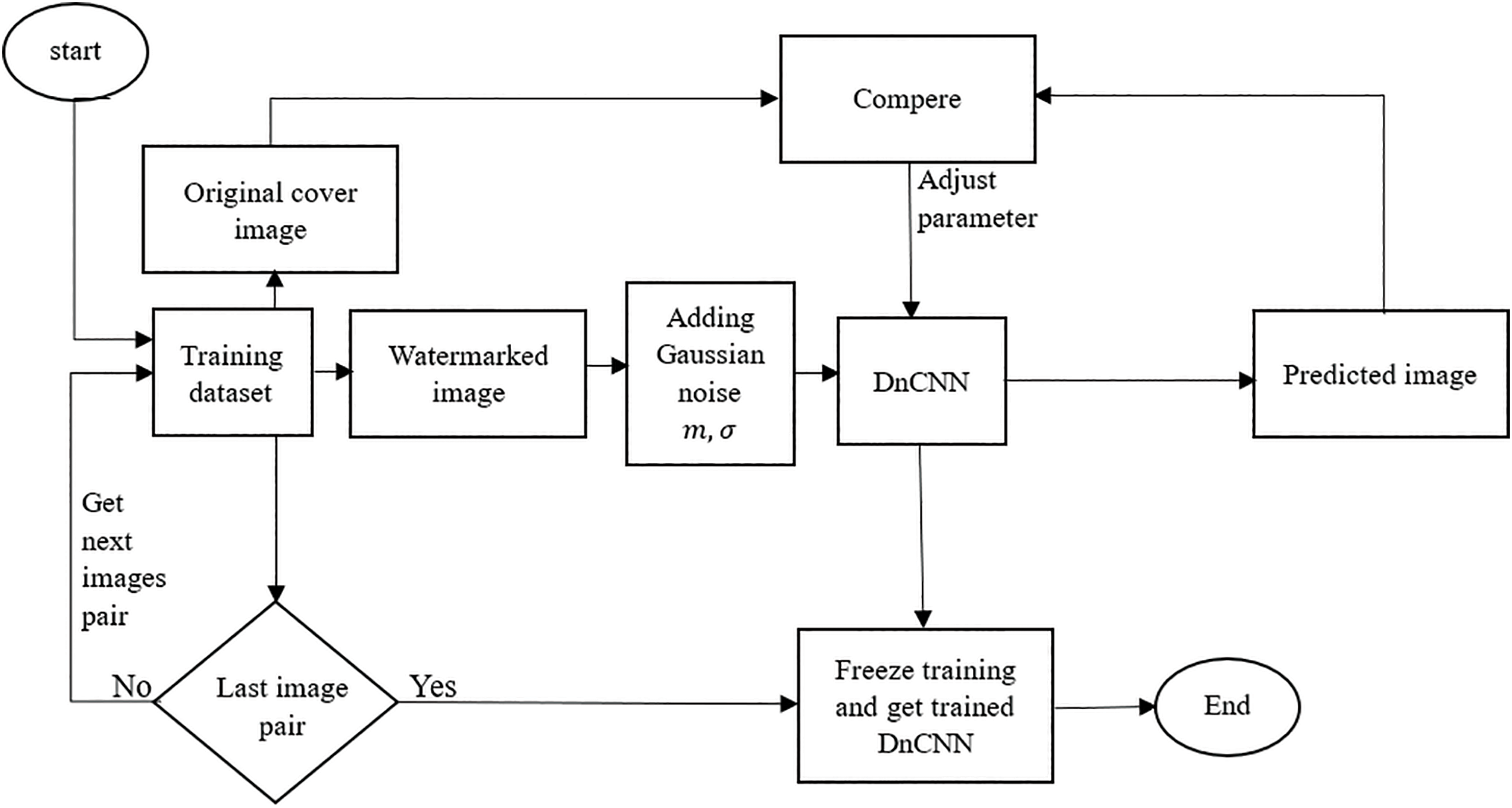
Figure 4: The DnCNN training phase utilizing the dataset generated in Fig. 3. Some additional Gaussian noise is added to each input watermarked image to increase the input data randomness and simulate real-world scenarios

Step 3: In the training phase, the DnCNN makes multiple parameter (weights) adjustments based on the loss functions that evaluate the similarity between the original cover image and the predicted output. This continuous process ensures that the DnCNN produces the best possible prediction results. Ultimately, this phase results in a trained DnCNN with its adjusted weights.

In the previous paragraph, we discussed how the DnCNN is trained using input data. Each training pair consists of an input watermarked image with added Gaussian noise \euscriptN (0, 1) and its corresponding pre-watermarking image as a label. The network continuously compares the predicted image with its corresponding label to make parameter adjustments until training convergence. As a result, the DnCNN becomes ready to handle any unseen watermarked image without knowledge of the watermarking algorithm (black box scenario).

Step 4: To verify the attack’s performance under such a scenario, a test watermarked image generated by an anonymous watermarking algorithm can be a useful choice (Fig. 5).

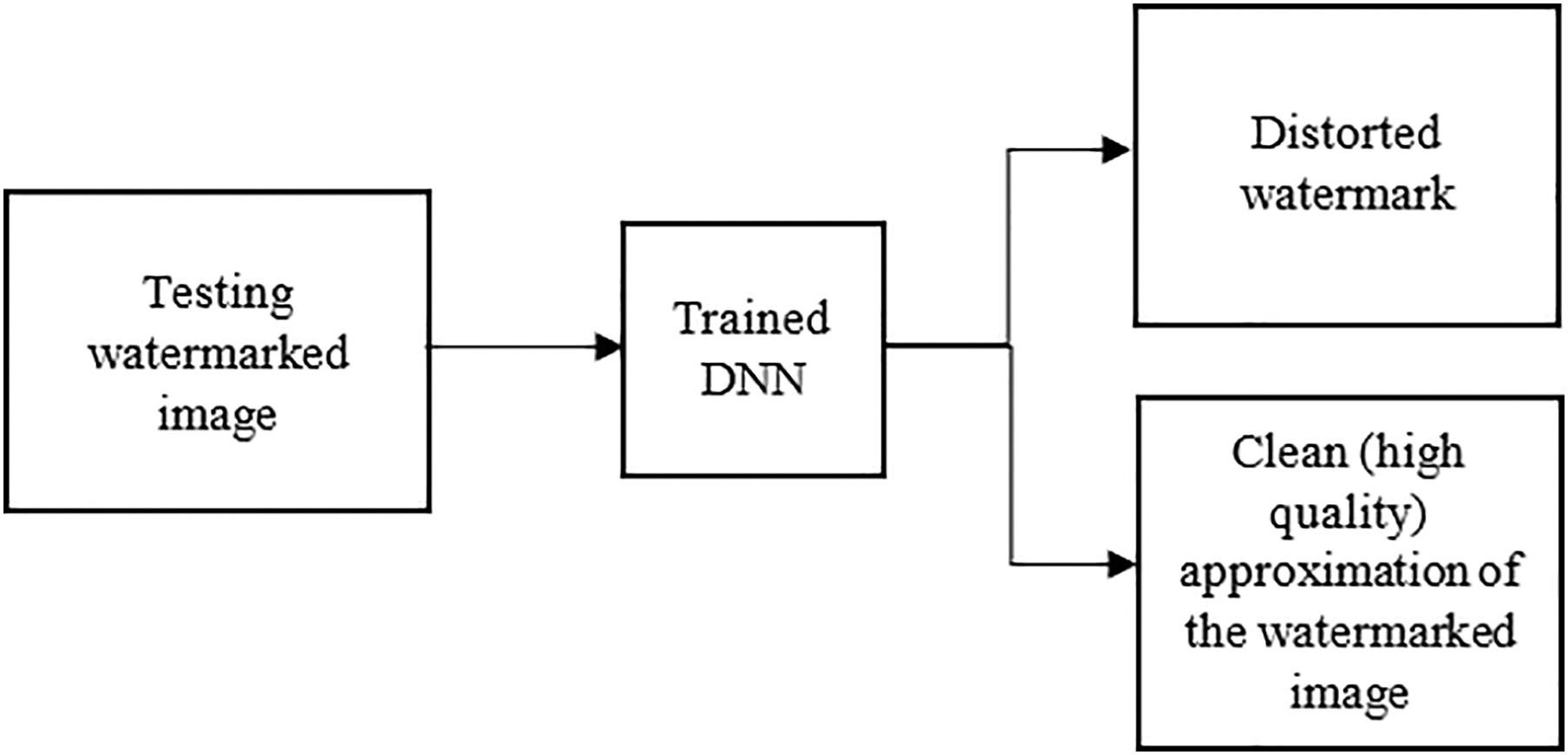
Figure 5: The result of the DnCNN attack is a severely scrambled watermark without producing much image fidelity degradation

Step 5: The trained DnCNN is used to assess the robustness of the proposed watermarking algorithm by subjecting the watermarked images to the proposed attack.

The structure of the used DnCNN network is shown in Fig. 6 below.

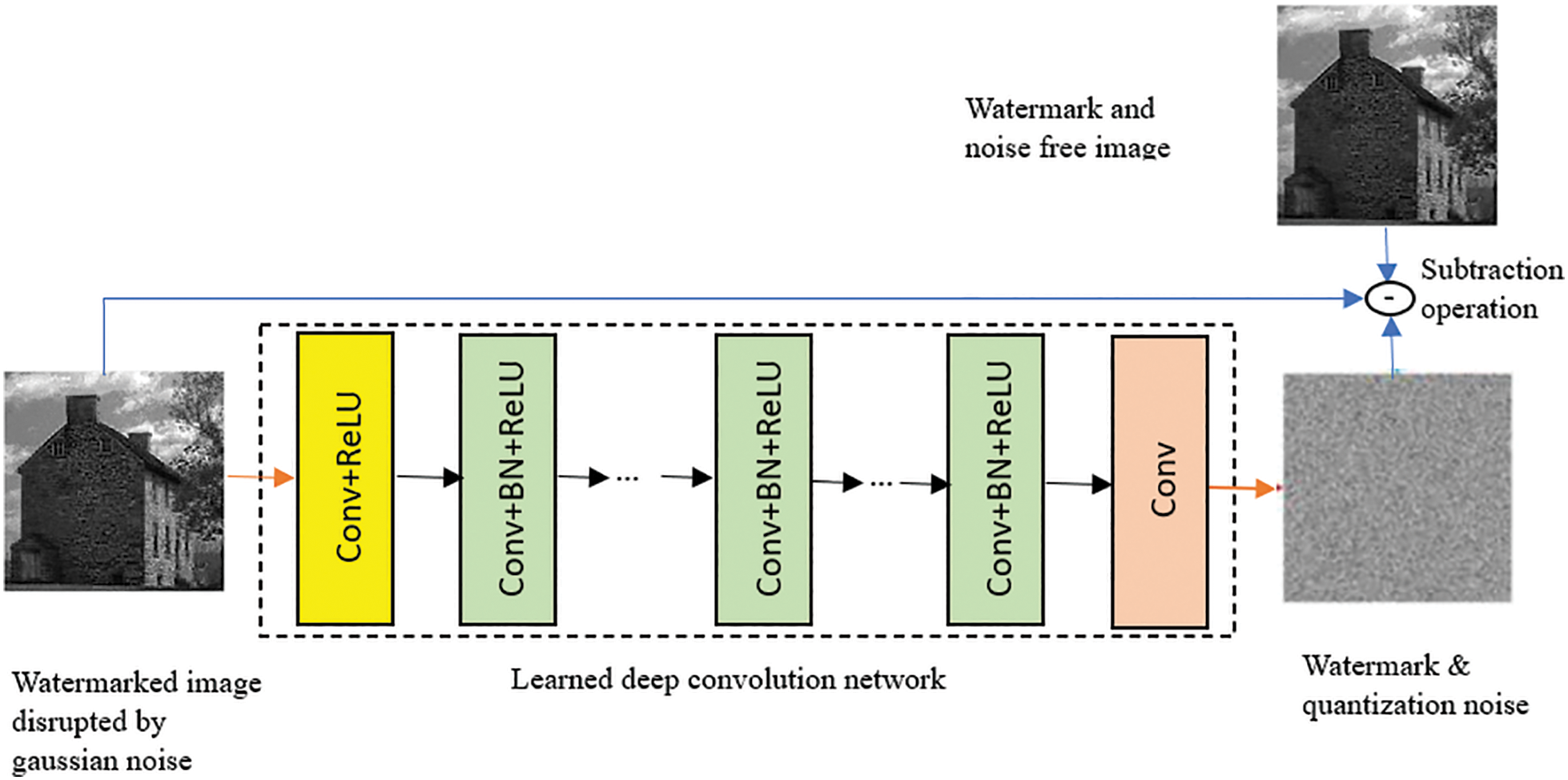
Figure 6: The structure of the watermark attacking DnCNN. The trained network on the original and the watermarked pairs become aware of the various noise types. It acts as a denoiser to destroy abnormal noisy form patterns (including watermarks)

4.2 The Procedure of the Proposed CSRWA

The common steps for the proposed watermarking algorithm are illustrated in Fig. 7 below.

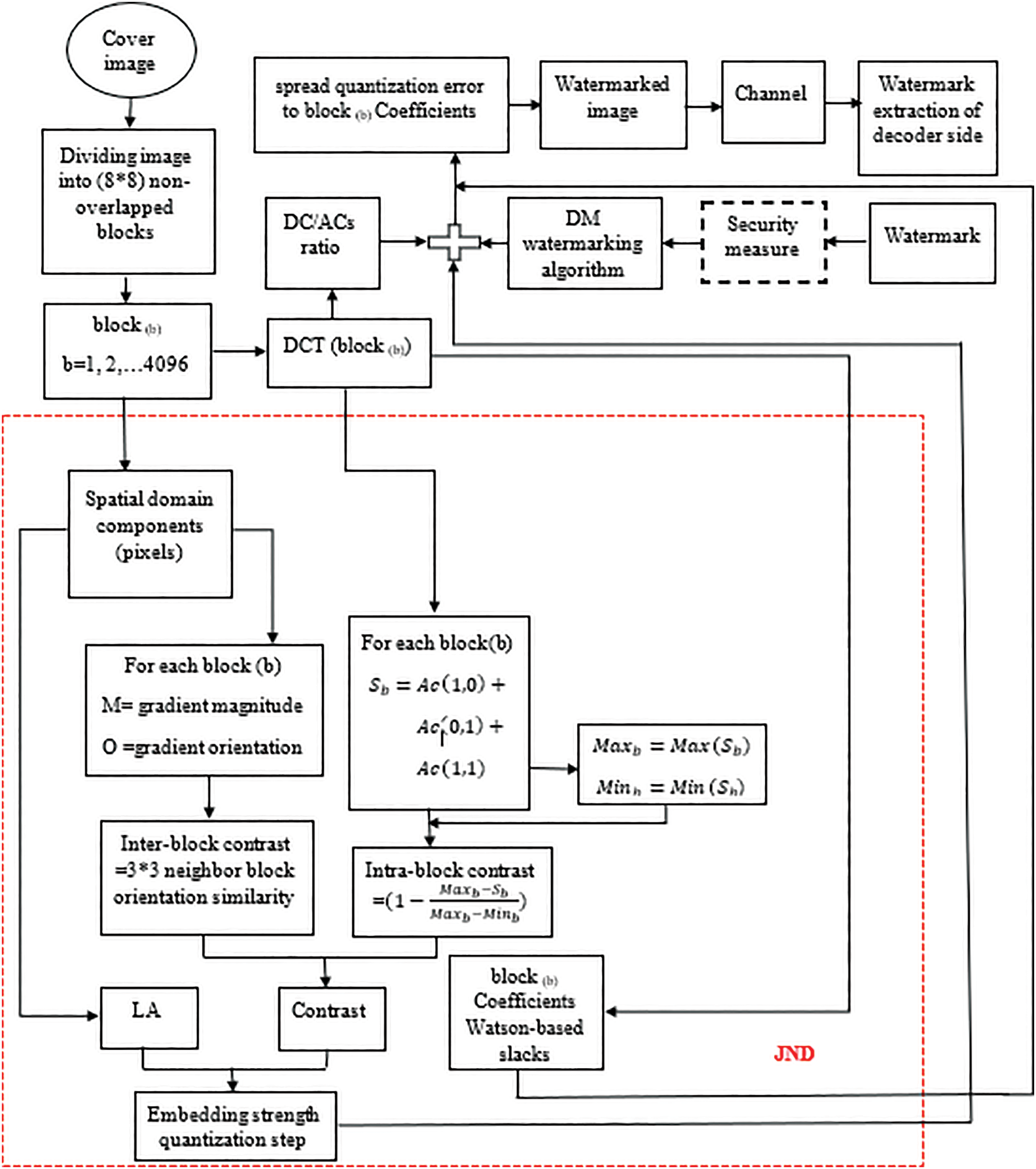
Figure 7: The flowchart of the proposed watermarking algorithm. The dashed line rounded the processes included in the JND calculations

The proposed algorithm flowchart presents a comprehensive overview of the general watermark embedding process. The detailed algorithm steps are as follows:

Step 1: As a preprocessing step, the algorithm divides the cover image into regions or blocks of defined dimensions (size).

Step 2: The quantized value for each block can be determined using the DC/sum (ACs) ratio, which is relatively invariant in image processing operations (volumetric and relative histogram equalization). This ratio will be used for watermark embedding and extraction.

Step 3: To determine an adaptive step size for each block regarding its luminance and texture, the JND model is going to utilize the regions LA of along with the contrast factor according to Eq. (15).

JND threshold=max (LA,Contrast)(15)

To get an accurate contrast, both inter and intra-contrast effects will be compounded together to calculate this factor. A block’s inter-contrast is calculated using its gradient orientation with respect to its neighbor blocks. Intra block’s-contrast is calculated by utilizing the normalized summation of the three upper left corners ACs coefficients of the DCT transform.

Step 4: The calculated value for the JND of the previous step is then multiplied by a pre-determined constant to determine the watermark embedding strength (quantization step size). The DM watermarking algorithm will use this step size to conduct the adaptive embedding processes. The distortion between the original signal and the watermarked one can be measured as the mean square error between them as in Eq. (16).

D(s,x)=1L‖s−x‖2(16)

where xands are the received and quantized watermarked images, respectively.

In this regard, the robustness of the embedded watermarked is determined according to the minimum distance between the reconstruction points of the quantizer pairs [29].

Step 5: watermark embedding is done by quantizing the DC/sum(ACs) ratio to the nearest predefined point from a set of such points. During the embedding process, one of two scalar quantizers is used based on the watermark bit that is to be embedded. The DM watermark embedding formula is given in Eq. (6).

Step 6: The extraction process is done utilizing the same quantizer pair used during the embedding process. The result of the quantizer with the nearest value to the received signal determines the extracted watermark’s bit.

Hence, the quantization result of a specific quantizer, which has the minimum distance to the received signal, will determine the embedded watermark bit according to Eq. (17).

m^=argminm∈{0,1}|x−s(x,m)|(17)

5  Experiment Results

In this section, we will present our DCT-based CSRWA algorithm. This will demonstrate how it can withstand the DnCNN attack by using the merits of the transform domain to select the most robust frequency components against such an attack. Additionally, we will show how spreading out the watermark energy across the frequency spectrum can preserve the DC/ACs ratio to some extent. This contributes to mitigating the effects of volumetric scaling, histogram equalization, and noise removal DnCNN attacks.

The results of this section are experienced utilizing the standard BOSSbase1.01dataset as cover images, along with the binary watermark of Fig. 8 below.

Figure 8: A binary watermark image of size 64 × 64

5.1 DnCNN Architecture

Network parameters must be configured appropriately, as the choice of their values depends on the type of application and its balance between prediction accuracy and time complexity. One key parameter to set is PatchesPerImage, which determines the number and size of patches used to segment the image for feature extraction. A greater number of patches can improve feature extraction accuracy, thereby increasing prediction accuracy. However, larger values for this parameter may require more memory resources and can sometimes lead to overfitting. Another important factor influencing the network learning process is the InitialLearnRate parameter. Larger values for this parameter can speed up the training process but may compromise learning efficiency, while smaller values can enhance learning at the cost of longer training times. Typically, a value of 0.001 is chosen for this parameter, which can be continuously adjusted to find the optimal rate using various algorithms throughout the training stages. Additionally, the MaxEpochs parameter—the total number of iterations through the entire dataset—can initially be set to a high value and modified throughout the learning process. Increasing MaxEpochs generally helps improve the learning outcome. The MiniBatchSize hyperparameter specifies the number of training examples used during each training iteration. This can vary based on the specific dataset size and the capabilities of the hardware used. Finally, shuffling the dataset before each epoch can enhance learning and reduce the risk of memorization.

The denoising attack on the watermarked image involves an architecture consisting of an input layer with dimensions 512 × 512 and one channel. This aligns with the standard BOSSbase1.01 sample images used. For feature extraction, a series of four convolution layers is utilized, with 16, 32, and 64 filters of sizes 3 × 3 and one filter of size 1 × 1. Batch normalization layers and ReLU layers are included between the convolution layers to speed up processing and perform non-linear operations.

Although we intentionally set the patches per image option in this network to “1” to accelerate the training phase, this resulted in the predicted denoised image not being the closest to the reference one. Increasing this option to a value of 3 or more can improve the prediction. The Adam loss function is used for fast convergence.

5.2 DC Coefficient as Part of the Solution

As it is known that the low-frequency coefficients constitute the main image’s informative components, denoisers can’t do a lot of modification within such coefficients, this is to avoid the main image’s features destruction. Thus, utilizing such coefficients for watermark hiding can provide more robustness against attacks. As the main informative coefficient of the DCT transform is the DC term, it may seem to be the best candidate for hiding the watermark information. This may be true for getting some extent of robustness, but certainly at the cost of losing imperceptibility. Furthermore, it shows a failure to some extent in resistance to volumetric and histogram equalization attacks due to the watermark energy concentration in a single frequency term.

Fig. 9 shows a sample of the BOSSbase1.01dataset watermarked image according to utilizing the DC for watermark information embedding, and its attacked versions by the various attack types. This figure also shows the extracted watermarks from their corresponding attacked cover images.

Figure 9: The image of the first row is a Watermarked image of size 512 × 512, the images of the second, and the fourth rows are attacked watermarked images by various attack types, the third and the fifth rows are for the extracted watermarks 64 × 64 from the attacked watermarked images

Table 1 shows three well-known fidelity measures which describe the MSE and structure similarity between the watermarked and the attacked watermarked image versions by various attack types. It is worth noting that, even though the PSNR and SSIM table entries show a high degree of watermarked image disruption due to the effects of the various attacks, the algorithm (utilizing the DC) withstands some attacks to some extent as it is obvious through the BER entries. It also shows high LA-SSIM values due to the implementation of the Weber-based JND model. Unfortunately, the algorithm fails to overcome the histogram equalization and volumetric scaling. The reason is that such attacks act to redistribute and modify the watermarked image pixels’ intensities and hence affect the watermark energy that is concentrated within the DC coefficient.

5.3 DC/ACs as a Complete Solution

For the sake of a fair assessment, the same sample image used in the previous DC implementation will be utilized to conduct the same experiments by implementing the DC/ACs ratio. Fig. 10 below shows the watermarked image according to this implementation along with its attacked versions by the various attack types. The extracted watermarks from their corresponding attacked cover images are also shown in this figure.

Figure 10: The image of the first row is a Watermarked image of size 512 × 512, the images of the second, and the fourth rows are attacked watermarked images by various attack types, the third and the fifth rows are for the extracted watermarks 64 × 64 from the attacked watermarked images

Spreading the watermark energy across multiple frequency terms instead of just focusing on the DC of the DCT transform helps retrieve more accurate watermark bits for histogram equalization and volumetric scaling. However, this approach can reduce the watermark’s robustness against some attacks (Table 2).

The algorithm spreads the embedded watermark energy across multiple coefficients of the cover image frequency domain. This makes attacks like histogram equalization and volumetric scaling have little degradation effect on the extracted watermark. However, the algorithm has limited resistance to JPEG compression attacks, as these attacks reduce data redundancy. This can cause loss to both the image and the embedded watermark information in removed coefficients. The algorithm depends on the Watson HVS-based model to determine the watermark energy share for each DCT coefficient based on their sensitivity before reaching one JND. This spreading process aims to make the watermark more imperceptible and less informative for the DnCNN feature extraction convolution layers. This may cause the network to mistake the network into determining watermarks as noise.

Histograms of Fig. 11 below show the absolute differences between the watermarked image and its various attacked versions. The difference dispersion across a wide range of these first row histograms reflects obvious dissimilarity between the image and its corresponding attacked versions, in terms of individual pixels. Thus, utilizing these pixels for the DM quantizers can lead to catastrophic watermark extraction BERs. the DC/ACs ratios for these image pairs tend to show less dispersion in this Figure’s second row. Thus, the stability of such ratios’ behavior before and after attacks leads us to use the quantization of these ratios for conducting the watermark embedding and extraction processes for their immunity against alteration under such attacks.

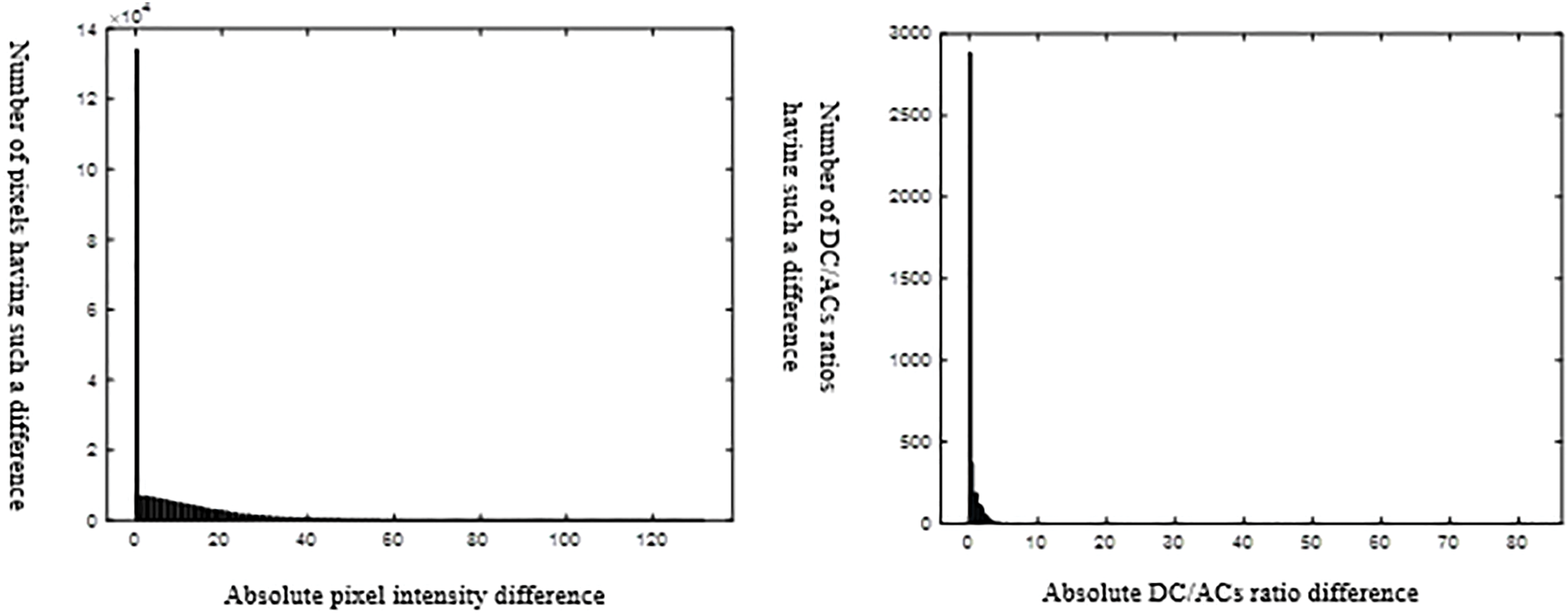
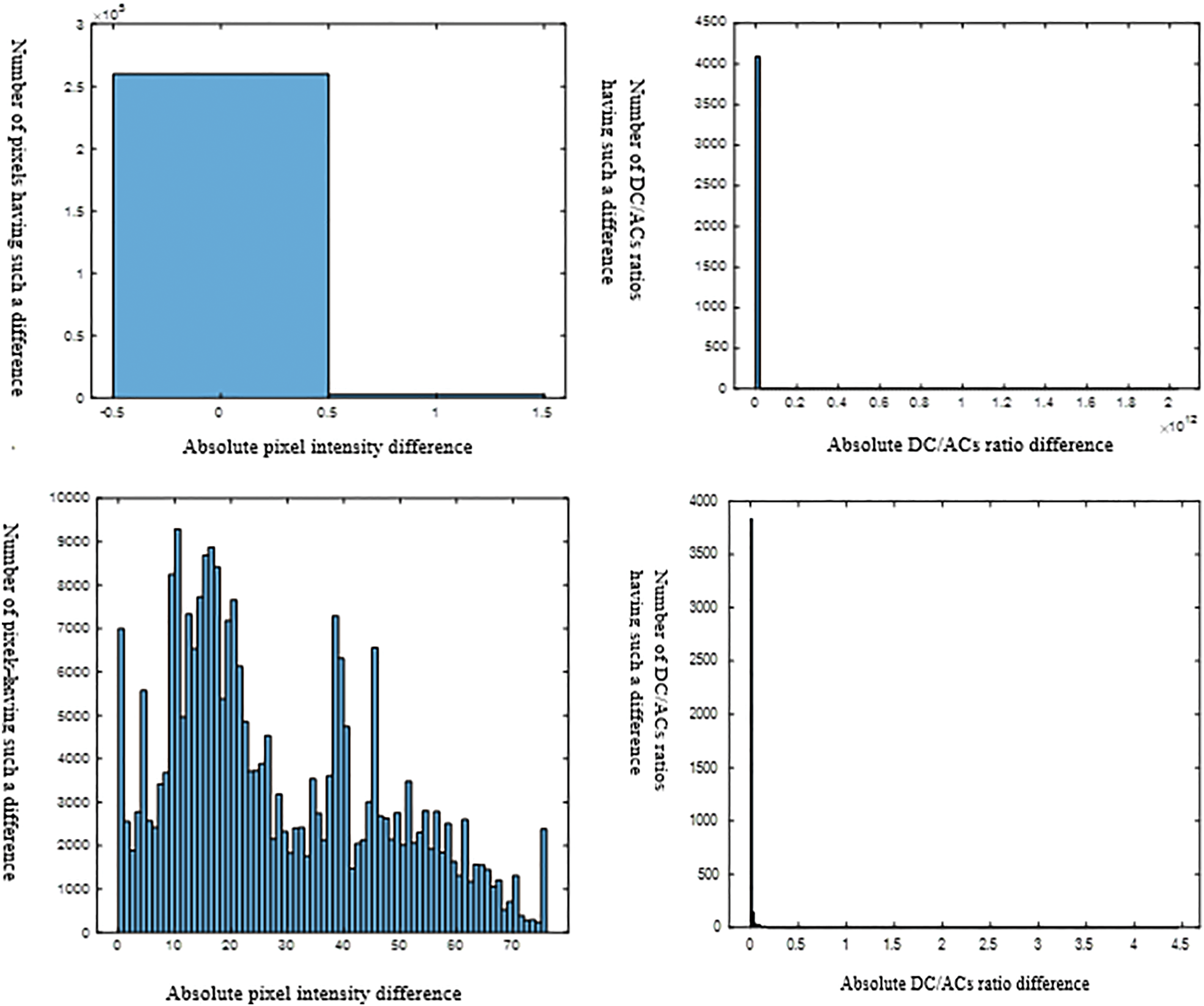
Figure 11: The first column, from top to bottom, displays histograms representing the absolute difference between the pixels of the watermarked image and the corresponding pixels of the attacked image for three types of attacks: denoiser, histogram equalization, and volumetric scaling respectively. The second column presents the same information, but instead of pixel values, it shows the absolute differences in terms of the DC/ACs ratio

Communication channels are designed to use the smallest file sizes possible for efficient transmission. As a result, files often need to be compressed and represented in various formats. Table 3 illustrates the effects of different compression formats on transmitted images, even with extreme compression ratios, such as a 30% quality factor, our proposed algorithm has a reasonable BER values.

6  Conclusion

In this paper, we implemented the DCT transform for watermark embedding. We conducted experiments using the low-frequency components of this transform to provide high protection for the embedded contents (watermark) against threats such as image processing operations and attacks. The experiments included using the direct current coefficient and the ratio of it to some mid-frequency AC coefficients. Both methods showed good resistance to the mentioned threats. The utilization of DM as one of the most robust watermarking algorithms contributed to increasing this robustness. We also considered watermark imperceptibility. To achieve this, we adopted Weber and Watson-based JND models to control the watermark embedding strength and its spread. The algorithm’s performance was evaluated using benchmark metrics to demonstrate its imperceptibility and robustness against threats. Additionally, we proposed a DnCNN architecture as a denoiser in this paper to serve as a basis for evaluating the algorithm’s robustness against recent trends of neural network attacks.

For future works, we should consider the system’s limitations to extend its utilization for various applications. For instance, this system is unsuitable for real-time applications due to its high complexity. To develop a more practical solution, future work should consider enhancing the system performance about time considerations and extending the used formats beyond the binary image currently used as a watermark. Additionally, while this system utilizes a single-channel (grayscale) image, it can be expanded to include three-channel (color) images, enhancing the watermark’s payload capacity. Furthermore, the system can be adapted for video applications, as each video frame can be treated as an image. Last, the system relies on a JND model to balance imperceptibility and robustness. However, JND models have intrinsic limitations, as they often rely on approximations of human perception that may not match all viewing conditions or all types of content. This bias may reduce the imperceptibility of the watermarking in some specific cases. In this sense, utilizing advanced artificial intelligent generative neural networks can contribute smartly for getting higher watermarked image fidelity and robustness.

Acknowledgement: It is our pleasure to express our appreciation and thanks to Ferdowsi University of Mashhad, Iran, and Imam Al-Kadhum College, Baghdad, Iraq, for their valuable assistance and encouragement in accomplishing this research.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Balsam Dhyia Majeed did the work design, analysis, and software writing. Amir Hossein Taherinia, Hadi Sadoghi Yazdi, and Ahad Harati drafted and revised the work, approved the publication of the version and agreed on all the aspects related to this work. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Available when requested.

Ethics Approval: Authors certify that they adhere to the ethical policies listed in this journal.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. L. Singh, A. K. Singh, and P. K. Singh, “Secure data hiding techniques: A survey,” Multimed. Tools Appl., vol. 79, no. 23–24, pp. 15901–15921, Jun. 2020. doi: 10.1007/s11042-018-6407-5. [Google Scholar] [CrossRef]

2. P. Kadian, S. M. Arora, and N. Arora, “Robust digital watermarking techniques for copyright protection of digital data: A survey,” Wirel Pers. Commun., vol. 118, no. 4, pp. 3225–3249, Jun. 2021. doi: 10.1007/s11277-021-08177-w. [Google Scholar] [CrossRef]

3. N. Agarwal, A. K. Singh, and P. K. Singh, “Survey of robust and imperceptible watermarking,” Multimed. Tools Appl., vol. 78, no. 7, pp. 8603–8633, Apr. 2019. doi: 10.1007/s11042-018-7128-5. [Google Scholar] [CrossRef]

4. S. B. B. Ahmadi, G. Zhang, and S. Wei, “Robust and hybrid SVD-based image watermarking schemes,” Multimed. Tools Appl., vol. 79, no. 1–2, pp. 1075–1117, Jan. 2020. doi: 10.1007/s11042-019-08197-6. [Google Scholar] [CrossRef]

5. S. Kumar, B. K. Singh, and M. Yadav, “A recent survey on multimedia and database watermarking,” Multimed. Tools Appl., vol. 79, no. 27–28, pp. 20149–20197, Jul. 2020. doi: 10.1007/s11042-020-08881-y. [Google Scholar] [CrossRef]

6. T. K. Araghi and D. Megías, “Analysis and effectiveness of deeper levels of SVD on performance of hybrid DWT and SVD watermarking,” Multimed. Tools Appl., vol. 83, no. 2, pp. 3895–3916, Jan. 2024. doi: 10.1007/s11042-023-15554-z. [Google Scholar] [CrossRef]

7. Y. Gangadhar, V. S. Giridhar Akula, and P. C. Reddy, “An evolutionary programming approach for securing medical images using watermarking scheme in invariant discrete wavelet transformation,” Biomed. Signal Process. Control., vol. 43, no. 12, pp. 31–40, May 2018. doi: 10.1016/j.bspc.2018.02.007. [Google Scholar] [CrossRef]

8. N. M. Makbol, B. E. Khoo, and T. H. Rassem, “Block-based discrete wavelet transform-singular value decomposition image watermarking scheme using human visual system characteristics,” IET Image Process., vol. 10, no. 1, pp. 34–52, Jan. 2016. doi: 10.1049/iet-ipr.2014.0965. [Google Scholar] [CrossRef]

9. C. X. Wang et al., “Robust image watermarking via perceptual structural regularity-based JND model,” KSII Trans. Internet Inf. Syst., vol. 13, no. 2, pp. 1080–1099, Feb. 2019. doi: 10.3837/tiis.2019.02.032. [Google Scholar] [CrossRef]

10. W. Wan et al., “Pattern complexity-based JND estimation for quantization watermarking,” Pattern Recognit. Lett., vol. 130, no. 9, pp. 157–164, Feb. 2018. doi: 10.1016/j.patrec.2018.08.009. [Google Scholar] [CrossRef]

11. T. Huynh-The, C. -H. Hua, N. A. Tu, and D. -S. Kim, “Robust image watermarking framework powered by convolutional encoder-decoder network,” in 2019 Digital Image Comput.: Techniq. Appli. (DICTA), IEEE, Dec. 2019, pp. 1–7. doi: 10.1109/DICTA47822.2019.8945866. [Google Scholar] [CrossRef]

12. L. Geng, W. Zhang, H. Chen, H. Fang, and N. Yu, “Real-time attacks on robust watermarking tools in the wild by CNN,” J. Real-Time Image Process., vol. 17, no. 3, pp. 631–641, Jun. 2020. doi: 10.1007/s11554-020-00941-8. [Google Scholar] [CrossRef]

13. A. Hmimid, M. Sayyouri, and H. Qjidaa, “Image classification using separable invariant moments of Charlier-Meixner and support vector machine,” Multimed. Tools Appl., vol. 77, no. 18, pp. 23607–23631, Sep. 2018. doi: 10.1007/s11042-018-5623-3. [Google Scholar] [CrossRef]

14. M. Yamni, H. Karmouni, M. Sayyouri, and H. Qjidaa, “Robust audio watermarking scheme based on fractional Charlier moment transform and dual tree complex wavelet transform,” Expert. Syst. Appl., vol. 203, Oct. 2022, Art. no. 117325. doi: 10.1016/j.eswa.2022.117325. [Google Scholar] [CrossRef]

15. S. S. Sharma and V. Chandrasekaran, “A robust hybrid digital watermarking technique against a powerful CNN-based adversarial attack,” Multimed. Tools Appl., vol. 79, no. 43–44, pp. 32769–32790, Nov. 2020. doi: 10.1007/s11042-020-09555-5. [Google Scholar] [CrossRef]

16. Q. Li and I. J. Cox, “Using perceptual models to improve fidelity and provide resistance to valumetric scaling for quantization index modulation watermarking,” IEEE Trans. Inf. Forensics Secur., vol. 2, no. 2, pp. 127–138, 2007. doi: 10.1109/TIFS.2007.897266. [Google Scholar] [CrossRef]

17. K. Zhou, Y. Zhang, J. Li, Y. Zhan, and W. Wan, “Spatial-perceptual embedding with robust just noticeable difference model for color image watermarking,” Mathematics, vol. 8, no. 9, Sep. 2020, Art. no. 1506. doi: 10.3390/math8091506. [Google Scholar] [CrossRef]

18. K. Zhang, W. Zuo, and L. Zhang, “FFDNet: Toward a fast and flexible solution for CNN-based image denoising,” IEEE Trans. Image Process., vol. 27, no. 9, pp. 4608–4622, Sep. 2018. doi: 10.1109/TIP.2018.2839891. [Google Scholar] [PubMed] [CrossRef]

19. C. Wang et al., “Wavelet-FCWAN: Fast and covert watermarking attack network in wavelet domain,” J. Vis. Commun. Image Represent, vol. 95, Sep. 2023, Art. no. 103875. doi: 10.1016/j.jvcir.2023.103875. [Google Scholar] [CrossRef]

20. M. W. Hatoum, J. -F. Couchot, R. Couturier, and R. Darazi, “Using deep learning for image watermarking attack,” Signal Process. Image Commun., vol. 90, Jan. 2021, Art. no. 116019. doi: 10.1016/j.image.2020.116019. [Google Scholar] [CrossRef]

21. Y. Zhang, Z. Wang, Y. Zhan, L. Meng, J. Sun and W. Wan, “JND-aware robust image watermarking with tri-directional inter-block correlation,” Int. J. Intell. Syst., vol. 36, no. 12, pp. 7053–7079, Dec. 2021. doi: 10.1002/int.22580. [Google Scholar] [CrossRef]

22. W. Wan, W. Li, W. Liu, Z. Diao, and Y. Zhan, “QuatJND: A robust quaternion JND model for color image watermarking,” Entropy, vol. 24, no. 8, Jul. 2022, Art. no. 1051. doi: 10.3390/e24081051. [Google Scholar] [PubMed] [CrossRef]

23. H. Fang, Z. Jia, H. Zhou, Z. Ma, and W. Zhang, “Encoded feature enhancement in watermarking network for distortion in real scenes,” IEEE Trans. Multimed., vol. 25, pp. 2648–2660, 2023. doi: 10.1109/TMM.2022.3149641. [Google Scholar] [CrossRef]

24. Y. Zhang, Y. Gong, J. Wang, J. Sun, and W. Wan, “Towards perceptual image watermarking with robust texture measurement,” Expert Syst. Appl., vol. 219, Jun. 2023, Art. no. 119649. doi: 10.1016/j.eswa.2023.119649. [Google Scholar] [CrossRef]

25. Q. Su and B. Chen, “Robust color image watermarking technique in the spatial domain,” Soft Comput., vol. 22, no. 1, pp. 91–106, Jan. 2018. doi: 10.1007/s00500-017-2489-7. [Google Scholar] [CrossRef]

26. P. Lefevre, D. Alleysson, and P. Carre, “A new blind color watermarking based on a psychovisual model,” J. Math. Neurosci., vol. 10, no. 1, Dec. 2020, Art. no. 17. doi: 10.1186/s13408-020-00094-9. [Google Scholar] [PubMed] [CrossRef]

27. S. -H. Bae and M. Kim, “A novel SSIM index for image quality assessment using a new luminance adaptation effect model in pixel intensity domain,” in 2015 Visual Commun. Image Process. (VCIP), IEEE, Dec. 2015, pp. 1–4. doi: 10.1109/VCIP.2015.7457810. [Google Scholar] [CrossRef]

28. M. W. Hatoum, R. Darazi, and J. -F. Couchot, “Normalized blind STDM watermarking scheme for images and PDF documents robust against fixed gain attack,” Multimed. Tools Appl., vol. 79, no. 3–4, pp. 1887–1919, Jan. 2020. doi: 10.1007/s11042-019-08242-4. [Google Scholar] [CrossRef]

29. Z. -R. Wang, J. Dong, and W. Wang, “Quantization based watermarking methods against valumetric distortions,” Int. J. Autom. Comput., vol. 14, no. 6, pp. 672–685, Dec. 2017. doi: 10.1007/s11633-016-1010-6. [Google Scholar] [CrossRef]