Hourglass-GCN for 3D Human Pose Estimation Using Skeleton Structure and View Correlation

1  Introduction

3D human pose estimation refers to estimating spatial coordinates of a set of specific joints of each human instance from images or videos. It has promising applications in monitoring, virtual reality, and human-robot interaction [1–4]. According to the view number of pose information adopted for estimating 3D poses, 3D pose estimation methods can be classified into monocular methods [5–7] and multi-view methods [8–11]. Under monocular camera configuration, not only the depth information in images is blurred but also partial joints are occluded [12,13], resulting in low pose estimation accuracy. The above problems are alleviated in multi-view methods on account of utilizing multi-view pose information.

To aggregate multiple-view pose information, some methods [14,15] projected estimated multi-view 2D heatmaps into 3D grids [16,17] as the 3D pose constraint space and applied 3D convolution neural networks [15,18] or Pictorial Structure Models [19] to estimate 3D poses. However, these methods associate the same joints in different views indirectly and require large amounts of computation, parameters, and memory. Some methods lifted 2D poses of the same joint from different views to 3D joint coordinates via the epipolar constraint [20,21] or differentiable Direct Linear Transform based on the Singular Value Decomposition [22] or Shifted Iterations method [14] when camera projection matrices were given. Although the triangulation method directly associates the same joints in different views, the algebraic approach cannot learn sufficient correlations between multi-view poses. Moreover, the correlations between different human joints are not exploited in above methods, illustrating that skeleton structure information was not utilized. Skeleton structure information has been verified to be beneficial to monocular 3D pose estimation [23–26] since skeleton priors alleviate the occlusion and depth ambiguity problem. However, there has been no research introducing the skeleton graph into multi-view 3D pose estimation.

Graph Convolutional Networks were introduced to process unstructured data such as skeleton graphs. GCNs can be divided into spectral-based GCNs [27,28] and non-spectral-based GCNs [29], spectral-based GCNs are suitable to deal with graphs with fixed topology such as the skeleton graph. In general graph convolutional operations [30,31], all pairs of neighboring nodes share the same correlation weight. To extract various graph features, neighborhood nodes of each node in a single-view skeleton graph were divided into three categories in the graph convolution operations [32,33], with different weights learned to represent the correlations between each node and its different categories of neighborhood nodes. Nevertheless, the correlations between the same joints from different views are not modelled. Additionally, extracted skeleton structure features are not elaborate enough since the correlation weights between all nodes in the graph and their neighborhood nodes of a certain category are still shared. For example, the shoulder, elbow, and hand joints have corresponding symmetric neighborhood nodes. It is unreasonable for each pair of symmetric nodes to share the same correlation weight because of the specificity of different joints. To be specific, these joints have different degrees of freedom or derive from different views.

To extract high-level skeleton structure features to estimate 3D poses from 2D skeleton graphs, some methods [34,35] stacked multiple graph convolution layers to perform on skeleton graphs at the original scale. Transformer architecture [36] used multi-head graph self-attention blocks to capture local information between adjacent nodes and long-range dependencies between joints in the spatiotemporal domain. High-order graph convolution utilized multi-hop neighborhoods [37] to capture dependencies between nodes at different hop distances. However, these methods make it difficult to extract global skeleton features efficiently in computation complexity and network parameters. To comprehensively analyze local-to-global skeleton graph structure, some methods [38–40] adopted the high-to-low and low-to-high architectures to extract structure features of multi-scale skeleton graphs. A local-to-global hierarchical graph convolution architecture [39,41] was adopted to exploit multi-scale graph representation. However, these methods construct complicated network structures or do not perform graph convolution operations in the low-to-high process to obtain deep-level semantic information at various scales.

To address the aforementioned problems, firstly, pre-estimated multi-view 2D poses are designed into a multi-view skeleton graph to introduce skeleton graphs into multi-view pose estimation, which fuses skeleton features and view correlations explicitly to process occlusion problem. As shown in Fig. 1, the skeleton-edge and symmetry-edge in each view of skeleton graph respectively represent the structure correlations between kinematically connected joints and the symmetry correlations between limb joints, the view-edge represent the view correlations between the same joints in different views. Subsequently, to express various skeleton structure priors and view fusion information, neighborhood nodes of each node are divided into seven categories consisting of three physically connected joints, one symmetry joint and three joints in the other views, with different correlation weights assigned to different categories. Based on this, different weights are assigned to each node in the graph to distinguish the characteristics of different joints for further representing more elaborate correlations between all nodes and their neighborhood nodes of the same category. Finally, according to the graph convolution operation proposed above, a Residual Graph Convolution (RGC) module is designed as the basic module. Inspired by the Stacked Hourglass Network [42], RGC module is combined with the simplified Hourglass architecture to construct the Hourglass-GCN as our 3D pose estimation network. Hourglass-GCN is a symmetrical network composed of graph convolution, graph pooling, graph upsampling and skip connection components which are all designed to be concise. Hourglass-GCN processes three scales of multi-view skeleton graphs to extract local-to-global scale and shallow-to-deep level skeleton semantic information and view correlations efficiently. Experimental results on common large 3D human pose dataset Human3.6M and MPI-INF-3DHP show that Hourglass-GCN outperforms some excellent methods in 3D pose estimation accuracy.

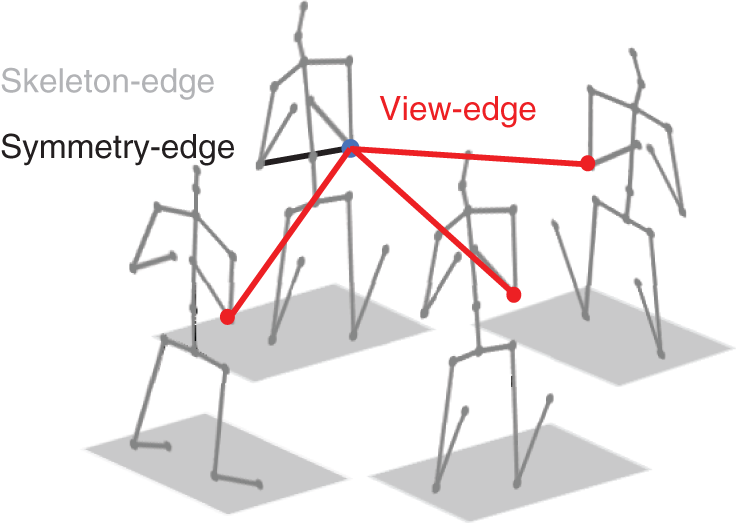
Figure 1: Constructed multi-view skeleton graph. To avoid messy lines, only the symmetry-edge (black line) and view-edge (red lines) associated with the right elbow joint (blue node) in one view, and all skeleton-edges (grey lines) in multiple views are represented, other edges are omitted

Main contributions of this study are summarized as follows:

(1)   Pre-estimated multi-view 2D poses are designed as a multi-view skeleton graph, with the skeleton-edge and symmetry-edge representing the skeleton structure information and the view-edge explicitly modelling the correlations between different views of joints.

(2)   To extract elaborate skeleton structure information and view correlations, neighborhood nodes of each node are divided into seven categories, with different correlation weights assigned to different categories of neighborhood nodes and different nodes in the graph to represent the correlations between all nodes and their neighborhood nodes of several categories.

(3)   A Residual Graph Convolution module is designed as the basic module and combined with the simplified Hourglass architecture to construct a symmetrical and concise Hourglass-GCN as our 3D pose estimation network. Hourglass-GCN processes three scales of multi-view skeleton graphs to extract local-to-global scale and shallow-to-deep level graph features efficiently.

2  Method

The general architecture of our multi-view 3D pose estimation model is described in Fig. 2. A set of 2D joint locations are estimated from multiple views of synchronous images respectively through an off-the-shelf trained cascaded pyramid network [43]. 2D poses are constructed to be a multi-view skeleton graph as the input of Hourglass-GCN to predict multi-view 3D joint locations. The loss function concludes the 3D pose loss and symmetry loss. Some individual components are introduced in detail below.

Figure 2: General framework of our 3D pose estimation model. Multi-view 2D poses are constructed to be a multi-view skeleton graph as the input of our 3D pose estimation network Hourglass-GCN

2.1 Fusing Skeleton Structure and View Correlation

As shown in Fig. 1, multi-view 2D poses are constructed as a multi-view skeleton graph ς=(V,ε,A) to fuse skeleton structure and view correlation, where V={vpm|p=1,…,P; m=1,…,M} denotes all nodes in the graph with P views and M joints in each view. ε={eij|i,j∈V} denotes all edges in the graph, representing the correlations between neighboring nodes. All edges are divided into three parts: (1) skeleton-edge: direct physical connections between adjacent joints in each view of skeleton graph; (2) symmetry-edge: indirect connections between symmetric limb joints; (3) view-edge: connections between the same joints in different views of graphs. The skeleton-edge and symmetry-edge represent the skeleton structure information, and the view-edge represent the multi-view pose correlation information. A=(aij)n×n with n=P×M is the adjacency matrix, representing the connectivity between all nodes, where aij=1 if (i,j)∈ε and aij=0 if (i,j)∉ε.

2.2 Extracting Elaborate Multi-View Skeleton Graph Features

A common graph convolutional operation [31] in Eq. (1) is applied as the baseline for processing multi-view skeleton graphs. Xl∈Rn×Dil and Xl+1∈Rn×Dol denote the node features of the input graph and output graph of the l graph convolution layer, respectively, where n denotes the node number in the graph, Dil and Dol represent the feature dimensions for each node. The graph convolutional operation involves the following steps. First, Xl is multiplied by Wl∈RDil×Dol, denoting a common convolution operation on the input graph through Dol filters with kernel size (Dil,1). Second, feature of each node is updated by associating with the correlative features of its neighborhood nodes through multiplying a normalized adjacency matrix A^=D−1/2A~D−1/2, where A~=IN+A and Dii=∑jA~ij. Finally, ReLU is adopted as the activation function σ(⋅) to increase the nonlinearity.

Xl+1=σ(A^XlWl)(1)

In Eq. (1), all edges in the graph represent the same correlation weight Wl. Considering the diversity of spatial connection structures between joints and the differences between multi-view pose information, neighborhood nodes of each node are first divided into four categories in each single-view skeleton graph and then divided into three categories to distinguish the pose information from other views. The multi-view skeleton graph in Fig. 2 depicts different colors of dots to denote different categories of neighborhood nodes: 1) the center node itself (black); 2) a node (green) which is directly connected to the center node in the skeleton and has a shorter path to the root node (grey); 3) a node (red) which is directly connected to the center node and has a longer path to the root node; 4) a node (yellow) which is symmetric with the center node; 5) a node (blue) that represents the same joint as the center node in the second view; 6) a node (purple) that represents the same joint in the third view; 7) a node (brown) that represents the same joint in the fourth view. The root node points to the abdomen joint. The right elbow joint is taken as an example of the center node. Colorful solid lines represent different correlations between one center node and its neighborhood nodes. Different learnable weights are set to represent the correlations between each node and different neighborhood nodes. Accordingly, the graph convolutional operation in Eq. (1) is transformed into Eq. (2), where c is the category index, Wcl is the convolution kernel weight for the c category of neighborhood nodes. A^c represents the adjacency matrix between n nodes and their c type of neighborhood nodes, where A^=∑c=17A^c.

Xl+1=σ(∑cA^cXlWcl)(2)

However, the specificity of different nodes in the graph is not considered in Eq. (2). Therefore, different learnable weights are assigned to each node when learning the correlations between all nodes and a certain category of neighborhood nodes to further learn elaborate skeleton structure information and view correlation information. Modified graph convolutional operation is written in Eq. (3), where Fc∈Rn×Dol is a learnable weight matrix for n nodes and Dol−dimensional features per node, and ⊙ denotes the dot product operation between two matrices.

Xl+1=σ(∑cA^cXlWcl⊙Fc)(3)

2.3 Hourglass-GCN for 3D Pose Estimation

Based on the graph convolution operation proposed above, a Residual Graph Convolution (RGC) module is designed as the basic module. In Fig. 3a, the RGC module is composed of a GCN Unit and a Per-Node Feature Fusion (FF) layer. GCN Unit in Fig. 3b implements the weighted feature fusion of neighboring nodes, where matrix multiplication operation is conducted between a learnable weight matrix FC for n nodes and constant adjacency matrix A^C to obtain the correlation weight matrix between neighboring nodes, which represents the skeleton structure information and view correlations. Per-Node FF layer in Fig. 3c performs 1×1 convolution to fuse multi-dimensional features for each node.

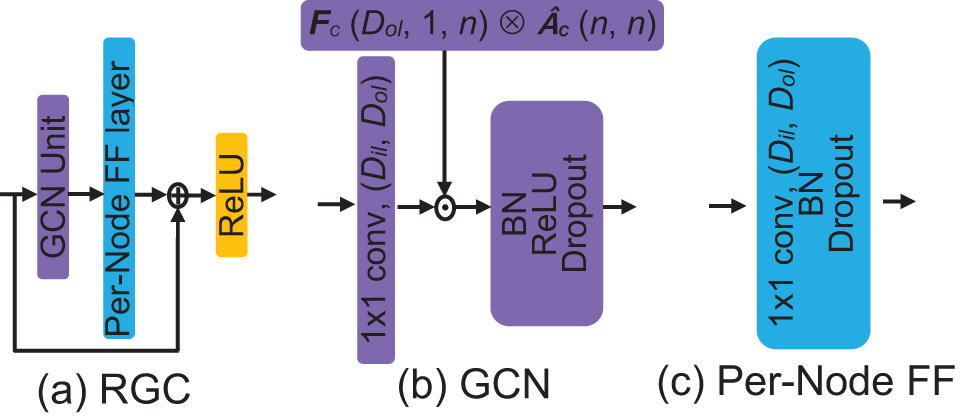
Figure 3: Structure of the Residual Graph Convolution (RGC) module. (b) and (c) represent the detailed GCN Unit and Per-Node FF layer in (a), ⨀ represents the element-wise product operation, ⊗ represents the matrix multiplication operation

RGC is combined with the simplified Hourglass architecture to construct the Hourglass-GCN as our 3D pose estimation network. In Fig. 4, Hourglass-GCN processes three scales of multi-view skeleton graphs to extract local-to-global scale and shallow-to-deep level skeleton semantic information and view correlations efficiently. High-to-low and low-to-high processes of the Hourglass-GCN are symmetrical. Hourglass-GCN is composed of graph convolution, graph pooling, graph upsampling, and skip connection components which are all designed to be concise. The graph pooling layer transforms large scales of skeleton graphs into small scales of graphs to obtain local-to-global graph representation. The first graph pooling layer pools the trunk and limb nodes separately. The second pooling layer pools the five nodes obtained above in each view of skeleton graph. Skip layer performs the element-wise sum operation between graph features at the same scale to preserve low-level graph spatial information.

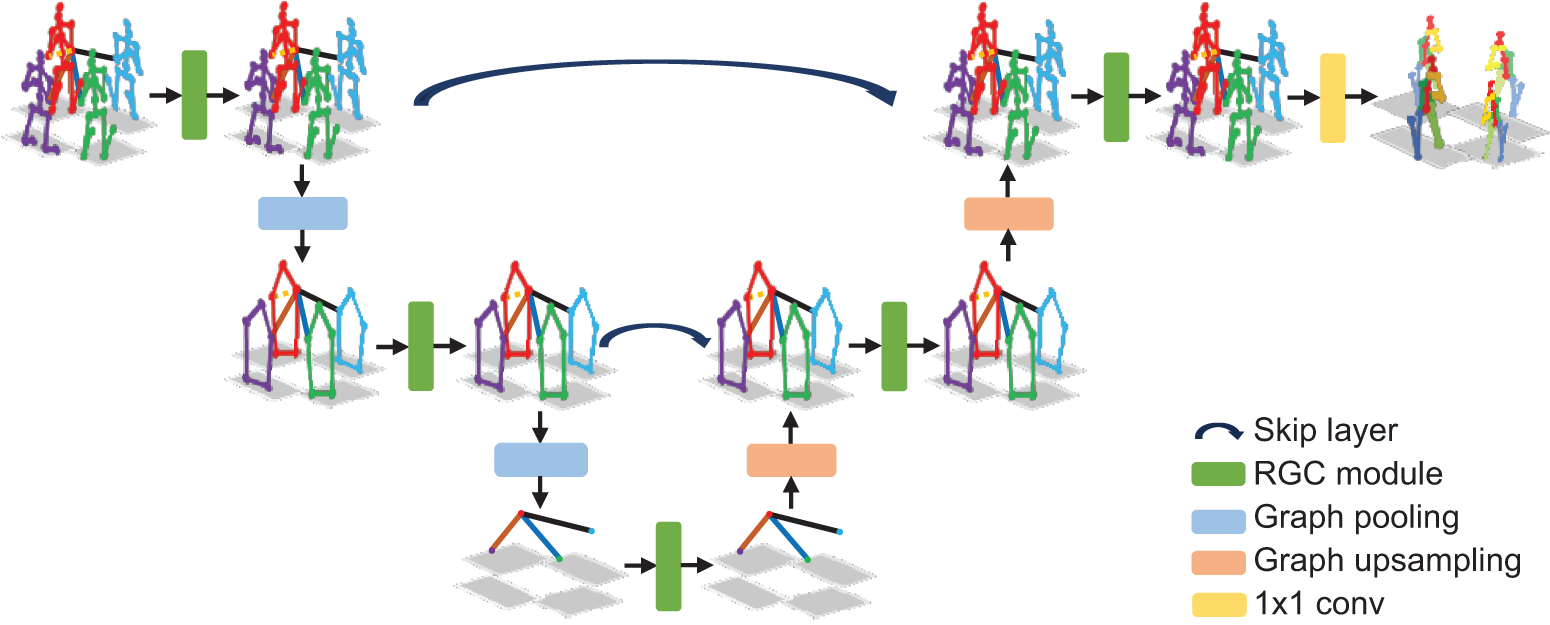
Figure 4: Network architecture of the Hourglass-GCN which processes three scales of multi-view skeleton graphs

2.4 Loss Function

When training Hourglass-GCN, the loss function consists of the 3D pose loss LP and symmetry loss LS. In Eq. (4), LP is defined as the mean square error of the estimated and ground truth 3D joint positions, where jpm~ and jpm represent the estimated and ground truth 3D joint position of joint m in view P.

In Eq. (5), LS measures the difference between corresponding bone pairs in the left and right body parts to make generated 3D poses structurally reasonable, where BPb is the length of bone b in the left body in view P and r(b) is the corresponding right bone. The final loss function L defined in Eq. (6) is taken as the linear combination of LP and LS, where λP=1 and λS=0.01.

LP=∑p=1P∑m=1M‖jpm~−jpm‖22(4)

LS=∑p=1P∑b‖Bpb−Bpr(b)‖22(5)

L=λPLP+λSLS(6)

3  Experiments

In this section, datasets and implementation details for training and evaluating the 3D pose estimation network are introduced first, then ablation studies on some components of our model are conducted. Finally, the results of our method are compared with some existing methods.

3.1 Dataset

Human3.6M Dataset. Human3.6M [44] is one of the largest datasets for 3D pose estimation, containing 3.6 million images captured from four different camera views. There are eleven subjects consisting of five women and six men performing fifteen typical activities in the indoor environment, such as discussion, talking on the phone, walking, and eating. S1, S5, S6, S7 and S8 are used for training and S9, S11 are used for testing. Ground truth 3D joint positions are recorded by the Vicon Motion Capture System, and the ground truth 2D joint positions of each human instance and camera parameters are also included in this dataset. The pose of each instance contains 17 specific joints. Most work adopts the mean per joint position error (MPJPE) between the estimated and ground truth 3D joint position as the performance evaluation index in millimeters (mm).

MPI-INF-3DHP. MPI-INF-3DHP [45] is a large 3D pose dataset containing more than 1.3 million frames deriving from four male and four female subjects taken from different views. Subjects perform diverse actions in indoor and outdoor scenes. Test set contains about 3000 frames from 6 subjects. Image sequences of two subjects and training sets are from indoor scenes with green screens, the other two sequences are from indoor scenes without green screens, the remaining two sequences are from outdoor scenes. The Percentage of Correct Keypoints (PCK) within 150 mm and the Area Under the Curve (AUC) are common test metrics.

3.2 Implementation Details

In our experiments, node features of the input graph were fed into a batch normalization layer to keep data distribution consistent. Our model was implemented under the PyTorch framework, which was trained for 200 epochs using Adam optimizer with a batch size of 256. The learning rate was initially set to 0.0005 and was reduced by 0.95 times after each epoch with a decay rate reduced by 0.5 times after every five epochs. All experiments were conducted on one GeForce GTX 1080 GPU with CUDA 9.0.

3.3 Ablation Studies

3.3.1 Influence of the Number of Views in the Graph

To explore the influence of the number of views in our constructed graph on 3D pose estimation, the number of views was set to one, two, three, and four, and experiments were conducted, respectively. The seventh, sixth, and fifth categories of neighborhood nodes in the four-view graph were gradually excluded with the view number decreasing from four to one. Table 1 shows the MPJPE of estimated 3D poses and the inference rate on a desktop computer with Intel(R) Core (TM) i7-7700 CPU @ 3.60 GHz when the number of views takes different values. With the number of views increasing from one to three, MPJPE is reduced from 51.55 to 30.55 mm, indicating that skeleton graphs with more views contain richer pose information and view correlations to be beneficial to pose estimation accuracy. When the view number changed from three to four, the pose error is reduced by only 0.9 mm, meaning that the pose information and view correlations are close to saturation. Moreover, the increase in the view number leads to the increased computational complexity of the model. The inference rate decreases from 59 frames/s to 18 frames/s. To balance the estimation accuracy and inference rate, the number of views was set to three in subsequent experiments.

3.3.2 Influence of the Types of Edges Contained in the Graph

To prove the effectiveness of a constructed skeleton graph, three variants of the three-view skeleton graph were designed: a) A graph with no edge; b) A graph with the skeleton-edge; c) A graph with the skeleton-edge and symmetry-edge. Experiments were conducted with graphs containing different types of edges. Since pose errors of extremity joints are relatively larger than those of the other joints, Table 2 shows pose errors of the hand and ankle joints and MPJPE to observe the influence of various edges on pose estimation. When the graph contains no edge, pose errors of the hand and ankle joints are larger than the errors in the graph with edges. Graph with no edge degenerates into a set of discrete nodes, meanwhile, corresponding graph convolutional operation transforms into ordinary convolution operation which cannot model joint correlations explicitly. With the skeleton-edge adding to the graph, MPJPE is reduced from 38.22 to 33.96 mm to verify the promotion of skeleton structure information between physically connected joints to pose estimation. With the symmetry-edge added subsequently, MPJPE is reduced by 0.81 mm. Skeleton symmetry has few constraints on pose estimation because of the weak symmetry of most human poses. Addition of the view-edge reduce MPJPE by 2.6 mm, indicating that extracting explicit correlations between the same nodes from different views completely fuse multi-view pose information.

To explore the effect of various edges on pose estimation intuitively, Fig. 5 shows the normalized correlation weights between the center nodes (take right elbow and left knee joints for example) and their neighborhood nodes in three variants and proposed three-view skeleton graph. In Fig. 5a, center nodes are affected by themselves since there are no edges in the graph. In Fig. 5b, addition of two skeleton-edges makes the weight associated with the right elbow node itself reduce from 1 to 0.292, indicating that adjacent joints contain more pose information than the center joint itself. In Fig. 5c, correlation weights represented by the symmetry-edge are 0.215 and 0.229, which are smaller than the other weights, confirming that the symmetry of limb joints is not strong in human poses. In particular, joints with a higher degree of freedom have weaker symmetry constraints. In Fig. 5d, weights of the newly added view-edge are larger than those of most other edges, indicating the significant relevance between the same joints in different views, hence explicit view correlations are critical for multi-view 3D pose estimation.

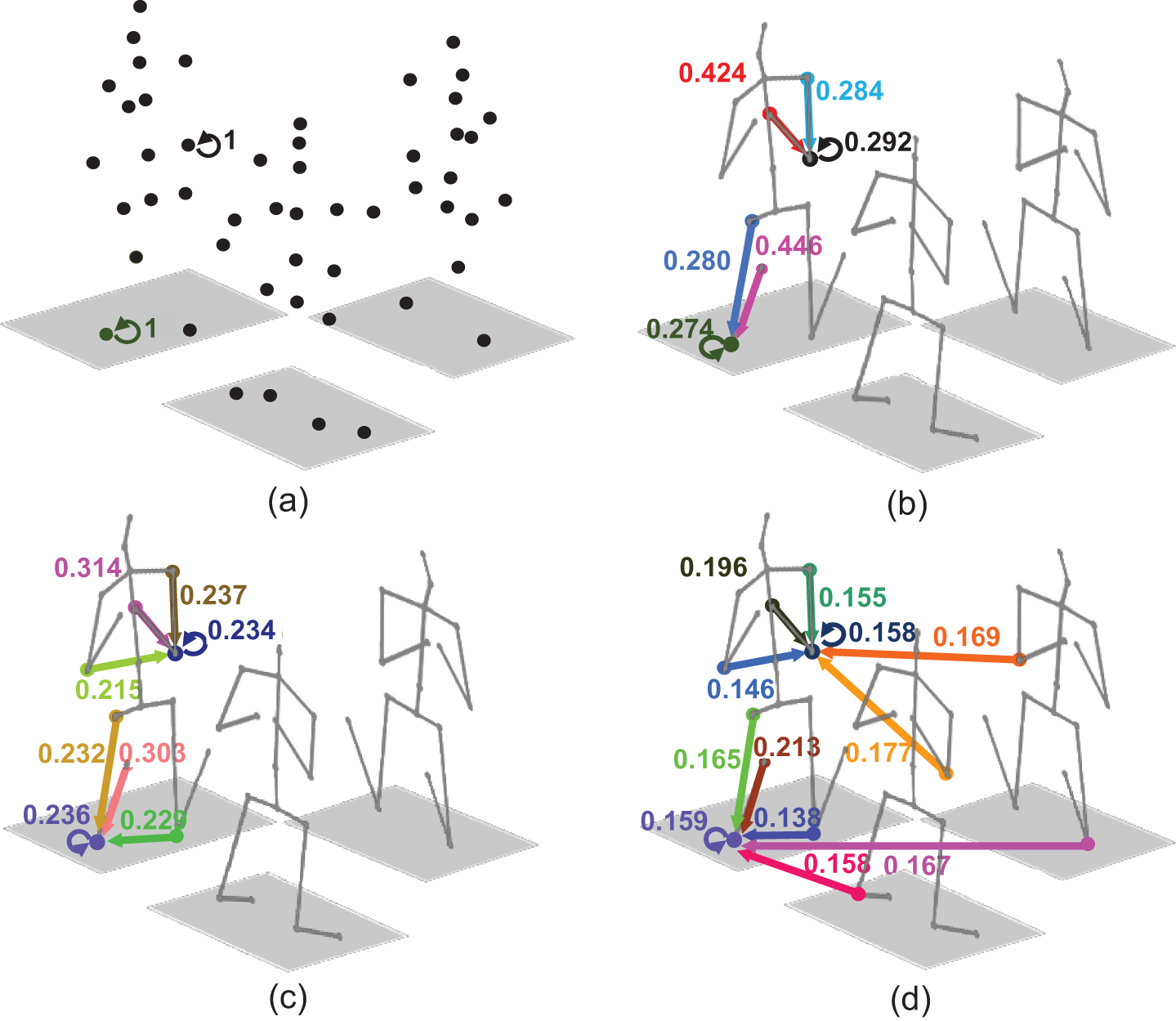
Figure 5: Normalized correlation weights between two joints and their neighborhood nodes in three variant graphs and proposed three-view skeleton graph. To avoid clutter lines, only the edges of the right elbow and left knee joints in one view are shown in (a)–(d), with different colors of solid lines representing different correlation weights

3.3.3 Influence of the Diversity of Correlation Weights between Nodes

To validate the influence of the diversity of correlation weights between nodes in the graph convolutional operation on 3D pose estimation, a variant of the graph convolutional operation proposed in Section 2.2 was designed that neighborhood nodes were divided into three categories including the nodes connected to the center node through the skeleton-edge, symmetry-edge and view-edge to represent different correlation weights. In addition, all pairs of neighboring nodes shared the same correlation weight in the baseline graph convolution. Based on Eq. (2) in Section 2.2, neighborhood nodes in the three-view skeleton graph were divided into six categories. In Eq. (3), when modeling the correlations between neighboring nodes in each of the six categories, adaptive weights were assigned to 51 nodes in the three-view graph, so 306 kinds of weights were learned to represent correlations between nodes.

When the diversity of correlation weights increases from 1 to 306, trends of the hand and ankle joint pose estimation errors and the average error are shown in Fig. 6. Errors decrease continuously as the diversity of weights increases. The average error is reduced by about 33% when the diversity increases from 1 to 306, indicating that more diverse correlation weights between nodes can extract more elaborate skeleton structure information and view correlations which are beneficial to multi-view 3D pose estimation.

Figure 6: Pose estimation errors of the hand and ankle joints and the average error of all joints when the diversity of correlation weights between nodes in the three-view skeleton graph is 1, 3, 6, and 306

Fig. 7 intuitively shows the influence of the diversity of correlation weights on the pose estimation. In Fig. 7a, correlation weights between the center nodes and six categories of neighborhood nodes are the same, so weights are all one-sixth. In Fig. 7b, sums of the correlation weights represented by three skeleton-edges, one symmetry-edge, and two view-edges are 0.429, 0.239, and 0.332, respectively. The skeleton-edge plays a more important role than the view-edge and the symmetry-edge. In Fig. 7c, different correlation weights are assigned to three skeleton-edges, where the weight (0.143) of the third category of neighborhood node is bigger than the weight (0.130) associated with the second category, indicating that the neighborhood node whose path to the root node is longer is more relevant to the center node. Different weights represented by two view-edges confirm that the left knee joints in the other two views contain different amounts of pose information about the joint in the main view. In Fig. 7d, correlation weights related to the left knee node are entirely different from those related to the right elbow node. Nodes in the graph have different characteristics, which should be distinguished to obtain elaborate graph representation.

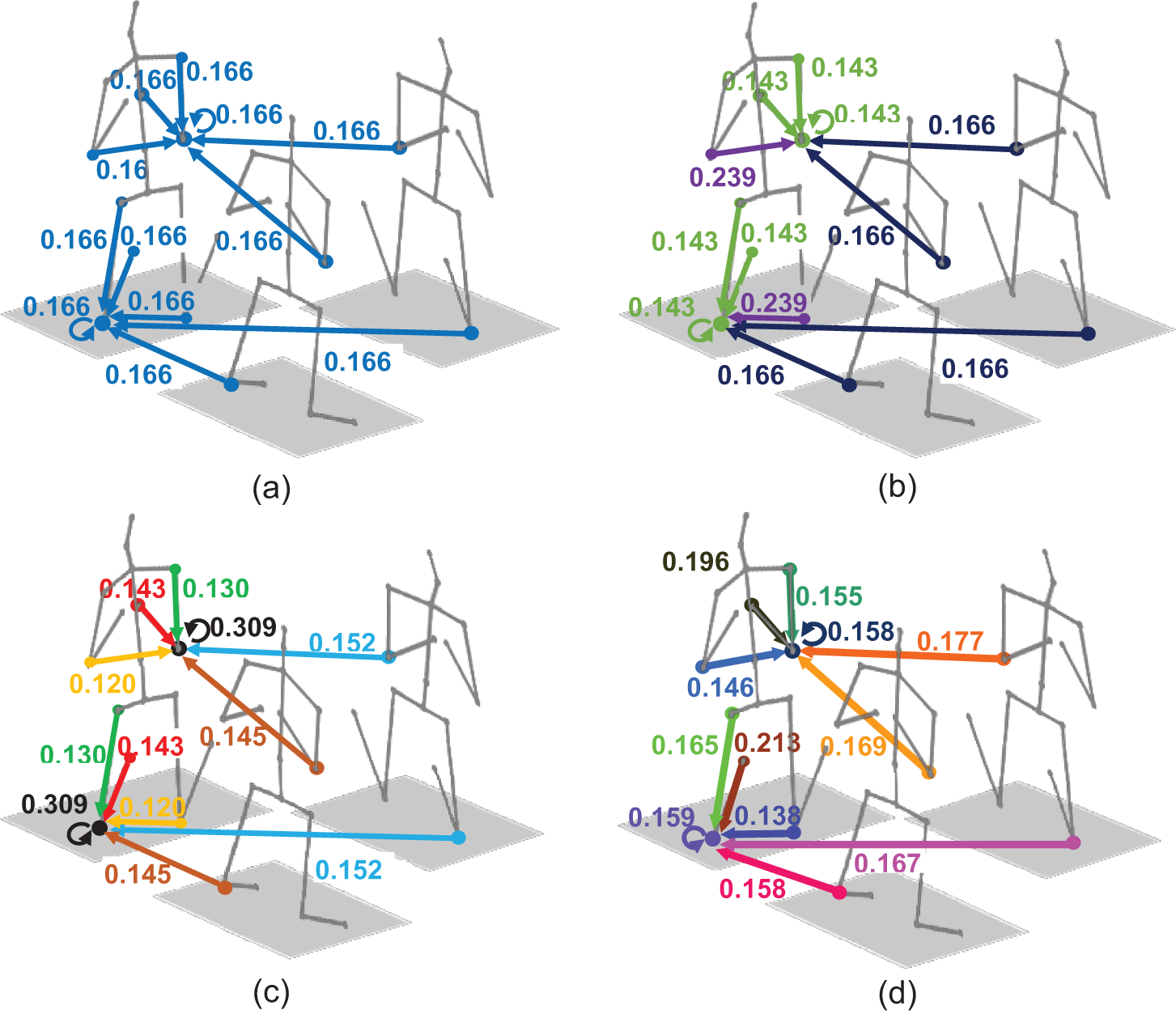
Figure 7: Normalized correlation weights between the center nodes (take the right elbow and left knee joint for example) and their neighborhood nodes. (a)–(d) respectively follow the baseline graph convolution operation, the variant, and two graph convolutional proposed in Section 2.2. Different colors of edges represent different weights

3.3.4 Influence of the Configurations of Hourglass-GCN

To explore the influence of several hyperparameters on the performance of Hourglass-GCN, a comparison of test errors on Human3.6M under different configurations is listed in Table 3. As can be seen, MPJPE decreases by 1.83 mm when the number of RGC modules contained in Hourglass-GCN increases from 4 to 6. However, increasing the number of RGC to 8 and 10 results in an increase in MPJPE from 30.55 to 30.75 and 30.92 mm, respectively. When the combination of node feature dimensions of three scales of multi-view skeleton graphs is (128, 256, 512), the model achieves the best performance. Increasing the dimensions to (192, 384, 768) or reducing them to (64, 128, 256) results in a performance degradation of 0.16 and 1.53 mm, respectively. Appropriate graph convolution depth and graph feature width are necessary to obtain discriminant graph representation to avoid underfitting and overfitting. Value change of batch size has a slight impact on MPJPE, and a batch size of 128 yields the best performance.

3.3.5 Influence of the 3D Pose Estimation Network Structure

To demonstrate the superiority of proposed Hourglass-GCN, four variants were designed: (1) ResGCN in Fig. 8a that stacked several RGC modules to perform on the origin-scale graph; (2) MSGCN in Fig. 8b that utilized RGC modules to process multiple scales of skeleton graphs in the high-to-low process and applied none graph convolution operation in the upsampling process; (3) HourglassGCN-NoSkip that represented the Hourglass-GCN without skip layer; (4) HourglassGCN-NoFF that represented the Hourglass-GCN without Per-Node FF layer. Four variants and Hourglass-GCN respectively process three-view skeleton graphs to estimate 3D poses, obtained test errors on Human3.6M are shown in Table 4.

Figure 8: Variants of the Hourglass-GCN. (a) ResGCN; (b) MSGCN

The test error of ResGCN is larger than the other networks. It is difficult to extract global and multi-scale graph features for ResGCN which only processes the single-scale skeleton graph. The error of MSGCN is 1.37 mm larger than that of the Hourglass-GCN because MSGCN neglects the upsampling process, thus not utilizing deep-level skeleton semantic information at multiple scales. Errors of HourglassGCN-NoSkip and HourglassGCN-NoFF are respectively 1.21 and 1.53 mm larger than that of the Hourglass-GCN. Since accurate graph spatial information is partially lost during the downsampling process, skip layers transfer the spatial information from shallow layers to deep layers. Besides, Per-Node FF layer fuses the multi-dimensional features of each node to generate deeper graph node features.

3.4 Quantitative Comparison with Existing Methods

Table 5 shows the quantitative comparison of our method with some existing 3D pose estimation methods on Human3.6M. MPJPEs of GCN-based monocular methods are generally smaller than common monocular methods, which is an inspiration to introduce skeleton structure information into the multi-view 3D pose estimation to improve the estimation accuracy. The average MPJPE of existing multi-view methods is 33.3 mm, confirming that fusing multiple views of pose information evidently improves the pose accuracy when compared with monocular methods. When the view number is four, our method achieves the minimum error of 29.4 mm, which is 3.9 mm smaller than the average error of multi-view methods. This progress is owing to constructing a multi-view skeleton graph and learning adaptive correlation weights between nodes to completely fuse multi-view pose information and extract elaborate skeleton features.

Table 6 shows the comparison with some existing methods on MPI-INF-3DHP. It can be observed that multi-view methods outperform monocular methods on account of richer pose information and view correlation features provided by multi-view model input. In comparison to the best performing multi-view method, our model exhibits relative improvements of 0.43% and 8.7% in terms of the PCK and AUC metrics on MPI-INF-3DHP, respectively, indicating that combining skeleton priors with multi-view pose information is effective in improving the pose estimation accuracy.

3.5 Qualitative Results of Hourglass-GCN

To evaluate the pose estimation performance of our model intuitively, qualitative 3D pose estimation results of some images in the Human3.6M test set are shown in Fig. 9. Three-view synchronized images are input into our model to estimate multi-view 3D poses. For simplicity, only the 3D poses corresponding to the middle-view images are displayed in the last two rows of Fig. 9. Estimated 3D skeleton graphs have high similarity with the target skeleton graphs. 3D positions of some occluded joints in the image can be estimated accurately on account of the precise skeleton structure and view correlation information. We also explored some instances with failure poses. The right two columns of Fig. 9 show failure cases from the “Sitting Down” action in Human3.6M. As can be seen, under some circumstances of severe occlusion or unusual human poses, estimated poses have low similarity with the target poses.

Figure 9: Qualitative results of our method on the Human3.6M test set. The first three rows list synchronized images from three views, and the last two rows display the ground truth and estimated middle-view 3D poses

4  Conclusion

In this paper, to fuse skeleton priors and view correlations to tackle the occlusion problem in multi-view 3D pose estimation, estimated multi-view 2D poses are designed into a multi-view skeleton graph. Different correlation weights are assigned to different categories of neighborhood nodes and further assigned to each node in the graph to make graph convolution operation mine elaborate skeleton graph features. Based on the proposed graph convolution operation, a Residual Graph Convolution module is designed as the basic module of a symmetric and concise Hourglass-GCN as our 3D pose estimation network to process three scales of multi-view skeleton graphs for extracting local-to-global scale and shallow-to-deep-level skeleton features efficiently. Experimental results on the Human3.6M and MPI-INF-3DHP datasets indicate that our method outperforms existing methods in 3D pose estimation accuracy and estimates 3D positions of some occluded joints accurately. The limitation of our method is that temporal information is not exploited to further tackle the occlusion problem. The performance of our method can potentially be improved by adding the long-term temporal consistency between frames.

Acknowledgement: The authors would like to thank the editors and reviewers for their valuable work.

Funding Statement: This work was supported in part by the National Natural Science Foundation of China under Grants 61973065, U20A20197, 61973063.

Author Contributions: Ange Chen: Conceptualization, Methodology, Software, Writing—original draft. Chengdong Wu: Supervision, Writing—review & editing. Chuanjiang Leng: Data curation, Visualization. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets generated and/or analyzed during the current study are available from the corresponding author on reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. A. K. Patil, A. Balasubramanyam, J. Y. Ryu, B. Chakravarthi, and Y. H. Chai, “An open-source platform for human pose estimation and tracking using a heterogeneous multi-sensor system,” Sensors, vol. 21, no. 7, 2021, Art. no. 2340. doi: 10.3390/s21072340. [Google Scholar] [PubMed] [CrossRef]

2. M. M. Afsar, S. Saqib, Y. Y. Ghadi, S. A. Alsuhibany, A. Jalal and J. Park, “Body worn sensors for health gaming and e-learning in virtual reality,” Comput. Mater. Contin., vol. 73, no. 3, pp. 4763–4777, 2022. doi: 10.32604/cmc.2022.028618. [Google Scholar] [CrossRef]

3. Y. Cheng, P. Yi, R. Liu, J. Dong, D. Zhou and Q. Zhang, “Human-robot interaction method combining human pose estimation and motion intention recognition,” in Proc. IEEE 24th Int. Conf. Comput. Support. Coop. Work. Des., Dalian, China, May 5–7, 2021, pp. 958–963. doi: 10.1109/CSCWD49262.2021.9437772. [Google Scholar] [CrossRef]

4. A. Arif, Y. Y. Ghadi, M. Alarfaj, A. Jalal, S. Kamal and D. Kim, “Human pose estimation and object interaction for sports behaviour,” Comput. Mater. Contin., vol. 72, no. 1, pp. 1–18, 2022. doi: 10.32604/cmc.2022.023553. [Google Scholar] [CrossRef]

5. T. Wehrbein, M. Rudolph, B. Rosenhahn, and B. Wandt, “Probabilistic monocular 3D human pose estimation with normalizing flows,” in Proc. IEEE Int. Conf. Comput. Vis., Montreal, QC, Canada, Oct. 10–17, 2021, pp. 11199–11208. doi: 10.1109/ICCV48922.2021.01101. [Google Scholar] [CrossRef]

6. Y. Xu, W. Wang, T. Liu, X. Liu, J. Xie and S. C. Zhu, “Monocular 3D pose estimation via pose grammar and data augmentation,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 44, no. 10, pp. 6327–6344, Oct. 2022. doi: 10.1109/TPAMI.2021.3087695. [Google Scholar] [PubMed] [CrossRef]

7. C. Li and G. H. Lee, “Generating multiple hypotheses for 3D human pose estimation with mixture density network,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit, Long Beach, CA, USA, Jun. 15–20, 2019, pp. 9879–9887. doi: 10.1109/CVPR.2019.01012. [Google Scholar] [CrossRef]

8. Z. Wu, Y. Tan, Y. Zeng, and C. Xu, “3D-label-free human mesh recovery using multi-view consistency,” in Proc. 15th Int. Conf. Digit. Image Process., New York, NY, USA, 2023, pp. 1–8. doi: 10.1145/3604078. [Google Scholar] [CrossRef]

9. D. C. Luvizon, D. Picard, and H. Tabia, “Consensus-based optimization for 3D human pose estimation in camera coordinates,” Int. J. Comput. Vis., vol. 130, no. 3, pp. 869–882, Feb. 2022. doi: 10.1007/s11263-021-01570-9. [Google Scholar] [CrossRef]

10. B. Gordon, S. Raab, G. Azov, R. Giryes, and D. Cohen-Or, “FLEX: Parameter-free multi-view 3D human motion reconstruction,” in Proc. Eur. Conf. Comput. Vis., Tel Aviv, Israel, Oct. 23–27, 2022, pp. 176–196. doi: 10.1007/978-3-031-19827-4_11. [Google Scholar] [CrossRef]

11. Z. Li, M. Oskarsson, and A. Heyden, “3D human pose and shape estimation through collaborative learning and multi-view model-fitting,” in Proc. IEEE Wint. Conf. Applica. Comput. Vis., Waikoloa, HI, USA, Jan. 5–9, 2021, pp. 1887–1896. doi: 10.1109/WACV48630.2021.00193. [Google Scholar] [CrossRef]

12. T. Chen, C. Fang, X. Shen, Y. Zhu, Z. Chen and J. Luo, “Anatomy-aware 3D human pose estimation with bone-based pose decomposition,” IEEE Trans. Circuits Syst. Video Technol., vol. 32, no. 1, pp. 198–209, Jan. 2022. doi: 10.1109/TCSVT.2021.3057267. [Google Scholar] [CrossRef]

13. C. Zheng, S. Zhu, M. Mendieta, T. Yang, C. Chen and Z. Ding, “3D human pose estimation with spatial and temporal transformers,” in Proc. IEEE Int Conf. Comput. Vis., Montreal, QC, Canada, Oct. 10–17, 2021, pp. 11636–11645. doi: 10.1109/ICCV48922.2021.01145. [Google Scholar] [CrossRef]

14. E. Remelli, S. Han, S. Honari, P. Fua, and R. Wang, “Lightweight multi-view 3D pose estimation through camera-disentangled representation,” in Pro. IEEE Conf. Comput. Vis. Pattern Recognit., Seattle, WA, USA, Jun. 13–19, 2020, pp. 6039–6048. doi: 10.1109/CVPR42600.2020.00608. [Google Scholar] [CrossRef]

15. H. Y. Tu, C. Y. Wang, and W. J. Zeng, “VoxelPose: Towards multi-camera 3D human pose estimation in wild environment,” in Computer Vision–ECCV 2020. ECCV 2020. Lecture Notes in Computer Science, Springer, Cham, Aug. 23–28, 2020, vol. 12346, no. 10, pp. 197–212. doi: 10.1007/978-3-030-58452-8_12. [Google Scholar] [CrossRef]

16. K. Iskakov, E. Burkov, V. Lempitsky, and Y. Malkov, “Learnable triangulation of human pose,” in Pro. IEEE Int. Conf. Comput. Vis., Seoul, Republic of Korea, Oct. 27–Nov. 2, 2019, pp. 7717–7726. doi: 10.1109/ICCV.2019.00781. [Google Scholar] [CrossRef]

17. Y. Chen, R. Gu, O. Huang, and G. Jia, “VTP: Volumetric transformer for multi-view multi-person 3D pose estimation,” Appl. Intell., vol. 53, no. 22, pp. 26568–26579, Aug. 2023. doi: 10.1007/s10489-023-04805-z. [Google Scholar] [CrossRef]

18. F. Huang, A. Zeng, M. Liu, Q. Lai, and Q. Xu, “DeepFuse: An IMU-aware network for real-time 3D human pose estimation from multi-view image,” in Proc. IEEE Wint. Conf. Applica. Comput. Vis., Snowmass, CO, USA, Mar. 1–5, 2020, pp. 418–427. doi: 10.1109/WACV45572.2020.9093526. [Google Scholar] [CrossRef]

19. H. Qiu, C. Wang, J. Wang, N. Wang, and W. Zeng, “Cross view fusion for 3D human pose estimation,” in Proc. IEEE Int. Conf. Comput. Vis., Seoul, Republic of Korea, Oct. 27–Nov. 2, 2019, pp. 4341–4350. doi: 10.1109/ICCV.2019.00444. [Google Scholar] [CrossRef]

20. Y. He, R. Yan, K. Fragkiadaki, and S. -I. Yu, “Epipolar transformers,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Seattle, WA, USA, Jun. 13–19, 2020, pp. 7779–7788. doi: 10.1109/CVPR42600.2020.00780. [Google Scholar] [CrossRef]

21. H. -K. Wang, M. Huang, Y. Zhang, and K. Song, “Multi-View 3D human pose and shape estimation with epipolar geometry and mix-graphormer,” in Proc. Int. Conf. Intell. Comput. Signal. Process, Xi’an, China, Apr. 21–23, 2023, pp. 28–32. doi: 10.1109/ICSP58490.2023.10248627. [Google Scholar] [CrossRef]

22. G. Hua, H. Liu, W. Li, Q. Zhang, R. Ding and X. Xu, “Weakly-supervised 3D human pose estimation with cross-view u-shaped graph convolutional network,” IEEE Trans. Multimedia, vol. 25, pp. 1832–1843, Apr. 2022. doi: 10.1109/TMM.2022.3171102. [Google Scholar] [CrossRef]

23. B. X. B. Yu, Z. Zhang, Y. Liu, S. -H. Zhong, Y. Liu and C. W. Chen, “GLA-GCN: Global-local adaptive graph convolutional network for 3D human pose estimation from monocular video,” in Proc. IEEE Int. Conf. Comput. Vis., Paris, France, Oct. 1–6, 2023, pp. 8784–8795. doi: 10.1109/ICCV51070.2023.00810. [Google Scholar] [CrossRef]

24. H. Li et al., “Pose-oriented transformer with uncertainty-guided refinement for 2D-to-3D human pose estimation,” in Proc. AAAI Conf. Artif. Intell., Washington, DC, USA, Feb. 7–14, 2023, pp. 1296–1304. doi: 10.1609/aaai.v37i1.25213. [Google Scholar] [CrossRef]

25. W. Zhao, W. Wang, and Y. Tian, “GraFormer: Graph-oriented transformer for 3D pose estimation,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., New Orleans, LA, USA, Jun. 18–24, 2022, pp. 20406–20415. doi: 10.1109/CVPR52688.2022.01979. [Google Scholar] [CrossRef]

26. Z. Zou and W. Tang, “Modulated graph convolutional network for 3D human pose estimation,” in Proc. IEEE Int. Conf. Comput. Vis., Montreal, QC, Canada, Oct. 10–17, 2021, pp. 11457–11467. doi: 10.1109/ICCV48922.2021.01128. [Google Scholar] [CrossRef]

27. Z. Zhang, Y. Li, H. Dong, H. Gao, Y. Jin and W. Wang, “Spectral-based directed graph network for malware detection,” IEEE Trans. Netw. Sci. Eng., vol. 8, no. 2, pp. 957–970, Apr.–Jun. 2021. doi: 10.1109/TNSE.2020.3024557. [Google Scholar] [CrossRef]

28. Y. Wang, Y. Xia, and S. Liu, “BCCLR: A skeleton-based action recognition with graph convolutional network combining behavior dependence and context clues,” Comput. Mater. Contin., vol. 78, no. 3, pp. 4489–4507, 2024. doi: 10.32604/cmc.2024.048813. [Google Scholar] [CrossRef]

29. K. J. Chen, H. Lu, Z. Liu, and J. Zhang, “Heterogeneous graph convolutional network with local influence,” Knowl.-Based Syst., vol. 236, no. 2, Jan. 2022, Art. no. 107699. doi: 10.1016/j.knosys.2021.107699. [Google Scholar] [CrossRef]

30. K. Liu, R. Ding, Z. Zou, L. Wang, and W. Tang, “A comprehensive study of weight sharing in graph networks for 3D human pose estimation,” in Proc. Eur. Conf. Comput. Vis., Aug. 23–28, 2020, pp. 318–334. doi: 10.1007/978-3-030-58607-2_19. [Google Scholar] [CrossRef]

31. H. Zhu and P. Koniusz, “Simple spectral graph convolution,” in Proc. Int. Conf. Learn. Represent., May 3–7, 2021. [Google Scholar]

32. L. Shi, Y. Zhang, J. Cheng, and H. Q. Lu, “Action recognition via pose-based graph convolutional networks with intermediate dense supervision,” Pattern Recognit, vol. 121, no. 11, Jan. 2022, Art. no. 108170. doi: 10.1016/j.patcog.2021.108170. [Google Scholar] [CrossRef]

33. Q. Wang, K. Zhang, and M. A. Asghar, “Skeleton-based ST-GCN for human action recognition with extended skeleton graph and partitioning strategy,” IEEE Access, vol. 10, pp. 41403–41410, 2022. doi: 10.1109/ACCESS.2022.3164711. [Google Scholar] [CrossRef]

34. M. T. Hassan and A. B. Hamza, “Regular splitting graph network for 3D human pose estimation,” IEEE Trans. Image Process., vol. 32, pp. 4212–4222, 2023. doi: 10.1109/TIP.2023.3275914. [Google Scholar] [PubMed] [CrossRef]

35. H. Lin, Y. Chiu, and P. Wu, “AMPose: Alternately mixed global-local attention model for 3D human pose estimation,” in Proc. IEEE Int. Conf. Acoust. Speech Signal Process., Rhodes Island, Greece, Jun. 4–10, 2023, pp. 1–5. doi: 10.1109/ICASSP49357.2023.10095351. [Google Scholar] [CrossRef]

36. Z. Islam and A. B. Hamza, “Multi-hop graph transformer network for 3D human pose estimation,” J. Vis. Commun. Image Represent., vol. 101, no. 1, May 2024, Art. no. 104174. doi: 10.1016/j.jvcir.2024.104174. [Google Scholar] [CrossRef]

37. J. Quan and A. B. Hamza, “Higher-order implicit fairing networks for 3D human pose estimation,” in Proc. Br. Mach. Vis. Conf., Nov. 22–25, 2021. [Google Scholar]

38. T. Xu and W. Takano, “Graph stacked hourglass networks for 3D human pose estimation,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Nashville, TN, USA, Jun. 20–25, 2021, pp. 16100–16109. doi: 10.1109/CVPR46437.2021.01584. [Google Scholar] [CrossRef]

39. V. T. Le, T. H. Tran, V. N. Hoang, V. H. Le, T. L. Le and H. Vu, “SST-GCN: Structure aware spatial-temporal GCN for 3D hand pose estimation,” in Proc. 13th Int. Conf. Knowl. Syst. Eng., Bangkok, Thailand, Nov. 10–12, 2021, pp. 1–6. doi: 10.1109/KSE53942.2021.9648765. [Google Scholar] [CrossRef]

40. H. Yang, H. Liu, Y. Zhang, and X. Wu, “HSGNet: Hierarchically stacked graph network with attention mechanism for 3D human pose estimation,” Multimedia Syst., vol. 29, no. 4, pp. 2085–2097, Apr. 2023. doi: 10.1007/s00530-023-01085-y. [Google Scholar] [CrossRef]

41. B. Xiao, H. Wu, and Y. Wei, “Simple baselines for human pose estimation and tracking,” in Proc. Eur. Conf. Comput. Vis., Munich, Germany, Sep. 8–14, 2018, pp. 466–481. [Google Scholar]

42. J. Si and S. Kim, “Restoration of the JPEG maximum lossy compressed face images with hourglass block-GAN,” Comput. Mater. Contin., vol. 78, no. 3, pp. 2893–2908, 2024. doi: 10.32604/cmc.2023.046081. [Google Scholar] [CrossRef]

43. Y. Chen, Z. Wang, Y. Peng, Z. Zhang, G. Yu and J. Sun, “Cascaded pyramid network for multi-person pose estimation,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Salt Lake City, UT, USA, Jun. 18–23, 2018, pp. 7103–7112. doi: 10.1109/CVPR.2018.00742. [Google Scholar] [CrossRef]

44. C. Ionescu, D. Papava, V. Olaru, and C. Sminchisescu, “Human3.6M: Large scale datasets and predictive methods for 3D human sensing in natural environments,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 36, no. 7, pp. 1325–1339, Jul. 2014. doi: 10.1109/TPAMI.2013.248. [Google Scholar] [PubMed] [CrossRef]

45. D. Mehta et al., “Monocular 3D human pose estimation in the wild using improved CNN supervision,” in Proc. Int. Conf. 3D Vis, Qingdao, China, Oct. 10–12, 2017, pp. 506–516. doi: 10.1109/3DV.2017.00064. [Google Scholar] [CrossRef]