An Iterated Greedy Algorithm with Memory and Learning Mechanisms for the Distributed Permutation Flow Shop Scheduling Problem

1  Introduction

Distributed manufacturing is emerging as a dominant model in various industrial scenarios such as steelmaking-continuous casting and furniture assembly. It has numerous advantages over traditional manufacturing, such as reducing transportation costs, accelerating response to demand, mitigating production risks, and enhancing resilience [1]. In recent years, distributed permutation flow shop scheduling problem (DPFSP) has been one of the fastest growing topics toward distributed manufacturing [2,3]. Compared to the permutation flow shop scheduling problem (PFSP), DPFSP requires additional consideration of jobs’ allocation across different factories. Once the assignment is determined, there is a PFSP within each factory.

Since the DPFSP is more complex than the PFSP, some effective designs on the PFSP may not be applicable to directly solve the DPFSP. For this reason, a number of meta-heuristic algorithms have been customized based on the characteristics of the DPFSP, e.g., iterated greedy algorithm (IGA) [4–6], scatter search [7], memetic algorithm [8,9], and artificial bee colony [10]. It can be found that IGA is a common optimizer to tackle the DPFSP. The main reason is that the single-solution evolution framework of IGA is more simple and effective than population-based evolutionary algorithms in solving DPFSPs. Meanwhile, IGA also has some limitations because it focuses more on the current best or better solutions, while it ignores useful historical information.

Furthermore, the combination of reinforcement learning (RL) and meta-heuristics is also a hot research topic [7]. Depending on the characteristics of scheduling problems, some model-free RL approaches, such as Q-learning and Sarsa, can be used to help meta-heuristics choose operators [11,12], local search strategies [13–15], heuristics [16] or other decisions [17] without increasing the algorithm’s complexity. To further improve the performance of IGA and approximate the solution’s optimality of the DPFSP, this paper develops an IGA with memory and learning mechanisms (MLIGA). The specific contributions are summarized below:

(1) A memory mechanism is introduced for IGA to make full use of the information from historical solutions. By mimicking human memory patterns, this mechanism not only collects and expands historical solutions, but also reconstructs and reinforces them to provide more appropriate initial solutions for each iteration of the IGA according to the historical information.

(2) A two-layer cooperative RL mechanism is designed to adaptively determine the critical parameters of the IGA and the operations of the memory mechanism.

(3) A probability curve based acceptance criterion is employed to ensure that the experience generated by each perturbation operator is fully learned and reduce the prior parameters of the algorithm. This criterion, which combines a cube root function with custom rules, provides a dynamic balance between exploration and exploitation in our algorithm.

(4) Inspired by linear warm-up techniques, a discrete adaptive learning rate is proposed to enhance the stability of the memory and learning mechanisms.

The rest of this paper is organized below. Section 2 reviews the related literature and summarizes some research gaps, followed by the developed MLIGA in Section 3. To evaluate the performance of MLIGA and the effectiveness of some internal designs, Section 4 conducts a series of comparative experiments and Section 5 analyzes the results in detail. Finally, Section 6 presents conclusions and future research directions.

2  Literature Review

In this section, we investigate the related works to emphasize the research gap between previous studies and this paper. A detailed and intuitive comparison can be found in Table S1 in the Supplementary Document. Since DPFSP is a classic standard problem, we will no longer provide a mathematical model here, but the model is available in [2].

2.1 DPFSP-Related Research

Since DPFSP was first proposed by [2], the related literature has been progressively enriched, leading to the proposal of a variety of meta-heuristic algorithms in succession. For example, Lin et al. [18] proposed a modified IGA. Naderi et al. [19] employed a scatter search algorithm with some advanced techniques. Zhao et al. designed a Q-learning enhanced fruit fly optimization algorithm [20].

Apart from those mentioned above, most of the research has focused on variants of the DPFSP. Lin et al. [21] proposed a backtracking search hyper-heuristic algorithm to solve the distributed assembly permutation flow shop scheduling problem. Lu et al. [22] addressed an energy-efficient scheduling of distributed flow shop with heterogenous factories and designed a hybrid multiobjective optimization algorithm to optimize both makespan and total energy consumption. Fernandez-Viagas et al. [23] dealt with the DPFSP for minimizing the total flowtime. Lu et al. [24] proposed a knowledge-based multiobjective memetic optimization algorithm to investigate a sustainable DPFSP with a non-identical factory with objectives of minimizing makespan, negative social impact, and total energy consumption. Guo et al. [25] employed an effective fruit fly optimization algorithm for the DPFSP with the optimization goal of minimizing the total flowtime. Lu et al. [26] designed a Pareto-based collaborative multiobjective optimization algorithm to study an energy-efficient scheduling of DPFSP with limited buffers with the optimization of makespan and total energy consumption. There has been scant literature on the standard DPFSP in the past five years. In this paper, we propose a more efficient algorithm for the standard DPFSP to explore better solutions on the benchmarks, which can also be easily extended to deal with variants of the DPFSP.

2.2 IGA-Related Research

IGA has been widely used in addressing DPFSPs due to its simple and effective single-solution evolution framework [4–6]. Despite previous efforts, it also has some limitations. On the one hand, it usually fails to utilize valuable information from historical solutions (i.e., memories), which may cause an imbalance between exploration and exploitation. Therefore, we design a memory mechanism to deal with the limitation. By mimicking human memory patterns, this mechanism not only collects and expands historical solutions, but also reconstructs and reinforces them to provide more appropriate initial solutions for each iteration of the IGA according to the historical information. This comprehensive approach to leveraging historical solutions is not commonly found in previous studies.

On the other hand, the majority of relevant literature uses the simulated annealing based acceptance criterion in the proposed IGA [27]. A potential drawback of this acceptance criterion is to introduce an extra parameter that needs to be tuned beforehand [4–6]. To improve such a deficiency, we propose a probability curve based acceptance criterion by combining the cube root function with customized rules for IGA, which does not introduce an additional parameter.

2.3 Application of RL in DPFSPs

Due to the superior performance of RL on decision-making problems [28], combining meta-heuristic algorithms with RL has become a hot topic in the field of scheduling, in which the widely used RL approach is Q-learning. For instance, Zhao et al. [11] utilized the Q-learning algorithm to choose the appropriate perturbation operators during iterations. Chen et al. [29] dynamically selected the scheme of task splitting as action by employing Q-learning algorithm. Zhao et al. [16] employed the Q-learning algorithm to choose an appropriate low-level heuristic. Jia et al. [17] adaptively adjusted the size of each subpopulation in the memetic algorithm via Q-learning. Yu et al. [30] embedded Q-learning algorithm into meta-heuristics to select the premium local search strategy during iterations.

Different from the above studies, Zhao et al. [14] employed two independent Q-learning algorithms to control two subpopulations in parallel. A major disadvantage is the lack of communication and cooperation between learning agents. In our work, we propose a two-layer cooperative reinforcement learning mechanism that intelligently determines key parameters of the IGA and controls operations of the memory mechanism. The learning mechanism, which features direct communication and cooperation between layers, is a novel concept not yet explored in the literature. Furthermore, inspired by linear warm-up techniques, we incorporate a discrete adaptive learning rate to enhance the stability of the learning mechanisms, which is another innovative aspect of our work.

3  The Proposed Approach

As discussed above, we propose a novel algorithm named MLIGA to solve the DPFSP aimed at minimizing makespan. Later in this work, Cmax as a convenient notation is used to denote the makespan of a solution. In this section, the framework of MLIGA is first presented, followed by the specific designs regarding IGA, memory and learning mechanisms.

3.1 The Framework of MLIGA

As shown in Fig. 1, MLIGA starts with an initial solution using NEH2_en and LocalSearchIG [5]. Subsequently, the solution first passes through an episode, whose size E is determined by the AcceptIG, which is the probability curve based acceptance criterion. An episode consists of three basic elements of IGA (i.e., perturbation, local search and acceptance) and the brainstrom, in which the solutions in OM will be extened by using swap operators and then stored in NM. After an episode, the first layer of RL, i.e., RLIG, will be used to learn the experiences from the episode, to control some parameters, and to pass information to the second layer of RL. And then, OM will be updated by MemoryUpdate for next iteration. After that, the local/global solutions will be updated by using AcceptMemroy, which is tailored to the framework of MLIGA. At last, the second layer of RL, i.e., RLMemory, is employed just like the first layer of RL. The whole process is repeated until the termination criterion is met. The detail procedure of MLIGA is described in Algorithm 1.

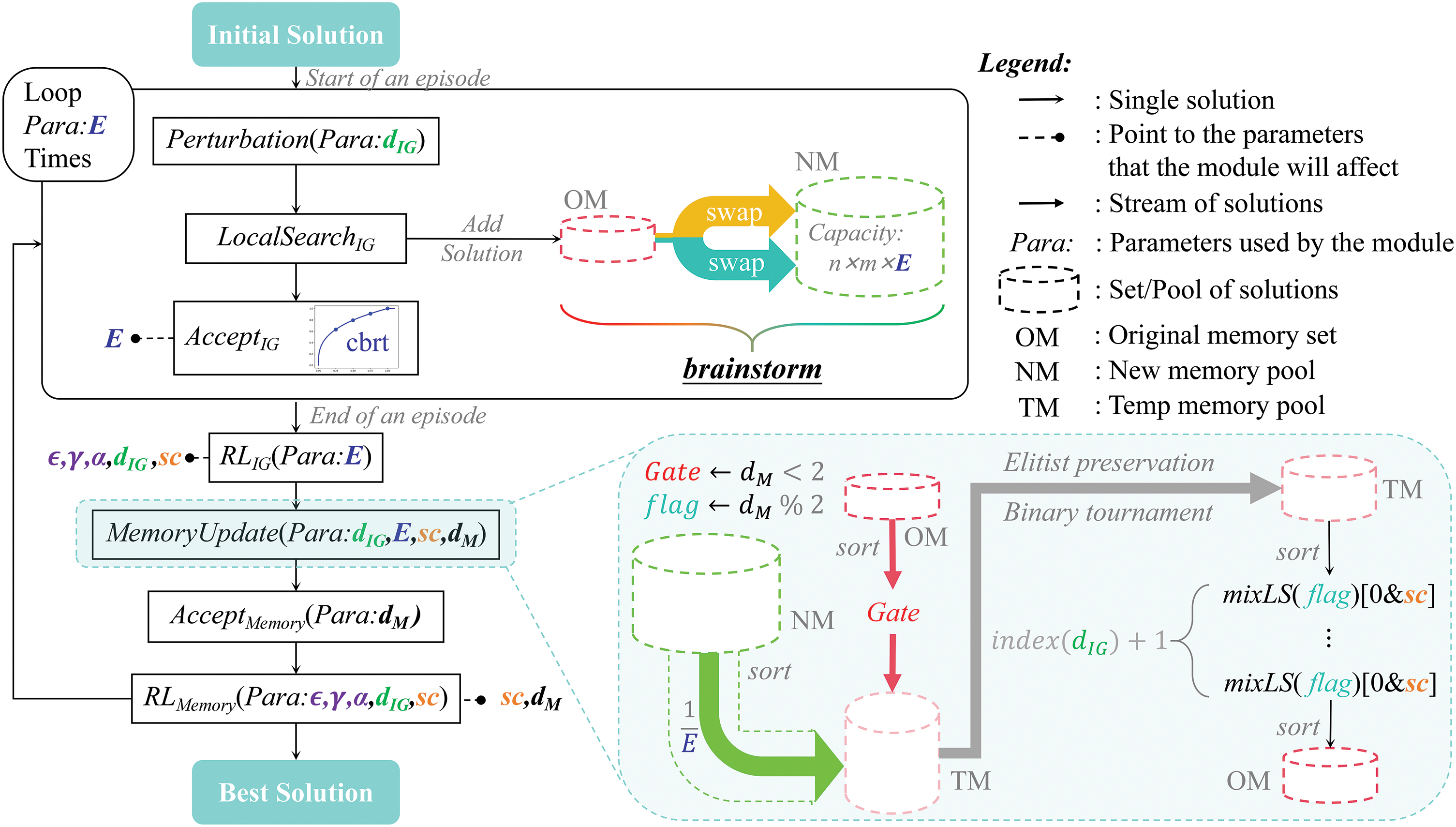
Figure 1: The framework of the proposed MLIGA

3.2 Design of the IGA

Apart from the acceptance, other elements of IGA have not been specifically designed and the details can be found in the Supplementary Document or related literature. First, for DPFSP, we adopt a widely-used solution representation proposed by [2], consisting of a set of F lists, each of which is a sequence of jobs processed within a factory. As for the initialization procedure, it comprises two steps: 1) First, we utilize the NEH2_en [5] to generate the initial solution; 2) Second, similar to other IGAs, we apply a local search to refine the initial solution just obtained. The perturbation consists of two parts: destruction and construction. We adopt the destruction employed by [5] and the construction proposed by [18]. The local search employed in IGA, denoted as LocalSearchIG, is the LS3 proposed by [5].

As illustrated in Fig. 1, each perturbation operator dIG is given an episode of size E to help solutions escape from the local optima and to learn sufficient and efficient experience for RLIG. When each perturbation operator acts only once (i.e., E=1), it resembles the basic IGA framework. However, in this scenario, the learned experience in RLIG will exhibit significant bias, and handling memories becomes challenging. When each perturbation operator acts for a fixed number of iterations (i.e., E>1), there is a trade-off: if the operator fails to yield improvements, the additional iterations can lead to wastage of computational resources; Conversely, if it consistently enhances solutions, insufficient iterations can limit its performance. Hence, determining the optimal E-value in advance is difficult. It is a good choice to adaptively adjust the E-values based on the performance of the operators.

Following the above analysis, we design a probability curve based acceptance criterion, i.e., AcceptIG. The cube root function is chosen as the probability generating function. Based on the characteristic of the problem, the formula of the probability curve is defined as (1).

cbrt(x)={x3,0≤x<11,x≥1(1)

when x=0, cbrt(x) is 0, indicating that accepting worse solutions is not allowed; when x≥1, cbrt(x) is 1, signifying that the worse solutions must be accepted. The acceptance probability P is defined as P=cbrt(s∗⋅Idx), where s∗ denotes the step-size, and Idx is a variable that records the number of times inferior solutions are not accepted in an episode, and its initial value is set 1 before an episode starts. A smaller (larger) s∗ leads to a smoother (more aggressive) increase in P, but results in larger (smaller) average sizes of the episodes. According to the primary experiments, we set s∗ to 0.25.

Additionally, the design of AcceptIG has the five characteristics: 1) As long as no worse solutions are accepted, P increases until it is 1. 2) After the first acceptance of an inferior solution, the episode is not terminated as long as there are local improvements. 3) After the second acceptance, the episode is not terminated only if global improvements exist. 4) Global improvements allow AcceptIG to be partly reset to the original state of the episode, but if worse solutions have already been accepted, Ecou is set to the state of the first acceptance. 5) Neither local nor global improvements can reset the P.

The detailed procedure of AcceptIG can be seen from Algorithm S3 in the Supplementary Document. Although both AcceptIG and traditional simulated annealing based acceptance criteria are able to accept inferior solutions, the former has two advantages over the latter in our problem: 1) It can fully utilize the potential of the operator dIG and enhance the quality of learning in RLIG. 2) There are no parameters to be determined in advance.

3.3 Memory Mechanism

The memory mechanism includes three main elements: brainstorm, MemoryUpdate and AcceptMemory. The brainstorm extends memories simply, while MemoryUpdate reconstructs and reinforces memories. Finally, the local/global solutions are updated by AcceptMemory. In this section, they will be introduced in turn. It is worth mentioning that memories are the solutions in our work.

3.3.1 Extension of Memories

As shown in Fig. 1, in each episode, every solution obtained after LocalSearchIG is added into the OM. Subsequently, memories in NM are extended using brainstorm, which is detailed in Algorithm 2. To adapt the memory mechanism to different instances, each expansion size of NM is determined by the instance characteristics (n×m, n and m represent the number of the jobs and machines). Moreover, solutions in OM undergo extension using the swap operator. To prevent stagnation in local optima, the binary tournament strategy is employed here to select better solutions from the OM.

3.3.2 Reconstruction and Reinforcement of Memories

Following RLIG, OM is reconstructed and reinforced by MemoryUpdate, which is illustrated in Algorithm 3. In this process, Gate, decided by dM, determines whether to forget the memories from the original OM. After the preservation of the elite solution(s) in OM (if any) and NM, the remaining memories in the new OM are supplemented from TM through the binary tournament strategy. To maintain diversity in OM, Cmax of the supplemented solutions differs from that of the preserved elite solution(s).

The aforementioned treatments are insufficient for the memory mechanism—not only should memories be collected, extended, and reconstructed, but they should also be reinforced. Therefore, considering the limited computational resources and the balance between exploration and exploitation, only two solutions OM[0] and OM[sc] are reinforced. OM[0] represents the best one, while OM[sc] denotes the worse one (the larger sc is, the worse OM[sc] is), where sc, decided by both RLIG and RLMemory (see Section 3.4), ranges from 1 to lennewOM−1. This reinforcement is achieved through using different numbers of mixLS. The number is calculated as index(dIG)+1, where index(dIG) is the index of dIG in dlist (defined in Table 1). A large (small) dIG indicates that IGA requires a large (small) perturbation, thus memories should be given a large (small) degree of local search. In mixLS, flag is first decided by dM (flag←dM%2) to employ insert or swap to improve solutions. After that, only the factories involved undergo LS1 [2]. Additionally, each call of mixLS extracts only int(n/len(d_{list}) jobs. The pseudo code of mixLS is presented in Algorithm S4 in the Supplementary Document.

3.3.3 Update of Solutions in the Memory Mechanism

After OM is updated, the local/global solutions (π and π∗) are updated using AcceptMemory. In preliminary experiments, we discovered that the design of the acceptance criterion significantly influences the performance of IGA by affecting the starting solution of the next episode. Hence, it needs to be carefully designed. Given the way OM is updated in MemoryUpdate, the design of AcceptMemory is guided by two principles: 1) Only if the best solution in OM outperforms π∗, π and π∗ are updated simultaneously. 2) If there is no global improvement, π is not allowed to accept the best solution in last OM. The details can be found in Algorithm S5 in the Supplementary Document.

3.4 Learning Mechanism

Inspired by [31], we design a two-layer cooperative RL mechanism to hierarchically and synergistically control the pivotal parameters of IGA and the memory mechanism. In accordance with the algorithm structure depicted in Fig. 1, the first layer of RL is denoted as RLIG, while the subsequent layer is named RLMemory. Both layers employ the Sarsa algorithm and there are direct communication and cooperation between them, which is different from those discussed in Section 2.3. The detailed information of parameters in the learning mechanism are provided in Table 1.

3.4.1 The First Layer of RL

In RLIG, SIG=[0,1]. The initial value of sIG is 0, and the initial value of dIG is selected randomly from dlist. If sIG=1(0), there are (no) global improvements in an episode. dlist is a list of different dIG-values, representing operators with different levels of perturbation for IGA. The reward is derived from two parts, i.e., local improvements and global improvements, which is designed by [12]. The details of RLIG are provided in Algorithm 4.

According to the design of AcceptIG (see Section 3.2), there are many possible E-values. In this situation, using the same learning rate for different E-values is unfair for RLIG. In AcceptIG, the smallest E-value is 2, i.e., in first iteration, the solution doesn’t yield an improvement and remains unimproved after being accepted (accept→end). The ideal E-value is 6, i.e., the algorithm goes through all designs of AcceptIG with minimal losses (accept→localimprove→accept→globalimprove→accept→end), where local/global improve represents that there is local/global improvement in one iteration. Therefore, it is reasonable to assume that the perturbation operator has been fully utilized when E≥6. Inspired by the linear warm-up technique, the learning rate α of RLIG can be adaptively adjusted according to the design of Line 2 in Algorithm 4. As for sc mentioned in Section 3.3.2, if a global improvement occurs in an episode, sc is set to 1; Otherwise, it is incremented by 1 to encourage exploration of worse solutions in OM. Finally, the ϵ-decay strategy [12] is utilized to choose actions and to reduce the value of ϵ and γ, facilitating the transition from exploration to exploitation in MLIGA.

3.4.2 The Second Layer of RL

In RLMemory, SM=[0,1] and mlist=[0,1,2,3]. The initial value of sM is 0, and the initial value of dM is selected randomly from mlist. Similar to RLIG, if sM=1(0), there are (no) improvements in the memory mechanism. Four kinds of dM in mlist control the combinations of the parameters Gate and flag discussed in Section 3.3.2. The reward calculation in RLMemory follows a similar method to RLIG, but consists of only one part. Algorithm 5 details the RLMemory.

Comparing to RLIG, RLMemory is obviously much simpler. If there is an improvement in memory mechanism, sc is set to 1. To avoid sc increases aggressively, RLMemory is not allowed to increase sc. Considering that ϵ and γ have been reduced in RLIG (see Section 3.4.1), they will not be reduced here. Finally, like RLIG, the learning rate α′ of RLMemory is dynamically tuned according to the following two ideas: 1) Since E-values affect the amount of memories collected and extended (see Section 3.3.1), they determine the upper limit of the learning rate α′, i.e., α is maximum of α′. 2) Considering that the memory mechanism employs different degrees of local search decided by dIG (see Section 3.3.2), the learning rate α′ should adjust within the upper limit α based on dIG, i.e., α′←α⋅(index(dIG)+1)/len(dlist).

4  Experimental Design

In order to investigate the performance of MLIGA and the effectiveness of some internal designs, we conducted comprehensive experiments. This section presents a detailed description of the experimental design as well as all relevant information.

4.1 Experimental Setting

For standard benchmarks, we utilized the Large test instances and Calibration instances employed by [5]. Further details about them can be found in the Supplementary Document. In addition, given the stochastic nature of the algorithms, each algorithm was independently repeated 10 times on each instance, and the results were subsequently averaged. The average relative percentage deviation (ARPD) [5] was chosen as the performance comparison metric. The relative percentage deviation (RPD) is first calculated as Equation (S3) in the Supplementary Document. As for the termination criterion, we adopted the maximum number of fitness evaluations utilized by [32]. To determine the maximum number of fitness evaluations, we employed the method proposed by [12], which is detailed in the Supplementary Document. Finally, all algorithms were coded by Python, and run on the PC: Intel(R) Core(TM) i9-13900K @ 3000 MHz with 64.0 GB RAM in the 64bit Windows 10 operation system.

4.2 Settings of Key Parameters

To avoid duplication of labor, the parameters in the learning mechanism were directly adopted from the combination of parameter values used by [12], i.e., αmax=0.6,ϵ=0.8,β=0.996,γ=0.8,η=0.3. Thus, calibration of the MLIGA involved only one parameter, dlist, which could be conducted by testing all possible dlist-values separately on the Calibration instances.

The dlist is a list of positive integers with continuous values. After reviewing relevant literature, the maximum value (dmax) in dlist is set to 10, and the minimum value (dmin) in dlist is set to 1, 2 and 3, respectively. dmin=3 is used to avoid the duplication between LocalSearchIG and perturbation. Moreover, since dlist is a set of actions in RLIG, the number of actions in dlist generally has to be greater than 2 to be meaningful. Therefore, the expression of the possible dlist-values is [dmin,⋯,dmin+Δ], Δ∈[2,dmax−dmin] and Δ∈N+.

4.3 Settings of Comparison Algorithms

To verify the effectiveness of MLIGA, we compared it with five state-of-the-art comparison algorithms, which are shown in Table 2.

4.4 Settings of Ablation Experiments

We also designed ablation experiments to examine specific designs and critical components in MLIGA. The first experiment was conducted to investigate the effect of different initialization procedures on MLIGA. In addition to the NEH2_en [5] utilized in MLIGA (see Section 3.2), we chose NEH2 [2] and RandInit as the other two initialization procedures, which are detailed in the Supplementary Document. The second experiment was designed to examine the impact of different probability curves (see Section 3.2) on both MLIGA and E-values. Inspired by some existing curves, we devised three additional probability curves: linear(x), sigmoid(x), and prob(x),which are illustrated in the Supplementary Document. Memory mechanism is the main innovation of our work. It is necessary to investigate how the memory mechanism influence MLIGA. Hence, in third experiment, we compared MLIGA with Memoryless MLIGA, which referred to the MLIGA without the memory mechanism and RLMemory.

5  Numerical and Statistical Results

In this section, we implemented all the experiments designed in Section 4, and subsequently analyzed the results using the Analysis of Variance (ANOVA) technique [34] and the Tukey’s Honest Significant Difference (HSD) with 95% confidence intervals [35]. More detailed analysis results are provided in Supplementary Document.

5.1 Calibration of MLIGA

The analysis of the results shows that there is no significant difference among these values, as the p-value of 1.000 exceeds the significance threshold of 0.050. This phenomenon is highly meaningful and ideal, because it demonstrates that MLIGA is insensitive to the parameter dlist. In other words, as long as the dlist-value falls within a reasonable range, the RLIG can effectively utilize the perturbation operator dIG, which precisely showcases the effectiveness and robustness of the learning mechanism. However, for subsequent experimental requirements, it remains necessary to determine a specific dlist-value. For convenience in plotting, we adopted the notation dmin−dmax instead of [dmin,⋯,dmax]. Thus, according to Fig. 2, we determined the dlist as [3,4,5,6], which had the smallest mean ARPD value.

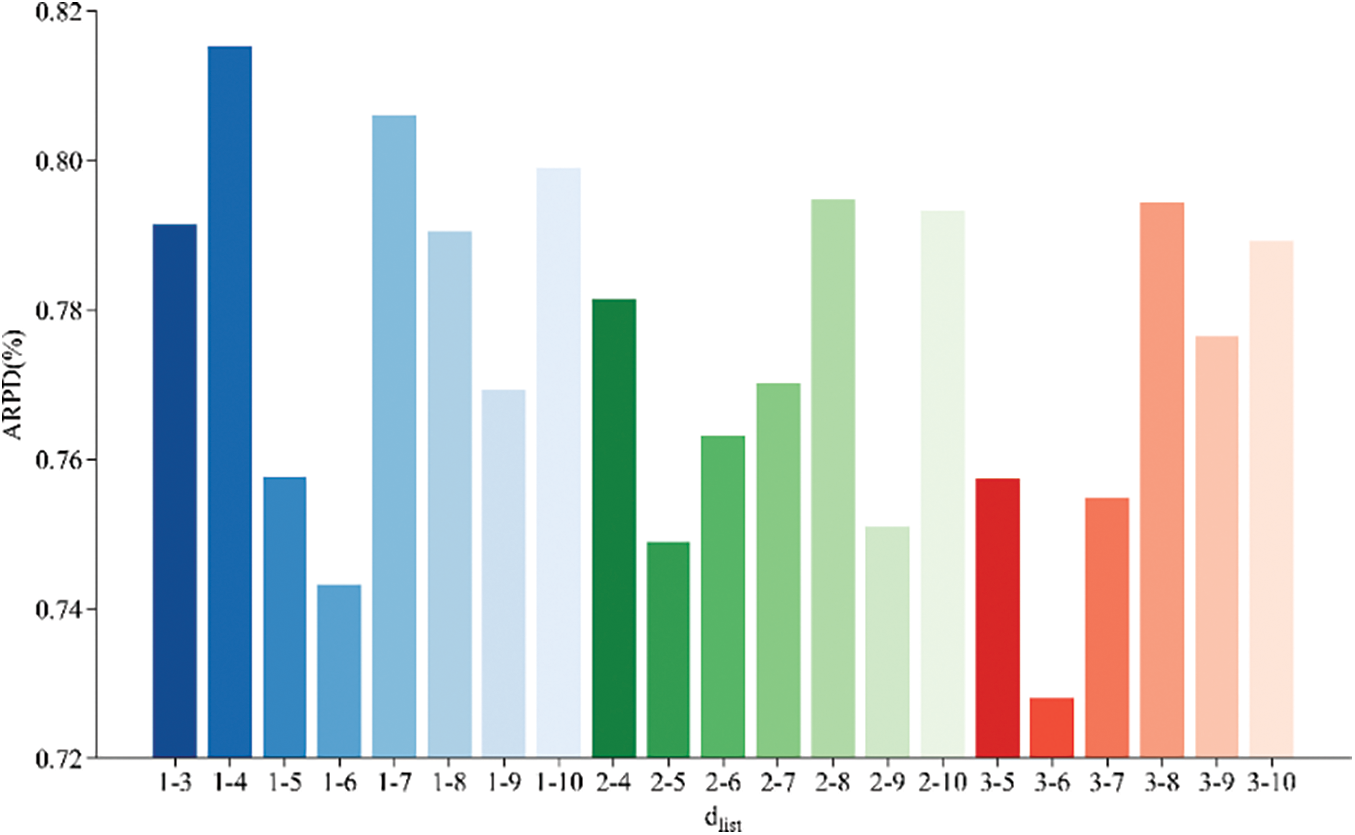
Figure 2: Means plots for all dlist-values

5.2 Effectiveness of MLIGA

As designed in Section 4.3, we conducted the comparison experiment. Fig. 3 shows the analysis of the results, and the smallest mean ARPD value is highlighted in bold. According to Fig. 3, MLIGA demonstrates superior overall performance compared to DABC, DFFO, QFOA, and QIGA. Moreover, given that QIGA utilizes a single-layer RL framework, the results can also indicate that the learning mechanism proposed in this paper is superior to the single-layer RL framework.

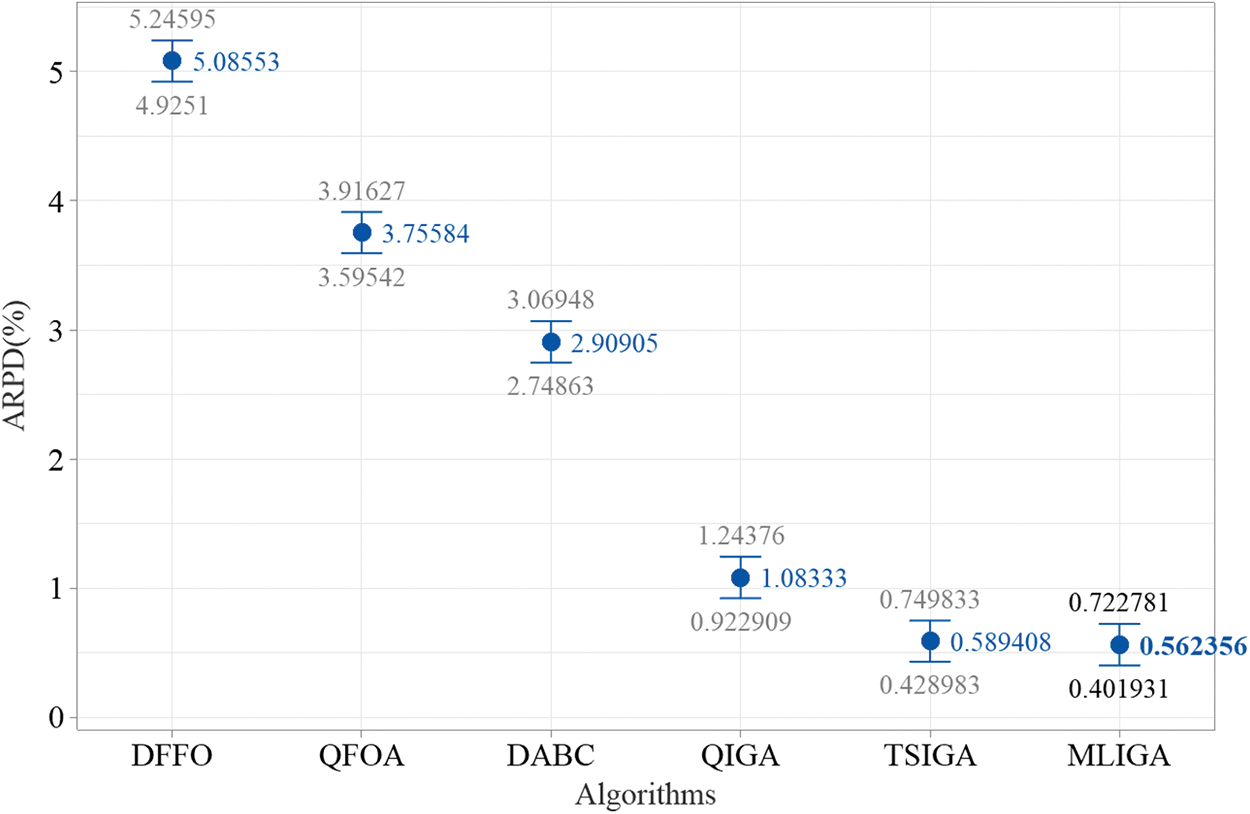
Figure 3: Means plots for all algorithms. All means have HSD 95% confidence intervals

However, the mean ARPD value of MLIGA is slightly lower than that of TSIGA, with no significant difference observed. Therefore, we need to further analyze MLIGA and TSIGA. The Large test instances used are not all large-scale instances, e.g., for an instance with 7 factories and 20 jobs in Large test instances, each factory contains fewer than 3 jobs on average. Small-scale instances are easily solved by most existing meta-heuristics for the DPFSP [5] and large-scale instances are more common in real-world distributed flow shop scheduling. Consequently, more attention should be paid to solving large-scale instances. Nevertheless, the definition of large-scale instances in DPFSP remains unclear, with much literature preferring to define instance scale based solely on the number of factories (F) or jobs (n). Considering these two key parameters in DPFSP and some spurious large-scale instances in the Large test instances, we thought that instance scale should be decided by both n and F. Based on the discussion above, we concluded that defining the instance scale in terms of the ratio between n and F, i.e., n/F, is a more appropriate approach. A higher ratio n/F indicates a larger instance scale. Hence, we further analyze TSIGA and MLIGA based on the ratio n/F. Moreover, considering that the overall performance of QIGA is not too much worse than these two algorithms, QIGA is also analyzed in Fig. 4.

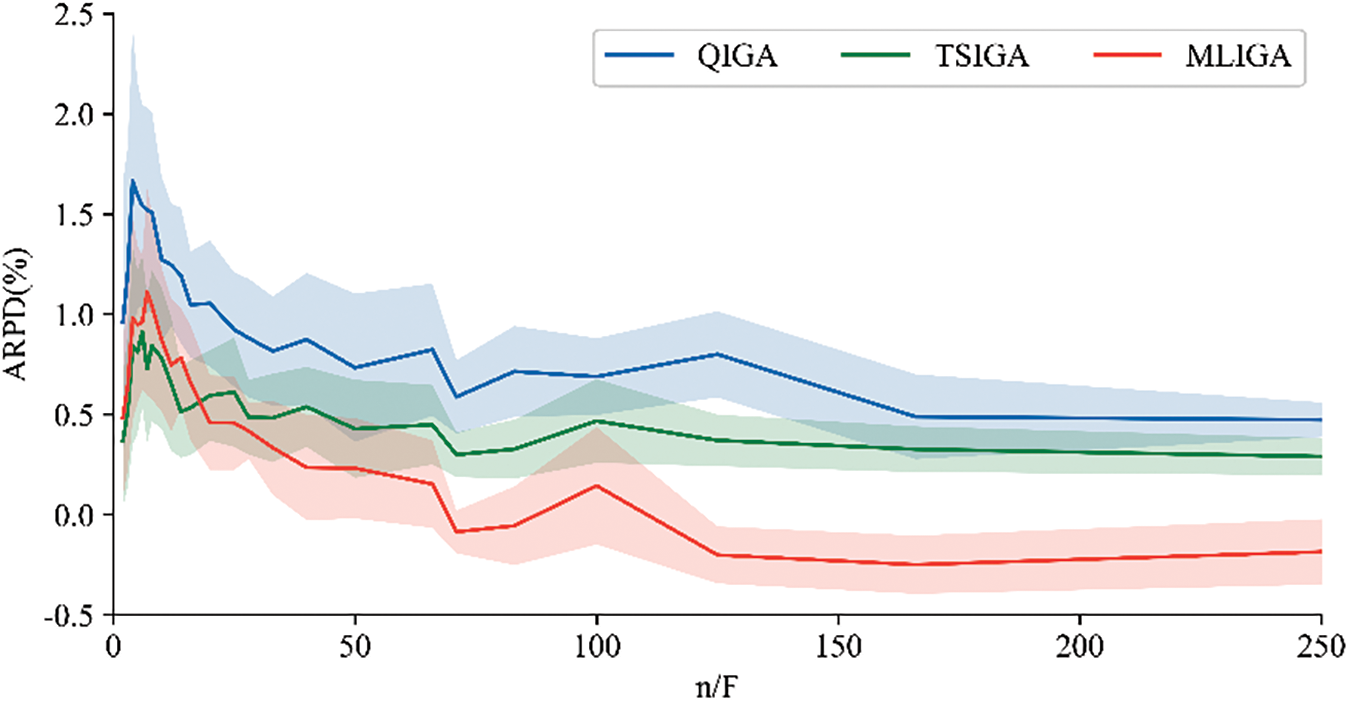
Figure 4: Line graph of ARPD of the three algorithms following the increase in the scale of instances

According to Fig. 4, MLIGA exhibits slightly inferior performance compared to TSIGA when n/F is approximately less than 20. After that, as the instance scale increases, the disparity between MLIGA and TSIGA gradually widens, with MLIGA’s superiority becoming increasingly evident. In summary, MLIGA has significant advantages over the comparison algorithms implemented in our work, especially in handling large-scale DPFSP instances.

5.3 Ablation Experiments

The analytical results of ablation experiments on initialization are shown in Table 3. It can be found that: 1) Compared to RandInit, both NEH2_en and NEH2 offer superior initial solutions; 2) The results obtained from NEH2_en are the best. However, the advantage of NEH2_en over NEH2 is not statistically significant, since the p-value between NEH2_en and NEH2 is bigger than 0.050; 3) The mean ARPD value of RandInit is better than that of DABC, DFFO, QFOA and QIGA in Section 5.2. Additionally, the mean ARPD value of NEH2 also outperforms all comparison algorithms in Section 5.2. In summary, MLIGA does not rely much on the initial solutions, and thanks to the presence of forgetting in the memory mechanism, MLIGA does not deteriorate even with worse initial solutions.

Table 4 lists the analytical results of ablation experiments on probability curves. From Table 4, it can be found that the cbrt(x) has the smallest mean ARPD value, which indicates that it is the best choice among the four curves. Nevertheless, although there is a slight disparity in the mean ARPD values among these four curves, the differences between them are not statistically significant, as the p-values among them were bigger than 0.050. This phenomenon suggests that AcceptIG is not particularly sensitive to different probability curves, namely, it is robust.

The impact of the probability curves is not only manifested in the result, but also more directly evident in the E-values. Thus, we collected and organized the E-values of these four probability curves across all instances in Fig. 5. In Fig. 5, we can find that: 1) Different probability curves lead to distinct distributions of E-values; 2) No particular E-value has a percentage of more than 50% across all probability curves, which indicates that there is indeed a necessity for adaptive adjustment of E-values during the search process, i.e., the design of AcceptIG is completely necessary.

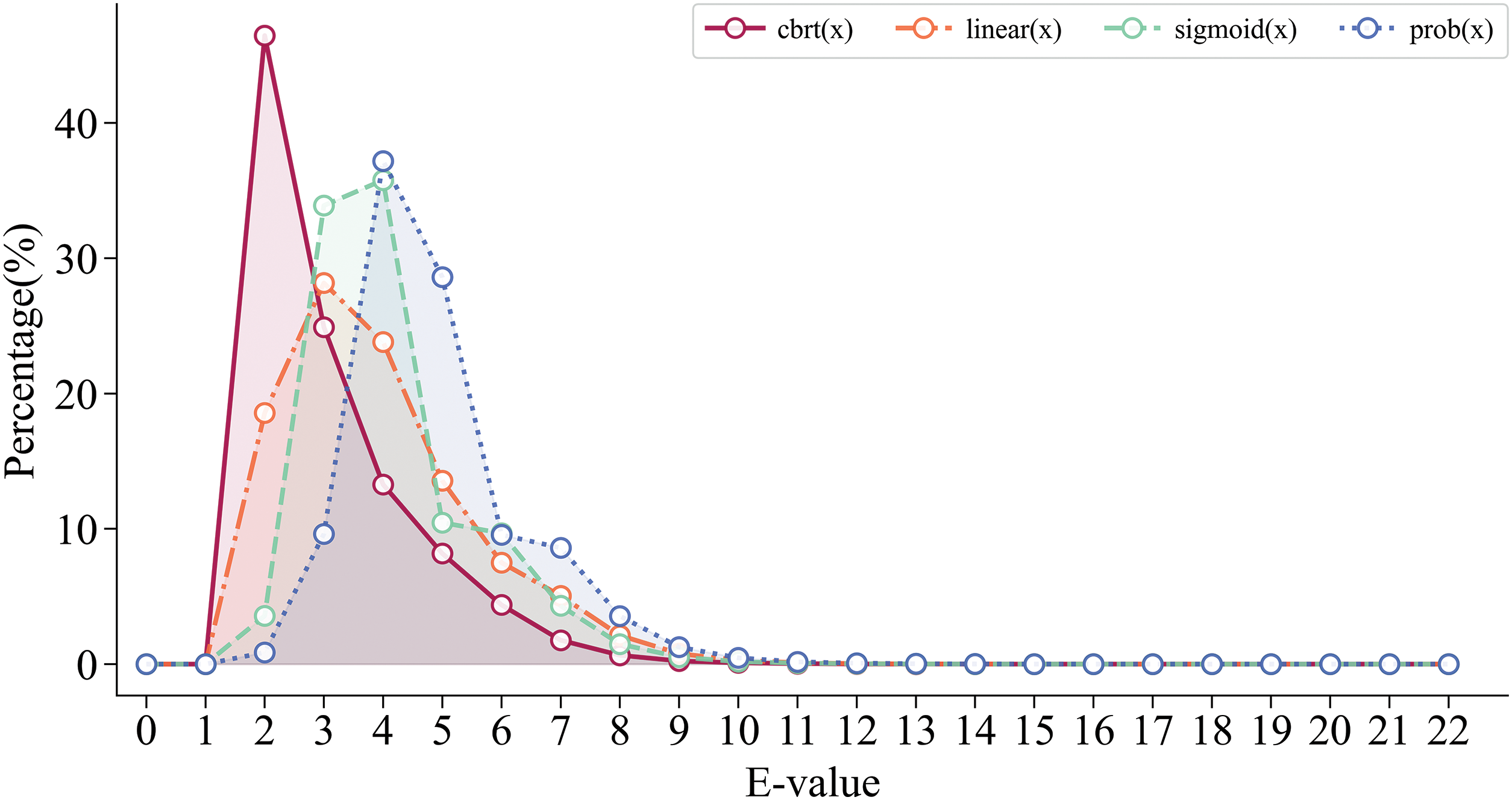
Figure 5: Line graph of percentage of each E-value for all probability curves

At last, the analytical results for MLIGA and Memoryless MLIGA are listed in Table 5. The results suggest that the memory mechanism can significantly improve the overall performance of the algorithm, with a significant difference observed between MLIGA and Memoryless MLIGA. This phenomenon effectively demonstrates the pivotal role of the memory mechanism in MLIGA’s performance.

6  Conclusion and Perspectives

In this paper, we developed a novel algorithm named MLIGA to solve the DPFSP with the objective of minimizing the makespan. One of main contribution is to incorporate a memory mechanism in IGA, which can help the algorithm escape from the local optima by collecting, extending, reconstructing (including forgetting), and reinforcing memories, with providing more appropriate starting solutions for IGA during iterations. In addition, we proposed a two-layer cooperative RL mechanism to determine the crucial parameters of IGA and the memory mechanism. Through a series of comprehensive experiments, it is clear that MLIGA exhibits excellent performance on large-scale DPFSP instances, indicating its potential applicability in real-world distributed flow shop scheduling.

However, there are also some limitations, including the performance is not as good as TSIGA in small-scale benchmarks, and there are some sorting operations in the memory mechanism. In the future, we will explore the feasibility of implementing switchable acceptance criteria based on the scale of instances to improve the performance of MLIGA on small-scale benchmarks, design more suitable acceptance strategies according to the structure of algorithm, or refine the framework of MLIGA to avoid some sorting operations. Furthermore, we will extend the application of MLIGA to tackle more variants of DPFSPs. More investigations on multi-objective evolutionary algorithms are also crucial for solving DPFSPs with multiple optimization objectives.

Acknowledgement: None.

Funding Statement: This work was supported in part by the National Key Research and Development Program of China under Grant No. 2021YFF0901300, in part by the National Natural Science Foundation of China under Grant Nos. 62173076 and 72271048.

Author Contributions: Study conception and design: Binhui Wang; data collection: Binhui Wang; analysis and interpretation of results: Binhui Wang; draft manuscript preparation: Binhui Wang; review and editing: Hongfeng Wang; funding acquisition: Hongfeng Wang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Supplementary Materials: The supplementary material is available online at https://doi.org/10.32604/cmc.2024.058885.

References

1. C. E. Okwudire and H. V. Madhyastha, “Distributed manufacturing for and by the masses,” Science, vol. 372, no. 6540, pp. 341–342, Apr. 2021. doi: 10.1126/science.abg4924. [Google Scholar] [PubMed] [CrossRef]

2. B. Naderi and R. Ruiz, “The distributed permutation flowshop scheduling problem,” Comput. Oper. Res., vol. 37, no. 4, pp. 754–768, 2010. doi: 10.1016/j.cor.2009.06.019. [Google Scholar] [CrossRef]

3. P. Perez-Gonzalez and J. M. Framinan, “A review and classification on distributed permutation flowshop scheduling problems,” Eur. J. Oper. Res., vol. 312, no. 1, pp. 1–21, Jan. 2024. doi: 10.1016/j.ejor.2023.02.001. [Google Scholar] [CrossRef]

4. V. Fernandez-Viagas and J. M. Framinan, “A bounded-search iterated greedy algorithm for the distributed permutation flowshop scheduling problem,” Int. J. Prod. Res., vol. 53, no. 4, pp. 1111–1123, Feb. 2015. doi: 10.1080/00207543.2014.948578. [Google Scholar] [CrossRef]

5. R. Ruiz, Q. -K. Pan, and B. Naderi, “Iterated Greedy methods for the distributed permutation flowshop scheduling problem,” Omega, vol. 83, no. 1, pp. 213–222, Mar. 2019. doi: 10.1016/j.omega.2018.03.004. [Google Scholar] [CrossRef]

6. Z. Shao, W. Shao, and D. Pi, “Effective heuristics and metaheuristics for the distributed fuzzy blocking flow-shop scheduling problem,” Swarm Evol. Comput., vol. 59, Dec. 2020, Art. no. 100747. doi: 10.1016/j.swevo.2020.100747. [Google Scholar] [CrossRef]

7. Q. -Y. Han, H. -Y. Sang, Q. -K. Pan, B. Zhang, and H. -W. Guo, “An efficient collaborative multi-swap iterated greedy algorithm for the distributed permutation flowshop scheduling problem with preventive maintenance,” Swarm Evol. Comput., vol. 86, Apr. 2024, Art. no. 101537. doi: 10.1016/j.swevo.2024.101537. [Google Scholar] [CrossRef]

8. S. -Y. Wang and L. Wang, “An estimation of distribution algorithm-based memetic algorithm for the distributed assembly permutation flow-shop scheduling problem,” IEEE Trans. Syst. Man Cybern. Syst., vol. 46, no. 1, pp. 139–149, Jan. 2016. doi: 10.1109/TSMC.2015.2416127. [Google Scholar] [CrossRef]

9. J. Deng and L. Wang, “A competitive memetic algorithm for multi-objective distributed permutation flow shop scheduling problem,” Swarm Evol. Comput., vol. 32, no. 6, pp. 121–131, Feb. 2017. doi: 10.1016/j.swevo.2016.06.002. [Google Scholar] [CrossRef]

10. J. Mao, Q. Pan, Z. Miao, and L. Gao, “An effective multi-start iterated greedy algorithm to minimize makespan for the distributed permutation flowshop scheduling problem with preventive maintenance,” Expert. Syst. Appl., vol. 169, May 2021, Art. no. 114495. doi: 10.1016/j.eswa.2020.114495. [Google Scholar] [CrossRef]

11. F. Zhao, G. Zhou, T. Xu, N. Zhu, and Jonrinaldi, “A knowledge-driven cooperative scatter search algorithm with reinforcement learning for the distributed blocking flow shop scheduling problem,” Expert Syst. Appl., vol. 230, Nov. 2023, Art. no. 120571. doi: 10.1016/j.eswa.2023.120571. [Google Scholar] [CrossRef]

12. M. Karimi-Mamaghan, M. Mohammadi, B. Pasdeloup, and P. Meyer, “Learning to select operators in meta-heuristics: An integration of Q-learning into the iterated greedy algorithm for the permutation flowshop scheduling problem,” Eur. J. Oper. Res., vol. 304, no. 3, pp. 1296–1330, Feb. 2023. doi: 10.1016/j.ejor.2022.03.054. [Google Scholar] [CrossRef]

13. F. Zhao, Z. Wang, and L. Wang, “A reinforcement learning driven artificial bee colony algorithm for distributed heterogeneous no-wait flowshop scheduling problem with sequence-dependent setup times,” IEEE Trans. Autom. Sci. Eng., vol. 20, no. 4, pp. 2305–2320, Oct. 2023. doi: 10.1109/TASE.2022.3212786. [Google Scholar] [CrossRef]

14. F. Zhao, T. Jiang, and L. Wang, “A reinforcement learning driven cooperative meta-heuristic algorithm for energy-efficient distributed no-wait flow-shop scheduling with sequence-dependent setup time,” IEEE Trans. Ind. Inform., vol. 19, no. 7, pp. 8427–8440, Jul. 2023. doi: 10.1109/TII.2022.3218645. [Google Scholar] [CrossRef]

15. F. Zhao, G. Zhou, and L. Wang, “A cooperative scatter search with reinforcement learning mechanism for the distributed permutation flowshop scheduling problem with sequence-dependent setup times,” IEEE Trans. Syst. Man Cybern. Syst., vol. 53, no. 8, pp. 4899–4911, 2023. doi: 10.1109/TSMC.2023.3256484. [Google Scholar] [CrossRef]

16. F. Zhao, S. Di, and L. Wang, “A hyperheuristic with Q-learning for the multiobjective energy-efficient distributed blocking flow shop scheduling problem,” IEEE Trans. Cybern., vol. 53, no. 5, pp. 3337–3350, May 2023. doi: 10.1109/TCYB.2022.3192112. [Google Scholar] [PubMed] [CrossRef]

17. Y. Jia, Q. Yan, and H. Wang, “Q-learning driven multi-population memetic algorithm for distributed three-stage assembly hybrid flow shop scheduling with flexible preventive maintenance,” Expert Syst. Appl., vol. 232, Dec. 2023, Art. no. 120837. doi: 10.1016/j.eswa.2023.120837. [Google Scholar] [CrossRef]

18. S. -W. Lin, K. -C. Ying, and C. -Y. Huang, “Minimising makespan in distributed permutation flowshops using a modified iterated greedy algorithm,” Int. J. Prod. Res., vol. 51, no. 16, pp. 5029–5038, Aug. 2013. doi: 10.1080/00207543.2013.790571. [Google Scholar] [CrossRef]

19. B. Naderi and R. Ruiz, “A scatter search algorithm for the distributed permutation flowshop scheduling problem,” Eur. J. Oper. Res., vol. 239, no. 2, pp. 323–334, Dec. 2014. doi: 10.1016/j.ejor.2014.05.024. [Google Scholar] [CrossRef]

20. C. Zhao, L. Wu, C. Zuo, and H. Zhang, “An improved fruit fly optimization algorithm with Q-learning for solving distributed permutation flow shop scheduling problems,” Complex Intell. Syst., vol. 10, no. 5, pp. 5965–5988, Oct. 2024. doi: 10.1007/s40747-024-01482-4. [Google Scholar] [CrossRef]

21. J. Lin, Z. -J. Wang, and X. Li, “A backtracking search hyper-heuristic for the distributed assembly flow-shop scheduling problem,” Swarm Evol. Comput., vol. 36, pp. 124–135, Oct. 2017. doi: 10.1016/j.swevo.2017.04.007. [Google Scholar] [CrossRef]

22. C. Lu, L. Gao, J. Yi, and X. Li, “Energy-efficient scheduling of distributed flow shop with heterogeneous factories: A real-world case from automobile industry in China,” IEEE Trans. Ind. Inform., vol. 17, no. 10, pp. 6687–6696, Oct. 2021. doi: 10.1109/TII.2020.3043734. [Google Scholar] [CrossRef]

23. V. Fernandez-Viagas, P. Perez-Gonzalez, and J. M. Framinan, “The distributed permutation flow shop to minimise the total flowtime,” Comput. Ind. Eng., vol. 118, pp. 464–477, Apr. 2018. doi: 10.1016/j.cie.2018.03.014. [Google Scholar] [CrossRef]

24. C. Lu, L. Gao, W. Gong, C. Hu, X. Yan and X. Li, “Sustainable scheduling of distributed permutation flow-shop with non-identical factory using a knowledge-based multi-objective memetic optimization algorithm,” Swarm Evol. Comput., vol. 60, Feb. 2021, Art. no. 100803. doi: 10.1016/j.swevo.2020.100803. [Google Scholar] [CrossRef]

25. H. -W. Guo, H. -Y. Sang, X. -J. Zhang, P. Duan, J. -Q. Li and Y. -Y. Han, “An effective fruit fly optimization algorithm for the distributed permutation flowshop scheduling problem with total flowtime,” Eng. Appl. Artif. Intell., vol. 123, Aug. 2023, Art. no. 106347. doi: 10.1016/j.engappai.2023.106347. [Google Scholar] [CrossRef]

26. C. Lu, Y. Huang, L. Meng, L. Gao, B. Zhang and J. Zhou, “A Pareto-based collaborative multi-objective optimization algorithm for energy-efficient scheduling of distributed permutation flow-shop with limited buffers,” Robot Comput.-Integr. Manuf., vol. 74, Apr. 2022, Art. no. 102277. doi: 10.1016/j.rcim.2021.102277. [Google Scholar] [CrossRef]

27. Z. Zhao, M. Zhou, and S. Liu, “Iterated greedy algorithms for flow-shop scheduling problems: A tutorial,” IEEE Trans. Autom. Sci. Eng., vol. 19, no. 3, pp. 1941–1959, 2021. doi: 10.1109/TASE.2021.3062994. [Google Scholar] [CrossRef]

28. J. Wang, H. Zheng, S. Zhao, and Q. Zhang, “Energy-aware remanufacturing process planning and scheduling problem using reinforcement learning-based particle swarm optimization algorithm,” J. Clean. Prod., vol. 476, Oct. 2024, Art. no. 143771. doi: 10.1016/j.jclepro.2024.143771. [Google Scholar] [CrossRef]

29. X. Chen et al., “Reinforcement learning for distributed hybrid flowshop scheduling problem with variable task splitting towards mass personalized manufacturing,” J. Manuf. Syst., vol. 76, no. 4, pp. 188–206, Oct. 2024. doi: 10.1016/j.jmsy.2024.07.011. [Google Scholar] [CrossRef]

30. H. Yu, K. -Z. Gao, Z. -F. Ma, and Y. -X. Pan, “Improved meta-heuristics with Q-learning for solving distributed assembly permutation flowshop scheduling problems,” Swarm Evol. Comput., vol. 80, Jul. 2023, Art. no. 101335. doi: 10.1016/j.swevo.2023.101335. [Google Scholar] [CrossRef]

31. Q. Yan, H. Wang, and F. Wu, “Digital twin-enabled dynamic scheduling with preventive maintenance using a double-layer Q-learning algorithm,” Comput. Oper. Res., vol. 144, Aug. 2022, Art. no. 105823. doi: 10.1016/j.cor.2022.105823. [Google Scholar] [CrossRef]

32. Q. Yan, H. Wang, and S. Yang, “A learning-assisted bi-population evolutionary algorithm for distributed flexible job-shop scheduling with maintenance decisions,” IEEE Trans. Evol. Comput., 2024. doi: 10.1109/TEVC.2024.3400043. [Google Scholar] [CrossRef]

33. Y. Yu, F. -Q. Zhang, G. -D. Yang, Y. Wang, J. -P. Huang and Y. -Y. Han, “A discrete artificial bee colony method based on variable neighborhood structures for the distributed permutation flowshop problem with sequence-dependent setup times,” Swarm Evol. Comput., vol. 75, Dec. 2022, Art. no. 101179. doi: 10.1016/j.swevo.2022.101179. [Google Scholar] [CrossRef]

34. M. G. Larson, “Analysis of Variance,” Circulation, vol. 117, no. 1, pp. 115–121, 2008. doi: 10.1161/CIRCULATIONAHA.107.654335. [Google Scholar] [CrossRef]

35. H. Abdi and L. J. Williams, “Tukey’s honestly significant difference (HSD) test,” in Encyclopedia of Research Design. SAGE Publications, Inc., 2010. [Google Scholar]