 Open Access
Open Access
ARTICLE
SEFormer: A Lightweight CNN-Transformer Based on Separable Multiscale Depthwise Convolution and Efficient Self-Attention for Rotating Machinery Fault Diagnosis
1 State Key Laboratory of Mechanics and Control for Aerospace Structures, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, China
2 School of Computer Science and Engineering, Nanyang Technological University, Singapore, 639798, Singapore
* Corresponding Authors: Hua Zhu. Email: ; Huafeng Li. Email:
(This article belongs to the Special Issue: Industrial Big Data and Artificial Intelligence-Driven Intelligent Perception, Maintenance, and Decision Optimization in Industrial Systems)
Computers, Materials & Continua 2025, 82(1), 1417-1437. https://doi.org/10.32604/cmc.2024.058785
Received 21 September 2024; Accepted 25 November 2024; Issue published 03 January 2025
Abstract
Traditional data-driven fault diagnosis methods depend on expert experience to manually extract effective fault features of signals, which has certain limitations. Conversely, deep learning techniques have gained prominence as a central focus of research in the field of fault diagnosis by strong fault feature extraction ability and end-to-end fault diagnosis efficiency. Recently, utilizing the respective advantages of convolution neural network (CNN) and Transformer in local and global feature extraction, research on cooperating the two have demonstrated promise in the field of fault diagnosis. However, the cross-channel convolution mechanism in CNN and the self-attention calculations in Transformer contribute to excessive complexity in the cooperative model. This complexity results in high computational costs and limited industrial applicability. To tackle the above challenges, this paper proposes a lightweight CNN-Transformer named as SEFormer for rotating machinery fault diagnosis. First, a separable multiscale depthwise convolution block is designed to extract and integrate multiscale feature information from different channel dimensions of vibration signals. Then, an efficient self-attention block is developed to capture critical fine-grained features of the signal from a global perspective. Finally, experimental results on the planetary gearbox dataset and the motor roller bearing dataset prove that the proposed framework can balance the advantages of robustness, generalization and lightweight compared to recent state-of-the-art fault diagnosis models based on CNN and Transformer. This study presents a feasible strategy for developing a lightweight rotating machinery fault diagnosis framework aimed at economical deployment.Graphic Abstract
Keywords
As modern mechanical systems advance swiftly, rotating machinery has emerged as a crucial component in intelligent manufacturing, attracting significant attention to its safety from both academic and industrial sectors [1]. Under high-intensity operating conditions, the core transmission components of rotating machinery unavoidably suffer from wear, crack, break, and other faults [2]. Faulty transmission components severely affect the operational reliability and stability of rotating machinery, potentially leading to major incidents, financial losses, and human casualties [3]. Consequently, research into rotating machinery fault diagnosis is of considerable value [4].
Traditional data-driven fault diagnosis methods depend on expert experience to manually extract effective fault features of signals, which has certain limitations [5]. Conversely, deep learning techniques have gained prominence as a central focus of research in the field of fault diagnosis by strong fault feature extraction ability and end-to-end fault diagnosis efficiency [6]. Particularly, methods based on CNNs and their variants prove effective in various fault diagnosis scenarios. He et al. [7] developed an ensemble CNN with multi-sensor fusion for rotating machinery fault diagnosis under different working conditions. Zhao et al. [8] designed a rotating machinery fault diagnosis method based on CNN with mixed information. Huang et al. [9] proposed a multi-scale CNN with channel attention mechanism for rolling bearing fault diagnosis. The CNN models excel at extracting local features within short-range sequences but lack the capability to establish global dependencies between long-range sequences. Nevertheless, when there is noise interference in the collected signals, it is a struggle to identify effective fault information using only local features [10].
As a rising star in natural language processing (NLP) and computer vision (CV), Transformer has a strong ability to capture fine-grained features and build temporal correlations from long-range sequences by assessing the resemblance among sequences [11,12]. Over the previous three years, various scholars have gradually employed Transformer in the domain of rotating machinery fault diagnosis. Tang et al. [13] developed a Signal-transformer architecture for rotating machinery fault diagnosis under variable operating conditions. Li et al. [14] designed a variational Transformer for rotating machinery fault diagnosis. Ding et al. [15] proposed a time-frequency Transformer for rolling bearings fault diagnosis. However, the Transformer models lack the local correlation extraction and spatial inductive bias capability of CNN models. Thus, training these models usually demands a significant number of samples to assure effective performance, which poses a challenge for fault diagnosis tasks [16]. Moreover, vibration signals are periodic and continuous, making it crucial not to overlook local features [17].
Approaches that combine CNNs with Transformers (CNN-Transformer) have recently been explored to jointly capture local features and global dependencies of temporal sequences. Fang et al. [18] developed a bearing fault diagnosis framework named CLFormer using multiscale convolution and linear self-attention. Han et al. [19] proposed a gearbox fault diagnosis framework named Convformer-NSE that utilizes local and global feature information. Yan et al. [20] designed a rotating machinery fault diagnosis framework called LiConvFormer using separable multiscale convolution and broadcast self-attention. Although existing CNN-Transformer models have demonstrated promise in the domain of fault diagnosis, they continue to face certain challenges in processing high-dimensional signal features: (1) the cross-channel convolution mechanism in CNN greatly raises the number of convolution operations; (2) the scaled dot-product attention in Transformer requires performing numerous high-dimensional exponential calculations and matrix multiplication operations. The preceding shortcomings contribute to excessive complexity in the cooperative model, which results in high computational costs and limited industrial applicability. Therefore, designing simple, lightweight, and efficient convolution and self-attention mechanisms is especially crucial for building a lightweight cooperative model that can maintain overall performance.
Inspired by the aforementioned research, this paper proposes a lightweight CNN-Transformer named SEFormer for rotating machinery fault diagnosis. The primary contributions are detailed below:
(1) A separable multiscale depthwise convolution block is designed to extract and integrate multiscale feature information from different channel dimensions of vibration signals.
(2) An efficient self-attention block is developed to capture critical fine-grained features of the signal from a global perspective.
(3) A lightweight CNN-Transformer named SEFormer for rotating machinery fault diagnosis based on separable multiscale depthwise convolution block and efficient self-attention block is proposed.
(4) Experimental results prove that the proposed framework can balance the advantages of robustness, generalization and lightweight compared to recent state-of-the-art fault diagnosis models based on CNN and Transformer.
The rest of this paper is organized below. Section 2 introduces the basic theory. Section 3 details the proposed lightweight SEFormer and rotating machinery fault diagnosis framework. Section 4 illustrates the two experimental studies and visualization analysis. Section 5 summarizes this paper and concludes future work.
2.1 Depthwise Separable Convolution
The depthwise separable convolution (DSC) [21] is a form of factorized convolution, as shown in Fig. 1. Standard convolution implements spatial-wise (filter) and channel-wise (combination) computation in a single stage, depthwise separable convolution divides the operation into two stages: depthwise convolution first applies a single filter kernel to each channel (capturing spatial-wise correlations), and then pointwise convolution constructs a linear combination of the results (capturing channel-wise correlations). This factorization requires fewer parameters than standard convolution, which can substantially reduce computational cost and model size, thereby improving computational efficiency [22,23]. Several studies have demonstrated that capturing spatial-wise correlations and channel-wise correlations separately is more efficient than capturing them simultaneously [23,24].
where
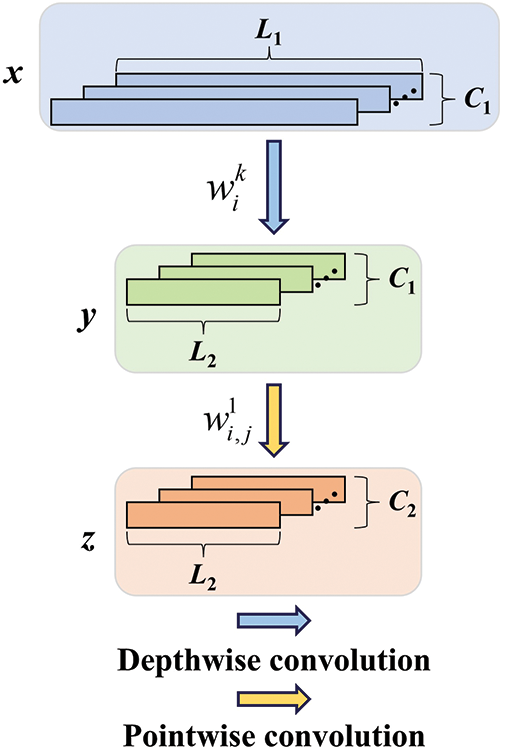
Figure 1: Depthwise separable convolution
The multiscale convolution (MC) [18], as visualized in Fig. 2, can parallelly extract multiscale features across different local receptive fields through filter kernels of multiple scales, compared to standard convolution with only filter kernels of the same scale. The extracted features are concatenated along the channel dimension, a batch normalization (BN) layer is then utilized to stabilize the feature distribution. Finally, the gaussian error linear unit (GELU) activation function is applied to execute nonlinear feature mapping. The formula describing the entire process is as follows:
where
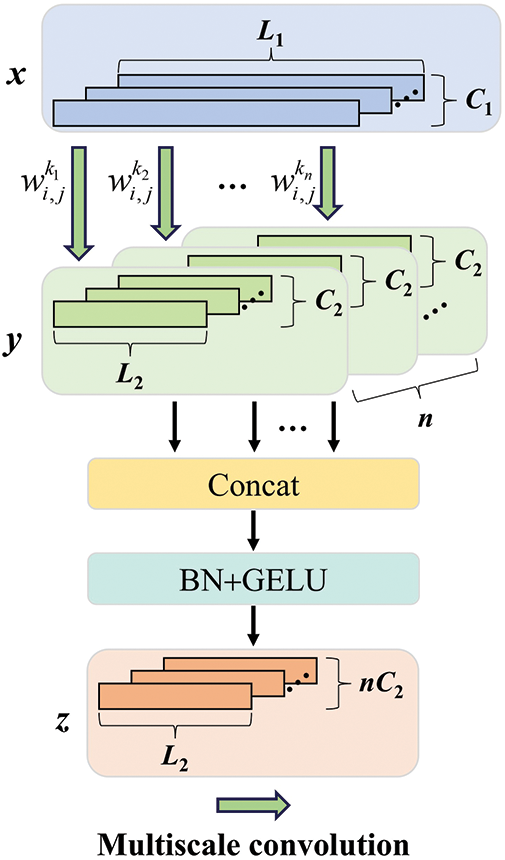
Figure 2: Multiscale convolution
Self-attention mechanism, a key part of Transformer [25], captures global feature representations across the temporal dimension through computing and assigning attention scores [26]. The scaled dot-product attention is currently the dominant method for calculating self-attention, and its mathematical formula is expressed as follows:
where
In Eq. (5), the matrix obtained by Q KT has a size of L × L, and its complexity is O(L2). Therefore, scaled dot-product attention demands high computational resources when the input dimension L is large. To address this, Shen et al. [27] proposed an efficient attention mechanism with linear complexity. Instead of using the Softmax operation, a matrix of size C × C is first obtained by KT · V according to the matrix association law, which has a complexity of O(C2). Since
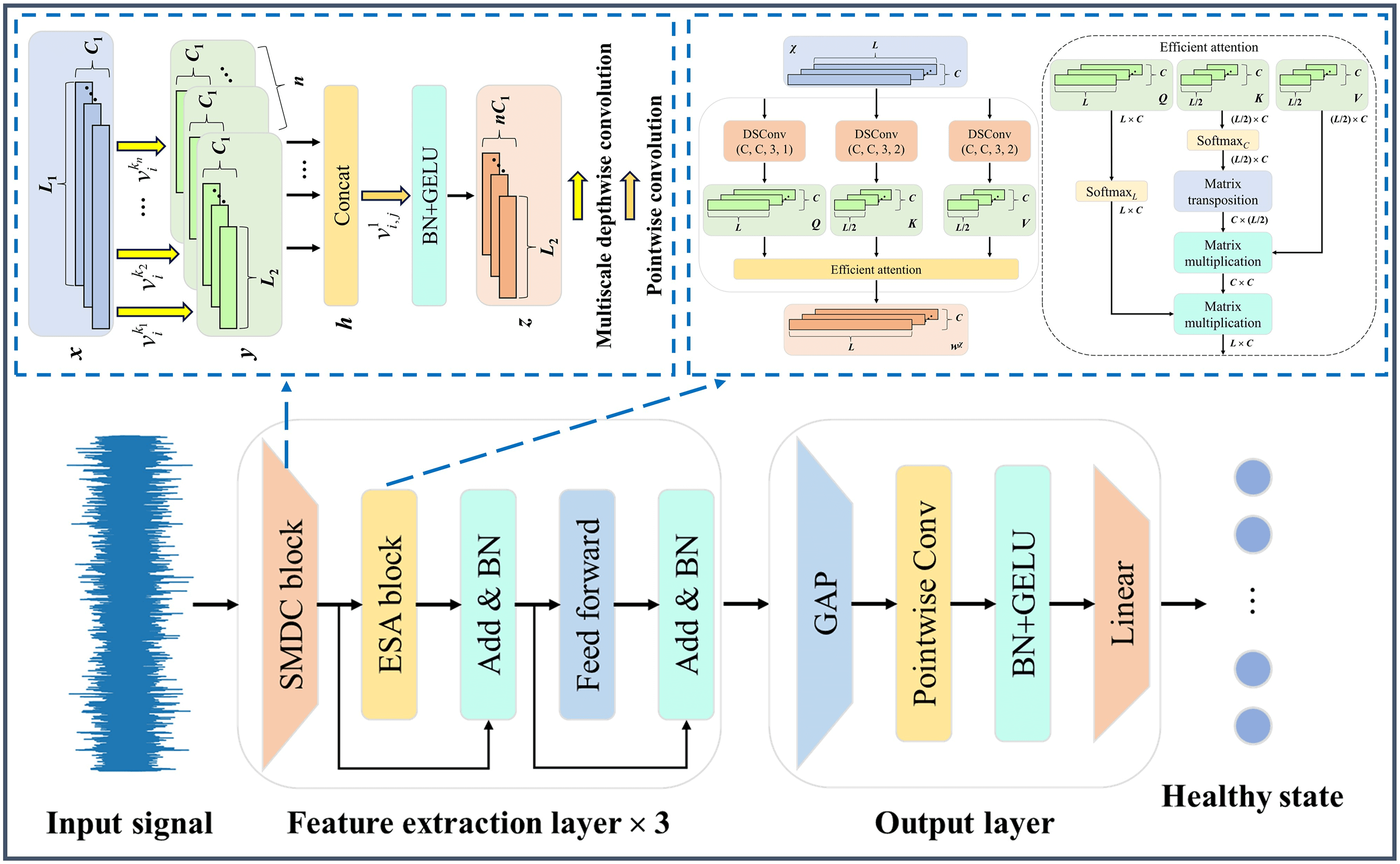
3.1 Separable Multiscale Depthwise Convolution Block
In order to efficiently extract and integrate multiscale feature information from different channel dimensions, a separable multiscale depthwise convolution (SMDC) block is designed by fusing DSC [21] and MC [18]. The depthwise separable convolution establishes a one-to-one direct mapping between input and output channels, thereby significantly lowering the computational cost of multiscale convolution. Unlike the separable multiscale convolution (SMC) block [20], the SMDC block adjusts the placement of multiscale depthwise convolution and pointwise convolution operations, first capturing multiscale spatial-wise correlations and then capturing channel-wise correlations, with the aim of aligning more closely with the DSC structure. Fig. 3 illustrates the structure of the SMDC block. First, multiscale features are extracted from different local receptive fields using parallel depthwise convolution kernels of various sizes. Then, these features are concatenated along the channel dimension. Next, pointwise convolution is utilized to integrate the feature information and capture channel-wise correlations. Finally, the BN and GELU are applied to stabilize feature distribution and perform non-linear mapping, respectively. The formula for these operations is defined as follows:
where
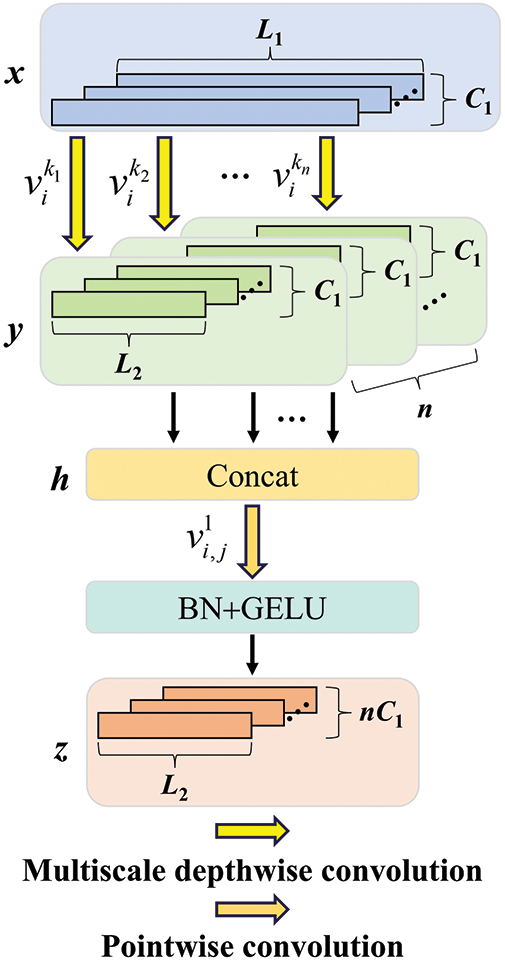
Figure 3: Separable multiscale depthwise convolution block
3.2 Efficient Self-Attention Block
To efficiently capture critical fine-grained features of the signal from a global perspective, an efficient self-attention (ESA) block is developed, as depicted in Fig. 4. First, to expand the representational capacity of each feature and reduce computation, three parallel DSC blocks are used to generate the input features for self-attention: the query matrix Q, key matrix K, and value matrix V. Then, efficient attention is employed to fully leverage global feature information transmission while lowering computational cost of self-attention calculation. Since output range of Softmax is (0, 1), it serves as a normalization operation suitable for the form of efficient attention. The matrices Q and K are normalized along the temporal and channel dimensions, respectively. Finally, attention weights are calculated through matrix transposition and multiplication operations. The formula for these operations is represented as follows:
where
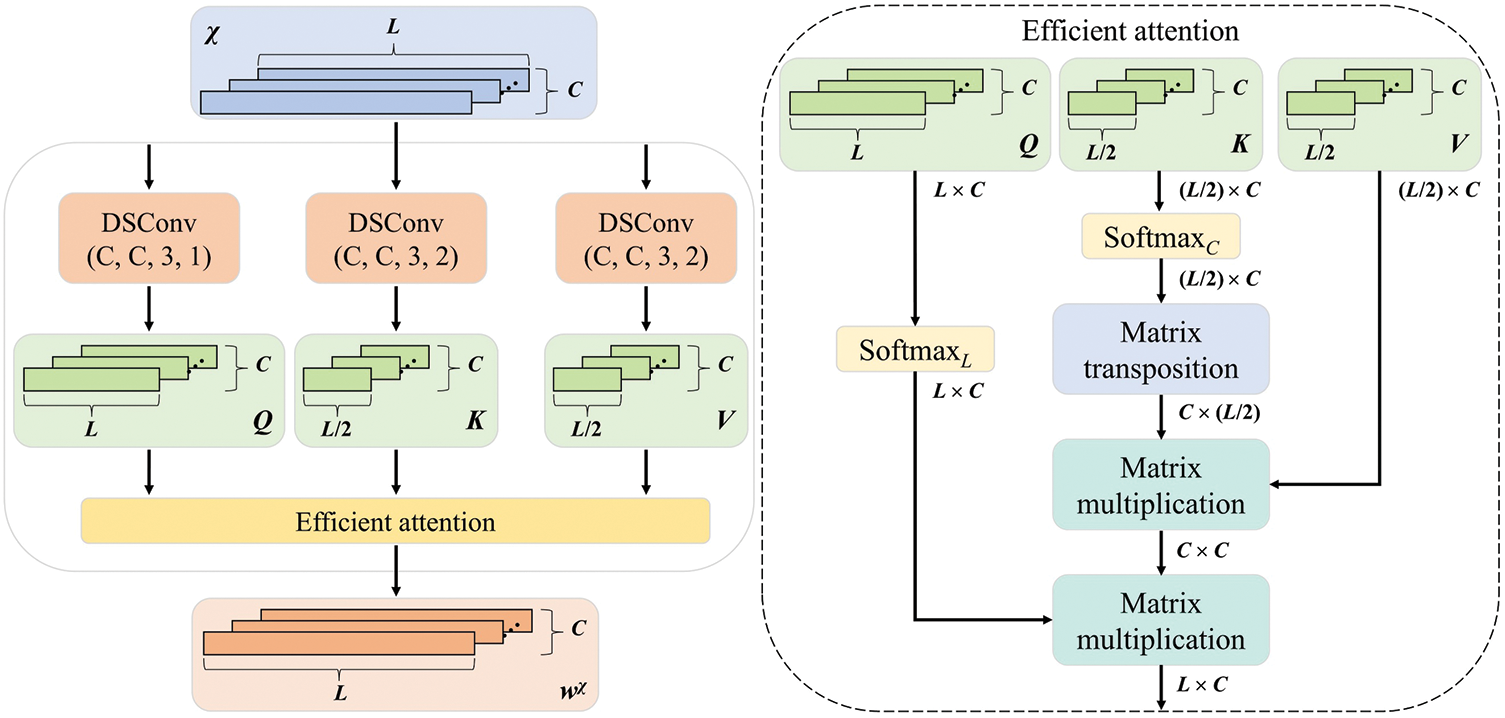
Figure 4: Efficient self-attention block
3.3 The Architecture of SEFormer
The architecture of SEFormer is simple and primarily includes three consecutively linked feature extraction layers along with a final output layer, as illustrated in Fig. 5.
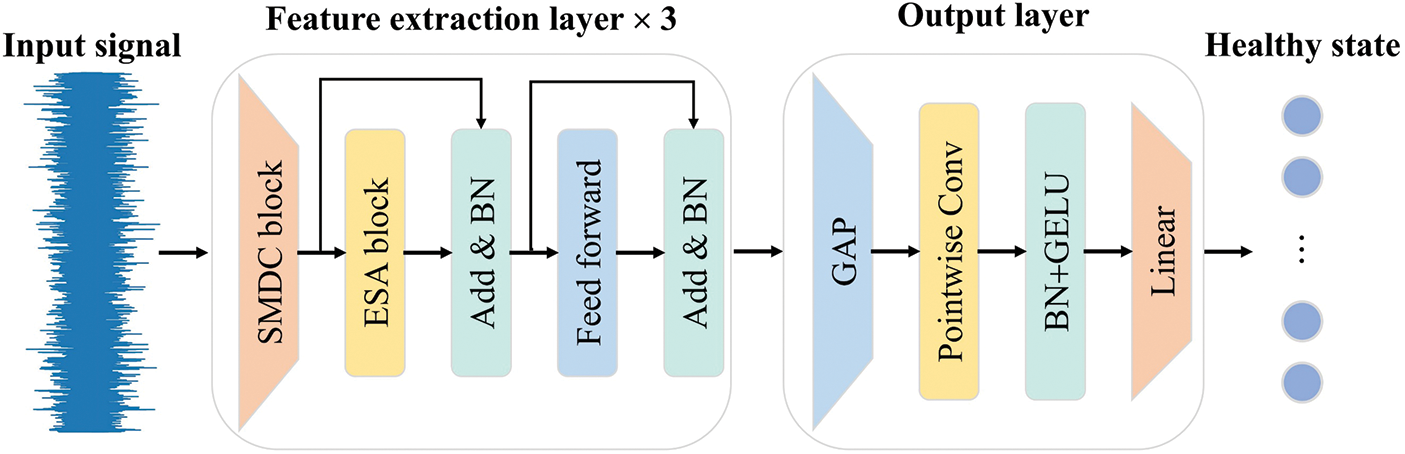
Figure 5: The architecture of SEFormer
The feature extraction layers serve as the crucial parts of SEFormer. To begin with, the SMDC block is applied to extract and integrate multiscale feature information of the signal from different channel dimensions. Next, the ESA block is employed to capture critical fine-grained features from a global perspective. A residual connection is introduced to mitigate the risk of overfitting, and BN is adopted to stabilize the distribution of feature information. Remarkably, inspired by Deng et al. [28], two trainable weights are incorporated into the residual connection to dynamically tune feature importance. Similar to the approach used by Mehta et al. [29], a lightweight feed forward network is then used to perform the non-linear feature transformation. Finally, the extracted features are output via a residual connection and BN. The specific flow and details of the feature extraction layer based on mathematical expressions are shown in Algorithm 1.

In the output layer, global average pooling (GAP) is first utilized for feature reduction in the temporal dimension. Next, a pointwise convolution block is used to integrate features across the channel dimension. Finally, a linear transformation is employed to project the high-dimensional features onto the healthy state.
Table 1 lists the detailed parameter configuration of SEFormer for an input signal with 1024 data points, including the core parameters and the output shape of each layer.

3.4 Lightweight Rotating Machinery Fault Diagnosis Framework
This paper proposes a lightweight rotating machinery fault diagnosis framework by incorporating the SEFormer model. As illustrated in Fig. 6, the specific procedure is described in the three stages below:
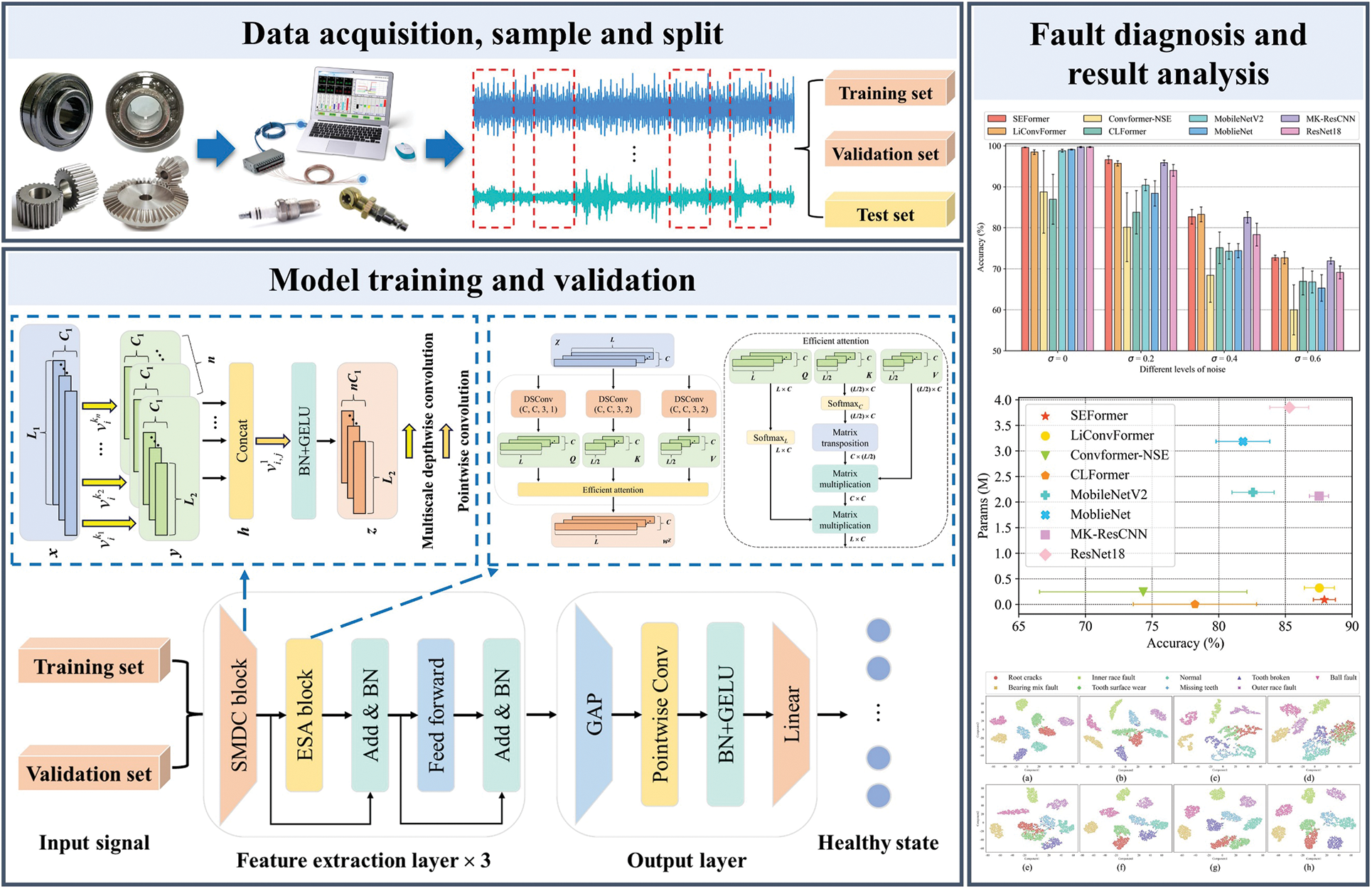
Figure 6: Lightweight rotating machinery fault diagnosis framework
Stage 1: Data acquisition, sampling, and splitting. Vibration signals are obtained through data acquisition devices from the components of rotating machinery. The collected signals are then divided into a sample set by sliding window sampling, and the sample set is split into training, validation, and test sets.
Stage 2: Model training and validation. The SEFormer model is trained using the training and validation sets. During the iteration process, the model with the highest validation accuracy is selected as the well-trained model.
Stage 3: Fault diagnosis and result analysis. The test set is input into the well-trained SEFormer model for fault diagnosis, and the results are visually analyzed from multiple perspectives.
The running configuration is as follows: CPU is an i7-14700HX with 16 GB of RAM; GPU is a RTX 4060 with 8 GB of memory. The running environment is as follows: the programming language is Python 3.8.13; the DL framework is Pytorch 1.13.1.
The cross-entropy function is applied to calculate the training loss, the Adam weight decay regularization (AdamW) [30] optimization algorithm is implemented to update the model parameters, and the learning rate is dynamically adjusted according to the loss of the validation set using an adaptive decay strategy. The initial learning rate is 0.001 in Case Study 1, and 0.01 in Case Study 2. The number of iterations for each training is 100, and the batch size is 64. In addition, unless otherwise stated, each experiment is performed five times to minimize the impact of randomness.
4.2 Case Study 1: Fault Diagnosis of Planetary Gearbox
The planetary gearbox dataset is acquired from the Institute of Aero-engine at Xi’an Jiaotong University, Xi’an, China [31]. The test rig is depicted in Fig. 7a. Two 1D-accelerometers are mounted in the X and Y directions of the planetary gearbox to gather vibration signals. During the experiment, the rotational speed of the motor and the sampling frequency are 1800 r/min and 20480 Hz, respectively. As illustrated in Fig. 7b, the fault types in the planetary gearbox consist of four gear faults and four bearing faults, one of which is a mixed fault. As a result, vibration signals are collected across nine healthy states, including the normal state.

Figure 7: The test rig of the XJTU Gearbox: (a) The test rig; (b) Healthy state of gears and bearings
The vibration signals for each health state are divided into 1200 samples using sliding window sampling. Of these, 500 samples are allocated for training, 300 samples for validation, and 400 samples for testing, with each sample comprising 1024 data points. To avoid test leakage, consecutive windows do not overlap and are spaced apart. While the original signals inherently carry some amount of noise, they still differ from the signals encountered in actual industrial manufacturing environments. Therefore, to assess the model’s anti-noise performance, two types of noises are sequentially added to the test samples. The specific formula for adding noise is as follows:
where Si denotes the i-th data point of a single test sample, α ~ N(0, σ) and β ~ N(1, σ) indicate the additive and the scaled Gaussian noise, respectively. σ is the variance of the Gaussian distribution, with larger values corresponding to stronger noise. To more realistically reflect the variability and uncertainty of noise, each sample has a 50% probability of randomly adding either type of noise. This approach allows the experimental results to be more random, better simulating the effects of noise in real-world scenarios.
This paper selects seven recent state-of-the-art models for comparative analysis with the proposed model, including three new end-to-end fault diagnosis models based on CNN-Transformer, called LiConvFormer [20], Convformer-NSE [19], and CLFormer [18], as well as four popular CNN models, called MobileNetV2 [23], MobileNet [21], MK-ResCNN [32], and ResNet18 [33]. When performing comparative analysis, each model may achieve different results under varying input signal lengths and training strategies. Therefore, to guarantee an equitable comparison, all models adopt the same input signal length and training strategy as the proposed model [6]. The average loss and accuracy from five repeated experiments for each model are depicted in Fig. 8. During the iteration process, the proposed model demonstrates minimal fluctuation at each stage and achieves lower validation loss and higher validation accuracy compared to the other models. In the early epochs, the training loss and training accuracy exhibit less fluctuation than those on the validation set for each model. The proposed model, LiConvFormer, MobileNetV2, MobileNet, MK-ResCNN, and ResNet18 show a rapid convergence rate, achieving convergence after 30 epochs, whereas Convformer-NSE and CLFormer require 80 epochs to converge. This delay in convergence is attributed to the feature dimension compression in these two models, which leads to some loss of fine-grained features and impedes their ability to adequately learn the multi-dimensional information within the signals.

Figure 8: The average loss and accuracy curves of the five repeated experiments: (a) Training loss; (b) Training accuracy; (c) Validation loss; (d) Validation accuracy
Table 2 presents the diagnostic result and model complexity under different levels of noise for each model. From the results, some baseline models exhibit somewhat higher average accuracy than the proposed model when σ = 0. However, the robustness superiority of the proposed model becomes significant as the noise level increases. Across all three noise levels, the proposed model performs well. Specifically, it achieves the highest average accuracies (96.63% and 72.72%) among all models, with small standard deviation values (0.89% and 0.59%) at σ = 0.2 and σ = 0.6. When σ = 0.4, the average accuracy of the proposed model is slightly lower than that of LiConvFormer, but it has a smaller standard deviation than LiConvFormer. In terms of overall performance, the second-best LiConvFormer shows comparable diagnostic accuracy to the proposed model. However, the proposed model demonstrates significant superiority in terms of model complexity over LiConvFormer. Although Convformer-NSE and CLFormer have relatively lower model complexity, their diagnostic performance significantly lags behind that of other models. Additionally, the optimal CNN model, MK-ResCNN, ranks third among all models.
The average diagnostic accuracy and model complexity under different levels of noise for each model is visualized in Fig. 9. The proposed model accomplishes the strongest diagnostic robustness among all models while maintaining model complexity. Specifically, the proposed model obtains an average accuracy of 87.92% and a standard deviation value of 0.83% across different noise levels, with 0.093 M Params and 9.315 M FLOPs. Compared with the second-best model, LiConvFormer, the proposed model reduces the Params by 0.23 M and FLOPs by 5.205 M, while enhancing the average accuracy by 0.38% and decreasing the standard deviation by 0.29%. Compared to the advanced CNN model, MK-ResCNN, the proposed model decreases the Params by approximately 23-fold and FLOPs by approximately 9-fold, while enhancing the average accuracy by 0.40%.
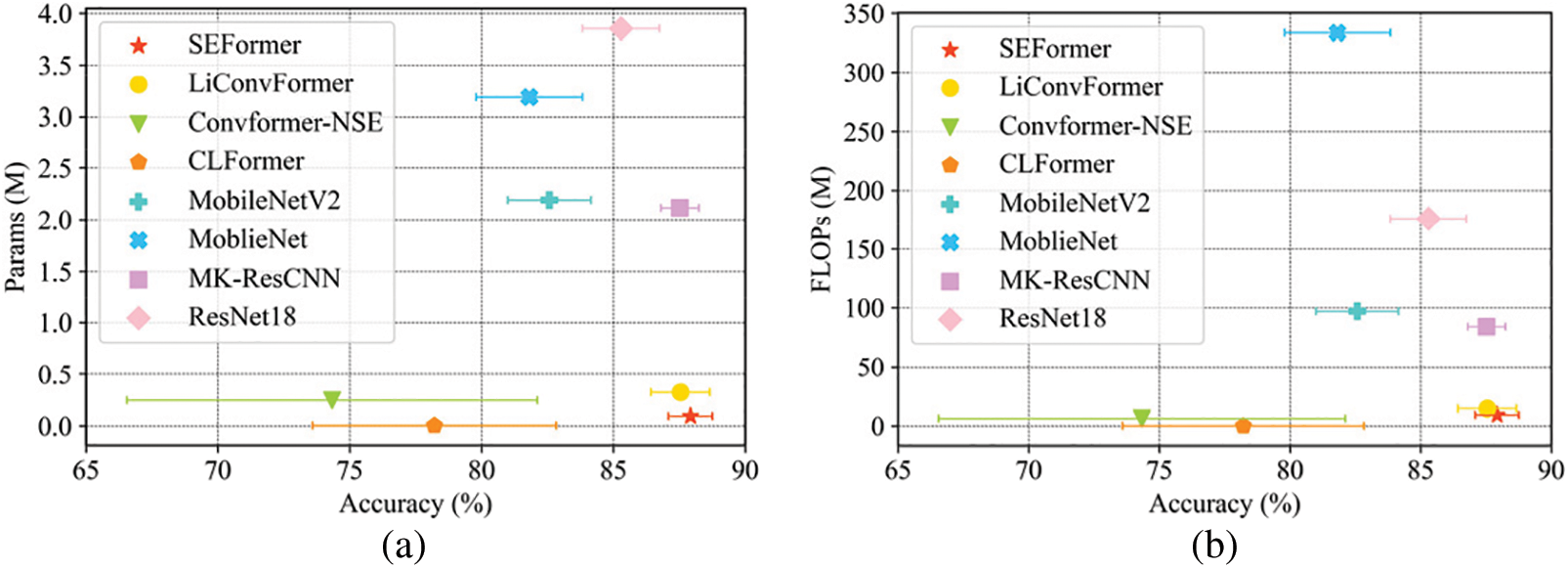
Figure 9: The average diagnostic accuracy and model complexity: (a) Performance of accuracy vs. Params; (b) Performance of accuracy vs. FLOPs
To additionally assess the feature extraction performance of each model under noise interference, feature distribution visualization is performed using t-distributed stochastic neighbor embedding (t-SNE) [35]. As shown in Fig. 10, the output features on the test set for each model are visualized in two dimensions, with different color shapes representing different healthy states. It is worth mentioning that the output features under different levels of noise for each model are combined to account for the effect of noise interference. In comparison with other models, the proposed model shows greater proficiency in distinguishing fault features across all health states, effectively clustering intra-class features of the same health state while differentiating between inter-class features of different health states. The second-best model, LiConvFormer, and the third-best model, MK-ResCNN, also demonstrate relatively good recognition of fault information across all health states. Moreover, other comparison models exhibit varying degrees of mixing between the four fault states, including root cracks, tooth surface wear, missing teeth, and normal state. This suggests that the feature information for these fault states is somewhat similar and more susceptible to noise interference.
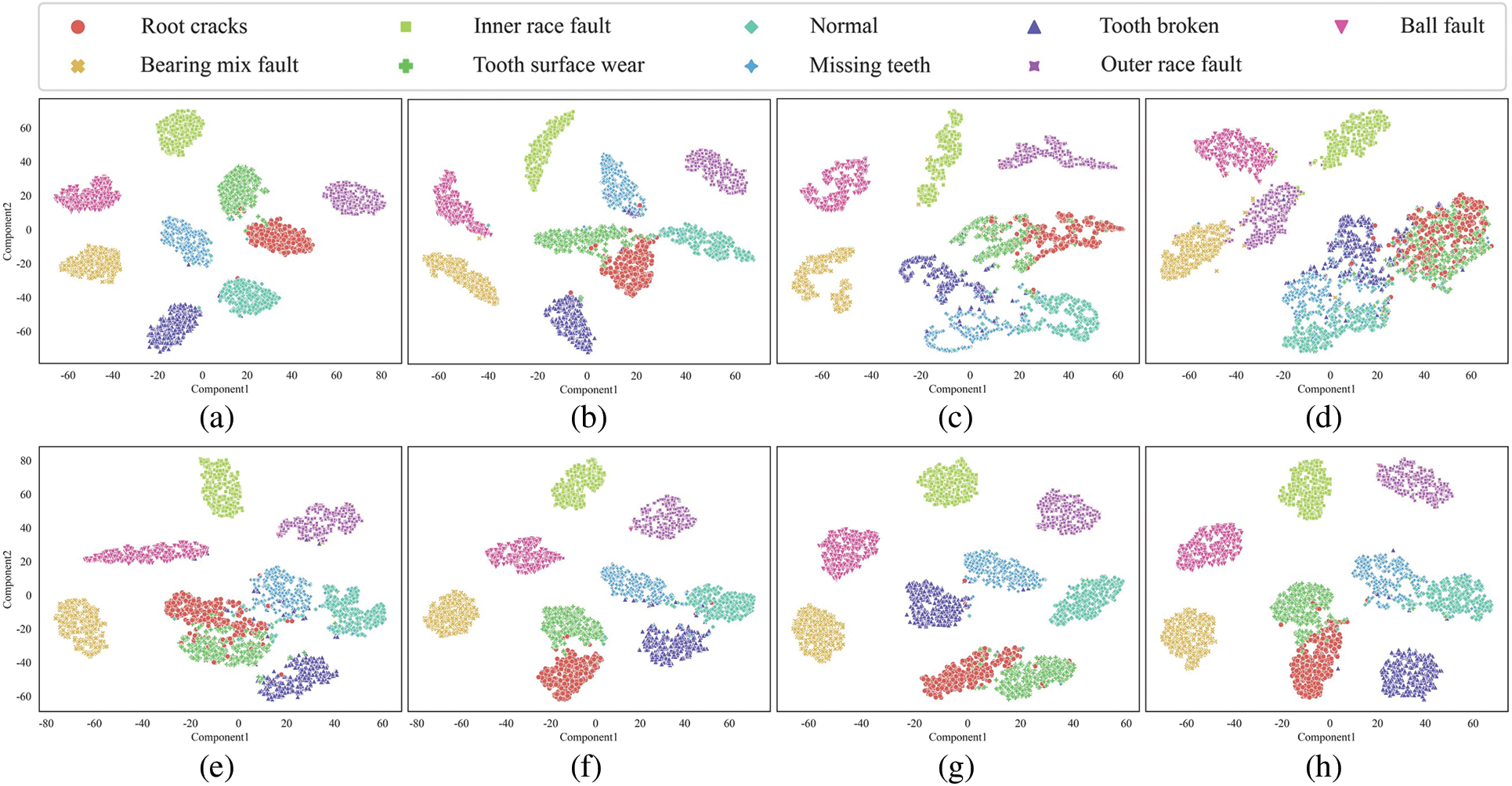
Figure 10: The feature distribution visualization by t-SNE: (a) SEFormer; (b) LiConvFormer; (c) Convformer-NSE; (d) CLFormer; (e) MobileNetV2; (f) MobileNet; (g) MK-ResCNN; (h) ResNet18
4.3 Case Study 2: Fault Diagnosis of Motor Roller Bearing
The motor roller bearing dataset is sourced from Jiangnan University (JNU), China [36], and includes three vibration datasets recorded at different motor rotational speeds (600, 800, and 1000 r/min) with a sampling frequency of 50 kHz. The experimental platform is illustrated in Fig. 11. The health states of the bearings include normal, inner race fault, outer race fault, and ball fault.
Figure 11: The illustration of test bench of the JNU Bearing
For each rotational speed, vibration signals corresponding to each health state are divided into 450 samples using sliding window sampling, with each sample comprising 1024 data points. As in Case Study 1, consecutive windows are spaced apart to avoid test leakage. To validate the generalization performance of the model, two cross-domain datasets are set up, as list in Table 3. The source domain dataset is split into training and validation sets at a ratio of 2:1, while the target domain dataset serves as the test set.

As in Case Study 1, seven comparison models are also utilized for comparative analysis with the proposed model, all with the same experimental setups. Additionally, a feature quantitative evaluation metric [37] based on between-class and within-class covariances is introduced to examine the quality of extracted features for each model in numerical terms. The between-class covariance is typically utilized to assess the extent of dispersion among distinct classes, while the within-class covariance is generally utilized to evaluate the extent of clustering within a single class. Therefore, the larger the value of the evaluation metric, the more distinguishable the output features of the model are, which is expressed as follows:
where J is the feature quantitative evaluation metric, and the larger J values indicate the better output feature quality. fi and
The feature quantitative evaluation and model complexity under the two cross-domain datasets for each model are detailed in Table 4. From the overall results, the J values on the D1 dataset are generally higher than those on the D2 dataset. This implies that the features on the D2 dataset are more difficult to extract than those on the D1 dataset. For both datasets, the proposed model has the highest mean J value (2.84 and 2.01) and min J value (2.47 and 1.62) among all models. This indicates that the proposed model remains effective in capturing fault features despite cross-domain influence. On the D1 dataset, the mean J value and min J value of the proposed model are approximately 21.37% and 43.60% higher, respectively, than those of the second-best MobileNetV2. On the D2 dataset, the mean J value is about 27.22% higher and the min J value is about 14.08% higher compared to the second-best MobileNetV2. Since Case Study 2 has fewer sensor channels for input signals than Case Study 1, the Params and FLOPs for each model are slightly reduced. While CLFormer has the smallest model complexity among all models, reducing feature dimensions leads to poor output feature quality. In comparison with the second-best MobileNetV2 and the third-best MobileNet, the proposed model shows a significant advantage in terms of model complexity while maintaining excellent feature extraction performance.

Fig. 12 depicts the diagnostic results under the two cross-domain datasets for each model, where precision and F1 score are also used to evaluate the diagnostic performance of each model in addition to accuracy. Since the features on the D2 dataset are more difficult to extract than those on the D1 dataset, the diagnostic results on the D1 dataset are generally higher than those on the D2 dataset, consistent with the feature quantitative evaluation. The proposed model obtains the best diagnostic results on both datasets, with the average of the three evaluation metrics on the D1 dataset reaching 97.24%, 97.28%, and 97.21%, respectively. On the D1 dataset, the three evaluation metrics are 1.81%, 1.65%, and 1.82% higher, respectively, than those of the second-best MobileNet. On the D2 dataset, the accuracy is 1.78% higher, precision is 4.15% higher, and the F1 score is 1.39% higher compared to the second-best MobileNet.
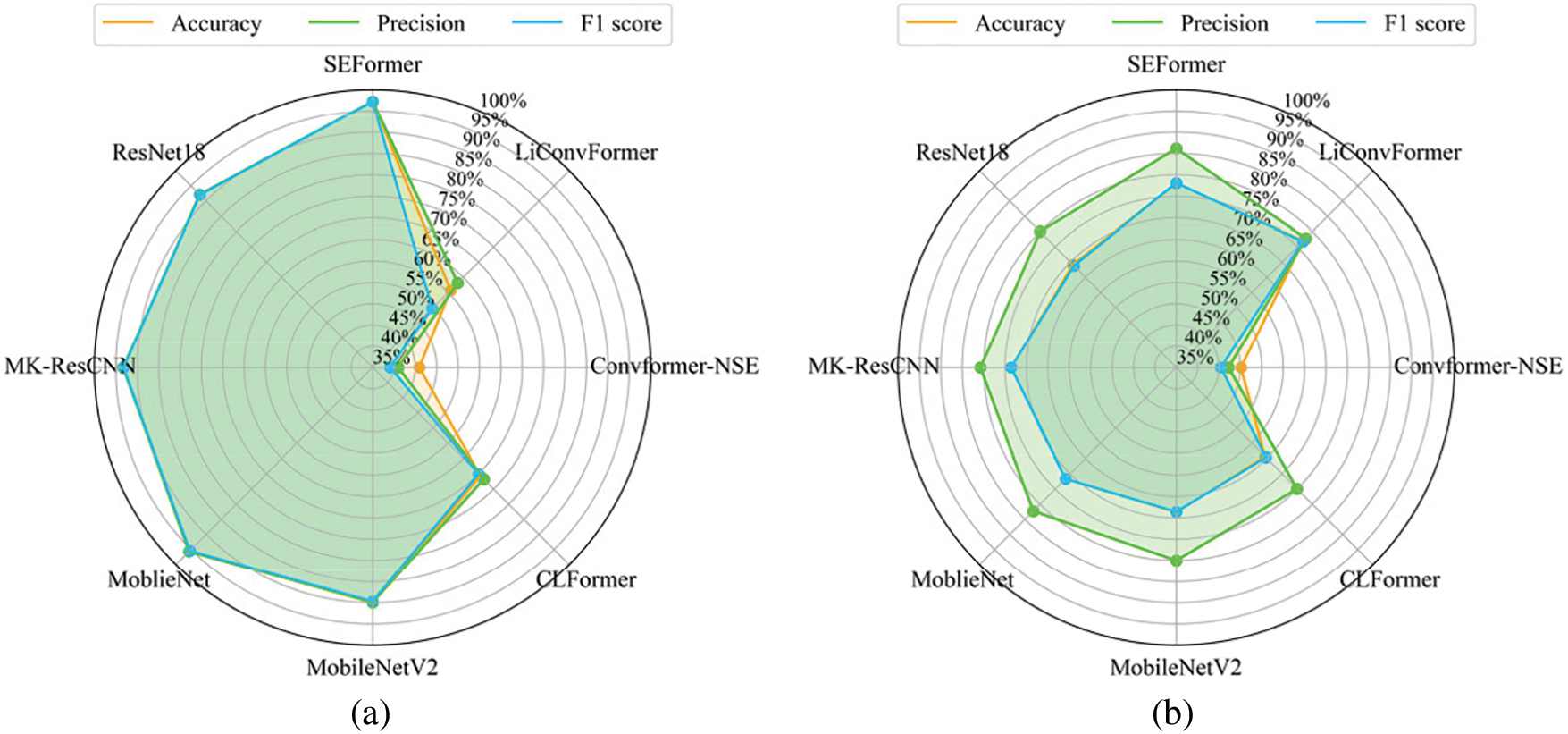
Figure 12: The diagnostic results under two cross-domain datasets: (a) D1; (b) D2
To more deeply investigate the feature extraction performance of each model under cross-domain influence, the confusion matrix is employed to evaluate the diagnostic details. As shown in Fig. 13, the confusion matrices from five repeated experiments on the D1 dataset for each model are integrated. In these matrices, IF, NS, OF, and BF on the coordinate axes correspond to the four health states of bearings: inner race fault, normal state, outer race fault, and ball fault. The proposed model achieves excellent classification results, with the recognition accuracy for each health state exceeding 92%, and accuracies for IF, NS, and OF reaching 99%. The classification results of the other comparison models are significantly lower than those of the proposed model. For the second-best MobileNet, the recognition accuracy for health states IF, NS, and OF exceeds 97%, but the accuracy for health state BF is relatively lower at 87%. Additionally, all models show lower performance in recognizing health state BF compared to other health states, indicating that the feature information of ball fault is more susceptible to cross-domain influences than that of the other health states.

Figure 13: The confusion matrix on the D1 dataset: (a) SEFormer; (b) LiConvFormer; (c) Convformer-NSE; (d) CLFormer; (e) MobileNetV2; (f) MobileNet; (g) MK-ResCNN; (h) ResNet18
To tackle the issue of high computational costs and limited industrial applicability posed by the cross-channel convolution mechanism in CNN and the self-attention calculations in Transformer, this paper proposes a lightweight CNN-Transformer named as SEFormer for rotating machinery fault diagnosis. The SEFormer comprises two core components: the SMDC block and the ESA block. The SMDC block is designed to extract and integrate multiscale feature information from different channel dimensions of vibration signals. The ESA block is developed to capture critical fine-grained features of the signal from the global scope. The experimental results on the planetary gearbox dataset and the motor roller bearing dataset prove that the proposed framework can balance advantages of robustness, generalization and lightweight compared to the recent state-of-the-art fault diagnosis models based on CNN and Transformer. This study presents a feasible strategy for developing a lightweight rotating machinery fault diagnosis framework aimed at economical deployment.
In future work, we will study the relationship between time complexity and model complexity, and further reduce the computational burden of the proposed model using techniques like model pruning, quantization, low-rank factorization, and knowledge distillation. Additionally, we will focus on further enhancing the reliability and practicality of the proposed model. To achieve this, we will investigate several advanced techniques, including multi-sensor fusion, interpretability, few-shot learning, and transfer learning [38,39]. These efforts will collectively contribute to achieving more reliable diagnostic results and more economical deployment.
Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.
Funding Statement: This work is supported by the National Natural Science Foundation of China (No. 52277055).
Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Hongxing Wang; methodology, Hongxing Wang; software, Hongxing Wang; validation, Hongxing Wang; formal analysis, Hongxing Wang; data curation, Hongxing Wang; writing—original draft, Hongxing Wang; investigation, Xilai Ju; resources, Xilai Ju; writing—review and editing, Hua Zhu and Huafeng Li; supervision, Hua Zhu and Huafeng Li; project administration, Huafeng Li; funding acquisition, Huafeng Li. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data available on request from the authors. The data that support the findings of this study are available from the corresponding author upon reasonable request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Y. Sun, J. Wang, and X. Wang, “Fault diagnosis of mechanical equipment in high energy consumption industries in China: A review,” Mech. Syst. Signal Process., vol. 186, 2023, Art. no. 109833. doi: 10.1016/j.ymssp.2022.109833. [Google Scholar] [CrossRef]
2. S. Bi et al., “A comprehensive survey on applications of AI technologies to failure analysis of industrial systems,” Eng. Fail. Anal., vol. 148, Jun. 2023, Art. no. 107172. doi: 10.1016/j.engfailanal.2023.107172. [Google Scholar] [CrossRef]
3. C. Lou, M. Atoui, and X. Li, “Recent deep learning models for diagnosis and health monitoring: A review of research works and future challenges,” Trans. Inst. Meas. Control., vol. 206, pp. 1–38, Mar. 2023. doi: 10.1177/01423312231157118. [Google Scholar] [CrossRef]
4. Z. Zhu et al., “A review of the application of deep learning in intelligent fault diagnosis of rotating machinery,” Measurement, vol. 46, Jan. 2023, Art. no. 112346. doi: 10.1016/j.measurement.2022.112346. [Google Scholar] [CrossRef]
5. Y. Lei, B. Yang, X. Jiang, F. Jia, N. Li and A. Nandi, “Applications of machine learning to machine fault diagnosis: A review and roadmap,” Mech. Syst. Signal Process., vol. 138, Apr. 2020, Art. no. 106587. doi: 10.1016/j.ymssp.2019.106587. [Google Scholar] [CrossRef]
6. Z. Zhao et al., “Deep learning algorithms for rotating machinery intelligent diagnosis: An open source benchmark study,” ISA Trans., vol. 107, pp. 224–255, Dec. 2020. doi: 10.1016/j.isatra.2020.08.010. [Google Scholar] [PubMed] [CrossRef]
7. Z. He, H. Shao, X. Zhong, and X. Zhao, “Ensemble transfer CNNs driven by multi-channel signals for fault diagnosis of rotating machinery cross working conditions,” Knowl.-Based Syst., vol. 207, Nov. 2020, Art. no. 106396. doi: 10.1016/j.knosys.2020.106396. [Google Scholar] [CrossRef]
8. Z. Zhao and Y. Jiao, “A fault diagnosis method for rotating machinery based on CNN with mixed information,” IEEE Trans. Ind. Inf., vol. 19, pp. 9091–9101, Aug. 2023. doi: 10.1109/TII.2022.3224979. [Google Scholar] [CrossRef]
9. Y. Huang, A. Liao, D. Hu, W. Shi, and S. Zheng, “Multi-scale convolutional network with channel attention mechanism for rolling bearing fault diagnosis,” Measurement, vol. 203, Nov. 2022, Art. no. 111935. doi: 10.1016/j.measurement.2022.111935. [Google Scholar] [CrossRef]
10. Y. Ding and M. Jia, “Convolutional transformer: An enhanced attention mechanism architecture for remaining useful life estimation of bearings,” IEEE Trans. Instrum. Meas., vol. 71, pp. 1–10, Nov. 2022. doi: 10.1109/TIM.2022.3181933. [Google Scholar] [CrossRef]
11. S. Islam et al., “A comprehensive survey on applications of transformers for deep learning tasks,” Expert Syst. Appl., vol. 241, no. 8, May 2024, Art. no. 122666. doi: 10.1016/j.eswa.2023.122666. [Google Scholar] [CrossRef]
12. K. Chitty-Venkata, S. Mittal, M. Emani, V. Vishwanath, and A. Somani, “A survey of techniques for optimizing transformer inference,” J. Syst. Archit., vol. 144, Nov. 2023, Art. no. 102990. doi: 10.1016/j.sysarc.2023.102990. [Google Scholar] [CrossRef]
13. J. Tang, G. Zheng, C. Wei, W. Huang, and X. Ding, “Signal-transformer: A robust and interpretable method for rotating machinery intelligent fault diagnosis under variable operating conditions,” IEEE Trans. Instrum. Meas., vol. 71, pp. 1–11, Apr. 2022. doi: 10.1109/TIM.2022.3217869. [Google Scholar] [CrossRef]
14. Y. Li, Z. Zhou, C. Sun, X. Chen, and R. Yan, “Variational attention-based interpretable transformer network for rotary machine fault diagnosis,” IEEE Trans. Neural Netw. Learn. Syst., vol. 35, pp. 6180–6193, Sep. 2022. doi: 10.1109/TNNLS.2022.3202234. [Google Scholar] [PubMed] [CrossRef]
15. Y. Ding, M. Jia, Q. Miao, and Y. Cao, “A novel time-frequency Transformer based on self-attention mechanism and its application in fault diagnosis of rolling bearings,” Mech Syst. Signal Process., vol. 168, Apr. 2022, Art. no. 108616. doi: 10.1016/j.ymssp.2021.108616. [Google Scholar] [CrossRef]
16. Z. Dai, H. Liu, Q. Le, and M. Tan, “CoAtNet: Marrying convolution and attention for all data sizes,” in 2021 Adv. Neural Inf. Process. Syst. (NeurIPS), 2021, pp. 3965–3977. [Google Scholar]
17. B. Tama, M. Vanis, S. Lee, and S. Lim, “Recent advances in the application of deep learning for fault diagnosis of rotating machinery using vibration signals,” Artif. Intell. Rev., vol. 56, pp. 4667–4709, Oct. 2022. doi: 10.1007/s10462-022-10293-3. [Google Scholar] [CrossRef]
18. H. Fang et al., “CLFormer: A lightweight transformer based on convolutional embedding and linear self-attention with strong robustness for bearing fault diagnosis under limited sample conditions,” IEEE Trans. Instrum. Meas., vol. 71, pp. 1–8, Dec. 2021. doi: 10.1109/TIM.2021.3132327. [Google Scholar] [CrossRef]
19. S. Han, H. Shao, J. Cheng, X. Yang, and B. Cai, “Convformer-NSE: A novel end-to-end gearbox fault diagnosis framework under heavy noise using joint global and local information,” IEEE/ASME Trans. Mechatron., vol. 28, pp. 340–349, Feb. 2023. doi: 10.1109/TMECH.2022.3199985. [Google Scholar] [CrossRef]
20. S. Yan, H. Shao, J. Wang, X. Zheng, and B. Liu, “LiConvFormer: A lightweight fault diagnosis framework using separable multiscale convolution and broadcast self-attention,” Expert Syst. Appl., vol. 237, Mar. 2024, Art. no. 121338. doi: 10.1016/j.eswa.2023.121338. [Google Scholar] [CrossRef]
21. A. G. Howard et al., “MobileNets: Efficient convolutional neural networks for mobile vision applications,” 2017. doi: 10.48550/arXiv.1704.04861. [Google Scholar] [CrossRef]
22. F. Chollet, “Xception: Deep learning with depthwise separable convolutions,” in 2017 IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Honolulu, HI, USA, 2017, pp. 1800–1807. [Google Scholar]
23. M. Sandler, A. Howard, M. Zhu, A. Zhmoginov, and L. -C. Chen, “MobileNetV2: Inverted residuals and linear bottlenecks,” in 2018 IEEE/CVF Conf. Comput. Vis. Pattern Recognit. (CVPR), Salt Lake City, UT, USA, 2018, pp. 4510–4520. [Google Scholar]
24. Y. Guo, Y. Li, R. Feris, L. Wang, and T. Rosing, “Depthwise convolution is all you need for learning multiple visual domains,” in 2019 AAAI Conf. Artif. Intell. (AAAI), Honolulu, HI, USA, 2019, pp. 8368–8375. [Google Scholar]
25. A. Vaswani et al., “Attention is all you need,” in 2017 Adv. Neural Inf. Process. Syst. (NIPS), Long Beach, CA, USA, 2017, pp. 8368–8375. [Google Scholar]
26. H. Lv, J. Chen, T. Pan, T. Zhang, Y. Feng and S. Liu, “Attention mechanism in intelligent fault diagnosis of machinery: A review of technique and application,” Measurement, vol. 199, Aug. 2022, Art. no. 111594. doi: 10.1016/j.measurement.2022.111594. [Google Scholar] [CrossRef]
27. Z. Shen, M. Zhang, H. Zhao, S. Yi, and H. Li, “Efficient Attention: Attention with linear complexities,” in 2021 IEEE Winter Conf. Appl. Comput. Vis. (WACV), Waikoloa, HI, USA, 2021, pp. 3530–3538. [Google Scholar]
28. J. Deng, W. Jiang, Y. Zhang, G. Wang, S. Li and H. Fang, “HS-KDNet: A lightweight network based on hierarchical-split block and knowledge distillation for fault diagnosis with extremely imbalanced data,” IEEE Trans. Instrum. Meas., vol. 70, pp. 1–9, Jun. 2021. doi: 10.1109/TIM.2021.3091498. [Google Scholar] [CrossRef]
29. S. Mehta and M. Rastegari, “Separable self-attention for mobile vision transformers,” 2022. doi: 10.48550/arXiv.2206.02680. [Google Scholar] [CrossRef]
30. I. Loshchilov and F. Hutter, “Decoupled weight decay regularization,” 2019. doi: 10.48550/arXiv.1711.05101. [Google Scholar] [CrossRef]
31. T. Li, Z. Zhou, S. Li, C. Sun, R. Yan and X. Chen, “The emerging graph neural networks for intelligent fault diagnostics and prognostics: A guideline and a benchmark study,” Mech. Syst. Signal Process., vol. 168, Apr. 2022, Art. no. 108653. doi: 10.1016/j.ymssp.2021.108653. [Google Scholar] [CrossRef]
32. R. Liu, F. Wang, B. Yang, and S. Qin, “Multiscale kernel based residual convolutional neural network for motor fault diagnosis under nonstationary conditions,” IEEE Trans. Ind. Inf., vol. 16, pp. 3797–3806, Jun. 2020. doi: 10.1109/TII.2019.2941868. [Google Scholar] [CrossRef]
33. K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” in 2016 IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Las Vegas, NV, USA, 2016, pp. 770–778. [Google Scholar]
34. K. He and J. Sun, “Convolutional neural networks at constrained time cost,” in 2015 IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Boston, MA, USA, 2015, pp. 5353–5360. [Google Scholar]
35. N. Pezzotti, B. Lelieveldt, L. Maaten, T. Höllt, E. Eisemann and A. Vilanova, “Approximated and user steerable tSNE for progressive visual analytics,” IEEE Trans. Vis. Comput. Graphics., vol. 23, pp. 1739–1752, Jul. 2017. doi: 10.1109/TVCG.2016.2570755. [Google Scholar] [PubMed] [CrossRef]
36. K. Li, X. Ping, H. Wang, P. Chen, and Y. Cao, “Sequential fuzzy diagnosis method for motor roller bearing in variable operating conditions based on vibration analysis,” Sensors, vol. 13, pp. 8013–8041, Jun. 2013. doi: 10.3390/s130608013. [Google Scholar] [PubMed] [CrossRef]
37. X. Zhao et al., “Intelligent fault diagnosis of gearbox under variable working conditions with adaptive intraclass and interclass convolutional neural network,” IEEE Trans. Neural Netw. Learn. Syst., vol. 34, pp. 6339–6353, Sep. 2023. doi: 10.1109/TNNLS.2021.3135877. [Google Scholar] [PubMed] [CrossRef]
38. T. Gao, J. Yang, and Q. Tang, “A multi-source domain information fusion network for rotating machinery fault diagnosis under variable operating conditions,” Inf. Fusion, vol. 106, Jun. 2024, Art. no. 12278. doi: 10.1016/j.inffus.2024.102278. [Google Scholar] [CrossRef]
39. T. Gao, J. Yang, W. Wang, and X. Fan, “A domain feature decoupling network for rotating machinery fault diagnosis under unseen operating conditions,” Reliab. Eng. Syst. Saf., vol. 252, Dec. 2024, Art. no. 110449. doi: 10.1016/j.ress.2024.110449. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF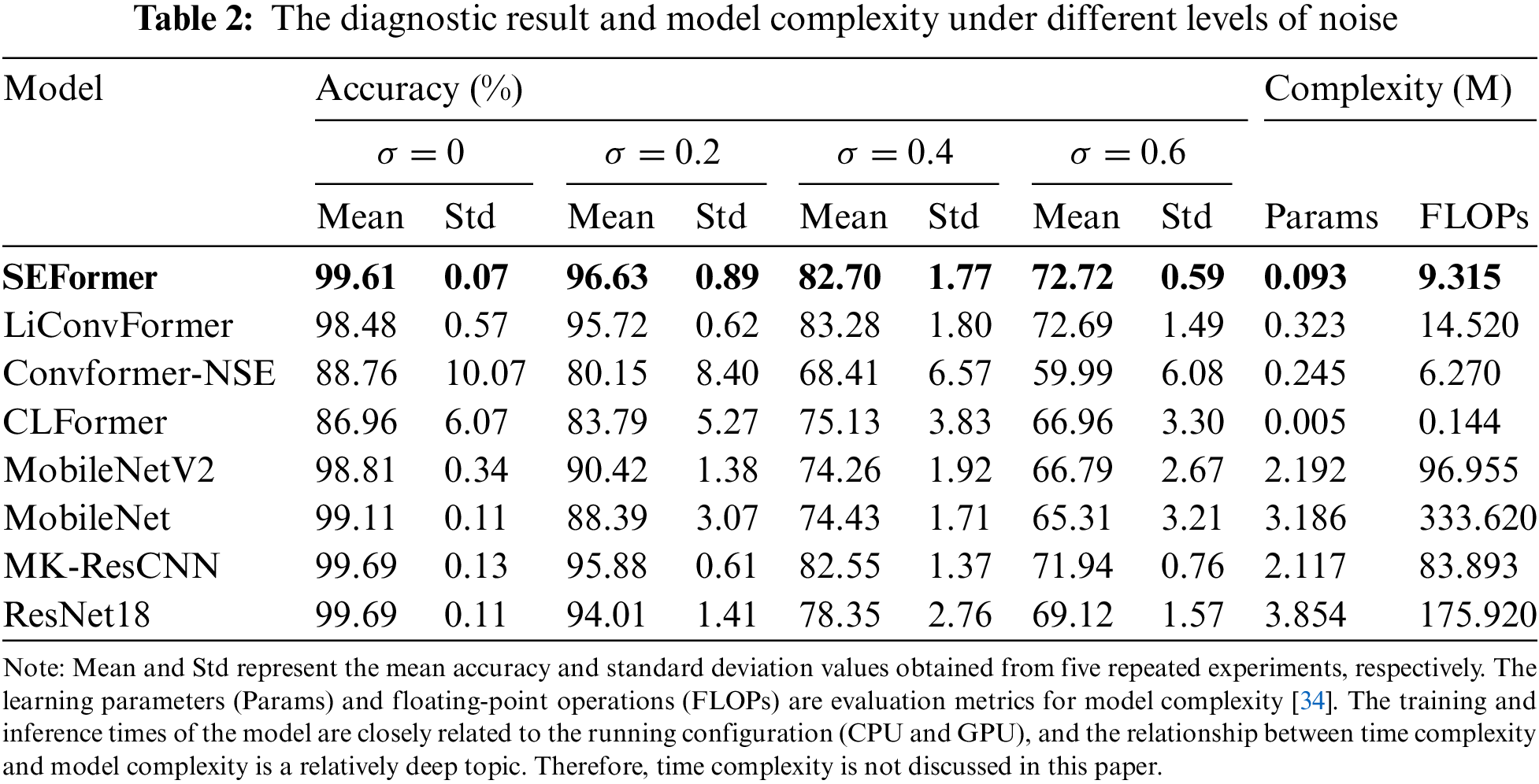
 Downloads
Downloads
 Citation Tools
Citation Tools