An Improved Practical Byzantine Fault-Tolerant Algorithm Based on XGBoost Grouping for Consortium Chains

1  Introduction

Blockchain can be categorized into public chains, private chains, and consortium chains based on its characteristics and application scenarios. Among them, the consortium chain, in which participants only target members of a specific organization and a limited number of third parties, takes into account the decentralization of the public chain and the efficiency of the private chain, as well as improves the security and scalability of the network, and has become the mainstream blockchain due to its strong ability to integrate with the business of the market, which has found widespread application in the field of supply chain management [1–3], financial services [4], energy [5], and so on.

The consensus algorithm, a core component of blockchain, plays a crucial role in its security and operational efficiency. Currently, the commonly used consensus algorithms in the consortium chain are Proof of Work (POW) [6], Proof of Stake (POS) [7], Practical Byzantine Fault-Tolerant (PBFT) [8], and Consistency Algorithm (RAFT) [9]. POW verifies the validity of the transaction by calculating the amount of workload, but its computation needs to consume significant resources and time, and it is prone to lead to the double-spend problem. POS is based on the holder’s equity to validate the transaction, but each time the reward is given to the miner with higher equity, once there is any delay, it will lead to synchronization problems. RAFT achieves node consensus through a voting mechanism and log replication mechanism, it outperforms the previous two in terms of performance, but due to the strong leader is prone to bring a single point of failure and data latency problems. PBFT with anti-Byzantine nodes and strong consistency performs especially well in the consortium chain compared with the previous three and becomes the first choice of consensus algorithm in consortium chains.

The design of the PBFT algorithm mainly focuses on the byzantine fault-tolerance problem in distributed systems, which can ensure that the system can still arrive at the correct consensus result even if there are f evil or downtime nodes in the case of the total number of nodes is 3f+1. PBFT ensures the stable operation of the system and efficient resource utilization through the view-switching protocol and the garbage collection mechanism. However, PBFT still exists in many practical scenarios, especially in the application of consortium chain, such as the trustworthiness of the master node cannot be guaranteed, the communication overhead is too large, and the support network scale is limited, which fails to meet the performance requirements of the application scenarios, and restricts the development of the consortium chain. Aiming at the above problems of the PBFT algorithm, scholars have proposed improvement of models [10–12].

Improved Practical Byzantine Fault-Tolerance (IPBFT) proposed in the literature [13,14] generates a master node through a credit model and a voting mechanism to ensure the reliability of the master node, literature [15] applied the method of selecting master nodes by reputation value to UAV-assisted environments, literature [16] applied the above method combined with the features of drug traceability to drug traceability systems, and literature [17] further optimized the consensus process by combining it with artificial bee colony, and applies it to constructing a federation chain for flight operation data. Although this method enhances the reliability of the master node, it is not suitable for dynamically changing network environments, and the algorithm’s performance deteriorates significantly as the number of nodes increases. WBFT proposed in the literature [18] introduced a dynamic weighting mechanism for consensus nodes to enhance the security of the blockchain system by diminishing the influence of malicious nodes. However, the computational efficiency of the weighting algorithm still needs to be improved. Literature [19] proposed a grouping PBFT consensus algorithm (GPBFT) based on feature trust, which assesses the trustworthiness of nodes during the transaction process using the EigenTrust trust model, and uses the trust of nodes as the basis for electing master and proxy nodes, the disadvantage is that it ignores the impact of historical trust information on the current trust value calculation and does not fully consider the time series coherence of transactions.

The improvement scheme of the above scholars is mainly to enhance the reliability of the master node by directly introducing the reputation value or trust model for grouping. This single reputation value selection method is easily influenced by outdated nodes, which can easily lead to the wrong selection of nodes, is not applicable to the rapidly changing network environment, and the updating and maintenance of the reputation system will become complicated when the data size is large. In recent years, the grouping of nodes by optimization algorithms and machine learning to improve consensus performance has become the main trend of scholars to improve PBFT. Literature [20] introduced a genetic algorithm to design the fitness function to iterate a consensus node group with better metrics. However, the time cost is high, and there is a tendency to get trapped in local optimization. Literature [21–23] introduced a decision tree algorithm to propose the optimization scheme of the PBFT algorithm based on improved C4.5, introduced the weighted average information gain to optimize C4.5 to improve the classification accuracy, chose the nodes with higher trust level to form the master consensus group, and introduced the integral voting mechanism to determine the master node. However, the accuracy of grouping still requires improvement.

To provide a PBFT algorithm with more reliable master node selection, this paper utilizes the features of XGBoost [24] such as automatic processing of missing values, strong generalization ability, and high classification accuracy, introduces SHAP to optimize the feature selection of XGBoost algorithm, and selects the nodes that have a significant impact on consensus serving as the foundation for grouping, and constructs a node grouping model based on XGBoost, and applies it to the PBFT node classification problem to select more reliable master nodes. The main contributions of this paper are as follows:

1.    Propose the XGBoost grouping model based on node classification. The model will be grouped according to the node’s historical performance characteristics, to reduce the chance brought by a single training and improve the reliability of the master node, the historical reputation value is introduced as a grouping feature;

2.    Improve the consensus protocol. The consensus protocol is enhanced by integrating the grouping model to address the high communication complexity inherent in the original PBFT algorithm;

3.    Set up multiple comparison experiments. To verify the advantages of the XG-PBFT algorithm, the algorithm is deployed to the Fabric consortium chain and other algorithms for performance comparison.

2  Overview of PBFT and XGBoost

2.1 PBFT Algorithm

The PBFT algorithm, first proposed by Miguel Castro and Barbara Liskov, addresses the inefficiencies of the original Byzantine fault-tolerant algorithm by reducing its complexity from exponential to polynomial levels, making Byzantine fault tolerance feasible for real-world applications.

2.1.1 Consensus Protocol

Fig. 1 shows the PBFT consensus protocol, where Client represents the client, Primary represents the master node, Replica0 and Replica1 represent the nodes in the consensus group, and Replica2 represents the nodes that are down or evil. The following is a detailed explanation of the optimization of the various stages of the protocol:

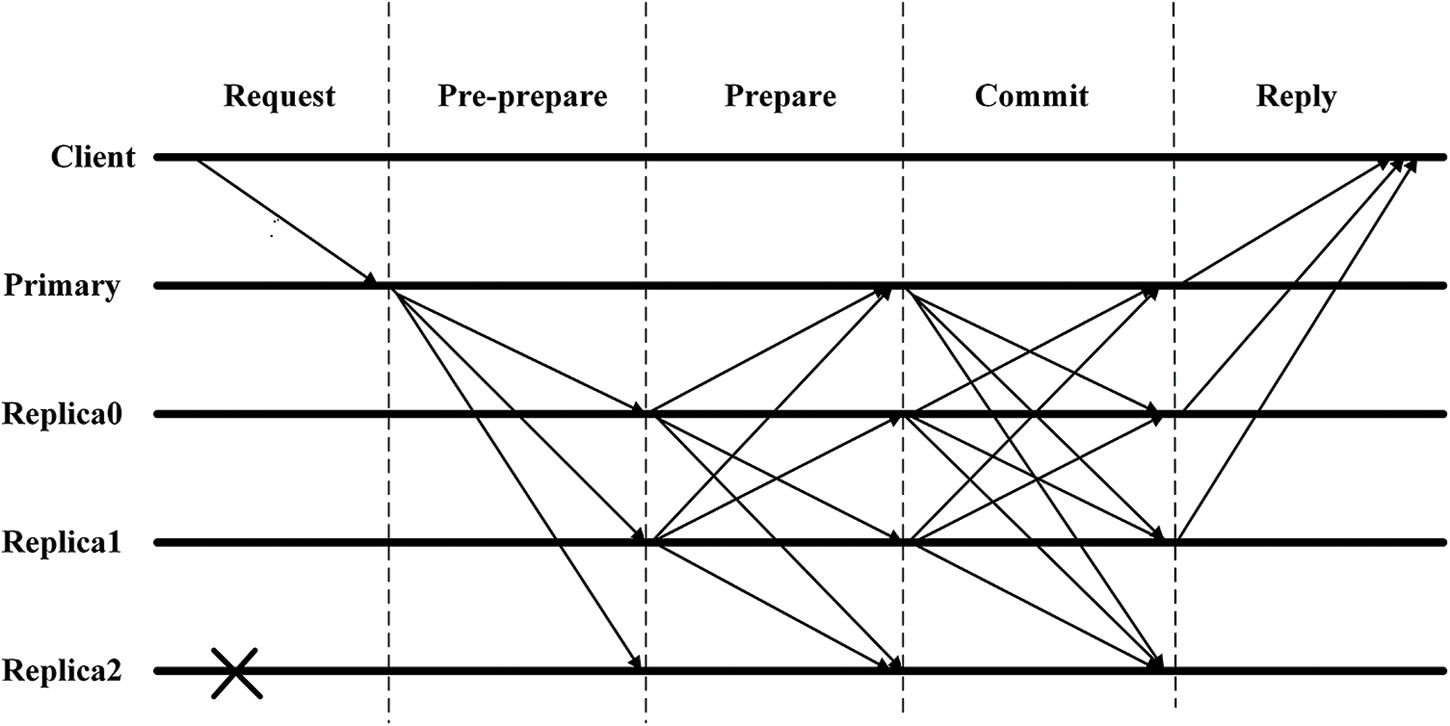
Figure 1: Execution process of the consistency protocol in the PBFT algorithm

Request: The client sends a transaction request message << REQUEST, O, T, C >> to the master node, O denotes the state machine that executes the request, T denotes the timestamp, and C denotes the number of the client.

Pre-prepare: The master node generates a pre-prepare message case << PRE-PREPARE, V, N, DIGEST >, MESSAGE>> broadcasting to the slave nodes from the view number N sent by the client, where V denotes the view number, MESSAGE denotes the client’s request information, and DIGEST denotes the summary of the disappearing MESSAGE.

Prepare: The consensus node receives the pre-preparation message and prepares the message <PREPARE, V, N, DIGEST>, and the master node receives the messages from all the slave nodes, then it enters into the acknowledgment phase.

Commit: The master node will receive feedback from the slave nodes for judgment and generate the message <COMMIT, V, N, DIGEST>, in the case of the same message, it will broadcast all the nodes in the network and inform the client.

Reply: Each node sends the consensus result to the client, and the entire network subsequently updates the ledger.

2.1.2 Other Mechanisms

The PBFT algorithm effectively prevents malicious attacks such as spoofing and replay in the blockchain by its unique consensus mechanism, which improves the security of the system and makes the system remain active when the master node fails. Mechanisms added by PBFT in the consensus process include garbage collection mechanisms, checkpoints, water level lines, and view-switching protocols.

The garbage collection mechanism is a mechanism in which the system removes the uncontested message records from the log to save memory. During the consensus process, each message received by a node is saved locally. When the node confirms that it has achieved synchronization and agreement with the majority of other nodes, it releases the previous consensus messages. Checkpointing is the mechanism used to process the recycled data periodically. When a node executes k requests consecutively, if a node receives 2k+1 checkpoints, the system considers that the majority of other nodes have reached a state of synchronization and agreement with itself, and will clean up the previous data, and this state of synchronization and agreement is a checkpoint, and the proven checkpoints are called stable checkpoints. To limit the master node to blindly assign sequence numbers, to ensure that the checkpointing protocol is normal, the consensus process adds a water level line mechanism, the water level line mechanism will be limited to the sequence number between the high and low water levels. The view-switching protocol is activated when the master node fails or behaves maliciously, preventing backup nodes from waiting indefinitely for the request to be executed.

2.2 XGBoost Algorithm

XGBoost is an integrated boosting algorithm based on decision trees, which improves the performance of the overall model by iteratively training the decision trees and continuously correcting the prediction errors of the previous trees. XGBoost improves the training speed and prediction accuracy by supporting parallelization of the training, has good generalization ability, and is now widely used in classification, regression, and sorting due to its good results and low computational complexity problems. The training process of XGBoost is shown in Fig. 2.

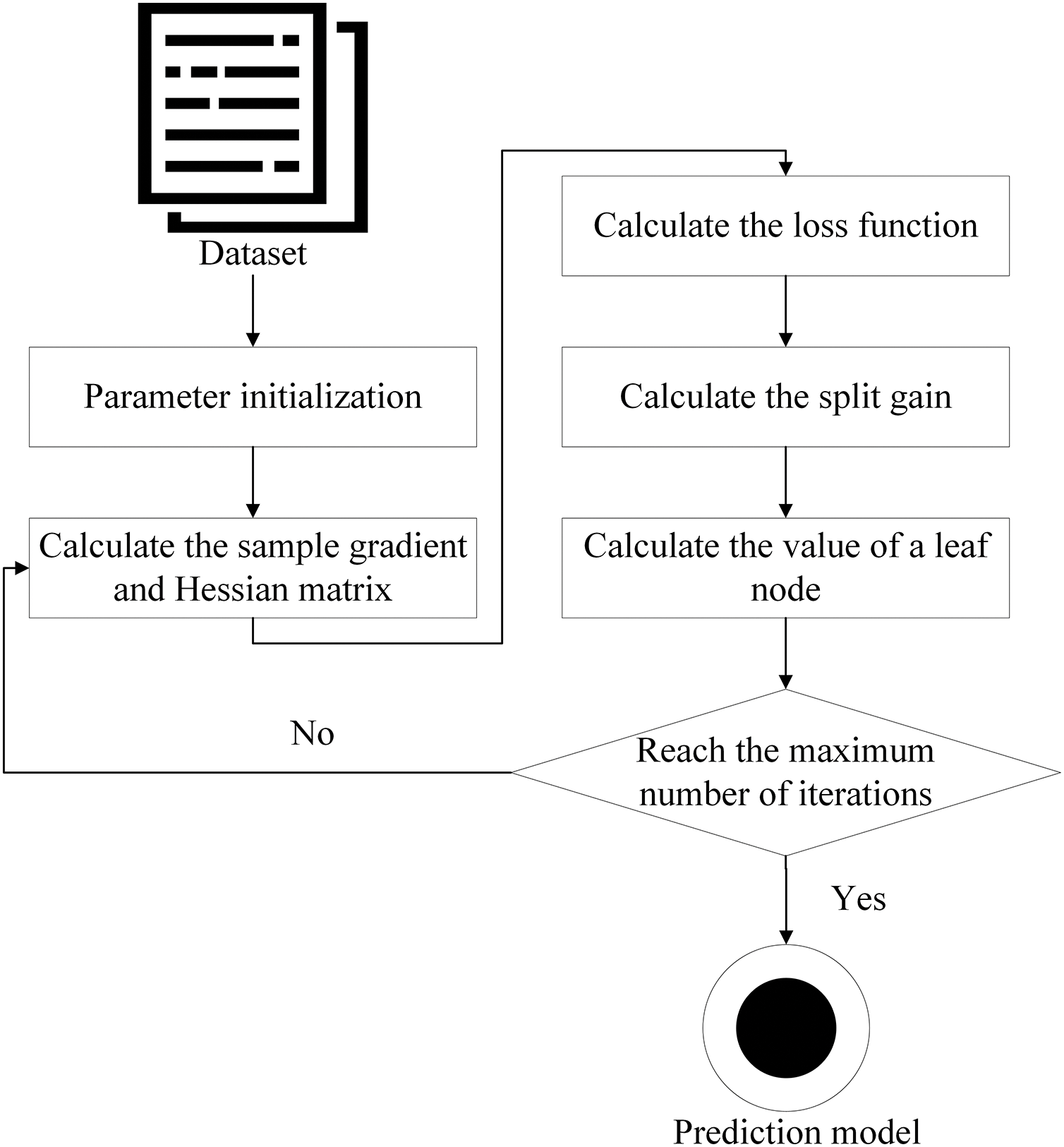
Figure 2: XGBoost training process

Step1 Parameter initialization. This includes the filling of data in the dataset with missing values and feature normalization, and the configuration of parameters that influence the model’s performance, such as the learning rate, the depth of the tree, and the regularization term.

Step2 Calculate the sample gradient and Hessian matrix. Calculate the gradient (first-order derivative) and Hessian matrix (second-order derivative) of the feature data samples of each node.

Step3 Calculate the loss function. The loss function is used to select the optimal tree structures. XGBoost incorporates a regularization term into the loss function to prevent overfitting, enhancing the model’s generalization capability. It determines the optimal weight values and tree scores using a second-order Taylor expansion. Generally, a smaller loss indicates a better tree structure, ultimately leading to the minimum value of the loss function, as illustrated in Eq. (1).

Obj(t)=−12∑j=1TGj2Hj+λ+ΥT.(1)

In the above equation, Gj2 and Hj represent the first and second-order derivatives of the jth leaf node, λ is the regularization parameter, Υ is used to control the minimum splitting gain of each tree, and T represents the number of leaf nodes of the tree.

Step4 Calculate the splitting gain. XGBoost uses the splitting gain to select the best splitting point to control the branching of the tree. The calculation of Gain is shown in Eq. (2).

Gain=12[GL2HL2+λ+GR2HR2+λ+(GL+GR)2(GL+GR)2+λ]−Υ.(2)

In the above equation, GL and GR denote the sum of the gradients of the left and right subsets of the partition, respectively. HL and HR denote the sum of the second-order derivatives of the left and right subsets of the partition, respectively.

Step5 Calculate the values of leaf nodes. Assign the samples to the leaf nodes and calculate the output value of each leaf node.

Step6 Threshold judgment. Judge whether the set number of iterations or the number of trees is reached, if not continue to repeat Step2 to Step5 for iteration to construct multiple decision trees. If the threshold is reached, the XGBoost prediction model is formed based on the combination of decision trees.

3  Improved Algorithm Design

3.1 System Model

To make the PBFT master node election more reliable, this paper proposes an XGBoost grouping based PBFT algorithm (XG-PBFT). XG-PBFT elects the features that have a greater impact on the consensus through SHAP, and the nodes joining the system will be grouped according to these features through the XGBoost grouping model. The system model of the XG-PBFT algorithm is shown in Fig. 3.

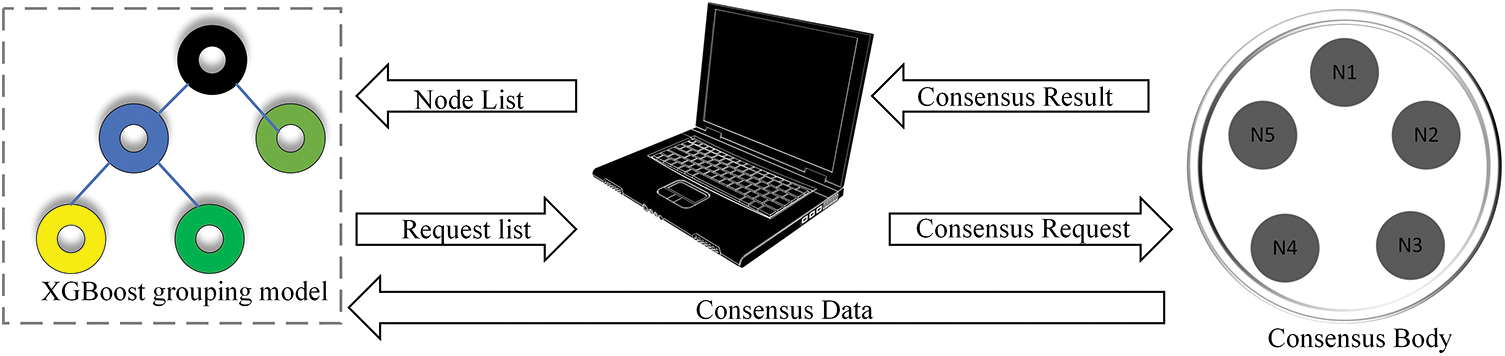
Figure 3: XG-PBFT system model

In the original PBFT algorithm, the client initiates a consensus request to the consensus body, and the consensus body feeds the consensus result back to the client after the end of the consensus, and then the master node broadcasts across the whole network. XG-PBFT introduces the XGBoost grouping model within the dotted line in the figure to group nodes in order to improve the reliability of the election of the master node and to improve the efficiency of the consensus. XG-PBFT will collect the node consensus performance data after each consensus body consensus, firstly, make a preliminary prediction by XGBoost, and then select the features that have greater influence on consensus as the basis of grouping by SHAP, so as to get the XGBoost grouping model, and the list of nodes initiating the consensus request will be grouped according to the grouping model, and the grouping result will be fed back to the client to wait for the initiation of the next consensus request. The system cycles through the consensus and grouping process to obtain nodes with good long-term performance to participate in the consensus, thus ensuring the reliability of the master node election.

3.2 Feature Selection

3.2.1 SHAP Explanatory Model

The core concept of SHAP (SHapley Additive exPlanations) is derived from game theory, which implements model interpretation by measuring the influence of each feature in the model. The method considers each feature in the model as a contributor to the final prediction and calculates their respective contribution. In short, the SHAP values reflect the importance of each feature in the model, thus providing quantitative support for model interpretation.

3.2.2 Feature Selection Process

To further improve the XGBoost grouping accuracy and master node election reliability, we utilized SHAP as an auxiliary tool to interpret the feature selection of XGBoost, and the interpretation process is shown in Fig. 4. The dataset of node consensus performance parameters is collected after the end of the PBFT consensus, and the prediction results are preliminarily derived from the XGBoost model, and SHAP can interpret the prediction results analysis to accurately locate the features required for PBFT node classification to select the features that have a greater impact on consensus as node classification features.

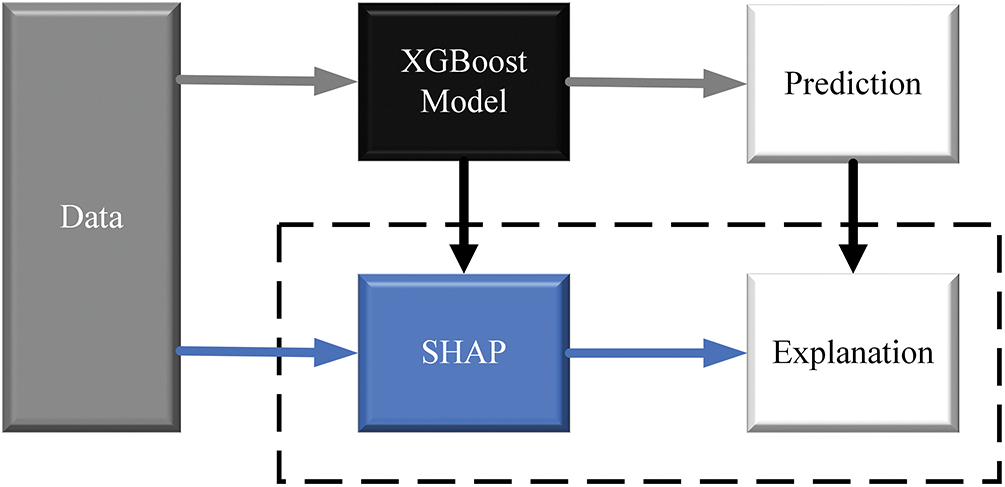
Figure 4: SHAP explains the XGBoost model

In the XGBoost model for classification tasks, the output is a probability value. SHAP (SHapley Additive exPlanations) calculates the Shapley value for each feature, providing a measure of each feature’s contribution to the final prediction. Assuming that f represents the XGBoost model to be interpreted, k represents the total number of features, and ∅ is the Shapley value of each feature, the SHAP value can be obtained as shown in Eq. (3), where f(n) is the model prediction, ∅0 is the predicted mean value of all the training samples, and ∅i is the attributed value corresponding to each feature.

f(n)=∅0+∑i=1n∅i.(3)

Additionally, the SHAP value reflects the influence of features on the model. When the SHAP value for a feature is positive, it indicates that the feature has a positive effect on the classification result; conversely, it reduces the classification accuracy of the XGBoost grouping model.

3.2.3 Node Classification Characteristics

The method of selecting consensus nodes with a single reputation value relies on the result of a single round of consensus, which is less reliable and not applicable to the dynamic network environment, and it is more complicated to update and maintain the reputation system. In this study, to improve the reliability of consensus node selection and the adaptability of the reputation value system to the dynamic network environment, by considering the eigenvalues after the SHAP analysis and introducing the historical reputation values as the classification features, Table 1 is the definition of the classification features.

H_rep is a weighted sum of the eigenvalues, reflecting the performance of the node over all historical consensus processes. The calculation process of H_rep is shown in the Eq. (4).

H_repit=α×H_repit−1+(1−α)Fit(Xit).(4)

In the above equation, H_repit denotes the reputation value of the ith node in the tth round, Xit denotes the set of eigenvalues of the ith node in the ith round [5 E_t], Fit(∗) denotes the computation function of the eigenvalues, and the eigenvalues need to be dimensionless during the computation, and α is the weight coefficient with the range of [0, 1] and the default value is 0.5. Among the above features, C_t, R_t and O_t reflect the performance characteristics of the node, and the weight is relatively low in the calculation; E_t and the H_rep are important features affecting the security of the node, and the weight is relatively high.

3.3 Node Grouping

After the client initiates the consensus, the anchor node in the coalition chain will detect the node behavior, and after each new round of consensus, the node consensus behavior data is collected and input into the grouping model. Based on the reputation values, nodes are then categorized into either the general group or the consensus group. Among them, the nodes classified into the consensus group need to be online for a long time, have less or almost no evil behavior, respond faster, and participate in the consensus for a sufficiently large number of times.

The node grouping step is shown in Algorithm 1, the reputation value obtained from the grouping model is used as the input of the grouping algorithm, the normal group and the consensus group are initialized to be empty, and the nodes are grouped based on their reputation value, with those having a value greater than 0.5 being assigned to the consensus group to participate in the consensus, and the rest of the nodes are in charge of accepting the results of the consensus by entering the normal group. In addition, to ensure that the algorithm successfully reaches consensus, the number of nodes in the consensus group should be no less than 4, when the number of nodes in the consensus group is less than 4, the nodes in the general group join the consensus group; to improve the efficiency of the consensus, the number of consensus groups is not greater than half of the total number of nodes when half of the total number of nodes is reached, the excess nodes are moved to the general group according to the reputation.

3.4 Improved Consensus Protocol

The consensus protocol is an important factor that affects the performance of the consensus algorithm such as communication complexity. In this paper, the consensus protocol of the PBFT algorithm is optimized for the problem of high communication complexity, which is shown in Fig. 5.

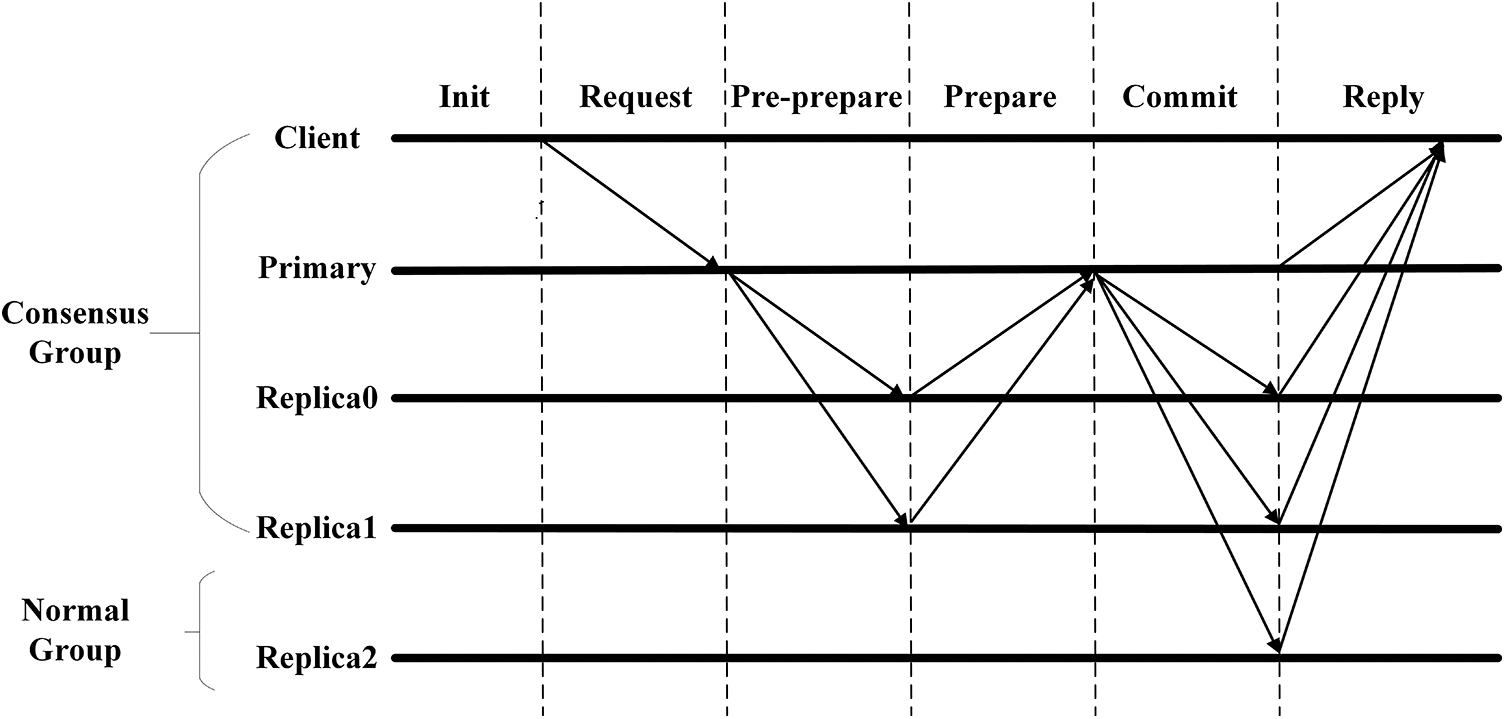
Figure 5: Execution process of the consistency protocol in XG-PBFT algorithm

In the above figure, Client represents the client, Primary represents the master node, Replica0 and Replica1 represent the nodes in the consensus group, Replica2 in PBFT represents the nodes that are down or evil and Replica2 in XG-PBFT represents the nodes in the normal group. The following is a detailed explanation of the optimization of each stage in the protocol:

A new initialization phase is added to XG-PBFT called Init, when XG-PBFT detects a node joining or dropping out, and when the master node is down the system will re-initialize and execute the XGBoost grouping model to group the nodes. To further verify the accuracy of the message, CREDIT of the reputation value information of the participating nodes evaluation and its hash computed value OUTCOME are added to the message in the pre-preparation phase with the preparation phase and OUTCOME is passed in the acknowledgment phase to validate the message accuracy further, if the message has tampered then OUTCOME will surely be changed. The preparation phase after optimization can also be called as feedback phase, when the master node receives the feedback from all the consensus group nodes then it enters into the confirmation phase. In the confirmation phase, the master node will receive feedback from all consensus nodes for judgment, in the case of the same confirmation message, it will be broadcast to all nodes in the network, and the message is increased to indicate whether the master node confirms the addition of the judgment information CONFIRM, all nodes receive the confirmation message to add the transaction information to the local memory. Eventually, each node replies to the consensus result to the client, and the whole network updates the ledger and counts the consensus performance of each node.

3.5 Algorithm Flow

The XG-PBFT algorithm execution flow is shown in Fig. 6. The client sends a request to the consensus group, and the system detects whether any node joins or quits. If a new node joins the system, the nodes will be grouped according to the XGBoost grouping model, after grouping, the view switching protocol is executed, if no node joins the system, the view switching is performed directly to elect the master node in the consensus group. The master node broadcasts a request to all the nodes in the consensus group to execute the consensus protocol, if the master node receives feedback from all the nodes, it means that consensus is reached, broadcasts the message to all the nodes, and generates the block. If it does not receive feedback from all the messages, it means that the master node is faulty, the master node will be downgraded to the normal group node and performs grouping again in order to get a new master node.

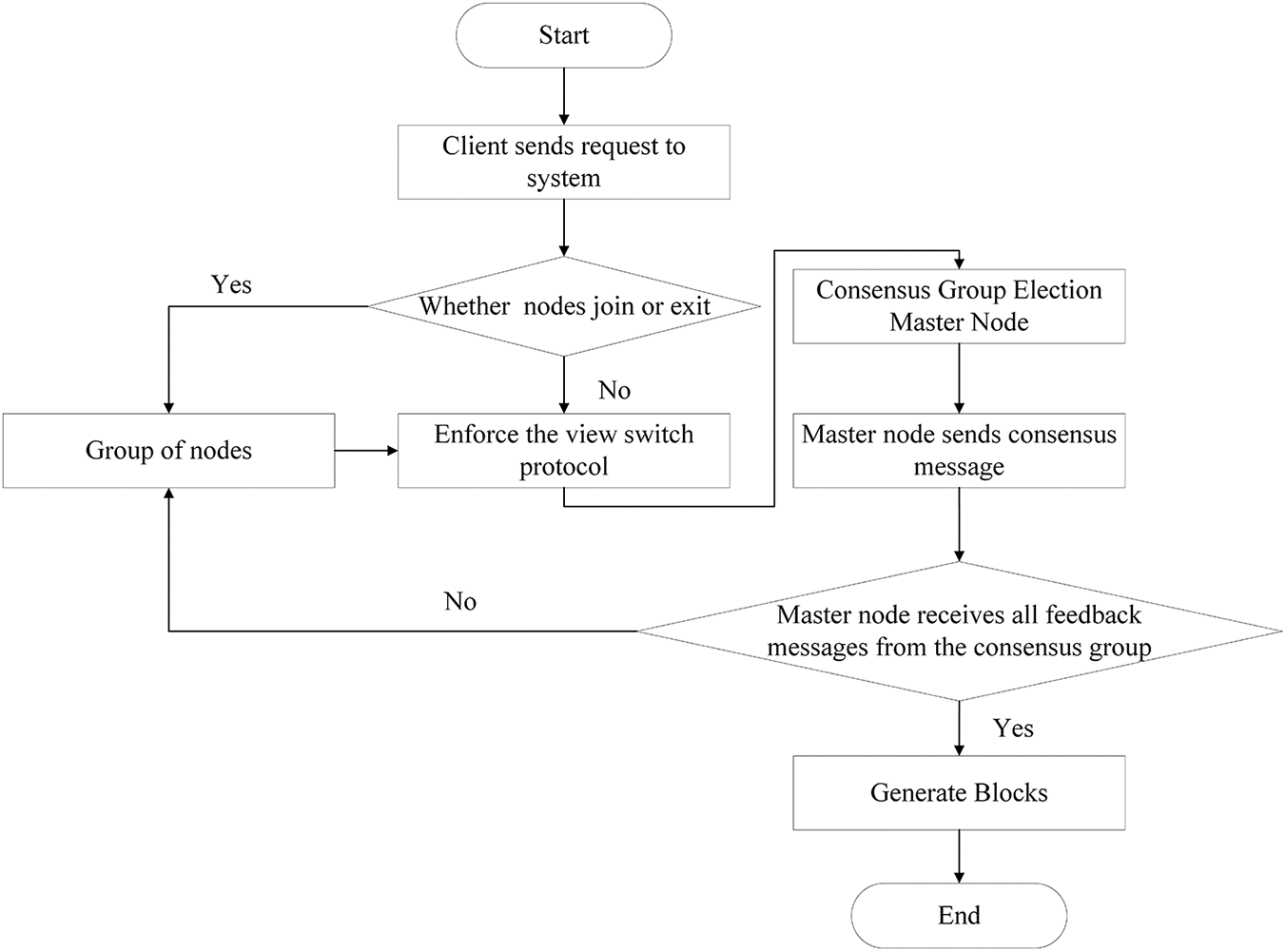
Figure 6: Algorithm execution flow

4  Experimental Results and Analysis

4.1 Experimental Setup

In this paper, we designed a blockchain transaction system based on Java, deployed the algorithm into the consortium chain according to Hyperledger Fabric’s feature of pluggable consensus algorithms, and used the Caliper test tool to experimentally verify the original PBFT algorithm, the DTBFT algorithm based on the improvement of the decision tree in the literature [23], the GPBFT algorithm based on the grouping of feature trusts in the literature [19], and the improved XG-PBFT algorithm in this paper.

The performance of the algorithms is compared and analyzed with respect to system security, transaction delay, throughput, and communication overhead. To reduce the error due to experimental chance, 20 experimental tests are conducted for each node and the average of the results is taken. The configuration of this experimental environment is shown in Table 2.

4.2 Classification Accuracy

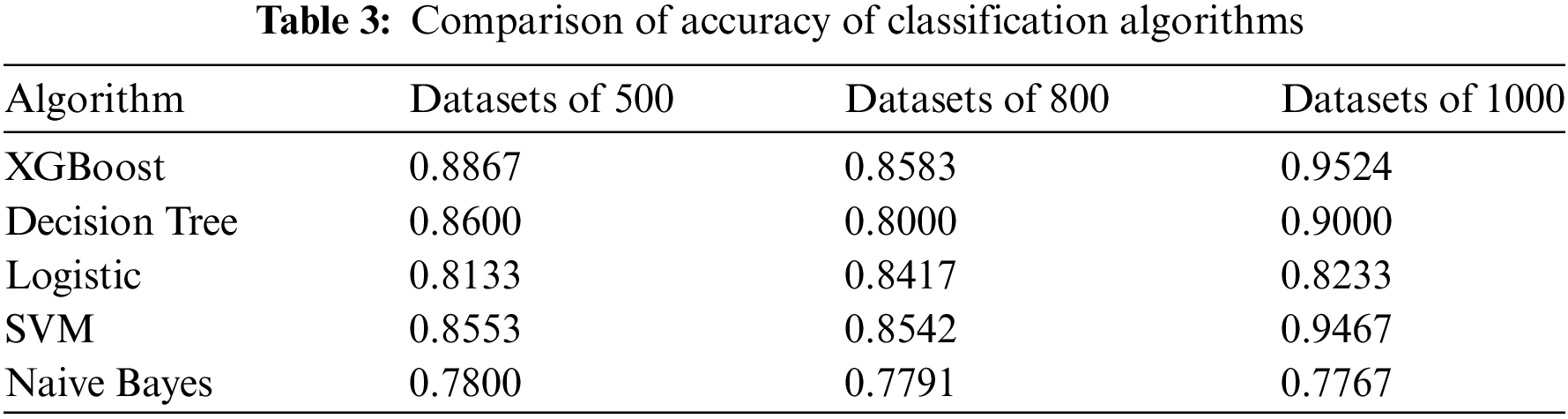
In this paper, we construct a grouping model based on XGBoost to classify nodes according to the characteristics of high classification accuracy of the XGBoost algorithm, which can effectively reduce the probability of malicious nodes becoming master nodes. The classification accuracy of commonly used classification algorithms such as XGBoost, Naive Bayes, Logistic, Decision Tree, and SVM are compared and analyzed using the consensus dataset obtained from the experiments, and the comparison results are shown in Table 3. We test for sample datasets of 500, 800 and 1000. The results show that the classification accuracy of XGBoost is greater than other classification algorithms, which can effectively improve the accuracy of classification, thereby improving algorithmic security.

4.3 Transaction Delay

Transaction delay is the time interval required for the consensus algorithm to reach agreement, specifically the duration between the client sending a request to the master node and the client confirming the completion of the consensus.

Fig. 7 is a comparison of the transaction latency of the four algorithms. As can be seen from the figure, when the number of nodes is less than 30, the transaction delay of each algorithm shows a slow growth trend, and the advantage of XG-PBFT is not obvious. When the number of nodes is greater than 30, the transaction delay of PBFT and DTBFT starts to show substantial growth, and at this time, the transaction delay of XG-PBFT and GPBFT still grows slowly. This is a result of the strict requirements on the reputation value of the nodes in the consensus group in XG-PBFT, i.e., the nodes in the consensus group in XG-PBFT perform well in the long run and the transactions are completed faster. As the number of nodes increases, the advantage of XGPBFT becomes more and more obvious.

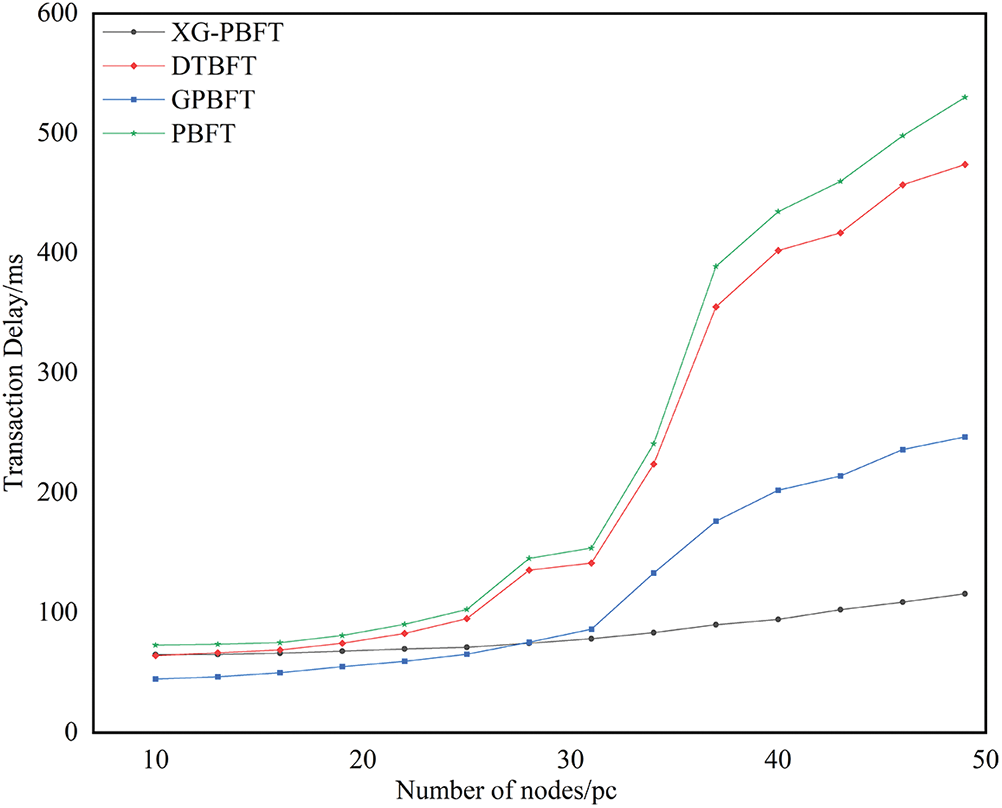
Figure 7: Comparison chart of transaction latency

4.4 Throughput

Throughput in a blockchain system refers to the number of transactions completed in a unit of time, commonly expressed as transactions per second (TPS). The steps for calculating throughput are shown in Eq. (5). Where the total number of successful transactions is the time consumed to complete the transaction.

TPS=NumtransactionΔt(5)

The throughput comparison graph of XG-PBFT with DTBFT, GPBFT, and PBFT algorithms is shown in Fig. 8, which shows that the throughput of the XG-PBFT algorithm is the same compared to other algorithms when the number of nodes is less than 30. When the number of nodes is greater than 20, the advantage of XG-PBFT is gradually obvious, with the increase of the number of nodes, the throughput of other algorithms decreases faster, but XG-PBFT can still maintain good performance.

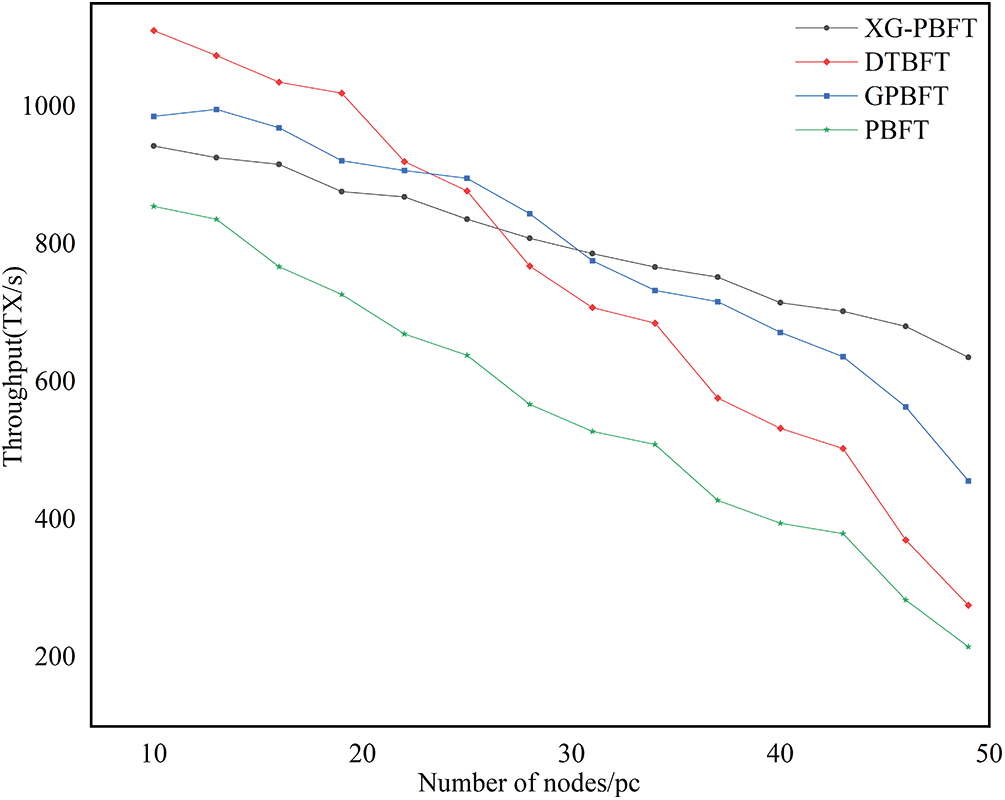
Figure 8: Comparison of TPS

4.5 Security Analysis

Security is a crucial attribute of blockchain systems. The XG-PBFT algorithm proposed in this paper introduces a grouping model, which, by considering the historical performance of multiple parameters, selects nodes with good long-term performance to enter the consensus group to select the master node, and at the same time prevents poorly performing nodes from participating in the consensus, which greatly improves the reliability of the master node and the security of the system. We demonstrate the security advantages of the proposed algorithm in this paper by simulating the change in reputation value.

As shown in Fig. 9, 20 rounds of reputation value changes of 5 nodes are simulated. The reputation value is initially set to 0.5 and the other parameters of the nodes are consistent. Among them, Node 1 is a consistently evil node, Node 5 is a consistently well-performing node, and the rest of the nodes show evil behavior in the middle. It can be seen that the reputation value of Node 1, which is consistently evil, falls below 0.5 after about five rounds of consensus and loses the possibility of participating in the consensus, and the rest of the nodes, once they show evil behaviors, will lose the possibility of participating in the consensus after a few rounds of the formula as well, whereas Node 5, which has been behaving well, will continue to remain in the consensus group. Since the reputation value of a node provides a comprehensive assessment of its behavior and historical performance in the consensus, the elected master node is more reliable than in the original PBFT algorithm, which relies on a single reputation value. This approach significantly reduces the likelihood of a malicious node becoming the master node, thereby greatly enhancing the system’s security.

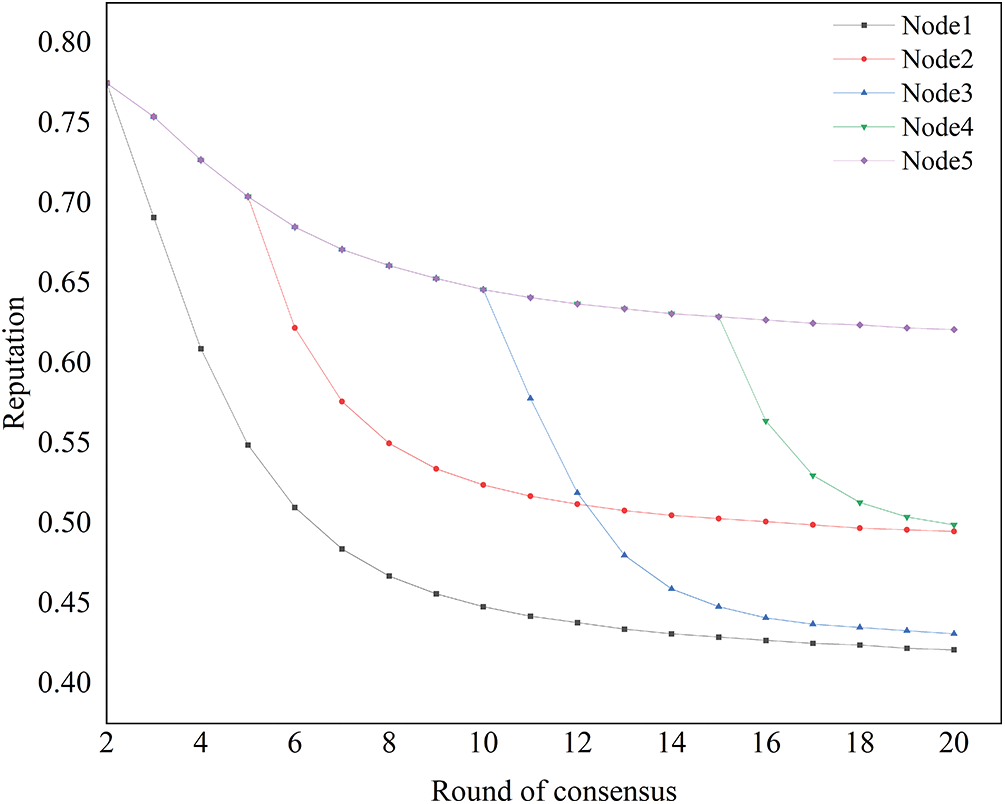
Figure 9: Change in reputation value

4.6 Communication Complexity

Algorithm communication complexity refers to the total volume of communication generated by all nodes in the network during the consensus process. XG-PBFT is optimized for the problem of high communication complexity and high communication overhead of PBFT. Table 4 shows the comparison of communication complexity between PBFT and XG-PBFT in each phase.

The communication complexity of the PBFT algorithm consists of the number of broadcast requests from the nodes in the prep phase n, the broadcast communications from the replica nodes in the prep phase n2, the number of communications required for the nodes in the acknowledgement phase to broadcast a message to each other n2, and the number of communications in the reply phase n. Hence, the total number of PBFT algorithm communications is 2n(n−1). In the case of ignoring the complexity of the grouping model, XG-PBFT only has a consensus group participating in the consensus, and the range of the number of nodes allowed in the consensus group is set to be between [4, n/2], which is calculated according to the maximum possible value of the nodes in the consensus group, and the communication complexity of the algorithm includes the master node broadcasting message n in the pre-preparation phase, the replica node feedback message n/2 in the preparation phase, the replica’s broadcasting message n/2 in the submission phase, and the number of nodes in the reply phase n, thus obtaining a communication complexity of 3n for XG-PBFT.

A comparison of the communication complexity of the four algorithms XG-PBFT, DTBFT, GPBFT, and PBFT is shown in Fig. 10. The communication complexity of all four algorithms increases with the increase in the number of nodes. Among them, the communication consumption of PBFT shows a steep increase, while the other three algorithms show a stable linear increase, and the communication complexity is reduced from O(n2) to O(n) for all PBFT algorithms, which greatly reduces the system resource consumption. Since XG-PBFT, DTBFT, and GPBFT algorithms all introduce other grouping mechanisms, the XG-PBFT proposed in this paper has a slight advantage over the other two without taking into account the impact of grouping mechanisms on communication complexity.

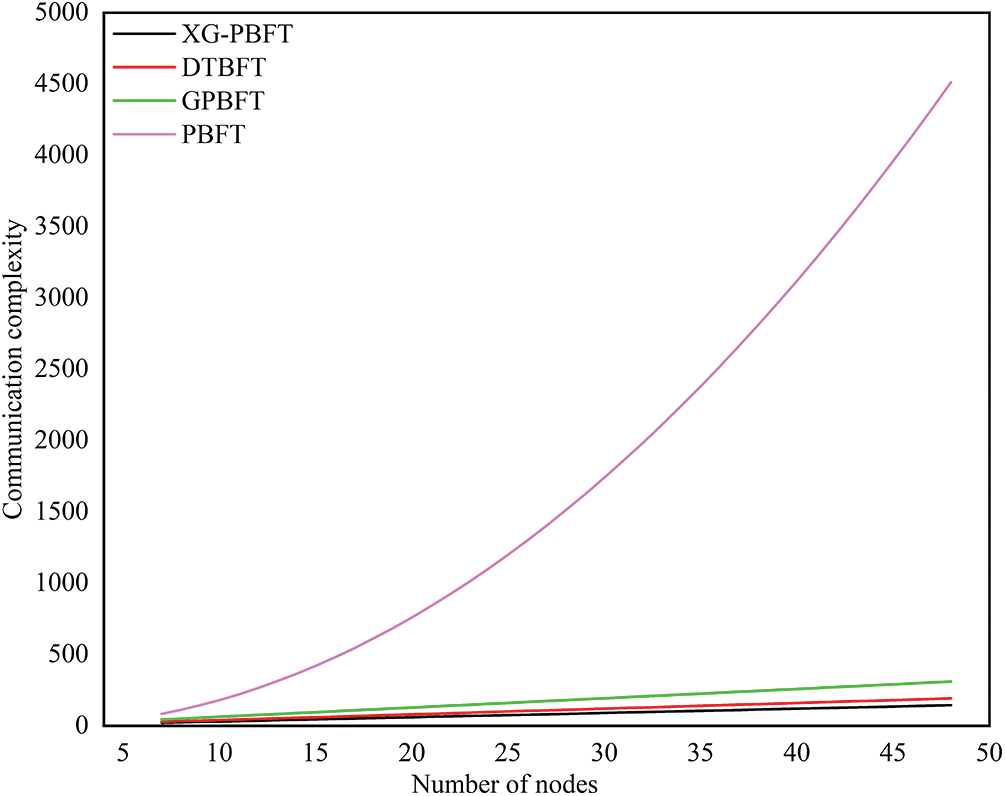
Figure 10: Comparison of communication complexity

5  Conclusion

This paper proposes the XG-PBFT algorithm, which is based on XGBoost grouping, to tackle issues related to unreliable master node election, low consensus efficiency, and the limited scalability of the PBFT algorithm. Several experiments are conducted to compare and validate the performance of XG-PBFT.

The experimental results demonstrate that the XG-PBFT algorithm proposed in this paper significantly enhances the reliability and security of master node election, thanks to the classification accuracy of XGBoost. By improving the consensus protocol, the communication complexity of the algorithm is reduced from a quadratic level to a linear level, which effectively reduces the communication overhead and resource waste of the system. Under the experimental conditions set in this paper, the XG-PBFT algorithm’s average consensus latency, throughput, security, and other performances have been greatly improved; in the case of a large number of nodes, the throughput and consensus delay of the XG-PBFT algorithm shows a greater advantage than that of DTBFT and GPBFT algorithm, which greatly improves the consensus efficiency of the system. Therefore, the XG-PBFT algorithm proposed in this paper is better suited for multi-node or large-scale consortium chain applications compared to other algorithms.

Although the XG-PBFT algorithm proposed in this paper is somewhat improved in terms of security, throughput, transaction latency, and communication complexity, it still has some shortcomings. The dataset in the SHAP-optimized XGBoost feature selection scheme proposed in this paper is not complete, and the complete dataset needs to be further collected due to the fact that some of the features are more difficult to deal with, so in the next phase of this research, we aim to fully validate the model with a comprehensive dataset.

Acknowledgement: We express our gratitude to the participants who generously dedicated their time and effort to contribute to our study. We would like to acknowledge the editor and the anonymous reviewers whose insightful comments and suggestions significantly enhanced the quality of this manuscript.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Xiaowei Wang; data collection: Jiasheng Zhang, Yingkai Ge; analysis and interpretation of results: Xiaowei Wang; draft manuscript preparation: Xiaowei Wang, Haiyang Zhang; revision of manuscripts: Lihua Wang, Kexin Cui, Zifu Peng, Zhengyi Li. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Partial data will be available upon request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Y. Liu, Z. Zhou, Y. Yang, and Y. Ma, “Verifying the smart contracts of the port supply chain system based on probabilistic model checking,” Systems, vol. 10, no. 1, Feb. 2022, Art. no. 19. doi: 10.3390/systems10010019. [Google Scholar] [CrossRef]

2. L. Cui, Z. Xiao, F. Chen, H. Dai, and J. Li, “Protecting vaccine safety: An improved, blockchain-based, storage-efficient scheme,” IEEE Trans. Cybern., vol. 53, no. 6, pp. 3588–3598, Jun. 2023. doi: 10.1109/TCYB.2022.3163743. [Google Scholar] [PubMed] [CrossRef]

3. C. Xu, Y. Qu, Y. Xiang, T. H. Luan, and L. Gao, “An optimized privacy-protected blockchain system for supply chain on internet of things,” IEEE Internet Things J., vol. 11, no. 5, pp. 9019–9030, Mar. 01, 2024. doi: 10.1109/JIOT.2023.3321889. [Google Scholar] [CrossRef]

4. L. Liu, Y. Li, and T. Jiang, “Optimal strategies for financing a three-level supply chain through blockchain platform finance,” Int. J. Prod. Res., vol. 61, no. 11, pp. 3564–3581, Jun. 03, 2023. doi: 10.1080/00207543.2021.2001601. [Google Scholar] [CrossRef]

5. J. Ye, H. Hu, J. Liang, L. Yin, and J. Kang, “Lightweight adaptive Byzantine fault tolerant consensus algorithm for distributed energy trading,” Comput. Netw., vol. 251, no. 4, 2024, Art. no. 110635. doi: 10.1016/j.comnet.2024.110635. [Google Scholar] [CrossRef]

6. S. Nakamoto, “Bitcoin: A peer-to-peer electronic cash system,” 2008. [Online]. Available: https://bitcoin.org/bitcoin.pdf [Google Scholar]

7. P. Gazi, A. Kiayias, D. Zindros, and Ieee, “Proof-of-stake sidechains,” in IEEE Symp. Secur. Priv., San Francisco, CA, USA, 2019, pp. 139–156. doi: 10.1109/SP.2019.00040. [Google Scholar] [CrossRef]

8. M. Castro and B. Liskov, “Practical Byzantine fault tolerance,” Jan. 01, 2000. Accessed: Aug. 10, 2024. [Online]. Available: http://mpaxos.com/teaching/ds/20fa/readings/pbft.pdf [Google Scholar]

9. D. Ongaro and J. Ousterhout, “In search of an understandable consensus algorithm,” in Proc. 2014 USENIX Conf. USENIX Annual Tech. Conf., Philadelphia, PA, USA, 2014, pp. 305–320. [Google Scholar]

10. M. Marco and M. Leonardo, “Analytical model for performability evaluation of Practical Byzantine Fault-Tolerant systems,” Expert. Syst. Appl., vol. 238, 2024, Art. no. 121838. [Google Scholar]

11. R. Hao, C. Yi, W. Dai, and Z. Zhang, “SimpleFT: A simple Byzantine Fault Tolerant consensus,” in Cryptology ePrint Archive, 2024. doi: 10.1109/TSUSC.2023.3341440. [Google Scholar] [CrossRef]

12. D. S. Antunes, A. N. Oliveira, A. Breda, M. G. Franco, H. Moniz and R. Rodrigues, “{Alea-BFT}: Practical asynchronous Byzantine Fault Tolerance,” in 21st USENIX Symp. Netw. Syst. Design and Implement. (NSDI 24), 2024, pp. 313–328. [Google Scholar]

13. Y. Wang, Z. Song, and T. Cheng, “Improvement research of PBFT consensus algorithm based on credit,” in Block. Trust. Syst.: First Int. Conf., BlockSys 2019, Guangzhou, China, Springer, 2020, pp. 47–59. [Google Scholar]

14. H. Wang and K. Guo, “Byzantine fault tolerant algorithm based on vote,” in 2019 Int. Conf. Cyber-Enabled Distrib. Comput. Know. Disc. (CyberC), IEEE, 2019, pp. 190–196. [Google Scholar]

15. Y. Zhang, Y. Gan, C. Li, C. P. Deng, and Y. Luo, “Primary node selection based on node reputation evaluation for PBFT in UAV-assisted MEC environment,” Wirel. Netw., vol. 29, no. 8, pp. 3515–3539, 2023. doi: 10.1007/s11276-023-03407-4. [Google Scholar] [CrossRef]

16. S. N. Liu, R. H. Zhang, C. Z. Liu, and D. Shi, “P-PBFT: An improved blockchain algorithm to support large-scale pharmaceutical traceability,” Comput. Biol. Med., vol. 154, no. 3, 2023, Art. no. 106590. doi: 10.1016/j.compbiomed.2023.106590. [Google Scholar] [PubMed] [CrossRef]

17. J. J. Xu, Y. L. Zhao, H. Y. Chen, and W. Deng, “ABC-GSPBFT: PBFT with grouping score mechanism and optimized consensus process for flight operation data-sharing,” Inf. Sci., vol. 624, no. 2, pp. 110–127, 2023. doi: 10.1016/j.ins.2022.12.068. [Google Scholar] [CrossRef]

18. H. Qin, Y. Cheng, X. Ma, F. Li, and J. Abawajy, “Weighted Byzantine Fault Tolerance consensus algorithm for enhancing consortium blockchain efficiency and security,” J. King Saud Univ.-Comput. Inf. Sci., vol. 34, no. 10, pp. 8370–8379, Nov. 2022. doi: 10.1016/j.jksuci.2022.08.017. [Google Scholar] [CrossRef]

19. Y. Wang, M. Zhong, and T. Cheng, “Research on PBFT consensus algorithm for grouping based on feature trust,” Sci. Rep., vol. 12, no. 1, Jul. 22, 2022, Art. no. 12515. doi: 10.1038/s41598-022-15282-8. [Google Scholar] [PubMed] [CrossRef]

20. J. Zhang, Y. Yang, D. Zhao, and Y. Wang, “A node selection algorithm with a genetic method based on PBFT in consortium blockchains,” Complex Intell. Syst., vol. 9, no. 3, pp. 3085–3105, Jun. 2023. doi: 10.1007/s40747-022-00907-2. [Google Scholar] [CrossRef]

21. J. Liu, W. Feng, Y. Zhang, and F. He, “Improvement of PBFT algorithm based on CART,” Electronics, vol. 12, no. 6, Mar. 2023, Art. no. 1460. doi: 10.3390/electronics12061460. [Google Scholar] [CrossRef]

22. X. Zheng, W. Feng, M. Huang, S. Feng, and F. Siling, “Optimization of PBFT algorithm based on improved C4.5,” Math. Prob. Eng., vol. 2021, no. 1, 2021, Art. no. 5542078. [Google Scholar]

23. W. Wang, Y. Bi, X. Chen, and C. Li, “A PBFT consensus algorithm for consortium chain optimization,” (In ChinaJ. Appl. Sci., vol. 41, no. 4, pp. 577–589, 2023. [Google Scholar]

24. T. Chen and C. Guestrin, “XGBoost: A scalable tree boosting system,” in Proc. 22nd ACM Sigkdd Int. Conf. Know. Disc. Data Min., 2016, pp. 785–794. [Google Scholar]