Collaborative Trajectory Planning for Stereoscopic Agricultural Multi-UAVs Driven by the Aquila Optimizer

1  Introduction

Agriculture is of critical importance to the development of human society. Currently, the quality of land in many areas is gradually degrading due to soil erosion, reduction of inorganic quality and pollution. Moreover, with the continuous development of urbanization, a lot of arable land has been used for the construction of infrastructure such as houses and highways, resulting in the continuous reduction of arable land area. Thus, to meet the challenges facing global agriculture in terms of land cultivation, it is necessary to actively adopt various means to improve the productivity and sustainability of agricultural cultivation and contribute to global food security and sustainable development [1].

Stereoscopic agriculture is a modern pattern of agriculture that utilizes stereoscopic space for agricultural production, which is a modern, efficient and sustainable model of agriculture compared to traditional horizontal farming, helping to meet the demands of agricultural development in the context of population growth and urbanization, as well as meeting the challenges posed by the environment and resources. Stereoscopic agriculture can maximize the use of limited land resources through the use of vertical space [2] and cultivation in multi-level agricultural systems at different altitudes. However, the operating area of stereoscopic agriculture is usually characterized by small cultivated areas and uneven terrain, which makes it difficult to adapt traditional agricultural techniques and mechanical equipment to the operating area of stereoscopic agriculture. On the contrary, unmanned aerial vehicles (UAVs) [3], as a new type of small machinery and equipment, can play a role in stereoscopic agriculture in a variety of aspects such as monitoring and investigation, fertilizer application and spraying, plant protection and disease monitoring, intelligent irrigation and water resource management, as well as automated and intelligent agricultural operations. Their ability to provide high-precision data and intelligent solutions can help the development of stereoscopic agriculture and improve the efficiency and sustainability of agricultural production.

Regarding the current challenges of UAV trajectory planning, decision makers find that there are usually many complex constraints, such as the flight speed, altitude, and flight radius of the UAV, as well as the need to avoid collisions with obstacles such as base stations and buildings. The combination of these factors makes it difficult for traditional optimization algorithms to deal with them comprehensively and effectively, thus making them prone to errors or impossible to apply. Application of metaheuristic algorithms has been introduced to provide a new solution to this challenge. And the main motivation for using meta-heuristic algorithms to solve the UAV trajectory planning problem lies in their excellent multiple constraints processing capability and global optimization ability, which can quickly adapt to changes in complex and dynamic agricultural environments and provide efficient, reliable and flexible path planning schemes, which in turn support the intelligent and refined management of agriculture.

Meta-heuristic algorithms [4] are a class of computational methods based on adaptive, iterative optimization to find near-optimal solutions to complex problems by simulating processes such as evolution and group intelligence in nature. Compared with traditional algorithms, metaheuristic algorithms have the advantages of high adaptability, low requirements on problem constraints, and high parallelism. Such algorithm types include, but are not limited to, Genetic Algorithm (GA) [5], Ant Colony Optimization Algorithm (ACO) [6], Particle Swarm Optimization (PSO) [7], Difference Algorithm (DE) [8], and so on. Meanwhile, metaheuristic algorithms currently show extraordinary potential in many problem domains. For example, in combinatorial optimization [9], traveler’s problem [10], path planning [11], and resource allocation [12], meta-heuristic algorithms are able to find near-optimal solutions efficiently. In addition, metaheuristic algorithms are widely used in many fields such as engineering optimization [13], image processing [14], data mining [15] and machine learning [16].

The Aquila Optimizer (AO) [17] is a new swarm intelligence-based optimization algorithm proposed by Abualigah et al. in 2021, which is inspired by the behavior of Aquila in nature during prey capture, and has a powerful global exploration capability, high search efficiency, and fast convergence speed. At present, due to the outstanding optimization ability of the AO algorithm has been widely applied in parameter optimization [18], scheduling optimization [19], system control [20], gene selection [21], and other related fields. In the face of the UAV trajectory path planning problem, the AO has a powerful global search capability, multi-objective optimization capability, constraint processing capability, adaptability and flexibility, and scalability, which makes it an effective algorithm to solve the UAV trajectory path planning problem, and it can help the UAV to find the optimal path to satisfy different objectives and constraints.

Nevertheless, the operational characteristics of stereoscopic agriculture will lead to the existence of different levels of operational objects and operational endpoints at different altitudes in the operational scheduling area. Then, UAVs performing multi-task trajectory planning operations in the background of stereoscopic agriculture will increase the complexity of the search space due to the increase in spatial dimensions, large coverage, multi-objective optimization, and dynamic environmental constraints, and it is difficult to some extent to generate a trajectory planning scheme with lower flight costs, higher stability, and higher safety. For this reason, to enhance the ability of UAVs to perform multi-task trajectory planning in the background of stereoscopic agriculture, and to enrich the current state of research in the field of UAVs performing multi-objective multi-task trajectory planning, this paper proposes an interferometric image enhancement model-based, adaptive weight factor-driven by Aquila optimizer (IEP-AO) for solving the problem of multi-task UAV trajectory planning in a stereoscopic agricultural environment. Among them, the main contributions of this paper are as follows:

• A multi-task trajectory planning model and algorithm (IEP-AO) that synthesizes flight safety and flight efficiency is proposed to address the need for UAVs to perform multi-task trajectory planning in stereoscopic agriculture.

• Proposed Aquila Optimizer (IEP-AO) driven by a combination of interferometric image enhancement model, adaptive weighting factors and Bernoulli mapping.

• Constructed a realistic three-dimensional stereoscopic agricultural trajectory planning scenario with a variety of constraints and obstacle models.

• Experimental results show that IEP-AO has stable and significant optimization and planning capabilities in four simulated trajectory planning tasks with different challenges.

2  Related Works

2.1 Literature Review

In recent years, with the rapid development of UAV technology, UAV trajectory planning has attracted extensive attention and research. This chapter will review the relevant literature on UAV trajectory planning and summarize the research directions and methods therein.

One common approach in the study of UAV trajectory planning is the optimization method based on heuristic algorithms. Among them, Zhang et al. [22] proposed a multi-objective evolutionary algorithm with a two-fold constraint-handling mechanism for multiple UAV path planning. Zhang et al. [23] proposed a beetle swarm optimization (BSO), which was used to generate a UAV path that minimizes the ground risk and flight cost. Chen et al. [24] proposed a UAV path planning method based on the opposition-based learning artificial bee colony (OABC) algorithm to obtain more building surface information with fewer images. Wang et al. [25] proposed an improved algorithm (GSPSODE) applied to UAV inspection path planning for urban corridors by introducing a collaborative game between Spherical Vector Particle Swarm Algorithm (SPSO) and Differential Evolution (DE) algorithm. Liu et al. [26] proposed a grey wolf optimization algorithm (NAS-GWO) incorporating multi-strategy improvement for the agricultural UAV trajectory planning problem. Phung et al. [27], for dealing with the UAV path planning problem in complex environments subject to multiple threats, transformed the path planning into an optimization problem containing requirements and constraints on the feasible and safe operation of UAVs and based on this proposed a spherical vector-based particle swarm optimization algorithm (SPSO).

Another common research method is UAV trajectory planning based on artificial intelligence technology. Technologies such as deep learning and reinforcement learning are introduced in order to achieve autonomous decision-making and route planning for complex environments. These techniques can learn and optimize the UAV’s trajectory planning process through a large amount of training data and intelligent algorithms so that it can adapt to different tasks and environments. Among them, Li et al. [28] proposed a UAV coverage path planning algorithm based on double-deep Q-network based on deep reinforcement learning theory and the characteristics of coverage path planning. Barnawi et al. [29] extracted the desired area through a deep learning based segmentation method, thus proposing an autonomous UAV-based mine detection framework to determine the coverage routes for scanning the target area. From the perspective of optimization efficiency, Pan et al. [30] found that deep learning (DL) has a high solution speed once it is trained with enough datasets, and thus proposed a deep learning algorithm called genetic algorithm trained (DL-GA) that combines the advantages of DL and genetic algorithm for improving the efficiency of multi-UAV data collection path planning. Not only that, Yang et al. [31] proposed a reinforcement learning algorithm based on intrinsic rewards and used it for the path planning problem of UAV base stations, which helped to provide stable communication for multiple mobile users.

In conclusion, UAV trajectory planning is a complex and challenging problem involving multiple aspects such as path search, constraint handling, and multi-objective optimization. In the above literature review, methods based on heuristic algorithms, artificial intelligence techniques, and multi-objective optimization are widely used in the field of UAV trajectory planning. Although the heuristic algorithms and artificial intelligence techniques mentioned above in the literature each have their own advantages in UAV trajectory planning, they are deficient in dealing with multi-tasking requirements in a stereoscopic agricultural environment. These algorithms usually have limited adaptability to complex terrains, poor multi-task coordination and real-time processing, and insufficient integrated processing capabilities when facing multiple constraints. Therefore, it is necessary to propose a new meta-heuristic algorithm and trajectory planning model, which can better adapt to the dynamics and complexity of stereoscopic agriculture, improve the coordination and execution efficiency of multi-tasking, as well as carry out effective path optimization under various constraints, so as to satisfy the needs of practical agricultural applications, and can provide strong theoretical support and solution for the research of trajectory planning in stereoscopic agriculture context.

2.2 Aquila Optimizer

The Aquila Optimizer is modeled by simulating four flight predation behaviors of Aquila, which can flexibly change the hunting strategy according to different prey, and each stage is described as follows:

A. Extended Exploration (X1)

In Expanded Exploration, the Aquila identifies prey areas and selects the best hunting area by soaring high in a vertical stoop. Here, the Aquila soars from a high altitude to identify the area of the search space, which represents the specific location of the prey to be searched. Eq. (1) below is the mathematical model of the extended exploration behavior.

X1(t+1)=Xbest(t)×(1−t/Maxiter)+rand•(Xmean(t)−Xbest(t))(1)

Xmean(t)=1N∑i−1NXi(t) ∀j=1,2,3,⋯,D(2)

where X1(t+1) is the solution obtained under the current t iterations generated based on the extended exploration behavior, Xbest(t) refers to the optimal solution generated during the iteration process and reflects the approximate location of the prey, and Xmean(t) denotes the average value of the current solution under the current t iterations. rand refers to a random number in the range of [0,1], t denotes the current number of iterations, Maxiter denotes the maximum number of iterations, D denotes the dimensional size of the problem, and N denotes the number of candidate solutions.

B. Narrowing of exploration (X2)

In the second method (X2), when the Aquila finds the prey area from high altitude, it hovers above the target prey and prepares to launch the attack, which is called isometric flight for short glide attack. At this time, the Aquila optimizer narrowly explores the selected area of the target prey in preparation for the attack, the mathematical model of this behavior can be expressed by the following Eq. (3):

X2(t+1)=Xbest•Levy(D)+Xr(t)+(y−x)•rand(3)

Levy(D)=s×u•σ|v|1β(4)

σ=(Γ(1+β)×sin⁡(πβ2)Γ(1+β2)×β×2β−12)(5)

y=r×cos⁡(θ),x=r×sin⁡(θ)(6)

r=r1+U×D1,θ=−ω×D1+3π2(7)

X2(t+1) represents the solution scheme generated in X2 mode, Levy(D) represents the number of Lévy flight distributions, Xr(t) represents the random solution within the population at the t-th iteration, and x,y are the behavioral expression models used to represent the spiral search pattern. Meanwhile, r1 is the number of fixed search cycles, r1⊂[1,20], D1 is an integer in the range [1,D1], and s,w,U all represent constants with values of 1.5, 0.005, and 0.00565, respectively.

C. Expanded development (X3)

During the third method (X3), when the Aquila locks on to the prey area, the Aquila prepares for landing and attacking, and then descends vertically and performs a preliminary attack to test the prey’s response, a behavior known as a low-flying and slow descending attack. The mathematical model of the Aquila performing the low-flying and slow descending attack behavior is shown in Eq. (8) below:

X3(t+1)=α⋅((Xbest(t)−Xmean(t))−rand+δ⋅((UB−LB)×rand+LB)(8)

There, X3(t+1) is the solution scheme generated iteratively by the search method, α and δ denote the mining tuning parameters in the range [0,1], and LB, UB represent the lower and upper boundaries of the search space.

D. Reduction in scope of development (X4)

In the fourth method (X4), the process of walking and catching the prey by the Aquila is mainly simulated, when the Aquila gradually approaches the prey and launches the attack according to the random movement of the prey, which is mathematically modeled as shown in Eq. (9).

X4(t+1)=Q•Xbest(t)−(G1•Xi(t)×rand)−G2•Levy(D)(9)

Q=2∗rand−1t(1−Maxiter)2(10)

G2=2∗(1−t/Maxiter)(11)

Among them, X4(t+1) is the solution scheme generated in the search method X4, Q is the quality function used to balance the search strategy, G1 denotes the various motions used to track the prey during the search for the prey, and G2 denotes the flight rate of the Aquila population, which decreases in value from 2 to 0.

3  Multi-Task UAV Trajectory Planning Model Construction in a Stereoscopic Agricultural Environment

3.1 Minimal Trajectory Path Constraints

The essence of the multi-task UAV trajectory planning problem is to find the shortest trajectory path by traversing the iterative search between the mission start point and multiple mission end points. Usually, assuming that the UAV’s trajectory path point in three-dimensional space is Rij=(xij,yij,zij), this path node can indicate that the UAV’s position at this time is located at the j-th node of the i-th path. Meanwhile, if the distance between two path points is to be obtained, then the distance between two path points can be denoted as ‖RijRi,j+1‖ by introducing the Euclidean distance calculation method. To this end, if Mi is denoted as a 3D array containing n path nodes, the cost function Function1 associated with the shortest trajectory path constraint can be constructed denoted as:

Function1(Mi)=∑j=1n−1‖RijRi,j+1‖(12)

3.2 Security Trajectory Altitude Constraints

Safety trajectory altitude is an important safety guarantee to safeguard UAVs during dispatching operations. In real flight rules, the navigational altitude of a UAV is usually influenced by both the maximum altitude hmax and the base altitude hmin. In the operation flight, suppose the height difference of UAV at Rij compared to the horizontal ground is Hij. When the sailing altitude of UAV exceeds the safe altitude constraint, the sailing altitude cost function Vij can be obtained based on the altitude penalty coefficient ϕ at a certain moment of time under the path point. In summary, the cost function Function2 related to the safe UAV trajectory altitude constraint can be expressed as:

Vij={ϕ⋅(Hij−hmax)Hij>hmax0ϕ⋅(hmin−Hij)∞hmin<Hij<hmax0<Hij<hminhmin<0(13)

Function2(Mi)=∑j=1nVij(14)

3.3 Safety Slope Constraints

Constructing slope constraint limitations is very important when multi-task UAV trajectory planning in stereoscopic agricultural environments. Slope variations are very large in stereoscopic agricultural environments, especially in multi-level greenhouses and crop stands. If the UAV trajectory planning does not consider the slope constraint limitations, it may lead to instability and insecurity throughout the flight, and may even lead to crashes and accidents. Assuming that the magnitude of the slope between two flight path nodes Rij and Ri,j+1 is Slij, and the maximum slope constraint in a stereoscopic agricultural environment is Slmax, then based on the slope penalty coefficient ε we can get the cost function of the flight slope under the path point at a certain moment Function3.

Slopec={ε⋅(Slij−Slmax)Slij>Slmax0Slij≤Slmax(15)

Function3=∑j=1nSlopecij(16)

3.4 Safety Corner Constraints

Multi-task trajectory planning tasks in stereoscopic agriculture usually require steering flights at critical positions because of the different target positions of the operational objects and the different operational areas, while the steering of UAVs usually includes horizontal and vertical steering. As shown in Fig. 1 below, the principle that the Euclidean distance between two consecutive path points can represent a flight path, assuming that ‖RijRi,j+1→‖ and ‖Ri,j+1Ri,j+2→‖ represent a complete flight path, the projection of the path segment in the two-dimensional plane can be denoted as Rij′Ri,j+1′, Ri,j+1′Ri,j+2′. For this purpose, the horizontal angle βij and vertical angle δij based on the projection plane can be obtained based on the forward unit vector a→ of the coordinate axis as:

|Rij′Ri,j+1′→|=a→×(Rij′Ri,j+1′→×a→)(17)

βij=arctan⁡(|Rij′Ri,j+1′→|×|Ri,j+1′Ri,j+2′→|Rij′Ri,j+1′×Ri,j+1′Ri,j+2′)(18)

δij=arctan⁡(Zi,j+1−Zi,jRij′Ri,j+1′)(19)

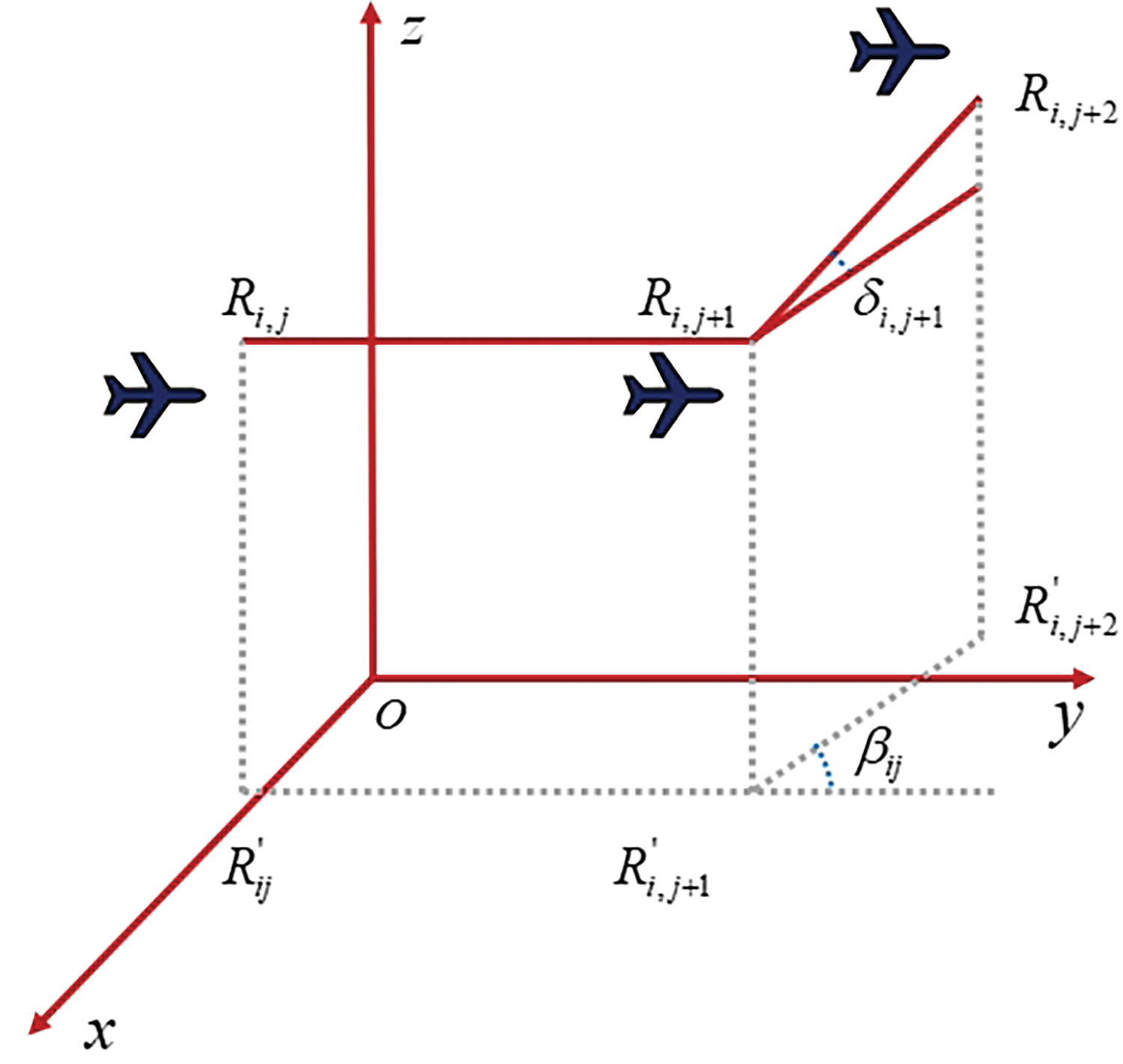
Figure 1: Schematic of UAV cornering model

Based on the above model, at this point, according to the horizontal cornering penalty coefficient ϑ and vertical cornering penalty coefficient ρ can be obtained the cost function Function4 related to the UAV navigation cornering constraint can be expressed as:

Function4(Mi)=ϑ⋅∑j=1n−2βij+ρ⋅∑j=1n−1(δij−δi,j−1)(20)

3.5 Obstacle Threat Constraints

Constructing obstacle minimum threat constraints is considered important when performing UAV trajectory planning in stereoscopic agriculture. This is because there are various obstacles in the stereoscopic agriculture environment, such as fixed structures, plants, and base stations, which may pose a threat to the safety and flight path of the UAV. By considering the location and threat level of the obstacles, the safe flight of the UAV can be ensured and the damage to plants, facilities, etc., can be minimized. To this end, as shown in the example in Fig. 2 below, it is assumed that the center coordinate of the threatening obstacle is χ, and the threatening radius of the obstacle is RT. From this, it can be obtained that the threatening area of the obstacle to which it belongs is AreaR. As can be seen from the illustration in Fig. 2, D represents the distance between a section of track ‖RijRi,j+1→‖ and the center of the obstacle. If the set consisting of obstacle threat zones is denoted as ν, and the obstacle threat penalty factor is denoted as η, the relevant cost function Function5 associated with the navigational obstacle threat constraint can thus be obtained as:

U(RijRi,j+1)={η⋅((AreaR+RT)−D)RT<D<AreaR+RT0AreaR+RT<D∞D<RT(21)

Function5(Mi)=∑i=1i−1∑j=1νU(RijRi,j+1)(22)

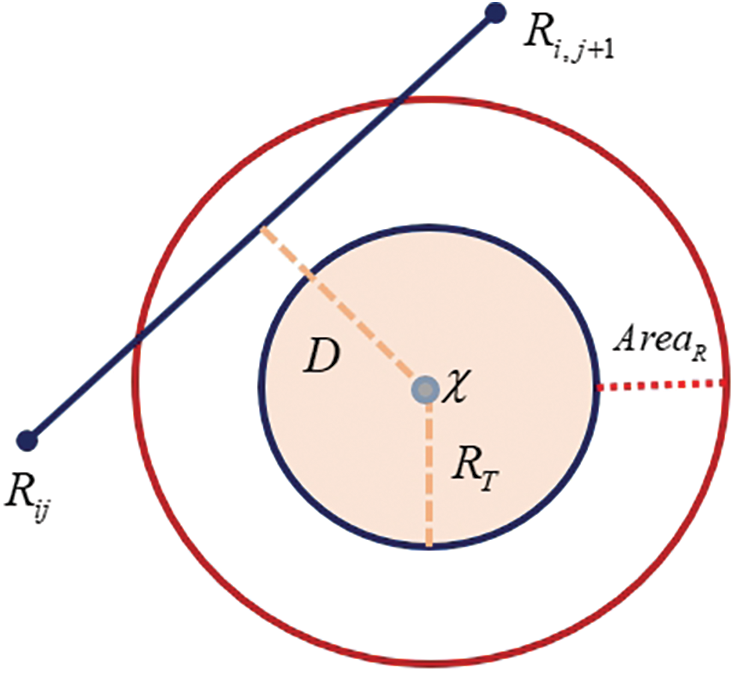
Figure 2: Schematic of the UAV obstacle threat model

3.6 Safety Energy Constraints

Energy consumption constraints are crucial to ensure the efficiency and safety of a mission. This research defines the energy consumption constraint as the maximum flight time constraint, then because the flight time is a direct indicator of energy consumption, which simplifies the complex energy consumption calculation, and ensures that the UAV can successfully complete the mission before running out of power by setting the maximum flight time. Assuming that the flight time at the path point Rij is Eij, if the maximum energy flight time that the UAV can reserve is MEmax, and the penalty factor for exceeding the maximum flight time is ψ, the cost function with the flight energy constraint can be shown by the definition of Function6.

Energij={ψ×(Eij−MEmax)Eij>MEmax0Eij≤MEmax(23)

Function6(Mi)=∑j=1nEnergij(24)

3.7 Multiple Factor Constraint-Based Cost Function

To uniformly portray the flight cost of UAVs in performing multi-task trajectory planning, this paper starts from the effectiveness of the model, and hereby constructs a flight cost function Fmuti−factors based on the weight ratio υ multi-factor constraints, as follows, which is the mathematical model of the function:

Fmuti−factors(Mi)=∑n=16υ⋅Functionn(Mi)(25)

4  Design of a Multi-Task UAV Trajectory Planning Algorithm in a Stereoscopic Agricultural Environment

4.1 Diversity Enhancement Mechanism Based on Bernoulli Mapping

Under the real operating scenarios of stereoscopic agriculture, due to the existence of different levels of operating objects and different altitudes of operating areas, these challenges will force the meta-heuristic algorithms to suffer from local adaptation degradation, weakening of path selection ability, and easy to fall into the local optimum at the early stage of the search in the process of performing multi-task trajectory planning for UAVs. As a result, to improve the local adaptability and the diversity of the trajectory search capability of UAVs executing the multi-task trajectory planning problem in stereoscopic agricultural environments, this paper will help the meta-heuristic algorithms to generate more reasonable path selections and overcome the path bottlenecks and other related problems in executing the UAV trajectory planning through the introduction of Bernoulli mappings.

Bernoulli mapping is a randomization technique that produces sequences that are random in nature and uniformly distributed. This allows the initial population information generated to have a high degree of diversity, which in turn allows for a better coverage of the search space and enables the algorithm to explore in multiple directions. When facing the path selection problem of UAV trajectory planning, Bernoulli mapping can enhance the diversity of the population through the stochastic character it possesses, thus improving the local adaptability of the algorithm and finding a better trajectory planning solution to a greater extent. The following is the mathematical model of Bernoulli mapping.

Bernoullik+1={Bernik/(1−λ),Bernik∈(0,1−λ](Bernk−1+λ)/λ,Bernik∈(1−λ,1)(26)

Here, Bernoullik+1 is the current value of the generated k-th generation chaotic sequence, and λ is the control parameter, which is tested in this paper and found to have strong traversal and better trajectory search effect when λ takes the value of 0.6.

4.2 Nonlinear Parameter Update Mechanism Based on Cosine Function

The terrain of the operating environment belonging to stereoscopic agriculture is complex and varied, this makes the search space for the multi-task UAV trajectory planning problem very large and complex. Meanwhile, the variation of operational targets and the diversity of features may lead to different trajectory planning schemes that may be adapted to different features and requirements. Therefore, in this paper, to balance and enhance the exploration and exploitation ability of the AO algorithm in performing the multi-mission UAV trajectory planning problem, a nonlinear parameter updating mechanism based on the cosine function is introduced as a way to improve the solution efficiency and better adapt to different task requirements.

The solution model of the AO algorithm, G2 is a control parameter that decreases linearly from a fixed value of 2 to 0, which represents the flight slope from the first to the last position when the Aquila is tracking the prey. Based on the above analysis, this paper proposes a nonlinear parameter decreasing model combined with the cosine function, the following Eq. (27) is the mathematical model of this optimization mechanism, and the following Fig. 3 shows the iteration curves before and after the model optimization schematically.

G2=2∗cos⁡((π•t)/2∗Maxiter)(27)

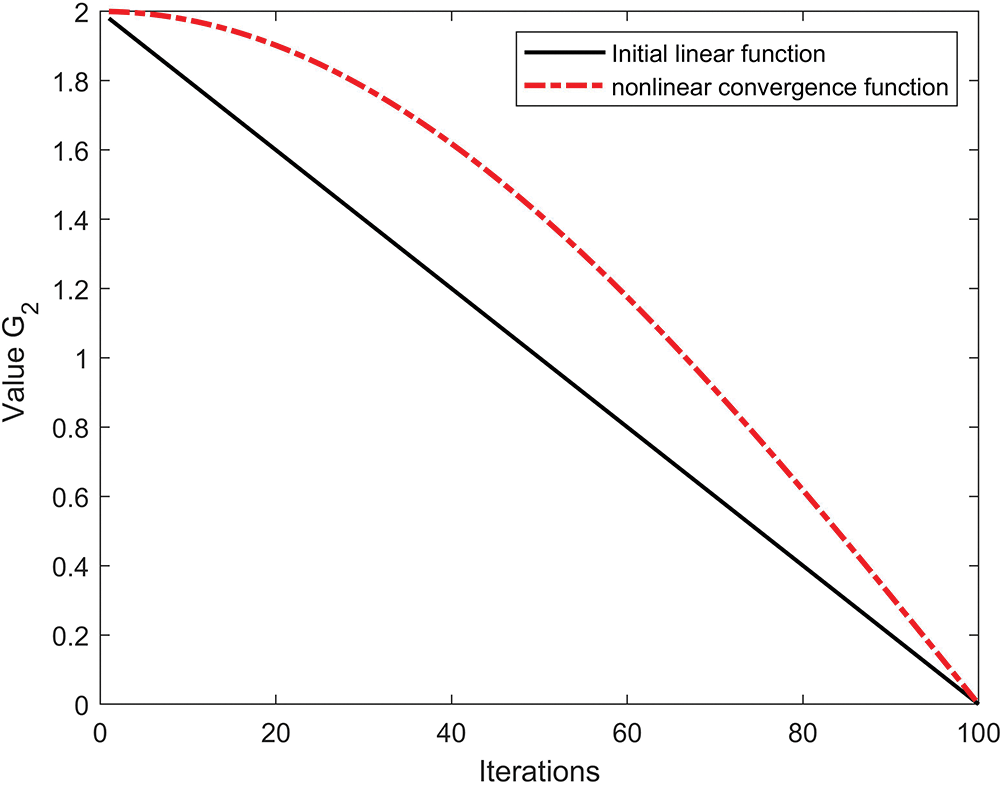
Figure 3: Schematic of parametric nonlinear convergence

Based on the new balance in the above equation, the algorithm retains larger parameter values in the early stage of iteration, which enables the algorithm to make full use of the optimization idea of Lévy flight in the original search model and maintains a larger search step size, which provides a better exploration capability and maximizes the trajectory search in the solution space. On the contrary, the parameter values of the algorithm decrease rapidly in the late iteration process, when the algorithm is less affected by the large step size search, which prompts the AO algorithm to strengthen the local search ability under the influence of the optimal solution and the historical optimal solution, thus improving the development ability of the algorithm in the late iteration.

4.3 Variational Perturbation Mechanisms Based on Interference Enhancement Modeling

Stereoscopic agricultural environments usually include vertically cascading crop cultivation systems, and thus UAVs need to fly and navigate between different heights and levels. At the same time, since UAVs need to perform multi-task trajectory planning in operational areas at different altitudes and levels, this will lead to meta-heuristic algorithms that are prone to fall into local optimality under the mutual interference and conflict of different constraints and are unable to jump out of the fixed trajectory track, thus making it difficult to find the optimal trajectory path scheme between different operational areas.

In this regard, from the actual difficulties faced in the stereoscopic agricultural environment, the optimal individual information generated by the initial search of the algorithm should be retained and used as the effective information for the algorithm to perform update iterations and jump out of the local optimum, due to the small influence of obstacle constraints, height constraints and slope constraints encountered by the UAV during the departure phase and initial search phase of the pre-setup trajectory search period. For this reason, in this paper, to improve the ability of UAVs to perform complex trajectory planning in stereoscopic agriculture, and also to effectively solve the challenges faced by UAVs in performing multi-task trajectory planning, a variational perturbation mechanism based on interference augmentation modeling is proposed.

Interference enhancement model is a kind of variational perturbation model inspired by the interference phenomenon independently proposed in this paper. The main idea of this model is to construct a perturbation model of the algorithm for the trajectory planning of stereoscopic agricultural multitasking UAVs by using the bright interference stripes produced by the interference of two beams as the optimal individual information retained by the algorithm in the pre-trajectory search period, and by using the difference in optical range between different beams as the basis for assigning weight values to individuals of different populations. The definition and construction process of the model is shown below:

Definition 1: From the physical properties of the interfering bright stripes, the n interfering enhancement points are defined as Pi, where Pi={P1,P2,…,Pn}, and Pi denotes the solution vector holding a higher fitness value in the iterative update of the algorithm.

Definition 2: Define the relative distance between the n interference enhancement points as Ji, where Ji={J1,J2,…,Jn}. In the algorithmic model, assume that Xi is the current individual position within the population, and Xbest is the best population individual abstracted from the interference enhancement points Pi, from which we can obtain the mathematical model of Ji as:

Ji=∑i=1n‖Xi−Xbest‖(28)

Definition 3: Define the weight of influence between n interfering enhancement points as Wi, where Wi={W1,W2,…,Wn}. In the algorithmic model, Wi denotes the weights of the currently stated population individuals affected by the optimal individual based on the relative distance Ji, from which the mathematical model of Wi can be obtained as:

Wi=1(1+Ji)⋅∑i=1nWi(29)

Definition 4: Define the interference enhancement perturbation model as Xi(t+1). In the algorithmic model, by combining the influence weights Wi and the individual position information Xi(t), while introducing the modulation parameters φ, γ and the random vector υ can be obtained as the mathematical computation model of Xi(t+1):

Xi(t+1)=φ⋅(Pi−Xi)−γ⋅(Wi⋅υ−Xi)(30)

4.4 Pseudo-Code for the IEP-AO Algorithm

The pseudo code of the algorithm generated by the proposed algorithm IEP-AO under combinatorial optimization is shown below. Besides, IEP-AO still simulates the foraging behavior of hawks in its algorithmic idea, and through extensive exploration and precise exploitation among the individuals representing the possible flight paths of UAVs in the initial population, it repeatedly evaluates and updates the adaptability of each path, especially focusing on the optimization of the path length, energy consumption, obstacle avoidance and other factors, so as to gradually converge to the optimal or nearly optimal flight trajectory that can meet the requirements of the complex dynamic environment, thus ensuring the realization of efficient, safe and economical trajectory planning schemes in the following trajectory planning:

5  Simulation Experiment and Result Analysis

5.1 Selection of Field Flight Scenarios for UAV Trajectory Planning

Scenario simulation in real terrain can help assess the adaptability of UAVs in different terrain conditions. This is critical for performing agricultural operations in different environments, as changes in the terrain may have an impact on the flight performance and stability of the UAV. Secondly, by using real terrain simulations, a comprehensive safety assessment of the flight path can be performed. This includes avoiding obstacles, identifying safe landing sites, and circumventing terrain features to ensure the safety of the UAV during agricultural operations.

In this regard, this paper decides to select Jiaoqiao Town, Nanchang City, Jiangxi Province, People’s Republic of China, as the main simulated flight scenario for the UAV to perform multi-task trajectory planning in this paper based on the geographic environment characteristics of stereoscopic agriculture. Jiaoqiao Town is located in Xinjian District, Nanchang City, Jiangxi Province, between latitude 28°41′53′′ N and 28°49′20′′ N and longitude 115°44′57′′ E and 115°51′45′′ E. The area of the town is 84.44 km2, and the slope range is 0–43.03°. The following map shows the topographic elevation of Jiaoqiao Township in Fig. 4.

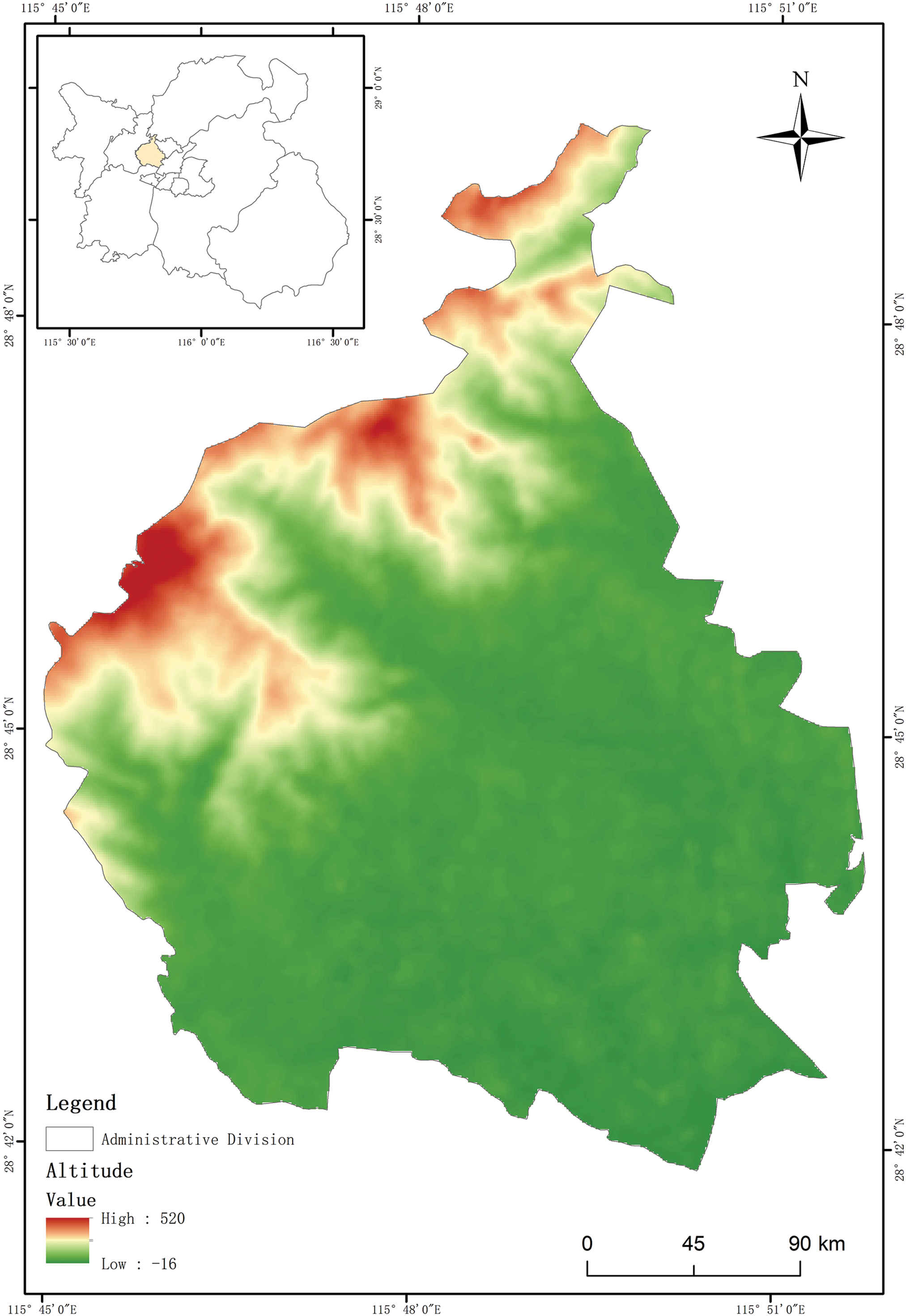
Figure 4: Elevation topographic map of Jiaoqiao Town

5.2 Three-Dimensional Model Construction of Flight Scene Based on the Real Elevation Map

The acquisition of elevation maps enables the transformation of elevation changes and terrain indication characteristics of the selected area through digital height values, which can be used as an important data source for UAV trajectory planning. This paper adopts the composite function of the following Eq. (31) and carries out simulation experiments of different scales and types in MATLAB simulation software. The following Eq. (31) is the composite function model for generating 3D digital elevation terrain:

M(a,b)=∑i=1nHiexp⁡[−(a−aias)2−(b−bibs)2](31)

In Eq. (31), M(a,b) represents the height value of the actual geographic coordinates, (ai,bi) represents the center value of the i-th mountain coordinate, Hi is the regulating parameter mainly used to control the height difference of the terrain. n represents the number of hills, and as,bs are used to constrain the inclination of the slope.

5.3 Simulation Experiments and Result Analysis of Trajectory Planning

Simulation experiments through real flight scenarios are an important way to test the effectiveness of these algorithms for multitasking trajectory planning and trajectory path searches performed by UAVs. In this paper, to confirm the theoretical validity of the proposed model and algorithms and their efficiency in the real scenario operation, five significant meta-heuristic algorithms PSO, SCA [32], WOA [33], AO, and IEP-AO are selected. Among them, PSO for stereoscopic agriculture in 3D terrain features can explore and utilize the space through the global search capability of particle swarm, and quickly adapt to the operational needs of different altitude layers. WOA due to its special encirclement and spiral ascent strategy, so that the other can provide effective encirclement and approximation strategy in the complex stereoscopic agricultural environment to help the UAV find the optimal path. While SCA can simulate sine and cosine functions to adjust the position, enabling the UAV to move accurately under subtle environmental changes. This is especially important in stereoscopic agriculture which requires precision operations.

Meanwhile, to guarantee the fairness of the simulated flight principle and to improve the adaptability of the simulated flight and the real flight, this paper, according to the terrain characteristics of the flight environment in Jiaoqiao Town, hereby sets the minimum flight altitude of 3 m, the maximum flight altitude of 520 m, and the maximum steering slope of 15°, Maximum one-way flight time is 45 s. Moreover, the maximum number of iterations of each trajectory optimization algorithm is 500, and each trajectory searching process is executed independently for 10 times.

Aiming to enhance the reducibility and realism of the simulation experiments in this work, the following Table 1 shows the component parts and parameter information of each trajectory task.

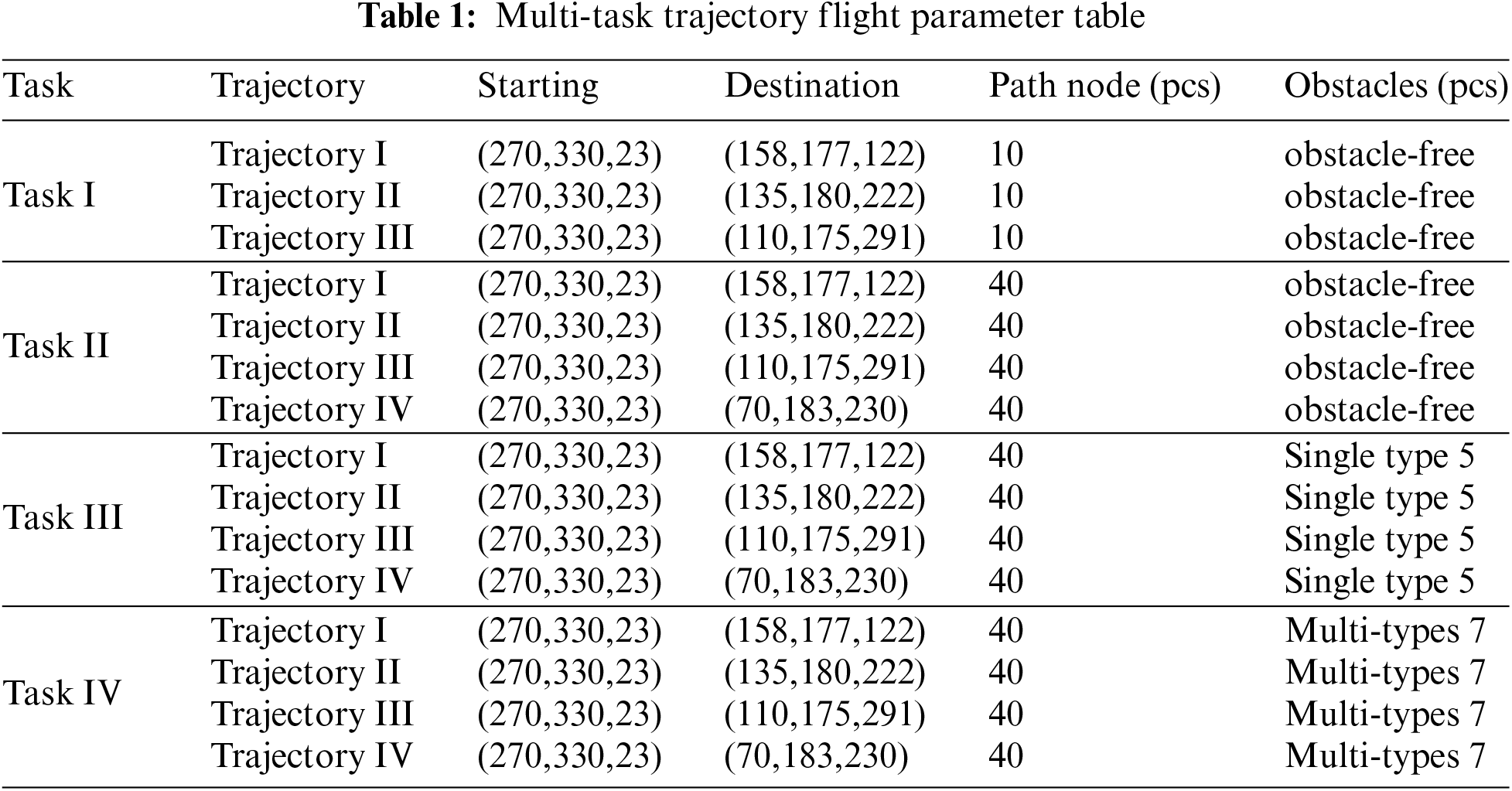
5.3.1 Multi-Task Trajectory Planning Based on Simple Trajectory Tasks and Base Scenarios

In Task Ⅰ, this paper presents the flight cost functions solved by each trajectory search algorithm at the start and end positions of each operational object as shown in Table 2 below, and summarizes the schematic diagrams of the multi-task trajectory path schemes solved by each algorithm as shown in Fig. 5 below. Because the operation scale and difficulty simulated by Task Ⅰ is small, it makes the various algorithms can find more similar solutions in the optimization process, thus leading to a small gap between the fitness value and the performance result. Among them, the maximum mean value of these algorithms to solve the sum of multi-task trajectory flight costs is WOA, the optimal one is IEP-AO, and the one with the strongest stability is SCA. It can be seen that, in the simulated flight of Task Ⅰ, not only does the effectiveness of these algorithms to perform multi-task trajectory planning in simple Stereoscopic agricultural environments is verified in terms of the solution of the multifactorial cost function, but also the effectiveness of IEP-AO algorithms to perform multi-task trajectory planning in the real stereoscopic agricultural operations when executing multi-task trajectory planning with a small degree of significance.

Figure 5: Path scheme for the flight path of Task I

Besides, another important consideration of the trajectory planning problem is the effectiveness of the resulting trajectory path scheme. The multi-task UAV trajectory planning problem, compared with the single-task, has different endpoints, which causes the algorithm to fail to jump out of the original search trajectory under the corresponding path nodes in the first and middle phases of the path search due to the similarity of the constraints, and it is difficult to traverse all the feasible path points. For this reason, there will be a large number of similar solutions in the planned trajectory scheme, reducing the effectiveness of real-time trajectory planning and the feasibility of executing operation scheduling.

In the trajectory path diagram of Task Ⅰ, it can be noticed that the WOA and SCA algorithms have a high degree of trajectory similarity and the problem of incomplete traversal search, which leads to the resulting trajectory path scheme is not sufficiently adapted to the actual operational requirements, and the feasibility is low. Secondly, for PSO and AO algorithms, although the feasible paths are obtained under the requirements of different operational altitudes and operational objects, the trajectory paths planned by them are less smooth due to the large changes in the search space at the later stage of the search, which greatly reduces the safety of the UAV’s trajectory flight. Conversely, the IEP-AO algorithm, due to its uniform and rich candidate populations under the optimization of chaotic mapping, can help to obtain more effective and feasible trajectory paths under the same path nodes with better smoothing and a more complete traversal search process.

5.3.2 Multi-Task Trajectory Planning Based on Complicated Trajectory Tasks and Base Scenarios

In Task II, this paper proposes to increase the scale of the trajectory path nodes and add the corresponding operational tasks to test the ability of UAVs to perform complex trajectory planning tasks in a stereoscopic agricultural environment.

As above, Table 3 below shows the cost function fitness values of each meta-heuristic algorithm in solving each mission in Task II. From the statistical data in the Table 3, it can be realized that, compared with Task Ⅰ, due to the increase of path nodes and task size, the size of the search space for the algorithm will be increased accordingly, which further leads to the algorithm needing to carry out stronger exploitation and exploration, and requiring it to find better quality solutions in a more complex search space. Meanwhile, the IEP-AO algorithm is still able to obtain large cost benefits in the comparison algorithms and test tasks in terms of the average cost fitness value and standard deviation of each task, but the standard deviation of the algorithm in Trajectory III is large, which affects the stability of the algorithm in the process of solving the total cost of the trajectory.

In addition, when the number of path nodes increases, the complexity and difficulty of the algorithm in traversing all the path nodes will increase. At this time, the ability to obtain effective and reasonable trajectory paths under multi-task and multi-constraint situations is also an important evaluation criterion for testing the model and search algorithm proposed in this paper.

As the following trajectory planning path diagram in Fig. 6 shows, when the operation scale is increased, the trajectory paths planned by different meta-heuristic algorithms at this time will have certain differences. Among them, except for the WOA algorithm whose trajectory plan reflects a weak effectiveness, the other four algorithms are able to find the optimal trajectory path according to their own model characteristics. For the SCA, PSO and AO algorithms, the smoothness of the SCA algorithm’s trajectory scheme in the late search of Trajectory I and Trajectory III is insufficient, which will increase the corresponding flight cost value. For the PSO algorithm, although the smoothness of the path curves obtained by the algorithm for each trajectory task is good, the differences of the path schemes in the pre-search stage are strong, which will lead to the lack of robustness of UAV trajectory planning, while the AO algorithm can be clearly found through the trajectory schematic diagrams, which shows that the effectiveness of the trajectory planning scheme presented by this algorithm is insufficient in the middle and late stages of the path search and fails to meet the requirements of path planning for the complex trajectory tasks. The IEP-AO algorithm maintains a stable and excellent global exploration capability in the adaptive updating of the nonlinear convergence factor. After ensuring sufficient population diversity and excellent exploration capability, the IEP-AO is able to fit the terrain characteristics of different operational levels and objects to obtain the most effective, least costly and most stable trajectory solution.

Figure 6: Path scheme for the flight path of Task Ⅱ

5.3.3 Multi-Task Trajectory Planning Based on Complicated Trajectory Tasks and Base Constraint Scenarios

Since UAVs fly through non-operational areas in different environments as they travel from their starting position to the operational area, which is mostly residential or flat farming areas, there are a variable number and type of obstacles to UAV flights. Therefore, to further test the ability of the UAV trajectory planning model and path search algorithm proposed in this paper to perform complex trajectory planning tasks under basic constraint environments, we propose to construct basic obstacles with different threat ranges in Task III, so as to test the ability of the IEP-AO algorithm to perform multi-task trajectory planning in the target operational area.

It is observed that the total trajectory costs of the WOA and PSO algorithms are slightly decreasing compared to those of Task II in Table 4, unlike the SCA, AO, and IEP-AO algorithms, but the standard deviation of WOA, which has a more pronounced fluctuation in the decrease, has increased by a factor of three, which indicates that the stability of some algorithms is greatly weakened under the influence of the obstacle threat. Nevertheless, the IEP-AO algorithm still maintains the optimal mean value of the total trajectory cost for the solved flight cost, which demonstrates the high performance and low cost of the algorithm in performing trajectory planning in complex scenarios.

Moreover, when obstacles threaten the trajectory, it is the most intuitive way to analyze the trajectory scheme obtained by each algorithm by observing and comparing them. By observing the trajectory paths in the following Fig. 7, it can be found that when the UAV encounters obstacle threats, in order to satisfy different constraints and limitations and ensure a safe and effective trajectory path, the algorithms will produce large differences in solving the trajectory paths for different tasks. Among them, for WOA and PSO algorithms, to avoid collision with obstacles and ensure effective trajectory path generation in their trajectory selection, both of them raise the flight altitude and carry out the phenomenon of leapfrogging flight, which is uncertain and dangerous in the real situation. As for the SCA and AO algorithms, the SCA algorithm has a higher degree of path overlap in the early stage, and shows a weaker strain and adaptability, while the AO algorithm carries out a larger degree of equal-area circling in order to ensure the effectiveness of the trajectory, leading to an increase in the cost of the flight, and it is difficult to satisfy the needs of the actual operation. In contrast, the IEP-AO algorithm can help the algorithm to have a certain diversity under the obstacle constraint limitations in the basic obstacle constraint task by perturbing the interference model with timely mutation perturbation, so as to obtain a safe, stable, and effective trajectory path scheme.

Figure 7: Path scheme for the flight path of Task Ⅲ

5.3.4 Multi-Task Trajectory Planning Based on Complicated Trajectory Tasks and Complicated Constraint Scenarios

To ensure the safety and adaptability of UAVs performing multi-task trajectory planning in the background of stereoscopic agriculture, this paper examines the trajectory planning capability of UAVs in complex trajectory tasks and complex constraint scenarios by adding the number and type of obstacle threats in Task IV.

As shown by the cost adaptation value statistics in Table 5 below, the vast majority of these algorithms produce varying increases in the statistical values of each of their cost evaluation metrics when confronted with multiple types and sizes of obstacle threat constraints. In particular, the WOA and SCA algorithms face complex threat constraints, at which point the robustness of solving the flight constraint cost function decreases substantially. However, unlike the PSO, AO and, IEP-AO algorithms, they are able to have stronger search capability and optimization stability in some cases when facing large-scale and high-complexity problems, which also proves the effectiveness of the classical PSO algorithm in solving real-time problems, and moreover verifies the potential of the AO algorithm in solving the multi-task UAV trajectory planning and the remarkable capability of the IEP-AO algorithm. The potential of the AO algorithm in solving multi-task UAV trajectory planning and the remarkable ability of the IEP-AO algorithm is also verified.

Similar to the above experimental analysis, Fig. 8 below shows the trajectory planning scheme of each algorithm obtained in Task IV. For the WOA algorithm, to ensure the effectiveness of the multi-task trajectory path, the WOA algorithm carries out the flight strategy around the obstacle within the reliable radius of the obstacle threat. Although the trajectory path generated in this mode has a certain degree of effectiveness, it is hard to meet the operational requirements in stereoscopic agricultural tasks due to the longer time and energy consumption costs. For the SCA, PSO and, AO algorithms, similarly, under the influence of multi-threat constraints, in order to ensure the smooth generation of trajectories, they choose to raise the flight altitude outside the radius of the obstacle threat to carry out leapfrog flight. Although the leapfrog flight around the obstacle can get the trajectory planning scheme smoothly, there is uncertainty and danger in the real situation. On the contrary, the IEP-AO algorithm is able to perform boundary flights within a reasonable threat radius under the limitations of complex constraints and perform effective avoidance flights under the influence of multi-obstacle constraints, obtaining the trajectory planning scheme with strong diversity, high adaptability, and excellent stability.

Figure 8: Path scheme for the flight path of Task Ⅳ

6  Discussion

This paper focuses on issues related to the execution of multi-task trajectory planning by UAVs in stereoscopic agricultural environments. To explore more thoroughly the contributions made and results obtained in this work, this section will discuss and analyze the relevant experimental results and experimental phenomena in a targeted manner based on the experimental results obtained from the simulation experiments of UAVs in 3D scenarios at different levels and at different operational altitudes.

The biggest difficulty of UAV trajectory planning in stereoscopic agricultural environments is the height variation and irregular vegetation shape. Compared with traditional 3D trajectory planning, the height and shape changes of vegetation in stereoscopic agricultural environments are more complex, and UAVs need to avoid obstacles through precise height control and more complex obstacle avoidance algorithms. Thus, this paper proposes an Aquila optimizer based on Interference Perturbation Model (IEP-AO) in order to address the ability of UAVs to perform multi-task trajectory planning in stereoscopic agricultural environments. The reason why the IEP-AO algorithm can help UAVs achieve significant trajectory planning effects in stereoscopic agricultural environments is mainly due to the following two aspects:

One, because of the existence of a large number of different levels and different altitudes in the stereoscopic agricultural environment, when the UAV performs multi-task trajectory operations, then for the meta-heuristic algorithm, the change of different operational endpoints and different operational terrains will require the algorithm to make the optimal response in a short period of time, which is characterized by a significant adaptability and rich diversity. In other words, the meta-heuristic algorithm iterates over the specified starting and ending positions to find the optimal solution, and the search space of the algorithm becomes complex and decreases when the operational altitude changes are elevated. When the information of individual populations is transmitted further, the optimal individual information will be lost due to the reduction of search space, and the optimal solution may not be found or may fall into the local optimum and fail to generate feasible paths. On the contrary, the IEP-AO algorithm greatly improves the population diversity in the pre-search stage by combining the Bernoulli mapping and the perturbation mechanism based on the interference-enhanced model, and the interference-enhanced perturbation model can carry out mutation perturbation on the basis of the optimal individuals, i.e., the individuals with the highest fitness values, to help the algorithm jump out of the local optimum in time. As a result, when the complexity of the search space increases or the effective range of the search space decreases, the IEP-AO algorithm can still traverse each candidate solution in the limited search space to find the optimal trajectory paths for different tasks.

Two, because obstacles such as different types of drainage base stations, irrigation pipes or plant stands are present in stereoscopic agricultural environments. Meta-heuristic algorithms often fail to generate effective and stable trajectory paths due to the lack of search capability when encountering obstacle threat constraints. Fortunately, the IEP-AO algorithm introduces a nonlinear parameter update mechanism based on the cosine function, which helps the algorithm not only to improve the exploration and survey capabilities, but also to balance the search weights of both exploration and survey capabilities during the trajectory search process, which prompts the UAV to obtain more comprehensive information, including various possible paths to avoid obstacles, and to be able to comprehensively consider factors such as flight distance, obstacle information, energy consumption and other factors to find the optimal trajectory planning solution.

7  Conclusion

Regarding the problems and challenges faced by UAVs in multi- task trajectory planning in the current background of stereoscopic agriculture, this paper proposes a multi-constraint integrated trajectory planning model and a trajectory planning algorithm (IEP-AO) based on the characteristics of UAV operation and algorithmic path optimization.

To verify the ability of IEP-AO algorithm to perform multi-task trajectory planning in stereoscopic agriculture. In this paper, the town of Jiaoqiao is selected as a simulation scene of 3D trajectory flight inspired by the geomorphological features of stereoscopic agriculture, and four kinds of trajectory missions with different scales, different difficulties and different test effects are arranged. The comprehensive results from the trajectory flight cost and trajectory path scheme can show that IEP-AO has significant trajectory planning capability and stable trajectory planning scheme in multi-task trajectory planning tasks.

Nevertheless, although this paper has initially conducted research on multi-task trajectory planning for UAVs in stereoscopic agricultural environments and achieved certain research results, the current research only focuses on multi-task single-trip trajectory planning. In the future research, we will further enhance the completeness and effectiveness of the study by constructing more targeted constraint models based on practical challenges, completing the study of UAV trajectory planning for multi-task and multi-travel in stereoscopic agricultural environments, and focusing on the effect of delay differences of different algorithms on UAV trajectory planning in complex environments.

Acknowledgement: We would like to express our appreciation to the participants who generously, volunteered their time and expertise for this study.

Funding Statement: This work was funded by the Jiangxi Provincial Social Science Planning Project (21GL12), Jiangxi Provincial Higher Education Humanities and Social Sciences Planning Project (GL22232), Jiangxi Province College Students’ Innovation and Entrepreneurship Training Program Project (S20241041027).

Author Contributions: Xinyu Liu: Conceptualization, Writing—original draft, Methodology; Longfei Wang: Resources, Data curation; Yuxin Ma: Investigation, Visualization; Peng Shao: Writing—review & editing, Supervision, Funding acquisition, Formal Analysis. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. M. S. Dimitrijević, “Technological progress in the function of productivity and sustainability of agriculture: The case of innovative countries and the Republic of Serbia,” J. Agric. Food Res., vol. 14, no. 2, 2023, Art. no. 100856. doi: 10.1016/j.jafr.2023.100856. [Google Scholar] [CrossRef]

2. S. Epting, “Participatory budgeting and vertical agriculture: A thought experiment in food system reform,” J. Agric. Environ. Ethics, vol. 29, no. 5, pp. 737–748, 2016. doi: 10.1007/s10806-016-9631-x. [Google Scholar] [CrossRef]

3. R. A. Pickett, J. W. Nowlin, A. A. Hashem, M. L. Reba, J. H. Massey and S. Alsbrook, “Small unmanned aircraft systems and agro-terrestrial surveys comparison for generating digital elevation surfaces for irrigation and precision grading,” Drones, vol. 7, no. 11, 2023, Art. no. 649. doi: 10.3390/drones7110649. [Google Scholar] [CrossRef]

4. O. E. Turgut, M. S. Turgut, and E. Kırtepe, “A systematic review of the emerging metaheuristic algorithms on solving complex optimization problems,” Neural Comput. Appl., vol. 35, no. 19, pp. 14275–14378, 2023. doi: 10.1007/s00521-023-08481-5. [Google Scholar] [CrossRef]

5. D. E. Golberg, “Genetic algorithms in search, optimization, and machine learning,” Addion Wesley, vol. 1989, no. 102, 1989, Art. no. 36. [Google Scholar]

6. M. Karimi, S. Kolahdouz-Rahimi, and J. Troya, “Ant-colony optimization for automating test model generation in model transformation testing,” J. Syst. Softw., vol. 208, no. 5–7, 2024, Art. no. 111882. doi: 10.1016/j.jss.2023.111882. [Google Scholar] [CrossRef]

7. J. Kennedy and R. Eberhart, “Particle swarm optimization,” Proc. ICNN’95—Int. Conf. Neural Netw., 1995, Perth, WA, Australia, vol. 4, pp. 1942–1948. doi: 10.1109/ICNN.1995.488968. [Google Scholar] [CrossRef]

8. P. Niloofar, R. Aghdam, and C. Eslahchi, “GAEM: Genetic algorithm based expectation-maximization for inferring gene regulatory networks from incomplete data,” Comput. Biol. Med., vol. 183, no. 5, 2024, Art. no. 109238. doi: 10.1016/j.compbiomed.2024.109238. [Google Scholar] [PubMed] [CrossRef]

9. M. Hemici and D. Zouache, “A multi-population evolutionary algorithm for multi-objective constrained portfolio optimization problem,” Artif. Intell. Rev., vol. 56, no. S3, pp. 3299–3340, 2023. doi: 10.1007/s10462-023-10604-2. [Google Scholar] [CrossRef]

10. S. Li, F. Wang, Q. He, and X. Wang, “Deep reinforcement learning for multi-objective combinatorial optimization: A case study on multi-objective traveling salesman problem,” Swarm Evol. Comput., vol. 83, no. 4, 2023, Art. no. 101398. doi: 10.1016/j.swevo.2023.101398. [Google Scholar] [CrossRef]

11. Y. Cui, W. Hu, and A. Rahmani, “Multi-robot path planning using learning-based artificial bee colony algorithm,” Eng. Appl. Artif. Intell., vol. 129, no. 11, 2024, Art. no. 107579. doi: 10.1016/j.engappai.2023.107579. [Google Scholar] [CrossRef]

12. Y. Han et al., “Two-stage heuristic algorithm for vehicle-drone collaborative delivery and pickup based on medical supplies resource allocation,” J. King Saud Univ.-Comput. Inf. Sci., vol. 35, no. 10, 2023, Art. no. 101811. doi: 10.1016/j.jksuci.2023.101811. [Google Scholar] [CrossRef]

13. H. Son, T. Nguyen, and V. N. Nguyen, “Hybrid sine cosine algorithm with integrated roulette wheel selection and opposition-based learning for engineering optimization problems,” Int. J. Comput. Intell. Syst., vol. 16, no. 1, 2023. doi: 10.1007/s44196-023-00350-2. [Google Scholar] [CrossRef]

14. W. Kong, J. Chen, Y. Song, Z. Fang, X. Yang and H. Zhang, “Sobel edge detection algorithm with adaptive threshold based on improved genetic algorithm for image processing,” Int. J. Adv. Comput. Sci. Appl., vol. 14, no. 2, pp. 557–562, 2023. doi: 10.14569/issn.2156-5570. [Google Scholar] [CrossRef]

15. S. M. Alshahrani, N. A. Khan, J. Almalki, and W. Al Shehri, “URL phishing detection using particle swarm optimization and data mining,” Comput. Mater. Contin., vol. 73, no. 3, pp. 5625–5640, 2022. doi: 10.32604/cmc.2022.030982. [Google Scholar] [CrossRef]

16. C. Cavallaro, V. Cutello, M. Pavone, and F. Zito, “Machine learning and genetic algorithms: A case study on image reconstruction,” Knowl.-Based Syst., vol. 284, no. 6, 2024, Art. no. 111194. doi: 10.1016/j.knosys.2023.111194. [Google Scholar] [CrossRef]

17. L. Abualigah, D. Yousri, M. A. Elaziz, A. A. Ewees, M. A. A. Al-qaness and A. H. Gandomi, “Aquila optimizer: A novel meta-heuristic optimization algorithm,” Comput. Ind. Eng., vol. 157, no. 11, 2021, Art. no. 107250. doi: 10.1016/j.cie.2021.107250. [Google Scholar] [CrossRef]

18. Z. Guo et al., “Optimal PID tuning of PLL for PV inverter based on Aquila optimizer,” Front. Energy Res., vol. 9, 2022. doi: 10.3389/fenrg.2021.812467. [Google Scholar] [CrossRef]

19. Z. Pang, B. Yang, R. Chen, Z. Zhang, and F. Mo, “A multi-phase scheduling method for reconfigurable flexible job-shops with multi-machine cooperation based on a Scout and mutation-based Aquila optimizer,” CIRP J. Manuf. Sci. Technol., vol. 46, no. 3, pp. 116–134, 2023. doi: 10.1016/j.cirpj.2023.08.003. [Google Scholar] [CrossRef]

20. S. Ekinci, D. Izci, and L. Abualigah, “A novel balanced Aquila optimizer using random learning and Nelder-Mead simplex search mechanisms for air-fuel ratio system control,” J. Braz. Soc. Mech. Sci. Eng., vol. 45, no. 1, 2023, Art. no. 68. doi: 10.1007/s40430-022-04008-6. [Google Scholar] [CrossRef]

21. E. Pashaei, “Mutation-based binary Aquila optimizer for gene selection in cancer classification,” Comput. Biol. Chem., vol. 101, 2022, Art. no. 107767. doi: 10.1016/j.compbiolchem.2022.107767. [Google Scholar] [PubMed] [CrossRef]

22. W. Zhang, C. Peng, Y. Yuan, J. Cui, and L. Qi, “A novel multi-objective evolutionary algorithm with a two-fold constraint-handling mechanism for multiple UAV path planning,” Expert. Syst. Appl., vol. 238, no. 4, 2024, Art. no. 121862. doi: 10.1016/j.eswa.2023.121862. [Google Scholar] [CrossRef]

23. X. Zhang, Y. Liu, Z. Gao, J. Ren, S. Zhou and B. Yang, “A ground-risk-map-based path-planning algorithm for UAVs in an urban environment with beetle swarm optimization,” Appl. Sci., vol. 13, no. 20, 2023, Art. no. 11305. doi: 10.3390/app132011305. [Google Scholar] [CrossRef]

24. H. Chen, Y. Liang, and X. Meng, “A UAV path planning method for building surface information acquisition utilizing opposition-based learning artificial bee colony algorithm,” Remote Sens., vol. 15, no. 17, 2023, Art. no. 4312. doi: 10.3390/rs15174312. [Google Scholar] [CrossRef]

25. C. Wang, L. Zhang, Y. Gao, X. Zheng, and Q. Wang, “A cooperative game hybrid optimization algorithm applied to UAV inspection path planning in urban pipe corridors,” Mathematics, vol. 11, no. 16, 2023, Art. no. 3620. doi: 10.3390/math11163620. [Google Scholar] [CrossRef]

26. X. Liu, G. Li, H. Yang, N. Zhang, L. Wang and P. Shao, “Agricultural UAV trajectory planning by incorporating multi-mechanism improved grey wolf optimization algorithm,” Expert. Syst. Appl., vol. 233, no. 3, 2023, Art. no. 120946. doi: 10.1016/j.eswa.2023.120946. [Google Scholar] [CrossRef]

27. M. D. Phung and Q. P. Ha, “Safety-enhanced UAV path planning with spherical vector-based particle swarm optimization,” Appl. Soft Comput., vol. 107, no. 2, 2021, Art. no. 107376. doi: 10.1016/j.asoc.2021.107376. [Google Scholar] [CrossRef]

28. S. Li, X. Chen, M. Zhang, Q. Jin, Y. Guo and S. Xing, “A UAV coverage path planning algorithm based on double deep Q-network,” J. Phys. Conf. Ser., vol. 2216, no. 1, 2022, Art. no. 012017. doi: 10.1088/1742-6596/2216/1/012017. [Google Scholar] [CrossRef]

29. A. Barnawi, K. Kumar, N. Kumar, N. Thakur, B. A. Alzahrani and A. Almansour, “Unmanned ariel vehicle (UAV) path planning for area segmentation in intelligent landmine detection systems,” Sensors, vol. 23, no. 16, 2023, Art. no. 7264. doi: 10.3390/s23167264. [Google Scholar] [PubMed] [CrossRef]

30. Y. Pan, Y. Yang, H. Liu, and W. Li, “UAVs and mobile sensors trajectories optimization with deep learning trained by genetic algorithm towards data collection scenario,” Mob. Netw. Appl., vol. 28, no. 2, pp. 808–823, 2023. doi: 10.1007/s11036-023-02106-w. [Google Scholar] [CrossRef]

31. S. Yang et al., “Path planning of UAV base station based on deep reinforcement learning,” Procedia Comput. Sci., vol. 202, no. 3, pp. 89–104, 2022. doi: 10.1016/j.procs.2022.04.013. [Google Scholar] [CrossRef]

32. S. Mirjalili, “SCA: A sine cosine algorithm for solving optimization problems,” Knowl.-Based Syst., vol. 96, no. 63, pp. 120–133, 2016. doi: 10.1016/j.knosys.2015.12.022. [Google Scholar] [CrossRef]

33. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Adv. Eng. Softw., vol. 95, no. 12, pp. 51–67, 2016. doi: 10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]