Machine Learning for QoS Optimization and Energy-Efficient in Routing Clustering Wireless Sensors

Nomenclature

1  Introduction

Several studies have proven that the deployment of a mobile data collector (MDC) improves the efficiency of wireless sensor networks (WSNs). However, some important design challenges have arisen, such as how to locate sensor nodes (SNs), how to locate a high density of SNs, and how to find the best MDC path. Accordingly, some new approaches have been developed for WSNs to address these issues. Although numerous research studies have focused on minimizing the routing protocols’ energy consumption, few have addressed other qualities of service (QoS), such as latency time. This prompts us to develop a routing protocol that takes into account the QoS criteria such as energy consumption, throughput, latency, and stability. In WSNs and the Internet of Things (IoT) [1], clustering has appeared as a leading technique for data mining to solve problems such as network lifetime, stability, data aggregation, energy consumption reduction, and reliability [2]. For numerous advantages, aggregation is recommended in the WSN data mining process. Clustering consists division of a WSN into groups known as “clusters”. Each cluster has a leader chosen from the SNs, who are called CHs. In a cluster, SNs collect the data streams, which are then aggregated by their CHs. In a cluster, SNs collect the data streams, which are then aggregated by their CHs. The CHs then forward the data to the sink. All WSN cluster protocols are based on rounds. Every round involves the creation of a cluster, the election of the CH, and the transfer of data [3]. By using the grid clustering algorithm [4], every cluster is created according to the size of each grid in the WSN. Specifically, this approach fixes cluster size and location. Grid clustering algorithms are popular due to their simplicity, scalability, and uniform energy consumption, but load balancing and energy efficiency remain open questions due to the random nature of WSNs [4].

Clustered WSN approaches comprise two major phases: first, the clustering phase, and second, the data transmission phase. A grid approach is considered as a cluster of clusters, whose elementary clusters are not dynamic. More precisely, this algorithm fixes cluster size and location [5]. On the other hand, a few other clustering algorithms proposed in the literature, such as the K-Means algorithm. It divides SNs into k clusters based on mean Euclidean distance, which optimizes intra-group similarity [6]. This research suggests a new protocol named (M-T), which is a combination of LEACH-G-K, LEACH-K, and MDC-K [7] approach and the traveling salesman problem (TSP) based MDC method. M-T utilizes the K-Means and the Grid clustering algorithms to reduce the CH election phase energy consumption and to improve the election of CH and a new intelligent MDC, which uses TSP to find the MDC optimal path for efficient latency time. In particular, our proposed protocol aims to extend the network lifetime and improve its QoS criteria. Our contribution is presented below:

•   Firstly, using the grid algorithm the regional network is divided into areas of equal size, and then the K-Means algorithm is applied to each grid cluster to search for the CH. In this case, every CH is allocated by the SN with the shortest distance from the centroid of each grid cluster.

•   Secondly, TSP is applied during the transmission step to find the optimal MDC path (where the MDC is an intermediate between the CH and the sink).

•   Finally, a simulated analysis comparing the proposed protocol with existing solutions was carried out, which showed that it was more effective.

This paper is organized as follows. Section 2 presents a literature review of the clustering protocol using the K-Means algorithm, Grid algorithm, and TSP in MDC. Section 4 presents the K-Means algorithm protocol. Section 3 presents the TSP algorithm protocol. Section 6 presents the proposed clustering protocol. Next, analyses and simulation results are presented in Section 7. Finally, Section 8 presents the conclusions.

2  Literature Study

Nowadays, Different researches focus on the MDCs implementation in routing protocols [7–11] to enhance the lifetime of WSNs. In addition, various research studies have been conducted to evaluate the performance impact of K-Means on the clustering protocol in WSNs [6,12–14]. Furthermore, other studies are applying grid clusters on clustering routing protocols to enhance WSN performance, such as [4,15,16]. Various research studies have applied MDC to the routing protocol, although others have employed K-Means and Grid-sizes clustering in the clustering protocol.

Reference [1] has proposed a new intelligent routing protocol named MDC-IR-DV-Hop, which combines the IR-DV-Hop localization algorithm, the K-Means algorithm and MDC. This approach employs the IR-DV-Hop localization algorithm to identify the precise location of error-free SNs in LS-WSNs and to determine CHs. Furthermore, the MDC is employed as an intermediary between the CH and the BS to improve WSN QoS criteria, minimize data collection delays, and extend WSN lifetime. Experimental results show that the MDC-IR-DV hop has a significant impact on energy consumption and QoS measurements. In particular, this protocol significantly improves energy consumption, latency, throughput, and stability gains compared to the EACBM, TCMDC, MDC maximum residual energy leach, MDC minimum distance leach, MDC-K, MDC-TSP-LEACH-K, AMWSN, and NDCM protocols. Authors of [8] discussing and performing LEACH-based MDC using a multi-hop routing approach. They demonstrate that this protocol shows a significant reduction in the energy consumption of SNs, improves network lifetime, and improves the data performance collection compared to the LEACH protocol. Specifically, only 40 SNs are used and the simulation area is equal to 1km2. Based on this approach, Reference [9] provides another protocol, where MDC provides multi-hop communication from SNs to the MDC and then finally. It allows for a decrease in the energy use for all network nodes. The MDC maximum residual energy approach, where MDC provides multi-hop communication from SNs to the MDC and then to sink. It allows for a decrease in the energy use for all network nodes. The MDC maximum residual energy approach [10] focuses on multi-hop communication between the SNs, the MDC, and the sink. Furthermore, it applies to a large-scale network. The results of the simulation demonstrate that this approach provides a performance gain over the LEACH protocol on SN energy consumption and the lifetime of the network. It does not enhance QoS, although, the simulation parameters were very limited [8]. Paper [7] proposed the MDC-K protocol, which is a combined approach of the LEACH-K protocol and the MDC protocol. Specifically, it uses the K-Means approach to reduce energy consumption during the CH election step. In addition, the MDC technology is used to enhance WSN QoS, decrease network data collection latency, and extend network lifetime. A simulation result demonstrated that MDC-K also reduced energy consumption and enhanced QoS performance, with lower energy consumption, higher throughput and latency, and stability over LEACH, TEEN, LEACH-K, and the maximum residual energy LEACH protocols. The objective of [11] is to attain different QoS parameters for WSNs by utilizing socially inspired reliable communication to decrease the SN’s energy consumption. Specifically, the total number of SNs is divided into an equal number of clusters. While one node serves as a BS, the closest BS node serves as a movable mobile data collector (MMDC) for reliable data collection from CHs and common SNs. On receiving a congestion alert from the CH, the MMDC seeks and moves to the CH to collect data and sends the collected packets to the BS. This technique controls congestion, BS traffic, and CHs. Using this technique, the WSN reliability, packet delivery rate, packet loss rate, and energy efficiency are archived. In addition to these parameters, the Socially inspired reliable communication (SIRC) protocol has successfully achieved the WSN delay and throughput parameters. This approach demonstrates the best protocol for reliable data collection in clustered WSNs.

In addition, many researchers have studied the impact of K-Means on WSNs. Various studies examine the impact of the K-Means method on the energy consumption of WSNs. Reference [13] examines the performance of LEACH based on machine-learning algorithms. The simulation results demonstrate a decrease in computing time using K-Means and higher residual energy by using Gauss. However, the proposed solution is limited in the fact that it was run on 100 SNs over 200 rounds. A K-Means algorithm was also performed in [12] in the LEACH protocol’s CH election stage. It showed that the proposed routing protocol reduced energy consumption and latency, and enhanced stability time and network throughput. Cluster-grid algorithms divide the area into grids of equal size, where every grid is considered a cluster, with one CH in each cluster [6]. On the other hand, Reference [14] proposed another method to improve the clustering phase of the LEACH protocol called Low Energy Adaptive Clustering Hierarchy-KMeans (LEACH-KMe) by using the K-Means algorithm. A Matlab simulation was performed with 100 SNs for 400 rounds to find out the performance of LEACH-KMe by considering four major metrics: energy consumption, number of live SNs, number of dead SNs, and residual energy. The simulation results showed that the LEACH-KMe protocol performs better than the LEACH protocol. The LEACH-KMe protocol is capable of providing a much more uniform distribution of SNs between clusters, and the network lifetime of the LEACHKMe protocol shows better improvement than the conventional LEACH protocol. LEACH-KMe can provide higher residual energy but with lower overall energy consumption in the process of data transmission. Moreover, LEACH-KMe can maintain SN energy, resulting in a larger number of live SNs than the LEACH protocol. Even with all the advantages of LEACH-KMe, it only improves 4 QoS criteria and this protocol has not been tested in large-scale WSN (LS-WSN).

Designing clustering algorithms for WSNs is a complex task, as clustering on WSNs is a difficult optimization problem in terms of QoS, with multiple constraints. Authors of [15] proposed a Query-Driven Virtual Grid-based Data Dissemination (QDVGDD) algorithm for WSN. In this approach, The monitoring field is partitioned into small equal-sized grids and mobile BS circles the sensing field by moving in a clockwise direction to gather the data for the injected query. As a result, the network control overheads decreased because of using virtual infrastructure. Also, The number of regions increased with the increase of the SNs number. The authors used a grid-based clustering algorithm to improve efficiency, reduce cost, and increase the reliability of the network. Additionally, in [16], the CHs rotation was based on a backoff timer. The back-off timer is calculated based on each SN residual energy level within a grid. In several grid cluster protocols, the algorithm selects one CH per grid based on its energy level, this CH is kept until its energy is completely depleted. Grid-cluster protocols have been used to optimize the CHs distribution to minimize the cluster area. However, the network energy consumed in these protocols is very high compared to a dynamic cluster-based protocol. The reason behind this is that the CHs selection is done only within a grid and not at the whole network level, as it is done in LEACH. Therefore, this method does not give a CH fair selection concerning all network nodes. Another reason for high energy consumption is that the clusters are not formed based on the distance to the closest CHs. Irrespective of the distance a node will always have to associate with the CH belonging to its grid. Reference [4] proposed Low Energy Adaptive Clustering-Grid-KMeans (LEACH-G-K) protocol This protocol divided the area into equal-sized clusters using the grid function. Then, for each cluster, the K-Means algorithm is applied to gather their nodes near the centroid, where the cluster head is located. The obtained simulation results showed that LEACH-G-K can decrease energy consumption and increase throughput compared to the Low Energy Adaptive Clustering Hierarchy protocol (LEACH), Threshold Sensitive Energy Efficient sensor Network protocol (TEEN), Low Energy Adaptive Clustering Hierarchy-KMeans protocol (LEACH-K) and MDC maximum residual energy LEACH protocols, but it did not improve other QoS criteria.

The TSP is one of the most studied problems in the field of combinatorial optimization, which finds applications in many fields such as logistics, planning, microchip manufacturing and testing, DNA sequencing, and many others [17]. Reference [18] examined TSP with a “Castalia” simulator and demonstrated that the TSP solution can be applied in WSNs to increase throughput and reduce network energy consumption. Various studies have employed TSP to determine the optimal MDC path. The researchers of this paper [19] develop an optional approach for data collection in large-scale WSNs, which is based on mobile networks. Furthermore, in [20], a round travels along the TSP path while the MDC moves through the SHDGP, the MDC can query the neighboring SNs one by one to collect data. When an SN receives the query request, the SN just sends its data to the MDC. Based on K-Means clustering and the approximate solution for the TSP using the simple local search algorithm (2-Opt), novel variants of the K-Means and the TSP-based mobility protocol have been developed in [11] to provide real-time solutions when the problem is disrupted by failures. Simulation results showed that, although this solution is very costly, it is interesting to implement when SN failure risk is high, and is more efficient than the original K-Means solution and TSP in terms of complexity. Reference [17] reviewed existing research and study TSP. Previous research has shown that the classical TSP can be solved efficiently in the parallel aisle structure of warehouses.

As illustrated above, various studies have implemented the Grid and K-Means algorithms in the clustering routing protocol, while others have applied the TSP algorithm in this protocol. However, the Grid and K-Means algorithms are used independently, as regrouping algorithms, to reduce energy consumption in the clustering routing protocols. While there are only a few research studies combining these two algorithms (Grid, K-Means) to enhance the QoS of the clustering protocol. But, to our knowledge, there are almost no research studies that have combined the Grid, K-Means, TSP, and MDC algorithms in the routing clustering protocol. Our research paper focuses on combining the K-Means and Grid algorithms in a clustering phase where the TSP algorithm is applied in the transmission stage of the LEACH protocol to improve the QoS of WSN.

Based on the above studies, it is concluded that using grids to create clusters, enables fixing the same cluster surface for all clusters, which reduces the computation complexity for all clusters and consequently the SNs’ energy consumption. Furthermore, based on the LEACH-G-K and MDC-K approaches, it is concluded that the election of CHs according to the K-Means algorithm can fix the same CH position in each cluster. Thus, reducing the distance between SNs and CHs and consequently reducing the SNs energy consumption which allows for decreasing WSN energy consumption and increasing throughput. But it is also noticed that the latency time is still high, which draws attention to the use MDC, which can solve this problem and later reduce the latency time, especially in the routing between the CHs and the BS. Also, MDC batteries are cheaper which means that it is more cost-effective rather than changing the sensors. Moreover, using the TSP algorithm, MDC can choose the optimal route, which can reduce energy consumption, and latency time, increase the number of packets transmitted between the CHs and the BS, and increase WSN stability. As a result, the routing cluster WSN protocol, which combines all these techniques can be more reliable and provide better QoS criteria.

3  The Traveling Salesman Problem (TSP)

A Traveling Salesman Problem (TSP) proposes a solution to the problem of determining the optimum route between various points and places to visit. The goal of the salesperson is to maintain the travel costs and the distance traveled as short as possible. Algorithms 1 and 2 present the process of TSP algorithm.

4  K-Means Algorithm

In the case of the K-Means algorithm, the selection of CHs is based mainly on Euclidean distances and depends on the residual energies of the SNs. Thus, here, the center node collects the identification, residual energy, and position of all SNs and saves this in a list in the center node. After it collects this information from all the SNs, it starts running the K-Means clustering algorithm [21,22]. The K-Means algorithm is as follows:

•   Step1: Set the initial number of centroids K on random locations.

•   Step2: For each cluster, calculate the Euclidean distance from each SN to all centroids and assign it to the closest centroid, and then the initial K clusters are created. Suppose there are N SNs where each of them belongs to DR. To find the minimum variance grouping of these nodes into K clusters, the problem is to find the K centroids [Ai]i=1K in DR where,

(1/N)×∑{mind2(Xj,Ai)};forj=1toN(1)

where, d (Xj, Ai) refers to the Euclidean distance between Xj and Ai. The SNs [i]j=1K are known as the centroid of the cluster.

•   Step3: Recalculate the locations of the centroids within every cluster and verify the change in location from the last one.

•   Step4: If the position of a centroid changes, proceed to step 2. Otherwise, the process of clustering is finished.

Fig. 1 comprehensively presents the process of K-Means algorithm.

Figure 1: The process of K-Means

5  Grid Clustering Algorithm

According to [4,16], the grid clustering algorithm is a clustering algorithm that forms clusters based on the density of each grid in a gridded WSN. Therefore, it is suitable for large-scale networks. The main basic idea of grid-cluster protocols is to divide the network area into equal-sized virtual grids where each grid is considered a cluster. A grid is considered a cluster where clusters are only fixed. Particularly, this method decreases the variations in sizes and locations of the clusters, due to the random deployment of nodes, it cannot create all equal-sized clusters. We choose the grid structure for clusters based on the following three considerations. Firstly, the grid structure can guarantee good cluster distribution. Secondly, the grid can guarantee the same cluster surface area and hence the same computational complexity at the level of each cluster. Thirdly, routing between CHs and SNs is simple in the grid structure. Cluster SNs can select one of several candidate routes to transmit data packets to CHs based on residual energy and load balance.

6  The Proposed M-T Protocol

We assume that the WSN is composed of 100 randomly deployed SNs of similar types. Each SN’s geographic location coordinates in the WSN are identified and assigned during the deployment stage. Every coordinate is considered the identifier of the given node. Furthermore, the network also includes a sink, which is the base station. This is located outside the network area. When the WSN deployment is complete, the process of network construction is launched based on their location. In our network model, we assume that:

•   SN homogeneous.

•   The SNs are static and know their locations.

•   Clustering is done through the Grid algorithm.

•   CH is elected through the K-Means algorithm, the node having the minimum distance with centroid from each grid will be CH.

•   sink gives the coordinates of all the CH to the MDC to use as input to the TSP algorithm.

•   There is a single intelligent MDC.

6.1 M-T Model

M-T extends the concept of LEACH-G-K [7] with the convergence of wireless mobile communication and improved WSN technology. We use the Grid and K-Means approach to improve the clustering stage and MDC as an interface between CHs and sink to improve the routing phase. The area of WSN is partitioned into grids of defined size. Each grid is a rectangular area of d × d as shown in Fig. 2. After the grid G is configured and all of the nodes are positioned, the K-Means algorithm is implemented on every grid cluster to minimize the intracluster communication distance and to deliver the centroid coordinates. The selection of the CH is based on the centroid distance. Suppose the number of nodes denoted by (Ni) is subdivided into K clusters. Then the centroid c is chosen to be the centroid of the K clusters. The K-Means step, therefore, begins by calculating the positions of each grid centroid. Allocate every CH to the SN with the minimum distance to the centroid. Each SN belongs to the Grid(i) with coordinates (xi, yi) then calculates the minimum distance as follows:

D(SN(j),c(i))=min{(xc−xi)2+(yc−yi)2};SN(j)∈Gc(i)(2)

Figure 2: The process of the M-T

As a consequence, the Grid-centroid coordinates, corresponding to the minimum distance to (x, y), are calculated. then the CH is selected for the given grid. Each CH diffuses its location in its transmission area using a special packet containing its coordinates to all the nodes of its grid cluster. The MDC does its job in a smart way that it only approaches the CHs closest to its neighbors. The MDC provides a dynamic trajectory using the Lin-Kernighan heuristic for solving the traveling salesman problem (LKH-TSP) algorithm. MDC collects the data that are broadcasted by the CH can broadcast data to MDC directly. Therefore, MDC completes the collection and finally delivers the data to the sink. Fig. 2 illustrates a straightforward MDC strategy in WSN.

In this scheme, a WSN based on a grid of clusters is used in the proposed system. For each Grid Cluster (GC), one SN is elected as the CH, which operates as an aggregator. The CH is responsible for aggregating the data received from its SNs and sending them to the sink through the MDC. The resolution of the TSP gives the MDC a dynamic trajectory. Because the CHs are nearly at the centroid, the MDC travels on a nearly linear path from the earliest centroid of the earliest GC to the final column of the GC. After that, it travels to the closest GC centroid to the entire GC. In the end, it transfers the full data to the sink. Therefore, energy and latency can be conserved by utilizing The TSP in MDC.

•   We propose a smart routing clustering protocol consisting of two phases: an initialization phase and a transmission phase. This approach is an improvement of the MDC-K, and LEACH-K protocols (which is an improvement of the LEACH protocol using the K-Means machine learning algorithm at the level of the initialization phase exactly the CH election phase and by integrating TSP at the MDC exactly at the level of the transmission phase).

•   Using MDC the energy consumption and latency in the transmission phase are reduced and the throughput is increased.

•   However, to demonstrate the advantages of our protocol, we have compiled a comparison with the native LEACH protocol and its enhancements (LEACH, TEEN, LEACH-K, LEACH-C, Improved-LEACH, Stable-Improved-LEACH, and MDC-maximum residual energy leach protocol).

M-T adapts the energy model of LEACH-G-K, as shown in Fig. 3.

Figure 3: M-T energy model

If the distance is less than a threshold D, the free space model (d2 power loss) is used; otherwise, the multi-path model (d4 power loss) is used. Or, for short-distance transmission, such as intra-cluster communication, the energy consumed by a transmitting amplifier is proportional to d2 and for long-distance transmission, such as inter-cluster communication, the energy consumption is proportional to d4. D is a threshold transmission distance, where,

D=εfs/εamp.(3)

Thus, if the transmitter sends a message of b bits to the receiver until d distance, the required energy to transmit b bits of data is modeled by (4):

ETransmitting=(Eeleb)+εAmpbd2,(4)

where, B is the number of transmitted bits, each SN is static and homogeneous, εfs is the power loss of free space, εAmp is the power multi path models, d is the distance between CH and MDC, Eele is The parameter Eelec is the per bit energy dissipations for transmission and reception.

The required energy to get B bits of data is modeled by (5):

EReceiving(B)=EeleB,(5)

where, Eele is the energy required to operate the electronic circuitry of the receiver. Energy consumed during a data collection cycle is calculated in (6).

ERound=ETransmitting+EReceiving.(6)

7  Simulation Results

In order to assess our protocol’s performance, it is compared with several other QoS-based protocols. We compared our M-T approach with LEACH and the ameliorated versions of LEACH [23] protocol namely TENN [24], LEACH-K [12], LEACH-C [25], Improved-LEACH [26], Stable-Improved-LEACH [27], MDC maximum residual energy leach [14], and MDC-K [7] protocols in terms of residual energy, packet latency time, and throughput. Table 1 depicts the common simulation settings for all scenarios.

The test scenarios considered and the performance measures adopted are discussed in this section. The analysis of these results is performed to make a trade-off between residual energy, throughput (packets received by the sink), and network latency as a function of the variation of K over 10,000 rounds. One hundred nodes have been chosen to test the performance of the M-T protocol. Fig. 4 displays the results of a study comparing the throughput in each round of the proposed protocol M-T and other improvements to the LEACH protocol.

Figure 4: Simulation throughput results of M-T, LEACH, TENN, LEACH-K, LEACH-C, Improved-LEACH, Stable-Improved-LEACH and MDC maximum residual energy leach protocols

Fig. 4 shows a variation of throughput of our proposed protocol as compared to Improved-LEACH, TENN, LEACH-K, LEACH-C, Improved-LEACH, Stable-Improved-LEACH, MDC-K, LEACH and MDC maximum residual energy leach protocols. The graphs in Fig. 4 show that the MDC implementation with the TSP algorithm enhances a significant amount of throughput. We observed in the previous figure that the throughput of M-T in round 10,000 is equal to 18,910 packets/round compared to 18,300 packets/round for MDC maximum residual energy leach protocol, 18,110 packets/round of LEACH-K protocol, 11,845 packets/round of Improved-LEACH protocol, 12,009 packet/round of Stable-Improved-LEACH protocol, 8012 packet/round of TEEN protocol and 8001 packet/round of LEACH protocol. However, our proposal enhances the Throughput value by reducing the path distance between BS and CH using the K-Means algorithm and decreasing the latency time by utilizing TSP in MDC.

The outcome of the comparison of latency time between M-T approach LEACH, TENN, LEACH-K, LEACH-C, Improved-LEACH, Stable-Improved-LEACH, and MDC maximum residual energy leach protocols is presented in Fig. 5.

Figure 5: Comparison between M-T, TENN, LEACH-K, LEACH-C, Improved-LEACH, Stable-Improved-LEACH, and MDC maximum residual energy leach protocols in terms of latency time

In Fig. 5, we can see how once using our protocol approach, also the latency decreases to 194.8 (ms) for the LEACH protocol, 154.11 (ms) for the LEACH-C protocol, 153.47 (ms) for the TEEN protocol, 123.07 (ms) for the Stable-Improved-LEACH protocol, 122.15 (ms) for the Improved-LEACH protocol, 96.1602 (ms) for the LEACH-K protocol, 55.97 (ms) for the MDC-K protocol, and 51.551 (ms) for the MDC maximum residual energy leach protocol compared to 45.9 (ms) for the M-T protocol to 45.9 (ms). However, we find that our approach provides optimal latency reduction over the previous routing protocols. Fig. 6 compares M-T approach LEACH, TENN, LEACH-K, LEACH-C, Improved-LEACH, Stable-Improved-LEACH, MDC-K, and MDC maximum residual energy leach protocols in terms of lifetime.

Figure 6: Comparison between M-T, LEACH, TENN, LEACH-K, MDC-K, LEACH-C, Improved-LEACH, Stable-Improved-LEACH, and MDC maximum residual energy leach protocols in terms of lifetime

As illustrated in Fig. 6, our protocol M-T improves the lifetime of the network with higher efficiency in terms of stability than LEACH, TENN, LEACH-K, MDC-K, LEACH-C, Improved-LEACH, Stable-Improved-LEACH, but it is less stable than MDC. It improves the SN’s residual energy as well. Results show that the proposed method can decrease the sensor nodes’ energy consumption. Fig. 7 presents the stability of the proposed protocol compared to the M-T approach LEACH, TENN, LEACH-K, LEACH-C, Improved-LEACH, MDC-K, Stable-Improved-LEACH and MDC maximum residual energy leach protocol.

Figure 7: Comparison between M-T, LEACH, TENN, LEACH-K, LEACH-C, Improved-LEACH, Stable-Improved-LEACH, MDC-K, MDC-K, and MDC maximum residual energy leach protocols in terms of stability

The stability improves slightly from 109 (rounds) in Improved-LEACH to 496 (rounds) in LEACH to (574) in LEACH-C to (637) in Stable-Improved-LEACH to 733 (rounds) in TEEN to 1607 (rounds) in LEACH-K to 1915 (rounds) in M-T to 1808 in MDC maximum residual energy leach to 1920 (rounds) MDC-K. The MDC (Maximum residual energy leach) protocol is more stable than ours. To assess the effectiveness of our MDC-K protocol in improving the QoS of the routing protocol Table 2 summarizes a comparison of our protocol and some similar protocols in the literature.

8  Conclusion

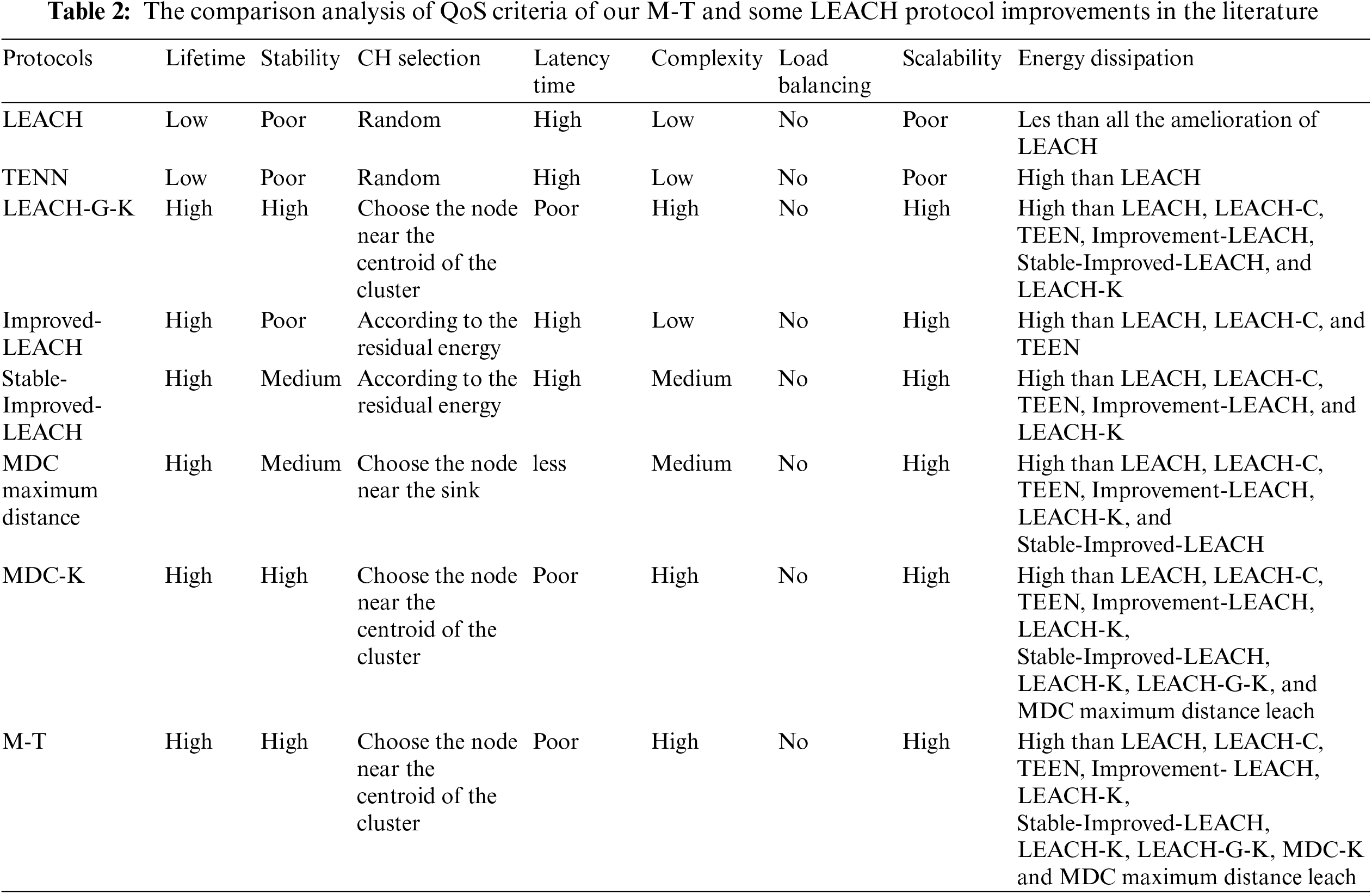
MDC represents one of the emerging technologies for diverse applications of WSNs. The main focus of these networks is latency time, throughput, lifetime, stability, and energy efficiency. This paper proposes the M-T protocol, which is a combination of the MDC-K protocol and the TSP to improve the transmission phase of the MDC-K protocol. To be more precise in our approach an MDC is employed as an interface between the CH and the sink to improve the QoS of WSN, to decrease delay during data collection, and to increase the lifespan of WSN. The simulation results showed that M-T had a significant impact on energy consumption and QoS than LEACH, TENN, LEACH-K, LEACH-C, Improved-LEACH, Stable-Improved-LEACH, MDC maximum residual energy leach and MDC-K protocols.

Acknowledgement: None.

Funding Statement: This research was supported by the Ministry of Education of the Republic of Korea and the National Research Foundation of Korea (NRF-2023S1A5C2A07096111).

Author Contributions: Rahma Gantassi: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Data curation. Zaki Masood: Validation, Data curation, Writing—original draft, Visualization. Yonghoon Choi: Validation, Resources, Writing—review & editing, Supervision, Project administration, Funding acquisition. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. R. Gantassi, S. Messous, Z. Masood, Q. A. Sias, and Y. Choi, “Enhanced network qos in large scale and high sensor node density wireless sensor networks using (IR-DV-Hop) localization algorithm and mobile data collector (MDC),” IEEE Access, vol. 12, no. 1, pp. 37957–37973, 2024. doi: 10.1109/ACCESS.2024.3370432. [Google Scholar] [CrossRef]

2. M. Abdullah, H. N. Eldin, T. Al-Moshadak, R. Alshaik, and I. Al-Anesi, “Density grid-based clustering for wireless sensors networks,” Procedia Comput. Sci., vol. 65, no. 4, pp. 35–47, 2015. doi: 10.1016/j.procs.2015.09.074. [Google Scholar] [CrossRef]

3. S. Zhong, G. Wang, X. Leng, X. Wang, L. Xue and Y. Gu, “A low energy consumption clustering routing protocol based on k-means,” J. Softw. Eng. Appl., vol. 5, no. 12, 2012, Art. no. 26263. [Google Scholar]

4. R. Gantassi, B. B. Gouissem, and J. B. Othman, “The use of grid-sizes clustering and k-means algorithms to enhance the qos in leach protocol,” in ICC 2021-IEEE Int. Conf. Commun., IEEE, 2021, pp. 1–6. [Google Scholar]

5. Y. Zhuang, J. Pan, and G. Wu, “Energy-optimal grid-based clustering in wireless microsensor networks with data aggregation,” Int. J. Parallel Emergent Distrib. Syst., vol. 25, no. 6, pp. 531–550, 2010. doi: 10.1080/17445760903548291. [Google Scholar] [CrossRef]

6. P. Sasikumar and S. Khara, “K-means clustering in wireless sensor networks,” in 2012 Fourth Int. Conf. Comput. Intell. Commun. Netw., IEEE, 2012, pp. 140–144. [Google Scholar]

7. R. Gantassi, B. Ben Gouissem, O. Cheikhrouhou, S. El Khediri, and S. Hasnaoui, “Optimizing quality of service of clustering protocols in large-scale wireless sensor networks with mobile data collector and machine learning,” Secur. Commun. Netw., vol. 2021, no. 1, 2021, Art. no. 5531185. doi: 10.1155/2021/5531185. [Google Scholar] [CrossRef]

8. M. Arshad, N. Armi, N. Kamel, and N. Saad, “Mobile data collector based routing protocol for wireless sensor networks,” Sci. Res. Essays, vol. 6, no. 29, pp. 6162–6175, 2011. [Google Scholar]

9. M. Arshad, M. Y. Aalsalem, and F. A. Siddqui, “Energy efficient cluster based routing scheme for mobile wireless sensor networks,” in 2014 5th Int. Conf. Intell. Adv. Syst. (ICIAS), IEEE, 2014, pp. 1–6. [Google Scholar]

10. R. Vishnuvarthan, R. Sakthivel, V. Bhanumathi, and K. Muralitharan, “Energy-efficient data collection in strip-based wireless sensor networks with optimal speed mobile data collectors,” Comput. Netw., vol. 156, no. 11, pp. 33–40, 2019. doi: 10.1016/j.comnet.2019.03.019. [Google Scholar] [CrossRef]

11. A. Ghabri, M. Bellalouna, and W. Khaznaji, “Improvement on k-means and tsp based mobility protocol of wireless sensor network,” in Fifth Int. Conf. Ambient Comput., Appl., Serv. Technol. (AMBIENTIARIA, 2015, pp. 56–64. [Google Scholar]

12. R. Gantassi, B. B. Gouissem, and J. B. Othmen, “Routing protocol leach-k using k-means algorithm in wireless sensor network,” In: Web, Artificial Intelligence and Network Applications, Cham: Springer, 2020, pp. 299–309. [Google Scholar]

13. E. Rabiaa, B. Noura, and C. Adnene, “Improvements in leach based on k-means and gauss algorithms,” Procedia Comput. Sci., vol. 73, no. 9, pp. 460–467, 2015. doi: 10.1016/j.procs.2015.12.046. [Google Scholar] [CrossRef]

14. A. S. Al-Zubaidi, B. M. Mahmmod, S. H. Abdulhussain, and D. Al-Jumaeily, “Re-evaluation of the stable improved leach routing protocol for wireless sensor network,” in Proc. Int. Conf. Inf. Commun. Technol., 2019, pp. 96–101. [Google Scholar]

15. A. W. Khan, J. I. Bangash, A. Ahmed, and A. H. Abdullah, “QDVGDD: Query-driven virtual grid based data dissemination for wireless sensor networks using single mobile sink,” Wirel. Netw., vol. 25, no. 1, pp. 241–253, 2019. doi: 10.1007/s11276-017-1552-8. [Google Scholar] [CrossRef]

16. Y. Zhuang, J. Pan, and G. Wu, “Energy-optimal grid-based clustering in wireless microsensor networks,” in 2009 29th IEEE Int. Conf. Distrib. Comput. Syst. Workshops, IEEE, 2009, pp. 96–102. [Google Scholar]

17. S. Bock, S. Bomsdorf, N. Boysen, and M. Schneider, “A survey on the traveling salesman problem and its variants in a warehousing context,” Eur. J. Oper. Res., 2024. doi: 10.1016/j.ejor.2024.04.014. [Google Scholar] [CrossRef]

18. J. E. Tito, M. E. Yacelga, M. C. Paredes, A. J. Utreras, W. Wójcik and O. Ussatova, “Solution of travelling salesman problem applied to wireless sensor networks (WSN) through the MST and B&B methods,” in Photonics Applications in Astronomy, Communications, Industry, and High-Energy Physics Experiments 2018. Bellingham, WA, USA: SPIE, 2018, vol. 10808, pp. 736–747. [Google Scholar]

19. M. Ma and Y. Yang, “Data gathering in wireless sensor networks with mobile collectors,” in 2008 IEEE Int. Symp. Parallel Distrib. Process., IEEE, 2008, pp. 1–9. [Google Scholar]

20. D. S. Johnson and L. A. McGeoch, “The traveling salesman problem: A case study,” in Local Search in Combinatorial Optimization. Princeton: Princeton University Press, 1997, pp. 215–310. [Google Scholar]

21. Saifullah, Z. Ren, K. Hussain, and M. Faheem, “K-means online-learning routing protocol (K-MORP) for unmanned aerial vehicles (UAV) adhoc networks,” Ad Hoc Netw., vol. 154, no. 2, 2024, Art. no. 103354. doi: 10.1016/j.adhoc.2023.103354. [Google Scholar] [CrossRef]

22. M. Upmanyu, A. M. Namboodiri, K. Srinathan, and C. Jawahar, “Efficient privacy preserving k-means clustering,” in Intell. Secur. Inform.: Pacific Asia Workshop, PAISI 2010, Hyderabad, India, Springer, 2010, pp. 154–166. [Google Scholar]

23. S. K. Singh, P. Kumar, and J. P. Singh, “A survey on successors of leach protocol,” IEEE Access, vol. 5, pp. 4298–4328, 2017. doi: 10.1109/ACCESS.2017.2666082. [Google Scholar] [CrossRef]

24. A. Manjeshwar and D. P. Agrawal, “TEEN: Arouting protocol for enhanced efficiency in wireless sensor networks,” in Proc. 15th Int. Parallel Distr. Process. Symp., IPDPS 2001, San Francisco, CA, USA, 2002, pp. 2009–2015. doi: 10.1109/IPDPS.2001.925197. [Google Scholar] [CrossRef]

25. M. Tripathi, M. S. Gaur, V. Laxmi, and R. Battula, “Energy efficient leach-c protocol for wireless sensor network,” in Third Int. Conf. Comput. Intell. Inf. Technol. (CIIT 2013), Mumbai, India, 2013, pp. 402–405. doi: 10.1049/cp.2013.2620. [Google Scholar] [CrossRef]

26. L. Liu, P. Guo, J. Zhao, and N. Li, “An improved leach protocol in wireless sensor networks,” Appl. Mech. Mater., vol. 743, pp. 748–752, 2015. doi: 10.4028/www.scientific.net/AMM.743.748. [Google Scholar] [CrossRef]

27. A. S. Al-Zubaidi, A. A. Ariffin, and A. K. Al-Qadhi, “Enhancing the stability of the improved-leach routing protocol for WSNs,” J. ICT Res. Appl., vol. 12, no. 1, pp. 1–13, 2018. doi: 10.5614/itbj.ict.res.appl.2018.12.1.1. [Google Scholar] [CrossRef]