AI-Enhanced Secure Data Aggregation for Smart Grids with Privacy Preservation

1  Introduction

The rise of smart grid technology marks a new era in power system management. By integrating advanced sensing and communication technologies, smart grids enable precise control over energy production, distribution, and consumption [1]. However, these advancements also introduce complexities in data management, particularly concerning data security and user privacy [2]. Although significant research has focused on data security and privacy protection within smart grids, existing solutions often focus on singular data types or isolated security mechanisms [3–5], making them insufficient for handling multi-source data integration and addressing evolving network threats. Therefore, a comprehensive approach is necessary for data aggregation in smart grids to manage data from various measurement points and devices while maintaining security and privacy [6].

Current technologies frequently compromise efficiency for security or lack comprehensive privacy protection. Ensuring data integrity and confidentiality is critical for maintaining user trust and system stability in smart grid applications [7]. Conversely, with the rapid growth of data volume, efficiently aggregating and analyzing this data while safeguarding user privacy has become an urgent challenge. To address these issues, this paper proposes an innovative artificial intelligence (AI)-assisted data aggregation strategy. The core of this research is the development of an AI-based multi-type data aggregation method, which effectively handles data from various modalities and protects user privacy during the aggregation process. By standardizing and normalizing the data, the approach eliminates scale and distribution discrepancies between different data sources, thereby enhancing aggregation efficiency. Additionally, Long Short-Term Memory (LSTM) [8] networks are introduced to process time-series data, extracting crucial features such as trends, seasonal characteristics, statistical metrics, and change points. These features are essential for pattern recognition, prediction, load analysis, and anomaly detection [9,10].

To further strengthen system security, we explore the application of Boneh-Lynn-Shacham (BLS) signatures for user authentication in smart grids. The efficiency and robustness of BLS signatures provide a secure user authentication mechanism, ensuring data integrity while protecting user privacy.

The final section of this paper demonstrates the practicality and security of the proposed scheme through rigorous security proofs and experimental analysis. These experiments validate the proposed method’s effectiveness in enhancing data aggregation efficiency and protecting user privacy. The specific contributions of this paper are as follows:

•   We propose a privacy-preserving scheme specifically designed for multiple types data aggregation, capable of aggregating various types of data. The scheme ensures data privacy through homomorphic encryption and leverages BLS signatures to verify user identity, as well as to ensure data integrity and confidentiality.

•   Our scheme extracts multiple time feature sequences from power consumption data, including trend features, seasonal features, statistical features, and change points. By employing LSTM to process these time feature sequences, the scheme efficiently facilitates pattern recognition, prediction, load analysis, and anomaly detection.

•   Security analysis and experimental results demonstrate that the proposed scheme effectively resists various attacks, ensuring both data security and the protection of user privacy.

2  Related Works

Gope et al. [11] designed a data aggregation scheme based on masking, utilizing lightweight primitives such as hash functions and exclusive OR operations to achieve efficient computation. However, the scheme cannot simultaneously ensure privacy protection and verifiable aggregation.

Bonawitz et al. [12] proposed a privacy-preserving scheme for multidimensional data aggregation, specifically designed for machine learning models. This scheme combines double blinding techniques with secure multiparty computation to ensure user privacy and verifiable aggregation. However, the scheme cannot guarantee fault tolerance for smart meter and aggregation gateway.

Wu et al. [4] designed a re-encryption-supported, verifiable homomorphic threshold proxy scheme. The scheme ensures system robustness through aggregation gateway clustering, allowing data aggregation to continue even if some aggregation gateways fail. However, it does not support aggregation of multiple types of data.

Zhan et al. [13] introduced an enhanced encryption algorithm that builds upon the foundational EC-ElGamal cryptosystem, incorporating a novel double live gate decryption approach. This algorithm exhibits homomorphic properties and facilitates data decryption and functional interrogation by SM and CC.

Yan et al. [14] proposed an efficient multi-task data aggregation scheme based on secret sharing, which can aggregate concurrent tasks from multiple requesters simultaneously. This scheme can aggregate different types of data uniformly and classify aggregation of the same type of data. However, the system needs to handle a large number of secret sharing interactions, which poses a significant burden on its performance.

Zhang et al. [15] proposed a multi-type data aggregation scheme based on homomorphic encryption and super-increasing sequences, allowing the control center to easily obtain aggregate values of different types of data. However, the scheme can only calculate the mean and variance of the same type of data and does not support finer-grained data analysis or the processing of multiple types data.

3  Problem Formalization

This chapter provides a detailed overview of the system model, threat model, and design goals. Additionally, the symbols used in this paper are explained in detail, as shown in Table 1.

3.1 System Model

The system model consists of three entities: smart meter (SM), aggregation gateway (AG), control center (CC) and trusted third party (TTP), as shown in Fig. 1.

•   SM is responsible for collecting various types of data, encrypting the collected data, and sending it to AG.

•   AG is responsible for aggregating data from different SMs and forwarding the summarized data to CC.

•   CC is responsible for processing the data, extracting time-series features, and implementing tasks such as load balancing and anomaly detection in the power grid.

•   TTP is responsible for distributing keys to other entities through secure channels.

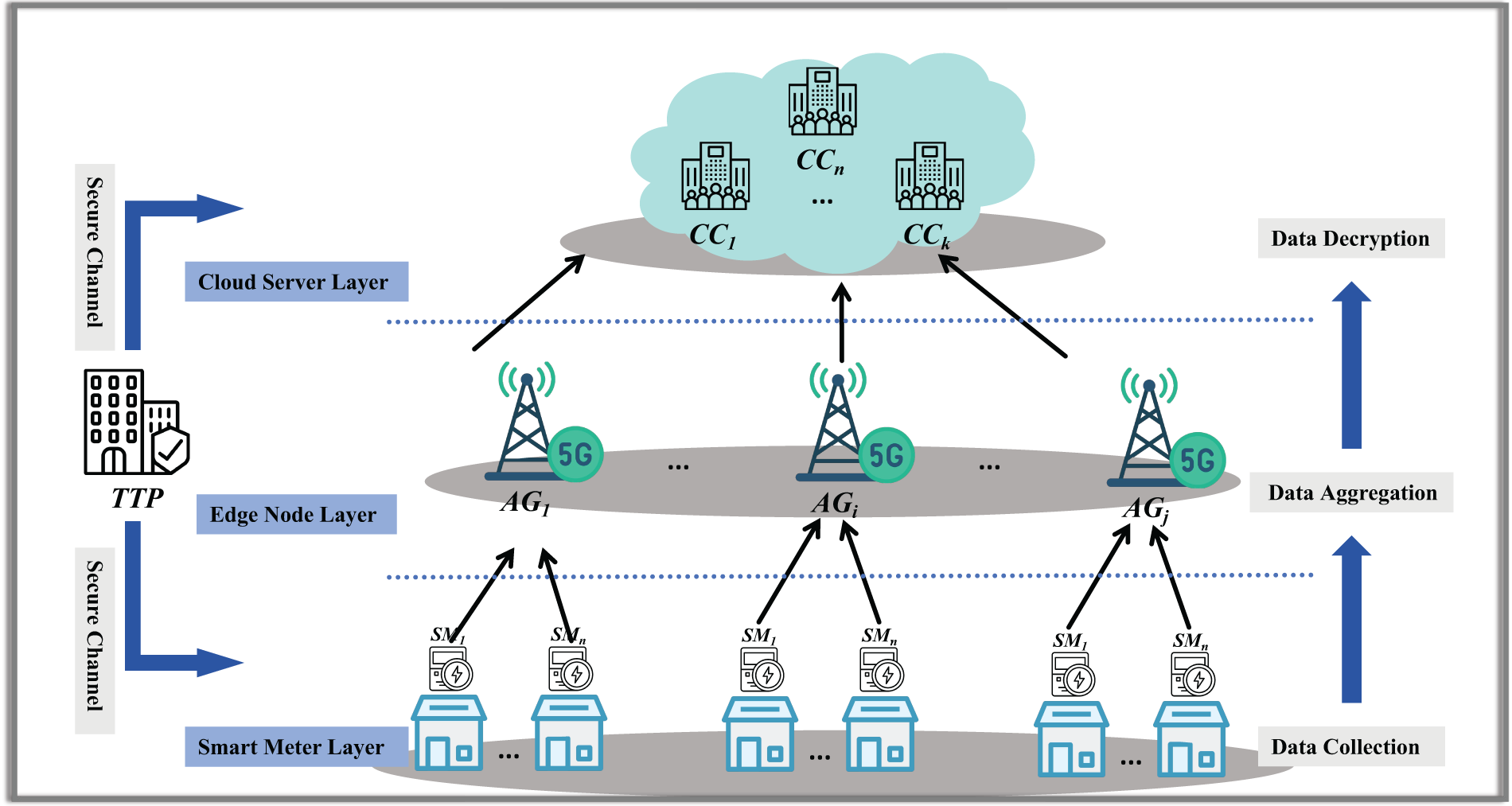
Figure 1: System model

3.2 Threat Model

In our system, we consider security threats posed by both internal and external attackers, and have constructed a threat model to address these two types of attacks.

Internal Attacks:

•   Threat from the AG: The AG operates honestly according to the instructions within the system, but it has a strong interest in the users’ data. Although the AG performs all operations as specified, it may attempt to extract sensitive information from the encrypted data.

•   Threat from the SM: Each SM is also honest yet curious, primarily interested in the data of other SMs. An SM might attempt to access data from other users. However, due to encryption protections and the isolation of critical information, the SM cannot access the plaintext data of other SMs.

•   Trust in the CC: The CC is considered a fully trusted entity within the system, responsible for key management and the final decryption of data. We assume that the CC does not engage in any improper actions with the data.

External Attacks:

•   Eavesdropping Attack: The attacker is passive, meaning that they can intercept and observe all communications between the SMs and the AG, but cannot alter or insert messages. The attacker’s goal is to recover plaintext from the intercepted ciphertext by passively listening to the communication between the SMs and the AG in an attempt to steal sensitive data.

•   Man-in-the-Middle Attack: The attacker acts as an intermediary, intercepting and modifying all messages between the two communicating parties. The attacker’s objective is to deceive one party by inserting their own public key or altering signatures, thereby impersonating one side of the communication to trick the other into accepting a forged signature.

•   Data Tampering and Replay Attack: The attacker may alter data during transmission or at its storage location, or they may intercept and save valid transmission data to replay it later in an attempt to deceive the system.

3.3 Design Goals

Our goal is to design a privacy-preserving scheme with efficient aggregation capabilities. Therefore, the following objectives must be met:

•   Security: The scheme must be able to resist various attacks as outlined in the threat model.

•   Efficiency: The scheme should balance computational load and system requirements effectively.

•   Functionality: The scheme should support various power grid functions, such as load forecasting and anomaly detection.

4  Preliminary

4.1 Paillier Cryptosystem

The Paillier cryptosystem is a homomorphic encryption method that allows operations on encrypted data. It supports adding two encrypted messages by multiplying their ciphertexts. The system consists of three main algorithms:

1.    Key Generation: KeyGen(1λ,p,q)→(pk,sk) produces a public key (N,g) and a private key (λ,μ) using a security parameter λ and two large primes p and q.

2.    Encryption: Encrypt(m,r)→c encrypts a message m with the public key and a random value r, resulting in a ciphertext c.

3.    Decryption: Decrypt(sk,c)→m retrieves the original message m from the ciphertext c using the private key.

4.2 Superincreasing Sequence

In this paper, a superincreasing sequence is an essential technique for handling multi-type data. This sequence consists of positive real numbers s1,s2,…, where each element is larger than the total sum of all preceding elements. Formally, it can be expressed as: sn+1>∑j=1nsj.

4.3 Composite Residuosity Problem (CRP) Assumption

Given a large integer N=qp, where p and q are large prime numbers, and an integer z∈ZN2, it is computationally difficult to determine whether z is a composite residuum modulo N. Specifically, the problem is to decide whether z belongs to ZN2∗ as a composite residuum, which is a hard computational task.

4.4 Computational Diffie-Hellman Problem (CDHP) Assumption

Given two elements g and ga in a bilinear group G, where a is a private key, and another element gb, it is computationally difficult to compute gab in polynomial time. Specifically, the problem is to determine the value of gab given g,ga and gb.

5  The Proposed Scheme

5.1 Overview

In summary, our goal is to propose an aggregation scheme that ensures both privacy protection and efficient load forecasting. To achieve this, we combine homomorphic encryption and BLS signature technologies. At the the SM level, the collected electricity usage data is encrypted to ensure data privacy and integrity. The encrypted data is then sent to the AG. Upon receiving encrypted data from multiple SMs, the AG first verifies the BLS signatures to ensure the security of user identity and the integrity of the data. Once the verification is successful, the AG aggregates all ciphertexts and signatures to generate aggregated ciphertext and signatures. Finally, the AG sends the aggregated ciphertext and signatures to the CC. The CC first verifies the correctness of the signatures, and once verified, decrypts the ciphertext to obtain the aggregated data. Subsequently, the CC uses a LSTM to train on the aggregated time series data, extract temporal features, and forecast future electricity usage. For various types of data, we employ the superincreasing sequence technique. Specifically, for each SMi, given k types of data (mi1,mi2,…,mik), a special superincreasing sequence is utilized, with each element satisfying the constraint: ω1=1, ωα>∑j=1α−1ωj(α=2,3,…,2k.j=1,2,…,k).

5.2 Initialization

The TTP begins by selecting two sufficiently large prime numbers p and q, and then computes N=p×q. The following parameter is then calculated: λ=lcm(p−1,q−1). Next, a random element g∈ZN2∗ is chosen, and the parameter μ is computed as follows: μ=(L(gλ mod N2))−1 mod N. Where the function L(x) is defined as: L(x)=x−1N. Finally, the TTP generates the public key pk=(N,g) and the private key sk=(λ,μ).

Let G1 and G2 be cyclic groups of prime order p, with generator g1 and g2. The bilinear map e is defined as G1∗G2→GT, where GT is another cyclic group of order p. The security hash function is denoted as H:{0,1}∗→G1. The TTP generates a superincreasing sequence consisting of 2k positive integers {ω1,…,ωk,ωk+1,…,ω2k}.

The TTP sends sk=(λ,μ) to CC via a secure channel, and respectively sends pk=(N,g) to SMi. The public parameters are represented as Ω=(G1,G2,GT,e,g1,g2,N,H,{ωα}1⩽α⩽2k).

5.3 Encryption

Data Encryption. The SMi selects a random number ri∈ZN2∗ and chooses x∈Z∗ as its private key. The corresponding public key is computed as y=g2x, where y∈G2. Thus, the public-private key pair for the signature is (x,y). The collected plaintext data mi is encrypted using the Paillier public key pk=(N,g). The ciphertext Ci is computed as follows:

Ci=gω1mi1+ωk+1mi12+ω2mi2+ωk+2mi22+…+ωkmik+ω2kmik2×riN( mod N2)(1)

where ri is a randomly chosen number, which ensures the randomness and security of each encryption.

Signature Generation. Using the BLS signature private key xi, the SM signs the ciphertext Ci along with the timestamp T. First, the ciphertext Ci and the timestamp T are combined and hashed using the hash function H to obtain the hash value H(Ci,T). The signature σ is then computed as: σ=gH(Ci,T) mod p. Where H is a hash function mapping the input to the group G1, and p is the order of the group G1.

Data Transmission. The SM sends the encrypted ciphertext Ci along with the corresponding signature σ to the AG.

5.4 Data Aggregation

Signature Verification. The AG first verifies the signatures using the BLS signature public key. For each received signature σi, AG computes the pairing equality e(σ,g)=e(yi,H(Ci,Ti)). Where e denotes the pairing function, yi is the public key associated with the signature, H is the hash function, Ci is the ciphertext, and Ti is the timestamp. The verification must hold true for all received signatures.

Data Aggregation. After successful verification of all signatures, AG aggregates the ciphertexts and signatures:

•   Compute the aggregated ciphertext C as:

C=∏i=1nCi mod N2=∏i=1ng∑j=1k(ωjmij+ωk+jmij2)⋅riN( mod N2)=g∑j=1k(ωj∑i=1nmij+ωk+j∑i=1nmij2)( mod N2)(2)

•   Compute the aggregated signature σ as σ=∑i=1nσi.

Transmission. AG then sends {C,σ} to the CC.

5.5 Decryption

Signature Verification. The CC begins by verifying the aggregated signature using the BLS signature verification process. Specifically, it checks the following pairing equality:

e(σ,g2)=∏i=1ne(υi,H(mi,T))(3)

where e denotes the pairing function, Ci is the individual ciphertext, and T is the timestamp. The verification must be successful for the aggregated signature to be considered valid.

Decryption of Aggregated Ciphertext. Upon successful verification of the signature, the CC proceeds to decrypt the aggregated ciphertext to obtain the aggregated result. The decryption process is as follows:

•   First, compute the intermediate value L(cλ mod N2) mod N. Where C is the aggregated ciphertext and λ is part of the Paillier private key.

•   Next, compute the final aggregation results R using the intermediate value and the Paillier decryption parameter μ:

R=∑j=1k(ωj∑i=1nmij+ωk+j∑i=1nmij2)=(L(cλ mod N2) mod Nμ) mod N(4)

    where μ is the decryption parameter from the Paillier private key. Thus, the CC could retrieve the aggregated multi-type data as R. Finally, the CC exploits Algorithm 1 to retrieve {M1,M2,…,Mk} and {RM1,RM2,…,RMk}, where Mj=∑i=1nmij, RMj=∑i=1nmij2 (j=1,2,…,k).

5.6 Load Forecasting

1.    Data Preprocessing. In our system, the SMs send data every fifteen minutes, allowing the CC to receive data at the same frequency. To ensure consistency of data across different time periods, the CC first preprocesses the data, which includes standardization and normalization. Standardization adjusts the data to have the same scale across different features, while normalization scales the data to a uniform range. This preprocessing ensures the accuracy and consistency of subsequent analyses.

•   Standardization: We treat each aggregated data point generated every fifteen minutes as an individual data point. To ensure that the data distribution has a mean of zero and a standard deviation of one, we standardize each data point. Specifically, we subtract the mean of the data from each data point and then divide by the standard deviation, as shown by the formula:

m′=m−τθ(5)

    where τ denotes the mean of the data, and θ denotes the standard deviation.

•   Normalization: After standardization, we further normalize the data by scaling it to the range [0,1] while preserving the relative distribution of the data. The normalization process involves subtracting the minimum value from the standardized data and then dividing by the range (i.e., the difference between the maximum and minimum values). The mathematical representation is given by:

m′′=m′−min(m′)max(m′)−min(m′)(6)

2.    Constructing Temporal Feature Sequences. In a smart grid system, load forecasting relies on extracting temporal features from historical data. The following temporal feature sequences can be derived from the data:

•   Trend Features: Utilize the long-term trend information from historical load data m(t) to identify changes in power demand trends. This feature is particularly crucial for long-term load forecasting.

•   Seasonal Features: Exploit periodic patterns in electricity usage (such as daily, weekly, and monthly usage patterns) to analyze load variations. For example, analyzing peak and off-peak load patterns within a day.

•   Statistical Features: Extract statistical features from the data, such as mean, variance, skewness, and kurtosis. These features help identify regular patterns and anomalies in electricity usage. The mean and variance are computed as follows:

avg=1T∑t=1Tm(t)(7)

avg=1T∑t=1T(m(t)−avg)2(8)

3.    Constructing the LSTM Model.

•   Input Layer: The processed temporal feature sequence X=x1,x2,…,xT is fed into the LSTM network, with the input sequence length being T.

•   Hidden Layer: The LSTM hidden layer recursively processes the input sequence and propagates information through time. The update formula for the hidden state ht at each time step t is given by:

ht=ξ(WhWt−1+Wxxt+b)(9)

     where Wh and Wx are weight matrices, b is the bias term, and ξ is the activation function (such as ReLU or sigmoid).

•   Output Layer: The output layer of the LSTM generates the load forecast results. The predicted load value is given by:

y^t+1=W0ht+b0(10)

     where W0 is the output weight matrix and b0 is the output bias.

4.    Training the Model. We use historical data as the training set and select Mean Squared Error (MSE) as the loss function to minimize the difference between predicted and actual values. The loss function is expressed as:

MSE=1N∑i=1N(y^i−yi)2(11)

       where y^i represents the model’s predicted value, yi denotes the actual value, and N is the number of samples. We adjust the model parameters using backpropagation and gradient descent algorithms until the model converges, meaning that the loss function reaches its minimum value.

5.    Implementing Load Forecasting. We use the trained LSTM model to predict future power grid loads. By inputting the latest time series data X=x1,x2,…,xT, the model can forecast the load for the next time step T+1 as y^T+1=W0hT+b0. Through rolling predictions, we can continuously predict multiple future time steps (e.g.,T+2,T+3,etc.) by incorporating each new prediction into the input sequence after each forecast.

hT+1=ξ(WhhT+Wxy^T+1+b))(12)

y^T+2=W0hT+1+b0(13)

h(T+2)=ξ(WhhT+1+Wxy^T+2+b)(14)

y^T+3=W0hT+2+b0(15)

      We use trend feature sequences for long-term forecasting, while seasonal feature sequences are suited for short-term and mid-term predictions. Additionally, statistical feature sequences serve as supplementary information, helping the model better understand the data’s distribution and variability, thereby enhancing the accuracy and robustness of the predictions.

6  Security Analysis

Based on the threat model, this section will prove the security of our scheme from both internal and external attack perspectives.

6.1 Internal Attacks

Theorem 1. No SM can obtain data from other SMs.

Proof. In our scheme, each SM encrypts its data using the Paillier homomorphic encryption algorithm. Even if a malicious SM intercepts encrypted data from other SMs during transmission, it cannot decrypt this data without the private key due to the security of the Paillier encryption algorithm. The security of Paillier encryption relies on the difficulty of the Composite Residuosity Problem (CRP), which ensures the ciphertext’s security in the absence of key disclosure. Since decryption requires the private key, which is securely stored only in the CC, no SM can access the plaintext data of other SMs.

Theorem 2. The AG cannot obtain the plaintext of aggregated data.

Proof. In our scheme, the AG performs data aggregation using homomorphic multiplication, meaning that the aggregated result remains encrypted. Additionally, public and private keys are separated in the scheme: the AG only possesses the public key for encryption operations, while the decryption private key is securely stored by the CC. Therefore, even though the AG can perform aggregation operations, it cannot decrypt any individual data or the aggregated data’s plaintext due to the lack of the private key. This design ensures that the AG cannot access sensitive information throughout the data processing.

6.2 External Attacks

Theorem 3. The proposed scheme is indistinguishable under chosen plaintext attack (IND-CPA).

Proof. Suppose there exists a polynomial-time adversary A capable of breaking the IND-CPA security of the Paillier encryption scheme, meaning A can distinguish between the ciphertexts of two plaintexts m0 and m1 with non-negligible probability.

Setup: The challenger prepares a Composite Residuosity Problem (CRP) instance by generating N=qp, where p and q are large primes, and selecting an element z∈ZN2. The task is to determine whether z is a composite residue modulo N2 without knowing the factorization of N. The challenger B provides A with the public key (N,g) of the Paillier cryptosystem, where g is a generator of ZN2∗.

Challenge: The A chooses two distinct plaintexts m0 and m1 and submits them to B. The challenger randomly selects a bit b∈{0,1} and computes the ciphertext:

c∗=gmb⋅rN mod N2(16)

The resulting ciphertext c∗ is sent back to A.

H-query: The B answers any hash queries made by A during the process. To do this, the B keeps a list H of queried messages and their corresponding hash outputs. If a hash query is repeated, the same result is returned; otherwise, a new value is randomly selected and recorded in H.

Response: The A eventually outputs a guess b′ for the bit b. The adversary succeeds if b′=b.

Probability analysis: Let the advantage of the adversary be defined as:

AdvA=|Pr[b′=b−12]|>ε(17)

where ε is non-negligible. This advantage implies that A can use the information from the ciphertext to make a correct guess more frequently than random chance. If A succeeds with a probability significantly better than 12, then B can leverage this success to solve the CRP by distinguishing whether z is a composite residue, which contradicts the assumption that this problem is hard to solve without factorizing N. Therefore, the probability that A can distinguish m0 and m1 must be close to random guessing: Pr[b′=b]≈12, making AdvA negligible.

Conclusion: Thus, the existence of such an adversary would contradict the intractability of the CRP, proving that the scheme remains secure against chosen plaintext attacks.

Theorem 4. The proposed scheme is unforgeable under chosen message attack (UF-CMA).

Proof. Assume there exists a polynomial-time adversary A capable of successfully executing a man-in-the-middle attack, meaning the A can forge BLS signatures and deceive the communicating parties into accepting the forged signature. In the proposed scheme, the signature is computed as σ=gH(Ci,T). Based on the capabilities of the adversary A, we can construct an algorithm B to solve the Computational Diffie-Hellman Problem (CDHP). The B receives a CDHP instance, specifically the elements g,ga, and gb in G, and attempts to compute gab by leveraging A’s man-in-the-middle attack capabilities.

Setup: The B places A in the middle of the communication process, allowing A to intercept, modify messages, and generate forged signatures. Specifically, the B generates a random number r and sends the generator g and the public key y=gx to A. Additionally, a random j∈{1,2,…,qH} is chosen as the guesse.

H-query: The B attempts to exploit A’s attack behavior, using the forged signatures to construct a valid solution to the CDHP, specifically to compute gab. To achieve this, the B creates an empty table to store the results of hash queries, with elements of the form (Ci,T,yi,bi). When A initiates the i-th (i∈[1,qH]), the response is provided as follows:

1)   If the tuple (ci,T,yi,bi) already exists in the Hlist corresponding to ci, then respond with yi.

2)   If it does not exist, randomly select a bi←Zq and proceed accordingly.

⋅ If i=j, compute h=yi⋅gybi=gyxi+bi∈G.

⋅ Otherwise, compute h=gbi∈G.

3)   Answer the query by using υi as the response for this query and store the tuple (mi,Ti,υi,bi) in the table.

Query: When A requests a signature for a message, identify i such that c=ci and T=Ti, where (ci,Ti) represents the query value of the i-th H query. Respond as follows:

1)   If i≠j, there exists a tuple (ci,Ti,yi,bi) in Hlist. Calculate σi=(yigr)bi to respond with σi. Due to σi=(yigr)bi=gbi(xi+r).

2)   If i=j, the process is aborted.

Forgery: A output is ((c,T),σ). If (c,T)≠(cj,Tj), the B aborts the game; otherwise, outputs h=gxi+bi.

The A returned a forged signature with an unverified message c. If message c is not the i-th message in the hash table, it will be aborted. According to the signature definition, σ=gbi(xi+r). Simulator B calculation σgrbi=gxbi+rbigrbi=gxbi.

Conclusion: As shown above, B can leverage A’s capabilities to solve the CDHP, which would imply that A can successfully carry out a man-in-the-middle attack and forge valid signatures. However, since the CDHP is intractable in polynomial time, this contradicts our assumption that A is an effective adversary. Therefore, we have proven that the proposed scheme is secure under the UF-CMA model; based on the CDHP assumption, an attacker cannot successfully forge BLS signatures or obtain the private key through a man-in-the-middle attack.

Theorem 5. The proposed scheme is secure against data tampering and replay attacks.

Proof. The attacker may attempt to tamper with data during transmission or at its storage location, or they may intercept and save valid transmission data to replay it later to deceive the system. To defend against such threats, our scheme incorporates timestamps in each data packet. The AG verifies the validity of these timestamps upon receiving data packets and rejects any data packets with expired timestamps. Furthermore, since BLS signatures are associated with both the data content and its timestamp, any replayed data with an outdated timestamp will result in invalid signatures, thereby preventing the system from accepting tampered or replayed data.

7  Performance Evaluation

In this chapter, we analyze the performance of the proposed scheme by evaluating both computational and communication overheads, and we also conducted load prediction experiments.

7.1 Computation Overhead

In our proposed scheme, the SM collects data every fifteen minutes and first encrypts the data, which requires one modular multiplication and two modular exponentiation operations. Next, the generated ciphertext is signed using a BLS signature, which involves one hash operation and one elliptic curve point multiplication. Simple addition operations are disregarded in this context. In comparison, Chen et al. [16]’s scheme requires the SM to perform one modular multiplication, three modular exponentiations, one bilinear pairing, and one hash operation. Liu et al. [17]’s scheme requires the SM to perform one exponentiation, three modular multiplications, and one hash operation. Zhang et al. [15]’s scheme requires the SM to perform three modular multiplications, three modular exponentiations, and three hash operations. As shown in Fig. 2, our scheme demonstrates the lowest computational overhead for the SM.

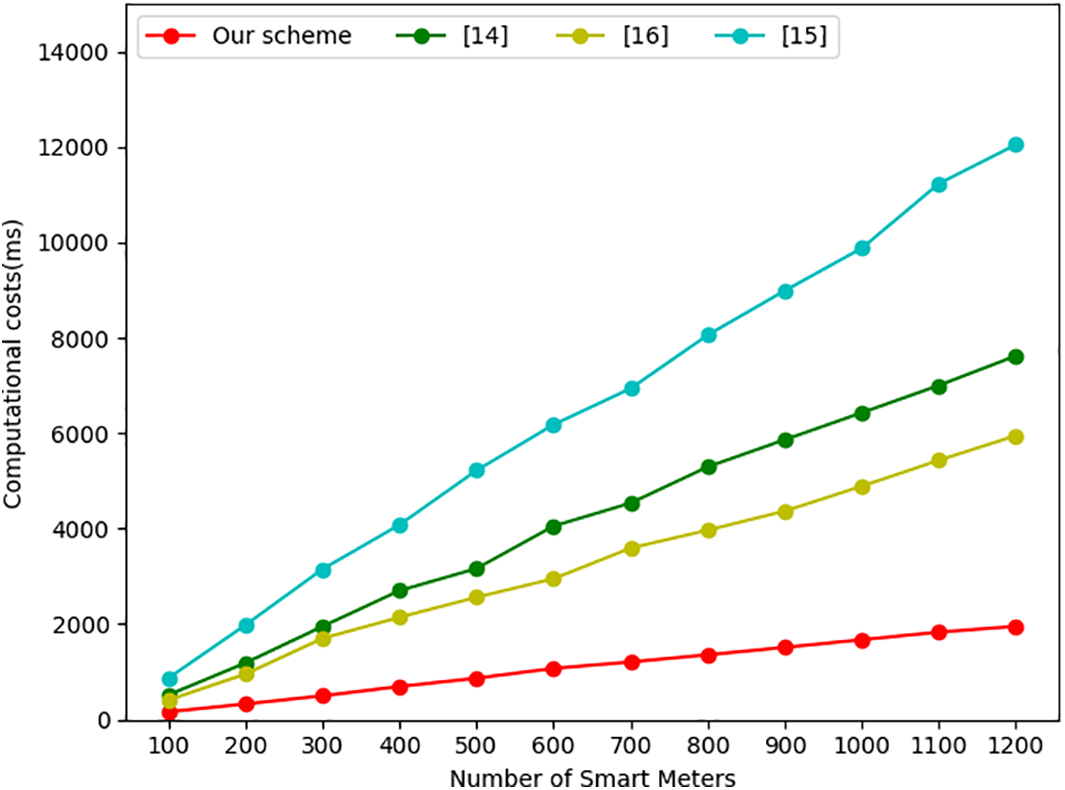
Figure 2: The computational cost of SM end

In our proposed scheme, the AG needs to perform n+1 hash operations, n bilinear mappings, and one multiplication operation. In comparison, Chen et al. [16]’s scheme requires the AG to perform n+1 bilinear pairings, 4(n+1) modular multiplications, and n+1 hash operations. Liu et al. [17]’s scheme requires the AG to perform 2(n−1) modular multiplications, n+1 hash operations, n+1 bilinear pairings, and n+1 elliptic curve additions. Zhang et al. [15]’s scheme requires the AG to perform n+1 modular exponentiations, 4n−2 modular multiplications, and one hash operation. As shown in Fig. 3, although our scheme has slightly higher computational overhead on the AG compared to Liu et al. [17], it remains within an acceptable range.

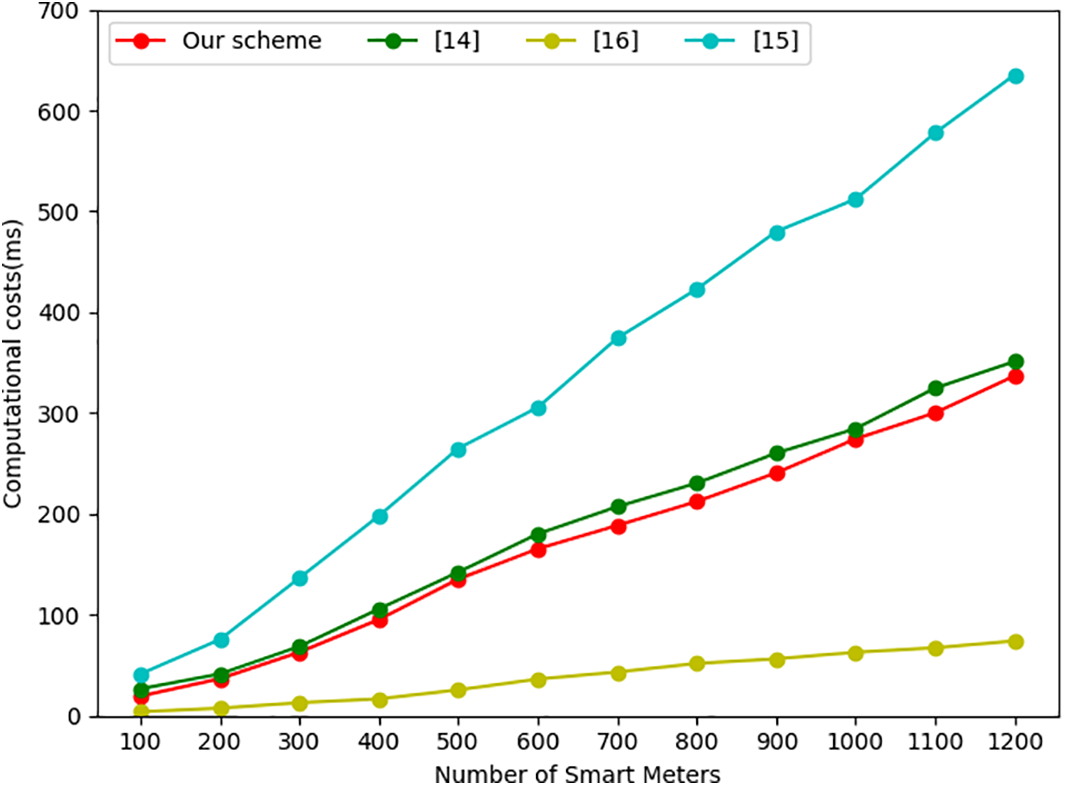
Figure 3: The computational cost of AG end

In the data decryption process of our scheme, the CC only needs to verify a single aggregated signature and decrypt the aggregated ciphertext. The CC in other schemes also performs these two operations, resulting in comparable computational overhead. Additionally, the CC can perform various other data operations, such as load prediction, calculating the mean, and variance, making it difficult to fairly compare the computational overhead across different schemes. Therefore, we did not separately list the CC’s computational overhead but instead provided a comparison of the total computational overhead for data aggregation across the three entities. As shown in Fig. 4, our scheme also leads in terms of total computational overhead.

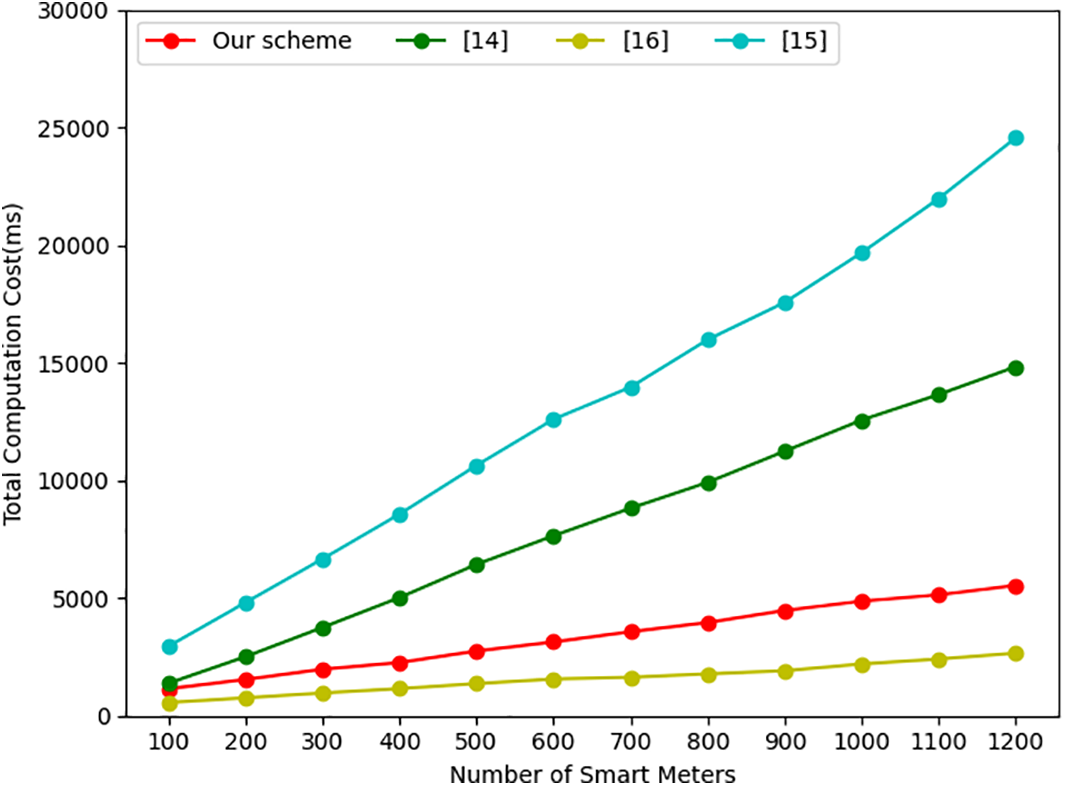
Figure 4: Total computational cost

7.2 Communication Overhead

In our proposed scheme, the smart meter (SM) needs to transmit a timestamp T, ciphertext ci, and a BLS signature σ. The timestamp occupies 64 bits, the Paillier-encrypted ciphertext is 2048 bits, and the BLS signature is 256 bits. Therefore, the communication overhead is 8n bytes(T)+256n bytes(c)+32n bytes(σ)=296n bytes. In comparison, Chen et al. [16]’s scheme has a communication overhead of 8n bytes(Id) + 8n bytes(T)+256n bytes(c)+32n bytes(σ)=304n bytes. Liu et al. [17]’s scheme requires 8n bytes(Id)+8n bytes(T)+256n bytes(c1)+256n bytes(c2)+32n bytes(σ)=656n bytes. Zhang et al. [15]’s scheme has a communication overhead of 8n bytes(T)+256n bytes(c)+64n bytes(σ)=328n bytes. The specific details are shown in Fig. 5.

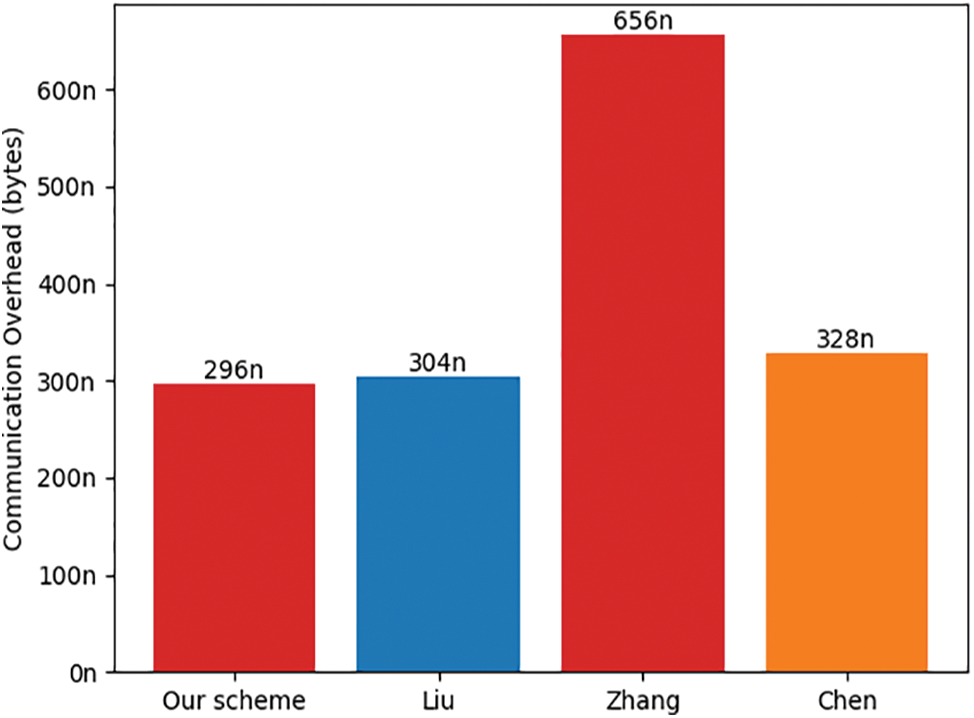
Figure 5: Communication overhead

7.3 Load Forecasting

We primarily employed the LSTM model to assess the performance of electric load forecasting. The dataset utilized was sourced from the public LibSVM dataset repository, specifically the dataset [18], which encompasses 45,781 data points, with each data point representing the electricity consumption for a one-hour period. Our approach involved the use of 100,000 data points as simulated data, where each data point corresponds to the electricity consumption collected over a fifteen-minute interval. As our focus was on forecasting aggregated electricity usage rather than predicting data for individual time points, the division of hourly consumption into four fifteen-minute intervals did not affect the ultimate results of our experimental analysis. The data were first normalized to the range of [0, 1]. In our experiment, we set the number of units in the LSTM layer to 50, with 100 training epochs and a batch size of 32. After training, the model was used to predict the data for future time periods, ranging from 1 to 10 periods ahead, with each period containing 100 data points. As shown in Fig. 6, our historical sample data size increased from 0 to 10,000, while the predicted data size ranged from 200 to 1000. The results demonstrate that the model achieved an accuracy close to 0.99 for both single-period and multi-period aggregated data forecasts.

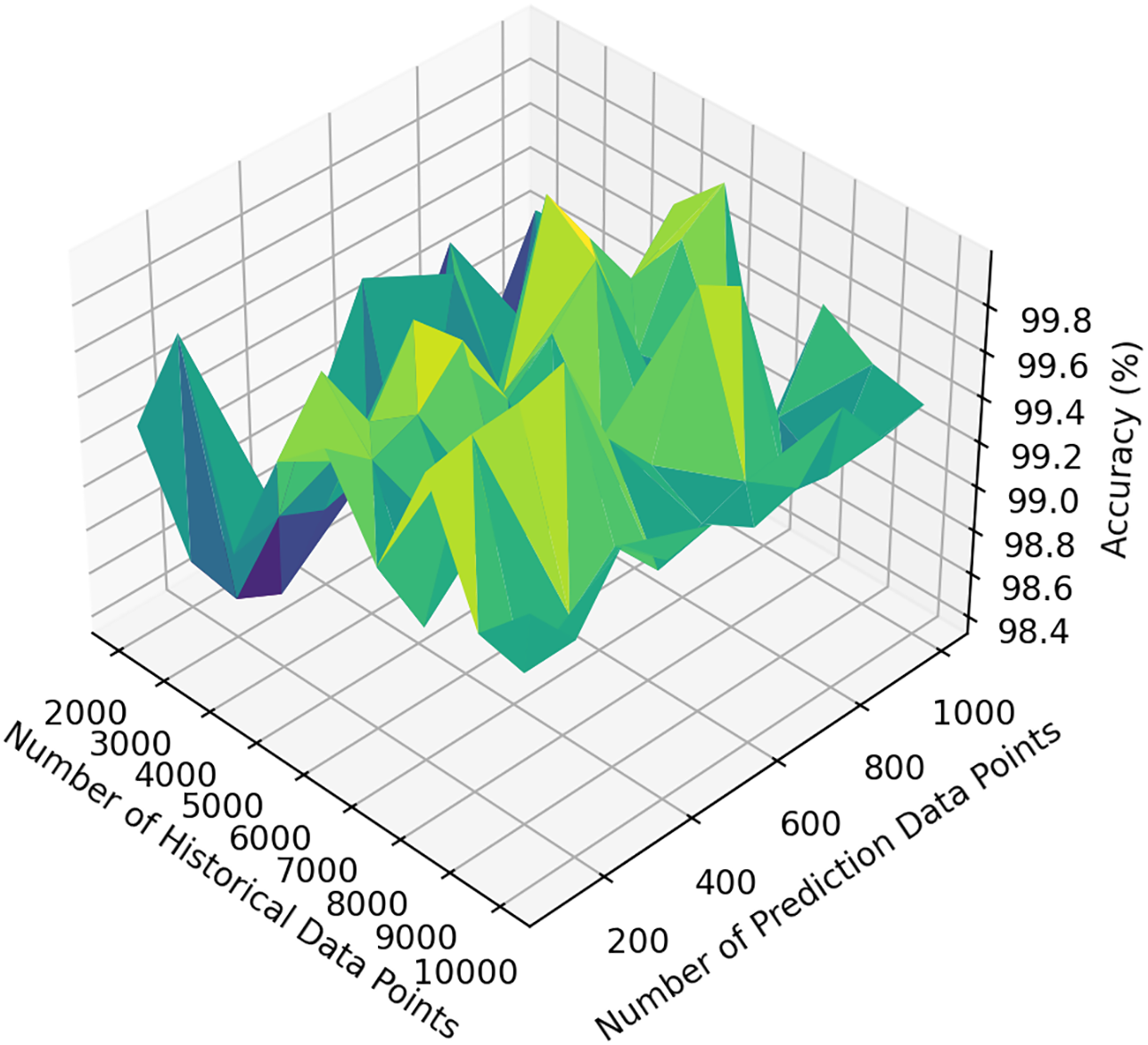
Figure 6: Load forecasting

As shown in Fig. 7, we fixed the prediction data size at 1000 points while gradually increasing the size of the historical data samples, ranging from 0 to 10,000 points. The results indicate that when the historical data falls within the ranges of 0 to 50,000 and 50,000 to 100,000, the accuracy generally exhibits a trend of initial decline followed by an increase. This trend may be related to seasonal variations, as electricity usage in spring and autumn is relatively equal, while consumption in summer and winter is significantly higher, with summer usage exceeding that of winter. The 1000 data points can be considered as the electricity consumption of a single user over ten days, with the smart grid collecting data every 15 min, resulting in 96 data points collected per day. A historical dataset comprising 18,000 points roughly corresponds to the total electricity usage during spring and summer. Using this data to predict the next ten days yields the highest accuracy. As the historical data gradually increases to 30,000 points, which represents the total electricity consumption during spring, summer, and autumn, the prediction accuracy for the next ten days decreases. However, when the historical data reaches 40,000 points, corresponding to the total electricity usage across all four seasons, the prediction accuracy gradually increases. Given that summer usage in the first half of the year is higher than winter usage, the accuracy peaks as the historical data approaches 50,000 points, displaying a cyclical pattern. The subsequent range of historical data from 50,000 to 100,000 points shows another cyclical change, maintaining the overall trend of initial decline followed by an increase. The average accuracy can exceed 80%. Notably, when the historical data sample consists of 20,000 points, the model achieves its highest prediction accuracy, approaching 100%. This is likely due to the use of half a year’s electricity data to predict consumption over the next ten days. After this point, the accuracy began to improve, which may be related to seasonal variations. Notably, when the historical data sample size was 20,000 points, the model’s prediction accuracy was highest, approaching 100%.

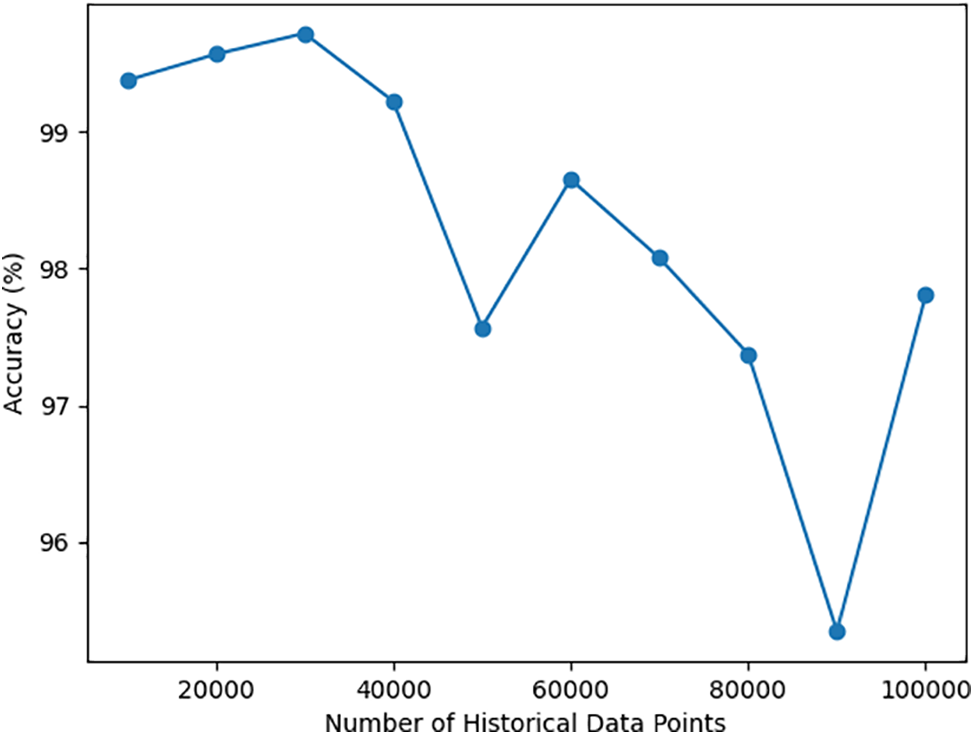
Figure 7: 1000 predicted data

Therefore, as shown in Fig. 8, we fixed the historical training data size at 20,000 points and gradually increased the predicted data size from 0 to 10,000 points. The results demonstrate that the prediction accuracy could be maintained around 0.99. This indicates that in our approach, using 20,000 historical data points for training can effectively predict the total electricity consumption in a region with approximately 10,000 users. This capability can contribute to better energy planning and management, as well as emergency preparedness.

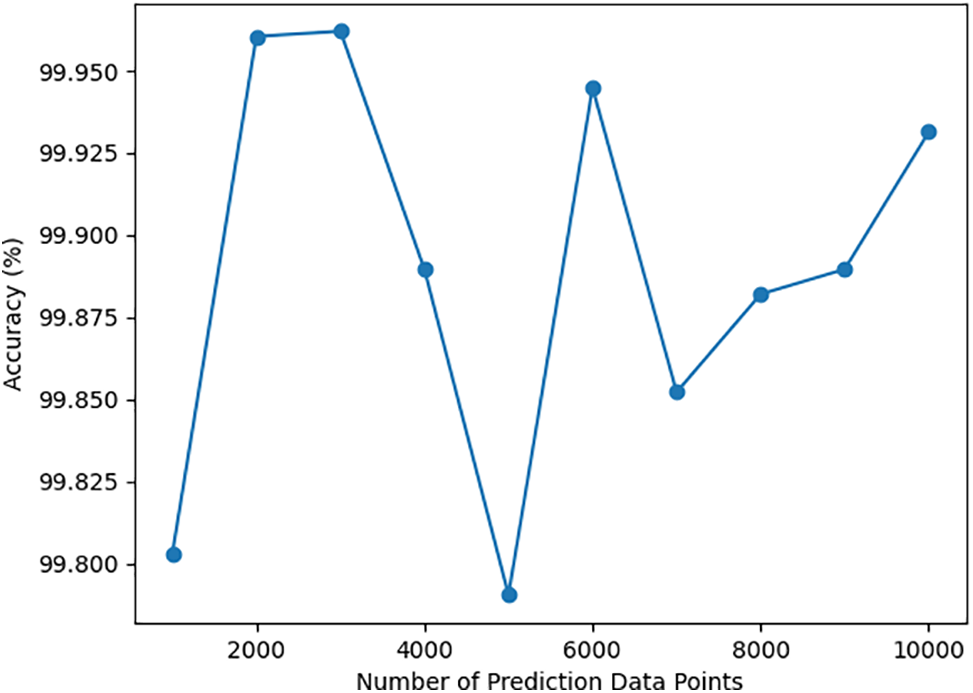
Figure 8: 20,000 historical data

8  Conclusion

This paper introduces an AI-assisted data aggregation scheme for smart grids, integrating homomorphic encryption and BLS signatures for secure data processing and robust authentication. LSTM networks efficiently handle time-series data, enabling effective load analysis and forecasting. The approach balances security, privacy, and performance, with experimental results confirming its effectiveness and resistance to attacks. Future work will extend the scheme to distributed environments for better scalability and fault tolerance and refine LSTM networks to improve prediction accuracy and adapt to diverse consumption patterns.

Acknowledgement: The authors are highly thankful to the National Natural Science Foundation of China.

Funding Statement: The work is supported by the National Key R&D Program of China (No. 2023YFB2703700), the National Natural Science Foundation of China (Nos. U21A20465, 62302457, 62402444, 62172292), the Fundamental Research Funds of Zhejiang Sci-Tech University (Nos. 23222092-Y, 22222266-Y), the Program for Leading Innovative Research Team of Zhejiang Province (No. 2023R01001), the Zhejiang Provincial Natural Science Foundation of China (Nos. LQ24F020008, LQ24F020012), the Foundation of State Key Laboratory of Public Big Data (No. [2022]417), and the “Pioneer” and “Leading Goose” R&D Program of Zhejiang (No. 2023C01119).

Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: Congcong Wang, Chen Wang; data collection: Wei Gu, Wenying Zheng; analysis and interpretation of results: Chen Wang, Wenying Zheng; draft manuscript preparation: Congcong Wang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are openly available in University of California, Irvine (UCI) Machine Learning Repository at https://doi.org/10.24432/C5KP4K (accessed on 22 October 2024).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Z. Bao, C. Tang, F. Lin, Z. Zheng, and X. Yu, “Rating-protocol optimization for blockchain-enabled hybrid energy trading in smart grids,” Sci. China Inf. Sci., vol. 66, no. 5, 2023, Art. no. 159205. doi: 10.1007/s11432-021-3390-7. [Google Scholar] [CrossRef]

2. J. Shen, H. Yang, P. Vijayakumar, and N. Kumar, “A privacy-preserving and untraceable group data sharing scheme in cloud computing,” IEEE Trans. Dependable Secur. Comput., vol. 19, no. 4, pp. 2198–2210, 2022. doi: 10.1109/TDSC.2021.3050517. [Google Scholar] [CrossRef]

3. C. Wang, T. Zhou, J. Shen, W. Wang, and X. Zhou, “Searchable and secure edge pre-cache scheme for intelligent 6G wireless systems,” Future Gener. Comput. Syst., vol. 140, no. 3, pp. 129–137, 2023. doi: 10.1016/j.future.2022.10.012. [Google Scholar] [CrossRef]

4. L. Wu, S. Fu, Y. Luo, H. Yan, H. Shi and M. Xu, “A robust and lightweight privacy-preserving data aggregation scheme for smart grid,” IEEE Trans. Dependable Secur. Comput., vol. 21, no. 1, pp. 270–283, 2024. doi: 10.1109/TDSC.2023.3252593. [Google Scholar] [CrossRef]

5. J. Zhang and C. Dong, “On the security of lightweight and escrow-free certificate-based data aggregation for smart grid,” IEEE Trans. Dependable Secur. Comput., vol. 21, no. 3, pp. 1242–1243, 2024. doi: 10.1109/TDSC.2023.3275972. [Google Scholar] [CrossRef]

6. C. Yan, C. Wang, J. Shen, K. Dev, M. Guizani and W. Wang, “Edge-assisted hierarchical batch authentication scheme for vanets,” IEEE Trans. Veh. Technol., vol. 73, no. 1, pp. 1253–1262, 2024. doi: 10.1109/TVT.2023.3305556. [Google Scholar] [CrossRef]

7. Z. Zhang and S. Link, “Mixed covers of keys and functional dependencies for maintaining the integrity of data under updates,” Proc. VLDB Endow., vol. 17, no. 7, pp. 1578–1590, 2024. doi: 10.14778/3654621.3654626. [Google Scholar] [CrossRef]

8. A. Cura, H. Küçük, E. Ergen, and I. B. Öksüzoglu, “Driver profiling using long short term memory (LSTM) and convolutional neural network (CNN) methods,” IEEE Trans. Intell. Transp. Syst., vol. 22, no. 10, pp. 6572–6582, 2021. doi: 10.1109/TITS.2020.2995722. [Google Scholar] [CrossRef]

9. T. N. A. Nguyen, N. N. Anh, T. N. Thang, V. K. Solanki, R. G. Crespo and N. Q. Dat, “Online SARIMA applied for short-term electricity load forecasting,” Appl. Intell., vol. 54, no. 11–12, pp. 1003–1019, 2024. doi: 10.1007/s10489-023-05230-y. [Google Scholar] [CrossRef]

10. M. Garralda-Barrio, C. Eiras-Franco, and V. Bolón-Canedo, “A novel framework for generic spark workload characterization and similar pattern recognition using machine learning,” J. Parallel Distributed Comput., vol. 189, no. 1, 2024, Art. no. 104881. doi: 10.1016/j.jpdc.2024.104881. [Google Scholar] [CrossRef]

11. P. Gope and B. Sikdar, “Lightweight and privacy-friendly spatial data aggregation for secure power supply and demand management in smart grids,” IEEE Trans. Inf. Forensics Secur., vol. 14, no. 6, pp. 1554–1566, 2019. doi: 10.1109/TIFS.2018.2881730. [Google Scholar] [CrossRef]

12. K. A. Bonawitz et al., “Practical secure aggregation for privacy-preserving machine learning,” in Proc. 2017 ACM SIGSAC Conf. Comput. Communicati. Security, CCS 2017, Dallas, TX, USA, ACM, 2017, pp. 1175–1191. [Google Scholar]

13. Y. Zhan, L. Zhou, B. Wang, P. Duan, and B. Zhang, “Efficient function queryable and privacy preserving data aggregation scheme in smart grid,” IEEE Trans. Parallel Distr. Syst., vol. 33, no. 12, pp. 3430–3441, 2022. doi: 10.1109/TPDS.2022.3153930. [Google Scholar] [CrossRef]

14. X. Yan, W. W. Y. Ng, B. Zhao, Y. Liu, Y. Gao and X. Wang, “Fog-enabled privacy-preserving multi-task data aggregation for mobile crowdsensing,” IEEE Trans. Dependable Secur. Comput., vol. 21, no. 3, pp. 1301–1316, 2024. doi: 10.1109/TDSC.2023.3277831. [Google Scholar] [CrossRef]

15. X. Zhang, C. Huang, Y. Zhang, and S. Cao, “Enabling verifiable privacy-preserving multi-type data aggregation in smart grids,” IEEE Trans. Dependable Secur. Comput., vol. 19, no. 6, pp. 4225–4239, 2022. doi: 10.1109/TDSC.2021.3124546. [Google Scholar] [CrossRef]

16. Y. Chen, J. -F. Martínez-Ortega, P. Castillejo, and L. López, “A homomorphic-based multiple data aggregation scheme for smart grid,” IEEE Sens. J., vol. 19, no. 10, pp. 3921–3929, 2019. doi: 10.1109/JSEN.2019.2895769. [Google Scholar] [CrossRef]

17. J. Liu, J. Weng, A. Yang, Y. Chen, and X. Lin, “Enabling efficient and privacy-preserving aggregation communication and function query for fog computing-based smart grid,” IEEE Trans. Smart Grid, vol. 11, no. 1, pp. 247–257, 2020. doi: 10.1109/TSG.2019.2920836. [Google Scholar] [CrossRef]

18. K. K. Kalyani, “Tamilnadu electricity board hourly readings,” UCI Mach. Learn. Rep., 2013. doi: 10.24432/C5KP4K. [Google Scholar] [CrossRef]