DIGNN-A: Real-Time Network Intrusion Detection with Integrated Neural Networks Based on Dynamic Graph

1  Introduction

Intrusion Detection Technology (IDT) monitors networks and systems to detect malicious activities or security policy violations to protect against unauthorized access, modification, and destruction. Its significance lies in real-time monitoring, security reinforcement, and event logging for timely threat detection and response [1]. The predominant methods are signature-based and rule-based techniques, which offer high accuracy and ease of management but struggle with detecting unknown threats and have high maintenance costs [2].

Artificial intelligence, notably machine learning, is increasingly used in Network Intrusion Detection Systems (NIDS), utilizing supervised, unsupervised, and semi-supervised learning to identify behavioral patterns [3–5]. Deep learning (DL) has further advanced NIDS by handling complex, large datasets with models such as convolutional neural networks (CNNs), recurrent neural networks (RNNs), and autoencoders (AE) [6–8]. Unlike traditional signature-based systems, machine learning-based NIDS offers automated feature extraction, adaptability, low false positives, and the ability to address zero-day attacks [9]. Deep learning techniques enhance detection accuracy and adaptability, making them highly effective for modern intrusion detection systems.

Despite advancements in intrusion detection, several research gaps remain unaddressed. Traditional deep learning methods, such as CNNs and RNNs, often fail to capture the intricate relationships between network nodes and the evolving interactions in network traffic. CNNs, though effective at modeling features like protocols and service categories, do not incorporate critical topological information about network structures. Similarly, RNNs excel in modeling traffic sequence features but overlook the complex interdependencies between communication flows over time. These limitations highlight the need for models integrating topological and temporal features to improve detection accuracy and robustness, particularly against sophisticated, evolving threats.

Recent focus has intensified on using Graph Neural Networks (GNNs) for intrusion detection, as the intrusion detection task benefits from the rich structural information inherent in network flow data, which can be directly encoded into graph formats [10]. Graph Neural Network (GNN) encode network flow data into graphs, showing network hosts and communication links as nodes and edges, highlighting host interactions. Various studies have explored modeling network traffic with different graph data forms to manage diverse attack characteristics and address complex patterns [11,12]. However, a critical limitation of traditional GNNs is their primary focus on node representations, often neglecting the rich information embedded in edges, which are crucial for accurately modeling communication flows and improving intrusion detection. Overcoming this challenge—specifically by optimizing edge representations—remains a crucial obstacle to fully realizing the potential of GNNs in network traffic analysis.

GNNs utilize static graphs to capture structural, topological, and edge attribute information efficiently, offering superior representation capabilities compared to flat data structures. Incorporating attention mechanisms into the message-passing process enhances the model’s ability to prioritize essential data and learn optimal vector representations from large-scale network data. However, dynamic graphs, with evolving structures or attributes, more accurately model complex network relationships, which is crucial for detecting sophisticated cyber-attacks, such as Advanced Persistent Threats (APTs) [13]. However, adequate data representation from dynamic graphs requires appropriate modeling techniques and algorithms. Existing GNN-based intrusion detection methods leverage the full spectrum of feature information from network traffic and host communication interactions to improve detection performance but treat all network traffic as static graph inputs, neglecting crucial temporal correlations between specific attack behaviors. To address this, recent studies [14] have adopted dynamic graphs with spatiotemporal features that capture additional information, particularly topological changes, which static graphs cannot. Despite this progress, challenges remain in generating edge embeddings for dynamic graphs and integrating advanced attention mechanisms.

Building on previous studies, we propose a novel dynamic integrated neural network with attention (DIGNN-A) for intrusion detection designed to address the critical challenges identified in existing methods. This model utilizes dynamic graphs as input, addressing the inherent limitations of static graphs in capturing the temporal evolution of network topology. To improve the spatial feature representation of graph data, we integrate graph convolution operations with multi-head attention mechanisms. Recognizing the significance of temporal and structural changes in dynamic graphs, we implement a hybrid approach combining integrated graph neural networks with line graphs, enabling efficient learning and capturing both temporal and spatial features from network traffic. The proposed DIGNN-A significantly enhances real-world intrusion detection by incorporating time evolution and attention mechanisms. It supports continuous network and system monitoring, rapid threat response, and protection for enterprises and critical infrastructure, crucial for traditional Information Technology (IT) security and emerging fields like Internet of Things (IoT), cloud computing, and industrial control systems. The key contributions of this paper are outlined as follows:

•   Modeling network traffic as a dynamic graph utilizing a line graph structure transforms the edge classification task into a node classification task while ensuring that the model remains unaffected by the changing structures and attributes of the dynamic graph. This approach facilitates the flexible representation of network traffic data in various sizes and forms for intrusion detection tasks. It can be applied to a broader range of graph neural network scenarios.

•   During the message-passing phase, a graph convolution operation with an attention mechanism allows the model to assign weights to messages from various neighbors. This improves the processing of complex messages and enhances overall performance.

•   An innovative integrated graph neural network is deployed to process dynamic graph inputs, learning a sequence-to-sequence representation of a succession of graph snapshots. This approach effectively captures the temporal and spatial information inherent in the graph data, enabling it to execute intricate intrusion detection tasks on dynamic graphs precisely.

•   Two public intrusion detection datasets were subjected to experimental analysis, and the results indicate that the proposed NIDS model demonstrates a slight superiority over existing methods in key metrics, including detection accuracy and the F1-score.

The remainder of the paper is organized as follows: Section 2 reviews related work. Section 3 presents the proposed NIDS methodology. Section 4 describes the experimental setup and evaluation metrics. Section 5 provides a comparative analysis of the results and ablation study. Finally, Section 6 summarizes the findings and suggests future research directions.

2  Related Works

2.1 DL-Based NIDSs

Inspired by deep learning frameworks in computer vision [15] and natural language processing (NLP) [16], recent research has increasingly utilized deep learning-based methods to analyze structured network traffic data from the outset. These methods leverage deep learning’s capacity to handle large, high-dimensional datasets, thus overcoming many limitations of traditional NIDS.

For example, Al-Turaiki et al. [17] introduced a two-step preprocessing approach combining dimensionality reduction and feature engineering within convolutional neural network architectures to enhance anomaly-based intrusion detection. Man et al. [18] proposed a model incorporating residual learning to address potential performance degradation in deep networks with many layers, along with an enhanced focal loss function to address category imbalance in the training set, improving the model’s ability to detect infrequent categories. Al-Haija et al. [19] developed an ensemble learning model using AdaBoost, RUSBoost, and bagged models for botnet detection in IoT networks. The ensemble achieved superior performance with a 99.60% detection rate, surpassing the individual classifiers.

Imrana et al. [20] identified high false alarm rates and difficulties detecting specific attacks like User-to-Root and Remote-to-Local as major limitations of traditional intrusion detection systems. To overcome these, researchers proposed a Bidirectional Long-Short-Term-Memory (Bi-LSTM) based intrusion detection system to capture temporal features. Sinha et al. [21] enhanced this by integrating CNN and Bi-LSTM for better spatial and temporal feature recognition. Cao et al. [22] developed a model combining CNN and Gated Recurrent Unit (GRU), utilizing hybrid and adaptive synthetic sampling for data imbalance and integrating Random Forest with Pearson correlation for feature selection. An attention mechanism assigns feature weights, reducing computational cost and improving performance, effectively addressing multi-class classification and class imbalance in intrusion detection.

While deep learning-based approaches have advanced intrusion detection, they struggle to model intricate network topologies and evolving traffic interactions. These methods focus on internal data characteristics, like communication ports and protocols, treating each traffic piece discretely and neglecting correlations, which reduces detection accuracy. Additionally, they often overlook network topology modeling, hindering the detection of attacks with distinct network patterns, such as Cross-Site Request Forgery (CSRF) and Distributed Denial of Service (DDoS), and proving inadequate for complex, variable intrusion tactics.

2.2 NIDSs Based on GNN

GraphSAGE [23] is a graph neural network algorithm for large-scale graphs, utilizing sampling and aggregation strategies. It samples neighboring nodes, aggregates their information using different functions, and learns embedded node representations for classification tasks. E-GraphSAGE [10], proposed by Lo et al., extends GraphSAGE to generate edge embeddings by combining edge features and topological patterns. Since intrusion detection datasets focus on edge features, the algorithm initializes node features as vectors of 1. It performs IoT intrusion detection on four NetFlow datasets, demonstrating superior performance over traditional machine learning methods.

Anomal-E [24] presents a static graph-based unsupervised intrusion detection method combining E-GraphSAGE, improved Deep Graph Infomax (DGI), and four traditional anomaly detection algorithms. This is the first method to integrate graph learning with anomaly detection for network attacks. FT-GCN [11] enhances intrusion detection with limited labels and constructs interval-constrained traffic graphs using three rules. Reference [25] introduced Traficaware Self-supervised model for Network Intrusion Detection (TS-IDS), a self-supervised learning framework for IoT network intrusion detection, using GNNs to capture traffic relationships and improve detection with node and edge features. It also employs a self-supervised approach using auxiliary attributes to enhance graph characterization without labeled data.

Graph construction for intrusion detection datasets can use IP and PORT fields or just IP fields. Reference [12] introduced a heterogeneous attribute graph with IoT traffic features and their values as nodes to reveal relationships between traffic features and topology. This is done by aggregating various node and edge types using an improved message-passing approach. Additionally, a data optimization strategy inspired by Huffman coding reduces the graph’s size and complexity, minimizing computational burden while maintaining predictive accuracy. IDS faces challenges in processing large volumes of network traffic while ensuring privacy protection. Insights from privacy-preserving recommender systems offer valuable approaches. For instance, Liu et al. [26] proposed a simplified graph convolutional network model in their work on privacy-preserving point-of-interest recommendations, which balances user preferences and privacy by generating a secure subset of data. Similarly, Qi et al. [27] used local sensitive hashing in their research to protect user privacy while recommending point-of-interest categories based on long- and short-term dependencies. These studies provide valuable inspiration for addressing privacy issues in intrusion detection systems.

While earlier GNN approaches incorporate data interaction and topology, they often overlook the temporal dimension. EULER [14] addresses this by combining GNNs and RNNs in an unsupervised intrusion detection system, leveraging both network topology and temporal characteristics. GNNs encode the network at specific moments, while RNNs track dynamic changes over time. The system also extends to a distributed framework for improved performance, highlighting the importance of temporal data. DLGNN [28], a semi-supervised method inspired by the 5G radio frame structure, monitors IP address communications by slicing streams into temporal graph snapshots. It uses placeholders for temporary communication absences, interpreting sparse behavior as a unique pattern. The method transforms edge classification into node classification by converting graph snapshots into line graph snapshots. Dynamic GNNs extract spatial information from each snapshot, capturing long-term communication patterns between IP pairs.

Previous methods have leveraged the graph-structured nature of network traffic for intrusion detection by utilizing intrinsic features and host interactions. However, studies [10–12] and [24,25] treated all traffic as a single graph, overlooking the dynamics of topology and node interactions. References [14] and [28] proposed partitioning traffic into discrete graph snapshots to capture spatial and temporal data. The EULER method combines GNNs and RNNs for node-level detection. However, existing NIDS datasets primarily focus on edge features rather than node-level data, and most GNN techniques emphasize node embeddings. DLGNN converts edge classification into node classification using a line graph structure, but monitoring host IP communications remains challenging in complex networks. Additionally, existing methods often neglect the differentiation of data types within models. Inspired by the human visual attention system, the attention mechanism in deep learning prioritizes critical data elements, enhancing model performance. Given the enormous volume of network data, integrating this mechanism helps identify the most relevant information. To sum up, Table 1 summarizes some facts and figures about some recent research below.

3  Methodology

In this section, we introduce DIGNN-A, a real-time intrusion detection model based on dynamic graph neural networks designed to optimally leverage the temporal and topological information inherent in network data. We begin by constructing a threat model tailored to the intrusion detection scenario, facilitating a deeper understanding and more effective mitigation of complex threats. Following this, we outline the overarching framework of the model, detailing the process of creating dynamic line graphs from network traffic. A graph convolution operation, enhanced by an attention mechanism, is then applied to each line graph snapshot, improving the spatial feature representation of the graph data. Each snapshot’s node features and adjacency matrix are subsequently fed into an integrated graph neural network model, generating node embeddings. These embeddings are used for node-level anomaly detection, enabling the identification of potential intrusion behaviors.

3.1 Threat Model

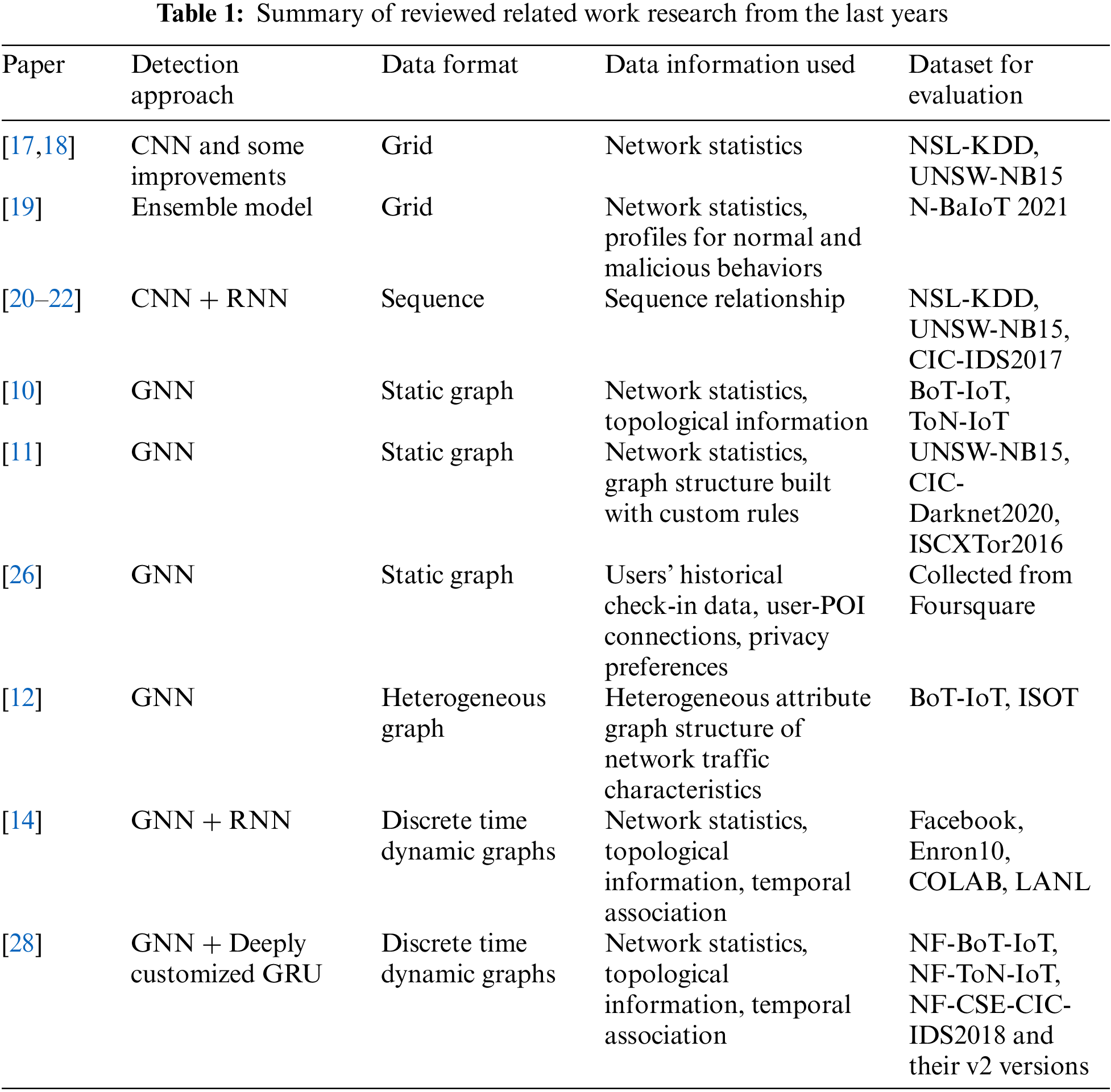
The proposed approach is based on a threat model applicable to most traditional network scenarios. An abstract representation of the threat model is illustrated in Fig. 1 below. It is assumed that all network traffic must traverse a firewall device, which may be situated on an upstream router. The firewall device collects and processes communication traffic between all hosts in the network. Each traffic record is collected and stored in a data format defined by a quintuple containing the source IP address, source port, destination IP address, destination port, and transport protocol [29]. Additionally, other statistical characteristics, such as communication status, communication byte size, and duration, are also recorded. The firewall device can inspect, store, export, and block the recorded traffic.

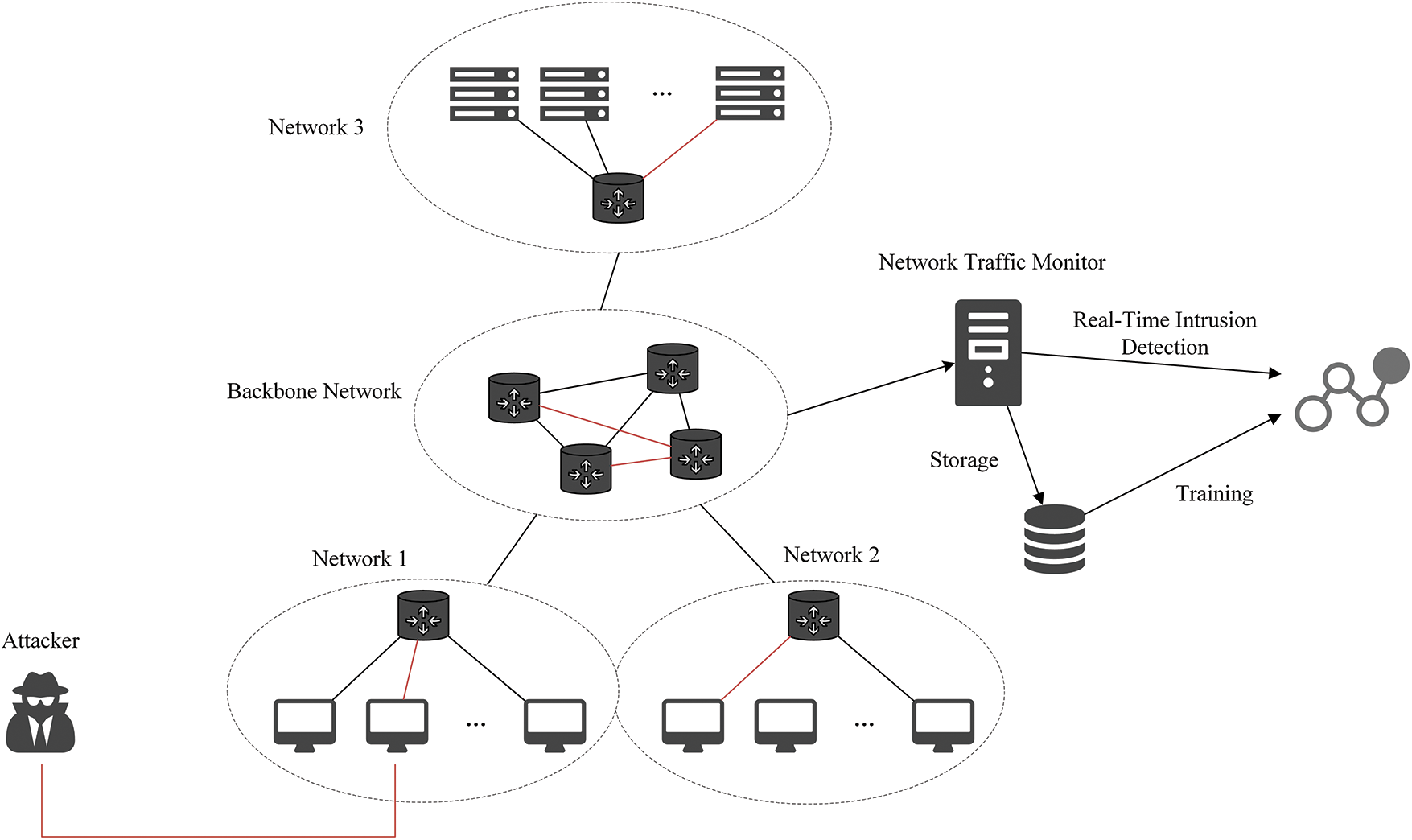
Figure 1: Overview of the threat model

Network devices can be categorized as either functioning correctly or compromised by attackers, who use them to perform malicious activities. Attackers exploit the network’s communication infrastructure for attacks like DDoS, injection, vulnerability exploitation, and executing shell code, affecting network traffic characteristics. Identifying compromised devices within mixed normal and abnormal traffic is crucial, as attackers disguise malicious traffic to mimic normal patterns. Instead of deep packet inspection, we use a statistical model for anomaly detection. Integrating a continuously updated anomaly detection model into network security allows real-time data monitoring from firewalls, real-time anomaly detection, and alert notifications.

3.2 Overview of the Model

This paper proposes a Dynamic Integrated Neural Network with Attention (DIGNN-A) model incorporating an attention mechanism. To overcome the limitations of classical GNNs, which typically prioritize node embeddings, we introduce a line graph structure as an alternative representation of the original graph. This approach provides a more efficient representation of graph structures while converting the intrusion detection edge classification task into a node classification task. Additionally, it addresses the challenge of changes in the node-set at different time steps due to the dynamic nature of the graph, ensuring the stability of node embeddings. Before the dynamic graph is input into the integrated graph neural network, a graph convolution operation with an attention mechanism is applied to enhance data representation, thereby improving the model’s ability to derive more effective vector representations from large datasets. Ultimately, the integrated graph neural network generates the corresponding node embeddings. The model consists of three principal components: the dynamic line graph processing module, the graph convolutional neural network module, and the integrated graph neural network module. The comprehensive architecture of the model is illustrated in Fig. 2 below.

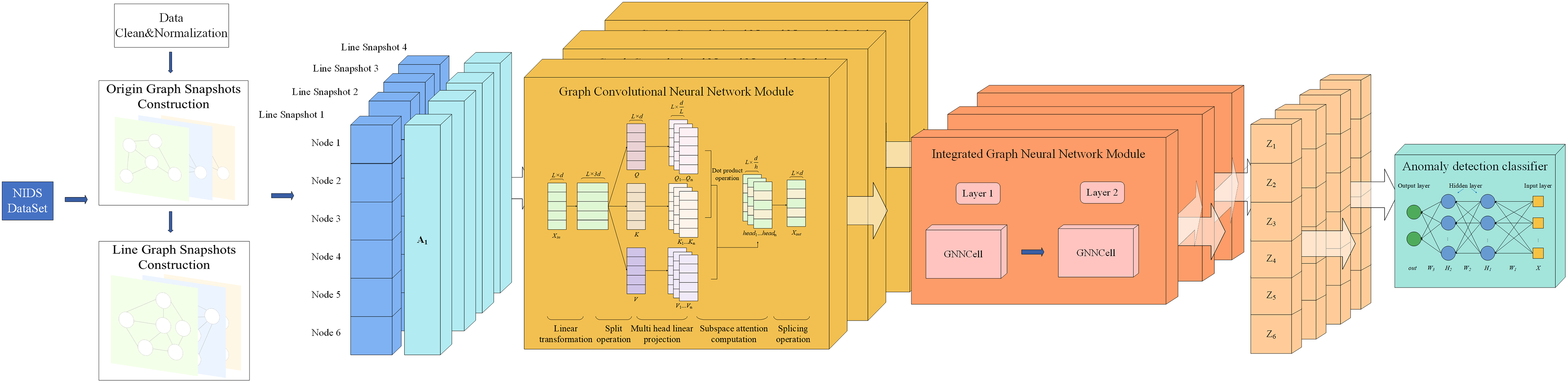
Figure 2: A framework for DIGNN-A model

The primary contributions of this study are as follows: We propose a dynamic graph modeling method based on a line graph structure, which transforms edge classification tasks into node classification tasks, thereby improving the model’s adaptability and flexibility to dynamic graph structure changes. By incorporating graph convolution operations with attention mechanisms, the model can effectively differentiate the significance of neighboring information, enhancing its capability to process complex data. Additionally, we employ an integrated graph neural network architecture to capture the spatiotemporal characteristics of dynamic graphs, enabling accurate handling of complex intrusion detection tasks.

3.3 Constructing Dynamic Line Graph Snapshots

Graph-based data effectively captures structural information through interactions among a set of objects. Additionally, the graph’s topology stores implicit relational information between these objects. By integrating a temporal dimension into graph data, dynamic graphs are used to represent both the network’s topology and its temporal changes. This method allows the model to encompass a more comprehensive scope of information.

In this study, we represent network traffic data as a series of discrete-time dynamic graphs for model input. Each discrete dynamic is composed of multiple static graphs. A static graph can be represented as G={V,E,A}, where V and E are the sets of nodes and edges of G, respectively. The topological information of the graph is represented by the adjacency matrix A∈R|V|×|V|, where Au,v=1 if there exists an edge between nodes u and v, and Au,v=0 otherwise. A discrete-time dynamic graph can be viewed as a sequence of T static graphs {G1,G2,⋯,GT} [30], which represent snapshots of different periods or windows. This definition of a snapshot of the static graph at a specific moment aligns with the definition of a single static domain.

The key features of network traffic used in constructing the static graph include source and destination IP addresses, source and destination port numbers, transaction protocols, transaction states, transaction bytes, and timestamps. In our approach, combinations of sockets—defined by IP addresses and port numbers—are treated as nodes in the graph, with communications between two sockets modeled as edges. This methodology is consistent with the approach used in most existing studies. Features such as communication protocol type, communication status value, and communication traffic byte size are incorporated as edge features.

To effectively obtain edge embeddings, one intuitive method is to incorporate edge feature information into the graph data during the message passing stage for transmission and aggregation. However, these methods still face the issue of oversmoothing. The line graph L(G) serves as an equivalent representation of the original graph G. Edges in the original graph are represented as nodes in the line graph, providing a more efficient method for modeling edge-to-edge relationships. Let G=(V,E) be a graph where E consists of ordered pairs (e1,e2,⋯,en). Then, L(G)=(E,E~) is the line graph of G, where (e1,e2)∈E~⇔e1∩e2≠∅. This structure also proves to be a more efficient method for detecting specific attack methods characterized by distinct structural features.

To align the dynamic graph data input with the sequence input format required by the integrated graph neural network module, a fixed batch size is used to partition the data and construct static graph snapshots. These snapshots are subsequently transformed into line graph structures, ensuring a consistent number of nodes in each line graph snapshot. The line graph snapshots are then assembled by specifying the time window size (similar to the sequence length in RNN) as the input of the model. The choice of batch size directly influences the sparsity of the graph data, which, in turn, affects the model’s computational complexity. The impact of batch size on the model is further analyzed in the parameter analysis section (Section 5.3).

In general, the process of converting raw one-dimensional network traffic data into a discrete-time dynamic graph is as follows: First, sort the traffic data by the time field and divide it into snapshots of a fixed batch size. Then, construct the original static graph snapshot with IP and port sockets as nodes and interactions between sockets as edges, and construct an equivalent line graph snapshot based on the line graph definition. Finally, multiple consecutive line graph snapshots are combined into a dynamic graph through a time window as input to the model. This transformation allows the anomalous edge detection task in intrusion detection systems to be recast as a node classification problem, making it compatible with a broader array of graph neural network models. It also preserves the topology and interaction information that evolves within the network traffic data. This is accomplished by using a consistent batch size and line graph structure that ensures uniform node count across line graph data sets, thereby meeting the model’s input requirements for dynamic graphs. The methodology for constructing the dynamic line graph module is depicted in Fig. 3 below.

Figure 3: Data preprocessing process

3.4 Graph Convolutional Neural Network Module

The graph convolution operation exemplifies a type-specific implementation that follows the message-passing paradigm. It is designed to effectively capture the interaction patterns among data, as well as the feature information of neighboring nodes. In accordance with the dynamic line graph data obtained in the preceding section, graph convolution operations are applied to each discrete-time static graph. This process aggregates neighbor information at each time step and generates node embeddings. However, existing graph convolution methods exhibit several shortcomings when handling complex graph structures. Firstly, these methods predominantly rely on local neighbor information for feature aggregation, which hampers their ability to capture dependencies between distant nodes effectively. Consequently, their performance tends to be suboptimal in some complex graph structures. Secondly, the aggregation operations in existing methods are typically fixed, lacking the flexibility to adapt to the varying needs of different graph structures, which can result in information loss or redundancy.

To address these issues, we introduced TransformerConv [31] to implement this part of the network, which leverages the strengths of the Transformer model from NLP and applies them to graph neural networks. The self-attention mechanism is combined with graph convolutional networks to capture long-distance dependencies between nodes and dynamically adjust their relationships, reducing information loss. Leveraging the parallel computing of Transformers, this approach efficiently handles large-scale graph data, reduces computational overhead, improves training efficiency, and better manages global information. Compared to other GNN models, TransformerConv more accurately captures the relationships and interactions between different flows. The TransformerConv layer calculates the output features of each node using the following formula:

xi′=W1xi+∑j∈N(i)ai,jW2xj(1)

where xi′ represents the feature vector of node i, which is derived by aggregating the information from its neighboring nodes, the xi indicates the feature vector of the input node i. The N(i) denotes the set of neighboring nodes associated with node i. All Ws are learnable parameters. The matrix of attention scores aij is computed using multiplicative attention as follows:

ai,j=softmax((W3xi)⊺(W4xj)d)(2)

where xi represents the feature vector of the input node i, xj represents the feature vector of the neighboring nodes of node i, and d denotes the size of the hidden layer of each head. If edge features exist as input features, the formula must be modified as follows:

xi′=W1xi+∑j∈N(i)ai,j(W2xj+W5ei,j)(3)

ai,j=softmax((W3xi)⊺(W4xj+W5ei,j)d)(4)

where ei,j represents the edge eigenvectors between nodes i and j. The attention score matrix, denoted by ai,j, enables the model to differentiate the relative importance of the various neighbors of each node in the network. The final node representation is obtained by multiplying the attention score matrix by the feature matrix of each neighboring node, xj.

In our study, we utilize the TransformerConv layer, which conducts convolutional operations on graph snapshots at each time step using a self-attention mechanism. The self-attention mechanism’s ability to adaptively adjust the weights of relationships between different nodes is crucial for intrusion detection in network traffic data. Attack traffic often shows a complex and nonlinear relationship with normal traffic. Moreover, the multi-head attention mechanism enables the model to extract features from various subspaces, enhancing its representational capacity. For network traffic intrusion detection, this means the model can analyze traffic patterns from multiple perspectives, increasing the accuracy and robustness of the detection process. By incorporating additional GNN convolutional layers before the integrated graph neural network module, we can more deeply explore the intricate relationships between nodes and their neighboring nodes, significantly enhance feature extraction capabilities, and further enrich the diversity of node representations, all while effectively minimizing potential information loss.

3.5 Integrated Graph Neural Network Module

Given that the input is structured data in the form of a line graph, the number of nodes representing line graph snapshots is fixed at each time step. However, the set of nodes varies over time steps, posing a challenge for the use of stacked dynamic graph neural networks due to the irregular nature of the data. Integrated graph neural networks effectively address this issue by leveraging their inherent properties [32]. Integrated graph neural networks are constituted by replacing linear change operations in GRU with GNN convolution operations, as illustrated in Fig. 4 below. This model is unaffected by changes in the node-set and can obtain the embedded representation of the line graph snapshot nodes at each time step. Additionally, by passing the hidden layer states, we obtain long-term evolution information of the line graph snapshots, further capturing temporal and spatial correlations between the network embeddings to generate the embeddings of each node. This process can be represented as follows:

Ht=GNN−GRU(Ht−1,Xt,At)(5)

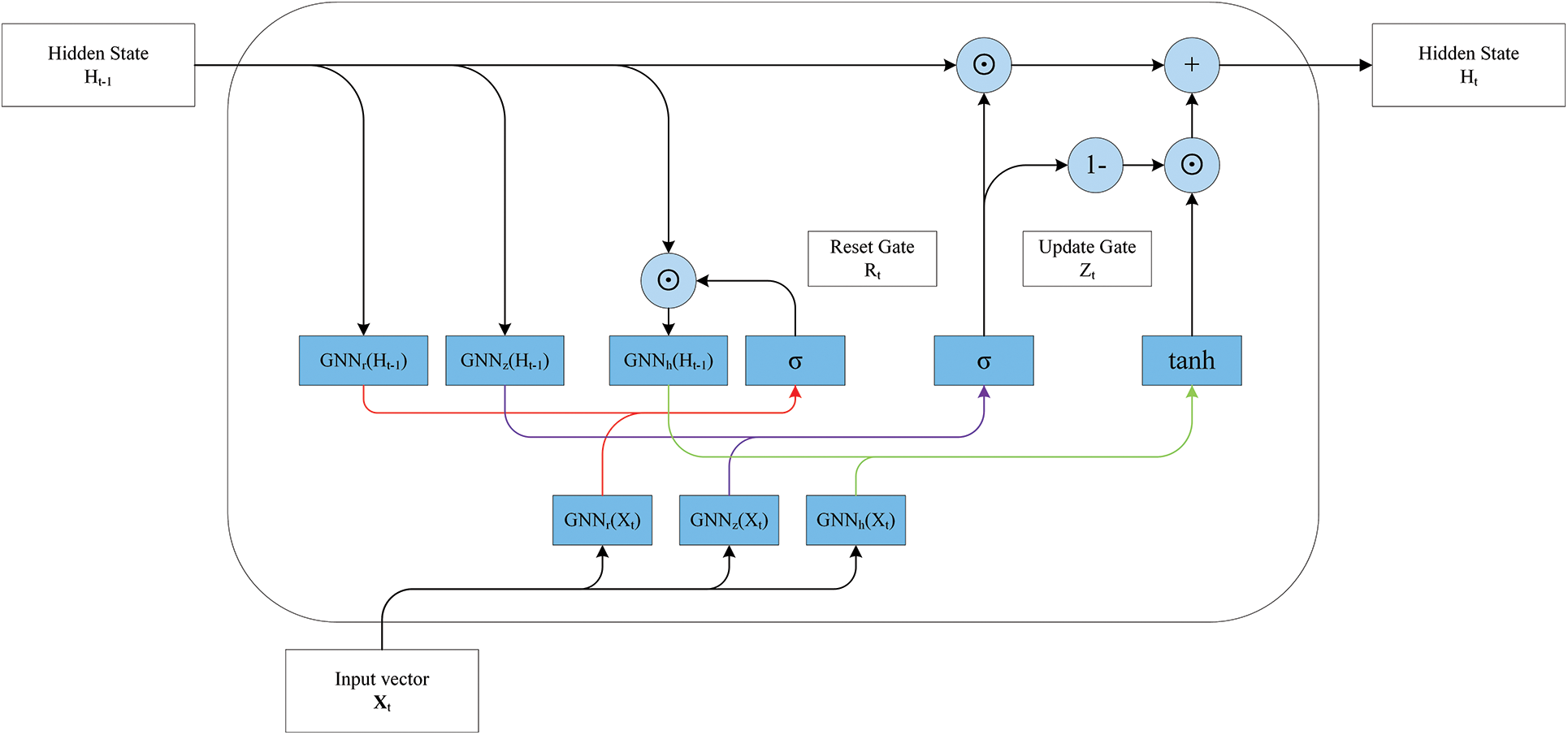
Figure 4: Overview of the architecture of the integrated graph neural network module

Following the preceding graph convolution module, neighboring nodes in the network receive an embedded representation that incorporates neighbor information through message passing. However, literature’s findings [33] indicated that the model’s performance significantly declines as the number of graph convolution layers increases. The incorporation of a more significant number of graph convolution operations into an integrated graph neural network inevitably leads to the oversmoothing issue within the model.

The GCNII [34] model incorporates initial residuals and constant mapping in its convolution operation, which helps prevent oversmoothing and consistently enhances performance as the network depth increases. Consequently, we selected GCNII as the convolution module in our integrated graph neural network. Subsequent experiments, detailed in Section 3.6, further validate the effectiveness of this structure. The integrated graph neural network module, GNN-GRUCell, can be represented by Eqs. (6)–(9).

rt=σ(GCNIIr(Xt,X0,At)+GCNIIr(Ht−1,X0,At))(6)

zt=σ(GCNIIz(Xt,X0,At)+GCNIIz(Ht−1,X0,At))(7)

h~t=tanh(GCNIIh(Xt,X0,At)+GCNIIh(rt⊙Ht−1,X0,At))(8)

Ht=(1−z)⊙h~t+zt⊙Ht−1(9)

where Xt denotes the node feature matrix at time t, while X0 represents the initial node feature matrix for the input with residual connections, the adjacency matrix at time t is denoted as At. The node feature matrix Ht captures both temporal and spatial information and serves as the output at each time step of the model. The graph convolution layers used for reset gates, update gates, and hidden state gates are denoted as GCNIIr, GCNIIz, and GCNIIh, respectively.

Given the necessity of classifying the nodes in each snapshot of the dynamic line graph (equivalent to classifying the edges in the original graph), it is evident that using the output of each time step for classification is a logical and appropriate approach. Therefore, the integrated graph neural network module is treated as a sequence-to-sequence model for both inputs and outputs. As with the named entity recognition task in the field of natural language processing, we consider the hidden state at each time step to be the output of the current time step and the input for the subsequent time step. The model generates a sequence that matches the length of the input sequence, producing a node representation of the input dynamic graph. This output effectively captures both temporal and spatial information, as the model allows the hidden state at each time step to incorporate information from both the current and preceding time steps, thereby capturing long-term dependencies in the sequence. The impact of the distinct GNN modules in the integrated model will be examined in the ablation experiment section.

3.6 Abnormal Traffic Classification

Following the previous modules, the node embedding representations of the discrete line graph snapshots, which incorporate temporal and spatial information, are obtained. These node representations of line graphs are equivalent to the edge embeddings of the original graphs. In this study, we consider abnormal traffic monitoring in intrusion detection as a binary classification problem. The line graph node feature matrix from Section 3.6, capturing temporal and spatial information, is fed into a neural network with a single hidden layer. Subsequently, the probability distribution is computed using the Softmax function, and the category with the highest probability is taken as the final classification result, as shown in Eq. (10).

P=softmax(W×Xt+b)(10)

where P represents the probability of an incorrect prediction, while W and b signify the parameters of the fully connected layer, normal traffic is labeled as 0, whereas abnormal traffic is labeled as 1.

Cross-entropy loss functions generally demonstrate better gradient properties during optimization, which enables more efficient parameter updates during backpropagation. The gradient calculation for the cross-entropy loss function involves comparisons among different classes, allowing for more practical guidance in parameter updates. This efficiency leads to faster convergence to the optimal solution during training. Therefore, we have chosen cross-entropy as the loss function for this study, as shown in Eq. (11).

L(y,p)=−∑j=1q[ylog⁡p+(1−y)log⁡(1−p)](11)

where L(y,p) denotes the binary cross-entropy loss, y represents the true label of the data, and p denotes the probability that the model predicts that the sample belongs to category 1. log denotes the natural logarithm.

4  Experimental Setup

In this section, the experimental environment, configuration, data sets used, and experimental evaluation criteria are described.

4.1 Dataset

In this work, the UNSW-NB15 [35] and NF-ToN-IoT [36] datasets are used, which are two datasets commonly used in the field of network intrusion detection. Table 2 shows the distribution of data and categories within each dataset.

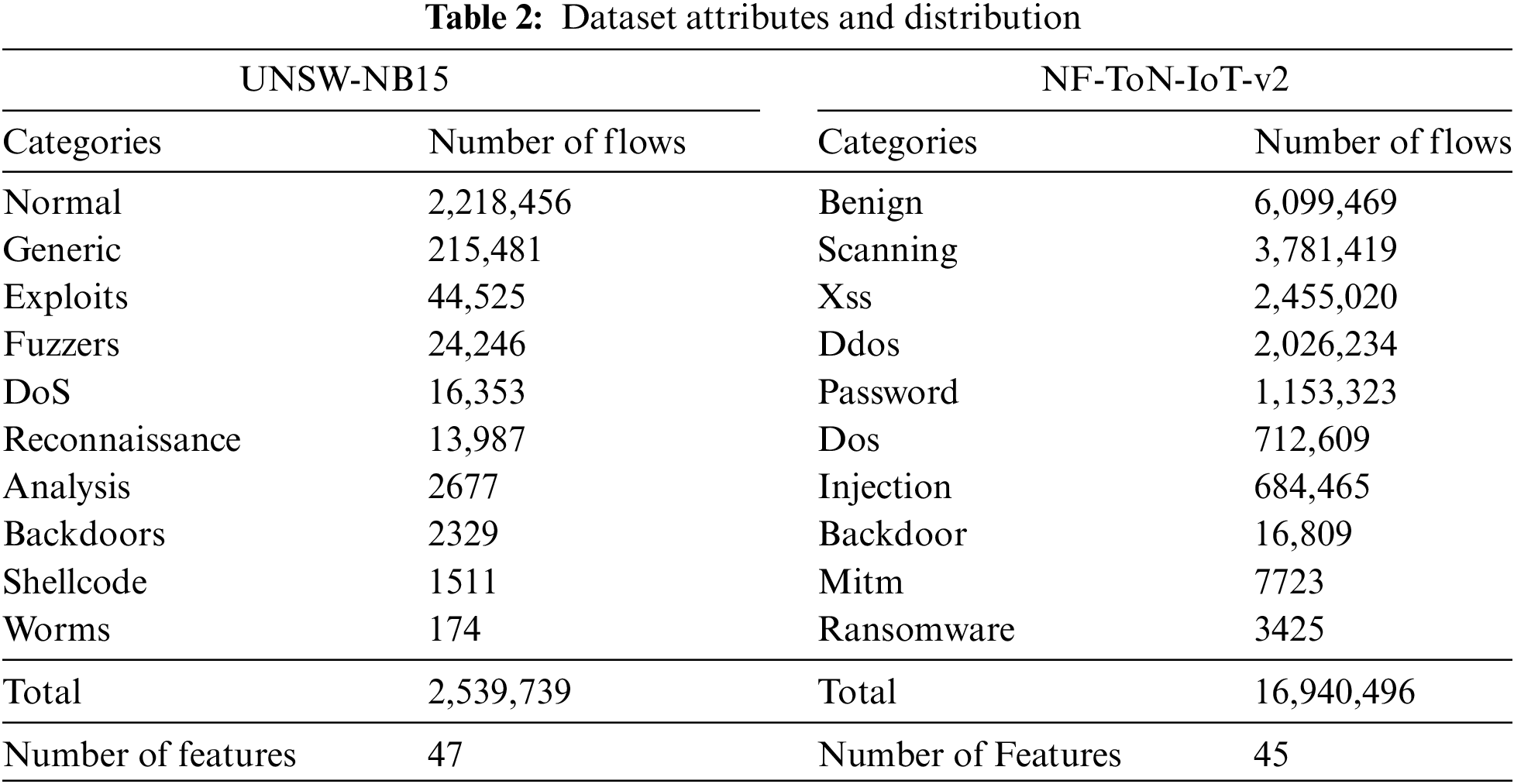
UNSW-NB15 dataset: developed by researchers at the University of New South Wales (UNSW) Cyber Security Laboratory to facilitate the study of network intrusion detection systems’ performance. The dataset includes a combination of typical network traffic and malicious traffic, categorized into various attack types. It is a standard dataset frequently used in cybersecurity research. The UNSW-NB15 dataset contains approximately 2.6 million records, encompassing nine distinct attack types: fuzzers, analysis, backdoors, DoS, exploits, generic, reconnaissance, shellcode, and worm. Using the Argus and Bro-IDS tools, the researchers developed twelve algorithms that generated 49 class-labeled features.

NF-ToN-IoT-v2 dataset: derived from the original NF-ToN-IoT dataset by converting its pcap-format file into a NetFlow-based feature set [37]. ToN-IoT, designed for cybersecurity research in IoT environments, includes traffic data from various IoT devices under normal and attack conditions. The NF-ToN-IoT-v2 dataset consists of 45 features and about 16 million records, with 63.99% attack samples and 36.01% normal samples, covering nine attack types.

4.2 Environments

The configuration of the experimental platform includes an Intel Core i7-8700K CPU, an NVIDIA GeForce RTX 3090 GPU with 24 GB of memory, 16 GB of RAM, and a Windows 10 operating system. The experimental environment consists of Python 3.9.16, PyTorch 2.0.0, CUDA 12.4, and PyTorch Geometric 2.4.0. The proposed algorithms are implemented using PyTorch and PyTorch Geometric, where the model comprises a three-layer TransformerConv and a two-layer GCNII-GRU module with a hidden layer size set to 64. Nonlinear activation functions are incorporated into both the TransformerConv and GCNII-GRU modules and Dropout is introduced between the hidden layers to mitigate overfitting in the neural networks. The Adam optimizer is utilized for backpropagation, and the training-test split ratio is set to 0.3. Additional hyperparameters are detailed in Table 3.

4.3 Evaluation

Due to the prevalence of data redundancy and imbalance in network traffic datasets, selecting appropriate evaluation metrics is crucial for accurately demonstrating model performance. The confusion matrix is employed to assess the model’s effectiveness, and its derived metrics—accuracy, precision, recall, and F1-score—provide a comprehensive reflection of the model’s performance. The confusion matrix categorizes the classification results as follows: True Positive (TP) represents the number of positive samples correctly predicted as positive; True Negative (TN) denotes the number of negative samples correctly predicted as negative; False Positive (FP) indicates the number of negative samples incorrectly predicted as positive; and False Negative (FN) signifies the number of positive samples incorrectly predicted as negative.

Accuracy indicates the proportion of correctly classified samples to the total number of samples. Precision represents the proportion of correctly predicted positive samples to the total predicted positive samples. The False Alarm Rate (FAR) indicates the proportion of samples incorrectly predicted to be attacks among all normal samples. Recall, based on the actual samples, represents the proportion of correctly predicted positive cases to the total actual positive cases. The F1-score is the harmonic mean of Recall and Precision. The formulas are shown in Eqs. (12) to (16), respectively.

Accuracy=TP+TNTP+FN+TN+FP(12)

Precision=TPTP+FP(13)

FalseAlarmRate=FPFP+TN(14)

Recall=TPTP+FN(15)

F1−Score=2×Recall×PrecisionRecall+Precision(16)

4.4 Baseline

We compare the performance of our proposed method on two datasets, UNSW-NB15 and NF-ToN-IoT-v2, with the following detection methods:

•   CNN-BiLSTM [21]: A network traffic intrusion detection method that combines the advantages of CNN and Bi-LSTM layers.

•   Stacked Random Forest [38]: Employs a balanced and stacked Random Forest classifier and uses the SHAP method to provide interpretable analysis of feature contributions.

•   VLSTM [39]: Learns low-dimensional feature representations from high-dimensional raw data using encoder-decoder neural networks and variational reparameterization methods. The reconstructed hidden variables are constrained by three loss functions and categorized by a lightweight estimation network, which is suitable for anomaly detection in industrial big data environments.

•   CTGNN [40]: A network anomaly detection framework based on Continuous Time Graph (CTG) neural networks designed to capture attributes and complex behavioral information of network interactions. The model utilizes a message aggregation scheme that fuses spatio-temporal neighborhood information, real-time distributions, and historical states to improve the learning ability of low-frequency interaction behaviors.

•   E-GraphSAGE [10]: An extension of GraphSAGE that captures edge features of graphs as well as topology information for intrusion detection in IoT networks.

•   DLGNN [28]: Semi-supervised learning addresses the high cost of data labeling by transforming network traffic into spatio-temporal graphs using a dynamic graph neural network. This method captures the evolution of communication between IP pairs through continuous snapshots. Additionally, the line graph structure enhances the edge-embedded representation of network communications and the message aggregation capability of graph convolution.

5  Results and Discussion

In this section, several state-of-the-art models are compared with DIGNN-A to demonstrate the feasibility of the designed model. Then, the usability of each module in the model is demonstrated by ablation experiments. Finally, the results of the experiment are discussed.

5.1 Experimental Results

The complete dataset underwent experimental validation. During the data processing stage, the training dataset was transformed into a data structure suitable for model input, following the dynamic line graph snapshot method proposed in Section 3. After training the model, binary classification results were obtained for the test set. Table 4 provides a detailed account of the outcomes of our methodology under the binary classification paradigm, including accuracy, precision, FAR, recall, and F1-score for both our proposed approach and the baseline model on both datasets. Overall, our method proves effective in intrusion detection binary classification scenarios, demonstrating higher accuracy, precision, and F1-score. For example, on the NF-ToN-IoT-v2 dataset, our method achieves 99.96% accuracy, 99.98% precision, a 0.03% FAR, 99.97% recall, and a 99.97% F1-score.

5.2 Analysis of Ablation Experiments

To evaluate model performance, key components, and features, as well as validate the effectiveness of the GNN and integrated graph neural network modules, we conducted a series of ablation experiments. The base model and parameters followed the default settings outlined in the Experimental Details section. For comparison, we used the binary classification results on the UNSW-NB15 dataset. The methods were divided into four processes: input graph structure processing, GNN convolution module, integrated GNN module, and anomaly detection module. The ablation results are presented in Table 5, focusing on the following variants:

•   DIGNNA-O: Using the original structure as model input, the convolution operation on the original graph produces node embeddings. The anomaly detection module employs EdgeEncoder to derive edge embeddings by aggregating the node embeddings at the ends of the edges. It is used to verify the validity of the line graph structure.

•   DIGNNA-E: Using the original graph as the model input, the graph neural network convolution module operation was replaced with the convolution operation from the E-GraphSAGE method. This modification was used to validate the effectiveness of TransformerConv.

•   DIGNNA-N: Removes the graph neural network convolution module, which is used to determine the relative importance of different modules in the proposed model from the side and to evaluate the contribution of this module to performance improvement.

•   DIGNNA-S: Remove the integrated graph neural network module and verify its effectiveness by replacing it with a simple RNN model.

•   DIGNN-A: We present the model unchanged.

The results of the ablation experiments are presented in Table 5.

The experimental results indicate that any modifications to the modules, such as replacing the original graph data used as model inputs or altering the graph convolutional neural network and integrated graph neural network modules, inevitably result in a decline in model performance. This observation underscores several key findings:

A comparison of DIGNNA-O and DIGNN-A reveals that using line graphs is a more advantageous approach than using original graphs for introducing edge features in the convolution operation.

A comparison of DIGNNA-O and DIGNNA-E reveals that, unlike E-GraphSAGE, TransformerConv utilizes an attention mechanism for graph convolution operations, assigning distinct weights to each node. This method allows the model to capture more intricate details of the graph structure.

DIGNNA-N excludes the graph convolutional neural network module compared to DIGNN-A. Nevertheless, the final results show only slight declines, suggesting that incorporating line graphs and the integrated graph neural network module is pivotal to our proposed methodology. Additionally, the graph convolutional neural network module contributes to the overall enhancement of the model.

In DIGNNA-S, we use the conventional recurrent neural network GRU to replace the integrated graph neural network module in the methodology, thereby giving the model a structure analogous to the stacked graph neural network described in previous sections. However, because the line graph structure is used as an input to the model, the set of line graph nodes at each time step is variable, making it impossible to correspond to the sequence data required by the GRU. Consequently, the model is ineffective.

5.3 Parameter Analysis

To investigate the influence of various module parameters on the model’s performance, we analyzed the results obtained by varying the values of several key parameters, as depicted in Fig. 5. Specifically, we evaluated the effect of batch size on the model by comparing four different sizes. Notably, when the batch size was set to 2048, the model achieved the best performance, particularly in terms of accuracy, recall, and F1-score. However, the highest precision rate was observed with a batch size of 1024. Additionally, the training time decreased proportionally with the increase in batch size.

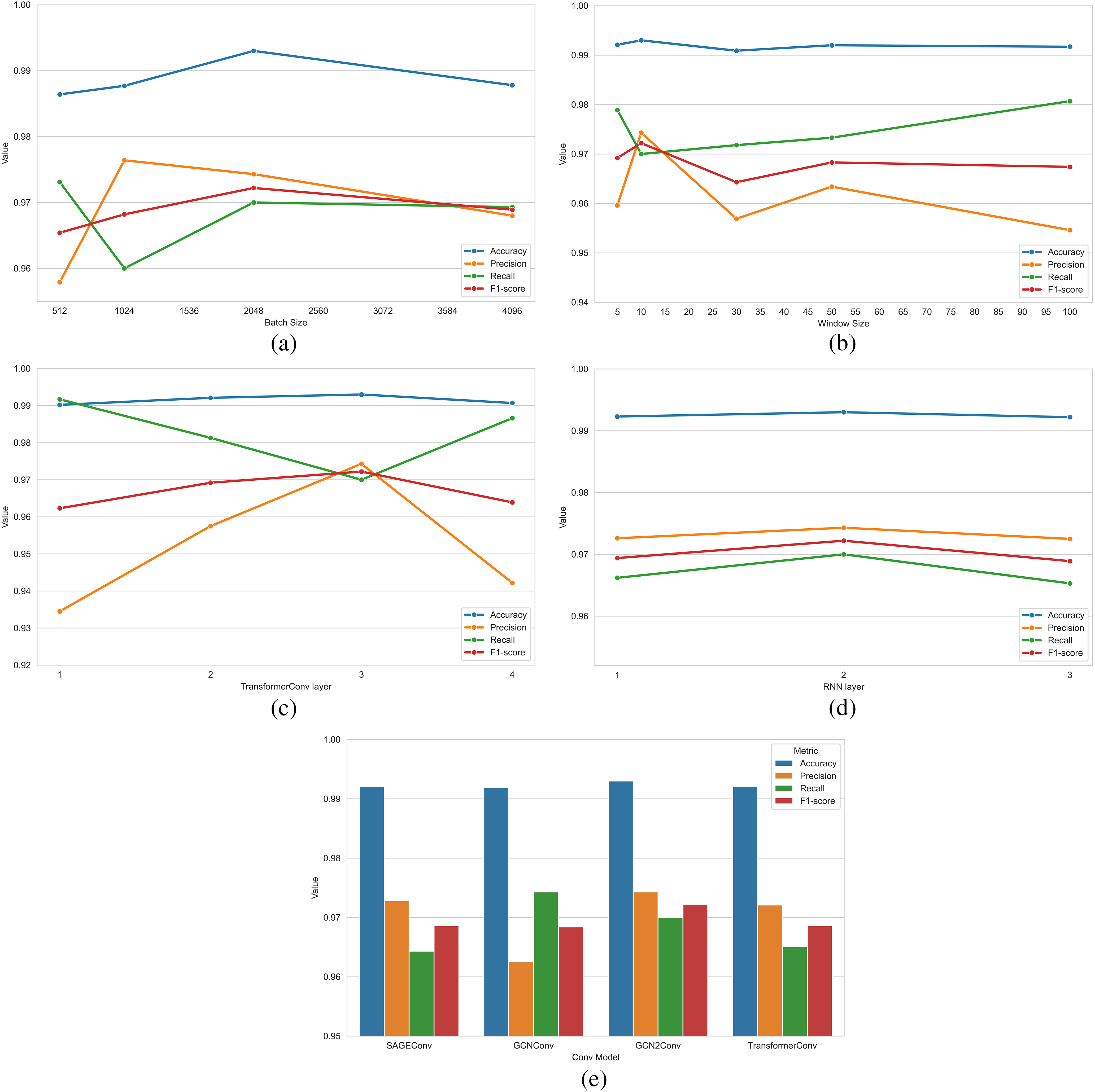
Figure 5: Effect of different parameters in the model on the experimental results. (a) Effect of batch size on model results; (b) Effect of window size on model results; (c) Effect of the number of TransformerConv layers on model results; (d) Effect of the number of RNN layers in the integrated graph neural network module on the model results; (e) Effect of different convolutional modules in integrated graph neural networks on model results

To explore the impact of window size, we tested five different time window sizes and found that the accuracy rate remained stable between 99.09% and 99.3% for all window sizes. A window size of 10 demonstrated a balanced performance with the highest accuracy rate and F1-score, while a window size of 100 was more suitable for prioritizing the reduction of false alarm rate.

We examined the impact of varying TransformerConv layers on model performance. As the number of layers increased, accuracy gains diminished while precision and recall fluctuated. The model showed the most stable performance with three layers. This balance likely stems from the fact that more layers allow better information aggregation from neighbors, but too few layers may miss information, and too many may introduce redundancy.

Furthermore, to validate the effect of the number of RNN layers in the integrated graph neural network module, we compared the performance of models with different numbers of RNN layers. Our findings indicated that the number of RNN layers had a minimal impact on the model’s performance, with the best performance observed when the number of layers was set to 2.

Lastly, to assess the impact of convolutional modules in the integrated graph neural network, we tested four modules: SAGEConv, GCNConv, GCN2Conv, and TransformerConv. SAGEConv and TransformerConv had similar Accuracy and F1-score but were more consistent, likely due to better capture of local structural information through message passing. GCNConv, which updates node features via weighted averaging of neighbors, requires more local smoothing. GCN2Conv performed the best, achieving the highest F1-score and balanced precision and recall, likely due to its residuals and identity mapping, which prevent oversmoothing or class bias.

5.4 Analysis of Line Graph

To further analyze the role of line graphs and their adaptability to other models, we conducted validation experiments by applying the line graph structure to the TransformerConv model. TransformerConv can directly incorporate edge feature information during message passing. We compared two implementations: one that adds edge features to the TransformerConv and another that uses the line graph structure. The results of these comparative experiments, as shown in Table 6, indicate that the TransformerConv model using the line graph structure achieves higher detection rates and F1-scores than the version incorporating edge features. These findings suggest that the line graph structure can enhance convolution operations beyond the models considered in this paper.

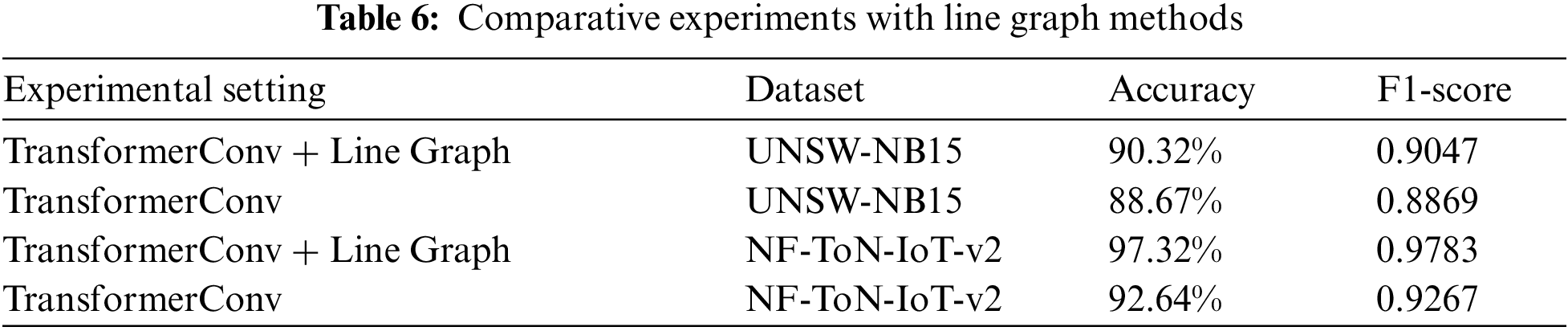
Fig. 6 shows the original graph and line graph visualizations for two randomly selected pairs of graph snapshots from the UNSW-NB15 test set, with red highlighting anomalous edges and nodes in the line graph. As evident from the figure, the line graph structure effectively aggregates anomalous edges from the original graph into significant clusters of anomalous nodes. This makes detecting these anomalies more straightforward and efficient in the line graph. The model can learn features associated with these clusters, thereby avoiding the high computational overhead required to identify and detect anomalous edges in the original graph. Additionally, communication interactions that occur only once in the original graph appear as isolated nodes in the line graph. For these isolated communications, the line graph reduces unnecessary message-passing operations during graph convolution and directly utilizes the original edge features for learning.

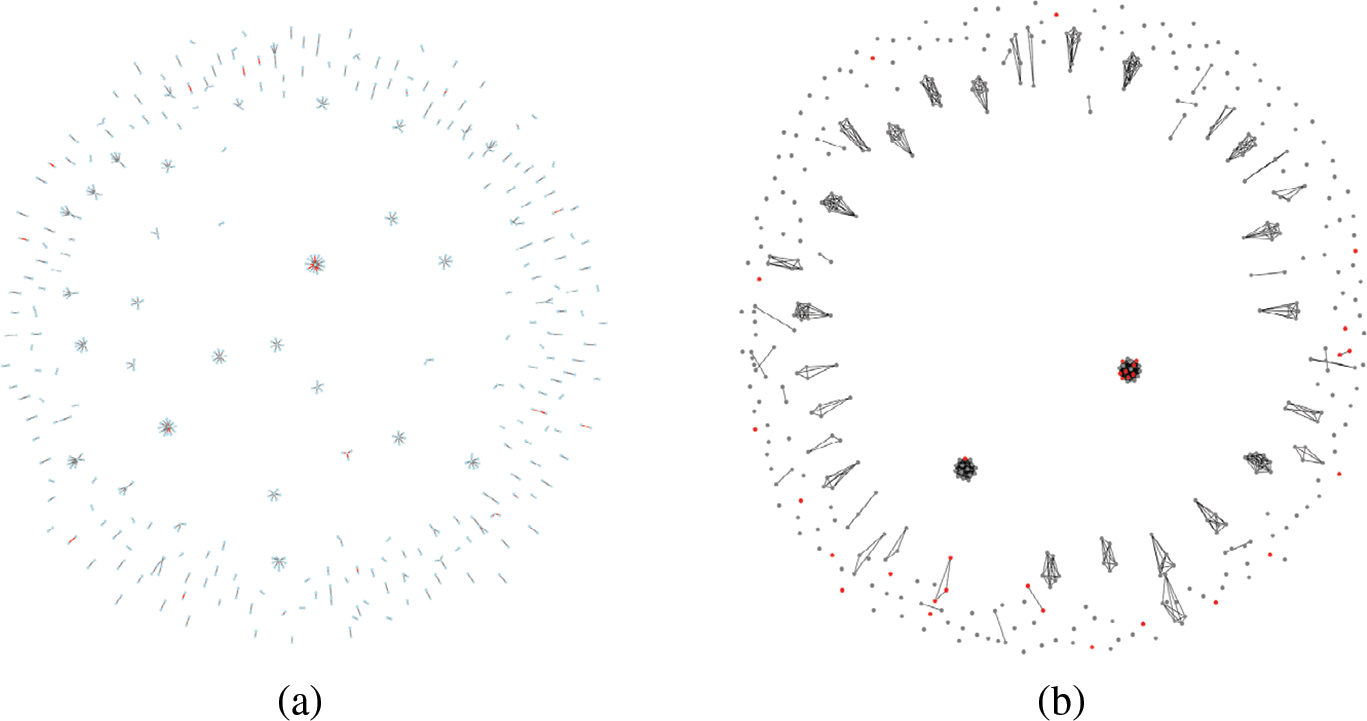
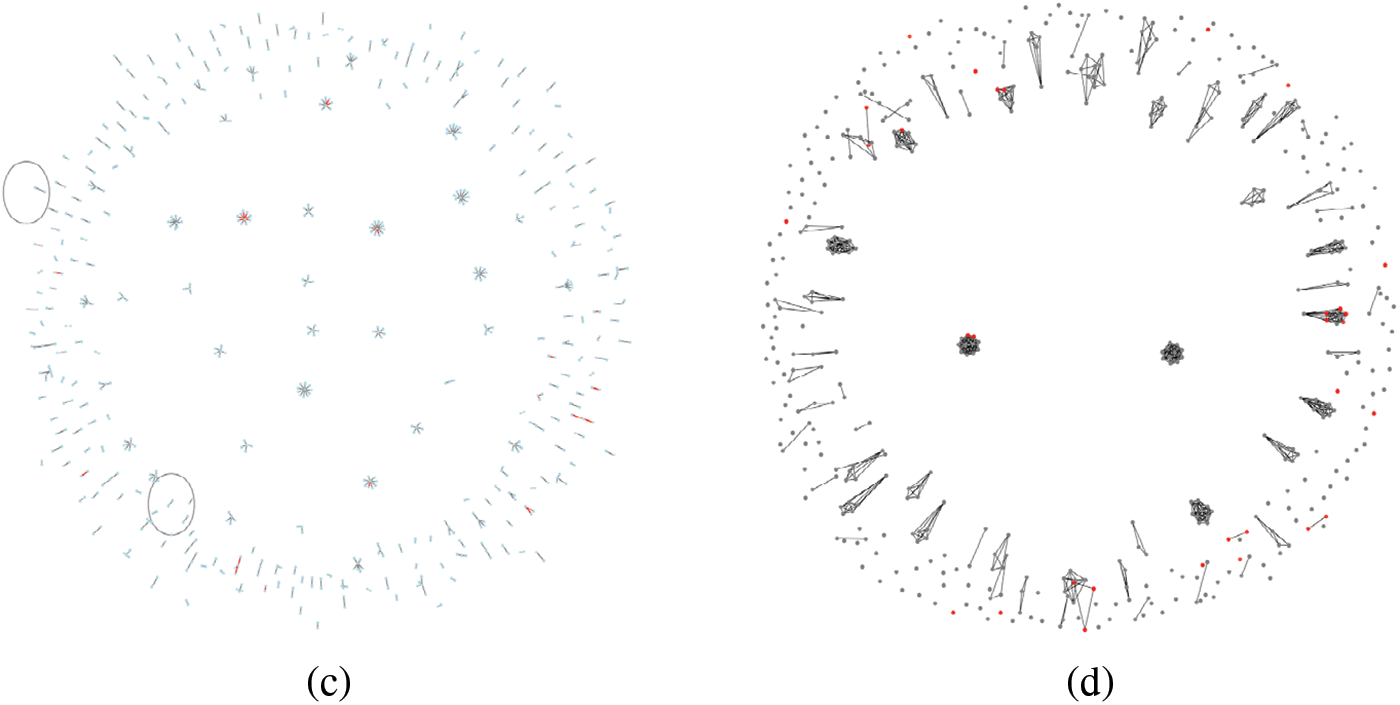
Figure 6: Distribution of original and line graphs. (a) Original graph 1 distribution; (b) Line graph 1 distribution; (c) Original graph 2 distribution; (d) Line graph 2 distribution

When addressing edge embedding challenges and potential trade-offs, several methods are worth noting: (1) generating edge embeddings through node embeddings, (2) combining node embeddings with edge features, and (3) converting the graph into a line graph. Each has its pros and cons. The first two methods are simple and efficient, suitable for large-scale graphs, but rely heavily on node feature quality. If edge features are limited or invalid, performance may suffer. Additionally, when edges significantly outnumber nodes, oversmoothing, information redundancy, and noise accumulation can degrade results. Line graphs, as an equivalent representation, retain topological structure and local information, naturally capturing high-order relationships. However, in extreme cases, such as when communication traffic forms independent pairs, line graphs may reduce to discrete points, weakening anomaly detection. Therefore, selecting the appropriate method depends on the application. In some scenarios, a multi-graph fusion approach, combining line graphs with other methods, can enhance model robustness by processing different structures from multiple perspectives.

In accordance with the definition of a line graph, each node within the line graph represents an edge from the original graph. When dynamic graphs are utilized to sort and divide data over time, the degree distribution in a specific snapshot of the original graph may seem markedly uneven. In contrast, in line graphs, edges from the original graph that share a common node are connected solely as nodes, redistributing the impact of high-degree nodes across multiple edge nodes and leading to a more uniform degree distribution. This characteristic enables the identification of nodes with dense communication in the original graph when represented in the line graph. Furthermore, converting a graph G to a line graph L(G) is a linear-time operation [42]. The complexity of message passing in graph neural networks correlates closely with node degrees, exhibiting a computational complexity of O(|V|⋅max(dv)), where |V| is the number of nodes, and max(dv) represents the maximum node degree in a graph. Due to the limited connectivity relationships per edge, the maximum degree of nodes in a line graph is typically lower than the maximum degree in the original graph. Additionally, the number of nodes in a line graph |E| is generally less than or equal to the square of the total number of nodes |V|, resulting in relatively low computational complexity.

To further verify the performance of the line graph method in adapting to highly dynamic environments, we recorded the time required to process the dataset into a dynamic graph suitable for input to the model under the default parameter settings described in the experimental section. The experimental results are presented in Table 7. As shown, the processing time is proportional to the number of data records; however, the time needed to process a single graph snapshot remains consistent. Additionally, it is essential to note that the NF-ToN-IoT-v2 dataset includes four more features than the UNSW-NB15 dataset, indicating that an increase in the number of features further affects the data processing time.

6  Conclusion

The paper presents a real-time intrusion detection method using integrated graph neural networks. This approach combines statistical data from network traffic with long-term sequence dependencies, improving anomaly detection on dynamic graphs. The method’s graph snapshot segmentation allows broader application across network intrusion datasets without performance loss. By converting graph snapshots into line graph snapshots, the edge detection problem is simplified to node detection, benefiting from graph neural networks for node classification. The model uses a graph convolution operation with an attention mechanism to enhance prediction accuracy. Experiments on UNSW-NB15 and NF-ToN-IoT-v2 datasets show the model’s superiority over benchmark models.

Despite its advantages, the proposed integrated graph neural network for real-time intrusion detection has limitations. The interpretability issue inherent in graph neural networks could be addressed through further research using the GNNExplainer [43]. Additionally, incorporating other data sources, such as host logs and user behavior, could enhance the detection of complex, multi-stage attacks. Future work may explore adapting the method to unsupervised or semi-supervised learning paradigms, reducing the reliance on labeled data and improving model adaptability and generalization. The development of heterogeneous graph neural networks could also enable the fusion of diverse data sources, better responding to evolving threats.

Acknowledgement: Thanks to our tutors and researchers for their assistance and guidance.

Funding Statement: The research received no funding grant from any funding agency in the public, commercial, or not-for-profit sectors.

Author Contributions: Study conception and design: Jizhao Liu, Minghao Guo; analysis and interpretation of results: Jizhao Liu, Minghao Guo; data collection: Minghao Guo; draft manuscript preparation: Jizhao Liu, Minghao Guo. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The dataset is available in two links below: https://research.unsw.edu.au/projects/unsw-nb15-dataset & https://staff.itee.uq.edu.au/marius/NIDS_datasets (accessed on 24 October 2024).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. M. Zhong, M. Lin, C. Zhang, and Z. Xu, “A survey on graph neural networks for intrusion detection systems: Methods, trends and challenges,” Comput. Secur., vol. 141, no. 3, Jun. 2024, Art. no. 103821. doi: 10.1016/j.cose.2024.103821. [Google Scholar] [CrossRef]

2. N. Shone, T. N. Ngoc, V. D. Phai, and Q. Shi, “A deep learning approach to network intrusion detection,” IEEE Trans. Emerg. Top. Comput. Intell., vol. 2, no. 1, pp. 41–50, Feb. 2018. doi: 10.1109/TETCI.2017.2772792. [Google Scholar] [CrossRef]

3. V. Morfino and S. Rampone, “Towards near-real-time intrusion detection for IoT devices using supervised learning and Apache Spark,” Electronics, vol. 9, no. 3, Mar. 2020, Art. no. 444. doi: 10.3390/electronics9030444. [Google Scholar] [CrossRef]

4. M. Verkerken, L. D’hooge, T. Wauters, B. Volckaert, and F. D. Turck, “Unsupervised machine learning techniques for network intrusion detection on modern data,” presented at the 2020 4th Cyber Secur. Netw. Conf. (CSNetLausanne, Switzerland, Oct. 21–23, 2020. [Google Scholar]

5. O. Y. Al-Jarrah, Y. Al-Hammdi, P. D. Yoo, S. Muhaidat, and M. Al-Qutayri, “Semi-supervised multi-layered clustering model for intrusion detection,” Digit. Commun. Netw., vol. 4, no. 4, pp. 277–286, Nov. 2018. doi: 10.1016/j.dcan.2017.09.009. [Google Scholar] [CrossRef]

6. I. Ullah and Q. H. Mahmoud, “Design and development of a deep learning-based model for anomaly detection in IoT networks,” IEEE Access, vol. 9, pp. 103906–103926, 2021. doi: 10.1109/ACCESS.2021.3094024. [Google Scholar] [CrossRef]

7. M. A. Khan, “HCRNNIDS: Hybrid convolutional recurrent neural network-based network intrusion detection system,” Processes, vol. 9, no. 5, May 2021, Art. no. 834. doi: 10.3390/pr9050834. [Google Scholar] [CrossRef]

8. B. Min, J. Yoo, S. Kim, and D. Shin, “Network anomaly detection using memory-augmented deep autoencoder,” IEEE Access, vol. 9, pp. 104695–104706, 2021. doi: 10.1109/ACCESS.2021.3100087. [Google Scholar] [CrossRef]

9. A. L. Buczak and E. Guven, “A survey of data mining and machine learning methods for cyber security intrusion detection,” IEEE Commun. Surv. Tutor., vol. 18, no. 2, pp. 1153–1176, 2016. doi: 10.1109/COMST.2015.2494502. [Google Scholar] [CrossRef]

10. W. W. Lo, S. Layeghy, M. Sarhan, M. Gallagher, and M. Portmann, “E-GraphSAGE: A graph neural network based intrusion detection system for IoT,” in Proc. NOMS, 2022 IEEE/IFIP Netw. Oper. Manag. Symp., Apr. 25–29, 2022, pp. 1–9. [Google Scholar]

11. X. Deng, J. Zhu, X. Pei, L. Zhang, Z. Ling and K. Xue, “Flow topology-based graph convolutional network for intrusion detection in label-limited IoT networks,” IEEE Trans. Netw. Serv. Manag., vol. 20, no. 1, pp. 684–696, Mar. 2023. doi: 10.1109/TNSM.2022.3213807. [Google Scholar] [CrossRef]

12. M. Gao, L. Wu, Q. Li, and W. Chen, “Anomaly traffic detection in IoT security using graph neural networks,” J. Inf. Secur. Appl., vol. 76, no. 5, Aug. 2023, Art. no. 103532. doi: 10.1016/j.jisa.2023.103532. [Google Scholar] [CrossRef]

13. A. Alshamrani, S. Myneni, A. Chowdhary, and D. Huang, “A survey on advanced persistent threats: Techniques, solutions, challenges, and research opportunities,” IEEE Commun. Surv. Tutor., vol. 21, no. 2, pp. 1851–1877, 2019. doi: 10.1109/COMST.2019.2891891. [Google Scholar] [CrossRef]

14. I. J. King and H. H. Huang, “EULER: Detecting network lateral movement via scalable temporal link prediction,” ACM Trans. Priv. Secur., vol. 26, no. 3, pp. 1–36, Jun. 2023. doi: 10.1145/3588771. [Google Scholar] [CrossRef]

15. A. Krizhevsky, I. Sutskever, and G. E. Hinton, “ImageNet classification with deep convolutional neural networks,” Commun. ACM, vol. 60, no. 6, pp. 84–90, Jun. 2017. doi: 10.1145/3065386. [Google Scholar] [CrossRef]

16. A. Vaswani et al., “Attention is all you need,” in Proc. 31st Int. Conf. Neural Inf. Process. Syst. (NIPS), Long Beach, CA, USA, Dec. 4–9, 2017, pp. 5998–6008. [Google Scholar]

17. I. Al-Turaiki and N. Altwaijry, “A convolutional neural network for improved anomaly-based network intrusion detection,” Big Data, vol. 9, no. 3, pp. 233–252, Jun. 2021. doi: 10.1089/big.2020.0263. [Google Scholar] [PubMed] [CrossRef]

18. J. Man and G. Sun, “A residual learning-based network intrusion detection system,” Secur. Commun. Netw., vol. 2021, 2021, Art. no. 5593435. doi: 10.1155/2021/5593435. [Google Scholar] [CrossRef]

19. Q. Abu Al-Haija and M. Al-Dala’ien, “ELBA-IoT: An ensemble learning model for botnet attack detection in IoT networks,” J. Sens. Actuator Netw., vol. 11, no. 1, Mar. 2022, Art. no. 18. doi: 10.3390/jsan11010018. [Google Scholar] [CrossRef]

20. Y. Imran, Y. Xiang, L. Ali, and Z. Abdul Rauf, “A bidirectional LSTM deep learning approach for intrusion detection,” Expert Syst. Appl., vol. 185, no. 8, Dec. 2021, Art. no. 115524. doi: 10.1016/j.eswa.2021.115524. [Google Scholar] [CrossRef]

21. J. Sinha and M. Manollas, “Efficient deep CNN-BiLSTM model for network intrusion detection,” in Proc. 3rd Int. Conf. Artif. Intell. Pattern Recognit. (AIPR), New York, NY, USA, Jun. 26–28, 2020, pp. 223–231. [Google Scholar]

22. B. Cao, C. Li, Y. Song, Y. Qin, and C. Chen, “Network intrusion detection model based on CNN and GRU,” Appl. Sci., vol. 12, no. 9, May. 2022, Art. no. 4184. doi: 10.3390/app12094184. [Google Scholar] [CrossRef]

23. W. Hamilton, Z. Ying, and J. Leskovec, “Inductive representation learning on large graphs,” in Proc. 31st Int. Conf. Neural Inf. Process. Syst. (NIPS), Long Beach, CA, USA, Dec. 4–9, 2017. [Google Scholar]

24. E. Caville, W. W. Lo, S. Layeghy, and M. Portmann, “Anomal-E: A self-supervised network intrusion detection system based on graph neural networks,” Knowl.-Based Syst., vol. 258, no. 1, Dec. 2022, Art. no. 110030. doi: 10.1016/j.knosys.2022.110030. [Google Scholar] [CrossRef]

25. H. Nguyen and R. Kashef, “TS-IDS: Traffic-aware self-supervised learning for IoT network intrusion detection,” Knowl.-Based Syst., vol. 279, Nov. 2023, Art. no. 110966. doi: 10.1007/s10115-012-0494-9. [Google Scholar] [CrossRef]

26. Y. Liu et al., “Privacy-preserving point-of-interest recommendation based on simplified graph convolutional network for geological traveling,” ACM Trans. Intell. Syst. Technol., vol. 15, no. 4, pp. 1–17, Aug. 2024. doi: 10.1145/3620677. [Google Scholar] [CrossRef]

27. L. Qi, Y. Liu, Y. Zhang, X. Xu, M. Bilal and H. Song, “Privacy-aware point-of-interest category recommendation in Internet of Things,” IEEE Internet Things J., vol. 9, no. 21, pp. 21398–21408, Nov. 2022. doi: 10.1109/JIOT.2022.3181136. [Google Scholar] [CrossRef]

28. G. Duan, H. Lv, H. Wang, and G. Feng, “Application of a dynamic line graph neural network for intrusion detection with semisupervised learning,” IEEE Trans. Inf. Forensic Secur., vol. 18, pp. 699–714, 2023. doi: 10.1109/TIFS.2022.3228493. [Google Scholar] [CrossRef]

29. B. Claise, B. Trammell, and P. Aitken, “Specification of the IP flow information export (IPFIX) protocol for the exchange of flow information,” Document RFC 7011, Sep. 2013. Accessed: Oct. 24, 2024. [Online]. Available: http://www.ietf.org/rfc/rfc7011.txt [Google Scholar]

30. L. Yang, C. Chatelain, and S. Adam, “Dynamic graph representation learning with neural networks: A survey,” IEEE Access, vol. 12, no. 70, pp. 43460–43484, Jan. 2024. doi: 10.1109/ACCESS.2024.3378111. [Google Scholar] [CrossRef]

31. Y. Shi, Z. Huang, S. Feng, H. Zhong, W. Wang and Y. Sun, “Masked label prediction: Unified message passing model for semi-supervised classification,” in Proc. 30th Int. Joint Conf. Artif. Intell. (IJCAI 2021), Aug. 19–27, 2021, pp. 1548–1554. [Google Scholar]

32. J. Skarding, B. Gabrys, and K. Musial, “Foundations and modelling of dynamic networks using dynamic graph neural networks: A survey,” IEEE Access, vol. 9, pp. 79143–79168, 2021. doi: 10.1109/ACCESS.2021.3082932. [Google Scholar] [CrossRef]

33. Q. Li, Z. Han, and X. Wu, “Deeper insights into graph convolutional networks for semi-supervised learning,” in Proc. AAAI Conf. Artif. Intell., New Orleans, LA, USA, Feb. 02–07, 2018. doi: 10.1609/aaai.v32i1.11604. [Google Scholar] [CrossRef]

34. M. Chen, Z. Wei, Z. Huang, B. Ding, and Y. Li, “Simple and deep graph convolutional networks,” in Proc. 37th Int. Conf. Mach. Learn. (ICML), Jul. 13–18, 2020, pp. 1725–1735. Accessed: Oct. 24, 2024. [Online]. Available: https://proceedings.mlr.press/v119/chen20v.html. [Google Scholar]

35. N. Moustafa and J. Slay, “UNSW-NB15: A comprehensive data set for network intrusion detection systems,” in Proc. Mil. Commun. Inf. Syst. Conf. (MilCIS), Canberra, ACT, Australia, Nov. 10–12, 2015, pp. 1–6. doi: 10.1109/MilCIS.2015.7348942. [Google Scholar] [CrossRef]

36. M. Sarhan, S. Layeghy, and M. Portmann, “Towards a standard feature set for network intrusion detection system datasets,” Mobile Netw. Appl., vol. 27, no. 1, pp. 357–370, Feb. 2020. doi: 10.1007/s11036-021-01843-0. [Google Scholar] [CrossRef]

37. M. Sarhan, S. Layeghy, N. Moustafa, and M. Portmann, “NetFlow datasets for machine learning-based network intrusion detection systems,” in Big Data Technologies and Applications, Z. Deze et al., Eds., Cham, Switzerland: Springer, 2021, vol. 13083, pp. 117–135. [Google Scholar]

38. T. Zebin, S. Rezvy, and Y. Luo, “An explainable AI-based intrusion detection system for DNS over HTTPS (DoH) attacks,” IEEE Trans. Inf. Forensic Secur., vol. 17, no. 9, pp. 2339–2349, Sep. 2022. doi: 10.1109/TIFS.2022.3183390. [Google Scholar] [CrossRef]

39. X. Zhou, Y. Hu, W. Liang, J. Ma, and Q. Jin, “Variational LSTM enhanced anomaly detection for industrial big data,” IEEE Trans. Ind. Informat., vol. 17, no. 5, pp. 3469–3477, May 2021. doi: 10.1109/TII.2020.3022432. [Google Scholar] [CrossRef]

40. G. Duan, H. Lv, H. Wang, G. Feng, and X. Li, “Practical cyber attack detection with continuous temporal graph in dynamic network system,” IEEE Trans. Inf. Forensic Secur., vol. 19, no. 1, pp. 4851–4864, Jan. 2024. doi: 10.1109/TIFS.2024.3385321. [Google Scholar] [CrossRef]

41. M. Sarhan, S. Layeghy, and M. Portmann, “Evaluating standard feature sets towards increased generalisability and explainability of ML-based network intrusion detection,” Big Data Res., vol. 30, no. 3, Nov. 2022, Art. no. 100359. doi: 10.1016/j.bdr.2022.100359. [Google Scholar] [CrossRef]

42. L. Cai, J. Li, J. Wang, and S. Ji, “Line graph neural networks for link prediction,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 44, no. 9, pp. 5103–5113, Sep. 2022. doi: 10.1109/TPAMI.2021.3080635. [Google Scholar] [PubMed] [CrossRef]

43. R. Ying, D. Bourgeois, J. You, M. Zitnik, and J. Leskovec, “GNNExplainer: Generating explanations for graph neural networks,” in Proc. 33rd Int. Conf. Neural Inf. Process. Syst. (NeurIPS), Vancouver, BC, Canada, Dec. 08–14, 2019, pp. 9240–9251. [Google Scholar]