Optimizing Fine-Tuning in Quantized Language Models: An In-Depth Analysis of Key Variables

1  Introduction

In recent years, Large-scale Language Models (LLMs) have established new benchmarks in Natural Language Processing (NLP) by delivering remarkable performance across a diverse array of tasks [1–5]. The widely adopted pre-training-fine-tuning paradigm allows these models to first learn general language representations during pre-training and then adapt to specific downstream tasks through fine-tuning, thereby offering significant cost savings for end-users by minimizing the need for extensive retraining [6–8]. Despite these advancements, fine-tuning LLMs remains a memory-intensive endeavor due to their massive parameter sizes, presenting a substantial barrier to their broader deployment, especially in resource-constrained environments. To address these challenges, Parameter-Efficient Fine-Tuning (PEFT) techniques [9,10] and parameter quantization strategies [11–14] have been developed. PEFT methods, such as Low-Rank Adaptation (LoRA) [15–17], focus on reducing memory overhead by updating only a small subset of parameters using low-rank matrices, while quantization compresses models by converting high-precision weights into lower-precision formats, thereby drastically cutting down memory requirements and accelerating inference speeds.

One of the most notable advancements in this area has been the development of QLoRA [18], which integrates PEFT with quantization, combining the strengths of both approaches. Specifically, QLoRA first compresses pre-trained models into low-bitwidth formats via quantization and then applies LoRA for efficient fine-tuning. This dual approach effectively reduces the memory footprint during fine-tuning, making it more feasible for practical applications. Building on this foundation, several QLoRA variants, including Q-BaRA and QA-HiRA [19], IR-QLoRA [20], and QA-LoRA [21], have been introduced to further optimize model performance and enhance fine-tuning efficiency through different innovative methodologies. However, despite the growing popularity and practical success of these methods, key variables that critically influence adapter fine-tuning have not been adequately explored, especially in terms of their quantitative impact on fine-tuning outcomes and overall model accuracy.

In well-established research fields, the influence of key variables on model performance has been thoroughly investigated. Examples include sparsity rates in pruning [22], bit width in mixed-precision training [23], the number of experts in each layer of Mixture of Experts (MoE) models [24–26], and scaling laws in LLM inference [27–29]. Yet, the combination of quantization and PEFT-a hybrid approach that holds immense potential-has not been thoroughly investigated within this context. Moreover, the diversity of key variables involved in this hybrid method, ranging from rank and balancing factors to input-output configurations, introduces a level of complexity that goes beyond the scope of single-variable studies conducted in prior research. Given the direct impact of these variables on the number of trainable parameters and the broader implications for fine-tuning efficiency, a comprehensive examination is warranted.

This paper takes a pioneering step by offering an in-depth analysis of the key variables affecting fine-tuning in quantized LLMs. Building upon existing research, we categorize LLM layers by type and depth, systematically examining how different settings of key variables influence fine-tuning accuracy. Our investigation reveals several critical trends: (1) The rank of the adapter significantly impacts fine-tuning accuracy, especially for larger layers (e.g., MLP layers), which can tolerate reductions in rank with minimal performance loss. In contrast, smaller layers (e.g., self-attention layers) are more sensitive to rank reductions. Layer depth shows minimal influence in this context. (2) The choice of balancing factors is primarily dependent on their specific values, with certain settings consistently performing better across layers, rather than varying based on layer type or depth. (3) Quantization-aware fine-tuning allows larger layers to use smaller adapters effectively, while smaller layers face challenges in maintaining performance with reduced adapter size. Additionally, adapter size is more strongly linked to layer type than to layer depth. Overall, our findings highlight that layer type plays a more significant role than layer depth in optimizing fine-tuning for quantized LLMs. By tailoring configurations based on these insights, it is possible to achieve similar fine-tuning results with significantly fewer trainable parameters, offering a more resource-efficient approach. Future work will delve further into understanding these relationships to refine fine-tuning strategies for quantized LLMs.

2  Related Work

2.1 Optimize the Efficiency of LLM

Quantization Quantization is a model compression technique that reduces the numerical precision of model weights and activation functions, converting floating-point numbers to lower-precision representations such as 8-bit or lower integer formats [30–32]. This approach significantly reduces the storage size of the model, accelerates model loading and inference processes, while maintaining model performance within acceptable bounds. In LLMs, Post-Training Quantization (PTQ) is a common method applied after model pre-training to optimize deployment efficiency [12–14,33,34]. PTQ quantizes the model weights, thereby reducing memory footprint and enabling the use of more efficient computational hardware such as specialized quantization accelerators or FPGAs [27,35].

Parameter-Efficient Fine-Tuning Parameter-Efficient Fine-Tuning (PEFT) techniques are designed to address resource constraints encountered when fine-tuning large pre-trained models [9,10]. By introducing a small number of trainable parameters, these techniques avoid updating the entire parameter set of the model, thus reducing computational and memory requirements during the fine-tuning process. A key advantage of PEFT is that it allows the model to quickly adapt to new tasks while retaining pre-trained knowledge. LoRA (Low-Rank Adaptation), a PEFT method, introduces low-rank matrices in critical layers of the model to adjust weights [15–17]. This method has proven effective across various tasks, significantly reducing the number of parameters needed for fine-tuning.

2.2 Combination of PEFT and Quantification

A well-known recent work QLoRA combines quantization and LoRA methodologies [18]. It first quantizes the pre-trained model’s weights using a 4-bit NormalFloat format, followed by fine-tuning using LoRA. This approach not only reduces memory usage but also maintains the efficiency of the fine-tuning process. Additionally, QLoRA can be integrated with Quantization-Aware Training (QAT) [19,21], where the adapter components are compressed to align with the low-precision representations of the pre-trained model. QAT allows the model to account for the effects of quantization during training, resulting in a more accurate low-precision inference model post fine-tuning. Recent work has focused on enhancing the accuracy of QLoRA by optimizing the fine-tuning of adapters [19] and preserving more information [20], thereby improving the overall accuracy.

2.3 Exploring the Optimization of Key Variables

Previous works have extensively investigated the underlying principles of traditional Deep Neural Network (DNN) model compression, such as the setting of different sparsity levels across layers [22,36,37] and the selection of bit-widths [23,38–40]. In recent years, with the rise of LLMs, researchers have shifted their focus towards understanding LLMs as well as fine-tuning [41]. For instance, in the case of MOE models, it has been observed that different MOE layers learn different representations, leading to varying optimal numbers of experts across layers [26]. And for the computer vision model, the layer close to the input learns the basic representation, so we can choose to freeze during fine-tuning [24,25]. Some studies have focused on exploring trade-offs in LLM through the lens of scaling laws, aiming to uncover the potential relationships between key variables and training outcomes [27–29]. For instance, research has examined how to balance bit width and the number of parameters under the same memory constraints, analyzed the impact of different data types on final performance, and evaluated the effects of network width and depth across various datasets. However, the scaling laws for LLMs primarily analyze inference, leaving a gap in the research on fine-tuning. Additionally, recent studies combining quantization with PEFT have introduced a variety of key variables that warrant further investigation.

3  Methodology

3.1 Preliminaries

In this section, we briefly introduce the principles of the methods involved in this paper to facilitate the explanation of the key variables.

Quantization. To save memory usage during model loading, the pre-trained model is first quantized into a low-precision representation before fine-tuning the LLM [33,35]. The quantization converts high-precision floating-point w into low-precision representations w^=⌈w−βα⌋. The parameters α and β serve as the quantization factors within the quantization block, respectively achieving the scaling and shifting of values. ⌈⌋ is the rounding function, and w^ is the low-precision representation. During fine-tuning, the low-precision representation needs to be dequantized back to a high-precision data format for computation:

w~=α⋅w^+β=α⋅⌈w−βα⌋+β(1)

LoRA introduces two low-rank matrices A and B as fine-tuning modifications for linear layer [15]. The dimension of A is (Dinput,Drank), and B is (Drank,Doutput), where Drank<<min(Dinput,Doutput). Thus, AB forms a matrix with the same dimensions as the original, but the actual count of trainable parameters is significantly lower than that of the base layer, specifically Dinput×Drank+Drank×Doutput<<Dinput×Doutput. The methods presented below are all based on a similar low-rank adaptation fine-tuning approach, while the number of trainable parameters can be adjusted by modifying the rank of adapter. The fine-tuning computation can be expressed as:

y=W⊤x+s⋅(AB)⊤x(2)

where x and y are the input and output for adapter, respectively. s is the scaling factor.

QLoRA combines quantization and LoRA, first quantizing the LLM parameters and then fine-tuning using LoRA [18]. The fine-tuning computation can be represented as:

y=W~⊤x+s⋅(AB)⊤x(3)

where replace the pre-trained W with W~.

IR-QLoRA uses the effective Information Elastic Connection (IEC) structure in the adapter part to enrich the adapter’s information without changing the structure of adapters [20]. The fine-tuning process can be expressed as:

y=W~ICQ⊤x+s⋅[B⊤(A⊤x+avg(x))+concat(A⊤x+avg(x))](4)

where W~ICQ is the weight of Information Calibration Quantization (ICQ), and avg(),concat() are the are non-parameter operators, which perform averaging and splicing operations respectively (defined in [20]).

Q-BaRA introduces a balancing factor λ in the QLoRA computation and simplifies the adapter input and output by compressing them by a factor of λ, while expanding the rank by λ (thus the number of trainable parameters remains unchanged) [19]. The fine-tuning computation can be represented as:

y=W~⊤x+s⋅repeat(B')⊤(A')⊤avg(x))(5)

where avg() and repeat() are implemented through AvgPool(λ) and repeat_interleave(λ), respectively. Both AvgPool() and repeat_interleave() are the function defined in PyTorch, see the official PyTorch documentation1 for a detailed explanation.

QA-HiRA uses a single matrix B as the fine-tuning adapter, with the dimensions (Dinputλ1,Doutputλ2) [19]. λ1⋅λ2 equals the block_size of the pre-trained model quantization. The fine-tuning computation can be expressed as:

y=W~⊤x+s⋅repeat((C')⊤avg(x))(6)

where avg() and repeat() are also implemented through AvgPool(λ1) and repeat_interleave(λ2) in PyTorch, respectively. Since the multiplication of two matrices is no longer used, the number of parameters of QA-HiRA no longer involves the rank of the adapter, but can be calculated as Dinputλ1×Doutputλ2

QA-LoRA compresses the adapter input to align with the group-wise quantization of the pre-trained model for QAT fine-tuning [21]. The compression factor is group size. The fine-tuning computation can be represented as:

y=W~⊤x+s⋅(AB)⊤avg(x)(7)

where avg() is implemented through AvgPool(group_size).

A comparison of these methods is shown in Fig. 1.

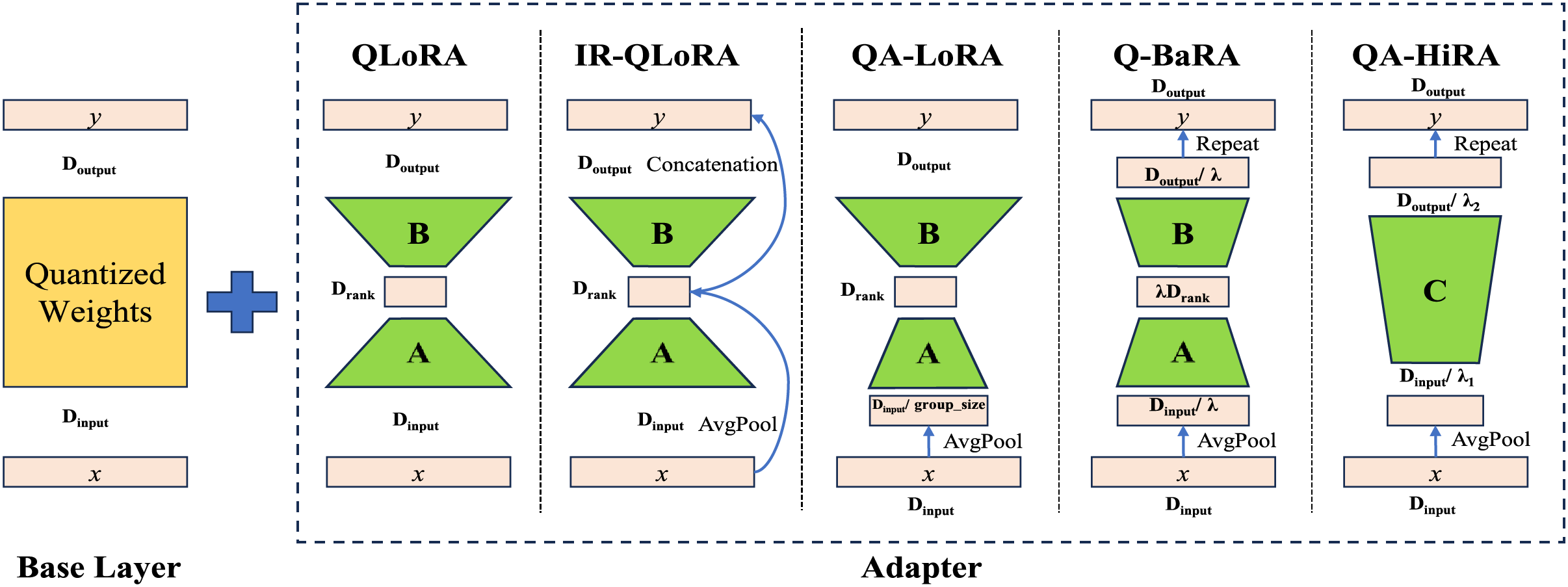
Figure 1: Comparison of QLoRA, IR-QLoRA, QA-LoRA, Q-BaRA, QA-HiRA

3.2 Key Variable

In the methods that fine-tune quantized LLMs using LoRA, three categories of key variables directly influence the adapter’s fine-tuning process. The first category pertains to the rank of LoRA, which controls the intrinsic rank of the low-rank adapter. The second category includes factors that balance the adapter’s capability with the difficulty of fine-tuning, such as the λ proposed in Q-BaRA. The third category comprises functional variables aimed at aligning the quantization of the pre-trained model to achieve QAT-based fine-tuning, such as λ1 and λ2 proposed in QA-HiRA, and the group size proposed in QA-LoRA. The detailed explanations of these key variables are as follows:

•   rank of adapter: This variable is the intrinsic dimension of the low-rank adapter fine-tuning, determining the complexity of the parameter space that the product matrix can represent, which is Drank of matrices A and B introduced in Section 3.1. Consequently, varying ranks correspond to different dimensions of the adapter. If the rank is too low, it may fail to capture sufficient task-specific information; if it is too high, it approaches full-parameter fine-tuning, losing the advantage of parameter efficiency. The methods involved include QLoRA, IR-QLoRA, QA-LoRA, and Q-BaRA.

•   Balancing factor λ (in Q-BaRA): This factor simplifies the adapter’s input and output, compressing the dimensions to 1/λ of the original while expanding the rank by λ times. In the corresponding methods, λ is utilized within the PyTorch functions AvgPool(λ) and repeat_interleave(λ) to adjust the adapter’s dimensions. The number of trainable parameters remains unchanged.

•   Compression factor λ1, λ2 (in QA-HiRA): These factors simplify the adapter’s input and output, compressing the input dimensions to 1/λ1 and the output dimensions to 1/λ2. In the corresponding methods, λ1, λ2 are also utilized within the PyTorch functions AvgPool(λ) and repeat_interleave(λ) to adjust the adapter’s dimensions. The adapter forms a matrix with dimensions (Dinputλ1,Doutputλ2).

•   group_size in QA-LoRA: This variable performs pooling operations on the adapter input, downpooling group size values with their average. It also reduces the number of parameters in matrix A. group_size is utilized within the PyTorch functions AvgPool(group_size). In the QA-LoRA method, it jointly affects fine-tuning along with rank.

•   A graphical explanation of these key variables can be found in Fig. 1.

3.3 Experimental Settings

Experimental design.In the aforementioned methods, researchers have already conducted analyses on the key variables within their approaches; however, two critical factors remain unexplored:

1) Layer-specific analysis: Considering the differences between various layers in LLMs, particularly between attention layers and MLP (Multi-Layer Perceptron) layers, we have conducted a more granular analysis of the key variables specific to each layer.

2) Integrated analysis for key variables: With the introduction of various methods, a diverse set of key variables has been identified, each serving different functions. In some approaches, multiple key variables simultaneously influence the fine-tuning of LLMs. Therefore, we have integrated these factors into our experiments to conduct a comprehensive analysis, providing deeper insights into the fine-tuning process.

Foundation models and datasets. We use LLaMA [4] and LLaMA2 [42] (ranging from 7B to 13B) as the foundation models for our experiments. Alpaca [43] is selected as the fine-tuning dataset for our study. Alpaca was created using only 52 K data with minimal training cost, achieving performance approximately equivalent to GPT-3.5.

Measurement metrics. We assess the performance of the LLMs in few-shot settings using the Massively Multitask Language Understanding (MMLU) benchmark [44], which is a comprehensive assessment tool designed to evaluate the capabilities of LLMs across a wide array of NLP tasks. It serves as a platform for measuring the generalization and transfer learning abilities of LLMs by challenging them with diverse datasets spanning multiple domains. MMLU encompasses a broad spectrum of subjects, including 57 tasks across various domains such as humanities, STEM, and social sciences. The benchmark is constructed with the intent to simulate real-world scenarios where language models must exhibit proficiency in understanding and generating human-like responses to various tasks. We evaluate the average score across all tasks. The official MMLU evaluation script and prompts are utilized for this purpose.

Additionally, we evaluate the zero-shot common sense reasoning capabilities of the models on tasks from HellaSwag [45], PIQA [46], WinoGrande [47], ARC [48], BoolQ [49], and OpenBookQA [50], with results generated using the OpenCompass Large Model Evaluation System 2.

Quantization. We rigorously follow the quantization methods specified for each approach to compress the pre-trained models. Specifically, QLoRA [18], IR-QLoRA [20], Q-BaRA, and QA-HiRA [19] employ NF4 combined with double quantization [35], while QA-LoRA uses GPTQ [33] for quantization.

Training details. During the fine-tuning phase, we set the constant LoRA α to 16 and apply no dropout. The optimization process utilizes a paged AdamW optimizer, with a maximum gradient norm of 0.3. We employ a batch size of 4 and accumulate gradients over 4 steps. A constant learning rate schedule is applied, with the rate set at 2×10−5 for the 7B and 13B models, and 1×10−5 for the 33B and 65B models. Fine-tuning involves 10 K steps for Alpaca.

Model details. We utilize the standard LLaMA [4] and LLaMA2 [42] models, which share a highly similar architecture consisting of multiple DecoderLayers, with each DecoderLayer comprising an Attention module and an MLP. Following the typical setup for LoRA fine-tuning of quantized LLM models, we incorporate LoRA into both the Attention and MLP components for fine-tuning. The specific layers involved and their respective dimensions are detailed in the accompanying Table 1.

4  Experimental Results

In this section, we report the impact of various key variables on different evaluation metrics under multiple experimental configurations. We summarize the underlying patterns observed across these different conditions. The results presented are the averages from 3 independent experiments.

In order to conveniently display the experimental results, we list the experimental list in Table 2.

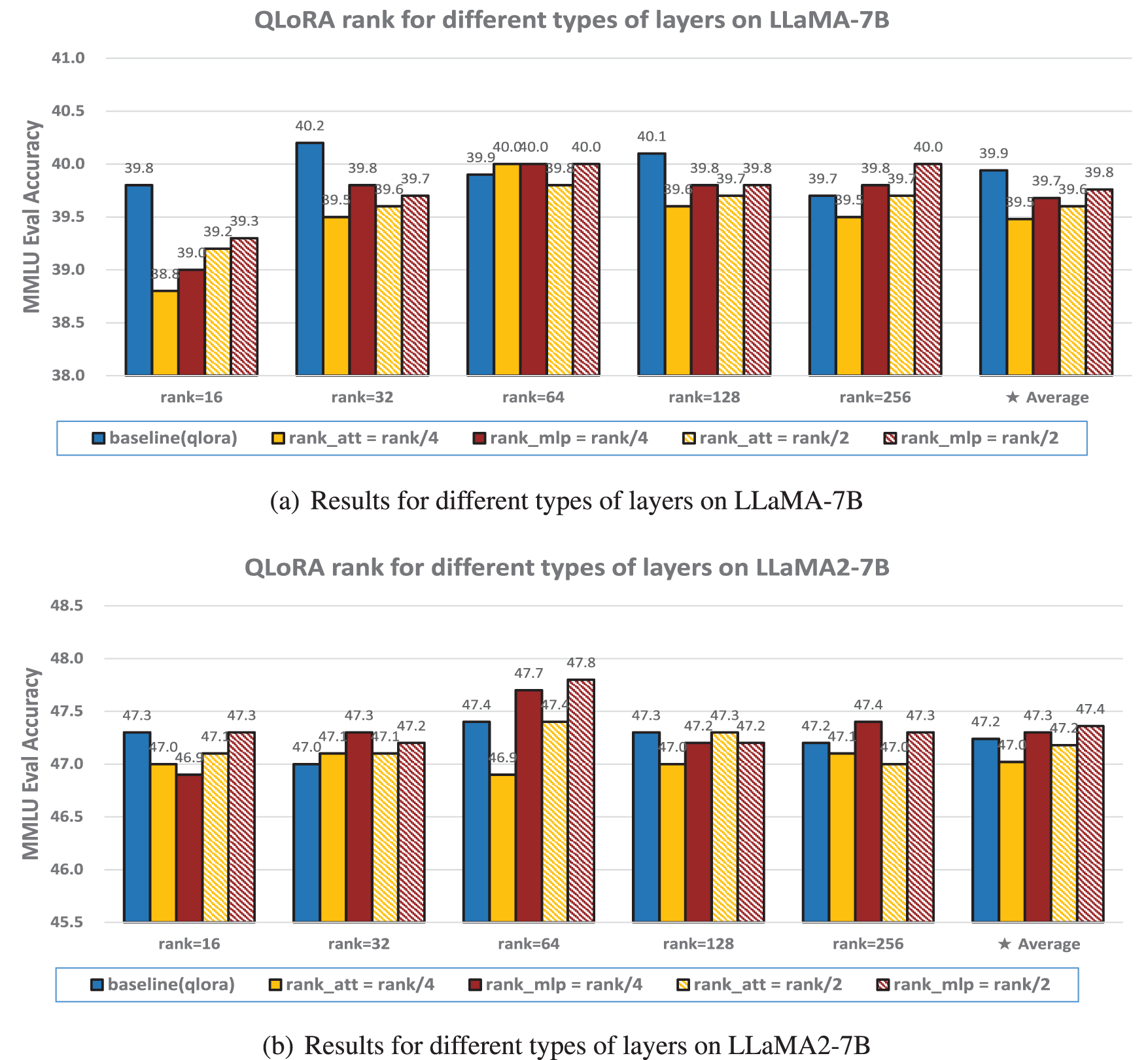
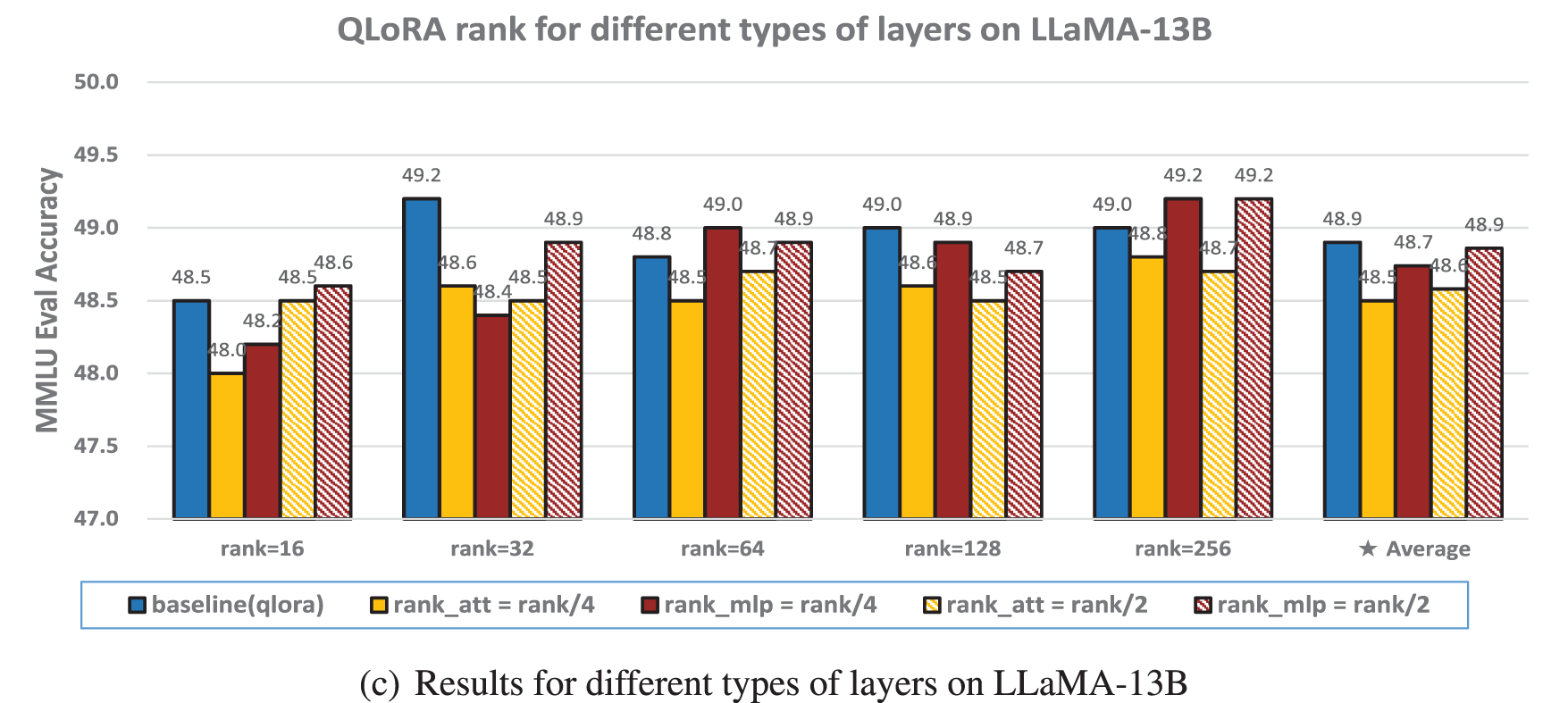
Figure 2: The 5-shot MMLU accuracy (%) of various ranks on different types of layers

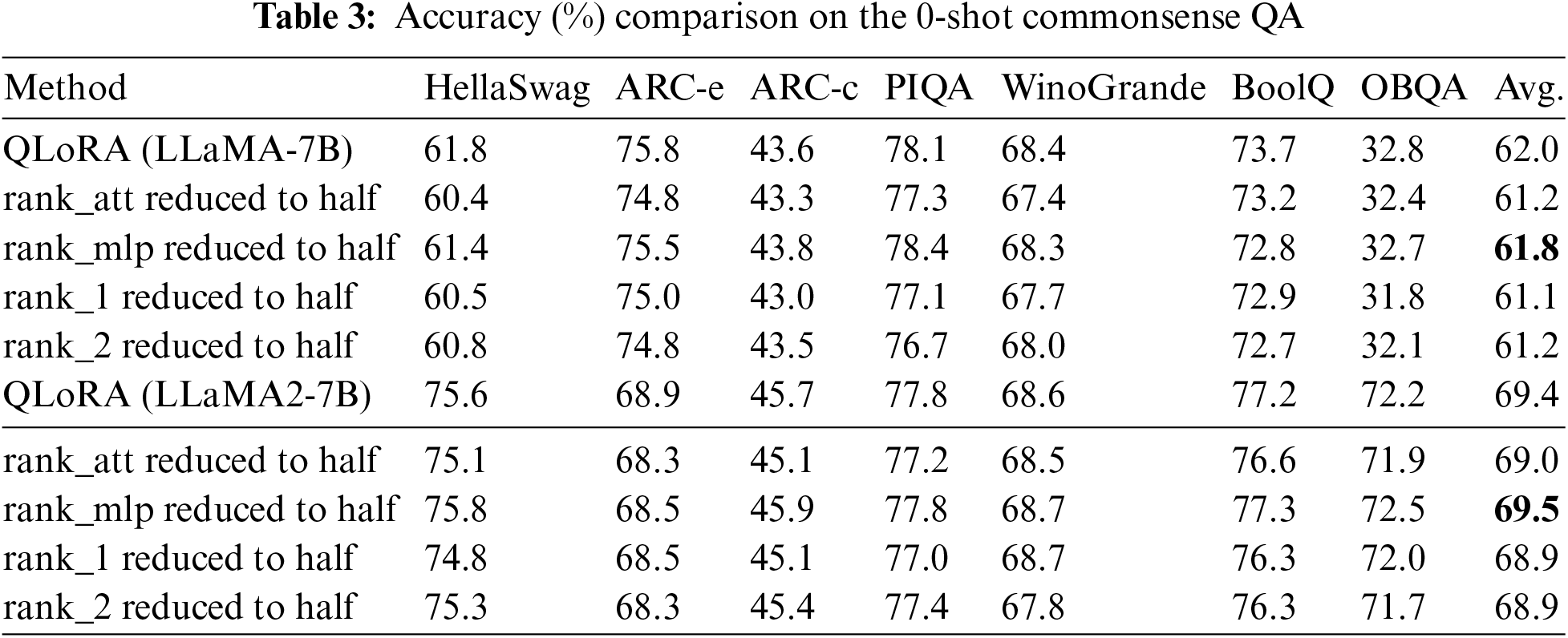
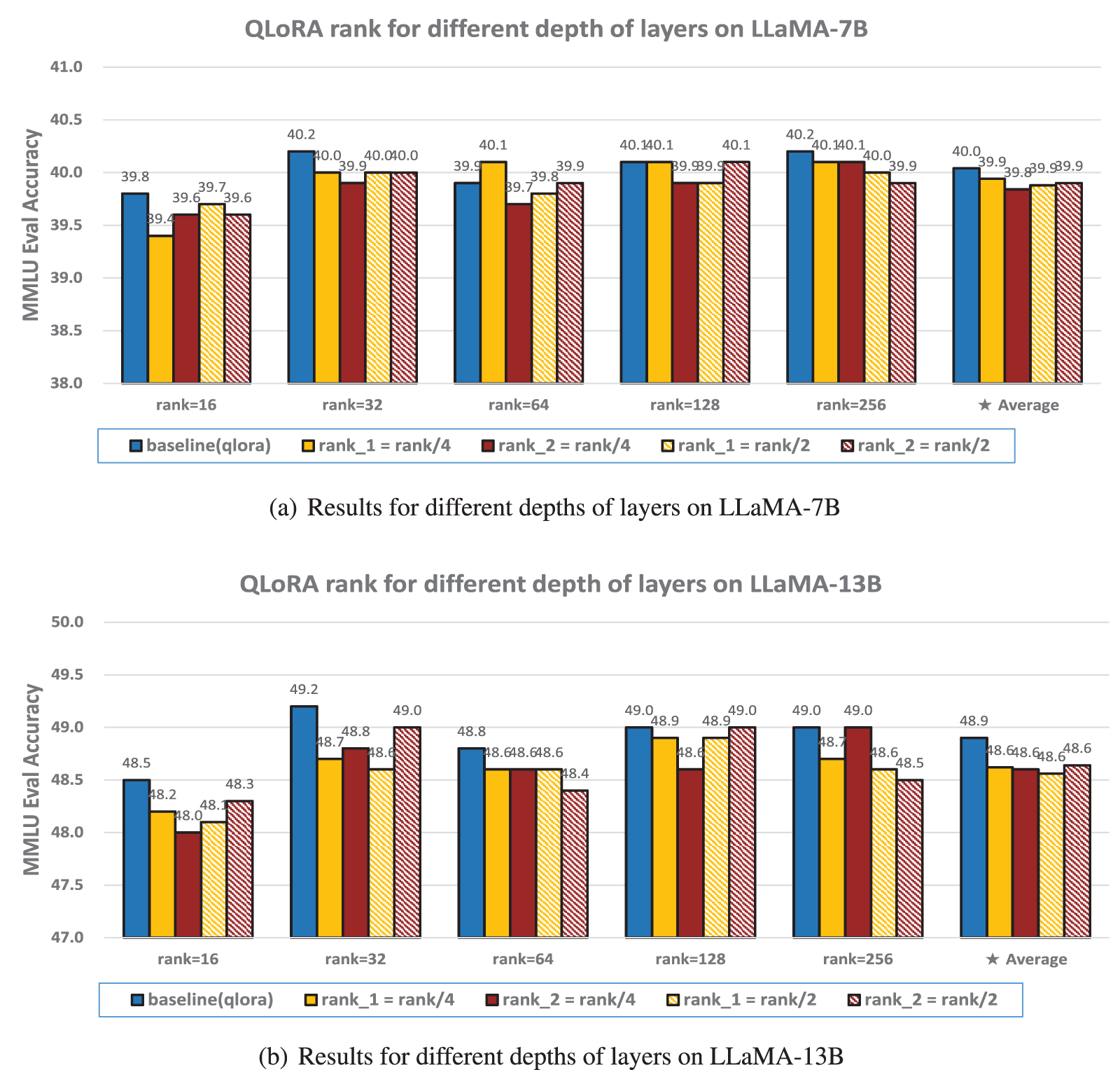
Figure 3: The 5-shot MMLU accuracy (%) of various ranks on different depths of layers

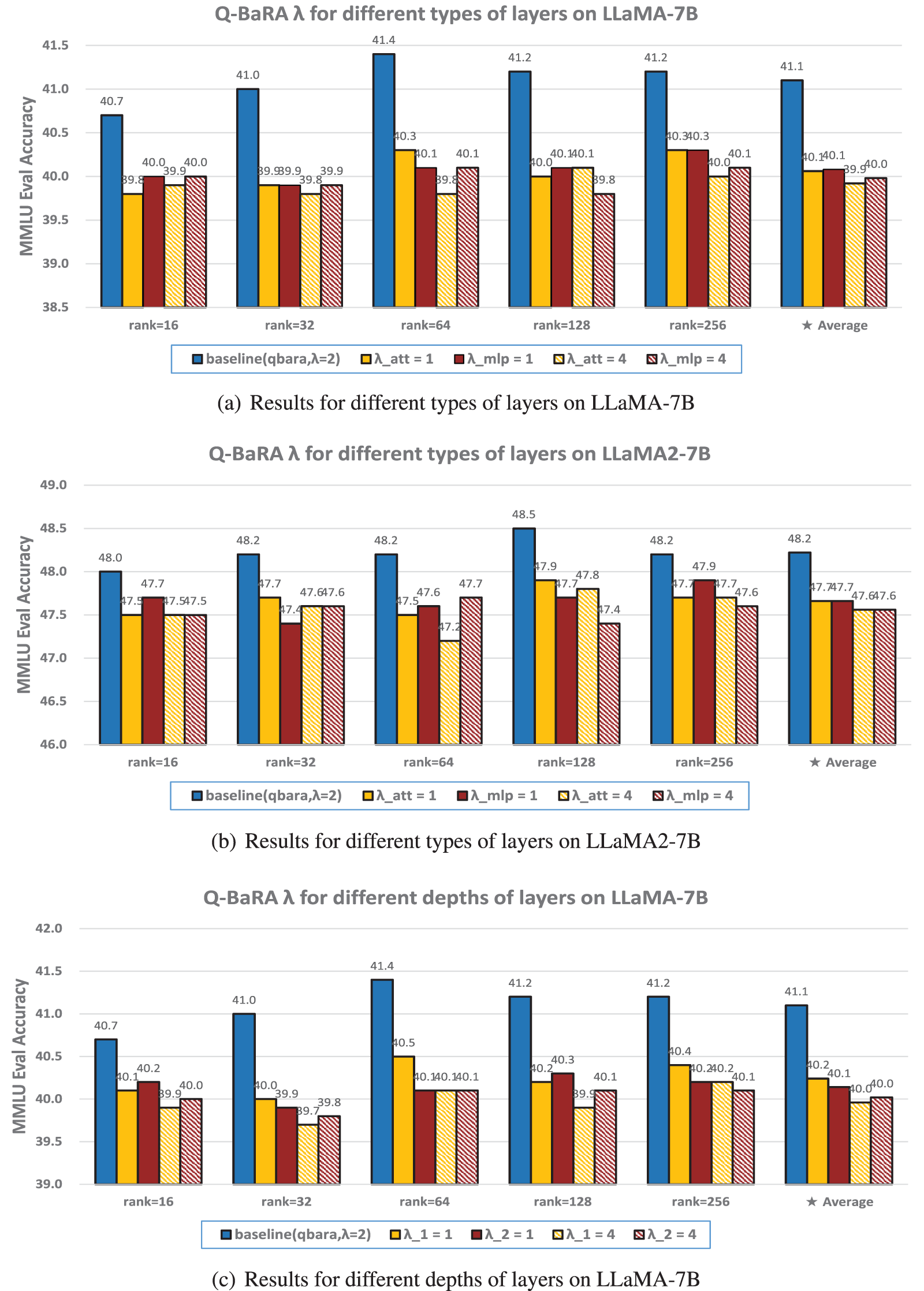
Figure 4: The 5-shot MMLU accuracy (%) of various λ on different layers

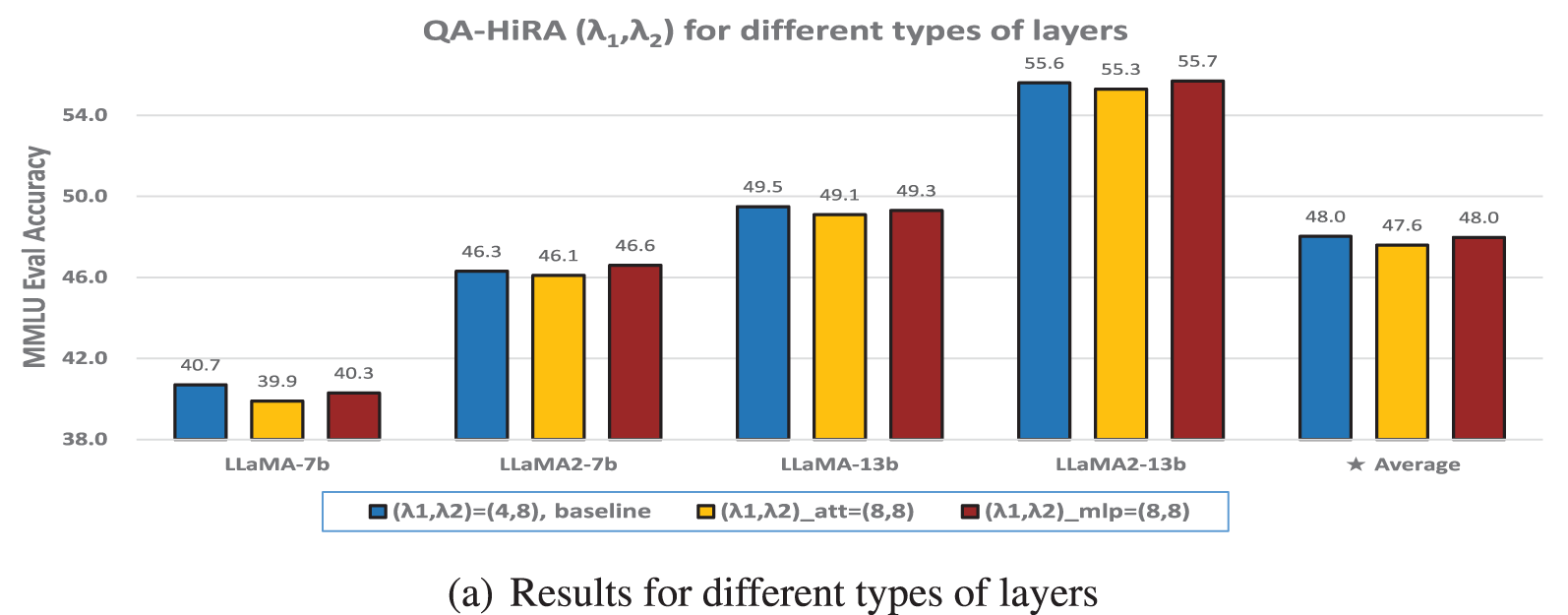
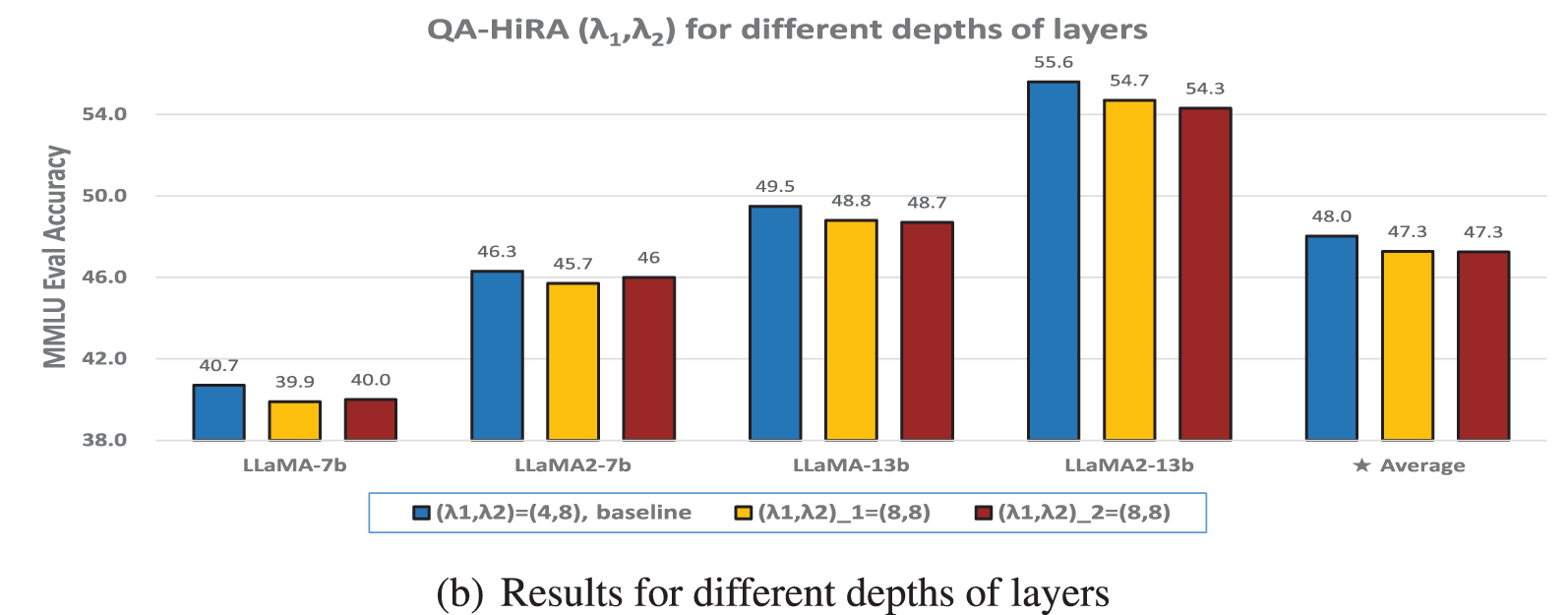
Figure 5: The 5-shot MMLU accuracy (%) of various λ1 and λ2 on different layers

4.1 Results of Experiments on LoRA Rank

We first present the impact of rank on the performance of different layers. The layers of the model are categorized based on their type (self-attention or MLP) and depth (the first half closer to the input or the second half closer to the output). We then examine the relationship between fine-tuning performance and rank.

Various ranks across different types of layers. In LLMs, the computational processes across layers differ significantly, as do the number of trainable parameters involved in each layer. To account for these variations, we assigned different ranks to distinct layer types during fine-tuning and evaluated their impact on MMLU test accuracy. As illustrated in Fig. 2, a clear trend can be observed: compared to self-attention layers (including q_proj, k_proj, v_proj, and o_proj) and MLP layers (including gate_proj, up_proj, and down_proj), the self-attention layers are more sensitive to rank reduction, whereas MLP layers exhibit greater robustness to such reductions (regardless of whether the rank is decreased by 2-fold or 4-fold, the height of the red bars in the histogram is generally higher than that of the yellow bars). When the rank of MLP layers is lowered, the impact on overall accuracy is noticeably smaller. Furthermore, when the rank is extremely low, fine-tuning performance degrades accordingly, with a sharper decline in accuracy as the rank is reduced further. However, when the initial rank is relatively high, a moderate reduction, particularly in MLP layers, does not significantly compromise accuracy. The decrease in rank corresponds to a decrease in the number of trainable parameters. It is noteworthy that halving or quartering the trainable parameters of larger multilayer perceptron (MLP) layers does not affect the final fine-tuning accuracy. Specifically, for the LLaMA-7B model, this results in a reduction of approximately 33.42% and 50.13% in overall trainable parameters, respectively, while for the LLaMA-13B model, the reduction is about 33.47% and 50.20%. These findings hold true for a rank of 64, which is commonly used in practice, as well as when considering the average across various ranks. This pattern is consistently observed across both LLaMA and LLaMA2 models, as well as in the IR-QLoRA, QA-LoRA and Q-BaRA setting (shown in Fig. A1), suggesting the broad applicability and robustness of this finding.

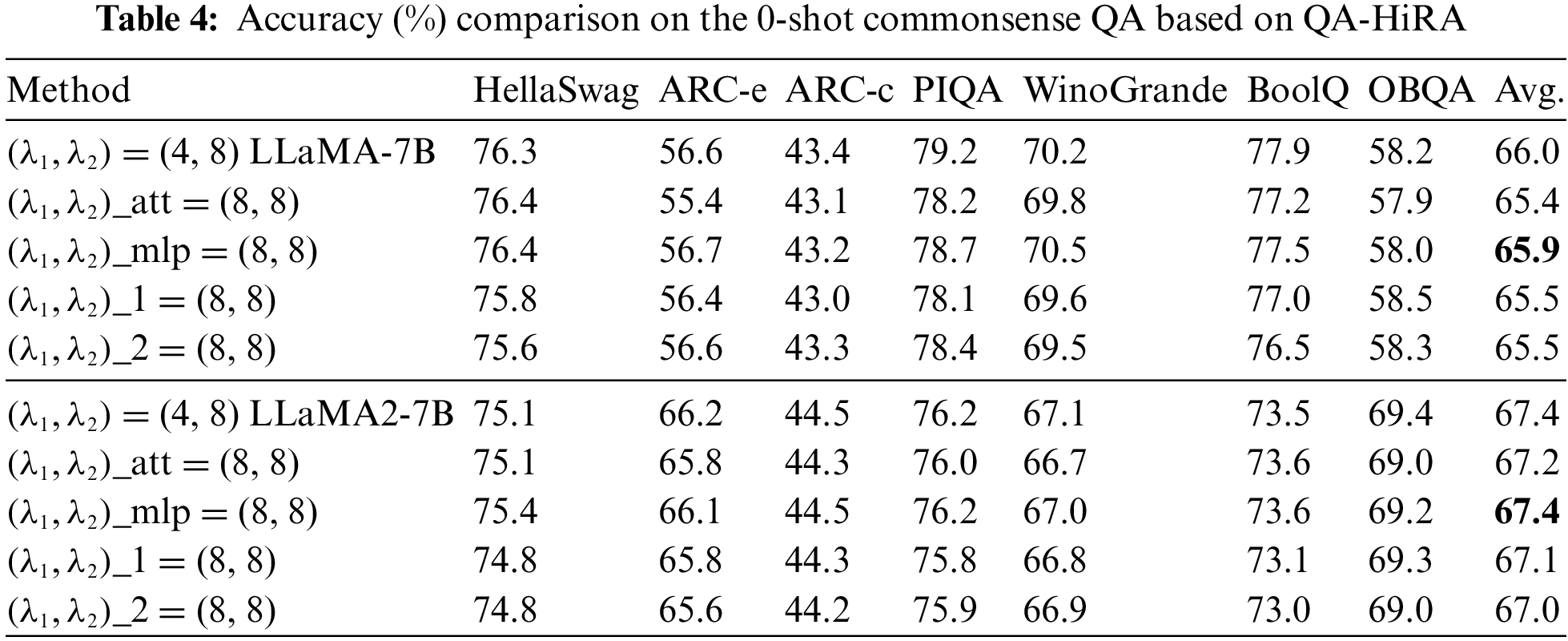
We also fine-tuned the models using these configurations and observed their performance on the 0-shot commonsenseQA, as depicted in Table 3. The same pattern emerged across various tasks: appropriately reducing the rank of MLP layers has a negligible impact on the final performance.

Various ranks on different depths of layers. Layers at different depths learn distinct representations, and many key variables are directly correlated with layer depth. However, when fine-tuning quantized LLMs, as illustrated in Fig. 3, we did not observe a significant correlation between accuracy and layer depth when varying the rank across different depths (rank_1 represents the rank of the first half of the model, close to the input, and rank_2 represents the rank of the second half of the model, close to the output). This lack of correlation may be attributed to the fact that quantizing a pre-trained LLM causes a loss of information due to low-precision representations. Consequently, during fine-tuning, the quantized LLM must not only learn new knowledge from the target dataset but also compensate for the information lost during quantization. Therefore, reducing the rank in either the earlier or later layers adversely impacts the final accuracy.

4.2 Results of Experiments on Balancing Factor

The balancing factor λ proposed in Q-BaRA [19] can be considered another key variable. Built upon the QLoRA framework, it balances the complexity between the adapter’s input and output and the rank size. Additionally, both λ and rank jointly influence the adapter’s fine-tuning performance. Therefore, we conducted comprehensive experiments by analyzing these factors in combination.

Various λ values on different layer types and depths. We evaluated the fine-tuning performance across different layer types and depths using various λ values under different rank settings. The configuration from Q-BaRA, where a uniform λ=2 is applied across all adapters, is used as the baseline for comparison. The experimental results, shown in Fig. 4, indicate no significant correlation between the choice of λ and the type or depth of the layers. Instead, the ultimate accuracy is related to the value of λ itself: setting λ=1 for some adapters outperforms setting λ=4 (The yellow and red bars with no patterns are taller than the yellow and red bars with spaced patterns), suggesting that excessive simplification of the adapter’s input and output is detrimental to fine-tuning. Additionally, deviating from the λ=2 setting (whether lowering to 1 or increasing to 4) leads to a decrease in accuracy, confirming that λ=2 serves as the optimal balance point for fine-tuning. Additional results regarding the selection of λ value can be found in Fig. A2.

4.3 Results of Experiments on Quantization-Aware Fine-Tuning

In some studies, a quantization-aware fine-tuning strategy is employed to ensure that the fine-tuned model can be directly represented in low bit-width formats. This is typically achieved by compressing the inputs and outputs of adapters to align with the quantization approach used in the pre-trained model. We conducted experiments to analyze the impact of varying compression factors on fine-tuning performance. For QA-LoRA [21], which similarly uses two low-rank matrices as adapters, the relationship between fine-tuning performance and rank has already been discussed in Section 4.1. However, since the group size in QA-LoRA must strictly match the GPTQ compression in the pre-trained model, it cannot be freely adjusted layer by layer. Therefore, our primary focus is on experiments involving QA-HiRA [19].

Various combinations of λ1 and λ2 across different layers. In QA-HiRA, the quantized blocks in the pre-trained model typically use sizes of 32 or 64, and it has been suggested in the study that the combination of (λ1,λ2) can take values from (4, 8) or (8, 8). As analyzed in Section 3.1, larger λ1×λ2 represents a larger compression factor and uses a smaller size adapter. We conduct experiments by categorizing layers based on type and depth, and test different combinations of (λ1,λ2) to observe their impact on fine-tuning performance. We use the default setting (λ1,λ2)=(4,8) for the whole model as the baseline, and change the setting of some adapters to (λ1,λ2)=(8,8) according to the types or depths of layers, respectively. As shown in Fig. 5, although larger block sizes increase quantization error, the results indicate that setting (λ1,λ2)=(8,8) for MLP layers does not degrade fine-tuning performance, suggesting that MLP layers can accommodate higher block sizes and thus reduce the number of trainable parameters. Additionally, no clear correlation was found between the optimal (λ1,λ2) configuration and layer depth. The same conclusion is also reflected in the 0-shot CommonsenseQA task, as shown in the Table 4.

5  Conclusion

In this work, we systematically analyzed fine-tuning strategies that combine PEFT with parameter quantization. Focusing on recent methodologies, we examined the influence of key variables within these approaches on the final fine-tuning performance. Based on extensive experiments, we reached the following conclusions:

•   The rank of the adapter significantly impacts fine-tuning accuracy, especially when the rank is set extremely low. Furthermore, the effect of reducing the rank varies across different types of layers: larger layers (e.g., MLP layers) can maintain similar accuracy even with reduced rank, while smaller layers (e.g., self-attention layers) cannot. However, layer depth shows no clear correlation with rank reduction effectiveness.

•   Adjusting balancing factors according to layer type or depth does not yield a consistent correlation with fine-tuning accuracy. Instead, performance is more closely linked to the specific value of the balancing factor itself: a value of 2 generally performs best, followed by 1, while further increasing the factor tends to degrade fine-tuning results.

•   In quantization-aware fine-tuning methods that compress the input and output of adapters, larger layers (e.g., MLP layers) can effectively utilize smaller adapters (with fewer trainable parameters), whereas smaller layers (e.g., self-attention layers) struggle to maintain performance with similarly reduced adapters. Additionally, there is no significant correlation between adapter size and layer depth.

These findings provide insights into the intrinsic patterns governing fine-tuning in quantized LLMs, enabling more targeted configurations based on specific needs. Notably, when it is necessary to reduce the number of trainable parameters during fine-tuning, prioritizing the reduction of trainable parameters in larger layers is more conducive to maintaining the original fine-tuning accuracy. This suggests that layer type has a more substantial impact on fine-tuning outcomes compared to layer depth. The likely reason for this is that fine-tuning not only involves learning new knowledge for specific tasks but also compensates for the performance loss introduced by model quantization. Further exploration and analysis of these aspects are left for future work.

Acknowledgement: We extend our sincere thanks to our friends and family for their unwavering support and encouragement throughout the duration of this research endeavor. Their understanding and patience have provided us with the stability necessary to pursue our academic goals with dedication and focus. Additionally, we are deeply grateful for the invaluable assistance and camaraderie received from our peers and colleagues. Their insights and collaborative spirit have significantly enriched our work and contributed to the advancement of our research. We acknowledge the collective effort that has been instrumental in bringing this study to fruition.

Funding Statement: This work was supported by the National Key R&D Program of China (No. 2021YFB0301200) and National Natural Science Foundation of China (No. 62025208).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Ao Shen; data collection: Ao Shen, Xiaoyu Hu; analysis and interpretation of results: Ao Shen, Xiaoyu Hu; draft manuscript preparation: Ao Shen; project administration: Zhiquan Lai; funding acquisition: Zhiquan Lai, Dongsheng Li. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data presented in this study are available or can be reproduced in QLoRA at https://github.com/artidoro/qlorahttps://github.com/artidoro/qlora (accessed on 07 October 2024), IR-QLoRA at https://github.com/htqin/ir-qlorahttps://github.com/htqin/ir-qlora (accessed on 07 October 2024), QA-LoRA at https://github.com/yuhuixu1993/qa-lorahttps://github.com/yuhuixu1993/qa-lora (accessed on 07 October 2024), qbaraqahira at https://github.com/xiaocaigou/qbaraqahirahttps://github.com/xiaocaigou/qbaraqahira (accessed on 07 October 2024) and OpenCompass Large Model Evaluation System at https://opencompass.org.cn/homehttps://opencompass.org.cn/home (accessed on 07 October 2024).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

1https://pytorch.org/docs/stable/index.html (accessed on 07 October 2024).

2https://opencompass.org.cn/home, (accessed on 07 October 2024)

References

1. J. Achiam et al., “GPT-4 technical report,” 2023, arXiv:2303.08774. [Google Scholar]

2. S. Bubeck et al., “Sparks of artificial general intelligence: Early experiments with GPT-4,” 2023, arXiv:2303.12712. [Google Scholar]

3. T. Le Scao et al., “Bloom: A 176b-parameter open-access multilingual language model,” 2022, arXiv e-prints, pp. arXiv–2211. [Google Scholar]

4. H. Touvron et al., “LLaMA: Open and efficient foundation language models,” 2023, arXiv:2302.13971. [Google Scholar]

5. J. Wei et al., “Emergent abilities of large language models,” 2022, arXiv:2206.07682. [Google Scholar]

6. T. Brown et al., “Language models are few-shot learners,” Adv. Neur. Inf. Process. Syst., vol. 33, pp. 1877–1901, 2020. [Google Scholar]

7. J. Devlin, M. -W. Chang, K. Lee, and K. Toutanova, “BERT: Pre-training of deep bidirectional transformers for language understanding,” 2018, arXiv:1810.04805. [Google Scholar]

8. W. X. Zhao et al., “A survey of large language models,” 2023, arXiv:2303.18223. [Google Scholar]

9. X. L. Li and P. Liang, “Prefix-tuning: Optimizing continuous prompts for generation,” 2021, arXiv:2101.00190. [Google Scholar]

10. N. Houlsby et al., “Parameter-efficient transfer learning for NLP,” in Int. Conf. Mach. Learn., PMLR, 2019, pp. 2790–2799. [Google Scholar]

11. T. Dettmers et al., “SpQR: A sparse-quantized representation for near-lossless llm weight compression,” 2023, arXiv:2306.03078. [Google Scholar]

12. J. Lin et al., “AWQ: Activation-aware weight quantization for llm compression and acceleration,” 2023, arXiv:2306.00978. [Google Scholar]

13. G. Xiao, J. Lin, M. Seznec, H. Wu, J. Demouth and S. Han, “SmoothQuant: Accurate and efficient post-training quantization for large language models,” in Int. Conf. Mach. Learn., PMLR, 2023, pp. 38087–38099. [Google Scholar]

14. X. Wei et al., “Outlier suppression: Pushing the limit of low-bit transformer language models,” Adv. Neur. Inf. Process. Syst., vol. 35, pp. 17402–17414, 2022. [Google Scholar]

15. E. J. Hu, P. Wallis, Z. Allen-Zhu, Y. Li, S. Wang, L. Wang, W. Chen et al., “LoRA: Low-rank adaptation of large language models,” 2021, arXiv:2106.09685. [Google Scholar]

16. S. Hayou, N. Ghosh, and B. Yu, “LoRA+: Efficient low rank adaptation of large models,” 2024, arXiv:2402.12354. [Google Scholar]

17. B. Zi, X. Qi, L. Wang, J. Wang, K. -F. Wong and L. Zhang, “Delta-LoRA: Fine-tuning high-rank parameters with the delta of low-rank matrices,” 2023, arXiv:2309.02411. [Google Scholar]

18. T. Dettmers, A. Pagnoni, A. Holtzman, and L. Zettlemoyer, “QLoRA: Efficient finetuning of quantized LLMs,” in Advances in Neural Information Processing Systems, 2024, vol. 36, pp. 1–28. [Google Scholar]

19. A. Shen, Q. Wang, Z. Lai, X. Li, and D. Li, “Accurate and efficient fine-tuning of quantized large language models through optimal balance,” 2024, arXiv:2407.17029. [Google Scholar]

20. H. Qin et al., “Accurate LoRA-finetuning quantization of LLMs via information retention,” 2024, arXiv:2402.05445. [Google Scholar]

21. Y. Xu et al., “QA-LORA: Quantization-aware low-rank adaptation of large language models,” in Twelfth Int. Conf. Learn. Represent., 2023. [Google Scholar]

22. S. Liu et al., “The unreasonable effectiveness of random pruning: Return of the most naive baseline for sparse training,” 2022, arXiv:2202.02643. [Google Scholar]

23. Y. Fu et al., “CPT: Efficient deep neural network training via cyclic precision,” 2021, arXiv:2101.09868. [Google Scholar]

24. J. Yosinski, J. Clune, Y. Bengio, and H. Lipson, “How transferable are features in deep neural networks?” in Advances in Neural Information Processing Systems 27 (NIPS 2014), 2014, pp. 3320–3328. [Google Scholar]

25. M. D. Zeiler and R. Fergus, “Visualizing and understanding convolutional networks,” in Comput. Vis.-ECCV 2014: 13th Eur. Conf., Zurich, Switzerland, Springer, 2014, pp. 818–833. [Google Scholar]

26. S. Rajbhandari et al., “DeepSpeed-MoE: Advancing mixture-of-experts inference and training to power next-generation AI scale,” in Int. Conf. Mach. Learn., PMLR, 2022, pp. 18332–18346. [Google Scholar]

27. T. Dettmers and L. Zettlemoyer, “The case for 4-bit precision: k-bit inference scaling laws,” in Int. Conf. Mach. Learn., PMLR, 2023, pp. 7750–7774. [Google Scholar]

28. J. Kaplan et al., “Scaling laws for neural language models,” 2020, arXiv:2001.08361. [Google Scholar]

29. T. Henighan et al., “Scaling laws for autoregressive generative modeling,” 2020, arXiv:2010.14701. [Google Scholar]

30. B. Jacob et al., “Quantization and training of neural networks for efficient integer-arithmetic-only inference,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., 2018, pp. 2704–2713. [Google Scholar]

31. S. Han, H. Mao, and W. J. Dally, “Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding,” 2015, arXiv:1510.00149. [Google Scholar]

32. H. Cai, C. Gan, T. Wang, Z. Zhang, and S. Han, “Once for all: Train one network and specialize it for efficient deployment,” in Int. Conf. Learn. Represent., 2020, pp. 1–15. [Google Scholar]

33. E. Frantar, S. Ashkboos, T. Hoefler, and D. Alistarh, “GPTQ: Accurate post-training quantization for generative pre-trained transformers,” in Eleventh Int. Conf. Learn. Represent., 2023. [Google Scholar]

34. X. Wu, Z. Yao, and Y. He, “ZeroQuant-FP: A leap forward in llms post-training W4A8 quantization using floating-point formats,” 2023, 2023, arXiv:2307.09782. [Google Scholar]

35. T. Dettmers, M. Lewis, Y. Belkada, and L. Zettlemoyer, “GPT3. int8(8-bit matrix multiplication for transformers at scale,” in Neural Information Processing Systems (2022), vol. 35, pp. 30318–30332, 2022. [Google Scholar]

36. D. C. Mocanu, E. Mocanu, P. Stone, P. H. Nguyen, M. Gibescu and A. Liotta, “Scalable training of artificial neural networks with adaptive sparse connectivity inspired by network science,” Nat. Commun., vol. 9, no. 1, pp. 1–12, 2018. doi: 10.1038/s41467-018-04316-3. [Google Scholar] [PubMed] [CrossRef]

37. U. Evci, T. Gale, J. Menick, P. S. Castro, and E. Elsen, “Rigging the lottery: Making all tickets winners,” in Int. Conf. Mach. Learn., PMLR, 2020, pp. 2943–2952. [Google Scholar]

38. S. Zhou, Y. Wu, Z. Ni, X. Zhou, H. Wen and Y. Zou, “DoReFa-Net: Training low bitwidth convolutional neural networks with low bitwidth gradients,” 2016, arXiv:1606.06160. [Google Scholar]

39. Z. Ma et al., “BaGuaLu: Targeting brain scale pretrained models with over 37 million cores,” in Proc. 27th ACM SIGPLAN Symp. Prin. Pract. Parall. Programm., 2022, pp. 192–204. [Google Scholar]

40. C. Yang, Z. Wu, J. Chee, C. De Sa, and M. Udell, “How low can we go: Trading memory for error in low-precision training,” 2021, arXiv:2106.09686. [Google Scholar]

41. T. Jiang et al., “MoRA: High-rank updating for parameter-efficient fine-tuning,” 2024, arXiv:2405.12130. [Google Scholar]

42. H. Touvron et al., “LLaMA 2: Open foundation and fine-tuned chat models,” 2023, arXiv:2307.09288. [Google Scholar]

43. R. Taori et al., “Stanford alpaca: An instruction-following llama model,” 2023. Accessed: Aug. 15, 2024. [Online]. Available: https://github.com/tatsulab/stanford_alpaca [Google Scholar]

44. D. Hendrycks et al., “Measuring massive multitask language understanding,” 2020, arXiv:2009.03300. [Google Scholar]

45. R. Zellers, A. Holtzman, Y. Bisk, A. Farhadi, and Y. Choi, “HellaSwag: Can a machine really finish your sentence?” 2019, arXiv:1905.07830. [Google Scholar]

46. Y. Bisk et al., “PIQA: Reasoning about physical commonsense in natural language,” Proc. AAAI Conf. Artif. Intell., vol. 34, no. 5, pp. 7432–7439, 2020. doi: 10.1609/aaai.v34i05.6239. [Google Scholar] [CrossRef]

47. K. Sakaguchi, R. L. Bras, C. Bhagavatula, and Y. Choi, “WinoGrande: An adversarial winograd schema challenge at scale,” Commun. ACM, vol. 64, no. 9, pp. 99–106, 2021. doi: 10.1145/3474381. [Google Scholar] [CrossRef]

48. P. Clark et al., “Think you have solved question answering? try ARC, the AI2 reasoning challenge,” 2018, arXiv:1803.05457. [Google Scholar]

49. C. Clark, K. Lee, M. -W. Chang, T. Kwiatkowski, M. Collins and K. Toutanova, “BoolQ: Exploring the surprising difficulty of natural yes/no questions,” 2019, arXiv:1905.10044. [Google Scholar]

50. T. Mihaylov, P. Clark, T. Khot, and A. Sabharwal, “Can a suit of armor conduct electricity? A new dataset for open book question answering,” 2018, arXiv:1809.02789. [Google Scholar]

Appendix A. More Experimental Results

From Fig. A1, it is observable that across all variant methods, a consistent pattern emerges: layers with larger sizes (MLP layers), exhibit a greater capacity to withstand reductions in rank.

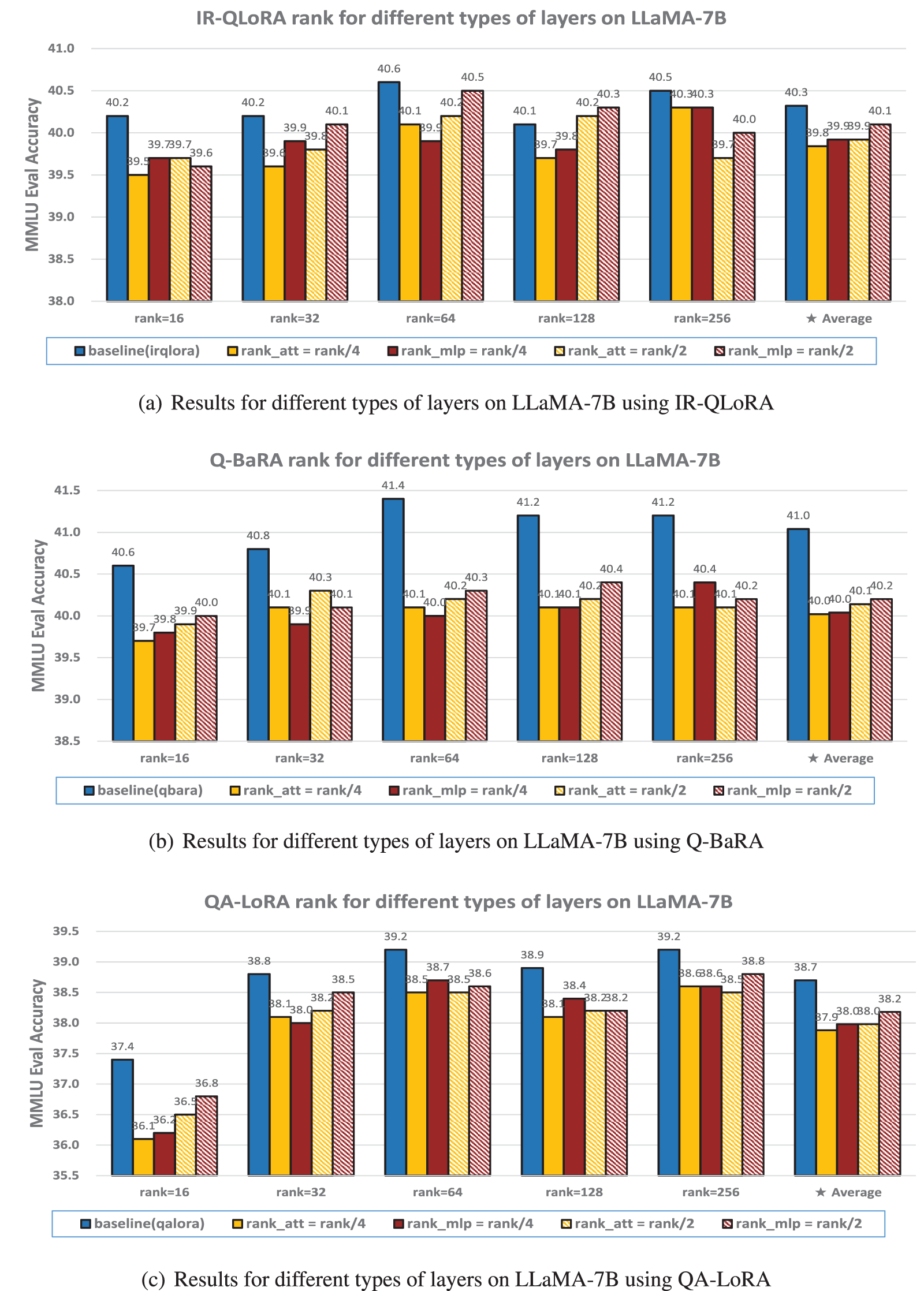
Figure A1: The 5-shot MMLU accuracy (%) of various λ on different layers

Fig. A2 reveals that, with the exception of scenarios where the rank is extremely low, a setting of λ=2 consistently yields optimal results. Utilizing higher values of λ (i.e., λ=4 or λ=8) does not surpass the performance achieved with the λ=1 configuration.

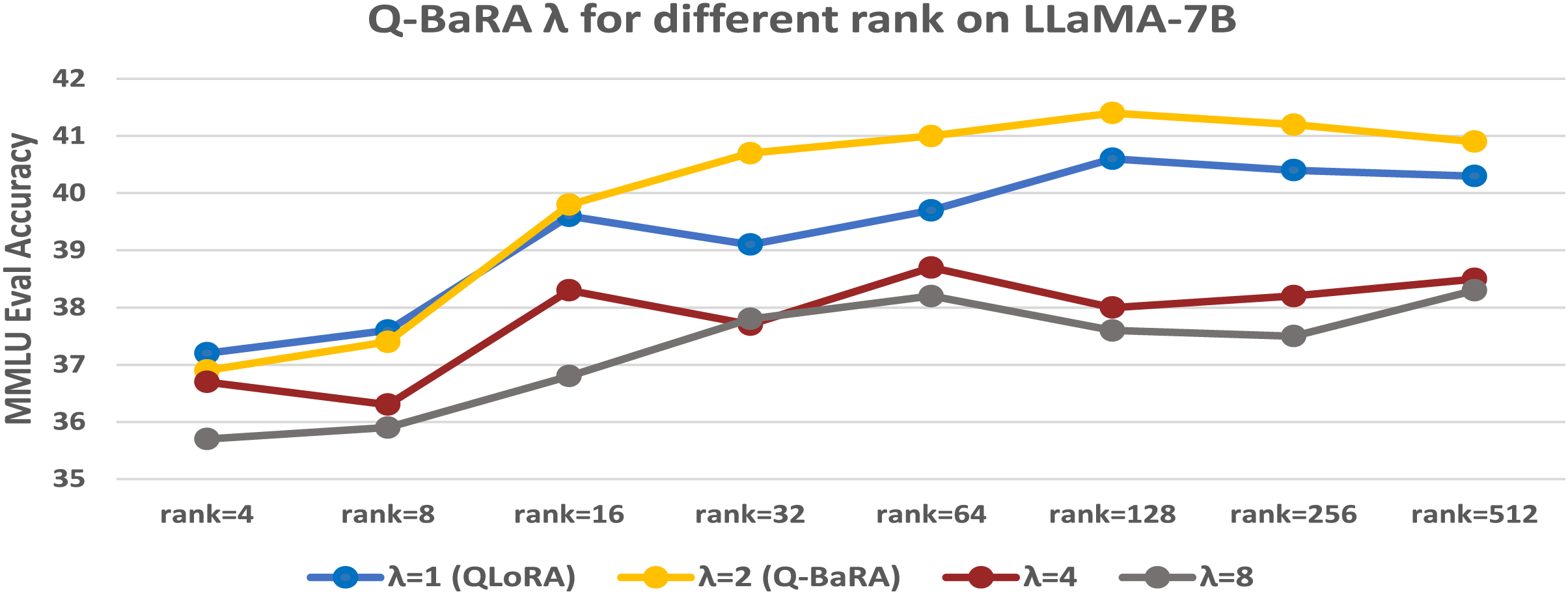
Figure A2: The 5-shot MMLU accuracy (%) of various values of λ