Offload Strategy for Edge Computing in Satellite Networks Based on Software Defined Network

1  Introduction

With the rapid advancement of communication technology, humanity is faced with the challenge of processing vast amounts of data. In different usage scenarios, users have varying requirements for task processing, such as the need for extremely low latency in certain situations [1]. Due to physical size and energy supply limitations, the computing power of devices is often limited, and local processing of tasks can increase computational delays and degrade user experience [2]. The European Telecommunications Standards Institute (ETSI) introduced Mobile Edge Computing (MEC). This technology offers IT and cloud computing capabilities near users within the network and can be deployed in various locations, including base stations, access points, and satellites [3]. Computing offloading technology enables users to leverage the computational power at the network edge [4–6].

Satellite edge networks utilize geostationary orbit (GEO) or low Earth orbit (LEO) satellites as network nodes to extend edge computing capabilities to the satellite level, allowing for long-distance data processing and storage, thereby reducing latency. Mobile edge networks offer high-density user services in localized areas, while satellite edge networks can cover remote regions and oceans that traditional mobile networks struggle to reach, finding applications in emergency communication, navigation, and positioning scenarios [7,8]. Satellite networks can enhance and expand terrestrial networks, achieving seamless global coverage [9]. Utilizing satellite networks allows us to bypass the constraints of terrestrial networks, particularly in regions with challenging terrain, while also offering multicast and broadcast functionalities.

Leveraging the strengths of satellite and ground-based networks, the hybrid architecture of satellite-terrestrial networks is expected to facilitate global coverage of 6G networks and provide ubiquitous communication support for the Internet of Things (IoT) [10,11]. Nonetheless, given the constraints on the computing capabilities of mobile devices, users aim to delegate as many tasks as they can to satellite-edge computing nodes to minimize the latency in processing. Nevertheless, due to the limited nature of satellite resources, how to effectively manage task scheduling and computation offloading in a satellite-terrestrial network environment to minimize task processing delays has become a major challenge in the current research on satellite network edge computing.

Thus, the following are the main contributions of this paper:

•   A model of application handling delay is developed regarding the dependencies between tasks in the case of satellite edge computing, where tasks need to be dealt with on multiple satellite edge nodes.

•   A task scheduling algorithm is proposed to derive the sequence of task performance. According to the priority of the tasks, the task execution sequence is obtained.

•   An improved Dueling-DDQN algorithm is presented to address the mission computation unloading problem. Improve the experience playback mechanism in the Dueling-DDQN algorithm.

•   An optical unloading strategy is obtained through the improved Dueling-DDQN algorithm. An optimal resource allocation strategy is obtained through DDPG.

The rest of the paper is organized as follows:

In Section 2, we analyze related work on satellite networks that integrate edge computing. Section 3 describes the system model, formulates the task latency model, and outlines the task scheduling algorithms, specifically the improved Dueling-DDQN algorithm and the DDPG algorithm. In Section 4, we conduct experiments to evaluate the performance of the proposed satellite edge computing offloading methods. Finally, Section 5 presents a summary of this paper.

2  Related Research

Currently, resource allocation in edge computing has become a research hotspot for scholars both domestically and internationally. Tang et al. [12] proposed a hybrid cloud-edge computing scheme that optimizes total energy consumption using the Alternating Direction Method of Multipliers (ADMM) algorithm; however, it only considered a single LEO satellite and did not account for collaborative offloading among multiple LEO satellites. Furthermore, Tang et al.’s subsequent research [13] constructed a three-layer computing framework based on distributed deep learning to address computing offloading issues and reduce execution latency but neglected the potential task dependencies. Within the framework of ground satellite IoT with MEC, Song et al. [14] proposed an energy-efficient computing offloading and resource allocation algorithm aimed at minimizing the total energy consumption of IoT devices, but did not consider the interference management between multiple satellite terminals. Yu et al. [15] introduced a framework for Space-Air-Ground Integrated Networks enhanced by edge computing, which incorporates a real-time decision-making offloading and caching algorithm based on Deep Imitation Learning (DIL), but it only considered a singular satellite edge server environment. Chen et al. [16] applied deep reinforcement learning (DRL) to address the integrated optimization challenges regarding computation offloading and resource distribution in mobile edge computing, thereby offering innovative insights to boost the overall system efficiency. Zhou et al. [17] proposed a distributed algorithm based on ADMM to address the mobile-aware computing offloading problem. Jiang et al. [18] proposed an online Joint Offloading and Resource Allocation (JORA) framework under persistent MEC energy constraints, utilizing Lyapunov optimization to maximize long-term Quality of Experience (QoE) and establishing an energy deficit queue to guide energy consumption, offering a solution for resource scheduling in the face of severe energy limitations. Zhang et al. [19] proposed a satellite peer offloading scheme that addresses the time-varying offloading cooperation problem under system resource and backlog constraints. However, the study assumes all tasks have the same priority, while in practice, different tasks may have varying priorities that require scheduling based on their urgency.

In addition, Wang et al. [20] developed a meta-reinforcement learning-driven approach for computation offloading, leveraging a tailored sequence-to-sequence neural network, proposing a collaborative training method incorporating first-order approximation and clipped target for the agent, but did not consider multi-task offloading. Sahni et al. [21] introduced a heuristic algorithm for joint task offloading and flow scheduling (JDOFH), which considered task dependencies and network flow scheduling aimed at minimizing average completion time, although their research primarily focused on handling task dependency relationships. Wei et al. [22] proposed an algorithm based on DRL to resolve issues related to joint trajectory planning and Directed Acyclic Graph (DAG) task scheduling. Song et al. [23] addressed the problem of dependent task offloading in multi-access edge computing, proposing a multi-objective reinforcement learning approach aimed at minimizing application completion time, energy consumption of mobile devices, and edge computing usage fees simultaneously. Fu et al. [24] assigned priorities to all sub-tasks executed on various edge devices and introduced a DAG task offloading algorithm that is based on these priority and dependency relationships. Zheng et al. [25] introduced a computation task processing scheduling (CTPS) mechanism based on Rubinstein’s bilateral bargaining game, aimed at reducing latency and energy consumption. Tang et al. [26] proposed a dual-time-scale framework to address the service deployment and task scheduling issues in satellite edge computing. By optimizing at two levels, the framework improves the computational performance of the network while ensuring service quality.

However, these studies have only singularly addressed either the handling of task dependency relationships or task resource allocation. This inspires us to consider the combined effects of task scheduling and resource allocation on task offloading. In conclusion, when numerous users concurrently offload a substantial number of latency-sensitive tasks, bottlenecks in offloading inevitably occur at a single satellite edge server. The dependency relationships between tasks and the locations where tasks need to be offloaded in a multiple satellite edge server environment significantly impact the completion time of applications. Thus, it is essential to consider the influence of task dependencies on task computing offloading and resource allocation, a consideration that has not been comprehensively addressed in existing research. Therefore, this paper considers the satellite edge environment and proposes a task scheduling and offloading algorithm among multiple satellite edge nodes.

3  System Model and Problem Formulation

3.1 Network Model

SDN-based satellite ground network structure is used for the network framework, in which three GEO satellites are placed with SDN controllers, and multiple LEO satellites are fitted with edge computing nodes to serve directly to terminal users, reducing the terminal equipment’s response delay. Multiple devices in the network scenes, including subscriber terminals, data monitoring equipment, and IoT devices, are accessed in the LEO satellite network, and the LEO satellites assume the calculation service. Each DAG task has different priority levels. The handling order of the tasks is derived based on the different priority levels. As shown in Fig. 1.

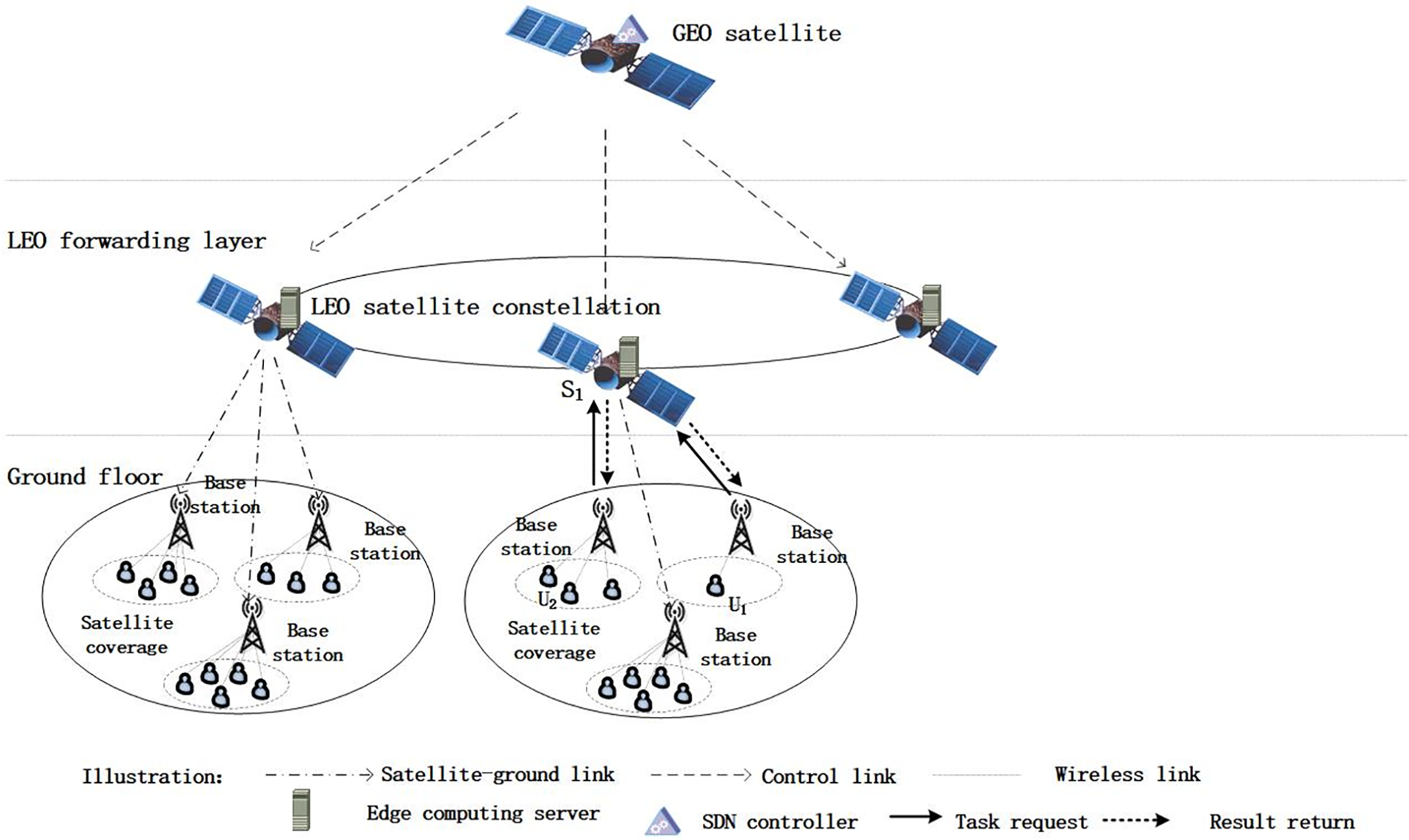
Figure 1: Schematic of the satellite edge network architecture

3.2 Task Model

3.2.1 Application Model

The application framework includes tasks that are interdependent and have strict deadlines. We consider that each application can be divided into several dependent tasks. We represent the application as a DAG with entry tasks. The entry tasks are simple, with no direct predecessor tasks, and the exit tasks have no direct successor tasks. We represent a collection of tasks within the application. These tasks must be completed before the application deadline.

In a system with a total of M mobile devices, M={1,2,3⋯m} is denoted as the set of device numbers, indexed by i, and the mobile device generates an application to be processed when each time slot starts. Generated applications on a mobile device can be partitioned into several interrelated tasks by computing the set of tasks denoted as N={1,2,3⋯n} and indexed by j. Since there are dependencies among the tasks of an application, its structure can be expressed as a directed acyclic graph, often referred to as Gi=(Vi,Ei), which Vi=(vi,1,vi,2…vi,n) denotes the sub-task nodes set in the ith application. In Gi=(Vi,Ei), for a sub-task vi,j=(Ci,j,Di,j), where Ci,j denotes the CPU cycles needed to process the task in cycles, Di,j expresses the current task’s size in bits, and the application ending latency is denoted as Tdi. Ei indicates the set of oriented edges between computational tasks Ei={ej,ki=(vi,j,vi,k)|vi,j,vi,k∈Vi}, where directed edges represent dependencies between computing tasks. In the set of directed edges, if there is a directed edge from vertex A to vertex B in the set of directed edges, it implies that task B must be processed after task A, meaning the ending moment of B cannot be earlier than the moment of A.

The satellite edge nodes that can provide task processing are s={1,2…S}. The MEC server allocates resources to a task when it is unloaded and does not release them until the task is done handling. Each mobile device requests to process one application and the task treatment process is described below:

① Multiple users on the ground send application processing requests to the corresponding covered satellites.

② The receiving satellites send task information to the GEO satellite, which hosts a global SDN controller. The SDN controller gathers information about the entire satellite network and task information, using a scheduling algorithm to calculate the optimal offloading location.

③ The GEO controller then transmits the corresponding control information to the LEO satellites.

④ The low Earth orbit satellites forward the tasks to the designated deployment locations using flow table control.

⑤ The edge computing nodes process the tasks and return the results to the ground users.

3.2.2 Delay Model

① The time taken by the sub-tasks to be delivered from a mobile device to a satellite edge computing server s. This transmission delay considers the time taken by the data to travel through the satellite network and is expressed as:

Ti,jus={Di,jRusi,js=accesssatellitesDi,jRusi,j+Di,jRssi,j+2d1,svotherwise(1)

d1,s represents the inter-satellite routing distance (single hop or multi-hop), Rssi,j represents the inter-satellite transmission rate, and v represents the speed of light. Rusi,j represents the uplink transmission rate (unit: Mbps) and it is expressed as:

Rusi,j=Blog2⁡(1+Pi,jgi,jN)(2)

The transmission power of sub-task vi,j is expressed as Pi,j, channel gain can be expressed as gi,j, Gaussian white noise power is expressed as N, representing the noise power in the transmission process, B indicating the transmission bandwidth (unit: MHz).

② The handling latency of the sub-tasks offloading to the satellite MEC server s can be expressed as follows, the handling latency is the time of the sub-task’s computing accomplishment on the satellite MEC server:

Ti,j,ssec=Ci,jFi,js(3)

Fi,js represents the computing resources (unit: cycle/s) allocated to the task by satellite edge node s.

③ The expression is: The handling latency of a local computing task involves processing latency and waiting latency. Since only a single task can be handled once locally, the task’s waiting time is summed by the computation time of all tasks before the task in the task set. The expression is:

Ti,jl=Ci,jFl+Ti,jl,w(4)

Fl indicates local computing capability (unit: cycles/s). Ti,jl,w represents the waiting time.

④ The actual handling latency of the task is:

Ti,j=(1−ai,js)Ti,jl+ai,js(Ti,j,ssec+Ti,jus+2hv)(5)

where ai,js is the task’s handling mode, the range from the mobile device to the satellite node is denoted as h, and the velocity of light is represented as v. If a task vi,j is processed locally, ai,js is denoted as 0 with s being 0. If a task vi,j is processed on a satellite, ai,js is denoted as 1 with the corresponding satellite number for s. In a DAG, each task is finished at a distinct time, and this requires us to properly indicate the point at which every task is completed to minimize the whole latency of the DAG. As a consequence of the dependencies among tasks, the completion delay of task vi,j is related to the delay required for the full accomplishment of its preceding tasks as well as the task’s data transmission delay, defining the actual completion time of task vi,j as EFTi,j.

⑤ The time delay for the actual completion of the mission is:

EFTi,j=Ti,j+maxk∈prep(j)EFTi,k(6)

where maxk∈prep(j)EFTi,k indicates the maximum accomplishment time for the precursor task of the task vi,j. When the task is the exit task of the DAG, its completion time is the completion delay of the entire DAG application.

⑥ To ensure that dependent tasks are executed before tasks they depend on to fulfill the relationship between tasks, the overall completion delay of the entire DAG application is calculated using equation:

EFTi,exit=Ti,exit+maxk∈prep(exit)EFTi,k=EFTi(7)

⑦ Optimization is required for task unloading decisions, scheduling decisions, and resource assignment jointly.

min1m∑i=1mEFTis.t.C1:∑i=1m∑j=1nai,jsFi,js≤Fmaxss∈{0,1,2…S}C2:Fi,js≥0 i∈M,j∈N,s∈{0,1,2…S}C3:ai,js∈{0,1}i∈M,j∈N,s∈{0,1,2…S}C4:EFTi≤Tdii∈M(8)

where m is the overall amount of applications to be addressed. When application i finishes within a bounded time latency Tdi and returns the result, EFTi≤Tdi, A is defined as the set of sub-task unloading strategies, A={ai,js} i∈M, j∈N. F is defined as computational resource assignment strategies set, F={Fi,js}. Fmaxs is the computational resources that can be assigned to the satellite edge node s.

3.3 Task Scheduling Models

3.3.1 Priority-Based Scheduling Model

Each task within different DAG applications may have dependencies, meaning that the execution of a task can be influenced by the tasks it is associated with. Therefore, it is essential to consider these dependencies before scheduling the sub-tasks. Different types of applications have varying requirements for completion times, so to reduce processing latency in the system and ensure that all applications complete within their respective deadlines, we first need to construct a priority queue at the outset. After receiving the application information, we sort the applications based on priority, which is represented by the deadline; the tighter the deadline, the greater the priority. Since there are dependencies between sub-tasks, we also need to sort the tasks to describe the current dependencies among them. To comply with the inter-dependencies among sub-tasks within the applications, we sequence the tasks in order of their decreasing order values, and the sub-tasks are prioritized as follows:

Pri(vi,j)={Ti,exitif Ti,jisexitsubtaskmaxvi,k∈succ(vi,j)Pri(vi,k)+Ti,jotherwise(9)

succ(vi,j) represents the set of successor nodes for vi,j. The priority of the last node in the sequence can be denoted by Ti,exit. Therefore, the sub-task preference sequence, sorted by the priorities of all sub-tasks, is derived.

3.3.2 Computational Offloading Method Based on Improved Dueling-DDQN’s Algorithm

Due to the dynamic nature of the satellite-ground link states in satellite edge computing scenarios, it is essential to update offloading strategies promptly to reduce computation offloading latency costs. In this paper, there are a total of s+1 offloading locations, and each satellite edge computing node can be allocated a certain amount of computing resources, allowing for different processing methods for the generated tasks. Deep reinforcement learning merges the advantages of deep learning with those of reinforcement learning, making it effective for solving sequential decision-making problems in complex systems. We first determine the computation offloading decisions based on the Dueling-DDQN network, followed by resource allocation decisions based on the DDPG network.

Extensive experiments indicate that the traditional DQN algorithm suffers from overestimation issues, non-uniqueness problems, and correlations among experience samples. To address these drawbacks, we employ the Double DQN algorithm, which improves the stability of learning by separating action selection from Q-value estimation. Dueling DQN is an enhancement of DQN that divides the Q-value into two components: the value function (Value) and the advantage function (Advantage). The Value represents the importance of the current state, while the Advantage corresponds to a value for each action indicating its advantage. Therefore, we use the Dueling-DDQN algorithm to solve the offloading problem by modeling it as a Markov Decision Process (MDP), defining the action space A, the state space S, and the reward function R.

(1) State Space

In the scenario studied in this chapter, the state will change over time, and can be represented as:

St={Da,Pr,F}(10)

where Da represents information about the currently pending DAG application, including the sub-task structure of the application, CPU processing cycles, and task sizes. Pr is the priority sequence information of the application and Ft={Ft,1,Ft,2…Ft,s} is the available computing resources.

(2) Action Space

Next, the action space should include the offloading position of the user’s current task and the resource allocation result. The resource allocation can be derived from the DDPG algorithm. Define the action of the sub-task as at={ai,j1,ai,j2,…,ai,jL,Fi,j1,Fi,j2,…,Fi,jL}, if ai,js is 0, it means that it is handled locally, and if the task vi,j is handled on the satellite, ai,js is 1. The set of all actions is At.

(3) Reward Function

The reward function is an essential component in achieving the optimal Q-network, as well as the rationale behind the algorithm’s convergence. This paper mainly focuses on minimizing the processing delay, thus the reward function Rt, which shall be inversely proportional to the delay, can be expressed as:

Rt=−1m∑i=1mEFTi(11)

Traditional DQN algorithm due to the use of maximization step leads to overestimation problem, while the DDQN algorithm makes the selection of action and the generation of target value decoupled so that the model learning speed achieves a faster and more stable state. The DDQN optimal action am is defined as:

am=arg⁡maxat+1Q(st+1,at+1,θ)(12)

θ are the parameters of the neural network.

The target Q-value is denoted as:

Qtar=Rt+γQ(st+1,am;θ−)(13)

θ− is the parameter of the target neural network, where γ represents the discount factor for reward importance.

Dueling Double DQN network structure is based on the Double DQN algorithm, Dueling DQN divides the Q-value into two parts: value function Value and advantage function Advantage, Value indicates the importance of the current state; this structure is suitable for the dynamically changing environment. The Q-value consists of the value function and advantage function, and its calculation formula is denoted as:

Q(st,at;θ)=V(st;θV)+A(st,at;θA)(14)

The Dueling Network structure changes the way of calculating Q-value, both are improvements to the DQN algorithm. Dueling-DDQN fuses them to find the loss function as in equation:

loss=E[(Qtar−Q(si,ai;θ))2](15)

The traditional DQN algorithm saves the empirical sample data acquired by the multi-agent interacting with the environment at every time step into an empirical pool, and adopts random sampling for the experience playback. Given that different data have different importance for the training of the model, random and uniform sampling may lead to low learning efficiency, or even overfitting. TD error signifies the discrepancy between the present estimation and the target value, whereby the TD error is denoted as:

δ=rt+γmaxaction′Q(st+1,at+1,θ−)−Q(st,at,θ)(16)

where θ and θ− represent the parameter values of the estimation network and the target network, respectively. The larger the empirical error, the higher the priority, which is defined as:

Pi=|σ|+ε,ε>0(17)

A sample’s TD error has a higher probability of being sampled the larger the absolute value of its TD error. The probability of the sample being sampled is dependent on the TD error. To solve the problems of learning inefficiency and overfitting, the random sampling method can be combined with pure greedy sampling and uniformly distributed sampling to ensure that the probability of sampling in the priority of the training data is monotonous, then the probability of preferential sampling can be expressed as:

P(i)=Pi∂∑jPj∂(18)

where ∂ is a hyperparameter that is used to regulate the degree of prioritization. When ∂ = 0 the sampling becomes uniform.

Due to the introduction of the degree of prioritization, a change in the distribution of sample data can result in training bias or overfitting. To mitigate this bias, the priority empirical replay algorithm corrects the bias through the importance sampling weight method (Algorithm 1). The important sampling weights of the samples are specified below:

Wis=(1N⋅1P(i))β(19)

3.3.3 Resource Allocation Method Based on DDPG Algorithm

The DDPG algorithm possesses symmetrical properties. It adheres to the Actor-Critic architecture and is capable of effectively addressing challenges in continuous action spaces by employing deep neural networks for policy approximation. The DDPG algorithm evaluates the quality of state-action pairs through the use of two neural network models: the policy function and the Q-value function. The Actor network determines actions based on the observed state, whereas the Critic network evaluates the actions taken by the Actor. We use the DDPG network to address resource allocation problems with continuous variables.

Each policy μ of DDPG defines an action-state pair value function Qμ(st,at), which denotes the expected return of an action when a given state st is executed, with a Q-value of:

Qμ(st,at)=E [Rt+γQ(st+1,μ(st+1))](20)

The update parameters for the action goal network and critic goal network are θμ and θQ, respectively. Similar to the structure of DQN, the critic network’s loss function can be derived below:

L(θQ)=E μ[(yt−Q(st,at|θQ))2](21)

yt=Rt+γQ(st+1,μ(st+1)|θQ)(22)

The strategy gradient can be figured out:

∇θμJ=1C∑j[∇aQ(s,a|θQ)|s=st,a=μ(st|θμ)][∇θμQ(s,a|θQ)|s=st,a=μ(st|θμ)θμ∇θμμ(st|θμ)|s=st](23)

To make the loss function, the critic network Q will be updated with a given optimizer. After that, the actor network will small batch the action critic network, which will result in the gradient change of action a. With these two gradients and the parameters (which can be derived from your optimizer), the actor network can be refined using the subsequent equation:

∇θμJ=1C∑j[∇aQ(s,a|θQ)|s=st,a=μ(st|θμ)∇θμQ(s,a|θQ)|s=st](24)

The DDPG algorithm uses the parameters θμ and θQ of the current actor and critic networks respectively and soft updates them as follows:

θQ′←θQ+(1−τ)θQ′θμ′←θμ+(1−τ)θμ′(25)

4  Simulation Experiment

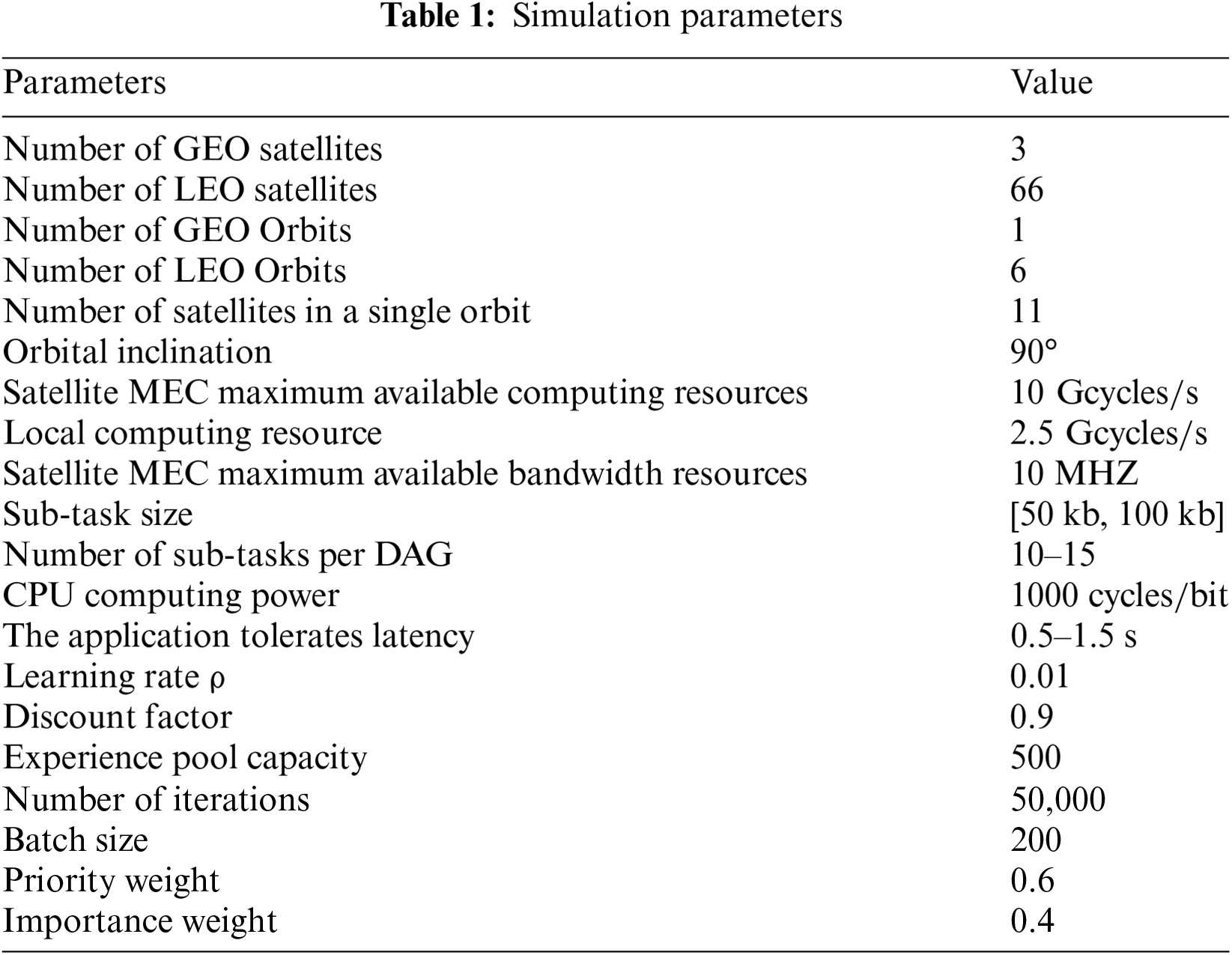
This simulation experiment uses STK simulation software to model the information transfer network and Python and Pytorch to build neural networks for training. In the simulation, the Walker constellation of 66 satellites is used, and the SDN controller is placed on the GEO satellites to monitor the individual satellites of the Walker constellation. The parameter settings for the simulation are shown in Table 1 [27–31].

Simulations are performed on the above parameters. This section will compare and analyze the completion rates of the applications. The simulation results will be shown and analyzed in terms of changes in resources, number of DAGs, and number of DAG sub-tasks.

As shown in Fig. 2, as the satellite computing resources increase, the completion latency of the application for all schemes shows a downward trend. The task processing based on DQN and DDPG (D-DDPG) and random processing (RA) have lower completion latency, while the method proposed in this chapter (combining Dueling-DDQN and DDPG, D3-DDPG) outperforms other algorithms in terms of completion latency. As the satellite computing resources gradually increase, the latency difference between D3-DDPG and RA decreases from 0.37 to 0.11 s. This is because as the satellite computing resources increase, the computational resources allocated to tasks also increase accordingly, reducing computation latency. The RA method randomly selects processing locations, failing to achieve optimal results, thus resulting in relatively high completion latency for this algorithm. The proposed method demonstrates lower processing latency compared to D-DDPG, indicating the effectiveness of the improved DQN algorithm. Additionally, compared to the RA method, the proposed D3-DDPG also exhibits lower completion latency, highlighting the importance of appropriate task offloading decisions. Finally, the average allocation algorithm (AV) has a higher latency, indicating the importance of reasonable resource allocation for tasks offloaded to the satellites.

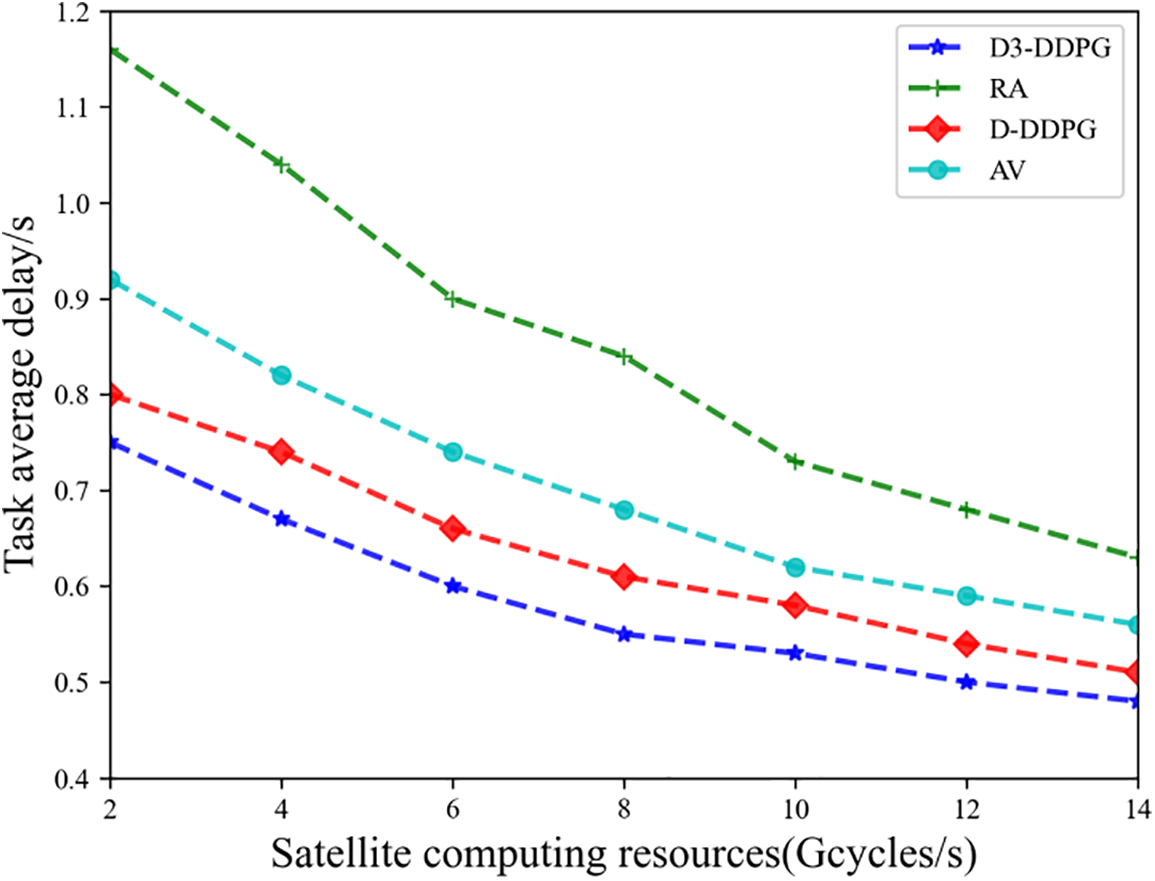
Figure 2: Task average delay vs. Satellite computing resources

As shown in Fig. 3, as local computing resources increase, the processing latency of the application for all schemes shows a downward trend. The task processing method based on D-DDPG and the random processing (RA) exhibit lower completion latency, while the method proposed in this chapter (D3-DDPG) demonstrates superior performance in terms of completion latency, primarily due to the increased computational resources available at the user end, effectively reducing task computation delays. The RA method selects processing locations randomly, and since it does not pursue an optimal solution, its completion latency is relatively high. The proposed D3-DDPG outperforms D-DDPG in processing latency, indicating a significant improvement achieved by the enhanced DQN algorithm. However, as local computing resources increase, the latency difference between D3-DDPG and D-DDPG gradually diminishes. This is because the improvements in this study mainly target satellite edge computing nodes, enhancing the user’s ability to independently compute tasks, thus reducing reliance on edge computing. Additionally, the proposed method shows lower completion latency compared to RA, highlighting the importance of reasonable task-offloading decisions for improving system efficiency. The scheme that offloads all tasks to the local (All local, AL) results in higher completion latency compared to the method proposed in this chapter, further confirming the necessity of rational offloading in task processing.

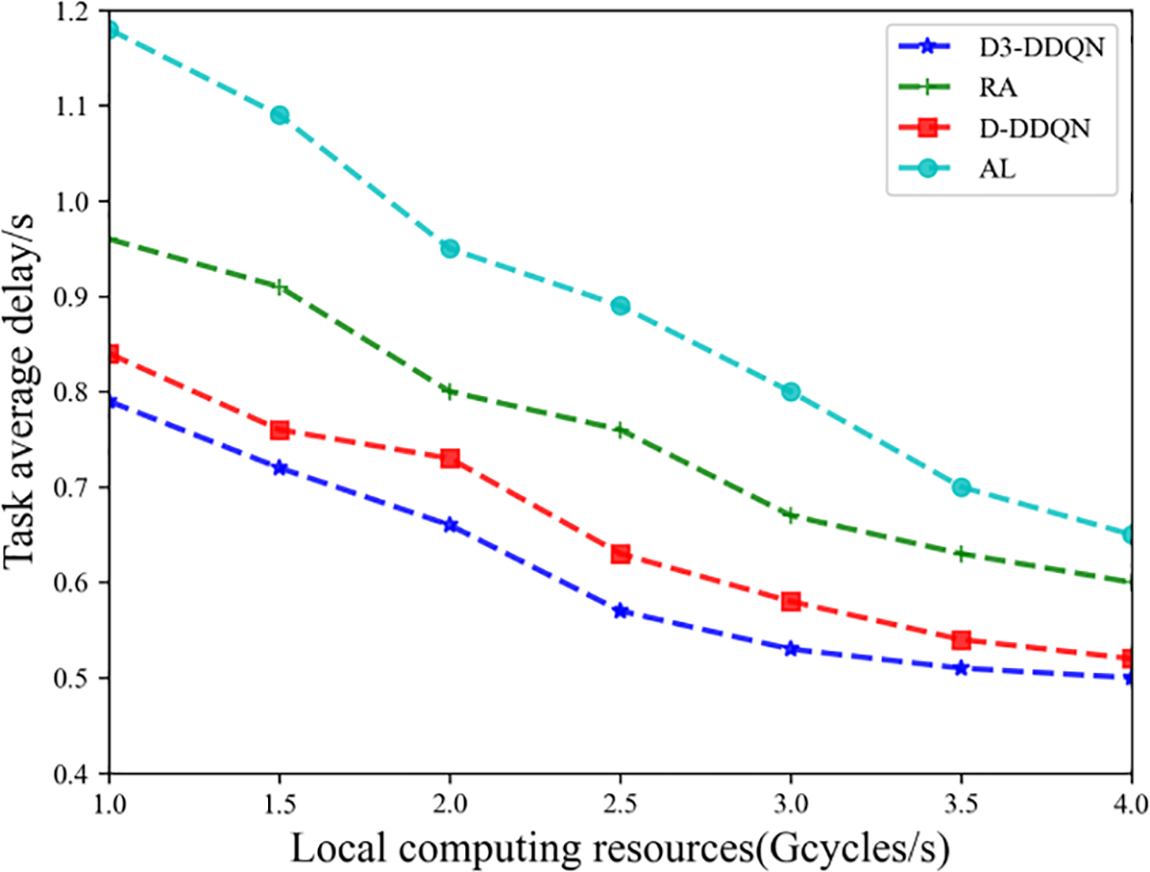
Figure 3: Task average delay vs. Local computing resources

As shown in Fig. 4, as the number of applications that need to be processed increases, the application processing latency for all schemes shows an upward trend. Additionally, the task processing method based on D-DDPG demonstrates superior performance in task processing latency compared to random processing (RA). Although the proposed D3-DDPG method also gradually increases in completion latency, it consistently remains below that of other algorithms. This is because, as the number of DAG tasks to be processed increases, the resources of the satellite edge nodes become increasingly limited. The RA method does not seek an optimal solution, resulting in relatively high completion latency for this algorithm. The processing latency of the proposed method is lower than that of D3-DDPG, further proving the effectiveness of the improved DQN-based algorithm. Simultaneously, the completion latency of this method is also lower than that of RA, emphasizing the importance of appropriate task-offloading decisions in enhancing system performance. Furthermore, the average allocation algorithm (AV) has a higher latency compared to the average completion latency of the proposed method, highlighting the critical importance of reasonable resource allocation when offloading tasks to satellites.

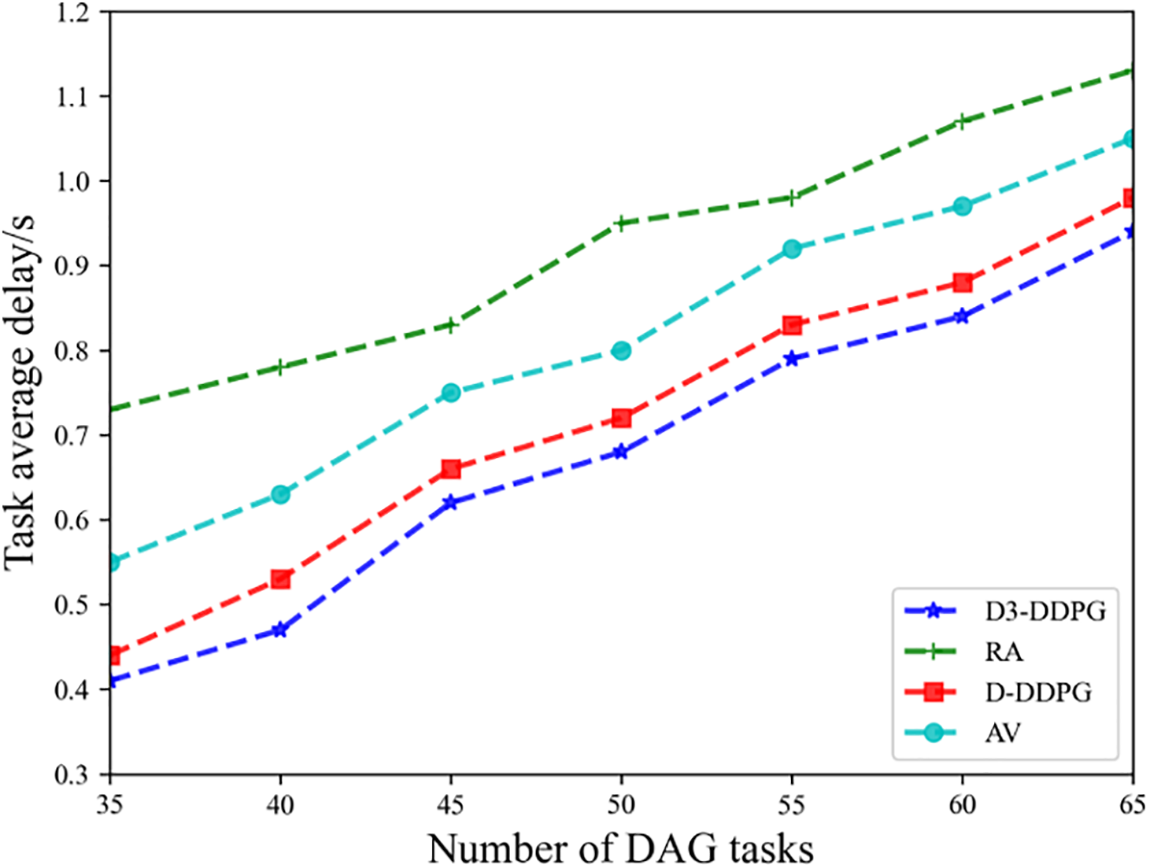
Figure 4: Task average delay vs. Number of DAG tasks

As shown in Fig. 5, as the number of sub-tasks increases, the processing latency of the application for all schemes shows an upward trend. This phenomenon reflects the direct impact of increased task complexity on system performance, especially in resource-limited scenarios. The task processing methods based on D-DDPG and random processing (RA) also experience an increase in completion latency as the number of tasks grows, highlighting the limitations of both approaches. However, the proposed D3-DDPG method consistently maintains a lower completion latency, outperforming other algorithms. This is mainly because as the number of DAG sub-tasks increases, the resources of the satellite edge nodes become increasingly constrained, leading to increased task computation delays. D3-DDPG optimizes task offloading decisions, making more efficient use of available resources and thereby reducing overall computation latency. The RA method relies on randomly selecting task processing locations and does not seek an optimal solution, which results in higher completion latency. This further emphasizes the importance of rational decision-making in enhancing system performance. The D3-DDPG method shows lower processing latency compared to D-DDPG, validating the effectiveness of the improved DQN algorithm, particularly in resource-constrained environments. Additionally, the completion latency of this method is lower than that of RA, underscoring the significance of appropriate task-offloading in improving system performance, as rational task-offloading can not only reduce delays but also enhance resource utilization efficiency. Finally, the average allocation algorithm (AV) exhibits higher latency than the proposed method, further indicating the importance of reasonable resource allocation in the distribution of resources.

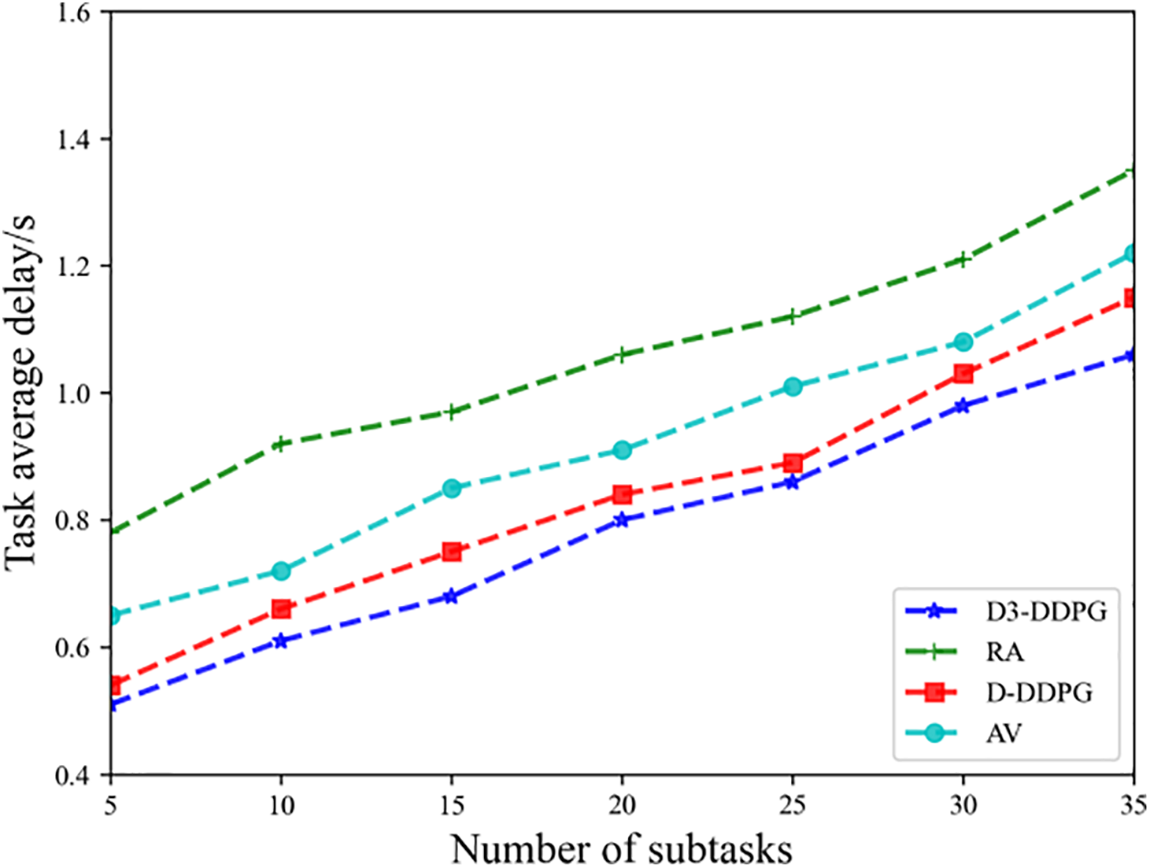
Figure 5: Task average delay vs. Number of sub-tasks

5  Conclusions

This paper addresses the offloading bottlenecks caused by the significant increase in demand for latency-sensitive tasks in a satellite-ground integrated network architecture. The insufficient computing power of a single satellite edge server requires effective scheduling to enhance user experience. It also considers that satellites can process tasks via inter-satellite links to reduce processing time. First, we propose an efficient priority-based task scheduling strategy to determine task priorities and clarify execution order. Then, we introduce an improved Dueling-DDQN algorithm to derive the computation offloading strategy by enhancing its experience replay mechanism. Using this improved algorithm, we obtain the optimal offloading strategy and apply the DDPG algorithm for resource allocation to reduce the processing latency of sub-tasks. Simulation results show that our proposed algorithm outperforms other solutions in reducing task processing latency.

Acknowledgement: We appreciate the insightful feedback from the anonymous reviewers, which has significantly contributed to enhancing the quality of this paper.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Zhiguo Liu; data collection: Yuqing Gui; analysis and interpretation of results: Lin Wang; draft manuscript preparation: Yingru Jiang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Given the nature of this research, the participants have not consented to public sharing of their data; therefore, supporting data is not accessible.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Y. Shi, Y. Zhou, D. Wen, Y. Wu, C. Jiang and K. B. Letaief, “Task-oriented communications for 6G: Vision, principles, and technologies,” IEEE Wirel. Commun., vol. 30, no. 3, pp. 78–85, 2023. doi: 10.1109/MWC.002.2200468. [Google Scholar] [CrossRef]

2. M. M. H. Shuvo, S. K. Islam, J. Cheng, and B. I. Morshed, “Efficient acceleration of deep learning inference on resource-constrained edge devices: A review,” Proc. IEEE, vol. 111, no. 1, pp. 42–91, 2023. doi: 10.1109/JPROC.2022.3226481. [Google Scholar] [CrossRef]

3. Y. Ma, W. Liang, M. Huang, W. Xu, and S. Guo, “Virtual network function service provisioning in MEC via trading off the usages between computing and communication resources,” IEEE Trans. Cloud Comput., vol. 10, no. 4, pp. 2949–2963, 2022. doi: 10.1109/TCC.2020.3043313. [Google Scholar] [CrossRef]

4. H. Zhang, H. Zhao, R. Liu, A. Kaushik, X. Gao and S. Xu, “Collaborative task offloading optimization for satellite mobile edge computing using multi-agent deep reinforcement learning,” IEEE Trans. Vehicular Technol., vol. 73, no. 10, pp. 1–16, 2024. doi: 10.1109/TVT.2024.3405642. [Google Scholar] [CrossRef]

5. M. Tang and V. W. S. Wong, “Deep reinforcement learning for task offloading in mobile edge computing systems,” IEEE Trans. Mob. Comput., vol. 21, no. 6, pp. 1985–1997, 2022. doi: 10.1109/TMC.2020.3036871. [Google Scholar] [CrossRef]

6. H. Zhou, K. Jiang, X. Liu, X. Li, and V. C. M. Leung, “Deep reinforcement learning for energy-efficient computation offloading in mobile-edge computing,” IEEE Internet Things J., vol. 9, no. 2, pp. 1517–1530, 2022. doi: 10.1109/JIOT.2021.3091142. [Google Scholar] [CrossRef]

7. L. Liu, W. Mao, W. Li, J. Duan, G. Liu and B. Guo, “Edge computing offloading strategy for space-air-ground integrated network based on game theory,” Comput. Netw., vol. 243, no. 10, 2024, Art. no. 110331. doi: 10.1016/j.comnet.2024.110331. [Google Scholar] [CrossRef]

8. P. Zhang, Y. Zhang, N. Kumar, and M. Guizani, “Dynamic SFC embedding algorithm assisted by federated learning in space-air-ground integrated network resource allocation scenario,” IEEE Internet Things, vol. 10, no. 11, pp. 9308–9318, 2022. doi: 10.1109/JIOT.2022.3222200. [Google Scholar] [CrossRef]

9. Y. Lin, W. Feng, Y. Wang, Y. Chen, Y. Zhu and X. Zhang, “Satellite-MEC integration for 6G Internet of Things: Minimal structures, advances, and prospects,” IEEE Open J. Commun. Soc., vol. 5, no. 1, pp. 3886–3903, 2024. doi: 10.1109/OJCOMS.2024.3418860. [Google Scholar] [CrossRef]

10. S. B. R. Tirmizi, Y. Chen, S. Lakshminarayana, W. Feng, and A. A. Khuwaja, “Hybrid satellite-terrestrial networks toward 6G: Key technologies and open issues,” Sensors, vol. 22, no. 21, 2022, Art. no. 8544. doi: 10.3390/s22218544. [Google Scholar] [PubMed] [CrossRef]

11. Y. Sun, M. Peng, S. Zhang, G. Lin, and P. Zhang, “Integrated satellite-terrestrial networks: Architectures, key techniques, and experimental progress,” IEEE Netw., vol. 36, no. 6, pp. 191–198, 2022. doi: 10.1109/MNET.106.2100622. [Google Scholar] [CrossRef]

12. Q. Tang, Z. Fei, B. Li, and Z. Han, “Computation offloading in LEO satellite networks with hybrid cloud and edge computing,” IEEE Internet Things J., vol. 8, no. 11, pp. 9164–9176, 2021. doi: 10.1109/JIOT.2021.3056569. [Google Scholar] [CrossRef]

13. Q. Tang, Z. Fei, and B. Li, “Distributed deep learning for cooperative computation offloading in low earth orbit satellite networks,” China Commun., vol. 19, no. 4, pp. 230–243, 2022. doi: 10.23919/JCC.2022.04.017. [Google Scholar] [CrossRef]

14. Z. Song, Y. Hao, Y. Liu, and X. Sun, “Energy-efficient multiaccess edge computing for terrestrial-satellite Internet of Things,” IEEE Internet Things J., vol. 8, no. 18, pp. 14202–14218, 2021. doi: 10.1109/JIOT.2021.3068141. [Google Scholar] [CrossRef]

15. S. Yu, X. Gong, Q. Shi, X. Wang, and X. Chen, “EC-SAGINs: Edge-computing-enhanced space-air-ground-integrated networks for internet of vehicles,” IEEE Internet Things J., vol. 9, no. 8, pp. 5742–5754, 2021. doi: 10.1109/JIOT.2021.3052542. [Google Scholar] [CrossRef]

16. J. Chen, H. Xing, Z. Xiao, L. Xu, and T. Tao, “A DRL agent for jointly optimizing computation offloading and resource allocation in MEC,” IEEE Internet Things, vol. 8, no. 24, pp. 17508–17524, 2021. doi: 10.1109/JIOT.2021.3081694. [Google Scholar] [CrossRef]

17. J. Zhou, Q. Yang, L. Zhao, H. Dai, and F. Xiao, “Mobility-aware computation offloading in satellite edge computing networks,” IEEE Trans. Mob. Comput., vol. 23, no. 10, pp. 9135–9149, 2024. doi: 10.1109/TMC.2024.3359759. [Google Scholar] [CrossRef]

18. H. Jiang, X. Dai, Z. Xiao, and A. Iyengar, “Joint task offloading and resource allocation for energy-constrained mobile edge computing,” IEEE Trans. Mob. Comput., vol. 22, no. 7, pp. 4000–4015, 2023. doi: 10.1109/TMC.2022.3150432. [Google Scholar] [CrossRef]

19. X. Zhang, J. Liu, R. Zhang, Y. Huang, J. Tong and N. Xin, “Energy-efficient computation peer offloading in satellite edge computing networks,” IEEE Trans. Mob. Comput., vol. 23, no. 4, pp. 3077–3091, 2024. doi: 10.1109/TMC.2023.3269801. [Google Scholar] [CrossRef]

20. J. Wang, J. Hu, G. Min, A. Y. Zomaya, and N. Georgalas, “Fast adaptive task offloading in edge computing based on meta reinforcement learning,” IEEE Trans. Parall. Distrib. Syst., vol. 32, no. 1, pp. 242–253, 2021. doi: 10.1109/TPDS.2020.3014896. [Google Scholar] [CrossRef]

21. Y. Sahni, J. Cao, L. Yang, and Y. Ji, “Multihop offloading of multiple DAG tasks in collaborative edge computing,” IEEE Internet Things J., vol. 8, no. 6, pp. 4893–4905, 2021. doi: 10.1109/JIOT.2020.3030926. [Google Scholar] [CrossRef]

22. X. Wei, L. Cai, N. Wei, P. Zou, J. Zhang and S. Subramaniam, “Joint UAV trajectory planning, DAG task scheduling, and service function deployment based on DRL in UAV-empowered edge computing,” IEEE Internet of Things J., vol. 10, no. 14, pp. 12826–12838, 2023. doi: 10.1109/JIOT.2023.3257291. [Google Scholar] [CrossRef]

23. F. Song, H. Xing, X. Wang, S. Luo, P. Dai and K. Li, “Offloading dependent tasks in multi-access edge computing: A multi-objective reinforcement learning approach,” Future Gener. Comput. Syst., vol. 128, no. 1, pp. 333–348, 2022. doi: 10.1016/j.future.2021.10.013. [Google Scholar] [CrossRef]

24. X. Fu, B. Tang, F. Guo, and L. Kang, “Priority and dependency-based dag tasks offloading in fog/edge collaborative environment,” in 2021 IEEE 24th Int. Conf. Comput. Support. Cooperat. Work Des. (CSCWD), Dalian, China, 2021, pp. 440–445. doi: 10.1109/CSCWD49262.2021.9437784. [Google Scholar] [CrossRef]

25. G. Zheng, Q. Ni, K. Navaie, and H. Pervaiz, “Semantic communication in satellite-borne edge cloud network for computation offloading,” IEEE J. Sel. Areas Commun., vol. 42, no. 5, pp. 1145–1158, 2024. doi: 10.1109/JSAC.2024.3365879. [Google Scholar] [CrossRef]

26. Q. Tang, R. Xie, Z. Fang, T. Huang, T. Chen and R. Zhang, “Joint service deployment and task scheduling for satellite edge computing: A two-timescale hierarchical approach,” IEEE J. Sel. Areas Commun., vol. 42, no. 5, pp. 1063–1079, 2024. doi: 10.1109/JSAC.2024.3365889. [Google Scholar] [CrossRef]

27. F. Chai, Q. Zhang, H. Yao, X. Xin, R. Gao and M. Guizani, “Joint multi-task offloading and resource allocation for mobile edge computing systems in satellite IoT,” IEEE Trans. Vehicular Technol., vol. 72, no. 6, pp. 7783–7795, 2023. doi: 10.1109/TVT.2023.3238771. [Google Scholar] [CrossRef]

28. Y. Zhang, J. Chen, Y. Zhou, L. Yang, B. He and Y. Yang, “Dependent task offloading with energy-latency trade off in mobile edge computing,” IET Commun., vol. 16, no. 17, pp. 1993–2001, 2022. doi: 10.1049/cmu2.12454. [Google Scholar] [CrossRef]

29. J. Sun, H. Wang, L. Nie, G. Feng, Z. Zhang and J. Liu, “A joint strategy for service deployment and task offloading in satellite-terrestrial IoT,” Comput. Netw., vol. 225, no. 14, 2024, Art. no. 109656. doi: 10.1016/j.comnet.2023.109656. [Google Scholar] [CrossRef]

30. J. Li, Y. Shang, M. Qin, Q. Yang, N. Cheng and W. Gao, “Multiobjective oriented task scheduling in heterogeneous mobile edge computing networks,” IEEE Trans. Vehicular Technol., vol. 71, no. 8, pp. 8955–8966, 2022. doi: 10.1109/TVT.2022.3174906. [Google Scholar] [CrossRef]

31. X. Cao, B. Yang, Y. Shen, C. Yuen, Y. Zhang and Z. Han, “Edge-assisted multi-layer offloading optimization of leo satellite-terrestrial integrated networks,” IEEE J. Sel. Areas Commun., vol. 41, no. 2, pp. 381–398, 2023. doi: 10.1109/JSAC.2022.3227032. [Google Scholar] [CrossRef]