Efficient OpenMP Based Z-curve Encoding and Decoding Algorithms

1  Introduction

Z-curve, proposed by Morton in 1966 [1], is an essential representative of the family of space-filling curves. It can map points in multidimensional space to one-dimensional space and maintain the local proximity property. Z-curve helps to improve the localization and continuity of data and facilitates the indexing, searching, and processing of spatial data. Compared with the Hilbert curve and many other space-filling curves, the mapping rules of the Z-curve are simple. Its range queries are efficient [2,3], so it is widely used in many fields, such as spatial data indexing and querying [4–6], image processing and compression [7,8], data mining [9–11], and deep learning [12].

In the realm of image compression, Ouni et al. [13] introduced a lossless image compression algorithm. This algorithm utilizes local image correlation to identify the direction of minimum pixel value change and employs a Z-curve for image compression and transmission.

In data mining, Lu et al. [10] proposed a fast distribution density peak clustering algorithm, FDDP. It utilizes the Z-curve for data dimensionality reduction and range partitioning based on Z-values to balance the load among processing nodes.

In deep learning, Z-curves and many other space-filling techniques can be used in a wide variety of fields, such as transforming two-dimensional data to one-dimensional [12], transforming one-dimensional data to two-dimensional, organizing convolution, or sorting two-dimensional data.

Unlike many Z-curve-based applications, we investigate the foundation of these applications: the encoding and decoding algorithms of the Z-curve. Specifically, we focus on the encoding and decoding algorithms for two-dimensional Z-curve. The process of encoding involves converting two-dimensional coordinates (X, Y) to their ordinal numbers (Z-values) on the Z-curve. Correspondingly, the process of computing the corresponding two-dimensional coordinates (X, Y) based on the Z-values is referred to as decoding. Z-curve encoding and decoding algorithms form the basis of Z-curve-based applications, and improving the efficiency of these algorithms contributes to the overall efficiency of processing in these applications.

Given that the Z-curve encoding and decoding algorithm is relatively simple, there is very little research on it compared to the Hilbert curve encoding and decoding algorithm [14–17]. Currently, the Bit Interleaving (BI) algorithm dominates the Z-curve encoding and decoding algorithm field [18]. The basic idea of BI is very simple. During encoding, it interleaves all bits of X=(x1x2…xn)2 and Y=(y1y2…yn)2 from left to right, resulting in the Z-value Z=(y1x1y2x2…ynxn)2. Here, xi, yi and zi=yixi denote the i-th order of X, Y and Z, respectively. During decoding, X and Y can be separated by extracting bits from Z in an interleaved manner.

Considering its simplicity and efficiency, the Bit Interleaving (BI) method is a dominant method in Z-curve-based applications, with subsequent applications predominantly adopting it. Despite its simplicity and widespread use, its interleaving process requires step-by-step coordinate shifting and bitwise operations. Thus, its efficiency needs to be further enhanced.

To tackle this problem, based on the depth analyses of the Z-curve, we consider the following three methods to improve the efficiency of the BI: 1) we design efficient lookup tables (LT) that convert the encoding and decoding operations into lookup table operations; 2) we utilize a bit detection mechanism to skip partial orders of a coordinate or a Z-value with consecutive zeros in the front, avoiding the need for iterative computations. To fully exploit the modern multi-core hardware, we further propose order-parallel and point-parallel Open Multi-Processing (OpenMP) based algorithms. We carry out extensive experiments on discrete datasets, skewed datasets, and real datasets. The results show that our algorithms effectively enhance the efficiency of Z-curve encoding and decoding algorithms, and our point-parallel algorithms can be up to 12.6× faster than the existing algorithms.

In this paper, we made the following contributions:

1) We design efficient lookup tables, which enable the encoding and decoding operations into simple lookup operations.

2) We implement novel and efficient encoding and decoding algorithms by exploiting LT, the bit detection mechanism, and multi-core hardware.

3) Extensive experiments show that our algorithms significantly outperform the existing algorithms.

2  Z-curve

The Z-curve grids the entire space, whereas the 1st-order Z-curve divides the square space into four sub-regions. Connecting these four sub-regions in the order of the lower left, upper left, lower right, and upper right of the square space forms an “N” type Z-curve of order 1. A Z-curve of order 1 in each sub-region can be obtained by embedding a Z-curve of order 2. Using this method, Z-curves of any order can be generated. The schematic diagrams of the Z-curve of orders 1, 2, and 3 are shown in Fig. 1.

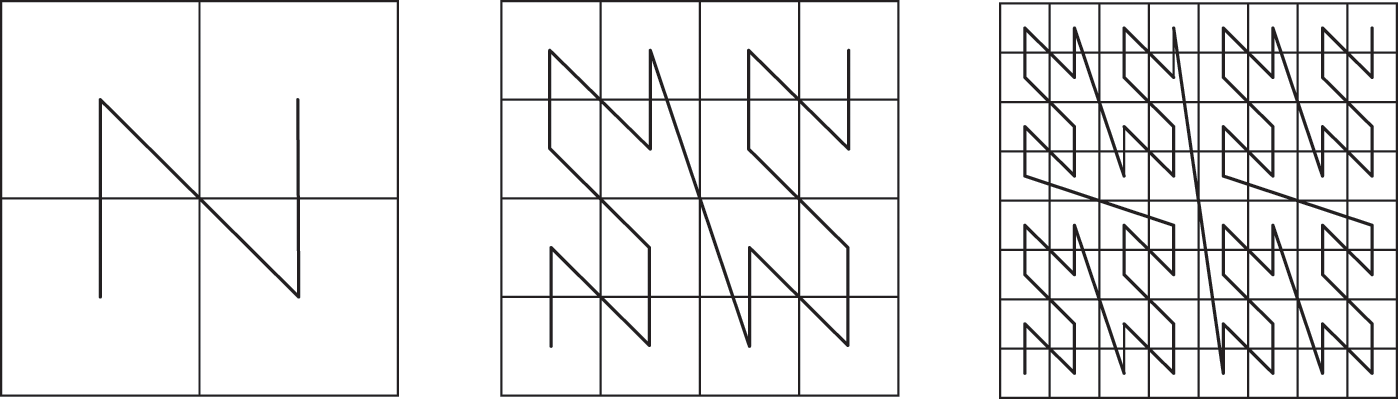
Figure 1: The schematic diagrams for the Z-curve of orders 1, 2 and 3

The Z-curve of order 1 has only one state, either “Z” type or “N” type, with the “N” type illustrated in Fig. 2. The numbers in the bracelet are the Z-values of order 1 and the numbers on top are the coordinates of order 1.

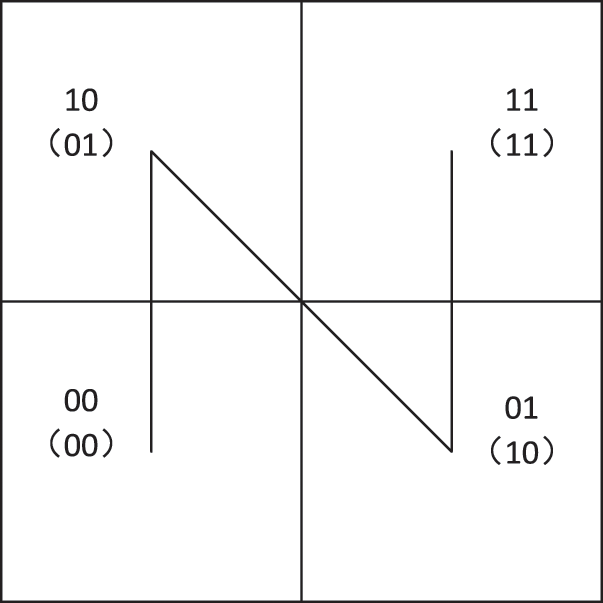
Figure 2: “N” type Z-curve

3  Z-curve Encoding and Decoding Algorithms

3.1 The Design of Lookup Tables

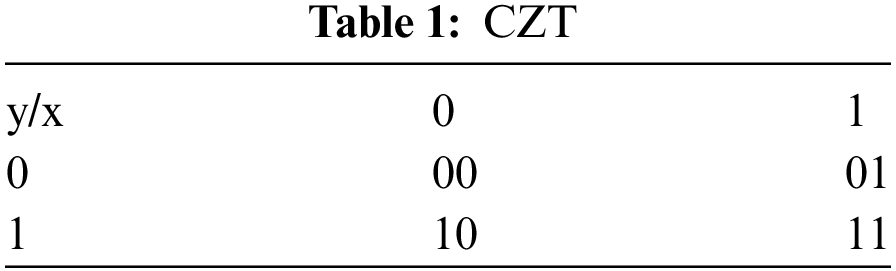
As shown in Fig. 2, there is a one-to-one mapping between the coordinates of order 1 and the Z-values of order 1. We store this mapping in lookup tables. Lookup tables are simple, intuitive, and efficient, so we implement the encoding and decoding algorithms based on lookup tables in this paper. For encoding, we create the coordinates for the Z-value lookup table (CZT), as shown in Table 1 Given (x, y), a coordinate of order 1, an entry in CZT implements a mapping from (x, y) to z, the corresponding Z-value of order 1. For descriptive convenience, the Z-values in Table 1 are expressed in binary.

3.2 Encoding Algorithms

Based on CZT, it is possible to iteratively query CZT to obtain the Z-values of each order, ultimately leading to the final encoding. This way, the encoding and decoding operations can be transformed into table-lookup operations. The lookup table-based encoding algorithm (LTe), implemented based on this concept, is illustrated in Algorithm 1.

LTe requires iterative encoding over each order of an input coordinate, leading to a time complexity of O(n), where n is the total number of orders.

Note that in real-world scenarios, the coordinates are usually skew-distributed, e.g., a large number of coordinates skewed to the original. In this case, these coordinates may have a lot of orders in the front with consecutive 0s. If we continue to encode all n orders in an order-wise manner, it will lead to a lower encoding efficiency.

We can easily observe from Fig. 2 that if x and y are zeros for the Z-curve, the corresponding Z-value of order 1, z, must be 0. Therefore, if the first m orders of a coordinate (X, Y) are all 0s, then the Z-value for these m orders must be 0, and there is no need to encode these orders iteratively.

Determining m efficiently is the fundamental problem we are facing. To address this problem, a bit detection mechanism is needed to detect m and improve algorithm efficiency quickly. Here, we use the First Set Bit (FSB) method provided by [19]; it quickly detects the first m orders with consecutive 0s using a binary search. Note that instead of executing FSB separately for X and Y, we only need to execute FSB once on max(X, Y). After obtaining m for a coordinate (X, Y), the first m orders can be safely skipped. We can iteratively encode the remaining n−m orders from the (m+1)-th order. Based on the discussion above, we implement a lookup table and FSB-based encoding algorithm, LTFe, incorporating first-bit detection on the basis of LTe, as shown in Algorithm 2.

Complexity analyses: The main cost of the algorithm lies in the iterative query operations on CZT. It requires a total of n−m iterations, each involving 1 table lookup operation. Therefore, the algorithm’s time complexity is O ((n−m)/k), where k is the number of threads for parallel execution. The algorithm’s space complexity mainly comes from the lookup table, as CZT uses char to store Z-values of order 1. Thus, the final space required is 4 × sizeof(char) = 4 bytes, and the space overhead can be essentially neglected.

3.3 OPenMP Based Parallel Algorithms

LTFe can effectively improve encoding efficiency; however, they do not fully utilize the parallel computing capabilities of modern multi-core processors. Therefore, its performance can be further enhanced.

OpenMP (Open Multi-Processing) is a parallel programming interface for shared-memory multiprocessor systems, widely used in various fields [20,21]. It is a convenient tool for for-loop parallelization, so we introduce it to speed up the iterative encoding further. By using simple compiler directives “#pragma omp parallel for”, the parallelization of the remaining n−m orders can be easily achieved, fully leveraging the potential of multi-core processors. OpenMP has four scheduling strategies: static, dynamic, runtime, and guided. Among them, guided is generally better than the others [22], we adopt this strategy to schedule parallel threads, achieving load balancing between the threads.

There are two ways for us to use OpenMP to speedup encoding efficiency. 1) Order- parallel: we parallelize the encoding of the remaining n−m orders for each coordinate and refer to this algorithm as OP-LTFe. In this case, we can insert “#pragma omp parallel for (guided)” between Lines 2 and 3 of Algorithm 2 to parallelize the for loop. As OP-LTFe is straightforward, we will not elaborate on it in detail here. 2) Point-parallel: we parallelize the encoding of all coordinates and refer to this algorithm as PP-LTPe. For PP-LTFe, as it is a point parallel algorithm, we perform parallel encoding for a collection of coordinates C and the encoded results are stored in an array V as shown in Algorithm 3.

3.4 Decoding Algorithms

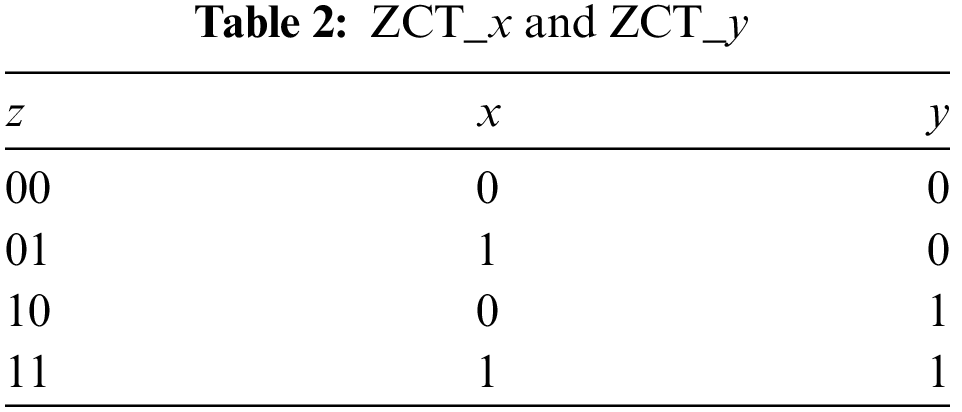
For decoding, two decoding lookup tables, ZCT_x and ZCT_y, are designed to implement the mappings from Z-values of order 1 to x and y, respectively. The designed decoding lookup tables are shown in Table 2. Here, we combine the lookup tables in Table 2.

Decoding is the inverse operation of encoding, involving the process of calculating coordinates from Z-values. Similar to encoding, we implement an iterative decoding algorithm, LTd. To further improve efficiency, we incorporate it with FSB to skip consecutive 0s in the front part. Based on these techniques, the final decoding algorithm, LTFd, is presented in Algorithm 4.

Complexity analyses: The main cost of the algorithm lies in the iterative decoding operations on ZCT_x and ZCT_y. It requires a total of n–m iterations, with each iteration involving 2 table lookup operations. Therefore, the time complexity of the algorithm is also. The algorithm’s space overheads mainly come from the lookup table. As ZCT_x and ZCT_y use char to store a 1-bit binary representation of the coordinate of order 1, the final space required is 2 × 4 × sizeof (char) = 8 bytes.

For decoding, we implemented similar OpenMP-based order-parallel decoding algorithms OP-LTFd and PP-LTFd. Due to space constraints, we do not provide the specific implementations here.

4  Experiments

4.1 Experimental Environment

The experiments are carried on a computer with an AMD Ryzen 7 5800H @ 3.20 GHz (8 cores, 16 threads) CPU and 16 GB memory. The operating system is Windows 10, and the compilation environment is Microsoft Visual Studio 2022.

4.2 Dataset

We use the following four datasets:

Discrete dataset (Discrete): In this paper, 25 million random coordinates of order n = 8, 16, 24, and 32 are generated as discrete datasets, respectively.

Skewed dataset (Skewed): To examine the impact of data skewness on the algorithms, we introduce two parameters: skewed order α and skewed rate β. Here, α represents the number of orders whose values are all 0, and β indicates the percentage of coordinates in which the values are all 0 in the first α orders among all coordinates. For instance, α = 8 and β = 50% mean that 50% of the generated coordinates have consecutive 0 in the first 8 orders. We generate 1 million random coordinates (for encoding) and Z-values (for decoding) for each specific α and β.

Real Datasets: We use the United States road dataset (Road) [23] and the Microsoft GPS trajectory dataset (Trajectory) [24] as real datasets. The Road dataset contains 24 million coordinates of major roads and bridges in the United States. The Trajectory dataset includes 25 million coordinates, recording users’ diverse outdoor activities, such as sightseeing, shopping, and commuting.

Considering decoding is the inverse operation of encoding, the encoding results are used as the decoding dataset. To test the efficiency of the proposed encoding algorithm, LTFe and LTFd are compared with the BI [18]. For simplicity, the BI encoding algorithm is referred to as “BIe,” and the corresponding BI decoding algorithm is referred to as “BId”.

4.3 Encoding

4.3.1 Impact of Lookup Tables on Encoding Efficiency

To assess the impact of lookup tables on the efficiency of Z-curve encoding, LTe and BIe are compared on three datasets: Discrete, Road, and Trajectory. The results are illustrated in Fig. 3a–c.

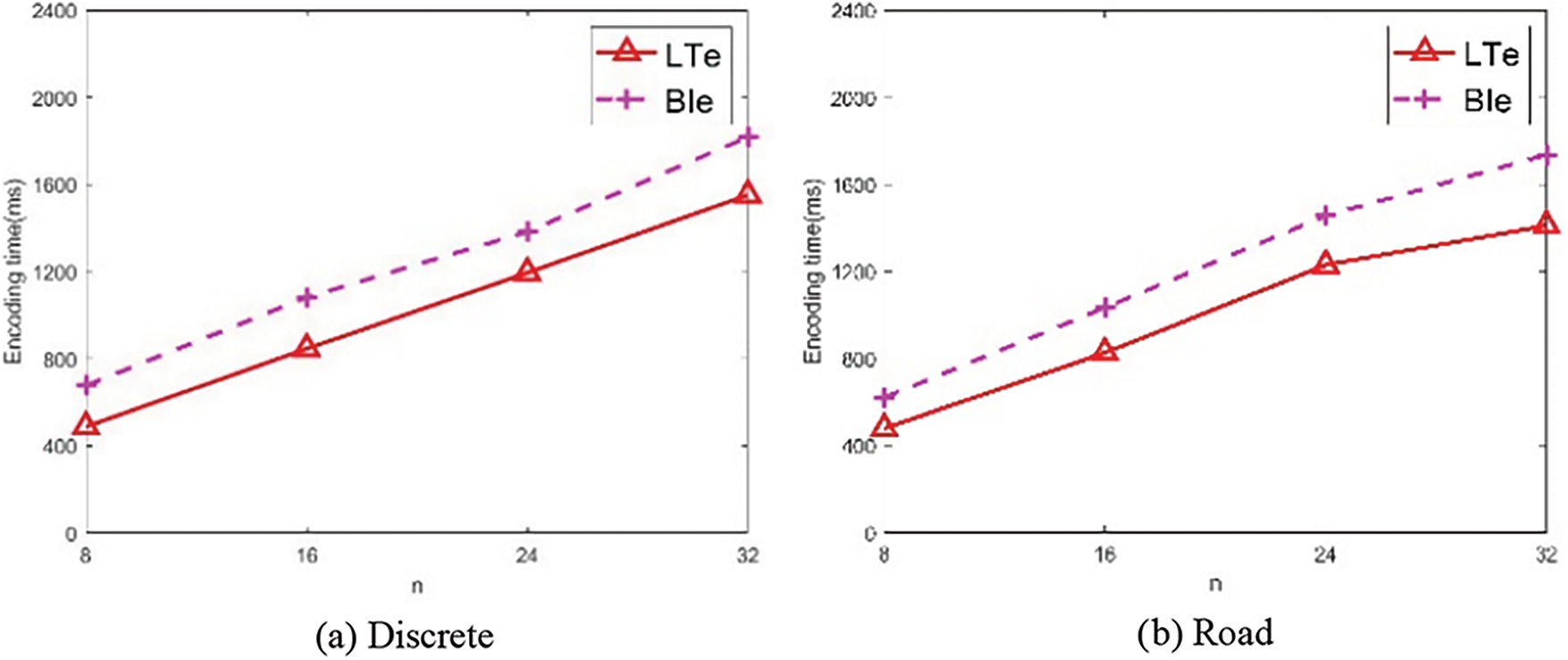
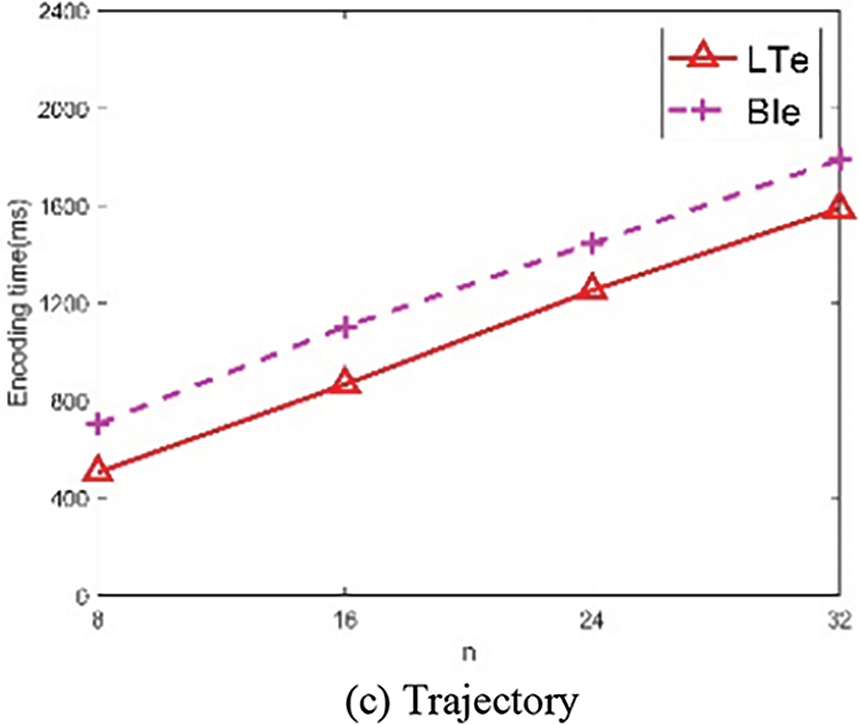
Figure 3: Comparisons between LTe and BIe

As seen from the above three figures, it can be observed that as n increases, the encoding time of each algorithm linearly increases. Overall, the efficiency of LTe is better than that of BIe, the reason lies in that LTe exploits the fast table lookup operations to obtain the Z-value of each order directly. At n = 32, the encoding times of LTe on the three datasets are 1551, 1411, and 1587 ms, while for BIe, these values are 1817 ms, 1736 ms, and 1787 ms. The efficiency improvements of LTe are 19%, 18.7%, and 11.2%, respectively.

4.3.2 Impact of Bit Detection Mechanism

To examine the impact of the bit detection mechanism under skewed distributions, LTFe and LTe were compared on Skewed datasets using the following two settings: (1) Fixing α = 16 and varying β at 25%, 50%, 75%, and 100%; (2) Fixing β = 50% and varying α at 4, 8, 16, 24. The experimental results are presented in Figs. 4 and 5, respectively.

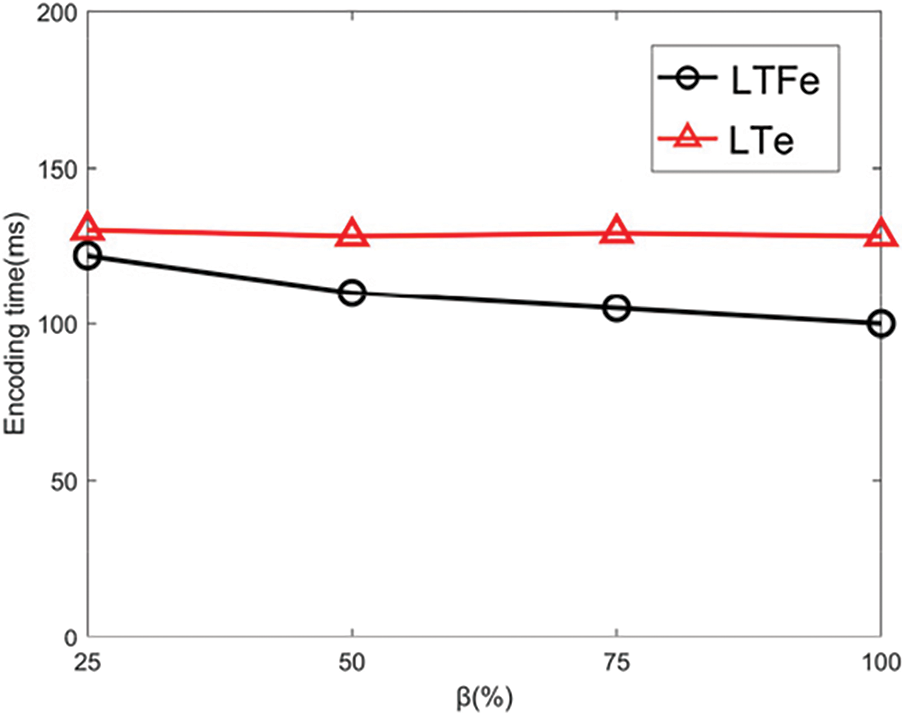
Figure 4: The effects on β

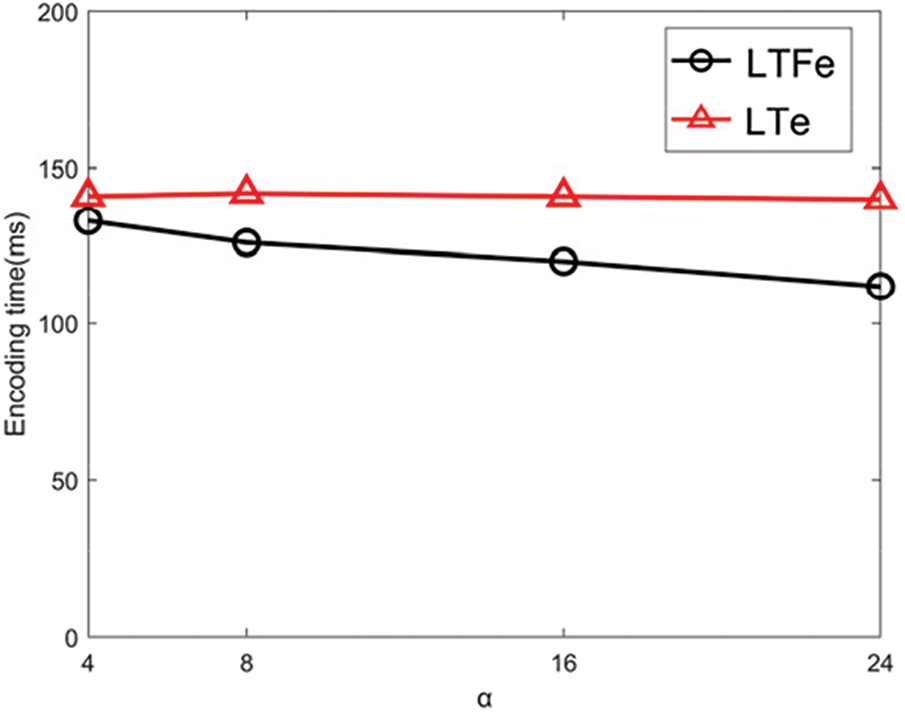
Figure 5: The effects on α

As seen in Fig. 4, it can be observed that as β increases, the number of orders that LTFe needs to encode decreases, resulting in an overall decrease in encoding time. In contrast, the number of orders that LTe needs to encode remains constant with the increase of β, leading to relatively stable encoding times. Overall, the efficiency of LTFe is better than LTe, indicating that skipping the first m orders can effectively improve encoding efficiency. When β = 100%, the encoding time of LTFe is 101 ms, while the corresponding encoding time for LTe is 128 ms, representing a 21% efficiency improvement.

As seen in Fig. 5, with the increase of α, the number of orders that LTFe needs to encode decreases, resulting in a reduction in encoding time for LTFe. Overall, the efficiency of LTFe is better than LTe. When α = 24, the encoding time of LTFe is 112 ms, while it is 140 ms for LTe, representing a 20% efficiency improvement.

4.3.3 Impact of the Number of Threads

To assess the impact of the number of threads, k, on Z-curve encoding efficiency, we set n to be 32 and k to be 4, 8, 12, 16, and 20, respectively. We compare LTFe, Op-LTFe and PP-LTFe on Discrete, Road, and Trajectory. The results are shown in Fig. 6a–c, respectively.

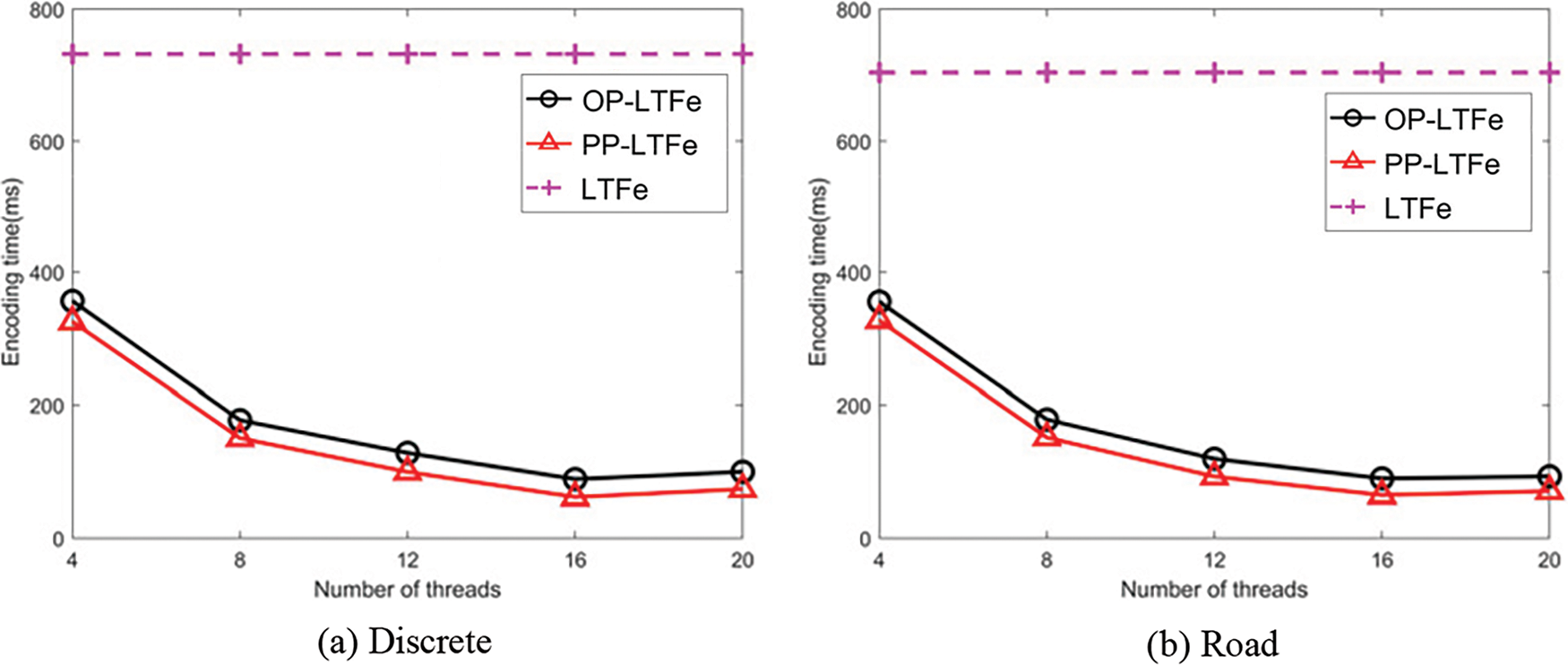
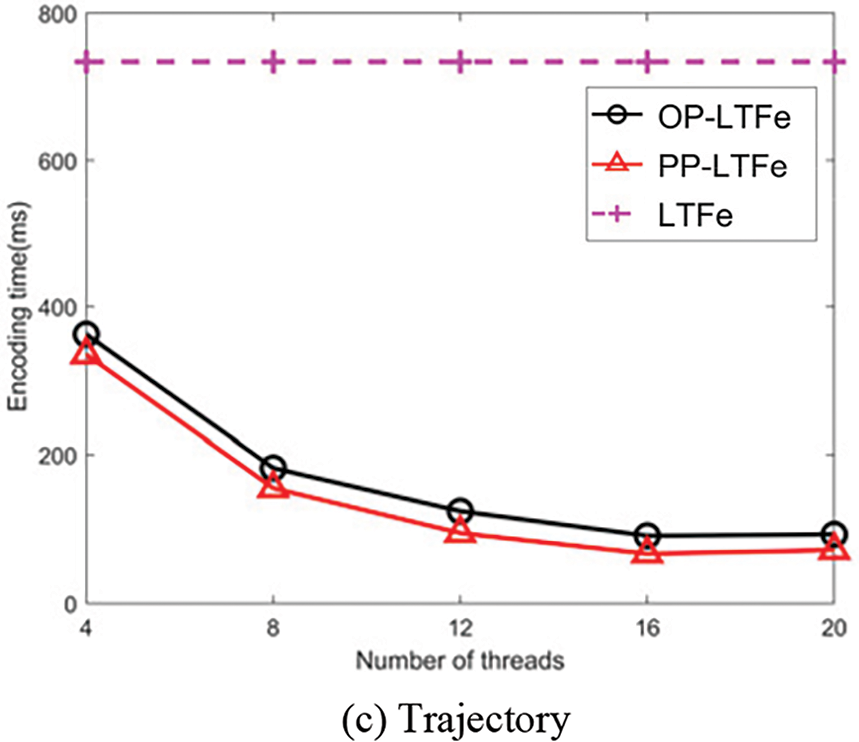
Figure 6: Comparisons of different number of threads

As seen from the above three figures, it is evident that the efficiency of OP-LTFe and PP-LTFe are far superior to LTFe across the three datasets because they can exploit OpenMP for parallel execution. When the number of threads is set to 16, the performances of OP-LTFe and PP-LTFe are close to optimal, consistent with the experimental setup of an 8-core, 16-thread CPU. Among the two parallel algorithms, although OP-LTFe has a finer parallel granularity, the efficiency of PP-LTFe is superior to OP-LTFe. This is because, in PP-LTFe, each thread encodes consecutive orders in a coordinate point, resulting in a better locality and lower thread switching overhead. The encoding times for PP-LTFe across the three datasets are 61, 64, and 66 ms for k = 16, representing 30.7%, 28.1%, and 26.7% efficiency improvements over OP-LTFd. The speedups of PP-LTFe over LTFe are 12.0×, 11.0×, and 11.1×, respectively.

4.4 Decoding

4.4.1 Impact of Lookup Tables on Decoding Efficiency

To assess the impact of lookup tables on Z-curve decoding efficiency, LTd and BId were compared across the Discrete, Road, and Trajectory datasets. The results are shown in Fig. 7a–c, respectively.

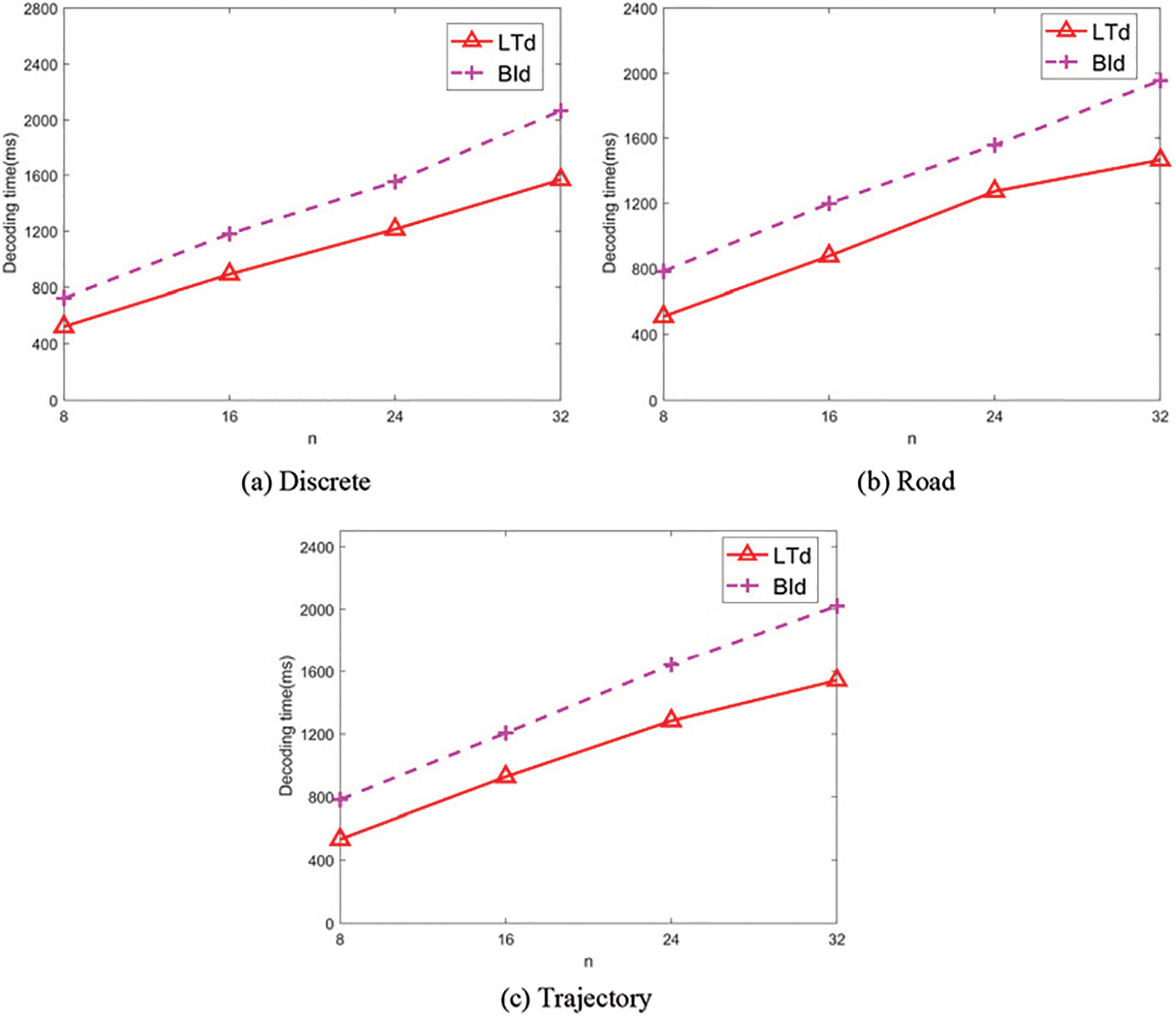
Figure 7: Comparisons between LTd and BId

The trends in the above graphs are similar to the encoding results. As n increases, the decoding times linearly increase for all algorithms. Overall, the efficiency of LTd is superior to BId due to the efficient lookup table we designed, which facilitates directly obtaining the Z-value of each order. At n = 32, the decoding times for LTd across the three datasets are 1568, 1464, and 1542 ms, while the corresponding decoding times of BId are 2066, 1956, and 2021 ms, representing efficiency improvements of 25%, 25.2%, and 23.7%, respectively.

4.4.2 Impact on Bit Detection

To examine the impact of the bit detection mechanism on Z-curve decoding efficiency under skewed distributions, LTFd and LTd were compared on the Discrete dataset using the following two settings: (1) Fixing α = 16 and varying β at 25%, 50%, 75%, 100%; (2) Fixing β = 50% and varying α at 4, 8, 16, 24. The experimental results are shown in Figs. 8 and 9, respectively.

Figure 8: The effects on β

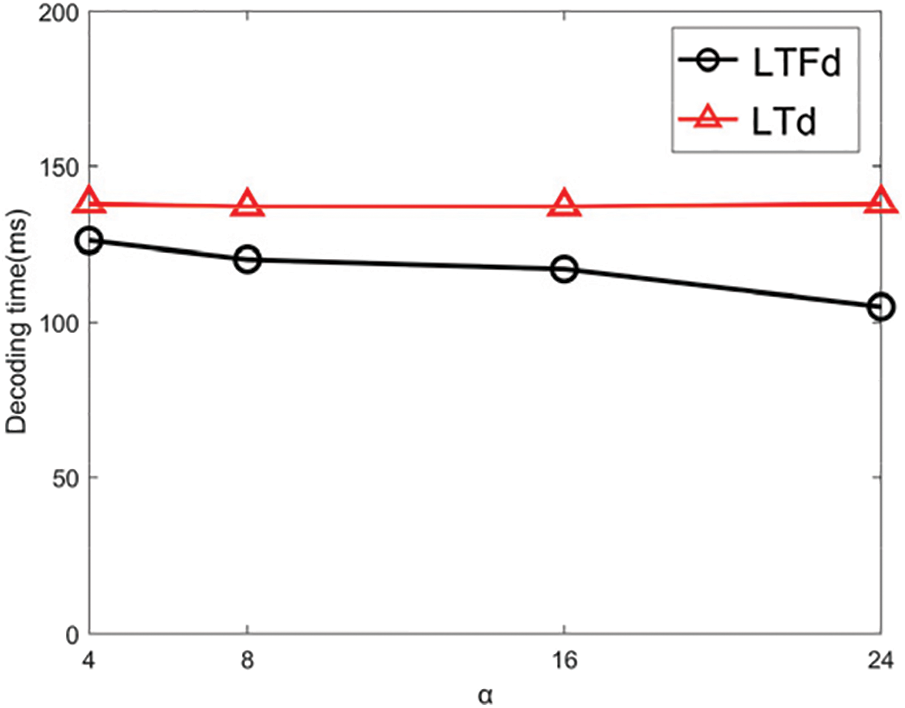
Figure 9: The effects on α

As seen in Fig. 8, the decoding time of LTFd decreases with the increase of β, while, relatively, the decoding time of LTd remains constant. As LTFd decodes less orders than LTd, the efficiency of LTFd is superior to LTd. At β = 100%, the decoding time of LTFd is 100 ms, while the corresponding LTd decoding time is 130 ms, resulting in a 23% efficiency improvement.

As seen in Fig. 9, with the increase of α, the decoding time of LTFd decreases. Overall, LTFd’s efficiency is superior to LTd’s. At α = 24, the decoding time of LTFd is 105 ms, while it is 138 ms for LTd, resulting in a 24% efficiency improvement.

4.4.3 Impact of the Number of Threads

To evaluate the impact of the number of threads on the decoding efficiency, we set n to be 32 and k to be 4, 8, 12, 16, and 20, respectively. LTFd, Op-LTFd and PP-LTFd are compared on Discrete, Road, and Trajectory. The results on the three datasets are shown in Fig. 10a–c, respectively.

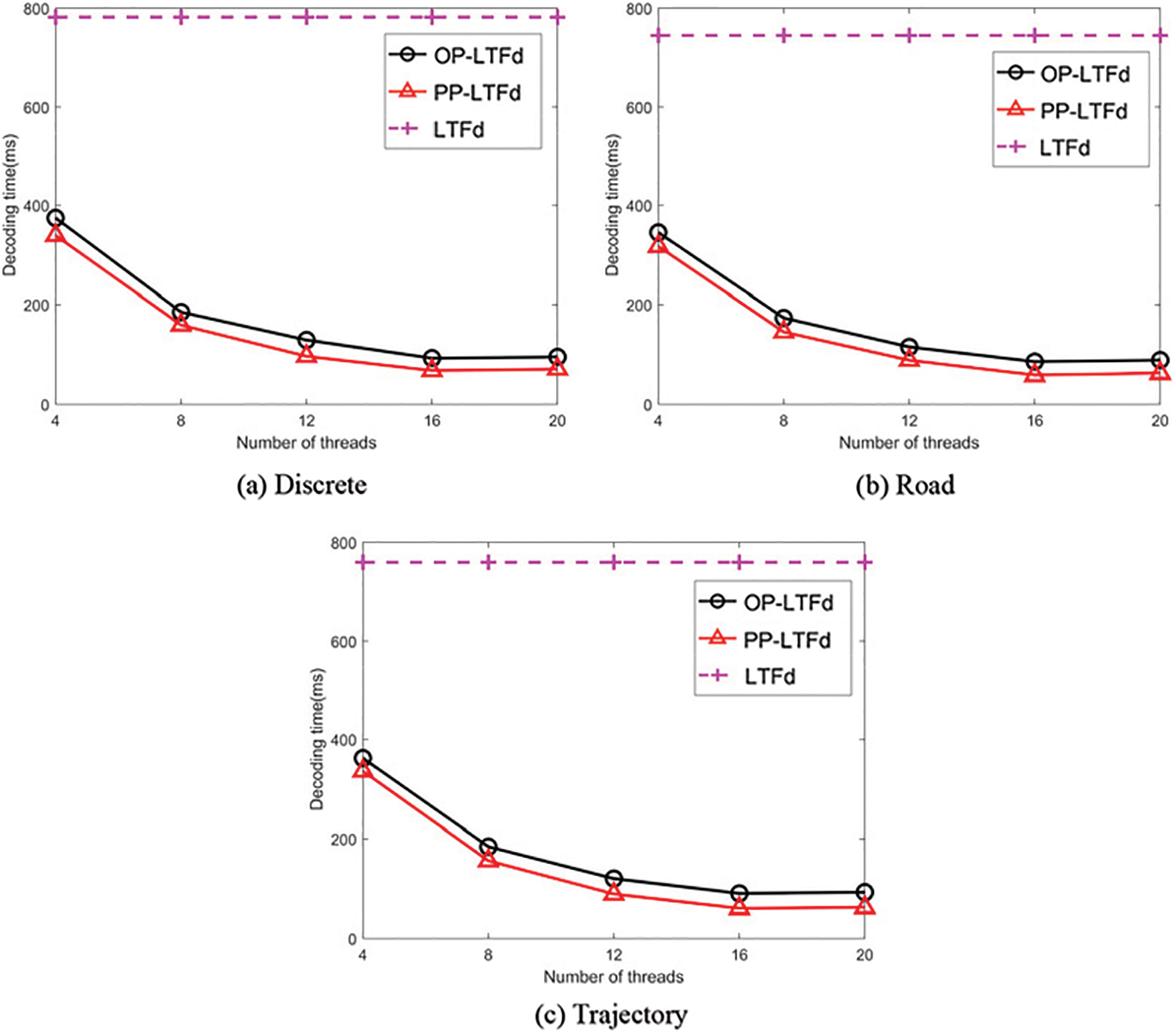
Figure 10: Comparisons of different number of threads

As seen from the above three figures, the efficiency of PP-LTFd is superior to LTFd and OP-LTFd. The reasons are similar to those of the encoding algorithm. First, it utilizes OpenMP to parallelize the encoding process; second, compared to OP-LTFd, PP-LTFd exhibits better locality and has lower thread switching overhead. When k is 16, the decoding times of PP-LTFd are 67, 58, and 60 ms on Discrete, Road, and Trajectory, respectively, exhibiting speedups over LTFd of 11.6×, 12.6×, and 12.6v.

5  Conclusion

This paper proposes optimized Z-curve encoding (LTFe) and decoding (LTFd) algorithms to boost the efficiency of the encoding and decoding algorithms. These algorithms utilize lookup tables and bit detection to address inefficiencies in bit interleaving. Additionally, two OpenMP-based parallel versions are introduced to leverage multi-core hardware. Experiments show that these algorithms outperform existing methods, making them ideal for indexing, image processing, and related applications.

Acknowledgement: The authors would like to thank Computer Technology Applications in Yunnan for providing the funding support.

Funding Statement: This research was funded by the Key Project of the Open Fund for Computer Technology Applications in Yunnan under Grant no. CB23031D025A.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Mengjuan Li, Fengling Xia; data collection: Teng Liang; analysis and interpretation of results: Fengling Xia, Zicheng Zhou, Shaowen Sun; draft manuscript preparation: Zicheng Zhou, Shaowen Sun. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on request from the authors.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. G. M. Morton, “A computer oriented geodetic data base and a new technique in file sequencing,” in Technical Report. Ottawa, Canada: IBM Ltd., 1966. [Google Scholar]

2. J. Gao, X. Cao, X. Yao, G. Zhang, and W. Wang, “LMSFC: A novel multidimensional index based on learned monotonic space filling curves,” Proc. VLDB Endow., vol. 16, no. 10, pp. 2605–2617, Jun. 2023. doi: 10.14778/3603581.3603598. [Google Scholar] [CrossRef]

3. G. Liu, L. Kulik, C. S. Jensen, T. Li, and J. Qi, “Efficient cost modeling of space-filling curves,” 2023, arXiv:2312.16355. [Google Scholar]

4. L. Jia, H. Tang, M. Li, B. Zhao, S. Wei and H. Zhou, “An efficient association rule mining-based spatial keyword index,” Int. J. Data Warehousing Min., vol. 19, no. 2, pp. 1–19, Jan. 2023. doi: 10.4018/IJDWM. [Google Scholar] [CrossRef]

5. D. Zhang, Y. Wang, Z. Liu, and S. Dai, “Improving NoSQL storage schema based on Z-curve for spatial vector data,” IEEE Access, vol. 7, pp. 78817–78829, 2019. doi: 10.1109/ACCESS.2019.2922693. [Google Scholar] [CrossRef]

6. P. Kilimci and O. Kalipsiz, “Indexing of spatiotemporal data: A comparison between sweep and z-order space filling curves,” in Int. Conf. on Inf. Soc. (i-Society 2011), London, UK, 2011, pp. 450–456. doi: 10.1109/i-Society18435.2011.5978495. [Google Scholar] [CrossRef]

7. R. Pajarola and P. Widmayer, “An image compression method for spatial search,” IEEE Trans. Image Process., vol. 9, no. 3, pp. 357–365, Mar. 2000. doi: 10.1109/83.826774. [Google Scholar] [PubMed] [CrossRef]

8. T. Bai, H. Yan, X. Jia, S. Jiang, G. Wang and X. Mou, “Z-index parameterization for volumetric CT image reconstruction via 3-D dictionary learning,” IEEE Trans. Med. Imaging, vol. 36, no. 12, pp. 2466–2478, Dec. 2017. doi: 10.1109/TMI.2017.2759819. [Google Scholar] [PubMed] [CrossRef]

9. Z. Yang, F. Li, and S. Xiao, “A nearest neighbor projection method based on Z curve,” presented at the ICBAIE 2022, Nanchang, China, Jul. 15–17, 2022. doi: 10.1109/ICBAIE56435.2022. [Google Scholar] [CrossRef]

10. J. Lu, Y. Zhao, K. L. Tan, and Z. Wang, “Distributed density peaks clustering revisited,” IEEE Trans. Knowl. Data Eng., vol. 34, no. 8, pp. 3714–3726, Aug. 1, 2022. doi: 10.1109/TKDE.2020.3034611. [Google Scholar] [CrossRef]

11. P. Cech et al., “Comparing MapReduce-based k-NN similarity joins on Hadoop for high-dimensional data,” presented at ADMA 2017, Singapore, Nov. 5–6 2017, pp. 63–75. [Google Scholar]

12. J. Qi, G. Liu, C. S. Jensen, and L. Kulik, “Effectively learning spatial indices,” Proc. VLDB Endow., vol. 13, no. 12, pp. 2341–2354. doi: 10.14778/3407790.3407829. [Google Scholar] [CrossRef]

13. T. Ouni, A. Lassoued, J. Ktari, and M. Abid, “Scan based lossless image compression scheme,” presented at SITIS 2011, Dijon, France, Nov. 28–Dec.1, 2011, pp. 454–460. doi: 10.1109/SITIS.2011.76. [Google Scholar] [CrossRef]

14. L. Jia, M. Kong, W. Wang, M. Li, J. You and J. Ding, “2-D Hilbert encoding and decoding algorithms on skewed data,” (in ChineseJ. Tsinghua Univ. (Sci. Technol.), vol. 62, no. 9, pp. 1426–1434, 2022. [Google Scholar]

15. C. Böhm, M. Perdacher, and C. Plant, “A novel hilbert curve for cache-locality preserving loops,” IEEE Trans. Big Data, vol. 7, no. 2, pp. 241–254, 1 Jun. 2021. doi: 10.1109/TBDATA.2018.2830378. [Google Scholar] [CrossRef]

16. Y. Lei, X. Tong, D. Wang, C. Qiu, H. Li and Y. Zhang, “W-Hilbert: A W-shaped Hilbert curve and coding method for multiscale geospatial data index,” Int. J. Appl. Earth Obs. Geoinf., vol. 118, Apr. 2023, Art. no. 103298. doi: 10.1016/j.jag.2023.103298. [Google Scholar] [CrossRef]

17. L. Jia, Y. Fan, J. Ding, X. Li, and J. You, “3D hilbert space filling curve encoding and decoding algorithms based on efficient prefix reduction,” J. Electron. Inf. Technol., vol. 46, no. 2, pp. 633–642, Feb. 2024. doi: 10.11999/JEIT230013. [Google Scholar] [CrossRef]

18. J. Li, Z. Wang, G. Cong, C. Long, H. M. Kiah and B. Cui, “Towards designing and learning piecewise space-filling curves,” in Proc. VLDB Endow., vol. 16, no. 9, pp. 2158–2171. doi: 10.14778/3598581.3598589. [Google Scholar] [CrossRef]

19. ROSETTA, “Find first and last set bit of a longinteger,” 2019. Accessed: Aug. 25, 2023. [Online]. Available: http://rosettacode.org/wiki/Find_first_and_last_set_bit_of_a_long_integer [Google Scholar]

20. S. Bak et al., “OpenMP application experiences: Porting to accelerated nodes,” Parallel Comput., vol. 109, Mar. 2022, Art. no. 102856. doi: 10.1016/j.parco.2021.102856. [Google Scholar] [CrossRef]

21. M. Aldinucci et al., “Practical parallelization of scientific applications with OpenMP, OpenACC and MPI,” J. Parallel Distr. Comput., vol. 157, pp. 13–29, 2021. doi: 10.1016/j.jpdc.2021.05.017. [Google Scholar] [CrossRef]

22. M. Li et al., “OpenMP based parallel set containtment query algorithm,” (in ChineseJ. Yunnan Univ. (Nat. Sci. Ed.), vol. 38, no. 3, pp. 376–382, 2016. [Google Scholar]

23. ROAD, 2010. Accessed: Sep. 1, 2023. [Online]. Available: http://www.diag.uniroma1.it//challenge9/download.shtml [Google Scholar]

24. Z. Yu, “T-Drive trajectory data sample,” Accessed: Sep. 10, 2023. [Online]. Available: https://www.microsoft.com/en-us/research/publication/t-drive-trajectory-data-sample/ [Google Scholar]