 Open Access
Open Access
ARTICLE
Occluded Gait Emotion Recognition Based on Multi-Scale Suppression Graph Convolutional Network
1 Beijing Key Laboratory of Information Service Engineering, Beijing Union University, Beijing, 100101, China
2 College of Smart City, Beijing Union University, Beijing, 100101, China
* Corresponding Author: Ning He. Email:
Computers, Materials & Continua 2025, 82(1), 1255-1276. https://doi.org/10.32604/cmc.2024.055732
Received 05 July 2024; Accepted 07 October 2024; Issue published 03 January 2025
Abstract
In recent years, gait-based emotion recognition has been widely applied in the field of computer vision. However, existing gait emotion recognition methods typically rely on complete human skeleton data, and their accuracy significantly declines when the data is occluded. To enhance the accuracy of gait emotion recognition under occlusion, this paper proposes a Multi-scale Suppression Graph Convolutional Network (MS-GCN). The MS-GCN consists of three main components: Joint Interpolation Module (JI Moudle), Multi-scale Temporal Convolution Network (MS-TCN), and Suppression Graph Convolutional Network (SGCN). The JI Module completes the spatially occluded skeletal joints using the (K-Nearest Neighbors) KNN interpolation method. The MS-TCN employs convolutional kernels of various sizes to comprehensively capture the emotional information embedded in the gait, compensating for the temporal occlusion of gait information. The SGCN extracts more non-prominent human gait features by suppressing the extraction of key body part features, thereby reducing the negative impact of occlusion on emotion recognition results. The proposed method is evaluated on two comprehensive datasets: Emotion-Gait, containing 4227 real gaits from sources like BML, ICT-Pollick, and ELMD, and 1000 synthetic gaits generated using STEP-Gen technology, and ELMB, consisting of 3924 gaits, with 1835 labeled with emotions such as “Happy,” “Sad,” “Angry,” and “Neutral.” On the standard datasets Emotion-Gait and ELMB, the proposed method achieved accuracies of 0.900 and 0.896, respectively, attaining performance comparable to other state-of-the-art methods. Furthermore, on occlusion datasets, the proposed method significantly mitigates the performance degradation caused by occlusion compared to other methods, the accuracy is significantly higher than that of other methods.Keywords
Gait emotion recognition is a technique that uses the characteristics of human walking patterns to identify an individual’s emotional state [1]. This recognition method is based on gait analysis, which infers possible emotional states such as happiness, sadness, anger, or anxiety by analyzing parameters like an individual’s steps, speed, stride length, and rhythm [2]. The application of this technology is extensive and can be found in fields such as security monitoring, healthcare, and human-computer interaction. Compared to traditional data types like RGB images, skeleton data provides direct structural information of the human body, which allows for a more accurate capture of core changes in human gait, such as joint angles and stride length [3–5]. Furthermore, skeleton data ignores environmental noise such as background and lighting conditions, focusing solely on analyzing dynamic information of the human body, thereby improving the accuracy of emotion recognition. As a result, human skeleton data is widely used in current research for gait emotion recognition tasks [6].
Overall, gait emotion recognition can be divided into methods based on handcrafted features and those based on deep learning. Handcrafted feature-based methods directly extract predefined features from gait data to classify emotions. These features typically include stride length, walking speed, body posture, and arm swing [7–10]. Although these methods can capture emotional information from gait to some extent, they are limited by the manual design of feature selection and extraction processes, which may not fully exploit the potential information in gait data [11,12]. Deep learning-based methods can generally be categorized into three types: Convolutional Neural Networks (CNN), Recurrent Neural Networks (RNN), and Graph Convolutional Networks (GCN) [13,14]. Since skeleton data can be viewed as a graph structure composed of human joints and connecting edges, GCNs can capture the spatial relationships between joints, allowing for more accurate recognition and analysis of human movements. Therefore, using GCNs to extract emotional features from gait has become the most popular method currently [15]. However, the aforementioned methods perform well on complete skeleton data but are ineffective in environments with occluded skeleton data. Specifically, when certain joints of the human skeleton are occluded or certain gait frames are missing, the recognition accuracy of these methods significantly decreases. As shown in Fig. 1, in real-life scenarios, captured skeleton data often experiences spatial occlusion and temporal occlusion due to factors such as camera line-of-sight obstruction, self-occlusion, and lighting variations. Thus, it is crucial to design an effective gait emotion recognition method that can handle occlusion. Given this situation, this paper proposes a Multi-scale Suppression Graph Convolutional Network (MS-GCN) to address various occlusion problems. MS-GCN consists of three core components: Joint Interpolation Module (JI Module), Multi-scale Temporal Convolution Network (MS-TCN), and Suppression Graph Convolutional Network (SGCN). Each part is specifically designed and optimized to ensure that the network can effectively recognize gait emotions even under complex occlusion conditions.
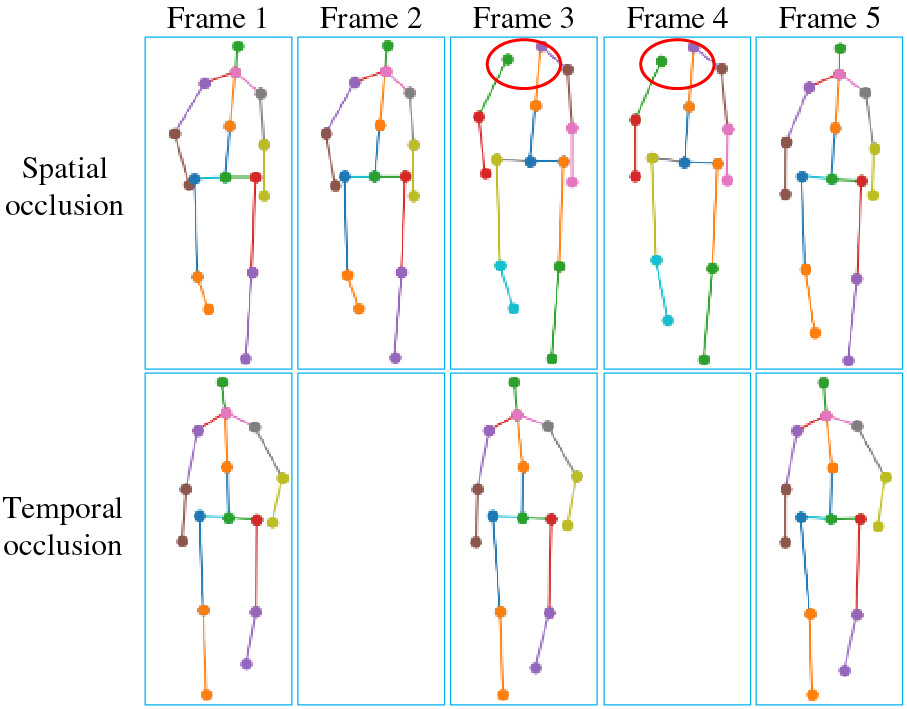
Figure 1: Occlusion illustration of gait emotion recognition
The JI Module is a method that uses K-Nearest Neighbors (KNN) technology to complete spatially occluded skeletal joints. When one or more joints are occluded, traditional skeletal data processing methods often lose information about these joints, leading to a significant drop in subsequent recognition accuracy. For example, in gait recognition, if key joints like the knee or ankle are occluded by other objects or the human body itself, the extracted human skeleton will be incomplete, and the final emotion recognition result will be severely affected. The JI Module predicts the possible positions of occluded joints by analyzing the spatial relationships between the unoccluded joints, thus restoring complete skeleton information. Specifically, the Joint Interpolation Module uses KNN technology to utilize the coordinates of known joints, calculates the distance between these points and the occluded joints, and estimates the most likely position of the occluded joints through a weighted average method. This operation not only improves the integrity of the skeleton data, but also facilitates the next step of feature extraction. The MS-TCN processes gait data at different temporal scales using convolutional kernels of various sizes. For instance, small convolutional kernels can capture subtle dynamic changes in gait, such as the variations of a single step, while large convolutional kernels can capture long-term trends in gait, such as emotional changes throughout the walking process. This design allows the network to capture both short-term dynamic changes and long-term emotional fluctuations in gait, thereby comprehensively capturing the emotional information contained in gait. Additionally, multi-scale temporal convolution helps compensate for temporally occluded gait frames. When some gait frame information is missing due to occlusion, large-scale convolutional kernels can use contextual information over a longer time range to infer these missing features, thus mitigating the impact of information loss. Therefore, MS-TCN can effectively compensate for short-term gait features missing due to occlusion by integrating information from different temporal scales. The design of the SGCN aims to extract more gait features beyond the key body parts by suppressing the extraction of features from these key body parts. This strategy is based on the observation that in the field of gait emotion recognition, graph convolutional network (GCN) tend to extract the most prominent features of the human skeleton for emotion classification, while less noticeable potential features are often overlooked. In other words, GCN rely on the most significant features of the human skeleton to recognize emotions. When the skeleton is complete, this does not affect recognition accuracy. However, under occlusion, if the skeleton joints containing these prominent features are missing, the accuracy of gait emotion recognition can significantly decrease. Therefore, this paper introduces a specially designed SGCN to suppress the extraction of prominent features in the human skeleton, enabling the network to fully extract less noticeable features, thereby reducing the negative impact of occlusion on emotion recognition results. The working mechanism of the SGCN includes the following aspects. First, during the training process, the network calculates the feature weights of each joint using a score evaluation module to identify the joints with significant features. Then, the joint suppression module performs a mask operation on the joints containing significant features. Finally, a GCN is used to extract non-significant features from the masked human skeleton. By repeating the above operations, the SGCN can fully extract non-significant features of the human skeleton. Through the collaborative work of the three modules, MS-GCN can effectively improve gait emotion recognition accuracy under occlusion conditions. Experimental results show that compared to existing gait emotion recognition techniques, MS-GCN demonstrates better performance and higher robustness in various occlusion scenarios. Overall, the main contributions of this paper can be summarized as follows:
1) Designed a JI Module based on KNN technology. By analyzing the unoccluded joints and their spatial relationships, this module completes the occluded skeletal joints spatially, thereby improving the completeness of skeletal data and the accuracy of recognition results.
2) Utilized MS-TCN, employing convolution kernels of different sizes to analyze gait data at multiple temporal scales, compensating for the loss of temporal information caused by occlusion.
3) Developed a SGCN to suppress the extraction of features from key body parts in gait emotion recognition. This allows the network to fully explore the latent features in the human skeleton that are not prominent, reducing the negative impact of occlusion on recognition results.
The remainder of the paper is organized as follows. Section 2 reviews the related work on gait-based emotion recognition and skeleton-based action recognition under occlusion. Section 3 presents the details of the proposed Multi-scale Suppression Graph Convolutional Network (MS-GCN), including the Joint Interpolation Module, Multi-scale Temporal Convolution Network, and Suppression Graph Convolutional Network. Section 4 describes the datasets used, implementation details, experimental results, an ablation study, and visualizations to validate the effectiveness of the approach. Finally, Section 5 concludes the paper and discusses potential future work.
2.1 Gait-Based Emotion Recognition
Based on different feature extraction methods, this paper categorizes gait-based emotion recognition into three types: sequence-based, image-based, and graph-based methods [13,14]. Sequence-based methods primarily extract features from time series data to analyze and recognize human emotional states. Bhattacharya et al. [16] proposed a semi-supervised method based on autoencoders, using hierarchical attention pooling to classify emotions from human gait captured in videos. Randhavane et al. [17] developed an LSTM-based method to obtain deep features by modeling long-term temporal dependencies in sequential 3D human poses. Zhang et al. [18] introduced a novel hierarchical attention neural network that extracts emotional features from motion information through position encoders and velocity encoders. Image-based methods transform continuous skeletal sequences into image-like representations, converting the sequence classification problem into an image classification problem. Hu et al. [13] proposed a novel dual-stream network named TNTC, which uses a Transformer-based complementary module TCM to hierarchically bridge the complementarity between two streams and capture long-range dependencies. Narayanan et al. [19] developed a model based on multi-view skeletal graph convolution for socially aware robot navigation in pedestrian environments. Graph-based methods treat the human skeleton as a graph, where each node represents a joint, and edges represent the physical connections between joints. These methods use GCN to capture the complex spatial relationships between human joints. Bhattacharya et al. [20] proposed a spatio-temporal graph convolutional network method to classify perceived human emotions from gait. Zhai et al. [21] introduced a network named BPM-GCN, which recognizes emotions in gait from both the pose stream and motion stream perspectives. Yin et al. [22] designed an adaptive spatio-temporal graph convolution method (MSA-GCN) that dynamically selects convolution kernels to learn spatio-temporal features under different emotions. The aforementioned methods focus on emotion recognition using complete skeletal data, but their accuracy significantly decreases under occlusion conditions. Therefore, based on these methods, this paper designs MS-GCN, which effectively improves recognition accuracy under occlusion conditions and fills a gap in related research.
2.2 Skeleton-Based Action Recognition under Occlusion Conditions
Traditional action recognition methods often perform poorly under occlusion conditions due to the loss of critical information. In recent years, with the development of deep learning technologies, several new methods have been proposed to address this issue. Shi et al. [23] proposed an occlusion-aware multi-stream fusion graph convolutional network (MSFGCN), which uses a multi-stream architecture where different streams handle different occlusion scenarios to improve the recognition accuracy of occluded skeletal data. Peng et al. [24] introduced a Transformer-based model called Trans4SOAR, which combines three data streams and a hybrid attention fusion mechanism to mitigate the negative impact of occlusion. Bian et al. [25] proposed a structural knowledge distillation scheme that uses high-quality skeletons as a teacher model to help train a student model with low-quality skeletons, enhancing the performance of low-quality skeletal data in action recognition tasks. Li et al. [26] proposed a novel encoding technique that converts the human skeleton into a feature matrix. By integrating an attention model into a GAN-based data interpolation model, it can effectively interpolate missing data. Ding et al. [27] introduced a generalized graph convolutional network that extracts discriminative features beyond physical joint connectivity. Vernikos et al. [28] proposed a novel deep convolutional recurrent neural network (CRNN) that alleviates the impact of occlusion by reconstructing the missing motion information of occluded skeleton parts. Yang et al. [29] presented a novel graph network learning framework that infers the positions of occluded key points by learning higher-order relationships and node topology information. Wang et al. [30] proposed an occlusion-aware contrastive representation method that optimizes occlusion-aware contrastive representations through pose completion and enhancement networks in an end-to-end iterative training strategy. Xing et al. [31] developed an improved spatio-temporal graph convolutional network that adaptively adjusts the graph structure according to spatial, temporal, and channel dimensions, further strengthening the dependencies between important joints.
To address the problem of gait emotion recognition under occlusion, this paper proposes MS-GCN. The overall network architecture of MS-GCN is shown in Fig. 2. The occluded skeletal data is first input into the JI Module to complete the occluded joints. Then, MS-TCN is applied to compensate for the temporal occlusion of gait information using different sizes of temporal receptive fields. Subsequently, the SGCN is used to suppress the prominent joints, allowing the network to fully capture gait emotion features. Finally, the four types of emotions are classified through a fully connected layer and a Softmax function.
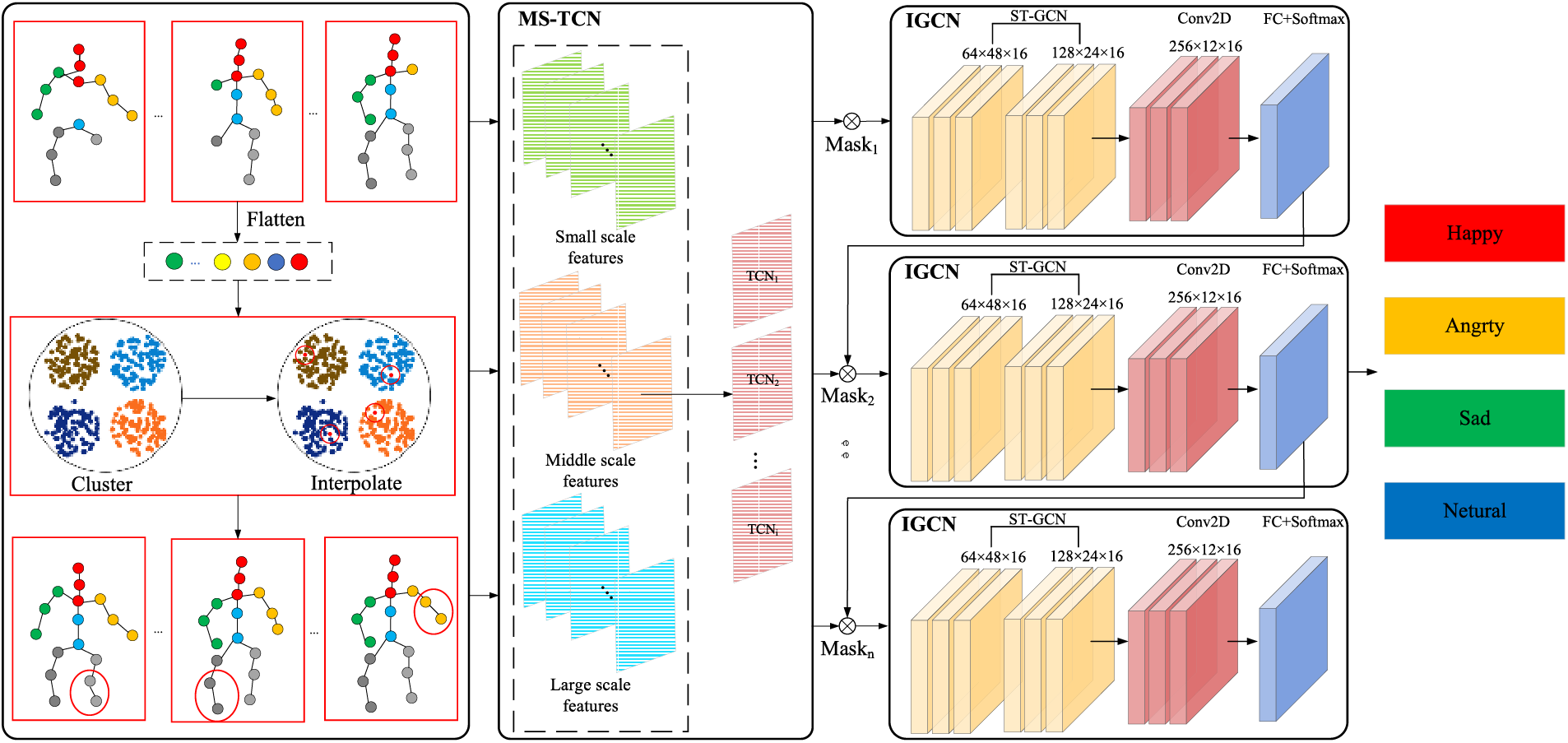
Figure 2: Overall network diagram of the proposed MS-GCN
3.1 Joint Interpolation Module
The method used in this paper to supplement occluded skeleton joints is KNN interpolation. The basic idea of KNN interpolation is that similar instances are likely to have similar data values. When the feature value of a data point is missing, it can be estimated using the K nearest neighbors that have the most similar feature values. This “nearest neighbor” method is based on the concept of spatial proximity, and the distance metric used here is Euclidean distance.
Due to the inefficiency of the KNN algorithm in handling large datasets, calculating the distance between each instance can be extremely time-consuming. To address this issue and improve the efficiency and performance of KNN imputation, this paper performs KNN imputation after clustering the data using the KMeans algorithm. The KMeans clustering algorithm can combine data with significantly similar step sequences into one cluster, thereby reducing computational complexity and enhancing the performance of the subsequent steps. In the initialization step of the KMeans algorithm, it is first necessary to choose the number of clusters k. Considering the model’s requirement to classify the data into four categories of emotions, the preliminary number of clusters k is set to 4. Next, k samples are randomly selected from the data as the initial centroids c1, c2,..., ck. For each step sequence xi in the data, the distances to all centroids are calculated, and the sequence is assigned to the cluster represented by the nearest centroid. The Euclidean distance is commonly used for calculating distance:
dist(xi,cj)=√D∑d=1(xi−cj)2(1)
where D is the dimensionality of the feature space. Each step sequence xi is assigned to the cluster Sj of the nearest centroid cj. Once all step sequences are assigned to the nearest clusters, each centroid is updated to the mean of all points in its cluster:
Cj=1|Sj|∑xi∈SjXi(2)
where |Sj| is the number of points in cluster Sj. The process of reassigning clusters and updating centroids iteratively continues until the step sequences converge into k clusters.
After performing KMeans clustering, KNN imputation is used to fill the missing values in the step sequences within each cluster. Here, because the neighboring samples may also have missing values, the standard Euclidean distance is not suitable. Therefore, a modified Euclidean distance is used:
dist(Sij,Sik)=√et−e×dignore(Sij,Sik)(3)
where t is the total number of joint points, and e is the number of existing joint points, i.e., the unblocked joint points. dignore (Sij, Sjk) is the Euclidean distance between samples j and k in cluster i ignoring missing values. After obtaining the distance of the missing values, the imputation of the skeleton key data can be expressed as:
v=∑Ki=1wi⋅vi∑Ki=1wi(4)
where v is the predicted value of the missing data, vi is the value of the i-th neighbor. The weight wi is inversely proportional to the distance from the neighbors and can be calculated as:
wi=1d(x,xi)2(5)
where d (x, xi) is the distance between the missing data point x and the i-th neighbor.
3.2 Multi-Scale Temporal Convolution Networks
Multi-Scale Feature Extraction. As shown in Fig. 3, to obtain multi-scale skeleton features, this paper modifies the single-scale input skeleton to the GCN by performing multi-scale operations. Here, multi-scale operations include both temporal and spatial multi-scale features of the skeleton, which helps in recognizing similar steps in different occlusion scenarios.
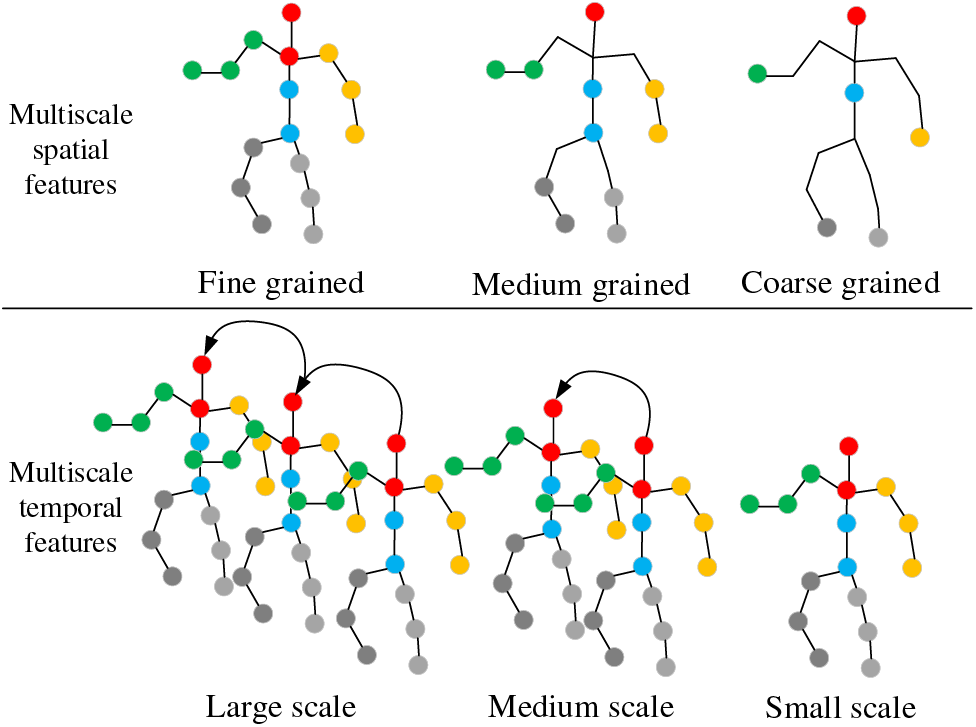
Figure 3: Multi-scale spatiotemporal features
At the temporal scale, the temporal features are divided into small-scale, medium-scale, and large-scale features. The temporal features for each scale can be represented as follows:
Xs={xti+1−xti|t=1,…,T,i=1,…,N}(6)
Xm={xti+j−xti|t=1,…,T,i=1,…N}(7)
Xl={xti+2j−xti|t=1,…,T,i=1,…N}(8)
where t represents a certain time step, and j represents the number of skipped frames. By concatenating, multi-scale temporal features can be obtained:Xtime=concat(Xs,Xm,Xl)(9)
At the spatial scale, each skeletal joint in the fine-grained graph is first connected to its adjacent joints, forming local neighborhoods that capture fine-grained spatial relationships. To extract meaningful skeletal joint features across different scales, we apply average pooling to these neighborhoods. This operation reduces the sensitivity to noise and minor variations while preserving the essential spatial information. The resulting joint features from the fine-grained graph are then aggregated across different granularities (coarse, medium, and fine) through concatenation operations. This multi-scale approach ensures that both global and local spatial patterns are effectively captured, facilitating a more robust representation of the skeletal structure. The corresponding formulas are:
Xc=AveragePooling(Xf1+Xf2+⋯+Xfn)(10)
Xskeleton=concat(Xc,Xm,Xf)(11)
where Xc denotes joint features in coarse-grained maps, and Xfn denotes joint features in fine-grained maps. Xskeleton denotes multi-scale joint features, and Xc, Xm, Xf denote coarse-grained, medium-grained, and fine-grained skeleton features, respectively.
Multiscale Temporal Convolutional Networks. As shown in Fig. 4, the MS-TCN is mainly composed of time dimension segmentation and multiple convolutional kernels. Specifically, the input gait feature X is first divided into temporal segments of approximately equal size through convolution operations in the temporal dimension, denoted as x1,x2,x3,…,xi. By adjusting the size of the convolutional kernels, the length of each temporal segment can be controlled. Then, different convolutional kernels are used to process these temporal segments. This operation allows each segment to focus on different temporal ranges, thereby enhancing the overall feature extraction process, which is formulated as follows:
Xt={Ti(xi)if i=1Ti(xi+yi−1)if i>1(12)
where Xt represents the features processed by the temporal convolution, Ti represents the temporal segment applied at the i-th segment, xi is the i-th segment of the input features, yi is the output after processing the i-th segment through the temporal convolution Ti, and yi−1 is the output of the previous segment, which is connected and added to the current segment xi to enhance features and prevent gradient vanishing, ensuring effective information transmission in the temporal dimension.
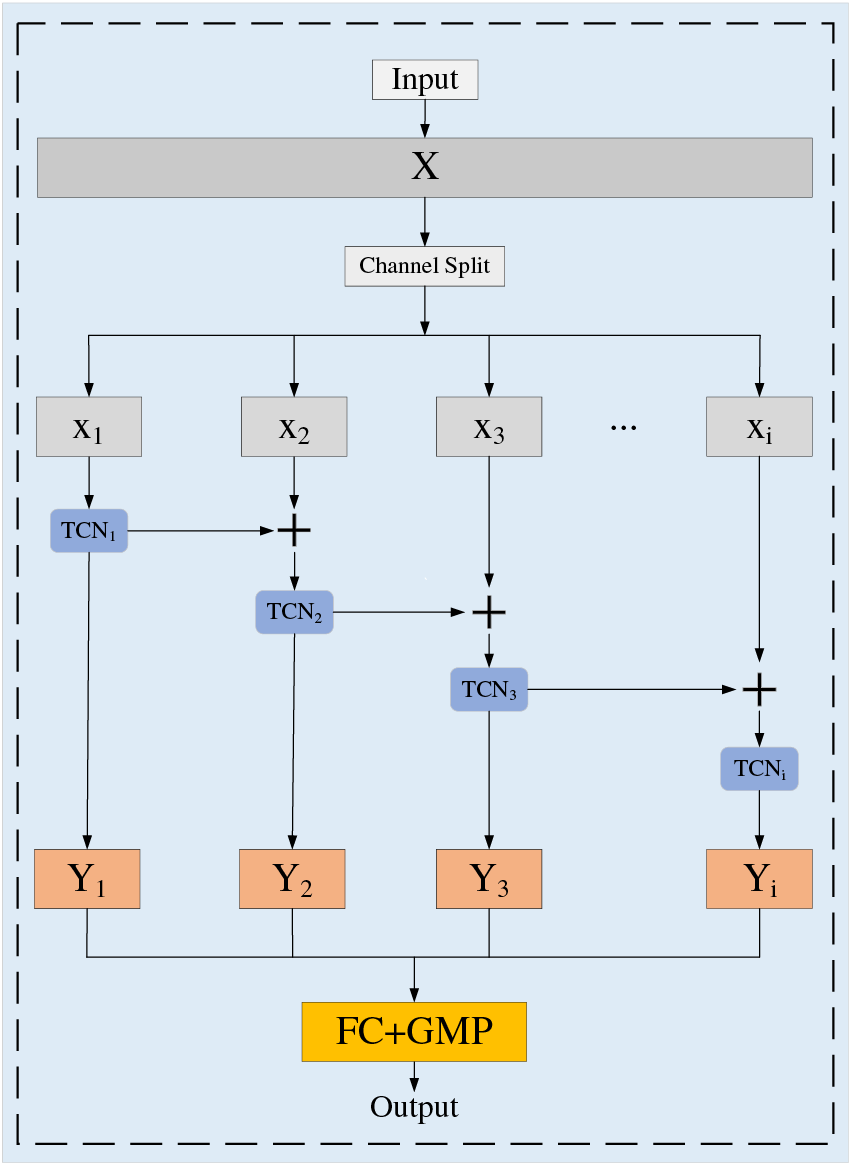
Figure 4: Multi-scale temporal convolution network
Each convolutional network with different-sized convolution kernels processes part of the features within the time range. By using residual connections and adding the output of the previous layer to the input of the current layer, information can be transmitted from one time scale to another, thereby enhancing the feature representation ability. After multiple convolutional processing, the features of each time segment need to be fused to form the final feature representation. To achieve this, global maximum pooling (GMP) and fully connected layers (FC) are used for information fusion and dimension reduction. The formula for this process is as follows:
Fout=FC(GMP(T1⊕T2⊕T3))(13)
where Fout represents the output value of multi-scale temporal convolution, ⊕ represents the connection operation, connecting the output features of different convolution kernels. FC represents the fully connected layer, GMP represents the global maximum pooling, and T1, T2, T3 respectively represent temporal convolutions with kernel sizes of 1, 3, and 9.
3.3 Suppression Graph Convolutional Network
The SGCN consists of three components: Graph Convolutional Network (GCN), Score Evaluation Module (SE Module), and the Joint Suppression Module (JS Module). The GCN primarily serves to extract skeletal features of the human body. The SE Module evaluates each joint of the human skeleton during the GCN’s feature extraction process, determining which joints contain significant features. The JS Module suppresses these significant features of the human skeleton, compelling the GCN to extract non-significant features from the skeleton, thereby improving the network’s recognition accuracy under occluded conditions.
Graph Convolutional Network. The method used in this paper is the GCN proposed by Kipf et al. [32]. The core components include the node feature matrix X, the adjacency matrix A, and the weight matrix W. The node feature matrix X contains the feature vectors of each node, the adjacency matrix A represents the topology of the graph, and the weight matrix W is used for feature transformation. The GCN consists of multiple convolutional layers, each of which takes the graph’s adjacency matrix and node feature matrix as inputs. Each convolutional layer updates the node representations by aggregating information from neighboring nodes. The convolutional formula is:
H(l+1)=σ(˜D−1/2˜A˜D−1/2H(l)W(l))(14)
where ˜A is the matrix obtained by adding self-loops to the original adjacency matrix A, and ˜D is the corresponding degree matrix. The activation function σ is usually ReLU, and W(l) is the learnable weight matrix. By using this formula, the GCN effectively aggregates the feature information of neighboring nodes and gradually extracts high-order structural features of the graph through multiple layers of convolution.
Score Evaluation Module. The SE Module consists of a fully connected layer and a softmax activation function. Inspired by [33], this paper extends the CAM technology in [34] from CNN to GCN. The original CAM performs global average pooling on the feature maps of each convolutional layer to calculate the average value of the activation values at all positions on each feature map Fk:
Fk=∑x,yfk(x,y)(15)
where fk (x, y) represents the activation value of the k-th feature map at the pixel point (x, y). Each class c that needs to be classified has a weight vector wc, which multiplies the output Fk of the average pooling to obtain the class score:
Sc=∑kwck∑x,yfk(x,y)=∑x,y∑kwckfk(x,y)(16)
where wck is the weight of the kth feature map for class c, and Sc is the score of the model for class c. In the GCN, given the human skeleton graph G = (X, W), where X is the set of joints, and W is the set of edges. A layer of graph convolution can be expressed as:
Hn=σ(˜D−12˜A˜D−12XW)(17)
where Hn is the joint feature matrix, ˜D is the degree matrix used to normalize the adjacency matrix ˜A, ensuring that the feature representation does not become unbalanced due to excessive degree differences of nodes in the graph. ˜A is the adjacency matrix with self-loops added, i.e., ˜A=A+I. X represents the human skeleton joints, and W is a learnable weight matrix.
Here, this paper replaces x in Formula (16) with gait T and y with X, obtaining the activation evaluation score of the gait T joints X:
SG=∑T,X∑kwckfk(T,X)(18)
where T represents the temporal frame sequence, and X denotes the feature information of each joint, including position coordinates, velocity, angle, and other relevant information.
Joint Suppression Module. Given a set of temporal skeleton sequence data G={st∈RX×D|t=1,2, …,T}, where T is the temporal frame sequence, X is feature information of each joint, and D is the dimension of each joint.
First, based on the activation estimation score S of the nodes, define a suppression probability P(T, X) for each node X at time step T:
P(T,X)=1−σ(S(T,X)maxS(T,X))(19)
where σ is the Sigmoid function used to normalize the importance scores to the interval (0, 1), and max denotes the maximum function.
Then, compute the suppression matrix M∈RT×J. This matrix is used to suppress the original skeleton data G. The suppression matrix M is calculated using the following formula, where each element mT,X represents the suppression probability applied to the node X at time step T:
mT,X={0,if uT,X<P(T,X)1,otherwise(20)
where uT,X is the average suppression probability of each node at time step T, and the calculation of P(T, X) follows Formula (19).
Finally, to extract features of the skeleton nodes without significant characteristics, this paper uses masking operations to suppress nodes with high feature scores. The formula is as follows:
˜G=G⊗mask(21)
where G represents the original skeleton, mask represents a floating-point mask matrix with the same dimension as X, and ⊗ denotes the matrix Hadamard product.
Emotion-Gait. The Emotion-Gait dataset [20] is a comprehensive collection containing 5227 gait samples, of which 4227 are real gaits and 1000 are synthetic gaits based on four emotional categories. These synthetic gaits are generated using STEP-Gen technology. The real gait samples come from various well-known sources such as BML [35], ICT-Pollick [36], and ELMD [37]. To process and analyze these gait data, all input gaits are converted into skeleton models containing 21 joints. The labeling of the gait data is done by 10 annotators aged between 20 and 28, from either the same or different cultural backgrounds as the subjects in the dataset, to ensure diversity and comprehensiveness in the annotations. In the final data processing, the emotion label with the most votes from the annotators is selected as the primary emotional category for each gait.
ELMB. The ELMB dataset [16] comprises 3924 gaits, of which 1835 gaits have emotion labels provided by 10 annotators, while the remaining 2089 gaits are unlabeled. Among the labeled data, approximately 58% are labeled as “Happy,” 32% as “Sad,” 23% as “Angry,” and 14% as “Neutral.” All input gaits are cropped or padded to 240 time steps and downsampled to every 5th frame, resulting in data with 48 time steps.
Since there is currently no publicly available human gait emotion recognition dataset for partial occlusion experiments, this paper simulates various real-world occlusion scenarios by applying temporal and spatial occlusions to the above two datasets to test the robustness of the proposed algorithm in occluded environments. Specifically, in terms of temporal occlusion, this paper randomly selects several frames from different gait sequences in the dataset and deletes them, with the deletion ratio and positions determined randomly to ensure diversity and authenticity in occlusions. For spatial occlusion, this paper employs a skeletal-based partial occlusion method, deleting joints from the left arm, right arm, two hands, two legs, and trunk to simulate real-world spatial occlusion scenarios.
Training. The proposed model is implemented based on the PyTorch deep learning framework. The experimental environment includes Ubuntu 22.04LTS, a 64-bit operating system, 128 GB of memory, an Intel® Xeon® Silver 4210 CPU @ 2.20 GHz processor, a GeForce RTX 2080Ti GPU, and the software platform comprises Python 3.8, PyTorch 1.4.0, CUDA 10.2, and CUDNN 7.6.5. The model uses the mini-batch stochastic gradient descent algorithm to learn the network parameters, with a batch size of 16 and an initial learning rate set to 0.1. The learning rate is divided by 10 every 40 epochs. During training, the cross-entropy loss function is used to measure the performance of the model.
Evaluation Criterion. This paper uses the accuracy metric to evaluate the model’s performance. Accuracy measures the overall prediction ability of the model on the entire dataset, representing the proportion of correctly predicted emotion labels among all predicted emotion labels. The calculation formula is as follows:
Accuracy=(TP+TN)/TD(22)
Precision=1nn∑1TP/(TP+FP)(23)
Recall=1nn∑1TP/(TP+FN)(24)
F1−Measure=2×Precision×Recall/(Precision+Recall)(25)
where TP represents the number of true positive samples, FP is false positive samples, TN is true negative samples, FN is false negative ones and TD represents the total number of samples.
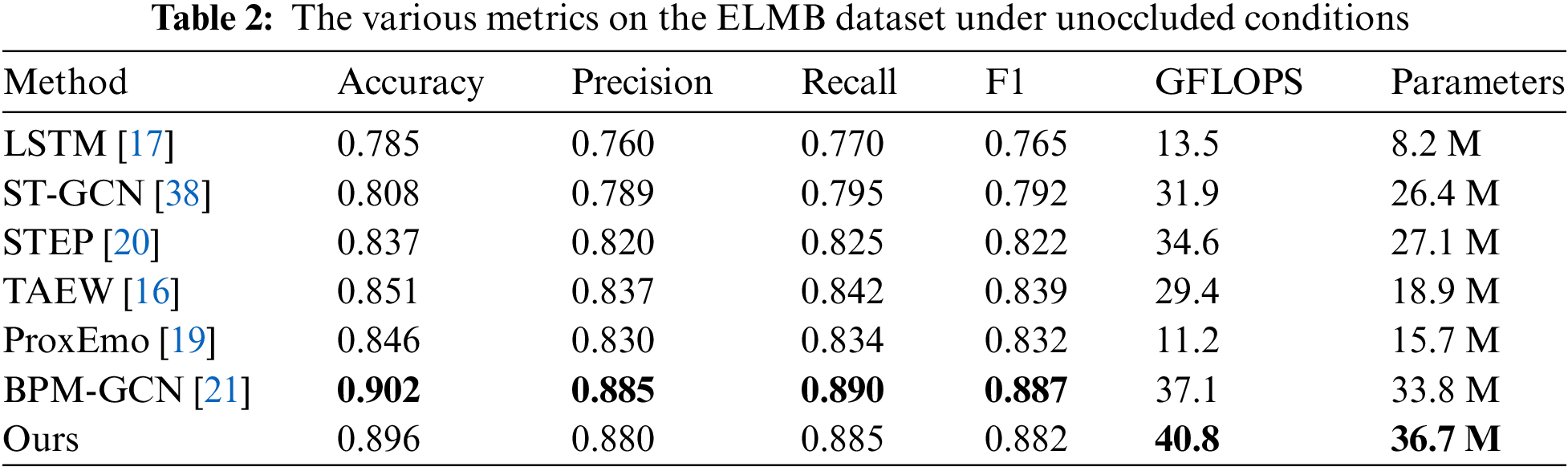
Unoccluded Dataset. As shown in Tables 1 and 2, the proposed method achieves good results on both the Emotion-Gait and ELMB datasets when the human skeleton is not occluded. In terms of metrics such as precision, recall and F1, MS-GCN performs outstandingly, significantly outperforming other methods except for BPM-GCN. The accuracy of MS-GCN reaches 0.900 and 0.896, respectively, only about 0.01 lower than BPM-GCN. Therefore, it can be considered that MS-GCN not only performs well under occlusion conditions but also remains one of the most advanced methods when the human skeleton is unobstructed. Additionally, MS-GCN has GFLOPS and Parameters values of 40.8 and 36.7 M, respectively, which are relatively high compared to other methods. This indicates that there is still considerable room for optimization in terms of computational efficiency and model complexity. Future research could focus on reducing the model’s computational complexity and parameter count while maintaining or improving performance, making the model more competitive in practical applications.
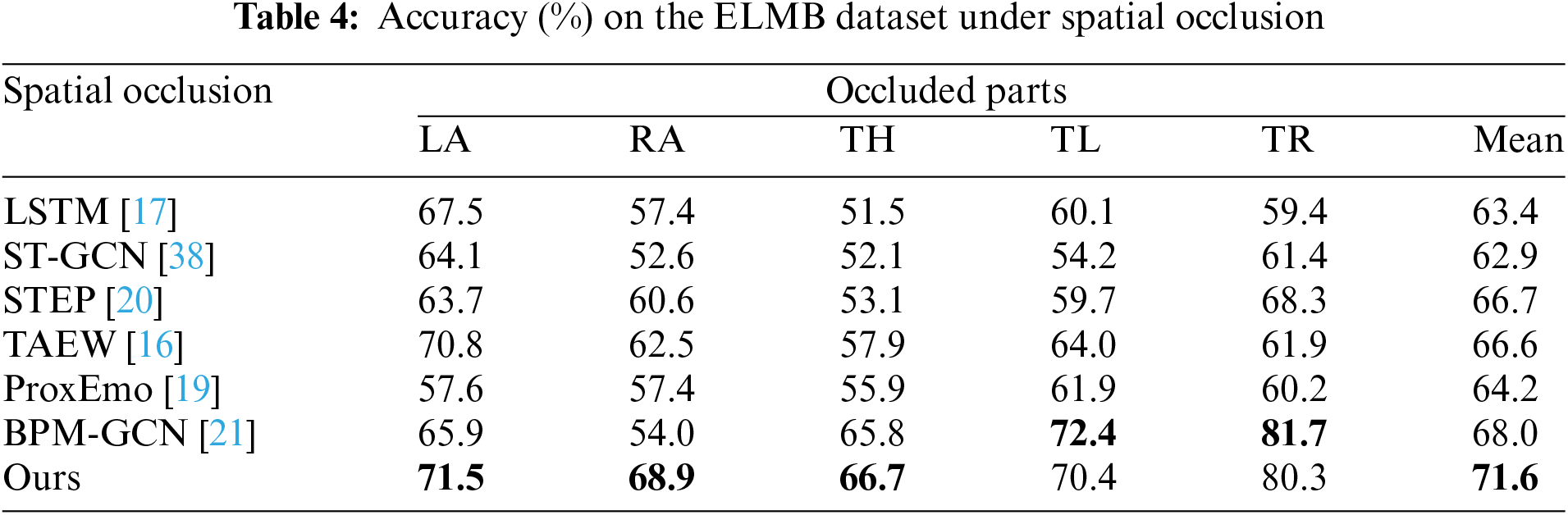
Occluded Dataset. As shown in Tables 3 and 4, this paper compares the proposed method with other state-of-the-art gait emotion recognition methods under spatial occlusion conditions on the Emotion-Gait and ELMB datasets. Specifically, we compare the accuracy of various models under different occlusion positions (LA, RA, TH, TL, TR) on the two datasets, where LA, RA, TH, TL and TR represent left arm, right arm, two hands, two legs, and trunk occlusion, respectively.
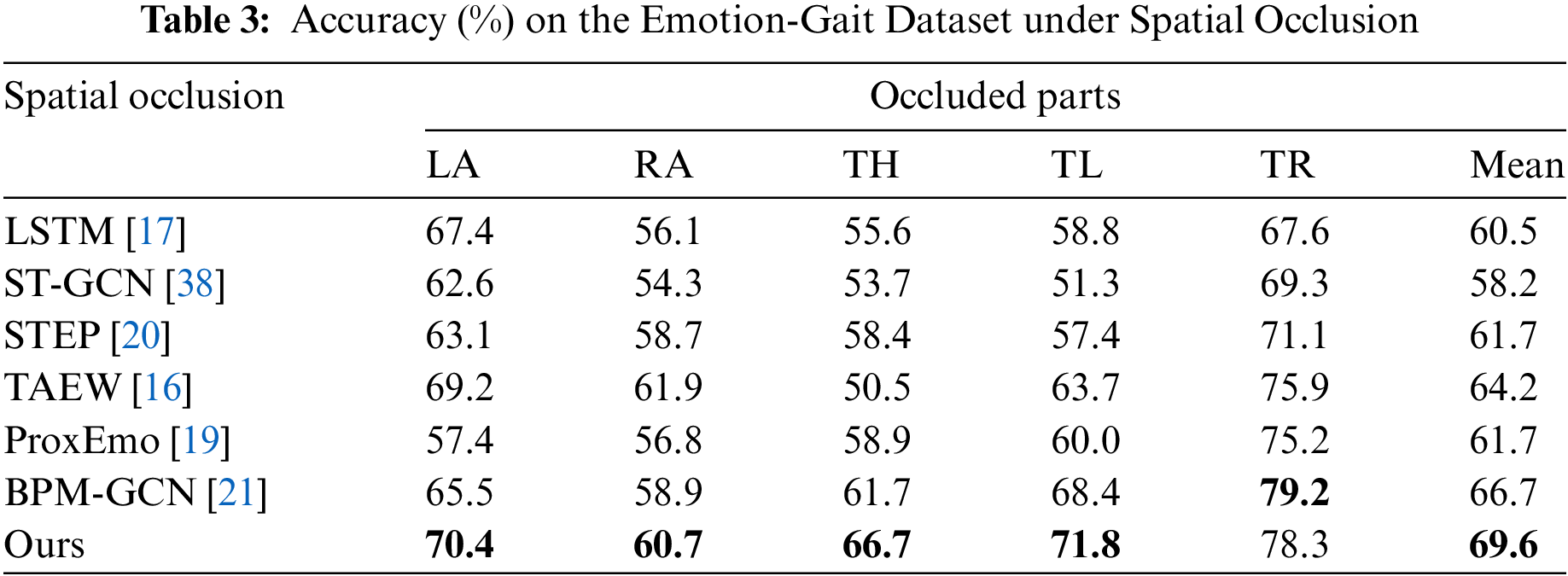
On the Emotion-Gait dataset, the proposed method demonstrates excellent performance in accuracy across all occluded regions, with an average accuracy of 0.696. In comparison, the second-best method, BPM-GCN, has an average accuracy of 0.667, which is significantly lower than our method. This indicates that the proposed method exhibits strong robustness and generalization ability in handling emotion gait recognition, regardless of the type of occlusion. Specifically, under left arm and right arm occlusion, our method achieves accuracies of 0.704 and 0.607, respectively, which may be due to the more distinct features contained in the right arm during walking. In cases of hand occlusion and leg occlusion, our method achieves accuracies of 0.667 and 0.718, respectively. Our method performs the best across these four metrics. Notably, under left arm and hand occlusion, the proposed method improves by nearly 0.05 compared to the second-best method, BPM-GCN, demonstrating that our approach can reconstruct occluded joints and fully extract remaining features, thereby enhancing recognition performance in complex occlusion scenarios. Under torso occlusion, the accuracy of our method is 0.783, slightly lower than BPM-GCN’s 0.792. We believe this may be because the torso features during walking are not particularly distinct or important, and therefore, occlusion has a relatively minor impact.
On the ELMB dataset, the proposed method achieves an average accuracy of 71.6%, once again outperforming all comparison methods, further validating its ability to handle gait occlusion across different datasets. Specifically, under LA, RA, and TH occlusion, our method achieves accuracies of 0.715, 0.689, and 0.667, respectively, which are significantly better than those of other methods. In the cases of TL and TR occlusion, our method achieves accuracies of 0.704 and 0.803, respectively, second only to the BPM-GCN method. In contrast, the ProxEmo method performs poorly on the ELMB dataset. Under TR occlusion, ProxEmo’s accuracy is only 55.9%, the lowest among all methods. This indicates that traditional time-series models exhibit significant shortcomings in feature extraction and model robustness when faced with complex occlusion conditions.
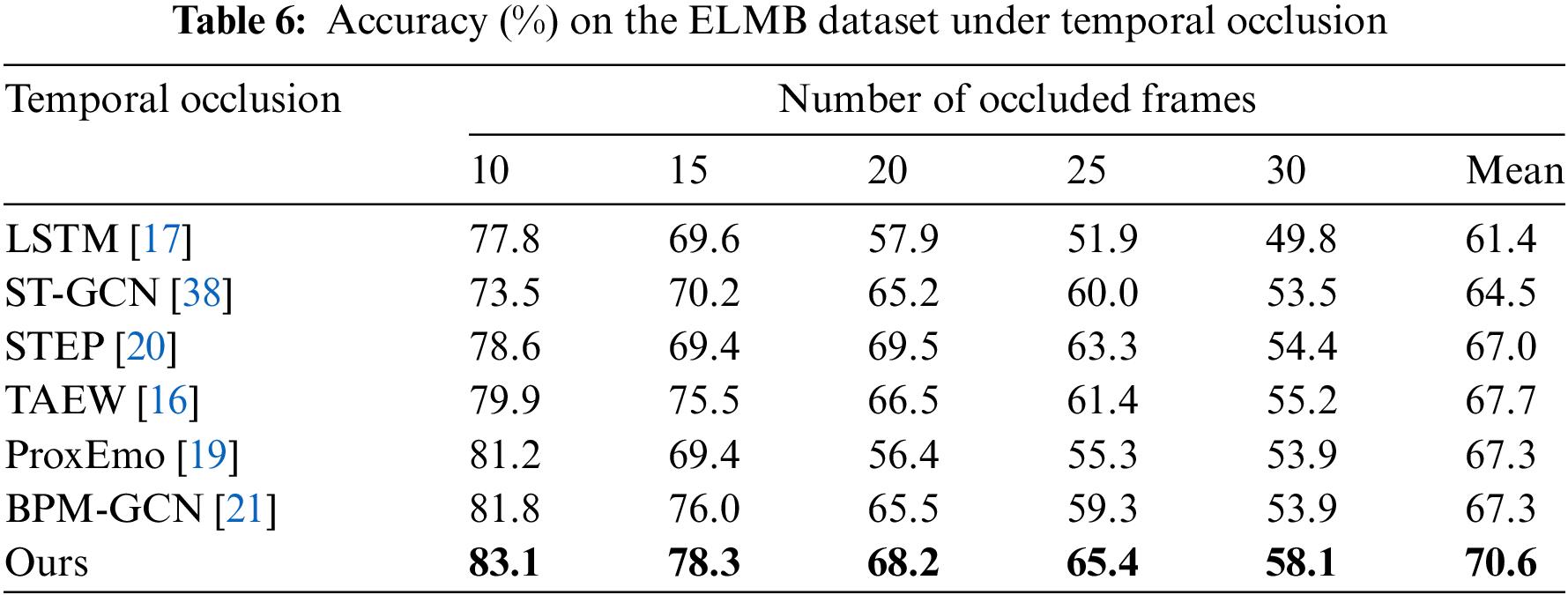
As shown in Tables 5 and 6, several methods are compared under temporal occlusion conditions. Specifically, we compare the accuracy performance of various methods on the Emotion-Gait and ELMB datasets under different numbers of occluded frames (10 frames, 15 frames, 20 frames, 25 frames, and 30 frames). It can be seen that the proposed method performs exceptionally well in handling temporal occlusion, especially achieving significantly better accuracy under multi-frame occlusion conditions compared to other methods.

On the Emotion-Gait dataset, as the number of occluded frames increases, the recognition accuracy shows a declining trend. The BPM-GCN method achieves an accuracy of 82.4% with 10-frame occlusion, but this drops to 0.556 with 30-frame occlusion. In contrast, the proposed method achieves an accuracy of 0.843 with 10-frame occlusion and still maintains an accuracy of 0.613 with 30-frame occlusion, with an average accuracy of 0.733, significantly higher than other methods. In comparison, other methods such as LSTM and ST-GCN show a rapid decline in accuracy as occlusion increases, indicating poor robustness to temporal occlusion. This demonstrates that the proposed MS-TCN can effectively capture and integrate multi-scale temporal features, providing reliable predictions even under severe occlusion conditions.
On the ELMB dataset, the proposed method also performs excellently. MS-GCN achieves an accuracy of 83.1% with 10-frame occlusion and 58.1% with 30-frame occlusion, with an average accuracy of 70.6%. Although the increase in the number of occluded frames significantly impacts all methods, MS-GCN consistently demonstrates the highest accuracy across different levels of occlusion, particularly excelling in the 25-frame and 30-frame occlusion scenarios, where it outperforms the second-best method, BPM-GCN, by more than 0.05.
Overall, the experimental results demonstrate that the proposed method has significant advantages in handling temporal occlusion. It not only performs well under mild occlusion but also maintains high accuracy even in more severe occlusion scenarios. This outcome proves that the MS-TCN shows clear superiority in addressing temporal occlusion issues. By performing convolution operations at different temporal scales, it effectively integrates both short-term and long-term dynamic information, enabling the model to maintain high predictive accuracy even in complex temporal occlusion environments.
Ablation Study of MS-GCN. As shown in Table 7, compared to the baseline ST-GCN, the proposed model shows a significant improvement in accuracy after incorporating the three modules proposed in this paper. Under spatial occlusion conditions, the accuracy reached 69.6%, which is much higher than the 58.2% of the baseline ST-GCN. Under temporal occlusion conditions, the accuracy reached 73.3%, which is 6.5% higher than that of ST-GCN. When using only the JI Module, the accuracy under spatial occlusion increased to 63.4%, and under temporal occlusion, it increased to 68.9%. This indicates that the JI Module can effectively supplement the missing key information in the gait, thereby improving the overall recognition accuracy under spatiotemporal occlusion. When using only the MS-TCN, the accuracy under spatial occlusion increased to 61.5%, and under temporal occlusion, it increased to 71.5%, proving that the proposed MS-TCN can comprehensively capture the emotional information contained in the gait in the temporal dimension, significantly improving the recognition accuracy of the model. When using only the SGCN, the accuracy under spatial occlusion increased to 65.2%, and under temporal occlusion, it reached 69.3%. This shows that the SGCN is effective in handling spatial occlusion. By finely extracting spatial information in the gait, the SGCN effectively improves the recognition ability under occlusion conditions. When using both the JI Moudle and the MS-TCN, the accuracy under spatial occlusion increased to 66.3%, and under temporal occlusion, it increased to 72.7%. This indicates that the combination of these two modules can further enhance the spatiotemporal feature extraction capability of the model, thereby improving recognition accuracy. When using both the JI Module and the SGCN, the accuracy under spatial occlusion reached 68.7%, and under temporal occlusion, it was 71.1%. This shows that the combination of the JI Module and the SGCN performs well in handling spatial information and also improves performance under temporal occlusion to some extent. When using both the MS-TCN and the SGCN, the accuracy under spatial occlusion was 67.1%, and under temporal occlusion, it increased to 72.0%. This shows that the combination of the MS-TCN and the SGCN has a good effect in enhancing the extraction of temporal and spatial features.

Ablation Study of Multi-Scale Temporal Convolution. Different sets of kernel sizes were selected for the experiments: 1, 3, 5, and 1, 3, 7, and 1, 3, 9, and 1, 3, 11. These different kernel sizes represent different temporal scales and can capture different levels of temporal features in gait emotion recognition. As shown in Fig. 5, when the kernel sizes were 1, 3, 5, the model achieved an accuracy of 69.3% under spatial occlusion and 71.0% under temporal occlusion. When the kernel sizes increased to 1, 3, 7, the accuracy under spatial occlusion increased to 69.0%, and under temporal occlusion, it increased to 72.5%. This indicates that appropriately increasing the kernel sizes can better capture the temporal features of the gait, thereby improving the model’s performance. Further increasing the kernel sizes to 1, 3, 9, the model achieved an accuracy of 69.6% under spatial occlusion and 73.3% under temporal occlusion. This result shows that the model achieved the best performance with a kernel size of 1, 3, 7. When the kernel sizes were further increased to 1, 3, 11, the accuracy of the model decreased to 68.9% under spatial occlusion and 72.8% under temporal occlusion. This result indicates that too large kernel sizes may lead to over-smoothing, losing the ability to capture subtle temporal features of the gait, thus affecting the model’s performance.
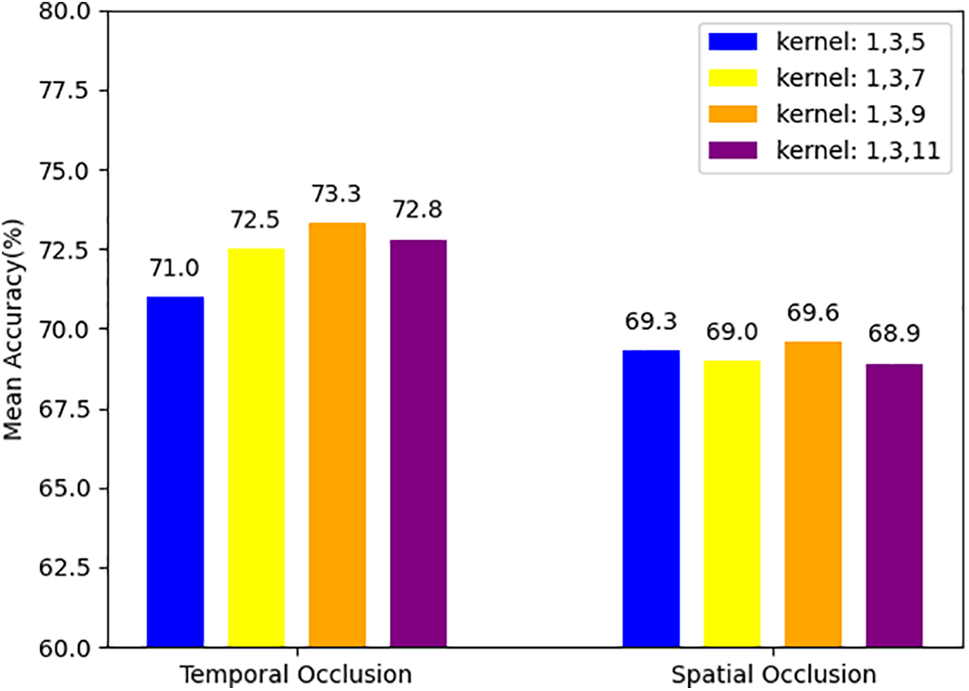
Figure 5: Ablation study of multi-scale temporal convolution
Ablation Study of Suppressive Graph Convolution Network. Additionally, the number of layers of the SGCN was varied to determine the optimal number of layers. As shown in Fig. 6, different numbers of layers were tested: 2 layers, 3 layers, 4 layers, 5 layers, 6 layers, and 7 layers. When the number of suppressive graph convolution layers was 2, the model achieved an accuracy of 63.1% under spatial occlusion and 69.0% under temporal occlusion. When the number of layers increased to 3, the accuracy under spatial occlusion increased to 68.4%, and under temporal occlusion, it increased to 72.8%. This indicates that appropriately increasing the number of layers can better capture gait features, thereby improving the model’s performance. Further increasing the number of layers to 4, the accuracy under spatial occlusion reached 67.9%, and under temporal occlusion, it was 72.5%. This result shows that the model achieved the best performance with 4 layers of the SGCN. When the number of layers was increased to 5, the accuracy under spatial occlusion slightly increased to 69.6%, and under temporal occlusion, it was 73.3%. When the number of layers increased to 6, the accuracy under spatial occlusion decreased to 67.5%, and under temporal occlusion, it decreased to 71.4%. When the number of layers was further increased to 7, the accuracy under spatial occlusion continued to decrease to 66.8%, and under temporal occlusion, it decreased to 70.5%. This result indicates that too many layers may cause the model to learn redundant features, thus affecting the model’s performance and reducing recognition accuracy.
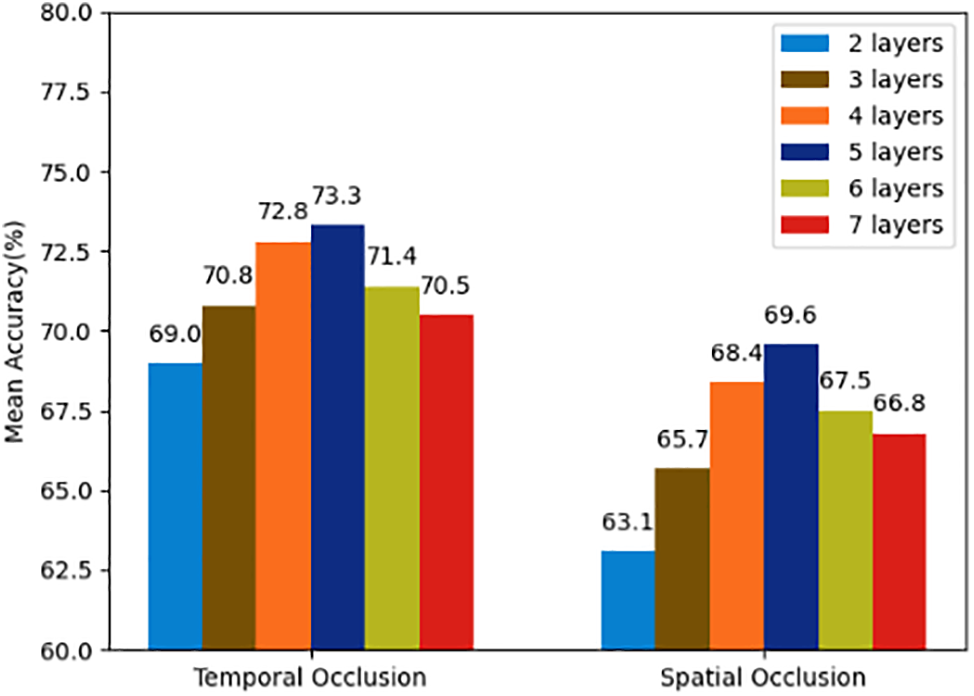
Figure 6: Ablation study of suppressive graph convolution network
As shown in Fig. 7, this paper presents the visualization results of several methods under occlusion conditions. The figure includes four emotion labels: Happy, Angry, Sad, and Neutral. The images under each label are divided into two parts: the upper part shows the human skeleton under occlusion, and the lower part shows the actual human skeleton without occlusion. Under each emotion label, the images show the results of four different methods: Step, Taew, BPM-GCN, and the proposed method. Incorrectly recognized emotions are indicated in red font, while correctly recognized emotions are indicated in black font. It can be seen that under occlusion conditions, the proposed method shows a significant advantage over other methods. For example, under the Happy emotion label, both Step and Taew incorrectly recognize the emotion as Angry under occlusion, while BPM-GCN and our method correctly recognize it as Happy. Similarly, under the Angry emotion label, Taew incorrectly recognizes the emotion as Sad, while our method correctly recognizes it as Angry. Under the Neutral emotion label, both Taew and BPM-GCN incorrectly recognize the emotion as Sad, while our method correctly recognizes it as Neutral. Therefore, the visualization results in the figure indicate that the Step and Taew methods have more recognition errors under occlusion conditions, especially under the Happy and Neutral emotion labels, where they tend to misjudge the emotions as Angry or Sad. The BPM-GCN method shows some improvement over the Step and Taew methods under occlusion conditions but still has misjudgments under certain emotion labels. In contrast, our method performs better than other methods in handling occlusion conditions, demonstrating higher robustness and accuracy, which helps improve the overall performance of gait emotion recognition.

Figure 7: Visualization comparison of different methods
To address the occlusion problem in the field of gait emotion recognition, this paper proposes a Multi-scale Suppressive Graph Convolutional Network. The network consists of a JI Module, MS-TCN, and a SGCN. The JI Module analyzes the unoccluded joints and predicts the possible positions of the occluded joints by leveraging the spatial relationships between them, thereby restoring complete skeletal information. The MS-TCN uses convolution kernels of different sizes to capture gait data at multiple temporal scales. By integrating information from different temporal scales, it compensates for the short-term dynamic features lost due to occlusion. The SGCN reduces the negative impact of occlusion on emotion recognition results by suppressing the extraction of features from key body parts, thereby fully extracting the non-significant features of the human skeleton. The main difference between the proposed method and existing methods lies in its overall approach to handling occlusion. Traditional methods tend to focus independently on either the spatial or temporal domain, whereas MS-GCN integrates these two domains through the JI Module and MS-TCN, offering a more comprehensive solution. Additionally, the JI Module’s method of enhancing recognition accuracy by completing occluded skeletal joints is being implemented in this field for the first time.
Experiments were conducted on the Emotion-Gait and ELMB datasets to validate the proposed method. The results show that the proposed method effectively mitigates the performance degradation caused by occlusion in both spatial and temporal domains, with recognition accuracy significantly better than other methods, demonstrating the effectiveness of the method. At the same time, MS-GCN has certain limitations in terms of computational complexity and model parameter count. Although it demonstrates excellent recognition performance, in practical applications, MS-GCN often leads to higher computational costs and a larger number of parameters, which can limit its applicability in resource-constrained environments. Therefore, reducing the model’s parameter count and constructing a flexible and lightweight model will be the focus of future research.
Acknowledgement: Not applicable.
Funding Statement: This work is supported by the National Natural Science Foundation of China (62272049, 62236006, 62172045), the Key Projects of Beijing Union University (ZKZD202301).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Yuxiang Zou, Ning He; data collection: Jiwu Sun, Xunrui Huang, Wenhua Wang; analysis and interpretation of results: Yuxiang Zou; draft manuscript preparation: Yuxiang Zou, Ning He. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: We use an open-source dataset to test our method. The Emotion-Gait dataset and ELMB dataset can be found in http://www.gamma.umd.edu/step and https://gamma.umd.edu/taew (accessed on 06 October 2024).
Ethics Approval: This study was conducted with human volunteers and was approved by the Human Research Ethics Committee of Beijing Union University. The study adhered to the ethical principles outlined in the Declaration of Helsinki, and the ethical approval certificate was granted with the reference number IRB2023-11. All participating human volunteers provided informed consent.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. T. Mittal, P. Guhan, U. Bhattacharya, R. Chandra, A. Bera and D. Manocha, “Emoticon: Context-aware multimodal emotion recognition using Frege’s principle,” in IEEE/CVF Conf. Comput. Vis. Pattern Recognit., Seattle, Washington, 2020, pp. 14234–14243. [Google Scholar]
2. X. Yao, D. She, S. Zhao, J. Liang, Y. Lai and J. Yang, “Attention-aware polarity sensitive embedding for affective image retrieval,” in IEEE/CVF Int. Conf. Comput. Vis., Seoul, Republic of Korea, 2019, pp. 1140–1150. [Google Scholar]
3. J. M. Montepare, S. B. Goldstein, and A. Clausen, “The identification of emotions from gait information,” J. Nonverbal Behav., vol. 11, no. 1, pp. 33–42, Mar. 1987. doi: 10.1007/BF00999605. [Google Scholar] [CrossRef]
4. S. Halovic and C. Kroos, “Not all is noticed: Kinematic cues of emotion-specific gait,” Hum. Mov. Sci., vol. 57, pp. 478–488, 2018. doi: 10.1016/j.humov.2017.11.008. [Google Scholar] [CrossRef]
5. C. L. Roether, L. Omlor, A. Christensen, and M. Giese, “Critical features for the perception of emotion from gait,” J. Vis., vol. 9, no. 6, pp. 15–31, 2009. doi: 10.1167/9.6.15. [Google Scholar] [PubMed] [CrossRef]
6. X. Li, Y. Makihara, C. Xu, Y. Yagi, and M. Ren, “Gait recognition via semi-supervised disentangled representation learning to identity and covariate features,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., 2020, pp. 13309–13319. [Google Scholar]
7. F. Noroozi, C. A. Corneanu, D. Kamińska, T. Sapiński, S. Escalera and G. Anbarjafari, “Survey on emotional body gesture recognition,” IEEE Trans. Affect. Comput., vol. 12, no. 2, pp. 505–523, 2018. doi: 10.1109/TAFFC.2018.2874986. [Google Scholar] [CrossRef]
8. S. Zhao et al., “An end-to-end visual-audio attention network for emotion recognition in user-generated videos,” in Proc. AAAI Conf. Artif. Intell., New York, NY, USA, 2020, pp. 303–311. [Google Scholar]
9. Z. Zhang, L. Tran, F. Liu, and X. Liu, “On learning disentangled representations for gait recognition,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 44, no. 1, pp. 345–360, 2020. doi: 10.1109/TPAMI.2020.2998790. [Google Scholar] [PubMed] [CrossRef]
10. H. Chao, K. Wang, Y. He, J. Zhang, and J. Feng, “GaitSet: Cross-view gait recognition through utilizing gait as a deep set,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 44, no. 7, pp. 3467–3478, 2021. doi: 10.1109/TPAMI.2021.3057879. [Google Scholar] [PubMed] [CrossRef]
11. M. Karg, K. Kühnlenz, and M. Buss, “Recognition of affect based on gait patterns,” IEEE Trans. Syst. Man Cybern. Part B (Cybern.), vol. 40, no. 4, pp. 1050–1061, 2010. doi: 10.1109/TSMCB.2010.2044040. [Google Scholar] [PubMed] [CrossRef]
12. W. Wang, V. Enescu, and H. Sahli, “Adaptive real-time emotion recognition from body movements,” ACM Trans. Interact. Intell. Syst., vol. 5, no. 4, pp. 1–21, 2015. doi: 10.1145/2738221. [Google Scholar] [CrossRef]
13. C. Hu, W. Sheng, B. Dong, and X. Li, “TNTC: Two-stream network with transformer-based complementarity for gait-based emotion recognition,” in IEEE Int. Conf. Acoust., Speech Signal Process. (ICASSP), Singapore, 2022, pp. 3229–3233. [Google Scholar]
14. H. Lu, S. Xu, S. Zhao, X. Hu, R. Ma and B. Hu, “EPIC: Emotion perception by spatio-temporal interaction context of gait,” IEEE J. Biomed. Health Inform., vol. 28, no. 5, pp. 2592–2601, 2024. doi: 10.1109/JBHI.2022.3233597. [Google Scholar] [PubMed] [CrossRef]
15. S. Xu et al., “Emotion recognition from gait analyses: Current research and future directions,” IEEE Trans. Comput. Soc. Syst., vol. 11, no. 1, pp. 363–377, 2024. doi: 10.1109/TCSS.2022.3223251. [Google Scholar] [CrossRef]
16. U. Bhattacharya et al., “Take an emotion walk: Perceiving emotions from gaits using hierarchical attention pooling and affective mapping,” in Eur. Conf. Comput. Vis. (ECCV), Glasgow, Scotland, 2020, pp. 145–163. [Google Scholar]
17. T. Randhavane, U. Bhattacharya, K. Kapsaskis, K. Gray, A. Bera and D. Manocha, “Identifying emotions from walking using affective and deep features,” 2019, arXiv:1906.11884. [Google Scholar]
18. S. Zhang, J. Zhang, W. Song, L. Yang, and X. Zhao, “Hierarchical-attention-based neural network for gait emotion recognition,” Physica A: Stat. Mech. Appl., vol. 37, 2024, Art. no. 129600. doi: 10.1016/j.physa.2023.129600. [Google Scholar] [CrossRef]
19. V. Narayanan, B. M. Manoghar, V. S. Dorbala, D. Manocha, and A. Bera, “ProxEmo: Gait-based emotion learning and multi-view proxemic fusion for socially-aware robot navigation,” in 2020 IEEE/RSJ Int. Conf. Intell. Robots Syst. (IROS), Las Vegas, NV, USA, 2020, pp. 8200–8207. [Google Scholar]
20. U. Bhattacharya, T. Mittal, R. Chandra, A. Bera, and D. Manocha, “Step: Spatial temporal graph convolutional networks for emotion perception from gaits,” Proc. AAAI Conf. Artif. Intell., vol. 34, no. 2, pp. 1342–1350, 2020. doi: 10.1609/aaai.v34i02.5490. [Google Scholar] [CrossRef]
21. Y. Zhai, G. Jia, Y. K. Lai, J. Zhang, J. Yang and D. Tao, “Looking into gait for perceiving emotions via bilateral posture and movement graph convolutional networks,” IEEE Trans. Affect. Comput., vol. 15, no. 3, pp. 1634–1648, 2024. doi: 10.1109/TAFFC.2024.3365694. [Google Scholar] [CrossRef]
22. Y. Yin, L. Jing, F. Huang, G. Yang, and Z. Wang, “MSA-GCN: Multiscale adaptive graph convolution network for gait emotion recognition,” Pattern Recognit., vol. 147, 2024, Art. no. 110117. doi: 10.1016/j.patcog.2023.110117. [Google Scholar] [CrossRef]
23. W. Shi, D. Li, Y. Wen, and W. Chen, “Occlusion-aware graph neural networks for skeleton action recognition,” IEEE Trans. Ind. Inform., vol. 19, no. 10, pp. 10288–10298, Oct. 2023. doi: 10.1109/TII.2022.3229140. [Google Scholar] [CrossRef]
24. K. Peng, A. Roitberg, K. Yang, J. Zhang, and R. Stiefelhagen, “Delving deep into one-shot skeleton-based action recognition with diverse occlusions,” IEEE Trans. Multimed., vol. 25, no. 5, pp. 1489–1504, 2023. doi: 10.1109/TMM.2023.3235300. [Google Scholar] [CrossRef]
25. C. Bian, W. Feng, L. Wan, and S. Wang, “Structural knowledge distillation for efficient skeleton-based action recognition,” IEEE Trans. Image Process., vol. 30, pp. 2963–2976, 2021. doi: 10.1109/TIP.2021.3056895. [Google Scholar] [PubMed] [CrossRef]
26. Z. Li and D. Li, “Action recognition of construction workers under occlusion,” J. Build. Eng., vol. 45, pp. 103352–103365, 2022, Art. no. 103352. doi: 10.1016/j.jobe.2021.103352. [Google Scholar] [CrossRef]
27. X. Ding, S. Zhu, W. Qu, and Y. Wang, “Generalized graph convolutional networks for action recognition with occluded skeletons,” in Proc. 2020 9th Int. Conf. Comput. Pattern Recognit., Xiamen, China, 2020, pp. 43–49. [Google Scholar]
28. I. Vernikos, E. Spyrou, I. A. Kostis, E. Mathe, and P. Mylonas, “A deep regression approach for human activity recognition under partial occlusion,” Int. J. Neural Syst., vol. 33, no. 9, pp. 47–63, 2023. doi: 10.1142/S0129065723500478. [Google Scholar] [PubMed] [CrossRef]
29. X. Yang, S. Li, S. Sun, and J. Yan, “Anti-occlusion infrared aerial target recognition with multisemantic graph skeleton model,” IEEE Trans. Geosci. Remote Sens., vol. 60, pp. 1–13, 2022. doi: 10.1109/TGRS.2022.3204062. [Google Scholar] [CrossRef]
30. J. Wang et al., “OCR-Pose: Occlusion-aware contrastive representation for unsupervised 3D human pose estimation,” in Proc. 30th ACM Int. Conf. Multimed., 2022, pp. 5477–5485. [Google Scholar]
31. Y. Xing, J. Zhu, Y. Li, J. Huang, and J. Song, “An improved spatial temporal graph convolutional network for robust skeleton-based action recognition,” Appl. Intell., vol. 53, no. 4, pp. 4592–4608, 2023. doi: 10.1007/s10489-022-03589-y. [Google Scholar] [CrossRef]
32. T. N. Kipf and M. Welling, “Semi-supervised classification with graph convolutional networks,” 2016, arXiv:1609.02907. [Google Scholar]
33. Y. F. Song, Z. Zhang, C. Shan, and L. Wang, “Richly activated graph convolutional network for robust skeleton-based action recognition,” IEEE Trans. Circ. Syst. Video Technol., vol. 31, no. 5, pp. 1915–1925, 2020. doi: 10.1109/TCSVT.2020.3015051. [Google Scholar] [CrossRef]
34. B. Zhou, A. Khosla, A. Lapedriza, A. Oliva, and A. Torralba, “Learning deep features for discriminative localization,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Las Vegas, NV, USA, 2016, pp. 2921–2929. [Google Scholar]
35. Y. Ma, H. M. Paterson, and F. E. Pollick, “A motion capture library for the study of identity, gender, and emotion perception from biological motion,” Behav. Res. Methods, vol. 38, no. 1, pp. 134–141, 2006. doi: 10.3758/BF03192758. [Google Scholar] [PubMed] [CrossRef]
36. S. Narang, A. P. Best, A. Feng, S. Kang, A. Shapiro and D. Manocha, “Motion recognition of self and others on realistic 3D avatars,” Comput. Animat. Virtual Worlds, vol. 28, no. 3, pp. 17–32, 2017. doi: 10.1002/cav.1762. [Google Scholar] [CrossRef]
37. I. Habibie, D. Holden, J. Schwarz, J. Yearsley, and T. Komura, “A recurrent variational autoencoder for human motion synthesis,” in Proc. British Mach. Vis. Conf. (BMVC), London, UK, 2017, pp. 119.1–119.12. [Google Scholar]
38. S. Yan, Y. Xiong, and D. Lin, “Spatial temporal graph convolutional networks for skeleton-based action recognition,” Proc. AAAI Conf. Artif. Intell., vol. 32, no. 1, pp. 7444–7452, 2018. doi: 10.1609/aaai.v32i1.12328. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF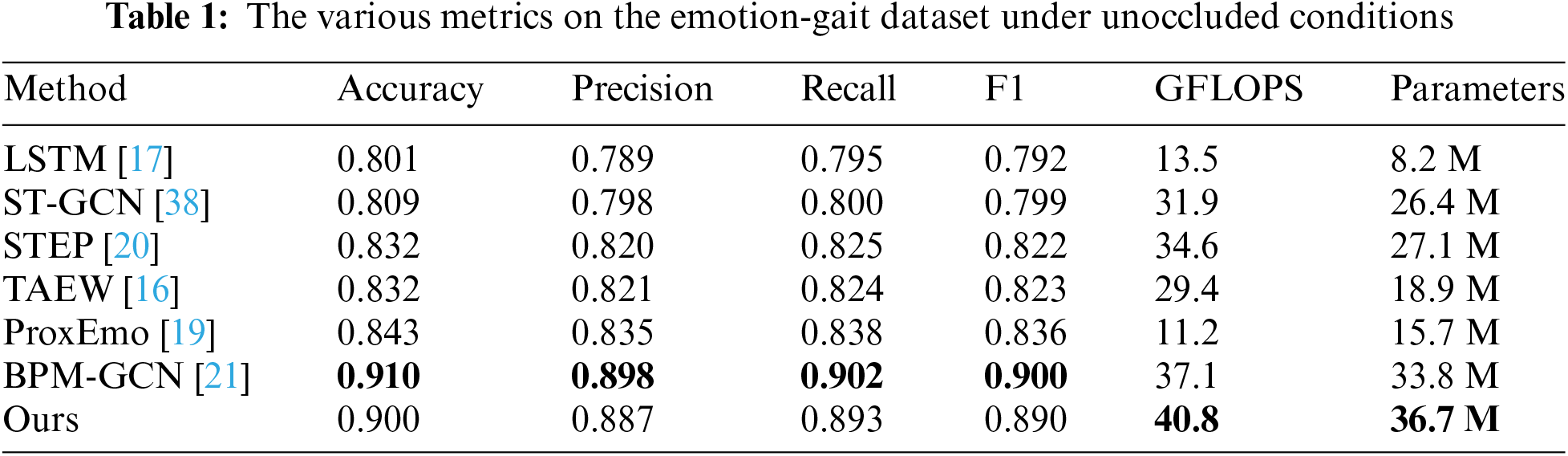
 Downloads
Downloads
 Citation Tools
Citation Tools
